Skip to main content
PMC home page
Iranian Journal of Radiology logoLink to Iranian Journal of Radiology
. 2015 Oct 17;12(4):e18286. doi: 10.5812/iranjradiol.18286

Velocity Measurement in Carotid Artery: Quantitative Comparison of Time-Resolved 3D Phase-Contrast MRI and Image-based Computational Fluid Dynamics

Ali Sarrami-Foroushani 1, Mohsen Nasr Esfahany 1,*, Abbas Nasiraei Moghaddam 2, Hamidreza Saligheh Rad 3, Kavous Firouznia 4, Madjid Shakiba 4, Hossein Ghanaati 4, Iain David Wilkinson 5, Alejandro Federico Frangi 6
PMCID: PMC4711029  PMID: 26793288

Abstract

Background:

Understanding hemodynamic environment in vessels is important for realizing the mechanisms leading to vascular pathologies.

Objectives:

Three-dimensional velocity vector field in carotid bifurcation is visualized using TR 3D phase-contrast magnetic resonance imaging (TR 3D PC MRI) and computational fluid dynamics (CFD). This study aimed to present a qualitative and quantitative comparison of the velocity vector field obtained by each technique.

Subjects and Methods:

MR imaging was performed on a 30-year old male normal subject. TR 3D PC MRI was performed on a 3 T scanner to measure velocity in carotid bifurcation. 3D anatomical model for CFD was created using images obtained from time-of-flight MR angiography. Velocity vector field in carotid bifurcation was predicted using CFD and PC MRI techniques. A statistical analysis was performed to assess the agreement between the two methods.

Results:

Although the main flow patterns were the same for the both techniques, CFD showed a greater resolution in mapping the secondary and circulating flows. Overall root mean square (RMS) errors for all the corresponding data points in PC MRI and CFD were 14.27% in peak systole and 12.91% in end diastole relative to maximum velocity measured at each cardiac phase. Bland-Altman plots showed a very good agreement between the two techniques. However, this study was not aimed to validate any of methods, instead, the consistency was assessed to accentuate the similarities and differences between Time-resolved PC MRI and CFD.

Conclusion:

Both techniques provided quantitatively consistent results of in vivo velocity vector fields in right internal carotid artery (RCA). PC MRI represented a good estimation of main flow patterns inside the vasculature, which seems to be acceptable for clinical use. However, limitations of each technique should be considered while interpreting results.

Keywords: Fluid Dynamics, Time-Resolved Three-Dimensional Phase-Contrast Magnetic Resonance Imaging (TR 3D PC MRI), Carotid Bifurcation

1. Background

In vivo assessment of physiologic and pathologic circulatory hemodynamics is of great importance in understanding the mechanisms of vascular diseases. Investigations on detailed hemodynamic behaviors of blood flowing in the vascular system could be useful in predicting the probability of adverse problems in pathologic vascular parts and may play an important role in designing more efficient treatment plans. Characterizing detailed hemodynamic properties of blood flow in the vascular system remains challenging regarding difficulties in direct measurement of important mechanical variables in vessels such as velocity, pressure and shear stress. Hence, finding some indirect methods to evaluate those variables is important. Time-resolved three dimensional phase-contrast magnetic resonance imaging (TR 3D PC MRI) also called 4D PC MRI or flow-sensitive 4D MRI as a noninvasive method encoding both spatially and temporally resolved velocity has been recently introduced and used in research work (1, 2).

The fact that MR signal is a vector quantity, with both magnitude and phase, is the basic principle of PC MRI. A bipolar gradient comprised of two gradients with the same amplitude and opposite polarities separates the stationary and moving spins associated with stationary tissue and moving blood in the vasculature. The phase shifts of the stationary spins under the effect of first gradient vanish while the second gradient with the same amplitude and opposite polarity is applied; however, for moving spins, an additional phase shift directly proportional to their velocity remains, which allows for quantification of moving spins velocity. For each spatial direction, an encoding gradient inducing a phase shift and an additional flow compensated or reference scan, which accounts for initial spins phase and system imperfections, would result in velocity component in that direction. In more recent phase contrast techniques, time-resolved PC MRI provides the opportunity to map temporal evolutions of velocity in a cardiac cycle. Due to the large amount of data collected at each temporal segment, an acquisition timing efficiently synchronized with cardiac motion allows for partially collecting data at one time point and then complete the acquisition at the same time point on other cardiac cycles. Hence, electrocardiogram (ECG) gating is needed for image acquisition.

3D velocity vector field, as an independent flow variable from which all the other hemodynamic variables like wall shear stress can be calculated, may also be predicted using image-based patient-specific computational fluid dynamic (CFD) simulations (3-10). Image-based CFD models are based on structural patient-specific angiograms acquired by magnetic resonance angiography (MRA), computed tomography angiography (CTA) or 3D rotational angiography (3DRA). They may use flow or pressure waveforms obtained from phase-contrast MRI as boundary conditions to numerically solve blood flow motion equations in the region of interest and predict hemodynamic parameters over the whole 3D computational domain.

Assessment of hemodynamics in carotid artery and its effects in vascular diseases such as carotid artery stenosis, atherosclerosis and evaluation of internal carotid artery aneurysms is of clinical interest. A number of studies in this area used PC MRI to analyze hemodynamics in intracranial arteries and aneurysms (3, 4, 6, 8, 11-15) and aorta (16, 17). Cebral et al. (3) qualitatively compared CFD and 4D PC MRI in intracranial arteries and showed a good qualitative agreement between the two techniques. Boussel et al. (4) also compared velocity and wall shear stress (WSS) fields obtained from these two techniques in intracranial aneurysms both qualitatively and quantitatively and showed that although velocity fields estimated by 4D PC MRI are acceptable for clinical use, spatial and temporal averaging associated with this technique make it incapable of providing accurate measurements of WSS. Hollnagel et al. (6) compared 4D PC MRI and CFD with the reference laser doppler velocimetry (LDV) technique in a phantom model of an intracranial aneurysm and showed a good qualitative and quantitative agreement between the results. However, among those concentrated on predicting hemodynamics in internal carotid artery (ICA) bifurcation, Harloff et al. (15) compared velocity vector fields obtained from TR 3D PC MRI and doppler ultrasound (US) and showed that TR 3D PC MRI is a promising technique for visualization of velocity vector field in ICA. Marshall et al. (7) qualitatively compared TR 3D PC MRI and CFD techniques in normal and stenosed ICA phantoms and presented a good agreement between velocity vector field and subsequent WSS estimates obtained from the two techniques. Rispoli et al. (18) proposed a combined CFD-MRI solver that integrates the nonlinear coupled system of blood equations of motion using MRI data as initial data and showed that this solver end in results which are in better agreement with PC MRI than CFD alone. Papathanasopoulou et al. (19) compared WSS fields obtained from 4D PC MRI and CFD in ICA phantom model and showed a general good agreement except for regions with disturbed flow at the divider wall. The current study compared velocity vector filed obtained by 4D PC MRI and CFD in a patient-specific carotid bifurcation model, not an idealized nor a phantom model, to show qualitative and quantitative agreement of the measured velocity values by the two techniques in the presence of flow complexities induced by patient-specific geometries.

2. Objectives

Velocity vector fields measured by TR 3D PC MRI in carotid artery were visualized and compared qualitatively with those predicted by CFD to assess their differences. Root mean square errors (RMSE) were used to quantitatively compare velocity fields obtained from CFD and MRI. Thus, the main purpose of this paper was to present a quantitative and qualitative comparison of carotid artery velocity vector fields obtained from CFD and PC MRI. Of course, in this study validation of CFD or PC MRI is not of interest; instead, the two techniques were compared to show their agreement in predicting velocity in large vessels.

3. Subjects and Methods

3.1. Magnetic Resonance Imaging

MR imaging was performed on a 30-year old male normal subject in Royal Hallamshire Hospital, Sheffield, UK. The study was approved by regional ethics committee for human research at University of Sheffield and informed consent was obtained before MR imaging. MRI examinations were performed on a clinical research 3T scanner (Philips Ingenia, Philips Medical Systems, Best, The Netherlands). The study included a high resolution time-of-flight MR angiography (TOF MRA) to produce a 3D model of the carotid artery and a TR 3D PC MRI in carotid artery to provide magnitude and phase images required in velocity calculation. 3D TOF MRA reconstructed voxel size is 0.4 mm × 0.4 mm × 0.6 mm. ECG gated TR 3D PC MRI is obtained with velocity encoding parameter (VENC) of 140 cm/sec in each of three spatial directions, TE/TR 2.5 ms/10 ms and then reconstructed with a voxel size of 0.94 mm × 0.94 mm × 2 mm into 35 frames per cardiac cycle.

3.2. PC MRI Post-Processing

The segmentation of vessel was performed for every time point at cardiac cycle using gradient vector flow (GVF) active contours method (20) applied on magnitude images. The provided mask is then used to remove vessel’s surrounding tissue and extract vessel wall from the phase difference images. Velocities for the points outside the region of interest were set to zero. These post-processing steps were all performed in MATLAB (Release 2011b, The MathWorks Inc. Natick, MA, USA).

3.3. Image-Based CFD Modeling

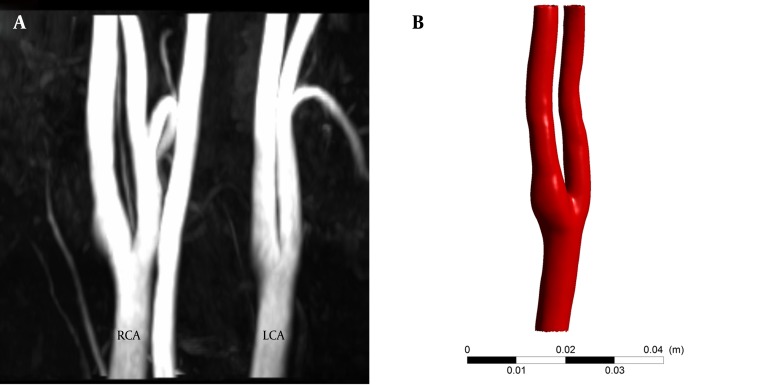
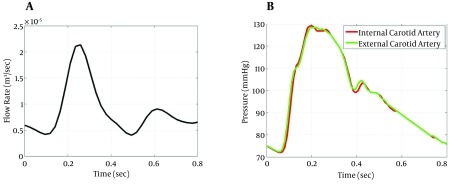
3D patient-specific geometric model of the right carotid artery was constructed after segmentation of 3D TOF MRA images in Materialise MIMICS 11.0 (Materialise Inc., Lueven, Belguim). As shown in Figure 1, the geometrical model includes right common carotid artery, where it bifurcates to internal and external carotid arteries. The geometric model is then used to generate a volumetric computational mesh of tetrahedral elements in Ansys ICEM CFD 14.5 (Ansys Inc., Canonsburg, PA, USA). Mesh and time-step dependency study, with velocity and pressure values monitored, ended to a mesh of 1260673 elements. The blood flow was modeled by unsteady 3D Navier-Stokes equations for incompressible Newtonian fluid. Blood is assumed to be a homogeneous Newtonian fluid with density of 1066 kg/m3 and viscosity of 0.0035 Pa.s. The assumption of blood to be a Newtonian fluid is demonstrated to be reasonable in large vessels with high shear rate (21). Despite compliance of the vessel walls, due to the lack of elastin in cerebral arteries (22) and observation of no remarkable wall motion in time-resolved images, vessel was assumed to be rigid with a non-slip boundary condition at walls. PC MRI flow measurements of the same patient were used to produce patient-specific flow waveform and assigned as inlet boundary condition (Figure 2 A). A straight tube of cross sectional area the same as model inlet was used as an extension proximal to the real inlet to ensure that blood flow entering the main computational domain has a fully-developed velocity profile and is independent of the entrance region effects. Pressure waveforms obtained from 1D model of systemic arterial tree (23) were used as outlet boundary conditions at internal and external carotid arteries (Figure 2 B). CFD simulations were run using ANSYS CFX 14.5 (Ansys Inc., Canonsburg, PA, USA) commercial package for three cardiac cycles with a time step of 0.005 seconds and results at the third cardiac cycle, where there is no initial transient effects, were used for comparison with 4D flow MRI.

Figure 1. MRA data and generated 3D model used for CFD. A, maximum intensity projection and B, 3D CAD model. CAD, computer aided diagnosis; CFD, computational fluid dynamics; LCA, left carotid artery; MRA, magnetic resonance angiography; RCA, right carotid artery.

Figure 1.

Open in a new tab

Figure 2. Boundary conditions for state 1; A, inlet flow waveform B, outlet pressure waveforms.

Figure 2.

Open in a new tab

3.4. Comparison and Statistical Analysis

To quantitatively compare velocity vector field determined by CFD and 4D PC MRI, 19 cross sectional cuts along the carotid axial direction were chosen in a way that covered the carotid bifurcation. Due to the fact that CFD grid is of a much higher resolution than 4D PC MRI, a rectangular grid of the same resolution as 4D PC MRI was fitted on the CFD results at each cross sectional cuts. Therefore, for every temporal point over the cardiac cycle, velocity vectors obtained from each technique could be compared at every spatial point over the 3D domain. Visual comparison was performed between CFD and 4D PC MRI velocity vector fields. Bland-Altman plots were produced to quantitatively compare CFD and 4D PC MRI velocity vector fields. To estimate error between the two techniques, the root mean square error (RMSE) was calculated for each spatial point at specific times during cardiac cycle.

4. Results

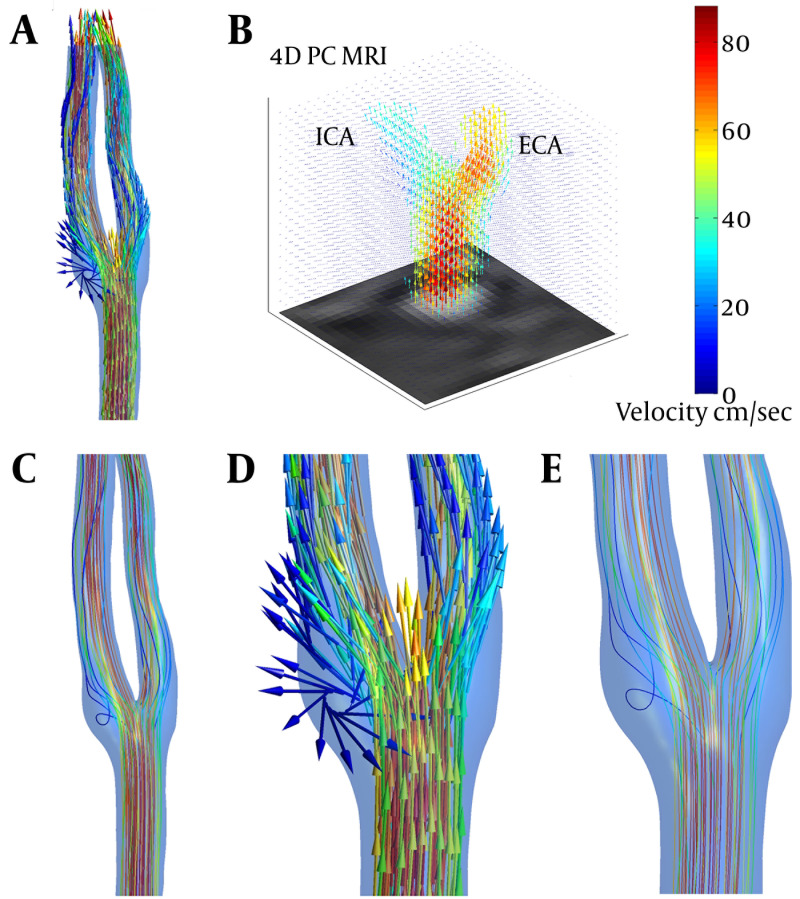
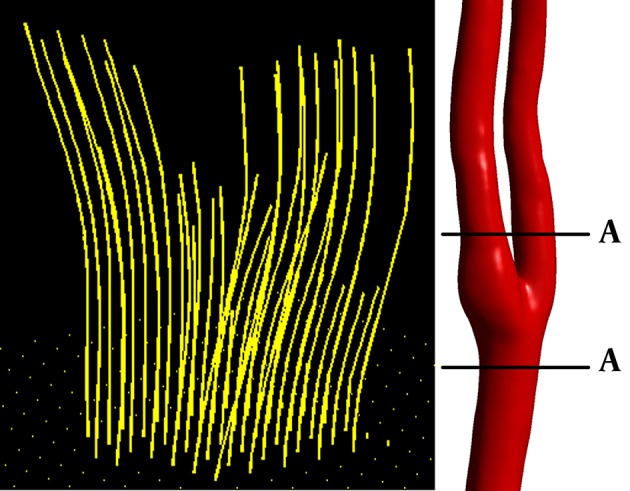
3D visualizations of blood flow in right carotid bifurcation of a healthy subject at peak systole are presented in Figure 3 to visually compare results from CFD and 4D PC MRI. The main flow patterns i.e. flow directions and secondary flows, are the same in both CFD and PC MRI maps; however, some differences can be visually recognized. CFD model generally overestimates the velocity compared to PC MRI. Secondary flows and recirculation zones near the bifurcation are of poorer quality in PC MRI compared to CFD; that is, in PC MRI map, streamlines tend to be parallel like in laminar flow. As illustrated in Figure 4, streamlines from PC MRI results stop suddenly inside the domain, which shows that velocity vector field produced by PC MRI is not divergence-free due to the noise. Therefore, although the velocity field obtained from PC MRI is acceptable for a comparison with CFD, more attention must be paid when such PC MRI velocity vector fields are to be used as an input in Navier-Stokes equations to determine pressure fields. However, as the purpose of this study was to compare velocity vector fields obtained from PC MRI and CFD, the current velocity field without any modification was used. For further usage of this velocity field to calculate pressure, the velocity field must be first mapped on a divergence-free vector field and satisfy the continuity equation.

Figure 3. 3D visualization of blood velocity vector field in the right carotid artery bifurcation at peak systole using CFD (A), and TR 3D PC MRI (B). The blood flow streamlines obtained from CFD (C), shows better resolution of CFD in mapping secondary and rotational flows. Circulation region in the carotid sinus can be clearly identified in velocity vector (D), and streamline (E), maps.

Figure 3.

Open in a new tab

Figure 4. 3D streamlines in right carotid artery (cut AA) from PC MRI results at peak systole.

Figure 4.

Open in a new tab

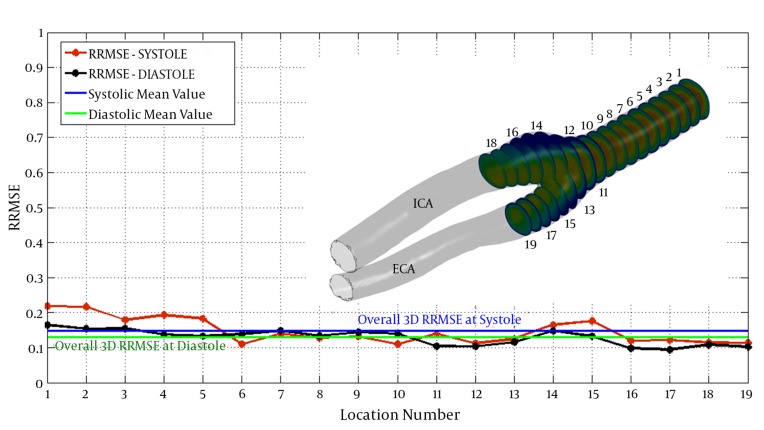
Relative RMSE was calculated at different locations at peak systole and end diastole for quantitatively comparing CFD and PC MRI. Overall RMSEs for all the corresponding data points in PC MRI and CFD are 14.27% in peak systole and 12.91% in diastole relative to maximum velocity measured at each phase. Hence, it seems that cardiac phase do not have any significant influence on relative RMSE; as overall RMSEs at the peak systole (14.27%) and end diastole (12.91%) are not remarkably far from each other. Figure 5 shows the relative RMSE in each of the 19 cross sectional areas along the axial direction in peak systole and end diastole. It is observed that greater errors exist in flow entering the domain and at the bifurcation. At the entering region, effects of inlet fully-developed velocity profile assumption are more dominant compared to other regions of the ICA geometry. Greater errors in this region could be attributed to the mentioned fully-developed velocity profile assumption at the inlet boundary.

Figure 5. Relative RMS error between CFD and 4D PC MRI results in 19 cross-sectional cuts at peak systole and end diastole. Blue line shows voxel-by-voxel RRMSE at peak systole (0.1472); and, green line shows the same at end diastole (0.1291). ECA, external carotid artery; ICA, internal carotid artery; RRMSE, relative root mean square error.

Figure 5.

Open in a new tab

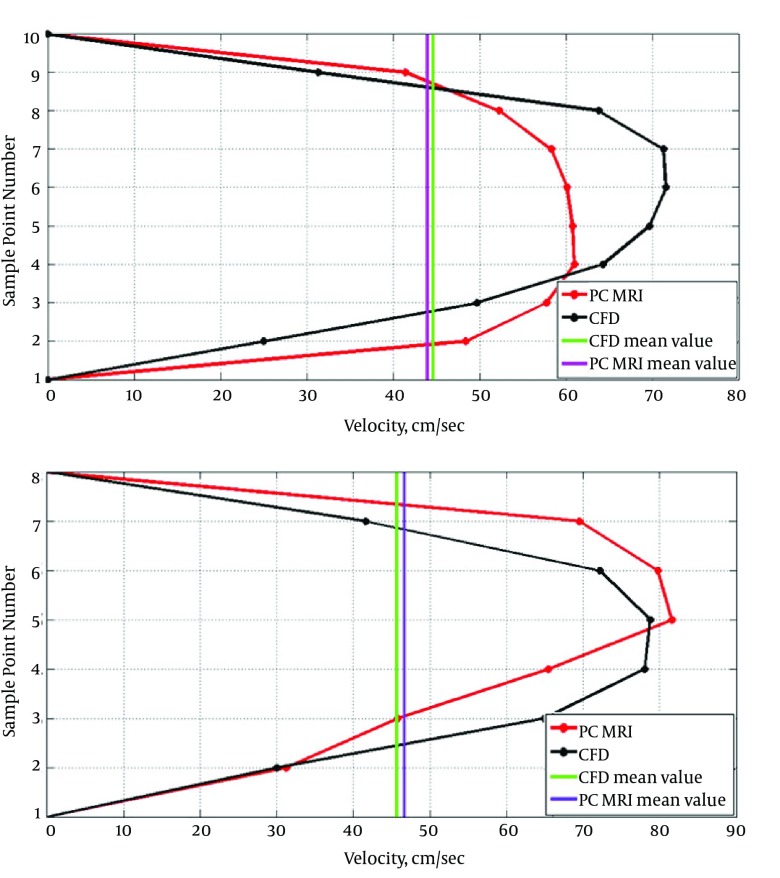
Figure 6 shows velocity profile on the main diameter of two arbitrarily chosen cross sections before bifurcation. Although CFD generally overestimates the velocity regarding visual comparison, that is not the case for cross section number 6. In both cross sections, average velocities from CFD and PC MRI showed very smaller differences compared to point-by-point differences. For cross section number 6, average velocity measured by PC MRI was 2.15% greater than what predicted by CFD, while in cross section number 12, CFD average velocity was 1.51% greater than PC MRI average velocity.

Figure 6. Velocity profiles for cross sections 12 (the first panel) and 6 (the second panel).

Figure 6.

Open in a new tab

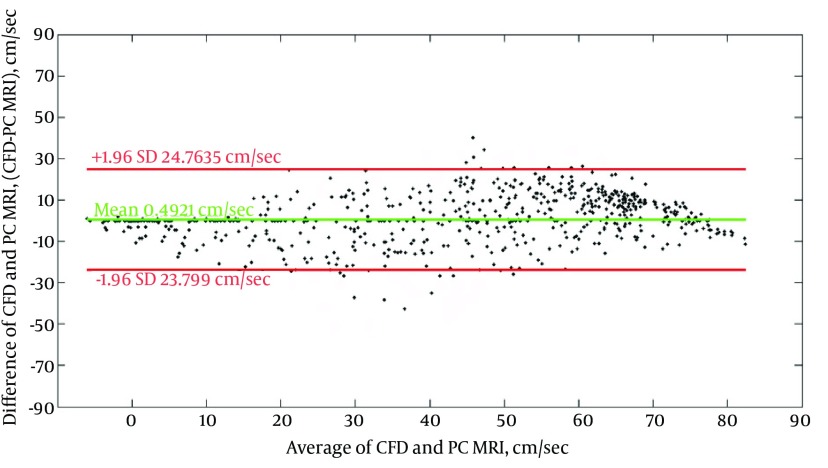
Bland-Altman plot comparing CFD and PC MRI results over the whole 3D voxel-by-voxel domain at peak systole is presented in Figure 7. Mostly all data points lie in the 95% limit band, which shows good agreement of CFD and PC MRI.

Figure 7. Bland-Altman plot of velocity values at different points within the computational domain obtained from CFD and 4D PC MRI. Red lines show 95% confidence bands and green line shows mean difference value.

Figure 7.

Open in a new tab

5. Discussion

This study used 4D PC MRI as a noninvasive feasible technique for in vivo velocity measurement in carotid artery. Visual and quantitative comparison of velocity vector field in carotid bifurcation from PC MRI and CFD showed a very good agreement between the two methods. However, due to limitations in each technique, there were some differences in results which are discussed below.

The first and principal source of error in PC MRI is spatial and temporal resolution (14, 15). This also has been spotted in other MR based tissue velocimetry or CSF transport assessment techniques (24, 25). Spatial averaging of velocity due to limitations in PC MRI spatial resolution leads to discrepancies in velocity measurements, especially in bifurcations and near vessel walls where the velocity gradients are large (14-17). Low temporal resolution of PC MRI results in averaging of velocity over time intervals, which reduces the ability of this technique to efficiently map transient patterns (17). Becauseof spatial and temporal averaging in PC MRI, this method fails to measure local and instantaneous changes in velocity vector fields and this leads to smoother profiles, which can be resulted in some sorts of underestimation. Again, due to the spatial averaging in PC MRI, less swirling flow and more parallel flow is observed in common carotid artery and the bifurcated internal and external carotid arteries immediately after the bifurcation. This reveals the poor quality of PC MRI in scanning the secondary flows and also complex flows in recirculation zones near the bifurcation (3). Secondary and complex flow patterns are of great importance for clinicians assessing the vascular pathologies and this would be a drawback for PC MRI not being able to map these behaviors with an acceptable resolution. Another limitation that may result in poor quality of scanning slow flows in PC MRI is related to the manually set parameter velocity encoding (VENC), which is usually chosen sufficiently high to avoid aliasing in high velocity regions which directly affects velocity to noise ratio in regions with low velocity magnitudes. However, despite these limitations, PC MRI is a very useful technique in measuring main flow patterns, major hemodynamic behaviors and volumetric blood flow rates and could be of great importance in assessment of vascular pathologies.

There are also a number of limitations for CFD. The main problem with CFD simulation is velocity profile. In this study, flow enters the vasculature after passing a length on 10 cm in a straight tube with a cross sectional area the same as vasculature entering region, leading to a fully-developed velocity profile different from realistic velocity profile. This leads to voxel-by-voxel errors between CFD and PC MRI, while the average velocities are very close to each other as shown in Figure 5. Rigid wall assumption may also lead to errors (3); although in this study, comparing the anatomical images in different cardiac phases, it was clear for authors that this assumption may not affect the results. Rotational angiography, computed tomography angiography, and MR angiography are currently being used for building 3D models of vascular anatomy (26); however, in this work, 3D geometrical model for CFD was constructed from high resolution time-of-flight MR angiograms that provided more accurate model than phase contrast magnitude images; however, in PC MRI, phase contrast magnitude images were used to segment the vessel from surrounding tissue, which might lead to underestimations of the vessel and this might result in errors while comparing CFD and PC MRI. However, CFD analysis is able to provide a detailed divergence-free velocity vector field with strong quality in rotational components of the velocity vectors.

However, in this study, time-resolved 3D phase-contrast MRI was compared with image-based patient specific computational fluid dynamics on a voxel-by-voxel basis in right carotid artery of a healthy subject. Both techniques provided quantitatively consistent results of in vivo velocity vector fields in RCA. PC MRI represented a good estimation of main flow patterns inside the vasculature that seems to be acceptable for clinical use. Nevertheless, above-mentioned limitations of each technique should be considered when interpreting their results.

Footnotes

Authors’ Contributions:Study concept and design: Ali Sarrami-Foroushani, Mohsen Nasr Esfahany, Abbas Nasiraei Moghaddam, Hamidreza Saligheh Rad, Madjid Shakiba, Kavous Firouznia and Hossein Ghanaati. Acquisition of data: Iain David Wilkinson. Analysis and Interpretation of data: Ali Sarrami-Foroushani, Mohsen Nasr Esfahany and Abbas Nasiraei Moghaddam. Drafting of the manuscript: Ali Sarrami-Foroushani. Critical revision of the manuscript for important intellectual content: Mohsen Nasr Esfahany, Hamidreza Saligheh Rad, Kavous Firouznia, and Madjid Shakiba. Statistical analysis: Ali Sarrami-Foroushani and Madjid Shakiba. Administrative, technical and material supports: Mohsen Nasr Esfahany, Hamidreza Saligheh Rad, Iain David Wilkinson, Alejandro Federico Frangi, Kavous Firouznia and Hossein Ghanaati. Study supervision: Mohsen Nasr Esfahany, Hamidreza Saligheh Rad, Kavous Firouznia and Hossein Ghanaati.

Funding/Support:This study did not receive any research funding.

References

  • 1.Barker A, Bock J, Lorenz R, Markl M. 4D flow MR imaging. Am J Neuroradiol. 2010;18:46–52. [Google Scholar]
  • 2.Markl M, Chan FP, Alley MT, Wedding KL, Draney MT, Elkins CJ, et al. Time-resolved three-dimensional phase-contrast MRI. J Magn Reson Imaging. 2003;17(4):499–506. doi: 10.1002/jmri.10272. [DOI] [PubMed] [Google Scholar]
  • 3.Cebral JR, Putman CM, Alley MT, Hope T, Bammer R, Calamante F. Hemodynamics in Normal Cerebral Arteries: Qualitative Comparison of 4D Phase-Contrast Magnetic Resonance and Image-Based Computational Fluid Dynamics. J Eng Math. 2009;64(4):367–78. doi: 10.1007/s10665-009-9266-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Boussel L, Rayz V, Martin A, Acevedo-Bolton G, Lawton MT, Higashida R, et al. Phase-contrast magnetic resonance imaging measurements in intracranial aneurysms in vivo of flow patterns, velocity fields, and wall shear stress: comparison with computational fluid dynamics. Magn Reson Med. 2009;61(2):409–17. doi: 10.1002/mrm.21861. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Ferrandez A, David T, Bamford J, Scott J, Guthrie A. Computational models of blood flow in the circle of Willis. Comput Methods Biomech Biomed Engin. 2000;4(1):1–26. doi: 10.1080/10255840008907996. [DOI] [PubMed] [Google Scholar]
  • 6.Hollnagel DI, Summers PE, Poulikakos D, Kollias SS. Comparative velocity investigations in cerebral arteries and aneurysms: 3D phase-contrast MR angiography, laser Doppler velocimetry and computational fluid dynamics. NMR Biomed. 2009;22(8):795–808. doi: 10.1002/nbm.1389. [DOI] [PubMed] [Google Scholar]
  • 7.Marshall I, Zhao S, Papathanasopoulou P, Hoskins P, Xu Y. MRI and CFD studies of pulsatile flow in healthy and stenosed carotid bifurcation models. J Biomech. 2004;37(5):679–87. doi: 10.1016/j.jbiomech.2003.09.032. [DOI] [PubMed] [Google Scholar]
  • 8.Isoda H, Ohkura Y, Kosugi T, Hirano M, Alley MT, Bammer R, et al. Comparison of hemodynamics of intracranial aneurysms between MR fluid dynamics using 3D cine phase-contrast MRI and MR-based computational fluid dynamics. Neuroradiology. 2010;52(10):913–20. doi: 10.1007/s00234-009-0634-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Steinman DA, Milner JS, Norley CJ, Lownie SP, Holdsworth DW. Image-based computational simulation of flow dynamics in a giant intracranial aneurysm. AJNR Am J Neuroradiol. 2003;24(4):559–66. [PMC free article] [PubMed] [Google Scholar]
  • 10.Alnaes MS, Isaksen J, Mardal KA, Romner B, Morgan MK, Ingebrigtsen T. Computation of hemodynamics in the circle of Willis. Stroke. 2007;38(9):2500–5. doi: 10.1161/STROKEAHA.107.482471. [DOI] [PubMed] [Google Scholar]
  • 11.Wetzel S, Meckel S, Frydrychowicz A, Bonati L, Radue EW, Scheffler K, et al. In vivo assessment and visualization of intracranial arterial hemodynamics with flow-sensitized 4D MR imaging at 3T. AJNR Am J Neuroradiol. 2007;28(3):433–8. [PMC free article] [PubMed] [Google Scholar]
  • 12.Bammer R, Hope TA, Aksoy M, Alley MT. Time-resolved 3D quantitative flow MRI of the major intracranial vessels: initial experience and comparative evaluation at 1.5T and 3.0T in combination with parallel imaging. Magn Reson Med. 2007;57(1):127–40. doi: 10.1002/mrm.21109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Cebral JR, Castro MA, Soto O, Löhner R, Alperin N. Blood-flow models of the circle of Willis from magnetic resonance data. J Eng Math. 2003;47(3-4):369–86. doi: 10.1023/B:ENGI.0000007977.02652.02. [DOI] [Google Scholar]
  • 14.Meckel S, Stalder AF, Santini F, Radu EW, Rufenacht DA, Markl M, et al. In vivo visualization and analysis of 3-D hemodynamics in cerebral aneurysms with flow-sensitized 4-D MR imaging at 3 T. Neuroradiology. 2008;50(6):473–84. doi: 10.1007/s00234-008-0367-9. [DOI] [PubMed] [Google Scholar]
  • 15.Harloff A, Albrecht F, Spreer J, Stalder AF, Bock J, Frydrychowicz A, et al. 3D blood flow characteristics in the carotid artery bifurcation assessed by flow-sensitive 4D MRI at 3T. Magn Reson Med. 2009;61(1):65–74. doi: 10.1002/mrm.21774. [DOI] [PubMed] [Google Scholar]
  • 16.Hope TA, Markl M, Wigstrom L, Alley MT, Miller DC, Herfkens RJ. Comparison of flow patterns in ascending aortic aneurysms and volunteers using four-dimensional magnetic resonance velocity mapping. J Magn Reson Imaging. 2007;26(6):1471–9. doi: 10.1002/jmri.21082. [DOI] [PubMed] [Google Scholar]
  • 17.Markl M, Draney MT, Hope MD, Levin JM, Chan FP, Alley MT, et al. Time-resolved 3-dimensional velocity mapping in the thoracic aorta: visualization of 3-directional blood flow patterns in healthy volunteers and patients. J Comput Assist Tomogr. 2004;28(4):459–68. doi: 10.1097/00004728-200407000-00005. [DOI] [PubMed] [Google Scholar]
  • 18.Rispoli VC, Carvalho LA, Nielsen JF, Nayak KS. Assessment of carotid flow using magnetic resonance imaging and computational fluid dynamics. In: Juarez LH, editor. Fluid dynamics, computational modeling and applications. InTech; 2012. pp. 513–36. [Google Scholar]
  • 19.Papathanasopoulou P, Zhao S, Kohler U, Robertson MB, Long Q, Hoskins P, et al. MRI measurement of time-resolved wall shear stress vectors in a carotid bifurcation model, and comparison with CFD predictions. J Magn Reson Imaging. 2003;17(2):153–62. doi: 10.1002/jmri.10243. [DOI] [PubMed] [Google Scholar]
  • 20.Xu C, Prince JL. Active contours, deformable models, and gradient vector flow. 2006. Available from: http://www.iacl.ece.jhu.edu/static/gvf/.
  • 21.Nichols W, O'Rourke M, Vlachopoulos C. McDonald's blood flow in arteries: theoretical, experimental and clinical principles. United States of America: CRC Press; 2011. [Google Scholar]
  • 22.Humphrey JD, Na S. Elastodynamics and arterial wall stress. Ann Biomed Eng. 2002;30(4):509–23. doi: 10.1114/1.1467676. [DOI] [PubMed] [Google Scholar]
  • 23.Reymond P, Merenda F, Perren F, Rufenacht D, Stergiopulos N. Validation of a one-dimensional model of the systemic arterial tree. Am J Physiol Heart Circ Physiol. 2009;297(1):H208–22. doi: 10.1152/ajpheart.00037.2009. [DOI] [PubMed] [Google Scholar]
  • 24.Zheng XZ, Yang B, Wu J. A comparison of the performance of myocardial videodensitometry, tissue velocity imaging and tissue tracking in discrimination between ST-segment elevation ischemic reperfusion injury and normal reperfusion state after non-beating cardiac operation. Iran J Radiol. 2014;11(4):e18286. doi: 10.5812/iranjradiol.11393. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Huang CW, Tsai YF, Hsiao CY. Different MRI Signs in Predicting the Treatment Efficacy of Epidural Blood Patch in Spontaneous Intracranial Hypotension: A Case Report. Iran J Radiol. 2013;10(3):172–174. doi: 10.5812/iranjradiol.3929. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Kayhan A, Koc O, Keskin S, Keskin F. The role of bone subtraction computed tomographic angiography in determining of intracranial aneurysms in non-traumatic subarachnoid hemorrhage. Iran J Radiol. 2014;11(2):e18286. doi: 10.5812/iranjradiol.12670. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Iranian Journal of Radiology are provided here courtesy of Brieflands

RESOURCES