In Silico Constraint-Based Strain Optimization Methods: the Quest for Optimal Cell Factories

SUMMARY

Shifting from chemical to biotechnological processes is one of the cornerstones of 21st century industry. The production of a great range of chemicals via biotechnological means is a key challenge on the way toward a bio-based economy. However, this shift is occurring at a pace slower than initially expected. The development of efficient cell factories that allow for competitive production yields is of paramount importance for this leap to happen. Constraint-based models of metabolism, together with in silico strain design algorithms, promise to reveal insights into the best genetic design strategies, a step further toward achieving that goal. In this work, a thorough analysis of the main in silico constraint-based strain design strategies and algorithms is presented, their application in real-world case studies is analyzed, and a path for the future is discussed.

INTRODUCTION

Since the early 1970s, modern biotechnology has started to emerge as a competitor of the chemical industry toward the production of chemicals, although it remains at a great disadvantage. However, the scenario is rapidly changing, given the increasing need for sustainable manufacturing processes. This context has given industrial biotechnology a new breath, boosting its use in the production of a number of valuable products, such as pharmaceuticals, fuels, and food ingredients. The Organization for Economic Cooperation and Development (OECD) predicts that by 2030, 35% of chemicals and other industrial products will be largely supported by industrial biotechnology (1).

In parallel, the development of industrial biotechnology is deeply intertwined with the recent evolution of molecular biology and genomics technologies. Two important technological advances must be emphasized, given their relevance to the field. In the early 1970s, the development of recombinant DNA technology (2–4) fostered efforts in genetic engineering and, eventually, gave rise to modern biotechnology. A few years later, in the mid-1970s, the development of the Sanger sequencing technique (5, 6) provided another boost, starting a real revolution in genome sequencing technologies. Indeed, the first automated sequencer was developed in the late 1980s, and in 1995, the first complete genome of a microbe, that of Haemophilus influenzae, was finished and published (7), followed by many others.

The importance of these technologies for industry is due to an obvious observation: since microbes have evolved according to their own intrinsic objectives, their metabolism needs to be manipulated to comply with industrial purposes. Indeed, a sustainable, environmentally friendly, and economically viable bio-based industry requires the use of cell factories tailored to deliver near-optimal yields of substrate-to-product conversion, as well as high titers and productivities.

The concept of metabolic pathway manipulation toward desirable behavior is an old one, with notable examples coming from the production of amino acids, vitamins, or antibiotics (8). These early methods relied mostly on the use of mating, hybridization, mutagenesis, and creative strain selection techniques (9, 10). As these traditional approaches for microbial improvement started to struggle to keep up with industrial requirements, it became necessary to resort to more rational approaches. Genetic engineering provides the way to more precisely modify specific genes/enzymes to create desirable strains (11).

In 1991, Bailey coined the term “metabolic engineering” (ME) to denote the use of recombinant DNA technology for the purpose of improving cellular activities via manipulation of enzymatic, transport, and regulatory functions of the cell (12). In contrast with previous experiences in genetic engineering, he envisioned a much more direct, target-oriented, and mechanistic approach. In parallel, Stephanopoulos and Vallino were applying branch point analysis techniques to promote the overproduction of specific metabolites (13), which would be evolved and applied in further endeavors (14, 15). Moreover, the introduction of already available mathematical frameworks, such as metabolic control analysis, into the ME arena only reinforced Bailey's views (16, 17). ME was also more attractive to the industry and led to less reluctance to deal with complementary approaches, like the ones provided by fields such as systems biology, since it was thought from the beginning to embrace knowledge from multiple disciplines.

The remarkable advances in genome sequencing technologies have played a decisive role in the change of perception regarding the genotype-phenotype relationship, which had been based mostly on qualitative analysis. With the recent developments in genome sequencing technologies, culminating in the surge of the so-called next-generation sequencing technologies (18) as well as semiautomated annotation techniques, an increasingly large number of fully annotated microbial genomes are being made available.

These full genome sequences provide comprehensive information about the genetic elements that compose an organism, which, when combined with the understanding of cellular processes such as metabolism, results in structured knowledge that can be mathematically represented. This knowledge explosion promoted the reconstruction of genome-scale metabolic networks for a large number of organisms (19). Although not directly usable for performing simulations, metabolic reconstructions can be combined with constraint-based modeling (CBM) methods for predicting the behavior of microbial strains and thus can support rational ME efforts.

CBM has been applied to the analysis of biochemical reaction networks for over 25 years (20). One of the major outcomes of this research has been the development of phenotype prediction methods supporting distinct genetic and environmental conditions, including the well-known flux balance analysis (FBA) (21–23). Based on these efforts, the time for the development of strain design methods had come, where bioengineering objectives could be rationally addressed. In 2003, Burgard and coworkers developed OptKnock (24), which would become the basis for a large portion of the constraint-based strain design methods for the following decade. Such in silico ME approaches are able to propose genetic changes (gene deletions in the case of OptKnock) based on computational simulation and mathematical optimization methods.

However, while this last decade has witnessed a rapid proliferation of strain optimization methods, mostly based on CBM approaches, in vivo proofs of concept are lagging far behind, as well as rigorous analyses of the predictive power of both simulation and design methods. Moreover, the concomitant proliferation of genome-scale metabolic models (GSMMs), often of organisms poorly characterized in physiological terms, adds a new layer of uncertainty to in silico predictions that also needs to be considered when designing novel and improved strains. In fact, most pathogens have few physiological data available, due to difficulties in performing controlled cultivations or even understanding nutritional requirements (25–28), but organisms commonly used in industry, such as the yeast Kluyveromyces lactis, also have very few data available that could be used for model construction and validation (29).

While recent reviews have discussed computational strain optimization methods (CSOMs), they either are not focused exclusively on this topic (30) or do not provide details about each method (31). Moreover, a rigorous assessment of the degree of in vivo validation of these methods has also been missing in previous surveys. Here, we aim to provide an in-depth and critical review of the currently available CBM-based strain optimization methods, including their strengths and limitations, as well as to discuss future trends in the field. The importance of these methods for ME and their relevance to boost modern industrial biotechnology efforts will be discussed, as well as the need for large-scale in vivo validation of rational-design-related methods.

We start by putting forward the main concepts and methods within CBM, which will serve as the context and support for strain optimization methods. We then cover in detail the main tasks in strain design and propose a novel taxonomy of the main strain optimization methods. These are presented in detail, their features and limitations are explored, and the connections among different methods are highlighted. That section closes with a global discussion on the merits and limitations of the distinct methods.

We then follow with an overview of selected practical applications of strain design in general and the contributions of the reviewed optimization methods in particular, focusing on experimentally and industrially validated applications. Successes and limitations of the approaches are discussed. We close with a discussion around the future challenges of ME and strain design and their relevance for a sustained bio-based economy over the coming years.

CONSTRAINT-BASED MODELING: CONCEPTS AND METHODS

Constraint-Based Models

Cellular functions are dependent on a series of intertwined mechanisms, such as metabolism or transcriptional regulation, which can be affected by a multitude of factors. Understanding the relationships between these mechanisms and the environment is key in developing correct and predictive models. Based on biochemical knowledge, classical kinetic models provide detailed dynamic and quantitative descriptions of the systems. However, they depend on many, usually difficult-to-measure, parameters and are also computationally expensive to solve in a genome-scale context (32–34). Indeed, to date, there are no dynamic genome-scale models of metabolism that can be used effectively in ME efforts, mainly because of the difficulty in obtaining the relevant kinetic data (35, 36). For several metabolic network analysis or metabolic engineering tasks, a simpler approach might be sufficient to obtain useful results. For these purposes, certain realistic assumptions can be adopted, avoiding the burden of determining kinetic rate equations and their parameters (33).

Since metabolic transients are usually faster than both microbial growth rates and dynamic environmental changes, internal metabolite concentrations can often be assumed to be in a quasi-steady state. This assumption is at the core of constraint-based metabolic modeling approaches, and its derived consequence is that all the metabolic fluxes leading to formation or degradation of any intracellular metabolite are mass balanced (37). This assumption can be represented in the form

$$S\cdot v=0$$ (1)

where S is an m × n matrix of stoichiometric coefficients, for a set of m metabolites and a set of n reactions, and v is the vector of n reaction rates (fluxes) (Fig. 1B). For each reaction, maximum and minimum flux values can also be imposed to define the thermodynamic feasibility (directionality) and flux capacity of the reactions, as follows:

$$\begin{array}{c}0\le v_i\le {\beta }_i,\forall \hspace{0.17em}i\hspace{0.17em}\in \hspace{0.17em}{N}_{irrev}\\ {\alpha }_i\le v_i\le {\beta }_i,\forall \hspace{0.17em}i\hspace{0.17em}\in \hspace{0.17em}{N}_{rev}\end{array}$$ (2)

where v_i is the flux carried over reaction i, N_rev and N_irrev are subsets of N composed of all reversible and irreversible reactions, respectively, and α_i and β_i are the lower and upper bounds for the flux over reaction i. For most GSMMs, the number of reactions surpasses the number of compounds; therefore, there are more variables than equations in the system defined by equation 1, which originates an infinite number of possible solutions leading to an underdetermined system.

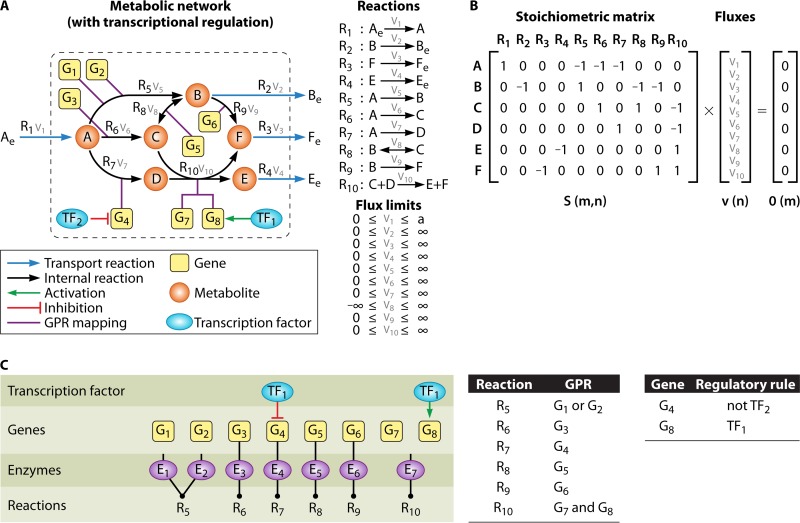
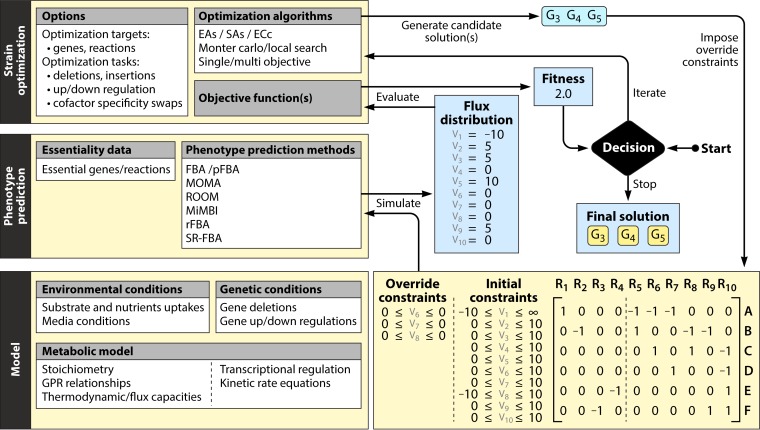
FIG 1.

Diagram of the various components commonly found in constraint-based metabolic (and integrated metabolic/regulatory) genome-scale models. The example includes a sample network composed of 10 reactions, 6 metabolites, 8 genes, and 2 transcription factors (A), the corresponding stoichiometric matrix (B), and the corresponding gene-protein-reaction and transcriptional regulation rules (C).

Further details, such as gene-protein-reaction (GPR) associations, are also typically included in the models (38). This additional knowledge enables the development of more realistic phenotype prediction and strain design methods. The representation of GPR associations usually resorts to Boolean logic, where the relationships between reactions and their encoding genes are modeled as logical “and/or” operations representing, among others, cases of protein complexes and isoenzymes, thus allowing, for instance, determination of the reactions inactivated after a set of gene deletions (Fig. 1C). While this is a useful approach, it is merely a functional representation of the connection between genes and reactions and does not provide a meaningful quantification of the relationship between transcripts and metabolic fluxes. Indeed, this typically depends on more complex interactions not depicted by the GPRs, regarding both the still poorly understood relationship between amounts of mRNA and proteins (39) and the highly nonlinear relationships between enzyme amounts and flux values (40).

Parallel efforts focused on the use of Boolean approaches to represent models of transcriptional regulation. By considering that each node in the network is in a binary state (active/inactive), Boolean networks try to approximate the dynamics of regulatory systems. For each node (representing a gene), a Boolean update rule is defined, which depends on the values of other nodes. Notable applications of Boolean networks include the elucidation of regulatory interactions (41, 42) and the simulation of system behavior under various genetic/environmental conditions (43). Despite the known fact that the expression of metabolic genes is affected by a plethora of different stimuli through regulatory mechanisms, few studies have focused on the integration of these approaches into GSMMs. The main efforts have been the inclusion of transcriptional regulation Boolean constraints, first by Covert and collaborators over an Escherichia coli GSMM (44) and more recently and in a more general way within the TIGER framework (45), as well as the inclusion of the transcriptional and translational machinery into the GSMMs of E. coli by Thiele et al. (46).

Reconstruction of GSMMs has skyrocketed in the last decade, with dozens of these models currently available for organisms from all the domains of life, including recent efforts to model complex eukaryotes, as is the case with human models. Recent reviews provide an historical perspective and analysis on the evolution of GSMMs and are readily available (47, 48). Moreover, several websites provide download access to GSMMs in standard formats (47; http://systemsbiology.ucsd.edu/InSilicoOrganisms/OtherOrganisms, http://darwin.di.uminho.pt/models). When used to support phenotype prediction and strain design methods (see below), GSMMs are a powerful tool to aid in various metabolic engineering tasks (49).

Constraint-Based Phenotype Prediction

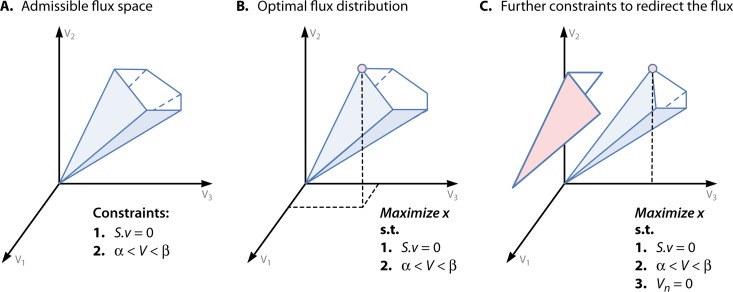
Phenotypic behavior can be predicted using a number of constraint-based approaches over the information kept in metabolic models. The intersection of the available biological constraints (e.g., steady state, reversibility, and flux capacity) defines the flux hypercone of admissible flux distributions (50) (Fig. 2A), representing the typical underdetermined nature of the system. Given that experimental measurements of internal fluxes are difficult to obtain, the usual approach to solve this underdetermined system is to transform it into an optimization problem (Fig. 2B). For this purpose, biological assumptions are usually adopted in the form of an objective function. One common approach is to rely on the rationale that organisms have been evolutionarily shaped toward metabolic operations that favor particular objectives. Extra constraints are commonly employed by many methods, which further reduce the flux cone, eventually changing the optimal solution (Fig. 2C).

FIG 2.

The flux cone. In the example, the admissible flux space is defined by the steady-state and reversibility constraints (A), an objective function defining an optimization problem is imposed (subjected to the previous constraints) (B), and further constraints are imposed to redirect the flux to a desired region of the flux cone (C).

In flux balance analysis (FBA) (21–23), these assumptions are modeled using linear objective functions, usually maximizing a given reaction rate (flux) and minimizing the global energy expenditures of the cell, or a panoply of other ones (51). With a linear objective function subjected to linear constraints, the problem is conveniently translated into a readily solvable linear programming (LP) problem. The most commonly used assumption is that microorganisms are evolutionarily adapted to maximize growth (52–54), which is modeled as a linear objective function (an artificially defined flux) that maximizes biomass formation.

Despite its utility, classical FBA is still fairly limited due to its obliviousness of several biological phenomena. As an example, the effects of regulatory constraints under certain medium/environmental conditions are not accounted for. For this purpose, specialized methods such as regulatory FBA (rFBA) (55) or steady-state regulatory FBA (SR-FBA) (56) have been developed. Both methods rely on additional information, such as transcriptional regulation constraints (44), being integrated in the models.

Regulatory FBA forecasts dynamic flux profiles in changing environments by predicting regulatory and metabolic steady states for short successive time intervals, while ensuring consistency with the previous state in each step. Alternatively, SR-FBA simulates an ensemble metabolic-regulatory steady state, under the assumption of a maximal biomass production rate satisfying both metabolic and regulatory constraints. A mixed-integer linear programming (MILP) problem is yielded by the superimposition of the regulatory constraints and GPRs as linear functions in the model. Although both these methods have provided interesting results in certain contexts, the Boolean nature of the representation used, together with the consideration of a limited domain of the full set of the regulatory interactions (only a limited set of transcriptional regulation is usually used), added to the lack of models containing this information, has severely limited the use of such methods.

While the assumption of maximal growth is acceptable under natural (wild-type) conditions, it is heavily disputed when the organism is subjected to genetic perturbations, for instance, when simulating the phenotypes of gene deletion mutant strains. To account for the burden of shifting from one operating region to another, Segrè and coworkers introduced the minimization of metabolic adjustment (MOMA) method (52). In contrast to FBA, MOMA is not growth coupled, meaning that the optimal flux distribution for a given set of conditions is not assumed to be dependent on the maximization of the organism's biomass production rate. Instead, it minimizes the sum of the squared differences between the wild type (typically calculated with FBA or given as a reference flux distribution) and the mutant flux distributions, thus defining a quadratic objective function, which translates into a quadratic programming (QP) problem.

With a similar purpose, Shlomi and coworkers developed the regulatory on/off minimization (ROOM) (57) algorithm, which minimizes the number of significantly changed fluxes, relative to the original flux distribution, after genetic perturbations. This approach requires the introduction of binary variables in the objective function, thus converting the LP problem into a MILP one, increasing its complexity. Both MOMA and ROOM formulations rely on the assumption that after genetic perturbations, the organism's metabolic and regulatory responses favor a new steady state close to the original operating region, rather than maximizing cellular growth.

More recently, Brochado and coworkers developed the minimization of metabolites balance (MiMBl) (58) as an alternative to MOMA, aiming at addressing some of its limitations. Instead of tackling the problem by finding linear combinations of fluxes, MiMBl resorts to metabolite turnovers, thus eliminating problems related to the sensitivity of the solutions to the stoichiometric representations, which can greatly affect phenotype predictions.

A panoply of methods have been proposed to improve phenotype predictions by taking into account complementary data, namely, different types of omics data with emphasis on gene expression data. Prominent examples are iMAT (59), GIMME (60), and RELATCH (61), which provide alternative objective functions and optimization approaches, combining the principles of constraint-based modeling with the consistency of fluxes with known data. In a recent study (62), these methods have been systematically evaluated, and the results obtained have been far from the ones expected, thus shedding some doubts on their applicability.

The previous methods, and more notably FBA, have an important limitation, since while they provide a solution with a unique optimal value for the objective function, a large number of flux distributions that lead to this value may exist; i.e., multiple optima may exist. One proposed way to address this issue was by the parsimonious enzyme usage FBA (63) algorithm, which chooses a particular flux distribution (or a smaller set of flux distributions) from these multiple optima by performing a second LP optimization that minimizes the sum of the flux values, while keeping the biomass flux (or another objective function) at an optimum level.

Flux variability analysis (FVA) (64) provides a distinct approach that aims to characterize the space of possible variation of specific fluxes, given a set of constraints. It can be used to define tight bounds for the fluxes in a GSMM if no further constraints are defined or to check the possible variation of a given flux in optimal or suboptimal solutions if a constraint over the objective function is defined. For instance, FVA is quite useful in checking if a flux can vary in optimal FBA solutions by setting a constraint that requires the biomass flux to be equal to its optimal value. Among other applications, FVA is used to assess the robustness of a flux distribution, for instance, in a mutant strain simulation, regarding its capability for production of a certain compound. FVA is typically applied to a given reaction flux by solving a pair of LP problems that maximize and minimize the target flux, obeying the set of defined constraints.

Unbiased Characterization of the Flux Cone by Pathway Analysis

Any attempt to enumerate all the possible flux steady-state distributions lies within the realm of the intangible for typical GSMMs with large numbers of reactions and metabolites, since their complexity scales exponentially with the size of the models (65, 66). This fact is the main driving force behind the development of the methods described in the previous section.

Still, within the field of pathway analysis, a number of methods have been put forward toward this purpose, even if currently these are mostly applicable to small- or medium-scale models. The two best known approaches for the enumeration of the possible flux distributions are elementary flux modes (EFMs) (67) and extreme pathways (ExPas) (66). Both these methods describe minimal (nondecomposable) subnetworks of the system that operate at steady state, defining the edges of a convex polyhedral hypercone (the flux hypercone [Fig. 2B]). In turn, linear combinations of the vectors representing these minimal subnetworks yield the totality of the solution space (all feasible flux distributions).

EFMs obey the following set of conditions (67).

1. Steady state: all elementary modes obey equation 1.

2. Feasibility: all irreversible reactions proceed in the forward direction; i.e., EFMs are thermodynamically feasible, obeying equation 2.

3. Nondecomposability: EFMs represent the minimal functional units in the network; therefore, no reaction can be removed from an EFM without violating either equation 1, equation 2, or both.

Moreover, these particular conditions yield some important properties.

• Property 1: there is a unique set of EFMs for a given metabolic network.

• Property 2: all the feasible steady-state flux distributions satisfying equations 1 and 2 are a nonnegative superimposition of the set of EFMs in the network.

• Property 3: when a reaction is removed from the network, the set of EFMs for the new network is equal to the one from the original network, but removing all the EFMs that include the removed reaction.

These properties render these approaches extremely interesting for metabolic engineering purposes (among others), since they describe the complete portfolio of steady-state phenotypes and are conveniently presented as minimal metabolic functions.

While the two methods are conceptually close to each other, the fact that ExPas resort to the decoupling of reversible reactions into equivalent forward and backward reactions translates into a noncomplete overlap of their corresponding enumerations in many cases. In fact, ExPas are a subset of EFMs, and in some cases the two sets coincide, namely, when the network is composed solely of irreversible reactions or, in most realistic cases, where only reversible exchange reactions occur (68).

Given that the previously mentioned enumerations, for genome-scale metabolic networks, are computationally unattainable, alternative methods based on random sampling of the flux space, such as a Monte Carlo Markov chain (MCMC) (69) or adapted canonical basis (70) approach, have been developed to circumvent this limitation. Moreover, alternative methods focused on achieving particular biological functions or searching a subset of the flux space (71, 72) are also suitable ways of exploiting this class of methods. The inclusion of GPR information as a means to omit biologically unfeasible solutions has allowed Jungreuthmayer and colleagues to significantly decrease computation times for the enumeration of EFMs (73). In this work, a maximum of 223 million EFMs were computed for the E. coli core model (74). Another recent effort by Hunt and coworkers tackled the problem by iteratively splitting the network into subnetworks and enumerating their EFMs in powerful computational clusters (75). This approach has allowed the full enumeration of EFMs (∼2.2 billion) for a Phaeodactylum tricornutum genome-scale model comprised of 318 reactions and 335 metabolites, the largest to date.

Finally, Bordbar and associates recently proposed the MinSpan algorithm (76), an alternative MILP formulation capable of computing a minimal set of pathways which are representative of the totality of the steady-state phenotypes. Unlike the previously stated convex analysis approaches, MinSpan is computationally tractable even for large genome-scale metabolic networks.

COMPUTATIONAL STRAIN OPTIMIZATION METHODS

Before a formal classification for computational strain optimization methods (CSOMs) is presented, our vision of what a CSOM is must be clarified. Computer-aided strain design efforts cover a broad range of applications and techniques, which leads some authors to mix together optimization approaches with others that can be considered phenotype prediction methods or even strain design algorithms that do not explicitly use any type of optimization algorithm. To clarify our approach to the classification of these methods and as a justification for the inclusion or absence of some well-known (and, nonetheless, very useful) approaches in this section, some rules have been drafted for whether or not to consider a method a CSOM.

1. A CSOM must (try to) provide an answer to a specific top-level question, in the form “Which set of perturbations applied to the model (organism) favors a desired engineering goal?”

2. The exhaustive enumeration of all possible solutions (designs), albeit highly desirable, is not considered a CSOM since it is considered a trivial approach (usually not attainable). Rather, an optimization algorithm that defines a strategy to sample the solution space must be defined to warrant the inclusion of the method below.

3. The algorithms covered in this review are solely the ones based on constraint-based approaches, following the framework highlighted in the previous section. We will not cover here other approaches, for instance, those based on graphs or hypergraphs and their underlying algorithms or any approach based on the use of dynamic models.

Computational Strain Optimization Tasks

CSOMs can be thought of as procedures which try to answer a practical question (or set of questions) relevant for strain design. These questions can be translated into mathematical formalisms and addressed by distinct optimization methods. Powered by phenotype prediction methods and guided by GSMMs, these methods automatically or semiautomatically search for answers to questions such as which genes should be deleted from the model to couple the production of compound X to growth or which foreign pathways must be added to acquire a desirable functionality in a given host. In fact, the latter question was probably the first one to arise when molecular biologists realized the inner potential of recombinant DNA technology.

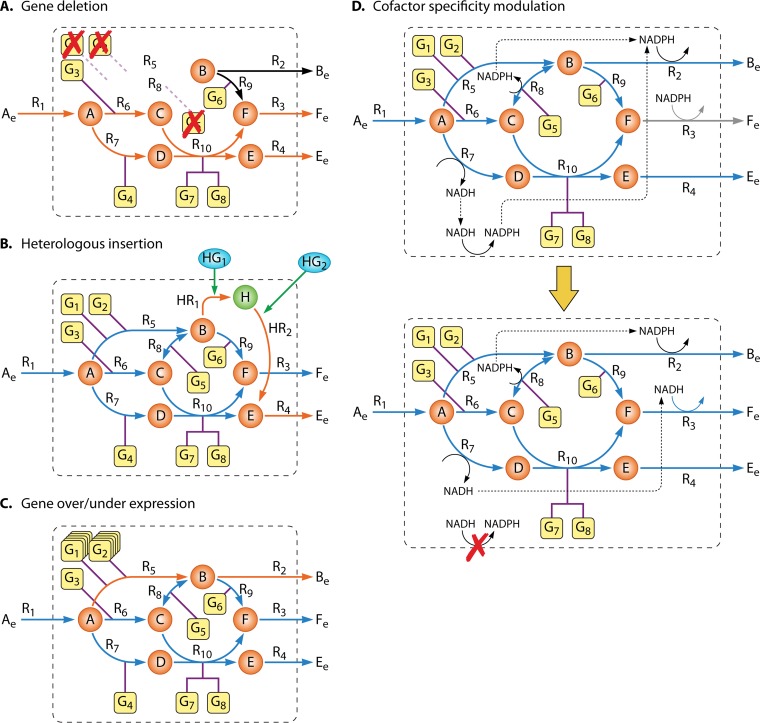
The most common tasks undertaken by CSOMs are gene deletion, gene over- or underexpression, heterologous insertion, and, more recently, cofactor specificity swapping. Some methods also attempt combinations of these tasks to find better phenotypes.

Gene deletion.

The suppression of a given metabolic function can be accomplished in vivo by disrupting the functioning of specific genes by targeted modifications through homologous recombination (77) or intron introduction (78). In silico CSOMs that account for gene deletion (Fig. 3A) usually search for combinations of metabolic function suppressions yielding desirable phenotypes. This task is commonly accomplished by imposing constraints that force the flux of the disabled reactions to zero, deterring the occurrence of flux over those reactions, followed by the evaluation of the effect of that perturbation.

FIG 3.

Computational strain optimization tasks. In the example, 3 gene deletions force the flux through reactions producing the desired compounds (A), the inclusion of two heterologous genes allow the production of an intermediary compound and subsequent excretion of the desired product (B), the overexpression of two enzymes allow the excess formation of compound B, which is subsequently excreted (C), and the enzyme catalyzing the transport reaction R3 is swapped by an heterologous enzyme using NADH (D). The deletion of a membrane oxidoreductase enzyme creates an excess of NADH that can be used by the new transport reaction to excrete compound F.

Some recent methods take advantage of the GPR information contained in the model and search for combinations of gene deletions (instead of searching for reaction suppressions) which more closely represent the in vivo scenario, since they inherently account for the occurrence of multifunctional and multimeric proteins, as well as isoenzymes (49).

Heterologous insertion.

Analogously, the inclusion of nonnative functionalities, via gene or pathway addition, might broaden the metabolic capabilities of desirable hosts, either by boosting the yields of native compounds or by allowing the production of entirely new ones (Fig. 3B). Typically, algorithms with this kind of capability will sort through databases of balanced reactions for the desired functionality and try to reconcile them with the original network. The augmented network can, afterwards, be engineered by other CSOMs to redirect flux in the desired directions. Most algorithms that are specialized only in the first task, that is, the sorting of heterologous enzymes and subsequent reconciliation with a target host, are not considered in this work since they are typically not constraint-based approaches. Examples of the aforesaid methods include DESHARKY (79), BioPathwayPredictor (80), or FindPath (81).

Gene over- or underexpression.

The up- or downregulation of gene expression has considerable importance in the ME community (82, 83). Gene over- or underexpression concerns the fine-tuning of enzyme levels and corresponding flux rates, which can be accomplished by using promoter libraries (84–86) or synthetic biology tools (87). This approach can be useful in situations where a gene deletion is lethal whereas downregulation is not and also can be a solution to overcome flux bottlenecks in certain steps toward a desired biological function (Fig. 3C). These tasks are usually undertaken through the addition of extra constraints on the fluxes, forcing them to operate closer to their maximal or minimal theoretical bounds. This task imposes some challenges given the fact that stoichiometric models often do not have capacity constraints for the majority of the fluxes, and thus wild-type simulations will determine a flux distribution that may already violate in vivo capacity constraints. Moreover, most methods simulate the effect of gene overexpression by imposing a flux through specific reactions, disregarding whether those reactions had zero flux in the wild type, thus artificially forcing flux distributions. Finally, a more fundamental question is related to the often nonlinear nature of the relationships between gene abundance and fluxes, which has been mentioned above.

Modulation of cofactor binding specificity.

A distinct approach is to tackle the scarcity of some cofactors required for essential steps of some ME efforts by modulating the cofactor binding specificities. A typical example is the modulation of NAD(H) or NADP(H) availability, due to their importance in the catabolic and anabolic processes. By manipulating the cofactor binding specificities, it is possible to establish driving forces in target pathways that require, for example, the regeneration of one particular cofactor (88). In vivo modulation of cofactor specificities has via protein engineering (89, 90) or by replacing native enzymes with heterologous ones with different cofactor specificities (91) been reported. This approach can be computationally simulated by swapping the cofactor specificities of some reactions in the network, followed by use of a phenotype prediction method to evaluate the effects of the perturbations (Fig. 3D).

A Taxonomy for Computational Strain Optimization Methods

The set of CSOMs reviewed in this work has been organized and classified according to several aspects, including the strain design task(s) addressed, the optimization algorithm, the mathematical formulation, the method's scalability, the validation case studies, and the availability of the method in a software implementation. This information is provided in Table S1 in the supplemental material, with the methods sorted chronologically.

A classification (or “taxonomy”) for CSOMs is proposed in this work based on the features of each method. An obvious classification would be to group them based on the tasks they try to accomplish, as explained in the previous section. While keeping this also in mind, we prefer to analyze them based primarily on their optimization frameworks and mathematical formulations. Following this principle, three main branches emerged in our analysis: bilevel mixed-integer programming (MIP)-, metaheuristics-, and elementary-mode analysis (EMA)-based methods.

Bilevel mixed-integer programming methods.

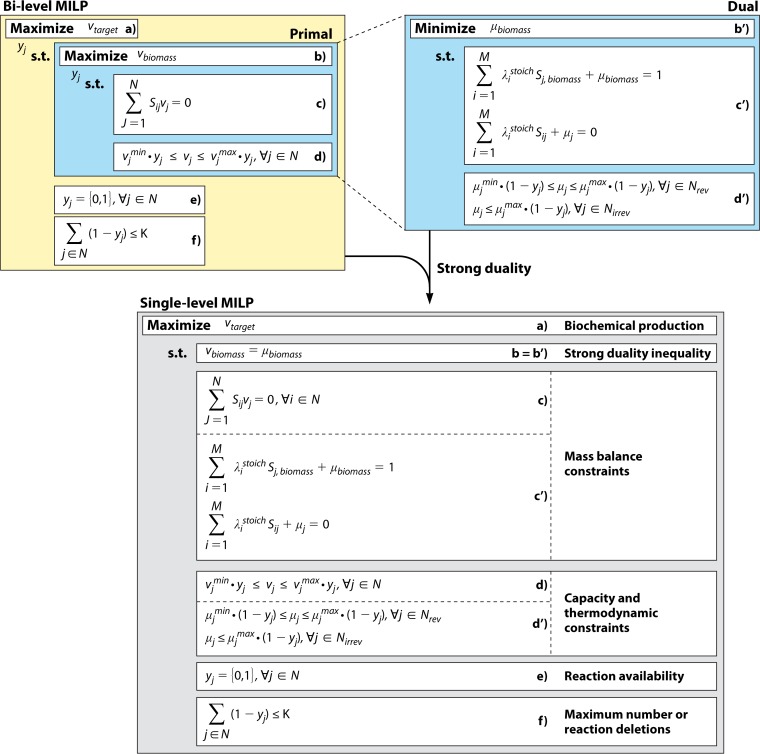
In 2003, Costas Maranas' group reported a specialized method to pursue productive gene deletion strain designs coupled to cellular growth. This method, OptKnock (24), proposed a bilevel framework, where two competing objective functions were simultaneously accounted for. The inner problem concerned the biological objective of the organism, in this case maximization of cellular growth, while the outer problem focused on the engineering goal, the overproduction of a desired compound. The method suggested reaction deletions, which were imposed as constraints for the inner problem. This elegantly formulated mathematical framework profited from the strong duality property, which states that if the primal and the dual optimal solutions are bounded, then at optimality, the gap between the objective function values must be zero (92). This property allows the bilevel formulation of OptKnock to be transformed into a single-level MILP by setting the primal and dual objectives equal to one another and accumulating their respective constraints. OptKnock represented a breakthrough in the field, establishing the framework used by many of the developed CSOMs until the present. Figure 4 summarizes the main properties of the bilevel formulation and its conversion to a single-level MILP, as introduced by OptKnock, which establishes the distinct characteristics of this category of CSOMs.

FIG 4.

Simplified example of the coupling strategy introduced by OptKnock, allowing the transformation of a bilevel MILP into a single-level one. The top region depicts the bilevel MILP problem (left) and the dual problem of the inner layer (right). For each constraint in the primal objective, there are one or more dual equivalents. Using strong duality theory and accumulation of constraints, the single-level MILP formulation is attained (bottom).

One of the properties of OptKnock solutions is that they are mathematically guaranteed to be optimal, given the defined task and objective function. However, they can often be considered overly optimistic in real-world scenarios. In fact, OptKnock selects the “best” solution, the one with highest product yield given a predefined minimum biomass flux value and a maximum number of reaction deletions, but is not able to account for competing pathways that might redirect the flux, lowering or even bringing to zero the expected product yield under the same biomass values.

To address this issue, Tepper and Shlomi (93) suggested the RobustKnock method, a reformulation of the OptKnock procedure that optimizes the worst-case scenario for product formation coupled to cellular growth, that is, the lower bound for the expected growth coupled to product formation. The maximum-minimum formulation of RobustKnock yields a triple-level problem, an outer maximum-minimum problem that searches for a set of knockouts maximizing the minimal production rate of the target compound (a bilevel problem) and an inner problem similar to that of OptKnock, searching for a feasible flux distribution maximizing biomass. The outer problem is transformed into a standard maximum-minimum problem using a procedure similar to that used in OptKnock and, subsequently, transforming it into a standard MILP problem.

Shortly after, Feist and coworkers, as an alternative approach to address the robustness issues brought up by OptKnock, introduced objective function tilting (94). Although not a CSOM by itself, objective function tilting represents a valid, computationally lighter alternative to RobustKnock, since it involves only small changes in the objective function of OptKnock (and also of OptGene, referred to in the next section) without increasing its computational complexity. In OptKnock, this approach involves adding the negative of the desired product yield multiplied by a very small weight to the inner problem's objective function. This forces the algorithm to identify the solution with the highest minimum production rate among the ones with optimal value for the inner problem.

More recently, Kim and coworkers introduced BiMOMA as an alternative to OptKnock (95). BiMOMA is a new bilevel CSOM for the design of gene deletion strategies. It is formulated as a mixed-integer quadratic constrained programming (MIQCP) problem, which uses MOMA as the inner phenotype evaluation method (as opposed to OptKnock's FBA). In their work, several techniques to reduce the scalability problems traditionally associated with MIP formulations were also suggested. These techniques include the tightening of the bounds of the dual variables using a sampling technique, the application of penalties for genetic perturbations (favoring smaller designs), reduction of the search space, and finally, the use of iterative methods as a way to improve the performance of the solvers. The applicability of BiMOMA was demonstrated for the production of glutamate and pyruvate in E. coli.

A similar approach was suggested by Ren and coworkers (96) with MOMAKnock. The adoption of MOMA to the inner problem once again yielded a mixed-integer bilevel quadratic programming (MIBQP) formulation, but, in contrast to BiMOMA, it was not converted to an MIQCP. Due to the heavy computational burden caused by the MIQCP formulation, the authors proposed the use of an adaptive piecewise linearized inner problem to approximate the quadratic objective function of MOMA. The proposed formulation was benchmarked against OptKnock results in the search for succinate productive E. coli strain designs.

Very recently, researchers from the Chinese Academy of Sciences questioned the validity of the duality theory transformation employed by OptKnock (97). They argued that by not including the lower-level primal variables in the dual objective, the single-level MILP problem on which OptKnock relies was erroneously derived. More explicitly, they argue that if the problem had been correctly formulated, a mixed-integer nonlinear programming (MINLP) problem would emerge instead of an MILP. Subsequently, they suggested a method based on the Karush-Kuhn-Tucker (KKT) technique (98) to reformulate mixed-integer bilevel linear problems (MIBLPs) as single-level MILPs (applicable only when the inner problem is continuous) and proposed ReacKnock as a more reliable alternative to OptKnock. However, more recently Chowdhury and coworkers released a new work (99) in which the details of the OptKnock formulation are more thoroughly explained. In particular, they elaborated on the application of the complementary slackness conditions to justify the absence of some of the lower-level primal variables in the dual-objective function, thus restating the formulation of OptKnock as completely valid.

The optimization of reaction deletions was not the only task addressed by this class of methods. Shortly after the publication of OptKnock, Maranas and coworkers extended the developed framework to support enhancing a desired host with nonnative functionalities via heterologous enzyme additions. This method was termed OptStrain (100) and was implemented as a multistep approach, using MILP formulations in the different steps. Profiting from the myriad of biological data sources available, such as KEGG (101, 102), MetaCyc (103), or BRENDA (104), the authors created a universal reaction database which OptStrain used as a core for finding the reactions that can be added to the host GSMM. With this knowledge base in place, the OptStrain procedure computes the maximum theoretical product yields for a given substrate, considering both native (from the GSMM) and nonnative (from the database) reactions. Afterwards, the minimal number of nonnative functionalities yielding balanced pathways is sought and included in the original stoichiometric model. Finally, the OptKnock framework is employed to find additional knockouts that further increase the yields. The OptStrain framework was used to identify metabolic engineering strategies for the production of hydrogen and vanillin in Clostridium acetobutylicum and E. coli, respectively.

In 2011, Kim and coworkers revisited and improved the OptStrain framework by considering both gene deletions and heterologous insertions simultaneously (95). This method, SimOptStrain, is aware of GPR relationships, which potentially allows for more biologically feasible designs. The new method was demonstrated in the design of succinate- and glycerol-productive strains of E. coli.

Yet, the portfolio of possible genetic manipulations was not complete with the development of OptKnock, OptStrain, and related methods. As stated above, the tuning of gene expression and related enzyme levels is another important task in strain optimization. The OptReg framework (105) was the first CSOM to allow searching for optimal gene expression levels, together with gene deletions as provided by OptKnock. In this MILP formulation, additional binary variables referring to up- and downregulations and knockouts were considered: y_j^d = 0 if reaction j is downregulated and 1 otherwise; y_j^u = 0 if reaction j is upregulated and 1 otherwise. These act as switches that restrict the flux in response to the respective perturbation (over- or underexpression) based on the supplementary constraints

$$v_j^{\text{min}}\le v_j\le [v_{j,L}^0\cdot (1-C)+v_j^{\min }\cdot \hspace{0.17em}C]\hspace{0.17em}\cdot \hspace{0.17em}(1-y_j^d)+v_j^{\max }\cdot y_j^d\hspace{0.17em},\forall j\in N$$ (3)

for downregulation and

$$[v_{j,U}^0\cdot (1-C)+v_j^{\max }\cdot \hspace{0.17em}C]\cdot (1-y_j^u)+v_j^{\min }\cdot \hspace{0.17em}{y}_j^u\le v_j\le v_j^{\max }\hspace{0.17em},\forall j\in N$$ (4)

for upregulation, where v_j^min and v_j^max are the lower and upper limits of flux j defined in the GSMM, v_j,U⁰ and v_j,L⁰ are the lower and upper limits of flux j determined by flux variability analysis (FVA) (106) and C is the regulation strength parameter considered in the interval [0, 1]. Higher values of C correspond to stronger regulation. Furthermore, constraints stating that a reaction can be subjected to only one manipulation (knockout, downregulation, or upregulation), constraints limiting the maximum number of manipulations allowed, and constraints forcing the mutual knockout of the two directions of reversible reactions are also taken into account. OptReg was illustrated with the determination of engineering strategies for the production of ethanol in E. coli.

Subsequently, Ranganathan and colleagues published an alternative method named OptForce (107), which was supported by a different but rather insightful concept. The workflow is initiated by a characterization of the wild-type strain, using FVA to determine the lower and upper bounds of each flux (this task can be aided by experimental data if available). By iteratively considering sets of reactions (pairs, triples, etc.), OptForce generates a set of those that are required to change to achieve a user-defined production yield (termed the MUST set). From this set, a new step proceeds to characterize the minimal set of reactions that need to be forced via genetic manipulation (termed the FORCE set). The proof of concept was performed in the production of succinate in E. coli. Posterior experimental validation led to interesting results for other targets in E. coli (108, 109) (further details are in the next section).

A similar approach, termed CosMos, was recently proposed by Cotten and Reed (110); it incorporates flux up- and downregulation in a more flexible manner than OptForce, since changes to bounds do not rely on previously calculated fluxes (as is the case with OptForce) but instead are subjected to continuous modifications. This MILP formulation was compared to OptForce, with additional solutions reported in a case study for succinate production with E. coli.

With the scalability problems of traditional MIP formulations in mind (94), Mahadevan and coworkers proposed the EMILIO (enhancing metabolism with iterative linear optimization) approach (111). The foundational framework employed by EMILIO is very similar to that of OptReg, with the exception that the inner problem's objective function enforces the maximization of a minimal production rate, thus addressing the concerns first raised by Tepper and Shlomi (93). The bilevel problem is reformulated into a nonconvex single-level mathematical program with complementary constraints (MPCC), which is solved using a three-step approach. First, iterative linear programming (ILP) is applied to establish the set of active constraints (flux bounds), followed by a recursive LP-based pruning method that identifies subsets of active constraints required to achieve a user-specified fraction of the maximum production rate. In the final step, for each subset, an MILP procedure similar to OptReg is employed to minimize the number of reaction modifications required to satisfy the user-specified fraction of the maximum production rate. EMILIO was demonstrated in the design of various deletion and over- or underexpression E. coli mutants for the production of succinate, l-glutamate, and l-serine.

A distinct method is OptORF, released in 2010 by Kim and Reed (112), which was the first to address strain optimization using metabolic-regulatory integrated models. Similarly to previous approaches, OptORF was formulated as a bilevel MILP problem, capable of suggesting metabolic engineering growth-coupled production designs. Uniquely, though, OptORF designs consisted of both metabolic and regulatory gene deletions, as well as metabolic gene overexpressions. These make use of Boolean rules defining the relations between reaction and metabolic genes (GPRs), as well as rules that define transcriptional regulation. Both are transformed into linear constraints. The applicability of this method was, however, limited by the scarcity of available integrated metabolic/regulatory models to profit from all its features. OptORF has been applied in the design of ethanol-, isobutanol-, and 2-phenylethanol-producing E. coli strains.

Complementary to the various described approaches for gene deletion, gene over- and underexpression, and heterologous insertion, some alternative CSOMs with unique characteristics have also been proposed.

An exquisite new method, OptSwap, was very recently proposed by King and Feist (88). OptSwap was the first and is so far the only method to consider cofactor binding specificities of enzymes as possible targets for computational strain optimization. More specifically, OptSwap focuses on oxidoreductase enzymes and their binding specificity for either NAD(H) or NADP(H). However, the authors state that the principles and framework can be extended to other specific sets of interest. A pool of swap candidate oxidoreductase enzymes is selected, based on literature and in silico limitations. The problem is formulated as an MILP, similarly to RobustKnock but including additional constraints to enforce swaps of the cofactor specificities of the previously selected reactions. This is accomplished by extending the model with a set of reactions with distinct cofactor specificity to the ones in the pool. Extra constraints are added to force the knockout of either the native or the swapped reaction and to limit the numbers of both swaps and deletions. The OptSwap procedure was used to identify nonintuitive designs for several end products in E. coli, some of which were not possible by gene deletions alone.

The most recent effort in MIP-based CSOMs combines the kinetic descriptions of metabolic steps with traditional stoichiometric models to improve their predictive power and suggest more accurate designs (113). By bridging the gap between stoichiometric- and kinetic-based models (114), k-OptForce may represent a game changer and a new chassis for future CSOM development efforts. In contrast to most CSOMs, k-OptForce does not rely on assumptions such as the maximization of biomass or minimization of metabolic adjustments as a fitness function but rather makes use of available kinetic rate laws to predict flux distributions. To meet this end, the reactions in the metabolic network are split into two sets, one containing reactions for which kinetic information is available (N^kin) and another for the reactions with only stoichiometric information (N^stoic). While the reactions in N^stoic are constrained by mass balances and thermodynamics, the ones in N^kin are subjected to enzyme kinetics, metabolite concentrations, and kinetic parameter values. Consequently, the N^kin part of the network is represented as a system of nonlinear ordinary differential equations (ODEs).

The k-OptForce procedure is subsequently solved in two steps. First, a characterization of the wild type is done by solving the system of ODEs to obtain a steady-state flux distribution for N^kin and by using FVA for the N^stoic reactions. Similarly, the characterization of the overproducing strain is performed subject to the kinetic and concentration constraints, where available. Finally, the computation of MUST and FORCE sets from OptForce (107) is reformulated to account for the newly introduced kinetic layer. The introduction of nonlinear kinetics into the formulation translates into a single-level mixed-integer nonlinear optimization problem (MINLP), which needs to be addressed using to NLP solvers. The k-OptForce formulation was contrasted with the original OptForce for the prediction of l-serine and triacetic acid lactone mutants of E. coli and Saccharomyces cerevisiae, respectively.

Overall, the class of methods described in this section presents numerous advantages and has led to several successful applications that will be covered below. Yet, although the formulation of strain optimization problems on the OptKnock framework yields exact solutions for the defined formulations, the methods have problems with the underlying computational complexity. This constrains, for instance, OptKnock and related methods to a relatively low maximum number of allowed transformations, as the consideration of higher numbers would make the methods hard to apply in current GSMMs. Also, the MIP framework restricts these methods to the use of linear objective functions that do not necessarily express the complexity of the bioengineering objectives. Lastly, these methods rely on a tight coupling of the two levels, the phenotype simulation and the strain optimization layers, which also reduces their flexibility. This is clearly illustrated by the fact that there is a need to define a new method when an optimization approach developed for a specific simulation method is to be applied to another one, such as changing from FBA to MOMA.

Metaheuristic CSOMs.

The problems associated with the previous methods stated above motivated the development of a separate class of approaches, supported on a more heuristic rationale. Heuristic methods are usually computationally less expensive approaches for a myriad of optimization problems. Although, due to their nature, they do not guarantee that the overall optimal solutions are found, they allow the definition of optimization frameworks with an enriched set of objective functions, fostering a clearer separation of the strain optimization from the phenotype simulation methods, while allowing optimization over larger search spaces (e.g., a higher number of gene deletions or other modifications). In Fig. 5, a generic workflow for a typical metaheuristic CSOM is presented.

FIG 5.

Workflow of generic metaheuristic CSOM. The separation of the several layers (model/phenotype prediction/strain optimization) is easily visible. Typically, an iterative procedure generates or modifies candidate solutions, which are translated into perturbations to the original network. Afterwards, the phenotype of the perturbed network is simulated and evaluated. The method stops when a desired phenotype or other termination criterion is attained.

The first effort to move in this direction was OptGene (115), presented by Patil and coworkers, which appeared shortly after the publication of OptKnock and OptStrain. Inspired by the Darwinian natural evolution theory, OptGene formulates a bilevel decoupled approach, supported by the use of a genetic algorithm (116). The idea is to encode solutions as individuals in an evolving population. Here, each solution is represented as a set of integer values encoding reaction deletions. The algorithm starts by the random generation of an initial set of candidate solutions (the initial population), and each is decoded into a set of reaction deletions, which are translated into constraints, which are flux distributions predicted using FBA. A fitness value is then assigned to each solution by a user-defined objective function, which can be nonlinear. Subsequently, the algorithm enters an iterative stage, starting with a selection step which chooses solutions as primary candidates for reproduction in a stochastic way that depends on their assigned fitness (fitter individuals have a higher probability of generating offspring solutions). Finally, by combining these individuals via crossover or mutation operators, a new population is attained and reevaluated. This cycle is repeated until a desired phenotype is achieved or another user-defined termination criterion is met (typically, a defined maximum number of generations or solutions evaluated).

Although these methods, like the previous ones, still follow a bilevel design, in this case the bioengineering and the biological optimization tasks are clearly decoupled and are performed independently. This decoupling of the outer and inner optimization problems is translated into some very powerful properties. For example, the inner phenotype evaluation method can easily be swapped among FBA, MOMA, ROOM, or any other phenotype simulation method, including the ones using regulatory constraints (such as rFBA or SR-FBA). Another important advantage is the flexibility in the definition of the objective function in the outer problem, which is here not bounded by linearity. Nonlinear objective functions (even discontinuous) can easily be included, as is the case with the biomass-product coupled yield (BPCY), which resembles productivity (115), allowing definition of more meaningful and powerful functions. The flexibility gained by the decoupling of the two layers also allows the easier switch of the optimization heuristic used to search for metabolic engineering strategies and allows the different optimization tasks to be addressed with a similar framework.

In the original publication, the OptGene method was first used to suggest S. cerevisiae designs for the production of vanillin, glycerol, and succinate. Since then, taking advantage of the flexibility provided by this approach, the framework has been thoroughly extended to support additional features and algorithms. Rocha and coworkers provided a reformulation of OptGene where set-based evolutionary algorithms (SEAs) and simulated annealing (SA) algorithms were used in the outer optimization problem (117), enabling a more compact representation and the simultaneous optimization of the number of knockouts. Also, extensions were proposed where metabolic engineering strategies consider both metabolic and regulatory genes as targets (118), gene over- or underexpression (119), and multiobjective optimization problems (120).

A very similar method, cipher of evolutionary design (CiED) (121), was also developed and experimentally validated in E. coli for the increased production of malonyl coenzyme A (malonyl-CoA).

More recently, Constanza et al. analyzed robustness issues involved in suggested genetic interventions (122). The proposed genetic design through multiobjective optimization (GDMO) is inspired by the nondominated sorting genetic algorithm II (NSGA-II) (123), a multiobjective evolutionary algorithm (MOEA) which uses the Pareto optimality principle to find the optimal (or near optimal) trade-off solutions in a multiobjective optimization problem. The procedure begins with the preprocessing stage, where a sensitivity analysis on the model ranks the various pathways according to their influence on the outputs. Subsequently, the MOEA searches for both gene deletions and nutrients in the medium, as specified by the defined objective functions. Finally, a robustness analysis task selects the most robust designs as ideal candidates for implementation by applying a random-noise function that causes small perturbations in the upper and lower bounds of the fluxes. The process is repeated for T trials, and the robustness of the design is defined as the number of robust trials with respect to the total number of trials. A design is considered robust if it still maintains the expected outcome after the perturbation. This procedure was applied in E. coli for the production of succinate and acetate, and its results were compared with those of OptGene, SEAs/SA algorithms, and OptKnock.

The genetic design through local search (GDLS) method (124) embraced the problem from a different perspective. By using iterative local search steps, building on previous solutions, GDLS is capable of suggesting efficient strain designs, involving a larger number of genetic interventions (both gene deletions and over- and underexpressions). However, as later pointed out (111), the complexity still increased exponentially with larger scopes of each local search. GDLS proof of concept was established by suggesting acetate- and succinate-productive E. coli strains.

Later, part of the GDLS team also participated in the development of the genetic design through branch and bound (GDBB) approach (125). GDBB uses a truncated branch and bound technique to tackle the scalability problems associated with the bilevel MILP problem introduced by OptKnock. The formulation, similar to that of OptKnock, makes use of the Gurobi solver (Gurobi Optimization, Houston, TX, USA) implementation of the truncated branch and bound algorithm and exploits its optimality and feasibility configuration options to fine-tune the truncation process. By not allowing the solver to reach optimality, but rather forcing it to stop at near-optimal solutions (considered sufficient for practical purposes), the performance of the method was improved significantly compared to that of previous approaches. Such a technique is readily applicable to any method whose foundational framework is a bilevel MIP for which a single-level MIP equivalent is attainable.

More recently, Rockwell and coworkers presented the Redirector approach (126). This method is based on the iterative local search technique used by GDLS but introduces a novel objective function reconstruction cycle in the iterative procedure. This novel cycle is composed of two steps: the first one, called “objective control,” finds metabolic engineering targets and adds them to the objective function, while the second one, designated “progressive target discovery,” iteratively adjusts the contribution of growth to the objective function, redirecting resources to the optimization of the target compound. Important in this method is the idea of simulating over- and underexpression of enzymes by including the fluxes in the objective function with positive and negative coefficients, respectively. This approach was applied to the discovery of novel E. coli designs for the production of fatty acids.

One of the latest noteworthy heuristic CSOMs presented is FastPros (127), an efficient screening procedure based on shadow price analysis. By relaxing or strengthening a given constraint in an LP problem, it is possible to measure the change in the value of the objective function, a variable which is termed the shadow price of the constraint. This algorithm introduces a novel score for knockout screening (μ_target) which corresponds to the shadow price of the constraint associated with the excretion reaction for the compound of interest (for an FBA problem maximizing biomass production rate). This new score represents the potential for target production and is calculated by the relationship μ_target = Δv_growth/Δv_target, where Δv_growth is the variation in the biomass production caused by an increase of Δv_target from zero flux. A positive value of μ_target represents growth-coupled production of the target compound. The procedure begins with the computation of every double-knockout strategy and corresponding μ_target values, from which a set of P parent sets is selected with regard to that score. At this point, the iterative procedure begins, consisting of the generation of knockout sets by adding every possible single knockout to every parent set in P (yielding P × N sets), recalculating the Δv_target values, and reinitializing the procedure with the new set of P parents. However, the value of Δv_target is related only to the benefit toward growth, rendering the iterative procedure insufficient for the purpose of finding high-productivity strain designs. For this purpose, the authors proposed a modification of the OptKnock procedure, where the candidates for reaction knockouts are limited to those selected by FastPros, which yielded very positive results. The FastPros procedure was used in the screening of geranyl diphosphate- and l-phenylalanine-producing E. coli designs.

EMA-based methods.

The final group of methods includes the CSOMs that use elementary-mode analysis (EMA) as their foundational framework.

Klamt and Gilles introduced the concept of minimal cut sets (MCSs) in 2004 (128), representing the first draft of what an EMA-based framework for strain optimization could look like. A minimal cut set describes an irreducible group of reactions required to disrupt a given network function (a targeted reaction, r_obj), and thus, in a certain way, MCSs are the opposite of EFMs, which describe the minimal functional modes. Similarly to EFMs, the set of MCSs in a network is also unique. As a limitation, the computation of the EFMs of the network is required a priori, which has limited the uses of MCSs to small to medium-size networks. After the computation of the EFMs is performed, the EFM set is divided in two subsets, one containing all the EFMs that involve the target reaction r_obj (the target modes, E^t) and another containing all the EFMs that do not involve the target reaction (the nontarget modes, E^nt). By ensuring that all the target modes become inactive after the removal of a set C of reactions, only nontarget modes will be left; hence, by the definition of EFMs, it is no longer possible to find a feasible flux distribution involving r_obj. An MCS “hitting” all target modes is termed a minimal hitting set, and the computation of the minimal hitting sets from the set of target modes can be performed using the Berge algorithm (129). In this work, several possible applications MCS were discussed, including target identification and repression of cellular functions, network verification and mutant phenotype predictions, and structural fragility and robustness analyses. Later, the concept of MCSs was refined and generalized to multiple targets, and its duality properties with EFMs were studied in more detail (130).

The main limitation of the MCS approach is that by being focused on a target functionality to be disrupted, it is rendered oblivious to possible side effects over other desired functionalities. To tackle this limitation, Hädicke and Klamt developed a generalized approach of MCSs termed constrained minimal cut sets (cMCSs), allowing for the inclusion of side constraints (131). A cMCS C is now admissible if it hits all target modes but also maintains a minimum number n of desired EFMs. It is not expected that this set (D) will keep all the desired modes, meaning that it is possible that some of the desired modes will also be hit by some MCSs. However, the set of desired modes not hit by any MCS (D^C) is bounded by |D^C| ≥ n. The introduction of these constraints indicated an adaptation of the Berge algorithm. This approach has been demonstrated for the production of ethanol in E. coli. The inclusion of regulatory constraints into cMCSs was later done by Jungreuthmaye and Zanghellini, who devised the regulatory constrained MCSs (rcMCSs) (132).

Concurrently, Srienc and collaborators presented another EMA-based approach, named minimal metabolic functionality (MMF) (133). This approach iteratively searches for all the combinations of gene deletions that will eliminate all undesired EFMs while keeping a set of optimal or near-optimal ones intact. Similarly to other approaches, coupling of biomass and product synthesis can be enforced by the selected knockout strategies. The application of MMF yields a network containing only its most efficient pathways, and its applicability was verified experimentally for the production of several secondary metabolites in E. coli.

The first EMA-based approach to consider other types of metabolic engineering interventions besides knockouts was FluxDesign (134). This procedure first computes the set of EFMs by using the EFMTool (135), followed by a normalization step that for a given EFM calculates the relative flux for each of its reactions, normalized to the substrate uptake. Finally, to decide whether or not a given reaction r represents a potential intervention target, a chosen set of EFMs is searched for (statistically) significant correlations between the flux through the objective reaction and the flux through reaction r. This strategy yields targets for both amplification (upregulation) and attenuation (downregulation). FluxDesign was demonstrated for lysine and enzyme production in Corynebacterium glutamicum and Aspergillus niger, respectively.

Another approach for suggesting multiple types of genetic interventions came from Hädicke and Klamt (136). The proposed computational approach for strain optimization aimed at high productivity (CASOP) is based on reaction importance measures, where their relative contributions to yield and flux capacity are taken into account. With the purpose of finding growth-coupled high-productivity strain designs for a target product P, the procedure begins by considering an artificial external metabolite (V), which is produced from biomass and the target product by the reaction (here simplified) R_v: (1 − γ)BM + γP(ext) → V, γ ∈ [0,1], with γ representing the relative production of P(ext) with respect to biomass (BM) synthesis. By iteratively increasing the parameter γ, computing the set of EFMs for the new scenario, and recalculating the EFM weights and reaction importance measures, the procedure yields a set of candidates for knockouts and overexpressions. Succinate-overproductive E. coli strain designs were suggested to demonstrate the applicability of this approach.

More recently, Trinh and coworkers presented the systematic multiple-enzyme targeting approach (SMET) (137). This method uses cMCS to find the set of modes maximizing a desired product yield and ensemble metabolic modeling (EMM) to generate ensemble models representing the steady-state phenotype of the wild-type strain. Afterwards, SMET is used to systematically identify sets of enzyme targets to engineer the wild-type strain to reach the desirable phenotype. The SMET approach is capable of suggesting designs based on deletions or over- or underexpressions and has been validated in the production of aromatic amino acids in E. coli.

An alternative method was suggested by Soons and coworkers (138), which combines both objective function-centered and pathway enumeration-centered approaches to achieve productive strain designs coupled to biomass growth. Their proposed method, iStruF, introduces the notion of structural fluxes, which are derived from the pathway enumeration of a metabolic network. The method is demonstrated for the production of ethanol and succinate in a medium-scale S. cerevisiae metabolic network.

Until recently, the use of EMA-based methods, including application to strain optimization, was limited to small- to medium-scale metabolic networks, as the number of possible EFMs increases exponentially with the network size. Indeed, all previously mentioned validation examples do not use GSMMs but rather use small or medium-size models with selected pathways.

Some approaches to circumvent this issue have been suggested in the past (139, 140) but have limited applicability in this context. A big step forward into bringing EMA-based CSOMs to the genomic scale was taken by de Figueiredo and collaborators, with the publication of a method to generate the shortest EFMs in a genome-scale metabolic network (141). While not being able to find all EFMs for the network, this method allows iterative calculation of sets of EFMs of interest for a given ME task (e.g., those achieving a given chemical transformation or a set of chemical transformations). As an illustration, the method has been employed within CASOP to extend it to genome-scale metabolic models via a heuristic approach named CASOP-GS (142).

Even more noteworthy is the latest work by von Kamp and Klamt, MCSEnumerator, published in early 2014 (145). The method begins by converting the original network and intervention objective to its dual form, following the approach of Ballerstein et al. (143), and then enumerates the k shortest EFMs in the dual network using a modified version of the approach of de Figueiredo et al. (141). The EFMs in the dual network correspond to the MCSs in the primal network, and thus the shortest EFMs in the dual network will correspond to the smallest MCSs in the primal network. The framework is formulated as an MILP problem, elegantly extended to represent sets. In their paper, MCSEnumerator is demonstrated first by enumerating all the synthetic lethal mutations up to 5 knockouts in a GSMM of E. coli (144) and then enumerating of all the cMCSs up to 7 reactions leading to growth-coupled ethanol production in the same model.

Comparative analysis of the different classes of CSOMs.

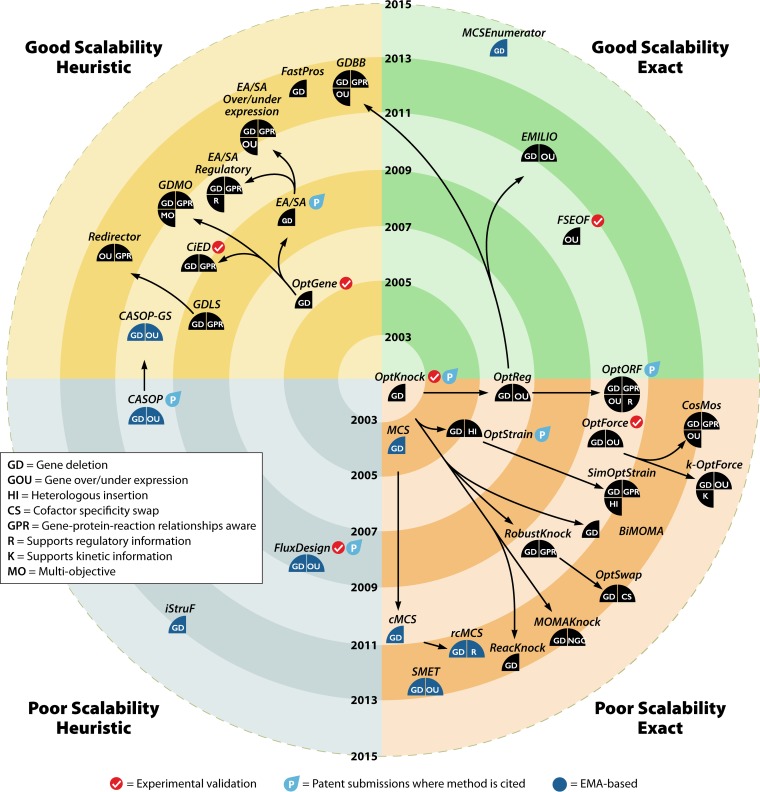
After reviewing all the relevant methods, it is important to provide an overall discussion of their merits and limitations. Figure 6 supports this discussion by organizing the most relevant methods according to several criteria, including scalability, ability to generate exact optimal solutions, and year of development. Also, other aspects related to the optimization task, experimental validation, and patent applications are also represented. Importantly, in Fig. 6, the links represent an attempt to define the methods' phylogeny, i.e., to identify methods that are extensions of or at least are strongly based on previous ones.

FIG 6.

Properties of CSOMs and their relationships. The target plot is sectioned into 4 discrete quadrants regarding scalability and exactness. Methods in the upper region are considered more scalable, while methods in the bottom region are considered less scalable. Similarly, the methods located in the right region of the figure guarantee that, if it exists, the optimal solution for the specified objective function is always found, while the methods in the left region, being inherently heuristic, do not. Other features are indicated on the figure.

One important trend that is clear from Fig. 6, looking at the dates of development, is the growing number of published methods over the last few years. This indicates the relevance of the problem and the growing need for efficient strain optimization methods. Another observable conclusion is the clear trade-off between scalability and the guarantee to reach the global optimal solution. The formulations of most MIP- and EMA-based methods guarantee that, for the implemented objective function, the global optimal solution is always found. To do this, the complexity of the mathematical formulations is usually incremented in such a way that, for larger models or for a higher number of tested perturbations, they usually do not scale well. Some authors addressed these scalability problems by suggesting ways to simplify the problems in MIP-based methods (95, 111) or by computing subsets of the solution space in EMA-based approaches (145). The recent developments from Klamt and coworkers (145) hold the promise to scale up EMA-based strain optimization and boost their utility in real-world applications.

Another approach is the use of metaheuristic CSOMs, which usually scale well with larger models or higher numbers of tested perturbations. However, there is no guarantee that the global optima will be found. When the solution space is large enough, they will usually reach optimal or near-optimal solutions faster than MIP- or EMA-based methods. However, even if they often perform better than these methods in large-scale problems, since further increasing the number of allowed perturbations will cause the solution space to grow exponentially, this might make it hard even for metaheuristic methods to find good solutions.

Metaheuristic methods are also more flexible when it comes to the specification of objective functions, since they are not bounded by linearity. For most MIP-based methods, the introduction of a nonlinear objective function will yield computationally very expensive MINLP problems.

The inclusion of support for gene-based intervention strategies, through GPR information, within the strain design methods is another trend adopted by several authors along the years. Although this increases the complexity of the overall approach, most solutions reached when only reactions are accounted for will be unfeasible once the GPR relationships are scrutinized. Common problems in this context are related to the existence of isoenzymes and, more importantly, to the fact that the same gene might be associated with several reactions, some of which can be essential for biomass growth and others important targets for redirecting the metabolic flux when removed.

One important aspect of the applicability of the discussed methods is how easily they can be accessed and used. Although descriptive formulations for most of the methods are provided in their respective publications, their implementations are generally not available. The methods from the OptGene family (EAs/SAs) and OptKnock can be readily accessed through the OptFlux workbench (146), and all the code is available under a GPL open-source license. The COBRA toolbox (147) also provides open-source implementations for some of these methods, such as OptKnock, OptGene, and GDLS; however, it depends on the commercial software MATLAB (The MathWorks, Inc., USA). Moreover, access to most of the methods from the Klamt group, such as CASOP and cMCS, is provided via CellNetAnalyzer (148), but the source code is not disclosed. Complete information regarding the availability of the discussed methods has been included in the Table S1 in the supplemental material, where the available methods are characterized by a set of features related to their aims, formulations, availability, and validation.

APPLICATIONS AND DISCUSSION

GSMM reconstructions and related querying methods have been employed as guiding tools for the development and optimization of bioprocesses for a wide range of industrially relevant chemicals, such as lycopene (149, 150), malate and succinate (151, 152), l-threonine (153), l-valine (154), and diapolycopendioic acid (155). Other applications include biofuels, such as bioethanol (156) or biohydrogen (157), and drug target discovery (158, 159). Recent reviews discussing the various applications of GSMMs are available (20, 48, 160–162).

Despite the positive results accomplished by employing GSMMs and related querying methods, elaborate strategies such as amplification/attenuation of gene expressions or strategies requiring multiple types of interventions are attainable neither by simple network inspection nor by exhaustive/iterative strategies (163). For these complex and nonintuitive strategies, the use of CSOMs is put forward. Academic researchers have concentrated some efforts on the validation of such methods; however, it is still not clear whether the application of CSOMs in guiding ME applications is already being used by the industry or whether it is limited only to the academic spectrum. Since CSOMs are centerpiece of this review, in the following discussion we focus mainly on applications where at least one of the discussed methods has been employed. To support this discussion, Table 1 provides a summary of the main experimental validations performed for CSOMs results, and Table 2 lists some industrial patents and patent applications referring to the use of at least one CSOM.

TABLE 1.

Experimental validation of CSOMs found in the literature

Organism (model)	Application	Yr	Method(s)	Results	Reference
E. coli (iJR904)	Lactate	2005	OptKnock	25% increase in pta-adhE strains, 73% increase in pta-pfk strains, 55% increase in pta-adhE-pfl-glk strains	164
G. sulfurreducens (iRM588)	Respiratory rate	2008	OptKnock	Higher respiratory rate and increased electron transfer; expected decrease in growth	165
E. coli (iJR904)	Malonyl-CoA	2009	CiED	Specific flavone yields increased by over 600%	121
S. cerevisiae (iFF708)	Sesquiterpene	2009	OptGene, MOMA	85% increase in titer	173
E. coli (EcoMBEL979)	Lycopene	2010	FSEOF	Maximum 3.2-fold increase in lycopene	178
E. coli (iJR904)	NADPH availability	2010	CiED, MOMA	4-fold increase in leucolyanidin, 2-fold increase in catechin	177
S. cerevisiae (iFF708)	Vanillin	2010	OptGene, MOMA, FVA, MMTa	5-fold increase compared to results in reference 174	189
C. glutamicum (ATCC 13032)	l-Lysine	2011	FluxDesign, EMA	Nearly 2-fold yield increase compared to results in reference 179	190
E. coli (iJR904)	1,4-Butanediol	2011	OptKnock	Over 3-fold increase in titer	166
E. coli (iJR904)	Malonyl-CoA	2011	OptForce	4-fold increase in intracellular levels of malonyl-CoA; highest yield of naringenin in a lab-scale fermentation ever achieved	108
E. coli (iAF1260)	Fatty acids	2012	OptForce	Over 20% yield increase among all tested strains	109
B. subtilis (iYO844)	Isobutanol	2012	FluxDesign, EMA	61% of maximum theoretical yield, a 2.3-fold increase	191
S. cerevisiae (iMM904)	2,3-Butanediol	2012	OptKnock	2,3-Butanediol titer of 2.29 g/liter and yield of 0.113 g/g under anaerobic conditions	167
S. cerevisiae (iMM904)	Succinate	2013	OptGene	30-fold improvement in succinate titer and 43-fold improvement in succinate yield compared to the reference strain	175

^aMMT, minimization of metabolite turnover (described in the supplemental material of reference 189).

TABLE 2.

Industrial patent application/grants for microorganisms, products, or processes referencing the use of at least one CSOM

Description	Patent no.	Yr	Assignee	CSOM	Reference
Microorganisms for production of adipic acid and other compounds	U.S. 7,799,545 B2	2010	Genomatica, Inc.	OptKnock	168
Microorganisms for production of 1,4-butanediol, 4-hydroxybutanal, 4-hydroxybutyryl-CoA, putrescine and related compounds, and methods related thereto	U.S. 20,110,229,946 A1	2011	Genomatica, Inc.	OptKnock	169
Primary alcohol-producing organisms	U.S. 7,977,084 B2	2011	Genomatica, Inc.	OptKnock OptStrain	172
Microorganisms and methods for production of 1,4-cyclohexanedimethanol	U.S. 20,120,156,740 A1	2012	Genomatica, Inc.	OptKnock	171
Cytosolic isobutanol pathway localization for production of isobutanol	U.S. 8,232,089 B2	2012	Gevo, Inc.	OptORF	192
Microorganisms for production of 1,4-butanediol and related methods	US8129169 B2	2012	Genomatica, Inc.	OptKnock	170
Methods of producing 6-carbon chemicals via CoA-dependent carbon chain elongation associated with carbon storage	U.S. 20,130,183,728 A1	2013	Invista North America S.A R.L.	OptFlux (EA/SA)	176
Method for prepn of 2,4-dihydroxybutyrate	WO2014009435 A1	2014	Adisseo France S.A.S.	CASOP	180
Microorganism modified for production of 1,3-propanediol	WO2014009432 A2	2014	Institut National des Sciences Appliquées	CASOP	181

Two years after the publication of OptKnock, Fong and coworkers implemented the predicted gene deletions for growth-coupled lactate production in E. coli and performed the first experimental validation of a CSOM (164). They concluded not only that the constructed strains were overproducing lactate but that this production was indeed coupled to growth, according to OptKnock predictions. Notwithstanding this positive confirmation, some discrepancies between the computationally predicted and experimentally observed growth rates were also reported. Since then, OptKnock has been employed in several other efforts, including increasing the respiratory rate in Geobacter sulfurreducens (165) and the production of 1,4-butanediol (166) and 2,3-butanediol (167) in E. coli and S. cerevisiae, respectively. More recently, particularly through the hands of Genomatica, Inc., several patent applications referring to the use of OptKnock have been filed, related to the development of microorganisms for the production of adipic acid (168), 1,4-butanediol (169, 170), and the polyester precursor cyclohexanedimethanol (171). Another patent application mentioning OptKnock and OptStrain in the engineering of primary alcohol producing microbes has also been filed (172).

Subsequently, the usefulness of some heuristic CSOMs was also gradually asserted. Asadollahi and coworkers used OptGene to find S. cerevisiae sesquiterpene-producing mutants with an 85% increase in titer (173). Here, the flexibility of the decoupled bilevel heuristics became evident, since the authors employed MOMA as the phenotype simulation method. A year later, Brochado and colleagues revisited S. cerevisiae, this time for the overproduction of vanillin, using OptGene as the strain design method, which resulted in a 5-fold increase compared to previously reported production (189). Discrepancies between the predicted results and the batch cultivations were attributed to the lack of kinetic and regulatory information, reinforcing the need to invest in the integration of such information with GSMMs and in the development of simulation and optimization methods that take this information into account. More recently, Otero and coworkers employed OptGene in the design of an S. cerevisiae strain which improved succinate yield on biomass by 43-fold in comparison with the reference strain (175). Moreover, in 2013, Invista (Invista North America S.A.R.L. USA) filed patent applications referring to the use of OptFlux (146), whose implemented strain optimization methods are direct descendants of OptGene, describing a method for producing 6-carbon chemicals (176).

Other heuristic approaches were also experimentally validated by Fowler and coworkers for the overproduction of malonyl-CoA (121) and by Chemler and colleagues (177) for the increased availability of NADPH, both in E. coli. The work of Fowler et al. culminated in flavone yields increased by over 600%, while that of Chemler et al. translated into a 4-fold increase in leucocyanidin and a 2-fold increase in catechin.

Naturally, validations of gene deletions suggested by CSOMs were the first to be performed, and they were indeed successful to a certain degree. However, other, more elaborate strategies are not so easy to attain. An obvious example is the identification of gene amplification/attenuation targets, which are not necessarily reflected by an increase in the metabolic flux, due to the complexity of the regulatory machinery. Despite the efforts directed to this subject, quantitative predictions of the flux distribution following this type of intervention are still in their infancy. OptReg was specifically designed for this purpose but has never been experimentally validated.

In fact, the first validation of a method suggesting over- or underexpression of genes was performed by Choi et al. for flux scanning based on enforced objective flux (FSEOF) (178), revisiting lycopene overproduction in E. coli. The FSEOF procedure consists of changing the objective function of the classic biomass maximization FBA problem by considering an additional constraint enforcing the production of the desired target. The iterative procedure progressively increases the enforced minimum value of the product while scanning the remaining flux distribution for relevant flux changes (relative to the wild type). The most commonly changing fluxes are considered preferential targets for manipulation. The best strain achieved in this work resulted in a 3.2-fold lycopene increase in comparison with that of the control strain and a titer slightly in excess of that reported by Alper and coworkers (150).

Another such method is OptForce, which was promptly validated in E. coli for the production of malonyl-CoA (108). OptForce application was translated into a 4-fold increase in intracellular levels of malonyl-CoA and the highest yield of naringenin in a lab-scale fermentation reported. OptForce was also successfully applied in the E. coli overproduction of fatty acids (109), with an overall 20% increase among all the strains.

The last class of methods discussed in this review, EMA-based CSOMs, has only one member for which experimental validation was performed. FluxDesign was validated first for the production of l-lysine in C. glutamicum, where a 2-fold increase in yield was achieved in comparison with an existing strain (179), and later for the production of isobutanol, where a strain operating at 61% of the maximum theoretical yield was engineered.

Although no academic validation has been performed for CASOP, it has recently been cited in a patent application by Adisseo (Adisseo France S.A.S., France) describing a method for the preparation of 2,4-dihydroxubutyrate (180) and another by the Institut National Des Sciences Appliquées (France) for the engineering of a 1,3-propanediol-producing microorganism (181).

Until recently, EMA-based approaches were limited to small to medium networks, which forced its application to be subjected to a biased selection process for the most promising pathway(s), which ultimately hinders the holistic vision characteristic of systems biology applications.

Overall, however, and despite these successful in vivo applications, the obtained improvements in yields, productivities, and titers are still far from the ones obtained with nonrational traditional approaches such as random mutagenesis. In fact, as an illustrative example, over 1,000-fold increase in the amount of penicillin produced in Fleming's original culture of Penicillium chrysogenum by the use of X rays, UV rays, or other mutagens since the 1950s has been reported (182). Although this time span is not compatible with the needs of modern biotechnology, this scale of improvement is clearly currently unattainable with rational methods.

One of the reasons for this is clearly the lack of relevant information in the models used, but it is also difficult to assess where additional developments should be focused, i.e., whether in the development of better models, in simulation methods, or in optimization tools, since most validation efforts are not exploited in sufficient detail. For example, there is a clear lack of studies that include more than one round of in silico design in in vivo implementation and where advanced omics data-based tools are used to characterize the developed strains, feeding and improving the in silico predictions. In the future, studies focusing on characterizing in detail the strains constructed from rational approaches, reporting failed efforts and several cycles of intervention, are necessary to assess where the main bottlenecks are. In fact, since most of the few reported validation efforts have been associated with specific CSOMs, which would be the final layer of an in silico approach, it is often impossible to decouple the effects of model predictions from the CSOM results themselves. More studies that would allow separation of the validation of GSMMs, simulation tools, and CSOMs are thus needed. To mention only an extreme example, the validation of simulation methods such as FBA, MOMA, or ROOM on a large scale has never been performed apart from the examples used when the methods have been developed or improved (52, 53, 57), a gap attributable in part to the scarcity of flux distribution experimental data.

Other studies that are lacking include the systematic utilization of the vast amount of information on strains developed using nonrational approaches to understand if the existing models/simulation/optimization tools allow reproducing the successful approaches and what can be learned from those strains.

In summary, although improvements are clearly needed in the development of novel CSOM methods that were very scarce until recently, it is probably also important to focus research efforts on the experimental validation of in silico approaches to foster the adoption of rational tools in industrial biotechnology.

CONCLUDING REMARKS

The shift from traditional chemical synthesis processes to biotechnological ones holds the promise to reshape the industrial landscape in the 21st century. Essentially driven by energy security and climate changes, the road toward a bio-based economy still faces several barriers. The investment in high-risk research-and-development infrastructure to support it and guarantees of a steady and controlled supply of raw materials (mostly agricultural products or by-products) are among the most sensitive issues to be addressed. Another barrier is the public perception of some biotechnologies, such as the use of genetically modified microorganisms (GMOs) in agriculture and food processing. Moreover, the use of farmable land for nonfood crops in a growing world population raises ethical concerns that must be properly addressed (183). Current worldwide revenue estimates for biotechnology-derived goods reach around EUR 60 billion, while some predictions for 2030 place this value at nearly EUR 300 billion (183). The adoption of these knowledge-based approaches is dependent on global policies supporting the improvement, validation, and scaling up of these technologies, reducing their risk and making them more attractive to the industry. In fact, both the United States, with the National Bioeconomy Blueprint (184), and Europe, with the Knowledge-Based Bio-Economy (KBBE) programs (185), are setting clear objectives and allocating public resources for these matters.

While the development and validation of rational approaches focused on the development of microorganisms for the production of biofuels and other bio-based chemicals are evolving steadily, the same cannot be said regarding agricultural efforts. A clear indicator of this gap is the relative scarcity of GSMMs in the plant kingdom, with reconstructions for only four higher plants available (186). The rational engineering of plants for both food crops and biomass (for other purposes, such as biofuels) will require a stronger investment at both the economic and at policy-making levels.

In the various research fronts toward a bio-based economy, the development of reliable GSMMs, robust phenotype prediction methods, and efficient strain optimization algorithms will increasingly become more relevant. GSMMs and phenotype prediction methods are already used to some extent to guide and evaluate rational engineering efforts (187), although, as mentioned above, further validation efforts are necessary on both fronts.

Specific limitations regarding the scalability of exact strain optimization methods, such as the ones supported by MIP-based or EMA-based implementations, are gradually being dealt with or circumvented by various researchers. More recently, these limitations are becoming more tractable, and a convergence between EMA-based and MIP-based approaches is to be expected. In fact, Hädicke and Klamt describe how both the OptKnock and RobustKnock methods can be reformulated as corresponding cMCS problems (131).

Another limitation affecting the precision and feasibility of the metabolic engineering strategies is intimately connected with the lack of kinetic and regulatory information available and considered in the discussed approaches. The recently proposed k-OptForce from Chowdhury and coworkers (113) is a step in this direction. While acquiring kinetic data will remain a difficult problem, already well-known phenomena and parameters can be exploited by this approach in tandem with the more commonly used stoichiometric representations of metabolism, improving the predictive capabilities of previous methods.

While improvements in scalability of MIP-based and EMA-based methods are gradually being made, these authors believe that the space for metaheuristic methods for strain optimization is not exhausted. The intrinsic simplicity, the flexibility allowed in the definition of (multi)objective functions, and the lack of complex implementation constraints allow these methods to be easily adapted to different tasks, as well as to efficiently inspect the search space, thus providing quick and useful solutions to problems of various dimensions and addressing distinct design aims.

As stated above, a large panoply of methods proposing the integration of omics data within constraint-based metabolic models and phenotype simulation methods have been proposed. However, their results are still not convincing (62), and probably for that reason the number of CSOMs exploring these capabilities is still scarce, leaving room for the emergence of new branches from previously proposed CSOMs or even entirely new ones.

In this review, we have presented a highlight of the main computational strain optimization methods. These methods were segmented into three distinct categories, and their functionalities and main applications were analyzed. As the number of genome-scale reconstructions increases each year and the complexity of these models is able to capture more and more information (188), new methods capable of exploring this information to generate new knowledge are expected to arise, holding the promise of finally bridging the gap between the academic-grade efforts and the industry-grade standards required for a full adoption of CSOMs as a standard tool for guiding metabolic engineering efforts. Nevertheless, this adoption is possible only if underlying tools such as modeling and simulation are also further developed and validated.