Race, Ethnicity, and Exposure to Alcohol Outlets

Abstract

Objective:

Prior studies suggest that Black and Hispanic minority populations are exposed to greater concentrations of alcohol outlets, potentially contributing to health disparities between these populations and the White majority. We tested the alternative hypothesis that urban economic systems cause outlets to concentrate in low-income areas and, controlling for these effects, lower demand among minority populations leads to fewer outlets.

Method:

Market potential for alcohol sales, a surrogate for demand, was estimated from survey and census data across census block groups for 50 California cities. Hierarchical Bayesian conditional autoregressive Poisson models then estimated relationships between observed geographic distributions of outlets and the market potential for alcohol, income, population size, and racial and ethnic composition.

Results:

Market potentials were significantly smaller among lower income Black, Hispanic, and Asian populations. Block groups with greater market potential and lower income had greater concentrations of outlets. When we controlled for these effects, the racial and ethnic group composition of block groups was mostly unrelated to outlet concentrations.

Conclusions:

Health disparities related to exposure to alcohol outlets are primarily driven by distributions of income and population density across neighborhoods.

Previous studies have found that areas in the United States with higher proportions of Black and Hispanic residents have greater concentrations of alcohol outlets (Berke et al., 2010; Gorman & Speer, 1997; LaVeist & Wallace Jr., 2000; Romley et al., 2007). This observation is highly relevant to public health because there is considerable evidence that problems such as intentional injuries (Cunradi et al., 2012; Gruenewald & Remer, 2006; Livingston, 2008, 2011; Mair et al., 2013; Toomey et al., 2012), road trauma (McMillan et al., 2007; Ponicki et al., 2013), and child abuse and neglect (Freisthler & Weiss, 2008; Freisthler et al., 2007) occur more frequently in areas with more alcohol outlets (Campbell et al., 2009). Exposure to outlets may therefore contribute to health disparities between these racial and ethnic minorities and the White majority population and may be an appropriate target for preventive intervention (Romley et al., 2007). However, these studies contain a number of key limitations, and theory regarding the spatial dynamics of retail markets predicts that Black and Hispanic groups will in fact have fewer outlets near their residences because these populations consume less alcohol. In that context, this study examined the claim that excess exposure to alcohol outlets is an issue of environmental justice for racial and ethnic minorities (Berke et al., 2010; LaVeist & Wallace Jr., 2000; Romley et al., 2007).

The guiding theory for the current study suggests that alcohol outlets are geographically distributed according to the dynamic processes that shape most retail markets (Morrison et al., 2015). From this perspective, the two primary determinants of outlet location are likely to be alcohol demand and income. Seeking to minimize convenience costs for potential consumers, outlets will locate in and near areas with greater demand (Aoyama et al., 2011). Population density, which varies by orders of magnitude between areas, accounts for most of the geographic variance in demand. To a lesser extent, income is also related to demand because lower income populations drink less alcohol than higher income populations (Pollack et al., 2005); thus, competition for market share will attract outlets to areas with wealthier residents. However, outlets will also be excluded from higher income areas because of greater land and structure rents (Aoyama et al., 2011; Hanson, 2005; Harris, 1954) and because higher income populations are better resourced than lower income populations to oppose undesirable land uses (DiPasquale & Wheaton, 1992). Greater concentrations of outlets will therefore be found in areas with greater population density and lower average income and will be located near higher income areas. We have previously demonstrated that the geographic distribution of outlets is consistent with theory regarding these economic geographic processes in both urban (Morrison et al., 2015) and rural (Morrison, 2015) areas of Australia. Regarding racial and ethnic minority populations in the United States, it is clear that Black and Hispanic individuals are more likely to abstain from alcohol than White individuals and less likely to drink heavily (Keyes et al., 2012). They also spend a smaller proportion of their income on alcohol and spend less money overall on alcohol (Bureau of Labor Statistics, 2014). The theory therefore predicts that there will be fewer outlets in areas with greater proportions of Black and Hispanic residents because of reduced alcohol demand.

Berke et al. (2010) conducted the largest study to date examining racial and ethnic correlates of outlet density. Using North American Industry Classification System (NAICS) business lists, the authors spatially smoothed the combined density of liquor stores, taverns and bars, grocery stores, gas stations, and convenience stores (representing potential outlets) across the surface of the continental United States and then constructed linear regression models for outlets per population within census tracts. Greater proportions of Black, Hispanic, and impoverished residents were independently associated with greater outlet density. Similarly, Romley et al. (2007) combined NAICS codes representing bars and off-premise outlets within urban zip codes in the United States, comparing mean outlet densities per roadway mile and per population within income and age strata. Zip codes with more Black and Hispanic residents also had greater concentrations of outlets in these data. Earlier studies by LaVeist and Wallace Jr. (2000) and Gorman and Speer (1997) examined counts of licensed off-premise outlets within 194 census tracts in Baltimore, MD, and 21 census tracts in Newark, NJ. Both found greater outlet densities in areas of these cities with lower income and more racial and ethnic minority residents, although Gorman and Speer noted some higher income areas also had more outlets.

These previous studies were conducted using the relatively large spatial units of census tracts (Berke et al., 2010; Gorman & Speer, 1997; LaVeist & Wallace Jr., 2000) or zip codes (Romley et al., 2007) in single-level models. However, the spatial dynamics of alcohol markets likely operate at multiple scales, possibly including smaller spatial scales than these units of analysis. We have previously demonstrated in Australian data that the spatial dynamics of alcohol markets are better observed in smaller spatial units (analogous to U.S. census block groups) than larger spatial units (analogous to U.S. census tracts); therefore, results of these previous studies may be affected by aggregation bias (Morrison et al., 2015). In addition, business lists such as NAICS do not account for regional variation in regulatory policy, a potential source of measurement bias (for example, alcohol sales are permitted in gas stations in Missouri but not Delaware [Mo. Rev. Stat. § 311; Del. Code tit. 4 § 516]). Also, none of the studies accounted for spatial autocorrelation, a potential source of type I error (Waller & Gotway, 2004).

The current study examined relationships between the density of alcohol outlets and the racial and ethnic compositions of census block groups in 50 mid-sized California cities. By calculating outlet density using real license data from the relevant authority (the California Department of Alcoholic Beverage Control) and using small spatial units in multilevel models with appropriate controls for spatial autocorrelation, we addressed the key limitations of prior studies in this field. With this construction, we first tested the general premise that outlet distribution in the 50 cities was spatially related to demand and income. We estimated demand using an approach we have previously used to approximate total alcohol consumption within areas of Melbourne, Australia (Morrison et al., 2015), and total marijuana consumption within areas of California (Morrison et al., 2014). These approximations of “market potentials” are the best available estimates for demand at high spatial resolutions given that real consumption data are impractical to collect (Hanson, 2005). We then tested the specific hypothesis that areas with greater concentrations of Black and Hispanic residents would have fewer outlets, and areas with greater concentrations of White residents would have more outlets. Understanding which populations are exposed to greater outlet concentrations and the mechanisms by which these exposures might arise is crucial for formulating effective interventions to reduce health disparities (Krieger, 2001).

Method

We conducted this study in stages. First, we used person-level data from a general population survey to assess the individual demographic correlates of alcohol consumption. Combining the coefficients from these regression analyses with area demographic data produced estimates of the market potential for alcohol within census block groups. Second, we assessed associations between outlet density and market potential and income in multilevel Bayesian spatial models. Separating the market potential estimate into its component demographic parts then enabled explicit assessment of associations between outlet density and racial and ethnic group composition.

Estimating market potential

Sample.

Person-level data were from a general population telephone survey of 8,790 adults ages 18 and older conducted between January 2009 and March 2010 in households across 50 cities in California (Gruenewald et al., 2014). The cities were randomly selected from among the 138 cities in the state with populations between 50,000 and 500,000, with each city separated by at least two unselected city or county areas (reducing spatial autocorrelation between sample units). Respondents were selected for a computer-assisted telephone interview using a list-assisted stratified random sample (Brick et al., 1995; Kempf & Remington, 2007; Tucker et al., 2002). The refusal rate for the survey was 45% of those contacted, and the response rate was 48%, calculated using standard definitions of the American Association of Public Opinion Research (2011).

Variables.

We developed two dependent variables from the survey data: a dichotomous measure of alcohol use over the past 12 months (M = 53.1% drinkers, SD = 49.9%), and the total volume consumed by every drinker (measured in total drinks) over the past 28 days (M = 11.14 drinks, SD = 23.06). We calculated total volume using self-reported frequencies of drinking one, two, three, six, or nine or more drinks over the past 4 weeks and the maximum drinks consumed on any occasion. Respondents who reported no alcohol consumption in the last month were asked about consumption over the last year, which we then rescaled to a 28-day equivalent. The resultant measure of adult drinking patterns has previously demonstrated good reliability and validity (test–retest reliabilities, .65 < r < .85; Gruenewald & Johnson, 2006).

To enable calculation of alcohol market potential at the census block group level, we selected independent measures from the person-level survey that best matched core census measures. These were the identity of each city, gender, educational level (less than high school, high school graduate, college graduate), number of adults in each household, age groups (a continuous measure categorized into 20–24, 25–29, 30–39, 40–49, 50–59, 60–69, and 70 years or older age groups), and racial (Native American, Asian, Black, Pacific Islander, and White) and ethnic (Hispanic) group membership. The survey-based measure of household income used categories somewhat different from those of the census. Thus, the survey-based measure was recoded to interval form using the central value for each group (e.g., income from $60,000 to $69,999 was recoded to $65,000).

Statistical analysis.

We examined the demographic predictors of the two dependent measures from the individual survey in two separate regression models. First, a fixed-effects logit model related a dichotomous measure of alcohol use to all independent measures. Second, a censored regression (Tobit) model related total volumes consumed to all independent measures among the 4,770 drinkers (Tobin, 1958). Low telephone survey response rates and potential nonresponse bias are now common problems in social science surveys of this kind (Kempf & Remington, 2007). Both models partially corrected for nonresponse bias using poststratification survey weights constructed in reference to the population of the 138 cities (based on population size of persons ages 18 and older classified by gender, age groups, and racial and ethnic group membership). Demographic characteristics reflected those of the 50 cities, with 90% of survey weights falling between 0.90 and 1.10.

Market potentials were estimated as follows: The demographic data considered were 2009 intercensal estimates of population size and proportions of the resident population within the aforementioned categories of race and ethnicity, highest educational achievement, employment status, median household income, and age (GeoLytics, 2010). We first estimated the contribution of these demographic characteristics to the total alcohol consumption in each block group by multiplying the point estimates from the censored regression model and the proportion of residents from each block group with the corresponding demographic characteristics. The sum of these values, the intercept from the Tobit model, and the point estimate of the city random effect produced an estimate of annual per capita alcohol consumption for current drinkers within each block group. The fixed-effects logit model provided an estimate of the proportion of block group residents who were current drinkers. Finally, the total alcohol consumption in block groups was calculated as the product of the block group population, the proportion of current drinkers, and the block-group-specific estimated per capita consumption for current drinkers.

Estimating exposure to outlets

Sample.

The unit of analysis for the spatial component of this study was block groups from the 2000 U.S. census nested within the 50 cities. We found in a prior study that marijuana dispensaries tended to be located just outside the limits of these cities (Morrison et al., 2014). This may also be the case for alcohol, so we included all block groups within a 3-mile buffer of the city boundaries. The final spatial sample was 8,877 block groups, including 151 located in the buffer regions of two cities.

Variables.

The dependent variable was counts of alcohol outlets within the included block groups. We geocoded all venues licensed to sell alcohol based on 2009 data from the California Department of Alcoholic Beverage Control and then calculated counts of bars (license types 23, 40, 42, 48, 61, and 75), restaurants (41 and 47), and off-premise outlets (20 and 21).

Independent variables were market potentials and demographic characteristics (population, median household income, racial and ethnic composition) calculated at three geographic levels: within local block groups, aggregated within lagged block groups (i.e., adjacent block groups that share a border with the local block group), and aggregated within cities. We aggregated market potential and total population by taking the sum, the racial and ethnic groups as proportions of the total population, and income as the population-weighted mean.

Statistical analysis.

To assess univariate relationships, we constructed a matrix of partial correlations between outlet densities (i.e., counts denominated by land area) and the characteristics of census block groups. The univariate correlations effectively included a fixed effect to control for variation among cities.

We then constructed hierarchical Bayesian conditional autoregressive Poisson models with random effects for cities predicting outlet counts within census block groups. Outcomes were counts of all outlets combined (Model 1) and then separated into bars (Model 2), restaurants (Model 3), and off-premise outlets (Model 4). There were two variants of each of the four models. The first (a) related counts of outlets to income and the market potential for alcohol at the three geographic scales (local, lagged, and city). The second (b) separated the market potential estimate into some of its component parts: population, income, and the proportion of Black, Hispanic, and White residents. We were not able to include any additional demographic characteristics because of collinearity. The proportion of Asian and other ethnicity residents was omitted as a comparison group. Block groups are not of uniform size; therefore, all models were adjusted for the logged area, with the effect that continuous and interval items (e.g., outlets) can be interpreted as density measures (Hilbe, 2011).

The eight models were fitted to the data using WinBUGS Version 4.3.1 (Lunn et al., 2000). After at least a 20,000 iteration burn-in during which all models had converged, we sampled 50,000 iterations to obtain parameter estimates. Two Markov chains produced a median estimate and a 95% credible interval (CI) that can be interpreted similar to the point estimate for the incidence rate ratio (IRR) and 95% confidence intervals in standard regression. Relationships are well supported where CIs do not include the null value (IRR = 1.00). This Bayesian procedure is appropriate for sparse data sets (i.e., with a large number of zeros), such as we used here (Waller & Gotway, 2004). Model errors were partitioned into a conditional autoregressive (CAR) spatial random effect and a nonspatial noise term. The CAR random effect accounted for spatially autocorrelated errors (Waller & Gotway, 2004) and controlled for overdispersion of the dependent measure (Lord et al., 2005).

Results

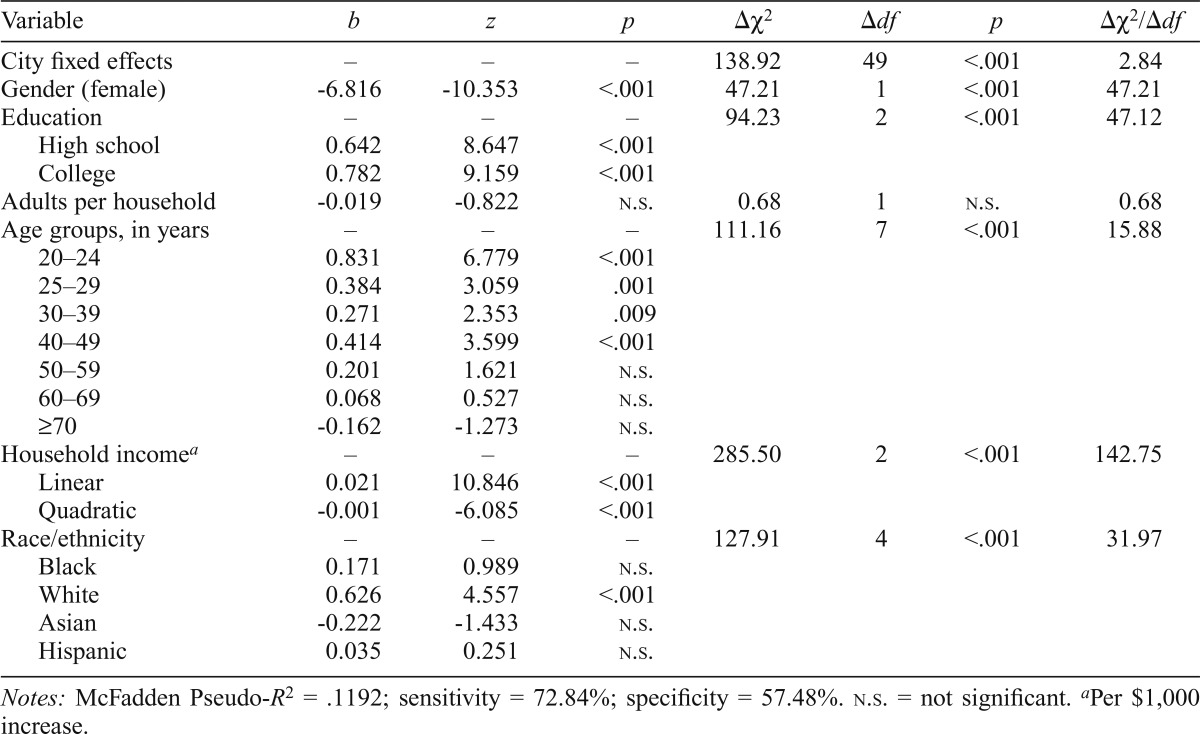
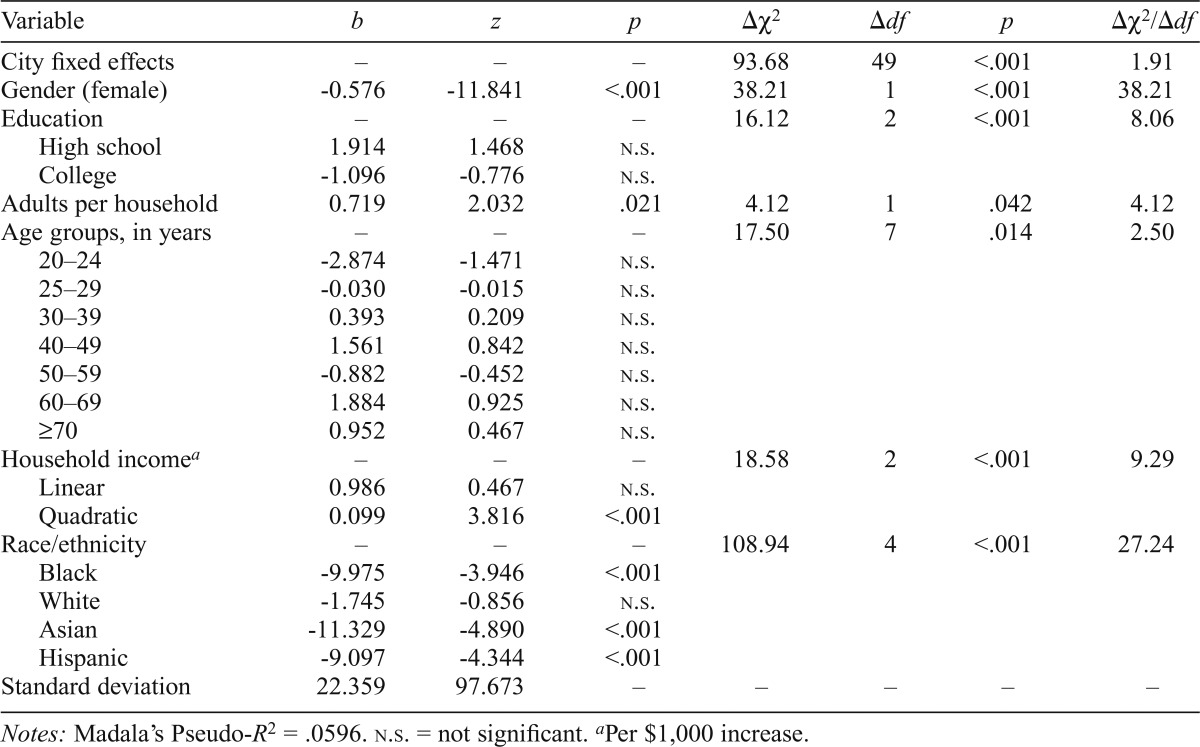
From the survey data, the logit model indicated that White respondents were significantly more likely to have consumed alcohol in the last year (b = 0.63; z = 4.56, p < .001); there was no detectable difference for Black, Hispanic, and Asian respondents (Table 1). Similarly, the censored regression model showed that Black (b = -9.98; z = -3.95, p < .001), Hispanic (b = -9.10; z = -4.34, p < .001), and Asian drinkers (b = -11.33; z = -4.89, p < .001) consumed significantly fewer drinks in the past 28 days (Table 2). Overall, the measures of household income, gender, education, and racial and ethnic group composition were the most substantive correlates in both analyses (measured in terms of χ²/df).

Table 1.

Logistic regression analysis of past year drinking status (use vs. abstention) among individual survey respondents (n = 8,790)

Variable	b	z	p	Δχ2	Δdf	p	Δχ2/Δdf
City fixed effects	–	–	–	138.92	49	<.001	2.84
Gender (female)	-6.816	-10.353	<.001	47.21	1	<.001	47.21
Education	–	–	–	94.23	2	<.001	47.12
High school	0.642	8.647	<.001
College	0.782	9.159	<.001
Adults per household	-0.019	-0.822	n.s.	0.68	1	n.s.	0.68
Age groups, in years	–	–	–	111.16	7	<.001	15.88
20–24	0.831	6.779	<.001
25–29	0.384	3.059	.001
30–39	0.271	2.353	.009
40–49	0.414	3.599	<.001
50–59	0.201	1.621	n.s.
60–69	0.068	0.527	n.s.
≥70	-0.162	-1.273	n.s.
Household incomea	–	–	–	285.50	2	<.001	142.75
Linear	0.021	10.846	<.001
Quadratic	-0.001	-6.085	<.001
Race/ethnicity	–	–	–	127.91	4	<.001	31.97
Black	0.171	0.989	n.s.
White	0.626	4.557	<.001
Asian	-0.222	-1.433	n.s.
Hispanic	0.035	0.251	n.s.

Notes: McFadden Pseudo-R² = .1192; sensitivity = 72.84%; specificity = 57.48%. n.s. = not significant.

^aPer $1,000 increase.

Table 2.

Censored regression analysis of drinking volume consumed (past 28 days) among current drinkers (n = 4,770)

Variable	b	z	p	Δχ2	Δdf	p	Δχ2/Δdf
City fixed effects	−	−	−	93.68	49	<.001	1.91
Gender (female)	-0.576	-11.841	<.001	38.21	1	<.001	38.21
Education	−	−	−	16.12	2	<.001	8.06
High school	1.914	1.468	n.s.
College	-1.096	-0.776	n.s.
Adults per household	0.719	2.032	.021	4.12	1	.042	4.12
Age groups, in years	−	−	−	17.50	7	.014	2.50
20–24	-2.874	-1.471	n.s.
25–29	-0.030	-0.015	n.s.
30–39	0.393	0.209	n.s.
40–49	1.561	0.842	n.s.
50–59	-0.882	-0.452	n.s.
60–69	1.884	0.925	n.s.
≥70	0.952	0.467	n.s.
Household incomea	−	−	−	18.58	2	<.001	9.29
Linear	0.986	0.467	n.s.
Quadratic	0.099	3.816	<.001
Race/ethnicity	−	−	−	108.94	4	<.001	27.24
Black	-9.975	-3.946	<.001
White	-1.745	-0.856	n.s.
Asian	-11.329	-4.890	<.001
Hispanic	-9.097	-4.344	<.001
Standard deviation	22.359	97.673	−	−	−	−	−

Notes: Madala’s Pseudo-R² = .0596. n.s. = not significant.

^aPer $1,000 increase.

From the spatial data, after we accounted for variance between cities, outlet density was negatively correlated with the median household income in areas (r = -.236). Correlations were negative for the proportion of White (r = -.088) and Black (r = -.049) residents, and positive for the proportion of Hispanic residents (r = .120). Figure 1 shows these univariate relationships in one of the 50 cities, Gardena. The central and northwestern areas of the city with the greatest outlet density also have the greatest population density and more Hispanic residents, and generally have lower income, fewer White residents, and fewer Black residents.

Figure 1.

Geographic distribution of alcohol outlets and major demographic predictors of demand (population density, income, and racial and ethnic composition) in Gardena, California. Darker regions represent higher values, and lighter regions represent lower values.

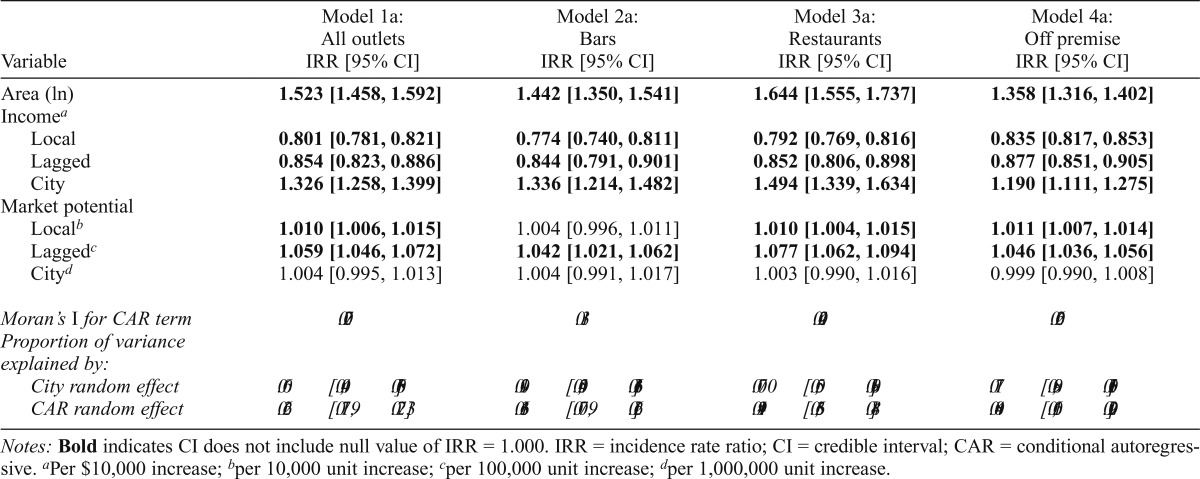
The results of the Bayesian spatial models are presented in Tables 3 and 4. Model 1a (Table 3) shows that market potential in local and lagged block groups was positively related to the number of all outlets. Specifically, a 10,000 unit increase in the estimated number of drinks consumed by block group residents (i.e., an 11.0% increase compared with the study area average) was associated with 1.0% more outlets within that block group (IRR= 1.010, 95% CI [1.006, 1.015]). Greater income in local and lagged block groups was associated with fewer outlets, whereas greater average income in the city in which the block group was located predicted more outlets. Models 2a, 3a, and 4a show similar relationships for bars, restaurants, and off-premise outlets, except that the local market potential did not predict counts of bars.

Table 3.

Hierarchical Bayesian Poisson models for counts of alcohol outlets in census block groups (n = 8,877) nested in 50 cities, with random effects for cities

Variable	Model 1a: All outlets IRR [95% CI]	Model 2a: Bars IRR [95% CI]	Model 3a: Restaurants IRR [95% CI]	Model 4a: Off premise IRR [95% CI]
Area (ln) Incomea	1.523 [1.458, 1.592]	1.442 [1.350, 1.541]	1.644 [1.555, 1.737]	1.358 [1.316, 1.402]
Local	0.801 [0.781, 0.821]	0.774 [0.740, 0.811]	0.792 [0.769, 0.816]	0.835 [0.817, 0.853]
Lagged	0.854 [0.823, 0.886]	0.844 [0.791, 0.901]	0.852 [0.806, 0.898]	0.877 [0.851, 0.905]
City	1.326 [1.258, 1.399]	1.336 [1.214, 1.482]	1.494 [1.339, 1.634]	1.190 [1.111, 1.275]
Market potential
Localb	1.010 [1.006, 1.015]	1.004 [0.996, 1.011]	1.010 [1.004, 1.015]	1.011 [1.007, 1.014]
Laggedc	1.059 [1.046, 1.072]	1.042 [1.021, 1.062]	1.077 [1.062, 1.094]	1.046 [1.036, 1.056]
Cityd	1.004 [0.995, 1.013]	1.004 [0.991, 1.017]	1.003 [0.990, 1.016]	0.999 [0.990, 1.008]
Moranʼs I for CAR term Proportion of variance explained by:	0.207	0.311	0.240	0.260
City random effect	0.060 [0.040, 0.086]	0.091 [0.054, 0.136]	0.070 [0.055, 0.089]	0.117 [0.089, 0.150]
CAR random effect	0.226 [0.179, 0.273]	0.163 [0.079, 0.266]	0.419 [0.356, 0.488]	0.048 [0.016, 0.092]

Notes: Bold indicates CI does not include null value of IRR = 1.000. IRR = incidence rate ratio; CI = credible interval; CAR = conditional autoregressive.

^aPer $10,000 increase;

^bper 10,000 unit increase;

^cper 100,000 unit increase;

^dper 1,000,000 unit increase.

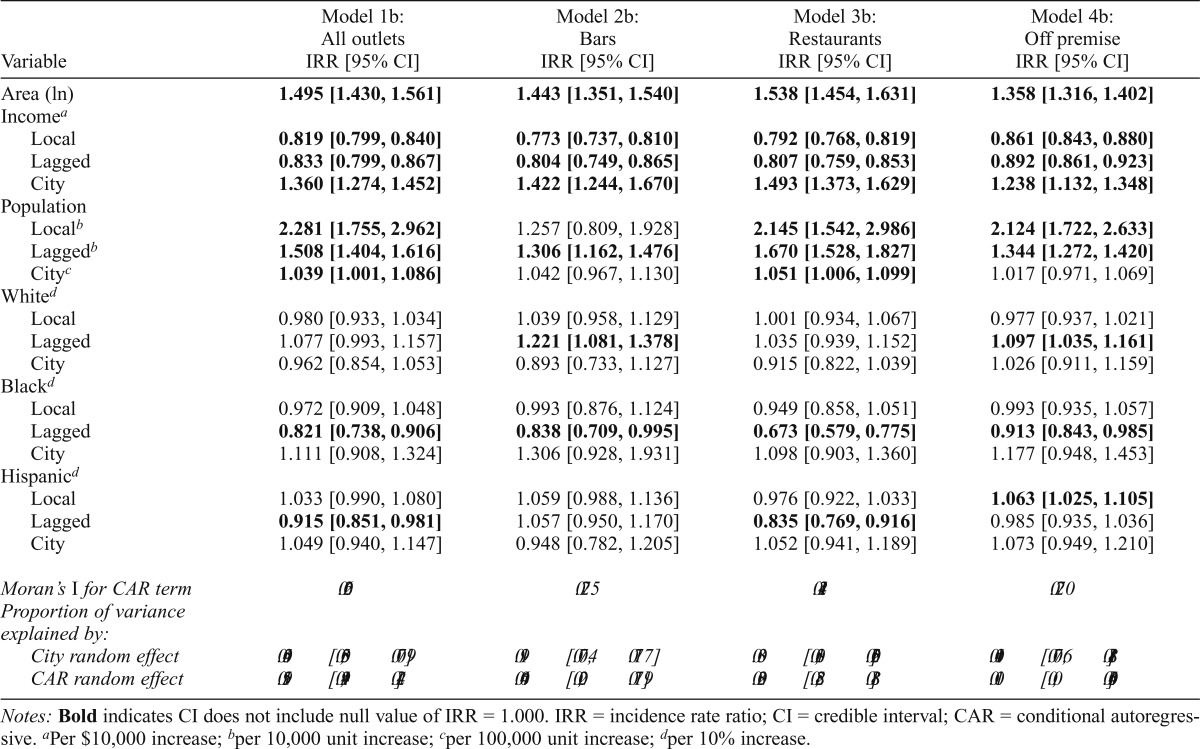
Table 4.

Hierarchical Bayesian Poisson models for counts of alcohol outlets in census block groups (n = 8,877) nested in 50 cities, with random effects for cities

Variable	Model 1b: All outlets IRR [95% CI]	Model 2b: Bars IRR [95% CI]	Model 3b: Restaurants IRR [95% CI]	Model 4b: Off premise IRR [95% CI]
Area (ln)	1.495 [1.430, 1.561]	1.443 [1.351, 1.540]	1.538 [1.454, 1.631]	1.358 [1.316, 1.402]
Incomea
Local	0.819 [0.799, 0.840]	0.773 [0.737, 0.810]	0.792 [0.768, 0.819]	0.861 [0.843, 0.880]
Lagged	0.833 [0.799, 0.867]	0.804 [0.749, 0.865]	0.807 [0.759, 0.853]	0.892 [0.861, 0.923]
City	1.360 [1.274, 1.452]	1.422 [1.244, 1.670]	1.493 [1.373, 1.629]	1.238 [1.132, 1.348]
Population
Localb	2.281 [1.755, 2.962]	1.257 [0.809, 1.928]	2.145 [1.542, 2.986]	2.124 [1.722, 2.633]
Laggedb	1.508 [1.404, 1.616]	1.306 [1.162, 1.476]	1.670 [1.528, 1.827]	1.344 [1.272, 1.420]
Cityc	1.039 [1.001, 1.086]	1.042 [0.967, 1.130]	1.051 [1.006, 1.099]	1.017 [0.971, 1.069]
Whited
Local	0.980 [0.933, 1.034]	1.039 [0.958, 1.129]	1.001 [0.934, 1.067]	0.977 [0.937, 1.021]
Lagged	1.077 [0.993, 1.157]	1.221 [1.081, 1.378]	1.035 [0.939, 1.152]	1.097 [1.035, 1.161]
City	0.962 [0.854, 1.053]	0.893 [0.733, 1.127]	0.915 [0.822, 1.039]	1.026 [0.911, 1.159]
Blackd
Local	0.972 [0.909, 1.048]	0.993 [0.876, 1.124]	0.949 [0.858, 1.051]	0.993 [0.935, 1.057]
Lagged	0.821 [0.738, 0.906]	0.838 [0.709, 0.995]	0.673 [0.579, 0.775]	0.913 [0.843, 0.985]
City	1.111 [0.908, 1.324]	1.306 [0.928, 1.931]	1.098 [0.903, 1.360]	1.177 [0.948, 1.453]
Hispanicd
Local	1.033 [0.990, 1.080]	1.059 [0.988, 1.136]	0.976 [0.922, 1.033]	1.063 [1.025, 1.105]
Lagged	0.915 [0.851, 0.981]	1.057 [0.950, 1.170]	0.835 [0.769, 0.916]	0.985 [0.935, 1.036]
City	1.049 [0.940, 1.147]	0.948 [0.782, 1.205]	1.052 [0.941, 1.189]	1.073 [0.949, 1.210]
Moranʼs I for CAR term Proportion of variance explained by:	0.206	0.275	0.214	0.270
City random effect	0.054 [0.035, 0.079]	0.119 [0.074, 0.177]	0.033 [0.018, 0.052]	0.104 [0.076, 0.138]
CAR random effect	0.195 [0.149, 0.242]	0.046 [0.002, 0.179]	0.320 [0.258, 0.383]	0.011 [0.000, 0.054]

Notes: Bold indicates CI does not include null value of IRR = 1.000. IRR = incidence rate ratio; CI = credible interval; CAR = conditional autoregressive.

^aPer $10,000 increase;

^bper 10,000 unit increase;

^cper 100,000 unit increase;

^dper 10% increase.

In Model 1b (Table 4), a 10% greater proportion of Black residents in lagged block groups was associated with 17.9% fewer alcohol outlets (IRR = 0.821, 95% CI [0.738, 0.906]); relationships were not supported at the local and city levels. Likewise, more Hispanic residents in lagged block groups was related to fewer outlets (IRR = 0.915, 95% CI [0.851, 0.981]), but not at the local or city level. Relationships were not supported between overall outlet density and the proportion of White residents in local block groups, lagged block groups, or in cities. Relationships for income and population were substantively similar to the relationships for income and market potential in Model 1a. Separating outlets into bars (Model 2b), restaurants (Model 3b), and off-premise outlets (Model 4b) revealed minor differences for the relationships between outlet density and racial and ethnic groups (e.g., the proportion of White residents in lagged block groups was not related to restaurants but was positively related to bars and off-premise outlets); however, the findings were generally consistent across outlet types.

Discussion

Alcohol-related harms have been reported to occur more frequently in areas with greater concentrations of alcohol outlets (Campbell et al., 2009); therefore, excess exposure to outlets may contribute to health disparities among populations. Evidence from the current study suggests that outlet density is strongly spatially related to lower income, but contrary to prior research (Berke et al., 2010; Gorman & Speer, 1997; LaVeist & Wallace Jr., 2000; Romley et al., 2007), we found no evidence that Black populations were exposed to greater densities of outlets. Hispanic populations appeared to be exposed to greater densities of outlets, but after accounting for income, population density, the multiscale nature of these spatial dynamics, and the spatial structure of the data, an association was only detectable for off-premise outlets. Thus, it appears that exposure to alcohol outlets contributes more substantially to health disparities between higher and lower income populations than between racial and ethnic groups.

As expected (Bureau of Labor Statistics, 2014; Keyes et al., 2012), areas with greater population density, higher income, and more White residents had greater market potential for alcohol. The underlying theory therefore predicts that these areas will also have greater densities of alcohol outlets, except that outlets will be excluded from higher income areas, appearing in lower income areas near higher income areas. Similar to our previous findings from Melbourne, Australia, the exclusionary effects of higher income appear to extend to at least the lagged block groups (Morrison et al., 2015). Here we add that the attractive effect of higher income operates across whole cities.

The expected negative associations for Blacks and Hispanics and positive associations for Whites were observable in lagged but not local block groups. It is here that observations of environmental injustice may be warranted (Romley et al., 2007). Assuming equilibrium between supply and demand, one would expect these relationships to also be observed in local block groups; however, just as higher income populations have greater financial and social resources to oppose undesirable land uses (DiPasquale & Wheaton, 1992), White populations may be better resourced to oppose establishment of the additional outlets that their greater demand attracts. Conversely, Black and Hispanic populations may have fewer resources to exclude outlets. Nevertheless, these drivers appear relatively minor compared with population density and income, the most substantive demographic contributors to demand within areas.

Model specification, spatial scale, and spatial structure may explain the difference between previous statistical epidemiological studies and the current theoretically oriented analysis. By using census block groups, the smallest spatial unit at which the requisite census data are released, and examining relationships at local, lagged, and city levels, we were able to separate the sometimes opposing multiscale effects. Aggregating within larger units (e.g., tracts, zip codes) and specifying only local effects would have averaged the mixed local, lagged, and city-level relationships, likely leading to biased estimates of associations within local units. In addition, Moran coefficients for the CAR random effects were between 0.21 and 0.31, suggesting the spatial component of the model residuals was significantly autocorrelated. Had we not adjusted our models appropriately, the likelihood of a type I error was high.

This study had some key limitations. First, market potential is an imperfect proxy for demand; however, such measures are commonly used in economic geography (Aoyama et al., 2011; Hanson, 2005; Harris, 1954). Taking into account the considerable range of population demographics from one census block group to another across cities, combining variations in the most substantive correlates of overall alcohol consumption (i.e., population density, household income, ethnic group composition) likely produces reasonable approximations of the differences in alcohol demand between spatial units. Nevertheless, an area for future research is the development of market potential estimates that account for other sources of variation between areas beyond the demographic correlates (e.g., due to geographic distributions of very heavy drinkers). Second, we could not assess the endogeneity between supply and demand in these cross-sectional data. Longitudinal analyses would provide better understanding of the dynamic economic and geographic processes that shape alcohol markets. They could also help determine the extent to which our results are affected by the modifiable areal unit problem, although the consistency between these results and those of our previous studies (conducted using different spatial scales in different geographic settings) supports our contention that the findings presented here are not artifacts of spatial unit construction but are attributable to a set of processes common to most retail markets.

Cumulatively, our findings suggest that the spatial distribution of alcohol outlets is consistent with economic geographic theory, with the result that lower income populations are disproportionately exposed to greater densities of outlets. These findings support intervention, such as density limits or the proactive use of planning and zoning ordinances, to address economic health disparities more than racial and ethnic health disparities. This is a crucial distinction which acknowledges that, unchecked, these differential exposures are the inevitable product of spatial retail market dynamics.