Abstract
Qualitative grading of milled rice grains was carried out in this study using a machine vision system combined with some metaheuristic classification approaches. Images of four different classes of milled rice including Low-processed sound grains (LPS), Low-processed broken grains (LPB), High-processed sound grains (HPS), and High-processed broken grains (HPB), representing quality grades of the product, were acquired using a computer vision system. Four different metaheuristic classification techniques including artificial neural networks, support vector machines, decision trees and Bayesian Networks were utilized to classify milled rice samples. Results of validation process indicated that artificial neural network with 12-5*4 topology had the highest classification accuracy (98.72 %). Next, support vector machine with Universal Pearson VII kernel function (98.48 %), decision tree with REP algorithm (97.50 %), and Bayesian Network with Hill Climber search algorithm (96.89 %) had the higher accuracy, respectively. Results presented in this paper can be utilized for developing an efficient system for fully automated classification and sorting of milled rice grains.
Keywords: Rice, Classification, Computer vision, Metaheuristic techniques
Introduction
Rice (Oryza sativa L.) is a primary source of food for energy consumed by almost half of the world population. It is an important source of vitamins, mineral elements and essential amino acids (Sadeghi et al. 2013). Because it is a staple food for serving many generations and many centuries in the world, the need for its production and consumption is increasing day by day. According to the census of Food and Agriculture Organization of the United Nations (FAO), world’s total rice production has been increased from 570 million tonnes in 2002 to 720 million tonnes in 2012.
In order to obtain white rice from paddy, from harvesting to final production, several operations such as threshing, handling, de-husking, milling and whitening are carried out on rice grains. If the adjustment of implements, used in the various mentioned operations, be not properly carried out, excessive losses in the rice final crop may occur (Zareiforoush et al. 2010a). Generally in rice mills, due to unavailability of continuous on-line measurement methods, quality grade of product is monitored visually by experienced operators at 1–2 h intervals (Yadav and Jindal 2007). This means that the operator, based on his experience and proficiency with the processing machinery, assesses the quality grade of the product by mere visual inspection of the machine output and making the required adjustments. Most of the time, this operation is neither carried out with enough accuracy nor performed in a short time. In this regard, development of automated systems which can work based on the operators’ expertise may be an efficacious method for fast and reliable quality grading of the product.
Soft computing is an innovative method for development of intelligent systems which has attracted increasing interest by the scientific communities during the past few decades. It has been stated that utilization of the machine vision and artificial intelligence can result in increased quality of the product, abolish inconsistent manual evaluation, and reduce dependence on available manpower (Li et al. 2009). In recent years, many scientists and researchers attempted to design and develop automatic system based on computer vision and artificial intelligence for quality evaluation and grading of rice.
Sansomboonsuk and Afzulpurkar (2006) developed shrinkage algorithms to extract features of rice kernels in two forms of point and line touching kernels. Area, perimeter, circularity and shape compactness were used as criteria for classifying the broken rice and long grain rice. Fuzzy logic method was used to organize and classify the kernels. From the experiments, it was found that the algorithms perform satisfactorily in evaluating the percentage of broken rice with overall accuracy of 92 %. The time required by automated counting and measuring compared to manual counting and measuring was 70 % less. However, the required time (approximately 1 min) may not be suitable for real-time processing operations. Emadzadeh et al. (2010) investigated the variations of geometric characteristics of three Iranian rice varieties, at different processing levels using micrometer and image processing methods. They reported that the true size and sphericity obtained using image analysis could be estimated with root mean square error (RMSE) of less than 6 % from the dimensional features provided by micrometer procedure. Shiddiq et al. (2011) declared that higher rice whiteness resulting from higher degree of milling (DOM) can be measured by extracting a histogram from the color components of RGB space. For proper simulation of human behavior in quality assessment, they have suggested an Adaptive Neuro-Fuzzy Inference System (ANFIS) in which the relationships between the system inputs (image color variables) and output (rice whiteness) is expressed in the form of if-then fuzzy rules. Some authors have attempted to incorporate vision techniques into metaheuristic classification algorithms and optimization methods for identifying rice kernels of different varieties. Liu et al. (2005) applied a digital color image analysis algorithm based on morphological features and artificial neural networks to identify six varieties of rough rice seeds. A two-layer tan-sigmoid/log-sigmoid neural network was used to classify the rice seeds based on the extracted color and morphological features. Upon completion of the training, the network was tested with 60 rice kernels as test dataset. They reported that classification accuracy of the network was 84.83 % on the average for the six rice varieties studied. Guzman and Peralta (2008) proposed the combination of a machine vision system and neural networks for automatic identification of 52 varieties of rice grains belonging to five varietal groups of the product in the Philippines. Images of three datasets consisting of 110 grains arranged in a singulated non-touching pattern were captured for each rice variety. From each individual grain image, 13 morphological features were extracted. A Multi-layer Perceptron (MLP) neural network was used for analysis of size, shape, and varietal type of the rice samples. The thirteen morphological features were set as input variables for the neural network while the output variables were either the size, shape, or variety. Results showed that the developed system was able to identify the grain sample sizes and shapes with overall average accuracies of 98.76 and 96.67 %, respectively. In a research, Mousavi Rad et al. (2012a) utilized this technique to select the best feature set for classification of seven Iranian rice varieties. Totally, 44 features (11 features × 4 orientations) were extracted from the bulk samples of rice images using normalized gray-level co-occurrence matrix (GLCM). A new feature selection method based on Imperialist Competition Algorithm (ICA) was prepared to optimize the number of features that contributed significantly to the classification. Furthermore, the best features were selected by Genetic Algorithm (GA) and its performance for classification of rice varieties was compared with the ICA. Results indicated that ICA-based method provided better classification performance than that of GA technique. Feature selection by both ICA and GA techniques showed a considerable increase in classification accuracy compared to when all the feature set is used for rice classification. Chen et al. (2012) applied the Least Squares Support Vector Machines for the classification of head rice and broken rice. They used GA method to optimize the parameter values of least squares SVM. Results of their study showed that head rice and broken rice could be effectively identified by Least Squares Support Vector Machines using machine vision. Similarly, Mousavi Rad et al. (2012c), Fayyazi et al. (2013), Prajapati and Patel (2013), Gujjar and Siddappa (2013), Kaur and Singh (2013) utilized neural networks and multi-class SVM for classifying and grading of Iranian and Indian rice varieties. Similar studies have been also carried out by Shantaiya and Ansari (2010), Prajapati and Patel (2013), and Silva and Sonnadara (2013) for classification of different rice varieties using artificial neural networks.
The objective of this study was to develop a computer vision-based system combined with appropriate metaheuristic algorithms to classify milled rice kernels based on the product visual features.
Materials and methods
Samples preparation
The laboratory analyses were performed in the Rice Research Institute of Iran (RRII). The evaluated rice variety, Hashemi, is one of the common varieties of rice in north of Iran (Zareiforoush et al. 2010b). This variety is categorized as “long kernel” rice according to the standard provided by the Institute of Standards and Industrial Research of Iran (ISIRI) (ISIRI 2012). Moisture content of the evaluated samples was determined by means of a digital moisture meter (GMK model 303RS, Korea) to be 11–13.5 % (w.b.). Before image acquisition, milled rice grains were classified by milling experts into four classes based on the standard provided by ISIRI (ISIRI 2012). The classes included Low-processed sound grains (LPS), Low-processed broken grains (LPB), High-processed sound grains (HPS), and High-processed broken grains (HPB). The mentioned grades were defined based on two quality indices, namely degree of milling and length of rice grains.
In order to achieve the desired quality levels, four sub-samples of rough rice each weighing 500 g were taken and kept separately in sealed polyethylene bags. The samples were hulled using two passes with a laboratory-scale-rubber-roll husker (IRE Model HT-3, Taiwan). The clearance between the two rubber rolls was set to 0.50 mm. This setting allowed obtaining brown rice with minimum amount of breakage and unhulled rough rice. The remaining rough rice kernels were manually removed from the husked samples. The obtained brown rice grains were polished using a laboratory abrasive type whitener (SATAKE, Model JNMS15, Japan). In each test run, 250 g of brown rice grains were poured into the rice whitener and milled to whiten the kernels. In order to achieve the desired levels of DOM, duration of whitening was altered and DOM was measured using a digital whiteness meter (KM, Model C-100, Japan). After obtaining the desired DOM level, the samples for each level of DOM having the initially existing broken grains were poured into a laboratory rice grader (Model JFQS, China) and sieved for 60 s to completely separate the broken grains from sound kernels. Size of the grader cylinder groove was 3 mm and the separated grains were collected in the grader container at a set angle of 30° from the vertical.
Research methodology
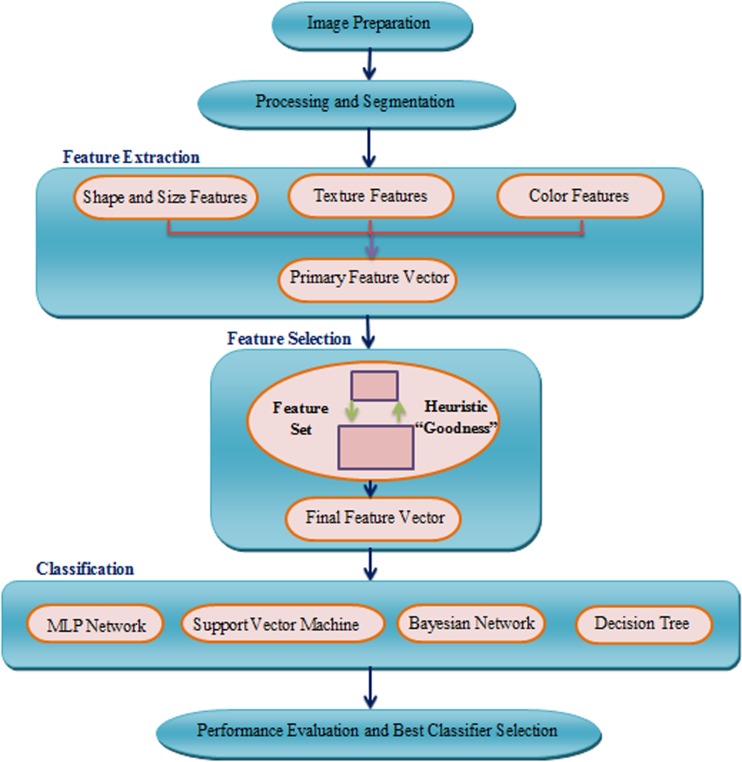
The methodology for qualitative grading of milled rice grains is shown in Fig. 1. In the developed system, first, images of milled rice samples are captured. The image processing operations are then executed to eliminate undesirable noises from images. After kernel segmentation, a primary feature vector is created based on some shape, size and color features. To have a high classification accuracy, it is necessary to prepare a proper input vector for the classifiers. For this purpose, the primary extracted features are subjected to a correlation-based feature selection procedure to reject the inferior features. Finally, the best classifier is selected for milled rice grading by examining four commonly used metaheuristic approaches. The entire applied methodology is described in the following sections.
Fig. 1.
Proposed methodology for qualitative grading of milled rice grains
Imaging setup
A machine vision system was developed to acquire images of milled rice samples (Fig. 2). The proposed system consisted of a color CCD camera (SAMSUNG, Model SCB-2000, Korea) equipped with a CS lens mount (3.5–8 mm focal length, 600 vertical TV lines resolution), a video capture card (Pinnacle 510-USB with a resolution 720 H × 576 V), a personal computer (PC) for image display and acquisition, and an appropriate illumination unit. The CCD camera was positioned about 15 cm above the samples and powered by a 12 VDC power supply. In order to provide uniform illumination, strip LED lights were used above the samples. A black cardboard was used as a background surface to simplify the segmentation process. In order to eliminate the environmental noises, the imaging chamber was covered by a black cover. Before image acquisition, the system was calibrated using a standard grey card to ensure light uniformity. Kernel samples of each class were manually separated from each other and placed under the camera. During image acquisition, signals from samples were captured by the camera, digitized and transferred to the PC using the capture card, subsequently stored on the PC in RGB color space.
Fig. 2.
Image acquisition setup
To acquire, record and process the captured images, a script was written in MATLAB R2010a version (MathWorks 2010). Based on quality grading of the samples, in each test, a certain number of milled rice grains were manually placed under the camera so that there was no contact between the grains. For each class, images of 320 grains were captured. In sum, images of 1280 grains were obtained from all classes. A sample of the captured images is presented in Fig. 3.
Fig. 3.
Typical images of rice grains: a Low-processed sound grains labeled as LPS, b Low-processed broken grains labeled as LPB, c High-processed sound grains labeled as HPS, d High-processed broken grains labeled as HPB
Image processing and segmentation
Image preprocessing operations were executed to prepare the images before feature extraction. The performance of classifiers is significantly dependent upon the success of image processing operations. In this study, the image processing stage consisted of removing background noises and separating each grain from the others in the image. In order to separate milled rice grains from the background, a global threshold was applied on the images using Otsu’s method. Otsu is a histogram-based thresholding method in which the normalized histogram is considered as a discrete probability density function. Otsu’s method selects the threshold value k that maximizes the value of G based on the following formula (Gonzalez et al. 2004):
| 1 |
where Pj is the proportion of the pixels of milled rice, Pb is the proportion of pixels of background, Ij is the mean gray value of milled rice, Ib is the mean gray value of background, and IT is the mean gray value of whole image. The threshold value is converted to a normalized value between 0 and 1. In this study, the threshold value was obtained as 0.203. After thresholding, the segmented images were converted into binary images. Finally, to carry out feature extraction, images of milled rice samples were labeled using the developed MATLAB script to analyze each grain separately in the segmented image. Result of the mentioned steps for a sample image is shown in Fig. 4.
Fig. 4.
An example of milled rice image preprocessing and segmentation operations: a Original image in RGB color space; b Image in binary mode after thresholding
Feature extraction
The result of segmentation operation specially after labeling was an image containing only one milled rice grain. From each segmented grain, a series of features was extracted. There are many defining features in image processing problems to describe the objects (Shouche et al. 2001). The feature analyses of milled rice samples included extraction of color, shape and size features. Totally, 57 features, including five regarding size and shape, four for texture, and 48 based on color information were extracted for each grain. Table 1 shows the list of defined features for quality classification of milled rice grains.
Table 1.
Shape, texture and color features of milled rice samples obtained from image analysis
| Shape and size features | ||||||||
| Feature | Major axis length | Minor axis length | Equivalent diameter | Perimeter | Solidity | |||
| Feature no. | F1 | F2 | F3 | F4 | F5 | |||
| Texture features | ||||||||
| Feature | Contrast | Energy | Correlation | Homogeneity | ||||
| Formula | ||||||||
| Feature no. | F6 | F7 | F8 | F9 | ||||
| Color features in RGB Space* | ||||||||
| Feature | Mean [μ=] for: | |||||||
| R | G | B | ||||||
| Feature no. | F10 | F11 | F12 | F13 | F14 | F15 | ||
| Feature | Mean [μ=] for: | |||||||
| R-G | G-B | R-B | ||||||
| Feature no. | F16 | F17 | F18 | |||||
| Feature | Variance [σ=] for: | |||||||
| R | G | B | ||||||
| Feature no. | F19 | F20 | F21 | F22 | F23 | F24 | ||
| Feature | Variance [σ=] for: | |||||||
| R-G | G-B | R-B | ||||||
| Feature no. | F25 | F26 | F27 | |||||
| Feature | Skewness [s=] for: | |||||||
| R | G | B | ||||||
| Feature no. | F28 | F29 | F30 | F31 | F32 | F33 | ||
| Feature | Skewness [s=] for: | |||||||
| R-G | G-B | R-B | ||||||
| Feature no. | F34 | F35 | F36 | |||||
| Feature | Kurtosis [k= ] for: | |||||||
| R | G | B | ||||||
| Feature no. | F37 | F38 | F39 | F40 | F41 | F42 | ||
| Feature | Kurtosis [k= ] for: | |||||||
| R-G | G-B | R-B | ||||||
| Feature no. | F43 | F44 | F45 | |||||
| Color features in HSV space | ||||||||
| Feature | Mean [μ=] for: | |||||||
| H | S | V | ||||||
| Feature no. | F46 | F47 | F48 | |||||
| Color features in L*a*b* space | ||||||||
| Feature | Mean [μ=] for: | |||||||
| L | a* | b* | ||||||
| Feature no. | F49 | F50 | F51 | |||||
| Color features in YCbCr color map | ||||||||
| Feature | Mean [μ=] for: | |||||||
| Y | Cb | Cr | ||||||
| Feature no. | F52 | F53 | F54 | |||||
| Color features in NTSC system | ||||||||
| Feature | Mean [μ=] for: | |||||||
| Yi | I | Q | ||||||
| Feature no. | F55 | F56 | F57 | |||||
*h(x) is the grey level of pixels in the image with a pixel position of x, x can take any value between 1 and z = m n, where m and n are row and column numbers in the image matrix, respectively
*μ, σ, S, and K are the Mean, Variance, Skewness, and Kurtosis of image pixels, respectively
Feature selection
After extraction of the visual features, the superior features were selected from the resulting feature vector. In classification approaches, the proper selection of feature vector is very important because it is the only database on which the classifiers work (Omid et al. 2013). Selection of the best features is one of the key factors in improving each classifier performance. In this regard, it is necessary to have a thorough feature vector. Nevertheless, features that may decrease classification accuracy must be removed from the feature vector. Several metaheuristic techniques are available for feature selection. The most frequently used applicable approaches for classification purposes include principal component analysis, correlation-based feature selection, factor analysis, and sensitivity analysis (Fielding 2007). Correlation-based feature selection is one of the prominent data mining methods to rank the relevance of features. It utilizes a search algorithm along with a function, Pearson’s correlation equation, to calculate which feature subsets deserve the final classification process (Mollazade et al. 2012). The heuristics by which correlation-based feature selection measures the goodness of feature subsets takes into account the usefulness of individual features for predicting the class label along with the level of intercorrelation among them (Hall 1999). In the current study, “Best First” procedure was chosen as the search algorithm. This algorithm searches the space of attribute subsets by “greedy hill climbing” augmented with a backtracking facility. The level of backtracking done can be controlled by setting the number of consecutive non-improving nodes allowed. Best first algorithm may start with an empty set of attributes and search forward, or it may start with a full set of attributes and search backward. It may even start at any point and search in both directions, by considering all possible single attribute additions and deletions at a given point (Witten and Frank 2005). The mentioned algorithm was implemented on the extracted features of milled rice using “CfsSubsetEval” attribute evaluator in WEKA software (Hall et al. 2009). The “CfsSubsetEval” algorithm evaluates the worth of a subset of attributes by considering the individual predictive ability of each feature along with the degree of redundancy between them. Subsets of features that are highly correlated with the class while having low intercorrelation are preferred. After feature selection operation, the size of feature vector showed a reduction from 57 features to 12, including 3 for size and shape, 1 for texture, and 8 for color features. As shown in Table 1, the selected features were: F1, F4, F5, F7, F12, F21, F39, F44, F50, F51, F53 and F54.
Qualitative classification of samples
Classification was the last stage of the milled rice grading process. Generally, classification is the process of training to assign a sample to pre-determined classes. The aim of classification was to find a rule based on the selected features or training elements, which allowed assigning each grain to its probable classes. Since the classification process contains training, cross-validation, and testing stages, the data set had to be divided into three parts: training set, cross-validation set, and testing set. The training set was used to train the classifier; whist cross-validation set was utilized to prevent overtraining and the testing set was employed to test the validity of the classifier. In this study, 50 % of the data set (640 samples) was randomly selected as the training set, 25 % (320 samples) for cross-validation, and the remaining 25 % of data set (320 samples) was used for testing. Several strategies can be implemented for the classification process. Most of them are categorized as metaheuristic techniques. Here, to find the best classifier for milled rice grading, four different metaheuristic techniques were evaluated using WEKA software (Hall et al. 2009). Each of the utilized techniques is described in the following sections.
Artificial neural networks
One of the most common types of artificial neural network for classification purposes is Multilayer perceptron (MLP). In general, MLPs consist of three main layers: input layers, hidden layers, and output layer. The layers belong to the class of feedforward networks, meaning that the information passes through the network nodes only in the forward direction. In order to classify the milled rice samples, the MLP model was trained using back-propagation algorithm. This algorithm calculates the weights of the activation function for each neuron (Karray and De Silva 2004). In the feedforward networks, error minimization can be performed using a number of procedures including gradient descent, gradient descent with a momentum, Levenberg–Marquardt, conjugate gradient, and etc. (Omid et al. 2010). The momentum parameter is utilized to prevent the system from converging to local minima. Although high values of momentum can increase the speed of convergence of the system, however, choosing the high values for the momentum parameter can increase the risk of minimum overshooting and consequently, cause the system to become unstable (Patterson 1998). In this research, the gradient descent with a momentum approach was used for error minimization with the momentum coefficient of 0.2. The number of neurons in input and output layers were fixed because they depend on independent (feature vector) and dependent (class) variables. The input layer consisted of 12 neurons (F1, F4, F5, F7, F12, F21, F39, F44, F50, F51, F53 and F54) based on feature selection operation (Table 1). Since milled rice grains must be graded into four classes, the output layer consisted of four neurons, each of which corresponded to one of the possible groups (LPS, LPB, HPS and HPB). Afterwards, hidden layers were applied for developing the MLP models.
Support vector machine
In machine learning, support vector machines are supervised learning systems based on the statistical learning theory that explore data and recognize patterns in classification and regression analysis problems. A support vector machine model is a representation of the samples as points in space, mapped so that the samples of the distinct classes are separated by a clear boundary which is as wide as possible. In this approach, the optimal boundary, known as hyper-plane, of two sets in a vector space is obtained independently on the probabilistic distribution of training vectors in the set. The hyperplane locates the boundary that is as far as possible from the nearest vectors to the boundary in both sets. The vectors situated near the hyperplane are called supporting vectors. If the space is not linearly separable, there may be no separating hyperplane to distinguish. In such cases, a kernel function may be used to solve the problem. The kernel function evaluates the relationships within the data and makes complex divisions in the space (Vapnik 2000).
Kernel trick is one of the common approaches for solving nonlinear solvable problems. This technique is based on the inner product of input data along with a definition of suitable kernel function. The idea of the kernel function is to enable operations to be performed in the input space rather than the potentially high dimensional feature space. Thus, the inner product is not required to be examined in the feature space. Selection of the right kernel would improve the performance of the classifier. In this study, four common kernel functions were utilized by trial and error on the test set. These kernel functions were namely Polynomial, Normalized Polynomial, RBF, and Universal Pearson VII (Cristianini and Shawe-Taylor 2000).
Decision tree
Decision trees are organized so that at each layer of the tree one class is rejected. The last remaining class at the bottom of the tree is considered as the designated class. The outgoing branches of each node correspond to possible outcome of the test at that node. There are a large number of decision tree algorithms introduced completely in the machine learning and applied statistic literatures. In the current research four different decision tree algorithms were used for classification of milled rice. The algorithms were namely J48 (C4.5 decision tree learner), REP (reduced-error pruning), LMT (logistic model trees) and Decision Stump algorithm. These algorithms have been frequently used in decision trees-based classification approaches (Gupta et al. 2012; Soltani and Omid 2015).
Bayesian networks
Bayesian networks are probabilistic graphical models representing a set of random variables and their conditional dependencies via a directed acyclic graph. Each node in the graph represents a random variable. The random variable refers to a feature about which we may be unsure. Each random variable has a set of mutually exclusive and collectively comprehensive possible values. That is, exactly one of the possible values is or will be the actual value, and we are not sure which one it is. The graph represents direct qualitative dependence relationships; the local distributions represent quantitative information about the strength of those dependencies. The graph along with the local distributions represent a joint distribution over the random variables denoted by the nodes of the graph (Neapolitan 2004). One of the most important features of Bayesian networks is that they offer a well-designed mathematical structure for modeling complex relationships among random variables while keeping a relatively simple visualization of these relationships (Heckerman et al. 1995).
When using Bayesian Networks for classification problems, the type of learning process is very important, because the accuracy of the network extremely depends on this factor. Generally, there are two learning procedures for these classifying networks: parametric learning and structural learning. The objective of structural learning is to find the best structure for the Bayesian network. The results of this process should be compatible with the data set adjustments. It should also be optimum in the case of complexity. The structural learning is comprised of two method categories: limit-oriented and point-oriented. In the point-oriented method, the best network is one that has answered better with Bayesian Networks and is defined by the independent relationships between nodes. In this study, five point-oriented methods, namely genetic search (Generation size: 100 and population size: 10), hill-climber search, K2 search, simulated annealing search (Start temperature: 10 °C, delta value: 0.999, and run number: 10,000) and TAN search methods were used in the learning stage of Bayesian networks. The selected algorithms have shown good performance in agricultural products classification (Mollazade et al. 2012). The purpose of this procedure was to find the best learning method in which Bayesian network gives the highest accuracy in milled rice sample classification.
Statistical analysis
The performance of the utilized metaheuristic techniques in milled rice classification was evaluated by forming a classification matrix (CM) and computing the statistical parameters such as sensitivity (Se), specificity (Sp), classification accuracy (Ac) and root mean squared error (RMSE). Sensitivity designates the classifier ability to identify a class correctly. Specificity represents the classifier ability to exclude a class correctly. For calculating the mentioned parameters, the following equations were used (Parker 2001; Teimouri et al. 2014):
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
where TP, FP, TN and FN are the number of true positives, false positives, true negatives and false negatives, respectively, while Tk and Zk are the actual and predicted values respectively; and N belongs to the total number of samples in the test set.
Results and discussion
In order to determine the best classifier, several items were examined for each method. The results of milled rice classification using the different data mining-based techniques are presented in the following sections.
Classification by artificial neural networks
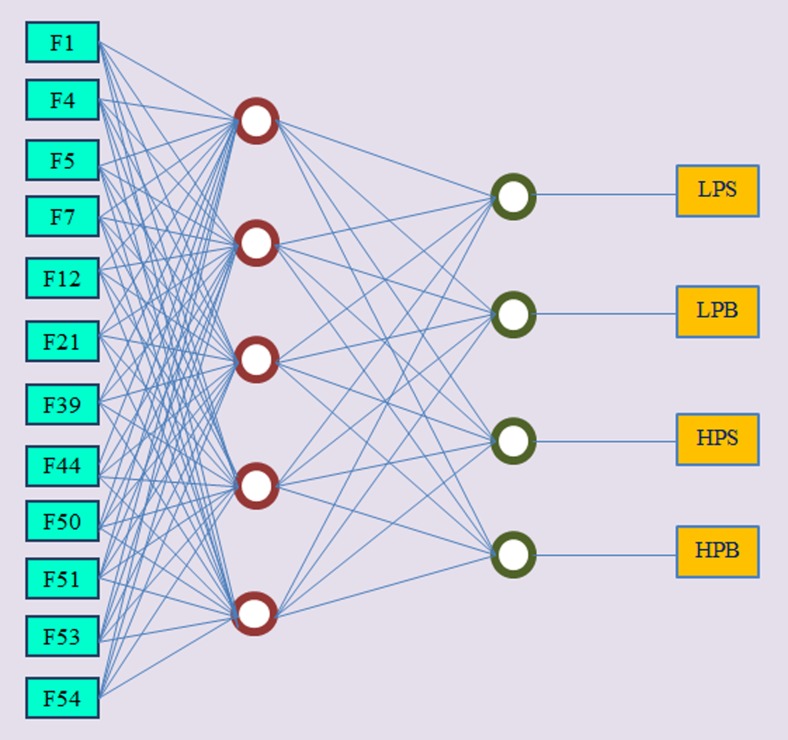
In order to achieve the optimal performance for the network, several arrangements for the number of neurons in the hidden layer and number of epochs were tested through trial and error procedure (Number of neurons in the hidden layer varied from 2 to 20 and number of epochs varied from 100 to 1000). The best arrangement for the network was determined based on the statistical parameters (Eqs. (2) to (6)). Results showed the hidden layer with five neurons (i.e., 12-5-4 topology) had the lowest classification error (0.0806 for RMSE) compared with the other configurations. One of the most significant points in design of artificial neural networks for online applications is proper determination of the hidden layers. The lower the number of neurons in the hidden layer, the lower the size of the network and analysis time. In this study, the 12-5-4 network topology was selected as the superior architecture for milled rice classification (Fig. 5). The CM (classification matrix) of this topology using the test data is presented in Table 2.
Fig. 5.
The selected artificial neural network architecture with 12-5-4 topology for milled rice classification
Table 2.
Classification matrix obtained from the evaluation of support vector machines with polynomial kernel function
Classified as 
|
LPS | LPB | HPS | HPB |
|---|---|---|---|---|
| LPS | 80 | 0 | 1 | 0 |
| LPB | 0 | 88 | 0 | 1 |
| HPS | 0 | 0 | 86 | 1 |
| HPB | 0 | 1 | 0 | 62 |
Values of the statistical parameters for the ANN classifier performance are given in Table 3. The Se values of the ANN classifier for identification of LPS, LPB, HPS and HPB classes were 100, 98.88, 98.85 and 96.87 %, respectively. S The ANN classifier Sp parameter in classification of LPS, LPB, HPS and HPB grades was equal to 99.58, 99.57, 99.57 and 99.61 %, respectively. The accuracy of the developed classifier in quality grading of milled rice samples into LPS, LPB, HPS and HPB classes was 98.76, 98.87, 98.85 and 98.41 %, respectively. The overall accuracy of the ANN was obtained as 98.72 %. The high accuracy of the neural network topology indicates the suitability of the selected features.
Table 3.
Values of the statistical parameters for the developed ANN classifier
| Quality class | S e (%) | S p (%) | A c (%) | RMSE |
|---|---|---|---|---|
| LPS | 100 | 99.58 | 98.76 | 0.0806 |
| LPB | 98.88 | 99.57 | 98.87 | |
| HPS | 98.85 | 99.57 | 98.85 | |
| HPB | 96.87 | 99.61 | 98.41 | |
| Average (%) | 98.65 | 99.58 | 98.72 |
Liu et al. (2005) applied a digital color image analysis algorithm based on morphological features and artificial neural networks to identify six varieties of rough rice seeds. A two-layer tan-sigmoid/log-sigmoid neural network was used to classify the rice seeds based on the extracted color and morphological features. Upon completion of the training, the network was tested with 60 rice kernels as test dataset which indicated that classification accuracy of the network was 84.83 % on the average for the six rice varieties studied.
Guzman and Peralta (2008) proposed the combination of a machine vision system and neural networks for automatic identification of 52 varieties of rice grains belonging to five varietal groups of the product in the Philippines. From each individual grain image, 13 morphological features were extracted. A Multi-layer Perceptron (MLP) neural network was used for analysis of size, shape, and varietal type of the rice samples. The thirteen morphological features were set as input variables for the neural network while the output variables were either the size, shape, or variety. Results showed that the developed system was able to identify the grain sample sizes and shapes with overall average accuracies of 98.76 and 96.67 %, respectively. When the sample images of the 52 varieties were included in a group classification, the average overall accuracy of the system was approximately 70 %. Similar studies were carried out by Shantaiya and Ansari (2010), Prajapati and Patel (2013), and Silva and Sonnadara (2013) for classification of different rice varieties using artificial neural networks.
Classification by support vector machines
Results showed that the Universal Pearson VII kernel function had the lowest RMSE (0.3139) compared to the other functions (Table 4). Hence, the Universal Pearson VII kernel function was selected as the best function for milled rice classification.
Table 4.
RMSE values for support vector machine classifiers using different kernel functions
| Kernel functions | RMSE |
|---|---|
| Polynomial | 0.3147 |
| Normalized polynomial | 0.3168 |
| RBF | 0.3513 |
| Universal Pearson VII | 0.3139 |
The CM of milled rice classification, using the Universal Pearson VII kernel function for LPS, LPB, HPS and HPB classes, is given in Table 5. The statistical measures presented in Table 6 have been obtained from Table 5. The Se value of the SVM classifier for classification of LPS, LPB, HPS and HPB grades was 98.78, 98.84, 100 and 95.38 %, respectively. The value of Sp for SVM classifier in classification of LPS, LPB, HPS and HPB grades was respectively equal to 100, 98.27, 100 and 99.61 %. The accuracy of the developed SVM classifier in quality assessment of milled rice grains into LPS, LPB, HPS and HPB classes was 100, 95.50, 100 and 98.41 %, respectively. The overall accuracy of the SVM model was equal to 98.48 %.
Table 5.
Classification matrix obtained from the evaluation of support vector machines with Universal Pearson VII kernel function
Classified as 
|
LPS | LPB | HPS | HPB |
|---|---|---|---|---|
| LPS | 81 | 0 | 0 | 0 |
| LPB | 1 | 85 | 0 | 3 |
| HPS | 0 | 0 | 87 | 0 |
| HPB | 0 | 1 | 0 | 62 |
Table 6.
Values of the statistical parameters for the developed SVM classifier
| Quality class | S e (%) | S p (%) | A c (%) | RMSE |
|---|---|---|---|---|
| LPS | 98.78 | 100 | 100 | 0.3139 |
| LPB | 98.84 | 98.27 | 95.50 | |
| HPS | 100 | 100 | 100 | |
| HPB | 95.38 | 99.61 | 98.41 | |
| Average (%) | 98.25 | 99.47 | 98.48 |
Chen et al. (2012) applied the Least Squares SVMs for the classification of head rice and broken rice. They used GA method to optimize the parameter values of least squares SVM. Results of their study showed that head rice and broken rice could be effectively identified by Least Squares SVMs using machine vision. Similarly, Mousavi Rad et al. (2012b), Fayyazi et al. (2013), Prajapati and Patel (2013), Gujjar and Siddappa (2013), Kaur and Singh (2013) utilized neural networks and multi-class SVM for classifying and grading of Iranian and Indian rice varieties.
Classification by decision trees
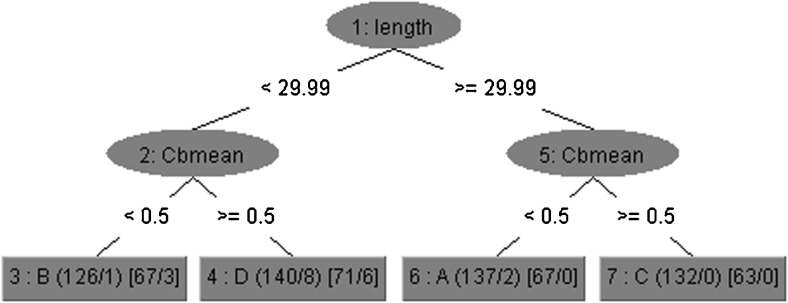
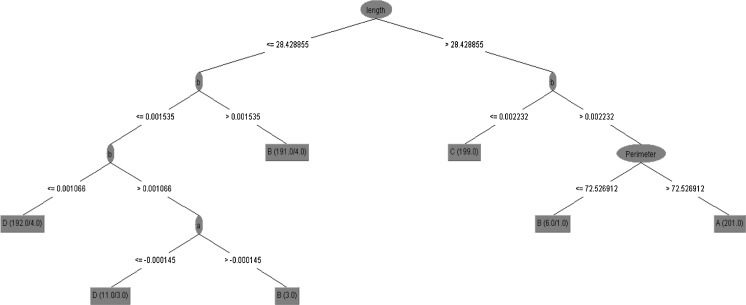
Based on the results presented in Table 7, the REP tree had the lowest RMSE (0.1104) compared with the other trees. Therefore, this tree was selected as the best tree for milled rice grains classification. As shown in Fig. 6, the structure of the REP tree consists of six branches and four leaves. Considering the overall form of the J48 tree (Fig. 7), which had the nearest RMSE to the REP tree, it can be seen that using the J48 tree, requires more branching to determine the qualitative class of a sample (12 branches compared to 4 branches in the REP tree). This can significantly affect the speed and accuracy of calculations in a decision-tree-based classifier.
Table 7.
RMSE values for decision tree classifiers using different induction algorithms
| Decision tree algorithm | RMSE |
|---|---|
| J48 | 0.1184 |
| LMT | 0.1697 |
| REP | 0.1104 |
| Decision stump | 0.3623 |
Fig. 6.
Structure of REP tree for classification of milled rice grains
Fig. 7.
Structure of J48 tree for classification of milled rice grains
According to the CM obtained from the validation stage (Table 8) and its relating statistical parameters (Table 9), The Se values of the REP decision tree classifier in identification of LPS, LPB, HPS and HPB classes were 98.78, 97.70, 98.84 and 93.85 %, respectively. The value of Sp in classification of LPS, LPB, HPS and HPB grades with REP decision tree classifier was respectively equal to 100, 98.27, 99.14 and 99.22 %. The accuracy of the REP classifier in quality grading of rice grains into LPS, LPB, HPS and HPB levels was 100, 95.50, 97.70 and 96.82 %, respectively. The overall accuracy of the REP decision tree was equal to 97.50 %.
Table 8.
Classification matrix obtained from the decision tree classifier with REP induction algorithm
Classified as 
|
LPS | LPB | HPS | HPB |
|---|---|---|---|---|
| LPS | 81 | 0 | 0 | 0 |
| LPB | 1 | 85 | 1 | 2 |
| HPS | 0 | 0 | 85 | 2 |
| HPB | 0 | 2 | 0 | 61 |
Table 9.
Values of the statistical parameters for the developed REP decision tree classifier
| Quality class | S e (%) | S p (%) | A c (%) | RMSE |
|---|---|---|---|---|
| LPS | 98.78 | 100 | 100 | 0.1104 |
| LPB | 97.70 | 98.27 | 95.50 | |
| HPS | 98.84 | 99.14 | 97.70 | |
| HPB | 93.85 | 99.22 | 96.82 | |
| Average (%) | 97.29 | 99.16 | 97.50 |
El-Telbany et al. (2006) investigated the Egyptian rice diseases using the C4.5 decision trees algorithm. The parameters for those classifiers were chosen to be the default one used by WEKA software. Seven attributes, namely variety, age, part, appearance, color, temperature and disease were selected for classification. Ten cross-validation bootstarps, each with 138 (66 %) training cases and 68 testing cases, were used for the performance evaluation. The SVM classifier was also compared with an ANN classifier for which a 52-33-5 architecture was considered in the form of a three-layer, fully connected feed-forward network. The network was trained using back propagation algorithm with learning rate of 0.3 and momentum of 0.2 for 500 iterations. Results indicated the classification accuracy of ANN and decision tree classifiers were respectively equal to 96.4 and 97.2 %.
Classification by Bayesian networks
Among the mentioned Bayesian-network-based methods, “Hill climber” was the best learning method for milled rice classification with the lowest RMSE (Table 10).
Table 10.
RMSE values for Bayesian networks classifier using different search algorithms
| Search algorithm | RMSE |
|---|---|
| Genetic search | 0.1473 |
| Hill climber | 0.1226 |
| Simulated annealing | 0.1303 |
| TAN | 0.1319 |
Results of Bayesian network with hill-climber-search algorithm for the validation data set are shown in the classification matrix (Table 11). The Se values of the hill climber algorithm in identification of LPS, LPB, HPS and HPB classes were 97.53, 97.67, 97.73 and 93.85 %, respectively. The value of Sp in classification of LPS, LPB, HPS and HPB grades with the hill climber algorithm was respectively equal to 99.16, 97.83, 99.57 and 99.22 %.
Table 11.
Classification matrix obtained from the Bayesian networks classifier with Hill climber search algorithm
Classified as 
|
LPS | LPB | HPS | HPB |
|---|---|---|---|---|
| LPS | 79 | 1 | 1 | 0 |
| LPB | 2 | 84 | 0 | 3 |
| HPS | 0 | 0 | 86 | 1 |
| HPB | 0 | 1 | 1 | 61 |
The accuracy of the hill climber algorithm in quality grading of milled rice grains into LPS, LPB, HPS and HPB levels was 97.53, 94.38, 98.85 and 96.82 %, respectively. The overall accuracy of the hill climber algorithm was equal to 96.89 % (Table 12).
Table 12.
Values of the statistical parameters for the Bayesian networks classifier with Hill climber search algorithm
| Quality class | S e (%) | S p (%) | A c (%) | RMSE |
|---|---|---|---|---|
| LPS | 97.53 | 99.16 | 97.53 | 0.1226 |
| LPB | 97.67 | 97.83 | 94.38 | |
| HPS | 97.73 | 99.57 | 98.85 | |
| HPB | 93.85 | 99.22 | 96.82 | |
| Average (%) | 96.69 | 98.94 | 96.89 |
Okamura et al. (1993) used the Bayes minimum risk classifier to separate raisins into three classes based on the degree of wrinkles and shape. They extracted some visual features of raisins from the acquired images and then fed these features into the classifier. According to the results, their grading system was more precise than human graders.
The performance comparison of the classifiers based on the statistical parameters is given in Table 13. As shown, all of the metaheuristic methods used in this research showed high levels of accuracy in classification of milled rice grains. The highest classification accuracy was attributed to ANN classifier. The highest classifier ability to properly recognition of the quality classes was corresponded to ANN classifier with Se value of 99.58 %, after which were SVM, DT and Bayesian classifiers, respectively. To the best of our knowledge, this is may be due to the fact that for such classifiers there are more possibilities to rearrange the classification algorithm parameters to achieve better performance.
Table 13.
Performance comparison of classifiers in terms of different statistical parameters
| Classifier | Se (%) | Sp (%) | Ac (%) | RMSE |
|---|---|---|---|---|
| ANN | 98.65 | 99.58 | 98.72 | 0.0806 |
| SVM | 98.25 | 99.47 | 98.48 | 0.3139 |
| DT | 97.29 | 99.16 | 97.50 | 0.1104 |
| Bayesian networks | 96.69 | 98.94 | 96.89 | 0.1226 |
Conclusions
In this research, four different metaheuristic classification techniques were utilized to classify milled rice grains into four qualitative grades based on color images. Performance evaluation of the classifiers indicated that MLP neural network with a 12-5-4 topology was the best classifier with an accuracy of 98.72 %. After the MLP ANN, support vector machines with Universal Pearson VII kernel function, decision tree with REP algorithm and Bayesian network with Hill Climber search algorithm had the higher accuracy, respectively. Comparison of classification matrices obtained from metaheuristic techniques showed that these approaches were quite efficient in classifying milled rice grains based on the defining features. Since most of the defined size and color features were selected in the final feature vector and contributed to the classification process, use of such features may meet the classifiers’ requirements for quality grading of milled rice with less need for texture features.
One of the most important problems associated with rice industry, is authenticity identification of rough rice varieties by providing a reliable, fast, yet accurate method. This issue is specially raised in the case of hybrid, local and aromatic varieties. For such products, it would be efficacious to develop an inspection system for distinguishing the impurity of seeds with a high level of accuracy. The ideas and plans presented in this research can be implemented for achieving further progress in this field. However, for more complex problems such as differentiation between milled rice varieties, it would be highly desirable to have a supplementary method such as electronic nose (E-nose), in which some characteristics of the kernels other than morphological features can be applied (Zhou et al. 2012). The heuristic algorithms presented in this research would lend itself for quality grading of the other cereal grains as well.
The forthcoming areas in this field may also include more advanced processing and sorting machines which can work based on the vision techniques. The feasibility of the application of computer vision along with machine learning and other branches of artificial intelligence to fully control and optimize rice processing operations in order to manage and reduce product losses during these operations can also be the subject of further development. For this purpose, it is suggested to develop algorithms similar to those proposed here, for other external qualitative indices of milled rice, such as fissure, chalkiness and et cetera. Determination of rice quality parameters by using computer vision techniques and instantaneous control of the processing machines based on the obtained information, will enable continuous monitoring of product processing in an objective manner, and thereby facilitate timely control of the changes in the product quality (Zareiforoush et al. 2015).
References
- Chen X, Ke S, Wang L, Xu H, Chen W (2012) Classification of rice appearance quality based on LS-SVM using machine vision. In: Information computing and applications. Springer, pp 104–109
- Cristianini N, Shawe-Taylor J (2000) An introduction to support vector machines and other kernel-based learning methods. Cambridge University Presss
- El-Telbany ME, Warda M, El-Borahy M. Mining the classification rules for Egyptian rice diseases. Int Arab J Inf Technol. 2006;3:303–307. [Google Scholar]
- Emadzadeh B, Razavi S. M. A., Farahmandfar R. Monitoring geometric characteristics of rice during processing by image analysis system and micrometer measurement. Int Agrophys. 2010;24:21–27. [Google Scholar]
- Fayyazi S, Abbaspour-Fard MH, Rohani A, Sadrnia H, Monadjemi SA (2013) Identification of three Iranian rice seed varieties in mixed bulks using textural features and Learning Vector Quantization neural network. Paper presented at the 1st International e-Conference on novel Food Processing, Mashhad, Iran, 26–27 Feb
- Fielding A. Cluster and classification techniques for the biosciences. UK: Cambridge University Press; 2007. [Google Scholar]
- Gonzalez RC, Woods RE, Eddins SL (2004) Digital image processing using MATLAB. Pearson Education India
- Gujjar HS, Siddappa DM. A method for identification of Basmati rice grain of india and its quality using pattern classification. Int J Eng Res Applic. 2013;3:268–273. [Google Scholar]
- Gupta D, Malviya A, Singh S (2012) Performance analysis of classification tree learning algorithms. IJCA Int J Comput Appl 55
- Guzman JD, Peralta EK (2008) Classification of Philippine rice grains using machine vision and artificial neural networks. In: World conference on agricultural information and IT, Tokyo, Japan, 24–27 August 2008. pp 41–48
- Hall MA (1999) Correlation-based feature selection for machine learning. The University of Waikato
- Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The WEKA data mining software: an update. ACM SIGKDD Explorations Newsl. 2009;11:10–18. doi: 10.1145/1656274.1656278. [DOI] [Google Scholar]
- Heckerman D, Mamdani A, Wellman MP. Real-world applications of Bayesian networks. Commun ACM. 1995;38:24–26. doi: 10.1145/203330.203334. [DOI] [Google Scholar]
- ISIRI (2012) Rice – specifications and test methods. Institute of Standards and Industrial Research of Iran. http://std.isiri.org/std/127.htm
- Karray FO, De Silva CW (2004) Soft computing and intelligent systems design: theory, tools, and applications. Pearson Education
- Kaur H, Singh B. Classification and grading rice using multi-class SVM. Int J Sci Res Public. 2013;3:1–5. [Google Scholar]
- Li X, Yuan J, Gu T, Liu X (2009) Level detection of raisins based on image analysis and neural network. In: The Sixth International Symposium on Neural Networks (ISNN 2009). Springer, pp 343–350
- Liu Z, Cheng F, Ying Y, Rao X. Identification of rice seed varieties using neural network. J Zhejiang Univ Sci. 2005;6:1095. doi: 10.1631/jzus.2005.B1095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MathWorks (2010) Matlab User’s Guide. The MathWorks Inc., USA
- Mollazade K, Omid M, Arefi A. Comparing data mining classifiers for grading raisins based on visual features. Comput Electron Agric. 2012;84:124–131. doi: 10.1016/j.compag.2012.03.004. [DOI] [Google Scholar]
- Mousavi Rad S, Akhlaghian Tab F, Mollazade K. Application of imperialist competitive algorithm for feature selection: a case study on bulk rice classification. Int J Comput Appl. 2012;40:41–48. [Google Scholar]
- Mousavi Rad S, Akhlaghian Tab F, Mollazade K. Design of an expert system for rice kernel identification using optimal morphological features and back propagation neural network. Int J Appl Inf Syst. 2012;3:33–37. doi: 10.4018/jismd.2012040102. [DOI] [Google Scholar]
- Mousavi Rad S, Tab FA, Mollazade K. Design of an expert system for rice kernel identification using optimal morphological features and back propagation Neural Network. Int J Appl Inf Syst. 2012;3:33–37. doi: 10.4018/jismd.2012040102. [DOI] [Google Scholar]
- Neapolitan RE (2004) Learning Bayesian networks vol 1. Prentice Hall Upper Saddle River
- Okamura NK, Delwiche M, Thompson J (1993) Raisin grading by machine vision Transactions of the ASAE (USA)
- Omid M, Mahmoudi A, Omid MH. Development of Pistachio sorting system using principal component analysis (PCA) assisted artificial neural network (ANN) of impact acoustics. Expert Syst Appl. 2010;37:7205–7212. doi: 10.1016/j.eswa.2010.04.008. [DOI] [Google Scholar]
- Omid M, Soltani M, Dehrouyeh MH, Mohtasebi SS, Ahmadi H. An expert egg grading system based on machine vision and artificial intelligence techniques. J Food Eng. 2013;118:70–77. doi: 10.1016/j.jfoodeng.2013.03.019. [DOI] [Google Scholar]
- Parker J. Rank and response combination from confusion matrix data. Inf Fusion. 2001;2:113–120. doi: 10.1016/S1566-2535(01)00030-6. [DOI] [Google Scholar]
- Patterson DW (1998) Artificial neural networks: theory and applications. Prentice Hall PTR
- Prajapati BB, Patel S. Algorithmic approach to quality analysis of Indian Basmati rice using digital image processing. Int J Emerg Technol Adv Eng. 2013;3:503–504. [Google Scholar]
- Sadeghi M, Nasrnia E, Masoumi A, Hemmat A. Head rice yield response to low and high drying and tempering conditions. Int Agrophys. 2013;27:219–223. doi: 10.2478/v10247-012-0088-5. [DOI] [Google Scholar]
- Sansomboonsuk S, Afzulpurkar N (2006) The appropriate algorithms of image analysis for rice kernel quality evalution. In: 20th Conference of Mechanical Engineering Network of Thailand, Bangkok, Thailand, 18–20 October 2006.
- Shantaiya S, Ansari U (2010) Identification of food grains and its quality using pattern classification. In: 12th IEEE International Conference on Communication Technology (ICCT), Nanjing, China, 11–14 November 2010. pp 3–5
- Shiddiq DM, Nazaruddin YY, Muchtadi FI, Raharja S (2011) Estimation of rice milling degree using image processing and adaptive network based fuzzy inference system (ANFIS). In: 2nd International Conference on Instrumentation Control and Automation (ICA), Bandung, Indonesia, 15–17 Novomber 2011. IEEE, pp 98–103
- Shouche S, Rastogi R, Bhagwat S, Sainis JK. Shape analysis of grains of Indian wheat varieties. Comput Electron Agric. 2001;33:55–76. doi: 10.1016/S0168-1699(01)00174-0. [DOI] [Google Scholar]
- Silva CS, Sonnadara U (2013) Classification of rice grains using neural networks. In: Proceedings of Technical Sessions, Sri Lanka, September 2013. pp 9-14
- Soltani M, Omid M (2015) Detection of poultry egg freshness by dielectric spectroscopy and machine learning techniques. LWT Food Sci Technol
- Teimouri N, Omid M, Mollazade K, Rajabipour A. A novel artificial neural networks assisted segmentation algorithm for discriminating almond nut and shell from background and shadow. Comput Electron Agric. 2014;105:34–43. doi: 10.1016/j.compag.2014.04.008. [DOI] [Google Scholar]
- Vapnik V (2000) The nature of statistical learning theory. Springer
- Witten IH, Frank E (2005) Data mining: practical machine learning tools and techniques. Morgan Kaufmann
- Yadav B, Jindal V. Modeling changes in milled rice (Oryza sativa L.) kernel dimensions during soaking by image analysis. J Food Eng. 2007;80:359–369. doi: 10.1016/j.jfoodeng.2006.06.005. [DOI] [Google Scholar]
- Zareiforoush H, Komarizadeh M, Alizadeh M. Effect of crop-screw parameters on rough rice grain damage in handling with a horizontal screw conveyor. J Food Agric Environ. 2010;8:494–499. [Google Scholar]
- Zareiforoush H, Komarizadeh M, Alizadeh M, Masoomi M, Tavakoli H. Performance evaluation of screw augers in paddy grains handling. Int Agrophys. 2010;24:389–369. [Google Scholar]
- Zareiforoush H, Minaei S, Alizadeh MR, Banakar A (2015) Potential applications of computer vision in quality inspection of rice: a review. Food Eng Rev :1–25
- Zhou B, Wang J, Qi J. Identification of different wheat seeds by electronic nose. Int Agrophys. 2012;26:413–418. doi: 10.2478/v10247-012-0058-y. [DOI] [Google Scholar]