Measurements of light absorption efficiency in InSb nanowires

Abstract

We report on measurements of the light absorption efficiency of InSb nanowires. The absorbed 70 fs light pulse generates carriers, which equilibrate with the lattice via electron-phonon coupling. The increase in lattice temperature is manifested as a strain that can be measured with X-ray diffraction. The diffracted X-ray signal from the excited sample was measured using a streak camera. The amount of absorbed light was deduced by comparing X-ray diffraction measurements with simulations. It was found that 3.0(6)% of the radiation incident on the sample was absorbed by the nanowires, which cover 2.5% of the sample.

Nanowires are important in many applications,¹ from nanoelectronics, where semiconductor nanowires can be used as field effect transistors,² to photonics³ and thermoelectrics.^4,5 Experimental studies on light absorption by nanowires can be important for the development of nanowire-based solar cells. The problem of measuring the absorbed-to-incident flux ratio has been addressed in several studies, in which high light absorption by nanowires was predicted theoretically^6–9 and demonstrated experimentally.^10,11 In the experimental studies, the photocurrent contribution from the nanowires and from the substrate cannot be separated.

Structurally sensitive time-resolved methods directly probe the atomic positions and enable studies of strain,¹² buckling,¹³ and phase-transitions^14,15 in semi-conductors. Time-resolved X-ray diffraction has been employed to study nanolayered materials^16,17 and the eigenmodes of nanowires as they bend and contract/expand along the lateral dimension of the nanowire.¹⁸

In this Letter, we present a method for measuring the temperature rise following light absorption in nanowires. We employed a laser pump/X-ray probe technique to measure the thermal strain in InSb nanowires. This can be used to measure how much of the incident light is converted to heat. It can also serve as a test for models of light-absorption in nanowires. When irradiating a low-bandgap material, electrons are excited. As the hot electrons equilibrate with the lattice, the deposited energy is converted to heat within ∼10 ps.¹⁹ Thus, the temperature rise directly corresponds to the amount of absorbed light energy. The heat results in thermal expansion, which can be studied using time-resolved X-ray diffraction. A similar behavior can be expected in higher-bandgap materials such as Si.²⁰

The samples were InSb (111)B nanowires grown on an InAs (111)B substrate.²¹ InSb was chosen due to the low bandgap, which ensures effective conversion of 1.5 eV light to heat. The length of the nanowires was 1.7 μm and the average diameter 80 nm. The wires are attached to the substrate via an InAs stem, which has a diameter of 50 nm and a length of 100 nm. They were grown by Metalorganic vapour phase epitaxy (MOVPE) using trimethylindium, trimethylantimony, and arsine precursors on an InAs (111)B substrate prepared with Au nanoparticles. The density of the nanowires on the surface of the substrate was 5 nanowires/μm². An SEM image of the sample can be seen in Fig. 1(a).

FIG. 1.

(a) SEM image of the InSb nanowire sample at an oblique angle of 14°. (b) Experimental setup.

The experiment was carried out at beam line D611 at the MAX II electron storage ring in Lund, Sweden. Beam line D611 is dedicated to laser-pump/X-ray probe experiments. It has a double-crystal InSb monochromator with a bandwidth of $\Delta \mathrm{E}/\mathrm{E}=4·{10}^{-4}$, which operates in the spectral range between 1.8 and 8 keV. A 400 × 200 μm² X-ray focal spot size can be obtained with 7 × 0.7 mrad² divergence (horizontal × vertical). The InSb (111) reflection was studied at a Bragg angle of 59° and normal laser incidence (see Fig. 1(b)). At this Bragg angle, the peak X-ray reflectivity occurs at an energy of 1.93 keV. Hence, the X-rays were impinging from the side and the full length of the nanowires was probed.

Short laser pulses were generated by a passively mode-locked, titanium-doped sapphire oscillator followed by a cryogenically cooled Ti:Al₂O₃ multipass laser amplifier. The amplifier was operated at 4.25 kHz and an average power of 2.5 W. The wavelength was centered around 780 nm, and the pulse duration was 70 fs. The laser system was synchronized to a single electron bunch in the MAX II storage ring with a jitter of 30 ps. The laser and the X-rays were overlapped in time and in space. Laser pulses with fluences up to 10 mJ/cm² were used to excite the sample, and the diffracted signal was measured with a streak camera.²² In the present study, the time window of the streak camera was extended to 300 ps, which limited the temporal resolution of the experiment to 10 ps.

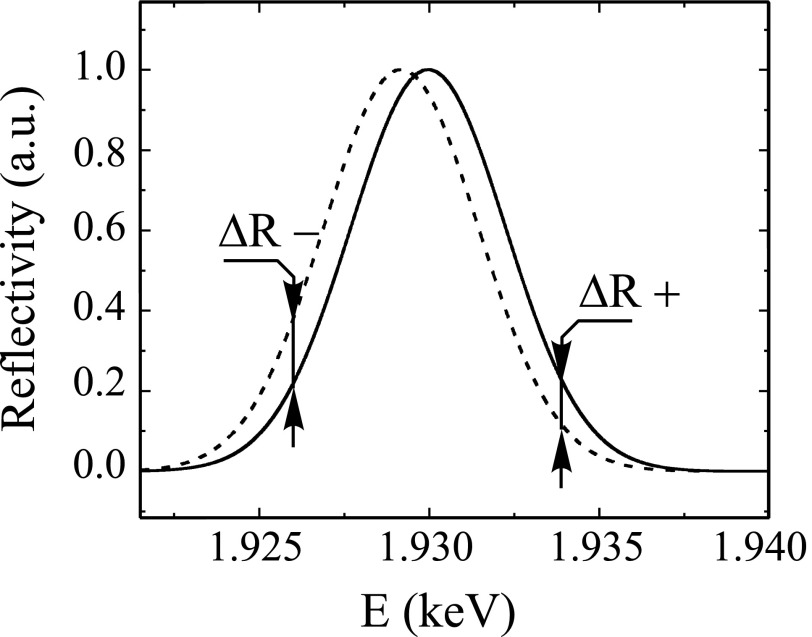
The X-ray intensity was first experimentally measured as function of X-ray energy for the unexcited sample. The X-ray scans were performed around the InSb(111) diffraction peak at 1.93 keV. These X-ray energy scans are important for use in the analysis. The interaction length of the X-rays is about 160 nm as the X-rays propagate through the 80 nm nanowires at an angle of 59°. This results in a relatively broad reflectivity curve due to the finite interaction length.²³ Theoretically, it would be expected that the peak in the X-ray energy scan for a single nanowire would have a width of 4.5 eV. The width of the peak in the measured energy scan was 5.3 eV due to angular dispersion of the nanowires.

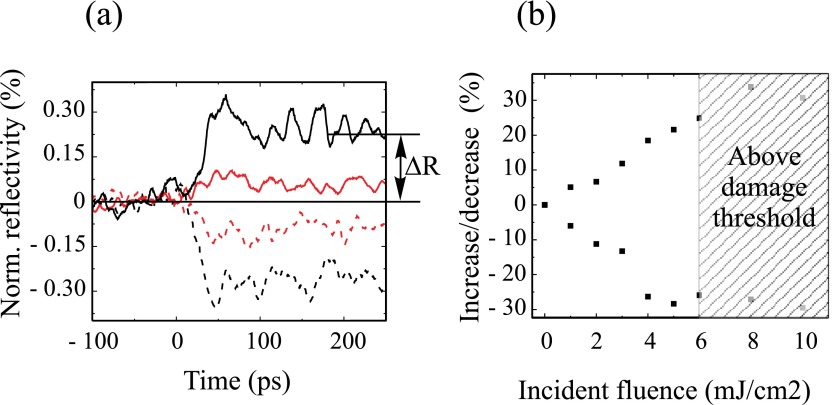
After the initial time-integrated energy scans, the X-ray intensity as function of time was measured for fixed energies. The streak camera is designed to measure the reflected intensity for a single energy at a time. As can be seen in Fig. 2, the size of the shift can be evaluated by comparing the reflectivity changes on the shoulders of the peak. So in order to deduce the shift of the energy scan induced by laser heating, the time-resolved change in reflectivity was measured for two X-ray energy offsets, 4 eV above and below, the peak X-ray energy. In order to obtain a reliable experimental value of the reflectivity change, the laser excitation was periodically turned on and off synchronized to the data acquisition. The normalized difference signal (R_on − R_off)/R_off was obtained from the X-ray reflectivities with (R_on) and without (R_off) the laser. The X-ray intensity changes following laser excitation for the two recorded X-ray energies are shown in Fig. 3(a) for a set of laser fluencies. After laser excitation, the reflectivity curve shifts towards lower energies, corresponding to expansion of the crystal lattice. The large initial strain, consisting of propagating¹² and stationary strain, builds up in 50 ps. The effect of the propagating strain wave decays due to dephasing²⁴ and after 200 ps only the stationary strain influences the X-ray intensity. Fig. 3(b) shows the change in normalized reflectivity 200 ps after laser excitation as function of incident laser fluence.

FIG. 2.

Experimentally measured X-ray reflectivity (R) as function of X-ray energy (E). The peak reflectivity has been normalized to 1. The solid line is an energy scan recorded from the unexcited sample, and the dashed line has been shifted to account for a uniform 0.05% change of the lattice constant. As can be seen, the reflectivity changes (ΔR⁺, ΔR⁻) measured off the peak will depend on the size of the shift.

FIG. 3.

(a) Experimentally measured change in X-ray reflectivity for two fluences (6 mJ/cm² black lines and 2 mJ/cm² red lines) as a function of time. Data were acquired for two X-ray photon energies −4 eV (solid lines) and +4 eV (dashed lines) off the peak in the energy scan. The way the change in reflectivity due to heating (ΔR) has been measured is indicated for one of the curves. (b) Normalized change in X-ray reflectivity as function of incident laser fluence.

For values exceeding 6 mJ/cm², the static X-ray reflectivity was permanently reduced, showing that fewer wires contributed to the signal. The laser damage was also investigated using SEM, and it was found that most wires had been broken at the stem for the highest laser fluences. This circumstance affects the reliability of the data above 6 mJ/cm². However, our evaluation of the amount of absorbed heat would not be significantly altered if the high fluence points are included in the analysis.

In order to calculate the heat stored in the nanowires from the reflectivity changes, we calculated energy scans for laser heated nanowires for a range of fluences. The first step was to calculate the heat distribution along the wire. This was based on simulating the light absorption and subsequently modeling the heat diffusion. We used Comsol Multiphysics™ to simulate laser absorption in InSb nanowires, using the optical properties for bulk InSb.²⁵ In the simulation, a plane wave with a wavelength of 800 nm was launched towards a nanowire and the underlying substrate. The wave propagation direction was parallel to the nanowire. The reflections from the wire and substrate surfaces were included, as well as diffraction, and the light absorption in the wire. The simulation was performed in 3D in order to correctly account for effects of the light polarization. The light absorption profile is shown in Fig. 4(a). We have not found other calculations for InSb on a substrate, but the data resemble those obtained by Wu et al. for InAs nanowires of similar dimensions.⁹

FIG. 4.

(a) Simulated light absorption of 800 nm radiation in an 80 nm diameter InSb nanowire for normal incidence to the top surface with the polarization of the light in the plane of the paper. The incident fluence was 1 mJ/cm². This corresponds to the heat distribution shortly after excitation before heat conduction has smeared out the distribution. (b) The heat distribution following 200 ps of heat diffusion using the bulk heat conductivity. After 200 ps, the initial radial distribution has evened out and is the time at which we evaluate the stored heat in the wire.

Subsequently we also used Comsol Multiphysics™ to calculate the heat diffusion to obtain the heat distribution after 200 ps, which is shown in Fig. 4(b). In this simulation, the heat diffusion into the substrate was included by keeping the base of the nanowire fixed at room temperature.

The energy deposited as heat in the nanowire leads to a temperature rise ΔT given by

$$\Delta T(z)=W(z)/C=Q\cdot W_{\mathit{N}\mathit{o}\mathit{r}\mathit{m}}(z)/C,$$ (1)

where C is the specific heat per unit volume. W(z) is the heat distribution that we calculated, Q is the total amount of heat in the wire that is to be experimentally determined, and W_Norm(z) is the normalized calculated heat distribution. After 200 ps, the radial heat distribution is uniform as can be seen in Fig. 4(b).

The change in the crystal lattice spacing is related to the temperature rise by

$$\frac{\Delta d}{d}=\beta \Delta T,$$ (2)

where $\beta$ is the linear expansion coefficient, and d is the lattice spacing. The strain is then defined as Δd/d × 100 (%), where $\Delta d$ is the change in crystal lattice spacing, and d is the crystal lattice spacing at thermal equilibrium.

Finally, we constructed simulated X-ray energy scans using the strain distribution calculated in Comsol Multiphysics™. The integration of the signal from the entire wire was carried out as follows. The nanowire is numerically divided into 10 nm thick discs. The temperature does not vary significantly within each disc and can be considered constant. The shift in the energy scan for each disc is given by Eq. (3), which is valid for the small strains considered here

$$\frac{\Delta E}{E}=-\frac{\Delta d}{d}.$$ (3)

Each disc was assigned an energy scan shifted according to Eq. (3). The energy scans of all the discs were then added. The reflectivity changes from these curves were compared to the experimental time-resolved data. The total amount of heat was set as free parameter and was varied to obtain the same reflectivity drop as the experimental data.

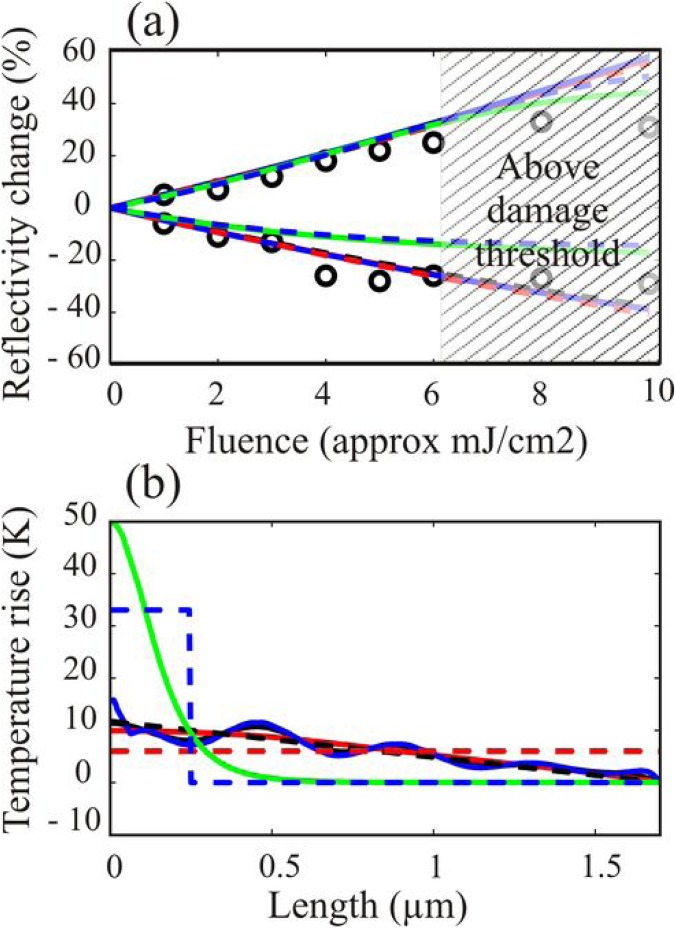
In order to ensure that the high laser intensity does not influence the results, i.e., that the results are also valid for normal solar cell conditions, we evaluated data for fluences ranging from 1 to 5 mJ/cm², and the results are shown in Fig. 5(a). We found that 3.0% of the incident energy was absorbed by the nanowires that cover 2.5% of the sample area.

FIG. 5.

(a) The sensitivity for the assumed heat distribution was tested by comparing experimentally measured and calculated changes in X-ray reflectivity (ΔR). The calculations were carried out using different heat distributions, shown in Figure 5(b). The solid black curve uses the heat distribution calculated with the bulk parameters. The solid blue curve has a 10 times lower heat conductivity, while the solid red curve has a 10 times higher heat conductivity. These three curves are nearly completely overlapping. The solid green curve is for an artificially constructed exponential absorption profile followed by 200 ps of heat diffusion using the bulk parameters. The dashed blue curve is for a 250 nm box, the dashed black curve is for a linear profile, and the dashed red curve is when for an even heat distribution. It can be seen that the two artificial curves with a very uneven distribution (box and exponential) deviate significantly from the experimental data well below damage threshold, while all other curves follow each other closely. (b) The different heat distributions used in investigating the robustness of the method. The solid black curve was calculated from the light absorption followed by thermal diffusion during 200 ps using bulk heat conductivity (18 W/m·K), the solid blue curve was calculated using 1.8 W/m·K. These two curves overlap each other almost completely. The solid red curve was calculated using (180 W/m·K). The solid green curve was calculated using exponential absorption from the top surface, the dashed black curve is a linear profile, the dashed blue curve is a 250 nm box, and the dashed red curve is when there is an even heat distribution.

Other methods measuring the photocurrent cannot measure the contribution only from nanowires but is influenced also by the substrate. Since the nanowires are grown on a stem and because heat propagation is slow, there is no thermal cross-talk between nanowires and substrate. In order to verify and quantify this statement, we have carried out simulations. The thermal energy that leaves the wire in 200 ps is less than 3% even if a 10 times higher heat conductivity is used.²⁶ Heat from the substrate propagated through the stem and heated the lower 50 nm of the nanowire by less than 3 K after 200 ps at an incidence fluence of 6 mJ/cm². The heat from the substrate propagating into the wire could give an error in the measured amount of absorbed light less than 2%.

To investigate the robustness of the method with respect to the model-dependent heat distribution, we also evaluated our data based on a number of other heat distributions. In order to investigate the influence of the thermal conductivity, we used two distributions which are similar to the calculated distribution above, but we artificially employed a 10 times too high and a 10 times too low heat conductivity. This is of particular importance since the heat transport properties can be changed by the confining nano-geometry.²⁷ It has also been observed that a large electron-hole density gradient may significantly modify the heat conductivity of bulk InSb.²⁶ Both of these effects modify the heat distribution within the wire but do not influence the deduced absorbed energy. We also tested the robustness by using a set of artificial heat distributions as shown in Figure 5(b).

We show the comparison between experimentally measured and calculated reflectivity changes for seven different heat distributions in Fig. 5(a). For all of them, there is a deviation from a linear behavior, which is due to the shape of the energy scan. A linear increase with fluence only occurs when the temperature changes in all parts of the wire are so small that the wing of the energy scan can be considered a linear function. The shape of the fluence dependence can be analyzed in order to see how accurate the assumed heat distribution is. In particular, the three curves calculated from the calculated absorption profile and different heat conductivities overlap almost completely. The values for the fraction of absorbed light are given in Table I. The values differ by <4%, showing that the method is insensitive to the actual heat distribution. For the exponential and the box distributions, there is a larger deviation, but there is also a deviation from the experimental data in Fig. 5(a) well below damage threshold showing that these distributions are not valid.

TABLE I.

Dependence on deduced amount of absorbed heat depending on the heat distribution profiles. The profiles are shown in Fig. 5(b).

Heat distribution	Fraction of incident energy absorbed (%)
Calculated using bulk heat conductivity (18 W/m K)	3.0
Calculated using (1.8 W/m K)	3.0
Calculated using (180 W/m K)	3.1
Calculated using exponential absorption from surface	2.5
Linear	2.9
Box	2.4
Even	3.0

We estimate the experimental uncertainty in this study to 20%, which is the error associated with measuring the laser fluence. This uncertainty is due to the difficulty of determining the beam profile at the point where the X-ray beam is probing the interaction. This dominating uncertainty accounts for the error bar.

In conclusion, we have demonstrated that it is possible to directly measure the light absorption in nanowires using time-resolved X-ray diffraction. This opens up the possibility to optimize nanowire solar cell materials by systematic studies in which the absorption in different materials and structures of different diameters can be studied as a function of incidence angle and wavelength.