Topical Review: Molecular reaction and solvation visualized by time-resolved X-ray solution scattering: Structure, dynamics, and their solvent dependence

Abstract

Time-resolved X-ray solution scattering is sensitive to global molecular structure and can track the dynamics of chemical reactions. In this article, we review our recent studies on triiodide ion (I₃^–) and molecular iodine (I₂) in solution. For I₃^–, we elucidated the excitation wavelength-dependent photochemistry and the solvent-dependent ground-state structure. For I₂, by combining time-slicing scheme and deconvolution data analysis, we mapped out the progression of geminate recombination and the associated structural change in the solvent cage. With the aid of X-ray free electron lasers, even clearer observation of ultrafast chemical events will be made possible in the near future.

I. INTRODUCTION

Chemistry in solution and liquid phases is an important field of research because many reactions in chemistry and biology occur in solution. The major challenge in understanding solution-phase chemistry arises from the presence of numerous solvent molecules surrounding solute molecules. Solvent serves as an energy source for activating a reaction as well as a heat bath to stabilize the products. As a result, the properties of solvent can significantly influence the energy landscape, rates, and pathways of a reaction in solution. Therefore, to have a better understanding of solution-phase chemical dynamics, it is important to consider complex influence of the solvent medium on the reacting molecules, i.e., solute-solvent interaction. Accordingly, the interplay of solute and solvent molecules and its effect on the outcome of chemical reactions have been a topic of much interest in the field of reaction dynamics.

Investigation of reaction dynamics in solution phase requires appropriate tools that can monitor the progress of the reactions and related dynamics processes. Over many decades, time-resolved optical spectroscopy has served as tools for measuring the dynamics of solution-phase reactions and solvation processes on the time scales down to tens of femtoseconds. The application of time-resolved optical spectroscopy to the studies of reaction dynamics has become possible with rapid advances in the laser technology, making ultrashort light pulses in the ultraviolet, visible, and infrared frequencies readily available with the pulse duration of femtoseconds to picoseconds. In particular, transient absorption and emission spectroscopies (a.k.a. pump-probe spectroscopy) based on electronic transitions of molecules have been most commonly used to study the time evolution of the populations of reactants and products with the progress of the reaction^1–4 because (1) electronic transitions usually have high oscillator strengths (and thus high sensitivity) and (2) visible laser pulses are most readily available technically. More recently, time-resolved vibrational spectroscopies, which employ infrared absorption (time-resolved IR spectroscopy)^5–7 or Raman scattering (time-resolved Raman spectroscopy)^8–11 as probe, have been increasingly used to study the reaction dynamics in solution. Compared to conventional transient absorption spectroscopy performed at visible and ultraviolet frequencies, the time-resolved vibrational spectroscopy has higher structural sensitivity because the frequencies of vibrational transitions are closely associated with molecular structure. Recently, transient absorption and vibrational spectroscopies have been extended to multidimensional frequency spaces, for example, two-dimensional (2D) electronic spectroscopy^12–16 and 2D-IR spectroscopy.^14,17–19 A measured 2D spectrum represents the instantaneous frequencies of transient absorption and emission mapped out in a two-dimensional frequency space in a correlated manner. From a series of 2D spectra measured along the population time period (i.e., a time axis scanned in the pump-probe spectroscopy), the population dynamics of multiple excited states and the excitation transfer among them can be kept track of unambiguously.

Besides the reaction dynamics of solute species, the dynamics of solvation resulting from solute-solvent interaction were also studied extensively using optical spectroscopic methods such as transient hole burning,^20–22 time-resolved fluorescence Stokes shift (TRFSS),^23–27 and photon echo peak shift (PEPS).^27–31 These third-order nonlinear spectroscopies monitor time-dependent spectral properties of the solute undergoing nonequilibrium relaxation, thus providing indirect information on the dynamic behavior of solvent in terms of spectral density. Later, higher-order coherent Raman techniques were developed to provide more direct view of the solvation response, for example, resonant-pump polarizability response spectroscopy (RP-PORS)^32,33 and resonant-pump third-order Raman probe spectroscopy (RAPTORS).^34,35 These techniques, which employ a pump pulse resonant with electronic excitation of the solute and an off-resonant impulsive Raman probe, are designed to measure the spectrum of low-frequency solvent motion (and its evolution) coupled to nonequilibrium relaxation of the solute. Therefore, these methods can directly probe the evolution of solute-solvent interaction in response to the chemical reaction of the solute, that is, instantaneous spectral density.

While the time-resolved spectroscopic methods described above are effective for resolving fast dynamics and spectral signatures of chemical reactions and solvation processes in solution, they provide only limited information on the changes of molecular structure associated with the dynamic processes. Such limitation arises from the fact that optical spectroscopic signals originate from absorption, emission, or Raman scattering of light. As a result, the spectroscopic signals are directly related to the populations of specific electronic, vibrational, or rotational states but not to the global molecular structure. As a means of overcoming this limitation in structural sensitivity of optical spectroscopy, time-resolved X-ray solution scattering (TRXSS) or time-resolved X-ray liquidography (TRXL) has emerged as an alternative method of probing the reaction dynamics in solution. By combining structural sensitivity of X-ray scattering and picosecond time resolution based on short X-ray pulses generated from synchrotrons, this technique is capable of resolving structural changes of rapidly reacting molecules. Thus far, TRXSS has been applied to the chemical reactions of many molecular systems in liquid and solution phases, revealing the dynamics, reaction mechanism, and structures of reaction intermediates of the reactions.^36–72 The molecular systems studied using this technique include diatomic or triatomic molecules (I₂, Br₂, HgI₂, HgBr₂, and I₃^–), haloalkanes (CBr₄, CHI₃, CH₂I₂, C₂H₄I₂, and C₂F₄I₂), organometallic compounds (Ru₃(CO)₁₂, Os₃(CO)₁₂, [Ir₂(dimen)₄]²⁺, [Fe(bpy)₃]²⁺, cis-[Ru(bpy)₂(py)₂]²⁺, and [Pt₂(P₂O₅H₂)₄]^4–), nanoparticles, and biological macromolecules (myoglobin, hemoglobin, homodimeric hemoglobin, photoactive yellow protein, cytochrome-c, and proteorhodopsin). These studies have established that TRXSS complements time-resolved optical spectroscopy because diffraction signals are sensitive to all chemical species simultaneously and each chemical species has a characteristic diffraction signal that can be quantitatively calculated from its three-dimensional atomic coordinates and thus can serve as a fingerprint of the chemical species. Since X-rays scatter from all atoms in the solution sample, including both the solute and the solvent, the analysis of TRXSS data provides the temporal behavior of the solvent as well as the structural progression of all the solute molecules in all reaction pathways, thus providing a global picture of the reactions and accurate branching ratios between multiple reaction pathways. In a typical application of TRXSS, the reaction intermediates are identified and their reaction rates are determined with time resolution of ∼100 ps, limited by the X-ray pulse width available at typical third-generation synchrotrons.

Recently, we have succeeded in advancing TRXSS to the next level in terms of structural details and achievable time resolution via the studies of triiodide (I₃^–) ion and molecular iodine (I₂) in solution, which will be reviewed in this article. These molecular systems are two of the simplest reactions occurring in solution and thus can be used as good model systems for demonstrating the powerfulness of TRXSS. By performing the TRXSS experiments on these simple molecules in various solvents, we comprehensively investigated the dynamical aspects of the photochemical reactions, including structural dynamics of solute and solvent molecules, reaction mechanism, and their solvent dependence. Compared with previous studies, in the case of triiodide ion, we determined the precise bond lengths and angles of the ground-state ion, which were found to exhibit strong solvent dependence. Extracting the structure of the solute is not trivial because the solute is the minor species accounting for only about 2% of the solution and thus the typical scattering signal from a solution is overwhelmed by the contribution from the solvent, the majority species of the solution. In the case of molecular iodine, by applying deconvolution data analysis to the data collected with time-slicing scheme, the time-dependent change of the bond length of a newly born iodine molecule was revealed with time resolution of ∼10 ps, which is substantially better than the typical time resolution achieved in previous studies. In addition, time-dependent structural progression of the solvent cage surrounding the solute, which is the spatial arrangement of the solvent molecules around the solute molecule, was also mapped out for the first time. Concluding this review, we provide the outlook of TRXSS studies in the near future.

II. PRINCIPLE OF TIME-RESOLVED X-RAY SOLUTION SCATTERING

A. Scattering signal directly related to molecular structure

The general theory of X-ray diffraction is well established for both ordered and disordered samples. Specifically, diffraction of X-rays from disordered samples is often called diffuse scattering so that it can be distinguished from the diffraction from well-ordered crystalline samples (i.e., Bragg diffraction). Since the target system of TRXSS experiment is randomly oriented molecules in liquid phase, and, therefore, we will use the term of “scattering” instead of “diffraction” in this paper. The X-ray scattering intensity is typically expressed as a function of q, the momentum transfer between the incident wave (k₀) and the elastically scattered X-ray wave (k). TRXSS offers the advantage over time-resolved spectroscopy in terms that the scattering signal from each molecule can be directly calculated from the three-dimensional atomic coordinates of the molecule using the following equation:

$$I(q)={\displaystyle \sum _{i=1}^N{I}_i(q)+2{\displaystyle \sum _{i=1}^{N-1}{\displaystyle \sum _{j=i+1}^N{F}_i(q)F_j(q)\frac{\sin q{r}_{\mathit{i}\mathit{j}}}{q{r}_{\mathit{i}\mathit{j}}}}}},$$ (1)

where i and j are the indexes for a pair of different atoms. F_i(q) and F_j(q) are the atomic form factors of the ith and jth atoms, respectively, and r_ij is the distance between the ith and jth atoms. Each chemical species has its own characteristic scattering pattern, which can therefore be used to monitor the time evolution of its concentration. In practice, quantum calculations generally predict the molecular structure more accurately than energy levels and spectra, therefore providing good starting points for the data analysis of TRXSS.

B. Experimental data measured in q space and its Fourier transform to r space

In the TRXSS experiment, scattering patterns from solution samples are measured before and after laser excitation and those patterns are subtracted from each other in order to extract only the contributions from structural changes induced by a chemical reaction, resulting in the elimination of all other background signals. Time-dependent difference scattering curves, ΔS(q,t), are obtained by azimuthal integration of two-dimensional (2D) scattering patterns and contain direct information on the structural changes of solute molecules in the solution. To achieve high signal-to-noise ratio, more than 50 scattering patterns are usually acquired and averaged at each time delay between the laser and X-ray pulses. Typically, an averaged ΔS(q,t) gives a signal-to-noise ratio up to 15. To emphasize the oscillatory features at high angles (or at low q values), ΔS(q,t) is often multiplied by q or q² values such that qΔS(q,t) or q²ΔS(q,t) (equivalently, rΔS(r,t) or r²ΔS(r,t) in r-space) is often used for data presentation.

Since X-rays scatter from all atoms in a solution sample, including both solute and solvent, the X-ray solution scattering signal can be decomposed into three contributions (see Figure 1): (1) the solute-only term reflecting the intramolecular atomic rearrangement of solute species, (2) the solute-solvent cross term (also called the cage term) induced by the changes in the intermolecular atomic configuration between solute and solvent pairs, and (3) the solvent-only term (hydrodynamics) arising from the changes in the temperature and density of bulk solvent as a result of heat transfer from photon-absorbing solute molecules. The fact that we have to deal with all three terms greatly complicate the data analysis but the reward is that we can extract structural dynamics information for not only the solute but also the solvent and the solvent cage (solute-solvent term). Theoretical difference scattering curves considering these three contributions can be expressed as follows:

$$\begin{array}{c}\Delta S{(q,t)}_{\mathit{t}\mathit{h}\mathit{e}\mathit{o}\mathit{r}\mathit{y}}=\Delta S{(q,t)}_{\text{solute-only}}+\Delta S{(q,t)}_{\text{solute-solvent}}+\Delta S{(q,t)}_{\text{solvent-only}}\\ =\Delta S{(q,t)}_{\text{solute-related}}+\Delta S{(q,t)}_{\text{solvent-only}}\\ =\left[{\displaystyle \sum _k{c}_k(t)S_k-S_g(q){\displaystyle \sum _k{c}_k(0)}}\right]+{(\partial S/\partial T)}_{\rho }\Delta T(t)+{(\partial S/\partial \rho )}_T\Delta \rho (t),\end{array}$$ (2)

where k is the index of the solute species (that is, reactants, intermediates, and products), c_k(t) is the concentration of kth species as a function of time delay t, S_k(q) is the solute-related (that is, solute-only and cage components) scattering intensity of kth species, and S_g(q) is the scattering intensity related to the reactants (g = reactants). (∂S(q)/∂T)_ρ is the change in the solvent scattering intensity in response to the temperature rise at a constant density, (∂S(q)/∂ρ)_T is the solvent scattering change with respect to the change of solvent density at a constant temperature, and ΔT(t) and Δρ(t) are the changes in temperature and density of the solvent, respectively, at a time delay t. By fitting the experimental difference scattering curves measured at various time delays using the theoretical difference scattering curves in Eq. (2), we can extract the dynamical information on the solute species, solute-solvent interaction, and solvent as described in detail below.

FIG. 1.

Schematic representation of the three principal contributions to the X-ray solution scattering for an I₃^– ion dissolved in water. The I, O, and H atoms are colored in purple, red, and white, respectively. Red arrows indicate atomic pairs of the solute only, while blue and green arrows represent solute–solvent and solvent-only atomic pairs, respectively.

Although ΔS(q,t) contains direct information on the structural changes of molecules in solution sample, the X-ray scattering data presented in the reciprocal space (that is, q-space) is not very intuitive. To make the scattering signal more intuitively interpretable, ΔS(q,t) can be sine-Fourier transformed into the real space (r-space) as follows:

$$\Delta S(r,t)=\frac{1}{2{\pi }^{2}r}{\displaystyle {\int }_0^{\infty }q\Delta S(q,t)\sin (qr)\exp (-q^2\alpha )\mathrm{d}q},$$ (3)

where the constant α is a damping constant to account for the finite q range of the experiment. This real-space representation of the difference scattering data corresponds to the distance distribution function of all the atom–atom pairs (that is, radial distribution function) present in the solution sample and represents structural evolution of reacting molecules with the progress of the reaction. For example, positive and negative peaks of ΔS(r,t) indicate the formation and depletion, respectively, of an atom-atom pair at the corresponding interatomic distance.

C. Pair distribution function connecting experiment and theory

In Eq. (2), S_k(q)'s are calculated from molecular dynamics (MD) simulations combined with quantum calculations. From MD simulations, atom-atom pair distribution function (PDF), g_R(r), is calculated for a particular atom–atom pair (R). Then, the S_k(q) curves are computed using an equation including a sine Fourier transform of g_R(r) – 1. The solute-only term is obtained by using g_R(r) for atomic pairs of only solute molecules while it can also be described by Debye scattering of isolated solute molecules in the gas phase. The cage term is calculated when g_R(r) for the solvent-solute cross pairs are used in the Fourier transform. In practice, g_R(r) for both solute-only atomic pairs and solute-solvent cross pairs is used to yield the solute-related terms, S_k(q). The solvent differential functions, (∂S(q)/∂T)_V and (∂S(q)/∂V)_T, can either be obtained by MD simulations or be measured from a separate experiment where the pure solvent is vibrationally excited by near-infrared light.⁴⁰ The latter gives superior agreement than the former does. In general, g_R(r) from MD simulation for a particular atomic pair can be used to calculate the contribution from that pair to the overall signal, thereby aiding the peak assignment. By combining the solute-related terms and solvent-only terms using Eq. (2), time-dependent theoretical difference scattering curves are constructed.

D. Extracting reaction dynamics and mechanism from TRXSS data

The treated experimental difference scattering curves, ΔS(q,t), are fit by the theoretical difference scattering curves using weighted least-squares fitting, whereby the difference between the experimental data and the theoretical model function, i.e., chi-square (χ²), is minimized. Since the experimental ΔS(q,t) curves at various time delays are related to each other through reaction kinetics, they are globally fit by minimizing the sum of “reduced” χ² values at all positive time delays

$${\chi }_{\text{reduced}}^2=\frac{1}{N-m-1}{\displaystyle \sum _{j=\text{time}\hspace{0.17em}\text{delay}}{\displaystyle \sum _i{\left(\frac{\Delta S_{\text{theory}}\left(q_i,t_j\right)-\Delta S_{\text{experiment}}\left(q_i,t_j\right)}{{\sigma }_{i,j}}\right)}^2}},$$ (4)

where N is the number of data points along q axis, m is the number of fitting parameters, and σ_i,j is the standard deviation of the experimental noise present in ΔS_experiment(q,t) at q_i and time delay t_j. Since the difference between the experimental and theoretical difference scattering curves is divided by the standard deviation of the experimental error, the reduced χ² can have a minimum value of 1, which means the theoretically allowed best fit. The reduced χ² is commonly used as a measure of the goodness of a fit.

The fitting parameters of the global fitting analysis usually consist of rate constants of various reaction pathways, branching ratios among photoproducts, the size of laser spot at the sample, etc. Time-dependent functions, c_k(t), ΔT(t), and Δρ(t), describing the reaction dynamics depend on those fitting parameters. Based on a kinetic model including all reasonable candidate reaction pathways, a set of rate equations are constructed in order to extract the mechanism of a reaction. Integrating the rate equations provides c_k(t)'s that are used to construct the theoretical scattering signal. The ΔT(t) and Δρ(t) are mathematically linked to c_k(t)'s and each other by energy conservation, mass conservation, and hydrodynamics. From c_k(t)'s, time-dependent heat released from photoexcited solutes to the solvent, Q(t), is calculated. Q(t) is used to compute ΔT(t) and Δρ(t) via thermodynamic and hydrodynamics relations. The solvent can be heated by processes such as vibrational cooling occurring on a time scale too fast to be captured with the ∼100 ps time resolution. The amount of heat caused by these processes is also included in Q(t) by considering the fraction that enters these processes among the initially photoexcited species. Further details of the X-ray solution scattering experiment and data analysis are described in Refs. 47, 48, and 57.

E. Structural analysis of TRXSS data combined with optimization of molecular structure

The analysis of TRXSS data described above focuses on characterizing the transition dynamics between various reaction intermediates. In this analytical approach, each reaction intermediate is assumed to be at quasi-equilibrium and, therefore, the molecular structure optimized by quantum calculation is used as the structure of each intermediate without any structural modification. Although this approach is appropriate for elucidating the reaction dynamics and mechanism of a complex reaction involving many reaction intermediates, it provides only limited information on the structure of chemical species participating in the reaction. Especially, this analysis might be ineffective for the reaction systems where the structure of a solute species changes sensitively with the reaction environment. For example, the structure of I₃^– ion in the ground state exhibits subtle changes depending on the hydrogen-bonding ability of the surrounding solvent. To overcome such limitation of the conventional TRXSS analysis, we applied an advanced approach of analysis to structural characterization of I₃^– ion as detailed in Sec. III B. Briefly, when we fit experimental difference scattering curves of I₃^– by theoretical scattering curves, we adjusted five structural parameters of I₃^– ion: three bond distances for I₃^– ion (R₁, R₂, and R₃ for the distance between I₁ and I₂, I₂ and I₃, I₁, and I₃, respectively, as shown in Figure 7), the bond distance for I₂^– fragment (R₄), and temperature change. By minimizing the deviation between the experimental and theoretical scattering curves by least-squares fitting, we determined the optimal structural parameters of I₃^– ion, elucidating the exact molecular structure of the ion. This analysis method is somewhat analogous to the structural refinement of the intermediates formed in the protein structural transition aided by Monte Carlo simulations.⁷³

FIG. 7.

Schematic of (a) our experimental approach using TRXSS experiment and (b) data analysis. Upon irradiation at 400 nm, I₃^– ion dissociates into I₂^– and I, and the temperature of the solution increases. By taking the difference between scattering patterns measured before and 100 ps after laser excitation, only the laser-induced changes are extracted with all other background contributions being eliminated. The structural information can be extracted by the maximum likelihood estimation using five fitting parameters. Three bond distances of I₃^– can be clearly identified, giving the exact structure of I₃^– ion in various solvents.

F. Improvement of time resolution using time-slicing scheme and deconvolution

Although TRXSS is an excellent tool for directly probing the structural dynamics of chemical and biological reactions, the time resolution of TRXSS measurement has been limited to 100 ps at third-generation synchrotrons. We expect that this limitation will be alleviated in the near future with the development of X-ray free electron lasers (XFELs), it is still desirable to improve the time resolution of the TRXSS experiments performed at synchrotron sources, especially considering the limited beamtimes at XFELs. As an effort to improve the time resolution, we applied the experimental approach of time slicing and deconvolution to geminate recombination of I₂ in solution as detailed in Sec. IV of this review. Briefly, we measured the time-resolved difference scattering curves, ΔS(r,t), with a time step much shorter than the X-ray pulse duration (100 ps). Subsequently, after elimination of solvent contribution and polychromatic correction, we deconvoluted the temporal profile of the X-ray pulse from ΔS(r,t) to extract the instantaneous response, ΔS_inst(r,t), of the sample molecules. With this experimental approach, we were able to directly obtain time-dependent distribution of I–I bond length of geminately recombining I₂ molecules in real space with much better time resolution. Although very detailed structural information on reacting molecules might be available for only well-studied simple molecules such as I₂, the experimental scheme of time slicing and deconvolution can be generally applied to various reaction systems to improve the time resolution of TRXSS experiment at synchrotron sources.

III. PHOTOCHEMISTRY AND MOLECULAR STRUCTURE OF TRIIODIDE ION

The solute-solvent interaction significantly influences chemistry in solution phase, and it becomes particularly important for ionic species due to the charge present in the ionic species. For example, the solute-solvent interaction sensitively changes with the type of solvent and thus affects the structure of the ions and energy landscape of their reactions. The interplay of ionic species and solvent molecules and its effect on the ion structure and the outcome of reactions have been a topic of intense research over several decades,^74–76 but it is still challenging to describe subtle changes induced by solute-solvent interaction, for example, change in the structure of ionic species.

The I₃^– ion in solution offers a good example that demonstrates the role of solvent in determining the structure of ionic species.^77–88 The candidate structures of I₃^– ion in solution suggested by previous studies are summarized in Figure 2(a). In the gas phase and aprotic solvents where the solute-solvent interaction is weak, the structure of I₃^– is linear and symmetric. In contrast, in protic solvents where strong solute-solvent interaction is present, an antisymmetric stretching mode, which is forbidden for molecules of D_∞h symmetry, was observed in the resonance Raman spectrum,⁸⁰ and a rotationally excited I₂^– fragment was detected in the transient anisotropy measurement of photoexcited I₃^– ion.⁸² These two observations suggest the existence of asymmetric and bent structure of I₃^– ion, respectively. Such lowered symmetry under strong interaction with surrounding environment is known as symmetry breaking.^89–91 The experimental evidences for the symmetry breaking of the I₃^– ion in solution have been supported by theoretical studies using MD and Monte Carlo simulations.^{85–88,92,93}

FIG. 2.

(a) Candidate structures of of I₃^– ion in solution. (b) Schematic of candidate reaction pathways for photodissociation of I₃^– ion in solution.

Despite these evidences, direct characterization of subtle structural change of the I₃^– ion in different solvents is not an easy task. To overcome this difficulty, we applied time-resolved X-ray solution scattering to photodissociation of I₃^– ion in three different solvents: water, acetonitrile, and methanol. TRXSS can directly detect the structures of reactants, intermediates, and products of the reaction and it is also sensitive to solute-solvent interaction (cage term). Therefore, by eliminating the solute term associated with intermediates and products as well as the cage term from the TRXSS signal of the solution, the structure of the ground-state reactant (that is, I₃^– ion) can be extracted. Thus, TRXSS is well suited for probing subtle structural change of I₃^– ion depending on the solvent.

A. Wavelength-dependent photochemistry of triiodide ion

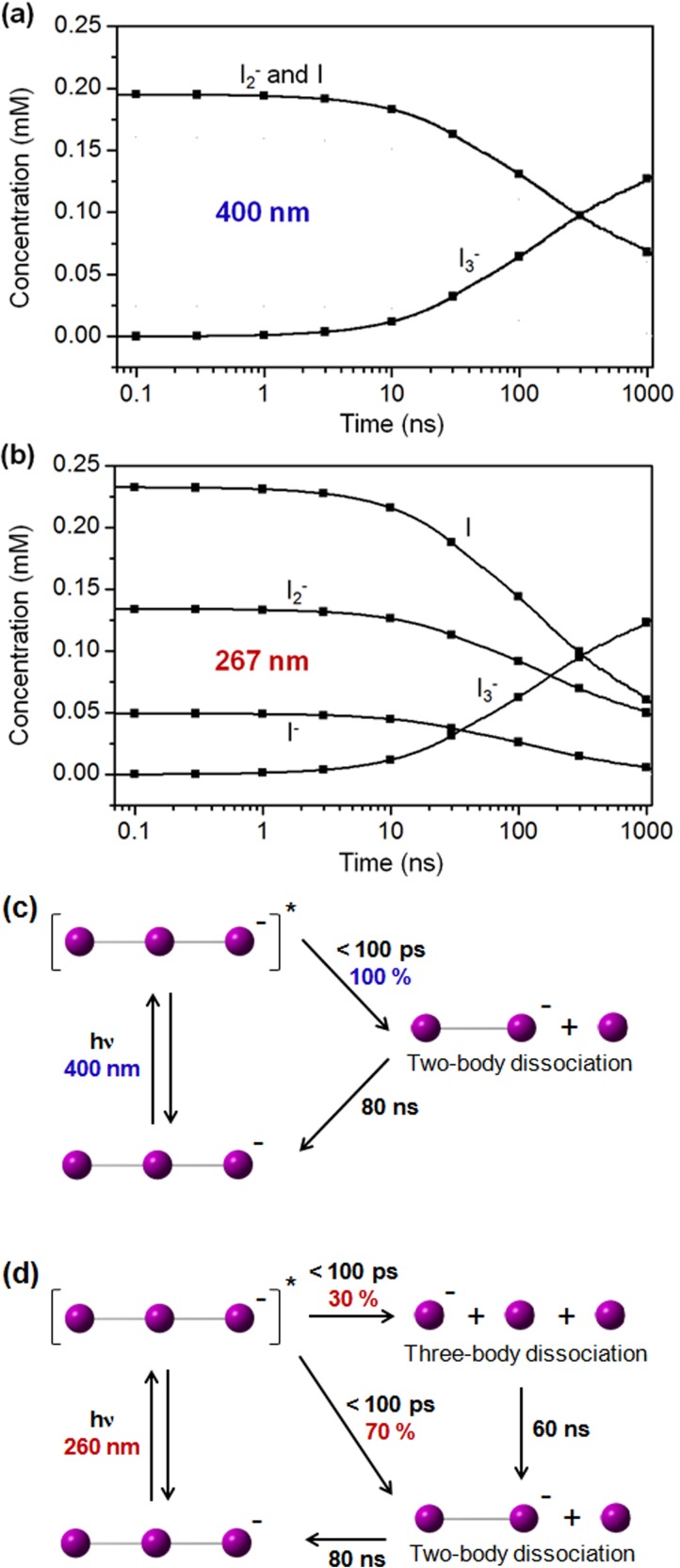
To characterize the exact molecular structure of I₃^– ion in the ground state using TRXSS measurement on photodissociation of I₃^–, we first need to identify the reaction pathways and reaction intermediates of the photochemical reaction so that the contribution of the I₃^– reactant can be extracted appropriately. Photodissociation of I₃^– ion in the solution has been studied using various time-resolved spectroscopic techniques.^77,79–84 One of main interests of those studies was the reaction mechanism that varies with the excitation wavelength. As shown in Figure 2(b), I₃^– ion has three candidate dissociation channels: two-body dissociation (I₂^– + I), three-body dissociation (I^– + I + I), and I₂ formation (I₂ + I^–). From transient absorption studies,^77,78,83 two-body dissociation of I₃^– was identified by detecting the signal from I₂^– fragment. From another transient absorption study,⁸¹ it was found that the quantum yield of two-body dissociation is almost unity with 400 nm excitation but decreases to 0.8 with 266 nm excitation. This reduced quantum yield was attributed to the increasing contribution of three-body dissociation (I^– + I + I) pathway. However, since transient absorption is only sensitive to I₂^– fragment, there has been no direct evidence of three-body dissociation. In contrast, since X-rays scatter off all the atoms in a system, TRXSS can detect any intermediates or products of the reaction and thus is well suited for studying the entire pathways of a reaction.^{36–69,71,72,94} In this section, we investigate the dynamics and mechanism of I₃^– photodissociation at two different excitation wavelengths using TRXSS.⁶¹

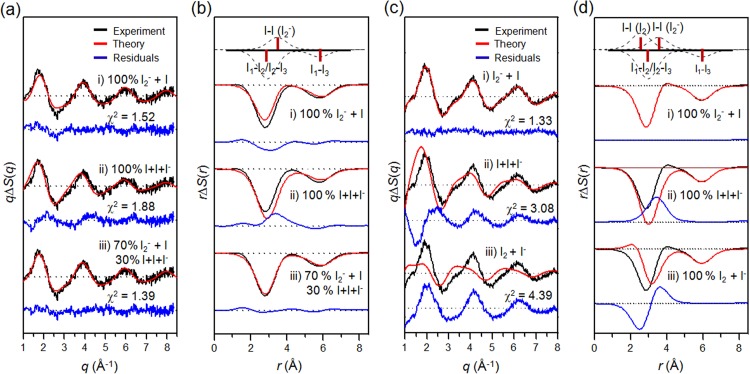
TRXSS measurement was performed using the laser pump–X-ray probe scheme at the beamline NW14A at KEK. Second harmonic generation and third harmonic generation of the output pulses from an amplified Ti:Sapphire laser system provided femtosecond pulses at 400 nm and 267 nm center wavelength, respectively, at a repetition rate of 1 kHz. The scattering curves were measured at the following time delays: −3 ns, −100 ps, 100 ps, 300 ps, 1 ns, 3 ns, 10 ns, 30 ns, 50 ns, 100 ns, 300 ns, 1 μs, and 3 μs. To achieve high signal-to-noise ratio, more than 50 images were acquired and averaged at each time delay. Time-resolved difference X-ray scattering curves measured with 400 nm and 267 nm laser excitations are shown in Figures 3(a) and 3(c), respectively.

FIG. 3.

Time-resolved difference X-ray scattering curves of I₃^– ion in methanol measured with ((a), (b)) 400 nm and ((c), (d)) 267 nm laser excitation. (a) Experimental difference scattering curves, qΔS(q,t), measured with 400 nm laser excitation (black) and their theoretical fits (red) are shown together. (b) Corresponding difference radial distribution functions, rΔS(r,t), obtained by sine-Fourier transformation of qΔS(q,t) in (a). (c) Experimental difference scattering curves, qΔS(q,t), measured with 267 nm laser excitation (black) and their theoretical fits (red) are shown together. (d) Corresponding difference radial distribution functions, rΔS(r,t), obtained by sine-Fourier transformation of qΔS(q,t) in (c).

TRXSS data were analyzed by considering all the possible candidate reaction pathways as shown in Figure 2(b). Details of the TRXSS data analysis are described in Sec. II and in our previous work.^47,48,57 Briefly, theoretical X-ray scattering intensities were calculated using standard diffuse X-ray scattering formulas. The theoretical difference X-ray scattering curve, ΔS(q,t)_theory, was constructed by combining solute-only term, solute-solvent cross term, and solvent-only term as in Eq. (3). The solute-only term was calculated by Debye equation using the molecular structures of solute species optimized by density functional theory (DFT) calculation. The solute-solvent cross term was calculated by Debye equation using the pair distribution functions obtained from MD simulation. The solvent-only term was obtained by a separate solvent-heating experiment where the pure solvent is vibrationally excited by near-infrared light.

With 400 nm excitation, as shown in Figure 4(a), two-body dissociation is the dominant reaction pathway since the model employing only the two-body dissociation pathway gives much better fit than the model employing the three-body dissociation or the I₂ formation pathway. Radial distribution functions (RDFs), rΔS(r,t), of solute-only term gives more intuitive view as shown in Figure 4(b). With the model employing only the two-body dissociation, the experimental and theoretical RDFs of solute-only term are in good agreement. With 267 nm excitation, as shown in Figure 4(c), the models employing both two- and three-body dissociation pathways give the best fitting qualities. Specifically, the optimum with the ratio of the contributions of two- and three-body dissociation was determined to be 7:3. Radial distribution functions, rΔS(r,t), of solute-only term gives more intuitive view as shown in Figure 4(d). With the model employing the two- and three-body dissociation pathways with the branching ratio of 7:3, the experimental and theoretical PDFs of solute-only terms are in good agreement. The population changes of intermediate species and the reaction mechanism of I₃^– photodissociation dependent on excitation wavelength is summarized in Figure 5. In contrast to the previous spectroscopic studies providing indirect evidences for the mechanism of the photodissociation reaction, we established the detailed reaction mechanism depending on the excitation wavelength by directly probing the structural changes of reacting molecules using the TRXSS measurement.

FIG. 4.

Determination of the reaction pathways of I₃^– photodissociation in methanol with ((a), (b)) 400 nm and ((c), (d)) 267 nm laser excitations in ((a), (c)) q-space and ((b), (d)) r-space. (a) Theoretical difference scattering curve (red) for each candidate pathway is shown together with the experimental difference scattering curve at 100 ps (black). The model employing only the two-body dissociation pathway gives much better fit than the models employing the three-body dissociation and I₂ formation pathways, indicating that two-body dissociation is the dominant reaction pathway with 400 nm laser excitation. (b) Radial distribution functions, rΔS(r,t), of solute-only term. Bond distances and their contributions of various I–I pairs are indicated as red bars and dashed curves, respectively, at the top. With the model employing only two-body dissociation, the experimental and theoretical RDFs of solute-only term are in good agreement. (c) The same analysis of (a) for 267 nm laser excitation. The models employing the two-body and three-body dissociation pathways give similarly good fitting qualities, indicating the possibility of multiple reaction pathways. The best fit was obtained with a model employing all three reaction pathways. The optimum ratio of the contributions of two-body and three-body dissociation was determined to be 7:3. (d) The same analysis of (b) for 267 nm laser excitation. With the model employing the two-body and three-body dissociation pathways with the branching ratio of 7:3, the experimental and theoretical PDFs of solute-only terms are in good agreement.

FIG. 5.

(a) Time-dependent concentration changes of various transient solute species after photodissociation of I₃^– ion in methanol with 400 nm excitation. (b) Time-dependent concentration changes of various transient solute species after photodissociation of I₃^– ion in methanol with 267 nm excitation. (c) Reaction mechanism of I₃^– photodissociation at 400 nm. (d) Reaction mechanism of I₃^– photodissociation at 267 nm.

B. Solvent-dependent structure of triiodide ion

The exact structure of the I₃^– ion has never been directly determined experimentally because characterization of subtle structural difference in solution is not an easy task. Extended X-ray absorption fine structure (EXAFS) technique can serve as an appropriate tool for revealing the structure parameters of the solute, which is usually minor species outnumbered by the solvent. Indeed the structure of the I₃^– ion was also studied by K edge EXAFS, and the study found that the peak corresponding to I–I bond distance of ∼3 Å broadens in protic solvents.⁹⁵ However, the broadening was attributed to high Debye-Waller (DW) factor, not to the symmetry breaking caused by solvent-solute interaction. In fact, the symmetry breaking of I₃^– ion was not identified by EXAFS due to its lack of structural sensitivity at long distances. Static X-ray solution scattering has been widely used for determining the shape and the size of large molecules in solution, but large background scattering arising from solvent molecules obscures the details of molecular structure. Large angle X-ray scattering was applied to determining the structure of small molecular systems such as binary solution, solvent-confined mesoporous materials, and ionic liquids,^96–104 but its spatial resolution is not high enough for distinguishing subtle structural changes of I₃^– ion studied in this work. We measured the static scattering of I₃^– ion in solution as shown in Figure 6, but failed to obtain a relevant scattering pattern that contains only the contribution from the solute molecules. Scattering patterns from pure solvent and air as well as the dark response of the detector were subtracted from the scattering pattern of the solution sample, but theoretical scattering curve (red) does not match the experimental difference curve due to the unknown background remaining. Therefore, we cannot obtain the exact structure of I₃^– ion within a reasonable error range with static X-ray solution scattering measurement.

FIG. 6.

(a) Atom-atom pairs probed by static X-ray solution scattering. Since X-rays scatter off from every atom in the solution, the scattering pattern is very complicated. (b) Scattering intensity of I₃^– ion extracted from static wide-angle X-ray solution scattering (black). Scattering patterns from pure solvent and air as well as the dark response of the detector were subtracted from the scattering pattern of the solution sample. The theoretical scattering curve (red) does not match the experimental difference curve due to the unknown background remaining. Therefore, we cannot obtain the exact structure of I₃^– ion within a reasonable error range.

To overcome the limited sensitivity of the static X-ray solution scattering caused by imperfect background subtraction, we applied TRXSS to I₃^– ion in three different solvents: water, acetonitrile, and methanol.¹⁰⁵ The key ideas of our experiment and data analysis are schematically summarized in Figure 7. Briefly, as overviewed in Sec. II E, we adjusted the molecular structure of reactant species (I₃^– ion) so that we can identify the exact structure of the ion. This approach is in contrast to the conventional analysis of TRXSS data focusing on the transition dynamics between various reaction intermediates that were assumed to be in quasi-equilibrium. According to our kinetic analysis presented in Sec. III A, two major changes occur by 100 ps time delay when I₃^– solution is excited by laser light at 400 nm; I₃^– ion dissociates into I₂^– and I, and the temperature of solution increases. By taking the difference between scattering patterns measured before and 100 ps after laser excitation, only the laser-induced changes of solution sample are extracted with all other background contributions being eliminated. Since the vibrational cooling of excited fragment (I₂^–) is much faster than 100 ps and the recombination of I₂^– and I is much slower than 100 ps, the changes related with those processes are irrelevant in our experimental data.

To extract the structure of I₃^– ion from the difference scattering intensity, the maximum likelihood estimation with chi-square estimator was employed^49,50,53 with five variable parameters. The parameters are three bond distances for I₃^– ion (R₁, R₂, and R₃ for the distance between I₁ and I₂, I₂ and I₃, I₁ and I₃, respectively, as shown in Figure 7), the bond distance for I₂^– fragment (R₄), and temperature change. The reduced chi-square (χ²) is given by the following equation:

$${\chi }_{\text{reduced}}^2(R_1,R_2,R_3,R_4,\Delta T)=\frac{1}{N-m-1}{{\displaystyle \sum _i\left(\frac{\Delta S_{\text{theory}}(q_i)-\Delta S_{\text{experiment}}(q_i)}{{\sigma }_i}\right)}}^2,$$ (5)

where N is the total number of q points (which is 1080 for our experimental data), m is the number of fitting parameters (which is 5 without constraint and 4 with constraint), and σ_i is the standard deviation at ith q-point. The likelihood (L) is related to χ² by the following equation:

$$L(R_1,R_2,R_3,R_4,\Delta T)\propto \exp (-{\chi }^2/2).$$ (6)

The errors of multiple fitting parameters are determined from this relationship by calculating boundary values of 68.3% of likelihood distribution. The calculation was done by MINUIT software package and the error values are provided by MINOS algorithm in MINUIT. Since the reduced χ² was normalized by the standard deviation of the experimental data, the quality of the fit becomes better as χ² approaches 1.

Theoretical X-ray scattering intensities were calculated using standard diffuse X-ray scattering formulas. The difference X-ray scattering curve, ΔS(q,t)_theory, includes solute-only term, solute-solvent cross term, and solvent-only term as in Eq. (3). The solute-only term was calculated using the Debye equation. The solute-solvent cross terms were calculated from the pair distribution functions obtained from MD simulation. The solvent-only term was obtained by a separate solvent-heating experiment where the pure solvent is vibrationally excited by near-infrared light. As a result, the lengths of the three bonds in I₃^– ion are identified with sub-angstrom accuracy, allowing us to determine the exact structure of I₃^– ion in solution.

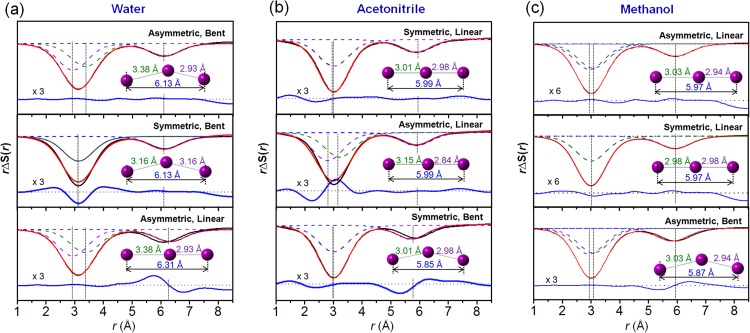
To reveal the symmetry breaking of I₃^– ion induced by hydrogen-bonding interaction with the solvent, the structure of I₃^– ion was characterized in three different solvents. Water, acetonitrile, and methanol have two, zero, and one functional groups available for hydrogen bonding, respectively. Figure 8 shows experimental and theoretical difference scattering curves at 100 ps for I₃^– ion in water, acetonitrile, and methanol solutions. In water solution, the asymmetric (R₁ > R₂) and bent (R₁ + R₂ > R₃) structure of I₃^– ion gave the best fit. If a symmetric structure (R₁ = R₂ constraint) or a linear structure (R₁ + R₂ = R₃) is assumed as a constraint, the fit between theory and experiment deteriorates. In contrast, in acetonitrile, the symmetric (R₁ = R₂) and linear (R₁ + R₂ = R₃) structure gave the best fit within the error range. If an asymmetric structure (R₁ > R₂, R₁ = 1.1 × R₂) or a bent structure (R₁ + R₂ > R₃, R₁ + R₂ = 1.05 × R₃) is assumed as a constraint, the agreement deteriorates. The optimized structure in methanol lies in between the ones in water and acetonitrile solutions, as expected from the number of functional groups available for hydrogen bonding. In methanol, I₃^– ion was found to have an asymmetric and linear structure (R₁ > R₂ and R₁ + R₂ = R₃). When other structure, for example, a symmetric (R₁ = R₂) structure, was assumed as a constraint, the agreement between experiment and theory became worse. Optimized bond distances and their errors are summarized in Table I.

FIG. 8.

Difference scattering curves measured at 100 ps after photoexcitation for the I₃^– photolysis in water, acetonitrile, and methanol solution. Experimental (black) and theoretical (red) curves using various candidate structures of I₃^– ion are compared. Residuals (blue) obtained by subtracting the theoretical curve from the experimental one are displayed at the bottom. (a) In water, I₃^– ion was found to have an asymmetric and bent structure. To emphasize the fine difference in fitting quality, the residuals shown were multiplied by a factor of 3. (b) In acetonitrile, I₃^– ion was found to have a symmetric and linear structure. (c) In methanol, I₃^– ion was found to have an asymmetric and linear structure.

TABLE I.

Structural parameters extracted from the data analysis and DFT calculation. R₁, R₂, and R₃ are the I–I distances of I₃^– ion and R₄ is the I–I distance of I₂^– fragment.

	R1 (Å)	R2 (Å)	R1 − R2 (Å)	R3 (Å)	<I1I2I3 (deg)	R4 (Å)
Water	3.38 ± 0.03	2.93 ± 0.03	0.45 ± 0.04	6.13 ± 0.14	153	3.43 ± 0.03
Water (DFT calculation)	3.21	2.74	0.47	5.94	172	…
CH3CN	3.01 ± 0.04	2.98 ± 0.04	0.03 ± 0.06	5.99 a	180	3.24 ± 0.06
MeOH	3.03 ± 0.04	2.94 ± 0.03	0.09 ± 0.05	5.97 a	180	3.59 ± 0.04

^aThe maximum value of R₃ was set to be R₁ + R₂ to avoid physically unacceptable structure. The R₃ values for the acetonitrile and methanol solvent hit the limit.

The distinction between the different structures of I₃^– ion can be emphasized when the contribution of I₃^– alone is extracted by subtracting the contributions of I₂^– ion, temperature change of solvent, and the cage component. Figure 9 shows the extracted real-space features of only I₃^– ion in water, acetonitrile, and methanol solutions. Each experimental curve (black line) can be fit by a sum of contributions from three I–I distances (red line) optimized in the fitting analysis described in Figure 8. Interestingly, for the peak around 3 Å, the peak is broader in water than in acetonitrile. This observation indicates that I₃^– ion in water has two different I–I bond distances around 3 Å and thus have an asymmetric structure. The asymmetric structure of I₃^– in water is supported by the poor fit when using a symmetric structure (middle panel of Figure 9(a)). The peak centered at ∼6 Å, which corresponds to the distance between the two end atoms, R₃, can be used for determining whether I₃^– ion has a linear or bent structure. In water, R₃ (6.13 Å) is shorter than the sum of R₁ and R₂ (6.31 Å), indicating the bent structure of I₃^–. If a linear structure is forced by using R₃ = 6.31 Å, the peak positions of the experimental and theoretical curves do not match well.

FIG. 9.

Structure reconstruction of I₃^– ion based on the extracted bond distances. The contribution of I₃^– alone (black solid line) was extracted. Theoretical curves (red) were generated by a sum of three I–I distances (dashed lines). The residuals (blue solid line) are displayed at the bottom. (a) In water solution, the theoretical curve calculated from the asymmetric and bent structure gave the best fit to the experimental curve (top panel). When one average distance (3.16 Å) instead of two unequal distances was used, the broad feature in the experimental curve cannot be matched (middle panel). When a linear and asymmetric structure is used, the sum of two I–I distances (6.31 Å) do not match the R₃ (6.13 Å) determined from the experimental scattering curve, indicating the bent structure (bottom panel). (b) In acetonitrile solution, a symmetric and linear structure gave the best fit (top panel). If two unequal distances (3.15 Å and 2.84 Å) were used, the theoretical curve becomes broader than the experimental curve (middle panel). When a bent structure was used, the peak at 5.99 Å is shifted to a smaller value, giving a worse fit to the experimental curve (bottom). (c) In methanol solution, a symmetric and linear structure gave the best fit (top panel). If two equal distances were used, the theoretical curve becomes slightly narrower than the experimental curve (middle panel). When a bent structure was used, the peak at 5.97 Å is shifted to a smaller value, giving a worse fit to the experimental curve (bottom).

The results from acetonitrile solution can be explained in the same manner. If an asymmetric structure of I₃^– ion with two different bond lengths (2.84 and 3.15 Å) is used, the theoretical curve has a broader width than the experimental data (middle panel of Figure 8(b)). The maximum value of the distance between the end atoms (R₃) was set to be R₁ + R₂ to avoid physically unacceptable structure and the R₃ values for the acetonitrile solvent reached the limit. The distance between the end atoms (5.99 Å) is the same as the sum of two other distances (5.99 Å), indicating the linear structure of I₃^–. If a bent structure is forced by using 5.85 Å, the peak position of the theoretical scattering curve is not in good agreement with that of the experimental curve. In methanol solution, the theoretical curve calculated from the asymmetric and linear structure gave the best fit to the experimental curve (top panel of Figure 9(c)). When one average distance (2.99 Å) instead of two unequal distances was used, the broad feature in the experimental curve cannot be matched (middle panel of Figure 9(c)). When a bent structure was used, the peak at 5.95 Å is shifted to a smaller value, giving a worse fit to the experimental curve (bottom panel of Figure 9(c)). Based on this analysis, the symmetry breaking is clearly observed in water and weakly present in methanol, but does not exist in acetonitrile.

Our experimental results well account for the results of the previous experimental and theoretical studies. For example, the I–I–I angle of the bent I₃^– ion in water was estimated to be 153° from transient anisotropy measurement.⁸² This estimated value well matches the value extracted from our data. Also, a theoretical study using MD simulation⁸⁸ suggested an asymmetric structure of I₃^– in water with one bond longer by 0.49 Å than the other. This prediction is very similar to the result of our measurement (0.45 Å).

In order to find the origin of the symmetry breaking, many theoretical studies have been performed. Although theoretical studies using MD or Monte Carlo simulation have ascribed the origin of the symmetry breaking of I₃^– in protic solvents to the hydrogen-bonding interaction between solute and solvent molecules, the structure of I₃^– with broken symmetry has never been optimized by quantum chemical calculation, mainly due to the difficulty of including explicit hydrogen-bonding interaction in the quantum chemical calculation.^86–88,93 Sato et al. found the flattening of the ground-state free-energy surface in aqueous solution,⁸⁵ but could not find an asymmetric structure as a minimum. In our work, we calculated the molecular structure of I₃^– by using DFT method by considering 34 explicit water molecules. All molecular structures were optimized using DFT method. Subsequently, harmonic vibrational frequency calculations were performed using the optimized molecular structures. We used the recently developed ωB97XD functional¹⁰⁶ as DFT exchange-correlation functional. To treat the scalar relativistic effect of iodine, we used aug-cc-pVDZ-PP small-core relativistic effective core potential (RECP).¹⁰⁷ For other atoms (O and H), 6-31++G(d) basis sets were used. We also used the integral-equation-formalism polarizable continuum model (IEFPCM) method¹⁰⁸ to describe solvent effect implicitly. The molecular structure of I₃^– was optimized with a total of 34 surrounding explicit water molecules to form the first solvation shell around I₃^– ion. We used the natural population analysis (NPA) for characterizing atomic charge. All DFT calculations were performed using the Gaussian09 program.¹⁰⁹ This approach is similar to a recent theoretical investigation of small molecules inside ice nanotube.¹¹⁰ The optimized structure yielded an asymmetric and bent structure of I₃^– ion. The structural parameters of the optimized structure are summarized in Table I. The difference between two I–I bond distances (0.47 Å) is well matched with that from the scattering experiment (0.45 Å). We note that the configuration of water molecules displayed in Figure 10 is not the only possible solution because the solvent molecules fluctuate significantly in reality. Still, it can be seen that the elongated iodine atom has more negative charge than normal and thus can strongly interact with the adjacent hydrogen atoms through hydrogen-bonding interaction. As a result, the solvated ion with broken symmetry can have much lower energy than the symmetric structure in the same solvation environment as shown in Figure 10. This DFT calculation confirms that the symmetry breaking of I₃^– ion is induced by hydrogen-bonding interaction.

FIG. 10.

Optimized structures and the relative energies of I₃^– ion with 34 explicit water molecules forming the first solvation shell by DFT method. The optimized structure of I₃^– ion has a broken symmetry (asymmetric, bent) and is stabilized by 51.2 kJ/mol compared with the linear symmetric one. The elongated iodine atom has more negative charge than the other iodine atom, resulting in stronger interaction with surrounding hydrogen atoms of water molecules.

As described in this section, we were able to characterize subtle structural change of I₃^– ion depending on hydrogen-bonding ability of the solvent. In water solution, we found that the I₃^– ion takes an asymmetric and bent structure, lowering the structural symmetry. This phenomenon is also weakly present in methanol but not in acetonitrile. These results provide the direct evidence for symmetry breaking of triiodide ion in hydrogen-bonding solvents and clarify the subtle effect of solute-solvent interaction on the structure of ionic species.

IV. GEMINATE RECOMBINATION AND VIBRATIONAL COOLING OF MOLECULAR IODINE

Geminate recombination of iodine atoms to form molecular iodine (I₂) in solution after photodissociation is a good example of prototype solution-phase reactions and has been investigated by spectroscopy and quantum chemistry for more than seven decades.^111–131 This reaction occurs due to collisions of dissociating I₂ molecule with surrounding solvent molecules, whereby the vibrational kinetic energy of the I₂ molecule is dissipated as the molecule reaches thermal equilibrium.^119–121 The dynamics of vibrational energy dissipation has been well characterized by spectroscopic studies of the photodissociation and subsequent recombination of I₂ in CCl₄, alkane liquids, and noble gas matrices.^{111–118,127–131} However, the change in molecular structure (i.e., bond length change) and the response of surrounding solvent cage have never been directly observed.

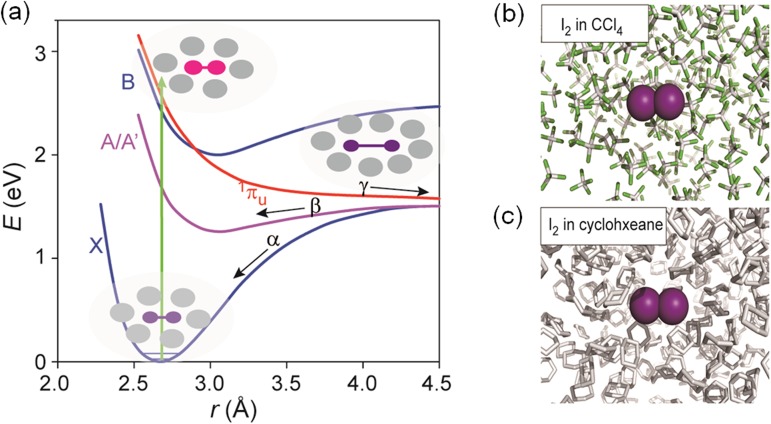
As described above, TRXSS is well suited for monitoring this solution-phase reaction because it directly probes the atom-atom distance distribution as a function of time. In the TRXSS experiment applied to the geminate recombination of I₂ in solution, optical laser pulses initially excite the solution sample and promote a fraction of I₂ molecules from the ground state X to the excited electronic states B and ¹π_u (Figure 11(a)). Then, the excited I₂ molecules in the solvent cage dissociate rapidly to form an activated complex (I₂)^* with an elongated bond length. A fraction of the (I₂)^* complexes escape the cage and recombine nongeminately in tens of nanoseconds.³⁷ The remaining (I₂)^* complexes recombine geminately along either the X or A/A′ potential energy surface while exhibiting large-amplitude vibrations. These geminate recombination and vibrational relaxation processes are monitored by time-delayed, 100-ps X-ray pulses from a synchrotron.

FIG. 11.

(a) Potential energy surface of I₂ in CCl₄. Low-lying electronic states (X, A/A′, B and ¹π_u) of I₂. The states A and A′ are closely spaced and can be viewed as a single electronic state A/A′. The processes α and β represent geminate recombination of two I atoms in the X and A/A′ states, respectively. The process γ represents nongeminate recombination through the solvent. Schematic snapshots of solute-solvent configuration at representative stages are depicted. (b) MD snapshot of I₂ in CCl₄. Purple sphere is iodine atom, grey rod is carbon atom, and green is chloride atom. (c) MD snapshot of I₂ in cyclohexane. Purple sphere is iodine atom, and grey rod is carbon atom.

A. Time-slicing scheme

The X-ray pulse generated from 3rd-generation synchrotrons has rather long pulse duration (∼100 ps), thus limiting the time resolution of TRXSS experiment. The instrumental time resolution is determined by a combination of X-ray pulse duration (100 ps), laser pulse duration (0.5 ps), and their relative jitter (3 ps), and thus the X-ray pulse duration is the limiting factor. In order to visualize the entire processes of geminate recombination and vibrational relaxation of I₂, we presented an experiment that circumvents this limitation by using the time-slicing scheme.^60,67 In this scheme, data are collected at earlier time delays and with finer time increments (down to 10 ps) than the X-ray pulse width (Figure 12). By subsequently applying deconvolution processing to the measured data, we can extract the dynamics that occur faster than the X-ray pulse width. Using this ingenious scheme, we monitored the time evolution of (1) atom-atom distance distribution of iodine atoms in CCl₄ (Figure 11(b)) and cyclohexane (Figure 11(c)) as well as (2) the solute-solvent distance distribution (i.e., solvation) at the early stages of I–I bond formation in CCl₄.⁶⁰

FIG. 12.

Schematic of the time-slicing experiment. At a negative time delay (e.g., −30 ps) close to time zero, the X-ray pulse arrives (effectively) earlier than laser pulse, but the X-ray pulse, which is much longer in time than the laser pulse, is still present after the interaction with the laser pulse and thus scattered off the laser-illuminated sample. At time zero, half of the X-ray pulse probes the laser-illuminated sample. At a positive time delay, most of the X-ray pulse is scattered off the laser-illuminated sample.

As the optical pulses (0.5 ps) used in the experiment are much shorter than the X-ray pulses (100 ps), at early time delays between −100 ps and 100 ps, the signal from the photoexcited sample is produced only by part of the X-ray pulse that arrives after the laser pulse (Figure 12). For example, at zero time delay, the laser pulse is temporally located in the middle of the X-ray pulse, and the excited sample is probed only by the truncated half of the Gaussian X-ray intensity. Time-resolved scattering patterns were collected as a function of the pump-probe time delay t from −200 ps to 400 ps with a time step of 10 ps. This time step is much smaller than the ones usually used in previous experiments and allows us to monitor the fast vibrational relaxation processes whose time scale is comparable to the full width at half maximum (fwhm) of the X-ray temporal profile (100 ps).

B. Removal of the solvent contribution

In order to extract only the dynamics of geminate recombination of I₂, the scattering from pure solvent (CCl₄ or cyclohexane) needs to be subtracted from the scattering of the solution sample. Especially, when a chemical reaction takes place, the elimination of solvent response becomes complicated because the temperature of the solvent unavoidably rises by the heat released from laser excitation and gives rise to an unwanted thermal response. To measure only the thermal response of pure solvent, a separate experiment was performed. In that experiment, pure CCl₄ or cyclohexane was irradiated by 100 fs laser pulses of ∼60 μJ pulse energy at the off-resonant wavelength of 390 nm (for CCl₄) or 1725 nm (for cyclohexane) so that the solvent can be heated through multi-photon absorption without inducing any chemical change. The time-dependent scattering curves of pure solvent, ΔS(r,t)_solvent-only, were recorded at t = 200 ps and 1 μs for the constant-volume and constant-pressure regimes, respectively. The measured thermal response of the solvent was subtracted from the solution signal after suitable scaling to match an ultrafast temperature jump.^40,51 The scaling factor used for the subtraction was determined by scaling ΔS(r,t)'s of the solution and the pure solvent to each other at r values much larger than the size of the I₂ molecule; r > 6 Å was used in this case as shown in Figures 13(a) and 13(b). As a result of the subtraction, we obtain solute-related ΔS(q,t) and ΔS(r,t) curves for I₂ in CCl₄ at various time delays as shown in Figures 13(c) and 13(d).

FIG. 13.

Difference scattering curves for solute and solvent-only contributions. (a) ΔS(r,426 ps) curve from I₂/CCl₄ solution (black) and ΔS(r,200 ps)_solvent-only curve from thermally excited CCl₄ (red). (b) Solute-related ΔS(r,426 ps) obtained by subtracting the solvent contribution from the solution signal. Note the negative peak arising from the depletion of I₂ in the ground (X) state and the positive peak corresponding to the A/A′ state. (c) Solute-related ΔS(q, t) curves with the solvent contribution eliminated. At early times, only a fraction of the X-ray pulse probes the laser-triggered molecules and thus the amplitudes of raw difference scattering signals at early times (black curves) are small. Considering the effect of this partial temporal overlap, the difference scattering curves at early times were scaled up (red curves) following the temporal rise of the signal in the form of an error function. (d) Solute-related ΔS(r, t) curves obtained by Fourier transform of the curves shown in (c). Note that the depth of the negative peak at 2.6 Å decreases with time as the geminate recombination progresses and leads to recovery of I₂ in the ground state.

C. Polychromatic correction

To maximize the intensity of X-rays, the raw quasi-monochromatic beam, which has a broad and asymmetric spectrum as shown in Figure 14(a), from the undulator fundamental was used in the experiment. The polychromaticity in the spectrum leads to a slight shift and damping of the scattered intensity ΔS(q) and its Fourier transform ΔS(r). The effect of the polychromatic beam on ΔS(r) is demonstrated in Figure 14(b). To avoid such distortion of the scattering signal, we corrected the polychromaticity as briefly described in Figure 14(b). The detailed procedure of polychromatic correction is described in Supplementary Material (SM).¹³² By using Eq. (S9) and least-squares fitting, ΔS(r) in monochromatic condition can be extracted from the polychromatic data as shown in Figure S1.

FIG. 14.

(a) The spectrum of X-ray pulse used in the experiment has a 3% bandwidth and a characteristic half-Gaussian shape. (b) A scheme for correcting the effect of polychromatic X-ray spectrum on the difference scattering curve. The polychromaticity of the X-ray spectrum induces the shift of ΔS(r) along r-axis (red curve). The black curve is a trial scattering curve obtained with a monochromatic X-ray beam. When the trial scattering curve is convoluted with the polychromatic spectrum, a blue curve is generated. By fitting the experimental data (red curve) with the convoluted trial curve (blue curve) using least-squares refinement of the trial curve, we can obtain ΔS[r] under monochromatic conditions.

D. Experimental data, r²ΔS(r), and radial distribution function, ρ(r)

Radial distribution function, ρ(r), represents the distribution of atom-atom distance in real space, and we can relate the experimental difference scattering curves, ΔS(r), with ρ(r). In principle, ρ(r) is equivalent to r²S(r) and therefore we multiplied the experimental data S(r) by r² and used r²S(r) from later on. Specifically, according to the step-by-step derivation from Eq. (S10) to Eq. (S15) in the SM,¹³² the relationship between r²S(r) and ρ(r) for an I₂ molecule is as follows:

$$\begin{array}{c}{r}^{2}S(r)=r^2\Delta S(r)+\sqrt{\frac{\pi }{\alpha }}\frac{N_{I_1}{N}_{I_2}}{2V}{\rho }_0(r)\ast \exp (-r^2/4\alpha )\\ =\sqrt{\frac{\pi }{\alpha }}\frac{N_{I_1}{N}_{I_2}}{2V}\left(\Delta \rho (r)+{\rho }_0(r)\right)\ast \exp (-r^2/4\alpha )\\ =\sqrt{\frac{\pi }{\alpha }}\frac{N_{I_1}{N}_{I_2}}{2V}\rho (r)\ast \exp (-r^2/4\alpha ).\end{array}$$ (7)

It can be seen that r²S(r) is the convolution of ρ(r) and a damping term (Gaussian function) and thus r²S(r) becomes broader than ρ(r). As a result, ρ(r) shows two maxima close to the turning points of the X state whereas this feature is much less apparent in r²S(r) shown in Figure 17(d). The loss of resolution along q axis arises from (1) finite q range of the experiment (0.04–9.0 Å⁻¹) and (2) the effect of X-ray form factor, that is, X-rays see atoms as “electron clouds” in contrast to neutrons that directly probe the positions of nuclei.

FIG. 17.

(a) Time-dependent I–I distance distribution functions, r²S_inst(r,t), of I₂ in CCl₄. (b) Cross sections of r²S_inst(r,t) at the time delays indicated by dotted lines in (a). (c) ⟨r(t)⟩ was calculated from (a) and compared with a single exponential fit (blue) and a double exponential fit (red). To obtain a satisfactory fit to the experimental data, a double exponential is necessary with the time constants of 16 ps and 76 ps and a relative amplitude ratio of about 2:1. (d) Time evolution of the I–I distance distribution function, r²S_inst(r,t) (blue, solid line), converted from ρ(r,t) of the I–I atomic pair obtained from MD simulation (black, dotted line). The potential energy curve corresponding to the X state is also shown (red, dashed line). (e) Time dependence of the average I–I distance, ⟨r⟩, calculated from the I–I distance distribution function, r²S(r,t). Fit of the average distance ⟨r⟩ (blue, solid line) by a double exponential function, g(t) = A_r exp(−t/τ₁^r) + B_r exp(−t/τ₂^r) + 2.67 Å (red, dashed line), gives the relaxation times τ₁^r = 3 ps and τ₂^r = 44 ps. The equilibrium distance (green, dash-dotted line) is also shown.

E. Retrieving r²ΔS_inst(r,t) by deconvolution

The difference scattering signal, r²ΔS(r,t), measured from the experiment is the convolution of the instantaneous response of the sample and the profile of X-ray pulse intensity

$$r^2\Delta S(r,t)={\displaystyle {\int }_{-\infty }^{\infty }d\tau I_{\mathrm{X}-\text{ray}}(t-\tau )r^2\Delta S_{\mathit{i}\mathit{n}\mathit{s}\mathit{t}}(r,\tau )},$$ (8)

where I_X-ray(t) is the temporal profile of X-ray pulse intensity recorded by a streak-camera and r²ΔS_inst(r,t) is the instantaneous response of the sample induced by an (hypothetical) ultrashort X-ray pulse.^133,134 While r²ΔS_inst(r,t) contains the desired information on the bond formation dynamics of I₂, the measured signal r²ΔS(r,t) is slightly blurred by the effect of X-ray pulse that has a finite temporal width. Therefore, it is necessary to deconvolute the X-ray pulse profile of finite pulse duration from experimentally measured r²ΔS(r,t) to extract r²ΔS_inst(r,t).

There are various deconvolution algorithms available, including constrained iteration, inverse filter, and least-mean-squares algorithms.^135–137 The last method was mainly used in this work.¹³⁵ We also tested the constrained iteration algorithm to check the method dependence of the deconvoluted signals, and the results confirm that the same result is obtained within experimental errors regardless of the deconvolution method used. Along with the deconvolution, a series of data processing procedures were employed to extract the structural changes more clearly. To assess the reliability of the used procedures, we applied the exact same procedures to mock data and examined the uncertainties introduced by the procedures. From this test, we confirmed that our procedures are reliable with spatial uncertainty of ∼0.06 Å and temporal uncertainty of ∼10 ps. The procedure of deconvolution is described in detail in the supplementary material.¹³²

The deconvoluted r²ΔS_inst(r,t) curves are shown in Figure 15(b) for I₂ in CCl₄ and in Figure 15(c) for I₂ in cyclohexane. While time-dependent changes of the measured signal are already distinct in r²ΔS(r,t) without deconvolution, they are enhanced in the deconvoluted r²ΔS_inst(r,t) curves as expected (Figure 15(b) for I₂/CCl₄ and Figure 15(c) for I₂/cyclohexane). In I₂/CCl₄, the negative peak at ∼2.67 Å, which corresponds to the depletion of I₂ in the ground state, is visible for all time delays, but its magnitude gradually becomes smaller with time as the ground state is repopulated. At early time delays up to 26 ps, positive peaks at distances above 4 Å are visible, but their magnitudes rapidly decay. At later time delays, only one positive peak around ∼3.1 Å, which we assign to the equilibrium A/A′ state (see below), remains and its magnitude decreases slowly with time.

FIG. 15.

(a) Concept of deconvolution. If the temporal duration of X-ray pulse is larger or comparable to the time scale of the process of interest, the dynamic features become blurred in the experimental data due to the convolution of the sample signal with the temporal profile of the X-ray pulse. Upper figure shows r²ΔS(r,t) with respect to time at r = 3.1 Å. For each r value, r²ΔS(r,t) results from the convolution of the sample signal r²ΔS_inst(r,t) with the X-ray temporal profile I_x-ray(t). The goal of deconvolution is to reconstruct r²ΔS_inst(r,t) from r²ΔS(r,t). (b) Time-dependent deconvoluted difference scattering curves r²ΔS_inst(r,t) for I₂ in CCl₄. (c) The same analysis for I₂ in cyclohexane.

In I₂/cyclohexane, the deconvoluted signals show quite different behavior compared with that of I₂/CCl₄. As in I₂/CCl₄, the negative peak at ∼2.67 Å (depletion of I₂ in the ground state) and the positive peak at ∼3.1 Å (A/A′ state) are observed and positive peaks at distances larger than 4 Å are also visible. However, the positive peak at ∼3.1 Å decays much faster than in I₂/CCl₄, indicating strong solvent dependence of the lifetime of the A/A′ state. As reported by Harris et al.,¹²⁸ in cyclohexane, the decay of A/A′ state occurs on the same time scale as vibrational cooling process. For this reason, in cyclohexane, the decay of the A/A′ state and vibrational cooling cannot be distinguished from each other in the deconvoluted signal, r²ΔS_inst[r,t]. The positive peak at ∼3.1 Å (A/A′ state) is noticeably smaller in cyclohexane than in CCl₄, indicating that the A/A′ state is relatively less populated in cyclohexane. This observation is consistent with previous spectroscopic studies.¹¹⁶

Two effects slightly distort the features in the r²ΔS_inst(r,t) curves. First, although the equilibrium I–I distance in the X and A/A′ state is 2.67 Å and 3.1 Å, respectively, the positions of the negative and positive peaks are slightly shifted from these values in the difference curves. This peak shift is due to partial overlap of positive and negative peaks. Second, the limited q range of the experimental data causes artificial oscillation in the Fourier transformed data, ΔS_inst(r,t). Because of the r² factor, these oscillations are enhanced in the high r region (r ⟩ 3.5 Å) of r²ΔS_inst(r,t) and generates wiggles in an otherwise monotonous distribution as shown in Figures 15(b) and 15(c). The period of this oscillation is 2π/q_max, where q_max is the maximum q used in Fourier transform. In our case, q_max is 9 Å⁻¹ and thus the period is ∼0.7 Å.

F. Double difference scattering curves, r²ΔΔS_inst(r,t)

In principle, r²ΔS_inst(r,t) reflects the motions of iodine atoms simultaneously occurring on the two electronic states, X and A/A′, complicating the interpretation. However, there is already a distinct peak at ∼3.1 Å corresponding to the equilibrium A/A′, even at the earliest time delays, suggesting that the relaxation in the A/A′ state is completed within our limited time resolution imposed by the 10 ps increment of the time delay. This is supported by the fact that no further growth of the ∼3.1 Å peak is observed. The A/A′ state has a rather long life time compared with the time range investigated in this measurement. In addition, a small fraction of I₂ completely dissociates into iodine atoms and do not return to I₂ in the investigated time range. To remove the contribution from these long-lived states, double difference signals, r²ΔΔS_inst(r,t) = r²ΔS_inst(r,t) – r²ΔS_inst(r,t_∞), were calculated, where t_∞ is a time delay (426 ps here) much longer than the time taken for vibrational relaxation in the X state. The r²ΔΔS_inst(r,t) curves for I₂ in CCl₄ are shown in Figure 16(a). Although the A/A′ life time is long (1.2 ns; extracted from the experiment data), r²ΔΔS_inst(r,t) is still affected by the decay of A/A′. To remove this effect, theoretical r²ΔΔS_inst(r,t) curves corresponding to this A/A′ decay were calculated and subtracted from r²ΔΔS_inst(r,t). For I₂ in CCl₄ he r²ΔΔS_inst(r,t) curves with the A/A′ decay eliminated are shown in Figure 16(b).

FIG. 16.

(a) r²ΔΔS_inst(r,t) for I₂ in CCl₄ obtained by subtracting r²ΔS_inst(r,426 ps) from r²ΔS_inst(r,t) to remove the contribution from the A/A′ state and dissociated iodine atoms remaining at 426 ps. (b) r²ΔΔS_inst(r,t) for I₂ in CCl₄ obtained by subtracting the contribution from the population decay of A/A′ (1.2 ns).

In contrast to I₂ in CCl₄, I₂ in cyclohexane shows faster population decay of A/A′, which is almost complete in 100 ps. As a result, it is difficult to decouple the population decay of the A/A′ state and the vibrational relaxation. Therefore, the double difference curves were not calculated for I₂ in cyclohexane. Harris et al.¹²⁸ also reported that the A/A′ decay for I₂ in cyclohexane is ∼71 ps, which is on the same time scale as the vibrational relaxation.

G. Time-dependent I–I distance distribution, r²S_inst(r,t)

Finally, we removed the negative peak at 2.67 Å corresponding to the depletion of the ground-state I₂ using the relationship of r²S_inst(r,t) = r²ΔΔS_inst(r,t) + r²S_I2,X(r), where r²S_I2,X(r) is the scattering curve of the ground state (X) of I₂. Considering the broadening effect of the damping and sharpening terms on r²S(r) up to ∼0.6 Å fwhm width, we used a Gaussian function with ∼0.6 Å fwhm to account for the contribution of the depleted ground state. The Gaussian peak for the depleted ground state, r²S_I2,X(r), was scaled by matching the intensity of the negative peak of r²ΔΔS_inst(r,1 ps) and added to r²ΔΔS_inst(r,t) at all time delays. As a result, we extracted time-dependent I–I distance distribution r²S_inst(r,t) arising from only recombining iodine atoms in the cage, as shown in Figures 17(a) and 17(b).

The time-dependent I–I distance distribution vividly visualizes the time-dependent progression of the I–I distance. At early times, the positive peak at ∼4 Å with a large width is clearly visible. At later time delays, the peak shifts to the shorter distances and eventually only one sharp, positive peak remains around 2.67 Å, representing the equilibrium X state. To quantify the shift of the peak, we calculated the average distance ⟨r(t)⟩ as a function of time by averaging the data from 1.5 Å to 4.5 Å as shown in Figure 17(c). The ⟨r(t)⟩ converges to 2.67 Å, the equilibrium I–I distance of the X state. The temporal decay profile is fit well by a double exponential function with time constants of 16 ps and 76 ps, while a single exponential function does not give a satisfactory fit. Therefore, the vibrational cooling in the X state can be described by a bi-exponential process.

This bi-exponential decay and the general time-dependent change of the I–I distance distribution is also supported by MD simulations. In Figure 17(d), the time evolution of the I–I distance distribution function, r²S_inst(r,t), obtained from the MD simulation is shown. The spread of r²S_inst(r,t) decreases with time as the ensemble of I₂ molecules relaxes towards the bottom of the potential well of the X state. As can be seen in Figure 17(e), the decay of the average I–I distance ⟨r⟩ extracted from the MD simulation is also fitted well by a bi-exponential function, in agreement with the bi-phasic decay behavior observed in the experimental data.

The bi-exponential dynamics of the vibrational relaxation for I₂ in CCl₄ found in this study provides an explanation for the result of a previous ultrafast spectroscopic study.¹²⁷ In that study, the decay of vibrational energy monitored from 50 ps to 200 ps shows single-exponential dynamics, but our bi-exponential behavior can be inferred indirectly. The vibrational energy decays from 2000 cm⁻¹ at 50 ps to 300 cm⁻¹ at 200 ps, and the decay profile was fit with an exponential of 70 ps time constant, which is in agreement with the time constant of the slower component in our measurement. Although the time range corresponding to a faster decay component was not investigated in that study, considering that the well depth of the X state is 12 000 cm⁻¹, the vibrational energy must have decayed by 10 000 cm⁻¹ within the first 50 ps. Therefore, this component should correspond to the first time constant of 16 ps obtained in our study.

As for the I₂/CCl₄ data, the negative peak for the ground-state I₂ was removed from the cyclohexane data to give the distance distribution r²S_inst(r,t) arising from only recombining iodine atoms, as shown in Figures 18(a) and 18(b). We note that, instead of double difference curves, r²ΔS_inst(r,t) was used to get r²S_inst(r,t) for I₂ in cyclohexane. As in I₂/CCl₄ data, the detailed time-dependent progression of I–I distance is mapped out in the I–I distance distribution. At early times, the positive peak has a larger width, reaching larger distances than in I₂/CCl₄. This observation indicates that iodine atoms can be separated into larger distances in cyclohexane than in CCl₄. The average distance ⟨r(t)⟩ is shown as a function of time in Figure 18(c). A single exponential function with a time constant of 55 ps provides a satisfactory fit to the decay profile. As both the population decay of A/A′ state and the vibrational cooling are mapped in ⟨r(t)⟩, the single-exponential behavior of ⟨r(t)⟩ suggests that both processes have similar time constants and single-exponential decay profiles. As discussed above, Harris et al.¹²⁸ also reported that the decay of A/A′ state is on the same time scale as the vibrational cooling process in cyclohexane. However, unlike in CCl₄ where the ⟨r(t)⟩ value converges to 2.67 Å within 400 ps, ⟨r(t)⟩ has not reached this equilibrium value in cyclohexane. This delay in reaching the equilibrium I–I distance may indicate that the 55 ps process corresponds to the fast phase of a bi-exponential relaxation. This time constant of 55 ps is considerably slower than 16 ps observed in CCl₄. The difference in maximum I–I separation and the time scale of vibrational cooling process in CCl₄ and cyclohexane can be explained by the difference in molecular mass of the two solvents. Cyclohexane is lighter than CCl₄ and, as the iodine atoms move away from each other with bond elongation, they experience smaller resistance force in cyclohexane than in CCl₄. As a result, the elongation of I–I bond will reach larger distance (and longer recombination time) in cyclohexane than in CCl₄.

FIG. 18.

(a) Time-dependent I–I distance distribution functions, r²S_inst(r,t), of I₂ in cyclohexane. (b) Cross sections of r²S_inst(r,t) at the time delays indicated by dotted lines in (a). (c) ⟨r(t)⟩ was calculated from (a) and fit by a single exponential fit (red). The single exponential gives a satisfactory fit to the experimental data with a time constant of 55 ps.

H. Solute-solvent structural dynamics

In addition to the change in the bond length of solute molecules, we can also extract the solvation dynamics from the TRXSS data. As the I–I bond length of the solute molecule changes in the low r region (1 – 5 Å), the experimental data also show changes of interatomic distance at r > 5 Å. The experimental r²S_inst(r,t) curves for I₂ in CCl₄ are plotted at r values from 5.0 to 9.0 Å in Figure 19(a). These changes represent time-dependent solute–solvent (mostly I–Cl) distance distribution in the distance regime of the first solvation shell surrounding the iodine molecule. As discussed in the Introduction, the dynamics of solvation associated with relaxation of electronic excited states have been measured using various spectroscopic methods.^20–35 As a result, the dynamics and the spectral signatures of solute-solvent interaction were elucidated extensively. However, those spectroscopic techniques do not give direct information on the evolution of solute-solvent distances. In contrast, the interatomic distance distribution shown in Figure 19(a) is a direct real-space representation of the spatial rearrangement of the solvent molecules with respect to the solute molecules.

FIG. 19.

(a) Experimental r²ΔS_inst(r,t) curves at large r values corresponding to time-dependent solute–solvent (mostly I–Cl) distance distribution functions, r²ΔS_cage(r,t). (b) Theoretical time-dependent solute–solvent distance distribution functions, r²ΔS_cage(r,t), based on the experimentally obtained I–I distribution (shown in Figure 17(a)) and the solute-solvent atom–atom pair distribution functions, g(r), calculated by MD simulation. (c) Interatomic pair distribution functions between a C atom of the solvent and an I atom of the solute, g_C–I(r). The red and blue curves are for the solute with the I–I distance of 4.0 Å and 3.1 Å, respectively, and the black curve is for the solute with the I–I distance of 2.65 Å. (d) Interatomic pair distribution functions between a Cl atom of the solvent and an I atom of the solute, g_Cl–I(r). The red and blue curves are for the solute with the I–I distance of 4.0 Å and 3.1 Å, respectively, and the black curve is for the solute with the I–I distance of 2.65 Å. (e) Theoretical solute–solvent distance distribution function, r²_cageS(r), is obtained from g(r) – 1 calculated from MD simulation. (f) Theoretical difference cage term r²ΔS_cage(r) is obtained by subtracting r²S_cage(r) of I₂ in the ground-state configuration from r²S_cage(r) of I₂ with the I–I distance in the range of 2.3 – 4.2 Å. With the decrease of I–I distance towards the equilibrium distance in the ground state, the width of negative peak at around 6 Å is narrowed, and positive peak between 7 and 8 Å is shifted to 7 Å.

To examine the origin of these changes, we performed a series of MD simulations of I₂ molecule in CCl₄ solvent molecules using MOLDY.¹³⁸ The detailed procedure of the MD simulations is described in SM.¹³² From the MD simulations, we extracted the atom–atom pair distribution functions, g(r), between an atom of the solute and an atom of the solvent (i.e., I–Cl and I–C) at various I–I bond lengths of the solute as shown in Figures 19(c) and 19(d), and transformed them to S(q) using Eq. (S10). Then, we obtained theoretical solute–solvent distance distribution, r²S_cage(r), at various I–I bond lengths of the solute by Fourier transform with a damping term and a sharpening function as shown by a contour plot in Figure 19(e). By subtracting theoretical r²S_cage(r) of the ground-state I₂ molecule (with the I–I distance of 2.65 Å) from theoretical r²S_cage(r) of the I₂ molecule with the I–I distance in the range of 2.3 – 4.2 Å, theoretical difference cage term, r²ΔS_cage(r) is obtained. Figure 19(f) shows r²ΔS_cage(r) as a function of I–I distance of the solute I₂ molecule. The r²ΔS_cage(r) at large r values obtained from the MD simulation clearly shows the shift of the peak positions with the change of I–I distance of the solute. With the decrease of the I–I distance towards the equilibrium distance in the ground state of I₂, the negative peak at around 6 Å becomes narrower, and the positive peak between 7 and 8 Å shifts to ∼7 Å.

Theoretical time-dependent solute–solvent distance distribution function was calculated by taking a linear combination of r²ΔS_cage(r) curves from the MD simulation at various I–I distances of the solute following the experimental time-dependent I–I distance distribution shown in Figure 17(a). For example, a theoretical difference cage term at a given I–I distance (r_i) of the solute, r²S_MDi(r), is weighted by the amplitude of experimental time-dependent I–I distance distribution curve at the corresponding r_i value, r²S_exp(r_i,t). Then, the theoretical time-dependent solute–solvent distance distribution function, r²ΔS_cage(r,t), at a given t was calculated as a sum of these weighted theoretical difference cage terms at various r_i values

$$r^2\Delta S_{\mathit{c}\mathit{a}\mathit{g}\mathit{e}}(r,t)={\displaystyle \sum _{r_{I-I}}{r}^2\Delta S_{M{D}_i}(r)\times r^2{S}_{\exp }(r_i,t)}.$$ (9)

Figure 19(b) shows the theoretical time-dependent solute–solvent distance distribution (i.e., cage term) as a function of time. As can be seen in Figures 19(a) and 19(b), the experiment and simulation show remarkably good agreement.

In Figures 20(a) and 20(b), we show examples of the difference pair distribution functions of Cl–I and C–I atomic pairs obtained from the MD simulation. As the I–I bond length of the I₂ molecule changes from 2.65 Å to 4.0 Å and from 2.65 Å to 3.1 Å, the Cl–I and C–I pair distribution functions change sensitively (see Figures 19(c) and 19(d)), giving an oscillatory pattern of the difference distance distributions as shown in Figures 20(a) and 20(b). As schematically described in Figure 20(c), the positive peaks at ∼7.7 Å (Cl–I distance in Figure 20(a)) and ∼8.5 Å (C–I distance in Figure 20(b)) represent the relatively increased population of the molecules with longer solute-solvent distances. In other words, the elongation of I–I bond in I₂ induces the expansion of the solvation shell. On the other hand, the negative peaks at ∼6.0 Å (Cl–I distance in Figure 20(a)) and ∼7.0 Å (C–I distance in Figure 20(b)) reflect the depletion of the solute–solvent distance in the ground-state configuration of the solute. Thus, we can infer that the first solvation cage expands by ∼1.5 Å along the I–I axis accompanying the elongation of I–I bond from 2.65 to 4.0 Å.

FIG. 20.

(a) and (b) Examples of the difference Cl–I pair distribution functions, Δg_Cl–I(r), and the difference C–I pair distribution functions, Δg_C–I(r), obtained from the MD simulation. The blue and red curves are for I–I distance changes from 2.65 Å to 4.0 Å and 2.65 Å to 3.1 Å, respectively. (c) Schematic for the change of the solvation shell due to the elongation of I–I distance. Dotted circles indicate the first solvation shell. The interatomic distance shown in this figure is the distance between the I atom of the solute and the C atom in the solvation shell. Because a CCl₄ molecule has one C atom surrounded by four Cl atoms and the Cl atom scatters much more strongly than the C atom, the scattering signal is dominated by the I−Cl contribution. Nevertheless, with the C atom being located at the center of the CCl₄ molecule, the I−C distribution provides a more intuitive picture of the size of the solvation shell.

In summary, we measured the real-time dynamics of geminate recombination and vibrational relaxation of I₂ in CCl₄ and cyclohexane using TRXSS combined with time slicing and deconvolution. From the measured data, we visualized in real space the recombination of I₂ molecules and the collective motions of surrounding solvent molecules in the form of time-dependent atom-atom distribution functions. Our scheme of using time slicing and deconvolution can serve as a general approach of circumventing the temporal limit imposed by X-ray pulse duration in the TRXSS experiment. For example, when femtosecond X-ray pulses are used in the future, even faster dynamics approaching attosecond time scale may be extracted using the time-slicing scheme.

V. CONCLUSION AND FUTURE PROSPECTS

As described in this paper, TRXSS demonstrated its power as an excellent tool for characterizing the transient structures of reacting molecules and elucidating the reaction dynamics and mechanism in solution phase. However, the time resolution of TRXSS studies performed thus far has been limited to 100 ps, which is imposed by the duration of X-ray pulses from third-generation synchrotrons. Due to the limited time resolution, ultrafast structural dynamics occurring on femtosecond time scales, for example bond breaking and bond formation, have not been studied with TRXSS. This limitation can be overcome with the recent advent of XFELs, which generates X-ray pulses of sub 100 fs duration and the intensity of ∼10¹³ photons per pulse. In the current experimental setup at third-generation synchrotrons, a single scattering image is recorded by accumulating the scattering of 5 × 10³ X-ray pulses and thus contains 5 × 10¹² X-ray photons in total. Thus, a single-shot of the X-ray pulse from an XFEL source contains enough photons to generate a scattering image comparable to an exposure of a few seconds at the third-generation synchrotron source. Therefore, it becomes possible to explore chemical processes occurring on femtosecond time scales using femtosecond TRXSS with improved time resolution and faster data acquisition rate.¹³⁹

For example, photochemistry of I₂ and I₃^– in solution that was reviewed in this article can be explored more extensively using femtosecond TRXSS. For I₂ in solution, besides the dynamics of geminate recombination reviewed in this paper, several interesting dynamic phenomena can be investigated in real time by femtosecond TRXSS (see Figure 21(a)). First, the time evolution of vibrational wave packet in the B state can be probed. When iodine molecules are photoexcited by ultrashort laser pulses, a vibrational wave packet is coherently prepared in the B state. As the wave packet evolves in the bound B state, the I–I bond length of I₂ will exhibit periodic oscillations until the population decays to a dissociative ¹π_u state, resembling the oscillating behavior of a classical harmonic oscillator. In time-resolved spectroscopy, the motions of such wave packet have been observed as quantum beats, i.e., the oscillation of nonlinear spectroscopic signals due to constructive and destructive interference between nuclear wave functions. In contrast, TRXSS will be able to detect the wave packet dynamics as a periodic change of the difference X-ray scattering pattern over time, thus providing a direct evidence of quantum mechanical wave packet dynamics in real space. Secondly, the ultrafast structural dynamics of nonadiabatic transitions among the electronic excited states of I₂ can be resolved. Although the previous TRXSS experiments on I₂ resolved the structural changes associated with vibrational relaxation in the hot ground or A/A′ state and rather slow relaxation of A/A′ state to the ground state,^60,140 the bond-breaking process of I–I bond along the dissociative ¹π_u state and the transition from ¹π_u to A/A′ state were not resolved. Even with the time-slicing experiment presented in this paper, A/A′ state was already fully populated at the earliest time delays. These photodissociation dynamics at the early stage of the reaction will be clearly resolved by femtosecond TRXSS experiment. In addition, the solvation dynamics on ultrafast time scales can be resolved by femtosecond TRXSS. From the spectroscopic studies of solvation dynamics, it was found that the solvation occurs in a bimodal manner, exhibiting ultrafast inertial motions of the solvent molecules on a time scale faster than 50 fs and slower diffusive motions at longer times.^20–35 While the latter component was already directly observed by the time-slicing experiment,⁶⁰ the faster component can be monitored as well using femtosecond TRXSS.

FIG. 21.

(a) Photodissociation dynamics of I₂ in solution phase. Upon photoexcitation by an optical pulse, coherent vibrational wave packet evolves in the B state to induce the periodic oscillation of I–I bond length (1, 2, and 3). Subsequently, the excited population relaxes to a repulsive ¹π_u state, leading to either dissociation of I₂ (4) or geminate recombination via A/A′ state (5) or hot ground state (6). (b) Photodissociation dynamics of I₃^– ion. Upon photoexcitation of I₃^– by an optical pulse, one I atom is dissociated (1), forming coherent vibrational wave packet in the hot ground state (²Σ_u⁺) of I₂^–. As the coherent wave packet evolves in the hot ground state of I₂^– ion, the I–I bond length of the I₂^– ion periodically oscillates (2). Subsequently, the population in the hot ground state of I₂^– relaxes vibrationally to the ground state of I₂^– (3).

Similarly, femtosecond TRXSS can keep track of the entire reaction processes of the photodissociation of I₃^– in solution in real time (see Figure 21(b)). When excited by an optical pulse at 400 nm, I₃^– dissociates into I₂^– and I with one of the I–I bonds being broken. This bond-breaking process, which was reported to take up to ∼300 fs,⁷⁸ can be monitored in real time. Subsequently, coherent vibrational wave packet is created in the hot ground state (²Σ_u⁺) of I₂^– fragment and evolves in the ²Σ_u⁺ state over time, leading to the periodic modulation of I–I bond length. We note that the “wave packet” term here is used in a loosely manner to describe both coherent states and incoherent ensembles of I₂^– fragments. As for I₂, we expect that the oscillation of the I–I bond length will be manifested as a periodic change of X-ray scattering pattern in time. Then, the population in the hot ground state of I₂^– relaxes vibrationally to the ground state in about 4 ps. Therefore, all these dynamic processes can be captured by the femtosecond TRXSS experiment.

As described above, by fully taking advantage of intense femtosecond X-ray pulses generated from XFEL, the TRXSS technique can take a step forward in the near future towards ultrashort time scales comparable to the vibrational period of molecules. However, to achieve that goal, many technical challenges in terms of experimental details, theory, and data analysis will await to be overcome. When these challenges are met by the efforts of researchers in the field, femtosecond TRXSS experiment will give insight to the very details of molecular movement during chemical reaction and stimulate further studies of more complex reactions using the technique.