Enzyme transient state kinetics in crystal and solution from the perspective of a time-resolved crystallographer

Abstract

With recent technological advances at synchrotrons [Graber et al., J. Synchrotron Radiat. 18, 658–670 (2011)], it is feasible to rapidly collect time-resolved crystallographic data at multiple temperature settings [Schmidt et al., Acta Crystallogr. D 69, 2534–2542 (2013)], from which barriers of activation can be extracted. With the advent of fourth generation X-ray sources, new opportunities emerge to investigate structure and dynamics of biological macromolecules in real time [M. Schmidt, Adv. Condens. Matter Phys. 2013, 1–10] in crystals and potentially from single molecules in random orientation in solution [Poon et al., Adv. Condens. Matter Phys. 2013, 750371]. Kinetic data from time-resolved experiments on short time-scales must be interpreted in terms of chemical kinetics [Steinfeld et al., Chemical Kinetics and Dynamics, 2nd ed. (Prentience Hall, 1985)] and tied to existing time-resolved experiments on longer time-scales [Schmidt et al., Acta Crystallogr. D 69, 2534–2542 (2013); Jung et al., Nat. Chem. 5, 212–220 (2013)]. With this article, we will review and outline steps that are required to routinely determine the energetics of reactions in biomolecules in crystal and solution with newest X-ray sources. In eight sections, we aim to describe concepts and experimental details that may help to inspire new approaches to collect and interpret these data.

I. CONFORMATIONAL ENTROPY AND ENTHALPY

Determination of the energetics of a chemical reaction is synonymous with the determination of the free energy surface on which that reaction proceeds. The energy of an instantaneous structure of a single protein molecule can be considered as a point $\overrightarrow{x}$ on a hypersurface called configurational energy surface with dimension 3N, with N the number of atoms in a molecule plus their weakly interacting solvent molecules. Each point on the surface corresponds to a different 3-dimensional arrangement of the atoms. The conformational free energy, G (free energy in short, Eq. (1), is an ensemble property. If the molecules distribute approximately in an even potential $U\left(\overrightarrow{x}\right)$, which is assumed for simplicity, the configurational energy of the mean structure represents the energy minimum, which is the conformational enthalpy. The difference between the enthalpy of formation of the macromolecule and the conformational enthalpy is that the conformational enthalpy does not consider covalent bonds that hold the primary structure together and rather considers non-covalent interactions that are responsible for the tertiary and quaternary structure formation. G also contains the conformational entropy S and the temperature T

$$G=H-S\cdot T.$$ (1)

A single configuration $\overrightarrow{x}$ on the configurational energy surface is not sufficient to determine the conformational entropy. The absolute conformational entropy is given by¹⁰

$$S\sim -{\displaystyle \int p\left(\overrightarrow{x}\right)}\ln p(\overrightarrow{x})d\overrightarrow{x},$$ (2)

where S may be given either in units of the Boltzmann constant k_B [1.381 × 10⁻²³ J K⁻¹] or the gas constant R [8.314 J mol⁻¹ K⁻¹]. $p\left(\overrightarrow{x}\right)$ is the probability density to find a molecule with configuration $\overrightarrow{x}$ on the energy surface. A sufficiently large area on that surface must be sampled to evaluate the integral (Eq. (2)), which can be challenging.¹⁰ Methods have been developed to estimate the absolute conformational entropy from theoretical calculations such as molecular dynamics simulation^10,11 or from experiment: Conformational entropy has been estimated from crystallographic B-factors assuming that the entire mean square deviation is caused by dynamic fluctuations,^12,13 from nuclear magnetic resonance order parameters,¹⁴ or from incoherent neutron scattering¹⁵ that provide dynamic mean square deviations 〈x²〉_dyn. For small proteins, the absolute conformational entropy is between 10 000 J mol⁻¹ K⁻¹ (Refs. 10 and 16) and 60 000 J mol⁻¹ K⁻¹,¹² for larger proteins it can be more than 100 kJ mol⁻¹ K⁻¹, which is enormous. The absolute free energy of a state, therefore, consists of the conformational enthalpy and the conformational entropy as a measure of structural variability.

II. ENZYMATIC REACTION PATHWAYS

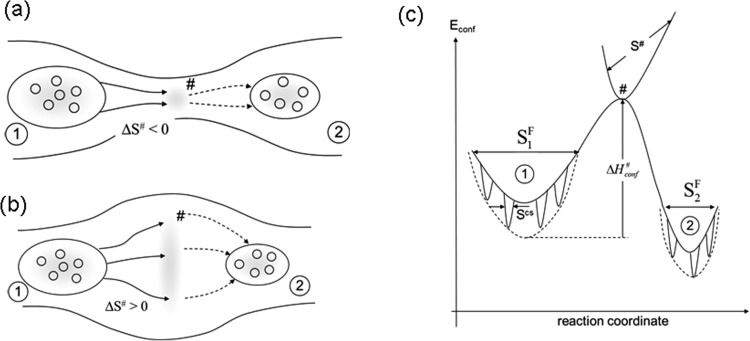
Proteins as one group of biological macromolecules may catalyze chemical reactions that take place in the active center of these molecules. Proteins are flexible and change their shape or conformation during the course of a reaction. Along the reaction, a protein molecule migrates on certain, energetically allowed pathways through conformational space (Fig. 1). These pathways are pre-determined by the structure of the protein and are therefore sometimes referred to as the reaction coordinate or the enzymatic reaction pathway.^17,18 The migration along these pathways is decisively determined by the local configurational energies and the number of microstates accessible at each point on the hypersurface. Both, conformational entropies and enthalpies play major roles in the description of these processes.¹⁹

FIG. 1.

Reaction coordinates of a general reaction (schematic). (a) and (b) two dimensional projection of the conformational hypersurface, iso-energy lines are schematically shown. Migration pathways of molecules through configurational space shown as arrows. (a) Transition state # has low entropy; reaction proceeds through a narrow path, ΔS^# is negative. (b) Similar to (a), transition state # has a larger entropy, the molecules are more flexible at the transition state, ΔS^# is positive. (c) One dimensional projection of the configurational energy hypersurface with energy E_conf along the reaction coordinate. S₁^F: conformational entropy of state 1 in the flexible state, S₂^F: conformational entropy of state 2 in the flexible state, S^cs: conformational entropy of conformational substates. Here, S₁^F > S₂^F > S^cs and reaction entropy ΔS is negative. S^#: entropy of transition state. ΔH^#_conf: change of conformational enthalpy from state 1 to the transitions state.

Protein folding is only one form of reaction that proceeds through energy landscapes. Conformational free energy differences between folded and unfolded states of a typical protein can be determined from melting curves²⁰ or even estimated from chain lengths.²¹ Conformational enthalpy differences, ΔH, are on the order of 500 kJ/mol for a medium sized protein, conformational entropy differences, ΔS, are around 1000 J mol⁻¹ K⁻¹.^20,22 This means that at physiological temperatures a few hundred kJ/mol of energy has to be used to break non-covalent bonds of a small protein to go from the folded to the unfolded state, and simultaneously a similar amount of energy is available through the gain of conformational entropy.²³ The typical free energy difference ΔG (Eq. (3)) of folding is consequently small on the order of 30–50 kJ mol⁻¹ in favor of the folded state

$$\Delta G=\Delta H-T\Delta S.$$ (3)

III. SHORT LIVED (TRANSIENT) STATES

A transient state is a synonym for an intermediate state that is shortly (transiently) populated by reacting molecules. Transient states are energy minima (holes) in configurational space, which are subsequently occupied by reacting molecules. The conformational enthalpy can be considered as the depth of the minimum and the entropy is equivalent to the width. A transient state represents an ensemble of molecules, all with approximately the same structure. Emphasis lies here on approximately since the structures of individual molecules are slightly different and exhibit deviations form a mean structure in the same way as is the case for stable equilibrium states. Molecules will voluntarily migrate from state to state when the difference of free energy between the states, ΔG, is negative. The reaction is exergonic. Endergonic reactions are made possible in biology by coupling them to hydrolysis of energy rich compounds such as ATP or GTP.

The free energy depends on the temperature (Eq. (1)). Equation (3) shows that the direction of a reaction cannot simply be changed by changing the temperature unless there is an entropy difference ΔS. Structural flexibility and, connected to this, the conformational entropy is dependent on the environment. When, for example, the solvent in which the protein is embedded becomes more mobile, the protein may exhibit a larger phase space and its conformational entropy increases. Populations of molecules previously in equilibrium may then change with temperature. A descriptive example is again the situation when the protein melts. The denatured state above the melting temperature T_m exhibits less interactions between the atoms and is disordered. Accordingly, it has a more positive conformational enthalpy (=less bonds) and also a larger conformational entropy compared to the folded state below T_m. At a temperature above T_m, the reaction proceeds towards the melted state, below T_m the protein folds. There are a number of experimental techniques that can contribute to the assessment of free energy surfaces in biological macromolecules by either determining enthalpies, entropies or both. The most frequently used techniques are based on spectroscopic methods such as UV/Vis absorption spectroscopy,^24,25 Moessbauer spectroscopy,^4,5,13,26 and nuclear magnetic resonance.¹⁴ However, also scattering methods, such as transient grating light scattering,²⁷ incoherent Neutron scattering,¹⁵ and X-ray diffraction,^4,28 are used to extract thermodynamic properties of biological macromolecules to determine free energy surfaces.

IV. EQUILIBRIUM DYNAMICS AND ITS RELATIONSHIP TO TRANSIENT STATE DYNAMICS

Dynamic properties of proteins at thermal equilibrium can be characterized by methods that allow for the dynamic autocorrelation function $c(\tau )=〈\overrightarrow{r}(t)\cdot \overrightarrow{r}(t+\tau )〉$ to be determined for a structural probe at a time dependent position $\overrightarrow{r}$ in the molecule. c(τ) is the average of the position of the probe at time t dotted into the position of the same probe at time t + τ. Once c(τ) is determined accurately, the dynamic mean square displacement ${〈x^2〉}_{\mathit{d}\mathit{y}\mathit{n}}$ can be determined from it¹³ and from this the conformational entropy.¹² Typically, c(τ) is measured by methods that probe an ensemble incoherently, such as inelastic, incoherent neutron scattering,²⁹ or Moessbauer spectroscopy.¹³ Incoherent means that scattering or absorption of one molecule in the ensemble has no (or an irrelevant) phase relation to a similar event in another molecule in the ensemble. If the dynamics is governed by phonons, c(τ) oscillates. On the other hand, non-oscillatory fluctuations exist which can be described by structural relaxations. The conformation is disturbed by random forces, for example, by fluctuating solvent molecules in the sample, and the structure adjusts slowly. Relaxations can be described mathematically by overdamped oscillations. Then the c(τ) decays exponentially within a characteristic time τ_relax which can be quite long if the system is strongly overdamped. The appearance of τ_relax requires that the method measures over a sufficiently large time τ_exp that τ_relax can be accurately determined.³⁰ The reciprocity between τ_exp and energy automatically means that the method must have energy resolution. A relaxation with τ_relax that is much longer than τ_exp must be considered static for the method. τ_exp is ∼140 ns for ⁵⁷Fe Moessbauer spectroscopy with an energy resolution (=line width) Γ on the order of 5 neV. For inelastic, incoherent neutron scattering experiments, τ_exp is a few picoseconds with an energy resolution of μeV.²⁹ Accordingly, different time scales are explored with different methods³⁰ that provide different estimates how much of conformational space is sampled by individual molecules during the time τ_exp. The important outcome is the dynamic mean square displacement ${〈x^2〉}_{\mathit{d}\mathit{y}\mathit{n}}$ characteristic to the method. During the limited time τ_exp, the individual molecules may not be able to sample the entire accessible conformational space and the ${〈x^2〉}_{\mathit{d}\mathit{y}\mathit{n}}$ may be an inadequate measure of the absolute conformational entropy.

Frauenfelder and colleagues^31–34 described how protein conformational substrates are hierarchically arranged within a conformation. Substrates represent a multitude of slightly different minima below the level of the top-tier conformation (Fig. 1), each minimum with a smaller width than the width of the hierarchically higher conformation. This means that each minimum represents an ensemble of molecules having restricted conformational entropy. Temperature dependent Moessbauer spectroscopic investigations can shine light on the nature of substrates, since these investigations are able to extract a dynamic mean square displacement, ${〈x^2〉}_{\mathit{d}\mathit{y}\mathit{n}}$, through the Lamb-Moessbauer factor. The ${〈x^2〉}_{\mathit{d}\mathit{y}\mathit{n}}$ observed below a characteristic temperature of T_c ∼ 180 °C is small. The ${〈x^2〉}_{dyn,T<{180}^{\hspace{0.17em}}°\mathrm{C}}$ can be explained by a normal mode analysis performed on the atomic structure of the protein.^26,35–37 The normal mode analysis provides an estimate for the conformational entropy S_conf.¹⁰ When the temperature increases, the molecules pass over to a more flexible state. This transition is known as the dynamic transition. Harmonic oscillations that are at the base of a normal mode analysis are not sufficient to explain the ${〈x^2〉}_{dyn,T>{180}^{\hspace{0.17em}}°\mathrm{C}}$. Diffusive motions described by relaxations in restricted space dominate the mean square displacement.⁵ At elevated temperature, a protein molecule can access and explore a larger phase space by populating a multitude of protein substrates by means of relaxations in the flexible state. The difference of conformational entropy of such a transition from a narrow structural distribution in the substrate to the broader distribution in the flexible state is known for certain proteins (Table I).^4,5 It is on the order of 100 J mol⁻¹ K⁻¹. At 300 K, the entropy contributes ∼30 kJ mol⁻¹ to the conformational free energy. It helps to keep the molecules in a flexible state ready to perform their function. At low temperatures, the entropic contribution to the free energy is small. As a consequence, the molecules stay in the rigid state and are non-functional. The free energy change of the dynamic transition from the rigid to the flexible state is relatively small (on the order of 1–5 kJ/mol at 30 °C, see Table I), since entropic and enthalpic contributions to the dynamic transition almost cancel. So far, no obvious differences in the dynamic transition temperature between molecules in the crystal and in solution are observed.^5,26,29 The dynamic transition has similarities to melting although T_c (∼180 K) is much smaller than T_m (∼350 K for photoactive yellow protein for example): T_c as well as T_m are points where ΔH and TΔS are equal. In both cases, entropy and enthalpy differences are positive when going from lower to higher temperatures. The difference is, however, that at temperatures above T_c diffusive motions in restricted space dominate the protein's 〈x²〉_dyn, whereas above T_m the molecules lose their structural integrity altogether.

TABLE I.

Thermodynamic parameters ΔH, ΔS, and ΔG (at 300 K) of the dynamic transition in heme proteins. The free energy is negative at 300 K, which means that the molecular population shift from the rigid states (CS) to the flexible state.

	Nitrophorin a (Fe3+)	Myoglobin b deoxy (Fe2+)	Myoglobin a met (Fe3+)
ΔH [kJ mol−1]	18.3 ± 3.7	25.9	21.0 ± 1.0
ΔS [kJ mol−1 K−1]	0.063 ± 0.020	0.107	0.080 ± 0.004
ΔGtrans at 300 K	−0.6 kJ/mol	−4.1 kJ/mol	−3 kJ/mol

^a,cReference 4.

^bReferences 5 and 6.

A reaction scheme such as the one depicted in Fig. 1 must be augmented by protein conformational substrates (CS) which are the small, local minima within a state's potential. For a reaction to occur, the molecules lift out of the CS and either surmount the barrier of activation (see below) or explore other CS. At lower temperatures, the CS decisively determines the time-dependence of the reaction, which becomes non-exponential.³¹ ΔH^# distributes along a range of energies. At temperatures higher than ∼200 K (Ref. 26) kinetic averaging, also called motional narrowing, restores exponential behavior.^26,38,39

V. TIME-RESOLVED TECHNIQUES TO EXPLORE CONFORMATIONAL SPACE

If a reaction is initiated in biological macromolecules, its progress can be followed by time-resolved techniques. Typical examples are mixing of substrate and enzymes or photoinitiating a process in a photoresponsive protein using an intense Laser pulse. For enzymes the difference of free energy between the substrate and the product will drive the reaction. In photoinitiated processes, a large amount of energy is injected into the system by the Laser pulse that dissipates through the reaction. The energy injected is usually absorbed by a central chromophore whose temperature can rise by several hundreds of K.⁴⁰ This energy is gradually released through different processes. A substantial amount of this energy is dissipated rapidly into the phonon modes of motion and results in a moderate adiabatic temperature change of the protein. For example, the activation of the photocycle in the photoactive yellow protein (PYP, see Fig. 2) requires an energy of 245 kJ/mol which is the energy of the blue photon that excites the central chromophore p-coumaric acid (PCA). With a molar mass of 14.7 kg/mol and assuming a heat capacitance of a typical protein being 5 kJ kg⁻¹ K⁻¹, the adjabatic temperature rise of a single PYP molecule would be $\Delta T=\frac{245\mathrm{k}\mathrm{J}\hspace{0.17em}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}\hspace{0.17em}}{14.7\mathrm{k}\mathrm{g}\hspace{0.17em}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}\times 5\hspace{0.17em}\mathrm{k}\mathrm{J}\hspace{0.17em}\mathrm{k}{\mathrm{g}}^{-1}{\mathrm{K}}^{-1}}\sim 3\mathrm{K}$, given that all the energy absorbed locally by the chromophore dissipates in the phonon modes of motion of the entire protein. However, in PYP, a substantial amount of the photon energy is used to twist the chromophore into a geometrically unfavorable configuration (Fig. 2(a)). The structural mechanism how this is achieved is subject to extensive theoretical and experimental work.^6,9,41–48

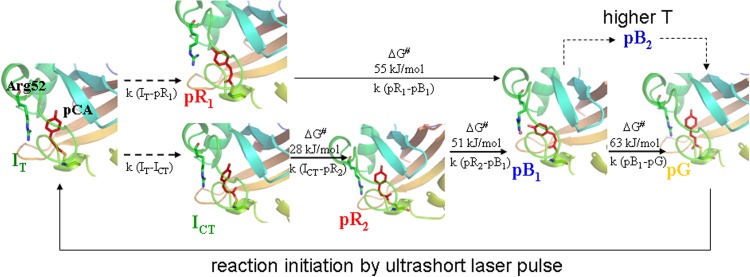
FIG. 2.

PYP photocycle from a time-resolved crystallographer's perspective. The early intermediate I_T crosses over to pR₁ and I_CT in a hula-twist and a bicycle pedal motion, respectively. I_CT decays to pR₂. pR₂ and pR₁ both react to pB₁ that may decay directly to the dark state. At higher temperatures pB₂ accumulates in addition. Mechanism is simplified by omitting less important transition pathways; see Ref. 2 for a more comprehensive mechanism. Free energies of the barriers of activation are shown as determined from five-dimensional crystallography for several transitions.

PYP features a quintessential photocycle, with a number of intermediates on time-scales from femtoseconds^49,50 to seconds (Fig. 2). The photocycle is active and can be investigated both in crystal and in solution. PYP and its photocycle were discovered in the 90th of the last century.⁵¹ Since then, a large number of publication report extensive details of the photocycle determined with methods with increasingly better time resolution. Initial time-resolved investigations were all performed using time-resolved spectroscopy in solution.^52–56 After the structure of PYP has been determined,⁵⁷ time-resolved crystallographic techniques were used to investigate the photocycle. First, the decay of a photostationary state produced by a long blue laser pulse (λ = 496.5 nm, 200 ms) was investigated on the millisecond time-scale with a single map collected with a 10 ms shutter opening from 2 to 12 ms.⁵⁸ That revealed the structure of the intermediate we know now as pB. With the advent of a global analysis based on the singular value decomposition (SVD),⁵⁹ the entire photocycle can be kinetically characterized using a comprehensive time-series of time-resolved X-ray data.^1,47,48,60 Recently, even the picosecond time-scale has been covered by two different publications.^6,9 Here, the results from Jung et al.⁹ are referred to, since in the other study crystals were grown in unusual conditions which might have changed to outcome. The structures of the photocycle intermediates I_T, I_CT, pR₁ (formerly pR_E46Q), pR₂ (formerly I_cw), pB₁ and pB₂ are now known (see Fig. 2) together with a plausible chemical, kinetic mechanism. In solution time-resolutions as good as 8 fs are reached.^61,62 However, with spectroscopy, structural information is sparse.⁶³ There are comparative investigations on crystal and solution on the μs to ms time scales.^64,65 The former study investigated the decay of a photostationary state at several temperatures to gain information on barriers of activation of that decay. In the latter study, single laser pulses were used to initiate the PYP photocycle and data were collected at a single temperature (15 °C). Results were comparatively analyzed on a time range from 1 μs to 150 ms by kinetic target analysis.⁵⁰ Both studies found kinetic differences between crystal and solution. The most striking difference is that the photocycle lasts about a factor 5 longer in solution than in the crystal. Obviously, barriers of activation in solution and in the crystal may be very different.

VI. BARRIERS OF ACTIVATION

Barriers of activation represent saddle points on the conformational energy surface that connect two adjacent states (Fig. 1). They decisively determine the magnitude of the microscopic rate coefficients k of a reaction. The transition state theory⁶⁶ accounts for the magnitude of k according to

$$k=\frac{\mathit{R}\mathit{T}}{N_{a}h}{e}^{-\frac{\Delta G^{\#}}{\mathit{R}\mathit{T}}}=\frac{\mathit{R}\mathit{T}}{N_{a}h}{e}^{\frac{\Delta S^{\#}}{R}}{e}^{-\frac{\Delta H^{\#}}{\mathit{R}\mathit{T}}},$$ (4)

where N_a is the Avogadro number, h is the Planck constant, R is the gas constant, ΔG^# is the free energy difference from a state to the transition state, and ΔH^# and ΔS^# are the enthalpic and entropic contributions, respectively. The saddle point that represents the transition state in Fig. 1 is denoted by a double dagger (#). Similar to transient states a transition state can be considered to have its own phase space with its own conformational entropy S^#. Transition states are notoriously difficult to characterize because their occupations are extremely low during a reaction. If, for example ΔG^# is 50 kJ/mol (see, e.g., the transition from pR to pB in Fig. 2), the probability to find a molecule on top of the barrier of activation is only $e^{-\hspace{0.17em}\hspace{0.17em}\frac{\Delta G^{\#}}{\mathit{R}\mathit{T}}}\sim {10}^{-9}$. Such an occupation is not measurable in any time-resolved experiment. However, transient states before and after the barrier can be characterized and the properties of the barrier deduced from this. Since the entropy change ΔS^# is included in Eq. (4), one can estimate the number of microstates ΔQ that are accessible at the transition state # compared to those in the transient states that flank the barrier by

$$\Delta Q=e^{\frac{\Delta S^{\#}}{R}},$$ (5)

where R is the gas constant and ΔS^# is measured in J mol⁻¹ K⁻¹. ΔQ might be smaller or larger depending whether ΔS^# is negative (number is smaller, Fig. 1(a)) and positive (number is larger, Fig. 1(b)). A larger number as in Fig. 1(b) will accelerate a reaction, since the transition state offers a large number of microstates that can be reached through a multitude of pathways. This makes the reaction more probable. If, however, a reaction is confined to a narrow pathway, the entropy difference is negative. The reaction slows down because it is less probable that the molecules thread through a narrow, confined path (Fig. 1(a)). It is important to notice that barriers of activation have to be determined for true chemical rate coefficients. Apparent rates Λ that are observable in a kinetic experiment are linear combinations of the true rate coefficients.⁸ The temperature dependence of the Λ can be fit with the Van't Hoff Arrhenius equation ${\Lambda }_T=\nu e^{-\frac{E_a}{\mathit{R}\mathit{T}}}$ to determine an energy of activation E_a and a prefactor ν, which can be understood as the number of attempts to surmount the barrier E_a. The Λ are fingerprints of a reaction, since they are, as mentioned, linear combination of k whose temperature dependences might be very different.

The appearance of diffusive motions in restricted space (see above) suggests that Kramer's theory⁶⁷ instead of the mentioned transition state theory should be used to describe the temperature dependence of the rate coefficients.⁶⁸ In Kramer's equation,⁶⁷ the prefactor $\frac{\mathit{R}\mathit{T}}{N_{a}h}$ in Eq. (4) is parameterized differently. Pre-factors from Kramer's equation are much smaller with correspondingly longer time-scales.^26,68 Parak et al.²⁶ modified Kramer's equation to contain the factor α₀, which is proportional to $1/{\tau }_{\mathit{r}\mathit{e}\mathit{l}\mathit{a}\mathit{x}}$, as the prefactor (Eq. (6)). α₀ can be obtained in a Moessbauer experiments from the linewidth of the broad Lorentzian that underlies the Moessbauer spectrum provided all molecules have left the conformational substrates and are in the flexible state

$$k=\frac{{\alpha }_0/\hslash }{2\pi }{e}^{-\frac{\Delta G^{\#}}{\mathit{R}\mathit{T}}}.$$ (6)

For α-helical as well as for β-sheet small proteins, such as myoglobin and nitrophorin, respectively, α₀ is known to be ∼40 mm/s derived from ⁵⁷Fe Moessbauer spectra,⁴ which corresponds to about 2000 neV that must be used in Eq. (6). From this a prefactor of ∼5 × 10⁸ 1/s is obtained. $\frac{\mathit{R}\mathit{T}}{N_{a}h}$ in Eq. (4) is 6 × 10¹² 1/s at 300 K. The difference in fitted values of ΔS^#/R between Kramer's theory and the transition state theory is on the order of ln(10⁴) = 9. The ΔS^# itself deviates by ∼70 J mol⁻¹ K⁻¹, which is relatively large. This has to be used as a caveat and trends rather than absolute values must be considered. The small prefactor in Kramer's equation also implies that transitions faster than about 2 ns should reveal their diffusive nature and might deviate from simple exponential behavior. There are indeed time-resolved crystallographic and time-resolved spectroscopic photoflash experiments on myoglobin at room temperature where the initial, fast kinetic phase is non-exponential in Refs. 69–71. Detailed experiments that structurally probe the fast picosecond time-regime are necessary for these small proteins. Relaxations and barrier crossings last even longer in larger proteins,⁶⁸ and the existing theories might need to be extended to describe their kinetics.⁷² However then, a molecular movie comes into reach that experimentally determines a trajectory through conformational space from an ensemble of reacting molecules.

VII. TRANSIENT STATE KINETIC EXPERIMENTS ON PYP TO DETERMINE BARRIERS OF ACTIVATION IN THE PHOTOCYCLE

Attempts to determine of barriers of activation in the PYP photocycle are sparse. All attempts so far used the transition state equation (Eq. (4)) or the Van't Hoff Arrhenius equation to fit the temperature dependence of the processes in the photocycle. Van Brederode et al., 1996²⁵ report barriers including entropy and enthalpy differences for the pR to pB and the pB to pG transition (Table II), and Ng et al.⁶⁵ report energies of activation for the decay of a photostationary state to pG determined from single crystal and solution spectroscopy (see also Table II). Recently, a time-resolved crystallographic experiment was performed by collecting comprehensive time-series from 2 ns to seconds at 14 different temperatures from −40 °C to +70 °C.² Global analysis with SVD and subsequent kinetic target analysis (posterior analysis) was used to extract apparent rates Λ_i for i = 1–3 processes as well as true rate coefficients of the mechanism shown in Fig. 2. Since the X-ray data were collected at 14 temperature settings, the temperature dependence of the rates and true rate coefficients could be used to determine activation energies, as well as entropy and enthalpy difference to transition states for six different rate coefficients. Since five variables, time, temperature, and space are involved, this method is called five-dimensional crystallography.⁷³ The following picture emerges: Spectroscopically, in crystals, the transition of pB to pG is biphasic.^2,64 Also the decay of a photostationary state to pG in crystals is biphasic with energies of activation of 23 kJ/mol and 48 kJ/mol for a fast and a slow phase respectively.⁶⁵ With five-dimensional crystallography, only the slow phase is observed at T < 50 °C with E_a = 49.6 kJ/mol.² pB₁ is the dominant species.⁵⁸ In solution the decay of the photostationary state is slower with E_a being about 6 kJ/mol larger than in the crystal.⁶⁵ This trend can also be observed when the reaction is initiated by a single laser pulse. In solution, the pB to pG barrier ( $\Delta G_{B-G}^{\#,sol}$) is about 6 kJ/mol larger than that obtained in crystals from five-dimensional crystallography (see Table II). The pR to pB transition on the other hand is similar in the crystal and in solution. In the crystal, there are two pR species (pR₁ and pR₂). Barrier heights for the pR to pB transitions are $\Delta G_{R1-B}^{\#}$ = 54 kJ/mol and $\Delta G_{R2-B}^{\#}$ = 51 kJ/mol, respectively. Since the latter (pR₂) is the species that is most populated with an approximate pR₂ to pR₁ ratio of 3:1, it dominates the transition. In solution $\Delta G_{R-B}^{\#,sol}$ is also 51 kJ/mol. Up to the pR relaxation the photocycles in crystal and solution show similar energetics. The energetics of even earlier intermediates such as I_CT is only available to date from five-dimensional crystallography. The free energy of the I_CT to pR₂ transition is 28 kJ/mol (Fig. 2) which accounts for the much faster decay of I_CT. So far, a consistent picture emerges, with the energetics in crystal and solution being similar except for the pB to pG transition. Apart from the difference of 6 kJ/mol between the barrier in the crystal and solution, significant differences emerge when entropy and enthalpy differences are inspected for the final pB to pG transition. In solution $\Delta H_{B-G}^{\#,sol}$ is only 9 kJ/mol. If the entropy would not play a role ( $\Delta S$^# ∼ 0), at 283 K (10 °C) pR would decay within 8 ps. However, $\Delta S_{B-G}^{\#,sol}$ is −196 J mol⁻¹ K⁻¹.²⁵ As a result, at 283 K the rate coefficient for the pB decay is 7.5 s⁻¹ with a characteristic time of 134 ms. It is the entropy of the transition state which decisively slows down the reaction. Since the entropy difference is negative, the transition state is much more ordered than the pB state itself. In solution, PYP refolds from a disordered structure with high conformational entropy through a well ordered transition state with a lower conformational entropy. In the crystal, the situation is different. There, $\Delta S_{B-G}^{\#}$ is positive (42 J mol⁻¹ K⁻¹). The transition state is more disordered than pB, which helps to accelerate the reaction. From the crystallographic data, the reason for this becomes clear. In pB, the chromophore has swung out to the solvent and is bound to Arg52 and to one or two water molecules by hydrogen bonds. For reisomerization, it has to swing back into the chromophore pocket. First the hydrogen bonds have to be broken, and some rotation about the double bond is necessary. This requires substantial energy of about 75 kJ/mol. The protein then provides an enlarged, relaxed chromophore pocket so that this reisomerization is facilitated.

TABLE II.

Thermodynamic parameters obtained from solution and crystal for barriers of activation for the pR to pB and the pB to pG transition by using Eq. (4). The activation energies (from the slopes of Arrhenius plots) of the decay of a photostationary state and for the pB to pR decay from single pulse experiments are also available.

	Solution a	Crystal b
	pR‐pB	pR1-pB1	pR2-pB1
ΔH# [kJ/mol]	66	50.0	48.1
ΔS# [J mol−1 K−1]	51	−15	−10.2
ΔG# [kJ/mol] at 300 K	50.7	54.5	51.2
	pB-pG	pB1-pG
ΔH# [kJ/mol]	9.2	75.2
ΔS# [J mol−1 K−1]	−196	41.9
ΔG# [kJ/mol] at 300 K	69	63

	Photostationary c		Single pulse b
	Solution	Crystal	Crystal, pR-pB
Ea [kJ/mol]	54.5	22.7/48.3 (biphasic)	49.6

^aReference 24.

^bReference 2.

^cReference 65.

Compared to the enormous conformational entropy of the entire protein (see above), entropy differences to the transition states are small. Protein structures may have been evolved that relatively small local entropy changes control catalytic reactions. It is interesting to note that although kinetic differences between crystal and solution are relatively large, free energies of activation differ by only a few kJ/mol. It would be highly desirable to determine the solution structure and follow its decay with time-resolved methods capable of determining structural changes.

VIII. TIME-RESOLVED STRUCTURES FROM SOLUTION

With the advent of fourth generation X-ray sources such as the Linac Coherent Light Source (LCLS) in Stanford, the determination of protein structures from solution have come within reach.^7,74,75 The coherent X-ray beam from these machines can be focused so much that the beamsize matches the size of a typical protein such as hemoglobin. The photon density becomes so large that a substantial number of photons can be scattered from a single molecule. Beamsizes as small as 100 nm are already achieved at the LCLS. Attempts to reduce the beam size further down are under way. In Fig. 3(c)), a beamsize of 10 nm is assumed into which 10¹² photons are focused, so the photon density is about 10¹⁰ photons/nm². The total scattering cross section of a PYP molecule is about 5000 × 10⁻¹⁰ nm². Accordingly, a total number of 5000 photons would be scattered per single PYP. However, it is exceptionally difficult to hit a single PYP molecules with such a small X-ray beam (Fig. 3(a)). One way out is to prepare an ensemble in a larger liquid jet (Fig. 3(b)) and accept that more than one PYP molecule scatters. The volume of the shaded area V in Fig. 3(c) is 2.4 × 10⁻²⁰ L. 40 mg/ml PYP corresponds to 16.4 × 10²⁰ molecules per Liter. Accordingly, V contains about 40 molecules of PYP that would diffract coherently. The question is, can the diffraction volume of a single PYP molecule be retrieved from the coherent scattering of this small ensemble? The answer is yes, subject to certain conditions. A recent approach^7,75 used pairwise correlations C₂ =  $〈I\left(q\right)I\left(q\prime ,\Delta \varphi \right)〉$ between intensities at q, I(q), and intensities I(q′,Δϕ) measured at q' an angular distance Δϕ apart in the diffraction pattern (Fig. 4(b)). It can be shown^75,76 that the pairwise intensity correlation of an ensemble is the same as the pairwise intensity correlation of a single molecule. Each data set may contain millions of diffraction pattern such as the one shown in Fig. 4(b). The angular correlations found in each individual diffraction pattern are averaged over all diffraction patterns. Since only correlations are used, an additional phase problem emerges that can be solved for a number of scenarios. (i) High symmetry imposes strong constraints, so that a unique solution can be found.^76–79 (ii) The existence of a reference structure in a time-resolved experiment allows structure determinations to be made independent of any symmetry of the structure.^7,75 Then two data sets are collected, a reference data set with the molecules in the initial (dark) state and a time-dependent data set, where a reaction is initiated by a laser for example. Two sets of pairwise correlations C₂ =  $〈I\left(q\right)I\left(q\prime ,\Delta \varphi \right)〉$ can be extracted from the two data sets. Young's fringes and other cross terms between different molecules that emerge from coherent illumination (Fig. 4(b)) average out to a flat background, because the relative distances and orientations of the different molecules are uncorrelated in solution.⁷⁵ The mathematics of this analysis is outlined in detail in two papers.^7,75 The C₂ can be related to the square of spherical harmonic expansion coefficients I_l,m of the diffraction volume.⁸⁰ The relevant quantity is $B_l\left(q,q\prime \right)=\sum _m{I}_{l,m}^{*}(q)I_{l,m}(q\prime )$, where m sums over the magnetic quantum number of the spherical harmonic expansion coefficients. The $B_l(q,q\prime )$ can be determined directly from C₂^7,81 collected separately a time t after reaction initiation, and in the dark as a reference (ref) without reaction initiation, respectively. If the structural changes are not too large the difference of the two sets of B_l(q,q′) is simply $\delta B_l\left(q,q\prime \right)=B_l{\left(q,q\prime \right)}^t-B_l{\left(q,q\prime \right)}^{\mathit{r}\mathit{e}\mathit{f}}$. The $\delta B_l\left(q,q\prime \right)$ are then related in a very specific manner (Eq. (7)) to the difference electron density⁷⁵

$$\delta B_l\left(q,q\prime \right)=M\delta \rho \left(\overrightarrow{r}\right).$$ (7)

Elements of matrix M are real numbers and are derived exclusively from known information provided by the dark state structure. δB_l(q,q′) is a measured quantity, and $\delta \rho \left(\overrightarrow{r}\right)$ is the difference electron density relative to the reference structure. $\delta \rho \left(\overrightarrow{r}\right)$ can be retrieved directly from the δBs by inverting matrix M. A result from a simulation⁷⁵ is shown in Fig. 4(c). $B_l{(q,q\prime )}^{\mathit{r}\mathit{e}\mathit{f}}$ were calculated from the dark state PYP model. Time-resolved $B_l{(q,q\prime )}^t$ were simulated by displacing the chromophore and a distant phenylalanine a significant amount. δρ was determined from the $\delta B_l{(q,q\prime )}^{t-ref}$ as described (Eq. (7)). Difference electron density δρ lights up in the frame of reference of the dark structure at the correct positions where the changes are made. This enables the difference electron density to be superimposed on the dark structure with standard crystallographic display software as in Fig. 4(c). With this method it might be possible for the first time to probe structures in solution at near atomic resolution and with ultra-fast time-resolution. For the PYP, it may become possible to directly observe the structural differences to the dark state in solution and compare those to known structural differences observed in the crystal.^2,9,48 A kinetic analysis would be as straightforward as for time-resolved crystallographic data using the same SVD-based approaches. Solution structures determined by nuclear magnetic resonance^82,83 as well as crystal structures^9,48 may be used as reference structures to construct matrix M (Eq. (7)). The X-ray photon densities available at the free electron lasers should be sufficient to extract the correlations to high resolution even in the presence of multiple particles.^84,85 By investigating the photocycle in terms of transient solution structures, it might well be that the structures of the transient states match those in the crystal, they might also be largely different, or a situation in between emerges. Results would shine light on why PYP behaves differently⁶⁴ in crystal and solution, which would also apply to other proteins and enzymes. Since the method averages over a large number of molecules present in millions of snapshots, it can be expected that the method provides a mean square deviation from which the conformational entropy can be estimated.¹² Moreover, by varying the temperature barriers of activation could be determined. Both conformational entropy and barriers can finally be compared to those obtained from crystals.

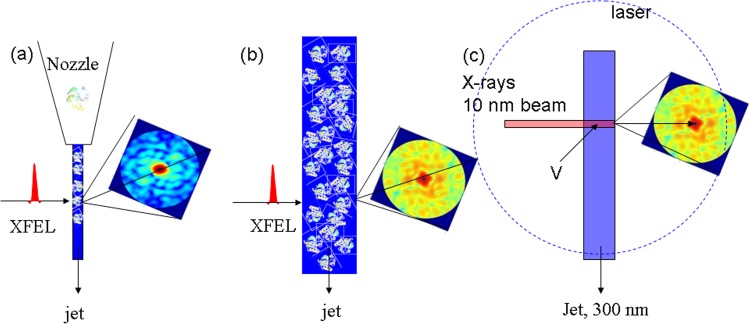
FIG. 3.

Geometry to determined time-resolved structures from solution. (a) Optimal setup: serial single molecule diffraction. Jet diameter is small. Due to jet and X-ray beam instabilities the hit rate is very small, if not non-existent. (b) More realistic scenario: Jet diameter is larger. The coherent XFEL beam interacts with an ensemble. (c) Geometry already in reach: X-ray beam is focused to 10 nm to increase the photon area density. Jet is large to allow for instabilities. With a PYP concentration of 40 mg/ml, the number of molecules in the intersecting volume V would be ∼40.

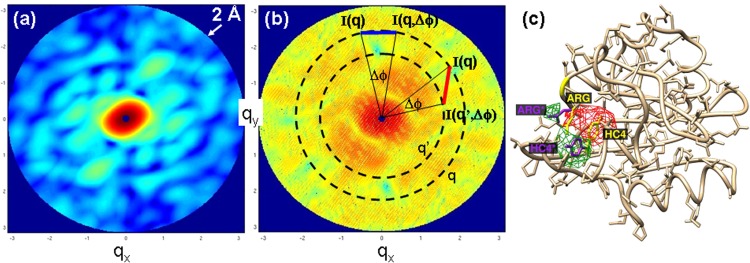
FIG. 4.

Structures from solution by analysis of the average angular correlations. (a) Intensity distribution from four molecules of random orientation and average distance of 150 Å from each other overlaid incoherently; $\left|\overrightarrow{q}\right|$ is 2π$\left|\overrightarrow{H}\right|$ with $\overrightarrow{H}$ the scattering vector; resolution at the edge: 2 Å. (b) Coherent diffraction from an ensemble of four molecules of random orientation and average distance of 150 Å. Young's fringes can be easily identified. Blue bar: I(q) and I(q, Δϕ) on same resolution ring; red bar I(q) and I(q′, Δϕ) on different resolution rings. (c) Difference electron density recovered from simulated δB_l(q,q′), courtesy of Kanupriya Pande. Position of the chromophore head as well as a Arg52 changed relative to the reference structure. Red: negative difference electron density, green: positive difference electron density.

IX. COMPARATIVE STRUCTURE BASED ENZYMOLOGY IN CRYSTAL AND SOLUTION

The European free electron laser for hard X-rays is designed to have X-ray pulse repetition rates of about 30 kHz.⁸⁶ With this rate, 1 million diffraction patterns can be collected in 330 s, and 10 million patterns in an hour. This makes it feasible to collect comprehensive time-series from the start of a reaction to the very end in less than an 8 h shift. All sorts of enzymatic reactions including those occurring in the largest complexes such as the ribosome^87–90 or other molecular machines that are prime drug targets⁹¹ could be investigated by this approach. To initiate an enzymatic reaction, the enzyme must be mixed with substrate and the mixture injected in the ultra-shortly pulsed X-ray beam. Diffusion times can then be as short as a few microseconds,^3,92 and the reaction can be swiftly initiated. Alternatively, small micron-sized or nanosized crystals can be injected after mixing with substrate. Diffusion times are acceptable and in the millisecond to microsecond time range when micro- and nanocrystals are used³ respectively. With these two mix-and-inject approaches, structure based enzymology and drug design become feasible. The structures of the transient states can be determined rapidly and free energy landscapes characterized routinely.