Femtosecond single-electron diffraction

Abstract

Ultrafast electron diffraction allows the tracking of atomic motion in real time, but space charge effects within dense electron packets are a problem for temporal resolution. Here, we report on time-resolved pump-probe diffraction using femtosecond single-electron pulses that are free from intra-pulse Coulomb interactions over the entire trajectory from the source to the detector. Sufficient average electron current is achieved at repetition rates of hundreds of kHz. Thermal load on the sample is avoided by minimizing the pump-probe area and by maximizing heat diffusion. Time-resolved diffraction from fibrous graphite polycrystals reveals coherent acoustic phonons in a nanometer-thick grain ensemble with a signal-to-noise level comparable to conventional multi-electron experiments. These results demonstrate the feasibility of pump-probe diffraction in the single-electron regime, where simulations indicate compressibility of the pulses down to few-femtosecond and attosecond duration.

I. INTRODUCTION

Ultrafast time-resolved electron diffraction (UED)^1–3 at keV energies is a versatile technique for investigating fundamental processes in numerous fields of research.^4–14 A femtosecond laser is used to initiate the dynamics of interest, and diffraction of ultrashort electron pulses provides a series of time-resolved structural snapshots with atomic resolution. However, the temporal resolution is usually limited by the duration of the probing electron pulses, which suffer from two different temporal broadening mechanisms: kinematic dispersion and intra-pulse Coulomb repulsion. In a typical UED setup, the latter is dominant for electron pulses containing more than 1000 electrons per pulse.¹⁵

Currently the highest resolution pump-probe experiments use microwave cavities to recompress multi-electron pulses. The effective resolution (instrument response function) is determined by, on the one hand, the duration of the individual dense electron pulses and, on the other hand, by laser-microwave synchronization jitter.^16–18 Reported pulse duration applied in UED experiments are in the range of 200–500 fs (full width at half maximum, FWHM).^18–21 Oudheusden et al.¹⁷ reported a pulse duration of 67 fs (rms), but the instrument response function was 104 fs (rms) due to jitter.¹⁷ This state-of-the-art in temporal resolution is not sufficient to observe many fast nuclear motions of interest.

The development of technologies that provide better temporal resolution in UED is therefore of large interest, and a variety of approaches to this problem exist.³ Laser-microwave jitter can be reduced to a level below 30 fs (rms) by time-stamping of the electron pulses.¹⁸ Combining this with the shortest individual dense pulses of Oudheusden et al.,¹⁷ one could reduce the instrument response function to approximately 80 fs (rms). Further improvements in laser-microwave synchronization, especially at higher repetition rates, could be made with intra-cavity phase detection,²² optically enhanced direct microwave generation,²³ or interferometric jitter detection.²⁴ Ultimately, however, ideal compression of individual dense electron pulses is prevented by a space-charge-induced emittance growth. Uniform ellipsoidal electron bunches, which have a reduced increase of emittance due to close-to-linear space charge fields, could help to reduce the duration of compressed multi-electron pulses.²⁵ However, the generation of such pulses is challenging.^26–28

An alternative approach, circumventing space-charge-induced emittance growth entirely is to work with single-electron pulses²⁹ for the complete trajectory, while compensating the remaining kinematic broadening effects (dispersion of vacuum) with microwave compression or a static dispersion compensator.³⁰ Simulations³¹ and first experiments²³ show that pulse durations down to few-femtoseconds or below are conceivable in this regime. Such pulses are required to eventually visualize coherent optical phonons,^32–34 photo-induced proton transfer,³⁵ the collapse of charge-density waves,^36,37 electron transfer,³⁸ or, in the long run, attosecond processes³⁹ with atomic resolution.

Single-electron pulses with about 500 fs (FWHM) duration at a high repetition rate of 500 kHz (Ref. 40) have been used in ultrafast electron microscopy (UEM), but the pulses contain more than one electron near the photocathode, causing emittance growth and temporal broadening. This can only be avoided by using single electrons over the entire trajectory.

However, the applicability of purely single-electron pulses to pump-probe experiments has been controversial,³ not because of the electron diffraction process, but because of the sample excitation. Roughly, ${10}^8$ incoming electrons are required for a suitable diffraction image^3,17 and about 100 different pump-probe delays must typically be applied for a complete picture of the dynamics. Hence, if the sample cannot be exchanged continuously,³ it must sustain approximately ${10}^{10}$ pump probe cycles reversibly without degradation. Ideally, pump-probe cycles would be repeated as fast as allowed by the rate of relaxation of the sample back to the initial state. In practice, however, the repetition rate is limited by the thermal load imposed by the excitation process³ to a few hundreds of kHz. We note that single-electron diffraction at 1–10 kHz used in the majority of UED experiments^6,41,42 would require net exposure times on the order of weeks.

In this work, we report on a time-resolved UED experiment using entirely single-electron pulses, which could in principle be compressed to few-femtosecond duration.^31,43 Although the experiment is performed with uncompressed pulses, it represents a proof-of-principle for the general feasibility of the single-electron pump-probe technique in the regime of reversible condensed matter dynamics.

II. EXPERIMENTAL SETUP AND DIFFRACTION GEOMETRY

Laser pulses of 60 fs duration (FWHM) and 500 nJ energy at a carrier wavelength of 800 nm were used for a laser-pump, electron-probe experiment in graphite thin films. The concept of the high-coherence single-electron source is described in Ref. 44. Here, the acceleration field was approximately 4 kV/mm and the final electron energy was 30 keV. The electron pulse duration is expected to be approximately 360 fs (FWHM) from laser-based streaking measurements in a comparable beamline.⁴⁵ The emittance of our single-electron source was improved with respect to the reported source⁴⁴ by inducing photoemission via two-photon absorption with frequency-doubled laser pulses and by tighter focusing with a 14.3 mm focal-length lens. The corresponding reduction of the transverse electron beam size at the sample (50 × 100 μm² FWHM) and on the screen (150 × 300 μm² FWHM) permits a significant reduction in the size of the pump beam, reducing the average thermal load at constant excitation flux on the sample. This advance enables repetition rates of hundreds of kilohertz. Linearly polarized pump laser pulses of roughly 350 nJ energy were focused to a diameter of 75 μm (FWHM) at the sample. Constant experimental conditions were achieved by actively and passively stabilizing laser power and beam pointing as well as magnetic fields around the experimental chambers. Stability of the single-electron generation and emittance of the beam was achieved by slightly heating the photocathode with a continuous wave laser. Under these conditions, fluctuations and long-term drifts of the electron beam intensity were less than a few percent over periods of more than 24 h.

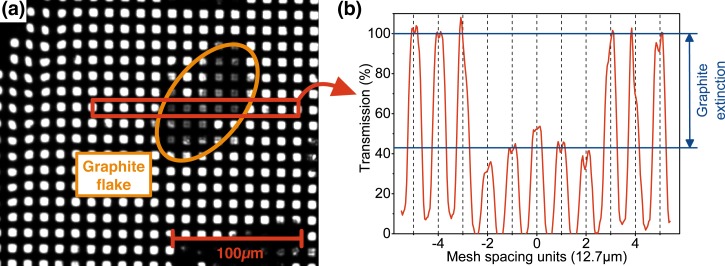
Graphite's carrier and phonon relaxation dynamics are interesting from a fundamental as well as technological perspective, because the population of phonon states influences the carrier mobility in graphene-based organic electronics.^12,46,47 Ultrafast dynamics of graphite thin films are well understood^46,47 and have been extensively studied using multi-electron diffraction.^5,12,48,49 For this reason, a graphite thin film was used for this single-electron proof-of-principle experiment. Using exfoliation, thin films of graphite were produced from highly oriented pyrolytic graphite (HOPG) and transferred to copper TEM grids with a spatial period of 12.7 μm (2000 mesh). The latter provides mechanical support as well as a highly efficient heat sink, significantly increasing the thermal damage threshold of the sample to >180 mW. Figure 1(a) shows an optical bright-field microscope image of the sample mounted on the TEM grid. Figure 1(b) shows the overall transmission along a horizontal slice (red rectangle in Figure 1(a)) dropping to roughly 45% at holes covered with graphite, corresponding to a layer thickness of 20–30 nm on average.⁵⁰

FIG. 1.

Fibrous graphite thin film sample. (a) Bright-field microscope image of the film (orange ellipse) on a 2000 mesh TEM grid. (b) Transmission profile along the red-marked area.

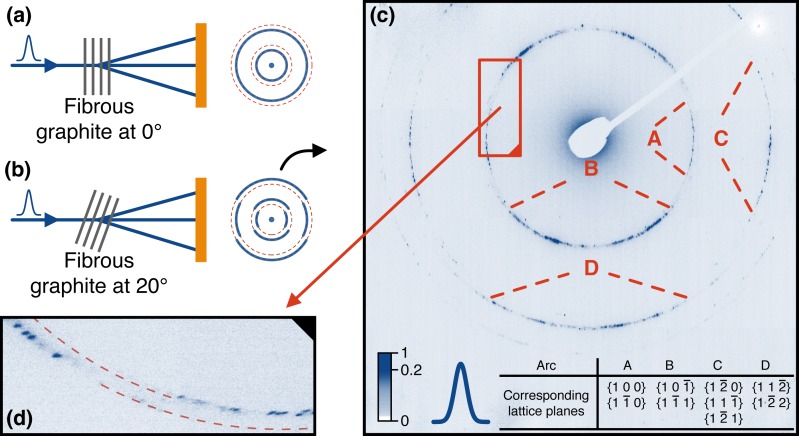
HOPG is a modification of graphite (space group P6₃/mmc, a = 246.4 pm, c = 671.1 pm) consisting of grains that are well aligned with the c-axis, but azimuthally disordered,⁵¹ forming a fibrous polycrystal.^52,53 Therefore, an incident electron beam propagating perpendicularly to the cleavage plane and parallel to the c-axis produces only rings with (hk0). This simple geometry prevents observation of atomic motion along the c-axis.^5,12,48 To be sensitive to dynamics along all spatial dimensions, we tilted our sample by about 20° with respect to the incoming electron beam.^5,48 For the fibrous polycrystal, the ring pattern is expected to break into a series of arcs, where new arcs appear featuring reflections with c-axis contributions.^52,54 This concept is illustrated in Figures 2(a) and 2(b).

FIG. 2.

Diffraction from tilted fibrous graphite thin films. (a) Diffraction geometry with a non-tilted sample (grey) and c-axis parallel to the electron beam (blue). The expected ring pattern (blue) on the screen only consists of rings corresponding to (hk0) while other rings are missing (red dotted lines). (b) Diffraction geometry with a sample tilted by 20° (grey). The expected ring pattern breaks into arcs (blue) and additional features with c-axis contribution appear. (c)Experimental diffraction pattern taken with 360 fs few-electron pulses. Several ring diameters are observable and the four smallest are labeled A-D, corresponding to the lattice planes listed in the inset. (d) Details of rings A and B, revealing their different diameters and individual Bragg reflections.

The measured diffraction pattern is shown in Figure 2(c). The inner four arcs are labeled A-D and correspond to the lattice planes listed in the table in Figure 2(c). In the case of the C-arc, lattice planes with slightly different spacings are listed together, because they cannot be clearly distinguished experimentally. Due to the superior beam quality in the single-electron regime, about 200 individual Bragg reflections can be distinguished within all of the arcs (see Figure 2(d)), indicating the limited number of grains probed by the electron beam.⁵⁵ This transitional regime between single-crystal and powder diffraction provides a unique opportunity to study different grains simultaneously by spot-wise evaluation of pump-probe dynamics.

III. PUMP-PROBE SINGLE-ELECTRON DIFFRACTION

Two different pump-probe data sets were recorded, one with ∼10 electrons per pulse on average at 128 kHz and 45 mW of incident average power, and one with ∼1 electron per pulse on average at 256 kHz and 90 mW. In both cases, the pump pulse energy was ∼350 nJ, corresponding to an incident fluence of ∼8 mJ/cm² under near-normal incidence, comparable to related studies.^5,11,48 By taking into account reflection and absorption for a graphite film of 25 nm thickness, the excited volume of $90 \mu {\mathrm{m}}^3$, the density $\rho \approx 2260 {\text{kg} \mathrm{m}}^{-3}$ (Ref. 51), and the temperature-dependent specific heat capacity $C_p\left(T\right)$⁵⁶ of graphite, the increase in temperature per pulse, $\Delta T$, can be estimated as ∼100 K. Limited heat diffusion causes a quasi-static accumulation of temperature that can be above $\Delta T$. Usually, this base temperature is determined via the Debye-Waller effect, but in our case the diffraction pattern is modified too much when the excitation laser is switched off. From the damage threshold, we roughly estimate the initial temperature to be below 2000 K for the single-electron data set and below 1000 K for the ten-electron data set, respectively. A slightly different sample alignment was used for the two data sets to access different grains. Both time-resolved measurements have been compiled from diffraction snapshots at 260 pump-probe delay times with accumulation of ∼10⁸ incoming electrons per delay step.

IV. RESULTS AND DISCUSSION

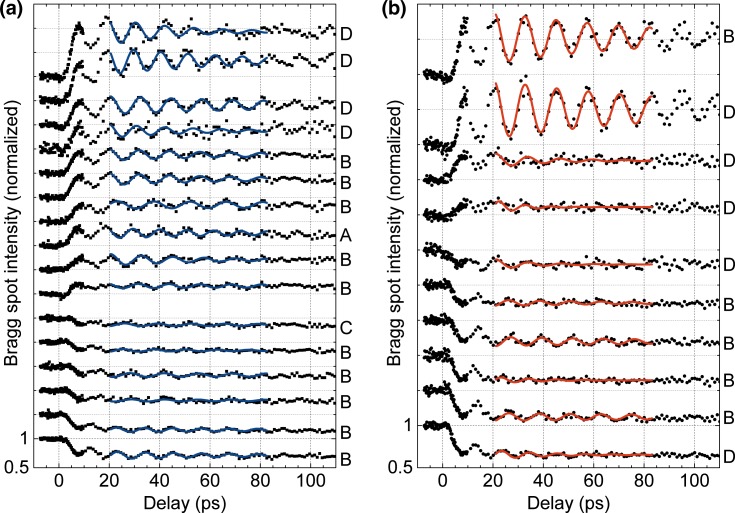
The time-dependent intensity of selected Bragg spots is shown in Figures 3(a) and 3(b). The measured data clearly reveals a fast change with varying sign and amplitude after laser excitation, followed by damped oscillations. Oscillations were observed only in arcs B and D sensitive to c-axis dynamics, with one exception from arc A probably related to multiple-scattering effects. These results are in agreement with comparable studies,^5,57–61 which identify thermal stress as origin of lattice expansion along the c-axis and as excitation mechanism of a coherent acoustic phonon mode.

FIG. 3.

Time-resolved intensity and fitting curves of 26 investigated Bragg reflections for (a) ten-electron pulses and (b) single-electron pulses on different arcs (see Figure 2(c)) as labeled on the right side on each plot. The individual traces were normalized and shifted for clarity; note the different intensity scales in (a) and (b). Error bars for each time step are not shown for convenience but were determined to be in the order of a few percent. Note that except one trace in (a), all traces correspond to lattice planes sensitive to c-axis dynamics. The non-normalized intensities before time-zero span the range of 1300–34 000 (a) and 1300–11 000 (b) total detected electrons; see also Fig. 6.

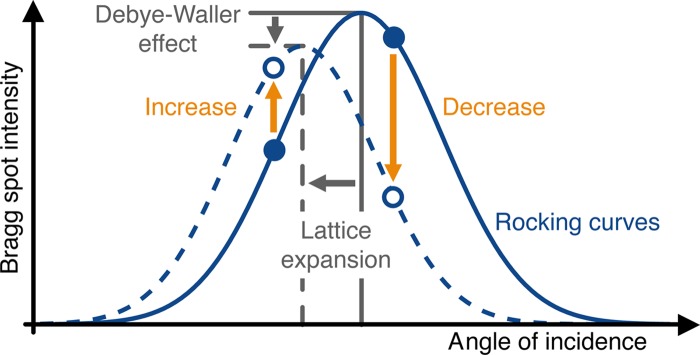
Variations of Bragg spot intensities are usually explained by changes of lattice spacing via the rocking curve.^58,59,62 Figure 4 illustrates the change in the rocking curve caused by thermal lattice expansion at a constant incident angle of the electron beam. The sign and amplitude of the observed change in diffraction intensity strongly depend on the difference between the incident beam angle and center of the initial rocking curves in the sample. This effect can compensate or even overcompensate decreases in diffraction intensity from the time-dependent Debye-Waller effect.^10,12,13

FIG. 4.

Mechanism of intensity change in Bragg spots due to thermal and expansion effects. The solid and dashed blue lines denote the rocking curves of the initial and the heated, expanded system. Depending on the angle of incidence between electron beam and sample, the initial intensity of Bragg spots (solid blue circles) can increase or decrease (orange arrows). This mechanism can dominate contributions from the Debye-Waller effect. An additional dynamical tilt of the sample's crystallographic axis corresponds in this picture to an additional change of the incidence angle.

However, the increase in temperature per pulse estimated in our experiment is rather low (∼100 K). The corresponding c-axis expansion alone cannot explain the observed magnitude of intensity change (−50% to +100%), taking into account a realistic rocking curve. This unexpectedly large intensity change could result from tilting of the local crystallographic axes with respect to the electron beam, for example induced by inhomogeneous excitation of the grains or their mechanical and thermal coupling to adjacent grains or the support structure.⁵⁹ Therefore, there can be a nonlinear relation between the measured intensity and the underlying c-axis dynamics, which must be taken into account to accurately fit time constants for graphite's phonon relaxation dynamics.^12,46,47

Our experimental setup did not allow us to deconvolve the aforementioned nonlinearity, but the very fast initial changes in intensity and position observed in some of the Bragg spots can be used to characterize our setup. Figure 5 shows phenomenological exponential fits to intensity and position of two selected Bragg spots. The time constants are $\left(600\pm 170\right) \text{fs}$ and $\left(730\pm 130\right) \text{fs}$, respectively. In both cases, a significant change in signal within 500 fs clearly demonstrates femtosecond temporal resolution of our setup, in agreement with the effective 360 fs resolution (FWHM) determined in a comparable beamline.⁴⁵ This is close to the state-of-the art (200–500 fs, FWHM) of temporal resolution in UED,^18–21 although no pulse compression was applied.

FIG. 5.

Exponential fits (solid lines) to measured change in data (black squares) of different Bragg spots after laser excitation. Fitted time-constants of several hundred femtoseconds demonstrate femtosecond temporal resolution. (a) Change in intensity recorded with ten-electron pulses and (b) change in position recorded with single-electron pulses.

From the data in Figure 3, we can evaluate the oscillation period of the laser-excited acoustic phonon. This is possible, because nonlinearities in the rocking curve are mostly irrelevant for oscillation periods and only cause minor distortions of the sinusoidal pattern. Fitting a damped sine function for delays of 20–85 ps (solid lines in Figure 3), we obtain a period of $\tau =\left(12.1\pm 0.3\right) \hspace{0.17em}\text{ps}$ on average. The small error is a consequence of the good data quality and the many Bragg spots observed. Equating $\tau$ with the round trip time of an acoustic wave in the thin film, the corresponding grain thickness is ${\mathrm{d}}_0={\mathrm{v}}_{\mathrm{s}}\tau /2$, with ${ \mathrm{v}}_{\mathrm{s}}=\left(4.14\pm 0.04\right)\hspace{0.17em}\hspace{0.17em}\text{km}/\mathrm{s}$ (Ref. 63) the speed of sound along the c-axis. Hence, the average sample thickness is $\left(25\pm 1\right) \hspace{0.17em}\text{nm}$. This is in nice agreement with the optical measurement. The damping constants show a large range between 25 ps and 300 ps, probably caused by different environmental conditions of each grain, such as inter-grain coupling and distance from the fixed supporting grid structure. In summary, our data is in agreement with intensity changes and coherent acoustic phonons obtained earlier on single-crystalline^5,48 and polycrystalline¹² samples, but here for the regime of a fibrous polycrystal.

V. SIGNAL-TO-NOISE

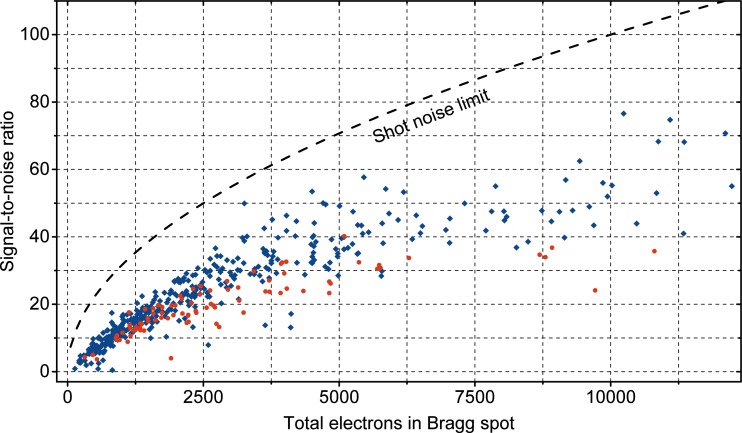
The signal-to-noise performance of our experiment can be determined from the variations of the measured Bragg spot intensities for negative pump-probe delays. Assuming that the diffraction pattern is identical for delays between −7 ps and −3 ps, we calculated the signal-to-noise ratio for each of the observed Bragg spots. Figure 6 shows the results, together with the shot noise limit, i.e., the signal-to-noise ratio only taking into account shot noise due to the number of detected electrons per Bragg spot.

FIG. 6.

Experimental signal-to-noise ratio of pump-probe single-electron diffraction (red) and ten-electron diffraction (blue) in comparison to the shot noise limit (dashed).

We find that the noise of our experiment approaches the shot noise limit within a factor of about two. We attribute this to some additional noise of our single-electron detection scheme.⁴⁴ Nevertheless, for many of the spots, the signal-to-noise ratio achieved here would allow seeing changes of a few percent in Bragg spot intensities, comparable to conventional multi-electron approaches.^6,10,64 There is no significant difference in noise between the one-electron and the ten-electron measurement.

VI. CONCLUSION

This study demonstrates the feasibility of femtosecond time-resolved diffraction utilizing single-electron pulses that are free of any space charge effects over their entire trajectory, thereby removing a difficulty in all UED experiments reported thus far, namely, the limitation of temporal resolution due to Coulomb repulsion. Data quality is comparable to multi-electron approaches. Without pulse compression, the temporal resolution is in the few-hundred-femtosecond regime. Crucial for single-electron diffraction at high repetition rates is minimization of the electron beam size at the sample, in order to avoid thermal load by the larger pump beam. More coherent single-electron sources based on needle emitters,^65,66 which can be focused smaller at the sample, could alleviate issues with elevated base temperature and ensure a homogeneous excitation. The single-electron approach, when combined with wave packet compression techniques,^23,30,31,43 may be a promising route towards direct observation of reversible condensed matter dynamics in an hitherto inaccessible resolution regime of few femtoseconds and below.