Ultrafast core-loss spectroscopy in four-dimensional electron microscopy

Abstract

We demonstrate ultrafast core-electron energy-loss spectroscopy in four-dimensional electron microscopy as an element-specific probe of nanoscale dynamics. We apply it to the study of photoexcited graphite with femtosecond and nanosecond resolutions. The transient core-loss spectra, in combination with ab initio molecular dynamics simulations, reveal the elongation of the carbon-carbon bonds, even though the overall behavior is a contraction of the crystal lattice. A prompt energy-gap shrinkage is observed on the picosecond time scale, which is caused by local bond length elongation and the direct renormalization of band energies due to temperature-dependent electron–phonon interactions.

INTRODUCTION

Electron energy-loss spectroscopy (EELS) in the electron microscope has become an invaluable tool for unraveling the chemical composition and structure of materials, enabling the imaging of individual atoms and their bonding states with unprecedented resolutions.^1–4 The low-energy (0–50 eV) region of the EEL spectrum delivers electronic information in the form of valence intra- and interband transitions, and plasmon excitations, rendering this part of the spectrum sensitive to changes in the overall electron density of the material. Conversely, the high-energy (>100 eV) region of the EEL spectrum is characterized by excitations of core-electrons into well-defined higher-lying empty states and into the continuum.⁵ Importantly, this core-loss spectroscopy provides a technique suitable for studying the chemical state, local geometric structure, and nature of chemical bonding centred around the absorbing atom. When combined with the nanoscale probing capabilities of transmission electron microscopy (TEM), core-loss spectroscopy becomes a powerful technique and has been used to probe chemical and structural properties of nanoparticles⁶ (carbon) nanotubes,^7–9 and interfaces.^10,11 However, until now, if one wishes to study dynamical processes, the temporal resolution has been limited by the speed of the acquisition time of the detector (∼30 ms). Crucially, this leaves inaccessible many phenomena that occur on shorter timescales.

Apart from relativistic effects,^12,13 electron energy-loss and X-ray absorption core-level spectra are essentially equivalent and provide the same information. Energy losses between 100 and 1500 eV are routinely accessible in TEM-EELS, which (partly) overlap with the soft X-ray region. Ultrafast X-ray spectroscopies have been subject to tremendous progress in recent years.¹⁴ Picosecond-resolved X-ray absorption spectroscopy (XAS) implemented at synchrotron facilities has enabled the characterization of the excited state structure and dynamics of a wide variety of chemical systems.^14–16 The advent of X-ray free electron lasers (XFELs) introduces a paradigm shift in terms of the temporal resolution of X-ray spectroscopies into the femtosecond regime.¹⁷

Importantly, due to the rather low interaction cross-section of X-rays with matter, in situ studies of nanoscale objects such as thin films and individual nanoparticles are challenging, especially for materials containing low-Z elements such as organic crystals, polymers, and biological molecules. This can be overcome by four-dimensional EM (4D-EM), which combines, in a tabletop apparatus, high spatial resolution and sensitivity to resolve individual nano-objects with the ultrashort temporal resolution needed to address nanoscale chemical dynamics immediately following laser excitation.^18–20

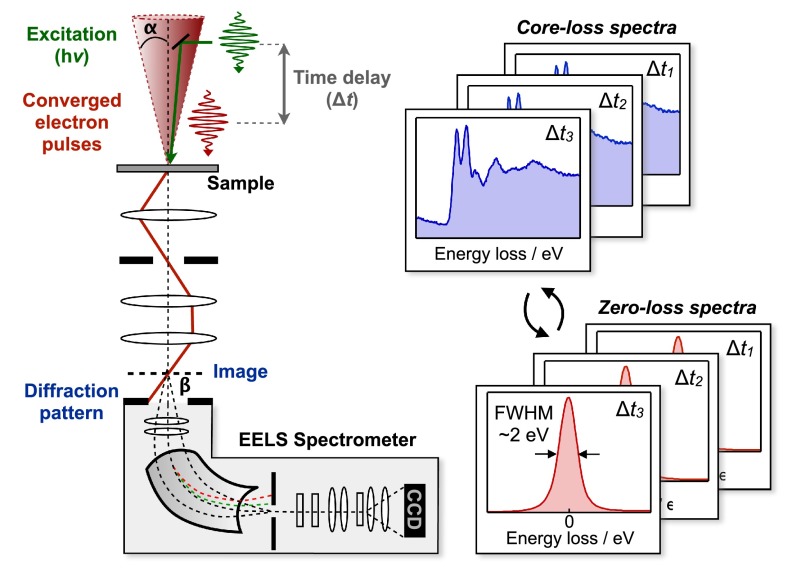
In this work, we introduce ultrafast core-loss spectroscopy in 4D-EM (Fig. 1). We use ultrashort, converged electron pulses with a diameter of ∼200 nm on the sample to probe the electronic and structural dynamics after laser excitation of a graphite nanometer-thin film, which is an ideal test case for the investigation of structural dynamics and coupling between electronic and lattice motions. For graphite, we report the structural dynamics with femtosecond and nanosecond resolutions following π-π* excitation with 2.33 eV (532 nm) photons.²¹ The electron energy-loss spectra are recorded by collecting the diffraction pattern of the converged electron beam at the spectrometer entrance aperture, and dispersing the pulsed electrons using a post-column spectrometer, achieving an energy resolution of ∼1–2 eV. Prerequisite for acquiring time-resolved core-loss spectra is a careful energy-drift correction, which is achieved by recording the spectrum of the elastically scattered electrons (zero-loss spectrum) prior to each core-loss spectrum, as shown in Fig. 1.

FIG. 1.

Ultrafast core-loss spectroscopy. The short laser pulse (hν, green) initiates the structural change at t = 0 and acts as a clocking pulse. The short, converged electron packet with convergence semi-angle α (red) illuminates a small area (∼100 nm) of the graphite nanometer-thin film and is time delayed with respect to the clocking pulse (Δt). Electron-propagation paths are schematically denoted as red lines. Electron energy-loss spectra are recorded by collecting the diffraction pattern of the converged electron beam at the spectrometer entrance aperture, and dispersing the pulsed electrons using a post-column spectrometer. The energy resolution (∼2 eV) is determined from the full-width-at-half maximum (FWHM) of the ZLP, corresponding to elastically scattered electrons passing through the aperture. Energy drifts are carefully corrected by alternatingly recording core-loss and zero-loss spectra and using the position of the ZLP to adjust the energy axis.

It is noted that the cross-section for inelastic scattering decays with a power-law energy dependence according to $A{E}^{-r}$, with r = 2–5.²² Therefore, deep core-level edges (>100 eV) are considerably more challenging to measure than shallow core-levels²³ and low-loss plasmon excitations²⁴ (0–100 eV). In the present work, we demonstrate the excellent sensitivity of the technique necessary to measure such weak time-resolved signals at deep core-level ionization edges like the carbon K-edge at ∼285 eV.

RESULTS AND DISCUSSION

Electron energy-loss spectroscopy of graphite thin films

EELS involves the measurement of the energy distribution of electrons that have interacted with a sample and changed momentum due to inelastic scattering (Fig. 2(b)). The magnitude and direction of the resulting momentum transfer q (i.e., the difference in momentum between the direct and scattered beams) are directly correlated to the specific electronic excitation in the sample.²²

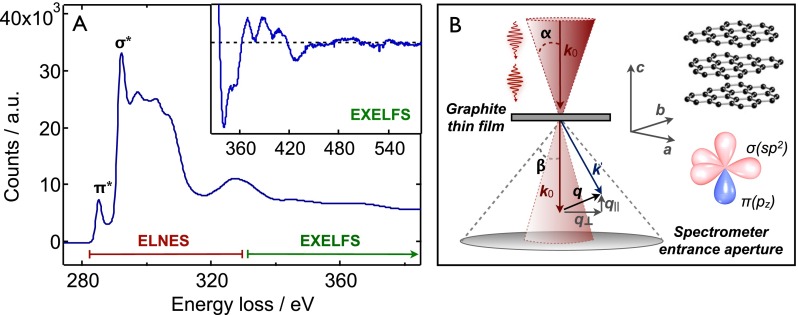
FIG. 2.

Electron energy-loss spectroscopy of graphite thin films. (a) Static K-edge core-loss spectrum of a ∼50 nm graphite thin film recorded using the setup described in Fig. 1. The near-edge (ELNES) spectrum is characterized by two main resonance features corresponding to excitations of the 1s core-electron into empty states above the Fermi level: (i) the π* resonance around 285 eV and (ii) the σ* resonance around 292 eV. The fine structure in the EXELFS spectrum (inset) at higher energy losses is due to constructive and destructive interference of the core-electron that scatters off neighboring atoms. The low-loss spectrum was deconvoluted from the core-loss spectrum (see the supplementary material³¹). (b) Schematic representation of the scattering geometry, with convergence semi-angle α, collecting semi-angle β, and momentum transfer q (with q_|| and q_⊥ components parallel and perpendicular to the c-axis, respectively). Only the direct beam (000) is collected by the aperture; higher-order diffraction peaks are excluded. The graphite crystal structure, unit cell axes, and hybridized σ- and π-orbitals are depicted on the right side.

The EEL spectrum of graphite is largely affected by the pronounced anisotropy of the layered structure. While strong σ(sp²)-bonds form the hexagonal graphene layers exhibiting excellent thermal and electronic properties,²⁵ weak interlayer bonding arises from van der Waals interactions and overlap of π(p_z)-orbitals oriented perpendicular to the plane.²⁶

The core-loss K-edge spectrum of graphite originates from the excitation of 1s core-electrons into empty bands and the continuum.^27,28 The spectrum of a ∼50 nm natural graphite film is shown in Fig. 2(a) and consists of two main parts: (i) the electron-energy near-edge spectrum (ELNES) extending ∼50 eV around the ionization edge, which contains transitions into empty states of π*- and σ*-character²⁹ and (ii) the extended electron energy-loss fine structure (EXELFS) starting ∼50 eV above the ionization edge. In the EXELFS region, the expelled core-electron has sufficient kinetic energy to scatter off neighboring atoms, causing modulations (interference) in the scattering cross-section that are a direct imprint of the local structure surrounding the absorbing atom.^22,30

In the present ultrafast core-loss spectroscopy experiments, the on-axis spectrometer entrance aperture (with collecting semi-angle β ∼ 10 mrad) selects a large range of momentum transfer values in the plane perpendicular to the c-axis (q_⊥) (see Fig. 2(b)). Due to the angular spread of the incoming converged electron beam (opening semi-angle α ∼ 5 mrad), momentum transfer components that are parallel to the c-axis (q_||) are also sampled, although to a lesser extent. The core-EEL spectrum is therefore sensitive to structural dynamics along the a,b- and c-axes of the graphite structure.

Nanosecond-resolved core-loss spectroscopy

Fig. 3(a) shows the static core-loss ELNES of a graphite thin film, together with the corresponding transient spectrum at Δt = 20 ± 10 ns after laser excitation (532 nm, ∼10 ns, and 10 mJ/cm²), which corresponds to the difference spectrum between the ELNES after laser excitation minus the averaged spectrum before excitation. Each static spectrum corresponds to a total integration time of 15 min (at 6 kHz), resulting in a maximum signal-to-noise level of S/N ∼ 15.

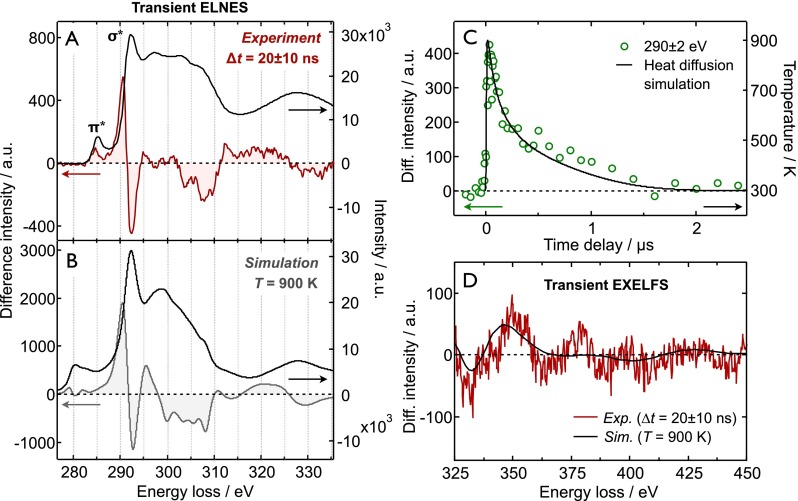
FIG. 3.

Nanosecond-resolved core-loss spectroscopy. (a) Experimental static (<t₀) and transient K-edge ELNES at Δt = 20 ± 10 ns after laser excitation at 532 nm. (b) Theoretical static and transient ELNES based on MD simulations at room temperature and 900 K, respectively. See text for details. The experimental and theoretical static spectra were normalized to the maximum of the σ* peak, and the transient spectra were scaled accordingly. (c) Temporal evolution of the nanosecond-resolved core-loss signal at 290 ± 2 eV, together with the simulated temperature profile. (d) Experimental and simulated transient EXELFS spectrum under the same conditions as in (a) and (b).

The transient ELNES exhibits pronounced derivative-like features around the σ* resonance and ionization threshold (∼290 eV), as well as less-pronounced features at higher energies (∼300–330 eV). It is noted that the transient spectrum is distinctly different from the difference spectrum that results from a simple red-shift of the spectrum as a whole, as is demonstrated in the supplementary material.³¹ In addition, multiple scattering contributions from the low-loss region are negligible because the graphite film (∼50 nm) is much thinner than the inelastic mean free path of the electrons (∼180 nm).³²

The time dependence of the transient ELNES signal at an energy loss of 290 ± 2 eV is shown in Fig. 3(c). This shows a non-exponential decay on the μs time scale, which can be satisfactory described with a simple one-dimensional heat diffusion model where the graphite film is in contact with a heat sink at room temperature (see the supplementary material for details).³¹ The resulting temperature profile is also depicted in Fig. 3(c). The maximum temperature reached at 20 ns after excitation amounts to ∼900 K. Transient low-loss spectra (0–55 eV) and time profiles that were measured simultaneously are provided in the supplementary material.³¹

On the nanosecond time scale, we assume that the graphite film is electronically relaxed. The changes in the electronic features of the ELNES therefore arise from the structural distortions accompanying the thermal excitation of the lattice. The thermal expansion coefficients (TECs) of natural graphite strongly depend on temperature.³³ In fact, the TEC in the basal plane is negative for a temperature range of 0–700 K, i.e., the unit cell contracts along the a,b-directions upon increasing the temperature, while the TEC along the c-axis is large and positive.³³ The temperature profile obtained from heat diffusion simulations (Fig. 3(c)) can be used to estimate the structural change along the perpendicular a,b- and c-directions by numerically integrating the TECs α(T), as $\Delta d/d_0={\int }_{T_0}^{T_0+\Delta T}\alpha (T)dT$. The resulting profiles are shown in the supplementary material.³¹

For a laser fluence of 10 mJ/cm² at the site of probing, the maximum contraction in the basal plane amounts to 0.023% at 130 ns after excitation, while the maximum c-axis expansion is 1.78% at 12 ns after excitation. This corresponds to a change of −5.6 × 10⁻⁴ Å in the a,b-unit cell dimension (2.456 Å),³⁴ and +0.12 Å in the c-unit cell dimension (6.696 Å).³⁴

In order to extract the structural dynamics from the transient ELNES spectra, we simulated the ELNES using the real-space multiple scattering package FEFF, which is commonly used in XAS.^35–37 By applying small distortions to the crystal lattice, it is possible to investigate the dependence of the spectrum on structural dynamics along the crystallographic a,b- and c-directions, shown in Fig. S4. The σ* edge onset is very sensitive to the carbon-carbon (C–C) bond length in the a,b-plane:³⁸ a uniform expansion (contraction) of 0.001 Å along the a,b-unit cell axes causes the σ* resonance to red-shift (blue-shift) by 20 meV. The π* resonance is very weakly affected by such bond length variations. This can be understood by considering a simple bond orbital approximation model, according to which an increase in nearest-neighbor spacing results in a reduction in band separation energy.⁸ The higher-energy σ* band is more sensitive to bond-length changes due to the strong directionality of the σ(sp²) C-C bonds and thus will have a larger red-shift than the π*(p_z) band upon lattice expansion because of its more delocalized nature (see Fig. 2(b)). The ELNES is much less sensitive to changes along the c-axis, i.e., the inter-plane separation, which mainly affect the higher-energy region around 295–325 eV (Fig. S4). As will be discussed later, increased electron-phonon coupling at elevated temperatures also causes a red-shift of the σ* band.

However, simulation of the transient ELNES using simply thermal expansions of a perfect graphite crystal along the a,b- and c-directions did not lead to a satisfactory agreement with the experimental data. In particular, the predicted thermal contraction in the a,b-plane, which should, in principle, give rise to a blue-shift of the σ* band, is contrary to the observed red-shift of this band in the transient ELNES (see Fig. 3(a)). This discrepancy is due to one important aspect which is still missing in such a simple distortion analysis, namely, dynamic disorder resulting from thermal lattice excitation. The absorbed laser energy gives rise to a temperature rise in the graphite film and causes the atoms to vibrate around their (thermally expanded) equilibrium positions.

Thermal disorder in EELS and XAS analyses is commonly accounted for by multiplying the scattering pathways by Debye-Waller factors that damp the fine structure in the spectrum.³⁹ Semiquantitative phenomenological⁴⁰ and ab initio methods based on density functional theory (DFT)³⁹ and molecular dynamics (MD)⁴¹ have been used to calculate Debye-Waller factors of anisotropic an non-periodic systems. A different approach to account for disorder, in general, is given by configurational averaging in combination with ab initio MD simulations, as demonstrated for various disordered systems.^42–44 Here, we apply the latter method to account for the pronounced anisotropy in the vibrational and thermal properties of graphite.

Molecular dynamics simulations

We performed ab initio MD simulations at room temperature (298 K) to represent the spectrum at t < 0, and at an elevated temperature of 900 K, corresponding to the temperature at ∼20 ns after laser excitation (see Fig. 3(c)). A representative set of 120 MD configurations was used to simulate the (transient) ELNES using the FEFF package.³⁵ Details about the simulations can be found in the supplementary material.³¹

The simulated static and transient ELNES spectra, depicted in Fig. 3(b), show good agreement with the experiment. All transient features, in particular, the red-shift of the σ* band, are reproduced by theory. The magnitude of the simulated transient is approximately a factor of ∼2–3 larger than that of the experimental transient, which we attribute to a slightly exaggerated distortion in the MD simulations (vide infra). The separation between the π* and σ* resonances is overestimated in the simulation, which has previously been attributed to the spherical (muffin-tin) approximation of the potential in the real-space multiple scattering calculation.³⁷ In addition, in the ground state, the simulated spectrum exhibits a larger decay in the scattering cross sections than observed in the experiment for energy losses between 295 and 310 eV. This causes the transient features in this part of the spectrum in the simulation to be overestimated and slightly shifted in energy.

The experimental and simulated EXELFS transient spectra >325 eV are given in Fig. 3(d). The agreement is only qualitative and less satisfactory than for the ELNES region. Nevertheless, the main feature around 350 eV is correctly reproduced and the overall signal magnitudes are satisfactorily reproduced. The simulation of the EXELFS region turned out to be challenging due to the large amount of scattering pathways that need to be included in the calculation for graphite. Whereas the full-multiple scattering approach in the ELNES region inherently includes all scattering paths within a certain cluster, the path expansion in the EXELFS region may not converge for reasonable cluster sizes and computation times.⁴⁵

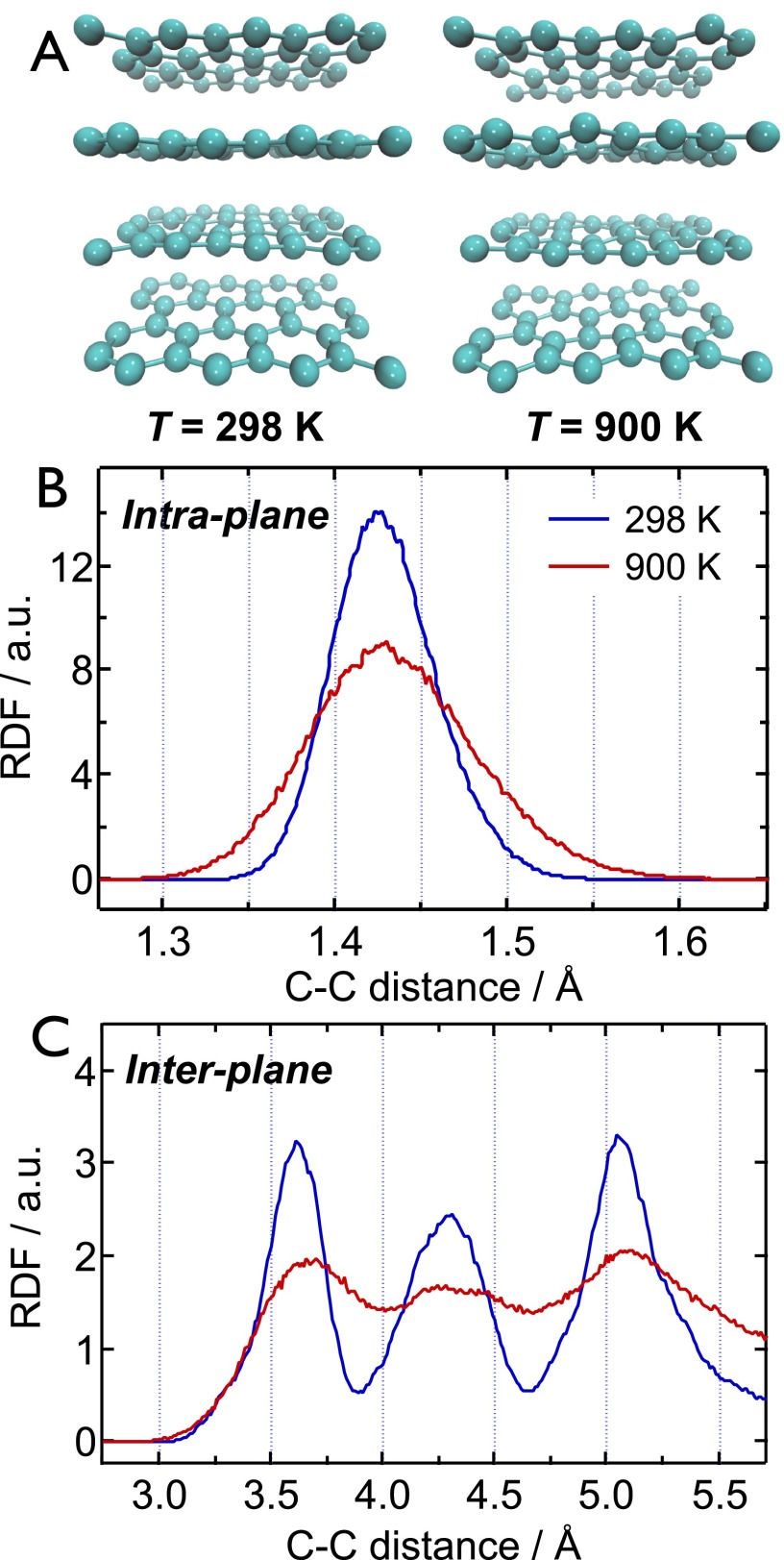
The graphite structures at 900 K obtained from MD simulation exhibit an increased dynamic disorder, which is more pronounced along the crystallographic c-direction than in the a,b-plane, in accordance with the large difference in Debye temperatures (θ_c = 800 K and θ_a,b = 2300 K).³³ This is visible in the two MD configurations at 298 K and 900 K depicted in Fig. 4(a), and more clearly seen in the corresponding Movies S1 and S2 in the supplementary material.³¹ The thermal disorder can be quantified by plotting the radial distribution function (RDF) for C–C distances obtained from the MD configurations at 298 K and 900 K. The RDF for the C–C bond distance in the basal graphite plane at 298 K exhibits a nearly Gaussian profile centered around 1.429 Å, as depicted in Fig. 4(b). At 900 K, this distribution broadens and becomes asymmetric towards larger bond distances, a manifestation of the anharmonicity of the interatomic potential, which causes the average C–C bond length to increase by ∼0.005 Å.

FIG. 4.

Molecular dynamics simulations. (a) Two snapshots from the MD simulations at 298 K (left) and 900 K (right). The corresponding movie is given in the supplementary material (Movie S1). (b) Radial distribution function (RDF) of the in-plane C–C bond length obtained from MD simulations at 298 K and 900 K. (c) RDF of the inter-plane C–C distances obtained from MD simulations at 298 K and 900 K.

In fact, this asymmetry in the RDF of the C–C bond is crucial for reproducing the salient transient ELNES feature around 285–295 eV. Contrary to diffraction techniques, core-loss spectroscopy measures the local structure surrounding the absorbing atom and may therefore be insensitive to changes in the overall lattice dimensions. In fact, although the C–C bond lengthens upon increasing the temperature, the overall lattice actually thermally contracts in the basal planes,³³ as discussed previously. This negative thermal expansion in graphite is caused by the population of low-frequency transverse acoustic modes with negative Grüneisen parameters.⁴⁶ The σ* resonance in the ELNES, however, is mainly sensitive to changes in the nearest-neighbor C–C bond length. This emphasizes the importance of accurately incorporating dynamic disorder in the interpretation of transient core-loss spectra, especially in the case of highly anisotropic materials such as graphite.

The partial RDF of the C–C distances between different graphite sheets is depicted in Fig. 4(c). Only inter-plane distances are plotted, while in-plane distances are omitted. Contrary to the in-plane RDF, the inter-plane RDF shows a clear shift of the peak centers towards larger bond distances at 900 K, as expected for the large positive thermal expansion along the crystallographic c-direction.³³ An inter-plane separation increase of ∼0.07 Å is derived from the simulations, corresponding to an increase of the c-unit cell dimension of 0.14 Å. The latter value is in good agreement with the expansion derived from the heat diffusion simulations (0.12 Å, see above) and reported expansions in the literature.^47,48 Besides the thermal expansion, Fig. 4(c) shows that the inter-plane RDF is also greatly affected by dynamic disorder, which is apparent as a pronounced broadening of the RDF. The increased distribution of C–C distances gives rise to a loss of interference, i.e., damping, in the EEL fine structure, analogous to the well-known Debye-Waller effect in ultrafast electron and X-ray diffraction studies.^47,49 Consequently, the overall effect of c-axis expansion is effectively reduced in the transient EEL spectrum, which eventually leads to a better agreement between the experimental and simulated spectra, as compared to a simple distortion of the crystal without including thermal disorder as previously described.

Femtosecond-resolved core-loss spectroscopy

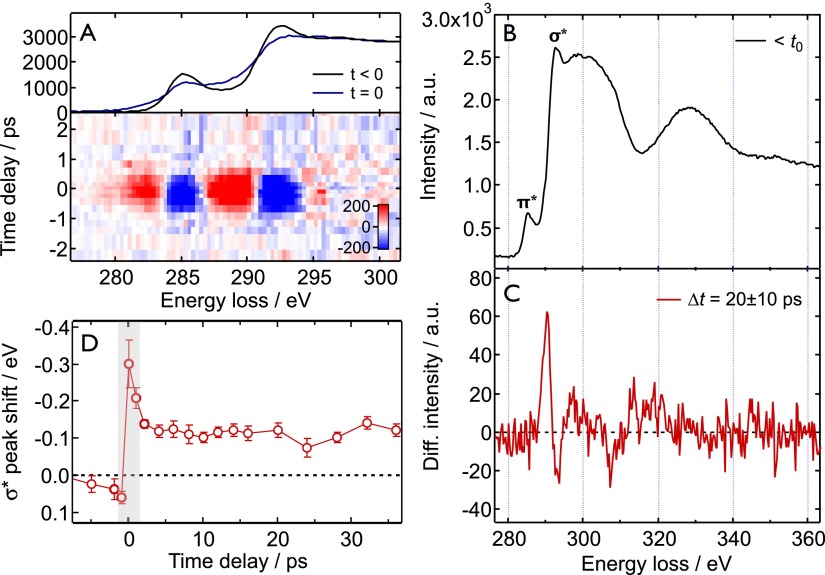
Fig. 5 depicts the femtosecond-resolved core-loss spectra of graphite after excitation at 519 nm (∼250 fs and 10 mJ/cm²). Before we turn to the discussion of the inherent graphite dynamics, we first point out the manifestation of a phenomenon around t = 0 that is caused by the interaction between photons scattered by the thin film and the fast probing electrons in the electron microscope. This phenomenon was dubbed photon-induced near-field microscopy (PINEM), as reported in several previous publications.^50,51 The PINEM effect is clearly visible as a broadening in the core-loss spectrum at t = 0, as depicted in Fig. 5(a) for a graphite film that was tilted by 45° with respect to the incoming laser and electron beams in order to enhance the laser scattering. At normal incidence, the PINEM effect is reduced, but it cannot be entirely avoided due to the convergence of the excitation laser and small steps and bulges on the surface of the graphite film. Therefore, caution is warranted in interpreting the dynamics between −1 and +1 ps.

FIG. 5.

Femtosecond-resolved core-loss spectroscopy. (a) The PINEM effect in core-loss spectroscopy. The electron-photon interaction causes a broadening of the core-loss spectrum around t = 0. (b) and (c) Static and transient ELNES at t = 20 ± 10 ps after excitation, respectively. A clear red-shift of the σ* band is visible. (d) Temporal evolution of the σ* peak position. The shaded area denotes the time window in which PINEM occurs.

The core-loss transient spectrum at t = 20 ± 10 ps (after the complete decay of the PINEM feature) and the corresponding static spectrum before t = 0 are shown in Figs. 5(b) and 5(c). Each static spectrum corresponds to a total integration time of 1 h (at 500 kHz), resulting in a maximum signal-to-noise level of S/N ∼ 5. A clear transient feature is seen at 290 eV, which corresponds to a red-shift of the σ* resonance and shows similarity to the nanosecond transient. The time evolution of the σ* resonance position is quantitatively depicted in Fig. 5(d). After a prompt rise and decay due to the PINEM effect on the femtosecond time scale, the red-shift remains constant at around −120 meV up to a time delay of t = 37 ps.

Due to the step-like temporal behavior of the transient core-loss signal, it can be excluded that electronic excitations contribute to the observed red-shift of the σ* resonance. Indeed, ultrafast optical^52–56 and electron diffraction^47,57 experiments have shown that 90% of the electronic energy decays within ∼500 fs upon π-π* excitation, after which the majority of the excitation energy resides in the form of lattice vibrations (optical and acoustic phonons). We therefore assign the prompt red-shift of the σ* band to an ultrafast energy-gap shrinkage, analogous to thermal band-gap shrinkage in semiconductors.^58–60

Graphite is a semimetal with a (nearly) vanishing band gap at the K-point in the Brillouin zone (BZ). The energy gap of interest here is therefore the overall energy separation between the filled π/σ- and empty π*/σ*-bands, rather than the smallest energy difference between the top of the valence and the bottom of the conduction band in semiconductors and insulators. The resonances in the ELNES correspond to maxima in the joint empty density of states (DOS) of the π*/σ*-band structure. The π* peak at 285 eV mainly probes the empty DOS near the M-point in the BZ, while the σ*-band onset at 293 eV indicates the lowest energy allowed transition to the conduction σ*-band near the Γ-point.^27,28 An ultrafast (<1 ps) band-gap shrinkage for the π-π* bands has been reported previously.⁶¹ Here, we observe the band gap shrinkage as a 120 meV red-shift of the σ*-band onset. Since the deep-lying 1s core level is hardly dependent on temperature, the observed red-shift is attributed mainly to a downward shift of the empty σ*-band. In principle, the π*-peak at 285 eV should display this shift as well; however, the π*-bands are only very weakly sensitive to in-plane structural changes,³⁸ and due to the rather small peak magnitude and the limited S/N we are not able to observe a shift.

There are two effects contributing to the energy-gap shrinkage:^59,60,62 (i) the temperature-dependent dilatation of the lattice, related to the change of the electron energies with the volume (minor contribution), and (ii) a shift in the relative position of the conduction and valence bands due to a temperature-dependent electron-phonon interaction (major contribution). In the present case, it is the thermal expansion of the individual C-C bonds, rather than the in-plane lattice, that leads to a small reduction of the π/π* and σ/σ* band gaps, as discussed above for the nanosecond-resolved experiment. However, on the ultrafast time scale, a large amount of energy is deposited into optical and acoustic phonon modes in the basal plane.⁴⁷ The second mechanism for energy-gap shrinkage, based on the increased electron-phonon coupling, is therefore expected to play an important role here.

CONCLUSIONS

We demonstrated here for the first time the feasibility of ultrafast core-loss spectroscopy in 4D-electron microscopy with femtosecond and nanosecond time resolutions, and at deep core-level ionization edges >100 eV. In contrast to electron diffraction⁶³ and low-loss spectroscopy,²⁴ core-loss spectroscopy is specially sensitive to chemical bonding properties in the close vicinity of the absorbing atom. By probing the ultrafast structural dynamics of graphite thin films, we have demonstrated that this local sensitivity of core-loss spectroscopy is a prerequisite to observe small bond length changes, such as the thermally induced increase in the C–C bond length in the basal plane of photoexcited graphite, independent of the thermal expansion properties of the material as a whole. Molecular dynamics simulations were crucial for the interpretation to adequately incorporate thermal disorder in the calculation of transient core-loss spectra of graphite. On the picosecond time scale, we observed an ultrafast energy-gap shrinkage that is governed by the increased electron-phonon interaction due to the efficient population of optical and acoustic phonons right after photoexcitation. By introducing core-loss spectroscopy to the palette of probing techniques in 4D-EM, we expect numerous future applications in the field of nanoscale chemical dynamics, including optical switching, charge-transfer, and phase transition dynamics.

METHODS

Experiments were carried out using the UEM-2 apparatus at Caltech, which is equipped with a Gatan post-column spectrometer.⁶⁴ EELS spectra were collected in the diffraction mode, which results in the best possible energy resolution of 1–2 eV (full-width-at-half maximum, FWHM) when compared to the image mode.²² The spectrometer entrance aperture only selects the direct (000) beam; higher-order diffraction peaks are excluded. Spectra were recorded with energy dispersions of 0.2 eV/pixel (nanosecond mode) and 0.3 eV/pixel (femtosecond mode). During the course of an experiment, the EELS spectrum undergoes a gradual energy drift of several eV/h caused by, for example, instabilities of the drift tube power supply. These energy drifts were carefully corrected for by recording a low-loss spectrum, including the zero-loss peak (ZLP) at ΔE = 0, with a short integration time (0.3 s) prior to each core-loss spectrum at a certain laser-electron time delay.

Switching between the energy windows (low-loss vs. core-loss) is achieved by changing the drift-tube voltage, which was entirely reproducible and does not exhibit any hysteresis.⁶⁵ During post-acquisition data analysis, the ZLPs were fitted with a Voigt profile and the energy drift during core-loss spectrum exposure was obtained from the energy shift between the two low-loss spectra using the fitted ZLP positions (estimated accuracy of σ ≅ 4 meV from fitting).

Time delay scans were alternatingly recorded towards positive and negative time delays and averaged during data analysis. In the nanosecond mode, the time delay was changed with a digital delay generator; in the femtosecond mode, the delay was scanned with a linear motor stage. A total of 30 time scans were averaged in the nanosecond mode, and a total of 61 scans were averaged in the femtosecond mode. The edge jump magnitudes of the core-loss spectra were normalized and the spectra were shifted vertically relative to a reference spectrum prior to averaging. The temporal evolution of the σ* band was determined by fitting an averaged spectrum before t₀ to each spectrum after t₀ with a horizontal shift and vertical scaling factor as fitting parameters.

Sample drifts were corrected for between time scans after a total drift of ∼2–3 μm. The laser beam position was monitored using a beam profiler setup⁶⁶ and corrected for when the peak was shifted >1 σ away from it initial position. Because the laser drifted systematically in one direction, the average laser-electron overlap was slightly (10 μm) offset from the ideal overlap. This offset was taken into account in the laser fluence determination and heat diffusion simulations. The laser spot size on the sample was ∼45 × 45 μm² (FWHM of Gaussian profile), as determined from the beam profiler, which was located at an equivalent image plane of the specimen. The electron beam was converged, resulting in a beam diameter of ∼200 nm at the sample.

The graphite thin film sample was obtained from a flake of natural Ontario graphite using a standard Scotch-tape cleaving procedure. The resulting graphite flakes were deposited on a 2000 Cu mesh and washed with acetone to remove glue residues. The free-standing flakes were highly crystalline as confirmed by electron diffraction and bright-field imaging. The film thickness of ∼50 nm was determined from the low-loss EELS spectrum according to the log-ratio method²² and the inelastic mean free path for graphite.³²

Short low-loss scans were recorded in order to determine whether transient electric fields (TEF)⁶⁷ from either the sample surface or the surrounding Cu frame were present. Except for the PINEM effect around t = 0, the fitted ZLP positions and widths did not show any systematic laser-induced shift or broadening at delays t > 1 ps, such that a TEF effect could be excluded.