Abstract
Single-particle structure recovery without crystals or radiation damage is a revolutionary possibility offered by X-ray free-electron lasers, but it involves formidable experimental and data-analytical challenges. Many of these difficulties were encountered during the development of cryogenic electron microscopy of biological systems. Electron microscopy of biological entities has now reached a spatial resolution of about 0.3 nm, with a rapidly emerging capability to map discrete and continuous conformational changes and the energy landscapes of biomolecular machines. Nonetheless, single-particle imaging by X-ray free-electron lasers remains important for a range of applications, including the study of large “electron-opaque” objects and time-resolved examination of key biological processes at physiological temperatures. After summarizing the state of the art in the study of structure and conformations by cryogenic electron microscopy, we identify the primary opportunities and challenges facing X-ray-based single-particle approaches, and possible means for circumventing them.
I. INTRODUCTION
Determining the structure and function of biological nanomachines is a key goal of molecular biology. Electron-microscopic single-particle imaging approaches, augmented by powerful algorithmic techniques, have served this goal by revealing the three-dimensional (3D) structure (Frank, 2006), discrete (Scheres, 2012) and continuous conformational changes, and energy landscapes (Dashti et al., 2014) from 2D snapshots of individual objects in unknown orientational and conformational states. These set a high bar for competing techniques. In order to delineate the opportunities for single-particle structure determination by methods based on X-ray free-electron lasers (XFEL's), it is necessary to begin with a summary of the state of the art in cryogenic electron microscopy (cryo-EM).
II. STRUCTURE OF BIOLOGICAL ENTITIES BY CRYOGENIC ELECTRON MICROSCOPY
Electron microscopy exploits the scattering of high-energy (100–300 kV) electrons passing through the sample of interest. Biological entities are captured in their “native” state in vitreous ice by plunge-freezing (Frank, 2006). This and the need to minimize radiation damage limit the signal-to-noise ratio (SNR) of cryoEM snapshots to the range of 0.1–0.01. Each electron micrograph represents a 2D “projection view” of a single particle in an unknown orientational and conformational state. The reliable extraction of conformational information has become possible only recently (Scheres, 2012 and Dashti et al., 2014).
Over fifty years of intensive research has resulted in a series of well-characterized data-analytical steps for recovering reliable 3D structural information from ultralow-signal electron micrographs of biological entities (Frank, 2006). Over this period, 3D structure recovery by cryoEM has moved systematically from relying on a few high-contrast (initially “stained”) snapshots, to utilize large collections of ultralow-signal snapshots obtained under exceptionally uniform imaging conditions. This trend has been driven by the need to preserve sample integrity and to minimize variations extraneous to the sample itself, often at the expense of signal-to-noise ratio. The realization that statistically meaningful structural information requires averaging over large homogeneous ensembles, particularly for the important class of conformationally flexible molecular machines (Moore, 2012), has fueled the development of powerful data-analytical approaches capable of extracting reliable information from large collections of ultralow-signal snapshots.
The past few years have witnessed a significant increase in the highest resolution with which 3D structure can be determined by CryoEM, to a level where secondary structure can be discerned. Specifically, the advent of direct-detection electron-counting techniques has resulted in near-atomic resolutions (see, e.g., Amunts et al., 2014), limited mostly by intrinsic sample heterogeneity. At the same time, it has been suggested that “the golden age of structure determination is drawing to a close, with the focus shifting to structural changes during function” (Moore, 2012). The growing realization that biological “function” involves conformational change rather than an immutable static structure has accelerated efforts to develop data-analytical methods capable of mapping complex conformational changes from large heterogeneous datasets of ultralow-signal 2D snapshots.
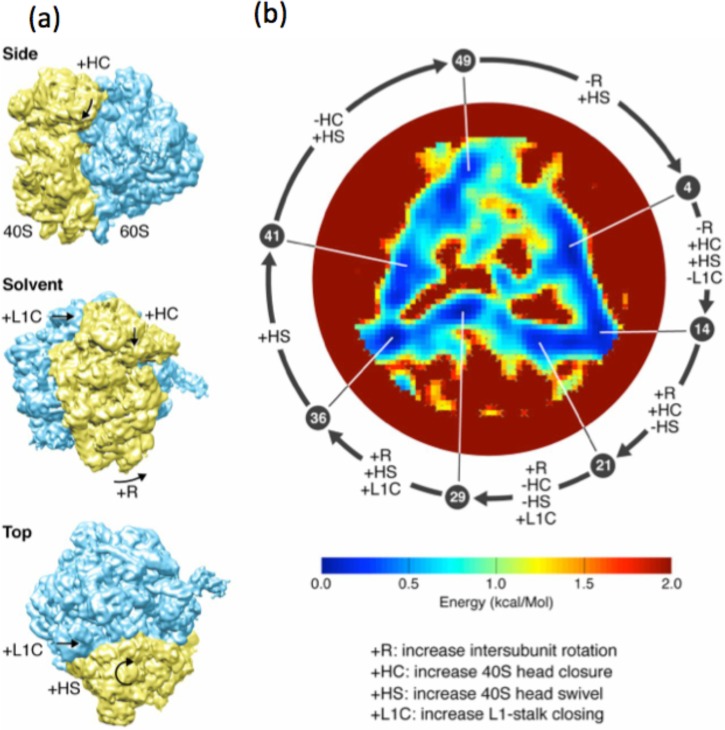
Bayesian clustering techniques (Scheres et al., 2007 and Scheres, 2012) have been highly successful in sorting discrete conformational states. Template-based methods have yielded exciting evidence of continuous conformational changes during function (Fischer et al., 2010). Most recently, manifold-based approaches have enabled ab initio, mathematically rigorous extraction of continuous conformational changes, without recourse to templates, pre-selected regions of interest, or other ad hoc assumptions (Dashti et al., 2014). It has thus been possible to compile molecular movies of the ribosome, map its energy landscape, and identify the trajectory on the energy landscape associated with function (Fig. 1). CryoEM is thus strongly positioned to lead the ongoing shift of emphasis from determining structure to elucidate function at the near-atomic level.
FIG. 1.
(a) 3D structure of ribosome shown in three standard views. (b) Energy landscape of ribosome. (Low-energy regions appear blue.) Conformational changes occurring between each of the seven numbered points along the trajectory are shown in letters. Movies showing the continuous conformational changes along the low-energy trajectory are available in Dashti et al. (2014). Reprinted with permission from Dashti et al., Proc. Natl. Acad. Sci. U. S. A. 111(49), 17492–17497 (2014). Copyright 2014 by PNAS.
III. DETERMINING THE 3D STRUCTURE OF BIOLOGICAL ENTITIES BY XFEL
Since the initial suggestion by Solem and Baldwin over three decades ago (Solem and Baldwin, 1982), the impressive simulations of Neutze et al. (2000) fifteen years ago, and the advent of XFELs capable of producing intense, ultrashort pulses of hard X-rays, the biostructural community has anticipated with excitement the 3D reconstructions of individual biological entities without radiation damage, or the need for crystals. Results are now beginning to emerge (Ekeberg et al., 2015), albeit with resolutions in the 100 nm range. These indicate the relative infancy of the field, whose progress will likely mirror the trajectory followed by CryoEM at the corresponding stage in its development.
Experimental challenges in single-particle imaging by XFEL are similar to those faced by the early CryoEM community: mitigation of shot-to-shot variations in the characteristics of the incident radiation; reproducible, artifact-free introduction of individual biological entities in their native states into beam; and the availability of well-characterized, linear detectors of sufficient dynamic range. From an algorithmic point of view, XFEL-based data-analytical methods initially focused on 3D reconstruction with ultralow-signal snapshots with Poisson noise (Fung et al., 2009 and Loh and Elser, 2009). The initial concentration on giant viruses, however, requires the algorithmic capability to deal with snapshots recording millions of scattered photons, a substantial proportion of which do not emanate from the object at all, but change unpredictably from shot to shot. These difficulties have led to the realization that an international collaborative effort is required for further experimental and algorithmic progress (Aquila et al., 2015). The advent of systematic efforts to identify optimum conditions for single-particle imaging by XFEL's will likely help to reduce artifacts due to shot-to-shot variations in extraneous scattering and detector nonlinearities. Such efforts must occur in tandem with the development of algorithms able to recover reliable 3D structure in the presence of remaining artifacts. The drive to experimentally reduce and algorithmically deal with artifacts represents a new and important direction in single-particle structure determination by XFEL's.
A. Present algorithms for 3D single-particle structure determination by XFEL
Since each diffraction snapshot is a 2D section through the center of a 3D diffraction volume, 3D structure recovery seems, at first sight, a classical tomographic problem. However, the snapshots emanate from unknown orientations of weakly scattering biological objects (Shneerson et al., 2008). In 2009, two apparently different Bayesian approaches (Fung et al., 2009 and Loh and Elser, 2009), later shown to be fundamentally the same (Moths and Ourmazd, 2011), demonstrated the capability to recover 3D structure from a collection of simulated snapshots at the SNR expected from a single 500 kD biological molecule. Since then, a growing number of publications have replicated the same capability (Tegze and Bortel, 2012 and Kassemeyer, et al., 2013). Some of these approaches have demonstrated success with ultralow-signal experimental snapshots obtained by cryoEM (Schwander et al., 2012), or even a conventional X-ray source (Philipp et al., 2012).
The same level of success, however, has not been achieved with experimental XFEL snapshots of biological entities, even from giant viruses. Since such large objects scatter millions of photons onto the detector, the scattering is visible to the naked eye as emanating from an icosahedral object (Fig. 2). The relative lack of success is thus, at first sight, surprising. When 3D structure recovery has been demonstrated (Xu et al., 2014 and Ekeberg et al., 2015), it has been based on a few (typically 10–200) individual snapshots—carefully selected from large collections containing ≥105 snapshots—so as to minimize the shot-to-shot variations in imaging conditions and detector response. In order to compete with alternative methods of structure recovery at nanometer and sub-nanometer levels and because of the need to compile ensemble averages as mentioned earlier, it is essential to develop the ability to recover 3D structure from large datasets.
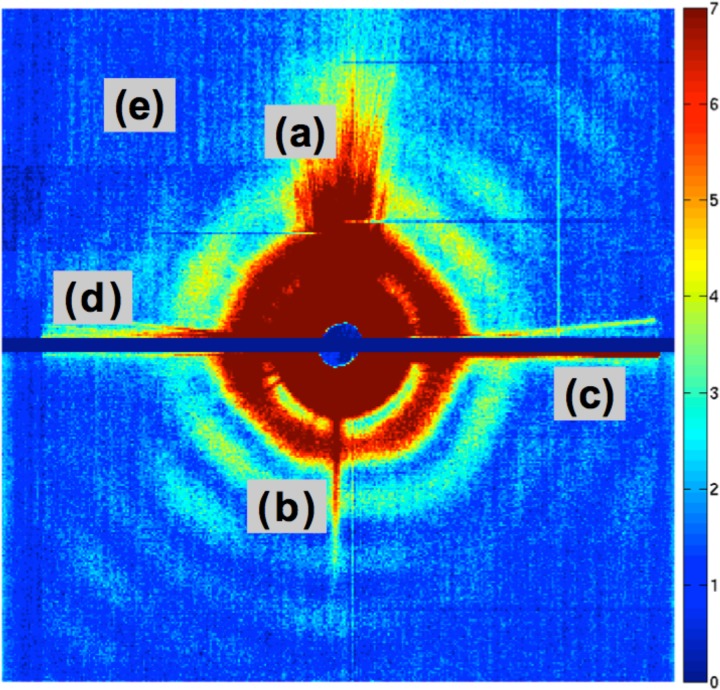
FIG. 2.
Some artifacts in a typical XFEL diffraction pattern from a large virus, obtained with a liquid-jet injector. Features marked (a) and (b) are due to the scattering from injector nozzle. Features (c) and (d) stem from movements in the position of the liquid jet containing the sample. Dark lines marked (e) represent the effect of electronic noise and dead pixels.
Two observations are appropriate at this point. First, when extraneous scattering and detector response dominate, they affect all methods based on similarity (Fung et al., 2009; Loh and Elser, 2009; and Giannakis et al., 2012), as well as those based on angular correlations (Saldin et al., 2009 and Kirian et al., 2011). Second, increases in the incident X-ray intensity are unlikely to solve this problem, because object and extraneous scattering effects often scale together, while detector nonlinearities tend to become worse at higher intensities.
B. Future algorithms for 3D structure determination by XFEL
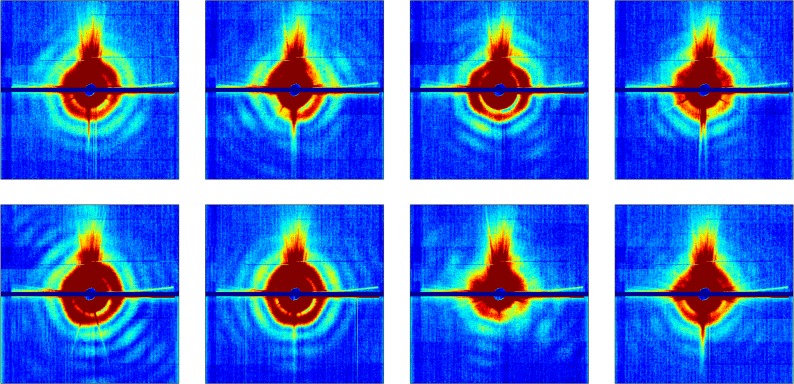
Future single-particle algorithms must be able to remove extraneous artifacts, which vary from shot to shot. These artifacts include: (i) Variations in the incident X-ray beam intensity, inclination, and position; (ii) scattering from upstream apertures and the sample injector; (iii) variations in beam-sample impact parameter; (iv) multi-particle hits; and (v) detector nonlinearities (Fig. 2). Unfortunately, each of these factors changes from shot to shot (Fig. 3).
FIG. 3.
Representative selection of snapshots showing shot-to-shot variations in effects extraneous to the particle under observation.
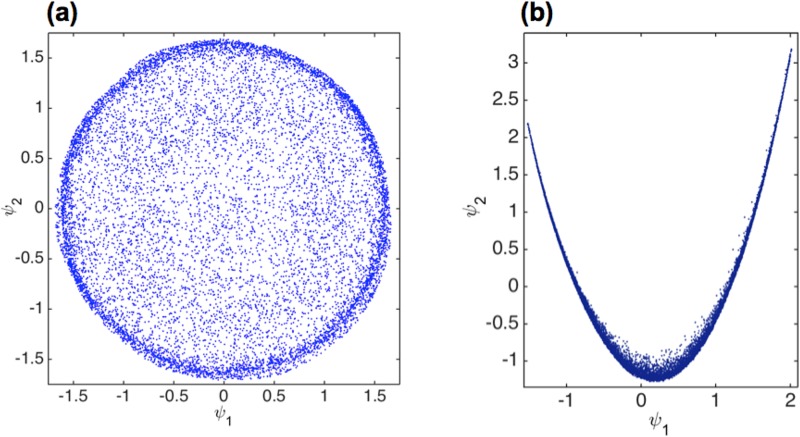
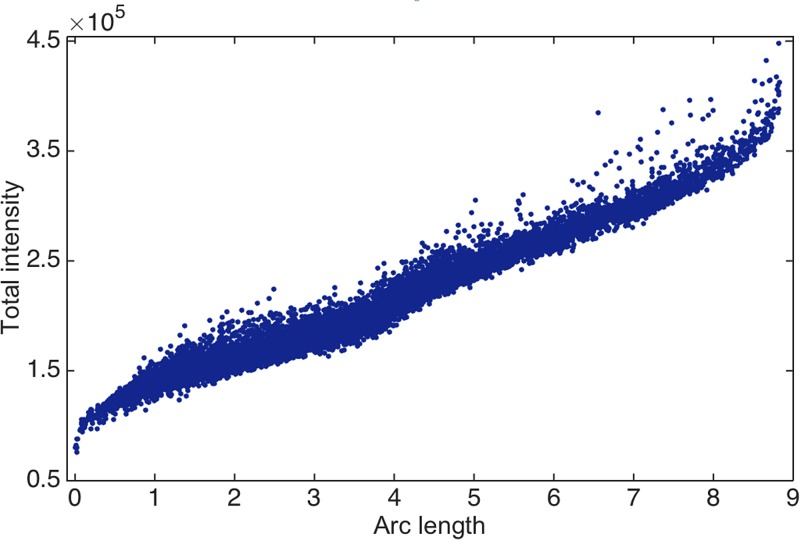
Algorithms designed to extract the object orientation from each 2D snapshot rely on some measure of similarity (or angular correlation) in order to determine the object orientation. However, in the presence of strong extraneous artifacts, such measures reveal the changes in the artifacts, rather than the particle orientation and/or conformation. Manifold-based approaches (Giannakis et al., 2012; Schwander et al., 2012; Hosseinizadeh et al., 2014; and Schwander et al., 2014) offer a geometric means of visualizing the effect of extraneous artifacts. In the absence of extraneous effects and conformational heterogeneities, the points representing a collection of snapshots from sightings of an object in different orientations lie on a specific hypersurface (“manifold”) (Giannakis et al., 2012; Hosseinizadeh et al., 2014; and Schwander et al., 2014). A two-dimensional representation of the hypersurface produced by snapshots of an icosahedral virus is shown in Fig. 4(a), to be compared with the hypersurface produced by experimental snapshots of a large virus [Fig. 4(b)]. This comparison makes it clear that the dominant similarity relationships between the snapshots contain little information about the orientation of the virus, reflecting, instead, the changes in extraneous effects. Fig. 5, for example, shows that the arc length along the experimental manifold of Fig. 4(b) reflects changes in the incident beam intensity.
FIG. 4.
(a) Manifold of simulated diffraction snapshots from an icosahedral virus. Each point in this plot represents a diffraction pattern. (b) 2D representation of the manifold of the experimental XFEL snapshots from a large icosahedral virus.
FIG. 5.
The total intensity of the snapshots (vertical axis) is correlated with the position along the parabolic manifold [arc length of parabola in Fig. 4(b)].
C. Post facto algorithmic correction of extraneous effects: Dynamic flat-fielding
One can regard the shot-to-shot changes in extraneous effects as changes in the detector response (background and gain). Corrections to detector response are traditionally implemented via so-called flat-fielding methods. As normally implemented, this involves a one-time correction to variations in detector response across a uniformly illuminated detector (Seibert et al., 1998).
In the case of XFEL snapshots, the incident imaging conditions vary from shot to shot, requiring a different “flat-field” correction for each snapshot. As little is known about the imaging conditions for each shot, this appears infeasible.
As described below, however, it is possible to design a “dynamic flat-fielding” correction for each snapshot based on the intrinsic properties of diffraction patterns themselves. The main assumption is that single-particle diffraction snapshots are collected in uniformly random orientations.
Provided that the snapshots are corrected for X-ray polarization, an average over a sufficiently large number of snapshots must be azimuthally uniform. In the presence of pixel-to-pixel variations in detector response, this symmetry is lost. One can therefore correct the combined effect of extraneous artifacts by applying a flat-field to each snapshot specifically designed to restore azimuthal symmetry to the ensemble-average of snapshots obtained under closely similar imaging conditions. This can be done with the help of manifold-based approaches, as outlined below.
First, one sorts the data-points along the parabolic manifold shown in Fig. 4(b), in order to identify subsets, within each of which the imaging conditions are closely similar. This “classification” can be performed by using bins along the arc-length of the parabola [Fig. 4(b)]. Specifically, one computes the angular average of diffracted intensities as a function of spatial frequency and the azimuthal angle on the snapshots within an interval , that is,
| (1) |
where N is the number of diffraction patterns in the selected interval. Next, a flat-field correction for the interval is designed
| (2) |
with .
This flat-field correction is applied to every image in the interval , in order to restore azimuthal symmetry to the ensemble-average over that interval, viz.,
| (3) |
where represents the corrected intensity .
The procedure outline above corrects for detector variations within a single class in the interval . In order to correct globally for all intervals of along the parabolic manifold, one makes in Eq. (2) independent of the interval by computing
Finally, each image in the dataset is corrected as follows:
| (4) |
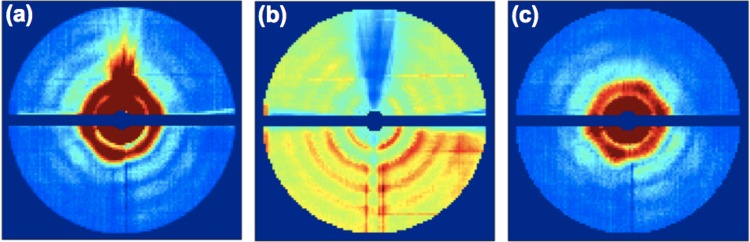
where is a diffraction pattern in the interval . This establishes identical azimuthal averages, and thus a global correction for all values of . The result is shown in Fig. 6. Horizontal and vertical streaks in the raw image are eliminated, and differences in overall intensity in top and bottom panels of the image corrected.
FIG. 6.
(a) A typical raw XFEL diffraction pattern obtained from a biological object injected by a continuous liquid jet. (b) The flat-field correction for this snapshot deduced from the collection of diffraction patterns themselves. (c) Corrected snapshot after dynamic flat-fielding.
IV. FUTURE DIRECTIONS
XFEL-based single particle methods can determine the structure of large objects, which are difficult to examine by other means. Determining the conformational spectra (“movies”) of molecular processes and the energy landscapes traversed in the course of function also represents a compelling goal. XFEL-based single-particle techniques have the potential to provide unprecedented access to such information under physiologically relevant conditions (temperature, pH, etc.).
Important challenges, however, remain. Experimentally, we must learn to reduce the effect of shot-to-shot variations in imaging conditions to a level where structural and conformational information can be reliably extracted. Algorithmically, we must develop the capability to remove remaining artifacts and mine the information content of large datasets to obtain statistically meaningful information. Finally, we must learn how to combine these capabilities with time-resolved single-particle approaches, to gain dynamical information on biologically important processes. Timing uncertainties, caused, for example, by “pump-probe jitter” when an optical pump is combined with an XFEL probe pulse, or by non-uniform reaction initiation in solution, can limit the available information. In order to exploit the exquisite short-pulse capability of the XFEL, we must develop the ability to extract accurate information from datasets collected in the presence of large timing uncertainty. The magnitude of these prizes and the challenges they pose require concerted international cooperation. It is gratifying that such efforts are gathering momentum.
ACKNOWLEDGMENTS
This work was supported in part by the U.S. National Science Foundation Award No. STC 1231306, the U.S. Department of Energy, Office of Science, Basic Energy Sciences Award No. DE-FG02-09ER16114, and the U.S. National Science Foundation Award No. MCB-1240590.
References
- 1. Amunts, A. , Brown, A. , Bai, X.-C. , Llácer, J. L. , Hussain, T. , Emsley, P. , Long, F. , Murshudov, G. , Scheres, S. H. W. , and Ramakrishnan, V. , “ Structure of the yeast mitochondrial large ribosomal subunit,” Science 343(6178), 1485–1489 (2014). 10.1126/science.1249410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Aquila, A. , Barty, A. , Bostedt, C. , Boutet, S. , Carini, G. , dePonte, D. , Drell, P. , Doniach, S. , Downing, K. H. , Earnest, T. , Elmlund, H. , Elser, V. , Gühr, M. , Hajdu, J. , Hastings, J. , Hau-Riege, S. P. , Huang, Z. , Lattman, E. E. , Maia, F. R. N. C. , Marchesini, S. , Ourmazd, A. , Pellegrini, C. , Santra, R. , Schlichting, I. , Schroer, C. , Spence, J. C. H. , Vartanyants, I. A. , Wakatsuki, S. , Weis, W. I. , and Williams, G. J. , “ The linac coherent light source single particle imaging road map,” Struct. Dyn. 2, 041701 (2015). 10.1063/1.4918726 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Dashti, A. , Schwander, P. , Langlois, R. , Fung, R. , Li, W. , Hosseinizadeh, A. , Liao, H. Y. , Pallesen, J. , Sharma, G. , Stupina, V. A. , Simon, A. E. , Dinman, J. D. , Frank, J. , and Ourmazd, A. , “ Trajectories of the ribosome as a brownian nanomachine,” Proc. Natl. Acad. Sci. U. S. A. 111(49), 17492–17497 (2014). 10.1073/pnas.1419276111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Ekeberg, T. et al. , “ Three-dimensional reconstruction of the giant mimivirus particle with an X-ray free electron laser,” Phys. Rev. Lett. 114, 098102 (2015). 10.1103/PhysRevLett.114.098102 [DOI] [PubMed] [Google Scholar]
- 5. Fischer, N. , Konevega, A. L. , Wintermeyer, W. , Rodnina, M. V. , and Stark, H. , “ Ribosome dynamics and tRNA movement by time-resolved electron cryomicroscopy,” Nature 466(7304), 329–333 (2010). 10.1038/nature09206 [DOI] [PubMed] [Google Scholar]
- 6. Frank, J. , Three-Dimensional Electron Microscopy of Macromolecular Assemblies ( Oxford University Press, New York, 2006). [Google Scholar]
- 7. Fung, R. , Shneerson, V. , Saldin, D. K. , and Ourmazd, A. , “ Structure from fleeting illumination of faint spinning objects in flight,” Nat. Phys. 5(1), 64–67 (2009). 10.1038/nphys1129 [DOI] [Google Scholar]
- 8. Giannakis, D. , Schwander, P. , and Ourmazd, A. , “ The symmetries of image formation by scattering. I. Theoretical framework,” Opt. Express 20(12), 12799–12826 (2012). 10.1364/OE.20.012799 [DOI] [PubMed] [Google Scholar]
- 9. Hosseinizadeh, A. , Schwander, P. , Dashti, A. , Fung, R. , D'Souza, R. M. D. , and Ourmazd, A. , “ High-resolution structure of viruses from random diffraction snapshots,” Philos. Trans. R. Soc., B 369(1647), 20130326 (2014). 10.1098/rstb.2013.0326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Kassemeyer, S. , Jafarpour, A. , Lomb, L. , Steinbrener, J. , Martin, A. V. , and Schlichting, I. , “ Optimal mapping of x-ray laser diffraction patterns into three dimensions using routing algorithms,” Phys. Rev. E 88(4), 042710 (2013). 10.1103/PhysRevE.88.042710 [DOI] [PubMed] [Google Scholar]
- 11. Kirian, R. A. , Schmidt, K. E. , Wang, X. , Doak, R. B. , and Spence, J. C. , “ Signal, noise, and resolution in correlated fluctuations from snapshot small-angle x-ray scattering,” Phys. Rev. E 84, 011921 (2011). 10.1103/PhysRevE.84.011921 [DOI] [PubMed] [Google Scholar]
- 12. Loh, N. T. and Elser, V. , “ Reconstruction algorithm for single-particle diffraction imaging experiments,” Phys. Rev. E 80(2 Pt 2), 026705 (2009). 10.1103/PhysRevE.80.026705 [DOI] [PubMed] [Google Scholar]
- 13. Moore, P. B. , “ How should we think about the ribosome?,” Annu. Rev. Biophys. 41, 1–19 (2012). 10.1146/annurev-biophys-050511-102314 [DOI] [PubMed] [Google Scholar]
- 14. Moths, B. and Ourmazd, A. , “ Bayesian algorithms for recovering structure from single-particle diffraction snapshots of unknown orientation: A comparison,” Acta Crystallogr., Sect. A: Found. Crystallogr. 67, 481–486 (2011). 10.1107/S0108767311019611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Neutze, R. , Wouts, R. , van der Spoel, D. , Weckert, E. , and Hajdu, J. , “ Potential for biomolecular imaging with femtosecond X-ray pulses,” Nature 406(6797), 752–757 (2000). 10.1038/35021099 [DOI] [PubMed] [Google Scholar]
- 16. Philipp, H. T. , Ayyer, K. , Tate, M. W. , Elser, V. , and Gruner, S. M. , “ Solving structure with sparse, randomly oriented x-ray data,” Opt. Express 20(12), 13129–13137 (2012). 10.1364/OE.20.013129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Saldin, D. K. , Shneerson, V. L. , Fung, R. , and Ourmazd, A. , “ Structure of isolated biomolecules from ultrashort x-ray pulses: Exploiting the symmetry of random orientations,” J. Phys.: Condens. Matter 21(13), 134014 (2009). 10.1088/0953-8984/21/13/134014 [DOI] [PubMed] [Google Scholar]
- 18. Scheres, S. H. , “ A Bayesian view on cryo-EM structure determination,” J. Mol. Biol. 415(2), 406–418 (2012). 10.1016/j.jmb.2011.11.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Scheres, S. H. , Gao, H. , Valle, M. , Herman, G. T. , Eggermont, P. P. , Frank, J. , and Carazo, J. M. , “ Disentangling conformational states of macromolecules in 3D-EM through likelihood optimization,” Nat. Methods 4(1), 27–29 (2007). 10.1038/nmeth992 [DOI] [PubMed] [Google Scholar]
- 20. Schwander, P. , Fung, R. , and Ourmazd, A. , “ Conformations of macromolecules and their complexes from heterogeneous datasets,” Philos. Trans. R. Soc., B 369, 20130567 (2014). 10.1098/rstb.2013.0567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Schwander, P. , Giannakis, D. , Yoon, C. H. , and Ourmazd, A. , “ The symmetries of image formation by scattering. II. Applications,” Opt. Express 20(12), 12827–12849 (2012). 10.1364/OE.20.012827 [DOI] [PubMed] [Google Scholar]
- 22. Seibert, J. A. , Boon, J. M. , and Lindfors, K. K. , “ Flat-field correction technique for digital detectors,” Proc. SPIE 3336, 348–354 (1998). 10.1117/12.317034 [DOI] [Google Scholar]
- 23. Shneerson, V. L. , Ourmazd, A. , and Saldin, D. K. , “ Crystallography without crystals. I. The common-line method for assembling a three-dimensional diffraction volume from single-particle scattering,” Acta Crystallogr., Sect. A: Found. Crystallogr. 64(Pt 2), 303–315 (2008). 10.1107/S0108767307067621 [DOI] [PubMed] [Google Scholar]
- 24. Solem, J. C. and Baldwin, G. C. , “ Microholography of living organisms,” Science 218(4569), 229–235 (1982). 10.1126/science.218.4569.229 [DOI] [PubMed] [Google Scholar]
- 25. Tegze, M. and Bortel, G. , “ Atomic structure of a single large biomolecule from diffraction patterns of random orientations,” J. Struct. Biol. 179, 41–45 (2012). 10.1016/j.jsb.2012.04.014 [DOI] [PubMed] [Google Scholar]
- 26. Xu, R. , Jiang, H. , Song, C. , Rodriguez, J. A. , Huang, Z. , Chen, C.-C. , Nam, D. , Park, J. , Gallagher-Jones, M. , Kim, S. , Kim, S. , Suzuki, A. , Takayama, Y. , Oroguchi, T. , Takahashi, Y. , Fan, J. , Zou, Y. , Hatsui, T. , Inubushi, Y. , Kameshima, T. , Yonekura, K. , Tono, K. , Togashi, T. , Sato, T. , Yamamoto, M. , Nakasako, M. , Yabashi, M. , Ishikawa, T. , and Miao, J. , “ Single-shot three-dimensional structure determination of nanocrystals with femtosecond X-ray free-electron laser pulses,” Nat. Commun. 5, 4061 (2014). [DOI] [PubMed] [Google Scholar]