Communication: Effects of thermionic-gun parameters on operating modes in ultrafast electron microscopy

Abstract

Ultrafast electron microscopes with thermionic guns and LaB₆ sources can be operated in both the nanosecond, single-shot and femtosecond, single-electron modes. This has been demonstrated with conventional Wehnelt electrodes and absent any applied bias. Here, by conducting simulations using the General Particle Tracer code, we define the electron-gun parameter space within which various modes may be optimized. The properties of interest include electron collection efficiency, temporal and energy spreads, and effects of laser-pulse duration incident on the LaB₆ source. We find that collection efficiencies can reach 100% for all modes, despite there being no bias applied to the electrode.

With ultrafast electron microscopy (UEM), the millisecond temporal resolutions typically accessible with conventional transmission electron microscopes (TEMs) and compatible digital detectors can be extended to the femtosecond (fs) timescale.^1,2 Via a pump-probe approach commonly employed in ultrafast spectroscopic experiments,³ UEM has been successfully used to conduct a wide range of studies on structural, electronic, and magnetic dynamics in nanoscale materials.^2,4 Conducting such pump-probe experiments in an electron microscope is made possible by modifying the TEM column such that optical access to both the electron-gun and specimen regions is enabled.^5,6 In the gun region, discrete photoelectron packets are generated from the emission source via the photoelectric effect; these discrete photoelectron packets are used to probe specimen dynamics induced with a pump laser pulse.^5–9 In this way, the wide-ranging capabilities common to conventional TEMs (e.g., bright- and dark-field imaging, parallel- and convergent-beam diffraction, spectroscopy, and energy filtering) can be extended to fs studies of atomic and nanoscale dynamics.⁴

The TEM platform upon which the first-generation fs UEM was based is an FEI Tecnai 120 kV instrument equipped with a self-biasing thermionic electron gun (TEG) and LaB₆ emission source.⁶ Modifications to this instrument consisted simply of the addition of optical elements (e.g., optical windows, and steering mirrors) at the gun and specimen regions of the column; the gun, electron optics, and detector were the same as those comprising the conventional microscope. In UEM mode, the LaB₆ source is typically held at room temperature (i.e., no resistive heating is applied) such that emission occurs only during laser illumination. Thus, the Wehnelt triode assembly is unbiased during UEM operation, and the lensing effect of the cylinder at the aperture is not present in the conventional sense. Despite this, both nanosecond (ns), single-shot and fs, single-electron studies (denoting the extremes of the time-resolved photoelectron parameter space) have been successfully demonstrated with the first-generation instrument.^10–13

Importantly, an as yet unrealized goal in the development and application of UEM is to reach the spatial-resolution limits of the base-TEM platform (e.g., 1.4 Å line resolution for the FEI Tecnai T20 G2) and combine this with the fs temporal resolution afforded by short-pulsed lasers. Indeed, images of nanometer and sub-nanometer lattice fringes have been obtained with UEM indicating a coherent beam of sufficient current can be generated (typically at high laser repetition rates),^1,7,14 but the challenge remains to image fs, real-space dynamics on these spatial scales. Reaching this goal requires balancing and optimizing a number of experimental parameters, including beam coherence and current, thermal drift and signal acquisition time, and robustness of specimen reversibility. Thus, development of a quantitative understanding of the effects of various electron-gun parameters on experimental observables in order to identify optimum conditions would aid in realizing the ultimate spatiotemporal resolutions for TEG-based UEMs.

Here, via ray-tracing simulations conducted with the General Particle Tracer (GPT) software package¹⁵ and field codes specific to the electron-optical design for a Tecnai T20 G2 (the platform upon which the FEI Tecnai Femto UEM is based), the effects of TEG and incident laser-pulse parameters—namely, LaB₆ position, Wehnelt aperture diameter, and laser-pulse duration—on various photoelectron-packet properties [e.g., collection efficiency (i.e., maximum beam current), duration, and energy spread] are described. Simulations were performed for three distinct UEM modes—single-electron (one electron per packet), burst (10³ electrons per packet), and single-shot (10⁷ electrons per packet)—for a Wehnelt at 0 V (i.e., no bias). In addition, the effect of LaB₆ size within the different modes was investigated. Electron paths were traced through standard TEM electric fields using a fifth-order Runge-Kutta method with adaptive stepsize control. At every time point, mutual electromagnetic forces between the electrons were evaluated using the Barnes-Hut tree algorithm.^16,17 Results of the simulations suggest there are experimentally accessible optimum settings for TEG-based UEMs, wherein beam current is maximized and coherence is preserved. Further, trends of photoelectron-packet temporal and energy spreads as a function of gun settings are predicted, thus serving as a potential guide for tailoring parameters to suit specific experimental requirements.

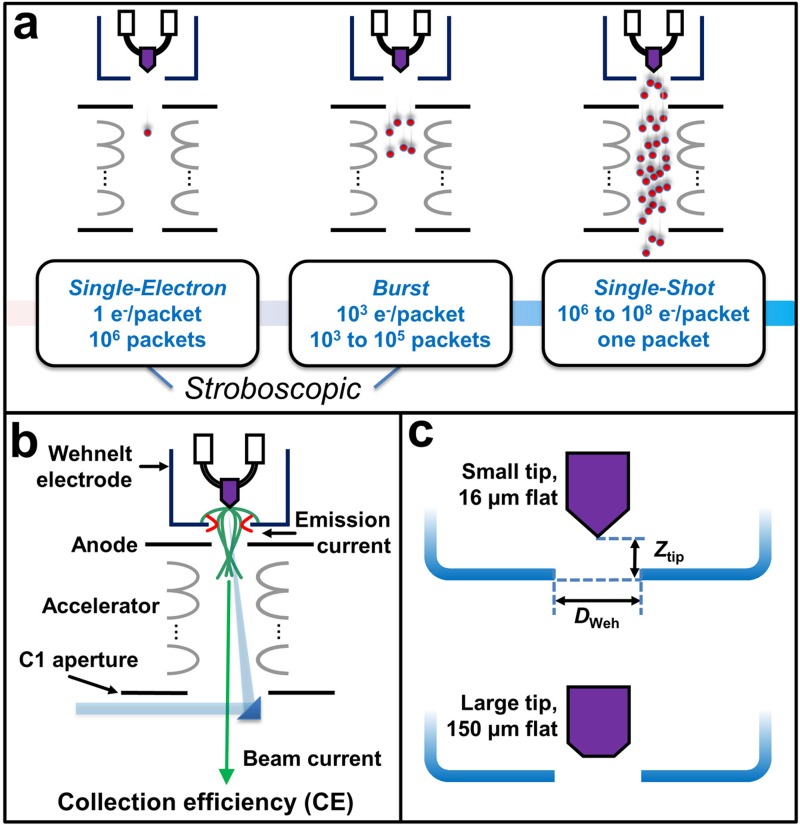
Figure 1 displays an overview of the qualitative simulation geometries and pictorial definitions of the parameters of interest. For the three distinct UEM modes examined here [Figure 1(a)], the single-electron and burst configurations consist of fs laser pulses used to generate the photoelectron packets stroboscopically, while the single-shot mode is of ns duration. For the latter mode, only the central portion of a 35-ps packet with equivalent current was considered, thus ignoring end effects. These end effects arise from a small percentage of the electrons comprising the packet and are of few-ps duration. Thus, they do not play a significant role on ns timescales (additional details provided below). Parameters for the three modes of interest are strictly set by space-charge effects^6,18–21 and represent experimentally accessible values for TEG-based UEMs. For all cases, the distance from the LaB₆ source to the anode is 5.5 mm, the Wehnelt electrode is at 0 V, and the anode is at −33.3 kV. Additionally, for the initial photoelectron energy spread, an exponential distribution with both a mean and standard deviation of 0.5 eV was used assuming Lambertian angular distributions. This implies that the radiant intensity is proportional to the cosine of the angle to the surface normal.

FIG. 1.

(a) Three distinct UEM modes—single-electron, burst, and single-shot—and the corresponding parameters (number of electrons per packet and total number of packets). (b) Electron-gun geometry of a self-biasing Wehnelt assembly and LaB₆ emission source. Pertinent components and beam properties are labeled. The probe-laser path and final steering mirror are also shown. (c) Illustration of the simulation parameters Z_tip (distance from LaB₆ tip to outer surface of the Wehnelt diaphragm) and D_Weh (diameter of the Wehnelt aperture). The two tip sizes investigated in the simulations (16 and 150 μm) are also noted.

A critical parameter of interest is collection efficiency (CE), which is defined here as the fraction of photoelectrons generated at the LaB₆ source that pass through the anode, acceleration tube, and C1 aperture (0.6 mm diameter) and enter the illumination system of the microscope [Figure 1(b)]; the defined number of photoelectrons per packet in Figure 1(a) is the fraction that enter the illumination system. In the simulations, the number of photoelectrons started at the source was adjusted for any non-unity CE values found. For fs UEM experiments, a CE of 100% with little to no loss of coherence is ideal, as this provides for the maximum-possible beam current, and thus the minimum signal acquisition time while preserving inherent instrument-limited resolutions. Note that a variety of practical experimental parameters were considered in the simulations. These included path-length differences arising from the emission process and size of the limiting aperture, electron-velocity distributions, and space-charge effects; variations arising across the three distinct modes were considered.

An additional electron-gun parameter varied in the simulations was LaB₆ tip size [Figure 1(c)]. For the single-electron mode, a standard, flat, 16-μm diameter LaB₆ source and incident laser-spot size of 16 μm with top-hat profile were used. Note that the geometrically-enhanced electric field around the tip reduces the time photo-emitted electrons spend at low velocities. For the burst and single-shot modes, however, a tightly focused laser would result in an initial spatially-confined photoelectron packet, which would produce significant Coulombic interactions at the source resulting in a broadening of the temporal and energy spreads.²¹ Consequently, for the burst and single-shot modes, it is preferable to use a larger laser-spot size in order to laterally distribute the photoelectrons and thus reduce space-charge effects. Note that brightness values are not reported owing to the relatively large surface emittance and, thus, the negligible degradation due to Coulombic interactions. Regardless, brightness will scale with laser power, number of electrons per packet, etc. Here, a laser-spot size of 80 μm, again with top-hat profile and a flat, 150-μm diameter LaB₆ emission source were used for the burst and single-shot modes. The tip-geometry parameters are summarized in Table I.

TABLE I.

Parameters (electrons per packet; LaB₆ tip size, and incident laser-spot size) used in the simulations of three distinct UEM operating modes.

UEM mode	Electrons/packet	LaB6 tip diameter (μm)	Incident laser-spot size (μm)
Single-electron	1	16	16
Burst	103	150	80
Single-shot	107	150	80

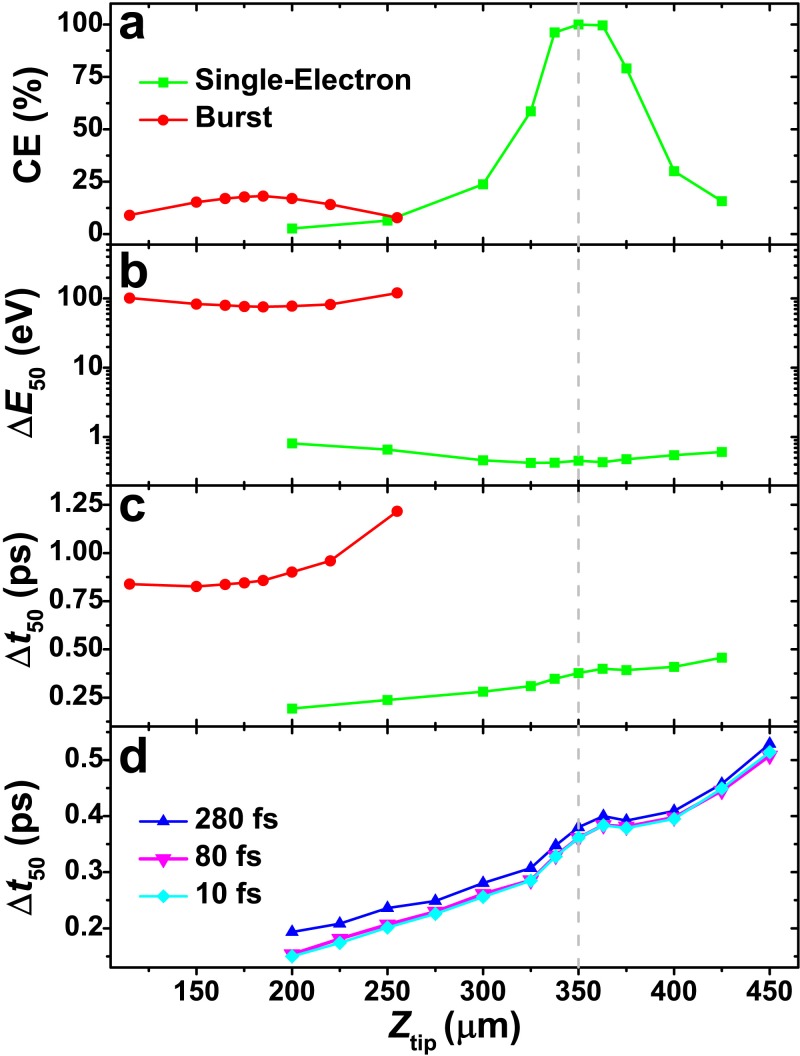
Figure 2 summarizes the simulation results for the stroboscopic single-electron and burst modes for critical photoelectron-packet properties—namely, the energy and temporal spreads (ΔE₅₀ and Δt₅₀, respectively)—and TEG-based UEM CE, all as a function of LaB₆ position [Z_tip, Figure 1(c)]. For this particular set of simulations, a fixed Wehnelt-aperture size [D_Weh, Figure 1(c)] of 0.7 mm (standard TEG size is 0.5–0.7 mm) was used, and the incident laser-pulse duration was fixed at 280 fs (entire pulse) [Figures 2(a)–2(c)]. In Figure 2(d), the effect of Z_tip on Δt₅₀ for the single-electron mode was simulated for three incident laser-pulse durations: 10, 80, and 280 fs. Here, Δt₅₀ and ΔE₅₀ are defined as the temporal and energy ranges, respectively, that contain the middle 50% of the Gaussian photoelectron (statistical) profile. Note that the simulations do not consider the effect of subtle experimental factors on Δt₅₀, such as photocathode response time or laser jitter. Further, the initial spatial and energy distributions of the photoelectrons are simplified such that calculated ΔE₅₀ values are true only for the specific assumptions made. The emphasis here is on general trends rather than absolute numbers, though both must be experimentally tested and verified, for example, by using the photon-induced near-field effect.^8,22–26

FIG. 2.

Dependence of (a) photoelectron collection efficiency (CE), (b) energy spread (ΔE₅₀), and (c) temporal spread (Δt₅₀) on LaB₆ position relative to the Wehnelt aperture (Z_tip) for the single-electron (green squares) and burst (red circles) modes. (d) Dependence of the statistical temporal spread for the single-electron mode on Z_tip for full, incident laser-pulse durations of 280 fs (blue triangles), 80 fs (purple inverted triangles), and 10 fs (light-blue diamonds). The key in (a) corresponds to (a)–(c), while the key in (d) is specific to that panel. The gray, dashed vertical line at Z_tip = 350 μm denotes a position at which the single-electron CE is 100%.

A key prediction arising from the simulations is that there are optimum Z_tip settings (e.g., 350 μm) at which 100% CE can be achieved in the single-electron stroboscopic mode, despite the absence of a bias applied to the Wehnelt cylinder [Figure 2(a)]; the electrode acts as an electrostatic lens even in the absence of an applied bias. As importantly, a strong dependence of CE on Z_tip is predicted, with values falling to near 0% at the simulation boundaries (i.e., 200 and 425 μm); the Z_tip distance affects the focusing of the photoelectrons. Conversely, due to the low electron-density per packet, ΔE₅₀ and Δt₅₀ do not greatly vary over this range [Figures 2(b) and 2(c)]. Further, as the electron-density per packet is increased from one to 10³ (i.e., transition from the single-electron to burst mode), (i) the optimum Z_tip shifts to shorter distances, (ii) the maximum CE reaches only 20%, and (iii) ΔE₅₀ significantly deteriorates due to space-charge effects such that high-resolution imaging and spectroscopy are likely not possible without filtering. Consequently, a balance must be struck between tip position, electron-density per packet, laser repetition rate, and specimen recoverability.

For the single-electron mode, the full duration of the laser pulse incident on the photocathode is predicted to have little to no effect on Δt₅₀ across the range of Z_tip investigated here [Figure 2(d)]. Indeed, at the optimum Z_tip, where CE = 100%, a reduction of the incident laser-pulse duration from 280 to 80 fs produced a commensurate drop in Δt₅₀ of only 20 fs; a further reduction in incident-pulse duration to 10 fs had no additional affect. This can be rationalized by again noting that the quoted laser-pulse durations correspond to the entire pulse, while that of the photoelectrons refers to the central region containing half the total population. Thus, the photoelectron durations studied here are, in most instances, significantly longer than the incident laser-pulse durations. Additionally, the simulations predict Δt₅₀ will increase with increasing Z_tip owing to weaker stray fields directly adjacent to the tip; the residence time of the photoelectrons at relatively lower kinetic energies increases, thus exacerbating their energy dispersion and mutual interactions. As such, a compromise must be made between temporal resolution and CE. The implication of the result shown in Figure 2(d) is that decreasing the pulse duration of the laser source alone beyond approximately 300 fs is insufficient for significantly increasing the temporal resolution of the type of TEG-based UEMs studied here; additional modifications and/or methods must be employed in order to push the instrument-limited resolution below 100 fs.^19,27–31

As previously noted, the simulations summarized in Figure 2 were performed with a fixed D_Weh = 0.7 mm. Thus, in order to determine the effect of Wehnelt-aperture diameter on CE, ΔE₅₀, Δt₅₀, and the optimum Z_tip (i.e., Z_opt), the simulations were repeated for various D_Weh ranging from 0.5 to 4 mm for burst mode and 0.5 to 3.5 mm for the single-electron and single-shot modes, the results of which are summarized in Figure 3. Here, the incident laser-pulse duration was held fixed at 280 fs, and Z_opt for each D_Weh was determined in the same manner as previously discussed. Likewise, the CE for each UEM mode and at each D_Weh was determined at the corresponding Z_opt for that particular setting. Note that Δt₅₀ for the single-shot mode is not included in Figure 3(c) because, by design, the packets are much longer in duration than the sub-ps timescales of interest for fs UEM.

FIG. 3.

Dependence of (a) photoelectron collection efficiency (CE), (b) energy spread (ΔE₅₀), (c) temporal spread (Δt₅₀), and (d) optimum LaB₆ tip position (Z_opt) on Wehnelt-aperture diameter (D_Weh) for the single-electron (green squares), burst (red circles), and single-shot (blue triangles) UEM modes. The key in (a) corresponds to all panels.

Recall from Figure 2 that, for a fixed D_Weh = 0.7 mm, the maximum CE for burst mode was 20% at Z_opt, while it reached 100% for the single-electron mode. The results summarized in Figure 3(a) show that CE for both the single-shot and burst modes increases linearly with increasing D_Weh, approaching 100% for both cases at the simulation limits. In addition, ΔE₅₀ generally decreases with increasing D_Weh for the burst and single-shot modes (no change is observed for the single-electron mode), while Δt₅₀ decreases for the burst mode and slightly increases for the single-electron mode [Figures 3(b) and 3(c), respectively].

Note the results summarized in Figure 3(b) indicate that the burst mode has a larger ΔE₅₀ than the single-shot mode due to relatively large end-effect contributions. The simulations indicate that for packets containing a large number of particles, electrons in the first few ps of the head and last few ps of the tail experience a charge imbalance and, thus, a net force that is directed forwards and backwards, respectively. Hence, these electrons are accelerated in the forward (head) and backward (tail) directions. In the burst mode, these end effects lead to a dominant correlated energy spread (with time). Conversely, for the single-shot mode, the number of electrons in the first and last few ps is small compared to the total packet population, and, thus, the end effects are negligible and can be ignored. This typically leads to smaller energy spreads in the single-shot mode, even for similar instantaneous current in the packet.

Finally, note that according to Figure 3(d), a nearly linear increase in Z_opt with increasing D_Weh is required in order to realize the trends in Figures 3(a)–3(c). Experimentally, this may result in practical challenges for Z_tip > 2 mm. Nevertheless, the simulations predict a large D_Weh will generally improve all parameters for all UEM modes. This is because the full beam can expand more before it is focused toward the C1 aperture, and the collected part is much wider throughout most of the accelerator; there is more distance between nearest-neighbor photoelectrons, and the Boersch effect is reduced.

In conclusion, via ray-tracing simulations performed with the General Particle Tracer software package and field codes specific to the electron-optical design of the Tecnai Femto UEM, optimum electron-gun settings and general trends have been identified for three distinct operating modes. Settings for achieving 100% collection efficiency with commensurate trends for energy and temporal spreads have been described, and negligible effects of the incident-laser pulse duration have been predicted. These results indicate that, despite the absence of an applied bias, the Wehnelt electrode acts as an electrostatic lens, and the LaB₆ position and Wehnelt aperture size can be tuned to optimize the focusing condition and UEM beam current for specific experimental requirements (e.g., ns, single-shot or fs, single-electron studies). On sub-ps timescales, however, operation within the (near) single-electron regime will be required to minimize post-specimen Coulombic interactions.³² Accordingly, the implications of this work are that, for particular electron-gun and laser settings combined with robust specimen reversibility and highly stable environmental conditions, sub-nanometer-scale real-space imaging of sub-ps dynamics should be possible with TEG-based UEMs. Work is currently underway to experimentally test the simulations reported here, the results of which will be detailed in a subsequent manuscript.