Fixed target matrix for femtosecond time-resolved and in situ serial micro-crystallography

Abstract

We present a crystallography chip enabling in situ room temperature crystallography at microfocus synchrotron beamlines and X-ray free-electron laser (X-FEL) sources. Compared to other in situ approaches, we observe extremely low background and high diffraction data quality. The chip design is robust and allows fast and efficient loading of thousands of small crystals. The ability to load a large number of protein crystals, at room temperature and with high efficiency, into prescribed positions enables high throughput automated serial crystallography with microfocus synchrotron beamlines. In addition, we demonstrate the application of this chip for femtosecond time-resolved serial crystallography at the Linac Coherent Light Source (LCLS, Menlo Park, California, USA). The chip concept enables multiple images to be acquired from each crystal, allowing differential detection of changes in diffraction intensities in order to obtain high signal-to-noise and fully exploit the time resolution capabilities of XFELs.

I. INTRODUCTION AND BACKGROUND

Proteins have evolved to direct chemical reactions into biological functions, but connecting the protein structure to the mechanism by which chemistry is coupled to functional outcome remains challenging. To understand this link requires high temporal and spatial resolution to unveil the small atomic dislocations involved in any correlated motion in real time.^1,2 While optical methods reveal many mechanistic details, they are fundamentally limited to connecting transient absorption spectra or localized vibration spectral changes to assumed structures. This gives the operative dynamics but not the global structural changes that are a key to revealing the structure-function relationship of these highly evolved systems. With the advent of ultrabright femtosecond electron and X-ray sources, like X-ray Free-electron Lasers (XFELs),^3–7 mechanistically relevant timescales lying in the femtosecond regime have become accessible, enabling the capture of protein motions with atomic resolution in order to follow the transduction of chemical energy into function.

Dynamic structure determination using the pump-probe method requires acquisition of diffraction images at many time delays. However, each sampling sequence of femtosecond laser excitation pulse and subsequent X-ray probe pulse damages the sample. This, combined with the non-reversibility of many biological systems, means a new crystal, or new region of a larger crystal, may be required for each sampling sequence. Thus, in order to ensure sufficient sampling of reciprocal space and time, time-resolved studies require far more crystals than is needed for conventional X-ray crystallographic analysis of static structures. Herein lies the challenge.

Any sample delivery system for time-resolved crystallographic measurements must allow the crystals to be non-frozen in order for the proteins to undergo their biologically relevant reaction.^8,9 Chapman et al. have demonstrated serial nano-crystallography for both static and time-resolved X-ray diffraction of sub-μm-sized crystals dispersed in mother liquor.^6,10,11 This liquid jet sample delivery method has been extremely successful. However, it is non-ideal for time-resolved studies as it does not allow differential detection, the mainstay of femtosecond spectroscopic methods, which generally leads to at least 2 orders of magnitude increased signal-to-noise for a given sampling time. As a result, there is a corresponding increase in the needed crystal quantity by at least two orders of magnitude over differential detection methods. The actual increase in number of crystals is likely to be significantly higher when we consider differences in crystal size, i.e., that the sampling size goes up with decreasing crystal size.

Further, in order to get above background, at least 10% of the proteins in the X-ray illuminated volume needs to be photoexcited, assuming unit quantum efficiency for the photoinduced process. Lower quantum yield processes require correspondingly higher excitation intensities. The incident peak power required to achieve this fraction of excited molecules is dependent on the strength of the absorption band. If the absorption is too weak the required peak power exceeds the linear range and leads to multi-photon absorption, which must be avoided. Strong absorption, on the other hand, leads to a large mismatch between the laser and X-ray penetration depth. This mismatch, although correctable to a certain degree with optimised crystal and crossed beam geometries, limits the time resolution of larger crystals in the crossed beam geometry to nominally subpicosecond.¹² Therefore, crystals on the order of 10 μm in thickness and photoexcitation with a laser beam almost parallel to the X-ray beam are required to approach the 10 fs time resolution capabilities of XFELs and capture the fastest possible nuclear motions.

An ideal approach for an ultra-fast XFEL time-resolved experiment is therefore to have a delivery system that is optimized for 10–100 μm size crystals and in which there is control over sample position to allow differential detection. Herein, we describe such a system based on a fixed target template that allows acquisition of multiple diffraction images per crystal while also providing thousands of crystals in known positions, which can be brought to the beam position. The crystals are sorted by fluid flow with random orientations onto a silicon nanofabricated crystallography chip, which can host thousands of protein crystals under ambient conditions, at defined positions, and nearly free of their mother liquor. The concept is scalable to enable mega-pixel crystal arrays of micron-sized crystals on centimeter formats. The general applicability of this approach to crystallography is first demonstrated for a number of model protein systems using a microfocus synchrotron beamline. We then show first results from a differential detection time-resolved XFEL study of myoglobin to demonstrate the utility of the chip for femtosecond time-resolved studies.

II. CRYSTALLOGRAPHY CHIP DESIGN

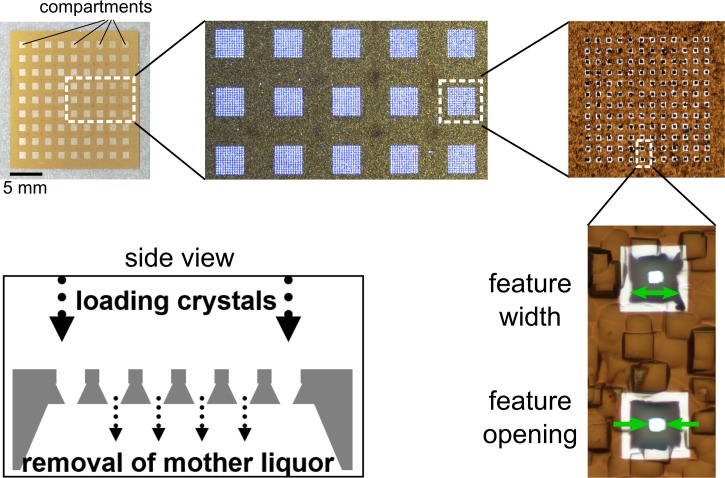
In comparison to our earlier generation of the crystallography chip,^13,14 we have redesigned the surface morphology, fabrication sequence, and loading design. The new chip can host crystals regardless of their mother liquor composition and viscosity, and loading is no longer based on sedimentation of the crystals in large droplets of mother liquor.¹³ Background contributions from tape, mother liquor, and silica beads, and stacking of multiple crystals were the major limitations of the previous methodology. A further limitation of the previous chip design was that it was not general, as the surface chemistry had to be tuned for different crystal types. The new chip design presented here (Figure 1) uses turbulent liquid flow through arrays of apertures to attain random crystal orientations and, as such, is completely general.

FIG. 1.

New crystallography chip design. The upper left picture shows a 20 × 20 mm chip with a 9 × 9 array of compartments. Each compartment is an array of tapered holes (“features,” 12 × 12 in the depicted chip). Two of the features are shown in the bottom right picture at high magnification. The width of the features at the top surface of the chip and the feature opening (width of the hole at the bottom surface) are indicated by green arrows. The structures in the surroundings are due to surface roughness of the unpolished Si substrate. They are also responsible for the grainy appearance of the substrate at lower magnifications. The white stripes around the features are a result of the fabrication process that leads to a local change in surface reflectivity. Side view: cross-section (schematic) along a line through the centers of the features in one row or column of a compartment (only 6 features are drawn, the real number of features per row/column is variable).

The redesigned crystallography chip has 2300–180 000 features per matrix and can easily be fabricated with varying feature sizes, thus enabling us to accommodate a variety of crystal sizes and conditions. The chip contains an array of 81 (9 × 9) compartments, which are composed of 5–100 μm sized features. The number of features per compartment and the total number of features on a chip depend on the feature size (∼2300 for 100 μm to ∼180 000 for 10 μm features per chip with inter-block space bars of 1 mm to retain rigidity on a 2 cm format).

The feature shape and the crystal-loading mechanism depicted at the bottom left of Figure 1 are a key to low background diffraction data and the efficient loading of thousands of small single crystals on the chip. As the fabrication is based on photolithography, the position of the features and their openings are regular to better than 1 μm accuracy and this regularity can be exploited to enable high-throughput, serial, room temperature crystallography using high speed translation stages.

III. RESULTS

A. In situ structure determination using the rotation method

1. Comparison to regular in situ approaches

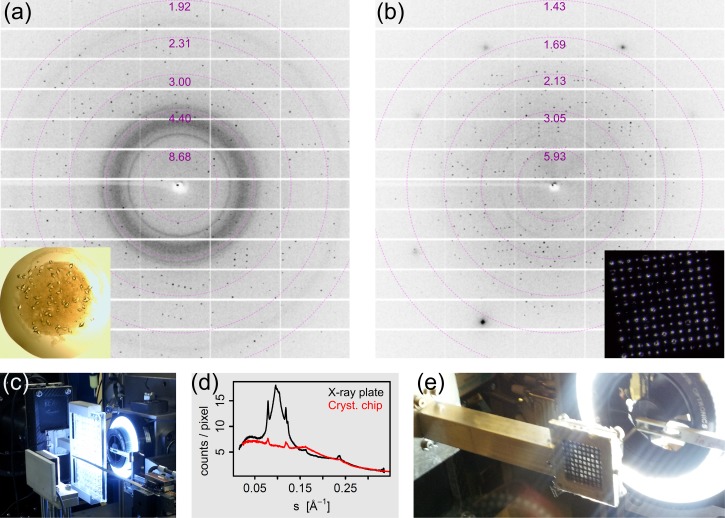
In Figure 2, we show a comparison of a commonly used in situ X-ray plate (Figure 2(a) or Figure 2(c)) and our chip (Figure 2(b) or Figure 2(e)). The crystallography chip is enclosed by a frame holder, which is sealed by two thin Mylar films. Background contributions from these films are negligible compared to the broad polymer rings appearing in data from the commercially available X-ray plates (cf. background around s = 0.1 Å⁻¹). Additionally, background contributions arising from the mother liquor and from precipitate forming throughout the crystallization droplet—both visible in the inset in Figure 2(a)—are heavily suppressed with this chip design (cf. rings at 0.08 and 0.12 Å⁻¹). The volume of mother liquor surrounding the crystals is also minimized as chips are loaded by applying a gentle pressure difference between the top and the bottom, driving the sample towards the bottom of the feature openings (see Figure 1 and Section VI for more details). Crystals are held within the tapered features without any further surface preparation. Undesired precipitate can easily be removed from the crystals by washing with mother liquor. It should be noted that the chemical composition or viscosity of the mother liquor has a negligible effect on the loading procedure. Background scattering from any source contributing to broad amorphous rings in the X-ray data is therefore minimized. If the beam and feature size are very similar, the wings of the X-ray beam may strike the silicon bulk of the chip. This situation results in clear diffraction spots, readily distinguishable from protein diffraction, rather than blurry amorphous rings (Figure 2(b)). Hence, the lower sample size limit for our approach is currently dictated by the X-ray beam size and the lithography based fabrication sequence of the crystallography chip. A comparison of room temperature data collected using the chip or the commercial in situ crystallography plate is given in Table I.

FIG. 2.

(a) X-ray diffraction pattern of a 40–50 μm T. daniellii thaumatin crystal located on a commercially available 96-well X-ray plate. The inset shows a photograph of the 1 μl crystallization droplet on the plate. (b) X-ray diffraction pattern of a 40–50 μm thaumatin crystal mounted on a crystallography chip with 50 μm sized features. The inset is a photograph of one compartment with 144 features at prescribed positions. The photograph in (c) shows the X-ray plate mounted at I24, Diamond Light Source. (d) Background scatter, radially averaged, as function of s = sinθ/λ. The photograph in (e) shows the crystallography chip mounted in its holder at beamline I24.

TABLE I.

Comparison of thaumatin diffraction obtained from a 1° wedge recorded using an X-ray plate or the crystallography chip.

	X-ray plate	Crystallography chip
Crystal parameters
Dominant size in sample (μm)	40–50	40–50
Feature width on chip (μm)	NA	50
Data collection
Rotation range: total, increment	1 deg, 0.1 deg	1 deg, 0.1 deg
Exposure time (seconds per image)	0.5	0.5
Number of images	10	10
Detector distance (mm)	399.28	271.31
Wavelength (Å)	0.9687	0.9687
Resolution, low (Å)	21.48	16.10
Resolution, high (Å)	1.51	1.55
Number of reflections	1779	2661
Number of reflections, unique	1741	2570
Completeness (%)	4.3	6.8
Multiplicity	1.022	1.035
Rmeas	0.144	0.043
⟨I/σ(I)⟩	25.0	22.20
Merging space group	P 4 2 2	P 4 2 2
Unit cell parameters: a = b, c (Å)	58.39, 151.09	58.37, 151.11

In addition to the reduction in background, it should also be noted that transfer and handling of the crystals from the crystallization plate to the chip matrix do not measurably affect the diffraction quality of the protein crystals tested so far (data not shown for all), for both soluble proteins (thaumatin, lysozyme, proteinase K, myoglobin, ferritin, and defluorinase) and membrane proteins (CorA, Mhp1). Maximum resolution and Bragg peak shape remain unchanged, indicating that our approach is a useful alternative to current in situ room temperature crystallography methods. Furthermore, the mother liquor can easily be exchanged during the process of crystal transfer, allowing manipulation of the molecular structure through variation of buffer conditions, in a similar way to that reported by Maire et al., who observed ligand exchange using an in situ X-ray plate.¹⁵ Our chip matrix approach is therefore suitable for the study of time-resolved reactions triggered by laser light or exchange of chemical environment, as well as determination of unknown protein structures, providing a broad platform for crystallography in different fields.

2. Crystal size and orientation

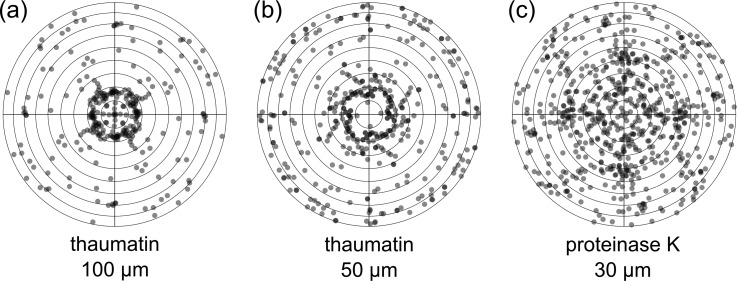
We investigated the impact of different crystal sizes on the performance of the chip and our loading protocol. Table II summarizes our findings for 100, 50, and 30 μm-sized crystals, which were loaded in the same fashion onto chips with matching feature sizes. In this initial work, we have used commercially available model systems, thaumatin and proteinase K (Sigma Aldrich). The diffraction images were automatically processed at beamline I24 with fast_dp,¹⁶ and afterwards the reduced datasets of the different crystals were merged using BLEND,¹⁷ a program using cluster analysis to generate an optimal, combined dataset (see Section VI for more information). In all cases, we were able to collect good quality, complete datasets. In order to further examine the distribution of crystals across a chip, an orientation analysis was carried out for thaumatin (100 and 50 μm in size) and 50 μm proteinase K crystals (Figure 3). This shows that diffraction data have indeed been collected from crystals in virtually all possible orientations. Certain orientations, however, do seem to occur more often than others, which is not surprising given the regular shape of crystals and the anisotropy of the features in the chip.

TABLE II.

Experimental specifications and data reduction/merging statistics for crystals of different sizes mounted in various crystallography chips. Values in parentheses are for the highest resolution shell.

Crystal type	Thaumatin	Thaumatin	Proteinase K
Experimental parameters
Dominant crystal size in sample (μm)a	100	40–50	30–40
Feature width on chip (μm)	100	50	30
Total number of shots (Nt)	114	188	183
Number of indexed datasets (Ni)b	76	110	173
Relative fill factor (Ni/Nt)	0.67	0.59	0.95
Data reduction/merging
Number of merged datasetsc	75	78	123
Space group	P41212	P41212	P43212
Cell parameters (Å): a = b, c	58.4, 150.9	58.4, 151.0	68.2, 103.6
Wavelength (Å)	0.96865	0.96865	0.96865
Resolution (Å)	29.18–2.12	29.15–2.18	29.27–2.07
	(2.18–2.12)	(2.25–2.18)	(2.13–2.07)
Rmerge	0.086 (0.108)	0.078 (0.185)	0.203 (0.278)
Rmeas	0.094 (0.117)	0.084 (0.198)	0.212 (0.289)
Rp.i.m.	0.036 (0.043)	0.028 (0.066)	0.058 (0.079)
⟨I/σ(I)⟩	32.2 (22.1)	28.5 (17.4)	24.3 (15.1)
Completeness (%)	97.5 (98.7)	99.6 (100.0)	100.0 (100.0)
Multiplicity	6.8 (7.0)	8.5 (8.8)	12.9 (13.1)
Mosaicity (average)	0.03	0.03	0.05

^aCrystal sizes were determined based on microscope measurements of the crystal solution. Values noted state the main sample size population.

^bNumber of data collections (“shots”) that produced diffraction images, which could be indexed by XDS during automatic processing with fast_dp.

^cNumber of datasets in the final cluster of datasets selected for merging on the basis of cluster analysis and ranking (by using BLEND).

FIG. 3.

(a) Overview of the orientation distribution of 100 μm thaumatin crystals (number of crystals n = 69), (b) 40–50 μm thaumatin crystals (n = 102), and (c) 30 μm proteinase K crystals (n = 165) mounted in crystallography chips of matching sizes (100, 50, and 30 μm features). The dots in transparent grey represent the beam directions relative to the crystal coordinate system in Lambert equal-area projection. Dark grey indicates overlap of two or more dots. The centers of the diagrams correspond to the tetragonal c axes, the outermost circle to directions in the a,b-plane. Each “observed” direction is replicated according to the point group (422) but, of all symmetry-related directions, only those pointing to the upper hemisphere are shown. In principle, three parameters are required to define the orientation of a crystal, but for the present purpose, the two angles shown in Figure 3 are sufficient. The third angle, representing rotation of the crystal around the beam direction, is superfluous as this parameter determines the orientation of the diffraction pattern in the detector plane, without changing the pattern itself. Figure prepared with R.³³

B. Ultra-fast structural dynamics by serial snapshots

1. Ratio method

Various strategies can be envisaged for time-resolved sampling of laser-induced structural changes using FEL X-ray pulses. Conceptually, the easiest way is to solve the structure quasi-statically for a series of time points defined by the delay between a laser “pump” pulse and an X-ray “probe” pulse. This approach is most expensive in terms of material, beam time, data storage space, and processing time. It requires acquisition of a huge number of partial reflection intensity data for every single time point, sufficient for statistical integration of full reflection intensities and their conversion to structure factors. In many cases, however, the structure of the initial state (ground state; before laser excitation) is known or can be determined with high accuracy by conventional methods. Furthermore, the structural changes are expected to be small, at least at short timescales. Thus, for ultra-fast time-resolved structure determination, it would be more appropriate to adopt a “difference method,” i.e., measuring intensity changes between the initial (dark, pump laser OFF) structure and the laser-induced (light, pump laser ON) structure of the same crystal in the same orientation. The fixed-target crystallography chip approach permits this strategy.

Using the known structure factors for the initial structure and the ratios, R(hkl), between reflection intensities measured before and after laser excitation, the structure factor amplitudes for the excited state can be calculated by F_hkl(laser ON, Δt) = F_hkl(ground state)R(hkl)^1/2. This “ratio method,” developed by Coppens et al.¹⁸ for small molecule crystals, and successfully applied to protein crystals by Schotte et al.,¹² should be much more efficient than the quasi-static approach, since it does not rely on the availability of integrated intensities from full reflections. The ratios, R(hkl) = I_rec(hkl; laser ON, Δt)/I_rec(hkl; laser OFF), can be calculated directly from the recorded (partial) intensities, I_rec, provided that these intensities are put on the same scale, and both images, ON and OFF, have been recorded under the same conditions. In principle, a single observation for every reflection should be sufficient. However, the ratio method puts high requirements on the stability of the experimental conditions and on the precision of the recorded intensities. More realistically, multiple observations must be acquired and averaged, and statistically evaluated as in conventional static structure determination.

2. Pump-probe experiment and data reduction

In order to test the suitability of the crystallography chip for differential detection measurements with FEL X-ray pulses, test diffraction data were collected at the LCLS, using a chip loaded with MbCO crystals (myoglobin bound with carbon monoxide) and a monochromatic X-ray beam reduced in intensity to less then 0.5% (on average) of the full pulse energy. Two diffraction images were recorded per chip feature, one for the ground state without laser excitation, and the second after a strong laser pulse sufficient for near 100% photolysis of the CO-Fe bond. Delay times ranged from −1 ps (probe before pump, as control) to 31.6 ps (for details see Section VI). The ground state diffraction pattern was accumulated from ten attenuated X-ray pulses in order to reduce the risk of beam-induced twitching of crystals and to increase the chance of collecting useful diffraction images, given the strong fluctuations of the X-ray pulse energies. Before calculating intensity ratios, laser ON and laser OFF diffraction images were scaled relative to each other by matching the total integrated reflection intensities.

Due to technical issues in detector readout and timing problems during the LCLS beam time, we were only able to collect a limited number of diffraction snapshots (2 × 2289 images, one dark and one light image per feature). This data acquisition period corresponded to only 8 min of error free operation yet still provided a significant amount of data, albeit insufficient to yield transient structures for given time steps. The information was, however, sufficient to clearly illustrate that photoinduced changes in structure are readily detectable with this approach (based on the photomodulation of a limited set of diffraction orders). All diffraction images were subjected to the same series of data analysis steps to eliminate the risk of losing useful data due to imperfect pre-filtering. The first step was to find diffraction spots and to determine the orientation of the crystals (see Section VI). For a small fraction of the ON/OFF pairs of images, spot finding and indexing was successful in the sense that both images, dark and light, could be indexed consistently. Only, these 42 image pairs were further processed and analyzed with regard to laser-induced intensity changes. An example difference diffraction pattern is shown in Figure 4. The main reasons for the small yield of useful patterns were the absence of bright spots due to small or missing crystals (indicating that the fill factor in loading the chip was lower than expected) and a high number of X-ray pulses with zero or close to zero intensities as part of normal operation of the LCLS, as well as non-ideal diffraction due to variable crystal quality, multiple crystals, or crystal fracture. Integration of the spot intensities from the 42 image pairs resulted in a dataset of 1747 reflections with partial intensities >3σ in both light and dark diffraction patterns, comprising all time delays, including control measurements (Table III).

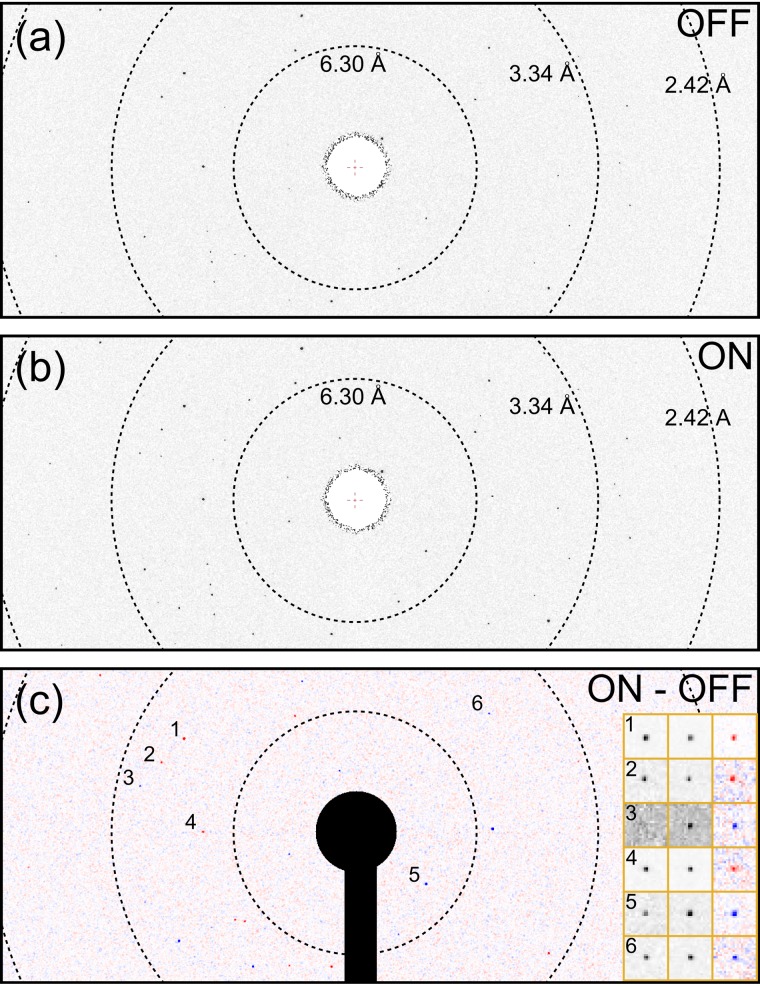
FIG. 4.

X-ray diffraction of a crystal of CO bound sperm whale myoglobin, SW-MbCO, (a) before and (b) after photoexcitation. The time delay was 0.9 ps. (c) is the difference pattern, (b)–(a), calculated after background subtraction and normalization for equal X-ray pulse energy. The inset in (c) shows the reference (OFF), pump-probe (ON), and difference diffraction (from left to right) in the vicinity of six reflections with higher magnification. Blue in the difference pattern is increasing, and red decreasing intensity relative to the reference.

TABLE III.

Numbers of reflections recorded in diffraction snapshots of MbCO crystals, grouped by resolution, and Z_I cutoff. Z_I = I/σ(I), with I and σ(I) recorded spot intensities and their estimated standard errors, respectively. Only reflections observed and indexed with XDS are counted, irrespective of the delay time (including controls) and the degree of partiality.

Resolution (Å)		Uniques possible	ON images			OFF images			ON and OFF
d.max	d.min	N	ZI > 3	ZI > 5	ZI > 10	ZI > 3	ZI > 5	ZI > 10	ZI > 3	ZI > 5	ZI > 10
19.77	3.44	2976	1706	1289	774	1268	879	438	1199	827	418
3.44	2.72	2975	688	403	182	416	197	62	389	185	61
2.72	2.38	2976	290	138	42	125	47	10	114	44	9
2.38	2.16	2975	142	64	13	43	14	2	37	14	2
2.16	2.00	2975	42	15	3	10	1	0	8	1	0
19.77	2.00	14 877	2868	1909	1014	1862	1138	512	1747	1071	490

3. Data screening and resolution of indexing ambiguity

Common indicators of data quality, like R_sym or R_merge, are not appropriate for the limited dataset reported here for the MbCO crystals. Statistical analysis is hampered by: (1) the fact that all observed intensities are “partials”; (2) the reflection indices are not defined uniquely; (3) the recorded data belong to different time points; and (4) by the overall scarcity of the data. With respect to this latter point, it should be born in mind that all the data presented were collected within only 8.3 min.

Reflection indices are not uniquely determined because of the hemihedry of space group P6, which leads to a two-fold ambiguity, even if all reflection indices are reduced to symmetrically equivalent, unique Miller indices. This ambiguity cannot be resolved easily by analyzing individual diffraction patterns and poses a general problem for serial crystallography and whenever data from different crystals have to be combined.¹⁹ In the present case, as the ground state structure (reference structure) is known, the ambiguity can be removed by comparing the observed reflection intensities with those expected from the reference structure, given the two possible orientations of the crystal. To this end, the diffraction of XFEL pulses was modeled in a kinematical approximation, using cell parameters, crystal orientation, mosaicity, beam divergence, and energy bandwidth as parameters. These parameters were optimized by least squares fitting of the calculated spot intensities to the recorded ones. Structure factors determined by Carver et al.,²⁰ protein data bank (PDB) entry 2SPL, served as the reference. The angular spread of mosaic blocks was described by a two-parameter Pearson type VII distribution, while beam divergence and bandwidth were assumed to be top-hat distributed. These distributions yielded slightly better results than computationally more efficient normal distributions. From the two possible indexing schemes, the one that is most consistent with the reference could be identified unambiguously by means of the residual sum of squares (RSS) for most diffraction patterns. However, 6 image pairs were rejected because no clear distinction between the two possibilities could be made on the basis of the RSS values and the plausibility of the fitted parameters.

4. Statistical distribution of intensity changes

The data collected from the remaining 36 crystals comprised of 920 observed reflections (ON-OFF pairs) with I/σ(I) > 5 in the resolution range from 19.8 to 2 Å (high resolution cutoff). These reflections came from 3 control measurements (set delay of −1 ps) and 33 pump-probe measurements with delays in the range from 200 fs to 32 ps, sampled at more than 10 significantly different time points if the timing jitter is taken into account (see Section VI).

The obvious way to assess the quality of the final data, i.e., the intensity ratio, R, consists of averaging equivalent ratios and analyzing the corresponding uncertainties using merging statistics similar to those commonly used for intensity data. However, in this case, the virtual absence of symmetry- and time-equivalent observations is prohibitive for this type of statistical analysis. Therefore, in order to show that the observed intensity changes are significant and can be attributed to light-induced structural dynamics, the variance and distribution of the intensity changes in real pump–probe measurements (Δt > 0) were compared with those in the control measurements (Δt < 0).

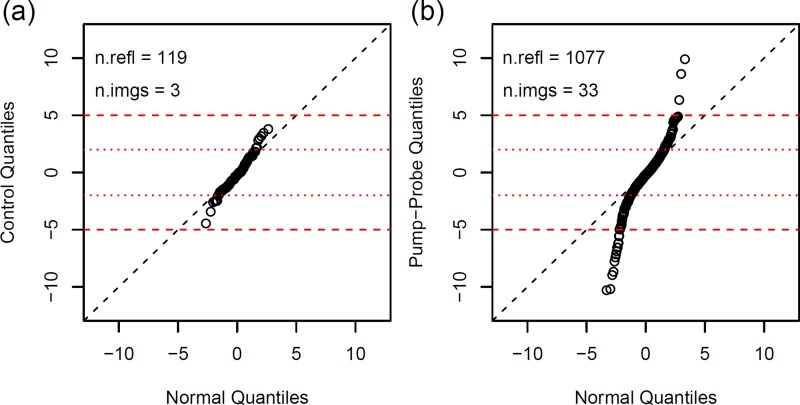
If I_ON and I_OFF are considered as random variables, the distribution of the ratio R = I_ON/I_OFF is nontrivial, in general, even for simple (e.g., Gaussian) distributions of I_ON and I_OFF. Therefore, the differences D = I_ON − I_OFF and their standardized versions Z_D = D/σ(D) with σ(D)² = σ(I_ON)² + σ(I_OFF)² were considered instead of the ratios R. Here, the σ values are the individual standard errors of the recorded intensities (scaled). Figure 5 shows that the variance of Z_D values obtained from the pump–probe data is significantly larger than that from the control data. The two distributions are clearly different, indicating that a substantial fraction of the observed intensity changes must be caused by laser-induced structural dynamics. In addition, the much lower variance of the control data indicates that our data collection protocol did not result in the accumulation of significant radiation damage during the accumulation of the OFF image.

FIG. 5.

Distributions of standardized intensity differences, Z_D. Quantile–quantile plots comparing the distribution of Z_D values for control data (a) and pump–probe data (b) with the standard normal distribution N(0, 1). The control data are almost normally distributed. Most of the intensity differences are within ±2σ from zero (dotted red lines), showing that the differences measured in control experiments are mainly due to counting statistics. Only a minor portion of the differences may be attributed to experimental instabilities (leading to systematic errors not included in the σ values) as indicated by the small deviation from the diagonal. By contrast, Z_D values for pump–probe data (b) are random samples from a much broader distribution with observations up to 10σ, as expected if the variance is dominated by light-induced changes of the crystal structure. Only reflections with recorded intensities >5σ have been used for the quantile–quantile plot. Figure prepared with R.³³

IV. DISCUSSION

The crystallography chip approach combines the advantages of serial crystallography with those of single crystal crystallography. In particular, it allows repeated measurements of the same crystal, essential for differential detection time-resolved measurements, and provides sufficiently random crystal orientations with minimum sample consumption. This opens up new possibilities for static and time-dependent structure analysis of bio-macromolecules, promising efficient use of valuable sample material and beam time, thus facilitating challenging, or seemingly impossible experiments.

A. In situ structure determination with synchrotron radiation

The primary advantage of the crystallography chip is that crystals are mounted on the chip in known positions and thus can be readily probed by the X-ray beam in an automated manner. In contrast, in continuous jet approaches and on commercially available X-ray plates, a large fraction of crystals are either not probed^6,21 or must be aligned manually. In the case of small protein crystals, from which it is not possible to obtain complete diffraction datasets, a single chip can be loaded and data completion can be achieved by merging data from many different crystals. In comparison to other sample preparation methods, all data can be acquired using a single chip without the need for time-consuming centering of individual crystals, but rather by rapid translation from one crystal to the next in a fully automated process. A variety of protein crystal sizes can be handled, highlighting again the broad application range of the crystallography chip. High throughput and high hit-rate serial crystallography based on a fixed target, as needed for ultrafast and high-power X-ray studies, thus becomes readily available. This approach will make optimal use of beam time and effectively make more beam time available for other studies.

Our shot efficiency has reached at least 50% (where shot efficiency is defined as the number of successfully processed datasets compared to the overall addressed features). This is largely due to the predefined location of the crystals in the chip. In the experiments described here, we followed a serial approach, addressing every feature in a compartment. Based on the shot efficiency, we can conclude that the fill factor on our chip was >50%. A fully filled chip may seem ideal, but this is not necessarily true: a high fill factor is likely to result in the stacking of multiple crystals within the features. For an ideal experiment, a fine balance of the optimal fill factor will be crucial. In the future, we plan to map the loaded chip prior to introduction to the X-ray beam such that, with an appropriate fiducial system, we can expect to achieve 100% hit rates even with low fill factors.

B. Femto-second structural dynamics by serial snapshot crystallography

In order to demonstrate the applicability of the crystallography chip for time-resolved XFEL experiments, time-dependent diffraction data were collected at the LCLS in the range from 200 fs to 32 ps probing the dynamics of CO dissociation from MbCO crystals. Though these data are far from complete, they serve to test the possible application of the chip approach for ultrafast time-resolved serial crystallography. That a large number of crystals can be directed automatically and with high reliability to the point of interaction is a major advantage of the crystallography chip over jet-based approaches, whose effectiveness is based on statistics. This ability to look at many oriented crystals automatically should be beneficial not only for structure determination, in general, but also for time-resolved studies, even if the most direct strategy is applied: solving the time-dependent structure for each time point individually. For the liquid jet method, this is the only available strategy, and it has been shown to be practicable only recently.^11,22

The fact that the chip approach allows multiple exposures of the same crystal can be exploited in pump–probe experiments to acquire diffraction images before and after laser excitation. In this way, changes in reflection intensities can be measured, which can be used to calculate time-dependent structure factors by following the ratio method.¹⁸ The ratio method is highly demanding in terms of stability and reproducibility of experimental parameters for laser ON and laser OFF measurements. In addition, photo-induced excitation of the crystals should be both homogeneous and as high as possible. This favors the use of small crystals, which in turn requires high X-ray intensities in order to increase the signal-to-noise ratio. High X-ray intensities, however, increase the risk of crystal twitching and radiation damage.

From the results of the pump–probe measurements (Figure 5), there is no doubt that intensity ratios can be measured with the crystallography chip, at least for reflections that are both strong and highly sensitive to light-induced structural changes. The number of observations collected so far is very limited, especially at resolutions better than 3 Å (cf. Table III). However, there is no reason to suspect that the numbers in Table III would be much different if all data had been taken at the same time point. Thus, these numbers can be used to estimate how many shots are needed per time point to collect sufficient data. Even without any further improvements, taking diffraction snapshots from 10 chips, all at the same time delay instead of the 10 different time delays in the present experiment would increase the number of data attainable for the given time delay in ∼80 min by a factor of 100. This would result in ∼100 000 strong reflections (I/σ(I) > 5) measured in the lower resolution range up to 2.7 Å, compared to ∼6000 unique reflections (including weak and strong). The average redundancy (∼17) would still be an order of magnitude lower than what is usually required for serial crystallography based on statistical integration of Bragg reflection.²³ Even so, it will be possible to calculate averaged intensity ratios and their figures of merit, at least for a substantial fraction of reflections. These data should be sufficient—if not for solving the structure right away—at least for refining model parameters derived from molecular dynamics simulation. It should also be noted that the number of useful observations will de facto increase above proportionality when a larger statistical basis is available. The reflections counted in Table III are only the clearly identified and trusted ones. Rather strict rules were applied to reject untrusted measurements due to the lack of any internal reliability test.

The shot efficiency of the pump–probe experiment was in the low percent region, much smaller than that attained in the static experiments. A certain reduction in shot efficiency is inevitable, since the success rate in the pump–probe experiment corresponds to the joint probability of successful ON and OFF diffraction. However, the small yield seen here is most likely due to a less than optimal loading of the chip. Improving the chip loading process, which ideally should be optimized for every preparation of protein crystals, is expected to increase the number of observations by a factor on the order of 10.

V. SUMMARY

In summary, the crystallography chip described here can help to overcome the restrictions in sample preparation and mounting that have limited the applicability of high-power and ultrafast pulsed X-ray sources to date. The chip design enables the exploration of functionally relevant protein motions involved in barrier crossings in time-resolved experiments that utilize the full brightness and spatiotemporal resolution of recently developed XFEL sources. Although the limited data collection time did not allow for sufficient collection of differential changes in Bragg reflections to determine the structural changes, this work demonstrates that it is possible to observe structure factor changes on the femtosecond time scale using differential detection. Even with this limited data set, there are clearly changes occurring on the sub-picosecond time scale that, with additional data, should be readily resolved structurally. We also show that the chip is useful on microfocus beam lines for high throughput serial crystallography of static crystal structures under room temperature conditions.

VI. MATERIALS AND METHODS

A. Fabrication of the crystallography chip

The procedure is described in detail by Mueller.¹³ In brief, we purchased single side polished silicon wafers, Si (100), 300–320 μm thick at WRS Materials, which were subsequently coated with 50 nm Low Pressure enhanced Chemical Vapour Deposition (LPCVD) silicon nitride on each side (Rogue Valley Microdevices). Following conventional photolithography, we patterned the backside of the chip first and removed the silicon nitride using SF₆/O₂ plasma etching. Subsequently, the silicon was thinned to a remaining thickness of 20–70 μm using KOH/isopropanol (40% (v/v) at 70 °C) wet etching. We then patterned the front side with the features later hosting the protein crystals. The feature sizes range from 5 to 100 μm and are always chosen to be square, forming regular blocks of features on the chip. The features are imprinted into the silicon wafer again using SF₆/O₂ plasma etching. A feature depth of 5–45 μm is achieved by this anisotropic dry etching step. An additional isotropic KOH/isopropanol (40% (v/v) at 50 °C) etch of the front side causes the squared features to be tapered along the Si(111) plane, with an angle of 54.7°. In a final step, the cone shaped features are opened from the backside of the chip, again using KOH/isopropanol (40% (v/v) at R.T.) wet etching.

B. Crystallization

Thaumatin from Thaumatococcus daniellii was purchased from Sigma Aldrich and dissolved to a final concentration of 50 mg/ml in a buffer of 100 mM 2-(N-morpholino)ethanesulfonic acid at pH 7. Crystallization was performed at 18 °C using the hanging drop method and sodium potassium tartrate (24% w/v) in the same buffer as precipitant.

Proteinase K from Tritirachium album was purchased from Sigma Aldrich and dissolved to a final concentration of 20 mg/ml in a buffer solution of 100 mM 2-(N-morpholino)ethanesulfonic acid at pH 6.2–6.3. Crystallization was performed at 18 °C using the hanging drop method and 0.80–1M ammonium sulphate in the same buffer as precipitant.

Recombinant wild-type sperm whale (Physeter catodon) myoglobin (SW-Mb) with the D122N mutation was expressed in the Escherichia coli strain BL21(DE3), and the protein was purified as described previously.^24,25 SW-Mb crystals were grown in concentrated ammonium sulfate following a protocol similar to the one described by Phillips et al.²⁶ To ensure that the SW-Mb crystals were grown in the reduced CO bound form (SW-MbCO), all purification and crystallization buffers were saturated with 1 atm of CO gas. The SW-MbCO crystals were grown in 3 ml Monoject Blood Collection Tubes (Covidien, Mansfield, MA) prefilled with gaseous CO. 250 μl of crystallization solution containing 40–50 mg/ml protein in 20 mM Tris-HCl pH 9.0 and 2.2–2.5M ammonium sulfate were added to the CO-filled tubes. Seeding was used to promote nucleation of a large numbers of small crystals. Pre-grown, large P6 SW-MbCO crystals were crushed in mother liquor containing 20 mM TrisHCl, 3.2M ammonium sulfate at pH 9.0 and then added to the tubes containing the concentrated myoglobin. The size of the final crystals was controlled by varying the dilution of the seed solution. This method produces crystals of appropriate sizes corresponding to the chip parameters as described previously.^14,27

C. Crystal harvesting and loading of the crystallography chip

The feature size of the chip was deliberately made to optimally isolate crystals of 30–60 μm in diameter. The feature size can be made from submicron to >100 μm as needed for a particular application. In all cases, smaller crystals than the feature size can still be harvested from the filtrate, and the larger crystals can be recovered by flushing the chip with mother liquor and collecting these crystals after loading. These features allow optimal use of the crystals.

Crystals of thaumatin and proteinase K crystals were harvested using 200 μl pipette tips. First, we added ∼10 μl of the precipitation solution to the droplet containing the crystals and mixed gently. The crystals were then transferred into 200 μl vials to be stored until application to the crystallography chip. Before application to the crystallography chip, the dense crystal suspensions were diluted with mother liquor to ∼50 μl volume. The crystals were gently applied to the chip and washed with a small amount of mother liquor before the loaded chip was transferred into the holder, sealed with Mylar film, and clamped shut. Further details of the procedure can be found in Ref. 13.

For pump–probe measurements on crystals of SW-MbCO, the chip was equilibrated with mother liquor saturated with gaseous CO, and 200–400 μl of the crystal suspension was pipetted onto the surface of the chip. A vacuum pump was used to generate a slightly reduced pressure below the chip to drive crystals into the features by pulling the solution through the holes. Mylar film was directly applied to the surface of the chip to prevent O₂ displacement of the CO from the Mb crystals and to prevent water loss and subsequent formation of ammonium sulfate crystals.

D. Data acquisition and analysis

1. Static diffraction data collected with rotation method using synchrotron radiation

Diffraction data from thaumatin and proteinase K crystals were acquired at the microfocus beamline I24 at Diamond Light Source (United Kingdom). We used a beam of 10 × 10 μm at an X-ray energy of 12.8 keV, 0.9686 Å. Each crystal was exposed for 500 ms with a total rotation of 1° or 2° in slices of 0.1° (10 or 20 frames per crystal). Data acquisition was performed at room temperature with a Pilatus3 6M detector at detector distances of 272 or 400 mm.

2. Time-resolved diffraction recorded with XFEL pulses

Time-resolved pump–probe data from SW-MbCO were collected at beamline XPP of the Linac Coherent Light Source (LCLS, California USA) at a nominal X-ray energy of 8.1 keV, 1.53 Å. X-ray pulses of 36 fs duration (FWHM) at a rate of 120 per second were energy-filtered with a Si(111) monochromator (ΔE/E ≈ 1.4 × 10⁻⁴). The beam was focused to about 10 μm at the sample. Diffraction images were recorded with a Rayonix MX170-HS detector at 70 mm distance from the chip. Within a total time of about 8 min, 109 × 21 = 2289 features of a single chip loaded with MbCO crystals were scanned through the beam focus. Two diffraction images were recorded for each feature, a “dark” image without laser excitation and a “light” image with a strong laser pump pulse (540 nm, 2.5 mJ/mm² at the sample, resulting in close to 100% excitation) preceding the X-ray probe at various time delays (sequence of set values: −1 ps [control], 0 [10×], 178 fs, 386 fs, 562 fs, 1 ps, 1.78 ps, 3.16 ps, 5.62 ps, 10 ps, 17.8 ps, and 31.6 ps). The exact time delays, as measured with the timing diagnostics tool,²⁸ differed from the set values by random corrections (jitter, s.d. = 0.09 ps) and a constant offset of 0.38 ps. Due to energy filtering and the spectral fluctuations of SASE (self-amplified spontaneous emission) XFEL pulses, the X-ray pulse energies displayed a high variance, including a large fraction (ca. 10%) of pulses with zero intensities. Dark images were obtained by accumulation of 10 pulses, each reduced in intensity by a factor of ∼10 using a fast attenuator. The light images were recorded with a single, unattenuated X-ray pulse.

E. Data analysis

1. Static diffraction of synchrotron radiation

Wedges of diffraction images recorded at beamline I24 (Diamond Light Source) from individual crystals on the crystallography chips were automatically processed at the beamline with fast_dp and xia2,^16,29 two data reduction pipelines based on crystallographic software packages CCP4³⁰ and XDS.³¹ Crystal orientations as determined by XDS during the fast_dp runs (if successful) were collected from the XPARM.XDS files and checked for plausibility by comparing the predicted cell parameters with values from the PDB. For each dataset that passed this test, the direction of the incident beam relative to the crystal coordinate system can be represented as a point at the unit sphere around the origin. Figure 3 shows the distribution of beam directions in Lambert azimuthal equal-area projection. An equal distribution of points in the Lambert projection would signify complete randomness of crystal orientations, except for a potential (but irrelevant) uneven distribution of the rotations around the incident beam. The reduced datasets from successful fast_dp runs were merged with BLEND,¹⁷ a program especially designed for the optimal combination of multiple partial datasets, using AIMLESS and POINTLESS³² of the CCP4 program suite. Proteinase K datasets exhibited a wide range of mosaicities, between 0.02 and 0.64. Only datasets with mosaicities <0.1 (i.e., 123 out of 173) were accepted for processing with BLEND. Statistics of the merged and scaled data are reported in Tables I and II.

2. Time-resolved diffraction of XFEL pulses

Snapshot diffraction images from pump–probe experiments at the LCLS were analyzed for intensity changes due to molecular motions induced by laser excitation. All images were processed with XDS to find and index diffraction spots (if present) using space group symmetry P6 and cell parameters from the PDB (2SPL²⁰). Since XDS has been designed for the rotation method, it cannot be used for indexing and integration of still images as such. In order to circumvent this limitation, the still images were treated as pseudo-rotation images by assuming a small (virtual) rotation angle of 0.1°. Integrated intensities calculated in this way are meaningless, indexing, and crystal orientation, however, should not be affected (within a fraction of 1°). To make sure that the reflection indices were correct, every diffraction image was processed twice, with the rotation axis horizontal and vertical. This resulted in 193 and 199 indexed images, respectively. Of these, 173 images were indexed in both runs and used for further analysis. All of them were indexed consistently, i.e., reflection indices assigned in both XDS runs were identical except for symmetry equivalence and indexing ambiguity of merohedral space group P6.

The final set of images that could be indexed consistently was composed of 57 dark (laser OFF) and 116 light (laser ON) images. This imbalance can be explained by the fact that OFF diffraction patterns were weaker by a factor of almost 2 (on average) than ON images, indicating that attenuation of X-ray pulses for dark images was not compensated for entirely by accumulation of 10 pulses due to large stochastic fluctuations in the beam intensity. As a result, intensity changes could be determined for only the 45 crystals with both images, ON and OFF, indexed successfully. Three crystals were rejected because of relatively large differences in the orientation parameters, which could be indicative of crystal twitching or beam instabilities, possibly distorting the results. Thus, the number of crystals (ON/OFF image pairs) amenable to further analysis was reduced to 42. Background corrected spot intensities and σ values were calculated for the predicted spot positions, using intermediate results of the XDS runs provided by the output of the INTEGRATE step.