A liquid flatjet system for solution phase soft-x-ray spectroscopy

Abstract

We present a liquid flatjet system for solution phase soft-x-ray spectroscopy. The flatjet set-up utilises the phenomenon of formation of stable liquid sheets upon collision of two identical laminar jets. Colliding the two single water jets, coming out of the nozzles with 50 μm orifices, under an impact angle of 48° leads to double sheet formation, of which the first sheet is 4.6 mm long and 1.0 mm wide. The liquid flatjet operates fully functional under vacuum conditions (<10⁻³ mbar), allowing soft-x-ray spectroscopy of aqueous solutions in transmission mode. We analyse the liquid water flatjet thickness under atmospheric pressure using interferomeric or mid-infrared transmission measurements and under vacuum conditions by measuring the absorbance of the O K-edge of water in transmission, and comparing our results with previously published data obtained with standing cells with Si₃N₄ membrane windows. The thickness of the first liquid sheet is found to vary between 1.4–3 μm, depending on the transverse and longitudinal position in the liquid sheet. We observe that the derived thickness is of similar magnitude under 1 bar and under vacuum conditions. A catcher unit facilitates the recycling of the solutions, allowing measurements on small sample volumes (∼10 ml). We demonstrate the applicability of this approach by presenting measurements on the N K-edge of aqueous NH₄⁺. Our results suggest the high potential of using liquid flatjets in steady-state and time-resolved studies in the soft-x-ray regime.

I. INTRODUCTION

Recent progress in soft-x-ray spectroscopy has enabled key insight into the local molecular interactions in neat liquids and in solutions. In particular, photoelectron spectroscopy,^1–13 x-ray absorption spectroscopy (XAS),^14–21 and resonant inelastic x-ray scattering (RIXS)^4,22–27 have been used to study neat liquid water, alcohols, and aqueous solutions. The development of ultrafast x-ray spectroscopic methods has opened new frontiers in ultrafast molecular science.^28–37 Among the various detection schemes for soft x-ray spectroscopy, the transmission mode is the most direct way of recording a soft x-ray absorption spectrum. For such experiments, however, it is necessary to probe samples with limited thicknesses, i.e., from submicrometer to a few micrometer range, dictated by the cross sections of the investigated molecular compounds in the soft-x-ray spectral range.³⁸

Use of thin sample cells with window consisting of Si₃N₄ (Refs. 31, 39–41) or SiC (Refs. 42 and 43) membranes enables, in principle, a direct control of sample thickness while remaining under normal pressure conditions. The advantages lie in the limited amount of sample needed, and the potential versatility in probing a large variety of samples, e.g., liquids, solutions, or molecular films. Numerous steady-state x-ray spectroscopic studies have now been reported using this approach.^40,43 Sample cells with Si₃N₄ windows have also been used in time-resolved studies of liquid water after excitation of the O-H stretching band,^44–47 or after optical excitation of molecular systems in solution.³¹ Even though nanofluidic cells can be designed to allow for liquid flow,⁴⁸ to date, no reports have been published on using such a design for (transient) soft-x-ray absorption spectroscopy in the transmission mode fully exploiting a sample flow fast enough to guarantee sample replacement between applied laser shots. Possible issues with sample degradation upon x-ray illumination (or upon pump laser illumination when pump pulses tuned in the ultraviolet or visible spectral range are used in time-resolved experiments) make this approach disadvantageous for photolabile molecular systems.

To guarantee a continuous replacement of liquid samples and to eliminate the potential influence of cell membranes affecting the measured signals, the use of a liquid jet with micrometer thickness is an attractive alternative for soft-x-ray absorption spectroscopy. Pumping a liquid through a nozzle with a small orifice diameter into the vacuum chamber and subsequently collecting it in a cold trap, or disposing it using a pump, warrants the vacuum conditions necessary for soft-x-ray spectroscopy. For XAS experiments in transmission mode, however, cylindrical jets with thicknesses of typically 6 μm to 50 μm cannot be applied because these thicknesses are too large compared to typical attenuation lengths of soft x-rays in liquids.

Free falling flatjets generated by pumping dye solutions through slit nozzles have been used for decades in dye laser systems,^49,50 and wire-guided gravity-driven jets have also been utilized as applications in high repetition-rate spectroscopy.⁵¹ These approaches have resulted in liquid sheets with several mm diameter and thicknesses clearly larger than 3 μm. We present here results on the implementation of a liquid flatjet with a thickness in the μm range, for XAS transmission measurements in the soft-x-ray regime. Obliquely colliding two identical laminar jets, the liquid expands radially, generating a sheet in the form of a leaf, bounded by a thicker rim, orthogonal to the plane of the impinging jets.^52–54 A fluid chain consisting of mutually orthogonal multiple sheets can be observed, and each subsequent link decreases in size until the chain merges into a single jet. Rayleigh-Plateau instabilities^55–57 of the rim cause the last link to break-up into droplets.

Whereas the formation of liquid sheets by collision of two jets under ambient conditions is well reported,⁵⁸ we present here the first demonstration of a liquid flatjet, fully operational under vacuum conditions. A catcher collects the liquid flatjet to enable an efficient transport out of the vacuum chamber, and by use of a recycle pump, it has become possible to use smaller volumes of solution. The liquid flatjet system is a versatile tool working with high stability under vacuum conditions (<10⁻³ mbar), opening up a new frontier of solution phase soft-x-ray spectroscopy with an easy implementation of time-resolved soft-x-ray experiments.

II. EXPERIMENTAL FLATJET SET-UP

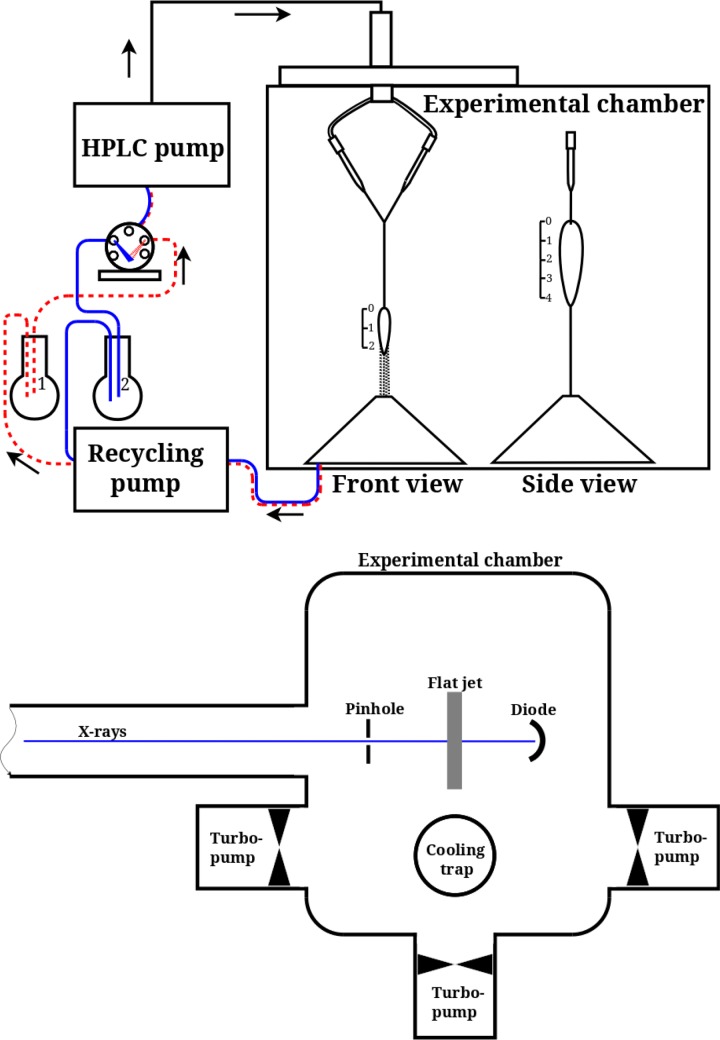
Figure 1(a) shows the general outline of the liquid flatjet system (Microliquids GmbH, Göttingen). A liquid solution is directed at room temperature by a pump, typically used in high performance liquid chromatography (HPLC), towards the vacuum chamber. The flow rate is set in the range from 5.8 to 6.2 ml/min for nozzles with 50 μm diameter. In order to minimize pulsations in a sample flow caused by the pump piston, a sequence of the capillaries made of polyether ether ketone (PEEK) with different inner diameters is used, placed in the order with increasing diameter. The capillary set serves as a kind of pulse damper, to ensure a more uniform flow. The liquid flow is divided into two equal arms and pumped through equal nozzles with 50 μm diameter positioned inside the vacuum chamber (Figure 1(b); <10⁻³ mbar working pressures). The resulting single laminar liquid jets obliquely collide under an angle of 2α = 48°. Such an approach is known to form a fluid chain which often consists of a succession of mutually orthogonal links, each composed of a thin oval film bound by relatively thick fluid rims.^55–57 In our case, the collision of the two single jets leads to the formation of two liquid sheets oriented orthogonally (Figure 2(a)). The second leaf is dipped into the catcher (not shown in Figure 2(a)) to enable collection of the liquid and pumping it out of the vacuum chamber. The beam catcher principle is utilized to pass the sheet-constriction neck through a small (∼400 μm diameter) orifice into a separate vacuum region where the jet waste is collected in liquid form at a vapour pressure >8–19 mbar.⁵⁹ The reverse gas flow through the 400 μm orifice is then of the order of 10⁻² to 10⁻¹ mbar l/s only. This can be pumped readily by the main vacuum chamber pumps and contributes to less than 10⁻⁵ mbar of pressure rise in the working vacuum. Using a peristaltic recycle pump (Lambda CZ, MaxiFlow), the liquid jet debris from the beam catcher are pumped back to an atmospheric pressure reservoir, thereby enabling the recycling.

FIG. 1.

Liquid flatjet system used for solution phase soft-x-ray absorption spectroscopy, consisting of an HPLC pump, directing the liquid solution from a reservoir to two nozzles placed in a vacuum chamber, resulting in two single laminar jets with 50 μm thickness obliquely colliding under an angle of 2α = 48°. The colliding jet geometry is shown from two orthogonal directions, showing the formation of two flatjet sheets with planes orthogonal to each other. The scaling is in mm units. The liquid jet is then directed to a catcher unit and recycled back to a solution reservoir. The vacuum chamber used in the UE52-SGM beamline, equipped with differential pumping,³⁴ is depicted underneath. For further details, see the text.

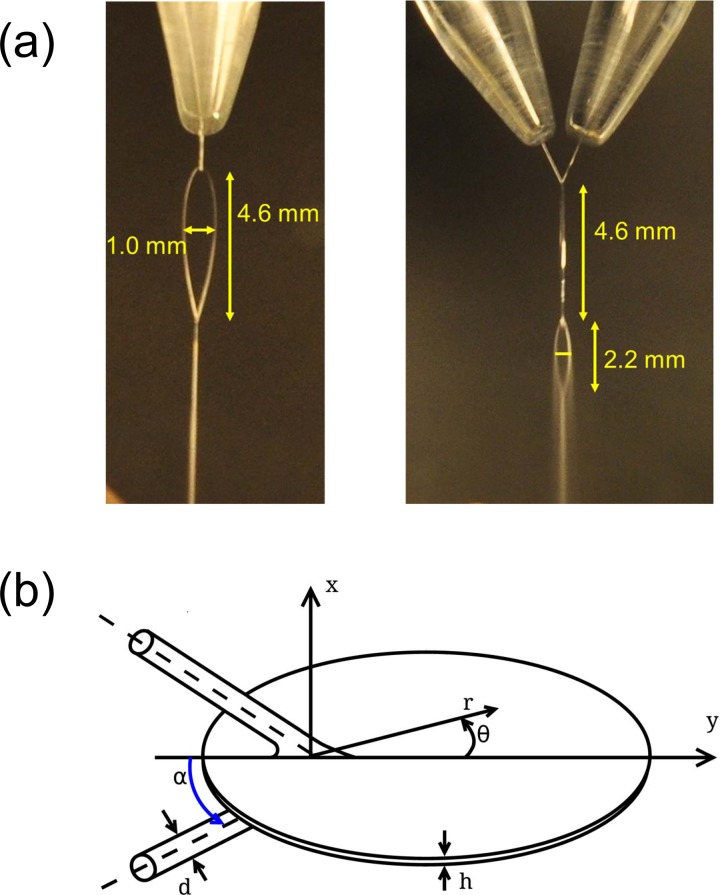
FIG. 2.

(a) Photo of the liquid flatjet taken from two orthogonal directions, showing the formation of a stable first sheet, as well as the second sheet exhibiting the onset of formation of small droplets. (b) Sketch of the flatjet with parameters as defined in Eq. (1). The x-direction indicates the transverse spatial extension of the first liquid sheet, the y-direction points to the flow direction of the flatjet, whereas the z-direction indicates, together with the flow direction, the plane of the two colliding single jets.

The flat liquid jet with elliptical sheet formation, used here for its shape with jet contraction at the end point flow region, is stable only in a narrow range of flow conditions. For our implemented setup with two 50 μm single jets colliding with 48° collision angle at 0.8 mm distance from the nozzle exits, the optimum flat sheet stability is obtained at a liquid flow rate between 5.7 and 6 ml/min. This is judged visibly from the appearance of a second and a third smaller flow sheet in the flow contraction region. The ellipse flow stability limits are reached when the ellipse-like sheet structure disappears completely, or the jet starts to disintegrate before it can form a first contraction. These are observed at a flow minimum of 3.9 ml/min and a maximum of 7.2 ml/ min, respectively. These flow limits vary strongly with the jet pair nozzle diameter and the intersection angle, as we have concluded from a not yet systematically investigated fashion.

At optimum stability settings, the jet thickness signal of the interferometric sensor readings vary over 0.5–1.0 μm when measuring near the center of the ellipse pattern over time periods from 5 min to 20 min of operation in quiet air and at stable temperatures of 20 °C. We have observed that, when after a flat area thickness profile scan we returned to the center starting point after more than an hour, the thickness and the scan profile track coincided within 0.1 μm variation with the initially measured track. The reproducibility of the interferometric method on the liquid flatjet is also illustrated in Figure SI-1 in the supplementary material,⁶⁰ where measurements made with an interval of 18 months are compared.

In Figure SI-2 and associated slide show in the supplementary material,⁶⁰ we show the snapshots of the flatjet taken over the course of an hour to demonstrate the long-time stability. A further illustration for the optical smoothness of the flat jet oval area is shown in the short video record of the liquid sheet, added as Figure SI-3 and associated movie in the supplementary material.⁶⁰ The optical inspection shows that the flowing film surface is flat with optical quality. At the jet boundary, only slight transient variations can be noticed, which appear in response to minimal irregularities in the fluid supply pump operation.

In vacuum environment, the jet thickness profiles have not been measured yet with the optical interferometry device, because this will require considerable technical effort. We note that at an HPLC pump flow rate of 5.8 ml/min, the first sheet has dimensions of 4.6 mm in length and 1.0 mm in width, whereas the second sheet is 2.2 mm long and 0.5 mm wide. Decreasing the HPLC pump flow rate by 10% leads to a length reduction of about 5%. Going to vacuum (10⁻³ mbar or better) also leads to a reduction in length of about 5%. From the small change of the geometrical shape of the flatjet sheet and from the measured vacuum evaporation loss of 5% of liquid during one vacuum passage, we can conclude that the liquid sheet thickness in vacuum is decreasing by 5%, at maximum, i.e., near the end point of the evaporating flat sheet structure.

The second sheet often shows signs of droplet formation, suggesting the onset of reaching the regime of fragmentation and formation of more evolved liquid structures such as the fishbone instability.^55–57 For our purposes of transmission mode soft x-ray absorption spectroscopy, however, the flatjet stability and dimensions, under vacuum conditions, are a more important objective than the formation of an extended fluid chain with multiple liquid sheets. In particular, a sheet stable in diameter and thickness for extended periods of time of up to hours is the pre-requisite for a successful implementation of such a flatjet system in soft-x-ray spectroscopic measurements. Operating the flatjet in high vacuum, we determined the evaporation rate by measuring the weight loss of the fluid in the recirculation reservoir to be 18 g of water vapour in 1 h, equivalent to a water vapour gas load in the main vacuum chamber of 6.7 mbar l/s. In relation to the total flatjet liquid flow rate of 369 g/h, this represents a liquid evaporational loss of 5% and a global decrease of the flatjet thickness profile by at maximum 5% at the lower contraction neck of the liquid sheet. Using this relative evaporation weight loss factor, the heat of evaporation, and the specific heat of liquid water, the average water temperature has lowered by 27 °C at the end point of the vacuum passage of the thin liquid sheet structure. Measurements of a spatial temperature profile, however, are to be left open for future experiments or theoretical simulation tasks.

From a single 50 μm liquid jet in high vacuum, the evaporation rate is significantly smaller than the prediction of the simple 1D free evaporation theory model. This had worked well in previous investigations for jets with diameters between 5 μm and 15 μm, where free molecular vacuum water jet evaporation conditions and adiabatic liquid jet cooling conditions were good approximations. Between 30 μm and 50 μm diameter, however, the liquid surface evaporation is already in the (much more difficult to model) molecular collisions dominated transition range of Knudsen flow numbers near 0.2, where the surface evaporation coefficient is decreased to 0.3, approximately, with the implication of an accordingly reduced water evaporation rate. In addition, at 50 μm diameter, the radial thermal relaxation time for the cylindrical water jet is increasing up to several 10–100 μs, resulting in incomplete cooling with warmer jet core temperatures. For a single 50 μm jet with a free vacuum path of 5–7 mm, with a nozzle temperature of 20 °C and a flow rate of 3 ml/min, the effective evaporation rate is 1.1–1.3 mbar l/s. The measured flatjet evaporation rate of 6 mbar l/s shows 3 times higher evaporation rates than the rate for two non-colliding jets, indicating a more efficient evaporation and cooling for the larger area and thinner flat jet ellipsoidal sheet. The flat jet evaporation increase, roughly, appears to correlate with the surface area increase in the flat jet system. The area of an ellipse is π × A × B with semi-axes A, B. For the liquid sheet with 4.6 × 1.0 mm extension, this gives an area of 3.6 mm² (for each side of the elliptical film sheet). A single jet with 50 μm diameter and a length of 5–7 mm has a surface of 0.8–1.1 mm². Thus, the flat jet surface, approximately, is 3–4 times larger than the surface area of an isolated jet pair and is in proportion with measured increase of the respective evaporation rates.

For our experiments, we have used water (typical conductivity >13 MΩ), filtered and degassed before each experiment. To prevent the orifices getting blocked by small particles, two filters are installed in the flow line. Ammoniumchloride (AnalaR Bio, NORMAPUR, ≥99%) was used without further purification.

The data in this work were acquired at the UE52-SGM beamline at the synchrotron radiation source BESSY II at the Helmholtz-Zentrum Berlin. BESSY II was operated in multi-bunch mode. Incident photon energies were calibrated by matching the measured spectral features in the water x-ray absorption spectra with previously measured and calibrated water spectra.^40,41 The exit slit of the x-ray monochromator was set to 100 μm for all measurements, resulting in a bandwidth of ranging from 152.9 meV at 480 eV to 289.7 meV at 700 eV. All measurements were performed in top-up mode of the electron storage ring. The incident flux on the sample typically amounted to ∼10¹¹ photons/s. The x-ray spot size diameter on the sample was 30 μm. To measure an XA spectrum, the soft-x-ray intensity transmitted through the sample is recorded while scanning the incident photon energy. For a correct measure of the incident intensity, a reference scan without the flatjet is performed under identical conditions.⁴⁰

III. FLATJET CHARACTERISATION UNDER 1 BAR CONDITIONS: MID-INFRARED TRANSMISSION AND VISIBLE LIGHT INTERFEROMETRY MEASUREMENTS

Interferometric determination of thin transparent samples using visible light is an approach that has been used to determine the thickness of liquid sheets^61,62 as well as thin liquid samples in standing cells for soft-x-ray spectroscopy.⁴⁰ For visible wavelength light sources, focal spot sizes can be clearly smaller than 50 μm, allowing for monitoring fine details of such spatial resolution, and ideally, the sample thickness can be measured with submicrometer precision. The thickness determination is possible upon applying a numerical routine to the recorded interferograms. We introduce here as an alternate means mid-infrared transmission probing using a cw-laser that can be utilized in an instantaneous detection mode, providing the option of online monitoring of the flatjet thickness without altering the sample due to extensive heating or sample degradation effects. Typical focal spot sizes in the mid-infrared are on the order of 200 μm, and alignment procedures of the long-wavelength mid-infrared light are less easy to perform than for the case of using visible light.

A. Interferometry measurements

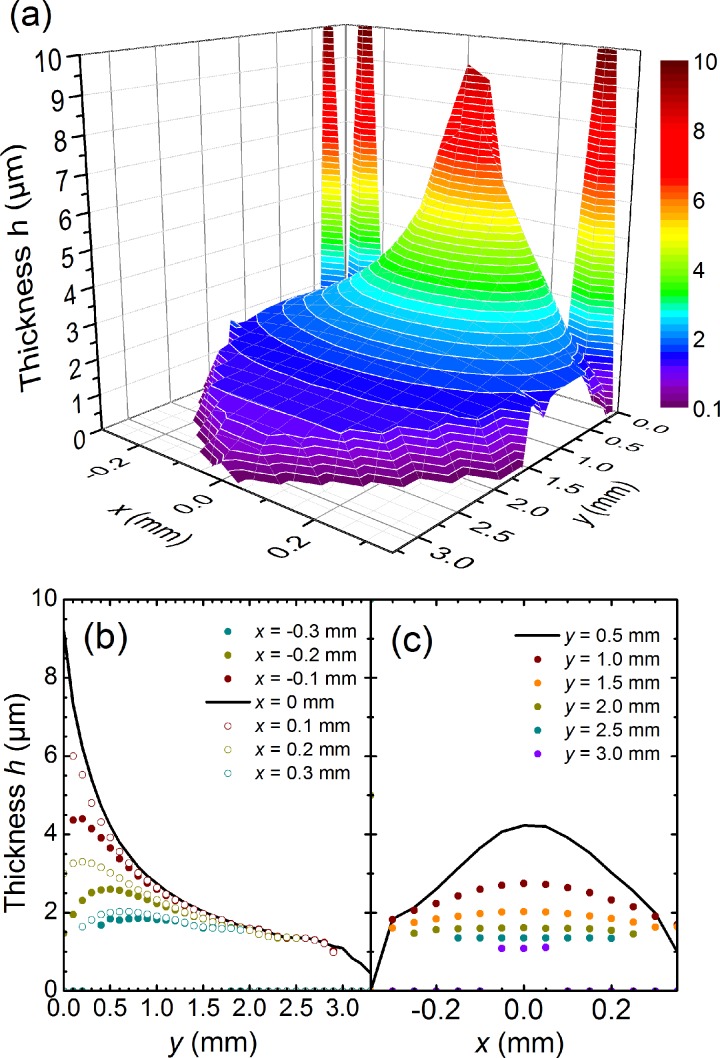
We have determined the thickness of the liquid flatjet under atmospheric conditions using interferometry (Figure 3). These measurements were taken with a “STIL-DUO” interferometric thickness sensor device, with a spot size of 40 μm. The total measurement time for the diagram was approximately 2 h. Successive data point positions were manually adjusted, using reading dial micrometers. The stability and reproducibility of thickness measurements were observed to be better than 0.1 μm over time periods longer than 20 min.

FIG. 3.

Thickness determination using interferometric measurements for a flatjet formed by colliding two 45 μm single jets with a flow rate of 3.9 ml/min under an angle of 2α = 45° under atmospheric conditions (Note: the orifice diameter and incident angle are slightly different from the soft-x-ray experiments). (a) 3D representation of the measured data. (b) Cut along the y-direction for different values of x, showing the gradual decrease of thickness along flow direction. (c) Transverse cuts along the x-direction for different values of y, showing the gradual flattening along the flow direction. The large values going off scale have resulted from the interferometric set-up probing the thicker rim boundary⁵⁵ of the flatjet.

Figure 3(a) clearly shows that the flatjet thickness h is largest near the point of collision of the two single jets. Along the propagation direction y, the thickness decreases (Figure 3(b)), as well as in the direction x perpendicular to that (Figure 3(c)). As such, the flatjet thickness h becomes smaller the further away one is located from the collision point, and the further away from the centre. This behaviour can be understood with the equation developed by Hasson and Peck assuming that the flow rate over the sheet is equal to that of the jet⁶³

$$h=\frac{d_j^2}{4r(\theta )}\times \frac{{\text{sin}}^3\alpha }{{(1+\text{cos}\hspace{0.17em}\theta \hspace{0.17em}\text{cos}\hspace{0.17em}\alpha )}^2}.$$ (1)

Here, d_j is the jet diameter which is set by the nozzle orifice diameter, r is the radial distance from the point of impact, 2α is the impact angle, and θ is the azimuthal angle (see Figure 2(b)). This model as well as other theoretical approaches for thickness prediction have their roots in the model provided by Taylor,⁵⁴ where it is made clear that the liquid sheet thickness at any point is inversely proportional to the radial distance and depends on the impact and azimuthal angles. Eq. (1) appears to hold well, up to the thicker rims, whose behaviour are not included in this approach (more sophisticated descriptions have included the spatial developments of the rim boundaries^55–57).

In the derivation of Eq. (1), it has been assumed that the velocity distribution is equal throughout the flatjet. A refinement where this assumption was relaxed (as suggested by experimental flow velocity measurements,⁶² or by assumption of a Poiseuille flow distribution^56,57) shows that the thickness behaviour remains the same, except for an overall magnitude scaling factor.⁶⁴ The flatjet dependence on the value of the impact angle α has been investigated in several studies.^62,63,65,66 From this, we derive that the small difference in impact angle (45° was the impact angle in the interferometry measurement at 1 bar; 48° is the impact angle used in the soft-x-ray spectroscopic measurements) has only minor influence. Our experience with the liquid water flatjet is consistent with the conclusions drawn from more sophisticated descriptions that have included the spatial developments of the thicker rim boundaries.^55–57 In these latter studies, it was found that a change of the flow rate results in a scaling of the flatjet in the transverse plane while roughly following the thickness distribution as defined by Eq. (1). We refer to a video taken of the liquid flatjet where the flow rate was changed from 5.2 to 6.2 ml/min to illustrate the role of the flow rate on the flatjet shape (see Figure SI-4 and associated movie in the supplementary material).⁶⁰ We also refer to Figure SI-1 in the supplementary material,⁶⁰ where we compare measured thicknesses for different flow rate values.

B. Infrared transmission measurements

To provide a direct means of probing the liquid sheet thickness, we have measured the intensity of a cw mid-infrared laser beam before (I₀) and after (I) transmission through the water film at atmospheric pressure. We utilized a cw He-Ne laser as light source operating at 3.39 μm wavelength exciting the water molecules in the region of the OH stretching band. The cw light beam was focused to a spot diameter of 440 μm in the centre part of the liquid sheet. Applying the Lambert-Beer law to estimate the sample thickness,

$$\text{log}\left(\frac{I_0}{I}\right)=\epsilon \times c\times h,$$ (2)

where ε is the molar extinction coefficient, c is the concentration of bulk water (55.5 mol/l), and h is the sheet thickness. Published literature values of ε (at 3.40 μm) range from 5.6 M⁻¹ cm⁻¹,⁶⁷ 6.1 M⁻¹ cm⁻¹,⁶⁸ to 6.5 M⁻¹ cm⁻¹,⁶⁹ respectively. We derive from our measurements a thickness of 3.5 ± 0.5 μm in the centre region of the flatjet. The uncertainty in the measurement is in part given by the spread in reported values, and in part by the thickness variation over the laser focal spot as discussed below.

To estimate possible averaging effects over the focal spot size, we have compared the experimental conditions of our liquid jet system with existing theoretical models used to predict the thickness distribution over the liquid sheet. We again use Eq. (1), and we find that the thickness of the water sheet is predicted to vary from 2.81 μm at the centre, to 2.80 μm at 30 μm from the centre, and to 2.47 μm at 220 μm from the centre. For the focal spot size of 440 μm in the mid-infrared experiment, the thickness is thus expected to vary by about 20%. Using better focusing optics and utilizing appropriate window materials for the vacuum chamber, we anticipate a steady-state IR diagnostics probing 200 μm sized regions of the flatjet, operating under vacuum conditions. A variation of the thickness over a focal spot size of 30 μm (as used in the soft-x-ray experiment, see below) is expected to be negligibly small.

IV. FLATJET CHARACTERISATION UNDER VACUUM CONDITIONS: OXYGEN K-EDGE ABSORPTION SPECTROSCOPY OF WATER

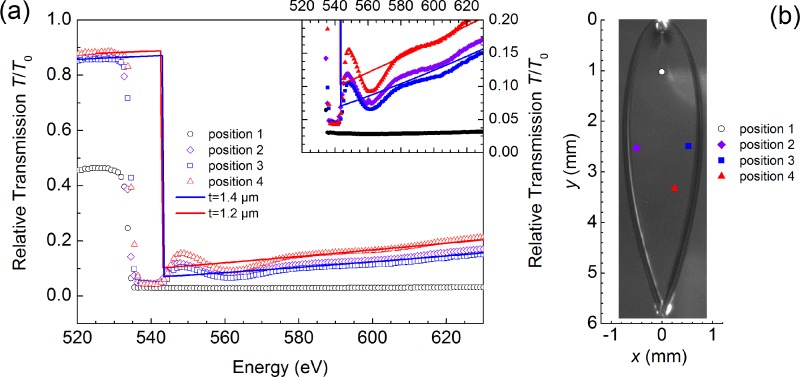
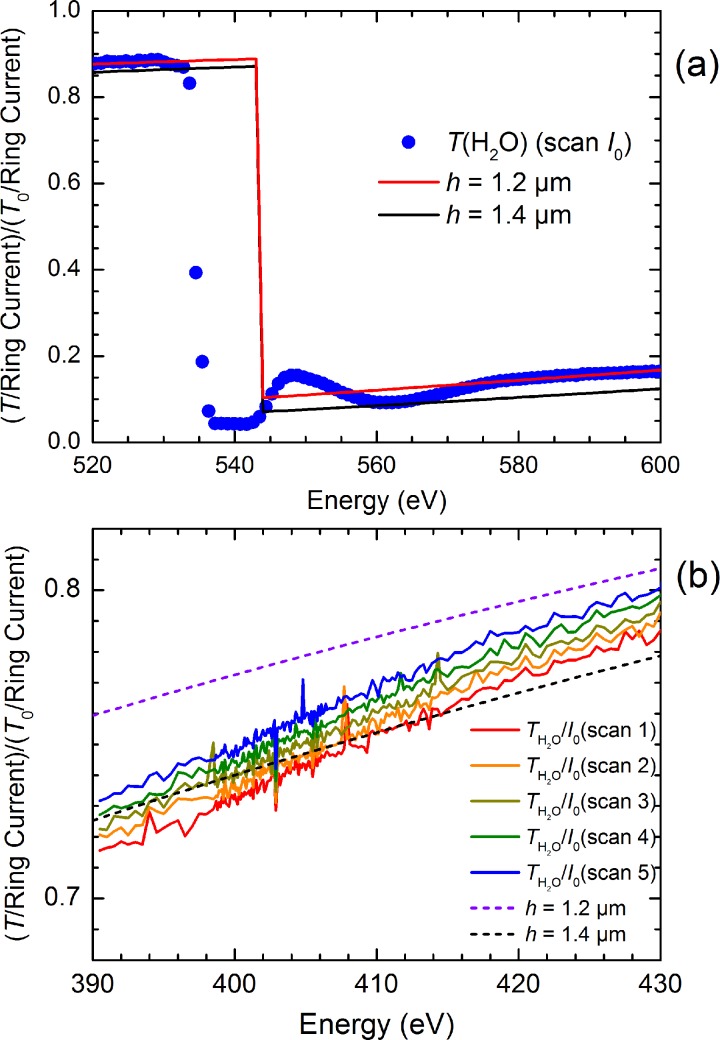
We have recorded O K-edge absorption spectra of the liquid water jet in transmission mode at different positions within the first liquid sheet (Figure 4). Typically, the transmission at the main edge of O decreases to values less than 2% for the working conditions used here. Comparing the measured transmission spectra with calculated ones using the Henke tables,³⁸ we determine the thickness of the liquid jet. Here, we have analysed the transmission at the high energy tail of the O K-edge absorption (in the region at around 580–630 eV, i.e., beyond the so called edge jump), as absorption around the pre-edge and main edge features is too strong to provide a reliable value and the region after these near-edge features and up until approximately 580 eV is strongly modulated by scattering or EXAFS (extended x-ray absorption fine structure) effects.^14,15,40 Our results suggest a stable working operation of the flatjet system for the parameters used here with thicknesses on 1.2–1.7 μm in the centre part of the first liquid sheet. These results show that measurement of the O K-edge of the water flatjet allows for an in-situ determination of the jet thickness during soft-x-ray spectroscopic studies. We have observed a variation in flatjet thickness in accordance to the expected flatjet profile (Figure 3), as exemplified by the position-dependent soft-x-ray transmission (as shown by the depicted traces in Figure 4).

FIG. 4.

Soft-x-ray transmission spectra of the liquid water flatjet near the O K-edge. Measurements were recorded at different positions in the flatjet. Experimental results (dots) are compared with values calculated using the Henke tables³⁸ (solid lines) using a water flatjet thickness h ranging from 1.4–2.1 μm. The inset shows a blow-up of the recorded transmission spectra around the edge jump absorption at the O K-edge. These spectra were each recorded on a 15 min time scale. The positions of the different scans are indicated in the sketch of the flatjet. The photo of the flatjet was not taken during these measurements and should only be considered as a guide.

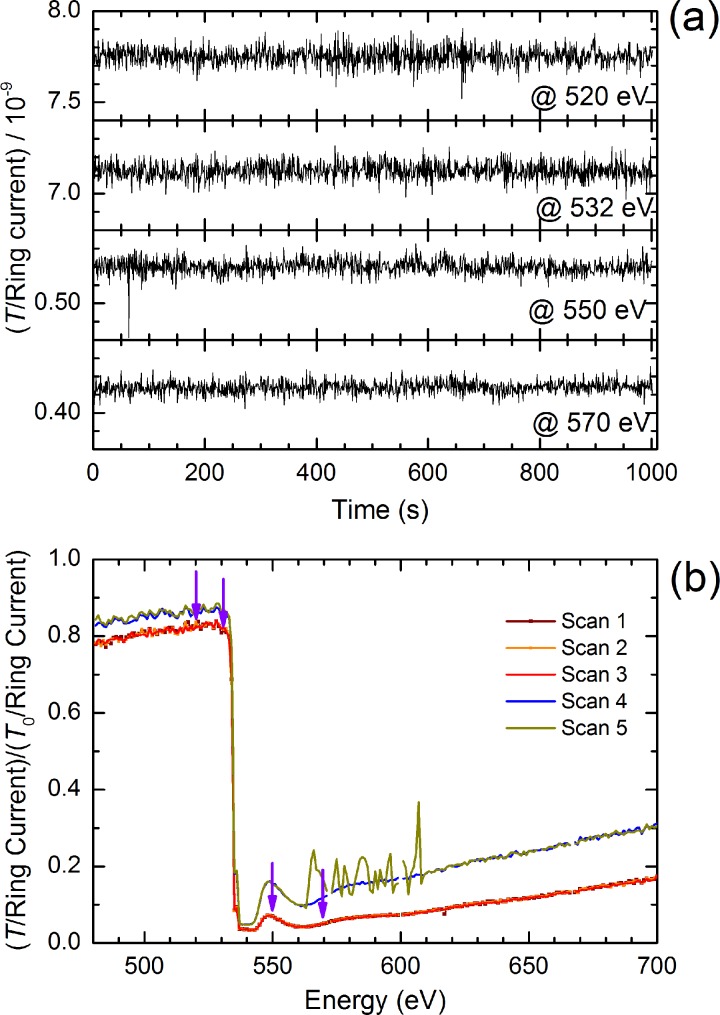
By translating the flatjet in transverse horizontal and vertical directions, an optimum position of the flatjet can be chosen for spectroscopic probing with the focused soft-x-ray beam. By scanning the transmission signal at the location of the pre-edge peak of liquid water (535 eV), we can identify a liquid sheet position with the highest transmission T/T₀ value (corresponding to the smallest value for the thickness h). After having found an appropriate jet position, with a transmission T/T₀ = 0.8 before the O K-edge, and T/T₀ = 0.03 at the O K-edge maximum, we have analysed the fluctuations of the measured signal at four spectral positions for a time period extending to 10 min (Figure 5(a)): at energies lower than the O K-edge band (520 eV), near the pre-edge feature (535 eV), in the O K main edge (550 eV), and beyond at 570 eV. Interestingly, the S/N ratio appears to be the similar, regardless of the spectral position the time scans were taken. The transmission changes at these selected energies differ by more than an order of magnitude, due to the different absorption cross sections. Noting that the measured soft-x-ray transmission signal T has been corrected with the BESSYII storage ring current, that in itself is directly proportional to the soft-x-ray signal without the flatjet (i.e., the unattenuated T₀), we can conclude that the observed fluctuations in Figure 5(a) should have their origin in the soft-x-ray beam propagation and/or the diode used to detect the soft-x-ray beam. Even more so, anticipated soft-x-ray beam intensity noise due to flatjet fluctuations in shape, size, and thickness appears to be of minor magnitude in these measurements. In fact, we argue that estimated thickness fluctuations of the flatjet are small enough for measurement times extending to (fractions of) hours, pointing at the potential of using the flatjet system for accurate spectroscopic measurements in the soft-x-ray regime. Interestingly, the stability of the flatjet is such that, in the occasion of a rare event of disruption of one of the single jets by an air bulb passing by, jet dimensions are restored to similar values, provided pump flow rates remain unchanged. In the measurement shown in Figure 5(b), the original jet thickness is actually fully restored after the disruptive event.

FIG. 5.

(a) Time scan measurements of the transmission signal at different energy positions near the O K-edge of water. (b) Energy scan measurements performed at different spatial positions. Note, the dark yellow curve shows a measurement during which a disruption event of the flatjet occurred, with a successful restoration of the initial thickness and stability parameters, after the disruption event passed by. These spectra were each recorded on a 15 min time scale. Scans 1, 2, and 3 were recorded for one position; scans 4 and 5 were recorded for a different position.

V. SOFT X-RAY SPECTROSCOPY OF THE NITROGEN K-EDGE OF SOLUTES

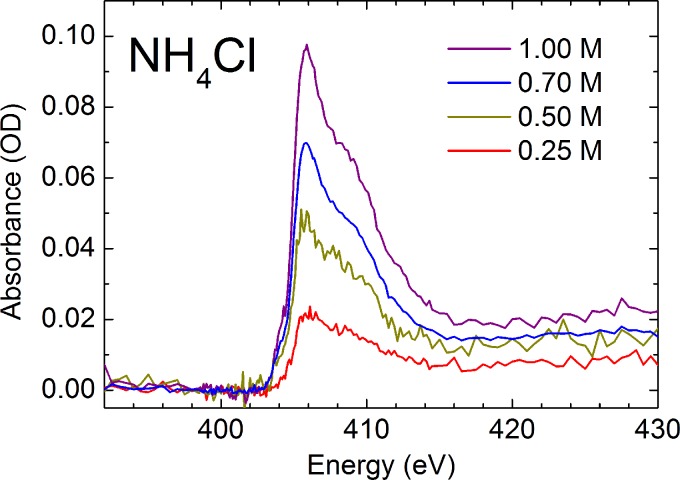
To assess the potential of using a flatjet system for solution phase soft-x-ray spectroscopy, we have measured soft-x-ray spectra of aqueous solutions of NH₄⁺. First, we have aligned the flatjet by recording the O K-edge of pure liquid water, followed by measuring the spectral response of the jet around 405 eV (Figure 6(a)). With this, we determined the background absorption of the solvent water in the flatjet with thicknesses of 1.2–1.4 μm (Figure 6(b)). After this, we switched to the aqueous solutions of NH₄⁺. Figure 7 shows the N K-edge spectra of NH₄⁺ measured at different concentrations. Typical measurements lasted 10 min. We note here that by measuring the O K-edge of the salt solutions and by comparing these with the pure water measurements, we can estimate the effect of adding salt to the solution on the flatjet thickness. Our findings are confirmed by the comparison of the NH₄⁺ measurements at different concentrations, where a 25% change in concentration leads to about 3% change in thickness, while realizing that these parameters may change more strongly when going to concentrations much higher than 1 M or when going to other solutes (which we, however, have not studied).

FIG. 6.

(a) Soft-x-ray transmission spectra of water at the O K-edge as well as in the spectral region of the N K-edge, suggesting a jet thickness of 1.2–1.4 μm. (b) Subsequent scans of transmission spectra of water in the N K-edge spectral region. Note the different y-axis scaling in panels (a) and (b). The O K-edge spectrum was recorded on a 15 min time scale. The N K-edge spectra were each recorded on a 10 min time scale.

FIG. 7.

N K-edge absorption of aqueous solutions of NH₄⁺, showing a linear concentration dependence in the absorption magnitude of the main edge feature. The spectra are the result of 3 scans (0.25 M and 0.70 M), or 1 scan (0.50 M and 1.00 M), where 1 scan typically lasted 10 min.

By measuring the magnitude of the absorbance of both the O K-edge band of the solvent water, and the N K-edge band of the solute NH₄⁺ in the flatjet, we can easily derive the relative magnitude in absorption cross sections. Knowing that viscosity of aqueous solutions remain close to that of pure water for sub-molar concentrations of simple salts, and knowing that the jet thickness remains largely unchanged when going from pure liquid to the solution (which one can check by determining the O K-edge absorption strength), we can determine the ratio of the absorption cross sections using

$$\frac{{\mathit{O}\mathit{D}}_{\mathrm{N}(405\hspace{0.17em}\text{eV})}}{{\mathit{O}\mathit{D}}_{\mathrm{O}(540\hspace{0.17em}\text{eV})}}=\frac{{\epsilon }_{\mathrm{N}(405\hspace{0.17em}\text{eV})}}{{\epsilon }_{\mathrm{O}(540\hspace{0.17em}\text{eV})}}\hspace{0.17em}\hspace{0.17em}\frac{c_{{\text{NH}}_4^{+}}}{c_{{\mathrm{H}}_2\mathrm{O}}}\frac{h}{h}\hspace{0.17em}\hspace{0.17em}.$$ (3)

Now, determination of the O K-edge absorption at the main edge near 538 eV does not lead to accurate values for our current flatjet thicknesses. However, comparing our measured value for the absorption at 600 eV, i.e., well beyond the scattering or EXAFS modulations, with those of thinner samples of H₂O measured in Si₃N₄ sample cells,⁴⁰ we can derive a ratio of absorbance for H₂O of $\frac{{\mathit{O}\mathit{D}}_{\mathrm{O}(538\hspace{0.17em}\text{eV})}}{{\mathit{O}\mathit{D}}_{\mathrm{O}(600\hspace{0.17em}\text{eV})}}$ = 2.9. For our measurements of Figures 5, we have a measured an absorbance of OD_O(538 eV) = 2.3 and OD_N(405 eV) = 0.1, and by knowing the concentrations of $c_{{\mathrm{H}}_2\mathrm{O}}$ = 55.6 M and $c_{{\text{NH}}_4^{+}}$ = 1.0 M, we derive $\frac{{\epsilon }_{\mathrm{N}(405\hspace{0.17em}\text{eV})}}{{\epsilon }_{\mathrm{O}(538\hspace{0.17em}\text{eV})}}$ = 2.4. We note that the absorption of NH₄⁺ in aqueous solution at the main edge around 405 eV is predominantly due to excitations to unoccupied molecular orbitals, as the ratio of the edge jump absorption at the K-edge as given by the Henke tables³⁸ suggests a value of $\frac{{\epsilon }_{\mathrm{N}(412\hspace{0.17em}\text{eV})}}{{\epsilon }_{\mathrm{O}(545\hspace{0.17em}\text{eV})}}$ = 1.05.

VI. CONCLUSIONS

We have presented here the first demonstration of a liquid water flatjet operating under vacuum conditions, to be successfully used in soft-x-ray transmission spectroscopy of water and aqueous solutions. By colliding two identical single jets, a liquid water flatjet is generated, in perpendicular direction from the plane formed by the two impinging single jets. The flatjet has 4.6 × 1.0 mm² surface dimensions. Interferometry measurements using visible light with a focal spot size of 40 μm and a thickness accuracy of 0.1 μm show a thickness profile of the liquid flatjet at 1 bar as described by Hasson and Peck⁶³ with values ranging from 1.5–3.0 μm at distances of >1 mm away from the collision point of the two single jets. A similar value of 3.5 μm with an accuracy of 0.5 μm was found using an infrared transmission measurement of the central part of the liquid flatjet using a HeNe laser operating at 3.39 μm wavelength with a larger spot size of 440 μm. Soft-x-ray transmission measurements of the O K-edge of water suggest thicknesses of 1.2–2.1 μm when going from the regions close to the outer rims to the centre of the flatjet. Further investigations will provide a more profound determination of the effect of vacuum conditions onto the liquid jet thickness profile.

The technological advance here is that the operation of the flatjet system occurs under vacuum conditions (<10⁻³ mbar) with thicknesses ranging from 1.4–2.0 μm and is stable for tens to hundreds of minutes. Furthermore, the addition of a catcher unit has enabled the implementation of a recycle option, allowing for sample volumes as small as 10 ml. Further promising developments appear to be a confinement to reach sub-micrometer thick water flatjet sheets, and the exploration of other solvents for flatjet formation. To reach these objectives, further exploration of the role of the nozzle size should be pursued. Our demonstration of a liquid water flatjet with thicknesses in the micrometer range, fully operational under vacuum conditions, opens up new frontiers in steady-state and time-resolved soft-x-ray spectroscopy of solution phase systems.