Signatures of nonthermal melting

Abstract

Intense ultrashort laser pulses can melt crystals in less than a picosecond but, in spite of over thirty years of active research, for many materials it is not known to what extent thermal and nonthermal microscopic processes cause this ultrafast phenomenon. Here, we perform ab-initio molecular-dynamics simulations of silicon on a laser-excited potential-energy surface, exclusively revealing nonthermal signatures of laser-induced melting. From our simulated atomic trajectories, we compute the decay of five structure factors and the time-dependent structure function. We demonstrate how these quantities provide criteria to distinguish predominantly nonthermal from thermal melting.

I. NONTHERMAL VS THERMAL MELTING

When an intense femtosecond-laser pulse excites silicon with a photon energy larger than the electronic band gap, most of the deposited energy is absorbed directly by the electrons. In addition, coherent phonons can be induced indirectly through Raman scattering, but their amplitude is so small, that in the present study we safely ignored this collective excitation.¹ While interacting with laser light, the electrons in silicon make transitions from bonding to antibonding orbitals.² As a consequence, interatomic bonds can be substantially weakened just by the presence of a hot electron plasma.³ When the density of excited carriers exceeds approximately 11% of the valence electrons, a saddle point develops and repulsive shear forces direct the atoms away from the equilibrium positions prior to the ultrashort laser excitation.^4,5 The so-induced atomic disordering, which results in a liquid state,⁶ is called nonthermal melting, because it is caused by the interaction of hot electrons with (initially) room-temperature atomic nuclei, which are out of thermal equilibrium with each other.

Competing in time with the above-mentioned nonthermal microscopic mechanism is the incoherent electron-phonon coupling,⁷ which leads to a heat flow from excited electrons to phonons until both reach the same temperature, which may be sufficiently high to cause melting. Aluminum is an example of a material that melts thermally after femtosecond-laser excitation, because the potential-energy surface on which the atoms move is not or only little affected by the electronic temperature,^8,9 leaving only the thermal mechanism of melting.¹⁰ It is important to mention that depending on the laser fluence, thermal melting can also be an ultrafast process, i.e., of shorter duration than 1 ps,¹¹ indicating that the time of laser-induced melting alone does not reveal its mechanism.

In silicon, the timescale of incoherent electron-phonon interactions has been found to increase from ≈240 fs for a single electron-hole pair to 1.2 ps and 2 ps, respectively, when 0.6% and 1.1% of the valence electrons are excited.^12,13 This increase has been attributed to electronic screening.¹⁴ The often used extrapolation¹⁵ of the result of Ref. 12 to an excitation density of 14.1%, which we applied in our ab-initio molecular-dynamics simulations below, gives a thermalization time of 530 ps, suggesting that ultrafast melting of silicon may be a purely nonthermal process. However, the extrapolation to such high densities is not supported by experiment or theory, leaving the question about the character of the femtosecond-laser-induced solid-liquid transition in silicon, i.e., predominantly nonthermal or thermal open.

In a recent experiment with femtosecond x-ray pulses at the Free-electron LASer in Hamburg (FLASH), a transition from a liquid with approximately the same density as solid silicon to a liquid with a higher density has been indirectly observed, starting 4.2 ps after femtosecond-laser excitation.¹⁶ We note that nonthermal melting of silicon has been predicted to induce a volume expansion,¹⁷ while the ordinary solid-liquid transition results in a volume contraction. We therefore think that a transition from nonthermal liquid silicon with hot electrons and holes to thermal liquid silicon with hot atoms has occurred. Its timescale is then indicative for the incoherent electron-phonon coupling time in liquid silicon, which therefore appears to be roughly two orders of magnitude faster than the above-mentioned extrapolation of Ref. 12 for solid silicon.

In order to find the signatures of nonthermal melting, we performed density-functional-theory molecular-dynamics simulations of silicon after intense femtosecond-laser excitation. We included only nonthermal processes, mainly because both the timescale and the relative matrix elements of the thermal electron-phonon interactions are unknown. From our simulated microscopic atomic pathways, we computed the time-dependent structure factors and structure function, which can be measured through the scattering of ultrashort x-ray or electron pulses.^16,18 As we will see below, the analysis of these quantities allowed us to pinpoint features that would not appear normally during melting under thermodynamic conditions but should be considered typical for nonthermal melting. Whereas our simulations do not resolve the thermal vs nonthermal melting issue, they provide criteria that can be used to conclude this open question. It is important to stress that our conclusions are not specific for silicon but can be applied to other materials as well.

II. SIMULATIONS

The past thirty-five years have seen increasingly sophisticated theoretical models of ultrafast melting of Si, which have developed from microscopic considerations¹⁹ through molecular-dynamics simulations based on tight-binding theory^4,17,20 to ab-initio molecular-dynamics simulations, at first for modest system sizes with N = 64 silicon atoms per supercell²¹ and recently for supercells with N = 640 and 800.^22,23 Size matters, because for the calculation of certain quantities, for example, the time-dependent structure function, it is necessary to sample a fine mesh of scattering vectors q between the main diffraction peaks, which can only be achieved by simulating a large supercell [see Eq. (2) below]. Therefore, in our present study, we used as many as N = 1200 atoms, for which we employed our in-house Code for Highly excIted Valence Electron Systems (CHIVES),²² which is a fast Gaussian density-functional-theory program.²⁴

In order to simulate an ultrashort laser excitation, we used electronic-temperature-dependent density-functional theory, in which the electronic temperature T_e is the key quantity describing the excitation of the system.²⁵ As pointed out above, we did not simulate incoherent electron-phonon scattering. Therefore, staying within the concept of the theory of Ref. 25, T_e was kept constant throughout the entire simulations, namely, T_e = 25 260 K. With this choice, we excited 14.1% of the valence electrons.

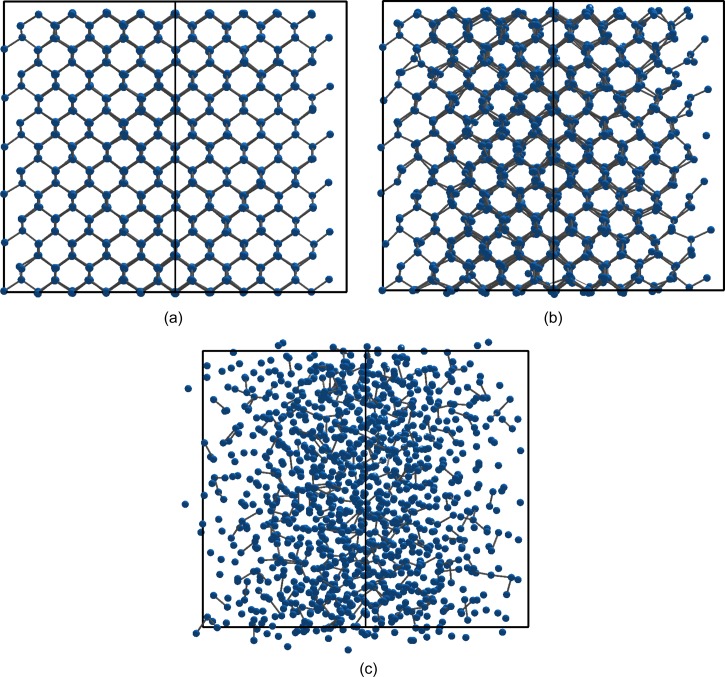
We initialized the atomic displacements and velocities according to a Maxwell distribution near room temperature using true random numbers²⁶ following the procedure outlined in Ref. 22. The dynamics of the atoms was obtained using the velocity Verlet scheme with a timestep of 2 fs, which is ≈1/40th of the period of the phonon mode with the highest frequency (see Fig. 5 below). During our simulations, we kept the volume of the supercell constant. To obtain good statistics, we performed twelve molecular dynamics runs with different, independent initial conditions and averaged the results. Snapshots of one such run shown in Fig. 1 visualize nonthermal melting of silicon.

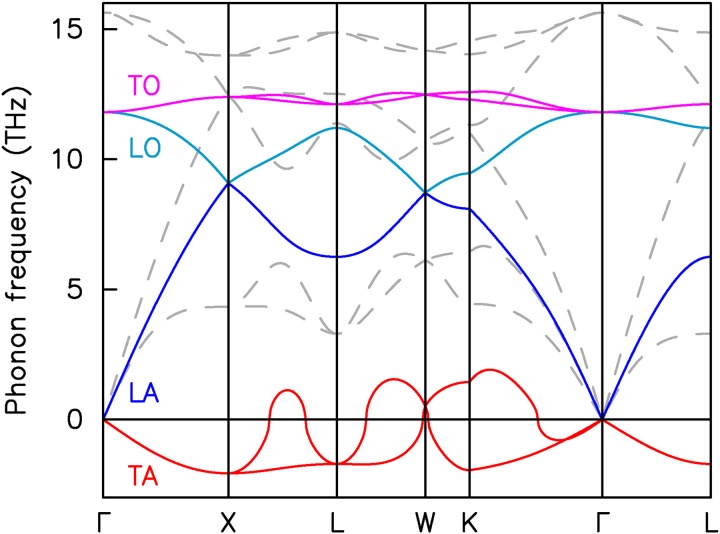
FIG. 5.

Phonon bandstructure in the femtosecond-laser-excited state with 14.1% of the valence electrons excited (colored, solid lines) and in the electronic ground state (gray, dashed lines). The colors represent transverse acoustic (TA, red), longitudinal acoustic (LA, blue), longitudinal optical (LO, cyan), and transverse optical (TO, pink) phonon branches, respectively. Imaginary phonon frequencies representing a repulsive potential-energy surface are drawn as negative values.

FIG. 1.

Snapshots of one ab-initio molecular-dynamics run with N = 1200 atoms per supercell projected in the [110] direction, respectively, 0, 100, and 450 fs after intense femtosecond-laser excitation. In (c), silicon is molten.

III. STRUCTURE FACTORS

Since we know the position of every atom throughout our molecular-dynamics runs, we can compute the time evolution of the experimentally accessible structure factor²⁷

$$F_{\mathbf{q}}(t)=\sum _{j=1}^N{e}^{i\mathbf{q}·{\mathbf{r}}_j(t)},$$ (1)

where i is the imaginary unit, r_j(t) is the position of atom j at time t, and q is a scattering vector of the form

$$\mathbf{q}=2\pi \left(\frac{n_x}{L_x},\frac{n_y}{L_y},\frac{n_z}{L_z}\right),$$ (2)

where n_x, n_y, and n_z are integers and L_x = L_y = 5a and L_z = 6a are the sizes of our supercell with a being the lattice parameter of silicon. If n_x = 5h, n_y = 5k, and n_z = 6l with h, k, and l being integers, one obtains the structure factor F_hkl(t) for the Miller indices (hkl), which label the main diffraction peaks. Structure factors for q vectors between the peaks describe background scattering. Scattering amplitudes are proportional to the intensities, which we define as

$$I_{\mathbf{q}}\left(t\right)=\frac{1}{N}{\left|F_{\mathbf{q}}\left(t\right)\right|}^2.$$ (3)

For the main diffraction peaks, we use the notation I_hkl.

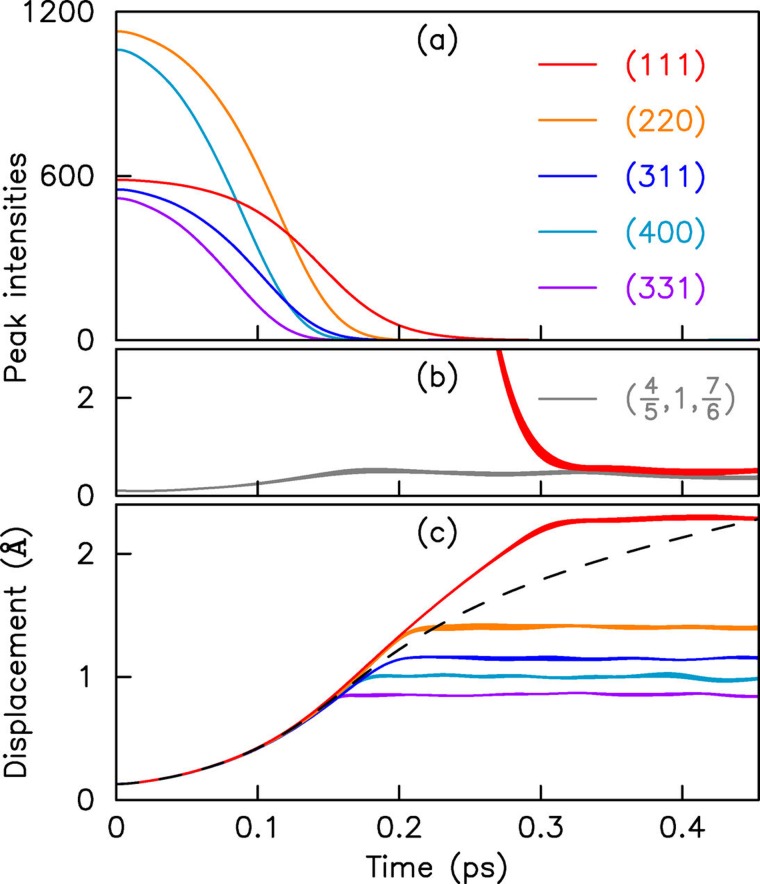
Figure 2(a) shows the time evolution of the five main diffraction peaks of silicon. Before laser excitation, at time zero, we note that peaks with odd h, k, and l have a value close to $I_{\mathit{h}\mathit{k}\mathit{l}}^{\max }=N/2$, whereas the structure factors of the even peaks are almost $I_{\mathit{h}\mathit{k}\mathit{l}}^{\max }=N$. The deviations of the peak heights from $I_{\mathit{h}\mathit{k}\mathit{l}}^{\max }$ are due to the thermal motions of the atoms, the so-called Debye-Waller effect.^28,29 The decays of the main diffraction peaks of silicon after femtosecond-laser excitation in Fig. 2(a) unambiguously confirm the ultrafast loss of crystalline order that we have already seen in Fig. 1.

FIG. 2.

(a) Time-dependent peak intensities for different scattering vectors indicated by their Miller indices after femtosecond-laser excitation. (b) Magnified decay of the (111) structure peak together with the time-resolved structure factor evaluated at a nearby q vector that is part of the background. (c) The root-mean-square atomic displacement reconstructed from the structure factors via time-dependent Debye-Waller theory [Eq. (4)]. For comparison, the dashed curve shows the time-dependent root-mean-square displacement calculated directly from the simulated atomic positions. All lines were obtained by averaging over twelve runs. The widths of the solid lines indicate the errors in the averages.

It is instructive to analyse these decays using time-dependent Debye-Waller theory,³⁰ which links small mean-square displacements of the atoms from their equilibrium positions, $⟨u^2⟩(t)$, to diffracted intensities via

$$⟨u^2⟩\left(t\right)=-\frac{3}{q^2}\text{log}\left(\frac{I_{\mathit{h}\mathit{k}\mathit{l}}\left(t\right)}{I_{\mathit{h}\mathit{k}\mathit{l}}^{\max }}\right),$$ (4)

with q being the norm of the scattering vector q, and log the natural logarithm. We note that Eq. (4) is not exact but is only valid for sufficiently small isotropic atomic displacements u. It is therefore interesting to find its range of applicability. With this aim in mind, we plotted results of Eq. (4) together with the directly computed root-mean-square atomic displacement in Fig. 2(c). We see that time-dependent Debye-Waller theory is valid during ultrafast melting of silicon for displacements up to ∼1 Å. For larger displacements, Eq. (4) holds only approximately, leading, for example, to an overestimation of the root-mean-square atomic displacement reconstructed from the (111) peak of 20% after 300 fs. Corrections to Eq. (4) are proportional to $⟨u^4⟩,\hspace{0.17em}⟨u^6⟩$, etc.³¹ It is amazing that time-dependent Debye-Waller theory apparently holds until $⟨u^2⟩\sim 1\hspace{0.17em}{\AA }^2$, where all correction terms become of the same order as Eq. (4).

Invariably, each reconstructed displacement reaches a plateau. We found that this happens when the corresponding structure factor has decayed to a value that is indistinguishable from the scattering intensity for nearby q vectors, i.e., when I_hkl has merged with the background intensity as exemplified in Fig. 2(b) for the (111) peak. We note that plateaus have also been observed in displacements reconstructed from experimental data obtained during ultrafast melting of InSb.³²

IV. STRUCTURE FUNCTION

From our simulations, we computed the time-resolved structure function³³ using

$$I(q,t)=\frac{{\sum }_{\mathbf{q}\prime }{I}_{\mathbf{q}\prime }\left(t\right)G\left(q-q\prime \right)}{{\sum }_{\mathbf{q}\prime }G\left(q-q\prime \right)},$$ (5)

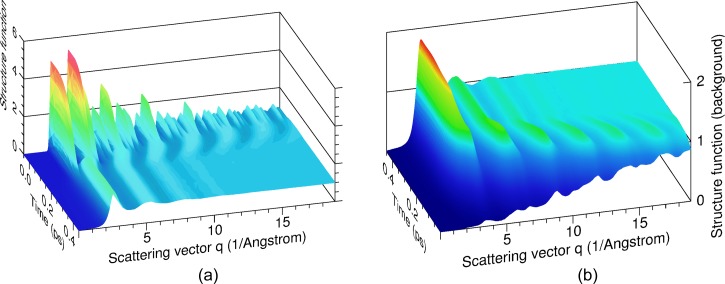
where $I_{\mathbf{q}\prime }(t)$ is given by Eqs. (1) and (2) and G is a Gaussian with full width at half maximum of 0.2 Å⁻¹, which we used to smoothen I(q, t) [cf. Ref. 27]. Our result is plotted in Fig. 3(a). Figure 3(b) shows only the background, i.e., the structure function excluding contributions from the main diffraction peaks. At time zero, before femtosecond-laser excitation, we see that the structure function is composed of the main diffraction peaks superimposed on a slowly varying background that is zero for small and approaches one for large scattering vectors. After excitation, the peaks disappear and after 150–450 fs the structure function obtains the typical shape of a liquid with a first broad peak around 2.6 Å⁻¹ followed by rapidly decaying fluctuations. After 100 fs, a transient periodic structure appears with maxima at scattering vectors that are neither present in solid silicon nor in the nonthermal liquid. See, in particular, Fig. 3(b).

FIG. 3.

(a) The structure function as a function of the scattering vector q and the time after femtosecond-laser excitation. (b) Background contribution to the structure function. Note that for reasons of clarity of presentation, the time after femtosecond-laser excitation runs in the opposite direction than in (a).

We can understand the transient behavior of the structure function from the pair-correlation function g(r), which is related to the structure function via

$$g\left(r\right)=1+\frac{1}{2{\pi }^2\rho r}{\int }_0^{\infty }\left[I\left(q\right)-1\right]\hspace{0.17em}\text{sin}\left(qr\right)q\hspace{0.17em}\mathrm{d}q,$$ (6)

where ρ = N/(L_xL_yL_z) is the atomic density. We note that, in contrast to time-dependent Debye-Waller theory, Eq. (6) is exact but the integration must be performed up to infinity. Circumventing this difficulty, we instead equivalently computed the pair-correlation function directly from

$$g\left(r\right)=\sum _{i,j}\frac{G(r-r_{\mathit{i}\mathit{j}})}{2\pi r^{2}N},$$ (7)

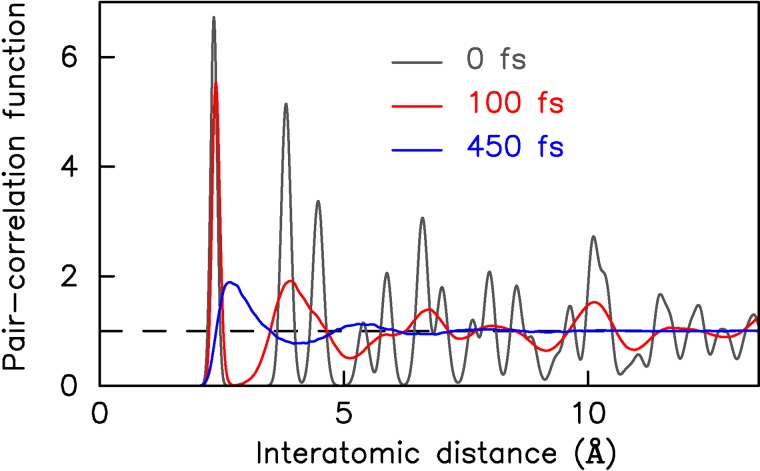
with G being a Gaussian with full width at half maximum of 0.1 Å and r_ij is the distance between atom i and j. Our results are shown in Fig. 4. Before laser excitation, at time zero, the pair-correlation function has peaks at the first, second, third, etc., nearest-neighbor distances of the silicon crystal lattice, which are broadened due to the thermal motions of the atoms. After 100 fs, the pair-correlation function still has one peak at the original nearest-neighbor distance; for r > 2.8 Å, g(r) is a smoothly varying function. The persistence of a single peak in the pair-correlation function in combination with the Fourier-like form of the inverse of Eq. (6):

$$I(q)=1+\rho {\int }_V{e}^{-i\mathbf{q}·\mathbf{r}}[g(r)-1]\mathrm{d}\mathbf{r}$$ (8)

explains the transient periodic structure in the structure function. After 450 fs, g(r) is smooth everywhere and has the typical shape of the pair-correlation function of a liquid.

FIG. 4.

Pair-correlation function 0, 100, and 450 fs after femtosecond-laser excitation.

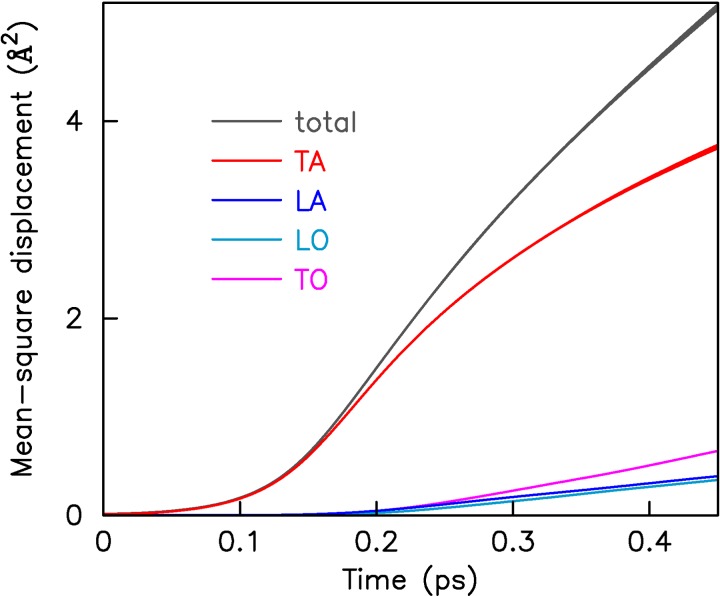
How can the nearest-neighbor peak in the pair-correlation function survive 100 fs after femtosecond-laser excitation with almost the same peak height as before the laser pulse while the other peaks have practically vanished? In order to understand the physical origin of this behavior, we computed the phonon band structure of silicon before and after ultrafast excitation following the procedure of Ref. 34. Our result is shown in Fig. 5. We see that while all phonon modes soften at high electronic temperature, only the transverse acoustic directions of the laser-excited potential-energy surface become repulsive as indicated by imaginary frequencies, plotted as negative values. In agreement, the mean-square atomic displacement $⟨u^2⟩$ projected onto the phonon modes at high T_e shown in Fig. 6 demonstrates that the atoms are displaced mainly in the transverse acoustic directions during the first stages of nonthermal melting (see Ref. 22 for details of the projection). Because transverse atomic motions are mainly perpendicular to the bonds between neighboring atoms, the change in the nearest-neighbor distances is to lowest order mostly proportional to u², but proportional to u for other distances. So, for small u, the peaks corresponding to the second and further nearest-neighbor distances become washed out much faster than the nearest-neighbor peak. The appearance of the transient periodic structure in the structure function 100 fs after ultrafast excitation is therefore a direct consequence of the microscopic atomic pathways followed during nonthermal melting.

FIG. 6.

Mean-square atomic displacement as a function of time as well as its projection onto the four different phonon types (TA, LA, LO, and TO).

V. SUMMARY

We performed density-functional-theory molecular-dynamics simulations of nonthermal melting of silicon, from which we computed the time evolution of five structure factors and the structure function. We found that the structure factors decay in agreement with time-dependent Debye-Waller theory up to a mean-square atomic displacement of ∼1 Å and that the structure function evolves from the peaked shape of solid silicon, through a transient periodic function that arises from the transverse character of the microscopic atomic melting paths, to a smooth function characteristic of a liquid.

VI. SIGNATURES

If we compare our simulations with a thermal melting process that proceeds through a melting front, it is clear that the diffraction pattern in the latter case would consist of a contribution from the solid part plus a contribution from the already molten part of the sample. So, for melting under thermodynamic conditions, diffraction peaks are expected to decay concertedly. This means that, in contrast, decay according to time-dependent Debye-Waller theory is a signature of nonthermal melting. Similarly, during conventional thermal melting, the structure function should be a superposition of the function of the solid and that of the liquid at all times. The transient periodic structure that we found 100 fs after femtosecond-laser excitation can clearly not be described as such a superposition and is therefore also a signature of nonthermal melting. Because diamond, silicon, and germanium as well as crystals with the zinc-blende structure, such as, GaAs, InSb, and InP, probably melt along the same atomic paths,⁴ we expect that the above signatures will show up in any of these solids as long as the femtosecond-laser-induced melting is predominantly nonthermal.

Experimentally, the validity of temperature-dependent Debye-Waller theory has been confirmed for InSb, which therefore apparently melts nonthermally. In silicon, diffraction peaks have been observed to decay concertedly.¹⁸ However, due to the poor signal-to-noise ratio arising from the limited number of single-shot snapshots, no definite conclusions can be drawn beyond the observed loss of order within 500 fs.³⁵ In case of silicon, we therefore consider the origin of laser-induced melting as a still open question.

Apart from nonthermal and thermal melting through a melting front, it has been proposed that a solid-liquid transition may be induced by a femtosecond laser through homogeneous nucleation of a superheated solid.^11,36,37 In this case, the melting would start from nucleation seeds distributed in the solid, which would give a similar diffraction pattern as conventional thermal melting if the density of liquid nuclei is relatively low. If, however, the density of nucleation seeds is of the order of one liquid nucleus per the volume of such a nucleus, the entire solid melts homogeneously, and the diffraction pattern could change unconcertedly. In contrast to both nonthermal and conventional thermal melting, changes in the diffraction patterns during homogeneous nucleation are expected to start with a delay, i.e., only after enough energy has been transferred from the excited electrons to the atoms, which distinguishes this mechanism from the other two.