Data collection strategies for time-resolved X-ray free-electron laser diffraction, and 2-color methods

Abstract

We compare three schemes for time-resolved X-ray diffraction from protein nanocrystals using an X-ray free-electron laser. We find expressions for the errors in structure factor measurement using the Monte Carlo pump-probe method of data analysis with a liquid jet, the fixed sample pump-probe (goniometer) method (both diffract-and-destroy, and below the safe damage dose), and a proposed two-color method. Here, an optical pump pulse arrives between X-ray pulses of slightly different energies which hit the same nanocrystal, using a weak first X-ray pulse which does not damage the sample. (Radiation damage is outrun in the other cases.) This two-color method, in which separated Bragg spots are impressed on the same detector readout, eliminates stochastic fluctuations in crystal size, shape, and orientation and is found to require two orders of magnitude fewer diffraction patterns than the currently used Monte Carlo liquid jet method, for 1% accuracy. Expressions are given for errors in structure factor measurement for the four approaches, and detailed simulations provided for cathepsin B and IC3 crystals. While the error is independent of the number of shots for the dose-limited goniometer method, it falls off inversely as the square root of the number of shots for the two-color and Monte Carlo methods, with a much smaller pre-factor for the two-color mode, when the first shot is below the damage threshold.

I. INTRODUCTION

In recent experiments aimed at the measurement of structure-factors using a free-electron laser (XFEL),¹ protein nanocrystals are sprayed in single-file across a pulsed hard-X-ray beam, using a technique known as serial femtosecond X-ray crystallography (SFX). The crystals, often of submicron dimensions, vary in size, are randomly oriented, and are destroyed by the beam after providing a high-resolution diffraction pattern. In addition, the intensity of the X-ray beam may vary from shot to shot by up to 15%, and the time-structure of the femtosecond pulses used also varies from shot to shot. Diffraction patterns are read out at perhaps 120 Hz, so that large amounts of data are collected. Nevertheless, using improved data analysis methods, the number of diffraction patterns needed to determine a structure at better than 0.2 nm resolution has recently been reduced to less than 6000.²⁴ The extraction of structure factors then requires an integration across the angular width of the Bragg reflections from these many “stills,” snapshots, or partial reflections, in each of which the Ewald sphere cuts through a small slice of the intensity distribution around each Bragg condition. For the smallest nanocrystals, containing perhaps just a few dozen unit cells, since the XFEL is spatially coherent, and assuming that the beam is wider than the crystal, the Bragg spots are broadened by “shape transform” functions;^1,11 for larger crystals, mosaicity may be present.² The case of a coherent beam smaller than the crystal (or smaller than one mosaic block, or unit cell) is discussed elsewhere.¹⁸ Where a wide beam illuminates a mosaic crystal, slightly tilted blocks of crystal monochromate different component wavelengths of the beam, scattering them into slightly different directions around the Bragg spots, across which an integration is required. The divergence of the incident beam and the energy-spread in the beam must also be considered, since these contribute to the "thickness" of the Ewald sphere. These considerations lead to the well-established multiple-scattering theory of primary and secondary extinction in mosaic crystals,¹⁹ which assumes incoherent multiple scattering between blocks but coherent multiple scattering within each block. We do not consider that here, since a modern XFEL coherent beam diameter of 200 nm is comparable with a typical mosaic block size, and the mosaic block model may not apply to the layer structures such a membrane proteins.²² In all cases, the precise deviation of the diffraction conditions from the ideal Bragg condition is needed for each spot in every shot in order to estimate the degree of partiality for each reflection. So far, it has not been possible to measure this quantity directly; however, several groups have recently used optimization methods to estimate partiality.^2,15,16,24

Building on earlier synchrotron work,²¹ pump-probe SFX experiments^3,4,20 have also been undertaken, aimed at imaging time-resolved changes (TR-SFX) in three-dimensional protein charge-density maps due to optical illumination, such as that which occurs in photosynthesis. In a typical experiment, alternate nanocrystals in a liquid jet stream might be illuminated optically (causing a change in structure factors) and the difference in the measured intensities between illuminated (bright) and un-illuminated (dark) angle-integrated Bragg reflections is used, after phasing, to provide a real-space density map showing the change in molecular structure due to illumination. The differences are taken between a very large number of bright and dark nanocrystals of different sizes (leading to large scale-factor differences covering orders of magnitude). In this paper, we obtain expressions for the number of patterns needed to reduce the errors in structure factor measurement to below that needed to observe optical pumping effects, using three different methods, which we compare.

In order to merge data (by adding together Bragg partial reflections with the same Miller indices from nanocrystals of different sizes), subject to these many sources of stochastic variation, it was suggested that the only reasonable method is a Monte Carlo (MC) type of angular integration across the Bragg reflections, in which the angular coordinate then consists of a random sample of abscissa (crystal orientation) values. This integration will then average over all stochastic fluctuations, such as shot-to-shot beam intensity variation and differences in crystal size. The contributions of these fluctuations to the final structure factor measurement might then be expected to add in quadrature, giving a signal-to-noise ratio (SNR) which improves as the square root of the number of diffraction patterns, and this behavior has been confirmed experimentally.⁵ Thus, a hundred times more data are needed to add one significant figure to the results. Improvements on this behavior require experimental characterization of the sources of error and their distributions and more accurate specification of experimental parameters, such as the assignment of a scattering vector to each pixel on the area detector and deviation from the exact Bragg condition. Model-based data analysis methods using the EMC (Expectation maximization and compression) algorithm also show great promise for the smallest crystals.⁶

More recently, we have been involved with experiments in which data are collected from larger crystals in a fixed orientation mounted on a goniometer, with provision to scan the sample to a new position laterally. For pump-probe experiments, the incident X-ray intensity can be adjusted for either destructive readout (in which case, the sample must be translated after each shot has drilled a hole in the sample) or defocussed to a level below the damage threshold, giving a poorer statistics.^7,8 In principle, this method allows measurements at equally spaced increments across the rocking curve, with a known abscissa error; however, the total dose for all exposures must fall below the Henderson safe dose.²⁸

Finally, new modes of XFEL operation have been demonstrated, dubbed “split and delay,” in which the coherent X-ray beam is split into two beams of slightly different wavelengths, with the femtosecond pulse in one beam delayed relative to the other.^9,10,25 Several methods are possible including a “slotted foil,” the use of mirrors (for softer X-rays with high efficiency) and Bragg crystal splitters (harder X-rays with lower efficiency). The two beams can be focused onto the same sample, arriving at slightly different times and beam energies, or from slightly different directions at the same energy. Delays are currently in the range of 100 fs but could, in principle, be extended to the range more useful for biology or organic chemistry (with very long path lengths), in which case a pump laser could be inserted between the two pulses of a pair, and both diffraction patterns then impressed on the same detector readout. For larger nanocrystals, the sharp partial Bragg spots at the two slightly different beam energies will then be displaced on the detector, and the intensity differences are merged to provide a difference density map after phasing. By obtaining pairs of diffraction patterns from the same nanocrystal (before and after optical illumination), errors due to both size and orientation variation are eliminated; however, the first pulse must clearly not destroy the sample, resulting in poorer SNR relative to the diffract-and-destroy mode. Among the methods developed at LCLS for split-and-delay research, different limitations apply. Use of mirrors limits the X-ray energy to below 2 keV and a short time delay, thus cannot provide high-resolution reflections needed for biological imaging. Bragg crystals used as beam splitters result in excessively collimated and monochromatic pulses giving low efficiency in structure factor measurement. Similarly, a two-color scheme based on use of two sets of undulators generates two X-ray pulses at slightly different energies (2% difference) and separated in time with an adjustable delay up to 40 fs, potentially extendable to up to 200 fs.⁹ This two-color approach, which is also applicable to hard-X-rays with time delay from a few femtoseconds up to 200 fs, is most suitable for the study of the earliest stages of conformational change and bond formation in biochemistry. We therefore focus our analysis and discussion on these two-color approaches in Secs. II B and III B.

In this paper, we compare the accuracy of structure factor measurement for each of these modes for pump-probe time-resolved diffraction experiments, in which the error should be less than the changes in structure factor due to pump illumination. Since many poorly characterized experimental factors influence such a complex comparison (such as crystal quality, jet hit rate, sample concentration, and fixed-sample scan time), we make here a simplified comparison which focuses on establishing signal-to-noise ratio as a function of number of shots for each method, with other factors equal. Some of the many additional experimental considerations might include the following. For irreversible processes, the pump laser must be directed to a new area (or crystal) for each shot. Since Laue diffraction is not possible using an XFEL, many shots (both bright and dark) are needed in the vicinity of every Bragg condition to perform the required angular integration over these partial reflections. With many pixels within the angular profile of the Bragg reflection, the intensity of these partial reflections is proportional to the square of the number of electrons in the illuminated region of the sample, while the angle-integrated intensity is proportional to the number of electrons or molecules. A doubling of beam size on a large crystal by defocus (with constant number of photons per shot) leaves the intensity of Bragg beams unchanged (in the absence of damage). The ideal maximum of diffraction information is obtained with the largest possible ideally imperfect crystal fully illuminated at a level below the Henderson safe dose. (This maximizes the number of undamaged molecules contributing to the diffraction pattern.) The use of diffract-and-destroy methods allows a dose of up to 100 times this safe dose without damage, in principle, providing much more intense high angle scattering and so better resolution, with data obtained from submicron regions of crystals, in some cases thereby reducing the contribution from defects. The use of femtosecond pulses allows us to outrun radiation damage effects at all beam intensity levels (including low intensity), while subsequent vaporization of the crystal at high intensities prevents the collection of pumped data from the same crystal. The theory of diffraction from protein nanocrystals is given elsewhere;⁵ the theory of diffraction from larger mosaic crystals is given in textbooks.¹⁹

II. XFEL-BASED APPROACHES FOR STRUCTURE FACTOR MEASUREMENT

A. Monte-Carlo approach

The MC approach⁵ merges all diffraction data from many crystal sizes and sample orientations and performs a simple average over microcrystal size, shot-to-shot beam intensity, and the partiality of the reflections. For different patterns, the Ewald sphere intersects the Bragg orders in reciprocal space at different points on the intensity distribution. The intensity of the reflection is thus dependent on the crystal size and orientation, assuming a parallelepiped crystal as¹¹

$$I^{\left(i\right)}=I_0^{\left(i\right)}{\left|F(\Delta \mathbf{k})\right|}^2{r}_e^{2}P\left({\mathbf{k}}_{\mathbf{0}}\right)\frac{\hspace{0.17em}{\text{sin}}^2\left(N_1^{\left(i\right)}{\Psi }_1^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_1^{\left(i\right)}\right)}\frac{\hspace{0.17em}{\text{sin}}^2\left(N_2^{\left(i\right)}{\Psi }_2^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_2^{\left(i\right)}\right)}\frac{\hspace{0.17em}{\text{sin}}^2\left(N_3^{\left(i\right)}{\Psi }_3^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_3^{\left(i\right)}\right)}\Delta \Omega ,$$ (1)

where the sin² terms are known as "shape transforms" and the N(i)'s represent the number of unit cells in a given dimension (hence crystal size), and

$${\Psi }_1^{(i)}=\pi \Delta \mathbf{k}\cdot {\mathbf{a}}^{(i)}\hspace{0.17em};\hspace{1em}{\Psi }_2^{(i)}=\pi \Delta \mathbf{k}\cdot {\mathbf{b}}^{(i)};\hspace{1em}{\Psi }_3^{(i)}=\pi \Delta \mathbf{k}\cdot {\mathbf{c}}^{(i)}.$$ (2)

The superscript index “(i)” indicates the “i”th shot event. a⁽ⁱ⁾, b⁽ⁱ⁾, and c⁽ⁱ⁾ are the lattice vectors of the nano-crystal in the frame fixed to the laboratory at the “i”th shot. The extracted structure factor is estimated from the average intensity of the Bragg beam over all shots with index⁽ⁱ⁾

$$\begin{array}{c}〈I^{\left(i\right)}〉=〈I_0^{\left(i\right)}{\left|F(\Delta \mathbf{k})\right|}^2\frac{\hspace{0.17em}{\text{sin}}^2\left(N_1^{\left(i\right)}{\Psi }_1^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_1^{\left(i\right)}\right)}\frac{\hspace{0.17em}{\text{sin}}^2\left(N_2^{\left(i\right)}{\Psi }_2^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_2^{\left(i\right)}\right)}\frac{\hspace{0.17em}{\text{sin}}^2\left(N_3^{\left(i\right)}{\Psi }_3^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_3^{\left(i\right)}\right)}〉r_e^{2}P\left({\mathbf{k}}_{\mathbf{0}}\right)\Delta \Omega ,\\ \approx 〈I_0^{\left(i\right)}〉{\left|F(\Delta \mathbf{k})\right|}^2〈\frac{\hspace{0.17em}{\text{sin}}^2\left(N_1^{\left(i\right)}{\Psi }_1^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_1^{\left(i\right)}\right)}\frac{\hspace{0.17em}{\text{sin}}^2\left(N_2^{\left(i\right)}{\Psi }_2^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_2^{\left(i\right)}\right)}\frac{\hspace{0.17em}{\text{sin}}^2\left(N_3^{\left(i\right)}{\Psi }_3^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_3^{\left(i\right)}\right)}〉r_e^{2}P\left({\mathbf{k}}_{\mathbf{0}}\right)\Delta \Omega ,\\ \approx 〈I_0^{\left(i\right)}〉{\left|F(\Delta \mathbf{k})\right|}^2〈\frac{\hspace{0.17em}{\text{sin}}^2\left(N_1^{\left(i\right)}{\Psi }_1^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_1^{\left(i\right)}\right)}〉〈\frac{\hspace{0.17em}{\text{sin}}^2\left(N_2^{\left(i\right)}{\Psi }_2^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_2^{\left(i\right)}\right)}〉〈\frac{\hspace{0.17em}{\text{sin}}^2\left(N_3^{\left(i\right)}{\Psi }_3^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_3^{\left(i\right)}\right)}〉\times r_e^{2}P\left({\mathbf{k}}_{\mathbf{0}}\right)\Delta \Omega .\end{array}$$ (3)

If we use $C_{(hkl)}^{(i)}$ to denote the combined effect of crystal size, orientation, and other constants, then Eq. (3) can be written in the following form:

$$I^{(i)}=I_0^{(i)}{\left|F(\Delta \mathbf{k})\right|}^2\cdot C_{(hkl)}^{(i)},$$ (4)

$$C_{\left(hkl\right)}^{\left(i\right)}=\left(\frac{\hspace{0.17em}{\text{sin}}^2\left(N_1^{\left(i\right)}{\Psi }_1^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_1^{\left(i\right)}\right)}\frac{\hspace{0.17em}{\text{sin}}^2\left(N_2^{\left(i\right)}{\Psi }_2^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_2^{\left(i\right)}\right)}\frac{\hspace{0.17em}{\text{sin}}^2\left(N_3^{\left(i\right)}{\Psi }_3^{\left(i\right)}\right)}{\hspace{0.17em}{\text{sin}}^2\left({\Psi }_3^{\left(i\right)}\right)}\right)r_e^{2}P\left({\mathbf{k}}_{\mathbf{0}}\right)\Delta \Omega ,$$ (5)

$$〈I^{(i)}〉=〈I_0^{(i)}〉{\left|F(\Delta \mathbf{k})\right|}^2〈C_{(hkl)}^{(i)}〉.$$ (6)

The structure factors can then be estimated from the average Bragg beam intensity using the following relation:

$${\left|F_{\left(hkl\right)}^{\exp }\right|}^2=\frac{〈I^{\left(i\right)}〉}{〈I_0^{\left(i\right)}〉〈C_{\left(hkl\right)}^{\left(i\right)}〉},$$ (7)

where $〈C_{(hkl)}^{(i)}〉$ includes the average shape transform, which can be modeled, based on experimental parameters. As shown elsewhere,²³ this average shape transform is a smooth curve, rather than the sinc-function profile of a single cubic nano-crystal.

B. Two-color approach for pump-probe experiments

The two-color approach offers the possibility of eliminating the randomness of several stochastic variables, as shown below. The first of a pair of pulses hits a nano-crystal and, after a set time delay, the second hits the same crystal in an identical orientation, since the rotational diffusion time of micron-sized microcrystals in the buffer solution of a liquid jet is much larger than the delay. Between these two pulses, the crystal may be pumped optically; however, the first X-ray pulse must not cause damage, and if it excites the crystal, sufficient time must be allowed for the excitation to decay before optical pumping. Both patterns are recorded by the detector within the same read-out event. Since the two patterns are from two pulses with slightly different wavelengths, they can be separated in data analysis, if the crystals are large enough to minimize an overlap of the diffraction spots at the two wavelengths. This method is not restricted to the use of a liquid or viscous jet, and our analysis can equally be applied to microcrystals mounted on a scanned fixed-target arrangement. Since the two diffraction patterns are from almost the same scattering geometry, the intensities may be expressed as

$$I_{1,(hkl)}^{(i)}=I_{01}^{(i)}\cdot {\left|F_{1,(hkl)}\right|}^2\cdot C_{1,(hkl)}^{(i)},$$ (8)

$$I_{2,(hkl)}^{(i)}=I_{02}^{(i)}\cdot {\left|F_{2,(hkl)}\right|}^2\cdot C_{2,(hkl)}^{(i)},$$ (9)

$$C_{1,(hkl)}^{(i)}\approx C_{2,(hkl)}^{(i)},$$ (10)

where the indices “₁” and “₂” indicate the first and the second of the paired pulses, or ground state and excited state. As can be seen from Eqs. (8)–(10), the beauty of the two-color approach is that we can now divide out the common orientation factor to obtain the change in structure factor amplitude

$$\begin{array}{c}{R}_{\left(hkl\right)}^{\left(i\right)}=\frac{\Delta \left(\left|F_{\left(hkl\right)}\right|\right)}{\left|F_{1,\left(hkl\right)}\right|}=\left|\frac{\left|F_{2,\left(hkl\right)}\right|-\left|F_{1,\left(hkl\right)}\right|}{\left|F_{1,\left(hkl\right)}\right|}\right|,\\ =\sqrt{\frac{{\left|F_{2,\left(hkl\right)}\right|}^2}{{\left|F_{1,\left(hkl\right)}\right|}^2}}-1=\sqrt{\frac{I_{2,\left(hkl\right)}^{\left(i\right)}}{I_{1,\left(hkl\right)}^{\left(i\right)}}\cdot \frac{I_{01}^{\left(i\right)}}{I_{02}^{\left(i\right)}}}-1,\\ =\sqrt{\frac{I_{2,\left(hkl\right)}^{\left(i\right)}}{I_{1,\left(hkl\right)}^{\left(i\right)}}\cdot k_{12}^{\left(i\right)}}-1=\sqrt{A_{\left(hkl\right)}^{\left(i\right)}}-1,\end{array}$$ (11)

$$k_{12}^{\left(i\right)}\equiv \frac{I_{01}^{\left(i\right)}}{I_{02}^{\left(i\right)}};\hspace{1em}{A}_{\left(hkl\right)}^{\left(i\right)}\equiv \frac{I_{2,\left(hkl\right)}^{\left(i\right)}}{I_{1,\left(hkl\right)}^{\left(i\right)}}\cdot k_{12}^{\left(i\right)},$$ (12)

where $k_{12}^{(i)}$ denotes the ratio of the first pulse intensity to the second for the (i)th shot. The ratio of the change in Bragg beam intensity is independent of crystal size and orientation. It is equal to the ratio of the change in the squared structure factor magnitudes. Experimentally, this means that each frame from paired pulses which contains two slightly displaced diffraction patterns gives exactly the same ratio of the change in the Bragg beam intensity. The randomness in crystal size and orientation are therefore eliminated, suggesting that this two-color approach might be superior to a Monte-Carlo approach in a liquid jet, where bright and dark differences are taken from crystals of different sizes. However, the weak signal from the first pulse (needed to avoid damaging the sample) degrades SNR.

C. Large crystal fixed on a goniometer

For fixed-sample experiments, the sample orientation can be controlled using a goniometer to allow a slow scan across reflections from a large single crystal at controlled increments for both bright and dark conditions. The total dose deposited in the sample must be lower the Henderson safe dose to obtain damage-free data. If the diffract-and-destroy mode is used (drilling holes with the beam in a large crystal), the many orientations and bright and dark conditions must all be obtained from different regions of the same crystal, separated by several microns to allow for the range of damage and strain caused by hole-drilling. This approach has the advantage of allowing a much higher dose¹³ (with resulting stronger high-angle scattering) and the absence of radiation damage on the Bragg data. A third possibility uses microcrystals trapped, perhaps by filtration, on the sites of a calibrated lattice in random orientations. Then, under diffract-and-destroy conditions, bright and dark data are collected from different microcrystals, and the methodology is similar to the GDVN (Gas Dynamic Virtual Nozzle) liquid jet, but with a hit rate approaching 100% and possibly slower readout, depending on scan speed. If a goniometer and large crystal are used (either above or below the damage threshold), the extracted structure factor from a series of exposures around Bragg conditions is

$$\begin{array}{c}{\left|F_{\mathit{e}\mathit{s}}\right|}^2=\sum _{i=1}^{N_s}\left(I_i\cdot \Delta \Psi \right),\\ \hspace{1em}\hspace{1em}=\Delta \Psi \sum _{i=1}^{N_s}{I}_i,\\ \hspace{1em}\hspace{1em}={\Psi }_T\frac{\sum _{i=1}^{N_s}{I}_i}{N_s},\end{array}$$ (13)

where ${\mathrm{\Psi }}_T$ is the effective angular width of the abscissa of Bragg reflection that is scanned across and $\Delta \mathrm{\Psi }$ is the sampling increment of the scanning process. $I_i$ is the measured intensity of the ith sampled point and $N_s$ is the number of sampling points across the reflection.

III. ERROR METRICS

In order to determine if the two-color (or split-and-delay) approach is more accurate than the Monte- Carlo method, the errors in structure factor extraction are estimated below for both approaches. In addition, we determine approximately the number of patterns needed to achieve a given accuracy in structure factor, and whether it is feasible for both approaches, with a 15% beam intensity fluctuation, to identify a 1% change in structure factors.

A. Monte-Carlo approach

The extracted structure factor converges to its true value by Monte-Carlo integration over crystal size, orientation, and beam intensity fluctuation.⁵ This convergence has a diminishing efficiency described by error reduction as $1/\sqrt{N}$, which makes Monte-Carlo approach wasteful of protein sample and beam resources. For the study of radiation damage dynamics or sub-pico-second time-resolved imaging, the change in structure factor is very small and likely to be less than 10% at best, and 1% in some cases. To recognize this small change from random errors, a huge number of patterns may be needed; nevertheless, near-atomic resolution “movies” of the photo-detection cycle in photo-sensitive bacterial yellow protein have recently produced by this approach.²⁰ In the following, we estimate this number based on error analysis.

The error in structure factor from each shot can be derived from Eq. (7) based on error propagation as¹¹

$$\frac{{\sigma }_{\mathit{M}\mathit{C}}^{\left(i\right)}\left(\left|F\right|\right)}{〈\left|F\right|〉}=\frac{1}{2}\sqrt{{\left(\frac{\sigma \left(I^{\left(i\right)}\right)}{〈I^{\left(i\right)}〉}\right)}^2+{\left(\frac{\sigma \left(C^{\left(i\right)}\right)}{〈C^{\left(i\right)}〉}\right)}^2+{\left(\frac{\sigma \left(I_0^{\left(i\right)}\right)}{〈I_0^{\left(i\right)}〉}\right)}^2},$$ (14)

where “σ” denotes the error (or standard deviation) in each random variable and “〈〉” represents the average value. After merging N patterns by Monte-Carlo integration over crystal size and orientation, the error in the structure factor is reduced by a factor of $1/\sqrt{N}$

$$\frac{{\sigma }_{\mathit{M}\mathit{C}}^{\left(N\right)}\left(\left|F\right|\right)}{〈\left|F\right|〉}=\frac{1}{2\sqrt{N}}\sqrt{{\left(\frac{\sigma \left(I^{\left(i\right)}\right)}{〈I^{\left(i\right)}〉}\right)}^2+{\left(\frac{\sigma \left(C^{\left(i\right)}\right)}{〈C^{\left(i\right)}〉}\right)}^2+{\left(\frac{\sigma \left(I_0^{\left(i\right)}\right)}{〈I_0^{\left(i\right)}〉}\right)}^2}.$$ (15)

If we now neglect the error in intensity detection due to shot noise for a relatively strong Bragg beam, then the first term in the parenthesis in Eq. (15) vanishes. Also, for the purpose of approximation, a Monte-Carlo simulation has been conducted to obtain the approximate percentage error (ratio of standard deviation to mean) in the C(i) factor, which represents the effect of crystal shape and orientation. For crystals of Trypanosoma brucei cysteine protease cathepsin B (TbCatB) used recently,¹² the value of the relative error in C(i) was found to be 5.7 for microcrystals of 0.9 × 0.9 × 11 μm average size and 10% deviation, with Gaussian distribution (see Appendix A). The shot-to-shot beam intensity fluctuation is 15%, so that the percentage error in a structure factor extracted using the Monte-Carlo approach is

$$\frac{{\sigma }_{\mathit{M}\mathit{C}}^{\left(N\right)}\left(\left|F\right|\right)}{〈\left|F\right|〉}=\frac{1}{2\sqrt{N}}\sqrt{{5.7}^2+15{\%}^2+0{\%}^2}=\frac{2.85}{\sqrt{N}}.$$ (16)

Therefore, for a 1% error tolerance in structure factor magnitude |F|, up to 8.12 × 104 patterns with the Bragg order (hkl) sampled are needed to achieve this accuracy.

From the above analysis, the dominant error contribution comes from the random variation in crystal size, shape, and orientation represented by the first term under the root sign in Eq. (16). The contribution from the shot-to-shot intensity fluctuation represented by the second term could be reduced or even eliminated by measuring the intensity of the incident beam for each shot; however, this required the assumption that the beam hits the center of the crystal, not the side, and these "impact parameters" also affect scaling. Although this effect is relatively small compared to the first term, it does make the Monte-Carlo integration converge faster, and the extracted structure factors achieve a higher accuracy.

B. Two-color approaches for TR-SFX

The two-color approach determines changes in structure factors from two diffraction patterns that are recorded by pulse pairs from the same crystal in the same orientation. Therefore, for each shot (i), $R_{(hkl)}^{(i)}$ is independent of the crystal size, shape, and orientation

$$R_{\left(hkl\right)}^{\left(i\right)}=\sqrt{\frac{{〈I_{2,\left(hkl\right)}^{\left(i\right)}〉|}^{\text{intensity}}}{{〈I_{1,\left(hkl\right)}^{\left(i\right)}〉|}^{\text{intensity}}}{k}_{12}^{\left(i\right)}}-1=R_{\left(hkl\right)},$$ (17)

where R_(hkl) denotes the true value of the change in magnitude of the structure factor (hkl), and k₁₂ is given by Eq. (12).

We estimate $R_{(hkl)}^{(i)}$ with $R_{(hkl)}^{\prime (i)}$ by replacing k₁₂ and the recorded intensities with their expectation values, giving

$$R_{(hkl)}^{\prime (i)}=\sqrt{\frac{I_{1,\left(hkl\right)}^{\left(i\right)}\cdot 〈k_{12}^{\left(i\right)}〉}{I_{1,\left(hkl\right)}^{\left(i\right)}}}-1=\sqrt{A_{\left(hkl\right)}^{\left(i\right)}}-1.$$ (18)

Thus, for each shot (i), the error in the estimate of the change in magnitude of structure magnitude $R_{(hkl)}^{\prime (i)}$ is

$$\begin{array}{c}\sigma \left(R_{(hkl)}^{\prime (i)}\right)=\frac{〈\sqrt{A_{\left(hkl\right)}}〉}{2}\cdot \sqrt{\frac{1}{I_{1,\left(hkl\right)}^{\left(i\right)}}+\frac{1}{I_{2,\left(hkl\right)}^{\left(i\right)}}+{\alpha }^2},\\ \hspace{0.17em}\alpha \equiv \frac{\sigma \left(k_{12}\right)}{〈k_{12}〉}.\end{array}$$ (19)

The percent error in $R_{(hkl)}^{\prime (i)}$ for one shot is inversely related to the intensity of the Bragg beam and directly related to the percentage error in k₁₂, which is denoted by α. Thus, brighter Bragg beams give smaller errors and weaker ones give larger errors. Even for a particular Bragg order and constant incidence fluence, different shots correspond to different points on the rocking curve and thus give different Bragg beam intensities. Therefore, to reduce the error in determination of the percent change in structure factor magnitude, we make use of data from all shots by assigning a weighting function which weighs brighter reflections more than weaker ones [Eq. (20)]. Alternatively, we may simply sum up the intensities from all shots for the same Bragg reflection (hkl) and take the ratio of the sums [Eq. (21)]. This is actually a self-weighted average with the weighting function being the intensity itself. These two methods can be shown to be equivalent, with a proper choice of the weighting function $W_{\mathit{o}\mathit{p}}^{(i)}$ as shown in Eq. (24)

$$1:\hspace{1em}{A}_{(hkl)}^{(N)}=\sum _{i=1}^N{W}^{(i)}{A}_{(hkl)}^{(i)};\hspace{1em}{R}_{(hkl)}^{\prime (N)}=\sqrt{A_{(hkl)}^{(N)}}-1,$$ (20)

$$2:\hspace{1em}{A}_{\left(hkl\right)}^{\left(N\right)}=\frac{\sum _{i=1}^N{I}_{2,\left(hkl\right)}^{\left(i\right)}}{\sum _{i=1}^N{I}_{1,\left(hkl\right)}^{\left(i\right)}}\cdot k_{12}-1;\hspace{1em}{R}_{\left(hkl\right)}^{\prime \left(N\right)}=\sqrt{A_{\left(hkl\right)}^{\left(N\right)}}-1,$$ (21)

$$W_{\mathit{o}\mathit{p}}^{\left(i\right)}=\frac{I_{1,\left(hkl\right)}^{\left(i\right)}}{\sum _{i=1}^N{I}_{1,\left(hkl\right)}^{\left(i\right)}}.$$ (22)

It is shown that $R_{(hkl)}^{\prime (i)}$ is indeed a valid estimate of $R_{(hkl)}$, the true value of relative change in structure factor magnitude $\left|F_{(hkl)}\right|$, and shows that the average value of $R_{(hkl)}^{\prime (i)}$ approaches the true value $R_{(hkl)}$ if the number of shots N is sufficiently large (Appendix B).

According to the theory of error analysis,¹¹ the errors in measured variables propagate into R′ according to

$$\begin{array}{c}\sigma \left(R^{\prime }\right)=\sigma \left(\sqrt{A}\right),\\ =\frac{1}{2}\sqrt{〈A〉}\cdot \sqrt{\frac{1}{\sum _{i=1}^N{I}_2^{\left(i\right)}}+\frac{1}{\sum _{i=1}^N{I}_1^{\left(i\right)}}+{\alpha }^2\cdot \frac{\sum _{i=1}^N{\left(I_2^{\left(i\right)}\right)}^2}{{\left(\sum _{i=1}^N{I}_2^{\left(i\right)}\right)}^2}},\\ =\frac{1}{2}\sqrt{〈A〉}\cdot \sqrt{T1+T2+T3}.\end{array}$$ (23)

We now discuss the error contributions from the terms T1, T2, and T3 above. In Eq. (23), T1, T2, and T3 can be approximately evaluated directly from experimental data, for an given value of the number of shots N. This requires simulations using a full data set of reflections $I_1^{(i)}$ and $I_2^{(i)}$. For a small value of N, this is necessary and can be readily undertaken. However, in case of a large value of N, it is impractical and unnecessary since the sampling can cover the whole intensity distribution of Bragg reflections ergodically, with much less fluctuation than for small values of N. We therefore estimate the error in R′ using the expectation value of the refection intensity $I_1^{(i)}$ and $I_2^{(i)}$ over the entire intensity distribution

$$\sigma \left(R^{\prime }\right)=\frac{1}{2}\sqrt{〈A〉}\cdot \sqrt{T1+T2+T3},$$ (24)

$$\hspace{1em}\hspace{1em}\hspace{0.17em}\underset{¯}{\underset{¯}{N\to \infty }}\frac{1}{2}\sqrt{〈A〉}\cdot \sqrt{\frac{1}{{〈I_2^{\left(i\right)}〉|}_{\text{shots}}^{\text{intensity}}}+\frac{1}{{〈I_1^{\left(i\right)}〉|}_{\text{shots}}^{\text{intensity}}}+\left(1+{\beta }^2\right){\alpha }^2}\cdot \frac{1}{\sqrt{N}},$$ (25)

where ${〈I_1^{(i)}〉|}_{\text{shots}}^{\text{intensity}}$ and ${〈I_2^{(i)}〉|}_{\text{shots}}^{\text{intensity}}$ are the expectation values over the distribution of Bragg reflection intensities from the first and second pulses, respectively. β is the relative standard deviation in $I_2^{(i)}$ over the rocking curve, and α denotes the relative error in $k_{12}$. The ratio of the intensities of the two pulses $k_{12}$ varies from shot to shot, and this fluctuation is characterized by α and determined by the stability of the emittance spoiler as well as the photon generating process (SASE (self-amplified spontaneous emission) or self-seeded).⁹ Using the two-color approach, this may depend on the stability of the seeding process.

As shown by Eq. (25), with a sufficiently large number of diffraction patterns, the error in R′ depends on the Bragg beam intensity via T1 and T2, the accuracy of the incident flux ratio α, and the statistics of nano-crystal size, shape, and orientation distribution β (which may be evaluated by Monte-Carlo simulation) via T3. Among the three contributing terms, T1 and T2 are dependent on experimental conditions, such as the flux of the two pulses and their ratio, while T3 is determined by the photon generation stability, and the nano-crystal samples.

Contributions from these terms are determined by the parameters of the sample and the experimental settings, such as the statistics of nano-crystal size, shape, orientation, X-ray flux, the relative intensity of the paired pulses, and the stability of the LCLS system. Without involving specific instrumental specifications and parameters, we can discuss below two different regimes of experiments: a relatively high flux of both of the paired pulses with unstable beam intensity ratio (e.g., two-color) and low flux for the first pulse, with perfect beam intensity control (as expected from a beam-splitting device).

In the case of high X-ray flux and unstable beam intensity, we expect small Poisson noise due to counting at the detector, but a large error in control of the relative intensity of the two pulses. Then, in Eq. (25), T3 would dominate over the negligible terms T1 and T2. Assuming the same value of β = 5.7 as in the Monte-Carlo approach, the error in R′ is

$$\sigma \left(R^{\prime }\right)\approx 2.89\sqrt{〈A〉}\cdot \alpha \cdot \frac{1}{\sqrt{N}},$$ (26)

which indicates that the error in the determination of the relative change of structure factor magnitudes is proportional to the relative error in the intensity ratio of the two paired pulses and hence depends on the stability of the emittance spoiler and the photon generation process. This error decreases as the square root of the number of patterns recorded, which is similar to the Monte-Carlo approach [Eq. (15)] but with a prefactor $\sqrt{〈A〉}\cdot \alpha$. Comparing split-and-delay and Monte-Carlo approaches, we can easily establish a criterion for superiority of the former over the latter

$$\alpha \cdot \sqrt{〈A〉}<1.$$ (27)

For 20% change in structure factor magnitude as an example, the critical value of α is 0.83. In other words, any two-color system with an error of less than 83% in intensity ratio makes the two-color approach preferable.

In the case of a weak first pulse (which does not destroy the sample) but with perfect beam intensity control, the Poisson noise T1 and T2 become the dominant error contribution rather than the negligible relative intensity fluctuation T3. Then, the error in R′ is

$$\begin{array}{c}\sigma \left(R^{\prime }\right)\approx \frac{1}{2}\sqrt{〈A〉}\cdot \sqrt{\frac{1}{\sum _{i=1}^N{I}_2^{\left(i\right)}}+\frac{1}{\sum _{i=1}^N{I}_1^{\left(i\right)}}},\\ \approx \left(\frac{\sqrt{2}}{2}\sqrt{〈A〉}\cdot \sqrt{\frac{1}{〈I〉}}\right)\frac{1}{\sqrt{N}}.\end{array}$$ (28)

Thus, the error is now independent of the specific statistics of the nano-crystal samples and is only determined by the summed reflection intensities from all patterns. Additionally, a smaller error is expected for a brighter Bragg reflection than a weaker one. For TbCatB crystals of 0.9 × 0.9 × 11 μm average size, assuming structure factors F ∼ 10⁴, an X-ray beam with photon energy of 9.4 keV, and beam diameter of 4 μm, at the Henderson "safe-dose" limit²⁸ of 1 MGy at room temperature (allowing study of dynamics), the average number of photons of a reflection in a pattern is estimated to be 77. Hence, the error in R′ is

$$\sigma \left(R^{\prime }\right)\approx 0.087\frac{1}{\sqrt{N}}.$$ (29)

For two-color experiments, the intensity or energy of each pulse can be measured by using a in-line spectrometer.²⁶ In this case, the uncertainty in k₁₂, denoted by α, becomes dependent on the accuracy of the intensity measurements. The error in R′ is then equal to that given by Eq. (28).

C. Fixed-sample experiments with goniometer

With sample fixed to a holder and a goniometer, the crystal orientation can be controlled accurately to facilitate scans across the rocking curve. In contrast to the stills obtained from different crystals in random orientations, this scan process may generate a sampling over the angular profile of the Bragg reflections with equally spaced increments and the relative error due to Poisson noise in intensity measurement is

$$\begin{array}{c}\frac{{\sigma }_R\left(\left|F_{\mathit{e}\mathit{s}}\right|\right)}{〈\left|F_{\mathit{e}\mathit{s}}\right|〉}=\frac{1}{2}\sqrt{{\left(\frac{\sigma \left(\Delta \Psi \right)}{{\Psi }_T}\right)}^2\left(1+{\beta }^2\right)N_s+\frac{1}{{〈I〉|}_{\text{intensity}}^{\text{shots}}{N}_s}},\\ =\frac{1}{2}\sqrt{E1+E2},\end{array}$$ (30)

where $\Psi$ is the angular variable, as the abscissa of the rocking curve. ${\Psi }_T$ is the total angular width of the rocking curve and $\Delta \Psi$ is the sampling increment. Ns is the number of sampling points and ${〈I〉|}_{\text{intensity}}^{\text{shots}}$ denotes the mean intensity of each sample point averaged over both Poisson noise and the entire rocking curve. $\beta$ is the relative standard deviation in measured intensity over the rocking curve, consistent with the previous discussion of the Monte-Carlo and two-color approaches. Beside the error contributions from goniometer control and intensity measurement, another contribution comes from the systematic error resulting from integration by quadrature. For one-point quadrature, the error is proportional to square of the sampling increment $\Delta \Psi$ and the first derivative of the curve $f^{\prime }$¹³

$${\sigma }_S\left({\left|F_{\mathit{e}\mathit{s}}\right|}^2\right)=O\left(f^{\prime }\cdot \Delta {\Psi }^2\right)\propto \frac{1}{N_s^2}.$$ (31)

In the destructive-readout mode, where the X-ray beam must be translated to a fresh point on the sample sufficiently far away from the hole drilled by the previous shot to avoid damage, fixed-sample experiments sampling rocking curves with even increments and maximum beam intensity would give a random error which goes as $\frac{1}{\sqrt{N_s}}$ as indicated by Eq. (30). (We assume perfect goniometer control.) In this regard, fixed-sample experiments and M.C. experiments are essentially equivalent from the point of view of error reduction and data efficiency. However, the prefactor in the M.C. approach is much larger than in the fixed-sample approach since the former uses a random sampling, whereas crystal orientation and sampling are totally controllable using a goniometer. For CXI beam line at LCLS, with a typical pulse energy of 2 mJ, the estimated average photon counts for the same condition are approximately 100 times than that of the non-destructive mode resulting in the prefactor of 0.0057. We must also note that, however, the number of shots we can take on a single large crystal Ns is limited by the crystal size as well as the safe distance between shots to avoid radiation damage caused by previous shots. Therefore, an upper limit might exist for the accuracy in structure factor measurement using this diffract-and-destroy mode in fixed sample experiments.

If the beam intensity is adjusted below the Henderson safe dose threshold so that the sample is not destroyed, the error from a fixed sample is then

$$\begin{array}{c}\frac{{\sigma }_{R,min}\left(\left|F_{\mathit{e}\mathit{s}}\right|\right)}{〈\left|F_{\mathit{e}\mathit{s}}\right|〉}=\frac{1}{2}\sqrt{E1+E2},\\ \approx \frac{1}{2}\sqrt{E2}=\frac{1}{2}\sqrt{\frac{1}{{〈I〉|}_{\text{intensity}}^{\text{shots}}{N}_s}},\\ \propto \frac{1}{2}{\left|F\right|}^{-1}\sqrt{\frac{1}{D_H\rho \text{LA}}},\end{array}$$ (32)

where $D_H$ is the Henderson safe dose, $\rho$ is the mass density, L is the attenuation length of the sample, $\left|F\right|$ is the magnitude of the structure factor, and $A$ is the effective beam area. Equation (32) indicates that the random Poisson error in detector counts is independent of the number of sampling points on the rocking curve and is only dependent on the sample and X-ray beam parameters. This is reasonable, since the total photon signal is limited by the Henderson safe dose no matter how many sampling points are used in a scan. Therefore, combining systematic and random errors for consideration, an optimal value of Ns exists for minimal error [Eqs. (31) and (32)].

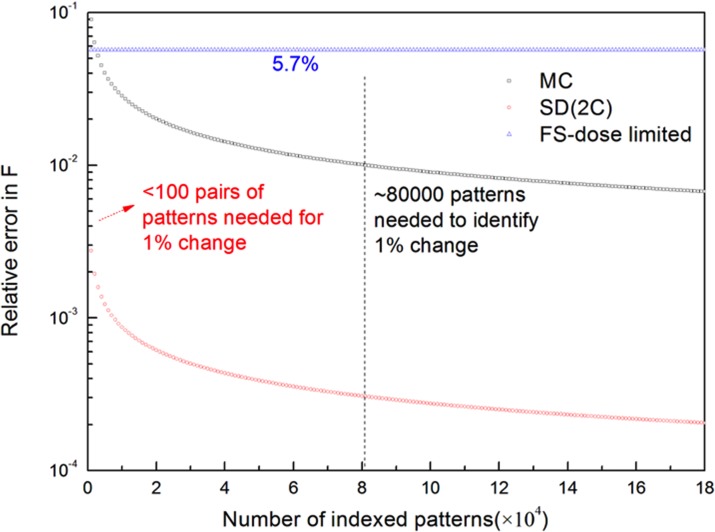
To determine the experimental design, detailed simulations need to be carried out to estimate the errors in the different approaches for specific samples. For TbCatB crystals¹² of 0.9 × 0.9 × 11 μm average size, assuming a structure factor F ∼ 10⁴, a photon energy of 9.4 keV, and a beam diameter of 4 μm, the Henderson dose limit of 1 MGy at room temperature, we show the number of patterns needed to achieve 1% accuracy in structure factor measurement for Monte-Carlo, two-color, and goniometer-based XFEL experiments in Fig. 1. The error follows the inverse square root rule ($1/\sqrt{N_s}$) in the Monte-Carlo, two-color, or split-and-delay approaches. However, the error falls more rapidly with number of diffraction patterns for the two-color or split-and-delay method than for the Monte-Carlo approach. To identify a 1% change in a structure factor in pump-probe experiments, less than 100 pairs of patterns with the corresponding Bragg order indexed are needed for the two-color or split-and-delay approach, whereas 80 000 patterns are required in the conventional Monte-Carlo approach. This improvement in error reduction and data efficiency is a direct result of the elimination of the stochastic factors, such as random orientation and varying size and shape of the crystals. Two-color or split-and-delay experiments have the advantage of sensitivity to change in structure factors over the other approaches, rather than any superior accuracy of direct structure-factor measurement. At the safe dose which minimizes damage, fixed-sample experiments give an error independent of sampling procedure, but limited by the X-ray dose the sample can tolerate. Complete data sets must be obtained to solve the time-resolved structure. The number of patterns required for this purpose is definitely much more than the number of patterns needed to achieve a certain accuracy in a single structure factor since we need sufficient patterns that cover the whole reciprocal space to produce the electron density maps. We assume that the number of patterns needed to form a complete data in two-color approach is about the same as that needed in liquid jet sample delivery, based on the Monte-Carlo approach, since the statistics of the crystal orientation distribution is the same for both methods. Also, in case that the crystal is much larger than the typical beam size of 4 μm, we can expand the beam to match the size of the crystal by defocussing, to maximize the total signal hence to reduce the error in structure factor measurement. An increase in the beam size by the factor of 25 (100 μm) reduces the error in fixed sample experiments to approximately 1%, which is comparable to the other approaches. But certainly, larger crystals not only favor the fixed sample experiments but are also preferred in all modes, since they yield stronger diffraction signals and so higher resolution data unless this is limited by crystal quality.

FIG. 1.

Relative error in structure factor magnitude measured in Monte-Carlo (MC, middle curve), split-and-delay or two-color (SD, 2C, lower curve), and non-destructive mode of goniometer-based fixed sample (FS, upper curve) approaches for TR-SFX. To identify 1% change in structure factor in pump-probe experiments, less than 100 pairs of patterns are needed in two-color or split-and-delay mode, compared to approximately 80 000 patterns required in the Monte-Carlo approach. The non-destructive mode of goniometer-based fixed sample approach gives an error limited by the X-ray dose, but independent of sampling. The diffract-and-destroy mode, using fixed samples, yields an error with a prefactor of 0.57%, but the number of patterns collected from one single crystal is limited by the crystal size and the distance between consecutive shots in order to avoid radiation damage. Diffraction from micro-crystals trapped on a calibrated lattice follows essentially the same error reduction behavior as the Monte-Carlo approach using the liquid jet delivery system.

IV. DISCUSSION AND CONCLUSION

The Monte-Carlo approach has been widely adopted for (SFX in recent years. Using tens of thousands of patterns, merged partial intensities converge accurately to yield the structure factors, allowing structures to be solved at better than 0.2 nm resolution which might not otherwise have been solved due to small crystal size or radiation sensitivity.²⁴ The low data efficiency mainly results from uncontrollable stochastic variables contributing to the error in structure factors. These contributions add in quadrature, and the large intensity variation of the same Bragg reflection on different shots (covering several orders of magnitude) due to partiality (i.e., different deviations from the exact Bragg condition) dominates the error in the Monte-Carlo approach.

To improve on the traditional Monte-Carlo integration and merging procedure, new methods of treating the partial intensities, intensity integration, scaling, and post-refinement have been proposed and studied. By modeling the angular profile of the Bragg spots from mosaic crystals,² an integration mask can be customized for each reflection. Using a geometrical model for partiality, the diffraction conditions for each pattern can be refined to estimate the partiality, so that full reflection intensities can be predicted, and this refinement procedure repeated iteratively to obtain the best estimate.¹⁴ Common reflections on different shots also assist scaling, using post-refinement and the Ewald offset correction, which assumes a Gaussian rocking curve for a sufficiently large crystal.¹⁵ Our two-color method complements these algorithmic approaches for improved accuracy, going beyond the Monte-Carlo method, for time-resolved diffraction.

The two-color approach eliminates variations in crystal size, shape, and orientation which dominate the Monte-Carlo approach, by probing the same crystal twice in the same orientation with two pulses of different energies, separated in time. The ratio of partial intensities of Bragg spots with identical Miller indices from two pulses is recorded for each pattern and then summed with a weighting to obtain the percentage change in structure factor. The accuracy in structure factor change is determined by the total signal summed over all patterns. Therefore, in spite of the low dose limit for the first pulse (which must not destroy the crystal), the accuracy improves with the number of patterns collected. For the TbCatB crystals used recently,¹³ at the Henderson safe dose limit of 1 MGy at room temperature, less than 100 patterns are needed to achieve 1% accuracy, compared to 80 000 patterns for the Monte-Carlo approach (Fig. 1). From the point of view of error reduction and data efficiency, the two-color approach appears to be a better choice for pump-probe time-resolved experiments, provided that a sufficiently long delay between X-ray pulses can be obtained for the process of interest.

A difference Fourier charge-density map is normally applied to study structural changes. The difference map shows changes in the electron density much more sensitively than a normal Fourier Map.²⁷ With unknown phases, the peak height in a map is half that with phase information¹⁷ if the conditions Δ|F|/|F| ≪ 1 and σ(Δ|F|)/Δ|F| ≪ 1 are satisfied. For most pump-probe experiments, these conditions are satisfied, making the difference Fourier map applicable to two-color data.

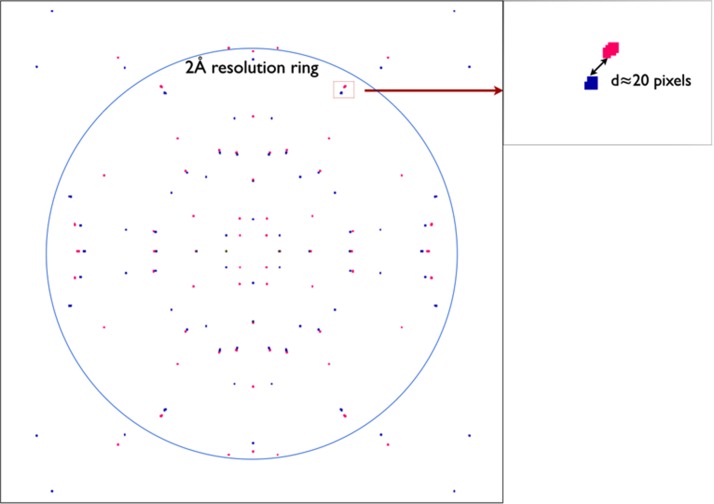
However, our two-color approach and error analysis are based on several essential assumptions which must be considered here. First, the time interval between the two pulses must be much shorter than the rotational diffusion time of the crystal in solution (typically milliseconds for a 1–μm crystallite in buffer) so that it can be treated as stationary. Second, the difference in wavelength between the two pulses must be sufficient to separate the two diffraction patterns in the same readout, but not too large so that the corresponding Ewald spheres are far from each other intersecting different Bragg reflections. Third, the crystal size must neither be too small such that the broad shape transform will not allow us to separate the two patterns nor too big to invalidate our shape transform analysis. (Our error analysis assumes that the two patterns are taken from almost the same point on the rocking curve.) To investigate these assumptions for future two-color experiments, diffraction patterns from I3C (“magic triangle”)²⁶ micron-sized inorganic crystals were simulated for X-ray pulses at energies of 6.6 keV and 6.685 keV, as shown in Fig. 2. Using the CSPAD (Cornell-SLAC hybrid pixel array detector) detector at LCLS with the minimum working distance of 5 mm, the 85 eV (1.3%) energy difference shifts the Bragg spots by approximately 20 pixels at the 2 Å resolution ring, which corresponds to the side edge of the detector. Since the relative displacement between the Bragg spots of the same Miller index increases with resolution, the Bragg reflections at low resolution can be separated by using a larger working distance or an additional back detector, illuminated by a central hole in the front detector. Over the past year, there have been dramatic advances in the ability to model partiality for SFX data from several groups, using iterative optimization algorithms and a suitable model for mosaicity.^2,15,16,24 If we use these methods to model the partiality for each wavelength separately on the same detector readout, the resulting more realistic results will fall somewhere between the Monte-Carlo error curve and two-color error curve (Figure 1), since curve “2C” assumes no difference in partialities of the two wavelengths.

FIG. 2.

Simulated diffraction pattern ((100) plane) from I3C (“magic triangle”) crystals (orthorhombic. Pbca, a = 9.214 Å, b = 15.735 Å, and c = 18.816 Å) using X-ray pulses at energies of 6.6 keV and 6.685 keV in two-color approach. Crystal size is 0.005 μm × 1.3 μm × 1.5 μm and identical intensity for all Bragg reflections is assumed just to show the Bragg spot positions. Red and blue colors indicate Bragg spots from 6.6 keV and 6.685 keV, respectively. Bragg spots of same index from two colors are clearly separated by detectable displacements. The displacement is approximately 20 pixels at 2 Å resolution ring on CSPAD detector at LCLS with the minimum working distance of 5 mm.

Goniometer-based fixed-sample experiments provide accurate control of the crystal orientation which our SFX experiments are not capable of. In destructive mode, each X-ray shot drills a hole in the crystal, which must be translated to a fresh point for the next shot. Beam intensity is maximized to obtain the highest SNR and the error decreases as the inverse square root of the number of patterns, which is similar to the Monte-Carlo approach, except that the prefactor is much smaller due to the accurate control of crystal orientation. With the beam attenuated or defocussed to a level below the damage threshold, goniometer-based experiments allow us to probe the same region of a sample in different orientations from which local information on structures or dynamics can be extracted. The low dose limit gives poorer statistics, and the error in the measured structure factor is found to be independent of the number of sampling points (or patterns from the same region) and is only determined by the total dose deposited into the probed region of the crystal.

APPENDIX A: STATISTICS OF TbCatB CRYSTAL SHAPE TRANSFORM CALCULATED BY MONTE-CARLO SIMULATION

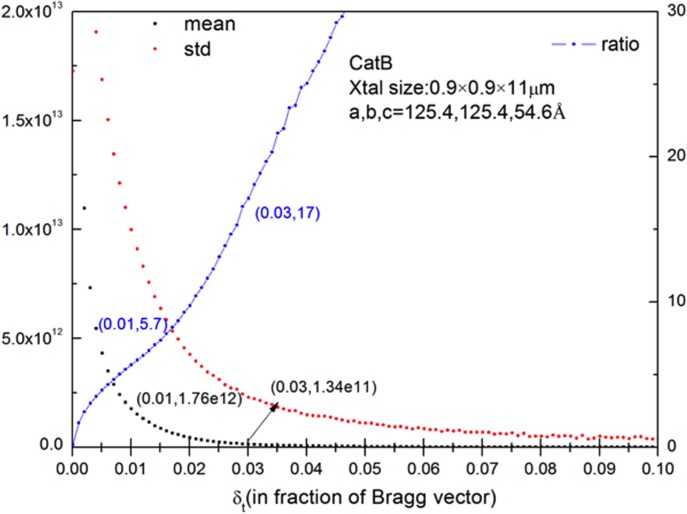
To characterize the source of errors in XFEL experiments, Monte-Carlo simulations were conducted to estimate the dominant contribution from the large intensity fluctuation across the shape transform based on its statistics. Shape transforms were modeled using Eq. (4) for TbCatB crystals¹³ of 0.9 × 0.9 × 11 μm average size with 10% Gaussian-distributed deviation. Statistics of intensity variation across the shape transform depends on the integration radius δ_t. Therefore, mean value, standard deviation, and their ratio (relative deviation) were calculated as functions of δ_t as a fraction of the scattering vector (Fig. 3). δ_t ranges from 0 to 0.1 with an increment of 0.01, and for each value of δ_t, 10⁶ sampling points on the shape transform were randomly generated for a uniform distribution. At δ_t = 0.01, which matches the average size of the crystal, the mean value and the relative deviation of the shape transform for TbcatB crystals were found to be 1.76 × 10¹² and 5.7, respectively.

FIG. 3.

Statistics (mean, standard deviation, and relative deviation/ratio) of TbcatB crystal shape transform obtained from Monte-Carlo simulation. 10% standard deviation in crystal size was assumed based on experimental data.¹² The abscissa δ_t is the integration radius around Bragg peaks; left vertical axis shows the mean and standard deviation values; right vertical axis shows the relative deviation/ratio.

APPENDIX B: ERROR ANALYSIS FOR TWO-COLOR APPROACH

According to error propagation theory,¹² errors in different variables are related as follows:

$$\sigma (R_{(hkl)}^{\prime (i)})=\sigma (\sqrt{A_{(hkl)}^{(i)}}),$$ (B1)

$$\frac{\sigma \left(\sqrt{A_{\left(hkl\right)}^{\left(i\right)}}\right)}{〈\sqrt{A_{\left(hkl\right)}^{\left(i\right)}}〉}=\frac{1}{2}\frac{\sigma \left(A_{\left(hkl\right)}^{\left(i\right)}\right)}{〈A_{\left(hkl\right)}^{\left(i\right)}〉},$$ (B2)

$$\frac{\sigma \left(A_{\left(hkl\right)}^{\left(i\right)}\right)}{〈A_{\left(hkl\right)}^{\left(i\right)}〉}=\sqrt{{\left(\frac{\sigma \left(I_{1,\left(hkl\right)}^{\left(i\right)}\right)}{I_{1,\left(hkl\right)}^{\left(i\right)}}\right)}^2+{\left(\frac{\sigma \left(I_{2,\left(hkl\right)}^{\left(i\right)}\right)}{I_{2,\left(hkl\right)}^{\left(i\right)}}\right)}^2+{\left(\frac{\sigma \left(k_{12}\right)}{k_{12}}\right)}^2},$$ (B3)

$$\sigma \left(I_{1,\left(hkl\right)}^{\left(i\right)}\right)=\sqrt{I_{1,\left(hkl\right)}^{\left(i\right)}}\hspace{0.17em};\hspace{1em}\sigma \left(I_{2,\left(hkl\right)}^{\left(i\right)}\right)=\sqrt{I_{2,\left(hkl\right)}^{\left(i\right)}}\hspace{0.17em};\hspace{1em}\alpha \equiv \frac{\sigma \left(k_{12}\right)}{k_{12}},$$ (B4)

$$\sigma \left(R_{(hkl)}^{\prime (i)}\right)=\frac{〈\sqrt{A_{\left(hkl\right)}}〉}{2}\cdot \sqrt{\frac{1}{I_{1,\left(hkl\right)}^{\left(i\right)}}+\frac{1}{I_{2,\left(hkl\right)}^{\left(i\right)}}+{\alpha }^2}.$$ (B5)

In order to analyze the error in ${R^{\prime }}_{(hkl)}^{(N)}$, we express it explicitly in terms of the experimentally measured parameters as below

$${R^{\prime }}_{\left(hkl\right)}^{\left(N\right)}=\sqrt{\frac{\sum _{i=1}^N{I}_{2,\left(hkl\right)}^{\left(i\right)}\cdot 〈k_{12}^{\left(i\right)}〉}{\sum _{i=1}^N{I}_{1,\left(hkl\right)}^{\left(i\right)}}}-1.$$ (B6)

To show that ${R^{\prime }}_{(hkl)}^{(N)}$ is indeed a valid estimate of $R_{(hkl)}$ which is the true value of the relative change in structure factor magnitude $\left|F_{(hkl)}\right|$, we show that the average value (expectation) of ${R^{\prime }}_{(hkl)}^{(N)}$ approaches the true value $R_{(hkl)}$ when the number of shots N is sufficiently large. The average value of ${R^{\prime }}_{(hkl)}^{(N)}$ is

$${〈{R^{\prime }}_{\left(hkl\right)}^{\left(N\right)}〉|}^{\text{intensity}}=\sqrt{\frac{\sum _{i=1}^N{〈I_{2,\left(hkl\right)}^{\left(i\right)}〉|}^{\text{intensity}}\cdot 〈k_{12}^{\left(i\right)}〉}{\sum _{i=1}^N{〈I_{1,\left(hkl\right)}^{\left(i\right)}〉|}^{\text{intensity}}}}-1.$$ (B7)

We define Δ⁽ⁱ⁾ as the discrepancy between $k_{12}^{(i)}$ and its expectation value $〈k_{12}^{(i)}〉$

$${\Delta }^{(i)}\equiv k_{12}^{(i)}-〈k_{12}〉.$$ (B8)

Then, Eq. (B7) can be rewritten as

$${〈{R^{\prime }}_{\left(hkl\right)}^{\left(N\right)}〉|}^{\text{intensity}}=\sqrt{\frac{\sum _{i=1}^N{〈I_{2,\left(hkl\right)}^{\left(i\right)}〉|}^{\text{intensity}}\cdot k_{12}^{\left(i\right)}}{\sum _{i=1}^N{〈I_{1,\left(hkl\right)}^{\left(i\right)}〉|}^{\text{intensity}}}-\frac{\sum _{i=1}^N{〈I_{2,\left(hkl\right)}^{\left(i\right)}〉|}^{\text{intensity}}\cdot {\Delta }^{\left(i\right)}}{\sum _{i=1}^N{〈I_{1,\left(hkl\right)}^{\left(i\right)}〉|}^{\text{intensity}}}}-1.$$ (B9)

If the number of shots N goes to infinity, or more practically, we have a sufficiently large number of shots from which diffraction patterns are collected; the second term under the square root sign approaches 0

$$\underset{N\to \infty }{\lim }\left(\frac{\sum _{i=1}^N{〈I_{2,\left(hkl\right)}^{\left(i\right)}〉|}^{\text{intensity}}\cdot {\Delta }^{\left(i\right)}}{\sum _{i=1}^N{〈I_{1,\left(hkl\right)}^{\left(i\right)}〉|}^{\text{intensity}}}\right)=〈{\Delta }^{\left(i\right)}〉=0.$$ (B10)

Hence, the average of ${R^{\prime }}_{(hkl)}^{(N)}$ approaches the true value $R_{(hkl)}$

$$\underset{N\to \infty }{\lim }{R^{\prime }}_{(hkl)}^{(N)}=R_{(hkl)}.$$ (B11)

Therefore, ${R^{\prime }}_{(hkl)}^{(N)}$ is a good estimate of the relative change in structure factor magnitude.

We now omit the Bragg order index (hkl) from subscripts and (N) from superscripts. Additionally, we define some auxiliary variables for notational convenience as follows:

$$R^{\prime }=\sqrt{A}-1,$$ (B12)

$$A=\frac{\sum _{i=1}^N\left(I_2^{\left(i\right)}〈k_{12}〉\right)}{\sum _{i=1}^N{I}_1^{\left(i\right)}}\equiv \frac{B}{D},$$ (B13)

$$B=\sum _{i=1}^N{B}^{(i)}\hspace{0.17em};\hspace{1em}{B}^{(i)}=(I_2^{(i)}〈k_{12}〉)\hspace{0.17em};\hspace{1em}D=\sum _{i=1}^N{I}_1^{(i)}.$$ (B14)

According to the theory of errors, the errors in the different variables are related as follows:

$$\sigma (R^{\prime })=\sigma (\sqrt{A}),$$ (B15)

$$\frac{{\sigma }^2\left(A\right)}{{〈A〉}^2}=\frac{{\sigma }^2\left(B\right)}{{〈B〉}^2}+\frac{{\sigma }^2\left(D\right)}{{〈D〉}^2},$$ (B16)

$$B^{(i)}=(I_2^{(i)}\cdot 〈k_{12}〉),$$ (B17)

$$\frac{{\sigma }^2\left(B^{\left(i\right)}\right)}{{〈B^{\left(i\right)}〉}^2}=\frac{1}{〈I_2^{\left(i\right)}〉}+{\left(\frac{\sigma \left(k_{12}\right)}{〈k_{12}〉}\right)}^2=\frac{1}{〈I_2^{\left(i\right)}〉}+{\alpha }^2,$$ (B18)

$$\begin{array}{c}{\sigma }^2\left(B\right)=\sum _{i=1}^N{\sigma }^2\left(B^{\left(i\right)}\right),\\ \hspace{1em}\hspace{1em}=\sum _{i=1}^N\left({〈I_2^{\left(i\right)}〉}^2{〈k_{12}〉}^2\left(\frac{1}{〈I_2^{\left(i\right)}〉}+{\alpha }^2\right)\right),\end{array}$$ (B19)

$${\sigma }^2(D)=\sum _{i=1}^N{\sigma }^2(I_1^{(i)})=\sum _{i=1}^N〈I_1^{(i)}〉.$$ (B20)

Combining Eqs. (B15)–(B20), we obtain the error in A, hence R′

$$\begin{array}{c}\frac{{\sigma }^2\left(A\right)}{{〈A〉}^2}=\frac{\sum _{i=1}^N\left({〈I_2^{\left(i\right)}〉}^2{〈k_{12}〉}^2\left(\frac{1}{〈I_2^{\left(i\right)}〉}+{\alpha }^2\right)\right)}{{〈\sum _{i=1}^N{I}_2^{\left(i\right)}〉}^2{〈k_{12}〉}^2}+\frac{\sum _{i=1}^N〈I_1^{\left(i\right)}〉}{{〈\sum _{i=1}^N{I}_1^{\left(i\right)}〉}^2},\\ =\frac{1}{\sum _{i=1}^N〈I_2^{\left(i\right)}〉}+\frac{1}{\sum _{i=1}^N〈I_1^{\left(i\right)}〉}+{\alpha }^2\cdot \frac{\sum _{i=1}^N{〈I_2^{\left(i\right)}〉}^2}{{〈\sum _{i=1}^N〈I_2^{\left(i\right)}〉〉}^2},\\ \approx \frac{1}{\sum _{i=1}^N{I}_2^{\left(i\right)}}+\frac{1}{\sum _{i=1}^N{I}_1^{\left(i\right)}}+{\alpha }^2\cdot \frac{\sum _{i=1}^N{\left(I_2^{\left(i\right)}\right)}^2}{{\left(\sum _{i=1}^N{I}_2^{\left(i\right)}\right)}^2},\\ \equiv T1+T2+T3,\end{array}$$ (B21)

$$\sigma \left(R^{\prime }\right)=\sigma \left(\sqrt{A}\right)=\frac{1}{2}\sqrt{〈A〉}\cdot \sqrt{T1+T2+T3}.$$ (B22)

In case of a large value of N, the sampling can cover the whole intensity distribution of Bragg reflections ergodically with much less fluctuation than for small values of N. Instead of using Eq. (B21), we estimate the error in R′ using the expectation value of the refection intensity $I_1^{(i)}$ and $I_2^{(i)}$ over the entire intensity distribution

$$\underset{N\to \infty }{\lim }T1=\frac{1}{N}\frac{1}{{〈I_2^{\left(i\right)}〉|}_{\mathit{s}\mathit{h}\mathit{o}\mathit{t}\mathit{s}}^{\text{intensity}}},$$ (B23)

$$\underset{N\to \infty }{\lim }T2=\frac{1}{N}\frac{1}{{〈I_1^{\left(i\right)}〉|}_{\mathit{s}\mathit{h}\mathit{o}\mathit{t}\mathit{s}}^{\text{intensity}}},$$ (B24)

$$\underset{N\to \infty }{\lim }\frac{\sum _{i=1}^N{〈I_2^{\left(i\right)}〉}^2}{{〈\sum _{i=1}^N{I}_2^{\left(i\right)}〉}^2}=\frac{N{\left({〈I_2^{\left(i\right)}〉}^2\right)|}_{\text{shots}}^{\text{intensity}}}{{\left(N{〈I_2^{\left(i\right)}〉|}_{\text{shots}}^{\text{intensity}}\right)}^2},$$ (B25)

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{N({(〈I_2^{\left(i\right)}〉{|}_{\text{shots}}^{\text{intensity}})}^2+{\sigma }^2(I_2^{\left(i\right)}))}{N^2{(〈I_2^{\left(i\right)}〉{|}_{\text{shots}}^{\text{intensity}})}^2},$$ (B26)

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{1}{N}\left(1+{\left(\frac{\sigma \left(I_2^{\left(i\right)}\right)}{{〈I_2^{\left(i\right)}〉|}_{\text{shots}}^{\text{intensity}}}\right)}^2\right),$$ (B27)

$$\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\frac{1}{N}\left(1+{\beta }^2\right),$$ (B28)

$$\beta \equiv \frac{\sigma \left(I_2^{\left(i\right)}\right)}{{〈I_2^{\left(i\right)}〉|}_{\text{shots}}^{\text{intensity}}},$$ (B29)

$$\underset{N\to \infty }{\mathit{l}\mathit{i}\mathit{m}}T3=\frac{1}{N}\left(1+{\beta }^2\right){\alpha }^2.$$ (B30)

Therefore, the error in R′ can be estimated as below

$$\sigma \left(R^{\prime }\right)=\frac{1}{2}\sqrt{〈A〉}\cdot \sqrt{T1+T2+T3},$$ (B31)

$$\hspace{1em}\hspace{1em}\hspace{0.17em}\underset{¯}{\underset{¯}{N\to \infty }}\frac{1}{2}\sqrt{〈A〉}\cdot \sqrt{\frac{1}{{〈I_2^{\left(i\right)}〉|}_{\text{shots}}^{\text{intensity}}}+\frac{1}{{〈I_1^{\left(i\right)}〉|}_{\text{shots}}^{\text{intensity}}}+\left(1+{\beta }^2\right){\alpha }^2}\cdot \frac{1}{\sqrt{N}},$$ (B32)

where ${〈I_1^{(i)}〉|}_{\text{shots}}^{\text{intensity}}$ and ${〈I_2^{(i)}〉|}_{\text{shots}}^{\text{intensity}}$ are the expectation values over the rocking curve of the reflection intensities from the first and second pulses, respectively. β is the relative standard deviation in $I_2^{(i)}$ over the rocking curve and α denotes the relative error in $k_{12}$. The ratio of the intensities of the two pulses $k_{12}$ varies from shot to shot, and this amplitude of fluctuation is characterized by α and determined by the stability of the emittance spoiler in the delay line.