Subsecond dopamine fluctuations in human striatum encode superposed error signals about actual and counterfactual reward

Significance

There is an abundance of circumstantial evidence (primarily work in nonhuman animal models) suggesting that dopamine transients serve as experience-dependent learning signals. This report establishes, to our knowledge, the first direct demonstration that subsecond fluctuations in dopamine concentration in the human striatum combine two distinct prediction error signals: (i) an experience-dependent reward prediction error term and (ii) a counterfactual prediction error term. These data are surprising because there is no prior evidence that fluctuations in dopamine should superpose actual and counterfactual information in humans. The observed compositional encoding of “actual” and “possible” is consistent with how one should “feel” and may be one example of how the human brain translates computations over experience to embodied states of subjective feeling.

Abstract

In the mammalian brain, dopamine is a critical neuromodulator whose actions underlie learning, decision-making, and behavioral control. Degeneration of dopamine neurons causes Parkinson’s disease, whereas dysregulation of dopamine signaling is believed to contribute to psychiatric conditions such as schizophrenia, addiction, and depression. Experiments in animal models suggest the hypothesis that dopamine release in human striatum encodes reward prediction errors (RPEs) (the difference between actual and expected outcomes) during ongoing decision-making. Blood oxygen level-dependent (BOLD) imaging experiments in humans support the idea that RPEs are tracked in the striatum; however, BOLD measurements cannot be used to infer the action of any one specific neurotransmitter. We monitored dopamine levels with subsecond temporal resolution in humans (n = 17) with Parkinson’s disease while they executed a sequential decision-making task. Participants placed bets and experienced monetary gains or losses. Dopamine fluctuations in the striatum fail to encode RPEs, as anticipated by a large body of work in model organisms. Instead, subsecond dopamine fluctuations encode an integration of RPEs with counterfactual prediction errors, the latter defined by how much better or worse the experienced outcome could have been. How dopamine fluctuations combine the actual and counterfactual is unknown. One possibility is that this process is the normal behavior of reward processing dopamine neurons, which previously had not been tested by experiments in animal models. Alternatively, this superposition of error terms may result from an additional yet-to-be-identified subclass of dopamine neurons.

Dopamine is an essential neuromodulator whose presence is required for normal learning, decision-making, and behavioral control (1, 2) and whose absence or dysfunction is associated with a variety of disease states including Parkinson’s disease, schizophrenia, addiction, and depression (3–7). Experiments in animal models support the hypothesis that changes in dopamine release at target neural structures encode reward prediction errors (RPEs) (the difference between actual and expected outcomes) important for learning and value-based decision-making (1, 8–12). In support of this claim, direct recordings of spike activity in mesencephalic dopaminergic neurons in nonhuman primates demonstrate that these neurons encode prediction errors in future reward delivery (8–10, 13, 14) and they may also encode other computations relevant for reward-guided actions (1, 15–17). However, action potential production in brainstem dopaminergic neurons can only be part of the story because activity in parent axons must be converted to changes in neurotransmitter release at synaptic terminals to have any impact on downstream neural systems (1, 18). There have been no direct measurements of dopamine release in human striatum that tests these ideas directly. In a large cohort of human subjects (n = 17), we tested the hypothesis that subsecond fluctuations in dopamine delivery to the human striatum encode RPEs generated during a sequential choice task.

Our measurements of dopamine release are made in patients undergoing deep brain stimulating (DBS)-electrode implantation for the treatment of Parkinson’s disease. This patient population provides a unique and important window of opportunity to investigate dopamine’s role in human brain function. Parkinson’s disease symptoms are treated with dopamine replacement therapies, and yet we know nothing about how rapid (subsecond) dopamine concentration changes contribute to their symptoms or changes in their decision-making abilities. The opportunity to measure dopamine release with subsecond temporal resolution in the brains of humans with Parkinson’s disease is an opportunity to learn about fundamental processes in human brain function as well as an opportunity to assess dopamine signaling in a patient population whose primary treatment is focused on replacing function lost as dopamine neurons degenerate.

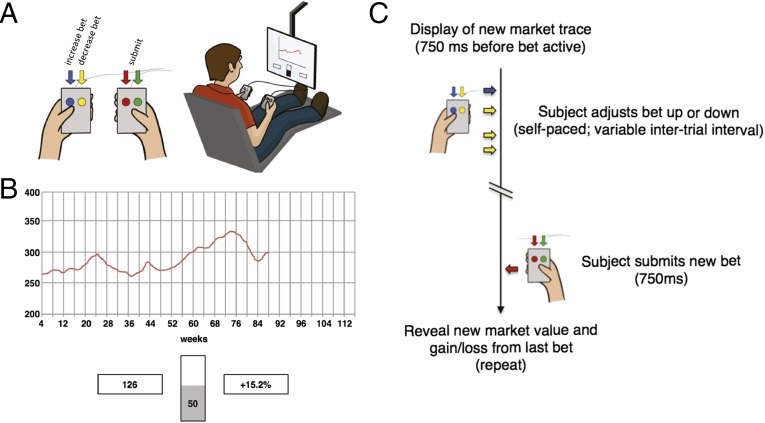
Participants (n = 17) in these experiments performed a simple, yet engaging, sequential investment game (Fig. 1 and refs. 19–21) while dopamine measurements with subsecond temporal resolution were made in the striatum (n = 14 in the caudate and n = 3 in the putamen). Participants were offered participation after they were deemed candidates for deep brain-stimulating electrode implantation (22, 23). The research protocol was explained to the participants verbally, and they were provided a written consent form, as required by dual-institutional review board (IRB)-approved protocols at Wake Forest University Health Sciences and Virginia Tech Carilion Research Institute. Patients thus indicated that they understood the research protocol and provided written informed consent to proceed with the research procedure.

Fig. 1.

Investment game. (A) Participants played a sequential-choice game during surgery using button boxes (Left) and a visual display (Right). For each patient, bet size adjustments (e.g., increase bet or decrease bet) and the decision to submit one’s answer were performed with button boxes. (B) Investment game (19, 21): participants view a graphical depiction of the market price history (red trace), their current portfolio value (bottom left box), and their most recent outcome (bottom right box) to decide and submit investment decisions (bets) using a slider bar in 10% increments (bottom center). Bet sizes were limited to 0–100% (in 10% increments) of the participant’s portfolio—no shorting of the market was allowed. During an experiment, a participant played 6 markets with 20 decisions made per market. (C) Timeline of events during a single round of the investment game.

The sequential investment game (Fig. 1 and refs. 19–21) consists of 120 investment decisions. On each trial ($t$), this game requires participants to use button boxes to adjust and submit an investment [bet ($b_t$), where bet sizes could range from 0% to 100% of the participants portfolio, in 10% increments], after which, participants experience a gain or loss (participant return) equal to the bet size times the fractional change in the market price [market return ($r$) at time $t$: $r_t=\hspace{0.17em}\frac{\mathrm{\Delta }{p}_t}{p_t}$, where $p$ is the market price and the participant return (i.e., gain or loss) at time $t$ is equal to $b_t{r}_t$]. Previous work used this task and functional magnetic resonance imaging to demonstrate that RPEs and CPEs over gains are tracked by blood oxygenation level-dependent (BOLD) responses in the striatum (19, 20). These reports also demonstrated at the behavioral level that humans use counterfactual information over choices that “might have been made” and RPE information over choices that were actually made to make their next choice (19, 20).

Results

Cross-Validated Penalized Linear Regression Approach Reliably Estimates Low Dopamine Concentrations.

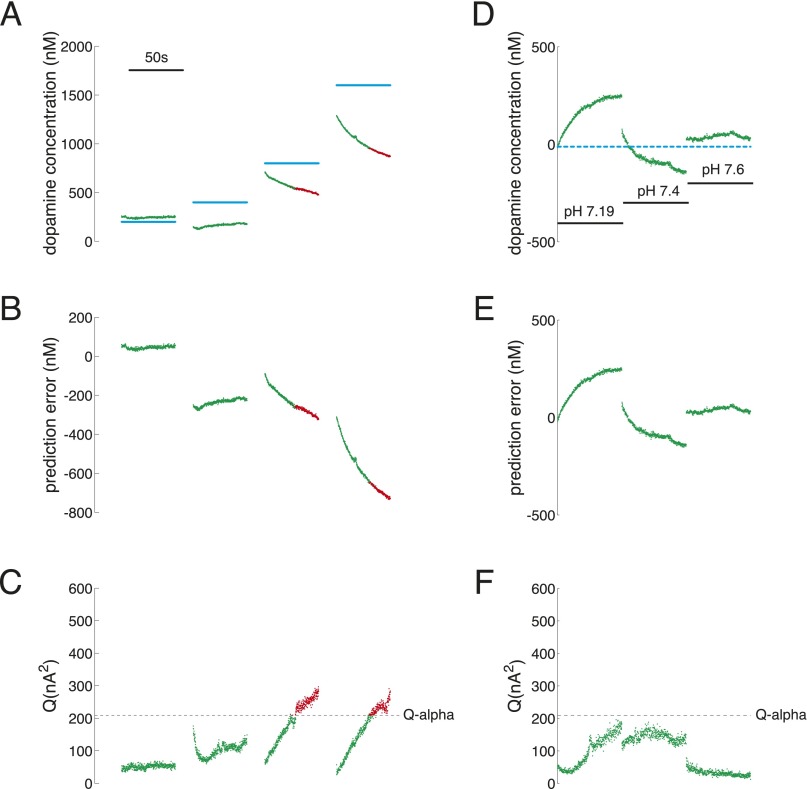
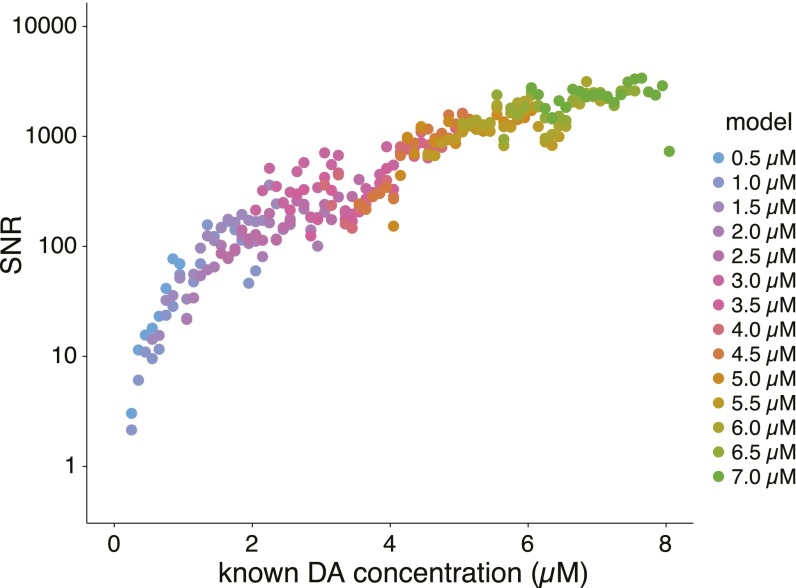
During the execution of the sequential investment game, an adaptation of fast-scan cyclic voltammetry (FSCV) was used to track subsecond dopamine fluctuations in the striatum. Standard approaches [see SI Methods, Principal Components Regression to Estimate Dopamine Concentration and Figs. S1–S3 and Table S1, which follow recommendations in ref. 24] for estimating dopamine concentration from FSCV measurements produced unreliable predictions for low dopamine concentrations in vitro (Fig. 2A). Furthermore, and also under controlled in vitro conditions, we observed that these methods produced predictions of dopamine concentration fluctuations that confused changes in pH for changes in dopamine (Fig. 2B). Thus, we sought to develop a novel approach that uses in vitro calibration data to fit a cross-validated penalized linear regression model for estimating dopamine concentrations from non–background-subtracted voltammograms [see SI Methods for details on our elastic net (EN)-based approach]. The new approach was sufficiently sensitive and stable to permit dopamine measurements at low levels expected in patients diagnosed with Parkinson’s disease (Fig. 2 C–E and Fig. S4). Fig. 2C shows our approach stably and accurately estimating dopamine levels in out-of-sample test cases from the same electrode and flow cell conditions used in Fig. 2 A and B. Fig. 2D shows that the cross-validated EN-based approach used to accurately track changes in dopamine concentration in Fig. 2C does not confuse changes in pH for dopamine fluctuations. Fig. S5 shows our approach achieving signal-to-noise ratios (SNRs) ranging from 2/1 to 5,000/1 for tonic dopamine concentrations ranging from 500 nM to 10 μM, respectively. For the results below, we use our EN-based approach to estimate dopamine levels from non–background-subtracted voltammograms measured in the striatum of humans undergoing DBS-electrode implantation surgery.

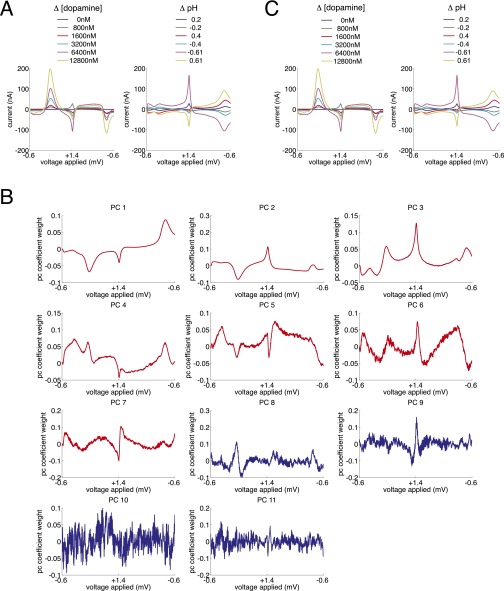
Fig. S1.

Principal components analysis of in vitro training data. (A) Background-subtracted voltammograms for six measurements of dopamine (Left) and six changes in pH (Right) are entered into a principal components analysis. (B) Resulting 11 principal components. Red traces (principal components 1 through 7) are retained for further analysis by the criteria set forth in refs. 24 and 56. (C) Representation of the training data in the reduced principal component space.

Fig. S3.

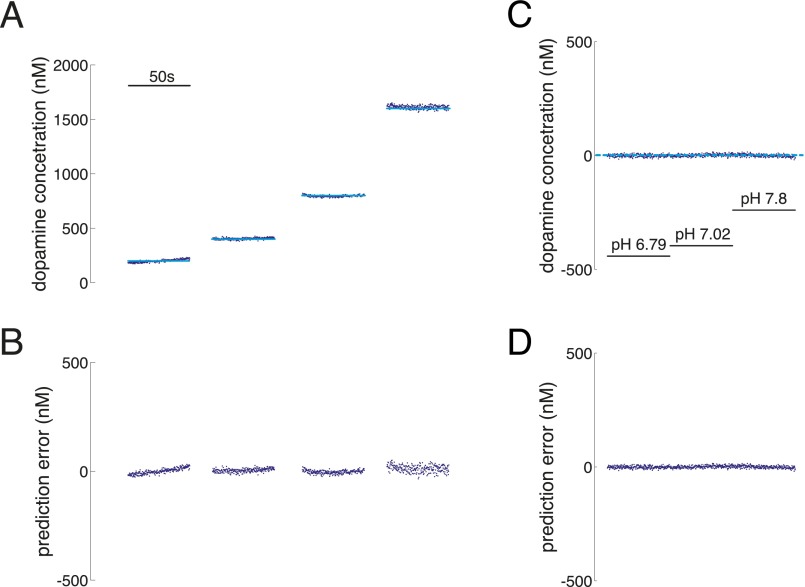
Performance of PC regression-based approach on out-of-sample test cases. (A–C) Changes in dopamine concentration under stable pH (pH 7.4). (D–F) Changes in pH under stable dopamine concentration (dopamine concentration for D–F is 0). (A) Prepared dopamine concentration (light blue: 200, 400, 800, and 1,600 nM) compared with the PC regression-based predictions for dopamine concentration (red and green). Green points: accepted by Q-value analysis; red points: rejected by Q-value analysis. The inset scale bar indicates measurement period of 50 s. (B) Prediction error of PC regression-based predictions of dopamine concentration over the range of dopamine concentrations shown in A. (C) Q-value analysis determined a Q-value threshold of Qα = 209.6 (dotted line) for significant variance explained by the retained principal components for the test dataset. (D) Predictions of dopamine concentration when pH is changed, but dopamine concentration is held constant (0). Dotted light blue line indicates actual concentration of dopamine is equal to 0. Insets indicate pH levels (pH range: 7.19, 7.4, 7.6). (E) Prediction error of PC regression-based predictions of dopamine concentration over the range of pH fluctuations shown in D. (F) Q-value analysis determined a threshold of Qα = 209.6 (dotted line) for significant variance explained by the retained principal components for the test dataset.

Table S1.

Principal components 1 through 7 retained for PC-regression analysis by Malinowski’s F-score threshold

Principal component no.	% variance explained	df	Malinowski's F score	P
PC 1	57.0219391	F(1,10)	71.5625781	7.20 × e−6
PC 2	39.61787313	F(1,9)	518.892365	2.87 × e−9
PC 3	2.861235738	F(1,8)	201.1369679	5.95 × e−7
PC 4	0.369182107	F(1,7)	77.1958539	4.99 × e−5
PC 5	0.089619474	F(1,6)	45.07042011	0.000530793
PC 6	0.01965172	F(1,5)	13.66101103	0.014056514
PC 7	0.013926391	F(1,4)	19.73411084	0.011313738
PC 8	0.003495778	F(1,3)	6.124811992	0.089679162
PC 9	0.001899128	F(1,2)	4.026631744	0.18260189
PC 10	0.000634205	F(1,1)	0.777518953	0.539945643
PC 11	0.000543236	NA	NA	NA

NA, not applicable.

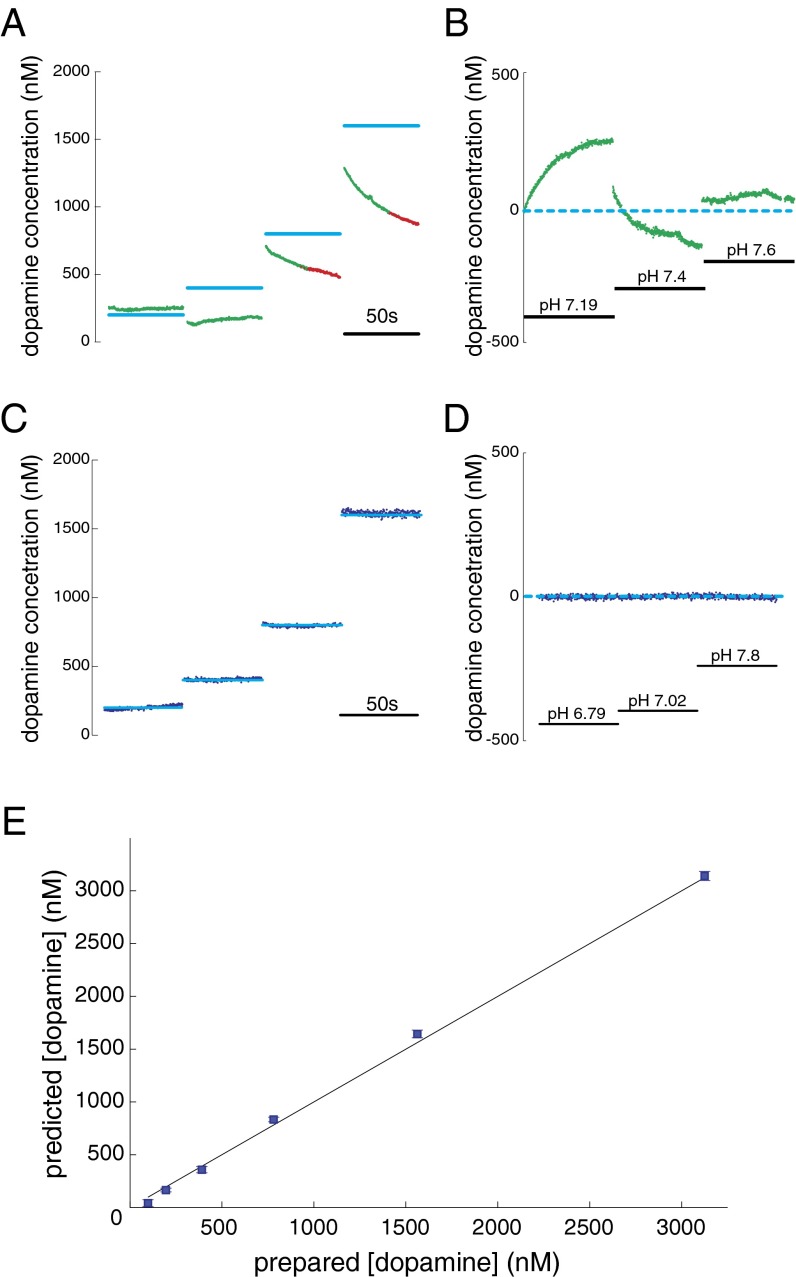
Fig. 2.

Performance of EN-based dopamine estimation algorithm. (A and B) Performance of PC regression-based approach on out-of-sample test cases. (C–E) Performance of EN-based approach on out-of-sample test cases. For A and B, light blue lines indicate dopamine concentration of prepared out-of-sample calibration solutions, green points indicate PC regression-based predictions accepted by Q-value analysis, and red points indicate PC regression-based predictions rejected by Q-value analysis. The inset scale bar indicates measurement period of 50 s. (A) PC regression-based prediction of changes in dopamine concentration under stable pH (pH 7.4). The prepared dopamine concentration (light blue; 200, 400, 800, and 1,600 nM) compared with the PC regression-based predictions for dopamine concentration (red and green). (B) PC regression-based predictions of dopamine concentration when pH is changed, but dopamine concentration is held constant (0 dopamine in solution). The dotted light blue line indicates actual concentration of dopamine is equal to 0. Insets indicate pH levels (pH range: 7.19, 7.4, 7.6). (C) EN-based predictions of changes in dopamine concentration under stable pH (pH = 7.4). The prepared dopamine concentration (light blue, 200, 400, 800, and 1,600 nM) compared with the EN-based predictions for dopamine concentration (dark blue). The inset scale bar indicates measurement period of 50 s. (D) EN-based predictions of changes in dopamine concentration when pH is changed, but dopamine concentration is held constant (0 dopamine in solution). The dotted light blue line indicates that actual concentration of dopamine is equal to 0. Insets indicate pH levels (pH range: 6.79, 7.02, 7.8). (E) Dopamine concentration predictions from the EN-based procedure gives accurate predictions of dopamine concentration (blue squares). Horizontal axis: concentration of prepared dopamine; vertical axis: predicted dopamine concentration. Plotted are mean predicted values for five measurements at each concentration ± SEM (note: SEM bars are plotted but are consumed by the marker).

Fig. S4.

Performance of EN-based approach on out-of-sample test cases. (A and B) Changes in dopamine concentration under stable pH (pH 7.4). (C and D) Changes in pH under stable dopamine concentration (dopamine concentration for C and D is 0). (A) Prepared dopamine concentration (light blue: 200, 400, 800, and 1,600 nM) compared with the EN-based predictions for dopamine concentration (dark blue). The inset scale bar indicates measurement period of 50 s. (B) Prediction error of EN-based predictions of dopamine concentration over the range of dopamine concentrations shown in A. (C) Predictions of dopamine concentration when pH is changed but dopamine concentration is held constant (0). Dotted light blue line indicates actual concentration of dopamine is equal to 0. Insets indicate pH levels (pH range: 6.79, 7.02, 7.8). (D) Prediction error of EN-based predictions of dopamine concentration over the range of pH fluctuations shown in C.

Fig. S5.

SNR of EN-based dopamine estimation as a function of dopamine concentration. Horizontal axis: concentration of prepared dopamine; vertical axis: SNR. Colored points indicate the value of the characteristic parameter (mean concentration of the training data) for each model generated (see inset legend for values).

Dopamine Transients Fail to Simply Encode RPEs.

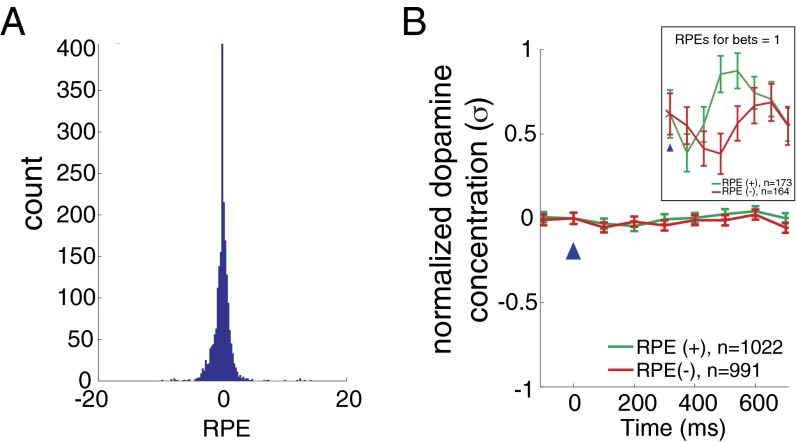
Dopamine measurements were made in 17 participants; each participant made 20 investment decisions per market in a total of six markets (120 decisions total per subject; one subject did not complete one market). At each decision within a market, an RPE was computed as the difference between the outcome (gain or loss as defined above) and the expected value of the outcome for that market (i.e., the average participant return up to that trial in that market); this difference is normalized to the variability of the preceding outcomes to facilitate comparison across markets and across participants (see Eq. 2 in Materials and Methods for equation and description of terms). The distribution of RPEs (Fig. 3A) is peaked around 0 but evenly distributed for positive and negative values. We divide these events into positive and negative RPEs and report the mean dopamine responses to positive (green; n = 17, n = 1,022) and negative (red; n = 17, n = 991) RPEs in Fig. 3B. The measured dopamine fluctuations in human striatum fail to distinguish RPEs categorized by sign [Fig. 3B; two-way ANOVA: F(1,7) = 1.67, P = 0.1965]. This null result holds even at lower sample sizes (n $\cong$ 200 per category, randomly sampled). Prior work strongly supports the hypothesis that dopamine fluctuations in striatum should track RPEs (1, 8, 10, 11, 13, 14). Our results contradict this expectation; however, the task we use was designed to also assess the impact of counterfactual feedback (e.g., difference between actual outcomes and what might have happened; Eq. 3). In this game, counterfactual prediction errors (CPEs) (Eq. 3) are parameterized by the distribution of participants’ bets. Instances where there is no CPE occur when the participants’ bet is equal to one (i.e., “all in”). In these specific instances, we observe (Fig. 3B, Inset) that dopamine transients to positive (n = 173) and negative (n = 164) RPEs indeed separate. Together, these results suggest that counterfactual information (as bet sizes decrease from 1) disrupts the expected standard response of dopamine release to positive and negative RPEs. We test this hypothesis below (Results, Dopamine Transients Integrate RPEs and CPEs) by examining the dopamine response to equivalent magnitude RPEs for different bet sizes.

Fig. 3.

Dopamine fails to simply track RPEs in the investment game. (A) Histogram showing the distribution of events for RPEs (n = 17 participants; n = 2,013 outcome revelations). (B) Mean normalized dopamine responses (±SEM) to positive (green; n = 1,022) and negative (red; n = 991) RPEs. Two-way ANOVA (RPE-sign and time: 700 ms following and including outcome reveal) reveals no significant difference comparing dopamine responses for positive and negative RPEs [F_RPE-sign(1,7) = 1.67, P = 0.1965]. Note, this null result holds even at lower sample sizes (n $\cong$ 200 per category, randomly sampled) comparable to those in Fig. 4. Horizontal axis: time (ms) from outcome reveal (blue arrow head); vertical axis: mean change in the dopamine response. Before averaging, dopamine traces are normalized to the SD (σ) of the fluctuations measured within patient. Error bars: SEM. Inset shows dopamine response to a subset of positive (green) and negative (red) RPE events (i.e., when the participants’ bet all in).

Dopamine Transients Integrate RPEs and CPEs.

Behaviorally, CPEs in this task have been shown to combine with RPEs to influence participants’ next decision (19, 20). Given the impact of bet size (and thus potentially counterfactual information) on the encoding of RPEs by dopamine fluctuations (Fig. 3B), we tested a novel hypothesis: subsecond dopamine transients encode a combination of RPEs and CPEs. To test our hypothesis, we follow the model of CPEs presented by Lohrenz et al. (19) and assume that dopamine encodes a linear combination of two separate computations: RPEs (Eq. 2) and CPEs (Eq. 3): $\text{dopamine}\hspace{0.17em}\text{transient}\propto \left\{\text{RPE}\right\}-\left\{\text{CPE}\right\}$, or

$$\text{dopamine}\hspace{0.17em}\text{transient}\propto \left\{\text{RPE}\right\}-\left\{r_t\left(1-b_t\right)\right\}.$$ [1]

Here, $b_t$ is the subject’s fractional bet at choice trial $t$ and $r_t$ expresses the relative fractional change in the market price ($r_t=\hspace{0.17em}\frac{\mathrm{\Delta }{p}_t}{p_t}$). The difference in what the participant earned and what the participant could have earned is the CPE (second term on the right in Eq. 1). The guiding intuition for the form of Eq. 1 is twofold: (i) that what might have been should adjust overall valuation estimates and encode this adjusted amount in a composite dopamine signal and (ii) that the RPE and CPE terms are computed in two separate pathways before being integrated at the level of dopamine release. Thus, the valuation error encoded by dopamine release is consistent with the intuition that “better-than-expected” outcomes (positive RPEs) that might have been better should be reduced in value and “worse-than-expected” outcomes (negative RPEs) that might have been worse should be increased in value. In this form, positive CPE terms (which occur for missed opportunities on positive-going markets) diminish the value of the RPE event, and negative CPE terms (which occur for avoided losses on negative-going markets) increase the value of the RPE event.

This model (Eq. 1) makes three testable predictions all of which derive from a dependence on the bet size $b_t$. We test these predictions for events that have the same magnitude of RPEs (positive and negative) but grouped for different size bets. According to the model in Eq. 1, we predict (and observe) the following.

Prediction 1: Impact of bet size equal to 1 (i.e., no CPE).

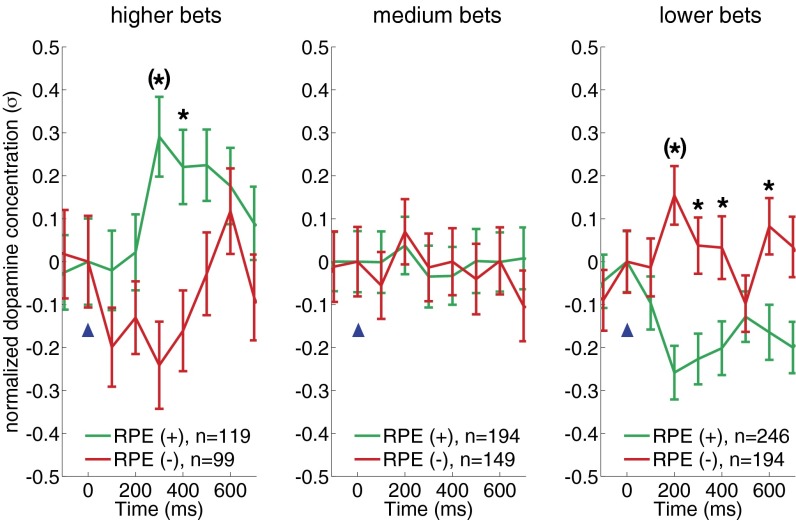
When the bet ($b_t$) is set near 1 (all in), the CPE is 0, so positive RPEs will be encoded as positive-going dopamine transients and negative RPEs will be encoded as negative-going dopamine transients [similar to experiments in rodents and nonhuman primates (8, 11, 25) and exactly what is observed in Fig. 3A, Inset, and for the “higher bets” graph in Fig. 4].

Fig. 4.

RPE encoding by dopamine transients invert as a function of bet size. Dopamine responses to equal absolute magnitude positive and negative RPEs (−0.75 > RPE > +0.75) when bets are high (higher bets, 100–90%) (Left), medium (medium bets, 80–60%) (Center), or low (lower bets, 50–10%) (Right). For all three plots, mean normalized dopamine responses (±SEM) to positive RPEs (green traces) and negative RPEs (red traces). Inset legends show sample sizes for event types. Two-way ANOVA (RPE-sign and time: 700 ms following and including outcome reveal) reveals a significant difference comparing dopamine responses for positive and negative RPEs following higher bets [F_RPE-sign(1,7) = 21.17, P = 0.00] and lower bets [F_RPE-sign(1,7) = 32.64, P = 0.00] but not medium bet sizes [F_RPE-sign(1,7) = 0.15, P = 0.6957]. Asterisks indicate significant difference between red and green traces: P < 0.05, post hoc, two-sample t test following ANOVA with time and RPE-sign as the two main factors. Asterisks with parentheses indicate Bonferroni correction for multiple comparisons. For low bets (i.e., large CPEs), only those events where the market price change and the RPE-sign are the same are considered. Horizontal axis: time (ms) from outcome reveal (blue arrowhead); vertical axis: mean change in normalized dopamine response.

Prediction 2: Impact of decreasing bet size on dopamine transient polarity for positive RPEs.

As the bet size decreases, the CPE grows in magnitude; thus, dopamine transients to positive RPEs will diminish (as is observed with the green traces in the “medium bets” graph in Fig. 4) and eventually will be encoded as a negative-going transients as the CPE term dominates (as is observed for green traces in the “lower bets” graph in Fig. 4).

Prediction 3: Impact of decreasing bet size on dopamine transient polarity for negative RPEs.

Again, as the bet size decreases the CPE grows in magnitude; thus, dopamine transients to negative RPEs will diminish (as is observed for red traces in the medium bets graph in Fig. 4) and eventually be encoded as a positive-going transients as the CPE term dominates (as is observed for red traces in the lower bets graph in Fig. 4).

Fig. 4 demonstrates that striatal dopamine measurements in humans follow predicted responses of the simple model expressed in Eq. 1. The three separate predictions are pertinent because in nonhuman primates dopamine neurons show asymmetrical modulation of their activity as a function of the RPE polarity (8, 10, 13, 15–17), and the integration of a CPE term has not previously been shown in experiments measuring changes in dopamine neuron firing rate. One possible interpretation here is that there is a separate class of midbrain dopamine neurons carrying the counterfactual information and these have yet to be recorded from in prior experiments. This hypothesis is particularly important because these subjects are patients with Parkinson’s disease, suggesting a class of dopamine neuron possibly preserved in the disease. Alternatively, these results suggest a previously untested mode of operation of reward processing dopamine neurons. Along these lines, different error terms for evaluating behavioral outcomes may be integrated before dopamine release. Both of these possibilities suggest two separate pathways for computing actual and counterfactual outcomes over past decisions. Where these computations may take place is unknown. Further work is needed to distinguish these and other possibilities.

SI Methods

Participant Recruitment.

All patients enrolled in this study were first diagnosed with Parkinson’s disease and deemed good candidates for DBS treatment. Once the patients agreed to the clinical procedure, they were deemed candidates for the research protocol and given the option to participate. Before obtaining written informed consent, the research study and how it would alter the participants’ clinical procedure were explained in detail to the patients—namely, the procedure would involve an additional research-exclusive probe (the carbon-fiber microelectrode) and that extra time (maximum thirty minutes) would be necessary to complete the experiment. The procedures to be used in the research study were verbally described and provided to patients in a written consent document.

During the surgical procedure to implant deep brain stimulating electrodes to treat Parkinson’s disease, we measured dopamine release in caudate and putamen in patients where the DBS target was the subthalamic nucleus and internal segment of globus pallidus, respectively. During surgery and the research protocol, all medications used to treat symptoms of Parkinson’s disease were withheld from the patients. No adverse or unanticipated events occurred during or as a result of these procedures.

Investment Game.

The investment game (Fig. 1 and refs. 19–21) requires participants to make decisions about how much of their portfolio they will invest in a stock market given three pieces of information: (i) the history of the market price, (ii) the participant’s current portfolio value, and (iii) the most recent fractional change in the participant’s portfolio value. The participant begins the game endowed with 100 points and plays six markets with 20 decisions in each market (n = 120 decisions per participant). For each decision, the participant chooses how much to invest at the market’s current price. Once the decision is lodged, the screen updates revealing the change in the market price and the change in the participant’s portfolio. The final portfolio value determines participants’ compensation. Each of the markets chosen is drawn from an actual historical market where large groups of humans actually decided the price levels. These participants had no prior knowledge of these markets, nor did the participants’ have professional expertise in market trading.

Participants viewed the game screen via a workstation monitor present in the operating room suite. These monitors hang from the ceiling from an adjustable arm that allow the monitor to be positioned within about two to three feet from the patients’ face, so that patients can view the screen in a comfortable viewing position.

The participants lodge their decisions using two handheld button boxes (Fig. 1A) that interface with the behavioral software via universal serial bus (USB) connections. Each button box contains two buttons. The hand contralateral to the electrochemical recording site was chosen as the hand to adjust the “bet size” slider bar. The hand ipsilateral to the recording site was chosen to lodge the decision to submit one’s final bet size decision. To adjust the bet size, the participant would press one button to raise the bet and the other button to lower the bet. The button box that signals the submit decision also contained two buttons, and either button could be used to submit one’s decision. Each of the button boxes are fitted with an additional sensor (internally) that tracks button presses and transmits this information as a voltage drop to the integrated mobile electrochemistry station.

One patient did not complete the full task within the allotted time; this patient lodged 100 out of 120 possible decisions. Additionally, a computer malfunction in the middle of one experiment resulted in the loss of dopamine data for seven consecutive decisions in one patient. The remaining data (n = 17; n = 2,013 decisions and outcome) were used in the present analyses.

Calculation of RPE and CPE.

In this game, participants invest a percentage (0–100% in 10% increments indicated by their bet size, $b_t$) of their portfolio. Investment returns are calculated as market price changes (market returns: $r_t=\hspace{0.17em}\frac{\mathrm{\Delta }{p}_t}{p_t}$) multiplied by the investment size; thus, participant returns (or outcomes) are $b_t{r}_t$ and correspond to monetary gains or losses depending on the sign of the price change.

RPEs are thus calculated per decision outcome as

$$\frac{b_t{r}_t-E\left(b_t{r}_t\right)}{{\sigma }_{b_t{r}_t}},$$

where $E\left(b_t{r}_t\right)$ is the expected value of $b_t{r}_t$, which is calculated as the mean of participant outcomes from the first trial of each market to trial $t-1$, and ${\sigma }_{b_t{r}_t}$ is the SD over those same events. For the first outcome of each market, the RPE is simply that outcome (assuming no expectations at that point of the market); the second outcome is that outcome minus the first outcome (without normalization); the third outcome (and beyond) uses the equation above.

CPEs are calculated per decision outcome as

$$r_t-b_t{r}_t.$$

The first term ($r_t$) reflects what could have been had the participant bet all in or $b_t=1$. For positive market price changes, r_t is the maximum possible gain; for a negative market price changes, r_t is the maximum possible loss. Depending on the size of the participants’ actual investment ($b_t$), the CPE as calculated here reflects the maximum difference between what could have been and what actually happened.

Description of Probe Placement for Clinical and Research Protocol.

Per standard clinical procedure, a Cosman–Roberts–Wells (CRW) stereotactic frame is placed on the patient’s head and a volumetric computed tomography (CT) scan of the head with frame is obtained. The CT scan and the patient’s preoperative MRI image sets are fused. The image sets are in turn fused with the Cranial Vault datasets and atlas (51), using a nonrigid coregistration algorithm on the Waypoint Navigator workstation. Once the images and atlases are fused, the target and trajectory for the DBS electrode is determined.

During surgery, the DBS electrode is targeted to the patients’ subthalamic nucleus or the internal segment of the globus pallidus per clinical indications; the implanted electrodes’ trajectory (for DBS treatment) thus typically passes through the caudate or putamen, respectively. Microelectrode recordings to determine the optimal DBS-electrode placement are made before placement of the DBS electrode. During this period of the surgery, we place our carbon-fiber microsensor in the caudate or putamen using one of the five possible microelectrode recording trajectories (five-hole “Ben-gun” array is used). Only one carbon-fiber microsensor is placed. The microsensor recording site is superior (in depth position) to the beginning of the microelectrode recording depth for any given trajectory and is thus in a location where (i) microelectrodes are deemed safe to pass through during planning stages and (ii) in a position that will not otherwise be used to collect clinical data.

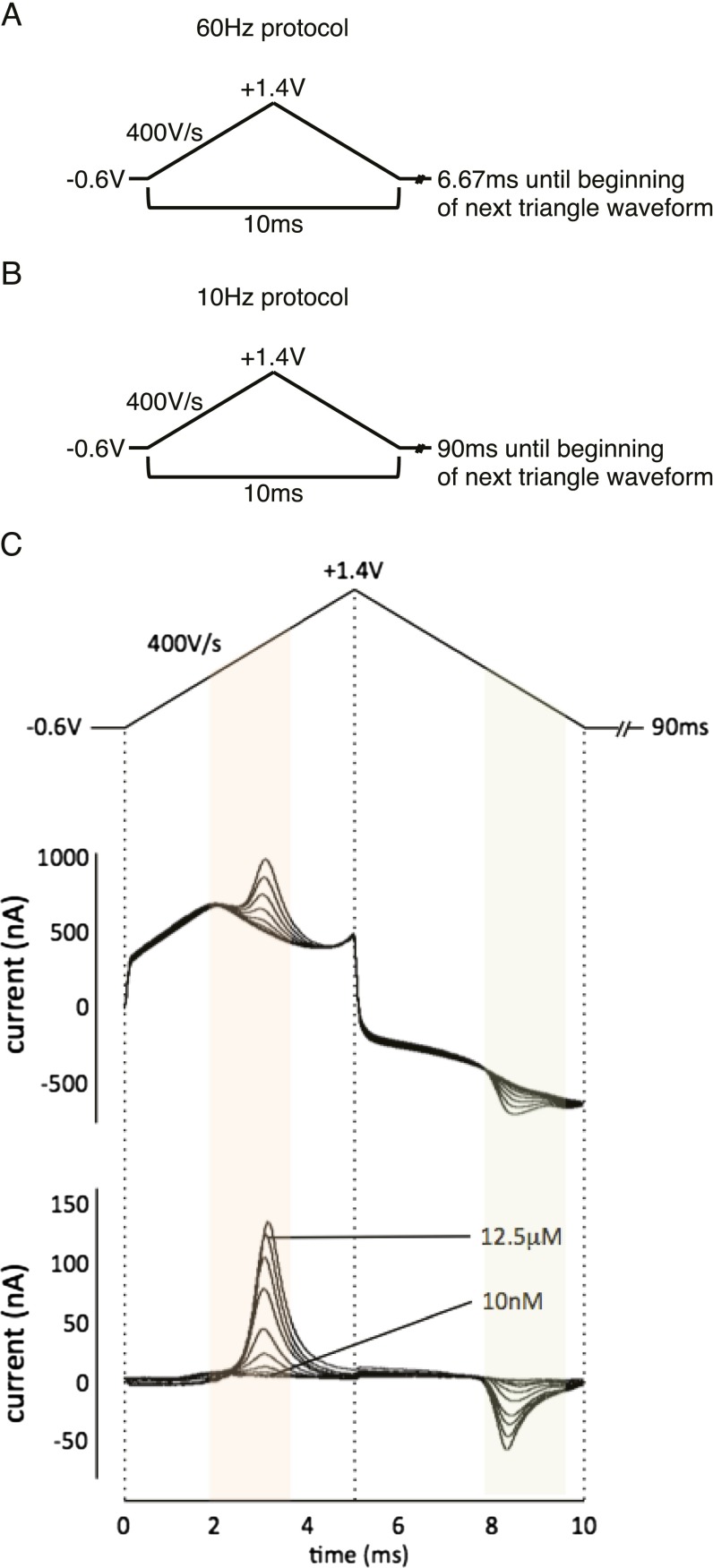
Once the carbon-fiber microsensor is positioned, a 400 V/s triangular voltammetry protocol is applied (Fig. S8A) at 60 Hz for 10 min to allow the microsensor to equilibrate. During this time, the patient is reminded of the game instructions, provided the handheld button boxes, and reinstructed about the operation of the handheld devices and game play. Game play begins after the 10-min precycling protocol is complete and the 10-Hz recording protocol is initiated (Fig. S8B).

Fig. S8.

FSCV protocols. (A) Triangular voltammetry protocol used for conditioning the carbon-fiber microsensor. (B) Triangular voltammetry protocol used for FSCV measurements of dopamine in vitro and in vivo. (C) In vitro-collected voltammogram for dopamine at increasing concentrations: triangular voltage waveform applied during FSCV measurements (Top), non–background-subtracted (Middle) and background-subtracted (Bottom) FSCV data collected in vitro for increasing concentrations of dopamine. Horizontal axis: time (ms). Vertical axis: current (nA). Orange and green shading indicates expected range of dopamine oxidation and dopamine-o-quinone reduction peaks, respectively.

Extended Carbon-Fiber Microsensor Dimensions and Construction.

Current technologies that detect dopamine release in humans (microdialysis or positron emission tomography) provide relatively good spatial resolution but poor temporal resolution (minutes to hours). The advent of FSCV in animal models (47, 48, 52) and humans (21) provides an increase in temporal resolution for dopamine measurements by roughly three orders of magnitude.

We preformed FSCV on extended carbon-fiber microsensors in the striatum of patients with Parkinson’s disease. The extended carbon-fiber microsensor is constructed to match the dimensions of the tungsten microelectrodes used for functional mapping during DBS-electrode implantation surgery. Fig. S7 shows the component parts and assembly of the extended carbon-fiber microsensor used in these experiments. Pacific BioLabs conducted a successful Ethylene Oxide Sterilization Exposure and Sterility Audit to ensure that the ethylene oxide treatment used before surgery renders the extended carbon-fiber microsensors completely sterile.

Fig. S7.

Diagram of extended carbon-fiber microsensor. From top to bottom, drawings of component parts and assembly steps for constructing the extended carbon-fiber microsensor. (A) 7-μm-diameter carbon fiber is threaded through a 1-cm-long (20-μm ID, 90-μm OD) fused-silica capillary with biocompatible polyimide coating and then held in place and sealed on one end with two-part epoxy. (B) Platinum-iridium wire (0.003 in diameter) is threaded through a 28-cm-long (100-μm ID, 238-μm OD) fused-silica capillary with biocompatible polyimide coating. (C) The recoding tip assembled in A is inserted 5 mm into the larger fused-silica capillary assembled in B. An electrical contact is made between the carbon fiber and the platinum-iridium wire using silver paint. A gold-plated connecting pin is soldered to the other end of the platinum-iridium wire. (D, Upper) The assembly in C is threaded into a guide tube purchased from FHC, which contains the reference electrode and connecting pin. (D, Lower) Colored drawing showing guide tube in gray and carbon-fiber biocompatible capillary assembly in orange. (E) The extended carbon-fiber microsensor is retracted (Lower) when not in use and during implantation, but when extended (Upper), the carbon-fiber working end extends 1 cm beyond the reference electrode tip contained on the end of the FHC guide tube. Two-part epoxy is used as a “stopper” to ensure that the probe extends the desired depth when deployed.

The carbon-fiber microsensors are manufactured in-house. A short segment of carbon fiber (1.2-cm long) is cut from a carbon-fiber spool (7-μm diameter; reference no. LS330423; Goodfellow) and threaded into a 1-cm-long piece of biocompatible polyimide-coated fused-silica capillary [1-cm length; inner diameter (ID), 20 μm; outer diameter (OD), 90 μm; Polymicro Technologies]. Once threaded, a small droplet of two-part epoxy is placed on one end of the carbon-fiber/fused-silica assembly, and the carbon fiber is pulled from the other end such that the epoxy is pulled into the fused-silica tubing and the working tip of the carbon fiber is secure. After the two-part epoxy cures, the carbon-fiber tip is trimmed to 120 μm $\pm$ 20 μm under a dissecting microscope. The other end of the carbon fiber is trimmed to a length of 1 mm. This working tip assembly is then threaded into a previously prepared assembly: A platinum-iridium wire (76.2-μm diameter; 29-cm length) is threaded into a 28-cm-long biocompatible polyimide-coated fused-silica capillary (2- to 8-cm length; ID, 100 μm; OD, 238 μm; laser cut; Polymicro Technologies). A 5-mm gap between the end of the capillary and the platinum-iridium wire is created so that approximately one-half of the working tip assembly can be inserted and held secure. Before inserting the working tip a small amount of conductive silver paint (GC Electronics) is fed into the large silica tube via capillary action. Once all excess silver paint is removed from the exterior of the large capillary, the working tip assembly is inserted and allowed to air dry ∼24 h before securing the assembly with two-part epoxy. All assembly steps are carried out by hand under a dissection microscope (Fisher Scientific Stereomaster). At the nonworking end of the platinum-iridium wire assembly, we solder a gold-plated connector pin (Newark), followed by application of a short length of medical-grade shrink tubing (HS-714; SPC Technology). This assembly is inserted into an FHC guide tube [GT(AR2)], which matches the specifications of the tungsten microelectrodes used for functional mapping during the DBS-electrode implantation procedure. The FHC guide tube contains a stainless steel ground contact near the working end of the microsensor assembly (where it protrudes) and a gold plated connector pin preassembled. Finally a droplet of two-part epoxy is placed at near the top of the microsensor assembly such that the working tip protrudes 1cm from the guide tube. To ensure that the electrical contacts are secure and stable, each microsensor is connected to the integrated electrochemical recording station (see Integrated Mobile Electrochemical Recording Station for a description), and the sensor is placed in a 1× PBS solution. A triangle waveform is applied, and the capacitive currents are assessed. Microsensors that did not show a current response of at least 200 nA were discarded; otherwise, microsensors were submerged in 10% (vol/vol) isopropanol solution for 24 h, allowed to air dry, and subsequently submitted for ethylene-oxide sterilization in preparation for use in surgery.

FSCV Protocol.

Our FSCV protocol follows previous work in rodents (21, 47, 48). Before experiment measurements, carbon-fiber microsensors require a conditioning procedure consisting of a 60-Hz application of the measurement waveform for approximately 10 min to allow equilibration of the recording surface and the measurement solution (Fig. S8A: hold at −0.6 V for 6.67 ms, ramp up to +1.4 V at 400 V/s, ramp down to −0.6 V at −400 V/s, and repeat). Following this conditioning procedure, a 10-Hz application of the same triangular waveform is applied for the duration of the experiment (Fig. S8B: hold at −0.6 V for 90 ms, ramp up to +1.4 V at 400 V/s, ramp down to −0.6V at −400 V/s, and repeat). This protocol (applied in vitro and with our microsensors) produces voltammograms characteristic of the oxidation and reduction of dopamine on the carbon-fiber surface (Fig. S8C). Example voltammograms from each patient using this protocol are shown in Fig. S9.

Fig. S9.

Examples of non–background-subtracted cyclic voltammograms from each participant and overlay of EN-determined linear regression weights used for prediction. (A–Q) FSCV sweep from each patient showing EN-determined linear regression coefficients overlaid in red and blue. As in Figs. S8 and S10, orange shading and arrowhead show expected range and peak of dopamine oxidation potential; green shading and arrowhead show expected range and peak of dopamine-o-quinone reduction potential. Horizontal axis: time (ms); vertical axis: current (nA).

Integrated Mobile Electrochemical Recording Station.

The mobile electrochemical recording station consists of a head stage (CV-7B/EC; Axon Instruments), an amplifier (700B; Axon Instruments Multiclamp), an analog-to-digital (A/D) converter (Digidata 1440A; Axon Instruments), and a laptop (MacBookPro; Apple). The entire station is contained in a portable rack (SKB component rack with caster kit; www.skbcases.com) that allows maneuverability in the operating room. This recording station was used in the operating room and for all in vitro experiments.

An electrochemistry-ready head stage (CV-7B/EC; Axon Instruments) was connected to the carbon-fiber microsensor working and ground pin connectors using a shielded trio of cables (two-feet long); the third cable attached to the guide cannula via a small alligator clip and served as an additional ground during electrochemical recordings. This cable and the carbon-fiber microsensors were submitted to the hospital for ethylene-oxide sterilization at least 48 h before surgery. The head stage was connected to a signal amplifier (Multiclamp 700B; Axon Instruments), which in turn was connected to an A/D converter (Digidata 1440A; Axon Instruments). The A/D converter was connected via USB to a laptop and controlled via software (pClamp10; Axon Instruments). The Digidata 1440A can record multiple streams of data with high temporal resolution; thus, we used the Digidata 1440A as the main hub for data collection. Additional data channels included (i) the button boxes (four buttons) used by the subject to play the game, (ii) a photodiode placed over the monitor used for game presentation, and (iii) an independent signal generator (Tektronix AFG320 Arbitrary Function Generator), which provided an analog square waveform (voltage step 0 to 5V, at 1Hz, with 1% duty cycle). This signal was split and sent to both the Behavioral recording system and Digidata 1440A and was used to temporally align the Digidata 1440A data stream with the Behavioral recording system. The entire system was powered via a power strip with surge protection and an isolation transformer (medical grade; IS500HG Isolation Transformer; Tripp Lite).

Behavioral Recording System.

In the operating room, a second laptop (MacBookPro; Apple) was used to control and record the behavioral data stream. The visual display of this laptop was split and shared with a hanging monitor in the operating room; this monitor could be positioned to be within comfortable viewing distance for the patient while in the stereotactic head frame. Custom written software (NEMO; labs.vtc.vt.edu/hnl/nemo) controlled the sequential investment game (19–21). NEMO handled the visual presentation of the game as well as maintaining a log of behavioral events. The sequential investment game script was modified such that a white box was briefly presented in the lower left hand side of the screen for every screen change. This area of the screen was covered with a photodiode and electric tape, which allowed the Digidata 1440A A/D converter to record screen changes with millisecond resolution. Additionally, a signal generator delivered a square wave pulse to NEMO (via a connection in the button box) and the Digidata 1440A A/D converter in parallel. NEMO received this input as a keystroke, which was logged in the behavioral data file; simultaneously, the Digidata 1440A A/D converter recorded the induced voltage fluctuations. These signals were used offline to reconstruct temporally aligned data streams between the sequential investment game behavioral variables and the physiological data steam recorded by the Digidata 1440A A/D converter.

Training Data Used to Fit EN-Penalized Linear Regression.

To create the training data matrix (X_DA-training), we performed FSCV measurements in vitro. The carbon-fiber microsensor and reference electrode is positioned in a glass capillary column containing PBS (1× PBS; pH 7.4) without dopamine. The glass capillary column allows complete fluid replacement with only 250-μL injections. Solutions of dopamine are prepared in PBS (pH 7.4). Powdered dopamine hydrochloride (Sigma-Aldrich) is dissolved in a 0.1 N solution of HCl to a concentration of 100 mM. Aliquots of this solution are diluted to 10 mM in 1× PBS and further diluted (in 1× PBS) to the desired concentration. Increasing concentrations of dopamine were injected into the flow cell while continuous (10 Hz) FSCV sampling occurred.

The data files consist of 2 min of sweeps (1,200 sweeps) collected at 10 Hz. During the 2-min-collection window, we replace the buffered solution with step increases in dopamine concentration within the first 10–20 s of the beginning of the file. The solution remains until the beginning of the next file. Data in the first 5–10 s are omitted from the training dataset, so that movement artifacts from replacing the solutions are ignored.

Training datasets were collected on a number of probes. Responses (voltammograms) are known to vary from probe to probe because of variations in probe construction. Considerable care is taken to minimize these variations. To improve a given model’s performance at predicting test samples, we sought to match the overall voltammogram shape between the probes used to collect human data and those used to generate the training datasets. We create several training datasets from multiple electrodes; the electrodes used to create these training datasets are chosen by their voltammogram response, and the training datasets are grouped for further model training. This process is motivated by two factors: (i) the observation that an electrode with a voltammogram that is more similar in shape to another electrode tends to give much more accurate cross-probe predictions than two electrodes whose voltammograms are very different; and (ii) the observation in in vitro tests that by training a model on multiple probes, we greatly improve the generalizability of the resulting model.

Segments (400 sweeps; i.e., 40 s of data) of the 2-min data file are selected for inclusion into the training dataset (X_DA-training). We select data that is collected after the injection of the new concentration is complete and before the data collection window is complete. Also, we determined training data subsets for various suspected ranges by subsampling the full range of collected data to generate subsets of training data that are approximately normally distributed, ∼N (μ, σ²), with a given mean μ and variance σ² that span the suspected in vivo range of possible dopamine concentrations. Thus, we train multiple models for prediction—each model is characterized by two parameters (the mean and variance of a Gaussian that is used to subsample the training data), which also characterize the target concentration range for that model. This step is motivated by five observations from in vitro tests: (i) models trained on small concentration ranges (i.e., low variance) perform better on out-of-sample tests than models trained on larger concentration ranges (i.e., high variance); (ii) a model trained targeting a low concentration but used to make predictions of test samples prepared at a high concentration tend to over shoot, and, vice versa, models trained targeting a high concentration but used to make predictions targeting a high concentration tend to under shoot; (iii) models characterized by different means and variances but that are similar and overlapping tend to give very similar predictions and are very close to the mean values that characterizes those models. For example, in vitro, we find that a model “X” trained to target the concentration range characterized by a Gaussian with mean μ = 400 nM and variance σ² = 100 nM will perform similarly compared with a model “Y” characterized by a Gaussian with mean μ = 500 nM and variance σ² = 100 nM, but a model “Z” characterized by a Gaussian with mean μ = 5,000 nM and variance σ² = 100 nM will undershoot considerably when the actual concentration is around 400–500 nM; (iv) prediction errors in in vitro test cases increase as the predicted value is further from the model’s characteristic mean value, so when a model makes a prediction that is more than 2 SDs from the characteristic mean (μ) with variance (σ²), we observe that those predictions have the greatest prediction error; (v) we do not actually know the concentration range in vivo, so a set of models with similar variance but mean values that span a wide range are generated, so that we may discover an appropriate model given the behavior of our approach in vitro.

The derivative of each probe’s response (non–background-subtracted voltammogram) in 1× PBS was entered into a clustering procedure that included representative responses (the derivative of one voltammogram from the midpoint of the experiment) for each probe used to collect human data. Clustering was performed using Matlab’s cluster.m function. The linkage function for generating hierarchical cluster trees using the method specified by the variable “ward,” which minimized the inner-squared distance of the derivative of the voltammogram response with other members of the group resulting in hierarchical clusters with groups that minimize the variance of voltammogram shape within groups versus across groups (53). Training data from those probes that were grouped with probes used to collect human data were used to train dopamine concentration predictive models for those corresponding human measurements. Thus, multiple probes’ in vitro data (n greater than or equal to two probes) entered as training data for our approach.

The derivative of each 1,000-data point voltammogram (cyclic voltammogram: 10-ms sweep, 100-kHz sampling rate, during triangle waveform; ${\stackrel{\rightharpoonup }{x}}_{1\hspace{0.17em}to\hspace{0.17em}p=1000}$) is labeled with the concentration of dopamine in nanomolar (nM) units; this vector of dopamine concentration labels ($\overrightarrow{y}$) is used to determine the coefficients $\stackrel{\rightharpoonup }{\beta }$ to fit the linear regression model $\overrightarrow{y}={\widehat{\beta }}_0+{\stackrel{\rightharpoonup }{x}}_1{\widehat{\beta }}_1+{\stackrel{\rightharpoonup }{x}}_2{\widehat{\beta }}_2+\hspace{0.17em}\cdots \hspace{0.17em}+{\stackrel{\rightharpoonup }{x}}_p{\widehat{\beta }}_p$ via the EN algorithm described in EN-Based Procedure to Predict Dopamine Concentration and as in ref. 49. Training data for different pH levels on two unique probes are also collected in the same manner where 1× PBS at a range of pH levels (pH 6.7–7.8) is injected and measured; these data are labeled as “0 nM dopamine” and are included in $\overrightarrow{y}$ and ${\mathit{X}}_{\mathit{DA}-\mathit{training}}$ to allow variations in electrochemical current nonspecific to dopamine to be accounted for in the EN procedure. All nonzero dopamine concentrations were measured in 1× PBS, pH 7.4.

Before fitting the linear regression model, the data in ${\mathit{X}}_{\mathit{DA}-\mathit{training}}$ is transformed in the following way: each row in ${\mathit{X}}_{\mathit{DA}-\mathit{training}}$ is the electrochemical current “I” measured at time samples “t” (collected at 100 kHz over a 10-ms window), so the approximate derivative, ∼dI/dt, for each subsweep (a row in ${\mathit{X}}_{\mathit{DA}-\mathit{training}}$) can be estimated (this was performed using the diff.m function in Matlab). The resulting matrix ${\mathit{X}}_{\mathit{DA}-\mathit{training},\hspace{0.17em}\mathit{dI}/\mathit{dt}}$ is reduced by one column (${\mathit{X}}_{\mathit{DA}-\mathit{training},\hspace{0.17em}\mathit{dI}/\mathit{dt}}$ has dimensions: [N_samples by 999 columns]) and is used to train the linear regression model using the EN.

A 10× concentrated solution of phosphate buffered saline (PBS) was prepared [PBS: NaCl (137 mM), KCl (2.7 mM), Na₂HPO₄ (10 mM), KH₂PO₄ (1.8 mM)]. Before use, a 900-mL sample was adjusted to the desired pH using HCl or NaOH. Once the desired pH was attained, milli-Q H20 was added to 1-L total volume. Powdered dopamine hydrochloride (Sigma-Aldrich) was dissolved in a 0.1 N solution of HCl to a concentration of 100 mM. Aliquots of this solution were frozen in a −20 °C freezer and thawed just before use. Aliquots were diluted to 10 mM in 1× PBS and further diluted (in 1× PBS) to the desired concentration for in vitro calibration of the carbon-fiber microsensors.

EN-Based Procedure to Predict Dopamine Concentration.

We use the EN to perform regularization and variable selection while determining a good fit for a linear regression model

$$\widehat{y}={\widehat{\beta }}_0+x_1{\widehat{\beta }}_1+x_2{\widehat{\beta }}_2+\cdots +x_p{\widehat{\beta }}_p$$

that will predict the concentration of dopamine ($\widehat{y}$) given a FSCV measurement ($\stackrel{\rightharpoonup }{x}$).

For our purposes, $\widehat{y}$ is the predicted concentration of dopamine; the vector of parameters, $x_1\dots \hspace{0.17em}{x}_p\hspace{0.17em}\left(\stackrel{\rightharpoonup }{x}\right),$ is the derivative (dI/dt) of a single cyclic voltammogram sweep (P = 999 values after calculating dI/dt for 1,000 data points in the cyclic voltammogram vector). The vector of betas, $\stackrel{\rightharpoonup }{\beta }$, are weights assigned to each value of $x_p$. The EN procedure for linear regression models minimizes the residual sum of squares with an additional penalty term, $P_{\alpha }\left(\beta \right)$:

$$\underset{\left({\beta }_0,\beta \right)\in {\mathrm{ℝ}}^{p+1}}{\min }\frac{1}{2N}{\displaystyle \sum }_{i=1}^N{\left(y_i-{\beta }_0-x_i^T\beta \right)}^2+\lambda P_{\alpha }\left(\beta \right).$$

The EN penalty $P_{\alpha }\left(\beta \right)$,

$$P_{\alpha }\left(\beta \right)=\left(1-\alpha \right)\frac{1}{2}{\Vert \beta \Vert }_{{\ell }_2}^2+\alpha {\Vert \beta \Vert }_{{\ell }_1}$$

$$={\displaystyle \sum }_{j=1}^p\left[\left(1-\alpha \right){\beta }_j^2+\alpha \left|{\beta }_j\right|\right],$$

is a mixture of the “ridge regression penalty” [${\ell }_2-\text{norm}:\hspace{0.17em}\frac{1}{2}{\beta }_{{\ell }_2}^2$ (54)] and “lasso penalty” [${\ell }_1-\text{norm}:\hspace{0.17em}{\beta }_{{\ell }_1}$ (55)] parameterized by $\alpha$, which takes a value between 0 and 1. To determine a best-fit linear regression model, we collect cyclic voltammetry measurements (sweeps, $\stackrel{\rightharpoonup }{x}$) for known concentrations of dopamine in vitro. Each sweep consists of 1,000 data points (measurements of current at 100kHz) collected during the application of a 10-ms triangular voltage waveform (hold at −0.6V for 90 ms, ramp up to +1.4 V at 400 V/s, ramp down to −0.6 V at −400 V/s, and repeat; Fig. S8). We have found that taking the derivative of the measured current leads to improved prediction performance. Thus, the derivative of the non–background-subtracted cyclic voltammogram is input into the linear regression model determined by EN regularization.

To perform the EN procedure, we use the toolbox provided by Qian et al. for Matlab (50). The range of $\lambda$ (a penalty weight) is determined for each $\alpha$ (a mixing term) by the cvglmnet.m function. The best $\alpha$ is determined via grid search ($\alpha$ for a range of $\lambda$); we searched $\alpha$ values between from 0 to 1 in 0.1 increments. We performed 10-fold cross validation within each training data subset and determined $\lambda$ that minimizes the average mean squared error over 10 iterations for each $\alpha$ tested. We chose the ($\alpha$, $\lambda$) pair that minimized the mean-squared error over the 10 iterations.

Model Selection Per Patient.

For each patient, dopamine concentration predictions were generated using each of the possible models, where each model indexed by m (m = 1, 2, 3, … M; M is the full set of possible models) has been trained on a different concentration range (concentration range characterized by the normal distribution with parameters μ_μ and σ²_μ as described in Training Data Used to Fit EN-Penalized Linear Regression) and multiple probes (per the probe clustering step above). A difference measure ($d_m$) for each model was calculated between the prediction vector generated from each model ($p_{m,t}$) and the mean concentration at which the model was trained (${\mu }_m$) as

$$d_m={\displaystyle \sum }_{t=1}^T{(p_{m,t}-{\mu }_m)}^2,$$

where t indexes each measurement within the experimental window and T is the total number of measurements within the experiment. Thus, we calculate d_m for each concentration-range specific model. The model yielding the smallest $d_m$ is selected, and the dopamine predictions resulting from this model are used as our best estimate of dopamine concentration in vivo. This step is motivated by three observations: (i) models that make predictions out of the range of training dataset used to generate that model make the biggest errors; (ii) as the actual dopamine concentration approaches the mean of a corresponding model (with characteristic μ), we see that the predictions error of the model significantly improves; and (iii) in vitro, we get the best performance from those models whose prediction minimize the difference between μ and the predicted concentration.

For the 17 participants analyzed in this report, our procedure yielded specific models that are consistent with known features in the voltammogram such as the oxidation and reduction peaks for dopamine (orange and green shading in Figs. S9 and S10). Our approach works on the derivative of the voltammogram signal (no background subtraction required); thus, the “peaks” are identified by the corresponding “upsweep” and “downsweep” components of each of the oxidation and reduction peaks: see red and blue circles around the oxidation (orange shaded areas in Figs. S9 and S10) and reduction (green shaded areas in Figs. S9 and S10) peaks in Figs. S9 and S10. Parts of the voltammogram in Figs. S9 and S10 that contain a red or blue circle are automatically selected by the EN procedure; other elements (that are not marked by red or blue circles) are ignored.

Fig. S10.

Examples showing derivative of cyclic voltammograms from each participant and overlay of EN determined linear regression weights used for prediction. (A–Q) Derivative of FSCV sweep from each patient showing EN-determined linear regression coefficients overlaid in red and blue. As in Figs. S8 and S9, orange shading and arrowhead show expected range and peak of dopamine oxidation potential; green shading and arrowhead show expected range and peak of dopamine-o-quinone reduction potential. Horizontal axis: time (ms); vertical axis: current (nA).

SNR.

To assess the sensitivity of each concentration range-based model, the SNR for each models’ predictions is calculated over a range of dopamine concentrations.

The SNR is calculated for a given concentration range; this calculation is performed for each concentration-range specific model compared against a test dataset collected in vitro with known dopamine concentration values. Thus, the SNR for a given concentration SNR_c, is calculated as the square of the RMS amplitude ratio of signal $c$ to noise $\stackrel{\rightharpoonup }{\epsilon }$:

$$SN{R}_c={\left(\frac{c}{\sqrt{\frac{1}{n}{{\displaystyle \sum }}^{}\left({\stackrel{\rightharpoonup }{\epsilon }}^2\right)}}\right)}^2,$$

where c is the known (i.e., prepared) concentration of dopamine, and $\stackrel{\rightharpoonup }{\epsilon }$ is the deviation of the predicted concentration ($\widehat{y}$) from the actual concentration ($c$) for n samples measured at that concentration

$$\stackrel{\rightharpoonup }{\epsilon }=\widehat{y}-c.$$

Two-Way Repeated-Measures ANOVA.

Two-way repeated-measures ANOVA was performed comparing the dopamine time series following an outcome for positive versus negative RPEs. For each dopamine time series plot shown (Figs. 3B and 4B), the two factors entered into the repeated-measures ANOVA were (i) the RPE category (positive or negative) and (ii) time. The time points included in the analysis were 0 (time of outcome reveal), 100, 200, 300, 400, 500, 600, and 700 ms. Post hoc two-sample t tests were performed comparing the dopamine measurement at each time point across RPE-sign category and Bonferroni corrected for multiple comparisons where indicated. All statistical analyses were performed using Matlab. The functions anovan.m and multcompare.m were used to perform the repeated-measures ANOVA and post hoc two-sample t tests with multiple comparisons correction, respectively.

Principal Components Regression to Estimate Dopamine Concentration.

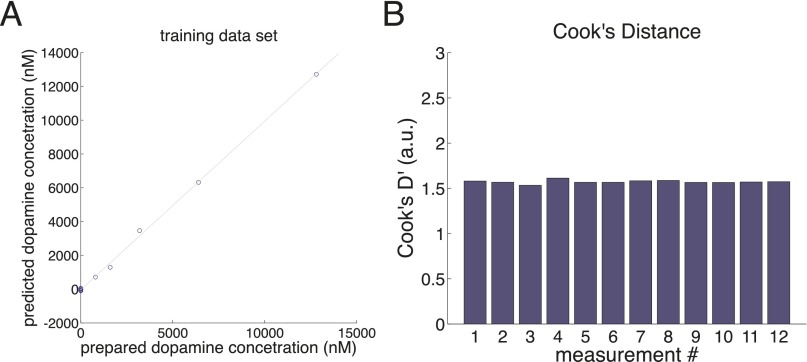
Principal components regression (PC-regression) was performed following recommended procedures described in ref. 24. A training dataset consisting of six background-subtracted voltammograms for six different dopamine concentrations (Fig. S1A, Left) measured in a flow cell and six voltammograms for six different pH levels (Fig. S1A, Right) were entered into a principal components analysis, which resulted in 11 principal components (Fig. S1B, red and blue traces). Malinowski’s F test (56) was used to determine the number of principal components to retain (Fig. S1B, red traces, and Table S1). Using the retained principal components, we reconstruct the training dataset (Fig. S1C) and observe that qualitative aspects indicative of the voltammograms for dopamine and pH changes are retained. Loading of these 12 measurements onto the seven retained principal components are used to fit a linear regression between the prepared concentrations and the predicted concentration (Fig. S2A). Cook’s distance was then calculated for each training data point (Fig. S2B), which shows that none of the 12 training data measurements should be considered outliers. Next, we perform predictions on out-of-sample test data (data collected during the same flow cell session as the training data) to determine the out-of-sample prediction accuracy of the resulting linear regression model (Fig. S3). Test data include changes in dopamine concentration (Fig. S3 A–C) and changes in pH (Fig. S3 D–F). For each prediction on the test dataset, prediction error (the difference between the actual concentration and the test concentration; Fig. S3 B and E) and Q values (following ref. 57) are calculated and compared with Qα (Fig. S3 C and F).

Fig. S2.

Cook’s distance analysis of training dataset. (A) Loadings of the 12 training data background-subtracted voltammograms on to the seven principal components are used to fit a linear regression by ordinary least squares. (B) Cook’s distances are calculated for each training data measurement to test for outliers in the training dataset.

Comparison of PC-Regression Approach to EN-Based Approach in Vitro.

Comparison of the PC-regression and EN-based approaches are shown in Figs. S3 and S4. The predictions shown are from the same electrode under the same flow cell conditions for both models. The main difference being the method for training a predictive linear regression model [PC-regression as outlined in ref. 24 (Fig. S3) or the EN-based approach outlined above (Fig. S4)]. The PC regression-based approach requires background subtraction; thus, predictions shown are for the change in dopamine or pH from the reference voltammograms (for the dopamine concentration measurements, the change was relative to voltammograms measured in 0 dopamine).

Our observation that changes in pH in vitro caused aberrant predictions in dopamine fluctuations when dopamine levels were held constant led us to rely on the EN-based approach for our analysis of human voltammetry data.

Discussion

We tested the hypothesis that fast fluctuations in dopamine concentration encode RPEs over monetary gains and losses using FSCV (to measure dopamine release) in 17 participants while they played a sequential investment game. The data show that a simple encoding of RPEs by dopamine release is not the case (Fig. 3B). Instead, our data are consistent with the idea that dopamine fluctuations integrate a RPE term with a CPE term (Fig. 3B, Inset, and Fig. 4). A model (Eq. 1) that subtracts a CPE term from the RPE term is consistent with our data (Figs. 3 and 4) and is consistent with how counterfactual experience should modulate actual experience but in computational terms. This model makes the surprising prediction that counterfactual outcomes can suppress and even invert dopamine responses to positive and negative RPEs.

Notably, our model and the dopamine responses it explains also capture qualitative aspects about how one should “feel” (e.g., good or bad) given one’s action, the resulting outcome, and the overall context of that outcome. For example, a better-than-expected outcome should feel good (i.e., rewarding); however, if the exact same outcome occurs when an alternative action could have resulted in an even better outcome, then the positive feelings associated with the better-than-expected experience should be diminished and in extreme cases such an experience should feel bad (i.e., aversive). This is consistent with feelings of “regret” and the negative feelings associated with missed opportunities. Likewise, a worse-than-expected outcome should feel bad (i.e., aversive), but, if that outcome is experienced when the outcome could have been much worse, then the overall experience should be driven toward the positive. These analogous feelings of “relief” are typically positive and rewarding for actions that avoid counterfactually large losses or severe punishment. Our model, and the impact of combining actual and counterfactual information to evaluate decision-making, has connections to regret-based theories of decision-making under uncertainty (26, 27). An interesting point here is that this combination of information in a single physical signal (the dopamine response) could be one way that the human brain translates computations about actual and simulated experience to embodied states of feeling.

These data are collected in humans undergoing DBS-electrode implantation for the treatment of Parkinson’s disease. In many respects, decision-making in patients with Parkinson’s disease remains largely intact: they make their own financial decisions, they are free to choose to consent in clinical and research procedures, and they make many other life critical decisions. However, prior work suggests that pharmacological agents, DBS therapies, and the Parkinson’s disease state have been associated with changes in patient behaviors associated with impulse control, adaptive decision-making, and goal-directed behaviors (28–30). The impact of significant dopamine neuron loss, which characterizes this disease, is important to consider. For example, it is unclear what aspects of the dynamics in the dopamine response we report are attributable to the normal state of dopamine neuron function in humans, to reduced dopaminergic signaling caused by Parkinson’s disease pathology, or perhaps downstream adaptive mechanisms resulting from patients’ history of pharmacotherapy. Thus, it is unclear whether the integration of these two error terms is representative of typical dopamine release in a non-Parkinsonian brain. For example (and speculatively), exogenously increased levels of dopamine via l-3,4-dihydroxyphenylalanine (l-DOPA) therapy could cause serotonergic terminals to inappropriately load dopamine through cellular reuptake mechanisms or directly convert l-DOPA into dopamine in terminals that normal release serotonin (31, 32); thus, signals normally encoded by serotonin release might then be misencoded by dopamine release. Although an integration of these terms is consistent with how a decision-making agent might account for these opponent feedback signals, it is not a priori necessary that dopamine release encodes this specific computation. Further experiments are required to determine whether dopamine release encodes the integration of actual and CPE terms in humans without Parkinson’s disease or model systems where the dopaminergic system is intact.

These present results are unanticipated by current models and data collected in nonhuman model organisms including nonhuman primate dopamine neuron recordings and dopamine release measurements in rodents. Work in nonhuman primates has demonstrated that neural activity (somatic spikes) in the anterior cingulate cortex (33), orbital frontal cortex and dorsolateral prefrontal cortex (34), and in rodent striatum (35) are able to track counterfactual information. These studies indicate that activity of single neurons in rodents and nonhuman primates are able to track counterfactual information reflected through changes in spike frequencies but do not demonstrate a mechanism by which these signals are integrated to represent modulations in value estimates of outcomes. Our results demonstrate that experience-dependent RPEs and simulated CPEs are combined at the level of extracellular dopamine fluctuations in the striatum within hundreds of milliseconds following the revelation of a decision–outcome.

In humans, it has been shown that lesions to the orbital frontal cortex impair counterfactual information processing as read out through decision-making behavior and subjective reports about feelings of regret and relief (36). Also, BOLD imaging experiments in humans support the idea that counterfactual information is represented by brain responses in the orbital frontal cortex (37) and striatum (19, 20, 38). However, BOLD imaging is unable to provide specific information about the neurotransmitters involved (39), nor do BOLD imaging experiments provide specific information about how the brain encodes this information at the level of neurotransmitter release, modulations in local field potentials, or somatic spike activity (39, 40). One report has demonstrated neural activity in human substantia nigra that was consistent with dopamine neuron activity (41). In that report, dopamine neuron spike rates were demonstrated to track RPEs as in the animal model literature; however, no association between dopamine neuron activity and counterfactual signaling could be made, nor could a direct link be made between dopamine neuron activity in the substantia nigra and dopamine release in downstream targets.

Our results show dopamine fluctuations combine evaluative information about actual outcomes (RPE) and feedback about outcomes that would have occurred had the agent performed a different action (CPE). These computations are related to temporal difference learning and related Q-learning methods (42, 43), both of with are constrained by experience-dependent learning signals, meaning that these approaches only update state–action value estimates on those states and actions actually experienced. This means that an agent must sample all state–action pairs to gain a full representation of the state–space. A more efficient approach would be to update representations independent of immediate state–action experiences as alternative forms of information become available. Thus, the ability to incorporate counterfactual information should speed up the process of learning because the agent could then update value estimates on multiple states in parallel. This kind of learning from fictive experiences could occur with counterfactual information coming from a variety of sources including other agents (social learning) or more complete information becoming available after certain actions have been made. For example, in the current task, the CPE signal is the difference between the best (or worst) possible outcome and the actual outcome (Eq. 3). This kind of counterfactual information has been shown to be an important signal for driving human choice behavior (19) and is similar to the supervised actor critic framework proposed in ref. 44 and discussed in ref. 45. Together with experience based learning, counterfactual learning signals like this one serve to speed up learning about the optimal strategy in complex and information rich environments.

How RPEs and CPEs are physically combined and contribute to the composite dopamine signal is not known. One possibility is that there are separate sets of dopaminergic neurons with activity modulations that specialize in either the prediction errors or CPEs. Such heterogeneity in dopamine neuron response profiles has been demonstrated (16, 46). This possibility has simply not been tested. Other possibilities are that such signal-dependent coding is multiplexed in a common set of mesostriatal dopamine neurons or that direct modulation of dopamine release and clearance in the terminal regions of the striatum provide direct control over the dynamics of error tracking by dopamine transients. Further work is required to separate these and other possibilities.

Methods

For more detail on all procedures, materials, and analyses presented below, refer to the SI Methods.

Informed Consent and Participant Recruitment.

Participants (n = 17) gave informed written consent and verbal assent to the dual IRB-approved research protocol. IRB committees at Wake Forest University Health Sciences (IRB00017138) and Virginia Tech (IRB 11-078) approved all procedures involving human experimentation. Once written and informed consent was obtained from the patient, the details of the computer task (i.e., the sequential-choice game) were described, and participants practiced a version of the game to gain familiarity with the game controls and game play.

Investment Game.

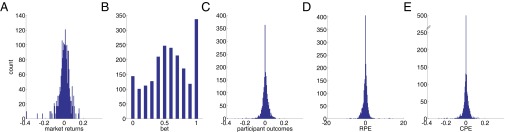
The investment game (Fig. 1 and refs. 19–21) requires participants to make decisions about how much of their portfolio they will invest in a “stock market” given three pieces of information: (i) the history of the market price, (ii) the participant’s current portfolio value, and (iii) the most recent fractional change in the participant’s portfolio value. The participant begins the game endowed with 100 points and plays six markets with 20 decisions in each market. The participants’ final portfolio value (after all 120 decisions have been made) determines the participants’ compensation. Fig. S6 shows the distribution of market returns (Fig. S6A), bets (Fig. S6B), participant returns (Fig. S6C), RPEs (Fig. S6D), and CPEs (Fig. S6E).

Fig. S6.

Distribution of decision-making variables in the investment game. (A–E) Histograms showing the distribution of events for each variable: market returns ($r_t=\hspace{0.17em}\frac{\mathrm{\Delta }{p}_t}{p_t}$) (A), bet size ($b_t$) (B), participant outcomes (gains and losses, $b_t{r}_t$) (C), RPEs ($\{b_t{r}_t-E\left(b_t{r}_t\right)\}/{\sigma }_{b_t{r}_t}$) (D), and CPEs ($r_t-b_t{r}_t$) (E).

RPE Calculation.

The term $b_t{r}_t$ corresponds to participant outcomes (gains or losses) depending on the sign of $r_t$. Positive $r_t$ results in a gain if participants’ bet size was greater than 0; likewise, negative $r_t$ results in a loss for bets greater than 0. RPEs are calculated as the difference between the actual participant return on that trial and the expected return on that trial. This term is then normalized by the variability in returns experienced up to that trial and within each market:

$$\frac{b_t{r}_t-E\left(b_t{r}_t\right)}{{\sigma }_{b_t{r}_t}},$$ [2]

where $E\left(b_t{r}_t\right)$ is the expected value of $b_t{r}_t$, which is calculated as the mean of participant outcomes from the first trial of the game to trial $t-1$, and ${\sigma }_{b_t{r}_t}$ is the SD over those same events.

CPE Calculation.

Participant outcomes ($b_t{r}_t$) are a fraction of the maximum possible outcome on any given trial. The “maximum possible” is revealed as the market return (i.e., price change) is revealed—had the participant bet all in or $b_t$, then the gain or loss (dependent on the sign of $r_t$) would have been the largest that it could have been on that trial. The difference between this value and the value of the participant’s actual return ($b_t{r}_t$) is the CPE − the difference between what could have been and what actually happened:

$$r_t\left(1-b_t\right).$$ [3]

FSCV Carbon-Fiber Microsensors.

We performed FSCV on extended carbon-fiber microsensors in the striatum (n = 14 caudate and n = 3 putamen) of patients (n = 17 total) with Parkinson’s disease. The extended carbon-fiber microsensor is constructed to match the dimensions of the tungsten microelectrodes used for functional mapping during DBS-electrode implantation surgery following ref. 21. Fig. S7 shows the component parts and assembly of the extended carbon-fiber microsensor used in these experiments.

FSCV Protocol.

Our FSCV protocol follows previous work in rodents (21, 47, 48). An electrochemical conditioning protocol (see Fig. S8A for depiction of applied waveform) is first applied consisting of a 60-Hz application of the measurement waveform for approximately 10 min to allow equilibration. Following this conditioning procedure, a 10-Hz application of the same triangular waveform is applied for the duration of the experiment (Fig. S8B). Examples of the resulting voltammograms (for each patient) and their derivatives, which were used for analysis, are shown in Figs. S9 and S10, respectively.

Estimation of Dopamine Concentration.

We estimate dopamine concentration, as measured by FSCV using linear regression models trained using in vitro data and the EN algorithm (refer to SI Methods for more information). The EN algorithm is an automatic shrinkage and regularization approach to fitting-regression models (49). We use the glmnet package developed for use in Matlab (50) to train and test cross-validated models against prepared solutions of known dopamine concentrations. Solutions of dopamine are prepared in PBS (pH 7.4). Powdered dopamine hydrochloride (Sigma-Aldrich) is dissolved in a 0.1 N solution of HCl to a concentration of 100 mM. Aliquots of this solution are diluted to 10 mM in 1× PBS and further diluted (in 1× PBS) to the desired concentration for in vitro calibration of the carbon-fiber microsensors.