Limitations of GCTA as a solution to the missing heritability problem

Significance

The genetic contribution to a phenotype is frequently measured by heritability, the fraction of trait variation explained by genetic differences. Hundreds of publications have found DNA polymorphisms that are statistically associated with diseases or quantitative traits [genome-wide association studies (GWASs)]. Genome-wide complex trait analysis (GCTA), a recent method of analyzing such data, finds high heritabilities for such phenotypes. We analyze GCTA and show that the heritability estimates it produces are highly sensitive to the structure of the genetic relatedness matrix, to the sampling of phenotypes and subjects, and to the accuracy of phenotype measurements. Plausible modifications of the method aimed at increasing stability yield much smaller heritabilities. It is essential to reevaluate the many published heritability estimates based on GCTA.

Abstract

Genome-wide association studies (GWASs) seek to understand the relationship between complex phenotype(s) (e.g., height) and up to millions of single-nucleotide polymorphisms (SNPs). Early analyses of GWASs are commonly believed to have “missed” much of the additive genetic variance estimated from correlations between relatives. A more recent method, genome-wide complex trait analysis (GCTA), obtains much higher estimates of heritability using a model of random SNP effects correlated between genotypically similar individuals. GCTA has now been applied to many phenotypes from schizophrenia to scholastic achievement. However, recent studies question GCTA’s estimates of heritability. Here, we show that GCTA applied to current SNP data cannot produce reliable or stable estimates of heritability. We show first that GCTA depends sensitively on all singular values of a high-dimensional genetic relatedness matrix (GRM). When the assumptions in GCTA are satisfied exactly, we show that the heritability estimates produced by GCTA will be biased and the standard errors will likely be inaccurate. When the population is stratified, we find that GRMs typically have highly skewed singular values, and we prove that the many small singular values cannot be estimated reliably. Hence, GWAS data are necessarily overfit by GCTA which, as a result, produces high estimates of heritability. We also show that GCTA’s heritability estimates are sensitive to the chosen sample and to measurement errors in the phenotype. We illustrate our results using the Framingham dataset. Our analysis suggests that results obtained using GCTA, and the results’ qualitative interpretations, should be interpreted with great caution.

In recent years, genome-wide association studies (GWASs) have become an important tool for investigating the genetic contribution to complex phenotypes. These studies use statistical techniques to find associations between single nucleotide polymorphisms (SNPs) and phenotype(s) (e.g., continuous traits such as height or discrete traits such as presence/absence of a disease). A widely used measure of genetic influence on a phenotype is the (narrow-sense) heritability, defined as the ratio of the additive genetic variance to the total phenotypic variance. A major conundrum revealed by many analyses of GWAS data has been that the small number of significant associations explain much less of the heritability than is estimated from correlations between relatives [i.e., much heritability is “missing” (1–3)]. To address this problem, Yang et al. (4) posited that heritability is not missing but is “hidden.” The authors developed a statistical framework [genome-wide complex trait analysis (GCTA)] in which each SNP makes a random contribution to the phenotype, and these contributions are correlated between individuals who have similar genotypes. Applied to many GWASs, GCTA yields estimates of heritability far larger than those obtained using earlier analyses. GCTA has been used to estimate the heritability of many phenotypes from schizophrenia (5) to scholastic achievement (6). Despite its current wide use, recent studies (7, 8) have questioned the reliability of GCTA estimates.

We show here that the results produced using GCTA hinge on accurate estimation of a high-dimensional genetic relatedness matrix (GRM). We show that even when the assumptions in GCTA are satisfied exactly, heritability estimates produced by GCTA will be biased, and it is unlikely that the confidence intervals will be accurate. When there is genetic stratification in the population, we show that GCTA’s heritability estimates are guaranteed to be unstable and unreliable, which is especially relevant because stratification is common in human GWASs.

Our analysis has two other important consequences: (i) the heritability estimate produced by GCTA is sensitive to the choice of the sample used; and (ii) the estimate is sensitive to measurement errors in the phenotype. We argue that this instability and sensitivity are attributable to the fact that GCTA necessarily overfits typical GWASs. We show that a direct approach to eliminating this overfitting leads back to the small SNP heritability estimates derived previously from association studies. We illustrate our results using the Framingham dataset (9, 10) comprising information on 49,214 SNPs in 2,698 unrelated individuals.

We conclude that application of GCTA to GWAS data may not reliably improve our understanding of the genomic basis of phenotypic variability. Even when the assumptions for GCTA all hold, we recommend the use of diagnostic tests, and we describe one such test. We also discuss several ways of moving toward better methods.

The Data and the GCTA Model

The Data.

A typical GWAS takes phenotypic values for N individuals and assays the individuals’ genotypes at P single nucleotide sites (SNPs). Typically, $N\ll P$ [e.g., our illustrations use the Framingham data on 2,698($=N$) unrelated individuals at 49,214($=P$) SNPs]. The genetic data can be represented as an $N\times P$ matrix $\mathbf{X}$ whose $\left(i,j\right)$ entry takes the value 0, 1, or 2 corresponding to the number of copies of the reference allele of the $j^{\text{th}}$ SNP in the $i^{\text{th}}$ individual.

Mixed-Effect Models.

To quantify how genes influence phenotypes, mixed linear models (11, 12) of the form

$$\mathbf{y}=\mathbf{F}\mathit{\beta }+\mathbf{Z}\mathbf{u}+\mathbf{ϵ}$$ [1]

are used in the animal-breeding literature. Here, $\mathbf{y}=\left\{y_i\right\}$ is a vector of phenotype values for the N individuals, $\mathbf{F}\mathit{\beta }=\mathit{\mu }$ is a vector of “fixed effects,” $\mathbf{u}$ is a vector of random effects of an individual’s genotype, $\mathit{ϵ}$ is a vector of residuals, and $\mathbf{Z}$ is a matrix describing how genetic effects are correlated between individuals. In animal-breeding studies and some human studies, the entries of $\mathbf{Z}$ are estimated from pedigrees.

What GCTA Assumes and Does.

GCTA applies Eq. 1 to GWASs, where genetic and phenotypic information are usually measured on unrelated individuals. Each individual’s genotype is given by P numbers, so the vector $\mathbf{u}$ of random effects is $P\times 1$ and the matrix $\mathbf{Z}$ is $N\times P$. GCTA estimates $\mathbf{Z}$ by centering and scaling the data matrix $\mathbf{X}$ using Hardy–Weinberg assumptions and assumes that $\mathbf{u}\sim \mathcal{N}\left(0,{\sigma }^2\mathbf{I}\right)$ and $\mathbf{ϵ}\sim \mathcal{N}\left(0,{\alpha }^2\mathbf{I}\right)$.

The fixed effects term $\mathit{\mu }$ is commonly dropped from the analysis and the GCTA model written as

$$\mathbf{y}=\mathbf{Z}\mathbf{u}+\mathbf{ϵ},$$ [2]

which we use henceforth. This model can be rewritten more clearly, with the same $\mathit{ϵ}$, as

$$\mathbf{y}=\mathbf{g}+\mathbf{ϵ},$$ [3]

where $\mathbf{g}\sim \mathcal{N}\left(0,V_g\mathbf{A}\right)$ is a random vector of genetic contributions to the phenotypes, $V_g=P{\sigma }^2$ is the variance of total additive genetic effects, and $\mathbf{A}=\mathbf{Z}{\mathbf{Z}}^{\text{T}}/P$ is the GRM between pairs of individuals.

GCTA obtains maximum-likelihood estimates (MLEs) of the parameters ${\alpha }^2$ and $V_g$ and then estimates the heritability as the ratio $V_g/V_p$, where $V_p=V_g+{\alpha }^2$ is the observed variance in the phenotype (4).

The relatively simple structure of Eq. 3 (linear, additive, and no environmental or epigenetic effects) relies on assumptions that GCTA has in common with the animal-breeding literature. GCTA assumes that the SNPs used are in linkage equilibrium; in practice, SNPs in linkage disequilibrium are avoided. In our analysis and example, we assume that this selection has been made. However, GCTA makes important additional assumptions: assumption 1, each SNP makes a random contribution to the phenotype independent of the others; assumption 2, the distribution of these random contributions is identical for all SNPs; and assumption 3, there is no genetic stratification in the population.

In this paper, we use a rigorous mathematical analysis of GCTA to answer two key questions. How reliable are the GCTA estimates when the assumptions in the model are satisfied exactly? How robust are the GCTA estimates to violations of assumption 3 (with or without a correction)?

We begin with the key point that any observed realization of the matrix $\mathbf{Z}$ in Eq. 2 is a sample from some underlying distribution of possible data. In fact, $\mathbf{Z}$ is a random matrix. Hence, the data (the entries of $\mathbf{Z}$) and the resulting GRM ($\mathbf{A}=\mathbf{Z}{\mathbf{Z}}^{\text{T}}/P$) will have sampling errors. As a consequence, the MLEs produced by GCTA are statistical estimates of the parameters in Eq. 3. To analyze the precision and stability of these MLEs, we now develop the connection between the MLEs and the geometry of $\mathbf{Z}$ (in terms of the matrix’s singular values and singular vectors).

Singular Values and GCTA.

The MLEs produced by GCTA depend on the properties of the GRM matrix ($\mathbf{A}=\mathbf{Z}{\mathbf{Z}}^{\text{T}}/P$). We prove here that these MLEs can be expressed in terms of the singular values and associated singular vectors—the spectral properties—of the data matrix $\mathbf{Z}$. Readers will be familiar with spectral properties in the context of principal component analysis (PCA). In PCA, we rank the N eigenvalues (and associated eigenvectors) of the symmetric matrix $\mathbf{Z}{\mathbf{Z}}^{\text{T}}$. PCA is equivalent to a singular value decomposition (SVD) of the matrix $\mathbf{Z}$, which produces a set of $k=\text{min}\left(N,P\right)$ real singular values ($\left\{w_i\right\}$ for $1\le i\le k$), a set of left singular vectors ($\left\{{\mathbf{u}}_i\right\}$ for $1\le i\le k$) of dimension $N\times 1$, and a corresponding set of right singular vectors ($\left\{{\mathbf{v}}_i\right\}$ for $1\le i\le k$) of dimension $P\times 1$. The eigenvalues of $\mathbf{Z}{\mathbf{Z}}^{\text{T}}$ in a PCA are the squares of the singular values of $\mathbf{Z}$ (the PCA eigenvectors are the left singular vectors of $\mathbf{Z}$).

We find (Appendix A) that the MLEs computed by GCTA are explicit functions of the singular values and singular vectors of $\mathbf{Z}$. We write the MLEs for ${\alpha }^2$ and ${\sigma }^2$ as the sum of three terms, the second of which (Eqs. A3 and A8) is a function of

$$\log \left({\displaystyle \prod _{i=1}^{i=k}\left(\left(1/w_i^2\right)+\left({\sigma }^2/{\alpha }^2\right)\right)}\right);$$ [4]

note the terms in $\left(1/w_i^2\right)$. Using ${\mathbf{y}}_1$ to represent a realization of $\mathbf{y}$, the third term (Eqs. A3 and A9) is a function of ${\mathbf{Z}}^{\text{T}}{\mathbf{y}}_1$ and of the left singular vectors ($\left\{{\mathbf{u}}_i\right\}$ for $1\le i\le k$) of $\mathbf{Z}$. We use these results to determine how sampling errors influence the estimates produced by GCTA in two cases.

Case 1: GCTA’s Assumptions Are Satisfied Exactly.

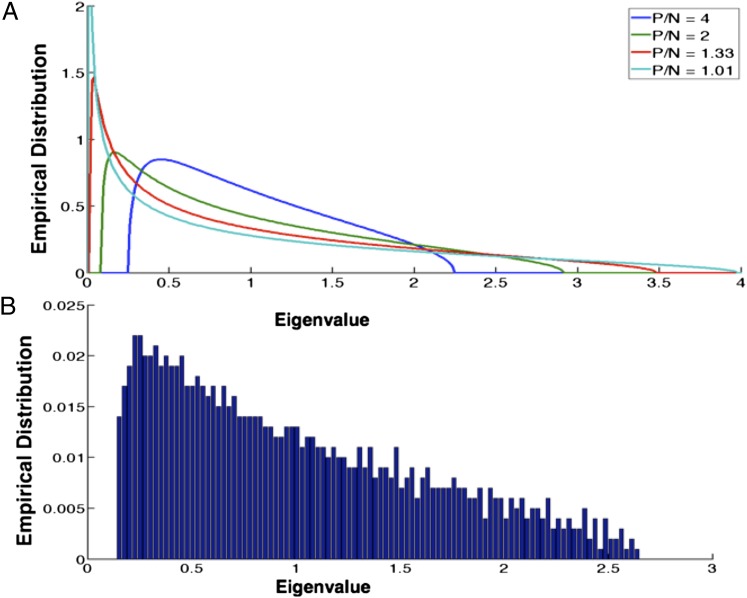
When assumptions 1 through 3 hold, the matrix $\mathbf{Z}$ (asymptotically) has an N variate Wishart distribution with P degrees of freedom. Marčenko and Pastur (13) (also see refs. 14 and 15 for more readable expositions) show that for samples $\mathbf{Z}$ from a Wishart distribution, the empirical distribution of the eigenvalues of $\mathbf{A}=\left(1/P\right)\mathbf{Z}{\mathbf{Z}}^{\text{T}}$ (Fig. 1A) converges to a limiting form when $N\to \infty$, $P\to \infty$, and $P/N$ is finite. This limit distribution depends only on the value of $P/N$ and, although asymptotic, accurately describes the eigenvalue distribution of $\mathbf{A}$ even for sample sizes as small as $N=\mathrm{1,000}$ (Fig. 1B). Note from Fig. 1A that for all values of $P/N$, almost all eigenvalues of $\mathbf{A}$ lie within the interval 0–4, and that as $P/N$ approaches 1, the spectrum of $\mathbf{A}$ becomes ill-conditioned (i.e., the ratio of its largest to its smallest eigenvalue becomes large).

Fig. 1.

The M-P distribution. (A) Plots of the M-P distribution of eigenvalues for different values of $P/N$. For $P/N$ values close to 1, the eigenvalues of the GRM are extremely skewed. As $P/N$ increases, the eigenvalues are concentrated on a smaller interval. (B) A frequency histogram of the eigenvalues for a sample GRM simulated using $N=\mathrm{1,000}$ and $P/N=4$. One eigenvalue had a magnitude greater than 400 (which is not represented in this plot). Note that even for sample sizes as small as 1,000, the M-P distribution accurately captures the distribution of the eigenvalues of the GRM.

In all available GWASs, there are more SNPs than people, so $P/N\gg 1$. For such cases, the known results above imply that the eigenvalues of the GRM are well-conditioned, so that the errors in the second term of the MLE [i.e., in $\left(\left(1/w_i^2\right)\right)$] will be small.

In addition to the eigenvalues, the third term in the MLE expression depends on the eigenvectors of the GRM. Because the eigenvectors of the true GRM are unknown, GCTA proceeds by approximating the eigenvectors of the true GRM by the eigenvectors of the sample GRM. This approximation will be valid if the eigenvectors of the true GRM are “similar” to the eigenvectors of the sample GRM. Standard results from perturbation theory show that the eigenvectors will be similar only if the eigenvalues of the sample GRM are not packed close to one another. However, because $N\sim O\left({10}^3\right)$ eigenvalues of the GRM are packed in the interval 0–4, the eigenvalues of the sample GRM are guaranteed to be packed close to one another (for our simulations in Fig. 1B, where $N=\mathrm{1,000}$ and $P/N=4$, the two closest eigenvalues have magnitudes 0.2412 and 0.2417, respectively). As a result of this close packing, the eigenvectors of the sample GRM can be drastically different from the eigenvectors of the true GRM and, these differences bias the MLEs of ${\alpha }^2$ and ${\sigma }^2$ by amplifying the sampling errors associated with the GRM (see Appendix B for details). If these biases in the MLEs are large, the heritability estimates produced by GCTA will not be representative of the true underlying heritability of the phenotype. Furthermore, because GCTA estimates the SE of the heritability as a function of the MLEs, large biases would make this SE meaningless.

To demonstrate this bias, we simulated a dataset comprising 50,000 SNPs in linkage equilibrium for 2,000 people [using PLINK software (16)] and a phenotype with a heritability of 0.75 (using GCTA). The simulation assumes that the entire additive genetic contribution to the phenotype comes from 45,000 out of the total 50,000 SNPs (the causal SNPs) whose effect sizes are normally distributed with mean 0 and variance 1.

Using GCTA on this dataset, we estimate the genotypic variance $V_g=P{\sigma }^2$ as $\approx 0.685$ with a SE of 0.151. This result, along with standard results from large sample theory (17), state that the MLE of ${\sigma }^2$ is approximately normally distributed with mean 0.685/50,000 = 1.37$\times \hspace{0.17em}{10}^{-5}$ and SD 1.51/50,000 = 3.1$\times \hspace{0.17em}{10}^{-6}$ which forms GCTA’s null hypothesis.

To test this hypothesis, we construct 500 genotype matrices, each comprising all 2,000 people but only 5,000 SNPs randomly chosen from the initial 50,000. We ran GCTA using each of these genotype matrices, and in each case, estimated ${\sigma }^2$ (Fig. 2). More than half of these estimates lie outside the 95% confidence interval (marked by red arrows), with the largest of these estimates ($4.497\hspace{0.17em}\times \hspace{0.17em}{10}^{-5}$) being more than 10 SDs away from the mean; these results suggest that GCTA’s null is almost certainly being violated.

Fig. 2.

Large deviations in ${\sigma }^2$ estimates. Estimates of ${\sigma }^2$ are produced by GCTA using 500 randomly sampled genotype matrices, each comprising 5,000 SNPs drawn at random from a simulated dataset (comprising 50,000 SNPs), which satisfies all of GCTA’s assumptions. When GCTA is run on the entire dataset, we get a ${\sigma }^2$ estimate of $1.37\hspace{0.17em}\times \hspace{0.17em}{10}^{-5}$ and SE of $3.1\hspace{0.17em}\times \hspace{0.17em}{10}^{-6}$; the 95% confidence interval corresponding to this estimate is marked with red arrows. Clearly, the confidence intervals produced by GCTA are grossly underestimating the uncertainty in the ${\sigma }^2$ estimates.

Although our results guarantee that each estimate of ${\sigma }^2$ in Fig. 2 will be biased, our results do not provide any general information about the magnitude of the bias. It is possible that the bias in some of these estimates is small, and some resampling procedure might resolve problems raised in this section; we do not pursue this here.

Case 2: There Is Genetic Stratification.

Assumption 3 is typically violated: stratification is widely observed in humans (18, 19) and animals (20, 21) and is a major reason for the high number of false discoveries in GWASs (22). GCTA claims to address this by incorporating eigenvectors of the GRM as fixed effects [as columns of $\mathbf{F}$ in Eq. 1, as suggested by Eigenstrat software (23)]. Surprisingly, GCTA finds that in most cases, the fixed-effect term has little influence (i.e., the heritability estimate from GCTA is nearly independent of the stratification). We will show that the analysis provided by GCTA is flawed and that stratification will induce large errors in the MLEs. We illustrate our points using the Framingham dataset (9, 10), which is known to be stratified.

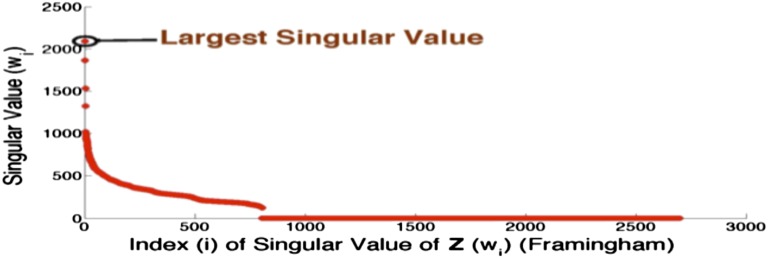
We begin by analyzing how genetic stratification influences the spectral properties of $\mathbf{Z}$. A plot of the singular values of $\mathbf{Z}$ for the Framingham dataset (Fig. 3) reveals that these values are extremely skewed. The first four singular values are greater than 1,000, and the next 20 or so are between 100 and 1,000, whereas thousands of singular values are close to 0: the largest singular value is $\sim {10}^{10}$ times the smallest singular value.

Fig. 3.

Skew in the singular values. Notice that $\mathbf{Z}$ has a long tail of near-zero singular values. The largest singular value of $\mathbf{Z}$ is $O\left({10}^3\right)$, and the smallest nonzero singular value of $\mathbf{Z}$ is $O\left({10}^{-7}\right)$, showing that $\mathbf{Z}$ has a very high condition number.

It is well known (see theorem 3 in ref. 24 and section 4.3 in ref. 25) that such skews must occur in stratified populations. In essence, these studies show that if N is large, and the markers are sampled from K different populations, the first $K-\hspace{0.17em}1$ singular values of $\mathbf{Z}$ will be much larger than the remaining $N-\hspace{0.17em}K+\hspace{0.17em}1$. Because in most cases, $N\gg K>1$, we expect most of the singular values of $\mathbf{Z}$ to be close to 0, as in Fig. 3.

This skew, and the long tail of near-zero singular values, have serious implications for the MLEs from GCTA. Recall that the second term in the MLE (Eq. A8) is sensitive to the near-zero singular values of $\mathbf{Z}$. The third term (Eq. A9) is a function of ${\mathbf{Z}}^{\text{T}}{\mathbf{y}}_1$ and so is also sensitive to the near-zero singular values when $\mathbf{Z}$ is ill-conditioned (i.e., the ratio of the largest to the smallest singular value of $\mathbf{Z}$ is large). Therefore, the accuracy of both terms in the MLE expression hinge on the precise estimation of the near-zero singular values of $\mathbf{Z}$. Stewart (26) shows that in the presence of noise, the estimation errors of a singular value whose “true” magnitude is 0 will be larger than the noise by a factor $\sqrt{P}$ (i.e., the estimates of the near-zero singular values are extremely imprecise). We now illustrate several problems with the GCTA estimates in genetically stratified populations, all of which stem from the imprecision of the near-zero singular values.

Sensitivity to the SNPs used in the study.

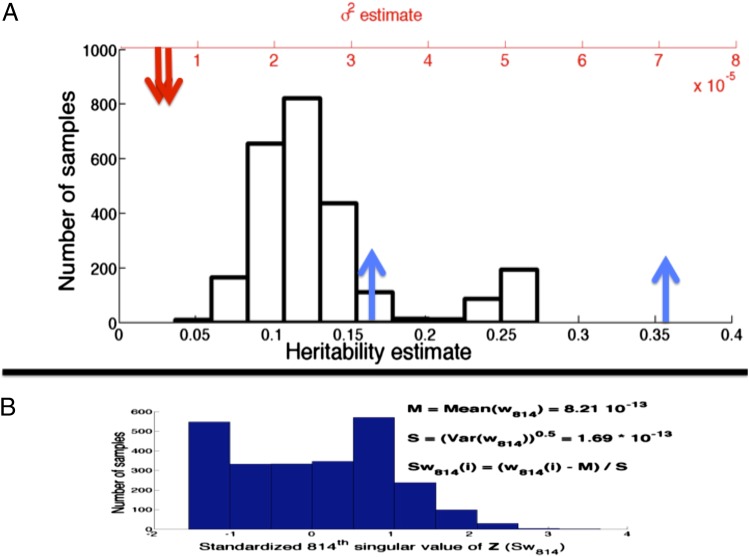
The heritability estimates from GCTA will be sensitive to the SNPs used in the study because the errors associated with the near-zero singular values (and in turn the MLEs) for datasets constructed using different sets of SNPs will be different. To demonstrate this, we construct 2,500 genotype matrices, ${\mathbf{X}}_i$ for $1\le i\le \mathrm{2,500}$, each comprising 5,000 (of the total 49,214 SNPs) randomly sampled SNPs, and use GCTA to estimate the heritability of systolic blood pressure (BP) (27) using each of these ${\mathbf{X}}_i$. Contrary to the claim in ref. 4, these heritability estimates show high variability (Fig. 4A), because of sampling errors associated with one or more of the near-zero singular values (Fig. 4B).

Fig. 4.

Sensitivity of GCTA estimates to SNPs retained in GWASs. (A) Heritability and corresponding ${\sigma }^2$ estimates from the Framingham dataset produced by GCTA using 2,500 randomly sampled genotype matrices comprising 5,000 SNPs each (from the total 49,214). When GCTA is run on the entire dataset, we get a ${\sigma }^2$ estimate of $5.34\hspace{0.17em}\times \hspace{0.17em}{10}^{-6}$ with a SE of $9.75\hspace{0.17em}\times \hspace{0.17em}{10}^{-7}$; the 95% confidence interval for the corresponding ${\sigma }^2$ and heritability estimates are marked with red and blue arrows, respectively. Note how drastically the null hypothesis is violated. (B) Histogram of the “standardized” ${814}^{\text{th}}$ singular value of $\mathbf{Z}$ ($w_{814}$) for the 2,500 samples. This singular value has an extremely small magnitude for all of the samples (∼O(10⁻¹³)) but has high estimation error and therefore can induce large errors in the heritability estimates produced using GCTA (see Eq. A8 in Appendix B for details).

Sensitivity to the measurement errors in the phenotype.

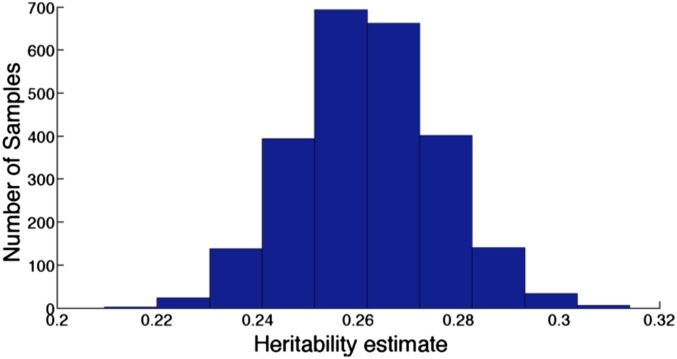
Because $\mathbf{Z}$ is ill-conditioned, small changes in the phenotype vector can cause large changes in the heritability estimates from GCTA. Hence, GCTA violates the “unspoken assumption that imprecision of measurement of phenotype will not have large systematic effects on the location of significant associations in GWAS” (28). To demonstrate this violation, we generate 2,500 noisy samples of the BP phenotype vector [for each sample, the $i^{th}$ entry of the vector is drawn uniformly over the minimum and maximum of the four BP readings available to us for person i; in general, BP readings are much noisier (29)] and use GCTA to estimate the heritability using each of these vectors. Even for the modest errors in this case, GCTA shows high variability in its heritability estimates (Fig. 5).

Fig. 5.

Sensitivity of GCTA estimates to measurement errors in the phenotype. Heritability estimates produced by GCTA using 2,500 “noisy” estimates of the phenotype (systolic blood pressure) vector; in our study, we used all 2,698 people and 49,214 SNPs.

Saturation of heritability estimates.

According to GCTA, each SNP makes a random contribution to the phenotype; therefore, the heritability estimate, $P{\sigma }^2/V_p$, is necessarily directly proportional to P (because $V_p$ is fixed). Several studies (see figure 5 in ref. 30) using GCTA have found results contradicting this; these studies report a threshold value above which, introducing more SNPs in the analysis produces only marginal increases in the heritability estimates from GCTA. This saturating behavior implies that above a threshold of P, $P{\sigma }^2$ is nearly independent of P (i.e., ${\sigma }^2$ is inversely proportional to P) which violates GCTA’s assumption that the contribution of each SNP to the heritability estimate is independent of the others.

Bias in the heritability estimates.

We have shown that for a stratified population, the MLEs produced by GCTA are guaranteed to be biased. The bias arises because thousands of eigenvalues of the GRM are closely packed (near 0) and have large sampling errors associated with their values (Appendix B). As a result of the bias, the heritability estimates produced by GCTA are not reflective of the “true” underlying heritability. Furthermore, the SEs reported by GCTA are functions of the MLEs, and so these SEs will also be unreliable.

To demonstrate this unreliability, we first ran GCTA on the Framingham dataset with BP as the phenotype. GCTA reports that $V_g=P{\sigma }^2$ has an estimate of 0.263 and a SE of 0.048. This result plus large sample theory imply that the MLE for ${\sigma }^2$ will be approximately normally distributed with mean 0.263/49,214 = $5.34\hspace{0.17em}\times \hspace{0.17em}{10}^{-6}$ and SD 0.048/49,214 = $9.75\hspace{0.17em}\times \hspace{0.17em}{10}^{-7}$ which forms GCTA’s null hypothesis.

To test this hypothesis, we computed the estimate and SEs of ${\sigma }^2$ for each of the samples used in Fig. 4A. The ${\sigma }^2$ for almost all of these samples lies outside the 95% confidence intervals predicted by GCTA’s null (marked by the red arrows), with the largest of these estimates (5.46 $\times \hspace{0.17em}{10}^{-5}$) being more than 50 SDs away from the mean; these results suggests that GCTA’s null is almost certainly being violated.

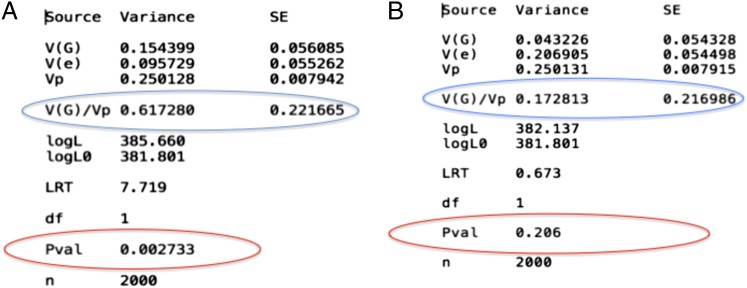
Resampling techniques like the bootstrap cannot be used to correct for the bias in heritability estimates because every run of the bootstrap will produce a biased estimate of heritability, and there is no way of estimating the magnitude of the bias in any of these samples. Are there other approaches to fixing GCTA when there is genetic stratification in the population? Two common approaches to fixing this problem are (i) constraining the random effects associated with only some of the SNPs to be relevant (sparsity) (31) or (ii) denoising the matrix $\mathbf{Z}$ (i.e., setting its lower noisy singular values to 0) before constructing it (32). We do not pursue the first approach because it violates the premise of GCTA that each SNP makes a random contribution to the phenotype. Using the latter approach, we show (Appendix C) that the contribution of the random effects term will not be significantly different from 0 (Fig. 6); these results are consistent with our findings on denoising the Framingham dataset. Because the random effects term is the sole driver of the “improved” heritability estimates produced by GCTA, in the term’s absence, the heritability estimates will be no better than those obtained using the significant SNPs in association studies.

Fig. 6.

Fixing GCTA by denoising the GRM. (A) Heritability estimates for a highly heritable phenotype computed using the GRM as prescribed by GCTA (the phenotype was simulated as a quantitative trait using GCTA; the desired heritability of the trait was set to 0.65). Notice that the P values suggest a significant contribution from the random effects term. (B) Heritability estimates for the same phenotype vector computed using a denoised GRM (obtained by setting the noise terms to 0). Notice that the random effects associated with the SNPs are no longer significant. This result shows that the pathologies of GCTA are general and not dataset-specific (we have verified a similar trend with the Framingham dataset; a significant random effect term loses significance upon denoising the GRM).

It is not surprising that the estimates produced by GCTA are sensitive and biased because the method estimates $NP+2$ parameters ($NP$ parameters for the N nonzero singular values and their corresponding left and right singular vectors, plus ${\alpha }^2$ and ${\sigma }^2$) from a dataset containing $NP$ entries and therefore overfits the data. In contrast, association studies insist on stringent P values for significance and so greatly reduce the effective number of parameters being estimated (see ref. 33 for details); the resulting effective number of parameters is much smaller than the size of the dataset, so overfitting is not a problem.

The MLEs produced by GCTA will be unreliable irrespective of the number of principal components that are included in the model (see Fig. 7, where the MLEs produced by GCTA are unreliable even when five principal components are used as fixed effects; similar unreliabilities were observed when one and three principal components were used as fixed effects, respectively). Price and coworkers (23, 24) have shown that principal components are useful for identifying population stratification and when used with reliable methods like association studies, are effective in correcting for population stratification. When principal components are used in conjunction with GCTA, the analysis step is unreliable as a result of the overfitting. Therefore, although the principal components are still able to accurately identify population stratification, they only serve to compound the bias of GCTA.

Fig. 7.

Using principal components as fixed effects do not resolve problems with stratification. Resampling experiments were identical to those performed in Fig. 4, with five principal components included as fixed effects; GCTA’s predicted 95$\text{\%}$ confidence intervals for the ${\sigma }^2$ and heritability estimates are marked with red and blue arrows, respectively. Note that the SEs are drastically underrepresenting the “true” variation in the ${\sigma }^2$ estimates, despite the inclusion of principal components as fixed effects. Near-identical plots are obtained when the simulations are run with one and three principal components, respectively.

Discussion

GCTA analyses have been widely accepted in large part because they produce heritability estimates that are many times larger than earlier estimates from GWAS data and are closer to those obtained from data with reliable pedigrees. The statistical model in GCTA assumes that each SNP makes a small random contribution to the variability in the phenotype. Our analytical and numerical results illustrate the problems with GCTA when (i) the assumptions of the model are satisfied exactly or (ii) the assumptions are violated as a result of genetic stratification. In both cases, the problems associated with GCTA stem from the fact that a high-dimensional correlation matrix is being estimated from a limited amount of data without dimensionality reduction.

When there is genetic stratification in the population, the GRM has a long tail of near-zero eigenvalues; here, GCTA will produce unreliable heritability estimates. GCTA claims that including the first few principal components as fixed effects (following ref. 23) will resolve the problem of stratification, but this is not the case; even after including principal components as fixed effects, the problems associated with the near-zero singular values of $\mathbf{Z}$ remain. Principal components are useful for dealing with stratification in the context of association studies because principal components reduce the dimensionality of the problem via stringent P value criteria. We believe that stratification is responsible for many of the counterintuitive results reported by studies using GCTA (a more detailed discussion of these studies can be found in ref. 8). Furthermore, numerous studies on sensitive subjects like childhood intelligence (34), Tourette syndrome (35), and schizophrenia (36) need to be critically reviewed.

Even when there is no genetic stratification, our analysis strongly suggests that the heritability estimates and their SEs produced by GCTA will be unreliable. These unreliabilities are illustrated by our simulations (Fig. 2). We do not prove that they will apply for all datasets where there is no genetic stratification. Our illustration does suggest a simple test of the reliability of GCTA’s estimates by a resampling procedure: first, construct many, say 500, genotype matrices by randomly sampling $\left(P/10\right)$ SNPs from the total P SNPs in the dataset and use GCTA to compute the ${\sigma }^2$ estimate corresponding to each of these genotype matrices. Next, compute the estimate ($e_1$) and SE ($s_1$) for ${\sigma }^2$ using all P SNPs. Under GCTA’s null, ∼99.5% of the distribution should lie in the interval [$e_1-4s_1$, $e_1+4s_1$]; if any of the 500 simulations estimates a ${\sigma }^2$ far outside this range, GCTA’s estimates should not be trusted.

Heritability estimates using methods other than GCTA are generally low $\approx 3\%\hspace{0.17em}\text{to}\hspace{0.17em}4\text{\%}$. These methods use, for example, either single SNP associations or polygenic scores constructed from a few significant SNPs. We have shown that GCTA grossly underestimates the uncertainties associated with the individual SNP contributions and as a result, the only reliable heritability estimates are the 3–4% produced by these other methods.

The problems in GCTA stem from the overfitting of a high-dimensional GRM. To make progress with GCTA-like mixed models, it is critical that the estimates of this matrix be refined. Some progress has been made in this direction using, for example, methods for covariance smoothing (37). There are several alternative methods of describing the relatedness between individuals (for a survey of these methods, see ref. 38), some of which could prove useful in improving the estimate of the GRM.

We have shown that a brute force approach to estimating the covariance structure of the random effects of SNPs (as in GCTA) does not resolve the problem stemming from the number of SNPs (P) being much larger than the number of subjects genotyped (N). We believe that future studies of GWAS data can make progress by incorporating prior information. Two possible ways of so doing are (i) insisting that the basis used for constructing the GRM is sparse (i.e., only some SNPs make random contributions and the rest have fixed contributions) and (ii) incorporating biological information about the relationships between elements in the random covariance matrix.

Appendices

Appendix A: The Likelihood Function and Sensitivity.

Expressing Eq. 2 in probabilistic form, we have

$$P\left(\mathbf{u}\right)=\mathcal{N}\left(\mathbf{u}|0,{\sigma }^2\mathbf{I}\right)\hspace{0.17em}\text{and}\hspace{0.17em}P\left(\mathbf{y}|\mathbf{u}\right)=\mathcal{N}\left(\mathbf{y}|\mathbf{Z}\mathbf{u},{\alpha }^2\mathbf{I}\right).$$ [A1]

Therefore, the marginal distribution of $\mathbf{y}$ will be given by

$$P\left(\mathbf{y}\right)=\mathcal{N}\left(\mathbf{y}|0,\mathbf{C}\right),\hspace{0.17em}\text{where}\hspace{0.17em}\hspace{0.17em}\mathbf{C}={\alpha }^2\mathbf{I}+{\sigma }^2\mathbf{Z}{\mathbf{Z}}^{\text{T}}.$$ [A2]

We have only one sample of the vector $\mathbf{y}$, namely our observed vector of phenotypes (which we call ${\mathbf{y}}_1$). Because $\mathbf{y}$ has a multivariate normal distribution, the log likelihood of observing ${\mathbf{y}}_1$ is

$$\log P\left({\mathbf{y}}_1|{\alpha }^2,{\sigma }^2\right)=\frac{-N}{2}\text{log}\left(2\pi \right)-\log \text{det}\left(\mathbf{C}\right)-\frac{1}{2}{\mathbf{y}}_1^{\text{T}}{\mathbf{C}}^{-1}{\mathbf{y}}_1.$$ [A3]

The Woodbury matrix identity (39) states that the inverse of a matrix $\mathbf{B}=\mathbf{A}+\mathbf{P}\mathbf{R}\mathbf{Q}$ is given by ${\mathbf{B}}^{-1}={\mathbf{A}}^{-1}-$${\mathbf{A}}^{-1}\mathbf{P}\left({\mathbf{R}}^{-1}+\mathbf{Q}{\mathbf{R}}^{-1}\mathbf{P}\right)\mathbf{Q}{\mathbf{A}}^{-1}$. Hence in Eq. A3 with $\mathbf{A}={\alpha }^2\mathbf{I}$, $\mathbf{P}={\sigma }^2\mathbf{Z}$, $\mathbf{Q}={\mathbf{Z}}^{\text{T}}$, and $\mathbf{R}=\mathbf{I}$, we have

$${\mathbf{C}}^{-1}=\frac{1}{{\alpha }^2}\mathbf{I}-\frac{{\sigma }^2}{{\alpha }^4}\mathbf{Z}{\left(\mathbf{I}+\frac{{\sigma }^2}{{\alpha }^2}{\mathbf{Z}}^{\text{T}}\mathbf{Z}\right)}^{-1}{\mathbf{Z}}^{\text{T}}.$$ [A4]

We now use this formulation to show that for a stratified population, the heritability estimates will be sensitive to the data used in the GWAS.

Instability of the second term in Eq. A3.

Using the SVD of $\mathbf{Z}$ ($\mathbf{Z}={\mathbf{U}}_1{\mathbf{W}}_1{\mathbf{V}}_1^{\text{T}}$) in Eq. A2, we have

$$\text{det}\left(\mathbf{C}\right)={\alpha }^{2N}\text{det}\left(\mathbf{I}+\frac{{\sigma }^2}{{\alpha }^2}{\mathbf{U}}_1{\mathbf{W}}_1^2{\mathbf{U}}_1^{\text{T}}\right).$$ [A5]

Sylvester’s theorem for determinants (40) states that for invertible matrices ${\mathbf{R}}_1,{\mathbf{R}}_2$, the determinant $\text{det}\left({\mathbf{R}}_1+\mathbf{P}{\mathbf{R}}_2{\mathbf{Q}}^{\text{T}}\right)=\text{det}\left({\mathbf{R}}_2^{-1}+{\mathbf{Q}}^{\mathbf{T}}{\mathbf{R}}_1^{-1}\mathbf{P}\right)\text{det}\left({\mathbf{R}}_2\right)\text{det}\left({\mathbf{R}}_1\right)$. Hence in Eq. A5, setting ${\mathbf{R}}_1=\mathbf{I}$, $\mathbf{P}=\mathbf{Q}=\left(\sigma /\alpha \right){\mathbf{U}}_1$, and ${\mathbf{R}}_2={\mathbf{W}}_1^2$, we obtain

$$\text{det}\left(\mathbf{C}\right)={\alpha }^{2N}\text{det}\left({\mathbf{W}}_1^{-2}+\frac{{\sigma }^2}{{\alpha }^2}{\mathbf{U}}_1^{\text{T}}{\mathbf{U}}_1\right)\text{det}\left({\mathbf{W}}_1^2\right).$$ [A6]

Therefore, because ${\mathbf{U}}_1^{\text{T}}{\mathbf{U}}_1=\mathbf{I}$,

$$\begin{array}{c}\text{log}\hspace{0.17em}\text{det}\left(\mathbf{C}\right)=2N\hspace{0.17em}\text{log}\left(\alpha \right)+\text{log}\left(\text{det}\left({\mathbf{W}}_1^2\right)\right)\\ +\text{log}\left(\text{det}\left({\mathbf{W}}_1^{-2}+\frac{{\sigma }^2}{{\alpha }^2}\mathbf{I}\right)\right).\end{array}$$ [A7]

To find the MLEs of ${\alpha }^2$, ${\sigma }^2$ using Eq. A3, we must differentiate $\text{log}\hspace{0.17em}\text{det}\left(\mathbf{C}\right)$ with respect to ${\alpha }^2$ and ${\sigma }^2$ and set the derivatives to 0. The derivative of the first term is independent of ${\mathbf{W}}_1$, and the derivative of the second term is 0 because $\text{log}\hspace{0.17em}\left(\text{det}\left({\mathbf{W}}_1^2\right)\right)$ is independent of ${\alpha }^2$ and ${\sigma }^2$. The last term in Eq. A7 is

$$\text{log}\left(\text{det}\left({\mathbf{W}}_1^{-2}+\frac{{\sigma }^2}{{\alpha }^2}\mathbf{I}\right)\right)=\log \left({\displaystyle \prod _{i=1}^{i=k}\left(\frac{1}{w_i^2}+\frac{{\sigma }^2}{{\alpha }^2}\right)}\right).$$ [A8]

For a stratified population, thousands of singular values, $w_i$ of $\mathbf{Z}$ will be close to 0, and Eq. A8 will be extremely sensitive to small changes in the values of w_i

Instability of the third term in Eq. A3.

From Eq. A4, we have

$${\mathbf{y}}_1^{\text{T}}{\mathbf{C}}^{-1}{\mathbf{y}}_1=\frac{1}{{\alpha }^2}{\mathbf{y}}_1^{\text{T}}{\mathbf{y}}_1-\frac{{\sigma }^2}{{\alpha }^4}{\mathbf{y}}_1^{\text{T}}\mathbf{Z}{\left(\mathbf{I}+\frac{{\sigma }^2}{{\alpha }^2}{\mathbf{Z}}^{\text{T}}\mathbf{Z}\right)}^{-1}\underbrace{{\mathbf{Z}}^{\text{T}}{\mathbf{y}}_1}.$$ [A9]

Consider just the factor with an underlying curly bracket. Suppose, we perturb ${\mathbf{y}}_1$ to ${\mathbf{y}}_1+\gamma {\mathbf{y}}_2$ for some small γ. Then, that factor becomes

$${\mathbf{Z}}^{\text{T}}\left({\mathbf{y}}_1+\gamma {\mathbf{y}}_2\right)=\left({\mathbf{Z}}^{\text{T}}+\gamma {\mathbf{E}}^{\text{T}}\right){\mathbf{y}}_1,$$ [A10]

where we chose ${\mathbf{E}}^{\text{T}}$ such that ${\mathbf{E}}^{\text{T}}{\mathbf{y}}_1={\mathbf{Z}}^{\text{T}}{\mathbf{y}}_2$ (the matrix ${\mathbf{E}}^{\text{T}}$ can be trivially constructed to have elements only on its primary diagonal). Because a small perturbation of $\mathbf{Z}$ causes a large change in its spectral properties (26), the vector $\left({\mathbf{Z}}^{\text{T}}+\gamma {\mathbf{E}}^{\text{T}}\right){\mathbf{y}}_1$ can be vastly different from ${\mathbf{Z}}^{\text{T}}{\mathbf{y}}_1$, and hence ${\mathbf{y}}_1^{\text{T}}{\mathbf{C}}^{-1}{\mathbf{y}}_1$ is extremely sensitive to measurement errors in the phenotype.

Appendix B: The Likelihood Function and Bias.

Here, we reformulate the likelihood function in terms of the eigenvalues [$a_i=\left(1/P\right)w_i^2$ for $1\le i\le N$] and the eigenvectors (${\mathbf{u}}_i$ for $1\le i\le N$) of the GRM, $\mathbf{A}=\left(1/P\right)\mathbf{Z}{\mathbf{Z}}^{\text{T}}$. Because $\mathit{ϵ}\sim N\left(0,{\alpha }^2\mathbf{I}\right)$, we have

$${\mathbf{U}}_1^{\text{T}}\mathit{ϵ}\sim N\left(0,{\alpha }^2\mathbf{I}\right).$$ [A11]

Using the SVD of $\mathbf{Z}$ described in Singular Values and GCTA, we have $\mathbf{A}=\left(1/P\right){\mathbf{U}}_1{\mathbf{W}}^2{\mathbf{U}}_1^{\text{T}}$. Now,

$${\mathbf{U}}_1^{\text{T}}\mathbf{g}\sim {\mathbf{U}}_1^{\text{T}}\mathcal{N}\left(0,{\sigma }^2{\mathbf{U}}_1{\mathbf{W}}^2{\mathbf{U}}_1^{\text{T}}\right)\sim \mathcal{N}\left(0,{\mathbf{W}}^2\right).$$ [A12]

Premultiplying Eq. 3 by ${\mathbf{U}}^{\text{T}}$ and using Eq. A12,

$${\mathbf{U}}_1^{\text{T}}{\mathbf{y}}_1={\mathbf{U}}_1^{\text{T}}\mathbf{g}+{\mathbf{U}}_1^{\text{T}}\mathit{ϵ}\sim \mathcal{N}\left(0,{\alpha }^2\mathbf{I}+{\sigma }^2\mathbf{W}\right).$$ [A13]

Setting the diagonal matrix, $\mathbf{S}={\alpha }^2\mathbf{I}+{\sigma }^2{\mathbf{W}}^2$, we note that ${\mathbf{U}}_1\mathbf{S}{\mathbf{U}}_1^{\text{T}}=\mathbf{C}$, where $\mathbf{C}$ is defined in Eq. A2. Using Eq. A13, we can write the likelihood function as

$$\text{log}\hspace{0.17em}P\left({\mathbf{y}}_1|{\alpha }^2,{\sigma }^2\right)=\frac{-N}{2}\text{log}\left(2\pi \right)-\text{log}\hspace{0.17em}\text{det}\left(\mathbf{S}\right)-\frac{1}{2}{\mathbf{y}}_1^{\text{T}}{\mathbf{U}}_1{\mathbf{S}}^{-1}{\mathbf{U}}_1^{\text{T}}{\mathbf{y}}_1.$$ [A14]

Because ${\mathbf{U}}_1$ is an orthogonal matrix, $\text{det}\left({\mathbf{U}}_1\right)\text{det}\left({\mathbf{U}}_1^{\text{T}}\right)$ = 1. Therefore, we have

$$\begin{array}{c}\text{det}\left(\mathbf{S}\right)=\text{det}\left({\mathbf{U}}_1\right)\text{det}\left({\mathbf{U}}_1^{\text{T}}\right)\text{det}\left(\mathbf{S}\right)=\text{det}\left({\mathbf{U}}_1\right)\text{det}\left(\mathbf{S}\right)\text{det}\left({\mathbf{U}}_1^{\text{T}}\right)\\ =\text{det}\left({\mathbf{U}}_1\mathbf{S}{\mathbf{U}}_1^{\text{T}}\right)=\text{det}\left(\mathbf{C}\right).\end{array}$$ [A15]

Using Eq. A15 in Eq. A14 and comparing with Eq. A3, we note that the first two terms in the likelihood function are identical. The only term whose derivative with respect to ${\alpha }^2$ and ${\sigma }^2$ depends on the eigenvectors is the third term, and therefore we analyze this term in more detail. The eigenvalues of $\mathbf{S}$ will be $s_i={\alpha }^2+{\sigma }^2{w}_i^2$ for $1\le i\le N$. The last term in Eq. A14 can be written as

$$J=\frac{1}{2}{\mathbf{y}}_1^{\text{T}}{\mathbf{U}}_1{\mathbf{S}}^{-1}{\mathbf{U}}_1^{\text{T}}{\mathbf{y}}_1={\displaystyle \sum _i\frac{1}{2s_i}{\left({\mathbf{y}}_1^{\text{T}}{\mathbf{u}}_1\right)}^2}.$$ [A16]

Now, suppose that the GRM, $\mathbf{A}$, estimated by GCTA differs from the “true” underlying GRM ($\tilde{\mathbf{A}}$) by a small sampling error $\mathbf{E}$. Using standard results from perturbation theory, we can express the eigenvectors of $\tilde{\mathbf{A}}$ in terms of the spectral properties of $\mathbf{A}$ and the error matrix, $\mathbf{E}$, as

$${\tilde{\mathbf{u}}}_i={\mathbf{u}}_i+{\displaystyle \sum _{j\ne i}\left(\frac{1}{a_i-a_j}\right){\mathbf{u}}_j^{\text{T}}\mathbf{E}{\mathbf{u}}_i}={\mathbf{u}}_i+{\displaystyle \sum _{j\ne i}\left(\frac{P}{w_i^2-w_j^2}\right){\mathbf{u}}_j^{\text{T}}\mathbf{E}{\mathbf{u}}_i},$$ [A17]

where $a_j=\left(1/P\right)w_j^2$ is the $j^{\text{th}}$ eigenvalue of $\mathbf{A}$, $w_j$ is the $j^{\text{th}}$ singular value of $\mathbf{Z}$, and ${\tilde{\mathbf{u}}}_i$ and ${\mathbf{u}}_i$ are the $i^{\text{th}}$ eigenvectors corresponding to $\tilde{\mathbf{A}}$ and $\mathbf{A}$, respectively. Using Eq. A17 in Eq. A16, we get

$$\begin{array}{c}J={\displaystyle \sum _i\frac{1}{2s_i}{\left({\mathbf{y}}_1^{\text{T}}{\mathbf{u}}_i\right)}^2}\\ +{\displaystyle \sum _i\frac{1}{2s_i}{\displaystyle \sum _{j\ne i}\frac{1}{{\left(a_i-a_j\right)}^2}{\left({\mathbf{y}}_1^{\text{T}}{\mathbf{u}}_j\right)}^2{\left({\mathbf{u}}_j^{\text{T}}\mathbf{E}{\mathbf{u}}_i\right)}^2}}\\ +{\displaystyle \sum _i\frac{1}{s_i}\left({\mathbf{y}}_1^{\text{T}}{\mathbf{u}}_i\right){\displaystyle \sum _{j\ne i}\frac{1}{\left(a_i-a_j\right)}\left({\mathbf{y}}_1^{\text{T}}{\mathbf{u}}_j\right)\left({\mathbf{u}}_j^{\text{T}}\mathbf{E}{\mathbf{u}}_i\right)}}.\end{array}$$ [A18]

Note that J is not symmetric in $\mathbf{E}$ (because the second term is not symmetric). Differentiating J with respect to ${\sigma }^2$, we have

$$\begin{array}{c}\frac{\partial J}{\partial {\sigma }^2}={\displaystyle \sum _i\frac{-w_i^2}{2s_i^2}{\left({\mathbf{y}}_1^{\text{T}}{\mathbf{u}}_i\right)}^2}\\ +{\displaystyle \sum _i\frac{-w_i^2}{2s_i^2}{\displaystyle \sum _{j\ne i}\frac{1}{{\left(a_i-a_j\right)}^2}{\left({\mathbf{y}}_1^{\text{T}}{\mathbf{u}}_j\right)}^2{\left({\mathbf{u}}_j^{\text{T}}\mathbf{E}{\mathbf{u}}_i\right)}^2}}\\ +{\displaystyle \sum _i\frac{-w_i^2}{s_i^2}\left({\mathbf{y}}_1^{\text{T}}{\mathbf{u}}_i\right){\displaystyle \sum _{j\ne i}\left({\mathbf{y}}_1^{\text{T}}{\mathbf{u}}_j\right)\left({\mathbf{u}}_j^{\text{T}}\mathbf{E}{\mathbf{u}}_i\right)}}.\end{array}$$ [A19]

Note in Eq. A19 that unless $\mathbf{E}$ is exactly 0, the MLE of ${\sigma }^2$ will always have a factor that does not average out to 0 (because the second term is not symmetric in $\mathbf{E}$), and therefore ${\sigma }^2$ is guaranteed to be biased. Similar derivations show that the MLE of ${\alpha }^2$ are also guaranteed to be biased.

Case 1: There is no stratification in the population.

When the assumptions of GCTA are met exactly, $\mathbf{Z}$ asymptotically has an N variate Wishart distribution with P degrees of freedom (15). Marčenko–Pastur theory (13) provides an empirical distribution (which we henceforth refer to as the M-P distribution) for the eigenvalues of the variance-covariance matrix (which in our case will be the GRM, $\mathbf{A}$) as a function of $P/N$, which although asymptotic, works well even for sample sizes as small as $N=\mathrm{1,000}$ (Fig. 1B). The distribution shows that most of the eigenvalues of the GRM will lie in 0–4. Note from Fig. 1A that when $P/N$ is close to 1, the eigenvalues will be skewed and as the value of $P/N$ becomes smaller, the eigenvalues become concentrated on smaller intervals. For example, when $P/N=4$, the eigenvalues lie within 0.25–2.25 (Fig. 1A).

Because the M-P distribution is continuous, we assume without loss of generality that the eigenvalues are unique (i.e., there are no repeated eigenvalues). Because N is large, the eigenvalues of $\mathbf{A}$ are necessarily packed extremely close to one another. To be specific, for $N=\mathrm{2,000}$ and $N/P=0.25$, the maximum value of the minimum separation between the eigenvalues will be $2/\mathrm{2,000}=0.001$. This upper bound is not tight; our ballpark estimate assumes a (best-case) uniform spread of eigenvalues on the interval. In reality, the distribution is peaked near 0.5 (Fig. 1A), and therefore we expect the eigenvalues near 0.5 to be a lot closer than 0.001 (for our simulation in Fig. 1B, the minimum spacing between the eigenvalues is $5\hspace{0.17em}\times \hspace{0.17em}{10}^{-4}$).

This small separation causes the eigenvectors of the estimated GRM to be drastically different from those of the true GRM. To see why, consider an eigenvalue (say the $p^{\text{th}}$ one) of $\mathbf{A}$, which is closely packed to another eigenvalue (say the $q^{\text{th}}$ one). From Eq. A17, the angle between ${\mathbf{u}}_p$ and ${\tilde{\mathbf{u}}}_p$ will have terms of the form $\left(1/\left(a_p-a_q\right)\right){\mathbf{u}}_p^{\text{T}}\mathbf{E}{\mathbf{u}}_q$, which will be large because $a_p-a_q$ is close to 0. This is just one of the terms; all eigenvalues that are “sticking” close to the $p^{\text{th}}$ eigenvalue will induce large differences between the estimated and true eigenvectors.

These differences are amplified in the expressions for the MLE and its derivatives (see the second and third summations in Eqs. A18 and A19). Therefore, the bias in the heritability estimates produced by GCTA can be large.

Case 2: The population is stratified.

In a stratified population, there are two sources of bias in the GCTA estimates. The first source of bias is identical to that described in the case when there is no stratification for a stratified population, thousands of eigenvalues of the GRM are tightly packed near 0, and therefore from Eqs. A18 and A19, there can be large errors associated with the MLEs produced by GCTA.

The second source of bias comes from the large errors associated with the eigenvalues of the GRM (26). Specifically, suppose there are sampling errors $\mathrm{\Delta }{a}_p$ and $\mathrm{\Delta }{a}_q$ associated with two closely packed eigenvalues whose true magnitudes are $a_p$ and $a_q$, respectively. We have

$$\begin{array}{c}\frac{1}{a_p+\mathrm{\Delta }{a}_p-\left(a_q+\mathrm{\Delta }{a}_q\right)}=\frac{1}{a_p-a_q-\left(\mathrm{\Delta }{a}_q-\mathrm{\Delta }{a}_p\right)},\\ \approx \frac{1+\kappa \left(p,q\right)}{a_p-a_q}\end{array}$$ [A20]

where $\kappa \left(p,q\right)=\left(\mathrm{\Delta }{a}_q-\mathrm{\Delta }{a}_p\right)/\left(a_p-a_q\right)$. Because the errors in the near-zero eigenvalues can be large, κ need not be close to 0. As a result, all of the error terms in Eqs. A18 and A19 will have additional amplification factors of the form $\left(1+\kappa \left(p,q\right)\right)$ for every pair (p and q) of near-zero eigenvalues of the GRM.

The bootstrap and GCTA.

Here, we show that resampling techniques (e.g., the bootstrap, jackknife, etc.) cannot be used to improve the estimates produced by GCTA. Loosely put, the bootstrap estimates the parameter in question (in this case, the heritability) by resampling from the original sample and relying on the fact that the sampling errors “average out” to 0. We have shown in Appendix B that the GCTA estimates are overly (erroneously) biased by local information.

For run i of a bootstrap, let the heritability estimate obtained by GCTA be ${\theta }_g\left(i\right)$, the biasing error be $\kappa \left(i\right)$, the sampling error (with mean 0) be $\pi \left(i\right)$, and the “true” heritability estimate be ${\theta }_0$. The $i^{\text{th}}$ bootstrap estimate can be expressed as

$${\theta }_g\left(i\right)={\theta }_0+\kappa \left(i\right)+\pi \left(i\right).$$ [A21]

Taking the mean in Eq. A21 over sufficient bootstrap samples, we have

$$\text{E}\left({\theta }_g\right)={\theta }_0+\text{E}\left(\kappa \right).$$ [A22]

The bootstrap will estimate $\text{E}\left({\theta }_g\right)$, which is not helpful because we have no handle on $\text{E}\left(\kappa \right)$. More importantly, $\text{E}\left({\theta }_g\right)$ provides no useful information about ${\theta }_0$.

Appendix C: Dynamics of GCTA and More Problems with Stratification.

Consider the most general case, where N random people and P random SNPs are used to construct the random genotype matrix $\tilde{\mathbf{X}}$ (of which one realization is the observed data matrix $\mathbf{X}$). From $\tilde{\mathbf{X}}$, we construct the matrix $\tilde{\mathbf{Z}}$ by centering and scaling so that the entries of matrix $\tilde{\mathbf{Z}}$ will be i.i.d., with mean 0 and variance 1. As a result, $\tilde{\mathbf{Z}}{\tilde{\mathbf{Z}}}^{\text{T}}$ and ${\tilde{\mathbf{Z}}}^{\text{T}}\tilde{\mathbf{Z}}$ will be random Wishart matrices (15), whose eigenvectors are known to be uniformly distributed over the unit sphere in N dimensions (41) which implies that with high probability, the eigenvectors of $\tilde{\mathbf{Z}}{\tilde{\mathbf{Z}}}^{\text{T}}$ ($\left\{\widetilde{{\mathbf{u}}_i}\right\}$ for $1\le i\le k$) and ${\tilde{\mathbf{Z}}}^{\text{T}}\tilde{\mathbf{Z}}$ ($\left\{\widetilde{{\mathbf{v}}_i}\right\}$ for $1\le i\le k$) satisfy ${\left|\widetilde{{\mathbf{u}}_i}\right|}_{\infty }=O\left(\sqrt{\log N/N}\right)$ and ${\left|\widetilde{{\mathbf{v}}_i}\right|}_{\infty }=O\left(\sqrt{\log P/P}\right)$, respectively (42) (the $\infty$ norm of a vector $\mathbf{x}$ = $\left\{x_1,x_2\dots x_n\right\}$ is defined as ${\left|\mathbf{x}\right|}_{\infty }$ = max$\left(\left|x_1\right|,\left|x_2\right|\dots \left|x_n\right|\right)$) [i.e., the maximum entries in the eigenvectors are very small (for n = 2,698 and P = 49,214, $\left(\log N/N\right)\approx 0.001$ and $\left(\log P/P\right)\approx 0.0001$)].

Suppose the first $k_1$ singular values of $\tilde{\mathbf{Z}}$ are much larger than the others. We analyze $\mathbf{g}=\tilde{\mathbf{Z}}\mathbf{u}$, the term primarily responsible for the high heritability estimates obtained using Eq. 3. First, we express $\mathbf{g}$ as a function of the singular values and singular vectors of $\mathbf{Z}$, namely

$$\begin{array}{c}\mathbf{g}={\displaystyle \sum _{i=1}^{i=k_1}\widetilde{w_i}\widetilde{{\mathbf{u}}_i}\left({\tilde{\mathbf{v}}}_i^{\text{T}}\mathbf{u}\right)}+{\displaystyle \sum _{i=k_1+1}^{i=k}\widetilde{w_i}\widetilde{{\mathbf{u}}_i}\left({\tilde{\mathbf{v}}}_i^{\text{T}}\mathbf{u}\right)}\\ ={\tilde{\mathrm{Z}}}_1\mathbf{u}+{\displaystyle \sum _{i=k_1+1}^{i=k}\widetilde{w_i}\widetilde{{\mathbf{u}}_i}\left({\tilde{\mathbf{v}}}_i^{\text{T}}\mathbf{u}\right)}.\end{array}$$ [A23]

In such cases, it is best to discard the near-zero singular values (26) while constructing the GRM. Accordingly, Eq. A23 becomes

$$\mathbf{g}={\displaystyle \sum _{i=1}^{i=k_1}\widetilde{w_i}\widetilde{{\mathbf{u}}_i}\left({\tilde{\mathbf{v}}}_i^{\text{T}}\mathbf{u}\right)}={\tilde{\mathbf{Z}}}_1\mathbf{u}.$$ [A24]

In this expression, note that ${\tilde{\mathbf{v}}}_i^{\text{T}}\mathbf{u}$ will be very close to 0 (because the $\infty$ norm of ${\tilde{\mathbf{v}}}_i$ is close to 0) for all $1\le i\le k_1$, and therefore the random effect term will never be significant. Because the $\infty$ norm of ${\tilde{\mathbf{u}}}_i$ for $1\le i\le k_1$ is also close to 0, we expect ${\tilde{\mathbf{Z}}}_1$ to be close to the 0 matrix, which is observed to be true in most cases.

GCTA tries to explain the variance of the phenotype vector $\mathbf{y}$ by k random projections onto a plane defined by the columns of $\mathbf{Z}$. In Eq. A23, we expressed these random projections using the left singular vectors of $\mathbf{X}$ as a basis. When N is fixed, $P\to \infty$ (i.e., as we collect more genotypic information on a fixed set of individuals) and one (or a few) of the singular values is much larger than the rest, the singular vector corresponding to these singular values will be consistent and the singular vectors corresponding to most of the remaining nonzero singular values will be strongly inconsistent (32) (informally put, consistency describes whether the singular vector estimates from the data matrix approach the “true” singular vector as more data are collected). This implies that the subspace defined by the higher singular vectors of the data matrix contain little biological information about the genotype matrix. [Similar inconsistency results hold for the case where $N\to \infty ,\hspace{0.17em}P\to \infty$, and $P/N\to c$ for some constant c (43)].

In Eq. A23, we showed that the random projection of $\tilde{\mathbf{y}}$ onto the first $k_1$ singular vectors (given by ${\tilde{\mathbf{Z}}}_1\mathbf{u}$) is almost surely 0. Because the subspace defined by the higher singular vector estimates (${\tilde{\mathbf{u}}}_{k_1+1},{\tilde{\mathbf{u}}}_3,\dots .{\tilde{\mathbf{u}}}_k$) is inconsistent, there is little biological connection between ${\displaystyle {\sum }_{i=k_1+1}^{i=k}{\tilde{w}}_i{\tilde{\mathbf{u}}}_i\left({\tilde{\mathbf{v}}}_i^{\text{T}}\mathbf{u}\right)}$ in Eq. A23 and the heritability estimate. It appears that it is this term that is responsible for the high values of the GCTA estimate (because the first term makes nearly 0 contribution to the projection). For every set of people and SNPs that are chosen, the data matrix generates a new set of $O\left(P\right)$ arbitrary singular vectors, which in turn generate arbitrary ${\alpha }^2$ and ${\sigma }^2$ estimates.