Skip to main content
NCBI home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2015 Dec 23;113(1):110–115. doi: 10.1073/pnas.1520483112

Molecular stripping in the NF-κB/IκB/DNA genetic regulatory network

Davit A Potoyan a, Weihua Zheng a, Elizabeth A Komives b, Peter G Wolynes a,1
PMCID: PMC4711861  PMID: 26699500

Significance

The classic models of genetic switches are based on thermodynamic control via binding affinities. Complex nonequilibrium eukaryotic gene networks with many targets such as the NF-κB/IκB/DNA system challenge this picture. Waiting for unbinding from the numerous NF-κB binding sites takes time that would allow wasteful overexpression of many genes. Active molecular stripping of NF-κB from the DNA by IκB solves the timescale problem raised in the classic picture based on thermodynamics alone.

Keywords: protein–DNA interaction, allostery, genetic switch, molecular dynamics, systems biology

Abstract

Genetic switches based on the NF-κB/IκB/DNA system are master regulators of an array of cellular responses. Recent kinetic experiments have shown that IκB can actively remove NF-κB bound to its genetic sites via a process called “molecular stripping.” This allows the NF-κB/IκB/DNA switch to function under kinetic control rather than the thermodynamic control contemplated in the traditional models of gene switches. Using molecular dynamics simulations of coarse-grained predictive energy landscape models for the constituent proteins by themselves and interacting with the DNA we explore the functional motions of the transcription factor NF-κB and its various binary and ternary complexes with DNA and the inhibitor IκB. These studies show that the function of the NF-κB/IκB/DNA genetic switch is realized via an allosteric mechanism. Molecular stripping occurs through the activation of a domain twist mode by the binding of IκB that occurs through conformational selection. Free energy calculations for DNA binding show that the binding of IκB not only results in a significant decrease of the affinity of the transcription factor for the DNA but also kinetically speeds DNA release. Projections of the free energy onto various reaction coordinates reveal the structural details of the stripping pathways.

The binding and release of protein transcription factors from DNA are fundamental molecular processes by which genes are regulated in the cell. The pioneering studies of Jacob, Monod, Ptashne, and Gilbert explained how these two processes, seeming inverses of each other, while being maintained in local chemical equilibrium, could still lead to robust genetic switches by coupling to protein synthesis and degradation, which are kinetically controlled far from equilibrium processes (1–4). This classic picture, with the law of mass action at its core (5, 6), suggests that understanding the molecular mechanism of the binding and release of transcription factors is of secondary interest compared with understanding the thermodynamics of protein–DNA recognition. The recent discovery of protein-induced release of a DNA-bound transcription factor in the NF-κB/IκB/DNA genetic switch changes this picture (7). The induced process, called “molecular stripping,” opens up the possibility of molecular kinetic control of binding and release, thus overturning the classic paradigm based only on thermodynamic control. In this paper, we use molecular dynamics simulations of coarse-grained but predictive energy landscape models of the proteins along with their interacting DNA to explore first how the NF-κB transcription factor binds individually both to DNA and to its inhibitor IκB and then to study how an approaching IκB can strip the NF-κB from a DNA molecule to which it has already been bound, by forming an intermediate ternary complex. These simulations show that each of the binary binding events involves conformational selection of different NF-κB global conformations. Molecular stripping then occurs that is induced by forming the ternary complex. Stripping involves changes in the patterns of local frustration in the proteins and an interchange of electrostatic interactions between the protein–protein and the protein–DNA partners. The simulations highlight the breaking of symmetry in the NF-κB heterodimer complex with IκB as well as the important role of the PEST sequence [protein sequence rich in proline (P), glutamic acid (E), serine (S), and threonine (T)] of IκB in the stripping.

Systems Biology of NF-κB/IκB/DNA

The transcription factor NF-κB is central to the regulation of inflammatory responses, immune responses to infections, and programmed cell death. NF-κB is a collective name for a family of homo- and heterodimeric proteins that serve as a bridge from the extracellular signals to gene expression (8). The NF-κB heterodimer p50p65 is the most abundant form, although other forms are also present in the cell. NF-κB is activated by a diverse set of extracellular stimuli that through an enzyme cascade mark the IκB moiety for degradation, subsequently freeing NF-κB from its inhibited complex. In its active, unbound form NF-κB translocates to the nucleus, thereby initiating the transcription of hundreds of genes. Owing to its wide range of influence NF-κB is considered a “master regulator switch” (9). Among the target genes of NF-κB is its own inhibitor IκBα, which we will refer to simply as IκB. Targeting IκB synthesis results in a negative feedback loop that governs the nuclear concentration of active NF-κB, leading to pulses of activation and inactivation (10, 11). IκB strips the NF-κB off from its DNA targets and masks the nuclear localization signal of the NF-κB (7). The resulting tightly bound NF-κB−IκB complex (12) is thus prevented from reentering the nucleus (13, 14), thereby terminating all of the associated genetic activities of NF-κB to restore the cellular resting state (Fig. 1A).

Fig. 1.

Fig. 1.

Open in a new tab

(A) Schematic systems biology view of NF-κB regulation by its inhibitor IκB. Shown are the key steps of a negative feedback cycle that includes the NF-κB activation by external stimuli (IKK), followed by NLS-mediated translocation to the nucleus, DNA binding, IκB synthesis, and molecular stripping of NF-κB by IκB. (B) Diagram showing the predicted structures used in the simulations. The names of complexes are shown at the bottom of the structures. Arrows indicate the thermodynamically favored directions for interconversion between the complexes given sufficient concentrations of the IκB and the DNA binding sites.

The most complete mathematical models of NF-κB signaling have assumed fast local equilibria for NF-κB binding to the DNA (15, 16). Recent in vitro kinetic measurements of IκB binding to the complex of NF-κB with DNA challenge this equilibrium view. NF-κB dissociates from DNA in an IκB concentration-dependent manner (7, 17). Including this enhancement in models requires going beyond the purely equilibrium picture that envisions fast dissociation/association and that ignores competing binding at other gene sites. A revised systems biology scheme showing the central role of molecular stripping is described in Fig. 1A. In vivo there are several thousand κB binding sites (18); thus, if dissociation from these target and decoy sites would not be fast enough there would be wasteful overexpression of genes. Rapid molecular stripping of NF-κB from its DNA results in efficient down-regulation of the NF-κB targets, ensuring the optimal expenditure of cellular resources. Our simulations demonstrate a feasible mechanism for this molecular stripping reaction.

Structures, Dynamics, and Thermodynamics

Structures of the p50p65 heterodimer of NF-κB bound with the DNA and with its inhibitor IκB have already been resolved with X-ray crystallography (14, 19, 20). Unfortunately, each of the available structures lacks at least one mechanistically crucial part of the NF-κB molecule. The structure of NF-κB−DNA (PDB ID code 1LE5) by Berkowitz et al. (19) lacks the crucial nuclear localization signal (NLS), and the entire p50 N-terminal binding domain is missing from the two existing crystal structures (14, 20) for NF-κB−IκB (PDB ID codes 1IKN and 1NFI). To understand the binding and stripping mechanisms, more complete structures are needed. To construct these structures (Fig. 1B) we carried out simulations with a coarse-grained protein–DNA force field. We added the missing molecular fragments and regenerated the full structures of the various complexes by using the Associative memory, Water mediated, Structure and Energy Model (AWSEM) for the interactions within and among the proteins (21) and the Three Sites Per Nucleotide (3SPN) model for the DNA (22, 23). DNA and protein are coupled through steric exclusion and electrostatics modeled at the mean field level. AWSEM is a coarse-grained predictive model based on the energy landscape formulation of protein folding theory (24). It accounts explicitly for physically motivated interactions such as hydrogen bonding and solvent interactions to model tertiary structure relationships and incorporates “evolutionary forces” via bioinformatic terms that act locally in sequence. Both kinds of interactions effectively sculpt the landscapes of naturally occurring proteins to be highly funneled toward the native state. AWSEM has proved successful in predicting structures of both protein monomers (21) and dimers (25). The 3SPN force field is a coarse-grained model for the DNA that also includes physically motivated terms, such as base pairing, base stacking, and electrostatic repulsion of phosphate groups that give rise to the double-helical structure of the DNA with appropriate thermal and mechanical properties (26, 27). It gives a good account of the range of structural diversity of double-helical DNA (26). Details of the models can be found in SI Appendix.

The 3D structures predicted by our code compare well with the available crystal structures of NF-κB−DNA. The tertiary and secondary levels of structure are reproduced in the simulations with high fidelity. The binding interface between protein and DNA is also well predicted. We also can compare the predicted complete structure of the complex NF-κB−IκB with the crystal structure of an NF-κB−IκB complex (PDB ID code 1IKN) in which the p50 binding domain has been removed (SI Appendix, Fig. S1). The crystal structure of the truncated complex aligns well with the simulated structure in the dimerization domain region. In the crystal structure of the truncated form, however, the p65 N-terminal binding domain has twisted further from its location in the NF-κB−DNA complex than it has in the predicted complete structure. This larger domain twist in the artificially truncated crystal structure results from the higher flexibility of the p65 N-terminal domain allowed by the absence of steric conflicts with the neighboring p50 N-terminal domain (SI Appendix, Fig. S1). When both N-terminal domains are present, the orientation of the domains is sterically forced to be closer to the orientation seen in the crystal structure of NF-κB−DNA. Simulations of a heterodimer in which the p50 N-terminal binding domain has been removed concur in predicting this additional twist. In the following sections we make use of our predicted full structures of the bound complexes to follow their formation dynamics and reaction pathways.

Naturally occurring proteins are minimally frustrated as a result of evolutionary development. The ability of proteins to fold into unique native configurations on reasonable timescales is successfully explained by folding theories resting on the principle of minimal frustration (28–30). Frustration is not completely eliminated via evolutionary selection because functional constraints also sculpt the energy landscapes to allow functional motions of the folded proteins in the folded states and binding reactions (30, 31).The folded protein ensemble occupies the dominant basin of the free energy landscape where frustration properly localized in key regions of the protein chain opens up routes for specific functional dynamics.

Frustration in biomolecules can be readily quantified and visualized using a spatially local version of the principle of minimal frustration (30). An algorithm to do this is implemented in the frustratometer (32), which estimates the energetic contribution of contacts to the stability of the native state and compares these energies in the native structure to the distribution of energies that would be obtained by performing residue substitutions in the local environment. Native contacts whose energies are sufficiently deep in the energetically stabilizing part of the distribution are called minimally frustrated and are drawn as green lines on the structure, whereas the native contacts that are found sufficiently far in the energetically destabilizing region are called frustrated and are drawn as red lines. The quantitative details of this algorithm including electrostatic effects have been discussed in previous papers (30, 32, 33).

The frustration patterns of the NF-κB were analyzed in the structure of free NF-κB, NF-κB bound with the DNA, and NF-κB bound with IκB. When electrostatic effects are included, localized high levels of frustration are found in the binding pocket of the NF-κB dimer when considered by itself (Fig. 2A) or when the protruding PEST sequence of the IκB is truncated in the NF-κB−IκB dimer (Fig. 2B). This frustration is largely caused by the positively charged residues which are located in close proximity to each other. Binding DNA or the IκB PEST sequence, both of which are negatively charged, mitigates this frustration so that the necklace of frustration in the binding pocket (Fig. 2 A and B) becomes unfrustrated after DNA binds (Fig. 2C) or when the PEST sequence of the IκB moves into the pocket (Fig. 2D). Thus, frustration analysis already hints that binding IκB with its PEST can facilitate the stripping of NF-κB from DNA by relieving frustration in the free NF-κB that forms if the DNA dissociates by itself.

Fig. 2.

Fig. 2.

Open in a new tab

Frustration analysis with electrostatics for the bound and free forms of the NF-κB. Shown are the frustration patters in (A) unbound NF-κB dimer, (B) NF-κB−IκB complex with the PEST sequence removed, (C) NF-κB−DNA complex, and (D) NF-κB−IκB complex.

This origin of stripping is underlined by free energy calculations using umbrella sampling simulations of DNA binding to NF-κB by itself and of DNA binding to a preexisting IκB−NF-κB complex. The starting structures for these simulations are the predicted structures previously described as well as a model of the ternary complex of IκB−NF-κB−DNA also created by AWSEM. From these starting points we used umbrella sampling to sample more broadly the complete ensemble of conformational states intermediate between those where the partners are fully bound and other conformations where they are completely released. These simulations capture the steps of molecular stripping.

The distances between either the center of mass of the dimerization domains with the center of mass of the DNA or with the center of mass of the IκB were used as harmonic biasing terms for the umbrella sampling. Whereas the in vitro experiments were carried out on the short piece of DNA that we used in simulations (SI Appendix, Fig. S2), we also carried out simulations that better mimic the way the transcription factor would approach a much longer full-length genomic DNA in vivo, by constraining the orientation of the DNA to remain parallel to the orientation of the initial bound state. Without this constraint an intermediate forms in which the protein complex binds to the apex of the short DNA fragment (SI Appendix, Fig. S3). Introducing the orientational constraint removes this artificial effect of the finite length of the DNA fragment studied in vitro.

The 1D free energy profiles for the biologically more relevant fixed orientation of the DNA (Fig. 3A) show that the binding of IκB not only changes the DNA binding free energy to NF-κB but also alters the detailed mechanism by which DNA associates with and dissociates from NF-κB. IκB lowers the barrier for DNA escape by at least 2–3 kcal (black arrows in Fig. 3A). This change implies that a considerable acceleration of the rate of dissociation from the DNA can be induced by binding IκB. Looking at the profile from the DNA association viewpoint one sees that there is a significant kinetic barrier for DNA to associate with a preexisting NF-κB−IκB complex, whereas DNA associates with free NF-κB in a diffusion-limited manner as shown by the purely downhill profile for binary association in the absence of IκB.

Fig. 3.

Fig. 3.

Open in a new tab

(A) The 1D free energy profile for IκB dissociation from the ternary complex IκB−NF-κB−DNA. (B) The 1D free energy profile for DNA dissociation from the binary complex of NF-κB−DNA (in blue) and from the ternary complex of IκB−NF-κB−DNA (in red). (C) A free energy surface combining the 1D plots in A and B. The initial, intermediate, and final configurations on a molecular stripping pathway can be seen in Fig. 6.

Examining the free energy profile for IκB dissociation from the ternary complex (Fig. 3B) shows that there is a larger barrier for releasing IκB from the complex than for releasing DNA. This is in harmony with kinetic mixing experiments that do not observe dissociation of the IκB on the laboratory timescale (7, 12). Combining the two 1D free energy profiles into a 2D free energy surface (Fig. 3C) maps out the interchange of the two binding partners, through the approach of IκB to the binary complex with DNA and the subsequent dissociation of the DNA from the resulting ternary complex. Such a representation is reminiscent of the 20th-century pioneering studies of elementary gas phase reactions that made use of semiempirical surfaces (34) and quasi-classic mechanics (35) for obtaining detailed dynamical features of reactions. The dynamical and thermodynamic aspects of molecular stripping can be studied at a higher level of structural detail by using additional collective coordinates as discussed below. The lower barrier for DNA dissociation from the ternary complex NF-κB−DNA−IκB compared with binary complex NF-κB−DNA and an even higher barrier for IκB dissociation (Fig. 3C) show that molecular stripping is not only thermodynamically but also kinetically favorable.

Essential Modes of Motion

Being a multidomain protein complex, as expected, the NF-κB heterodimer can bend around the connecting hinge while the individual domains themselves remain relatively rigid. To characterize this and other global slow timescale motions we performed many exhaustive simulations with a cumulative run time equivalent to more than 500 μs of real time. The long sampling times are made possible by using our coarse-grained model. Using long constant temperature simulations we first carried out principal component analysis in the Cartesian space spanned by the backbone Cα atoms of the free NF-κB alone to uncover the dominant large amplitude modes of motion. Principal component analysis of well-sampled trajectories of proteins in their native states provides a convenient simplifying lens to characterize their functional collective motions (31, 36).

The first principal component is the predominant motion that accounts for more than 70% of the amplitude of motion in unbound NF-κB (SI Appendix, Fig. S4), but a second component also plays a role. Projection of the equilibrium ensemble of structures onto these two modes reveals that these large-amplitude motions are not quasi-harmonic in the free NF-κB dimers, leading to multipeak distributions for these collective coordinates in the free form (Fig. 4A and SI Appendix, Fig. S5). The first principal component is largely a domain twist motion (SI Appendix, Fig. S6 and Movie S1). The second principal component for the free NF-κB is an overall domain breathing motion, resembling the opening and closing of the DNA binding cavity (SI Appendix, Fig. S6 and Movie S2). In contrast to the free NF-κB case, for both binary complexes the distribution of these coordinates is essentially single-peaked, with peaks in different locations for NF-κB−IκB and for NF-κB−DNA (Fig. 4A). IκB binding and DNA binding couple to distinct motions of the free NF-κB, namely dominantly to the twist when forming IκB−NF-κB but to the breathing mode when forming NF-κB−DNA.

Fig. 4.

Fig. 4.

Open in a new tab

(A) Distribution of conformational ensembles for free and bound forms of NF-κB along the twist mode coordinate of free NF-κB. (B) The p50 domain of the binary complex (gray) was aligned with the p50 domain of the ternary NF-κB−DNA−IκB complex (p50, green; p65, yellow; DNA, red; IκB, not shown). The IκB induces a twist in the relative orientation of the p50 and p65 domains (angle θ).

Projecting the equilibrium ensemble of the binary complexes on principal components determined now by including both backbone atoms of NF-κB and the backbone atoms of its binding partners (either DNA or IκB) reveals the motions of the partners with respect to each other. The principal motion of the NFκB−DNA complex corresponds to sliding the NF-κB along the DNA strands (SI Appendix, Fig. S6), supporting the view that NF-κB can easily perform a 1D diffusional motion along the DNA without being released. The second largest principal component for NF-κB−DNA as a whole complex corresponds to what was the domain twist motion of the free NF-κB. The domain breathing motion that is displaced upon DNA binding is heavily suppressed in fluctuating amplitude after the DNA binds.

When IκB binds to free NF-κB the induced twist orients the domains so that only one of the NF-κB monomers can now contact the DNA very closely (Fig. 4B). This observation is one of the key results of this work. We see that IκB acts as an allosteric effector precisely by selecting a conformation in the NF-κB−DNA most favorable for DNA dissociation. Once the IκB binds the NF-κB, the DNA remains held by only a single N-terminal domain of NF-κB coming from the p50 subunit (Fig. 4B). In contrast, both N-terminal domains contribute to holding strongly to the DNA before the twist transition has taken place. The allosteric change through twisting ultimately allows the stripping of NF-κB from its genomic binding sites on the DNA.

Mechanistic Picture of Molecular Stripping

By mapping the free energy profile simultaneously onto the dissociation distances (Fig. 3) and onto the principal components of free NF-κB we can uncover the key mechanistic steps by which DNA dissociates from NF-κB after the complex with IκB forms. Following how the domain twist coordinate changes as the partners approach each other we see that the minimal free energy paths for dissociation of DNA have two stages (Fig. 5). In the first stage the domains twist (note the solid arrows in Fig. 5 A and B), thereby loosening the steric and electrostatic grip of the transcription factor on the DNA. This twist is then followed by a subsequent step in which the DNA separates from the complex whereas only one of the two domains holds on strongly to the DNA. The free energy surface for DNA dissociation from the binary complex NF-κB−DNA (Fig. 5C) shows a bifurcation: The DNA can be induced to dissociate by rotating either one of the two DNA binding domains. The two dissociating paths do not have equal barriers, which highlights the symmetry breaking in the heterodimer of NF-κB.

Fig. 5.

Fig. 5.

Open in a new tab

(A–D) Free energy surfaces mapped onto relevant dissociation/association distances and the domain twist mode. Dark arrows indicate the the direction of the most favorable path leading to formation of stable complexes. (A) Free energy surface for NF-κB binding to IκB forming a binary complex IκB−NF-κB. (B) Free energy surface for NF-κB−DNA binding to IκB forming a ternary complex NF-κB−DNA−IκB. (C) Free energy surface for DNA dissociation from the binary complex NF-κB−DNA to form free NF-κB. (D) Free energy surface for DNA dissociation from the ternary complex NF-κB−DNA−IκB to form the binary complex NF-κB−IκB. (E) Free energy surface mapped onto the DNA dissociation distance and the PEST distance from the binding pocket of the NF-κB in the ternary complex of the NF-κB−DNA−IκB. (F) Free energy for dissociation of the DNA−NF-κB complex mapped onto the DNA dissociation distance and onto the breathing mode that opens and closes the DNA binding cavity.

Dissociation of DNA from the ternary complex proceeds by a different route (Figs. 5D and 6) than does DNA dissociation from the binary complex because the binding of the IκB to the NF-κB−DNA binary complex has already induced the necessary domain twist of the p65 domain via a conformational selection mechanism (Fig. 5B). In forming the ternary complex the DNA binding domain has already come to a more favorable orientation for releasing DNA, leading to lower kinetic barriers (Fig. 5D). We see the first step of molecular stripping occurs through an allosteric transition caused by the IκB acting on the domain twist mode of the NF-κB heterodimer. This conformational change facilitates the stripping of the NF-κB from DNA by decreasing the barrier for further domain twist. Once DNA leaves the ternary intermediate, the resulting bound complex of NF-κB−IκB is thermodynamically much more stable (Fig. 5A) than the starting complex with NF-κB bound only to the DNA (Fig. 5B). It is then no surprise that the reverse reaction of DNA stripping the IκB moiety from its complex with NF-κB has not been observed in kinetic experiments (7). The thermodynamic stability of the NF-κB−IκB complex as well as the origin of barrier for the reverse reaction of DNA binding can be explained using electrostatic arguments as follows. In the second step of stripping, as the DNA begins to leave, the IκB reconfigures through the motion of the PEST sequence. By being highly negatively charged the PEST sequence begins to compete with the DNA for binding to the positively charged NF-κB binding pocket (Fig. 5E). This exchange of partners lowers the barrier for DNA dissociation.

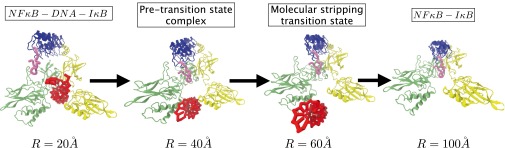
Fig. 6.

Fig. 6.

Open in a new tab

The progression of structural changes on the molecular shipping path starting from the ternary complex DNA−NF-κB−IκB and going through the states of the pretransition state complex, the molecular stripping transition state, and ending at the stable binary complex of IκB−NF-κB. The pink tube highlight shows the PEST sequence and its motion with respect to the NF-κB throughout the DNA dissociation. The partial collapse of the binding cavity once the DNA has left is also evident.

As is seen on the free energy surface, once the DNA has completely left the cavity, the PEST sequence moves still further to occupy the cavity, thereby finally resolving the electrostatically frustrated interactions (Figs. 5E and 6). Looked at hypothetically in the reverse direction of association, the occupation of the DNA binding pocket by the PEST sequence leads to a free energy barrier inhibiting association of the DNA with the NF-κB−IκB complex. This barrier gives another way by which IκB controls the transcriptional ability of the NF-κB. Note that in both the pretransition state complex and the molecular stripping transition state itself the DNA remains bound transiently to the p50 subunit for which it has the higher affinity (37).

One may use other collective modes for investigating different mechanistic aspects of NF-κB domain motions. For instance, using the breathing mode as a collective coordinate (Fig. 5F) reveals a displacement in the breathing mode coordinate when DNA dissociates or binds to the free NF-κB. The two DNA binding domains of NF-κB first open and then close, approaching each other to seal the cavity between them, thus locking onto the target DNA.

Materials and Methods

A detailed description of the materials and methods is given in SI Appendix, Materials and Methods. Briefly, the simulations were carried out using electrostatically enhanced version of AWSEM force field for proteins (33) and 3SPN2c force field for DNA (22, 23). All simulations were done under constant temperature conditions, following the standard protocols of minimization and equilibration starting from either computationally predicted or available crystal structures. Principal component analysis was performed on an ensemble of structures generated by carrying out multiple independent constant temperature simulations with a cumulative time equivalent to over 500 μs of real time. Close to 100 large-scale domain change events have been registered in the simulations, each of which is estimated to take place on a 1- to 10-μs timescale. Free energy profiles were computed by carrying out umbrella sampling by restraining protein–protein and protein–DNA center of mass distances with harmonic constraints.

Concluding Remarks

Single-cell experiments on NF-κB regulation in vivo, mathematical modeling, in vitro kinetics, and structural studies have provided many important clues to NF-κB signaling systems biology. The present simulations show that a detailed molecular-level understanding of the functional dynamics of the key NF-κB−IκB−DNA genetic switch elements can add more to the story. In this work exhaustive long timescale, coarse-grained simulations for the free NF-κB heterodimer and its bound complexes with DNA and IκB have allowed us to explore structures, thermodynamics, and motions that have not been accessible to direct crystallographic study. Our simulations demonstrate that the NF-κB/DNA/IκB switch functions via an allosteric mechanism that involves conformational selection of a collective mode of domain twist accompanied by opening and closing of the cavity between the two DNA binding domains of the heterodimer. The molecular stripping process of NF-κB from its target genetic sites by IκB proves both kinetically and thermodynamically favorable, suggesting a novel nonequilibrium mechanism for the efficient control of gene expression in this important master regulator system.

Supplementary Material

Supplementary File
Supplementary File
Download video file (660KB, mpg)
Supplementary File
Download video file (632KB, mpg)

Acknowledgments

We thank Holly Dembinsky, Kristen Ramsey, Bin Zhang, and Patricio Craig for numerous stimulating discussions. This work was supported by PPG Grant P01 GM071862 from the National Institute of General Medical Sciences. This work was also supported by the D. R. Bullard-Welch Chair at Rice University, Grant C-0016 (to P.G.W.).

Footnotes

The authors declare no conflict of interest.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1520483112/-/DCSupplemental.

References

  • 1.Ptashne M. Gene regulation by proteins acting nearby and at a distance. Nature. 1986;322(6081):697–701. doi: 10.1038/322697a0. [DOI] [PubMed] [Google Scholar]
  • 2.Ptashne M. A Genetic Switch: Phage Lambda Revisited. Vol 3 Cold Spring Harbor Lab Press, Cold Spring Harbor; NY: 2004. [Google Scholar]
  • 3.Gilbert W, Müller-Hill B. Isolation of the lac repressor. Proc Natl Acad Sci USA. 1966;56(6):1891–1898. doi: 10.1073/pnas.56.6.1891. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Jacob F, Monod J. Genetic regulatory mechanisms in the synthesis of proteins. J Mol Biol. 1961;3:318–356. doi: 10.1016/s0022-2836(61)80072-7. [DOI] [PubMed] [Google Scholar]
  • 5.Ackers GK, Johnson AD, Shea MA. Quantitative model for gene regulation by lambda phage repressor. Proc Natl Acad Sci USA. 1982;79(4):1129–1133. doi: 10.1073/pnas.79.4.1129. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Phillips R, Kondev J, Theriot J, Garcia H. Physical Biology of the Cell. Garland; New York: 2012. [Google Scholar]
  • 7.Alverdi V, Hetrick B, Joseph S, Komives EA. Direct observation of a transient ternary complex during IκBα-mediated dissociation of NF-κB from DNA. Proc Natl Acad Sci USA. 2014;111(1):225–230. doi: 10.1073/pnas.1318115111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Oeckinghaus A, Ghosh S. The NF-kappaB family of transcription factors and its regulation. Cold Spring Harb Perspect Biol. 2009;1(4):a000034. doi: 10.1101/cshperspect.a000034. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Krappmann D, et al. The IkappaB kinase complex and NF-kappaB act as master regulators of lipopolysaccharide-induced gene expression and control subordinate activation of AP-1. Mol Cell Biol. 2004;24(14):6488–6500. doi: 10.1128/MCB.24.14.6488-6500.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Hoffmann A, Levchenko A, Scott ML, Baltimore D. The IkappaB-NF-kappaB signaling module: Temporal control and selective gene activation. Science. 2002;298(5596):1241–1245. doi: 10.1126/science.1071914. [DOI] [PubMed] [Google Scholar]
  • 11.Nelson DE, et al. Oscillations in NF-kappaB signaling control the dynamics of gene expression. Science. 2004;306(5696):704–708. doi: 10.1126/science.1099962. [DOI] [PubMed] [Google Scholar]
  • 12.Bergqvist S, et al. Thermodynamics reveal that helix four in the NLS of NF-kappaB p65 anchors IkappaBalpha, forming a very stable complex. J Mol Biol. 2006;360(2):421–434. doi: 10.1016/j.jmb.2006.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Baeuerle PA, Baltimore D. I kappa B: A specific inhibitor of the NF-kappa B transcription factor. Science. 1988;242(4878):540–546. doi: 10.1126/science.3140380. [DOI] [PubMed] [Google Scholar]
  • 14.Jacobs MD, Harrison SC. Structure of an IkappaBalpha/NF-kappaB complex. Cell. 1998;95(6):749–758. doi: 10.1016/s0092-8674(00)81698-0. [DOI] [PubMed] [Google Scholar]
  • 15.Williams RA, Timmis J, Qwarnstrom EE. Computational models of the NF-KB signalling pathway. Computation. 2014;2(4):131–158. [Google Scholar]
  • 16.Cheong R, Hoffmann A, Levchenko A. Understanding NF-kappaB signaling via mathematical modeling. Mol Syst Biol. 2008;4:192. doi: 10.1038/msb.2008.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Bergqvist S, et al. Kinetic enhancement of NF-kappaBxDNA dissociation by IkappaBalpha. Proc Natl Acad Sci USA. 2009;106(46):19328–19333. doi: 10.1073/pnas.0908797106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Martone R, et al. Distribution of NF-kappaB-binding sites across human chromosome 22. Proc Natl Acad Sci USA. 2003;100(21):12247–12252. doi: 10.1073/pnas.2135255100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Berkowitz B, Huang DB, Chen-Park FE, Sigler PB, Ghosh G. The x-ray crystal structure of the NF-κ B p50.p65 heterodimer bound to the interferon β -κ B site. J Biol Chem. 2002;277(27):24694–24700. doi: 10.1074/jbc.M200006200. [DOI] [PubMed] [Google Scholar]
  • 20.Huxford T, Huang DB, Malek S, Ghosh G. The crystal structure of the IkappaBalpha/NF-kappaB complex reveals mechanisms of NF-kappaB inactivation. Cell. 1998;95(6):759–770. doi: 10.1016/s0092-8674(00)81699-2. [DOI] [PubMed] [Google Scholar]
  • 21.Davtyan A, et al. AWSEM-MD: Protein structure prediction using coarse-grained physical potentials and bioinformatically based local structure biasing. J Phys Chem B. 2012;116(29):8494–8503. doi: 10.1021/jp212541y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Hinckley DM, Freeman GS, Whitmer JK, de Pablo JJ. An experimentally-informed coarse-grained 3-Site-Per-Nucleotide model of DNA: Structure, thermodynamics, and dynamics of hybridization. J Chem Phys. 2013;139(14):144903. doi: 10.1063/1.4822042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Freeman GS, Hinckley DM, Lequieu JP, Whitmer JK, de Pablo JJ. Coarse-grained modeling of DNA curvature. J Chem Phys. 2014;141(16):165103. doi: 10.1063/1.4897649. [DOI] [PubMed] [Google Scholar]
  • 24.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
  • 25.Zheng W, Schafer NP, Davtyan A, Papoian GA, Wolynes PG. Predictive energy landscapes for protein-protein association. Proc Natl Acad Sci USA. 2012;109(47):19244–19249. doi: 10.1073/pnas.1216215109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Potoyan DA, Savelyev A, Papoian GA. Recent successes in coarse-grained modeling of DNA. WIRES Comp Mol Sci. 2013;3:69. [Google Scholar]
  • 27.de Pablo JJ. Coarse-grained simulations of macromolecules: From DNA to nanocomposites. Annu Rev Phys Chem. 2011;62:555–574. doi: 10.1146/annurev-physchem-032210-103458. [DOI] [PubMed] [Google Scholar]
  • 28.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84(21):7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins. 1995;21(3):167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
  • 30.Ferreiro DU, Komives EA, Wolynes PG. Frustration in biomolecules. Q Rev Biophys. 2014;47(4):285–363. doi: 10.1017/S0033583514000092. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Zhuravlev PI, Papoian GA. Protein functional landscapes, dynamics, allostery: A tortuous path towards a universal theoretical framework. Q Rev Biophys. 2010;43(3):295–332. doi: 10.1017/S0033583510000119. [DOI] [PubMed] [Google Scholar]
  • 32.Jenik M, et al. Protein frustratometer: A tool to localize energetic frustration in protein molecules. Nucleic Acids Res. 2012;447:1. doi: 10.1093/nar/gks447. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Tsai MY, et al. Electrostatics, structure prediction, and the energy landscapes for protein folding and binding. Protein Sci. August 8, 2015 doi: 10.1002/pro.2751. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Eyring H, Polanyi M. Uber einfache gasreaktionen. Z Phys Chem Abt B. 1931;12:279. [Google Scholar]
  • 35.Hirschfelder J, Eyring H, Topley B. Reactions involving hydrogen molecules and atoms. J Chem Phys. 1936;4:170. [Google Scholar]
  • 36.Potoyan DA, Papoian GA. Energy landscape analyses of disordered histone tails reveal special organization of their conformational dynamics. J Am Chem Soc. 2011;133(19):7405–7415. doi: 10.1021/ja1111964. [DOI] [PubMed] [Google Scholar]
  • 37.Phelps CB, Sengchanthalangsy LL, Malek S, Ghosh G. Mechanism of κ B DNA binding by Rel/NF-κ B dimers. J Biol Chem. 2000;275(32):24392–24399. doi: 10.1074/jbc.M003784200. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File
pnas.1520483112.sapp.pdf (4.9MB, pdf)
Supplementary File
Download video file (660KB, mpg)
Supplementary File
Download video file (632KB, mpg)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES