Turning statistical physics models into materials design engines

Significance

A fundamental tenet of science is that the properties of a material are intimately linked to the nature of the constituent components. Although there are powerful methods to predict such properties for given components, a key challenge for materials design is the inverse process: identifying the required components and their structural configuration for given target properties. This paper presents a new approach to this challenge. A formalism is introduced that generates algorithms for materials design both under equilibrium and under nonequilibrium conditions and operates without the need for user input beyond a design goal. This formalism is broadly applicable, fast, and robust, and it provides a powerful tool for materials optimization as well as discovery.

Abstract

Despite the success statistical physics has enjoyed at predicting the properties of materials for given parameters, the inverse problem, identifying which material parameters produce given, desired properties, is only beginning to be addressed. Recently, several methods have emerged across disciplines that draw upon optimization and simulation to create computer programs that tailor material responses to specified behaviors. However, so far the methods developed either involve black-box techniques, in which the optimizer operates without explicit knowledge of the material’s configuration space, or require carefully tuned algorithms with applicability limited to a narrow subclass of materials. Here we introduce a formalism that can generate optimizers automatically by extending statistical mechanics into the realm of design. The strength of this approach lies in its capability to transform statistical models that describe materials into optimizers to tailor them. By comparing against standard black-box optimization methods, we demonstrate how optimizers generated by this formalism can be faster and more effective, while remaining straightforward to implement. The scope of our approach includes possibilities for solving a variety of complex optimization and design problems concerning materials both in and out of equilibrium.

Computer programs that can design material properties have led to exciting, new directions for materials science (1–3). Computational methods have been used to predict crystal (4) and protein (5, 6) structures, yielding the toughest crystals known to mankind (4) and de novo protein configurations unseen in nature (5). Applied to polymers, Monte Carlo methods (7–9) and evolutionary algorithms (10, 11) have paved the way toward optimizing directed self-assembly. Similar methods have been used to identify the crystal structures of patchy, colloidal particles (12). For far-from-equilibrium systems like jammed, metastable aggregates of particles (3), simulation-based optimization has been successfully used to design bulk properties like stiffness (13) and packing density (14) by way of tuning complicated microscale features like particle shape.

However, despite these successes, most of the existing methods work only for narrowly defined classes of materials: Optimization techniques that prove successful at designing one class of materials may struggle or fail on other systems. Thus, designing new materials can require a large investment in trial and error at the level of the algorithm itself, even if, for given parameters, the material’s behavior can be simulated easily.

In black-box approaches, the algorithm tunes the material by adjusting control parameters without considering the likelihood of finding the material in microscale configurations. Instead, the optimizer operates in some auxiliary space, defined outside the physical model, and remains ignorant of the statistics in the physical configuration space. On the other hand, for the overwhelming majority of materials, an accurate description of macroscale behavior comes about by explicitly considering the probability of finding the system in certain microscopic configurations. Several materials optimization approaches exist that take this statistical nature into account, examples include optimizers that design spin configurations (15, 16), patchy colloidal particles (17), and self-assembly driven by short-ranged interactions (18). These approaches build heavily upon the specific model defining the material. As a consequence, it is difficult to extend them beyond the material class they are designed for. Evidently, microscale configurations present key statistical information about a material, which is completely ignored by black-box approaches, yet there is no formalism that generically incorporates this information into materials design.

The question we ask is whether microstate information not only can be used to enhance an optimizer’s speed and range of applicability, but also can become the cornerstone of an approach that automatically transforms a design goal and a statistical model into an optimizer. One can then construct optimizers that can work on material classes that are as broad as those described by statistical mechanics, without the need for ad hoc modification.

Here we take some first steps toward such a framework. We present a formalism that can be used to transform the capacity to predict material behavior into an optimizer that tunes it. Furthermore we find that our formalism often solves optimization problems faster and more reliably than approaches built around black-box methods.

Deriving the Optimization Equations

Our approach starts by assuming a given model $\rho \left(x|{\lambda }_i\right)$ that predicts the probability of finding a material in some configuration, x. The model depends on the adjustable parameters ${\lambda }_i$ and by tuning ${\lambda }_i$, a user can impact the emergent, bulk properties, averaged over configuration space. Thus, design proceeds by tweaking ${\lambda }_i$ to promote a desired, user-specified response.

We work toward this goal, starting from the heuristic equation

$$\dot{\rho }\left(x|{\lambda }_i\right)=\rho \left(x|{\lambda }_i\right)\left[f\left(x\right)-\langle f\left(x\right)\rangle \right],$$ [1]

where the angle brackets denote an average over configurations weighted by ρ, the overdot denotes a derivative with respect to an artificial time that indexes the optimization steps, and $f\left(x\right)$ is a function that quantifies how well configuration x represents the user-specified goal. In this way, Eq. 1 attempts to increase the probability of finding the system in states with better than average values of $f\left(x\right)$: If a configuration x has a value of $f\left(x\right)$ greater than the average, then the probability of finding the system near x increases, for average $f\left(x\right)$ it does not change, and for worse than average it decreases.

As written, Eq. 1 assumes that $\rho \left(x|{\lambda }_i\right)$ can be independently set for every possible point in the configuration space, despite the fact that $\rho \left(x|{\lambda }_i\right)$ is constrained by the physics behind the material of interest. In actuality, $\rho \left(x|{\lambda }_i\right)$ can offer only a limited flexibility through the parameters ${\lambda }_i$. Thus, for many problems it will not be possible to exactly satisfy Eq. 1, although it is possible to make a best approximation to Eq. 1, given a particular physical distribution. We achieve this by setting the changes to ${\lambda }_i$ such that they minimize the average error between the updates implied by Eq. 1 and the actual changes to $\rho \left(x|{\lambda }_i\right)$. Explicitly, we rewrite Eq. 1 as ${\dot{\lambda }}_i{\partial }_{{\lambda }_i}\log \left[\rho \right]=f\left(x\right)-\langle f\rangle$ and select the ${\dot{\lambda }}_i$ that minimize the average value of the squared error, $\mathit{ϵ}=\langle {\left({\dot{\lambda }}_i{\partial }_{{\lambda }_i}\log \left[\rho \right]-\left[f\left(x\right)-\langle f\rangle \right]\right)}^2\rangle$. The equations of motion for ${\lambda }_i$ that minimize ε at a given instant in time are found by setting the partial derivatives with respect to ${\dot{\lambda }}_i$ equal to zero (Supporting Information):

$${\dot{\lambda }}_i\left(t\right)={\langle {\partial }_{{\lambda }_i}\log \left(\rho \right){\partial }_{{\lambda }_j}\log \left(\rho \right)\rangle }^{-1}\langle \left[f\left(x\right)-\langle f\left(x\right)\rangle \right]{\partial }_{{\lambda }_j}\log \left(\rho \right)\rangle .$$ [2]

Eq. 2 is now a closed expression for ${\lambda }_i$ that depends only on expectation values. Thus, it can function as an algorithm: one can draw samples from $\rho \left(x|{\lambda }_i\right)$, use the samples to evaluate the right-hand side of Eq. 2, and then integrate the equations of motion to generate new, improved parameter settings.

Eq. 2, and its motivating Eq. 1, overlap with a surprising number of different fields. For example, the matrix elements in Eq. 2 resemble kinetic coefficients, suggesting the interpretation that $f\left(x\right)$ generates a thermodynamic force that pushes the system to solve the design goal (19). Alternatively, Eq. 2 appears in the optimization and mathematics literature as natural gradient descent: It bears the interpretation of a gradient descent method that takes the steepest step such that the change in entropy stays bounded (20–22). Indeed, the matrix in front of Eq. 2 is the Fisher information metric and is constraining the driving force to move in directions of small entropy change (21). This interpretation is also associated with state-of-the-art optimizers like the covariance matrix adaptation evolution strategy (CMA-ES) (22–24); however, here the design parameters ${\lambda }_i$ are treated as random variables drawn from a Gaussian distribution irrespective of the design problem, and a version of Eq. 2 is used to update the mean and covariance of this auxiliary distribution. This is in contrast to our proposition that ${\lambda }_i$ should be treated as deterministic variables that evolve according to Eq. 2 with randomness entering only at the level of material configurations. If the task considered is changed to finding the best-fit model parameters to a given set of data, then Eq. 2 represents the direction in parameter space that decreases the fit error most efficiently per unit of behavioral change in the model (25). In this scenario, one can consider regularizing Eq. 2 to produce the Levenburg–Marquart algorithm modified to account for the geometric aspects of the optimization. Finally, one can note that the motivating equation, Eq. 1, is the replicator equation from game theory and evolutionary biology (26–28). Thus, one could also interpret the dynamics as a process of reproduction and competition in a continuous parameter space (26, 27), projected onto $\rho \left(x|\lambda \right)$.

Whatever the picture, Eq. 2 has a number of powerful properties. In particular, Eq. 2 is invariant to any invertible reparameterization of ${\lambda }_i$, including rotations, dilations, and translations in parameter space. If the reward function, $f\left(x\right)$, is chosen correctly, the velocity flow is also invariant to rank preserving changes in the design goal (22). Thus, there will be no difference in performance between two design problems that differ by coordinate choice over ${\lambda }_i$ and/or a rank preserving change in the design goal [e.g., $g\left(x\right)$ vs. $\exp \left(g\left(x\right)\right)$], provided the initial values of ${\lambda }_i$ are the same. These invariances also provide stability to the algorithm: by making the search algorithm invariant to both the goal function magnitude and the parameterization, the effect of sampling errors gets bounded in a parameterization invariant way. Thus, errors from sampling parameters in Eq. 2 will not cascade, even if the matrix in Eq. 2 becomes ill-conditioned. Altogether, these features greatly simplify the optimization task because, now, the designer is free from worrying about trivial choices surrounding ${\lambda }_i$ and the goal function. Details on these points can be found in Supporting Information.

For the task of optimizing materials, we stress one further property: By using Eq. 2 optimization takes place in configuration space, rather than in an auxiliary space introduced to define an optimizer. As we will show, this gives a unique advantage in applying Eq. 2 to materials design: More information is used by the optimizer when updating parameters, without incurring an increase in computational cost. Perhaps best of all, this optimizer is constructed by straightforwardly applying the formalism encoded in Eq. 2 to the relevant statistical model. For example, when $\rho \left(x|{\lambda }_i\right)$ is given by the canonical ensemble, $\rho \left(x|{\lambda }_i\right)\propto \exp \left[-{\lambda }_i{h}_i\left(x\right)\right]$, the optimizer follows immediately from Eq. 2 as ${\dot{\lambda }}_i=-\mathrm{Cov}{\left[h_i\left(x\right),h_j\left(x\right)\right]}^{-1}\mathrm{Cov}\left[h_j\left(x\right),f\left(x\right)\right]$. Ultimately, Eq. 2 makes the transition from describing a material to designing a material in just one step.

Comparison Against Black-Box Optimizers

To demonstrate these strengths, we test our method against standard approaches that feed simulation parameters into a model by way of a black-box optimizer. We use adaptive simulated annealing (ASA) (29) and the CMA-ES (24). In each test, we allow the optimizers a fixed budget of material simulations, and each simulation requires a fixed amount of computational power. Thus, in our comparisons, computational cost and number of simulations are equivalent and an efficient optimizer is one that solves a design problem simulating as few candidate materials as possible. Implementation details are in Supporting Information.

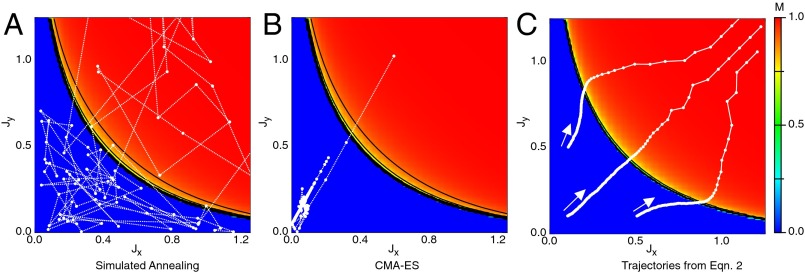
As a first example, we task these two black-box algorithms and our approach with designing a square-lattice Ising model to maximize the magnitude of its magnetization. To do so, each method is allowed to vary the coupling constants that define the energy of spin alignments in the horizontal ($J_x$) and vertical ($J_y$) directions. To implement the black-box methods, we allow each optimizer to guess a set of coupling constants and evaluate the quality of that guess by computing the average magnetization. We find that both ASA and the CMA-ES struggle when searching entirely in the zero magnetization phase. This is an obvious consequence of the fact that the optimizer sees no variation in the quality for each parameter setting. Consequently, it receives no guidance about how to update its parameter guesses and can at best walk randomly until finding the phase boundary (Fig. 1 A and B).

Fig. 1.

Phase transitions and flat landscapes. If a materials design problem features a phase transition as part of the search space, black-box optimizers can struggle or fail due to inefficient use of simulation data. For example, if optimizing the magnetization, M, of a 2D Ising model by changing the coupling constants along the x and y directions ($J_x/kT$ and $J_y/kT$, respectively), black-box methods like simulated annealing (A) and the CMA-ES (B) walk randomly if initialized in the zero magnetization state. Our method (C) interprets fluctuations in solution quality against model components as encoded by Eq. 2 and thus can navigate to the magnetized state regardless of initialization.

By contrast, the updates encoded in Eq. 2 navigate a path that links one phase to the other: Fig. 1C shows the flow field generated by Eq. 2 upon taking $\rho \left(x|\lambda \right)$ to be the canonical ensemble with the Ising Hamiltonian, $H=-J_x{\displaystyle {\sum }_{{\left[ij\right]}_x}{s}_i{s}_j}-J_y{\displaystyle {\sum }_{{\left[ij\right]}_y}{s}_i{s}_j}$, where ${\left[ij\right]}_x$ denotes summing over nearest neighbors along the x direction, likewise for ${\left[ij\right]}_y$, and $s_i$ denote the spin variables. Given this statistical model, the control parameters ${\lambda }_i$ for optimization become ${\lambda }_x=J_x/kT$ and ${\lambda }_y=J_y/kT$. Finally, the quality function $f\left(s\right)$ is set to reward states with higher magnetizations (Supporting Information). If, for shorthand, we call the individual energy components $h_x={\displaystyle {\sum }_{{\left[ij\right]}_x}{s}_i{s}_j}$ and $h_y={\displaystyle {\sum }_{{\left[ij\right]}_y}{s}_i{s}_j}$, then Eq. 2 gives the velocity field ${\dot{\lambda }}_x=\left(1/\left|C\right|\right)\left(\mathrm{Cov}\left[h_y,h_y\right]\mathrm{Cov}\left[h_x,f\right]-\mathrm{Cov}\left[h_x,h_y\right]\mathrm{Cov}\left[h_y,f\right]\right)$, where $\left|C\right|=\mathrm{Cov}\left[h_x,h_x\right]\mathrm{Cov}\left[h_y,h_y\right]-\mathrm{Co}v{\left[h_x,h_y\right]}^2$. A similar equation holds for ${\dot{\lambda }}_y$ but with the variables x and y appropriately interchanged.

In this form, it is clear that our method will optimize as long as there is covariation between the quality function, f, and the energy components, $h_i$. Because magnetization and energy are correlated, even if the average magnetization is zero, Eq. 2 can purposefully optimize even when operating in regions of parameter space where the black-box methods fail. The difference between these approaches lies in the fact that black-box methods are trying to solve a problem defined over the space of ${\lambda }_i$, whereas our approach is tasked to solve a problem defined on the space of configurations, x, via Eq. 1. The CMA-ES generates multiple guesses of parameters from a Gaussian distributed over all possible λ and ASA samples by assigning an energy value to each choice of λ. These methods associate only one piece of information, the quality function, to full ensembles of configurations defined by each choice of parameters. This is in contrast to our approach that tries to solve the problem of reproducing configurations, x, that are better than average. Consequently, Eq. 2 is able to use information about how fluctuations in configurations correspond to fluctuations in quality because it has been built to exploit the extra fact that the simulation data were generated from a known distribution, ρ.

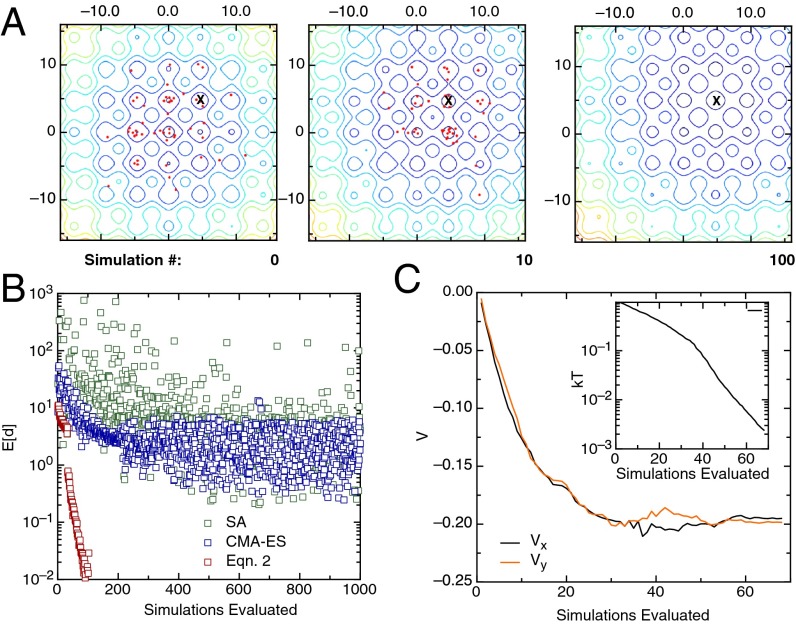
As a second example, we consider a thermalized particle trapped on a 2D substrate, defined on the $x_1-x_2$ plane and at thermal equilibrium. The substrate applies a potential to the particle, making some positions more likely than others. We task the optimizer with trapping the particle in a specific potential well. To do so, we give the optimizer the freedom to tune the interaction strength with the substrate, and we give it control over a linear electric field to drive the particle. To make the problem interesting, we use a rough substrate potential: $h_s={\displaystyle {\sum }_i\left(-\cos \left[x_i\left(2\pi /5\right)\right]+x_i^2/25\right)}$. With the field included, the total Hamiltonian becomes $H=h_s+v_{x_1}{x}_1+v_{x_2}{x}_2$, where $v_{x_1}$ and $v_{x_2}$ represent the field strength in the two coordinate directions. To simplify the form of Eq. 2, we represent these effects to the optimizer by defining ${\lambda }_s=1/kT$ and absorb a factor of $kT$ into the field coupling constants so that $\rho \propto \exp \left[-{\lambda }_s{h}_s-{\lambda }_{x_1}{x}_1-{\lambda }_{x_2}{x}_2\right]$. In discussing the optimizer’s performance, however, we will convert the results to the original, physical variables $kT$, $v_{x_1}$, and $v_{x_2}$.

The solution to this problem requires the design engine to make the target well the global minimum, and cool the system to zero temperature to trap the particle. For definiteness, the target well is the point $\left(\mathrm{5,5}\right)$ and we initialize the algorithm with the substrate at $1kT$ and the field parameters set to zero.

In Fig. 2A we plot the energy landscapes generated by the optimizer, as well as the points sampled during each iteration. Indeed, the optimizer quickly learns to tilt the landscape, correctly making the target well the global minimum, and then cools the system (Fig. 2B), trapping the particle in the well. By comparing the performance against black-box approaches (Fig. 2C), our approach is both faster and more reliable: It correctly tilts the well after only 35 iterations, whereas it takes $\sim 100$ simulations for the CMA-ES and ASA. Further, neither of the black-box methods learns to completely cool the system in the allotted 1,000 simulated ensembles.

Fig. 2.

Trapping a particle in a well. Here we treat the problem of a thermalized particle, trapped on a sinusoidal energy landscape superimposed on a quadratic background with a minima at the origin, depicted by the energy contours in A. The optimizer is given control over the system temperature $kT$ plus a linear field potential in the two coordinates $v_{x_1}$ and $v_{x_2}$. Its task is to trap the particle in a specific well located off center at $\left(\mathrm{5,5}\right)$ in the $x_1-x_2$ plane, marked by a cross in A. The sampled particle locations, given each choice of parameters generated, after evaluating 0, 10, and 100 iterations of Eq. 2 are plotted as red points. The optimizer uses the field to first tilt the potential and make the target well the global minimum, and then it cools the system. In tasking the same problem to black-box optimizers, we find that both ASA and the CMA-ES are able to tilt the well, but never learn to cool the system (B). Comparing how the temperature and field parameters change at each iteration (C) against $d_{\text{ave}}$ in B shows that the exponential convergence occurs in concert with an exponential decrease in system temperature. We note that the field parameters $v_{x_1}$ and $v_{x_2}$ track one another, reflecting the fact that the optimizer is invariant to rotations in the configuration space: The optimizer moves the field along the direction associated with the greatest improvement in solution quality and is insensitive to the fact that the problem was parameterized in the arbitrary coordinates $x_1$ and $x_2$.

We speculate that this shortcoming is again a consequence of indirect problem representation. We note that when $kT\approx 0.1$, the particle is almost evenly distributed between both the central well and the four nearest neighbors that surround it. Thus, for black-box methods, noise in the average particle position can play an overpowering role during parameter updates. By contrast, Eq. 2 considers covariances at the finer scale of configuration space. As with our prior example, this extra information makes our method appreciably more robust to flat regions in the search landscape and in this case yields an essentially exponential convergence to the optimized state (Fig. 2B).

Designing a Polymer to Fold into an Octahedron

The success of the two simple examples in the previous section invites more complicated design problems. As an example, we consider a basic model for a polymer: a string of hard, colored balls interconnected by rigid rods. The balls are weakly attractive, interaction strengths determined by the colors. For example, red and blue may be attracted more strongly than blue and green.

In principle, by tuning the color interactions, it should be possible to fold the chain into specific, desired shapes. To make a concrete task, we take a chain of six particles and create an optimizer to fold them into an octahedron, defined by minimizing the sum of the distances to the center of mass. Note that the search space is appreciably larger than in the prior examples (dimension 10), and that simply setting all of the interaction strengths to large values will not produce the optimal solution. By choosing the interaction appropriately, the same energy can be given to the octahedral and polytetrahedral configurations for identical coupling constants. Entropic arguments imply that the polytetrahedron will dominate the chain configurations unless the optimizer carefully adjusts the coupling constants to take on unique values (30, 31).

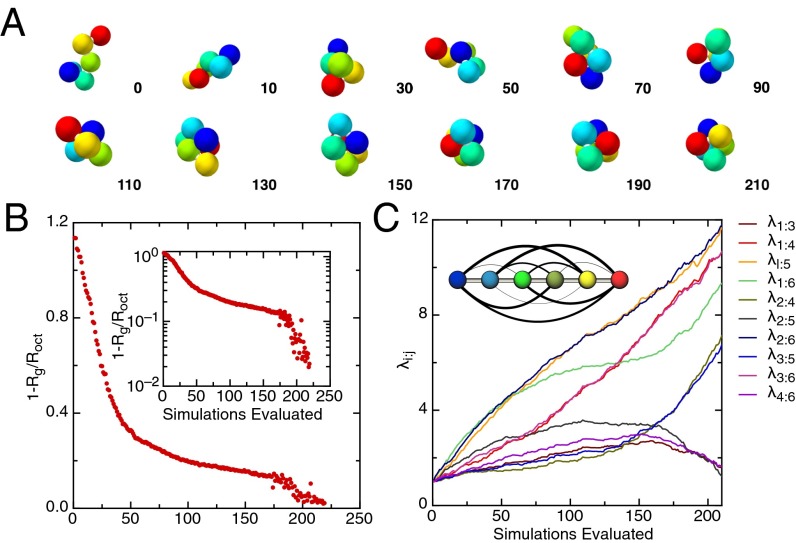
Fig. 3A shows a typical chain configuration from each generation, and Fig. 3B shows the median sum of distances to the center of mass, normalized relative to that of a perfect octahedron. Initially, the coupling constants are set to $1kT$, and random chain configurations are typical. However, as the optimizer drives the interaction energies to larger values, the shapes become compact and structured. Around 200 generations, virtually every shape generated is octahedral (Fig. 3A).

Fig. 3.

Folding an octahedron out of a linear chain. (A) Typical chain configurations that result after iterating Eq. 2. Numbers indicate the iteration number. Early on, the polymer configurations are dominated by thermal energy and random, yet as the interaction strengths increase and differentiate, more structured objects appear, and ultimately only the octahedron configuration exists (iterations 190–210). (B) Plotting the median percentage of deviation between the polymer’s radius of gyration $R_g$ and the radius of gyration for an octahedron $R_{\text{oct}}$ at each iteration shows that the optimizer again produces a monotonic decrease at each step, with an effectively exponential convergence in the last 30 iterations. By the last 10 iterations, the median deviation from a perfect octahedron is roughly 1%. (C) In plotting the coupling constants against iteration number, we find that the optimizer adjusts coupling constants in groups. It is clear that the active coupling constants form the contact network for an octahedron (C, Inset).

By plotting the values of the interaction strengths against iteration number, we find the optimizer’s solution is simple, logical, and arguably optimal. Early on, the optimizer attempts to meet the design goal by simply increasing the coupling strengths to make more compact objects (Fig. 3A). However, as the coupling constants are undifferentiated, the results are predominately polytetrahedral geometries. To compensate, the optimizer deactivates three coupling constants around 100 generations and sends the remainder to infinity (Fig. 3C). The logic behind this maneuver becomes clear by plotting the interactions as a network: The active interactions plus the polymer backbone form the contact graph of an octahedron. This strategy, transforming the contact matrix to an interaction matrix, has been identified as an approach to programing, by hand, the optimal interaction parameters for self-assembly (18). In fact, the specific problem of creating a self-assembling octahedron has been solved using a virtually identical motif (32). Evidently our optimizer can reproduce a well thought-out approach to self-assembly, and it does so automatically, requiring only a model and a design goal.

Optimization of an Out-of-Equilibrium System

Because Eq. 2 holds for any parameterized probability distribution function, it can be used to create optimization schemes beyond the canonical ensemble in the prior examples. The only essential ingredients are a model that predicts the probability of microstates, an engine that samples configurations from said model, and a design goal. As simple extensions, chemical potentials or constraints on pressure could be included as tunable parameters (33). A new theoretical concept, termed “digital alchemy,” extends statistical mechanics to account for microscale geometric parameters, such as the particle shape in a colloidal-nanoparticle assembly (34). Thus, by coupling this approach with our optimization formalism, particle geometry can be tuned to produce optimized bulk responses. One can also note that the range of parameters to design is at the user’s discretion: Eq. 1 can be used to rederive Eq. 2, assuming that some of the model parameters are not controllable by taking them to be time independent. Indeed, for the particle in a well problem, the wavelength of corrugation was taken as a fixed parameter and the resulting optimizer was quite effective. One can also consider optimization for global quality functions that exist over multiple a range of parameters (35). For instance, our approach can optimize the density of a crystal lattice over a range of pressures and system volumes by defining $\rho ={\rho }_0\left(x|\lambda ,V,P\right)U\left(V,P\right)$, where $U\left(V,P\right)$ is a uniform distribution for V and P over a range of consideration and ${\rho }_0$ is the appropriate distribution for microstates given a fixed volume and pressure. Eq. 2 can then be applied to optimize in this extended parameter space to find choices of λ that work well over a range of possible densities and pressures. Abstracting the concept, statistical models could be based on calculations like self-consistent field theory or experiments with the code directly measuring correlation functions in the laboratory and tuning physical parameters.

Moreover, nonequilibrium processes, provided they have a statistical description, are fair game. For example, if one simulates diffusion by adding white noise to a mean drift, then the paths are distributed by a product of Gaussian distributions conditioned on the prior steps. Clearly, the paths are statistical objects, with diffusion and drift as the distribution parameters, λ. Thus, one can build an optimizer that tunes these control parameters using Eq. 2, even if they are time-dependent functions.

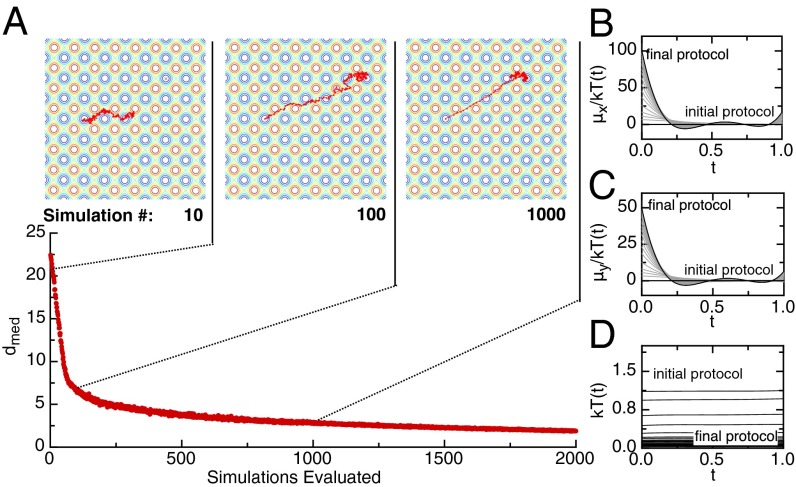
As proof of this point, we return to the problem of a particle trapped on a substrate, but now simulate the particle dynamics. The applied field and the system temperature are treated as functions of time and the optimizer is tasked with moving the particle from one well to another in a given interval.

Fig. 4A shows the median distance to the target well after executing the optimizer’s processing protocol in each generation. In the first 60 generations, the optimizer learns to transport the particle from its starting location to the target well via a large, deterministic driving force. It then spends the remaining iterations monotonically decreasing the system temperature while developing a trapping protocol with the field. After 2,000 iterations, the optimizer seems to traps the particle by oscillating the driving force, changing its direction before the particle can transition to another well. In effect, the optimizer learns to drag the particle to the target and trap it in place, using both the temperature and the field. By 2,000 iterations, $\sim 90\text{\%}$ of the points in the path fall within the target well. When left to run longer, the optimizer continues to improve the quality of solutions, but at the cost of becoming unphysical, the optimizer generates extremely large fields that move the particle to the well faster and faster. To optimize beyond the proof of concept demonstrated here, one may have to restrict the range of parameters allowed to the optimizer or account for arbitrary velocities by increasing the number of steps in the walk.

Fig. 4.

Optimizing a nonequilibrium process. By using Eq. 2 we can tune processing protocols for a Brownian particle walking on a rough energy landscape controlled by a time-dependent temperature, kT, and linear mean drift components, ${\mu }_x$ and ${\mu }_y$. The optimizer has been tasked to adjust to place and trap the random walker in a well located at the x–y coordinates $\left(\mathrm{10,10}\right).$ (A) Ensemble median distance to the objective well after executing a processing protocol at each iteration of the algorithm. Callouts show representative paths taken by the particle, and contours in the callouts show lines of constant energy over the substrate potential. The large image represents the protocol executed after 2,000 iterations. Every protocol attempted at 10-iteration intervals is illustrated in B–D, where the temperature, $kT$ (D) as well as the applied fields in the x direction and y direction normalized by temperature, ${\mu }_x/kT$ (B) and ${\mu }_y/kT$ (C), are plotted against time. At $t=0$ the particle is released from its initial position at $\left(-\mathrm{10,0}\right)$ and allowed to wander and the processing protocol is executed until the simulation is stopped at $t=1$. At each iteration, the optimizer works to monotonically decrease the temperature, while arriving at a field protocol that quickly drives the particle to the target well and then oscillates the fields to trap it there.

Optimization of Directed Self-Assembly

As a final demonstration of our approach we consider the real-world problem of designing the directed self-assembly of block copolymers on a chemically patterned substrate. This represents a task at the forefront of both materials design and sublithographic fabrication (1, 7–11, 36, 37). The goal is to lithographically pattern a substrate with a small number of chemical features such that these features promote block copolymers to self-assemble into a desired target morphology. Here, we consider a task that has been identified as a promising candidate for the manufacture of next-generation semiconductor devices and high-density storage media: self-assembly of AB-diblock copolymers into an ordered striped or lamellar morphology (1, 9–11).

We use a theoretically informed coarse-grain model for block copolymer simulations (36). Polymer chains are simulated as beads that are linked together. The system is considered at fixed temperature and volume, and thus the probability of finding a given microstate configuration is defined in terms of an energy given by three parts. The first is a linear spring bond energy between beads in each polymer chain. The second is a nonbonded interaction energy that characterizes repulsion from unlike species and the material compressibility. Details are in Supporting Information (36). Both the model and the parameters in it represent a polystyrene-block-poly(methyl methacrylate) (PS-b-PMMA) diblock copolymer with a number-averaged molecular weight of 22,000-b-22,000 and a stripe period of 28 nm.

The final contribution to the energy is the substrate interaction. The substrate consists of two regions: the patterned stripes of width w and the background. Both are defined to have short-ranged effects on the polymer beads and assume the form $H_s/kT=\mathrm{\Lambda }\left(\alpha \right)/d_s\exp \left[-{\left(z/2d_s\right)}^2\right]$, where $d_s$ defines the decay length of the interaction, z is the distance from the plane of the substrate, and $\mathrm{\Lambda }\left(\alpha \right)$ is the interaction strength between the substrate and a bead of type α. Thus, if the particle is over the guiding stripe and of type A, $\mathrm{\Lambda }\left(A\right)={\mathrm{\Lambda }}_s$. If the particle is of type A and over the background region, $\mathrm{\Lambda }\left(A\right)={\mathrm{\Lambda }}_b$. Following ref. 11, we simplify our model by assuming the interactions are antisymmetric: ${\mathrm{\Lambda }}_s\left(A\right)=-{\mathrm{\Lambda }}_s\left(B\right)$ and ${\mathrm{\Lambda }}_b\left(A\right)=-{\mathrm{\Lambda }}_b\left(B\right)$. The design problem is to adjust the width of the strips w and the two energy parameters ${\mathrm{\Lambda }}_s$ and ${\mathrm{\Lambda }}_b$ so the target stripe phase replicates itself m times between two guiding stripes spaced by the polymer period multiplied by m.

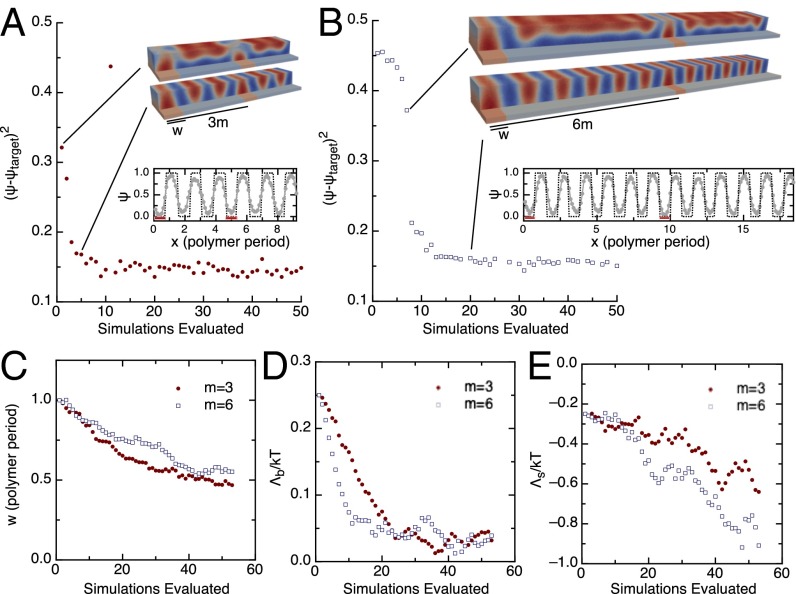
The results for $m=3$ and $m=6$ density multiplication are shown in Fig. 5. For the $m=3$ problem, we ran the optimization four times, varying the time step used in integrating Eq. 2. In every instance, the optimizer not only brought the system to a state that successfully met the design goal, but also, within noise, converged to the same state. The optimized parameters suggest that directed self-assembly is best achieved by setting the stripe width equal to roughly half the polymer period, ${\mathrm{\Lambda }}_s\approx -1kT$ and ${\mathrm{\Lambda }}_b=0.05kT$. All of these parameters agree with simulation results obtained by a brute-force solution to the problem and experimental verifications performed on the real polymer system (37) and are physically consistent with optimization results obtained for triblock copolymer pattern multiplication (11). These results can be explained by considering the interfacial energies in the system. The background interaction is required to be weak because the background region has roughly equal coverage between the A and B phases and is significantly larger in area than the size of the stripe. Moreover, the interaction strength for the stripe components is larger in the $m=6$ problem (Fig. 5D), because the larger distance between patterned regions requires stronger anchoring to guide assembly.

Fig. 5.

Optimizing directed self-assembly. Here we design the width of the stripe, the strength of its attraction to the red polymer beads ${\mathrm{\Lambda }}_s$, and the attraction strength of the background substrate ${\mathrm{\Lambda }}_b$ toward the blue polymer beads, to match the self-assembled phase as closely as possible to the target of alternating stripes. We quantify the success of our optimizer by comparing an order parameter $\mathrm{\Psi }\left(x\right)=\left(n_a\right)/\left(n_a+n_b\right)$ binned along the x axis of the box and averaged over y and z to the target stripe pattern. With Eq. 2, we are able to produce optimized parameters for 3× (A) and 6× (B) density multiplication after simulating 10 and 20 parameter choices. Two characteristic configurations are plotted in A and B, Insets, separated by just a handful of iterations, yet displaying markedly different phases of the polymer. Asymptotic configurations depicting Ψ (solid, marked line) and the target (dashed line) (A and B, Insets) show that the optimized parameters match the desired morphology, typically within $80\text{\%}$ or better. In plotting the parameters generated by Eq. 2 (C–E), we find that the interaction with the background brush is the most relevant parameter in directed self-assembly. For both the 6× and 3× problems, the rapid convergence toward the optimized state takes place once the background strength is reduced to ${\mathrm{\Lambda }}_b\approx 0.05$. After a weak background is established, the strip width and strength function as fine-tuning parameters that facilitate defect-free assembly.

When the optimizer was run at the most aggressive time step, we were able to achieve convergence for m = 3, (m = 6) in less than 10 (18) iterations, despite the fact that the material required the simulation of roughly 50,000 (100,000) polymer beads. We stress that the performance obtained here is not a consequence of initializing the system too close to an optimal state, but rather evidence of the power behind Eq. 2. Fig. 5 shows that indeed the initial parameters do not produce a solution to the design problem, let alone a stripe pattern of any kind.

This particular problem also has been attempted in some variant using other materials design methods. In fact, our initial conditions were selected to match those given to an implementation of the CMA-ES, solving the same design problem but using triblock copolymers (11). For that problem, the CMA-ES took roughly 50 generations to converge, simulating 32 ensembles in parallel per iteration, each requiring 200,000 Monte Carlo steps. Our approach also used 200,000 Monte Carlo steps per iteration, but required only 10 iterations to converge. If algorithm performance is measured in terms of the number of microstates simulated, then solving directed self-assembly problems by way of the CMA-ES requires at least 5 times as much compute power as the approach proposed here. If it is not possible to run the ensemble simulations in parallel, our approach is roughly 130 times faster than the CMA-ES and completes a full optimization process before the CMA-ES has completed a single iteration. Additionally, inverse Monte Carlo methods have been used to solve directed self-assembly problems involving the placement of guiding posts instead of stripes (8). Although there are relevant physical differences, we note that the results presented for inverse Monte Carlo converge after simulating roughly 30 million microstates. Because this number of microstates simulated is roughly 15 times larger than what was used here, we can speculate that our proposed methods could also be faster for such applications.

Conclusions

To the extent that the goal of materials design is a unified framework that handles a wide range of complex inverse problems, we believe the formalism introduced here represents a significant step forward. By applying Eq. 2, we can solve problems with flat search landscapes (Fig. 1) and multiple-interaction types (Fig. 2), incorporate constraints (Fig. 3), tune processing conditions (Fig. 4), and address application scale design and optimization tasks (Fig. 5). Furthermore, in all of the examples presented, the end result is intuitive even though it was achieved in a complicated search landscape where other optimization schemes struggle or fail. Finally, the fact that processing conditions such as applied fields or temperature protocols and model parameters like internal interaction energies can be optimized with the very same framework presents an unexplored direction for materials design. Because these are the essential aspects that determine the properties of any material, the capacity to tune both simultaneously, one accounting for the other, opens the doors to a more coherent and conceptually complete design program.

Eq. 2 as a Best Approximation

As stated in the main text, Eq. 2 can be derived by choosing parameter updates that minimize the average squared error $\mathit{ϵ}=\langle {\left({\dot{\lambda }}_i{\partial }_{{\lambda }_i}\log \left[\rho \right]-\left[f\left(x\right)-\langle f\rangle \right]\right)}^2\rangle$. In other words, one updates λ so that $\dot{\lambda }$ minimizes ε. This requires that ${\partial }_{{\dot{\lambda }}_j}\mathit{ϵ}=0$ for all of the ${\dot{\lambda }}_j$, which gives the condition

$$0=2\langle {\partial }_{{\lambda }_j}\log \left(\rho \right){\partial }_{{\lambda }_i}\log \left(\rho \right)\rangle {\dot{\lambda }}_i-2\langle {\partial }_{{\lambda }_j}\log \left(\rho \right)\left[f\left(x\right)-\langle f\rangle \right]\rangle .$$ [S1]

Multiplying on the left by the pseudoinverse for $\langle {\partial }_{{\lambda }_j}\log \left(\rho \right){\partial }_{{\lambda }_i}\log \left(\rho \right)\rangle$ and moving the second term to the left-hand side, we arrive at Eq. 2:

$${\dot{\lambda }}_i={\langle {\partial }_{{\lambda }_i}\log \left(\rho \right){\partial }_{{\lambda }_j}\log \left(\rho \right)\rangle }^{-1}\langle {\partial }_{{\lambda }_j}\text{log}\left(\rho \right)\left[f\left(x\right)-\langle f\left(x\right)\rangle \right]\rangle .$$ [S2]

We comment briefly on how to select an $f\left(x\right)$ that leads to a rank-invariant optimizer. Whereas in principle $f\left(x\right)$ can be anything that rewards solutions that conform well to the design goal, one can gain an added invariance property by designing $f\left(x\right)$ to reward good configurations based on relative rank rather than absolute value. This makes the optimizer invariant to trivial changes in the design problem that preserve the rank of candidate solutions. To achieve this, we took $f\left(x\right)$ to equal the probability of selecting another configuration that performs as well as or worse than the current configuration x when drawn randomly from the current distribution, $\rho \left(x|{\lambda }_i\right)$. Explicitly, this requires

$$f\left(x\right)={\displaystyle \int dx\prime \mathrm{\Theta }\left(g(x\prime )\le g\left(x\right)\right)\rho \left(x\prime |\lambda \right)},$$ [S3]

where $g\left(x\right)$ is a raw quality function that determines how well solutions meet the design goal, and $\mathrm{\Theta }\left(a\le b\right)$ is equal to 1 whenever the inequality in the argument is satisfied and zero otherwise. For example, in the Ising model problem $g\left(x\right)$ was taken to be the average magnetization of a given configuration, x. Thus, $f\left(x\right)$ rewards the configurations that have magnetizations that are likely to be larger than others drawn from the same distribution. This rescaling indeed satisfies the requirement that any rank preserving transformation of the raw quality function $g\left(x\right)$ will not change the flow of parameters. In other words, any rewriting of $g\left(x\right)$ that preserves the ranking of configurations will not alter the optimizer performance.

We note in passing that by choosing this form for $f\left(x\right)$, Eq. 1 in the main text becomes the continuous space replicator equation from evolutionary game theory (26, 27). Thus, we can also interpret $f\left(x\right)$ in the rank-invariant form as a fitness function that rewards the configuration at x with a unit of fitness for every competitor configuration drawn from the ensemble $\rho \left(x\right)$ that performs at a lower or equal quality.

Eq. 2 as a Projection of Eq. 1

Here we derive Eq. 2, starting from the motivating expression $\dot{\rho }\left(x|{\lambda }_i\right)=\rho \left(x|{\lambda }_i\right)\left[f\left(x\right)-\langle f\left(x\right)\rangle \right]$ without introducing the concept of an error minimization. We begin by noting that $\rho \left(x|{\lambda }_i\right)$ has time dependence only through the ${\lambda }_i$ terms. Thus, via the chain rule the left-hand side can be expanded as

$${\partial }_{{\lambda }_i}\log \left(\rho \left(x|\lambda \right)\right){\dot{\lambda }}_i=\left[f\left(x\right)-\langle f\left(x\right)\rangle \right].$$ [S4]

To isolate update rules for each ${\lambda }_i$, we project the equation onto the functions ${\partial }_{{\lambda }_j}\log \left(\rho \right)$ by multiplying both sides by $\rho {\partial }_{{\lambda }_j}\log \left(\rho \right)$ and integrate over configuration space:

$$\langle {\partial }_{{\lambda }_j}\log \left(\rho \right){\partial }_{{\lambda }_i}\log \left(\rho \right)\rangle {\dot{\lambda }}_i=\langle {\partial }_{{\lambda }_j}\text{log}\left(\rho \right)\left[f\left(x\right)-\langle f\left(x\right)\rangle \right]\rangle .$$ [S5]

The matrix on the left-hand side is identified as the Fisher information matrix and can be inverted to produce

$${\dot{\lambda }}_i={\langle {\partial }_{{\lambda }_i}\log \left(\rho \right){\partial }_{{\lambda }_j}\log \left(\rho \right)\rangle }^{-1}\langle {\partial }_{{\lambda }_j}\log \left(\rho \right)\left[f\left(x\right)-\langle f\left(x\right)\rangle \right]\rangle .$$ [S6]

As desired, this form is Eq. 2 and the basis of our optimizer.

In this derivation, we essentially multiplied by ${\langle {\partial }_{{\lambda }_i}\log \left(\rho \right){\partial }_{{\lambda }_j}\log \left(\rho \right)\rangle }^{-1}\langle {\partial }_j\log \left[\rho \right]|$. Structurally, this is a projection and this gives an alternate interpretation of Eq. 2 as the projection of Eq. 1 onto the basis functions ${\partial }_{{\lambda }_i}\log \left[\rho \right]$.

Invariance Properties of Eq. 2

As stated in the main text, Eq. 2 hosts a range of invariance properties that yield robust performance over a large class of design problems. One of the most important is that the velocity field generated by Eq. 2 is invariant to any reparameterizations of the design parameters λ, provided the structure of the distribution ρ is left intact. By this we mean that if there is a change of coordinates so that ${\lambda }_i^{\prime }={\lambda }_i^{\prime }\left(\lambda \right)$ and ${\lambda }_i={\lambda }_i(\lambda \prime )$, then the velocity field generated by Eq. 2 is the same in both parameterizations. This can be shown by direct substitution:

$${\dot{\lambda }}_i=\frac{\partial {\lambda }_i}{\partial {\lambda }_j^{\prime }}{\dot{\lambda }}_j^{\prime }={\langle \frac{\partial \log \left[\rho \right]}{\partial {\lambda }_i}\frac{\partial \log \left[\rho \right]}{\partial {\lambda }_k}\rangle }^{-1}\langle \left[f-\langle f\rangle \right]\frac{\partial \log \left[\rho \right]}{\partial {\lambda }_k}\rangle .$$ [S7]

Rewriting everything in terms of the primed variables requires the substitution $\frac{\partial \log \left[\rho \right]}{\partial {\lambda }_i}=\frac{\partial {\lambda }_j^{\prime }}{\partial {\lambda }_i}\frac{\partial \log \left[\rho \left(\lambda \prime \left(\lambda \right)\right)\right]}{\partial {\lambda }_j^{\prime }}$, which gives us that

$$\frac{\partial {\lambda }_i}{\partial {\lambda }_j^{\prime }}{\dot{\lambda }}_j^{\prime }={\langle \frac{\partial {\lambda }_l^{\prime }}{\partial {\lambda }_i}\frac{\partial \log \left[\rho \right]}{\partial {\lambda }_l^{\prime }}\frac{\partial {\lambda }_m^{\prime }}{\partial {\lambda }_k}\frac{\partial \log \left[\rho \right]}{\partial {\lambda }_m^{\prime }}\rangle }^{-1}\langle \left[f-\langle f\rangle \right]\frac{\partial {\lambda }_n^{\prime }}{\partial {\lambda }_k}\frac{\partial \log \left[\rho \right]}{\partial {\lambda }_n^{\prime }}\rangle$$ [S8]

$$\frac{\partial {\lambda }_i}{\partial {\lambda }_j^{\prime }}{\dot{\lambda }}_j^{\prime }={\left(\frac{\partial {\lambda }_l^{\prime }}{\partial {\lambda }_i}\langle \frac{\partial \log \left[\rho \right]}{\partial {\lambda }_l^{\prime }}\frac{\partial \log \left[\rho \right]}{\partial {\lambda }_m^{\prime }}\rangle \frac{\partial {\lambda }_m^{\prime }}{\partial {\lambda }_k}\right)}^{-1}\frac{\partial {\lambda }_n^{\prime }}{\partial {\lambda }_k}\langle \left[f-\langle f\rangle \right]\frac{\partial \log \left[\rho \right]}{\partial {\lambda }_n^{\prime }}\rangle .$$ [S9]

Now we use the fact that ${\delta }_{ij}=\frac{\partial {\lambda }_i^{\prime }}{\partial {\lambda }_k}\frac{\partial {\lambda }_k}{\partial {\lambda }_j^{\prime }}$ and the matrix identity ${\left(ABA\right)}^{-1}=A^{-1}{B}^{-1}{A}^{-1}$ to get

$${\dot{\lambda }}_j^{\prime }={\langle \frac{\partial \log \left[\rho \right]}{\partial {\lambda }_j^{\prime }}\frac{\partial \log \left[\rho \right]}{\partial {\lambda }_k^{\prime }}\rangle }^{-1}\langle \left[f-\langle f\rangle \right]\frac{\partial \log \left[\rho \right]}{\partial {\lambda }_k^{\prime }}\rangle ,$$ [S10]

which is the velocity equation that results when initially working from the primed coordinates.

The key idea expressed here is that Eq. 2 assigns a velocity to each possible ${\lambda }_i$ in the search space that is independent of how ${\lambda }_i$ is parameterized. Thus, an optimizer starting at a given ${\lambda }_i$ position will evolve along the same trajectory as another optimizer written in a different coordinate choice. This can provide a big advantage compared with black-box methods. To see why, consider the fact that two different coordinate choices may lead to search spaces that are more or less corrugated in λ space. Because black-box methods will see the search landscapes as distinct, the performance will be better or worse, depending on a trivial reparameterization of ρ. By contrast, optimizers based on statistical mechanics models see no difference whatsoever, provided they are initialized to the same λ point. This means the designer is free to choose any coordinate system without having to worry whether the optimizer performance will degrade.

Error Propagation via Eq. 2

In this section we examine what effect errors in evaluating Eq. 2 can have on the algorithm performance. In particular, the matrix inverse in Eq. 2 might suggest that small errors could be amplified to produce large parameter variations. Here we show that whereas small errors may indeed introduce large variations into the parameters λ, for our algorithm, this occurs only for parameters that have little effect on the simulated material properties. Specifically, we focus on implementations of Eq. 2 that use the rank-based $f\left(x\right)$ defined in the previous section, integrate Eq. 2 using a small numerical time-step τ, and evaluate expectation values using a Monte Carlo approximation. To assess the fidelity of these approximations, we compare the information lost when representing the true target distribution defined by Eq. 2 with one constructed using the stated assumptions. In bits, this is given by the Kullback–Leibler divergence or $K={\displaystyle \int dx\rho \left(x|{\lambda }_i\left(t\right)\right)\log \left[\frac{\rho \left(x|{\lambda }_i\left(t\right)\right)}{\rho \left(x|{\lambda }_i\left(t\right)+\delta {\lambda }_i\left(t\right)\right)}\right]}$, where $\delta {\lambda }_i\left(t\right)$ represents the error due to sampling. If we expand to leading order in the error, we find

$$K=\delta {\lambda }_i{g}_{ij}\delta {\lambda }_j,$$ [S11]

where we have used the notation $g_{ij}=\langle {\partial }_i\log \left[\rho \right]{\partial }_j\log \left[\rho \right]\rangle$. Because we are interested in whether an ill-conditioned matrix inverse is problematic, we focus our analysis on the case where the largest contribution in error comes from computing the $\langle {\partial }_j\log \left[\rho \right]\left[f\left(x\right)-\langle f\rangle \right]\rangle$ terms in Eq. 2. Thus, we have that to leading order in the time step, $\delta {\lambda }_i=\tau g_{ij}^{-1}\delta C_j$, where $\delta C_j$ is the error on the estimates for $\langle {\partial }_j\log \left[\rho \right]\left[f\left(x\right)-\langle f\rangle \right]\rangle$. Inserting this relationship into the equation for K and taking the expectation value over sampling realizations for $\delta C_j$, we find that to leading order in τ,

$$K=\mathrm{Cov}\left[{\partial }_j\log \left[\rho \right]\left[f\left(x\right)-\langle f\rangle \right],{\partial }_i\log \left[\rho \right]\left[f\left(x\right)-\langle f\rangle \right]\right]g_{ij}^{-1}{\tau }^2/N,$$ [S12]

where we have used the fact that, averaged over realizations, the mean squared errors for $\delta C_i$ should be given by the covariance on the estimated parameters divided by the number of samples N. We now bound our error estimate, using the fact that

$$\mathrm{Cov}\left[{\partial }_j\log \left[\rho \right]\left[f\left(x\right)-\langle f\rangle \right],{\partial }_i\log \left[\rho \right]\left[f\left(x\right)-\langle f\rangle \right]\right]g_{ij}^{-1}\le \langle {\left[f\left(x\right)-\langle f\rangle \right]}^2{\partial }_j\log \left[\rho \right]{\partial }_i\log \left[\rho \right]\rangle g_{ij}^{-1}.$$ [S13]

This equation follows because $g_{ij}^{-1}$ is a positive definite matrix and so the term $\langle {\partial }_j\log \left[\rho \right]\left[f\left(x\right)-\langle f\rangle \right]\rangle g_{ij}^{-1}\langle {\partial }_i\log \left[\rho \right]\left[f\left(x\right)-\langle f\rangle \right]$ appearing in the covariance expression is strictly positive. Inserting this into our expression for K gives

$$K\le \langle {\left[f\left(x\right)-\langle f\rangle \right]}^2{\partial }_j\log \left[\rho \right]{\partial }_i\log \left[\rho \right]\rangle g_{ij}^{-1}{\tau }^2/N.$$ [S14]

The final step is to note that the rank-based $f\left(x\right)$ used to define algorithms in this paper is bounded and the bounds are independent of λ. Specifically, for the system described in the prior section, $0<f\left(x\right)<1$ and $\langle f\rangle =0.5$ for all λ. Thus, we have that ${\left(f\left(x\right)-\langle f\rangle \right)}^2<\frac{1}{4}$, which gives us that

$$K\le \langle {\left[f\left(x\right)-\langle f\rangle \right]}^2{\partial }_j\log \left[\rho \right]{\partial }_i\log \left[\rho \right]\rangle g_{ij}^{-1}\frac{{\tau }^2}{N}\le \frac{{\tau }^2}{4N}{g}_{ij}^{-1}{g}_{ij}=\frac{{\tau }^{2}d}{4N},$$ [S15]

where d is the number of parameters ${\lambda }_i$ in the model. Thus, we find the surprising result that to leading order in τ, the information lost by approximating Eq. 2 is bounded and that the bound is independent of both λ and $g_{ij}$. In other words, to leading order in τ, an approximation to Eq. 2 using the methods described in this paper will lose no more than $\frac{{\tau }^{2}d}{4N}$ bits due to sampling noise, for any λ selected by the optimizer.

Methodology for the Ising Model Problem

As discussed in the main text, applying Eq. 2 to the Ising model Hamiltonian gives the optimization equation ${\dot{\lambda }}_{x_l}=\mathrm{Cov}{\left[h_{x_l},h_{x_m}\right]}^{-1}\mathrm{Cov}\left[h_{x_m},f\right]$, where the $h_{x_i}$ represent the energy contributions of neighbors along the horizontal and vertical directions. To maximize the average magnetization, we set $f\left(x\right)$ equal to the probability that another configuration drawn at random from ρ has a lower instantaneous magnetization, $m\left(x\right)$, than that of configuration x (Supporting Information, Eq. 2 as a Best Approximation). Specifically, we set $f\left(x\right)={\displaystyle \int dx\prime \mathrm{\Theta }\left(m(x\prime )\le m\left(x\right)\right)\rho \left(x\prime |\lambda \right)}$, where $\mathrm{\Theta }\left(a\le b\right)$ is unity when the inequality in the argument is satisfied and zero otherwise. With this definition all of the terms in the update equation are expressible as expectation values, and they can be evaluated by making a Monte Carlo approximation with samples drawn from $\rho \left(x|\lambda \right)$.

To draw these samples from the Ising Hamiltonian at equilibrium, we implemented the Wolff cluster algorithm with variable coupling constants for the horizontal and vertical directions (38). In this Markov chain Monte Carlo method, a single spin is chosen at random and flipped. The neighbors of this site are then flipped randomly based on the energy associated with the old and new configurations. If flipped, any neighbors of the altered site are considered for manipulation, and the process iterates until no new sites are added to the cluster. For our simulations, we used a 25 × 25 grid of spin sites. To minimize correlation between the samples, we ran a burn-in period with 1,000 spin-flip cycles, logging the average number of spins flipped in each iteration. Once this finished, we continued to iterate the spin-flip algorithm and logged samples once every q iterations. We selected q so that the average number of spins flipped per cycle multiplied by the number of cycles between logged samples equals the system size. The process was repeated until 1,000 configurations were saved.

To integrate Eq. 2 we used a modified Euler scheme with a fixed time step of 0.5. We suggest future work could improve this aspect of the algorithm, yet for a proof of concept this simple choice was effective. We note that moving to higher order or variable time-step integrators will have to account for the fact that the Monte Carlo approximation introduces error that can be larger than the truncation error associated to the integration scheme. Thus, using more sophisticated integrators may require a careful analysis of how noise in the velocity terms impacts the optimizer trajectories.

Methodology for the Equilibrium Particle on a Substrate Problem

Following the discussion in the main text, we chose our optimization parameters so that $\rho \left(x|{\lambda }_i\right)$ is given by a canonical ensemble of the form $\rho \propto \exp \left[-{\lambda }_s{h}_s-{\lambda }_{x_1}{x}_1-{\lambda }_{x_2}{x}_2\right]$, where the ${\lambda }_s$ represents control parameters for the temperature and ${\lambda }_{x_i}$ is the control parameter for the field contributions. With this choice, Eq. 2 takes the form

$$\frac{d}{dt}\left[\begin{array}{c}{\lambda }_s\\ {\lambda }_{x_1}\\ {\lambda }_{x_2}\end{array}\right]={\left[\begin{array}{ccc}\mathrm{Cov}\left[h_s,h_s\right]& \mathrm{Cov}\left[h_s,x_1\right]& \mathrm{Cov}\left[h_s,x_2\right]\\ \mathrm{Cov}\left[h_s,x_1\right]& \mathrm{Cov}\left[x_1,x_1\right]& \mathrm{Cov}\left[x_1,x_2\right]\\ \mathrm{Cov}\left[h_s,x_2\right]& \mathrm{Cov}\left[x_2,x_1\right]& \mathrm{Cov}\left[x_2,x_2\right]\end{array}\right]}^{-1}\left[\begin{array}{c}\mathrm{Cov}\left[h_s,f\right]\\ \mathrm{Cov}\left[x_1,f\right]\\ \mathrm{Cov}\left[x_2,f\right]\end{array}\right].$$ [S16]

As all of the terms in this equation are expectation values, we approximate them by averaging over samples drawn from ρ. Given a set of interaction strengths ${\lambda }_i$, we generated samples for the particle position by running a Metropolis–Hastings random walk. The proposals were generated by adding Gaussian noise to each particle position. For the data shown, the SD of the noise was set equal to $5/\sqrt{\max \left[\lambda \right]}$. The factor of 5 corresponds to the characteristic spacing between wells in the random walk problem and thus represents the characteristic length scale of the problem. To decrease the correlation between samples, we discarded the first 10,000 steps in the random walk and took 50,000 more steps, recording the position every 1,000 cycles. These 50 particle locations were then sent to the optimizer as samples.

As with the Ising model example, we integrated Eq. 2 with a modified Euler scheme (time step set to 0.5) and used a rank-based quality function for $f\left(x\right)$. Specifically, we used the choice $f\left(x\right)={\displaystyle \int dx\prime \mathrm{\Theta }\left(d(x\prime )\le d\left(x\right)\right)\rho \left(x\prime |\lambda \right)}$, where $d\left(x\right)$ is the distance between x and the target well and where $\mathrm{\Theta }\left(a\le b\right)$ is unity when the inequality in the argument is satisfied and zero otherwise. With this definition, $f\left(x\right)$ is the probability that another configuration drawn at random from ρ is farther away from the target well than configuration x.

Methodology for the Polymer Folding Problem

By construction, we required particles to remain a fixed distance D from their neighbors along the chain. Thus, we used a Metropolis–Hasting algorithm with proposal states designed to respect this condition (39, 40). In each iteration, we selected a particle to manipulate at random. If the particle was at the end of the chain, it was given a new position distributed uniformly at random on a unit sphere surrounding its one neighbor. If the particle was in the interior of the chain, then all of the possible new positions for the particle lived on a circle defined by the condition that the particle remains a unit distance from its two neighbors. In this case, we assigned the interior particle a new position drawn at random and uniformly distributed on the circle.

To deal with deep local minima that might trap the Metropolis–Hastings walk, we implemented a parallel tempering scheme (41). We ran two other Monte Carlo simulations in parallel with identical coupling constants, but one with a temperature twice as big and the other with a temperature 10 times as big. The ensembles were allowed to attempt an exchange of configuration with the next closest temperature ensemble every 100 iterations. The probability of exchange was set according to the standard replica-exchange algorithm (41). With these two temperature ratios we found empirically that the probability of accepting an exchange move was roughly 0.30 and always fell between 0.1 and 0.5.

We iterated this process with a burn-in period of 10,000 steps and then took 1,000,000 steps, saving samples every 1,000 cycles. The resulting 1,000 configurations were then used by the optimizer to evaluate the expectation values in Eq. 2. For our quality function, we used a rank-based reward system and defined $f\left(x\right)={\displaystyle \int dx\prime \mathrm{\Theta }\left(R_g(x\prime )\le R_g\left(x\right)\right)\rho \left(x\prime |\lambda \right)}$, where $R_g\left(x\right)$ is radius of gyration for the polymer configuration x and where $\mathrm{\Theta }\left(a\le b\right)$ is unity when the inequality in the argument is satisfied and zero otherwise. With this definition, $f\left(x\right)$ is the probability that another configuration drawn at random from ρ has a larger radius of gyration than the configuration x. With all these parameters in place, Eq. 2 was integrated with a modified Euler scheme, using a time step of 0.25.

We checked that simply setting all of the energy parameters to large, identical values will not produce an octahedron. This comes about by tuning a Lennard-Jones potential $V=4\left({\left(\frac{a}{r}\right)}^{12}-{\left(\frac{a}{r}\right)}^6\right)$ with a cutoff distance, $r_c$, such that $V=0$ for any $r\ge r_c$. We shift the raw Lennard-Jones potential by its value at $r_c$ to keep the potential continuous.

The specific value for $r_c$ was picked by ensuring that, in the octahedron geometry, the only contribution to the particle energy would come from contacting particles. This was achieved by setting the cutoff parameter to be $r_c=\sqrt{2}D$. Because the polytetrahedron geometry has the exact same number of particle contacts (12 contacts) and no two points closer than $r_c$, these two geometries will have exactly the same energy given the short-ranged potential.

We note, in passing, that there is some residual in our optimizer’s coupling constants. Beyond deactivating the three interactions, some coupling constants have larger values than others. Further, we note that the active coupling constants can be placed in four groups that respect the symmetry around the center of the chain. For instance, the binding energy between the second and the last particle is almost exactly the same as the energy between the first and the second to last particle (Fig. 3 C and D). These variations show that the optimizer is responsive to the chain’s influence on configurations, even though the chain binding the particles together is not programmed explicitly into the structure of the Hamiltonian. In other words, the optimizer can learn constraints programmed implicitly in a model and react using its explicit control parameters.

Methodology for the Nonequilibrium Particle on a Substrate

Here we show how to derive an optimizer that works on an out-of-equilibrium problem. This particular optimizer treats the problem of a particle walking randomly on a substrate and takes the random path traveled by the particle as its configuration space. To model the process, we discretize the path into N steps, each spaced in time by a small interval τ. We pick N and τ so that $N\tau =1$ and set up the problem so that the random walk takes place over a time interval $0<t<1$. The path is generated by adding white noise with variance of $\tau k{T}_i$ and a mean drift of ${\overrightarrow{v}}_i$ to update the particle position ${\overrightarrow{x}}_i$ at each time step i. Convolving these random additions gives the probability for a full path:

$$\rho \propto \text{exp}\left[-{\displaystyle \sum _{i=0}^N\frac{1}{2\tau k{T}_i}{\left({\overrightarrow{x}}_{i+1}-\left({\overrightarrow{x}}_i+\tau v\left({\overrightarrow{x}}_i,i\right)\right)\right)}^2}\right].$$ [S17]

By expanding the square and absorbing all of the terms independent of $x_i$ into the proportionality constant we get

$$\rho \propto \text{exp}\left[{\displaystyle \sum _{i=0}^N-\frac{1}{2\tau k{T}_i}\left({\left({\overrightarrow{x}}_{i+1}-{\overrightarrow{x}}_i\right)}^2-2\left({\overrightarrow{x}}_{i+1}-{\overrightarrow{x}}_i\right)\overrightarrow{v}\left({\overrightarrow{x}}_i,i\right)\tau \right)}\right].$$ [S18]

For our particular problem, the mean velocity term $\overrightarrow{v}\left({\overrightarrow{x}}_i,i\right)$ is made up of a contribution from the substrate, which depends on the particle position $-\overrightarrow{\nabla }U\left({\overrightarrow{x}}_i\right)$, where $U\left({\overrightarrow{x}}_i\right)=-\cos \left(\frac{2\pi }{5}x\right)-\cos \left(\frac{2\pi }{5}y\right)$ is the substrate potential, and a contribution from the field ${\overrightarrow{\mu }}_i$ that provides a directional bias and depends only on the time index i. Writing these two parts explicitly gives us

$$\rho \propto \exp \left[-{\displaystyle \sum _{i=0}^N\frac{1}{2\tau k{T}_i}\left({\left({\overrightarrow{x}}_{i+1}-{\overrightarrow{x}}_i\right)}^2-2\left({\overrightarrow{x}}_{i+1}-{\overrightarrow{x}}_i\right)\left({\overrightarrow{\mu }}_i-\overrightarrow{\nabla }U\left({\overrightarrow{x}}_i\right)\right)\tau \right)}\right].$$ [S19]

At this stage, we need to assume a particular form for how the control parameters $k{T}_i$ and ${\overrightarrow{\mu }}_i$ depend on time. One choice is to expand the parameters, using a set of orthogonal basis functions. We used the Chebyshev polynomials (42) of the first kind, $T_n\left(t\right)$. Specifically, we define $\frac{1}{k{T}_i}={\displaystyle {\sum }_{n=0}^4\left(T_n\left(i\tau -1\right)+1\right)a_n}$ for the temperature variables and $\frac{{\overrightarrow{\mu }}_i}{k{T}_i}={\displaystyle {\sum }_{n=0}^4{T}_n\left(i\tau -1\right){\overrightarrow{b}}_n}$ for the fields. Note the vector notation signifies that there are two sets of $b_n$, one for the field contributions in the x direction and one for the field component in the y direction. Using this choice of basis functions, we can rewrite the probability function for the path ρ as

$$\rho \propto \exp \left[{\displaystyle \sum _{n=0}^4{a}_n{\mathrm{\Phi }}_n\left[x\right]}+{\overrightarrow{b}}_n{\overrightarrow{\mathrm{\Psi }}}_n\left[x\right]\right],$$ [S20]

where

$${\mathrm{\Phi }}_n\left[x\right]={\displaystyle \sum _{i=0}^N\left(1+T_n\left(i\tau -1\right)\right)\left(\nabla U\left(x_i\right)-\frac{1}{2\tau }{\left({\overrightarrow{x}}_{i+1}-{\overrightarrow{x}}_i\right)}^2\right)}$$ [S21]

and

$${\overrightarrow{\mathrm{\Psi }}}_n\left[x\right]={\displaystyle \sum _{i=0}^N{T}_n\left(i\tau -1\right)\left({\overrightarrow{x}}_{i+1}-{\overrightarrow{x}}_i\right)}.$$ [S22]

In this form, the distribution is in the same family as all of the prior examples. As far as the optimization engine is concerned, we can treat ${\mathrm{\Phi }}_n$ and ${\overrightarrow{\mathrm{\Psi }}}_n$ as though they were “energy” components and can produce a version of Eq. 2, using covariances between ${\mathrm{\Phi }}_n$, ${\overrightarrow{\mathrm{\Psi }}}_n$, and the reward function f:

$$\frac{d}{ds}\left[\begin{array}{c}{a}_n\\ \overrightarrow{b_n}\end{array}\right]={\left[\begin{array}{cc}\mathrm{Cov}\left[{\mathrm{\Phi }}_n,{\mathrm{\Phi }}_m\right]& \mathrm{Cov}\left[{\mathrm{\Phi }}_n,{\overrightarrow{\mathrm{\Psi }}}_m^{†}\right]\\ \mathrm{Cov}\left[{\overrightarrow{\mathrm{\Psi }}}_n,{\mathrm{\Phi }}_m\right]& \mathrm{Cov}\left[\overrightarrow{{\mathrm{\Psi }}_n},{\overrightarrow{\mathrm{\Psi }}}_m^{†}\right]\end{array}\right]}^{-1}\left[\begin{array}{c}\mathrm{Cov}\left[{\mathrm{\Phi }}_m,f\right]\\ \mathrm{Cov}\left[{\overrightarrow{\mathrm{\Psi }}}_m,f\right]\end{array}\right].$$ [S23]

Here we use the variable s to denote the optimizer’s time parameter to avoid confusion with the t, the time parameter for the random walk. For the particulars of our optimizer, we again chose a modified Euler integrator with a time step of 0.5 and calculated average values by sampling 100 paths per iteration. We used a rank-based quality function for the $f\left(x\right)$ in Eq. 2. Specifically, we calculated the distance to the target well averaged over every point in the path $d_{\text{target}}\left[x\right]$ and then set $f\left(x\right)$ equal to the probability that another path drawn at random from the same distribution parameters has a value of $d_{\text{target}}$ greater than or equal to the given path.

Methodology for the Directed Self-Assembly Problem

In this section we provide a brief overview of the key components used to model diblock copolymer directed self-assembly as well as how we implemented Eq. 2 to optimize them. The primary focus of this section is on how one can take a generic Monte Carlo description of a material and convert it into an optimizer via Eq. 2. Because the polymer model has been presented previously in the literature, we provide only a broad level description and, for details, we direct the reader to previously published work (40).

As stated in the main text, the energy for the full system of polymer chains interacting with a chemically modified substrate is given in three parts. The first part is the bonded contribution between polymer beads in a given chain,

$$\frac{H_b}{kT}=\frac{3}{2}{\displaystyle \sum _j^{n_p}{\displaystyle \sum _i^{N-1}{\left(r_j\left(i+1\right)-r_j\left(i\right)\right)}^2/b^2}},$$ [S24]

where b is the statistical length segment of the polymer, N is the number of beads in a chain, $n_p$ is the number of polymer chains in the system, and $r_j\left(i\right)$ is the position of the ith bead in the jth chain. The second contribution to our model is given by the nonbonded energy between polymer elements of different chains. This contains two parts: one describing compressibility of the polymer melt and the other describing repulsion between different monomers,

$$\frac{H_{nb}}{kT}=\frac{\sqrt{\overline{N}}}{R_e^3}{\displaystyle \int dx\left[\chi N{\varphi }_A{\varphi }_B+\left(\kappa N/2\right){\left(1-{\varphi }_A-{\varphi }_B\right)}^2\right]},$$ [S25]

where ${\varphi }_A$ and ${\varphi }_B$ are the local densities of the A- and B-type beads, respectively, $R_e^2=N{b}^2$ is the mean squared end-to-end distance, and the invariant degree of polymerization is given by $\sqrt{\overline{N}}={\rho }_0{R}_e^3/N$, where ${\rho }_0$ is the average bead density. Here the first term characterizes the repulsion between unlike monomers and is scaled by a Flory–Huggins parameter for the model (χ). The second term defines the compressibility and its model parameter κ is inversely proportional to the material’s modulus of compression. Note that the local densities ${\varphi }_A$ and ${\varphi }_B$ are evaluated using a particle-to-mesh method.

As noted in the main text, the final energy contribution comes from the particle interaction with the substrate. Each substrate has lithographically patterned stripes of width w and a background material. The two substrate types interact with the particles by way of an energy $H_s/kT=\mathrm{\Lambda }\left(\alpha \right)/d_s\exp \left[-{\left(\frac{z}{2d_s}\right)}^2\right]$, where $d_s$ defines the decay length of the interaction, z is the distance from the plane of the substrate, and $\mathrm{\Lambda }\left(\alpha \right)$ is the interaction strength between the substrate and a bead of type α. In other words, when a particle of type A is above the patterned region of the substrate, $\mathrm{\Lambda }\left(A\right)={\mathrm{\Lambda }}_s$, whereas if it is over the background region, $\mathrm{\Lambda }\left(A\right)={\mathrm{\Lambda }}_b$. As stated in the main text, we assume that the model parameters are antisymmetric: ${\mathrm{\Lambda }}_s\left(A\right)=-{\mathrm{\Lambda }}_s\left(B\right)$ and ${\mathrm{\Lambda }}_b\left(A\right)=-{\mathrm{\Lambda }}_b\left(B\right)$.

Parameters for the simulation model were selected to agree with experiments performed on polystyrene-block-poly(methyl methacrylate) (PS-b-PMMA) diblock copolymers with a number-averaged molecular weight of 22,000-b-22,000 (41). Specifically, we took $\sqrt{\overline{N}}=83$, $\kappa N=22$, and $\chi N=17$. The substrate interaction length was set to $d_s=0.15$, in units of the polymer length. Each polymer chain was composed of 32 beads, 16 of type A followed by 16 of type B.

The design goal posed in the main text is to optimize the stripe width, w, and the two interaction energy scales ${\mathrm{\Lambda }}_b$ and ${\mathrm{\Lambda }}_s$ to promote self-assembly into a striped phase. Because microstate configurations are distributed according to the canonical ensemble, Eq. 2 is given by

$$\frac{d}{dt}\left[\begin{array}{c}w\\ {\mathrm{\Lambda }}_b\\ {\mathrm{\Lambda }}_s\end{array}\right]=-{\left[\begin{array}{lll}\mathrm{Cov}\left[{\partial }_w{H}_s,{\partial }_w{H}_s\right]\hfill & \mathrm{Cov}\left[{\partial }_w{H}_s,{\partial }_{{\mathrm{\Lambda }}_b}{H}_s\right]\hfill & \mathrm{Cov}\left[{\partial }_w{H}_s,{\partial }_{{\mathrm{\Lambda }}_s}{H}_s\right]\hfill \\ \mathrm{Cov}\left[{\partial }_{{\mathrm{\Lambda }}_b}{H}_s,{\partial }_w{H}_s\right]\hfill & \mathrm{Cov}\left[{\partial }_{{\mathrm{\Lambda }}_b}{H}_s,{\partial }_{{\mathrm{\Lambda }}_b}{H}_s\right]\hfill & \mathrm{Cov}\left[{\partial }_{{\mathrm{\Lambda }}_b}{H}_s,{\partial }_{{\mathrm{\Lambda }}_s}{H}_s\right]\hfill \\ \mathrm{Cov}\left[{\partial }_{{\mathrm{\Lambda }}_s}{H}_s,{\partial }_w{H}_s\right]\hfill & \mathrm{Cov}\left[{\partial }_{{\mathrm{\Lambda }}_s}{H}_s,{\partial }_{{\mathrm{\Lambda }}_b}{H}_s\right]\hfill & \mathrm{Cov}\left[{\partial }_{{\mathrm{\Lambda }}_s}{H}_s,{\partial }_{{\mathrm{\Lambda }}_s}{H}_s\right]\hfill \end{array}\right]}^{-1}\left[\begin{array}{c}\mathrm{Cov}\left[{\partial }_w{H}_s,f\right]\\ \mathrm{Cov}\left[{\partial }_{{\mathrm{\Lambda }}_b}{H}_s,f\right]\\ \mathrm{Cov}\left[{\partial }_{{\mathrm{\Lambda }}_s}{H}_s,f\right]\end{array}\right],$$ [S26]

where we have used the fact that $-{\partial }_{{\lambda }_i}\log \left[\rho \right]={\partial }_{{\lambda }_i}H-\langle {\partial }_{{\lambda }_i}H\rangle$.

The partial derivatives involving ${\mathrm{\Lambda }}_s$ and ${\mathrm{\Lambda }}_b$ are straightforward to evaluate,

$$\begin{array}{l}{\partial }_{{\mathrm{\Lambda }}_s}{H}_s={\displaystyle \sum _A\frac{\theta (x,y)}{d_s}}\exp [-{\left(\frac{z}{2d_s}\right)}^2]-{\displaystyle \sum _B\frac{\theta (x,y)}{d_s}}\exp [-{\left(\frac{z}{2d_s}\right)}^2]\mathbf{[S27]}\hfill \\ \hfill \end{array}$$

$${\partial }_{{\mathrm{\Lambda }}_b}{H}_s={\displaystyle \sum _A\frac{(1-\theta (x,y))}{d_s}}\exp [-{\left(\frac{z}{2d_s}\right)}^2]-{\displaystyle \sum _B\frac{(1-\theta (x,y))}{d_s}}\exp [-{\left(\frac{z}{2d_s}\right)}^2],$$ [S28]

where $\theta \left(x,y\right)=1$ if the particle is over a stripe and zero otherwise, and the sums ${\mathrm{\Sigma }}_A$ and ${\mathrm{\Sigma }}_B$ are over all beads of types A and B. To evaluate the partial derivatives with respect to w we decided to approximate the derivatives via a central, finite difference. Because the method already uses a particle-to-mesh approximation, we have a small length cutoff, l. This gave us the approximation

$${\partial }_w{H}_s\left(w,{\mathrm{\Lambda }}_s{\mathrm{\Lambda }}_b\right)\approx \frac{H_s\left(w+l,{\mathrm{\Lambda }}_s{\mathrm{\Lambda }}_b\right)-H\left(w-l,{\mathrm{\Lambda }}_s{\mathrm{\Lambda }}_b\right)}{2l}.$$ [S29]

To finalize the algorithm, we used a Monte Carlo scheme detailed in ref. 36 to draw samples for polymers distributed in a box. The box dimensions, measured in units of the polymer length, were scaled to $2m\times 2\times 1$, where m is the multiplication target for directed self-assembly. Stripes were automatically drawn by the algorithm at $x=0,z=0$ and $x=m,z=0$ along the y axis. The polymer chains were then randomly initialized in the simulation region to fill to a desired density and were then allowed to equilibrate. In the 3× density multiplication problem, we used 50,000 polymer beads, whereas in the 6× problem this was doubled to roughly 100,000.

We allowed the system a burn-in time of 20,000 Monte Carlo steps before we began sampling. Samples were recorded every 10,000 steps and the full system was run for 200,000 iterations. We decided on 10,000 steps by examining the autocorrelation time for the substrate energy contributions. We found that after roughly 5,000 Monte Carlo steps samples were effectively independent. We drew samples half as frequently to be sure samples remained independent even if the optimizer explored unusual regions of parameter space.

Because this system was appreciably larger than other examples in the text, some care was taken to make integration of Eq. 2 as efficient as possible. Our protocol was to integrate Eq. 2, using a modified midpoint method, initially taking the time step to be 0.5. We allowed this cursory run 100 iterations. We found that it converged in fitness after 80 cycles and had halved the initial fitness value after roughly 20 cycles. This suggested we could dramatically increase the time-step parameter without causing the integration to become unstable. We scaled our time step by a factor of 8 so that the fitness would halve after just 3 iterations and the optimization would complete in 10 cycles. Indeed, we found this was the case in both the 3× and 6× problems as noted in the main text. We then reran the optimizer three times at these settings to find essentially identical results in each case.