Aquatic carbon cycling in the conterminous United States and implications for terrestrial carbon accounting

Significance

Inland waters provide habitat for aquatic organisms; are sources of human drinking water; and integrate, transport, and process carbon across continents. Estimates of the accumulation of carbon in terrestrial environments suggest that agricultural and forest ecosystems have annual net gains in carbon storage. These ecosystems are considered sinks of atmospheric carbon dioxide. None of these estimates have considered the loss of carbon to and also through aquatic environments at the national or continental scale. We show that aquatic ecosystems in the conterminous United States export over 100 teragrams of carbon (TgC) per year, highlighting the need to attribute the sources of aquatic carbon more accurately, and assert that inland waters play an important role in carbon accounting.

Abstract

Inland water ecosystems dynamically process, transport, and sequester carbon. However, the transport of carbon through aquatic environments has not been quantitatively integrated in the context of terrestrial ecosystems. Here, we present the first integrated assessment, to our knowledge, of freshwater carbon fluxes for the conterminous United States, where 106 (range: 71–149) teragrams of carbon per year (TgC⋅y⁻¹) is exported downstream or emitted to the atmosphere and sedimentation stores 21 (range: 9–65) TgC⋅y⁻¹ in lakes and reservoirs. We show that there is significant regional variation in aquatic carbon flux, but verify that emission across stream and river surfaces represents the dominant flux at 69 (range: 36–110) TgC⋅y⁻¹ or 65% of the total aquatic carbon flux for the conterminous United States. Comparing our results with the output of a suite of terrestrial biosphere models (TBMs), we suggest that within the current modeling framework, calculations of net ecosystem production (NEP) defined as terrestrial only may be overestimated by as much as 27%. However, the internal production and mineralization of carbon in freshwaters remain to be quantified and would reduce the effect of including aquatic carbon fluxes within calculations of terrestrial NEP. Reconciliation of carbon mass–flux interactions between terrestrial and aquatic carbon sources and sinks will require significant additional research and modeling capacity.

Management of terrestrial carbon stocks and fluxes is considered a sustainable approach to reducing the anthropogenic contribution to increasing atmospheric CO₂ (1). Therefore, accurate accounting of carbon storage and flux is essential to understand the role that natural ecosystems can play in regional, national, and global carbon cycles. However, current modeling approaches for estimating net ecosystem production [NEP = GPP − R, where GPP is gross primary production and R is autotrophic and heterotrophic respiration (2, 3)] assume that carbon is converted to terrestrial storage terms only without adequate accounting of aquatic carbon processes. These aquatic carbon processes include downstream carbon transport, lake and reservoir sedimentation, and CO₂ emission. Recent studies (4–6) indicate that downstream export of carbon through rivers, carbon burial in lakes and reservoirs, and carbon emissions across water surfaces are large enough to alter the calculation of terrestrial NEP significantly. Therefore, when the processing and removal of carbon through inland waters is properly accounted for, the calculated capacity of soils and biomass to store carbon is reduced (7, 8).

Most studies that have made concurrent measurements of terrestrial and aquatic fluxes of carbon were conducted in small watersheds and have used different metrics to estimate total carbon accumulation across terrestrial landscapes. For example, recent efforts suggest that upward of 10% of the net ecosystem exchange (NEE) in Sweden is represented by the evasion of CO₂ from stream and river surfaces (9). On a larger scale, Striegl et al. (10) suggest that about 6% of net primary production (NPP) is exported downstream in the Yukon basin. When combined with river CO₂ emission (11, 12), the total aquatic carbon flux amounts to 12% of NPP for the basin. Across smaller watersheds, the magnitude of the freshwater carbon flux can reach 34% of the estimated NEP, excluding carbon burial via sedimentation (13). These studies are beneficial in identifying the diversity of carbon sources and potential influences of different carbon cycle processes, and they also document removal via lateral carbon export and CO₂ emissions.

The total mass fluxes of carbon moving out of aquatic systems are poorly constrained at the global scale, yet recent estimates suggest these fluxes may exceed 3 petagrams of carbon (PgC) per year (14, 15). Data are lacking at this scale to apportion these fluxes across the landscape. Emerging research highlights the difficulty in identifying the major sources of carbon to freshwater ecosystems, which is critical to link the terrestrial and aquatic carbon cycles properly. Efforts in the Brazilian Amazon River basin produce differing results depending upon geographic location and prevailing hydrologic conditions. Research suggests upstream terrestrial carbon previously degraded in soil and stream environments can fuel heterotrophy in the lower river reaches (16), whereas in another study, respiration and organic carbon (OC) from fringing wetlands may provide significant CO₂ to match the supersaturated chemistry of the larger central Amazon (17). These two sources are not mutually exclusive. In the conterminous United States, input of supersaturated ground water is more important in small streams, whereas internal production of CO₂ is higher in larger river systems (18).

In lake and reservoir ecosystems, CO₂ supersaturation is common, but the processes maintaining elevated CO₂ concentrations are diverse and regionally variable (19–21). Respiration of allochthonous OC results in net heterotrophy in many lake systems (22). Inorganic carbon inputs can also contribute substantially to CO₂ emissions from lakes (19, 23). Furthermore, freshwater systems have strong seasonal patterns (22). Changes in precipitation alter stream and river flow and carbon concentrations (24). Lakes can vary between net heterotrophy and net autotrophy with changes in temperature and across spatial gradients (19). Man-made reservoirs can function like natural lake systems; however, they also sequester large amounts of carbon through sedimentation (25). Much of the OC delivered to sediments is potentially remineralized to CH₄ and CO₂ and returned to the atmosphere over millennia (26–28).

Here, we present the first combined estimates of the major removal fluxes, to our knowledge, including burial in lakes and wetlands, downstream transport to coastal areas, and the CO₂ emission to the atmosphere for the conterminous United States. In this effort, we aggregate vertical gas evasion, lake and reservoir sedimentation, and the lateral fluxes of carbon by modified versions of major two-digit US Geological Survey (USGS) hydrologic regions (HUCs) and compare estimates across each of these regions (Fig. S1). In its simplest form, the calculated total US aquatic carbon flux is represented by Eq. 1 (expanded methods are provided in SI Materials and Methods):

$$Total\hspace{0.17em}US\hspace{0.17em}Flux\hspace{0.17em}(\text{TgC}\cdot {\text{y}}^{-1})={\displaystyle \sum }_{HUC}Stream\hspace{0.17em}Emission+Lateral\hspace{0.17em}Flux+Lake\hspace{0.17em}\&\hspace{0.17em}Reservoir\hspace{0.17em}Emission-Lake\hspace{0.17em}\&\hspace{0.17em}Reservoir\hspace{0.17em}Burial,$$ [1]

where $Stream\hspace{0.17em}Emission$ represents the vertical evasion of CO₂ from stream and river surfaces in teragrams of carbon (TgC) per year, $Lateral\hspace{0.17em}Flux$ represents the total dissolved inorganic plus OC fluxes draining from the landscape to coastal systems in TgC per year, $Lake\hspace{0.17em}\&\hspace{0.17em}Reservoir\hspace{0.17em}Emission$ represents the vertical evasion of CO₂ across lake and reservoir surfaces in TgC per year, and $Lake\hspace{0.17em}\&\hspace{0.17em}Reservoir\hspace{0.17em}Burial$ represents the total organic carbon (TOC) burial in lakes plus reservoirs in TgC per year. This total flux was calculated for only the conterminous US land area, because adjustments were made to reduce vertical emission and sedimentation for those areas of each contiguous basin in Fig. S1 that originate outside of the United States. Because fluxes were calculated using consistent national methodologies, we are able to make regional comparisons in aquatic flux magnitudes across systems as well as explore the importance of terrestrial drivers on aquatic flux variability.

Fig. S1.

USGS two-digit HUC regions used for analysis of both aquatic carbon and terrestrial carbon balance. HUCs 17 and 18 have been modified as identified in SI Materials and Methods to represent differences in precipitation regimes across the Coastal and Cascade mountain ranges.

North America has been identified as a potentially large carbon sink ranging from 0.1 to 2 PgC⋅y⁻¹ (29). Although much of this sink may be attributed to increasing rates of forest regrowth (30), there remains significant variability among the current suite of terrestrial biosphere models (TBMs) to identify and account for a terrestrial sink in any one component of the biosphere (31). Here, we use aggregated results of the Multiscale Synthesis and Terrestrial Model Intercomparison Project (MsTMIP) part of the North American Carbon Program to capture both the variability that exists across models and the uncertainty associated with the calculation of terrestrial carbon stocks and flows across large spatial scales. The transport and processing of carbon in aquatic systems is not estimated in any of the predictive models. In this context, the inputs of terrestrial carbon into aquatic environments in both inorganic and organic forms, as particles or dissolved, represent either a loss of either terrestrial carbon uptake or relocation of respiration as CO₂.

SI Materials and Methods

Expanded Discussion on Autochthonous Production of Carbon and Model Spatial Scales.

There is growing evidence that the proportion of carbon in fluvial systems derived from autochthonous vs. allochthonous sources is scale-dependent, where the contribution of terrestrial carbon is greater in smaller watersheds (18, 56). In a lentic environment, there is evidence that overall carbon fluxes can be supported by allochthonous inputs of both inorganic carbon and OC (19, 20); conversely, the recycling of atmospheric CO₂ has been shown to support heterotrophy in some systems (57). A spatially explicit accounting of the magnitude of (f_a) is outside the scope of this article but is needed to apportion the contribution of terrestrial carbon to total aquatic carbon fluxes correctly. However, there is strong evidence that the majority of carbon in aquatic environments is derived from terrestrial OC and inorganic carbon (58). It is within this framework where exploring the correlations between measurements of terrestrial carbon and aquatic carbon can be most informative to identify possible driving mechanisms.

Given the differing spatial scales between the TBM output and the aggregated aquatic carbon fluxes presented here, it is important to comment on the potential for double accounting of the net uptake and removal of carbon through different pathways. The MsTMIP modeling scheme runs at a resolution of 0.25° at the global scale. Within each of these grid cells, there exist many differing water features that are not specifically partitioned into their own carbon sources and sinks. Therefore, when aggregated to a grid cell of this size, calculated respiration implicitly includes aquatic efflux, just as calculated NEP will implicitly include carbon burial in lakes, streams, and reservoirs. However, none of these grid cells include the movement of carbon laterally through the riverine network.

Modified Two-Digit HUC Boundaries.

Each two-digit HUC represents contiguous drainage regions where possible. The Mississippi River basin is represented by HUCs 05, 06, 07, 08, 10, and 11; the Colorado River basin includes HUCs 14 and 15; and specific modifications have been made to HUCs 17 and 18. Due to the distinct ecological variability driven by very high precipitation regimes and forest cover between the Coastal and western Cascade mountain ranges in the states of Washington, Oregon, and California, this combined area of HUCs 17 and 18 is designated as 17 Coast, whereas the remaining portions are now designated as 17 Dry and 18 Dry.

Stream and River Efflux by HUC.

Detailed methods for calculating the total carbon flux and average carbon yield for each two-digit HUC are available in studies by Butman and Raymond (32) and Stackpoole et al. (33). Modification to those methods are outlined below. In brief, for estimates across the conterminous United States:

$$\left[fC{O}_{2}C\right]\left(\text{Tg}\right)=\hspace{0.17em}{\displaystyle \sum }_{HUC}\left[{\displaystyle \sum }_{SO}\left[\left[C{O}_{2-water}-\hspace{0.17em}C{O}_{2-air}\right]\ast kC{O}_2\ast SA\right]\right].$$ [S1]

The term fCO₂C is the total net emission of CO₂ from riverine systems of the conterminous United States. CO_2-water is the riverine CO₂ concentration (moles per liter), CO_2-air is the CO₂ equilibrium concentration of atmospheric CO₂ in water (moles per liter), kCO₂ is the gas transfer velocity of CO₂ across the air–water interface (meters per day), and SA is the riverine surface area (square meters). The total flux was calculated by the summation of all mean annual fluxes for a stream order [SO] within each two-digit HUC.

Dissolved CO₂ concentrations (CO_2-water) were estimated from stream and river chemistry measurements of pH, temperature, and total alkalinity available through the USGS NWIS (waterdata.usgs.gov/nwis). CO₂ was then calculated from the known disassociation constants for carbonic acid in freshwater systems at ambient atmospheric pressure using the CO2SYS program within the MATLAB (Mathworks, Inc.) computing environment (59). For the 18 HUCs evaluated here, a total of 6,986 USGS gaging station locations had an adequate chemistry record and were used for the CO₂ efflux calculation. A minimum of 12 sampling dates were required for inclusion in this analysis. A total of 435,030 matched daily chemical measurements were identified. The concentration of CO₂ in the atmosphere (CO_2-air) was assumed constant at 390 ppm for all HUCs.

The gas transfer velocity (kCO₂) was modeled based on a metaanalysis of measurements of gas exchange and the gas transfer velocity made by direct tracer injections across small to midsized river systems in the United States (49, 60). Physical parameters of stream slope and water velocity were used to predict gas transfer velocity according to the following equation (49):

$${\text{k}}_{600}\left(\text{m}\cdot {\text{d}}^{-1}\right)=\text{S}\hspace{0.17em}*\hspace{0.17em}\text{V}\left(\text{m}\cdot {\text{s}}^{-1}\right)\hspace{0.17em}*\hspace{0.17em}2,841\text{.}6+2\text{.}03\text{.}$$ [S2]

The term k₆₀₀ is the gas transfer velocity of CO₂ (meters per day) normalized to the Schmidt number (a dimensionless ratio that approximates the relationship between the viscosity and gas diffusivity across a boundary layer) for CO₂ at standard temperature (20 °C) and standard atmospheric pressure (61), S is the average slope of a stream reach, and V is the average velocity of water in meters per second.

Average slope was derived from the National Hydrography Dataset (NHD; NHDPlus, 2005) for each stream order within each two-digit HUC of the conterminous United States (Fig. S1). Velocity estimates were calculated from hydraulic geometry coefficients derived for each of the 19 HUCS using the USGS NWIS database of in situ measured slope and velocity at 12,975 gaging stations for the period between 1940 and 2011. A total of 1,547,878 instantaneous discharge measurements, along with concurrent measurements of stream width and velocity, were used to derive hydraulic geometry coefficients specific to each HUC. Each HUC specific regression to predict both width and velocity from instantaneous discharge was evaluated using a bootstrapping with replacement technique, and fifth through 95th confidence intervals for the regression parameters were estimated and include in the Monte Carlo model discussed below (Table S1). Additional discussion regarding the use of hydraulic geometry coefficients is presented in a study by Raymond et al. (49).

Table S1.

Regression model results for each two-digit HUC derived from the hydraulic geometry relationship between that natural log of discharge (cubic meters per year) and both width (meters) and velocity (meters per second)

				Width			Velocity
HUC	No. of sites	No. of measurements	SO range	Slope	Intercept	r2	Slope	Intercept	r2
01	458	36,977	1–7	0.484 (0.469–0.499)	1.953 (1.915–1.991)	0.90	0.172 (0.159–0.186)	−1.152 (−1.186 to 1.117)	0.58
02	1,589	203,570	1–7	0.484 (0.475–0.493)	2.154 (2.134–2.174)	0.88	0.192 (0.182–0.202)	−1.255 (−1.277 to 1.234)	0.49
03	2,069	224,935	1–8	0.47 (0.461–0.479)	2.106 (2.081–2.13)	0.83	0.14 (0.13–0.149)	−1.419 (−1.445 to 1.392)	0.5
04	653	58,818	1–7	0.501 (0.486–0.516)	2.001 (1.965–2.037)	0.87	0.161 (0.142–0.179)	−1.156 (−1.201 to 1.11)	0.45
05	1,066	149,787	1–9	0.475 (0.465–0.486)	1.975 (1.944–2.007)	0.88	0.132 (0.123–0.141)	−1.128 (−1.156 to 1.1)	0.42
06	323	31,355	1–8	0.482 (0.463–0.5)	2.086 (2.039–2.133)	0.89	0.148 (0.127–0.168)	−1.186 (−1.24 to 1.132)	0.38
07	892	121,268	1–10	0.504 (0.493–0.515)	1.901 (1.868–1.934)	0.90	0.142 (0.132–0.152)	−1.187 (−1.217 to 1.156)	0.45
08	257	25,334	1–10	0.452 (0.424–0.481)	2.089 (1.988–2.19)	0.79	0.167 (0.132–0.202)	−1.538 (−1.66 to 1.416)	0.26
09	133	17,242	1–7	0.495 (0.46–0.531)	1.802 (1.707–1.897)	0.85	0.147 (0.113–0.18)	−1.233 (−1.322 to 1.144)	0.36
10	1,265	170,656	1–9	0.502 (0.491–0.512)	1.802 (1.776–1.827)	0.88	0.128 (0.119–0.137)	−0.978 (−0.999 to 0.956)	0.39
11	689	80,126	1–9	0.47 (0.456–0.483)	1.972 (1.932–2.011)	0.87	0.107 (0.095–0.119)	−1.08 (−1.115 to 1.045)	0.31
12	459	78,868	1–7	0.465 (0.441–0.489)	1.783 (1.714–1.852)	0.77	0.111 (0.091–0.132)	−1.156 (−1.216 to 1.095)	0.2
13	134	18,253	1–8	0.549 (0.516–0.582)	1.906 (1.837–1.975)	0.89	0.141 (0.107–0.175)	−0.777 (−0.848 to 0.705)	0.34
14	480	56,148	1–8	0.516 (0.502–0.529)	1.769 (1.742–1.797)	0.92	0.166 (0.155–0.177)	−0.705 (−0.728 to 0.682)	0.64
15	306	33,320	1–9	0.503 (0.481–0.526)	1.897 (1.848–1.946)	0.86	0.155 (0.135–0.175)	−0.903 (−0.947–0.86)	0.42
16	327	49,752	1–7	0.518 (0.501–0.535)	1.754 (1.721–1.786)	0.92	0.148 (0.129–0.167)	−0.786 (−0.822 to 0.75)	0.42
17 Dry	784	71,445	1–8	0.493 (0.481–0.505)	1.86 (1.83–1.89)	0.90	0.145 (0.133–0.158)	−0.784 (−0.817 to 0.752)	0.4
17 Coast	524	52,978	1–8	0.465 (0.451–0.479)	1.932 (1.893–1.971)	0.89	0.184 (0.167–0.2)	−0.98 (−1.026 to 0.933)	0.48
18 Dry	571	67,046	1–7	0.476 (0.46–0.491)	1.778 (1.743–1.814)	0.86	0.14 (0.124–0.156)	−0.928 (−0.964 to 0.892)	0.34

Values in parentheses represent the fifth–95th percentiles derived from a bootstrapped regression with replacement. All regression models were statistically significant to P < 0.001. All data used to derive these equations are available with the USGS NWIS (waterdata.usgs.gov/nwis).

Hydraulic geometry of stream reaches showed remarkable consistency within and across watersheds to approximate channel width, velocity, and depth from measured discharge (62, 63). All scaling relationships derived by the calculation of hydraulic geometry exponents were statistically significant (P < 0.001; Table S1). However, velocity measurements had r² values ranging from 0.2 to 0.6, whereas r² values for width ranged from 0.85 to 0.98. Modeled average annual discharge from the NHDPlus data was used to estimate average channel width and velocity utilizing the regression models derived for each ecoregion (Table S1). Average slope and velocity were then calculated by stream order to estimate the gas transfer velocity of CO₂ according to Eq. 4.

Stream surface area was calculated based on the same hydraulic geometry coefficients discussed above for width within each HUC. Average discharge from the NHDPlus data was then used to calculate an average width for each stream order within a HUC. The total stream length was then calculated for each stream order within a HUC. Stream and river surface area was then calculated as the product of the average width and total length of streams by stream order.

A Monte Carlo simulation was performed for each stream order estimate of the total flux (TgC per year) from riverine surfaces with each individual HUC. The fifth through 95th confidence intervals derived from the bootstrapping discussed above were used to bound the Monte Carlo simulation for each parameter of Eq. 3. One thousand replications of the total flux calculation were performed for each stream order in a HUC. This approach is considered conservative because it allowed for the same probability of all combinations of each parameter in the total flux equation to be selected for each stream order and may have overestimated the error associated with the riverine evasion flux.

All estimates derived from the Monte Carlo simulation were adjusted to account for monthly temperatures below freezing under the assumption that stream and river efflux did not occur when monthly temperatures averaged below 0 °C. All carbon fluxes by stream order were reduced by the proportion of time that stream order fell within a region where monthly average temperatures fell below freezing. This improvement in method presented here better represents the presence of small streams within high elevations and/or cold environments, and appropriately weights the reduction in the overall flux more accurately. These changes result in an overall reduction across the conterminous United States of 14%, ranging from no effect of freezing temperatures in HUC 12 to a 30% reduction in both HUCs 01 and 04.

Lake and Reservoir Efflux.

Lake efflux estimates are presented in Table S3. Water chemistry data were obtained from the National Lakes Assessment (NLA) of the US Environmental Protection Agency. The NLA used a probability-based survey design to select 1,028 lakes in the contiguous United States that met the following criteria: (i) were greater than 4 ha in area, with a minimum of 0.1 ha of open water; (ii) were at least 1 m deep; and (iii) were not treatment or disposal ponds, brackish, or ephemeral. Sampling took place during the summer of 2007; 50% of the samples were obtained between July 12 and August 23, and nearly all (99%) were obtained between June 1 and September 30. NLA data can be accessed at www2.epa.gov/national-aquatic-resource-surveys/national-lakes-asessment. Data were partitioned geographically by HUC.

Table S3.

Lake carbon efflux by two-digit HUC

Two-digit HUC	Lake area, km2	Lake surface flux, TgC⋅y−1	Lake surface yields, gC⋅m−2⋅y−1
01	6,179	0.66 (0.17–0.21)	106.34 (78.76–140.54)
02	4,040	0.6 (0.27–0.47)	148.69 (80.83–265.25)
03	15,702	2.51 (0.86–1.24)	159.87 (104.84–238.62)
04	7,246	1.1 (0.3–0.4)	152.13 (110.2–207.36)
05	3,431	0.43 (0.13–0.2)	125.22 (87.82–184.55)
06	2,722	0.24 (0.2–0.36)	89.48 (16.24–220.02)
07	11,156	0.72 (0.27–0.39)	64.11 (40.19–99.37)
08	10,014	2.31 (0.85–1.14)	230.34 (145.53–343.7)
09	7,940	1.12 (0.48–1.03)	141.66 (81.57–270.98)
10	15,703	1.15 (0.25–0.28)	73.38 (57.54–91.44)
11	8,295	1.81 (0.41–0.5)	218.43 (169.04–278.23)
12	8,984	2.01 (0.74–1.28)	223.33 (140.59–365.59)
13	1,313	0.14 (0.1–0.15)	107.04 (32.08–222.06)
14	1,755	0.09 (0.06–0.1)	51.68 (15.02–109.2)
15	1,372	0.07 (0.04–0.06)	47.61 (15.49–87.76)
16	7,951	0.49 (0.26–0.28)	61.47 (28.97–96.84)
17 Coast	1,133	0 (0–0)	18.84 (0.93–43.89)
17 Dry	6,210	0.1 (0–0.3)	18.84 (0.93–43.89)
18 Dry	6,006	0.4 (0.1–0.9)	74.5 (24.47–155.72)
Total	127,151	16.0 (14.3–18.7)	111.21 (64.79–182.37)

Lake surface area was determined by the NHD by HUC. Total carbon flux is calculated according to (17). Errors in parentheses represent the fifth and 95th confidence intervals around the mean.

A number of biological, physical, and chemical indicators were measured for the NLA; only a subset of water chemistry and physical data were used: acid-neutralizing capacity (assumed to be equal to alkalinity), pH, temperature, and DOC. Although many studies ignore the contribution of noncarbonate alkalinity to total alkalinity when calculating partial pressure of CO₂ (pCO₂), parallel calculations using alkalinity/pH/temperature and DIC/pH/temperature have indicated that ignoring noncarbonate alkalinity can lead to an overestimation of pCO₂ and, subsequently, CO₂ fluxes (64). In typical naturally occurring freshwaters, the only major contributor to noncarbonate alkalinity is organic acid anions, primarily humic and fulvic acids (65). The concentration of free organic ions was estimated for the NLA lakes using the empirical relationships described by McDonald et al. (19).

Because flux calculations were performed using mean parameter (pCO₂, temperature, etc.) values, the data were examined for outliers before computation. Although pH and temperature data exhibited minimal skewness and did not contain any extreme values, corrected alkalinity values were highly positively skewed and did contain several very high values (three observations with corrected alkalinity >20,000 μEq/L). After sorting corrected alkalinity data by ecoregion, any observations that fell outside of the interval Q1–1.5 * IQR, Q3 + 1.5 IQR were excluded, where Q1 is the first quartile, IQR is the interquartile range, and Q3 is the third quartile. Any values less than zero were also removed.

Dissolved CO₂ ([CO₂]_aq, μmol/L) was computed using the equilibrium geochemical model PHREEQC (66). Water, temperature, pH, estimated organic anion concentration, and concentration of inorganic major ions were specified, and total inorganic carbon was optimized [Nelder–Mead simplex method documented by Parkhurst and Appelo (66)] such that the calculated alkalinity was equal to observed alkalinity.

The CO₂ flux across the air–water interface (millimoles per square meter per day) was calculated according to Eq. 3. Atmospheric pCO₂ was determined regionally based on summer (June to September) averages from five monitoring locations throughout the United States. These sites included Key Biscayne (FL), Niwot Ridge (CO), Southern Great Plains (OK), Wendover, (UT), and Trinadad Head (CA). These data are available at www.esrl.noaa.gov. The station within or nearest to each two-digit HUC was assigned to that region. Observations were corrected to 2012 based on a linear regression of annual means from 1998–2010 (mean = 390 μatm, range = 381–394 μatm). Partial pressures were converted to molar concentrations using Henry’s law constant, which was estimated from mean water temperature using the empirical relationships of Plummer and Busenberg (67) (mean = 0.034 μmol⋅L⁻¹⋅μatm⁻¹, range = 0.030–0.040 μmol⋅L⁻¹⋅μatm⁻¹).

The gas transfer velocity (k) was calculated according to Cole and Caraco (68), using an exponent of −0.67 to relate the transfer velocity at a Schmidt number of 600 to ambient conditions. Mean summer (June–September) wind speeds (u₁₀) for each ecoregion were determined from National Aeronautics and Space Administration surface meteorology and solar energy data (available at https://eosweb.larc.nasa.gov/sse/). The Schmidt number was calculated for each region as a function of water temperature (61). Lake and reservoir surface areas were tabulated for each HUC, following the method of McDonald et al. (69). Recent studies have identified shortcomings in simple models based only on wind speed (70). Surface renewal models based on measurements of near-surface turbulence produce enhanced gas transfer velocities (70). These results suggest that the models presented by Ward et al. (16) are underestimated, and that lake efflux may be larger than those values calculated herein.

Many of the parameters involved in these calculations violated normality assumptions. Therefore, nonparametric confidence intervals (95%) were determined on 1 million ordinary bootstrap replicates. Confidence intervals for calculated fluxes were determined via propagation of uncertainty derived from the bootstrapping results, with the exception of the total values (e.g., sum of regional estimates). In that case, confidence intervals were assumed to be additive (i.e., uncertainty was not propagated), because potential errors in the regional estimates are likely to be systematic.

Lateral Fluxes.

All lateral fluxes estimates are presented in Table S2. A benefit of presenting aquatic carbon flux results by HUCs is that carbon export from the major two-digit HUCs can be captured in one riverine flux. For example, HUC 05 carbon export is represented by the Ohio River flux (site 03612500; Ohio River at Dam 53 near Grand Chain, IL) minus the Tennessee River flux (site 03609750; Tennessee River at Highway 60 near Paducah, KY). HUC 06 is represented solely by the Tennessee River flux. HUC 07 is represented by the flux from the Mississippi River (site 05587455; Mississippi River at Grafton, IL), and HUC 10 is represented by the flux from the Missouri River (site 06934500; Missouri River at Herman, MO). HUC13 is represented by the Rio Grande (site 08475000; Rio Grande at Brownsville, TX), but it should be noted that the precipitation, soil OC, and NEP values in this analysis represent only the drainage area of the Rio Grande within the United States, because comparable data were not available for the portion of the drainage area that lies in Mexico.

Table S2.

Summary of lateral fluxes of carbon and the flow-weighted yields used to calculate the total carbon flux by HUC

HUC	No. of DIC sites	Total DIC flux, TgC⋅y−1	Total DIC flux error, TgC⋅y−1	Weighted DIC yield, gC⋅m2⋅y−1	DIC yield as % of TC yield	No. of TOC sites	Total TOC flux, TgC⋅y−1	Total TOC flux error, TgC⋅y−1	Weighted TOC yield, gC⋅m2⋅y−1	TOC yield as % of TC yield
01	13	0.441	0.035	2.783	40.0	10	0.661	0.077	4.172	60.0
02	21	1.233	0.083	4.289	66.2	21	0.631	0.071	2.194	33.8
03	42	1.584	0.069	2.270	43.1	38	2.089	0.221	2.993	56.9
04	32	4.904	0.019	10.630	74.7	19	1.657	0.058	3.592	25.3
05	1	4.382	0.045	10.382	77.3	1	1.285	0.025	3.045	22.7
06	1	0.629	0.008	5.933	81.1	1	0.147	0.003	1.387	18.9
07	1	5.081	0.074	10.331	80.3	1	1.250	0.053	2.542	19.7
08	3	0.763	0.011	2.908	41.0	3	1.098	0.034	4.186	59.0
09	3	0.246	0.091	1.597	55.1	3	0.200	0.046	1.303	44.9
10	1	2.892	0.019	2.184	75.6	1	0.932	0.019	0.704	24.4
11	3	1.750	0.036	2.728	71.3	3	0.704	0.020	1.097	28.7
12	12	0.914	0.185	1.967	66.6	12	0.458	0.095	0.986	33.4
13	3	0.012	0.003	0.034	79.4	1	0.003	0.001	0.009	20.6
14	1	0.524	0.001	1.784	73.7	1	0.187	0.010	0.638	26.3
15	14	0.034	0.002	0.094	56.7	5	0.026	0.007	0.072	43.3
16	58	0.697	0.009	1.896	89.0	30	0.086	0.011	0.234	11.0
17 Coast	2	0.803	0.040	4.800	84.0	2	0.153	0.045	0.912	16.0
17 Dry	25	1.699	0.054	2.983	77.2	17	0.503	0.094	0.883	22.8
18 Dry	11	1.197	0.298	2.995	74.9	10	0.401	0.063	1.004	25.1

The total lateral carbon flux to coastal systems is represented by multiple rivers for coastal regions of the United States, including the Atlantic Coast, Pacific Coast, Gulf Coast, and Great Lakes (HUCs 01, 02, 03, 04, 12, 17 Coast, and 18). It is important to note that this estimate does not represent the total movement of carbon from terrestrial systems into aquatic systems, but the final flux of carbon beyond the conterminous United States. The three rivers (the Red, Souris, and Rainy Rivers) representing HUC 09 drain northward into Canada, whereas the three rivers that represent HUC 11 (the White, Arkansas, and Red Rivers) drain into HUC 08. HUC 16 is unusual in that it is an endorheic basin, so we summed the total fluxes of data from eight major rivers (the Bear, Humboldt, Provo, Quinn, Sevier, Truckee, Walker, and Weber Rivers) that originated and terminated within this region.

For several HUCs, the representation of major riverine export was less straightforward. For example, because this study is interested in comparison of precipitation, soil organic carbon (SOC), and NEP from within HUCs, we chose to represent the carbon flux for HUC 08 with 22 rivers that originated within that region. Therefore, the carbon flux value for HUC 08 does not include the main stem Mississippi River flux where its drains into the Gulf Coast. This main stem flux was excluded from HUC 08 because it represented carbon export from the headwaters in HUC 07, along with input from tributaries in HUC 05 and HUC 06.

In the western United States, the riverine carbon flux value for the Columbia River as it exits HUC 17 Dry (site 14105700; Columbia River the Dalles, OR) was adjusted by subtracting off the carbon influx from Canada (site 12400520; Columbia River at Northport, WA). We also adjusted the HUC 17 Coast flux value so that the Columbia River component of HUC 17 Coast flux is its terminus (site 14246900; Columbia River at Beaver Army Terminal near Quincy, OR) minus the input from HUC 17 Dry (site 14105700; Columbia River the Dalles, OR). We added in the carbon flux for the Willamette River as well as the carbon fluxes for 23 smaller rivers that originated within HUC 17 Coast.

HUC 14 is represented by fluxes from the Colorado River (site 09180500; Colorado River near Cisco, UT) plus two major tributaries, the Green River (site 09315000; Green River at Green River, UT) and the San Juan River (site 09379500; San Juan River near Bluff, UT). HUC 15 is represented by the flux on the Colorado River below Hoover Dam (site 09421500; Colorado River below Hoover Dam, AZ/NV) minus the flux from HUC 14 (site 09380000; Colorado River at Lees Ferry, AZ) plus the Gila River (site 09518000; Gila River above Diversions at Gillespie Dam, AZ), one of the major tributaries in the region. We did not use the most downstream site on the Colorado River (site 09522000; Colorado River at Northern International Boundary, above Morelos Dam, AZ) because of the major flow diversions that occurred upstream from that location.

We summed the observed mean carbon export from all sites within HUCs and then corrected for the drainage area and discharge known to be missing from our database for each HUC. The values for A_TOT/A_IN used in the DIC correction ranged from 0.6 to 3.8. Because of a more limited TOC concentration dataset, the maximum for total organic carbon (TOC) reached 5.9. For missing exorheic drainage area, the total carbon export estimate (Total EC) was calculated as:

$${\text{Total}\hspace{0.17em}\text{E}}_{\text{C}}={\text{E}}_{\text{C}\left(\text{IN}\right)}\mathrm{\times }\left({\text{A}}_{\text{TOT}}/{\text{A}}_{\text{IN}}\right),$$ [S3]

where E_C(IN) is the carbon export estimated from sites included in our database, A_TOT is the total exorheic drainage area for rivers draining the conterminous United States, and A_IN is the total drainage area in our dataset. This correction assumes an equivalent watershed carbon yield from the remaining (unmeasured) exorheic drainage area.

Carbon concentration and flow data to estimate longitudinal carbon fluxes were obtained from the NWIS (waterdata.usgs.gov/nwis/). Carbon fluxes (kilograms per day) were estimated from water quality and daily stream flow data, using the USGS Load Estimator Model (LOADEST) (55, 71). Half of the TOC concentrations represent values taken directly from the NWIS (p00680), and half were calculated as the sum of dissolved (p00681) and particulate OC (p00689). We calculated inorganic carbon concentration from pH, temperature, and either filtered or unfiltered alkalinity (34). LOADEST is a multiple regression adjusted maximum likelihood estimation model that uses measured concentration values to calibrate a regression between constituent flux and stream flow. Input data were log-transformed to avoid bias and centered to avoid multicollinearity. Mean flux estimates (teragrams per year) with SEs were used to develop 95% confidence intervals. Carbon yields (gC per meter per year) were calculated by dividing mean fluxes by drainage area.

DOC concentrations were taken directly from water quality data, but DIC concentrations were estimated from pH, temperature, and either filtered or unfiltered alkalinity (34). [CO₂]_aq was not included in the lateral flux calculation because it comprised a small portion of the DIC and because [CO₂]_aq is an ephemeral portion of the DIC pool, which is likely to reach atmospheric equilibrium as rivers reach coastal boundaries. This decision had a minimal effect on the DIC fluxes at the large scales presented in this paper because median molar [CO₂]_aq/DIC was 5.8% for all rivers included in lateral flux estimates and rivers; where [CO₂]_aq/DIC was higher tended to be smaller rivers with low overall DIC concentrations, and therefore small DIC lateral flux. The DIC calculations assumed that carbonate and bicarbonate ions comprised nearly all of the species contributing to alkalinity, as opposed to other potential contributions from particulate inorganic carbon or organic acids. Paired measurements of OC, alkalinity, and pH were inconsistent in our dataset; thus, to estimate organic acid contribution to alkalinity, we assumed that 10% of the natural OC contained organic acid anions (72). We multiplied mean OC concentration by 10% to arrive at an approximate estimate of organic acid concentration and compared this value with the mean reported alkalinity. For all sites with both OC and DIC estimates, we determined that organic acid contribution to alkalinity was small, <1.5% of the estimated alkalinity measurement.

We compare our study’s method for estimates of longitudinal flux for HUC 08 with an estimate that can be obtained by summing fluxes from HUCs 05, 07, 08, 10, and 11. This method produces an average total flux of 17 TgC⋅y⁻¹, where 13.2 TgC is DIC. This rate of DIC export is very close to the 13.5 Tg of DIC per year presented by Cai et al. (73); however, these estimates are well below a recent synthesis that presents a total of 22.5 TgC⋅y⁻¹ with 17.4 TgC as DIC (34).

OC Burial in Lakes and Reservoirs.

Methods for calculating OC burial in lakes and reservoirs of the CONUS are described by Clow et al. (35), and results are presented in Table S4; a brief summary is provided here. OC burial was estimated for each water body in the CONUS using the following equation:

$${\text{OC}}_{\text{burial}}\left(\text{TgC}\cdot {\text{y}}^{-1}\right)=\left[{\text{WB}}_{\text{area}}\left({\text{m}}^2\right)\times \text{SedRt}\left(\text{g}\cdot {\text{m}}^{-2}\cdot {\text{y}}^{-1}\right)\times {\text{OC}}_{\text{conc}}\left(\text{\%}\right)/100\times \text{BE}\left(\text{\%}\right)/100\right]{\times 10}^{-12},$$ [S4]

where OC_burial is the OC burial rate, WB_area is water body area, SedRt is sedimentation rate, OC_conc is OC concentration in sediments (percentage by dry weight), BE is burial efficiency, and 10⁻¹² is a conversion factor from grams to teragrams (35).

Table S4.

Lake and reservoir OC burial by two-digit HUC

Two-digit HUC	Lake area, km2	Lake/reservoir sedimentation flux, TgC⋅y−1
01	6,006	0.5 (0.3–0.9)
02	3,903	0.4 (0.2–1)
03	15,828	3.1 (1.2–11.7)
04	7,798	0.6 (0.3–1.5)
05	3,432	0.5 (0.3–0.9)
06	2,679	0.4 (0.2–0.6)
07	11,081	0.9 (0.5–2.2)
08	10,778	5.4 (1.3–25.4)
09	7,336	0.4 (0.1–1)
10	15,196	1.8 (1–3.6)
11	8,357	1.2 (0.7–2.9)
12	8,793	1.9 (0.8–7.1)
13	1,076	0.2 (0.1–0.3)
14	1,782	0.3 (0.2–0.5)
15	1,377	0.3 (0.2–0.5)
16	7,960	0.6 (0.3–1.3)
17 Coast	1,133	0.2 (0.1–0.4)
17 Dry	6,159	1 (0.7–1.5)
18 Dry	5,951	0.9 (0.5–1.8)
Total	126,793	20.6 (9–65.1)

Lake surface area was determined by the NHD by HUC. Total carbon flux is calculated according to Huang et al. (37). Errors in parentheses represent the range of 1 SD from the mean. Sedimentation is considered a negative flux.

Similar to the methods used to calculate lake efflux, water body areas were derived from the high-resolution (1:24,000) USGS NHD (nhd.usgs.gov/). Water bodies were classified as either reservoirs or lakes/ponds based on geocoding in the NHD (35).

Sedimentation rates for reservoirs were calculated from repeat bathymetric surveys for 1,771 reservoirs in the national Reservoir Sedimentation Database [water.usgs.gov/osw/ressed/index.html (74, 75)]. Reservoir sedimentation rates were regressed against basin characteristics, including land use, vegetation, soils, hypsography, and climate, using a stepwise multiple linear regression (MLR) approach (35). The resulting MLR equation was used to estimate sedimentation rates for all reservoirs in the CONUS. To estimate uncertainty in impoundment sedimentation rates, a Monte Carlo simulation was performed in which model coefficients were allowed to vary randomly within the bounds of the associated 95% confidence interval; this operation was repeated for 1,000 iterations, yielding 100 estimates of the sedimentation rate in each impoundment.

Sediment OC concentrations in reservoirs were estimated using a similar geostatistical approach. A generalized linear model was built using sediment OC data collected during the 2007 NLA (35); these data were regressed against the same explanatory variables as in the reservoir sedimentation rate analysis, except that water body type was added as a categorical variable; the resulting predictive equation was applied to all reservoirs in the CONUS (35).

Sedimentation rates and sediment OC concentrations in lakes/ponds were compiled from peer-reviewed literature, and included sites from across the CONUS that spanned a range in land use and trophic conditions (35). OC burial rates at these sites were regressed against landscape and climate characteristics, as in the reservoir sedimentation rate analysis, to develop a predictive equation that was applied to lakes/ponds across the CONUS (35).

TBM Data Processing.

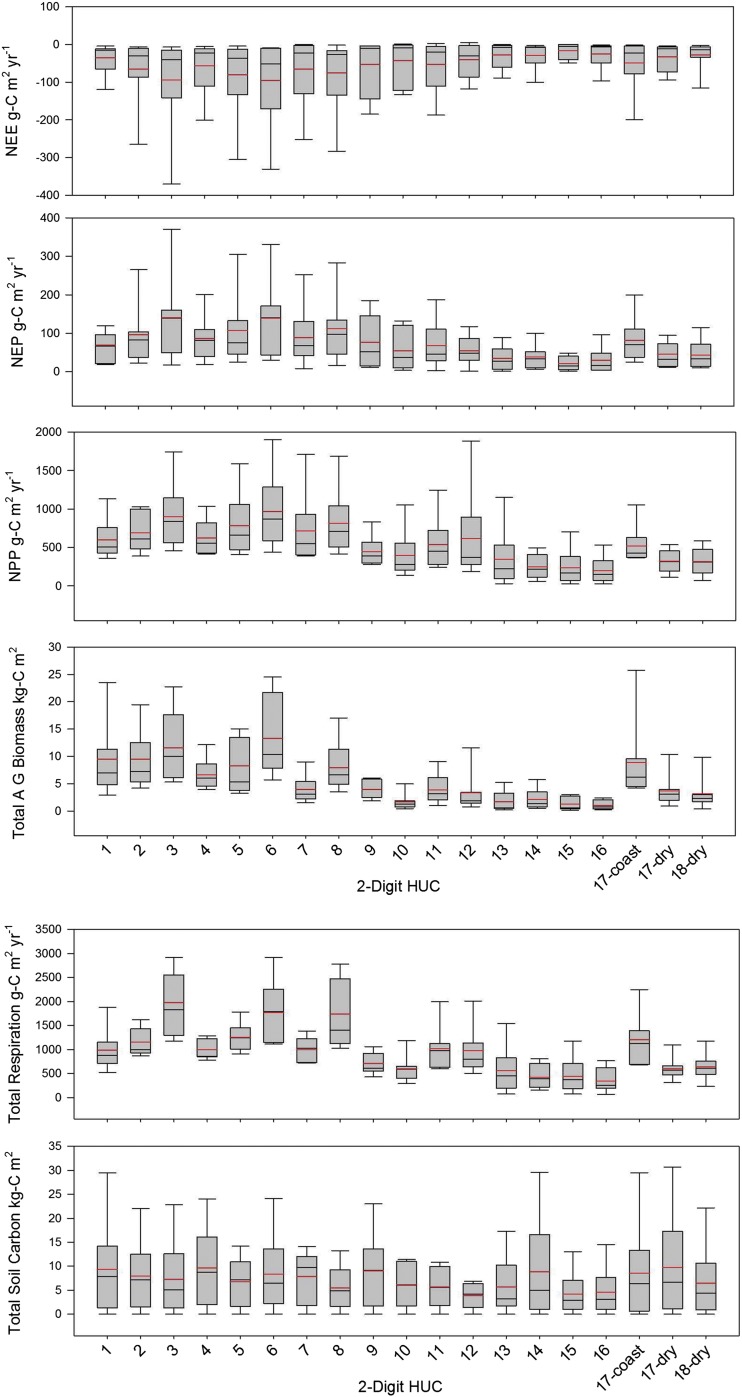
All model data for this effort are available as NetCDF files from (MsTMIP; nacp.ornl.gov/mstmipdata/). The 0.25° gridded monthly estimates for each model output parameter (NEE in gC per square meter per year, NEP in gC per square meter per year, NPP in gC per square meter per year, total live biomass in kilograms of carbon per square meter, total respiration in gC per square meter per year, and total soil carbon in kilograms of carbon per square meter) within Fig. S1 were annualized for years 1990–2010. Average annual estimates were then calculated for each of the two-digit HUCs and aggregated by modified two-digit HUCs presented in Fig. 1. Averages were calculated for each of six models: the Biome-BGC (36), the CLASS-CTEM-N (37), the CLM4 (38), the CLM4-VIC (39), the DLEM (40), and the ISAM and TRIPLEX-GHG (41). All model averages for the period 1990–2010 were then averaged into an ensemble mean across each of the HUCS and used within the study for comparison with aquatic systems. The average and SDs were calculated for all individual model means, whereas the average, SD, and minimum and maximum values were calculated for the ensemble and are presented in Fig. S2 and presented in Table S5.

Fig. 1.

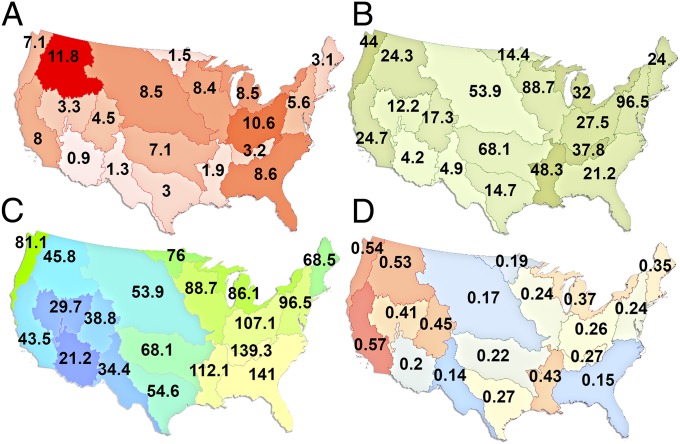
(A) Total aquatic carbon flux measured in TgC per year by modified two-digit HUCs. (B) Normalized aquatic carbon yields in gC per square meter per year per area of each HUC using Eq. 2. (C) Average NEP gC per square meter per year for the years 1990–2010 derived from the MsTMIP model outputs. (D) Maximum potential fraction of NEP accounted for by aquatic carbon if all aquatic carbon is derived from terrestrial sources [does not include (f_a) from Eq. 2] represented as in B and C. Uncertainty ranges are presented in Table S5.

Fig. S2.

Box plots by two-digit HUCs for the MsTMIP model ensemble terrestrial carbon stocks and flux estimates. Boxes represent the 25th and 75th percentiles, black lines represent the median, red lines represent the mean, and whiskers represent the 10th and 90th percentiles.

Table S5.

Summarized carbon fluxes and yields for each two-digit HUC within the conterminous United States (fifth and 95th percentiles in parentheses) and summarized mean NEP calculated from the MsTMIP terrestrial biogeochemistry model (SDs in parentheses)

Two-digit HUC	Carbon yield, gC⋅m2⋅y−1 (Eq. 2)	MsTMIP NEP, gC⋅m−2⋅y−1	Maximum potential NEP, % (Eq. 2)	NPP AVG, gC⋅m2⋅y−1	Total biomass, kgC⋅m2	Total respiration, gC⋅m−2⋅y−1
01	24 (16.5–33)	68.5 (48.4)	35.0	599 (134.6)	9.5 (2.7)	982 (270.8)
02	23.2 (15.1–33.5)	96.5 (97.3)	24.0	689.8 (286)	9.5 (4.5)	1,158.8 (461.5)
03	21.2 (15.5–28.2)	141 (125.8)	15.0	903.3 (355)	11.5 (5.7)	1,977 (640.6)
04	32 (28.2–36.4)	86.1 (75)	37.1	623.6 (264.8)	6.6 (4.6)	996.7 (376.2)
05	27.5 (20.9–35.3)	107.1 (97.5)	25.7	782.8 (307.4)	8.3 (4.7)	1,253.6 (381.9)
06	37.8 (21.7–56.6)	139.3 (134)	27.1	966.4 (246.5)	13.3 (4.7)	1,765.8 (408.2)
07	20.8 (17.5–25)	88.7 (94)	23.5	713.4 (296.1)	3.9 (3.7)	996.5 (327.3)
08	48.3 (38.4–61.3)	112.1 (132.7)	43.1	812.8 (240.8)	7.9 (6)	1,734.9 (586.9)
09	14.4 (7.6–24.2)	76 (73)	18.9	446.2 (219.3)	3.9 (4.8)	705.6 (360.7)
10	9.1 (7–12)	53.9 (73.5)	17.0	395.7 (240.5)	1.7 (2.2)	598.8 (328.8)
11	14.8 (10.7–19.6)	68.1 (108.2)	21.7	539.2 (258.4)	3.9 (4.6)	1,013.7 (540.2)
12	14.7 (10.6–20.5)	54.6 (111.5)	26.9	615.4 (375.2)	3.3 (4.2)	974.9 (626.3)
13	4.9 (2.5–7.6)	34.4 (64.7)	14.2	346.1 (194.4)	1.7 (1.7)	560.3 (229.9)
14	17.3 (10.2–26.2)	38.8 (51.9)	44.5	250.8 (141.3)	2.1 (2.2)	424.7 (211.8)
15	4.2 (2.4–6.5)	21.2 (57.5)	19.6	239.1 (137.1)	1.3 (1.2)	439.9 (211.3)
16	12.2 (7.6–18)	29.7 (50.4)	41.0	200.7 (109.7)	1 (1.1)	347.5 (169.9)
17 Coast	44 (26.4–63.3)	81.8 (57)	53.8	521.6 (159.9)	8.9 (3.1)	1,202.9 (346)
17 Dry	24.3 (14.9–35.3)	45.8 (56.3)	53.1	322 (166.3)	3.7 (3.2)	595.9 (299.2)
18 Dry	24.7 (14.4–36.4)	43.5 (66.4)	56.8	319.2 (229)	3.2 (3.2)	643.5 (432.7)
Average	18.8 (13.8–24.8)	70.0 (84.0)	26.8	522.2 (242.6)	4.7 (3.5)	925.4 (391.6)

Maximum potential NEP is the calculated potential contribution of aquatic systems to the NEP term when not accounted for in terrestrial carbon models using Eq. 2 and without (f_a). Maximum potential NEP is the hypothetical maximum reduction of NEP that would occur if all carbon in aquatic systems is derived from terrestrial sources and is unaccounted for in a regional carbon balance. Average yields are all calculated weighted by area. AVG, average; kgC, kilograms of carbon.

Results and Discussion

Total Carbon Fluxes.

The total flux of freshwater carbon from the conterminous United States is 106 (range: 71.4–148.9) TgC⋅y⁻¹ (Table 1) as calculated by Eq. 1. Aggregated to the conterminous United States, the atmospheric flux of CO₂ from streams and rivers represents 65.4% of the total positive flux of inland water carbon at 69.3 (range: 36–109.6) TgC⋅y⁻¹ (Table 1). This estimate for stream efflux is 27.7% lower than a previous estimate of 97 TgC⋅y⁻¹ (32). The difference between the water surface emissions presented here and in the study by Butman and Raymond (32) is predominantly due to modifications in the modeling related to estimating the total surface areas of streams and rivers and the gas transfer velocity coefficient across the air–water interface (33). In particular, the gas transfer velocity was not allowed to exceed 30 m⋅d⁻¹, derived from new hydraulic geometry coefficients (Table S1), and this restriction affected the magnitude of fluxes in small-order streams in steep topography (SI Materials and Methods).

Table 1.

Total carbon fluxes by two-digit HUCs across the conterminous United States using Eq. 1

Two-digit HUC	Stream efflux, TgC⋅y−1	Total lateral flux, TgC⋅y−1	Lake efflux, TgC⋅y−1	Lake burial, TgC⋅y−1	Total aquatic carbon, TgC⋅y−1	Carbon yield, gC⋅m2⋅y−1 (Eq. 1)	Carbon yield gC⋅m2⋅y−1 (Eq. 2)
01	1.8 (0.9–2.9)	1.1 (1–1.2)	0.7 (0.5–0.9)	0.5 (0.3–0.9)	3.1 (2–4.4)	18.1 (11.8–25.9)	24 (16.5–33)
02	3.6 (1.8–5.7)	1.9 (1.8–2)	0.6 (0.3–1.1)	0.4 (0.2–1)	5.6 (3.6–8.3)	20.3 (13–29.9)	23.2 (15.1–33.5)
03	5.5 (2.8–8.8)	3.7 (3.4–4)	2.5 (1.6–3.7)	3.1 (1.2–11.7)	8.6 (4.8–13.3)	12.3 (6.9–19.1)	21.2 (15.5–28.2)
04	1.5 (0.8–2.3)	6.6 (6.5–6.6)	1.1 (0.8–1.5)	0.6 (0.3–1.5)	8.5 (7.6–9.7)	28 (25–31.8)	32 (28.2–36.4)
05	5 (2.5–8)	5.7 (5.6–5.7)	0.4 (0.3–0.6)	0.5 (0.3–0.9)	10.6 (8–13.7)	25.1 (19–32.5)	27.5 (20.9–35.3)
06	2.6 (1.3–4.2)	0.8 (0.7–0.7)	0.2 (0–0.6)	0.4 (0.2–0.6)	3.2 (1.7–5)	30.2 (16–47.2)	37.8 (21.7–56.6)
07	2.3 (1.2–3.7)	6.3 (6.2–6.5)	0.7 (0.4–1.1)	0.9 (0.5–2.2)	8.4 (7–10.3)	17.2 (14.2–20.9)	20.8 (17.5–25)
08	3.1 (1.6–5.1)	1.9 (1.9–1.9)	2.3 (1.5–3.4)	5.4 (1.3–25.4)	1.9 (−0.1 to 4.7)	7.2 (−0.4 to 17.9)	48.3 (38.4–61.3)
09	0.3 (0.1–0.5)	0.4 (0.4–0.5)	1.1 (0.6–2.1)	0.4 (0.1–1)	1.5 (1–2.4)	9.3 (6.4–15.3)	14.4 (7.6–24.2)
10	5.3 (2.8–8.5)	3.8 (3.8–3.9)	1.2 (1–1.5)	1.8 (1–3.6)	8.5 (6–11.9)	6.4 (4.5–9)	9.1 (7–12)
11	4 (2.1–6.4)	2.5 (2.4–2.5)	1.8 (1.4–2.3)	1.2 (0.7–2.9)	7.1 (4.9–9.8)	11.1 (7.6–15.3)	14.8 (10.7–19.6)
12	1.5 (0.8–2.4)	1.4 (1.1–1.7)	2 (1.3–3.3)	1.9 (0.8–7.1)	3 (1.5–5.3)	6.5 (3.2–11.4)	14.7 (10.6–20.5)
13	1.4 (0.7–2.2)	0 (0–0)	0.1 (0–0.3)	0.2 (0.1–0.3)	1.3 (0.5–2.3)	3.8 (1.4–6.5)	4.9 (2.5–7.6)
14	4 (2–6.5)	0.7 (0.7–0.7)	0.1 (0–0.2)	0.3 (0.2–0.5)	4.5 (2.4–7.1)	15.3 (8.2–24.2)	17.3 (10.2–26.2)
15	1.1 (0.6–1.8)	0.1 (0–0)	0.1 (0.1–0.2)	0.3 (0.2–0.5)	0.9 (0.5–1.6)	2.5 (1.4–4.3)	4.2 (2.4–6.5)
16	2.6 (1.3–4.3)	0.8 (0.8–0.8)	0.5 (0.2–0.8)	0.6 (0.3–1.3)	3.3 (1.8–5.2)	8.9 (4.9–14.2)	12.2 (7.6–18)
17 Coast	6.3 (3.4–9.6)	1 (0.9–1)	0.02 (0–0.04)	0.2 (0.1–0.4)	7.1 (4.1–10.4)	41.6 (24-60.9)	44 (26.4–63.3)
17 Dry	10.5 (5.7–16.2)	2.2 (2–2.4)	0.1 (0–0.3)	1 (0.7–1.5)	11.8 (6.9–17.7)	20.8 (12.1–31.1)	24.3 (14.9–35.3)
18 Dry	6.8 (3.6–10.5)	1.6 (1.2–2)	0.4 (0.1–0.9)	0.9 (0.5–1.8)	8 (4.1–12.4)	20.1 (10.4–31.3)	24.7 (14.4–36.4)
Total	69.3 (36–109.6)	41.5 (39.4–43.5)*	16 (14.3–18.7)	20.6 (9–65.1)	106.2 (71.4–148.9)	13.5 (9.1–19)	18.8 (13.8–24.8)

Values in parentheses represent error terms; fifth and 95th percentiles for both lake and stream efflux; SE associated with DIC, DOC, and total lateral fluxes; and the SD for the burial of OC. Lateral fluxes represent the net fluxes at the most downstream point within each contiguous HUC. Total aquatic carbon flux errors represent the ± sum of all presented error terms. Carbon yield is expressed on a per unit area of the two-digit HUC.

^*Total lateral flux represents only those HUCS that drain off of the land mass into coastal oceans and the Great Lakes, and exclude HUC 16, the Great Basin.

The total lateral flux, representing only the export of carbon to coastal systems, is 41.5 (39.4–43.5) TgC⋅y⁻¹. This estimate is similar to past research, which suggests a lateral export of 41–49 TgC⋅y⁻¹ developed from USGS gaging station discharge and water quality data (34). The dominant component of the lateral flux is dissolved inorganic carbon (DIC) at ∼70% of the total flux, whereas the remaining 30% of the total flux is dissolved organic carbon (DOC), which aligns with previous large-scale flux estimates (14, 34) (Table S2). In this effort, the methods to calculate both the CO₂ emission and the lateral export of DIC use the same underlying dataset on alkalinity, temperature, and pH to calculate inorganic carbon in freshwaters. CO₂ uptake in terrestrial soils by mineral weathering contributes to the total DIC in inland waters. However, degassing of inorganic carbon to the atmosphere is determined by the concentrations of H₂CO₃ and dissolved CO₂ in surface waters.

Total CO₂ efflux from lake surfaces is 16 (range: 14.3–18.7) TgC⋅y⁻¹, whereas TOC burial is 20.6 (range: 9.0–65.1) TgC⋅y⁻¹. Aggregated at the national scale, lakes and reservoirs accumulate carbon through sedimentation in equal proportion to the release of carbon across the air–water interface. However, the level of uncertainty associated with the burial of OC and emission of CO₂ from lakes and reservoirs highlights a gap in our understanding of the processes involved, and reinforces that these numbers are best estimates from existing data (35).

Identifying appropriate terrestrial modeling products to evaluate against the cycling of aquatic carbon remains difficult. Here, we have included a subset of the MsTMIP model intercomparison efforts to look at the potential relationships between NEE in grams of carbon (gC) per square meter per year, NEP in gC per square meter per year, NPP in gC per square meter per year, total live biomass in kilograms of carbon per square meter, total respiration in gC per square meter per year, total soil carbon in kilograms of carbon per square meter, and the fluxes of carbon in inland waters. Here, we have averaged for the period 1990–2010 only the results of the Biome-Biogeochemical Model (BGC) (36), the Canadian Land Surface Scheme and Canadian Terrestrial Ecosystem Model (CLASS-CTEM^N+) (37), the Community Land Model (CLM4) (38), the CLM4-Variable Infiltration Capacity (VIC) (39), the Dynamic Land Ecosystem Model (DLEM) (40), and the Integrated Science Assessment Model (ISAM) and TRIPLEX-GHG (41), given the data availability through Oak Ridge National Laboratory (42, 43). These data only include the scenarios that allowed for land use change to occur and for nitrogen deposition. This scenario was chosen to represent the model ensemble averages for the best estimate of carbon stocks and flows under naturally varying conditions.

Average annual NEP for the conterminous United States was 70.0 (SD = 84.0) gC⋅m⁻²⋅y⁻¹. NEP varies across HUCs from a low of 21.2 (SD = 1.0) gC⋅m⁻²⋅y⁻¹ in HUC 15, representing the desert southwest, to a high of 141.0 (SD = 12.6) gC⋅m⁻²⋅y⁻¹ in HUC 03, dominated by the productive and dense forests of the southeastern United States (Fig. 1C). Additional results of the aggregation of the TBM outputs are presented in Fig. S2.

Regional Variability of Aquatic Carbon Fluxes.

There is significant variability across each of the 19 HUCs for all of the inland water carbon fluxes. Total carbon fluxes ranged from 0.9 (range: 0.5–1.6) TgC⋅y⁻¹ in HUC 15, the southern portion of the arid Colorado River Basin, to 11.8 (range: 6.9–17.7) TgC⋅y⁻¹ in the eastern portion of HUC 17 inclusive of the Columbia River (Fig. 1A and Table 1). Previous work has suggested stream and river efflux is the dominant flux of carbon from freshwater ecosystems at the national scale (14, 32), but that finding is not uniform across all regions presented here (Table 1). HUCs 04, 05, 07, 08, 09, and 12 were dominated by either the lateral export of carbon (4, 5, 7) or the efflux of carbon from lake surfaces (9, 12). Estimates for the burial of carbon in lake sediments for HUC 08 are 5.4 TgC⋅y⁻¹, and represent the dominant removal and storage term for aquatic carbon.

The gaseous evasion of CO₂ from streams and rivers ranged from 0.3 (range: 0.1–0.5) TgC⋅y⁻¹ in HUC 09 to 10.5 (range: 5.7–16.2) TgC⋅y⁻¹ in HUC 17 Dry (Table 1). Stream and river efflux dominated those regions where there are high slopes (the western United States inclusive), and where there existed a combination of moderate alkalinity, lower pH, and high estimated water velocity. Water velocity is an important variable for the modeling of gas transfer coefficients (SI Materials and Methods), and is a function of both high slopes (HUCs 13, 14, 15, 16, and 17 Dry) or high precipitation (HUCs 02, 03, and 17 Coast).

Lateral fluxes of inorganic carbon and OC varied significantly across regions as well. Total DIC fluxes were largest from HUC 04 [4.9 (range: 4.9–4.9) TgC⋅y⁻¹], HUC 05 [4.4 (range: 4.3–4.4) TgC⋅y⁻¹], and HUC 07 [5.1 (range: 5.0–5.2) TgC⋅y⁻¹] (Table S2). This large inorganic carbon flux has been attributed to agricultural practices in the upper midwestern United States contributing bicarbonate, as well as weathering interactions within soils derived from underlying carbonate bedrock (34, 44). In our flux estimates, DIC was calculated from alkalinity and pH, and it was dominated by HCO₃⁻ and CO₃⁻². These ions are formed through weathering reactions in the soil, with as much as 36% originating from geological sources through carbonate weathering (45). These weathering reactions do not represent the rapid transit of atmospheric CO₂ into inland waters and require further investigation to account correctly for the temporal imbalance involved with the use of total DIC from terrestrial sources when compared with the cycling of carbon in terrestrial systems over decades and not millennia. In general, DIC exports were three- to fivefold greater than OC in the upper Midwest. OC dominated the lateral carbon fluxes from HUCs 01, 03, and 08 only. These high organic carbon fluxes are predominantly the result of significantly higher average concentrations of TOC. However, the proportion of wetlands within these HUCs was relatively high at 8%, 18%, and 20%, respectively, providing a large DOC source. There is strong correlation between weighted TOC yields and the proportion of wetlands within a region (r² = 0.5, P < 0.01).

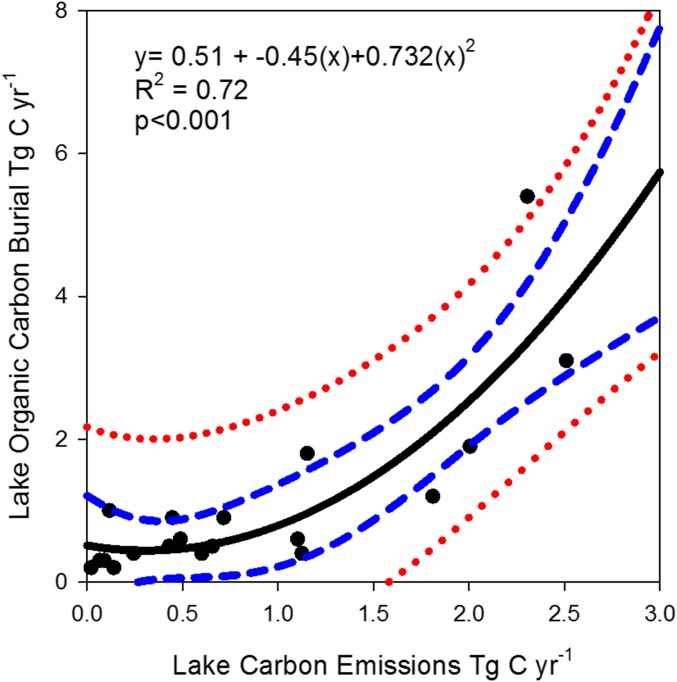
Because of human activities, including agriculture and dam construction, sediment transport and burial in reservoirs and lakes has been assumed in the past to comprise a large component of the aquatic carbon budget (46). At the national scale, CO₂ emission from the water surfaces and burial in lakes and reservoirs is correlated (r² = 0.73, P < 0.001; Fig. S3 and Tables S3 and S4), but the residuals of the relationship reveal some distinct geographic trends. Overall, burial exceeds lake emissions by 28% and is nonlinear, where proportionally more burial takes place as lake emissions increase. However, this estimate is driven by the imbalance presented in HUC 08, where burial is more than double CO₂ emission. Carbon burial in lakes, ponds, and reservoirs correlates with the presence of wetlands. This drives the high carbon burial rates within HUC 08 (35). In arid regions of the United States dominated by large river systems, including the Columbia River and Colorado River (HUCS 14, 15, 17 Dry, and 18 Dry), carbon burial exceeds CO₂ emission by up to 900%, possibly reflecting the combined effects of greater soil loss through erosion due to sparse vegetation cover and agricultural nutrient enrichment of water bodies resulting in higher levels of autochthonous primary productivity (primary productivity in aquatic environments). Conversely, lake and reservoir CO₂ emission is greater than burial in HUCs 01, 02, 09, and 11. We do not currently have a unified hypothesis as to why emissions are larger than burial across such distinctly different regions. HUC 09 is dominated by lake systems shown to be net heterotrophic in the past (23), whereas carbon burial remained a small component over short time periods.

Fig. S3.

Nonlinear correlation between the emission of CO₂ from lakes and the burial of OC across two-digit HUCs in the conterminous United States. Red lines indication the 95% prediction interval, and blue lines represent the 95% confidence interval. Error bars represent the SD about the mean.

Carbon yields, defined as the carbon flux on a per unit watershed basis within a HUC, are a useful way to examine aquatic carbon export because they help to illustrate the connectivity between the aquatic fluxes and contributing terrestrial drainage area (Fig. 1B, Table 1, and Tables S5 and S6). HUC 17 Coast, representing the western Cascade and Coastal mountain ranges in the US Pacific Northwest, has an estimated yield of 41.6 (range: 24–60.9) gC⋅m⁻²⋅y⁻¹. This high flux is dominated by high emission rates from stream and river surfaces. HUC 15 represents the lowest carbon yields at 2.5 (range: 1.4–4.3) gC⋅m⁻²⋅y⁻¹, where total inland water carbon fluxes are smallest across all components of the aquatic ecosystem.

Table S6.

Summarized TBM outputs for each two-digit HUC within the conterminous United States (SDs in parentheses)

HUC	NEP AVG, gC⋅m2⋅y−1	NPP AVG, gC⋅m2⋅y−1	Total biomass, kgC⋅m2	Total respiration, gC⋅m2⋅y−1
01	68.5 (48.4)	599 (134.6)	9.5 (2.7)	982 (270.8)
02	96.5 (97.3)	689.8 (286)	9.5 (4.5)	1,158.8 (461.5)
03	141 (125.8)	903.3 (355)	11.5 (5.7)	1,977 (640.6)
04	86.1 (75)	623.6 (264.8)	6.6 (4.6)	996.7 (376.2)
05	107.1 (97.5)	782.8 (307.4)	8.3 (4.7)	1,253.6 (381.9)
06	139.3 (134)	966.4 (246.5)	13.3 (4.7)	1,765.8 (408.2)
07	88.7 (94)	713.4 (296.1)	3.9 (3.7)	996.5 (327.3)
08	112.1 (132.7)	812.8 (240.8)	7.9 (6)	1,734.9 (586.9)
09	76 (73)	446.2 (219.3)	3.9 (4.8)	705.6 (360.7)
10	53.9 (73.5)	395.7 (240.5)	1.7 (2.2)	598.8 (328.8)
11	68.1 (108.2)	539.2 (258.4)	3.9 (4.6)	1,013.7 (540.2)
12	54.6 (111.5)	615.4 (375.2)	3.3 (4.2)	974.9 (626.3)
13	34.4 (64.7)	346.1 (194.4)	1.7 (1.7)	560.3 (229.9)
14	38.8 (51.9)	250.8 (141.3)	2.1 (2.2)	424.7 (211.8)
15	21.2 (57.5)	239.1 (137.1)	1.3 (1.2)	439.9 (211.3)
16	29.7 (50.4)	200.7 (109.7)	1 (1.1)	347.5 (169.9)
17 coast	81.8 (57)	521.6 (159.9)	8.9 (3.1)	1,202.9 (346)
17 dry	45.8 (56.3)	322 (166.3)	3.7 (3.2)	595.9 (299.2)
18 dry	43.5 (66.4)	319.2 (229)	3.2 (3.2)	643.5 (432.7)

Terrestrial and Aquatic Carbon Accounting.

There are two ways to evaluate the carbon fluxes through aquatic systems in the context of terrestrial carbon accounting depending on the goals of the analysis. As presented in Eq. 1, the end accounting of carbon represents the net balance of carbon for the conterminous United States, where carbon burial in lakes, ponds, and reservoirs is considered stored within the national boundaries. This estimate is most relevant for the total accounting of carbon at the national level when considering the various natural and anthropogenic sources and sinks over time. However, to begin developing a broad framework to account for carbon in aquatic systems that may have originated from terrestrial vs. aquatic sources, summing all of the components of Eq. 1 reveals the total carbon moving into and out of aquatic systems aggregated to these modified two-digit HUCS (Fig. 1 B–D and Table 1). In addition, some fraction of each carbon flux must be accounted for as originating from autochthonous production and respiration:

$$HUC\hspace{0.17em}Flux\hspace{0.17em}(\text{TgC}\cdot {\text{y}}^{-1})={\displaystyle \sum }_{HUC}\left[Stream\hspace{0.17em}Emission-\hspace{0.17em}\left(f_a\right)\right]+\left[Lateral\hspace{0.17em}Flux-\left(f_a\right)\right]+[Lake\hspace{0.17em}\&\hspace{0.17em}Reservoir\hspace{0.17em}Emission-\left(f_a\right)]+[Lake\hspace{0.17em}\&\hspace{0.17em}Reservoir\hspace{0.17em}burial-\left(f_a\right)].$$ [2]

The (f_a) term in each of the aquatic carbon fluxes represents a fraction of the related flux derived from autochthonous sources. In this analysis, we are unable to quantify the internal production and consumption of carbon within aquatic systems at such a large scale, but the effect of this process will reduce the overall mass of terrestrial carbon needed to support these flux estimates. Research suggests that the internal production of DOC and mineralization to CO₂ may contribute up to 28% of the total CO₂ efflux in rivers (18). However, the origin of that DOC is not quantified, suggesting that this DOC could remain a source from terrestrial carbon. Supersaturation in lakes across the conterminous United States has been shown to be supported by riverine DIC inputs; however, research is still unable to attribute the source of this inorganic carbon spatially (19). To our knowledge, there do not exist large-scale attempts to identify (f_a) that would be relevant for the accounting of carbon within the conterminous United States, which represents a significant knowledge gap requiring future research (an expanded discussion on autochthonous inputs and model spatial scales is provided in SI Materials and Methods). The net effect of autochthonous production for the attribution of total carbon fluxes will reduce the importance of terrestrial inputs by an unknown quantity.

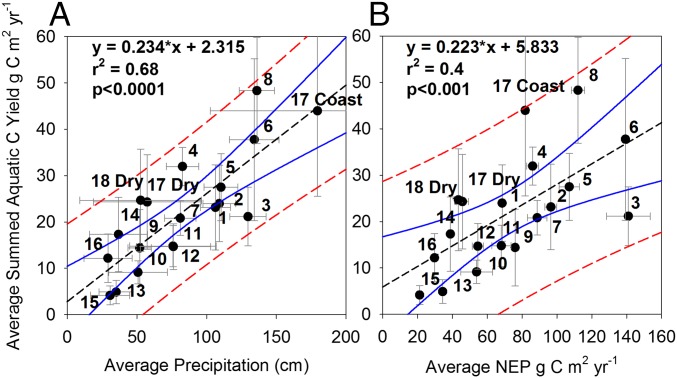
A strong correlation exists between the total aquatic carbon yields calculated using Eq. 2 and average annual precipitation (r² = 0.68, P < 0.001; Fig. 2A). This correlation suggests that areas with high rates of water throughput, and available water storage in soils, have higher rates of carbon export into aquatic environments. Precipitation is emerging as a driver of many components that comprise the carbon chemistry in freshwaters (14, 32, 47). In contrast to previous work, we show that this relationship is maintained across regions where the lateral export of carbon or the surface evasion of carbon is dominant. These findings show that broad climatic patterns influence the movement of carbon across the terrestrial–aquatic interface and can provide insight into how aquatic carbon cycling can be integrated into a modeling framework.

Fig. 2.

Correlation between the summed aquatic carbon yield (Eq. 2) and average annual precipitation (PRISM Climate Group, Oregon State University; prism.oregonstate.edu) (A) and NEP (MsTMIP model ensemble mean) (B) by HUC. Points are labeled by HUC. Red lines indicate the 95% prediction interval, and the blue lines represent the 95% confidence interval. Error bars represent the SD about the mean.

Estimated freshwater carbon yields also correlate strongly with terrestrial NEP across the United States (r² = 0.4, P < 0.01; Fig. 2B) as well as terrestrial NPP (r² = 0.35, P < 0.01), total above-ground biomass (r² = 0.49, P < 0.01), and total respiration (r² = 0.45 P < 0.01) (data presented in Table S6). There was not a significant correlation between total soil carbon and total aquatic carbon yields. This last point is surprising because we hypothesize that landscapes with higher soil carbon stores will offer an opportunity for additional inorganic carbon and OC to be mobilized into aquatic environments. Given the strong correlation between aquatic carbon yields and precipitation, the relationship between terrestrial NEP and aquatic carbon yield is to be expected because precipitation is a significant variable that determines the turnover and processing of carbon within each of the models. Precipitation is a primary driver that determines the presence and form of above-ground biomass over time, as well as many of the surface energy balance terms (42). These relationships also support the intuitive notion that systems having high rates of carbon processing and larger estimates of NEP potentially have more carbon available for mobilization into the aquatic system (48). The finding that total soil carbon did not correlate with aquatic carbon yield may indicate that the rates of processing of carbon are more influential on aquatic ecosystems, and not on the long-term standing stock of carbon for the conterminous United States.

By comparing summed regional aquatic carbon fluxes with the MsTMIP model output, where each model produces only an estimate for terrestrial carbon sources and sinks, we can assess the maximum potential proportion of NEP that is offset by the removal of carbon through streams, rivers, lakes, and reservoirs. For this analysis, we consider aquatic carbon fluxes and burial to be a removal of terrestrial carbon only across each of the two-digit HUCs. The inability to assess (f_a) from Eq. 2 biases these estimates high. At the national scale, a maximum of 26.8% of the estimated net uptake of carbon in terrestrial ecosystems may be offset by the inclusion of freshwater carbon cycling (Tables S5 and S6), calculated as the ratio of the average carbon yield from Eq. 2 (Fig. 1B) to the average terrestrial NEP from the MsTMIP output (Fig. 1C). There are significant regional differences in the relative importance of freshwater systems to terrestrial carbon accounting. Our analysis indicates that in the Pacific Northwest, between 53% and 56.8% of the total NEP in region 17 could potentially be redirected to freshwater ecosystems, and returned to the atmosphere through remineralization and respiration (reduced NEP) or deposited in coastal and ocean environments (net sink) (Fig. 1D and Table S5). These estimates are potentially biased high due to poorly constrained estimates of the surface gas transfer velocities in streams within steep topography (49). HUC 03 represents the smallest differential between the positive aquatic carbon flux and the terrestrial sink of carbon (15%). This small ratio is driven by the high rate of NEP in the southeastern United States, 141 (SD = 125.8) gC⋅m⁻²⋅y⁻¹ (Fig. 1C). These potential reductions in the net terrestrial sink of carbon would reduce regional estimates of the efficiency of managed forested and agricultural ecosystems as a means to reduce greenhouse gas emissions. However, further work is needed to partition the contribution of internal production of inorganic carbon and OC (f_a) within inland waters spatially to constrain the linkages across terrestrial and aquatic ecosystems better (18).

Reconciling Carbon Budgets Across Ecosystems: Future Needs.

For larger scale studies, the extent to which aquatic carbon cycling is included in carbon budgets depends upon the accounting methods used. Atmospheric inversion modeling includes the degassing of CO₂ from water surfaces within the model domain, and eddy covariance measurements capture emissions from water surfaces within the tower footprint; however, lateral fluxes are missed. Inventory-based methods of calculating NEP, designed to measure the accumulation of carbon in soils and biomass physically at the scale relevant for national carbon accounting, exclude any loss of inorganic carbon and OC to aquatic systems, and hence any relocation of carbon in soils.

The terrestrial carbon fluxes presented here are derived from dynamic TBMs. The ability to use spatially explicit aquatic carbon models to match terrestrial ecosystems models has not yet been developed but is critical to identify fully where and how freshwater ecosystems may affect the calculated uptake of carbon in both land and water and to provide resource managers integrated tools to strategize policy decisions for carbon sequestration at differing landscape scales (50).

At 106 TgC⋅y⁻¹, the removal of carbon by inland waters within the conterminous United States is substantial at the national scale. However, this analysis represents a snapshot of a dynamic environment that is continuously processing both allochthonous and autochthonous carbon (22, 51). Developing a model framework that couples the biogeochemical processing of inorganic carbon and OC in soils to the movement of water through soils to inland waters is needed to quantify (i) terrestrial carbon sources to inland waters, (ii) seasonal inputs of carbon to freshwater systems under a changing climate, and (iii) anthropogenic influences on freshwater carbon processing (47, 52, 53). There are few direct measurements of the suite of carbon-based greenhouse gases in freshwater ecosystems, particularly methane (11). Methane is emerging as a persistent significant greenhouse gas from freshwater systems (54). Similarly, large uncertainty remains for calculations of lake and reservoir sedimentation and the impacts of physical processes that affect the distribution of sediments along lake and reservoir beds. Continued monitoring and the integration of new measurement techniques for dissolved carbon and carbon gases are important to begin developing both the modeling and databases needed to understand fully the role of inland waters in the carbon cycle.

Materials and Methods

An expanded description of all methods used in this analysis is presented in SI Materials and Methods. Total flux estimates for carbon emissions with each two-digit HUC from water surfaces are described by Stackpoole et al. (33) using the general equation:

$$\left[fC{O}_{2}C\right]\left(\text{Tg}\right)=\hspace{0.17em}{\displaystyle \sum }_{HUC}\left[{\displaystyle \sum }_{SO}\left[\left[C{O}_{2-water}-\hspace{0.17em}C{O}_{2-air}\right]*kC{O}_2*SA\right]\right].$$ [3]

The term fCO₂C is the total net emission of CO₂ from riverine, lake, and reservoir systems of the conterminous United States. CO_2-water is the aquatic CO₂ concentration (moles per liter) derived from calculated estimates of dissolved CO₂ using measured alkalinity, temperature, and pH available at the National Water Information System (NWIS; waterdata.usgs.gov/nwis/) for streams and rivers, and from the Environmental Protection Agency National Lakes Assessment (www2.epa.gov/national-aquatic-resource-surveys/national-lakes-assessment) for lakes and reservoirs. CO_2-air is the CO₂ equilibrium concentration of atmospheric CO₂ in water (moles per liter). kCO₂ is the gas transfer velocity of CO₂ across the air–water interface (meters per day). SA is aquatic surface area (square meters). Lateral carbon flux is represented by multiple rivers for coastal regions of the United States, including the Atlantic Coast, Pacific Coast, Gulf Coast, and Great Lakes (HUCs 01, 02, 03, 04, 12, 17 Coast, and 18). Carbon concentration and flow data to estimate longitudinal carbon fluxes were obtained from the NWIS (waterdata.usgs.gov/nwis/). Carbon fluxes (kilograms per day) were estimated from water quality and daily stream flow data, using the USGS Load Estimator Model (LOADEST) (55). Methods to estimate OC burial in lakes and reservoirs are fully described by Clow et al. (35) and outlined in SI Materials and Methods. OC burial was estimated for each water body in the conterminous United States (CONUS) using the following equation:

$${\text{OC}}_{\text{burial}}\left(\text{TgC}\cdot {\text{y}}^{-1}\right)=\left[{\text{WB}}_{\text{area}}\hspace{0.17em}\left({\mathrm{m}}^2\right)\times \text{SedRt}\left(\text{g}\cdot {\text{m}}^{-2}\cdot {\text{y}}^{-1}\right)\times {\text{OC}}_{\text{conc}}(\%)/100\times \text{BE}(\%)/100\right]\times {10}^{-12},$$ [4]

where OC_burial is the OC burial rate, WB_area is water body area, SedRt is sedimentation rate, OC_conc is OC concentration in sediments (percentage by dry weight), BE is burial efficiency, and 10⁻¹² is a conversion factor from grams to teragrams (35). Water bodies are derived from similar sources as those sources used for efflux calculations. All TBM data processing is available as NetCDF files from the MsTMIP model (nacp.ornl.gov/mstmipdata/).