Abstract
Purpose
The purpose of this investigation was to create an equation for continuous percentile rank of maximal oxygen consumption (VO2 max) from ages 20 to 99.
Methods
We used a two-staged modeling approach with existing normative data from the American College of Sports Medicine for VO2 max. First, we estimated intercept and slope parameters for each decade of life as a logistic function. We then modeled change in intercept and slope as functions of age (stage two) using weighted least squares regression. The resulting equations were used to predict fitness percentile rank based on age, sex, and VO2 max, and included estimates for individuals beyond 79 years old.
Results
We created a continuous, sex specific model of VO2 max percentile rank across the lifespan.
Conclusions
Percentile ranking of VO2 max can be made continuous and account for adults aged 20 to 99 with reasonable accuracy, improving the utility of this normalization procedure in practical and research settings, particularly in aging populations.
Keywords: cardiopulmonary exercise test, treadmill test, aging, physical endurance
Introduction and Purpose
The standard method of quantifying capacity for aerobic activity is maximal oxygen consumption (VO2 max) during a graded exercise test on a treadmill1. Maximal VO2 provides information about the state of the cardiorespiratory and musculoskeletal system as well as the functional capacity of the individual2. Clinicians may use VO2 max to assess baseline function or therapeutic response. For many studies, it is common practice to compare VO2 max with other physiologic measures to assess the influence of maximal oxygen consumption on an outcome of interest such as brain volume, muscle mass, hemoglobin A1c3–7. However, for clinicians or researchers seeking to quantify exercise capacity or physiologic change in response to exercise intervention, aging can be a confounding variable even within the limits of an inclusion criterion. For example, in a typical study of “older adults” ages 65 to 85 years old, there is significant decline in VO2 max due to a confluence of factors including sarcopenia, neuromuscular deterioration and cardiopulmonary decline7–9.
To study fitness in populations using VO2 max, particularly in a heterogeneous population of older males and females, fitness measured by VO2 max can be percentile ranked in relationship to sex and decade of life to minimize these confounding factors. The ACSM publishes percentile rankings of estimated VO2 max in five percent increments from the third through the eight decade of life1. These rankings allow for comparison between individuals over several decades. That is, percentile ranks make it easy to tell who is performing at a high level across age groups even while estimated VO2 max levels decline substantially from 25 years to 75 years. However, binning ranks within a decade obscures meaningful differences between individuals in the same decade of life. This is especially true when year over year differences are exacerbated, as in old age. Further, the ACSM does not publish ranks for individuals 80 years and older, a fast growing segment of the US population10.
To address these concerns we sought to model a continuous estimate of percentile rank, based on those published by the ACSM. Further, we sought to estimate percentile rank values for individuals in their 80s and 90s, based on the trajectory of decline over age.
Methods
We used the most recently published estimated VO2 max (mL/kg/min) values with corresponding percentile ranks from the Cooper Institute as reported by the ACSM1. The rankings are split by decade of life (20s through 70s) and sex, binned in five percent increments, with the extremes at a ceiling at the 99th percentile and floor at the first percentile. All analyses were performed using R (Ver 3.1.1, R Core Team Vienna, Austria) including the use of the package MASS for modeling of logistic functions11.
We used a two-stage modeling approach and performed all analyses separately for males and females. We first modeled the percentile rank as a function of estimated VO2 max within each decade of life and sex (i.e., as 12 separate logistic functions). Estimated VO2 max was used as the explanatory variable and percentile rank was used as the response variable. Thus, each model (stratified by decade and sex) produced an intercept (as) and a slope parameter (bs) estimate for the specific decade and sex in the first stage of our two-stage approach. The stage one models for each age decade-by-sex stratum were of the form:
| (1) |
such that ps,d represents a given percentile for a specified VO2 max value for sex s and decade d.
In stage two, we modeled these resultant intercept and slope parameter estimates of each logistic model (Table 2) as functions of age (within each sex stratum separately) using weighted least squares regression. For these stage two models the middle value of each decade (i.e. 25, 35, …75) were used as the explanatory variable, the parameter estimate was used as the response variable, and the number of subjects reported by ACSM for that decade were used as the weight; thus, age-sex specific fitness percentiles based on a larger number of subjects were weighted more heavily in this estimation of the stage two parameters than those based on fewer subjects. After first visually inspecting scatter plots of the estimated stage one parameters by age, we allowed the stage two models of age predicting these stage one parameter values to include both linear and quadratic relationships. We then further assessed the need for the quadratic terms in the models by comparing predicted percentiles to the published percentile data and found these indicated less error in predicting these values using the models that allowed for the quadratic terms. The general form for modeling the intercept parameter changes for sex s as a function of age (ignoring weight) was thus:
| (2) |
…and for the slope parameters were
| (3) |
Table 2.
Mean Absolute Difference Between Published and Predicted Percentile Rank is Lower Using Quadratic Modeling.
| Males | Females | |||
|---|---|---|---|---|
| Age | Linear | Quadratic | Linear | Quadratic |
| 25 | 5.46 | 1.20 | 7.04 | 1.20 |
| 35 | 1.17 | 1.01 | 1.68 | 1.67 |
| 45 | 1.99 | 1.22 | 3.28 | 1.36 |
| 55 | 1.07 | 1.26 | 1.09 | 1.39 |
| 65 | 4.17 | 0.78 | 5.16 | 2.06 |
| 75 | 7.33 | 4.25 | 5.22 | 4.98 |
| Mean | 3.53 | 1.62 | 3.91 | 2.11 |
Logistic functions that included a quadratic modeling of age effects resulted in smaller differences between published and predicted percentiles.
The resultant functions (Equation 2 and 3) based on these stage two models were substituted into the standard logistic function (Equation 4) to estimate a percentile rank given the participant’s age and VO2 max as:
| (4) |
We evaluated the mean difference and absolute mean difference between the categorized percentile rank data used in stage one and our predicted percentile rank, again using the middle value of each decade as the assumed age for the categorized percentiles from the limited range. Finally, we performed face validity checks for individuals 20 years to 89 years, which included extrapolations beyond the range of data presented by the ACSM test criteria, using a convenience sample of older adults that met ACSM test criteria for maximal oxygen consumption during testing as part of existing institutional review board (IRB)-approved aging and fitness projects in our labs.
Results
Slope and intercept parameter estimates for stage one models are presented in Table 1. We then fit linear and quadratic functions to the intercept (a) and slope (b) coefficients separately for each sex, using weighted least squares regression. The quadratic functions of intercept and slope coefficients for males (Equations 5 and 6) and females (Equations 7 and 8) are provided.
| (5) |
| (6) |
| (7) |
| (8) |
Substituting these equations into the corresponding values of as,d and bs,d from Equation 4 produced our predicted percentile rank based on VO2 max, adjusted for the confounding effects of age and sex.
Table 1.
The Intercept and Coefficient of the Regression Models of the Logit Transformation of Estimated VO2 peak Percentiles for Each Age Group and Sex.
| Males | Females | |||||
|---|---|---|---|---|---|---|
| Age | Intercept (as) |
Slope (bs) |
N | Intercept (as) |
Slope (bs) |
N |
| 25 | −10.15 | 0.2314 | 2,328 | −9.48 | 0.2504 | 1,280 |
| 35 | −10.37 | 0.2442 | 12,730 | −9.27 | 0.2553 | 4,257 |
| 45 | −10.06 | 0.2486 | 18,104 | −9.52 | 0.2755 | 5,908 |
| 55 | −9.56 | 0.2552 | 10,627 | −9.82 | 0.3116 | 3,923 |
| 65 | −8.83 | 0.2591 | 2,971 | −9.88 | 0.3430 | 1,131 |
| 75 | −8.22 | 0.2649 | 417 | −9.88 | 0.3629 | 155 |
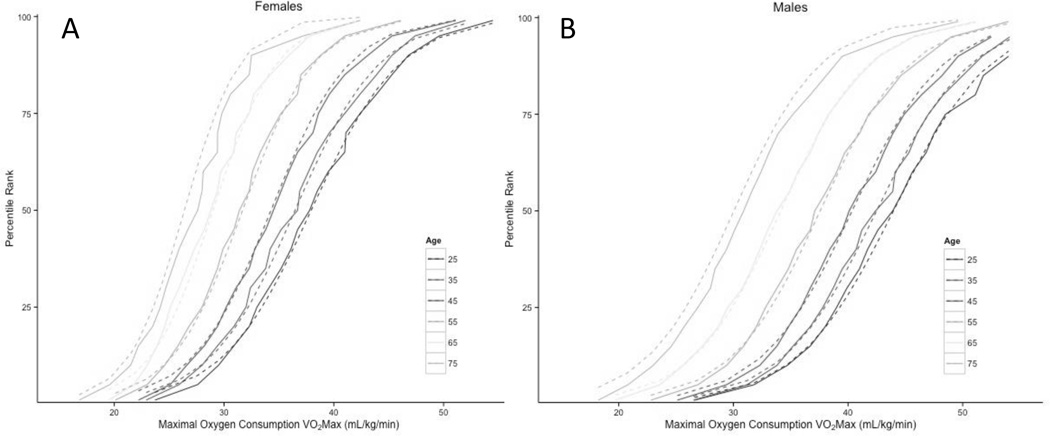
To evaluate our two-stage model results and compare models in stage two that both excluded and included quadratic terms, we calculated mean difference and absolute mean difference between our predicted percentile rank and the published percentile rank (again, using the midpoint of the age categories as the age value). Absolute mean difference for both linear and quadratic relationships, for each decade can be found in Table 2. Based on lower absolute mean difference, we included the quadratic functions in the two-stage model to create a continuous, sex specific model of VO2 max percentile rank across the lifespan. That is, we found that ou\r model most closely fit the published norms as a quadratic function rather than a linear function, in agreement with prior work showing a non-linear decline in fitness with age9. These modeled functions can be seen plotted against the true curves reported by ACSM in Figure 1. Using the quadratic models we calculated predicted percentile ranks and matching VO2 max values for individuals in their 80s and 90s (Table 3).
Figure 1. Percentile Rank Models Compared to American College of Sports Medicine Curves.
The modeled functions (dashed) can be seen plotted against the true curves (solid) reported by ACSM.
Table 3.
Projected Percentiles for Individuals in Their 80s and 90s with Corresponding Estimated VO2 Max.
| Males | Females | |||
|---|---|---|---|---|
| Age 80–89 | Age 90–99 | Age 80–89 | Age 90–99 | |
| Percentile | Estimated VO2Max | |||
| 99 | 42.7 | 37.1 | 34.4 | 31.0 |
| 95 | 36.4 | 30.8 | 30.6 | 27.7 |
| 90 | 33.6 | 28.0 | 29.0 | 26.2 |
| 85 | 31.8 | 26.3 | 27.9 | 25.3 |
| 80 | 30.5 | 25.0 | 27.1 | 24.6 |
| 75 | 29.4 | 23.9 | 26.5 | 24.0 |
| 70 | 28.5 | 22.9 | 25.9 | 23.5 |
| 65 | 27.6 | 22.0 | 25.4 | 23.1 |
| 60 | 26.8 | 21.2 | 24.9 | 22.7 |
| 55 | 26.0 | 20.5 | 24.4 | 22.3 |
| 50 | 25.3 | 19.7 | 24.0 | 21.9 |
| 45 | 24.5 | 18.9 | 23.5 | 21.5 |
| 40 | 23.7 | 18.2 | 23.1 | 21.1 |
| 35 | 22.9 | 17.4 | 22.6 | 20.6 |
| 30 | 22.0 | 16.5 | 22.1 | 20.2 |
| 25 | 21.1 | 15.6 | 21.5 | 19.7 |
| 20 | 20.0 | 14.5 | 21.0 | 19.1 |
| 15 | 18.7 | 13.2 | 20.1 | 18.4 |
| 10 | 16.9 | 11.4 | 19.0 | 17.5 |
| 5 | 14.1 | 8.6 | 17.3 | 16.0 |
| 1 | 7.8 | <3.0 | 13.6 | 12.7 |
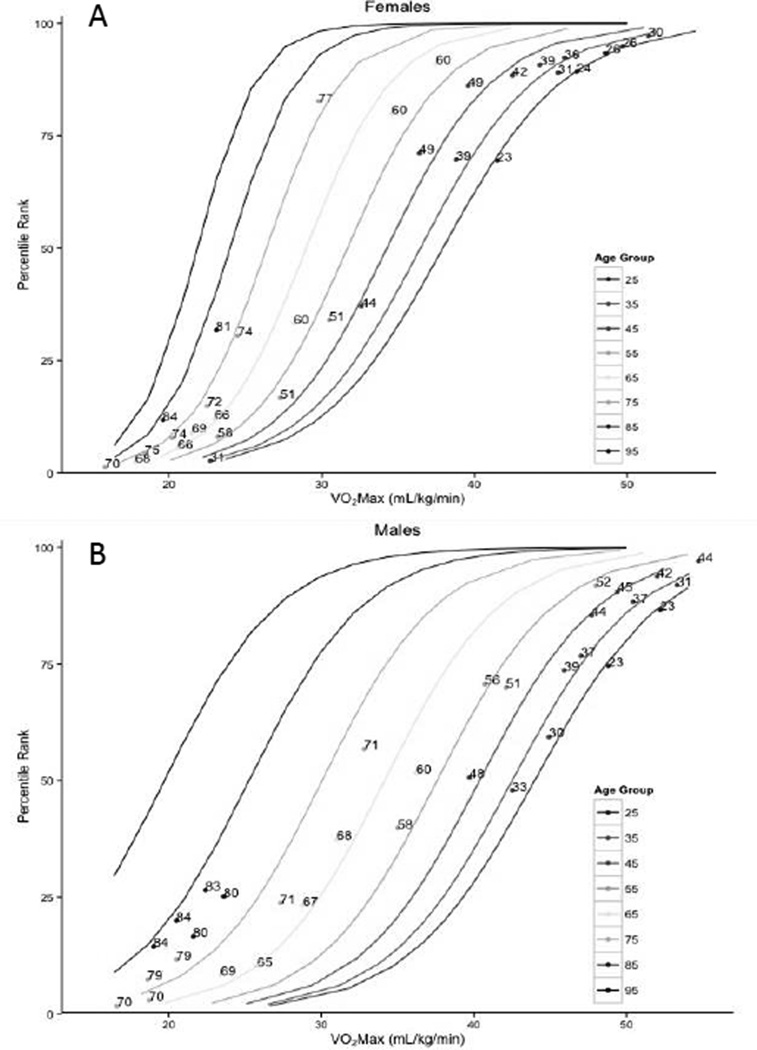
Finally, we selected a convenience sample of VO2 max values with good age dispersion from individuals from 20 to 89 meeting ACSM criteria for VO2 max from existing IRB approved aging and fitness projects in our labs. Figure 2 shows real data plotted against our estimated curves at the midpoint of each decade. Within the same decade of life, older individuals are given a higher percentile rank compared to a younger individual with a similar VO2 max. For example, we plot 80 and 83 year-old males with nearly the same fitness level (22.1 ml/kg/min vs. 22.4 ml/kg/min). In our model, the 83 year old is given a higher percentile rank (26.5%) than the 80 year-old (18.5%) by virtue of his age. Neither would have been ranked due to age by ACSM, but if one were to apply the norms of 8th decade of life, the 83 year-old would be ranked in the 10th percentile and the 80 year old in the 15th percentile.
Figure 2. VO2 max Data Demonstrates Face Validity of Our Modeled Percentile Ranks.
Each plotted point is the real VO2 max from an individual in a prior study, labeled with their age. The lines show our modeled functions at the midpoint of each decade. The plot demonstrates the face validity of our equations; within the same decade of life, older individuals are given a higher percentile rank compared to a younger individual with a similar VO2 max.
Discussion
We sought to develop a continuous model of VO2 max percentile ranks that could be useful across the lifespan. We modeled an age-dependent logistic function that closely fits the percentile rankings published by the ACSM. In doing so, we were able to extend the existing percentile ranking for individuals in their 80s with reasonable face validity. This later ability is likely to become increasingly important as the population ages and there is an increased focus on maintaining functional fitness.
By modeling age as a continuous variable, we have allowed for increased specificity in assigning percentile ranks. Consider two males, 70-years old and 78, both with a VO2 max of 32.3 mL/kg/min. With the current ACSM ranking system, both would be classed in the same 60th percentile. However, our model acknowledges that the 78-year old (percentile rank 72%) has maintained maximal oxygen consumption better than his 70-year old counterpart (percentile rank 51%). This specificity is particularly useful for comparing individuals over a wide age range, for example a clinical trial with inclusion criteria that span two or more decades (e.g. 65-years old to 85) or a comparison of fitness levels in a fitness program at an independent continuing care retirement community. That is, incremental changes in VO2 max due to intervention can be weighted appropriately for age and compared across decades of life.
A second strength of the present model is the extension beyond 79-years old. With existing ACSM rankings, individuals in their 80s either could not receive a percentile rank or would be penalized by being grouped with those in their 70s. As previously reported, the five percent per decade decline in VO2 max that begins after 30-years old increases substantially after 709. We used the trends from 25 to 75 years of age to predict further decline in the 80s and 90s. By including a quadratic function of age, we captured this precipitous decline and assigned percentile ranks with face validity in our own dataset. Currently, there are not enough studies reporting VO2 max of individuals over 80 to accurately define percentile ranks. Fleg et al.9 reported 26.1% and 21.1% decrease in peak oxygen consumption from age 70 to 80 for males and females, respectively. Our model predicted slightly less decline from 75 years to 85, 18.1% for men and 13.0% for women. It is not clear what accounts for these differences, but they may be related to our use of maximal versus peak oxygen consumption values. Our inclusion of only those meeting ACSM maximal oxygen consumption criteria1 likely biases norms toward individuals with greater physical function. In contrast, Fleg et al.9 used only achievement of > 85% age-predicted heart rate as a threshold for an acceptable test.
We expect percentile rank modeling to become increasingly valuable as a research tool to allow for comparison of individuals across several decades. By expanding the rankings along the age continuum we have allowed for more accurate comparison between age peers. Further, the percentile rank can be treated as a continuous measure rather than an ordinal variable biased towards individuals in the middle of a given decade. As such, this continuous measure can be compared to other biomarkers or as its own outcome measure with greater precision.
For researchers or individuals in the fitness field, Equation 4 can be easily implemented in a spreadsheet format to automatically convert VO2 max to a percentile rank. Alternatively, we have created a web application deployable to any device that can use an internet browser. The user inputs the age, sex and VO2 max and the application returns a percentile rank (http://bit.ly/KUADCFitRank).
Conclusion
We modeled existing percentile ranking of VO2 max values from 25-years old to 75. In doing so, we were able to create a continuous measure, rather than one binned by half-decade, that we could project into the 9th and 10th decade of life where there are currently no published norms. The application of this model will allow clinicians, researchers and others in the exercise field such as personal or athletic trainers to more accurately compare age-peers or account for a wide age range in comparing measures.
Supplementary Material
Acknowledgments
Portions of this work were supported by the following grants R01AG034614, R01AG033673 & U10NS077356. Rasinio S. Graves and Eric D. Vidoni were supported in part by the Foundation for Physical Therapy through the Magistro Family Foundation Research Grant. Rasinio S. Graves, Jonathan D. Mahnken, and Eric D. Vidoni were also supported by the University of Kansas Alzheimer’s Disease Center, P30AG035982. Sandra A. Billinger’s work on this project was supported in part by K01HD067318. Rodrigo D. Perea’s work on this project was supported in part by K01AG035042. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or the Foundation for Physical Therapy.
References
- 1.American College of Sports Medicine. ACSM's Guidelines for Exercise Testing and Prescription. 9th. Baltimore, MD: Lippincott Williams & Wilkins; 2014. [Google Scholar]
- 2.Cress ME, Meyer M. Maximal voluntary and functional performance levels needed for independence in adults aged 65 to 97 years. Phys Ther. 2003 Jan;83(1):37–48. [PubMed] [Google Scholar]
- 3.Honea RA, Thomas GP, Harsha A, et al. Cardiorespiratory fitness and preserved medial temporal lobe volume in Alzheimer disease. Alzheimer Dis Assoc Disord. 2009 Jul-Sep;23(3):188–197. doi: 10.1097/WAD.0b013e31819cb8a2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Erickson KI, Voss MW, Prakash RS, et al. Exercise training increases size of hippocampus and improves memory. Proc Natl Acad Sci U S A. 2011 Feb 15;108(7):3017–3022. doi: 10.1073/pnas.1015950108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Church TS, Blair SN, Cocreham S, et al. Effects of aerobic and resistance training on hemoglobin A1c levels in patients with type 2 diabetes: a randomized controlled trial. JAMA. 2010 Nov 24;304(20):2253–2262. doi: 10.1001/jama.2010.1710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Vaitkevicius PV, Fleg JL, Engel JH, et al. Effects of age and aerobic capacity on arterial stiffness in healthy adults. Circulation. 1993 Oct;88(4 Pt 1):1456–1462. doi: 10.1161/01.cir.88.4.1456. [DOI] [PubMed] [Google Scholar]
- 7.Fleg JL, Lakatta EG. Role of muscle loss in the age-associated reduction in VO2 max. J Appl Physiol (1985) 1988 Sep;65(3):1147–1151. doi: 10.1152/jappl.1988.65.3.1147. [DOI] [PubMed] [Google Scholar]
- 8.de Oliveira RJ, Bottaro M, Motta AM, et al. Association between sarcopenia-related phenotypes and aerobic capacity indexes of older women. J Sports Sci Med. 2009;8(3):337–343. [PMC free article] [PubMed] [Google Scholar]
- 9.Fleg JL, Morrell CH, Bos AG, et al. Accelerated Longitudinal Decline of Aerobic Capacity in Healthy Older Adults. Circulation. 2005;112(5):674–682. doi: 10.1161/CIRCULATIONAHA.105.545459. [DOI] [PubMed] [Google Scholar]
- 10.Ortman BJM, Velkoff VA, Hogan H. An Aging Nation : The Older Population in the United States. P25-1140. United States Census Bureau. Washington, D.C.: 2014. [Accessed June 2015]. Issued May 2014. [Google Scholar]
- 11.Venables WN, Ripley BD. Modern Applied Statistics with S. 4th. New York: Springer; 2002. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.