Programmable Extreme Pseudomagnetic Fields in Graphene by a Uniaxial Stretch

Abstract

Many of the properties of graphene are tied to its lattice structure, allowing for tuning of charge carrier dynamics through mechanical strain. The graphene electro-mechanical coupling yields very large pseudomagnetic fields for small strain fields, up to hundreds of Tesla, which offer new scientific opportunities unattainable with ordinary laboratory magnets. Significant challenges exist in investigation of pseudomagnetic fields, limited by the non-planar graphene geometries in existing demonstrations and the lack of a viable approach to controlling the distribution and intensity of the pseudomagnetic field. Here we reveal a facile and effective mechanism to achieve programmable extreme pseudomagnetic fields with uniform distributions in a planar graphene sheet over a large area by a simple uniaxial stretch. We achieve this by patterning the planar graphene geometry and graphene-based hetero-structures with a shape function to engineer a desired strain gradient. Our method is geometrical, opening up new fertile opportunities of strain engineering of electronic properties of 2D materials in general.

Being able to influence the motion of charge carriers, strain-induced pseudomagnetic fields in graphene have been explored as a potential approach to engineering the electronic states of graphene. There has been experimental evidence of enormous pseudomagnetic fields (up to 300 T) in locally strained graphene nanobubbles [1] and graphene drumheads [2], which inspires enthusiasm in exploring the abundant potential of strain engineering of graphene, as well as charge carrier behavior under extreme magnetic fields that otherwise do not exist in normal laboratory environments [3–9]. Enthusiasm aside, there exist significant challenges that hinder further explorations of these fertile opportunities to full potential. For example, existing experiments demonstrate pseudomagnetic fields in highly localized regions of graphene with a non-planar morphology [1,2], which poses tremendous challenge for experimental control and characterization of the resulting fields. Further challenge originates from the dependence of the symmetry of the strain-induced pseudomagnetic field on the strain gradient in graphene. As a result, an axisymmetric strain field in graphene leads to a pseudomagnetic field of rotational threefold symmetry [2,4–7]. By contrast, a uniform pseudomagnetic field in a planar graphene with tunable intensity is highly desirable for systematic investigations [10]. In principle, such a uniform pseudomagnetic field can be achieved by introducing a strain field of threefold symmetry in graphene [4,8], which requires equal-triaxial loading of atomically thin graphene, a technical challenge already prohibitive in bulk materials. So far, a viable solution to generate a pseudomagnetic field in graphene with controllable distribution and amplitude over a large planar area under a feasible loading scheme still remains highly desirable but elusive.

The ever-maturing programmable patterning [11–22] and functionalization [23–30] of graphene has enabled a class of graphene-based unconventional nanostructures with exceptional functionalities, such as nanoribbon [31], nanomesh [16] and hybrid superlattices [23]. Significant progress has also been made on fabricating high quality in-plane heteroepitaxial nanostructures that consist of different monolayer two-dimensional (2D) crystals, such as graphene, hydrogenated graphene (graphane) and hexagonal boron nitride (h-BN) [32–35]. Furthermore, controllable and nondestructive generation of uniaxial strains (up to more than 10 %) in graphene has been successfully demonstrated recently [36]. Motivated by these advances, here we reveal a feasible and effective mechanism to achieve programmable pseudomagnetic fields in a planar graphene by a simple uniaxial stretch. We demonstrate two new possible approaches: 1) by tailoring the planar edge geometry of a graphene strip, and 2) by patterning in-plane graphene-based hetero-structures. These feasible-to-implement approaches yield rich features necessary for systematic studies of pseudomagnetic fields in strain engineered graphene geometries, as demonstrated below.

When the graphene lattice is strained, the main effect is to modify the hopping energy between the two graphene sublattices. The modified energies add a term to the momentum operators in the low energy Dirac Hamiltonian, in the same way a vector potential is added for electromagnetic fields. This gives a very useful way to relate the mechanical deformation in graphene with a gauge field that acts on the graphene electronic structure [2–9]. The pseudomagnetic field, B_ps, is given by the 2D curl of the mechanically derived gauge field. For elastic deformations, the pseudomagnetic field in graphene is related to the strain field in the plane of the graphene as [2–9]

$$B_{\mathrm{p}\mathrm{s}}=\frac{t\beta }{e{v}_{\mathrm{F}}}[-2\frac{\partial {\epsilon }_{xy}}{\partial x}-\frac{\partial }{\partial y}({\epsilon }_{xx}-{\epsilon }_{yy})],$$ (1)

where β = 2.5 is a dimensionless coupling constant, t = 2.8 eV is the hopping energy, ν_F = 1 × 10⁶ m s⁻¹ is the Fermi velocity, and ε_xx, ε_yy, and ε_xy are the components of the strain tensor of the graphene. The x-axis is along the zigzag direction of graphene lattice. The field in Eq. (1) is for one graphene valley, with opposite sign for the other valley.

We consider the pseudomagnetic field under the special case of uniaxial stretch (see Section I in Supplemental Material [47]) given by,

$$B_{\mathrm{p}\mathrm{s}}=\frac{3t\beta }{e{v}_{\mathrm{F}}}(1+\nu )\frac{\partial {\epsilon }_{yy}}{\partial y}.$$ (2)

The above formulation reveals that a programmable pseudomagnetic field is achieved if the strain gradient $\frac{\partial {\epsilon }_{yy}}{\partial y}$ in graphene can be engineered under a simple uniaxial stretch. For example, a constant strain gradient $\frac{\partial {\epsilon }_{yy}}{\partial y}$ in graphene (i.e., a linear distribution of tensile strain in the armchair direction) can result in a uniform pseudomagnetic field over a large area of graphene; a highly desirable feature to enable direct experimental characterization of the resulting field.

To demonstrate the feasibility to engineer the strain field in graphene under a simple uniaxial stretch, we first consider a graphene nanoribbon of length L that is patterned into a shape with a varying width W(y) and subject to an applied uniaxial tensile strain ε_app along its length in the y direction [Fig. 1(a)]. The geometry of the two long edges of the graphene nanoribbon is defined by a shape function f(y) = W(y)/W₀, where W₀ = W(0) denotes the basal width of the graphene nanoribbon. When L ≫ W(y), it is reasonable to assume that ε_yy is constant along any cross-section cut in x direction and only varies along y direction. This assumption is justified in the majority part of the graphene nanoribbon except in the vicinity of its four corners, as verified by both finite element modeling and atomistic simulations [47]. Considering the force balance along any cross-section cut in x direction, it is shown that [47]

$$\frac{\partial {\epsilon }_{yy}}{\partial y}=-\frac{F}{E_g{W}_{0}h}\frac{1}{f^2}\frac{df}{dy},$$ (3)

where F is the applied force at the ends of graphene nanoribbon necessary to generate the uniaxial tensile strain ε_app, E_g and h are the Young’s Modulus and thickness of graphene, respectively.

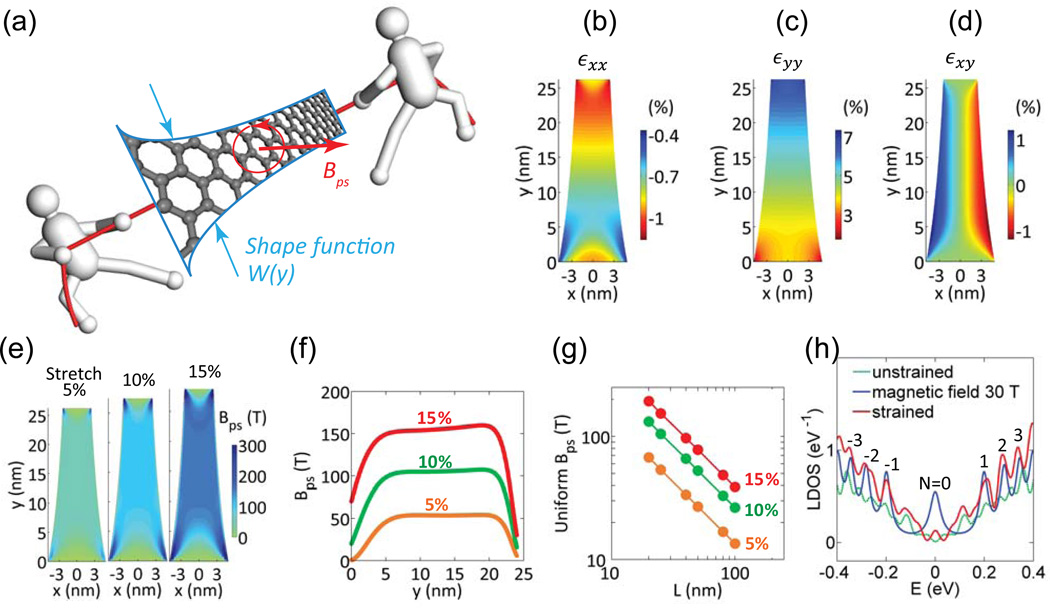
FIG. 1.

(color online). Producing uniform pseudomagnetic fields in a planar shaped graphene strip under a uniaxial stretch. (a) Schematic showing a graphene nanoribbon of varying width under a uniaxial stretch producing a pseudomagnetic field, B_ps. The red circle denotes cyclotron orbits in the field giving rise to pseudo-Landau levels in (h). (b to d) Contour plots of the resulting strain components in the graphene, ε_xx, ε_yy and ε_xy, respectively, under a 5 % uniaxial stretch. (e) Resulting pseudomagnetic fields in the graphene nanoribbon shown in (a) under a uniaxial stretch of 5 %, 10 % and 15 %, respectively. (f) Intensity of the pseudomagnetic field as the function of location along the centerline of the graphene ribbon for various applied uniaxial stretches. (g) Intensity of the pseudomagnetic field is shown to be linearly proportional to the applied uniaxial stretch and inversely proportional to the length of the graphene ribbon L. (h) Local density of states of unstrained graphene and graphene with a constant strain gradient determined by density functional theory calculations. N=0 and N=±1, ±2, ±3 Landau levels, corresponding to cyclotron motion in a magnetic field are seen to emerge in the strained graphene, demonstrating a uniform pseudomagnetic field. The wiggles in the results for the unstrained case result from finite size effects in the calculations. See Supplemental Material for further discussion [47].

Thus from Eq. (2), the resulting pseudomagnetic field in such a patterned graphene nanoribbon is given by,

$$B_{\mathrm{p}\mathrm{s}}=-\frac{3t\beta F}{e{v}_{\mathrm{F}}{E}_{\mathrm{g}}{W}_{0}h}(1+\nu )\frac{1}{f^2}\frac{df}{dy}.$$ (4)

Equation (4) reveals that a tunable pseudomagnetic field is achieved under a uniaxial stretch by engineering the shape of the graphene nanoribbon. For example, to achieve a uniform pseudomagnetic field, the corresponding shape function is shown to be

$$f(y)=\frac{f_{\mathrm{r}}L}{f_{\mathrm{r}}(L-y)+y},$$ (5)

where f_r = f(L) denotes the ratio between the widths of the top and bottom ends of the graphene nanoribbon. The intensity of the resulting uniform pseudomagnetic field (see Section III in [47] for details) is given by,

$$B_{\mathrm{p}\mathrm{s}}=\frac{6t\beta }{e{v}_{\mathrm{F}}}\frac{{\epsilon }_{\text{app}}}{L}\frac{(1-f_{\mathrm{r}})}{(1+f_{\mathrm{r}})}(1+\nu ).$$ (6)

To verify the above elasticity-based theoretical prediction, we performed numerical simulations using both finite element method and atomistic simulations (Sections V and VII in [47] for simulation details) to calculate the strains and pseudomagnetic field using Eq. (1), which lead to results well in agreement with the above theory, Eqs. (2–6), as elaborated below.

Figure 1(a) shows the schematic of a graphene nanoribbon of L = 25 nm, W₀ = 10 nm, f_r = 0.5, with two long edges prescribed by the shape function in Eq. (5). The ribbon is subject to an applied unidirectional stretch of 5 % in its length direction. Figure 1, (b) to (d), plots the components of the resulting strain in the graphene, ε_xx, ε_yy and ε_xy, respectively, from finite element simulations. In the majority portion of the graphene except its four corners, ε_xx and ε_yy show a linear distribution along y direction [also see Fig. S1(a)], while ε_xy shows a linear distribution along x direction. From Eq. (2), such a strain distribution will result in a rather uniform pseudomagnetic field in the graphene nanoribbon.

Figure 1(e) plots the resulting pseudomagnetic fields in the graphene nanoribbon under an applied uniaxial stretch of 5 %, 10 % and 15 %, respectively, all of which clearly show a uniform distribution in nearly the entire graphene ribbon except at its four corners. The intensity of the pseudomagnetic field as the function of location along the centerline of the graphene ribbon is shown in Fig. 1(f), for various applied uniaxial stretches (See Section V in [47] for detailed discussions). For each case, the plateau in a large portion of the curve shows a rather uniform and strong pseudomagnetic field along the centerline of the graphene nanoribbon (e.g., ≈150 T under a 15 % stretch). Further parametric studies [Fig. 1(g)] reveal that the intensity of resulting pseudomagnetic field is linearly proportional to the applied uniaxial stretch ε_app and inversely proportional to the length of the graphene ribbon L, in excellent agreement with the dependence from the theoretic prediction in Eq. (6) (See Section V in [47] for details). Our atomistic simulation results [Fig. S4] further verify both the uniform distribution of the resulting pseudomagnetic field in the graphene nanoribbon and the agreement on the field intensity with the results from finite element simulations. As additional verification, our density functional theory calculation produces pseudo-Landau levels, corresponding to cyclotron motion in a magnetic field [Fig. 1(h)], attesting to the presence of a strain-induced pseudomagnetic field for a graphene under a strain field of constant $\frac{\partial {\epsilon }_{yy}}{\partial y}$ (See Section II in [47] for details).

Equation (6) also suggests another geometric dimension to tailor the intensity of pseudomagnetic field: tuning the top/bottom width ratio f_r of the graphene nanoribbon. For nanoribbons with the same length, a smaller f_r leads to more strain localization (i.e., a higher strain gradient) in the graphene nanoribbon, and thus a higher intensity of the pseudomagnetic field. Figure S3 shows the geometry of 25 nm long graphene nanoribbons with three top/bottom width ratios, f_r = 0.35, 0.5, and 0.7, with the two long edges of each nanoribbon prescribed by Eq. (5). The corresponding intensities of the resulting pseudomagnetic field from finite element simulations, as shown in Fig. S3(b), are in excellent agreement with the prediction from Eq. (6).

The programmable pseudomagnetic field in planar graphene demonstrated above essentially originates from determining a shape function that yields a tunable effective stiffness in various locations of the graphene, which in turn leads to non-uniform distribution of strain under a uniaxial stretch. From a different point of view, the graphene nanoribbon in Fig. 1(a) can be regarded as a lateral 2D hetero-structure, consisting of a pristine graphene nanoribbon and two patches on its side made of 2D material (vacuum) with zero stiffness [e.g., Fig. 2(a)]. As a result, the effective stiffness of the graphene nanoribbon at different cross-section decreases from the wider end to the narrower end. The above mechanistic understanding indeed opens up more versatile approaches to achieving a programmable pseudomagnetic field in planar graphene hetero-structures, which we further explore as follows.

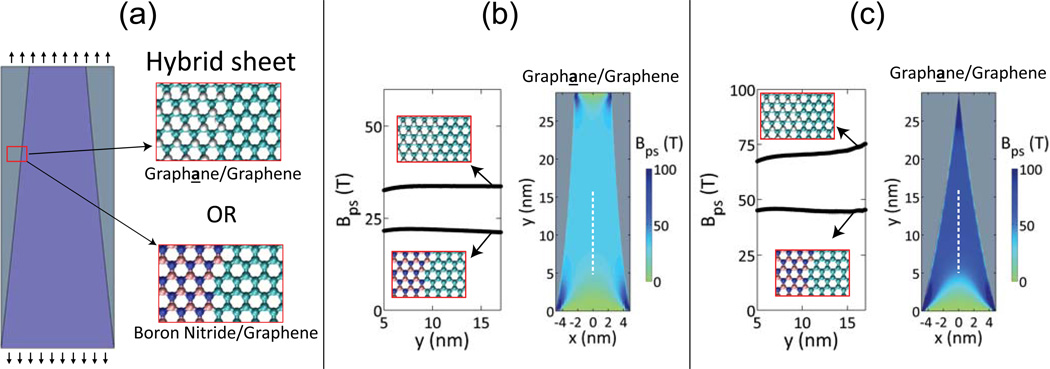
FIG. 2.

(color online). Producing uniform pseudomagnetic fields in planar graphene-based hetero-structures under a uniaxial stretch. (a) Schematic showing a 2D hetero-structure consisting of graphene and graphane (or h-BN) bonded to a center piece of graphene under a uniaxial stretch. (b) Left: Intensity of the resulting pseudomagnetic field in the graphene domain of a graphene/graphane and a graphene/h-BN hetero-structure, respectively, under a 15 % uniaxial stretch. Here the top/bottom width ratio of the graphene domain f_r = 0.5; Right: Contour plot of the resulting pseudomagnetic field in the graphene/graphane hetero-structure. (c) Left: Intensity of the resulting pseudomagnetic field in the graphene domain of a graphene/graphane and a graphene/h-BN hetero-structure, respectively, under a 15 % uniaxial stretch. Here the top/bottom width ratio of the graphene domain f_r = 0; Right: Contour plot of the resulting pseudomagnetic field in the graphene/graphane hetero-structure.

Recent experiments demonstrate facile fabrication of high quality in-plane hetero-epitaxial nanostructures such as graphene/graphane and graphene/h-BN hetero-structures in a single 2D atomic layer [32–35]. The more corrugated lattice structures of graphane and h-BN lead to an in-plane stiffness smaller than that of pristine graphene. It is expected that such in-plane hetero-structures with proper geometry (shape function) can be tuned to have a suitable variation of effective stiffness, and thus allow for a desirable strain distribution to enable programmable pseudomagnetic fields in the graphene portion under a uniaxial stretch.

Consider a rectangular 2D hetero-structure with a graphene nanoribbon and two patches of another 2D crystal of effective stiffness E_h [e.g., graphane or h-BN, Fig. 2(a)]. Following a similar theoretical formulation as for the graphene nanoribbon shown above, it is shown that a programmable pseudomagnetic field in the graphene domain can be achieved by tailoring its geometry in the 2D hetero-structure. For example, a suitable shape function f(y) of the two long edges of the graphene domain can be solved so that a uniaxial stretch in y direction can generate a uniform pseudomagnetic field in the graphene domain (see Section IV in [47] for details).

To verify the above theoretical prediction, we carried out both finite element modeling and atomistic simulations of two types of 2D hetero-structures, graphene/graphane and graphene/h-BN, respectively, under uniaxial stretch, as shown in Fig. 2(a). The intensity of the resulting pseudomagnetic field in the graphene domain of a graphene/graphane and a graphene/h-BN hetero-structure, are shown in Fig. 2(b), respectively. Here the top/bottom width ratio of the graphene domain f_r = 0.5, and the applied stretch is 15 %. A rather uniform distribution of the pseudomagnetic field is clearly evident, with an intensity of ≈33 T (graphene/graphane) and ≈22 T (graphene/h-BN), respectively, in good agreement with theoretical predictions. There exists a unique advantage of using a 2D hetero-structure over a pure graphene nanoribbon. It is shown that a stronger pseudomagnetic field can be generated in a graphene nanoribbon (or domain in 2D hetero-structure) with a smaller top/bottom width ratio f_r, with all other parameters kept the same (Eq. (S20) in [47]). To maximize such a tunability on field intensity, a graphene nanoribbon with f_r = 0 (the narrower end shrinks to a point) is desirable, but applying uniaxial stretch to such a nanostructure becomes prohibitive given its sharp tip. By contrast, a tipped graphene domain in a 2D hetero-structure is feasible to fabricate and a uniaxial stretch can be readily applied to the rectangular 2D hetero-structure. Figure 2C demonstrates the resulting pseudomagnetic field in two types of such a hetero-structure, with an elevated average intensity of ≈70 T (graphene/graphane) and ≈45 T (graphene/h-BN), respectively, in comparison with those in Fig. 2(b) (f_r = 0.5, all other parameter being the same). Further atomistic simulations [Fig. S5] show good agreement with the above finite element modeling results in terms of both distribution and intensity of the resulting pseudomagnetic field.

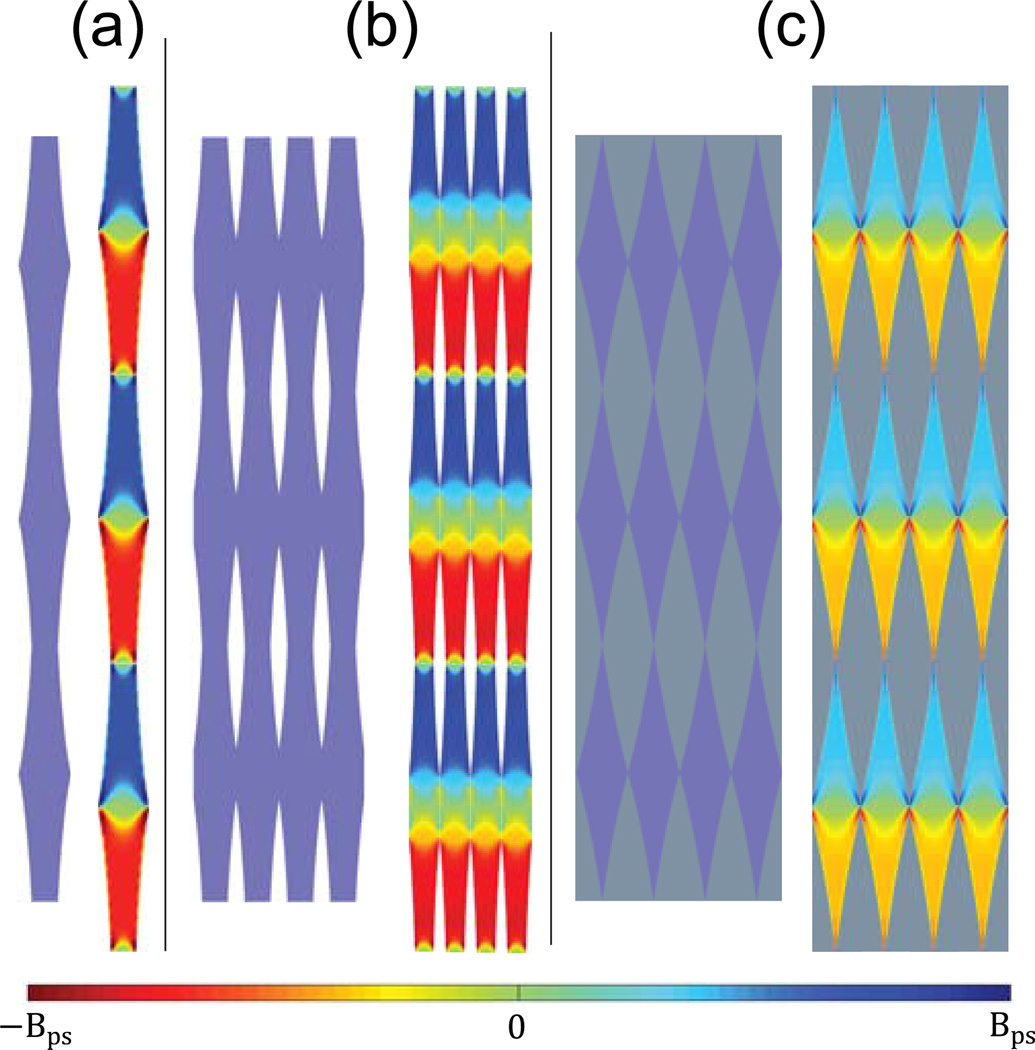
In conclusion, we offer a long-sought solution to achieving a programmable pseudomagnetic field in planar graphene over a large area via a feasible and effective strain-engineering mechanism. Our method utilizes a shape function applied to a planar graphene sheet to achieve a constant strain gradient when applying a simple uniaxial stretch to a graphene ribbon [Fig. 1(a)]. We demonstrate such a mechanism in both graphene nanoribbons and graphene-based 2D hetero-structures with resulting pseudomagnetic fields possessing a uniform distribution and a tunable intensity over a wide range of 0 T to 200 T. Such a programmable pseudomagnetic field under a uniaxial stretch results from the tunable effective stiffness of graphene by tailoring its geometry, so that the challenge of generating controllable strain gradient in graphene can be resolved by patterning the shape of a graphene nanoribbon or the graphene domain in a 2D hetero-structure, a viable approach with the ever advancing 2D nanofabrication technologies. These feasible-to-implement approaches can yield rich rewards from systematic studies of pseudomagnetic fields in graphene, which are extreme fields compared to normal laboratory field strengths, and can be arbitrarily patterned in 2D. For example, a repeating programmable pseudomagnetic field can be generated in a wide range of structures over large areas by repeating the suitable geometrical patterns, e.g., a long graphene ribbon [Fig. 3(a)], a graphene nanomesh [Fig. 3(b)], and a graphene-based 2D superlattice structure [Fig. 3(c)]. The geometrical nature of the concept demonstrated in the present study is applicable to other 2D materials, and thus sheds light on fertile opportunities of strain engineering of a wide range of 2D materials for future investigations.

FIG. 3.

(color online). Pseudomagnetic fields in patterned graphene hetero-structures supperlattices. (a) Schematic of a suitably patterned long graphene nanoribbon (left) and the contour plot of the resulting pseudomagnetic field under a 15 % uniaxial stretch (right). (b) Schematic of a suitably patterned graphene nanomesh (left) and the contour plot of the resulting pseudomagnetic field under a 15 % uniaxial stretch (right). (c) Schematic of a suitably patterned graphene-based 2D superlattice structure (left) and the contour plot of the resulting pseudomagnetic field under a 15 % uniaxial stretch (right). The scale for B_ps is from – 200 T to 200 T.