Abstract
While it has become axiomatic that mechanical signals promotes in-vitro engineered tissue formation, the underlying mechanisms remain largely unknown. Moreover, efforts to date to determine parameters for optimal extracellular matrix (ECM) development have been largely empirical. In the present work, we propose a two-pronged approach involving novel theoretical developments coupled with key experimental data to develop better mechanistic understanding of growth and development of dense connective tissue under mechanical stimuli. To describe cellular proliferation and ECM synthesis that occur at rates of days to weeks, we employ mixture theory to model the construct constituents as a nutrient-cell-ECM triphasic system, their transport, and their biochemical reactions. Dynamic conditioning protocols with frequencies around 1 Hz are described with multi-scale methods to couple the dissimilar time scales. Enhancement of nutrient transport due to pore fluid advection is up-scaled into the growth model, and the spatially dependent ECM distribution describes the evolving poroelastic characteristics of the scaffold-engineered tissue construct. Simulation results compared favorably to the existing experimental data, and most importantly, distinguish between static and dynamic conditioning regimes. The theoretical framework for mechanically conditioned tissue engineering (TE) permits not only the formulation of novel and better-informed mechanistic hypothesis describing the phenomena underlying TE growth and development, but also the exploration/optimization of conditioning protocols in a rational manner.
Keywords: multi-scale modeling, functional tissue engineering, growth and remodeling, heart valve, reaction-diffusion, poro-elasticity
1. INTRODUCTION
The development of engineered tissue replacements results from the needs from diverse potential applications, from dense connective tissues (e.g. skin, cartilage, or bone) to complete complex organs (e.g. heart, liver, kidney, etc.). Their appeal arises mainly due to (i) limitations of conventional prosthetic devices, (ii) risk of complications with transplantation, and (iii) critical shortage of donor tissues (Mendelson and Schoen 2006). The long-term goal of the engineered tissue paradigm is the formation of living tissues that functionally duplicate the native target tissue. Thus, from a functional biomechanical perspective any engineered tissue must lead to sufficient mechanical function for an implant to perform after in-vivo implantation (Sacks et al. 2009). This must start with a deeper understanding of native tissue function (Woo and Seguchi 1989), coupled to the delineation of critical native tissue behaviors essential for duplication in the replacement tissue (Butler et al. 2000).
A major issue is the often-obtained lack of structural organization of the engineered tissue that generally leads to insufficient mechanical properties for in-vivo functional performance. Consider the in-vitro engineered tissue development paradigm (Lanza et al. 2000; Park et al. 2007) - during both in-vitro incubation and the initial phase of in-vivo deployment engineered tissue implants are commonly living tissue-synthetic scaffold composites possessing sufficient mechanical integrity to support acute function and allow subsequent in-vivo remodeling (Hoerstrup et al. 2000a; Rabkin et al. 2002). In this paradigm, the effective mechanical properties include contributions from the de novo ECM and the scaffold prior to its resorption. The mechanical performance of the engineered tissue implant is dependent on the spatial-temporal distributions of its components and includes the effects of their micromechanical interactions. Most importantly, the ECM constituents are evolving over time – not only increasing in quantity, but also improving their quality due to active remodeling of the living tissue component. Underlying the process of growth and development of de novo ECM in functional tissue engineering is the modulation of cellular responses, which have been extensively studied, e.g. by Madri et al. (1992), Freed et al. (1999), Stegemann and Nerem (2003), Lutolf and Hubbell (2005). Moreover, the critical mechanical interactions between the scaffold and ECM clearly dictate local mechanical environment experienced at the cellular level and its influence in cellular behavior (Engelmayr and Sacks 2008).
However, significant problems exist on connecting the cellular and tissue scales. In particular, heterogeneous cell growth and ECM synthesis are generally observed when engineered tissue constructs whose dimensions exceed a critical length scale (Demol et al. 2011; Obradovic et al. 2000; Radisic et al. 2006). This is largely due to diffusional limits and robust cellular nutrient consumption, which results in cellular proliferation and ECM synthesis generally observed in the periphery of tissue engineered constructs. However, the inner regions are hindered of nutrient supply, which lead to localized hypoxia, cell death, and diminished ECM proliferation (Brown et al. 2007; Lewis et al. 2005). Construct perfusion (Mizuno et al. 2001) and other strategies (e.g. finite-sized transport channels (Bian et al. 2009)) have been attempted to mitigate nutrient depletion from the inner regions of the growing construct, but so far have only enjoyed limited practical success mainly due to their empirical-based approaches.
While the rudimentary aspects of engineered tissue development (e.g., cell proliferation, collagen secretion) can be simulated in-vitro by growth factors under static conditions (Fu et al. 2004), the formation of dense collagenous structures characteristic of functional connective tissues (Rabkin et al. 2002) is difficult to achieve and has yet to be observed without mechanical stimulation (Bishop and Lindahl 1999; Costa et al. 2003; Mol et al. 2003). Multiple studies have been conducted to assess the role of biomechanics and dynamic mechanical conditioning on TE outcomes. Supporting evidence has been obtained from (i) experiments at the tissue level in idealized and highly controllable in-vitro environments with custom made bioreactors providing biomimetic mechanical conditioning (Engelmayr et al. 2003; 2008), and (ii) incubation of geometrically accurate scaffolds in organ level bioreactors mimicking the dynamic flow and mechanical environment of the native environment (Hoerstrup et al. 2000b; Ramaswamy et al. 2010). These studies have extensively demonstrated that mechanical conditioning promotes engineered tissue formation in-vitro in comparison to static culturing (e.g. Kim et al. (1999) on engineered smooth muscle, Mol et al. (2003) on engineered heart valve tissues, or Bian et al. (2010) on tissue engineered cartilage). Yet, despite this demonstrated evidence, optimal in vitro mechanical conditioning protocols for initial development of engineered tissue remain unknown, and most importantly, the underlying theoretical models to develop them do not exist.
In general, a myriad of external stimuli is available in current in-vitro conditioning regimes and may depend on a wide-range of variables, including type/magnitude of stresses applied, construct motion and geometry, conditioning timeframes, cell source(s), scaffold materials, and media formulation, to name a few (Berry et al. 2010). All of these variables (and potentially many others) require knowledge of their effects on initial and subsequent post-implant tissue formation. However, a rational methodology to obtain fully functional and clinically robust engineered tissue implants remains nonexistent, and the current alternative is difficult and expensive trial-and-error iterations following a largely empirical approach. Thus, the systematic translation of the empirically collected knowledge to functional tissue engineering or to the subsequent in-vivo stage has reached only limited success. To achieve the long-term goal of engineering mechanically stable implants exhibiting tissue function equivalent to native tissues, fully integrated experimentation/modeling approaches are necessary. Experimental exploration, the development of theoretical frameworks, and subsequent validating experiments must start with highly controlled in vitro experiments at the bench in bioreactors under well-known and well-defined conditions. Sufficient level of understanding of the process of growth and development of engineered tissue must be achieved with systematic in vitro experiments, which knowledge can then be extended to the in-vivo milieu. The improvement of the general awareness of the underlying mechanisms of engineered tissue development is crucial to rationally design for and develop in-vivo function in animal models, and certainly, to subsequently achieve the goal of obtaining tissue engineering implants with practical clinical relevance.
Our objective herein is to lay the foundation for development of robust theoretical models and reliable simulation tools applicable to engineered tissue implants during all stages of their in vitro development and subsequent in vivo function. We aim for sufficient generality that renders our framework applicable to diverse functional tissue engineering conditions (specifically, diverse in vitro mechanical conditioning or other perfusion protocols) and extendable to other tissue engineering stages (i.e. in vivo where more complex biochemistry is present). The inclusion of cytokines, growth factors, and other biochemical functional triggers, explicit cell-cell and cell-ECM interactions, or more complex descriptions of the de novo ECM (as multi-component structure with multiple types of collagen, elastin, proteoglycans), are natural extensions of the present framework, however require not only the addition of further modeling hypothesis but also critical experimental characterization.
As first step, we develop our framework based on the fundamental in-vitro experiments of Engelmayr et al. (2003; 2005; 2008) at the tissue level. Specifically, we aim to model and quantify the influence of mechanical conditioning in dense connective formation and support the optimization of conditioning protocols allowing for in silico pre-exploration of outcomes of different conditioning regimes. The pivotal experimental model of Engelmayr et al. (2003; 2005; 2008) facilitates theoretical treatment and interpretation, permits the development of tractable and realistic models framing all the salient elements of functional tissue engineering, and covers many of the problems associated with organ-level tissue engineering. Heart valves undergo complex deformations in-vivo, are subjected to large internal tensile and external shear forces, and are in contact with blood (Sacks and Yoganathan 2008). Although it had been extensively shown that these stimuli work as developmental triggers on de novo ECM growth and development (Engelmayr et al. 2005; 2006; 2008; Ramaswamy et al. 2010), current knowledge and understanding of their effects is very limited and is hampering the development of engineered tissue heart valves.
2. METHODS
2.1 Experimental data
Specific details of the experimental methods and findings have been previously presented. In brief, Engelmayr et al. (2003; 2005; 2008) were the first to demonstrate that cyclic flexure can independently influence the in vitro development of a tissue engineered heart valve (TEHV). The goal of these studies was not to reproduce the material properties of semilunar valve native tissues or engineered valve tissue properties obtained in vivo after implantation in sheep in the pulmonary position (Sutherland et al. 2005), but rather to develop a fundamental understanding how cyclic flexural loading affects the development of TEHV, in particular, the development of ECM in TEHV, and, concomitantly, its stiffness. The choice of a highly controllable culture system with idealized geometry is crucial to this be able to discern and establish cause-effect relationships (a brief summary of the experimental protocols of Engelmayr et al. (2003; 2005; 2008) is summarized in Table 1).
Table 1.
Experimental findings previously presented in Engelmayr et al. (2003; 2005; 2008).
| Scaffolds | non-woven 50:50 PGA-PLLA fibers, Rectangular with dimensions 25 × 7.5 × 1 mm |
| Cells | Ovine vascular smooth muscle cells (carotid artery, adult Dover sheep) Seeded at 17 × 106 cells/cm2 |
| Mechanical training | Uni-direction cyclic flexure at 1 Hz with central displacement of 6.35 mm for 3 weeks Static control group for 3 weeks |
| Biochemical assaying | DNA (PicoGreen dSDNA), Collagen (Sircol), Elastic (Fastin), S-GAG (Blyscan) Conducted at t = 3wk for both training regimes |
| Histology and staining | Hematoxylin and Eosin, Movant pentachrome, picro-sirius red Conducted at 3 weeks for both training regimes Transmural cell distribution obtained from nuclei count on Movat-stained photomicrographs Transmural collagen distribution obtained from fluorescent intensity in picro-sirius red grayscale images |
| Effective stiffness | 3-point flexure (applied moment vs change in curvature) Flexural rigidity from least squares fit of the Bernoulli-Euler moment-curvature relationship Conducted at t = 0 and at t = 3 wk for both training regimes |
These studies (2003; 2005; 2008) utilized rectangular shaped scaffolds of nonwoven 50:50 blend PGA/PLLA scaffolds seeded with vascular smooth muscle cells (VSMCs) subjected to cyclic flexure, one of the primary modes of valvular deformations, with a frequency of 1 Hz for a period of 3 weeks. A 63% increase in collagen concentration when compared with static culture was observed, indicating that mechanical conditioning enhances ECM production. Moreover, cyclic flexure was found to improve significantly the homogeneity of the distribution of ECM across the thickness of the construct, as opposed to cell and ECM deprived regions observed in the middle of the statically cultured construct. An amplifying effect on the stiffness of the construct with the amount of ECM deposited occurred due to an increase of the number of rigidly-bonded fiber-fiber cross-over points (Engelmayr and Sacks 2008). A trend of increased stiffness of the ECM deposited in addition to a substantially augmented ECM concentration was observed – mechanical conditioning primarily affected collagen quantity, but it also appeared to affect the structural-mechanical quality of the ECM produced.
2.2. Modeling engineered tissue growth
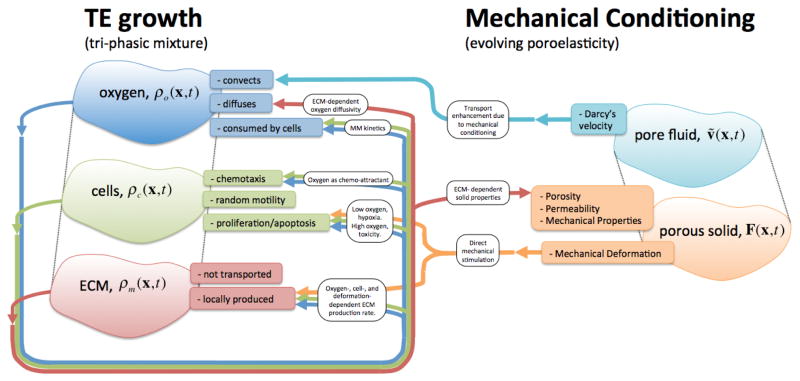
We model the TE construct as an evolving triphasic mixture composed of (Figure 1): (i) a dissolved chemical agent representing the combined nutrients needed for the cells to operate, which we consider as oxygen, with partial density ρo(x,t); (ii) a cellular phase ρc(x,t) onto which we lump all different types and stages of existing cells; and (iii) a ECM phase ρm(x,t), which comprises the forming engineered dense connective tissue.
Figure 1.
Schematic of the engineered tissue growth and development model, the ECM-evolving poroelastic material, and their two-way couplings. The tri-phasic mixture model describes the interplay between nutrient, cells, and ECM in an evolving construct. Upon mechanical conditioning, not only nutrient transport is augmented by convection through seepage velocity, but also cell proliferation and ECM synthesis are directly stimulated by the deformation.
2.2.1. Nutrients
Oxygen diffuses accordingly to a Fick-like diffusion law with an ECM-dependent diffusivity Do = Do(ρm), is transported with solvent velocity field v̂ = v̂(x,t) (respective to the construct), and is consumed by cells with reaction rate qo = qo(ρc, ρo) (Figure 1). Balance of mass results in the governing equation for dissolved oxygen, which assuming incompressible solvent (i.e. ∇·v̂ = 0), is given by
| (2.1) |
ECM-dependent oxygen diffusivity decreases as the empty volume of the scaffold is occupied by cells and newly synthesized ECM. Wood et al. (2002) have found that effective diffusivity in cellular systems is somewhat insensitive to the detailed geometric structure of the system, whereas it is primarily influenced by the volume fractions of the extra- and intra-cellular spaces. We employ , a non-dimensional measure of ECM, to modulate oxygen diffusivity as the construct grows and evolves over time: ρ̃m → 0, represents the initial diffusivity of oxygen in the scaffold devoid of ECM material, whereas ρ̃m → 1, corresponds to the diffusivity of oxygen in native tissue or in engineered tissue at the limiting steady-state of cultivation at a balance of production, degradation, and incorporation of collagen. The functional form of the ECM-dependent oxygen diffusivity Do = Do(ρm) is detailed in Appendix.
Oxygen consumption rate qo = qo(ρc, ρo) by the cellular phase is widely reported to follow Michaelis-Menten kinetics in engineered tissues (Galban and Locke 1999a; 1999l; Obradovic et al. 2000; Pathi et al. 2005; Zhao et al. 2005), i.e.
| (2.2) |
where Qo is the maximal oxygen consumption rate and is the oxygen for half-maximal consumption.
2.2.2. Cells
Cells proliferate or apoptose accordingly to their local nutrient environment, and move by chemotaxis in response to chemo attractants (Figure 1). With the objective of enriching the model, we allow cells to move due to chemotaxis with the nutrient phase acting as chemo attractant. We consider a “volume-filling” Keller-Segel-type chemotaxis model (Hillen and Painter 2009; Keller and Segel 1971). Balance of cell population results in the governing equation for the cell phase, given by
| (2.3) |
where Dc is the diffusivity of the cell phase (which describes random movement and drives cellular spatial spreading), χ is the chemotactic sensitivity (which drives cellular movement in the direction of increasing oxygen gradients), and gc = gc(ρc, ρo) is the cellular growth rate. If oxygen concentration is held fixed over time, cellular growth occurs in a sigmoidal kinetics
| (2.4) |
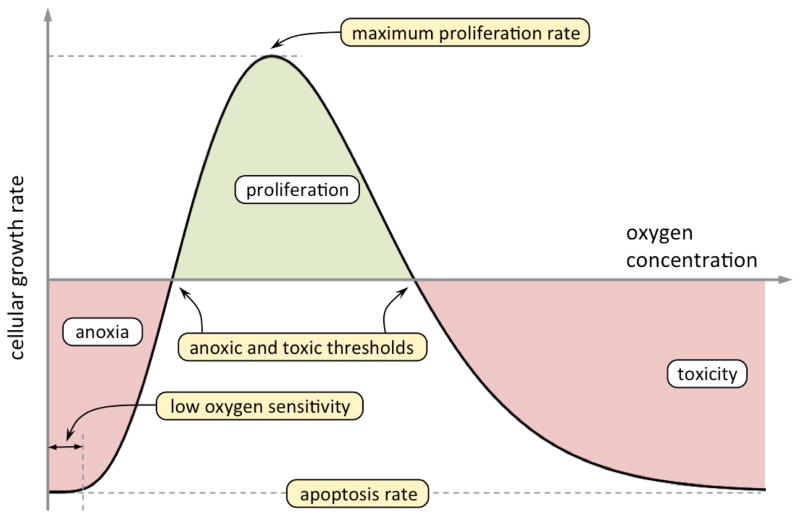
with an oxygen-dependent cellular proliferation/apoptosis rate, kc = kc(ρo). Cellular proliferation is slower when cell density is low due to replication limitations and when cell density is close to maximum upon confluency. Furthermore, cells experience growth inhibition and apoptosis at toxic and anoxic oxygen concentrations. Oxygen is the growth-limiting phase and we specify rate of proliferation/apoptosis kc based on Moser’s growth kinetics to describe anoxia insensitivity (Kovarova-Kovar and Egli 1998), and Aiba et al. (2000) inhibition kinetics to describe high oxygen concentration toxicity. Practically, this results in results in kc < 0 for low and high concentrations of oxygen, and in kc > 0 for a region in between where oxygen conditions allow proliferation to occur (Figure 2, functional form detailed in Appendix).
Figure 2.
Schematic plot of the oxygen-dependent rate of cell proliferation/apoptosis. Cellular apoptosis occurs at low and at high levels of oxygen (anoxia and toxicity respectively, labeled in red), whereas cells proliferate when fed with optimal conditions of oxygen (labeled in green). The 5 constants in the growth kinetics function (in Equation (A.6)) can be determined by experimental data reduction over the entire curve or by educated estimation of 5 independent measures in the curve (maximum rates of proliferation and apoptosis and anoxic and toxic thresholds, highlighted in yellow).
2.2.3. Extracellular matrix
Oxygen-fed cells synthesize collagen and mediate its self-assemblage into the extracellular matrix (Figure 1). In healthy tissues in-vivo, cells maintain steady-state metabolism of ECM by balancing its continuous production and degradation. In engineered constructs, growth and development of dense connective tissue is not driven by homeostatic equilibrium, but instead, by programmed developmental cues in pro-development environments. Matrix deposition usually begins at the periphery where an oxygen-rich environment promotes higher cell density and more ECM synthesis, but a limiting steady-state is approached at which there is balance of production, degradation, and incorporation of collagen. Locally produced matrix is tightly bound and consequently does not diffuse nor is transported. The governing equation for the matrix phase is given by
| (2.5) |
where km = km(ρo) is the oxygen-dependent ECM production rate. We consider km ≥ 0 as the net production rate of ECM in the growing engineered tissue, as opposed to traditional growth & remodeling frameworks where production and degradation terms are explicitly split such that homeostatic ECM turn-over and remodeling can occur (Humphrey and Rajagopal 2002) – the driving force of de novo ECM synthesis in tissue engineering has substantially different characteristics.
We consider a threshold oxygen concentration that changes cell phenotype from quiescent (rate of ECM production km = 0 if to synthetic. In the synthetic regime, we employ Obradovic et al. (Obradovic et al. 2000) assumption of 1st order kinetics. Lastly, ECM production can be modulated directly by mechanical stimulation, i.e.
| (2.6) |
where is a basal matrix production rate (when strains are zero) and k̄m(C) is a strain-dependent production rate where C is the right Cauchy-Green stretch tensor representing the deformation of the construct, defined as C = FTF with F being the deformation gradient.
2.3. Modeling dynamic mechanical conditioning
Engineered tissue constructs are time evolving porous materials. Scaffolds are usually highly porous by design such that cells and newly produced ECM occupy their voids and form tissue. Macroscopic deformations translate to microstructural deformations and ultimately act as direct cellular mechanical stimuli and may trigger biochemical changes and modulate cellular behavior. Mechanical conditioning also promotes fluid movement in the pore space, resulting in enhanced oxygen transport, augmented ECM production, and better biological outcomes. The coupling between mechanical deformation and enhanced oxygen transport is properly described with the employment of poroelastic models. We employ the u-p classical formulation of finite poroelasticity (Coussy and Coussy 2004) (see Appendix).
Extracellular matrix plays major role in modulating the porosity φ0, permeability k, and mechanical properties of the construct (Figure 1). These material parameters to be material functions of the local amount of ECM instead of material constants, i.e.
| (2.7) |
| (2.8) |
linear on ρ̃m changing from properties pertinent to the initial scaffold to properties characterizing native tissue or engineered tissue at its final steady-state cultivation stage (when ρ̃m = 0 and ρ̃m = 1 respectively).
The poroelastic material evolves and stiffens as more ECM is produced, and we model the solid constituent mechanical response with a stored energy density function modulated by the amount of ECM present locally
| (2.9) |
where the first term Ws represents the contribution of the scaffold (existing alone initially when ρ̃m = 0 and not changing over time) and the second term Wm represents the contribution from the ECM currently existing. We consider a deformation-dependent stiffening effect, i.e. mechanical stimulation acts as trigger for the development of stiffer ECM. Specifically, ECM that is produced under high strains is stiffer than ECM produced at lower strains. We employ a similar form of Humphrey and Rajagopal (2002) and consider the ECM contribution towards the stored energy function of the solid constituent as function of the strain history and matrix production rate, i.e.
| (2.10) |
where and Ct(s) = C(t − s) with s ∈ (0,t) are the histories of ECM composition and deformation. Stiffening rate W̄m = W̄m(Ct(s)) modulates the contribution of each infinitesimal portion of produced ECM towards the total stored energy density function of the ECM and is given by
| (2.11) |
where is a basal stiffening, that results in ECM obtained without any mechanical conditioning, and a deformation-dependent stiffening enhancement w̄m(Ct(s)) that depends on the deformation experienced at the time that each infinitesimal portion of ECM was produced. Equation (2.9) implicitly assumes that the stress free configuration of the ECM component is the same as the scaffold – however, a more general setting could be considered where residual stresses on the ECM are relevant and could be accounted either with a pre-stress term or with a different reference configuration for the ECM component.
Although any hyperelastic material model can be employed in Equation (2.9), we consider both contributions onto the stored energy to follow compressible neo-Hookean specific form given by
| (2.12) |
where μ and K are the shear and bulk moduli respectively, and Ī1 is the first principal invariant of the deviatoric strain tensor C̄ defined as C̄ = J−2/3C. In the small strain limit, shear and bulk moduli can be estimated from mechanical properties inferred experimentally by Englemayr et al. (2005) using 3-point bending through μ = E/2(1+ν) and K = E/3(1−2ν) respectively, where E and ν are the Young’s modulus and the Poisson’s ratio. The material model of the solid constituent is thus a two-parameter family of neo-Hookean solids modulated by its evolving mechanical properties (not material constants, but material functions dependent on the spatial distribution of ECM ρ̃m). Poisson’s ratio of the solid mixture of scaffold and deposited ECM evolves linearly from the highly compressible scaffold to the nearly incompressible tissue as
| (2.13) |
where νs and νt are the Poisson’s ratios of initial scaffold and steady-state cultured tissue respectively. Young’s modulus is history-dependent to allow the description of the effects of ECM-strengthening due to deformation, and from Equation (2.10) its evolution results in
| (2.14) |
where Es is the Young’s modulus of the scaffold and the second term represents the stiffening effect of ECM produced at different deformations. No ECM-strengthening effects are present under static conditions, and thus the Young’s modulus of the solid constituent results in when no conditioning regime is applied to the construct.
2.4. Solution methods
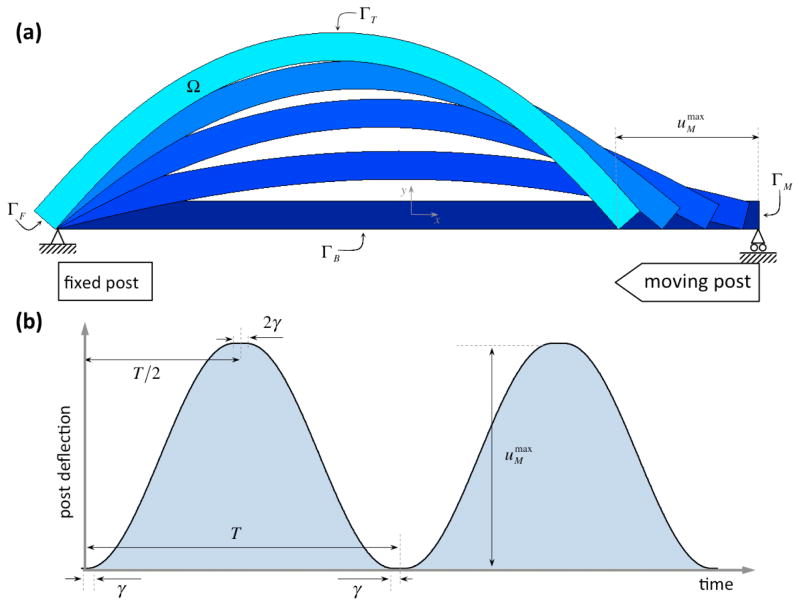
We simulate growth and development of dense connective tissue in rectangular constructs subjected to the flexure cycles of Engelmayr et al. (2003; 2005; 2008) of period of T = 1 s and moving post translation of (Figure 3). We non-dimensionalize the dependent variables of the governing equations and model parameters were determined with available data in the literature. Initial and boundary conditions, the non-dimensionalization procedure, and parameter determination are detailed in Appendix (model parameters are summarized in Tables 2 and 3).
Figure 3.
Schematic plot of (a) the bioreactor setup and (b) the temporal evolution post deflection uM (t). We define the motion to be smooth in order to ensure computational ease: (i) the period T and amplitude fully characterize each conditioning protocol, (ii) inward and outward motions are described with sinusoidal functions, and (iii) a short threshold time γ ≪ T during which the straight at flexed positions are held at rest before motion reversal is considered.
Table 2.
Parameter set of the TE growth model.
| Non-dimensional Parameter | Dimensional values in Equations (2.1), (2.3), and (2.5) | Reference | Non-dimensional Values in Equations (A.1)–(A.3) | |||
|---|---|---|---|---|---|---|
|
|
|
Zhao et al. (2005) | ||||
|
|
|
Engelmayr et al. (2005) | ||||
|
|
|
Lis et al. (1987) | ||||
|
|
Qo = 1.25·10−17 molO2·cell−1·s−1 | Pathi et al. (2005), Zhao et al. (2005) | Q̃o = 8.393·10−4 | |||
|
|
|
Pathi et al. (2005), Zhao et al. (2005) |
|
|||
|
|
|
Engelmayr et al. (2006) |
|
|||
|
|
χ = 0 | χ̃ = 0 | ||||
|
|
ka = 705 [cell·cm−3]−1·s−1 | Galban and Locke (1999a; 1999l) | k̃a=1·10−5 s−1 | |||
|
|
|
Galban and Locke (1999a; 1999l) |
|
|||
|
|
k̃p = 2.6·109 | |||||
|
|
k̃i =14 | |||||
|
|
|
|||||
|
|
|
|
||||
|
|
|
Obradovic et al. (2000) | k̃m = 1.675·10−7 | |||
| k̄m | k̄m = 0 |
Table 3.
Parameter set of the evolving poroelastic model.
| Parameter | Value | Reference | ||
|---|---|---|---|---|
| Es | Es = 174 ± 22 kPa | Engelmayr et al. (2005) | ||
|
|
|
Engelmayr et al. (2005) | ||
| νs | νs = 0.1 | |||
| kρ̃m=0 | kρ̃m=0 = 10kρ̃m=1 = 3.66·10−8 cm·s−1 | Galban and Locke (1999a; 1999l) | ||
|
|
|
Lovich and Edelman (1996) | ||
| νt | νt = 0.45 | |||
| kρ̃m=1 | kρ̃m=1 = 3.66·10−7 cm·s−1 | Harrison and Massaro (1976) | ||
|
|
|
Engelmayr et al. (2005) |
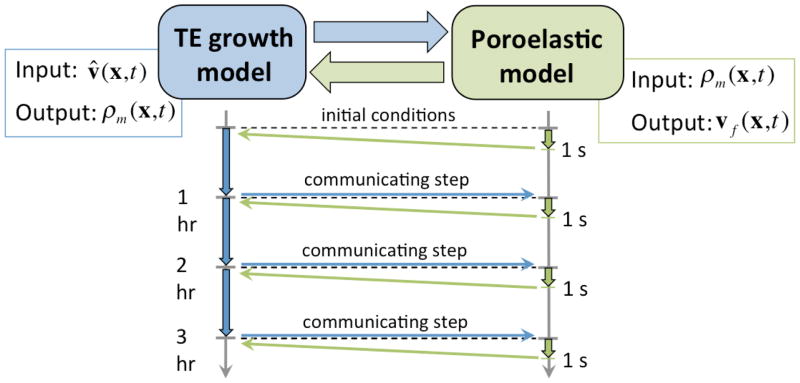
Two distinct time scales characterize this problem: (i) nutrient consumption, cellular proliferation and ECM synthesis occurs at very slow rates over the course of several weeks to months, whereas (ii) cyclic mechanical conditioning protocols are usually conducted at frequencies of around 1 Hz. Tissue engineering constructs undergo millions of conditioning cycles during the time period of interest and each cycle individually has little impact on cellular proliferation and ECM synthesis. However mechanical conditioning impacts ECM growth and development on longer time scales. We develop a time-lumping alternating scheme strategy composed of: (i) solve the mechanical deformation for a single cycle with current state of construct; (ii) lump its impact into the growth model through enhanced nutrient transport resulting from convection due to seepage; (iii) solve the TE growth model for a larger time period (Figure 4).
Figure 4.
Schematic of the multiscale methodology coupling the TE growth model and the mechanical conditioning poroelastic model. Nutrient transport and consumption, cellular proliferation and ECM synthesis occur at rates of days to weeks, whereas effective mechanical conditioning protocols are highly dynamic with frequencies around 1 Hz. Pore fluid velocity is obtained as a solution of the poroelastic model and is upscaled into the advection term TE growth model to enhance nutrient transport due to mechanical deformation. Conversely, spatial dependent ECM distributions are obtained as solutions of the TE growth model and are employed to modulate the poroelastic characteristics of the TE construct.
The initial poroelastic step is characterized by ρm = 0 everywhere and its solution for one cycle results in the Darcy’s velocity field vf(x,t) for all x and t ∈ [0,T]. Darcy’s velocity field is time averaged over the cycle to obtain the convection velocity field v̂ present in Equation (2.1) through
| (2.15) |
where C is a lumping constant. It must be noted that if the fluid is incompressible and changes in porosity are small, then div vf ≈ 0, and consequently div v̂ ≈ 0. Convection velocity field v̂ is then employed to solve the growth model for a larger period of time t ∈ [0,Tg], which we set as Tg = 20,000 s ≈ 5.5 hr. Subsequently, ECM present at the end of this timestep ρm(x,Tg) is employed to solve the next cycles of the poroelastic model (for t ∈ [Tg,Tg + T] but now with different poroelastic properties), and results in another convection velocity field v̂, which then is employed during the next step of the growth model for t ∈ [Tg,2Tg] (Figure 4).
2.5. Computational Simulations
We implement the present framework into Abaqus (Dassault Systemes, Waltham, MA) and conduct simulations to predict results of both conditioning regimes studied by Engelmayr et al. (2005; 2008): (i) static for t = 3 weeks, and (ii) dynamic flexure at 1 Hz for t = 3 weeks. Lastly, we investigate the impact on cellular proliferation and ECM production of multiple conditioning frequencies and degrees of flexure. We perform parametric variations on T and on – more precisely, we will consider two additional scenarios on each conditioning parameter, (i) doubling and halving the frequency of the mechanical conditioning, and (ii) increasing and decreasing flexure curvature considering post displacements of 10.00 mm and 2.50 mm respectively.
3. RESULTS
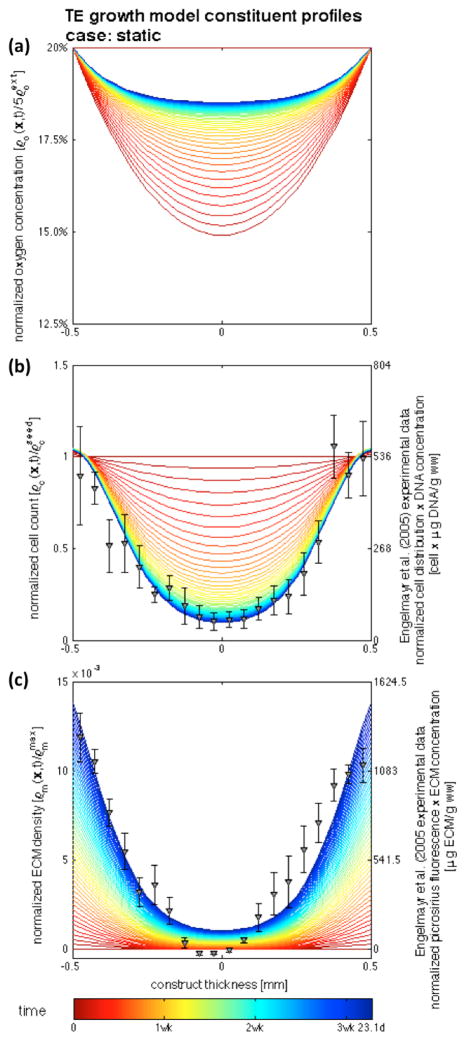
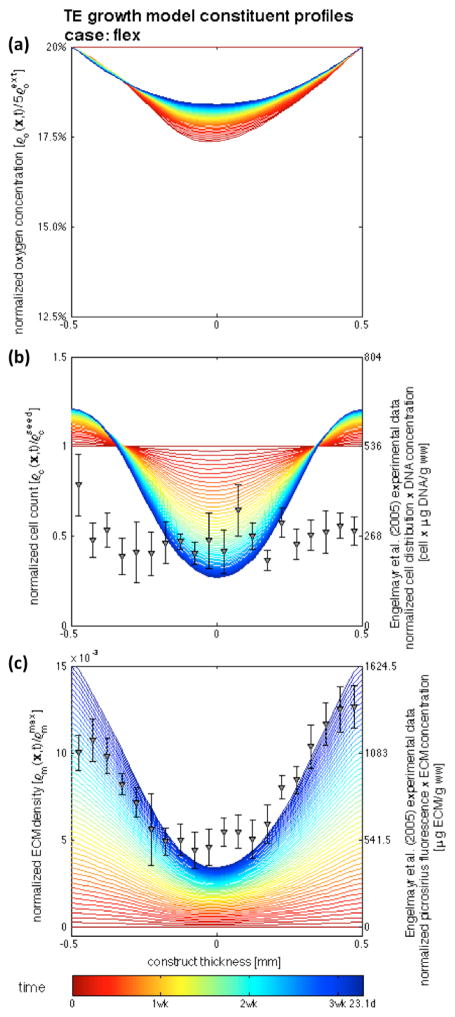
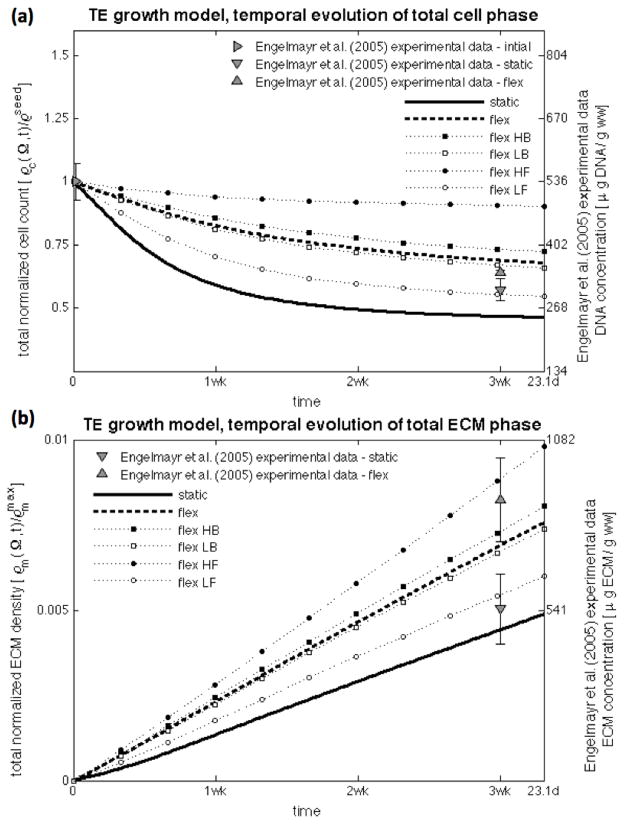
Simulations conducted up to 3.31 weeks demonstrated good agreement on the cell and ECM profiles with the experimental findings of Engelmayr et al. (2005; 2008) of engineered tissue construct development under static culture and mechanical dynamic conditioning. The chief feature of the model is its ability to distinguish the substantial differences in between both incubation regimes (Figures 5 and 7, dots – experimental data at 3 weeks, lines – model results at the central transmural section from t = 0 (red) to t = tmax = 2,000,000 s (blue) with Δt = 200,000 s). Experimental cellular profiles were obtained with a combination of: (i) DNA assay of the construct, which resulted in 536±38 μg/g ww after 30 hours seeding period, and 307±23 and 344±5 μg/g ww for the static and flex groups after 3 weeks of incubation, and (ii) transmural normalized cell count distribution determined by nuclei counts on Movat-stained histological sections. ECM experimental measurements were obtained similarly with: (i) biochemical assay data, which resulted in 0.546±0.111 and 0.846±0.113 mg/g ww on the static and flex groups respectively; and (ii) spatial determination of fluorescence micrographs of picro-sirius red collagen stained engineered constructs (cf. Engelmayr et al. (2005; 2008) for full details).
Figure 5.
Temporal evolution of nutrient, cell, and matrix profiles at the central transmural cross-section of the construct for the static case. Colored lines represent the evolution of the model solution, markers represent experimental data of Engelmayr et al. (2005; 2008) – (a) the nutrient flux across the boundary is not able to supply and maintain the initially seeded cell profile, (b) leading to cellular apoptosis in the middle of the construct due to oxygen deprivation, while (c) cell proliferation and an augmented rate of ECM production occur near the boundaries of the construct.
Figure 7.
Temporal evolution of nutrient, cell, and matrix profiles at the center of the construct for the flex case: (a) nutrient transport is enhanced with convection of pore fluid, (b) the increase of available nutrient supply is able to sustain more cells at deeper regions of the construct, and consequently (c) more ECM is synthesized. The chief feature of the framework is the ability of distinguish between both incubation regimes.
3.1. Engineered Tissue Growth under Static Conditions
Cellular oxygen consumption decreases the amount of oxygen in the construct (Figure 5a), and apoptosis occurs in the middle region due to oxygen deprivation (Figure 5b). Cellular proliferation occurs near the boundaries, which in turn increases produced ECM and further hinders the supply of oxygen. The process of cellular proliferation/apoptosis balances locally with the processes of oxygen consumption and supply – a certain specific cellular quantity is able to be sustained at each location of the construct, causing the cellular and oxygen profiles to balance and tend towards an equilibrium and remain mostly unchanged for the latter periods of the simulations.
The production of ECM in the inner region of the construct is substantially lower than in the periphery – as time progresses, the ECM profile observed experimentally by Engelmayr et al. (2005; 2008) is achieved (Figure 5c). The model prediction agrees generally well with the experimental data, however slight disagreement occurs in the middle of the construct where measurements of near-zero and negative fluorescence were reported experimentally. The representative micrograph (cf. Figure 5 of Engemayr et al. (2008)) exhibits minimal ECM presence in this region; however, this might be an artifact of the fluorescence normalization (cf. the modified Movat Pentacrome stained sections in Figure 3 of Engelmayr et al. (2005) clearly demonstrate the existence of collagen in the middle of the statically cultured constructs).
3.2. Mechanically Conditioned Engineered Tissue Growth
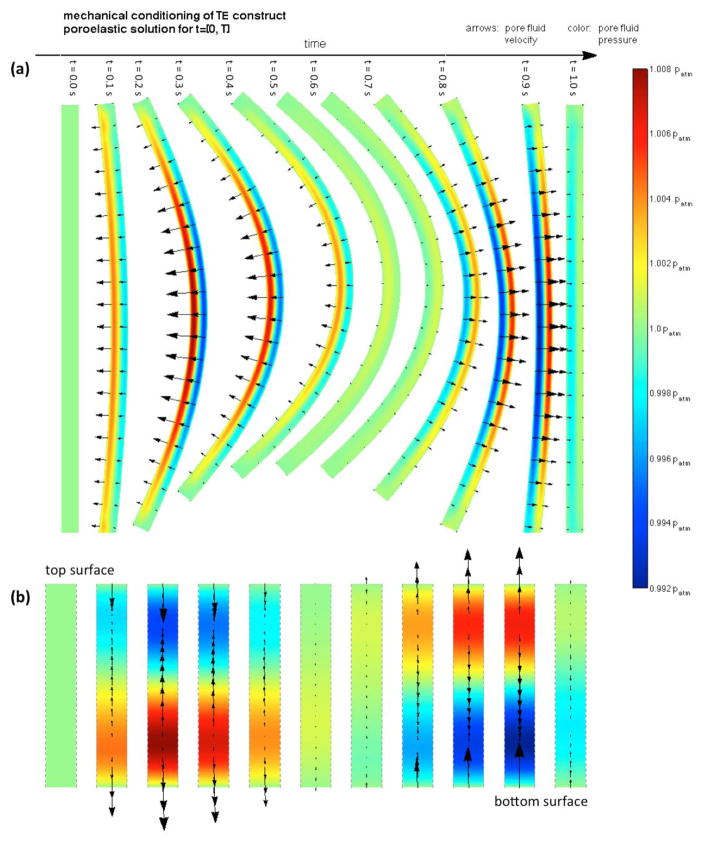
Complex fluid flow patterns occur through the pores of the construct during each mechanical cycle due to the deformation of the poroelastic material (Figure 6 showing the pore flow field observed at t = [0,T], ρ̃m = 0). A strong initial ejection of fluid occurs from the bottom surface when flexion initiates as this region is compressed, the current porosity decreases, and the pore pressure increases. At the same time, the top layers are subjected to tension/expansion – the porosity increases, pressure decreases, and fluid uptake occurs in the top surface to saturate the augmented void space. Consequently, pore fluid is driven upwards upon flexion during most of the first half of flexing cycle. Fluid then comes to rest in the fully bent configuration, and upon deflection, reversed but approximately similar flow fields occur. A certain degree of lateral flow is observed, but with velocities several orders of magnitude lower than transversal flow velocities. The flow field evolves as ECM is deposited in the porous construct in an inhomogeneous process and its poroelastic characteristics evolve (not shown).
Figure 6.
Poroelastic solution of the mechanical conditioning cycle occurring at t ∈ [0,T]. The flow field inside the construct during each cycle is substantially complex: (a) entire construct, (b) detail of the flow field occurring at the central transmural cross-section. A strong initial ejection of fluid from the bottom surface occurs when flexion initiates as this region compresses, its pore space decreases and pore pressure increases. On the other hand, fluid uptake occurs at the top surface as pore space increases. Upon deflection, reversed but approximately flow fields occur.
The experimental observations of Engelmayr et al. (2005; 2008) of tissue engineering subjected to flexure conditioning are also well approximated (Figure 7). Nutrient transport and supply is enhanced with convection of pore fluid and is able to sustain more cells at deeper regions of the construct – and consequently, more ECM is synthesized. Engelmayr et al. (2005; 2008) has observed similar tissue formation in the regions near the edges of the construct in both the static and flexed conditions, whereas a significantly different amount of ECM was present in the middle – the simulation results describe effectively such behavior (Figure 7c for the flex conditions, Figure 5c for the static conditions). In regard to cell amount, the simulation is able to approximate acceptably well the middle region, yet fails to match the regions near the edges of the scaffold – a higher amount of cells than actually observed experimentally is predicted.
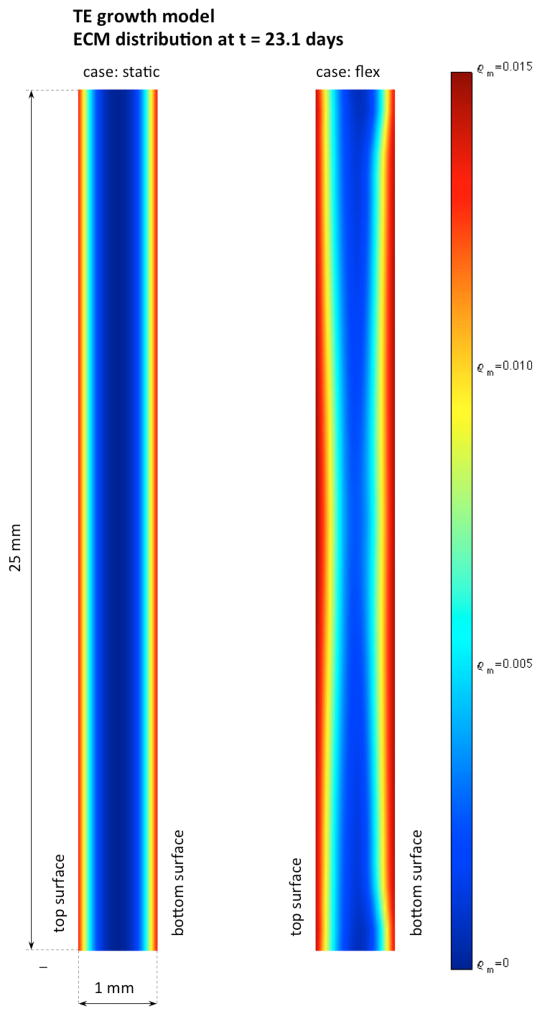
The highly localized and inhomogeneous pore flow field leads to spatially dependent growth and development of engineered tissue (Figure 8, not drawn to scale). Nutrient supply, cellular growth, and ECM synthesis are highest at the middle cross-sectional profile of the construct, while the edges of the construct suffer substantially lesser effects of mechanical conditioning. Although obtained with only one experimental point (at 3 weeks), the model is able to describe the differences in total mass of ECM and DNA due to the impact of mechanical conditioning (Figure 9a and 9b, lines – model simulation, markers – experimental observation). Higher ECM synthesis near the nutrient rich edges is also responsible for limiting nutrient transport to the middle region decreasing oxygen diffusivity, and construct porosity and permeability. Although this negative feedback mechanism would hamper tissue development, at the early development stage experimented by Engelmayr et al. (2005; 2008) with small collagen content is not very significant.
Figure 8.
Spatial distributions of ECM present at the end of the simulated time frame (23.1 days). Nutrient consumption, cellular proliferation/apoptosis, and ECM synthesis are highly inhomogeneous. The major impact of mechanical conditioning is observed at the center cross section where pore fluid convection is more intense, whereas the ends of the construct where pore fluid flow is negligible evolve in a similar fashion in both conditioning regimes.
Figure 9.
Temporal evolution of total mass of DNA (top) and ECM (bottom) in the construct for the static and flex cases (solid and dashed lines), and for parametric variations of the conditioning protocol (marked lines). Modeling allows the in-silico investigation of different conditioning regimes, and we observed that changing frequency has a more significant effect than changing the amount of flexure.
We have investigated the effects of different conditioning regimes in-silico, and have observed that changing frequency has a more significant effect than changing amount of flexure (Figure 9). Increases of each condition lead to augmented convection of pore fluid inside the construct, richer nutrient supply, increased ability to support a higher amount of cells across the construct, and consequently, enhanced ECM production. Decreased frequency of conditioning or less flexure leads to the reverse effect. The model is more sensitive to changing frequencies rather than changing amount of flexure – changing frequency inherently increases significantly the number of conditioning cycles.
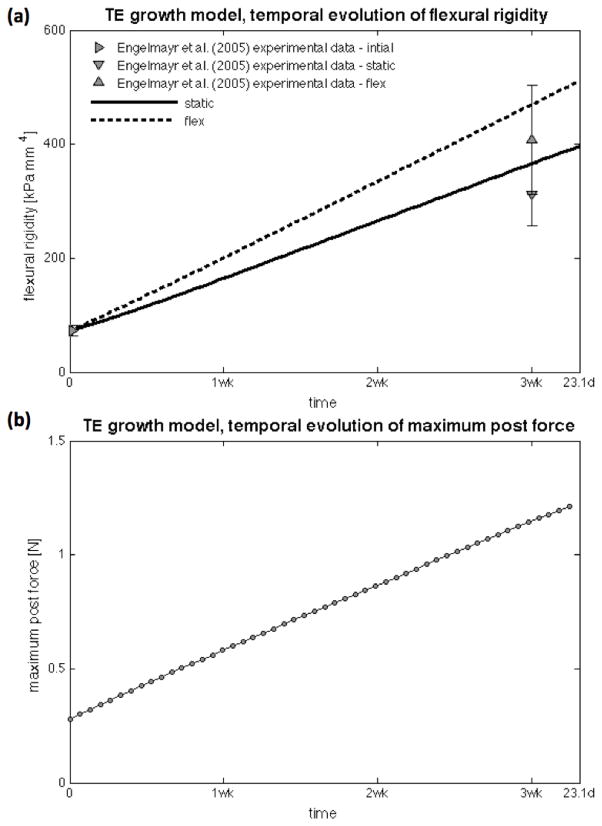
Lastly, as more ECM is produced and deposited in the construct, its flexural rigidity increases in a mildly nonlinear fashion as more ECM is deposited near the boundaries of the construct (Figure 10a). Flexural rigidity predicted by the framework was computed at the central transmural cross-section, whereas experimental flexural rigidities are computed with the experimentally obtained Young’s modulus by Engelmayr et al. (2005) assuming an homogeneous beam, i.e. EI = Eh3d/12 with Es = 174±22, Estatic= 748±130, and Eflex =978±228 kPa. Consequently, more force is necessary to perform the same conditioning cycle as time progresses (Figure 10b showing the maximum force occurring at the fully bent configuration), which is a direct measure of the strengthening effect of TE growth, can be easily predicted by the framework, and was not performed experimentally by Engelmayr et al. (2003; 2005; 2008).
Figure 10.
Temporal evolution of flexural rigidity EI(t) (top) and necessary maximum post force for the conditioning cycle (bottom). As more ECM is deposited near the edges of the construct, its flexural rigidity increases in a nonlinear fashion. As expected, a higher force is necessary to perform the same mechanical conditioning cycle as the TE construct growths.
4. DISCUSSION
4.1. A novel triphasic model for mechanically conditioned engineered tissues
We have developed a novel theoretical framework for mechanically conditioned TE based on a triphasic mixture composed of nutrient, cell, and matrix components. Specific mechanisms included are: (i) nutrient transport and consumption throughout the construct; (ii) cell transport, proliferation and apoptosis; and (iii) localized ECM synthesis as a function of nutrient and cell availability. To account for the effects of mechanical conditioning, we allow the triphasic mixture to undergo mechanical deformation and employ general class of evolving poroelastic models with ECM-dependent properties (porosity, permeability and elasticity). Augmented ECM production and quality may occur not only because of enhanced nutrient availability due to pore fluid convection, but also by direct mechanical stimulation (Figure 1).
The significantly disparate characteristic time scales of mechanical conditioning regimes (generally conducted with frequencies of or around 1 Hz) and engineered tissue growth and ECM synthesis (generally on the order of weeks to months) requires a numerical strategy to couple both time scales in a computationally efficient manner and we have devised an alternating scheme with different decompositions of the time domain (Figure 4). We have not observed any problems with the behavior of our numerical methods – the nonlinearities present in the model are mild, the staggered algorithm couplings are rather direct, and solutions generally well-behaved. We demonstrate the ability of the framework to differentiate experimental data of Engelmayr et al. (2005; 2008) obtained with VSMC-seeded scaffolds under static and mechanically flexed conditions (Figures 5 and 7). Lastly, and with the objective of illustrating the utility of developing such rational tools for the in-silico investigation of different mechanical conditioning regimes, we conduct a parametric analysis of different conditioning protocols, namely changing the frequency and the amplitude of flexure (Figure 9).
Our framework improves current existing modeling approaches by including a third phase to describe independently cells and ECM. The advantage of a triphasic model over a biphasic one is directly related with the experimental dataset collected by Engelmayr et al. (2005; 2008), where independent measurements of the spatial distribution of cells and ECM were performed. However, we attempted to simplify the problem while still being able to capture the underlying phenomena and describe/predict quantitatively the experimentally observed outcomes. Our goal is not to develop an all-encompassing theory of engineered tissue growth, but instead to develop a theoretical framework to: (i) describe a specific dataset of the phenomena in question; (ii) provide further insight into hypothesis formulation on the mechanistic causes of the observed outcomes; and (iii) provide an applicable tool for the exploration of different conditioning regimes and guide further experimentation. To our knowledge, the integration of mechanical conditioning in TE growth models in connection with experimental data has never been pursued and that aspect is the major novelty of our approach. This phenomena has been extensively established experimentally by our group with VSMCs and bone marrow derived mesenchymal stem cells (MSCs) subjected to cyclic flexure and to large uniaxial stretches (Engelmayr et al. 2005; Engelmayr et al. 2006; Stella 2011), as well as by many others (cf. e.g. (Butler et al. 2000; Martin et al. 2004; Nerem 2003) and references therein).
However, the limited knowledge and available data hampers the development of rigorous thermodynamically-consistent frameworks stemming from the general postulates of the theory of reactive mixtures – an immense number of modeling assumptions would be necessary to be made, e.g.: (i) the number of constituents and their interactions, not only their interconnected mass productions/consumptions, but also their mechanical and electrochemical interactions; (ii) the formulation of conservation laws (of mass, momentum, and energy) for each constituent of the mixture would be rather difficult to reason, cast, or measure; and (iii) the mechanical contributions of individual mixture components, and most importantly, their evolution, along with the natural difficulty arising from the imposition of boundary conditions in mixtures.
Taking these difficulties into consideration, we have resorted to the strategy of simplification, while still being able to depict the phenomena at hand. From the biochemical standpoint, a higher number of phases would certainly be necessary to capture with fidelity all the details involved in TE growth and development: (i) multiple chemical species, e.g. oxygen, glucose, lactic acid, and a multitude of growth factors, signaling agents, transport proteins, do exist in the growing tissue, play a significant role in the process, and could/should be considered; (ii) the cellular phase could in fact be subdivided into multiple subspecies representing different cell types, e.g. cellular heterogeneity due to inhomogeneous differentiation, aging, or inherent functional differences such as proliferative or synthetic phenotypes; and (iii) ECM is indeed composed of distinct components, e.g. multiple types of collagen, elastin, and other proteic components, and glycosaminoglycans, which often happen with a large degree of heterogeneity. Although it is possible to differentiate some of the ECM constituents as the load-carrying components and some efforts have been made to model their effects and interactions at the microstructural level (distributions of collagen fiber orientation, crimping and recruitment), filler components are often disregarded but sometimes play a significant role (e.g. non-homogenous tissue swelling and Donnan osmotic pressure effects due to negatively charged proteoglycan content). Notwithstanding, the tractability of such complex approach would be minimal with the need for characterization of so many inter-relationships.
From the mechanical standpoint, we simplify the phenomena to an evolving poroelastic material of one solid and one fluid constituent. The evolution of the solid phase is determined by the current biochemical composition dictated by the reaction equation governing ECM production. ECM production is thus not directly associated with any particular configuration of the deformable poroelastic evolving material – we implicitly assume that de novo ECM is being laid down stress free at the straight configuration (as translated by Equation (2.9)). Certainly residual stresses can play very important roles in biological tissues and in growth and remodeling phenomena, specifically in long-term quasi-static adaptive processes driven by homeostatic equilibrium (Baek et al. 2006; Humphrey and Rajagopal 2002), however we are of the opinion that the quality and maturity of the ECM produced in our specific tissue engineering system is rather low to grant residual stresses in the construct. Moreover, with the inability to observe any related phenomena experimentally, this can only be contemplated as a valid hypothesis that would need extra modeling assumptions to be introduced and tackled, however, of sufficient importance and relevance to grant further investigation.
4.2. Mathematical Modeling in Tissue Engineering
Mathematical modeling of TE has been scant and mainly focused towards the understanding of the observed heterogeneity in engineered tissues. Galban and Locke (1997; 1999a; 1999l) must be recognized for bringing mathematical modeling into the field – their seminal transport and growth modeling of chondrocytes established the direction the field needs to take. Freed and co-workers (1998, 1994) had investigated and identified experimentally key physical/chemical parameters to aid in determining the most favorable conditions for in-vitro chondrogenesis (e.g. scaffold thickness and initial cell density) and have concluded that cell growth in the inner parts of the constructs was inhibited due to transport limitations. With this empirical evidence, Galban and Locke (1997; 1999a; 1999l) systematized engineered tissue growth under static conditions with a two-species (cells and nutrients) volume-averaged reaction-diffusion model and have qualitatively predicted trends observed by Freed et al. (1998; 1994). Galban and Locke fairly recognize the two-fold limitations of their modeling effort: (i) the influence of extracellular matrix on cell growth was not accounted, and (ii) experimentation is necessary to render the model quantitative and obtain a more detailed understanding of the factors governing engineered tissue growth. Whereas the former has, to our knowledge, never been tackled in full, Locke and co-workers have established a couple attempts to connect their modeling effort with a detailed experimental system – with the objective of improving the productivity of their perfusion bioreactor and sustaining a spatially uniform construct development with high cellular and ECM densities, Pathi et al. (2005) and Zhao et al. (2005) have conducted experiments and simulations to investigate the role of nutrient (oxygen) transport in the proliferation of granulocyte progenitor cells and human MSCs.
Obradovic et al. (2000) developed a two-species (oxygen-GAGs) reaction-diffusion system to rationalize GAG concentration profiles measured as a function of cultivation time in disc-shaped cartilage constructs under static conditions. Model simulations and experimental data reduction supported two hypothesis on GAG synthesis: (i) first-order dependence on oxygen concentration, and (ii) product inhibition, albeit the authors correctly recognize that the exact mechanisms that regulate the process remain largely unknown. Although their model grossly approximates the processes that control tissue development and their assumptions and simplifications at least do not distort actual behavior, Obradovic et al. (2000) acknowledge that other aspects of tissue development such as cell growth and collagen deposition must be incorporated in order for the model to serve as a predictive tool.
Only sufficient experimental data and careful validation may render any modeling effort with practical use, and only a few attempts have been pursued and reported – similar reaction-diffusion systems have been employed by others to other engineered tissue growth experiments, most often biphasic models (cells and nutrient) with disk geometries under static culture conditions: (i) Lewis et al. (2005) employed the experimental data of Malda et al. (2004) with bovine chondrocytes in PEGT/PBT scaffolds cultured up to 6 weeks in spinner flasks to develop an single phase model of oxygen transport and consumption and have concluded that growth heterogeneity is an inevitable outcome of cellular consumption and transport limitations; (ii) Brown et al. (2007) obtained engineered heart tissues from neonatal rat ventricular myocytes in a cell culture incubator and developed a single-species reaction-diffusion equation to investigate the role of oxygen consumption and transport in cardiac TE; (iii) Demol et al. (2011) conducted experiments with human periosteum derived cells seeded in fibrin hydrogels for bone TE applications and developed a biphasic cell-oxygen reaction-diffusion model to corroborate quantitatively the spatiotemporal distribution of cells; and lastly (iv) Sacco et al. (2011) fitted results of Raimondi et al. (2006) with a model that builds up on the volume average method employed by Galban and Locke (1999a; 1999l) and the biphasic approach of Chung et al. (2007) based on Stokes equation with Brinkman correction to treat perfused TE constructs.
These phenomenological based models were essentially developed towards the enrichment of the understanding of cartilage TE and modeled the effect of oxygen transport and the resultant inhomogeneity of cell and ECM distributions, but always, under static conditions only. Modeling of perfusion bioreactors with dynamic flow fields with rigid porous media have been subject of considerable attention (cf. e.g. Klein and Sah (2007) or O’Dea et al. (2013)). However, the effect of mechanical conditioning on cellular responses occurring in TE constructs has never been systematized and analyzed, at least with the objective of rendering the model practical and descriptive of a particular dataset.
On the other hand, the theory of mixtures has been employed by many in attempts to describe adaptive biological tissues that grow and remodel – efforts date back to Humphrey and co-workers in the vasculature, Mow and co-workers in cartilage, or Cowin and co-workers in bone, cf. (Ambrosi et al. 2011; Ateshian and Humphrey 2012). Several rigorous theoretical generalizations encompassing more phenomena associated with biochemical transport and deformation-modulated growth and remodeling, and their particularizations into models of this class for specific applications have been proposed (cf. Athesian and co-workers (2007, 2010, 2013), Garikipati and co-workers (2004), Klisch and co-workers (2005), among many others). Specifically targeting mechanically-conditioned tissue engineering applications, Sengers et al. (2004) have recast the classical equations of reactive mixtures into an abstract framework of an evolving biphasic poroelastic material, but have not particularized or rendered it practical and have fairly recognized the limit of its usefulness due to the lack of proper validation. Penta et al. (2014) developed a mathematical model for the macroscopic behavior of a porous, linear elastic deformable solid, saturated with a slowly flowing incompressible, viscous fluid, with surface accretion of the solid phase resulting in growth of the solid phase through mass exchange from the fluid. Penta et al. (2014) proposed engineered tissue growth under mechanical training as a possible application, but tactfully noted that model parameterization is a much broader issue given that mechanical, chemical and kinetic properties are both tissue and species-specific, and that motivates collaboration between biologists and mathematicians to close the data gap.
4.3 Modeling as a rational tool for experimental design
Several interesting features are observed with our simulations – the framework predicts the inhomogeneous evolution of cell and ECM distributions (cf. Figure 5b,c, Figure 7b,c, and Figure 8), and that both conditioning regimes are asymptotically similar at the longitudinal ends of the construct. One key aspect of our modeling effort is to guide and inform further experimentation, and consequently, to allow for a better design of conditioning protocols and experimental measurement techniques on subsequent experimental attempts. Particular examples of the former is the incorporation of more controllability of the conditioning cycle with multiple flexures and frequencies (Figure 9a,b), whereas examples of the latter is the extension of histologic protocols to longitudinal cross sections (Figure 8) or the measurement of the force necessary to perform the mechanical conditioning to allow the determination of its evolution (Figure 10b).
A more critical evaluation of the existing experimental data is also possible with our modeling framework – Engelmayr et al. (2005) have observed lower cell density near the boundaries of the flexed constructs when compared with the static constructs, however the fundamental mechanisms incorporated in our framework translate to enhanced proliferative conditions in this regions and a slightly increased amount is predicted (Figures 5b and 7b). This disagreement is debatable at first glance, but it must be remarked that cells near the boundaries of the construct are exposed to the outside environment, are subjected to the highest magnitude cyclic compressive/tensile strains, and also to high amplitude displacements. The combination of these experimental aspects might be responsible for some cells to fall from the construct, and consequently, result in a lower than expected experimental observation of cells and ECM near the boundaries of the construct. Modeling allows for a reassessment of the interpretation of experimental observations and may alert for possible phenomena or mechanisms that were not initially accounted for – in this particular case, cells falling out of the construct due to the high amplitude high frequency movement and the breakdown of the validity of the no-flux boundary condition for the cellular phase in the flex case. The experimental analysis of longitudinal cross sections would be crucial to analyze and possibly improve modeling aspects such as the imposition of boundary conditions – specifically, we assume that oxygen is held fixed at exterior concentration independent of length and face (top or bottom). These do not take into account any sort of exterior flow fields developing in the bioreactor with substantial length dependent surface pressure and shear stress (Ramaswamy et al. 2014), factors that might lead to an important and significant departure from the assumed conditions, specifically in the flex case.
With the aid of the proposed framework, development of further experimentation/validation can occur at three different levels: (i) to employ the same experimental set up of Engelmayr et al. (2005) and further validate the framework predictions with different conditions, specifically with different flexure conditioning regimes; (ii) to critically determine the parameters needed for the model, e.g. nutrient diffusivity with changing collagen content, or proliferation rate with changing oxygen concentration – in order to obtain them, new experiments with completely different concept must be designed and conducted; and lastly (iii) to scale up to richer mechanical problems such as e.g. biaxial stretch bioreactors or full blown TEHVs in organ level bioreactors (cf. experiments of Ramaswamy et al. (2010)). The governing equations would have to be solved with a completely different initial and boundary value problem, predictions could be computed and validated (particularly, the effects of different transvalvular pressures on ECM synthesis), and corroborated by another set of experiments, the framework would be a robust TE design tool to optimize in-silico conditioning parameters.
4.4. Modeling as a predictive tool for in-silico investigation and hypothesis formulation
Our framework also predicts other specific features – some obvious, e.g. the nonlinearity observed in the augmentation of the flexural rigidity over time (Figure 10a) can be reasoned directly from the observation of the inhomogeneity of the ECM transmural distribution and simple arguments of beam theory, while others are nontrivial and are only able to be discerned by conducting parametric investigations on the problem. One of such is the analysis of the effects of changing frequencies or changing degrees of flexure in the conditioning protocol, where we have found that the former has a more intense effect than the latter (Figure 9a,b). The reason for such is mainly due to a combined contribution of not only an augmented pore fluid flow, but also a substantial increase in number of conditioning cycles that changing frequencies entails.
Other rather interesting feature we have observed was the inherent equilibration of the dynamics of oxygen consumption and transport and cellular proliferation/apoptosis at each point of the construct. Oxygen and cell distributions change until equilibrium is reached, which occurs readily within the first week of incubation (Figures 5a,b and 7a,b). This equilibrium can be thought of as the local amount of oxygen maintains the current amount of existing cells (in particular, at the y axis intersection in Figure 2, the anoxic threshold). If pushed to marginally anoxic conditions, a fraction of cells die and deem the present oxygen supply sufficient or enough for the remaining to proliferate slightly; whereas under marginally proliferative conditions, a higher number of cells consume more oxygen, which results in an insufficient oxygen supply and slight apoptosis to adjust the cell population to the conditions present. Furthermore, the diffusional transport of oxygen is changed as more ECM is deposited, and consequently, the cell-oxygen equilibrium is slowly shifted over time (Figures 5a,b and 6a,b). Most importantly, our modeling framework allows us to determine the importance of convection in shifting this equilibrium state, as more nutrient can be supplied and a higher cell amount can be achieved. Several strategies are employed to promote convection as a developmental trigger to support higher and better cellular and ECM distributions than on static constructs: (i) mechanical training of porous constructs is a pumping mechanism that results in a convection flow field, and (ii) perfusion bioreactors drive nutrient-rich fluid flow through static constructs by means of a pressure differential (Pathi et al. 2005; Raimondi et al. 2006; Zhao et al. 2005).
Experimentation has been able to shed some light into the underlying mechanisms of engineered tissue growth, either mechanically conditioned or not. However, only with the aid of a sound theoretical framework further experimentation can be carefully designed to obtain relevant information not only to improve the fundamental understanding of the biochemical and biomechanical processes involved in TE but also to inform the next modeling steps and increase and advance the level of fidelity any particular framework can aim/achieve. Engelmayr et al. (2003; 2005; 2008) have conducted experiments to establish fundamental behavior, i.e. the authors have hypothesized and shown that if TE constructs were subjected to mechanical deformation, the cells are indeed led to produce and deposit more ECM in the construct over time. However, no particular mechanisms could be discerned with those experiments. The chief feature of our modeling framework relies on the hypothesis that the flow field occurring inside the porous construct due to mechanical condition is the mechanism responsible for a significant enhancement of the biochemical environment inside the construct, i.e. more nutrients are supplied to the cells.
The formulation and testing of further mechanistic hypothesis in TE is another crucial facet of our modeling effort. Convection enhanced nutrient transport due to pore fluid flow arising from mechanical deformation of the constructs seem to be enough to describe Engelmayr et al. (2005; 2008) experimental observations, but still, other mechanisms might play a major role and a sound theoretical framework allows the exploration of such. One particular mechanism that seems not to occur appreciably in Engelmayr et al. (2005; 2008) experiment is augmented ECM production and enhanced ECM quality due to mechanical stimulation (cf. the deformation dependent term in the ECM production term in Equation (2.6), and the deformation dependent term in the stored energy function of the porous construct in Equation (2.10)). Stella (2011) has demonstrated a dramatic increase of dense connective tissue formation upon stretching electrospun elastomeric scaffolds that are able to undergo much larger deformations than Engelmayr et al. (2003; 2005; 2008) non-woven scaffolds subjected to bending. Also, Stella (Stella 2011) has determined a significant increase in ECM stiffness, i.e. not only were cells stimulated to produce more quantity of collagen but also collagen of a better quality. Although we have included such possibilities in our modeling framework (cf. equations (2.6) and (2.10)), we are not able to ascertain any of these effects from Engelmayr et al. (2005; 2008) experiments and therefore we have chosen to disregard them, while still being able to discern the impact of mechanical conditioning upon ECM production. A similar argument was employed to disregard the effects of chemotaxis. These effects certainly enable a richer model (in the sense that a richer set of phenomenological behavior is able to be describe), but we have not included them due to the lack of critical data to characterize such complex phenomena.
Another key influencing factor in TE outcomes are the effects of pressure and oscillatory shear stress exerted on the surfaces of the construct due to exterior flow. Engelmayr et al. (2006) have conducted TE experiments with a similar set up but with MSCs and adding a component of exterior flow at physiological ranges, i.e. static, flex, flow, and flex-flow conditions. The authors have observed that mechanical conditioning and exterior flow have a synergistic effect on the response of MSCs in regard to matrix synthesis. When compared with their previous experiment with VSMCs, the observed DNA content with MSCs was significantly lower. On the other hand, the MSCs produced more GAGs than the VSMCs in all conditions. However, only the flex-flow conditions produced similar amounts of collagen as the flex condition with VSMCs, while under all other conditioning protocols, the amount of collagen produced was comparable to VSMCs under static conditions. Based on these experimental findings, Engelmayr et al. (2006) have extrapolated that this particular cell line (MSCs) require external flow to effectively differentiate to ECM-synthesizing cells. Although these experiments were conducted with a completely different goal and concept, they provide optimal insight for extensions of our modeling framework such as: (i) the influence of the exterior flow onto the growing construct, which can be included with the resolution of the external flow field with computational fluid dynamics and external flow-dependent mass convection and pressure boundary conditions supplied to the TE growth model and poroelastic model; and (ii) the inclusion of a more complex and descriptive framework that takes into account MSC differentiation, i.e. accounting for multiple cellular phases, and a differentiation pathway with a transported biochemical signaling agent as a differentiation mechanism.
4.5. Limitations
Accurate parameters are a necessity for the development of any model, and systematic experimental results are key for its validation. The dataset of Engelmayr et al. (2005; 2008) is the most complete experimental data currently available on both aspects; however, a complete working set of constants for the particular VSMC line is unavailable. We have employed constants of previously published studies, and/or reasonable estimates obtained from other relevant TE studies (e.g. Locke and co-workers (Pathi et al. 2005; Zhao et al. 2005) or Vunjak-Novakovic and co-workers (Freed et al. 1998; 1994; Obradovic et al. 1999; 2000)). This certainly limits predictive capability of the framework when particularized with the current parameter-set, but nonetheless, our framework is able to describe/predict Engelmayr et al. (2005; 2008) dataset with acceptable quality. Most importantly, our framework is cast in a general form such that extension to other conditions can be rendered, and trends upon changing conditions are able to be inferred – and that is our ultimate goal, to provide a methodology able to inform on how to improve dense connective tissue formation with mechanical conditioning to achieve better TE outcomes.
5. SUMMARY
We proposed a novel theoretical framework based on a triphasic mixture of nutrient-cell-ECM, governed by the mechanisms of: (i) nutrient transport (diffusion and convection), (ii) cellular nutrient consumption, (iii) nutrient-dependent cellular proliferation/apoptosis, and (iv) nutrient- and cell-dependent ECM synthesis. Mechanical conditioning enhanced engineered tissue growth is mainly due the augmentation of the nutrient supply upon convection of pore fluid inside the evolving porous TE construct, although direct stimulation improving not only ECM synthesis but also ECM stiffness can be accounted. Due to the disparate time scales of engineered tissue growth (weeks to months) and mechanical conditioning (with frequencies of 1 Hz), we devised a multi-scale time-coupling that allows the incorporation of the pore fluid flow field into the transport equation of oxygen. The proposed theoretical framework is, to our knowledge, the first to incorporate the effects of mechanically conditioning in engineered tissue growth in a systematic fashion and in connection with real experimental data. The framework is able to describe the experimental data observed by Engelmayr et al. (2005; 2008), and most importantly, to distinguish between the static and the flex conditioning regimes. Afterwards, we explored the impact of different regimes of the conditioning protocol – we conducted parametric studies on the influence of the frequency and the extent of flexure and have found that the former has a greater effect mainly due to the inherent increase in number of cycles associated with its variation.
The major driving force for our modeling effort is to add critical rationality to the field of tissue engineering in general by providing a framework that can be extended to the multiple variables existing in present day tissue engineering. Our particular goal is to obtain a robust tool that can be employed to: (i) optimize in-silico and cost-effectively mechanical conditioning protocols; (ii) formulate, explore and verify hypothesis of fundamental mechanisms of biological, biochemical and biomechanical function in TE; and (iii) aid further experimental design for parameter determination, model refinement, and ultimately, clinical translation.
Acknowledgments
Funding for this work was supported by NIH/NHLBI Grant R01 HL- 068816 and R01 HL-089750. We thank and acknowledge the constructive suggestions made by four anonymous reviewers.
Nomenclature
- ρo
Partial density of oxygen (nutrient) phase
- ρc
Partial density of cellular phase
Maximal partial density of cellular phase at steady-state limit of cultivation
- ρm
Partial density of ECM phase
Maximal partial density of ECM phase at steady-state limit of cultivation
- Do
ECM-dependent oxygen diffusivity
Oxygen diffusivity in the scaffold (devoid of ECM)
Oxygen diffusivity in native or engineered tissue (at limit of cultivation)
- v̂
Oxygen convection velocity (solvent velocity)
- vf
Darcy velocity (seepage velocity)
- Dc
cellular phase diffusivity
- χ
cellular phase chemotactic sensitivity
- qo
oxygen consumption rate (by cells)
- Qo
maximal oxygen consumption rate
oxygen concentration at half-maximal consumption
- gc
cellular phase growth/apoptosis rate
- kc
oxygen-dependent cellular proliferation/apoptosis rate
- km
oxygen-dependent ECM production rate
threshold oxygen for ECM production
basal ECM production rate (at no deformation)
- k̄m
deformation-dependent ECM production rate
- φ0
porosity (in the reference configuration)
porosity in the scaffold (devoid of ECM)
porosity in native or engineered tissue (at limit of cultivation)
- k
permeability
- kρ̃m=0
permeability in the scaffold (devoid of ECM)
- kρ̃m=1
permeability in native or engineered tissue (at limit of cultivation)
- Ws
Stored energy density function of scaffold
- Wm
Stored energy density function of the de novo ECM
- W̄m
Stiffening rate of the de novo ECM
Basal ECM stiffening rate (at no deformation)
- w̄m
Deformation-dependent ECM stiffening rate
- νs
Poisson ratio of the scaffold (devoid of ECM)
- νt
Poisson ratio of native or engineered tissue (at limit of cultivation)
- Es
Young’s modulus of the scaffold (devoid of ECM)\
Basal ECM modulus stiffening rate (at no deformation)
- Ēm
Deformation-dependent ECM modulus stiffening rate
Appendix
A.1. Non-dimensionalization of the governing equations
We non-dimensionalize the dependent variables of the governing equations of the growth model – for that we employ 5 times the exterior oxygen concentration , initial cell seeding , and maximum ECM density resulting in , and respectively. The specific form of the governing equations does not change, but upon non-dimensionalization, constants present in the model equations are updated accordingly (and their non-dimensionalized forms and values are recorded in Table 2). Non-dimensional forms of the governing equations (2.1), (2.3), and (2.5) will have tildes in all their members and are
| (A.1) |
| (A.2) |
| (A.3) |
and their parameters are adjusted to their non-dimensional form (listed in Table 2). As we will always refer to their non-dimensional form, tildes on the dependent variables and parameters will not be carried.
A.2 ECM-dependent diffusivity and oxygen-dependent cellular proliferation/apoptosis kinetics
We employ , a non-dimensional measure of ECM, to modulate oxygen diffusivity as the construct grows and evolves over time: ρ̃m → 0, represents the initial diffusivity of oxygen in the scaffold devoid of ECM material, whereas ρ̃m → 1, corresponds to the diffusivity of oxygen in native tissue or in engineered tissue at the limiting steady-state of cultivation at a balance of production, degradation, and incorporation of collagen. Wood et al. (2002) have found that effective diffusivity in cellular systems is somewhat insensitive to the detailed geometric structure of the system, whereas it is primarily influenced by the volume fractions of the extra- and intra-cellular spaces. Wood et al. (2002; 2000) have shown that the analytical solution obtained from Chang’s unit cell (1983), composed of a periodic array of spheres and accounting for diffusion in the extracellular and intracellular spaces and finite mass transport across the cellular membrane, provides reasonable estimates of the experimentally measured effective diffusivity of several solutes in diverse biological tissues. We specify the ECM-dependent oxygen diffusivity as a function of ρ̃m:
| (A.4) |
Where κ and ψ are non-dimensional material parameters, the former is a ratio of the diffusivities in extra- and intra-cellular media and the latter weights transmembrane transport properties with extra-cellular diffusion. If membrane resistance is negligible, equation (A.4) recovers Maxwell’s solution of heat conduction in a heterogeneous two-phase system (Wood and Whitaker 2000). At ρ̃m → 1, and equation (A.4) results in
| (A.5) |
and from which specific values for parameters κ and ψ can be estimated.
The oxygen-dependent cellular proliferation/apoptosis rate kc = kc(ρo) describes the phenomena of growth inhibition and even apoptosis at very high oxygen toxic concentrations, and at very low oxygen anoxic concentrations, and is given by
| (A.6) |
The first term of equation (A.6) is based on Moser’s growth kinetics (driven by exponent n) and Aiba et al. inhibition kinetics (driven by the exponential contribution on the first term) to describe the inability for proliferate at low and at high oxygen concentrations respectively. Kinetic constant kp is a maximum proliferation rate, is the oxygen concentration for half-maximal proliferation rate, and exponent n is the anoxic inhibition coefficient for the Moser-type growth term. Kinetic constant ki is the oxygen’s toxicity inhibition rate for Aiba-type inhibition term, and ka the maximum apoptosis rate. Practically, equation (A.6) results in kc < 0 for low and high concentrations of oxygen, and in kc > 0 for a region in between where oxygen conditions allow proliferation to occur (Figure 2).
A.3 Poroelasticity formulation
Let us consider a mixture composed of a porous solid saturated with fluid. As the mixture deforms, particles of the constituents that co-occupied a point move along different paths and this allows the description of the diffusion or flow of fluid with respect to the solid. We employ the u-p classical formulation of finite poroelasticity (Coussy and Coussy 2004). The dependent variables are the displacement field of the poroelastic mixture, denoted by u, and the pore pressure, denoted by pf (Figure 1). Let the elementary volume of the porous mixture in the reference and current configurations be represented by
| (A.7) |
| (A.8) |
which is made up of volume occupied by the solid constituent (dVs and dvs) and the fluid saturated void space (dVf and dvf).The porosity of the medium φ is the ratio of the volume of fluid to the total volume of a representative volume element, i.e. φ = dvf/dv and φ0 = dVf/dV in the current and reference configurations respectively, and related by
| (A.9) |
where Jf = dvf/dVf is the change in volume of void space, and J = dv/dV is the change in volume of the porous mixture. Balance of mass of fluid is given by
| (A.10) |
where vf is the average velocity of the fluid relative to the solid (seepage velocity or Darcy’s velocity). The total stress acting at a point, T, is assumed to be composed by an average pressure stress in the fluid, pf and the effective stress in the solid Ts, and is defined by
| (A.11) |
Balance of linear momentum of the mixture in the absence of body forces and restricting the analysis to quasi-static motions is given by
| (A.12) |
The constitutive behavior of pore fluid flow is governed by Darcy’s law. Darcy’s law states that the volumetric flow rate of the fluid through a unit area is proportional to the negative of the gradient of pore pressure, i.e.
| (A.13) |
where K is the permeability of the poroelastic mixture (units of length/time). We consider that permeability is isotropic, i.e. K = k1, with k the scalar permeability. The effective stress in the solid is assumed to follow classical hyperelasticity. The Cauchy stress tensor in the solid Ts relates to the 1st Piola-Kirchhoff stress tensor P by
| (A.14) |
where F is the deformation gradient computed from the gradient of displacements as
| (A.15) |
and J = dv/dV = det F. Finally, P is derivable from a stored energy function W = W(F) through P = ∂W/∂F.
A.4. Initial and boundary value problems
The rectangular constructs have dimensions L = 25 mm, d = 5 mm, and h = 1 mm, and are modeled as a two dimensional domain Ω along their length under the state of plane strain – it is implicitly assumed that Ω represents the middle longitudinal cross-section of the construct, and that changes in longitudinal sections are not appreciable at least far from the boundary effects existing near their side edges. To aid the specification of the boundary conditions, we will consider a (x, y) Cartesian system with the axes x and y aligned with the length and the thickness of the construct respectively. The origin is defined in the middle of the construct, thus Ω={−L/2 < x < L/2,−h/2 < y <h/2}. The fixed post is the boundary at ΓF={x =−L/2, −h/2 < y < h/2} whereas the moving post is represented by the boundary ΓM={x = L/2, −h/2 < y < h/2}. Top and bottom surfaces are defined by ΓT={−L/2 < x < L/2, y =−h/2} and ΓB={−L/2 < x <−L/2, y = h/2} (Figure 3a).
Initial and boundary conditions must be specified to particularize the solution of governing equations of the TE growth model (equations (2.1), (2.3) and (2.5)). Equation (2.5) governing matrix production does not necessitate boundary conditions, as it is a reaction-only equation. Oxygen concentration is imposed on top and bottom surfaces (Dirichlet) with the exterior concentration
| (A.16) |
which is assumed to be constant along the length and not time-varying. No-flux boundary conditions (Neumann) are imposed on the cellular phase
| (A.17) |
with the meaning that cells will not leave the construct through its top and bottom boundaries. Lastly, the two ends of the construct are considered impervious for both nutrients and cells as these portions of the construct are connected to the rigid metal posts and no flux is considered to occur across these boundaries. As for initial conditions, we consider that nutrient and cells are homogeneously distributed at initial time, with exterior oxygen concentration (i.e. no oxygen tension), initial cell seeding, and no ECM,
| (A.18) |
Governing equations of poroelasticity (A.10) and (A.12) require boundary conditions to be solved. Similarly as before, we consider that the two ends of the construct are impervious to fluid flow,
| (A.19) |
whereas top and bottom surfaces allow fluid movement in and out the poroelastic body. The exterior fluid pressure is imposed in the pores, i.e.
| (A.20) |
All edges of the construct are traction free, and displacement is imposed at two corners of the construct to describe the effects of the fixed and moving posts, xF= (−L/2, −h/2) and xM = (L/2, −h/2) respectively,
| (A.21) |
Where uM(t) is a periodic function describing the movement of the post along the length direction. For computational ease, we consider the motion to be sufficiently smooth, with period T and amplitude (Figure 3b), and the following piece-wise form was chosen
| (A.22) |
Where γ ≪ T is a short threshold time during which the initial and max deflected positions are held to ensure sufficient smoothness of the motion. The maximum deflection of the construct, if pure bending would be assumed (i.e. the deformed shape would lay in a circular arc of radius R and spanning angle 2θ), is given by δmax = R(1−cosθ) where R and θ are the solutions of the following system of equations: 2θR = L and . In order to achieve a maximum deflection of δmax = 6.36 mm, the deflection employed by Engelmayr et al. (2005; 2006), the maximum displacement of the moving post is .
We neglect inertial effects and restrict our analysis to quasi-static motions, therefore initial conditions on mixture velocity u̇(x, 0) are not required. Pore pressure is considered to be homogeneously distributed and equal to the exterior pressure at initial times
| (A.23) |
which with Darcy’s law results in fluid velocity initially zero everywhere, i.e. vf(x,0) = 0.
A.5. Results of interest for experimental validation
Quantities of interest are the evolution of the distribution of cells and ECM over time, i.e. ρc(x,t) and ρm(x,t). Whereas the control case results in a one-dimensional problem (due to the particular form of the boundary conditions, the solution is independent of x), mechanical conditioning introduces a degree of inhomogeneity in the equation governing oxygen transport and consumption. Results will be presented either in the form of profiles at a given time t along the thickness of the scaffold at the mid-plane plane x = 0, y∈[−h/2,h/2] and contours over the entire length-section Ω (both corresponding to immunohistochemistry images of construct sections), and lastly, a single scalar corresponding to the total mass in the whole construct (corresponding to the assays conducted experimentally to the entire constructs) obtained with
| (A.24) |
The temporal evolution of the flexural rigidity of the construct, which considering no stiffening effect due to deformation, is computed at the middle section with
| (A.25) |
Lastly, the temporal evolution of the force necessary to deform the constructs is obtainable from the poroelastic solutions.
A.6. Parameter estimation
Exterior oxygen concentration of 20% O2 is reported by Zhao et al. (2005) and Pathi et al. (2005), who have employed a similar boundary condition in their simulations, as . We consider experimental data obtained by Lis et al. (Lis et al. 1987) on the collagen content of the human mitral valve to set – the authors have obtained a leaflet composition of 1.4 g wet weight, 81% of the wet weight composed by water, and 57% of dry weigh composed by collagen. Initial cell seeding in TE is usually conducted at sufficiently high values as similar to native tissue cell content, and during the initial periods of incubation, cell content decreases substantially. Engelmayr et al. (2006) reported that the DNA content measured for native juvenile ovine PV leaflets as 701±42 μg/g ww. Assuming DNA content of 7.6 pg/cell and a wet tissue density of 1 g/cm3, cell density in native tissue is set as . On their experiment with VSMCs, the DNA content of 536±38 μg/g ww after 30 hours seeding period (Engelmayr et al. 2005) – thus we set seeding density as .
To characterize the Michaelis-Menten consumption kinetics of oxygen (cf. Equation (2.2)) we employ constants used by Pathi et al. (2005) and set Qo = 1.25·10−17 molO2·cell−1·s−1 and . Obradovic et al. (2000) considered that diffusivity of oxygen in TE scaffolds to be half of the diffusivity in water; Galban and Locke (1999a; 1999l) considered that diffusivity in tissue to be 10 times lower than diffusivity in water – we set and . To fully characterize the dependence of diffusivity on existing ECM (cf. Equation (A.4)), we will further assume that trans-membrane transport is 10 times higher than intracellular diffusivity, thus we obtain κ = 0.43 and ψ = 23.07. Relationship (A.4) is only mildly nonlinear (not shown) and a parametric study on its parameters has shown it to be somewhat insensitive to ψ (the ratio between transmembrane transport and extra-cellular diffusivity) and mainly governed by κ (the ratio between extra- and intra-cellular diffusivities).
Cellular proliferation/apoptosis and extracellular matrix production rate constants are determined/estimated with the scant data existing in the literature. Galban and Locke (1999a; 1999l) have conducted a parameter analysis on several growth parameters using a modified Contois growth kinetics function and have obtained cellular growth and death rates (with respect to dimensionless cellular volume fraction in between 0 and 1) on the orders of magnitude of ±1·10−5 s−1; using a similar formalism, Pathi et al. (2005) and Zhao et al. (2005) estimated a maximum proliferation rates of 5.99·10−5 s−1 and 3.875·10−7 s−1 respectively – notwithstanding, it must be stressed that these proliferation and death rates are inherent to Galban and Locke’s framework, but can be employed to estimate the oxygen dependent cellular proliferation/apoptosis rate function kc(ρo) (Equation (A.6) and Figure 3). Experimental data and rate constants for the VSMCs employed by Engelmayr et al. (2005) do not exist, thus we assume apoptosis rate k̃a = 1·10−5 s−1 and maximum proliferation rate , both specified with respect to changes in non-dimensional variable ρ̃c and in agreement with orders of magnitude proposed by Galban and Locke (1999a; 1999l). In order to obtain this behavior, we set constants in Equation (A.6) as: proliferation rate k̃p = 2.6·109, inhibition kinetics rate k̃i = 14, Moser’s growth kinetics parameters n = 5 and . Units of these parameters involve multiple powers of [molO2/cm3] because of exponent n, and are of much lesser relevance than the dimensionality of the full expression of k̃c, [s−1]. Engelmayr et al. (2005) has observed a marked region of non-ECM producing cells inside the construct, and we employed solutions of the oxygen governing equations with values of oxygen consumption kinetics and oxygen diffusivity above to estimate ECM production threshold of . Obradovic et al. (2000) have determined a GAG production rate of occurring in cartilaginous TE experiments conducted by Vunjak-Novakovic and co-workers (Freed et al. 1998; 1994; Obradovic et al. 1999) – we employ such finding to estimate the ECM production rate .
Engelmayr et al. (2005) reported Young’s modulus of the scaffolds as Es = 174±22 kPa, with initial porosity of , and that they are highly compressible – therefore we set Poisson’s ratio of scaffold of νs = 0.1 and employ relationships μ = E/2(1+ν) and K = E/3(1−2ν) to determine shear and bulk moduli of scaffold as μs = 39.54 kPa and Ks = 72.5 kPa respectively, characterizing the initial condition of the two-parameter family of compressible neo-Hookean material describing the evolving poroelastic solid when no ECM is present. Engelmayr et al. (2005) has also observed a markedly linear relationship between collagen concentration and Young’s modulus of TE constructs (cf. Figure 8 of Engelmayr et al. (2005)) – although their range of observation is restricted to the initial stages of TE growth when a still small amount of ECM is present (up to a maximum of ρm ≈ 1.5 mg/g ww at 9 weeks of culture of TEHVs), it allows for parameter appearing in Equation (2.14) to be obtained from its slope and set to . Finally, we assume that engineered tissue at its final steady state stage of cultivation (when ρm→1) is nearly incompressible, thus setting νt = 0.45.
Variations of porosity and permeability with tissue evolution (set as linear relationships shown in equations (2.7) and (2.8)), require the specification of scaffold and tissue porosities and permeabilities and were estimated as follows: (i) Harrison and Massaro (1976) determined the water flux through a 2 mm thick porcine aortic tissue due to a hydrostatic pressure gradient of 110 mmHg and have determined a hydraulic conductivity (corresponding to flux times thickness divided by pressure drop) of 7·10−13 cm4·dyne−1·s−1 from which we set permeability of tissue kρ̃m=1 = 3.66·10−7 cm·s−1; (ii) we employ the same reasoning as Galban and Locke (1999a; 1999l) for the specification of the permeability of the scaffold (mainly due to lack of existing data) as 10 times greater than permeability of native tissue, i.e. kρ̃m=0 = 10kρ̃m=1; and finally, (iii) Lovich and Edelman (1996) have determined experimentally the fractional space in arterial media, adventitia and myocardium and we employ their result on arterial media to set porosity in tissue as . The remaining parameter employed for the poroelastic formulation are fluid density, set to density of water ρf = 1 g/cm3, and external pressure, set to atmospheric pressure pext = 101.325 kPa.
Lastly, under static conditions nutrient transport occurs due to diffusion only, i.e. v̂ = 0 in Equation (2.1) and the framework, together with the parameter set above, is able to describe with sufficient accuracy the existing experimental data set (cross sectional profiles, bulk measures and bulk mechanical properties). When subjected to mechanical conditioning, the mechanism of nutrient convection plays a significant role in changing the behavior of the system. Time lumping constant C present in Equation (2.15) was set to C = 70 such that the departure from the static solution represents the observed differences in between both regimes by Engelmayr et al. (2005) with the same parameter set. Although we have included in our model the effects of chemotaxis and of deformation dependent ECM production (both in quantity and in quality), we have chosen to disregard these effects mainly due to the lack of critical experimental data to determine their impact. Consequently, chemotactic flux in equation (2.3) is not accounted, and matrix production rate and stiffness (equations (2.6) and (2.10)) are indifferent to deformation, i.e. k̄m(C) = 0 and w̄m(Ct(s)) = 0. Notwithstanding, it must be stressed that in general these effects might be relevant and significant in engineered tissue growth, and that motivates our reasoning to explicitly account deformation-dependent ECM production rate and stiffness at the model development stage. The determination of these effects must be carried on with different experimental programs than the one conducted by Engelmayr et al. (2003; 2005; 2006) and are subject of our future studies.
References
- Aiba S, Shoda M, Nagatani M. Kinetics of product inhibition in alcohol fermentation (Reprinted from Biotechnology and Bioengineering, vol 10, pg 845, 1968) Biotechnology and Bioengineering. 2000;67:671–690. doi: 10.1002/(Sici)1097-0290(20000320)67:6<671::Aid-Bit6>3.0.Co;2-W. [DOI] [PubMed] [Google Scholar]
- Ambrosi D, et al. Perspectives on biological growth and remodeling. J Mech Phys Solids. 2011;59:863–883. doi: 10.1016/j.jmps.2010.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA. On the theory of reactive mixtures for modeling biological growth. Biomech Model Mechanobiol. 2007;6:423–445. doi: 10.1007/s10237-006-0070-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian GA, Humphrey JD. Continuum mixture models of biological growth and remodeling: past successes and future opportunities. Annu Rev Biomed Eng. 2012;14:97–111. doi: 10.1146/annurev-bioeng-071910-124726. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Ricken T. Multigenerational interstitial growth of biological tissues. Biomech Model Mechanobiol. 2010;9:689–702. doi: 10.1007/s10237-010-0205-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek S, Rajagopal KR, Humphrey JD. A theoretical model of enlarging intracranial fusiform aneurysms. J Biomech Eng. 2006;128:142–149. doi: 10.1115/1.2132374. [DOI] [PubMed] [Google Scholar]
- Berry JL, Steen JA, Koudy Williams J, Jordan JE, Atala A, Yoo JJ. Bioreactors for development of tissue engineered heart valves. Ann Biomed Eng. 2010;38:3272–3279. doi: 10.1007/s10439-010-0148-6. [DOI] [PubMed] [Google Scholar]
- Bian L, et al. Influence of decreasing nutrient path length on the development of engineered cartilage. Osteoarthritis Cartilage. 2009;17:677–685. doi: 10.1016/j.joca.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bian L, Fong JV, Lima EG, Stoker AM, Ateshian GA, Cook JL, Hung CT. Dynamic mechanical loading enhances functional properties of tissue-engineered cartilage using mature canine chondrocytes. Tissue Eng Part A. 2010;16:1781–1790. doi: 10.1089/ten.TEA.2009.0482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop JE, Lindahl G. Regulation of cardiovascular collagen synthesis by mechanical load. Cardiovasc Res. 1999;42:27–44. doi: 10.1016/s0008-6363(99)00021-8. [DOI] [PubMed] [Google Scholar]
- Brown DA, MacLellan WR, Laks H, Dunn JC, Wu BM, Beygui RE. Analysis of oxygen transport in a diffusion-limited model of engineered heart tissue. Biotechnol Bioeng. 2007;97:962–975. doi: 10.1002/bit.21295. [DOI] [PubMed] [Google Scholar]
- Butler DL, Goldstein SA, Guilak F. Functional tissue engineering: the role of biomechanics. J Biomech Eng. 2000;122:570–575. doi: 10.1115/1.1318906. [DOI] [PubMed] [Google Scholar]
- Chang HC. Effective Diffusion and Conduction in 2-Phase Media - a Unified Approach. Aiche Journal. 1983;29:846–853. doi: 10.1002/Aic.690290521. [DOI] [Google Scholar]
- Chung CA, Chen CW, Chen CP, Tseng CS. Enhancement of cell growth in tissue-engineering constructs under direct perfusion: Modeling and simulation. Biotechnol Bioeng. 2007;97:1603–1616. doi: 10.1002/bit.21378. [DOI] [PubMed] [Google Scholar]
- Costa KD, Lee EJ, Holmes JW. Creating alignment and anisotropy in engineered heart tissue: role of boundary conditions in a model three-dimensional culture system. Tissue Eng. 2003;9:567–577. doi: 10.1089/107632703768247278. [DOI] [PubMed] [Google Scholar]
- Coussy O, Coussy O. Poromechanics. 2. Wiley; Chichester: 2004. [Google Scholar]
- Demol J, Lambrechts D, Geris L, Schrooten J, Van Oosterwyck H. Towards a quantitative understanding of oxygen tension and cell density evolution in fibrin hydrogels. Biomaterials. 2011;32:107–118. doi: 10.1016/j.biomaterials.2010.08.093. [DOI] [PubMed] [Google Scholar]
- Engelmayr GC, Jr, Hildebrand DK, Sutherland FW, Mayer JE, Jr, Sacks MS. A novel bioreactor for the dynamic flexural stimulation of tissue engineered heart valve biomaterials. Biomaterials. 2003;24:2523–2532. doi: 10.1016/s0142-9612(03)00051-6. [DOI] [PubMed] [Google Scholar]
- Engelmayr GC, Jr, Rabkin E, Sutherland FW, Schoen FJ, Mayer JE, Jr, Sacks MS. The independent role of cyclic flexure in the early in vitro development of an engineered heart valve tissue. Biomaterials. 2005;26:175–187. doi: 10.1016/j.biomaterials.2004.02.035. [DOI] [PubMed] [Google Scholar]
- Engelmayr GC, Jr, Sacks MS. Prediction of extracellular matrix stiffness in engineered heart valve tissues based on nonwoven scaffolds. Biomech Model Mechanobiol. 2008;7:309–321. doi: 10.1007/s10237-007-0102-1. [DOI] [PubMed] [Google Scholar]
- Engelmayr GC, Jr, Sales VL, Mayer JE, Jr, Sacks MS. Cyclic flexure and laminar flow synergistically accelerate mesenchymal stem cell-mediated engineered tissue formation: Implications for engineered heart valve tissues. Biomaterials. 2006;27:6083–6095. doi: 10.1016/j.biomaterials.2006.07.045. [DOI] [PubMed] [Google Scholar]
- Engelmayr GC, Jr, et al. A novel flex-stretch-flow bioreactor for the study of engineered heart valve tissue mechanobiology. Ann Biomed Eng. 2008;36:700–712. doi: 10.1007/s10439-008-9447-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freed LE, Hollander AP, Martin I, Barry JR, Langer R, Vunjak-Novakovic G. Chondrogenesis in a cell-polymer-bioreactor system. Exp Cell Res. 1998;240:58–65. doi: 10.1006/excr.1998.4010. S0014-4827(98)94010-1 [pii] [DOI] [PubMed] [Google Scholar]
- Freed LE, Marquis JC, Langer R, Vunjak-Novakovic G. Kinetics of chondrocyte growth in cell-polymer implants. Biotechnol Bioeng. 1994;43:597–604. doi: 10.1002/bit.260430709. [DOI] [PubMed] [Google Scholar]
- Freed LE, Martin I, Vunjak-Novakovic G. Frontiers in tissue engineering. In vitro modulation of chondrogenesis. Clin Orthop Relat Res. 1999:S46–58. [PubMed] [Google Scholar]
- Fu P, et al. Effects of basic fibroblast growth factor and transforming growth factor-beta on maturation of human pediatric aortic cell culture for tissue engineering of cardiovascular structures. Asaio J. 2004;50:9–14. doi: 10.1097/01.mat.0000104815.21056.08. [DOI] [PubMed] [Google Scholar]
- Galban CJ, Locke BR. Analysis of cell growth in a polymer scaffold using a moving boundary approach. Biotechnology and Bioengineering. 1997;56:422–432. doi: 10.1002/(Sici)1097-0290(19971120)56:4<422::Aid-Bit7>3.0.Co;2-Q. [DOI] [PubMed] [Google Scholar]
- Galban CJ, Locke BR. Analysis of cell growth kinetics and substrate diffusion in a polymer scaffold. Biotechnol Bioeng. 1999a;65:121–132. doi: 10.1002/(sici)1097-0290(19991020)65:2<121::aid-bit1>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Galban CJ, Locke BR. Effects of spatial variation of cells and nutrient and product concentrations coupled with product inhibition on cell growth in a polymer scaffold. Biotechnology and Bioengineering. 1999l;64:633–643. doi: 10.1002/(Sici)1097-0290(19990920)64:6<633::Aid-Bit1>3.0.Co;2-6. [DOI] [PubMed] [Google Scholar]
- Garikipati K, Arruda EM, Grosh K, Narayanan H, Calve S. A continuum treatment of growth in biological tissue: the coupling of mass transport and mechanics. J Mech Phys Solids. 2004;52:1595–1625. [Google Scholar]
- Harrison RG, Massaro TA. Water Flux through Porcine Aortic Tissue Due to a Hydrostatic-Pressure Gradient. Atherosclerosis. 1976;24:363–367. doi: 10.1016/0021-9150(76)90128-3. [DOI] [PubMed] [Google Scholar]
- Hillen T, Painter KJ. A user’s guide to PDE models for chemotaxis. Journal of mathematical biology. 2009;58:183–217. doi: 10.1007/s00285-008-0201-3. [DOI] [PubMed] [Google Scholar]
- Hoerstrup SP, et al. Functional living trileaflet heart valves grown In vitro. Circulation. 2000a;102:III44–49. doi: 10.1161/01.cir.102.suppl_3.iii-44. [DOI] [PubMed] [Google Scholar]
- Hoerstrup SP, Sodian R, Sperling JS, Vacanti JP, Mayer JE., Jr New pulsatile bioreactor for in vitro formation of tissue engineered heart valves. Tissue Eng. 2000b;6:75–79. doi: 10.1089/107632700320919. [DOI] [PubMed] [Google Scholar]
- Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Mathematical models and methods in applied sciences. 2002;12:407–430. [Google Scholar]
- Keller EF, Segel LA. Model for Chemotaxis. J Theor Biol. 1971;30:225. doi: 10.1016/0022-5193(71)90050-6. [DOI] [PubMed] [Google Scholar]
- Kim BS, Nikolovski J, Bonadio J, Mooney DJ. Cyclic mechanical strain regulates the development of engineered smooth muscle tissue. Nat Biotechnol. 1999;17:979–983. doi: 10.1038/13671. [DOI] [PubMed] [Google Scholar]
- Klein TJ, Sah RL. Modulation of depth-dependent properties in tissue-engineered cartilage with a semi-permeable membrane and perfusion: a continuum model of matrix metabolism and transport. Biomech Model Mechanobiol. 2007;6:21–32. doi: 10.1007/s10237-006-0045-y. [DOI] [PubMed] [Google Scholar]
- Klisch SM, Sah RL, Hoger A. A cartilage growth mixture model for infinitesimal strains: solutions of boundary-value problems related to in vitro growth experiments. Biomech Model Mechanobiol. 2005;3:209–223. doi: 10.1007/s10237-004-0060-9. [DOI] [PubMed] [Google Scholar]
- Kovarova-Kovar K, Egli T. Growth kinetics of suspended microbial cells: from single-substrate-controlled growth to mixed-substrate kinetics. Microbiology and molecular biology reviews: MMBR. 1998;62:646–666. doi: 10.1128/mmbr.62.3.646-666.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanza RP, Langer RS, Vacanti J. Principles of tissue engineering. 2. Academic Press; San Diego: 2000. [Google Scholar]
- Lewis MC, Macarthur BD, Malda J, Pettet G, Please CP. Heterogeneous proliferation within engineered cartilaginous tissue: the role of oxygen tension. Biotechnol Bioeng. 2005;91:607–615. doi: 10.1002/bit.20508. [DOI] [PubMed] [Google Scholar]
- Lis Y, Burleigh MC, Parker DJ, Child AH, Hogg J, Davies MJ. Biochemical characterization of individual normal, floppy and rheumatic human mitral valves. Biochem J. 1987;244:597–603. doi: 10.1042/bj2440597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lovich MA, Edelman ER. Computational simulations of local vascular heparin deposition and distribution. Am J Physiol. 1996;271:H2014–2024. doi: 10.1152/ajpheart.1996.271.5.H2014. [DOI] [PubMed] [Google Scholar]
- Lutolf MP, Hubbell JA. Synthetic biomaterials as instructive extracellular microenvironments for morphogenesis in tissue engineering. Nature Biotechnology. 2005;23:47–55. doi: 10.1038/Nbt1055. [DOI] [PubMed] [Google Scholar]
- Madri JA, Bell L, Merwin JR. Modulation of vascular cell behavior by transforming growth factors beta. Molecular reproduction and development. 1992;32:121–126. doi: 10.1002/mrd.1080320207. [DOI] [PubMed] [Google Scholar]
- Malda J, et al. The effect of PEGT/PBT scaffold architecture on oxygen gradients in tissue engineered cartilaginous constructs. Biomaterials. 2004;25:5773–5780. doi: 10.1016/j.biomaterials.2004.01.028. [DOI] [PubMed] [Google Scholar]
- Martin I, Wendt D, Heberer M. The role of bioreactors in tissue engineering. Trends Biotechnol. 2004;22:80–86. doi: 10.1016/j.tibtech.2003.12.001. [DOI] [PubMed] [Google Scholar]
- Mendelson K, Schoen FJ. Heart valve tissue engineering: Concepts, approaches, progress, and challenges. Annals of Biomedical Engineering. 2006;34:1799–1819. doi: 10.1007/s10439-006-9163-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizuno S, Allemann F, Glowacki J. Effects of medium perfusion on matrix production by bovine chondrocytes in three-dimensional collagen sponges. J Biomed Mater Res. 2001;56:368–375. doi: 10.1002/1097-4636(20010905)56:3<368::aid-jbm1105>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- Mol A, et al. The relevance of large strains in functional tissue engineering of heart valves. Thorac Cardiovasc Surg. 2003;51:78–83. doi: 10.1055/s-2003-38993. [DOI] [PubMed] [Google Scholar]
- Myers K, Ateshian GA. Interstitial growth and remodeling of biological tissues: Tissue composition as state variables. J Mech Behav Biomed Mater. 2013 doi: 10.1016/j.jmbbm.2013.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nerem RM. Role of mechanics in vascular tissue engineering. Biorheology. 2003;40:281–287. [PubMed] [Google Scholar]
- O’Dea R, Byrne H, Waters S. Computational Modeling in Tissue Engineering. Springer; 2013. Continuum Modelling of In Vitro Tissue Engineering: A Review; pp. 229–266. [Google Scholar]
- Obradovic B, Carrier RL, Vunjak-Novakovic G, Freed LE. Gas exchange is essential for bioreactor cultivation of tissue engineered cartilage. Biotechnol Bioeng. 1999;63:197–205. doi: 10.1002/(SICI)1097-0290(19990420)63:2<197::AID-BIT8>3.0.CO;2-2. pii. [DOI] [PubMed] [Google Scholar]
- Obradovic B, Meldon JH, Freed LE, Vunjak-Novakovic G. Glycosaminoglycan deposition in engineered cartilage: Experiments and mathematical model. Aiche Journal. 2000;46:1860–1871. doi: 10.1002/Aic.690460914. [DOI] [Google Scholar]
- Park H, Cannizzaro C, Vunjak-Novakovic G, Langer R, Vacanti CA, Farokhzad OC. Nanofabrication and microfabrication of functional materials for tissue engineering. Tissue Eng. 2007;13:1867–1877. doi: 10.1089/ten.2006.0198. [DOI] [PubMed] [Google Scholar]
- Pathi P, Ma T, Locke BR. Role of nutrient supply on cell growth in bioreactor design for tissue engineering of hematopoietic cells. Biotechnology and Bioengineering. 2005;89:743–758. doi: 10.1002/Bit.20367. [DOI] [PubMed] [Google Scholar]
- Penta R, Ambrosi D, Shipley RJ. Effective Governing Equations for Poroelastic Growing Media Q. J Mech Appl Math. 2014;67:69–91. doi: 10.1093/Qjmam/Hbt024. [DOI] [Google Scholar]
- Rabkin E, Hoerstrup SP, Aikawa M, Mayer JE, Jr, Schoen FJ. Evolution of cell phenotype and extracellular matrix in tissue-engineered heart valves during in-vitro maturation and in-vivo remodeling. Journal of Heart Valve Disease. 2002;11:308–314;. discussion 314. [PubMed] [Google Scholar]
- Radisic M, Malda J, Epping E, Geng W, Langer R, Vunjak-Novakovic G. Oxygen gradients correlate with cell density and cell viability in engineered cardiac tissue. Biotechnol Bioeng. 2006;93:332–343. doi: 10.1002/bit.20722. [DOI] [PubMed] [Google Scholar]
- Raimondi MT, Moretti M, Cioffi M, Giordano C, Boschetti F, Lagana K, Pietrabissa R. The effect of hydrodynamic shear on 3D engineered chondrocyte systems subject to direct perfusion. Biorheology. 2006;43:215–222. [PubMed] [Google Scholar]
- Ramaswamy S, Boronyak SM, Le T, Holmes A, Sotiropoulos F, Sacks MS. A Novel Bioreactor for Mechanobiological Studies of Engineered Heart Valve Tissue Formation Under Pulmonary Arterial Physiological Flow Conditions. J Biomech Eng-T Asme. 2014;136:Artn 121009. doi: 10.1115/1.4028815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramaswamy S, et al. The role of organ level conditioning on the promotion of engineered heart valve tissue development in-vitro using mesenchymal stem cells. Biomaterials. 2010;31:1114–1125. doi: 10.1016/j.biomaterials.2009.10.019. S0142-9612(09)01106-5 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sacco R, Causin P, Zunino P, Raimondi MT. A multiphysics/multiscale 2D numerical simulation of scaffold-based cartilage regeneration under interstitial perfusion in a bioreactor. Biomech Model Mechanobiol. 2011;10:577–589. doi: 10.1007/s10237-010-0257-z. [DOI] [PubMed] [Google Scholar]
- Sacks MS, Schoen FJ, Mayer JE. Bioengineering challenges for heart valve tissue engineering. Annu Rev Biomed Eng. 2009;11:289–313. doi: 10.1146/annurev-bioeng-061008-124903. [DOI] [PubMed] [Google Scholar]
- Sacks MS, Yoganathan AP. Heart valve function: a biomechanical perspective. Philos Trans R Soc Lond B Biol Sci. 2008;363:2481. doi: 10.1098/rstb.2008.0062. 814417U817GQHL00 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengers BG, Oomens CW, Baaijens FP. An integrated finite-element approach to mechanics, transport and biosynthesis in tissue engineering. J Biomech Eng. 2004;126:82–91. doi: 10.1115/1.1645526. [DOI] [PubMed] [Google Scholar]
- Stegemann JP, Nerem RM. Phenotype modulation in vascular tissue engineering using biochemical and mechanical stimulation. Ann Biomed Eng. 2003;31:391–402. doi: 10.1114/1.1558031. [DOI] [PubMed] [Google Scholar]
- Stella JA. A Tissue Engineering Platform to Investigate Effects of Finite Deformation on Extracellular Matrix Production and Mechanical Properties. University of Pittsburgh; 2011. [Google Scholar]
- Sutherland FW, et al. From stem cells to viable autologous semilunar heart valve. Circulation. 2005;111:2783–2791. doi: 10.1161/CIRCULATIONAHA.104.498378. [DOI] [PubMed] [Google Scholar]
- Woo SLY, Seguchi Y. Tissue Engineering - 1989. 14. Asme; New York: 1989. BED edn. [Google Scholar]
- Wood BD, Quintard M, Whitaker S. Calculation of effective diffusivities for biofilms and tissues. Biotechnology and Bioengineering. 2002;77:495–516. doi: 10.1002/Bit.10075. [DOI] [PubMed] [Google Scholar]
- Wood BD, Whitaker S. Multi-species diffusion and reaction in biofilms and cellular media. Chem Eng Sci. 2000;55:3397–3418. doi: 10.1016/S0009-2509(99)00572-2. [DOI] [Google Scholar]
- Zhao F, Pathi P, Grayson W, Xing Q, Locke BR, Ma T. Effects of oxygen transport on 3-d human mesenchymal stem cell metabolic activity in perfusion and static cultures: experiments and mathematical model. Biotechnol Prog. 2005;21:1269–1280. doi: 10.1021/bp0500664. [DOI] [PubMed] [Google Scholar]