Supplementary Eye Field Encodes Confidence in Decisions Under Risk

Abstract

Choices are made with varying degrees of confidence, a cognitive signal representing the subjective belief in the optimality of the choice. Confidence has been mostly studied in the context of perceptual judgments, in which choice accuracy can be measured using objective criteria. Here, we study confidence in subjective value-based decisions. We recorded in the supplementary eye field (SEF) of monkeys performing a gambling task, where they had to use subjective criteria for placing bets. We found neural signals in the SEF that explicitly represent choice confidence independent from reward expectation. This confidence signal appeared after the choice and diminished before the choice outcome. Most of this neuronal activity was negatively correlated with confidence, and was strongest in trials on which the monkey spontaneously withdrew his choice. Such confidence-related activity indicates that the SEF not only guides saccade selection, but also evaluates the likelihood that the choice was optimal. This internal evaluation influences decisions concerning the willingness to bear later costs that follow from the choice or to avoid them. More generally, our findings indicate that choice confidence is an integral component of all forms of decision-making, whether they are based on perceptual evidence or on value estimations.

Introduction

During decision-making, one option is selected among a number of alternatives. However, the same option can be selected with varying degrees of confidence, the belief that this choice was correct. Confidence represents an evaluation of the choice process, based on the balance of evidence supporting the alternatives that were considered (Vickers 1979), and it may influence future decisions that are contingent on the initial choice (Kiani and Shadlen 2009; Kepecs and Mainen 2012).

Recently, neurophysiological evidence of confidence signals has been reported using perceptual decision tasks (Kepecs et al. 2008; Kiani and Shadlen 2009). The confidence signals in these studies reflect the belief in the accuracy of the judgment with respect to the objectively given external stimuli or states. However, studies on perceptual decision-making do not address how confidence is represented in most real-life decisions, which often have no obvious objective criteria for the accuracy of judgments (Sugrue et al. 2005). An additional problem is that, in these previous studies, the relation between confidence and expected reward has not been straightforward (Mainen and Kepecs 2009). In the perceptual decision tasks used in these studies, accurate judgments were rewarded with a fixed amount of reward. Hence, the degree of belief in the accuracy of a choice is highly correlated with the probabilistic assessment of the chance to get a reward.

A value-based decision framework can address both of these issues. First, in value-based decision-making, choices are based on a comparison of subjective value estimations, not of objective sensory information. Choice confidence reflects the balance of evidence in favor of the different response options. In our gambling task, confidence depends therefore on the difference in subjective value of the 2 options. These value estimations are noisy, due to the probabilistic nature of the gamble option's outcome and the resulting uncertainty about whether it is better or worse than the alternative sure option. Secondly, in our gambling task, we use gambles and sure reward options in 2 different value ranges (Fig. 1A). Across high- and low-value trials, choices with a similar degree of difference in their subjective value, and therefore a similar degree of confidence, are associated with different reward expectations (Fig. 1B). Thus, our gambling task makes it possible to disassociate confidence from reward expectation.

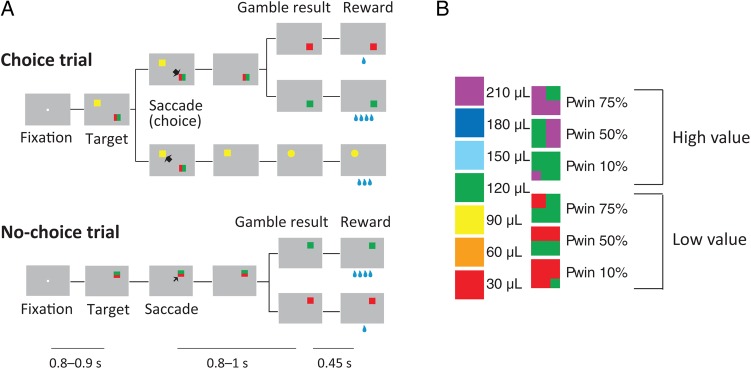
Figure 1.

Gambling task. (A) Sequence of events during choice trials and no-choice trials in the gambling task. In this study, we focused our analyses on choice trials and excluded the neurons showing no significant difference in activity between choice and no-choice trials. Below is indicated the duration of various time periods in the gambling task. The first line indicates the first fixation period. The second line indicates the post-choice delay, in which the monkey has to wait for the result of the trial when he had made a saccade to a gambling option. The third line indicates the interval between visual indication of the gamble result and reward delivery. Note that the decision time between target onset and saccade initiation depends on the monkey. (B) Visual cues used in the gambling task: (left) sure options and (right) gamble options. The rewards are 1–7 units of a minimum unit of reward (30 µL). Note that across high- and low-value trials choices with a similar degree of confidence are associated with different reward expectations. For instance, the choice of any low-value gamble (30 or 120 µL fluid reward) is clearly better than receiving the smaller amount for sure (the sure 30-µL option). Thus, the monkey can be very confident that he made the right choice. A similar degree of confidence should accompany the choice of a high-value gamble (120 or 210 µL fluid reward) over the option to receive the smaller amount for sure, despite the fact that the monkey is expecting a much larger amount of reward.

Using a standard decision-making model (Vickers 1979; Kiani and Shadlen 2009), we show that choice confidence is monotonically related to the difference in the value of the chosen and unchosen option. Using the difference in a subjective value as a proxy for choice confidence, we found the corresponding neuronal signals were represented in the supplementary eye field (SEF), a higher order oculomotor area that has been shown to represent the signals relevant for the control and evaluation of saccades (Amador et al. 2000; Stuphorn et al. 2000, 2010; Roesch and Olson 2003; Stuphorn and Schall 2006; So and Stuphorn 2010, 2012). These signals were observed after the choice has been made, and were mostly negatively correlated with the value difference. In other words, most SEF neurons showed higher activity when the monkey made a less optimal choice. These signals were stronger during those trials in which the monkeys eventually broke fixation and aborted a trial. This suggests that the confidence signals in SEF evaluate the quality of the choice process and are used to avoid costs (such as having to fixate a target to wait for reward) that arise from choices that were likely suboptimal.

Materials and Methods

General

Two rhesus monkeys (both male; monkey A: 7.5 kg and monkey B: 8.5 kg) were trained to perform the tasks used in this study. All animal care and experimental procedures were approved by Johns Hopkins University Animal Care and Use Committee. During the experimental sessions, each monkey was seated in a primate chair, with its head restrained, facing a video screen. Eye position was monitored with an infrared corneal reflection system (Eye Link, SR Research Ltd, Ottawa, Canada) and recorded with the PLEXON MAP system (Plexon, Inc., Dallas, TX, USA) at a sampling rate of 1000 Hz. We used a newly developed fluid delivery system that was based on 2 syringe pumps connected to a fluid container that were controlled by a stepper motor. This system was highly accurate across the entire range of fluid amounts used in the experiment.

Behavioral Task

In the gambling task, the monkeys had to make saccades to peripheral targets that were associated with different amounts of water reward (Fig. 1A). The targets were squares of various colors, 2.25° by 2.25° in size. They were always presented 10° away from the central fixation point at a 45°, 135°, 225°, or 315° angle. The task consisted of 2 types of trials, namely choice trials and no-choice trials. In choice trials, 2 targets appeared on the screen and the monkeys were free to choose between them by making an eye movement to the target that was associated with the desired option. In no-choice trials, only one target appeared on the screen so that the monkeys were forced to make a saccade to the given target. No-choice trials were designed as a control to compare the behavior of the monkeys and the cell activities when no decision was required.

Two targets in each choice trial were associated with a gamble option and a sure option, respectively. The sure option always led to a certain reward amount. The gamble option led to 1 of 2 possible reward amounts with a certain set of probabilities. We designed a system of color cues, to explicitly indicate to the monkeys the reward amounts and probabilities associated with a particular target (Fig. 1B). Seven different colors indicated 7 reward amounts (increasing from 1 to 7 units of water, where 1 unit equaled 30 µL). Targets indicating a sure option consisted of only 1 color. Targets indicating a gamble option consisted of 2 colors corresponding to the 2 possible reward amounts. The portion of a color within the target corresponded to the probability of receiving that reward amount. In each trial, the exact color configuration of the gamble target was randomized across 4 different variants that were derived from 90° rotations of the target around its center. Thus, for 10% and 75% gamble targets, the smaller color patch could appear in each of the 4 corners. For 50% gambles, the middle color partition could be horizontal or vertical and each color could appear either on the right/left or up/down.

In the task, we used 2 different reward amount sets for the gamble options (minimum/maximum pair was either 1 vs. 4 [low-value gamble] or 4 vs. 7 [high-value gamble] units of water). Each of the reward amount sets was offered with 3 different probabilities of getting the maximum reward (10%, 50%, and 75%), resulting in 6 different gambles. In each choice trial, 1 of these 6 gamble options was compared with 1 of 4 sure options, ranging in a value from the minimum to the maximum reward outcome of the gamble. This resulted in 24 different combinations of options that were offered in choice trials.

A choice trial started with the appearance of a fixation point at the center of the screen (Fig. 1A). After the monkeys successfully fixated for 800–900 ms, 2 targets appeared on 2 randomly chosen locations among the 4 quadrants on the screen. Simultaneously, the fixation point went off and the monkeys were allowed to make their choice by making a saccade toward one of the targets. Following the choice, the unchosen target disappeared from the screen. The monkeys were required to keep fixating the chosen target for 800–1000 ms, after which the target changed either color or shape. If the chosen target was associated with a gamble option, it changed from a two-colored square to a single-colored square associated with the final reward amount. This indicated the result of the gamble to the monkeys. If the chosen target was associated with a sure option, the target changed its shape from a square to either a circle or a triangle. This change of shape served as a control for the change in visual display during sure choices and did not convey any behaviorally meaningful information to the monkeys. Following the change in visual display, the monkeys were required to continue to fixate the target for another 450 ms, until the water reward was delivered. If the monkey broke fixation anytime before the reward delivery, the trial was aborted and no reward was delivered. After the usual intertrial interval, a new trial started. In this trial, the target or targets represented the same reward options as in the aborted trial. In this way, the monkey was forced to sample every reward contingency evenly. The location of the targets, however, was randomized, so that the monkey could not prepare a saccade in advance.

The sequence of events in no-choice trials was the same as in choice trials, except that only one target was presented (Fig. 1A). The location of the target was randomized across the same 4 quadrants on the screen that were used during choice trials. In no-choice trials, we used individually all 7 sure and 6 gamble options that were presented in combination during choice trials. We presented no-choice and choice trials interleaved in a pseudorandomized schedule in blocks of trials that consisted of all 24 different choice trials and 13 different no-choice trials. This procedure ensured that the monkeys were exposed to all the trial types equally often. Within a block, the order of appearance was randomized and a particular trial was not repeated, so that the monkeys could not make a decision before the targets were shown. Randomized locations of the targets in each trial also prevented the monkeys from preparing a movement toward a certain direction before the target appearance. In addition, presenting a target associated with the same option in different locations allowed us to separate the motor decision from the value decision.

For reward delivery, we used an in-house built fluid delivery system. The system was based on 2 syringe pumps connected to a fluid container. A piston in the middle of the 2 syringes was connected with the plunger of each syringe. The movement of the piston in one direction pressed the plunger of one syringe inward and ejected fluid. At the same time, it pulled the plunger of the other syringe outward and sucked fluid into the syringe from the fluid container. The position of the piston was controlled by a stepper motor. In this way, the size of the piston movement controlled the amount of fluid that was ejected out of one of the syringes. The accuracy of the fluid amount delivery was high across the entire range of fluid amounts used in the experiment, because we used relatively small syringes (10 mL). Importantly, it was also constant across the duration of the experiment, unlike conventional gravity-based solenoid systems. During an experimental or training session, we delivered a total amount of fluid reward (150–300 mL), which was much larger than the capacity of a single syringe. The fact that a second syringe was filled, while the first syringe was emptied allowed us to overcome this limitation. We moved the piston in one direction until the corresponding syringe was almost empty, before we reversed the direction of the piston movement and started to empty the other syringe.

Estimation of Subjective Value of Gamble Options

In everyday life, a behavioral choice can yield 2 or more outcomes of varying value with different probabilities. A decision-maker that is indifferent to risk should base his decision on the sum of values of the various outcomes weighted by their probabilities, that is, the expected value of the gamble. However, humans and animals are not indifferent to risk and their actual decisions deviate from this prediction in a systematic fashion. Thus, the subjective value of a gamble depends on the risk attitude of a decision-maker. In this study, we measured the subjective value of a gamble and the risk attitude of the monkeys with the following procedures.

We described the monkey's behavior in the gambling task by computing a choice function for each of the 6 gambles from each day's task session. The choice function of a particular gamble plots the probability of the monkey to choose this gamble as a function of the reward amount of the alternative sure option (Fig. 2A). When the amount of the alternative sure option is small, monkeys are more likely to choose the gamble. As the sure option's reward amount increases, monkeys increasingly choose the sure option. We employed a logistic regression analysis to estimate the probability of choosing the gamble as a continuous function of the reward amount, or value, of the sure option [EVs], that is, the choice function:

$$\text{log[}P(\mathrm{G})/\text{1}-P(\mathrm{G})]=b0+b\text{1}{}^{\ast }\text{EVs}.$$ (1)

Figure 2.

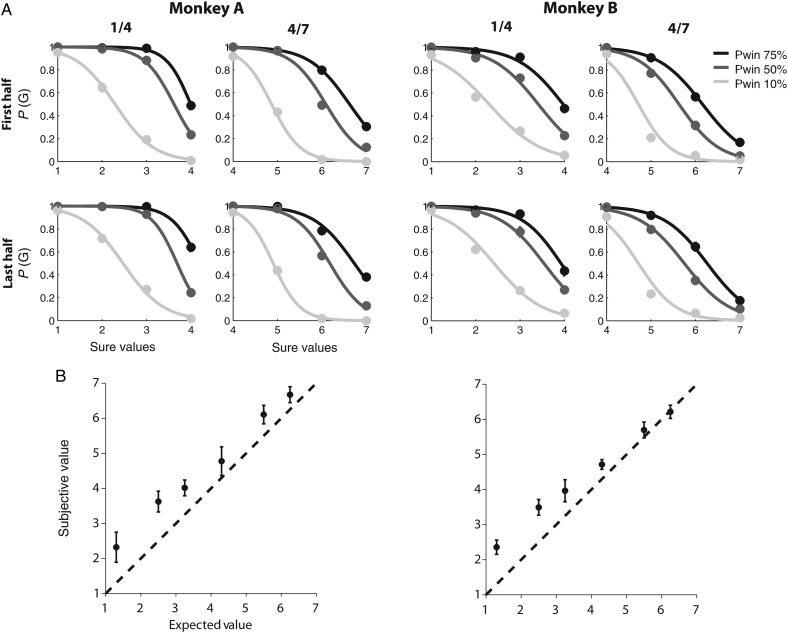
Subjective value estimation. (A) Choice functions of monkeys A (left) and B (right). The probability that the monkey chooses a particular gamble option is plotted as a function of the value of the alternative sure option. The reward size is indicated as multiples of a minimal reward amount (30 µL). The left column shows gamble options that yield either 30 µL (1 unit) or 120 µL (4 units) with a 10% (light gray line), 50% (dark gray line), and 75% (black line) chance of receiving the larger outcome. The right column shows gamble options that yield either 120 µL (4 units) or 210 µL (7 units) with a 10% (light gray line), 50% (dark gray line), and 75% (black line) chance of receiving the larger outcome. All trials are split so that the upper row shows behavior from the first half of each experimental session, while the lower row shows behavior from the second half of each session. There is no difference in the choice functions, indicating that the overall preferences are conserved throughout each session. Also, note that the choice functions for most gambles indicate that the monkeys had variable preferences with respect to a wide range of alternative sure options. (B) Comparison between subjective value (utility) and expected value of a gamble option. The subjective value of a gamble option was estimated from behavior and plotted against its expected value (the weighted average of the 2 possible outcomes). The subjective value is consistently larger than the expected value, indicating that the monkey overvalued the gamble options and behaved in a risk-seeking fashion. The figure represents the grand average over all choice trials recorded across different sessions from monkeys A (left; 42 sessions with average 800 trials per session [SEM = 64.3]) and B (right; 29 sessions with average 1030 trials per session [SEM = 81.9]).

The choice function reached the indifference point (ip) when the probability of choosing either the gamble or the sure option are equal [P(G) = 0.5]. By definition, at this point, the subjective value of the 2 options must be equal, independent of the underlying utility functions that relate physical outcome to value. Therefore, the subjective value of the gamble [SVg] is equivalent to the sure option value at the indifference point [EVs(ip)]. This value, sometimes also referred to as the certainty equivalent (CE; Luce 2000), can be estimated by using equation (1) at the indifference point

$$\text{EVs(ip)}=\text{SVg}=-b0/b\text{1}.$$ (2)

During the initial training stages, we observed that, overall, the monkeys preferred gambles over sure options. To offer combinations of gamble and sure options that elicited a varied set of responses ranging from preference of sure to preference of gamble options, we opted for gamble options with a 10%, 50%, and 75% chance of winning. The asymmetry in the winning probabilities reflects the overall gamble preference of the monkeys.

Relationship Between Confidence and Value Difference

Any type of decision process can be understood as the comparison of the various factors that support or oppose a particular choice (“the evidence in favor of choosing x”). In the case of perceptual decisions, the evidence is primarily the sensory information that supports hypothesis x about the state of the world being true (Gold and Shadlen 2007). In value-based decision-making, the evidence supporting an option x is primarily the subjective value that the agent expects to receive following choosing x. If an option x is chosen over an alternative y that was supported by substantially less evidence, the choice is likely to be optimal and confidence in the choice should be high. Conversely, if the same option x is chosen over an alternative y′ that was supported by an almost similar amount of evidence, the choice is less likely to be optimal and confidence should be low. This relation between the balance of evidence and confidence is independent of the particular outcome of the choice (e.g. reward amount), since the confidence signal evaluates the quality of the decision process, not its eventual outcome.

It is important to distinguish choice confidence from response conflict, another monitoring signal that is also related to the difference in evidence supporting the generation of competing responses. Response conflict is thought to be a cognitive signal that monitors the degree to which mutually exclusive responses are prepared by the brain and is used to regulate the level of executive control over response selection (Botvinick et al. 2001). In the context of value-based decision-making, response conflict is therefore defined as the absolute difference in value (|Vd|), independent of which option is chosen. Response conflict should be maximal when both options are likely to be chosen. In this case, both alternatives are supported by similar amounts of evidence, so that choice confidence should be low. Conversely, response conflict should be minimal, when choice confidence is high. However, the 2 signals are not simply the inverse of each other, since their function and timing is different. Since response conflict is defined independent of the eventual choice, it can be computed instantaneously during the ongoing decision process to evaluate the “momentary” difficulty in making a choice. In contrast, choice confidence is defined with respect to the actual choice and can therefore only be computed after the decision process is finished as a post hoc evaluation.

In our data set, the difference of evidence on which the decision was based, that is, value difference, was not immediately observable on a trial-by-trial basis. Instead, using a simple choice model (Fig. 3), we could predict how mean confidence in a particular choice chosen over a particular alternative should be related to observable task variables.

Figure 3.

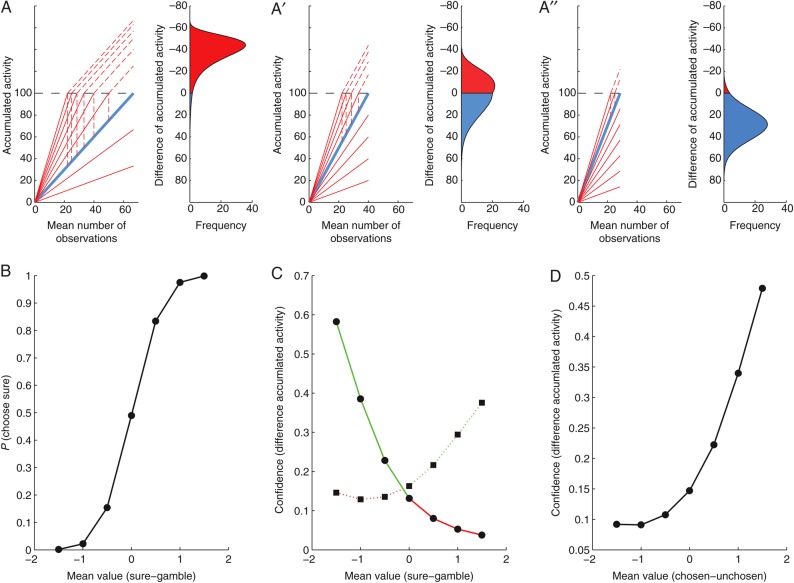
A schematic diagram relating choice confidence to the value difference between the chosen and unchosen target. (A) The competition between the gamble and the sure option is modeled as a race between 2 competing linear ballistic accumulators. The expected value of the gamble option varies across trials (family of red lines), whereas the expected value of the sure option is constant (single blue line). The gamble accumulator is matched against a sure accumulator representing a value that is smaller (A), equal to (A′), or larger (A″) than the average gamble value. (B) Probability of choosing the sure option as a function of mean difference in the value of sure and gamble options. (C) Confidence as a function of mean difference in the value of sure and gamble options. (D) Confidence as a function of mean difference in the value of chosen and unchosen options.

The decision process in our task was modeled as a race between 2 accumulators, namely the sure and the gamble choice accumulators. In accumulator models, the increase in activity reflects the integrated information supporting a particular choice. For value-based decisions, the rise in activity is therefore proportional to the subjective value of each option, which takes the place of sensory evidence in similar models of perceptual decision-making (Gold and Shadlen 2001, 2007). The monkeys showed a highly consistent preference ranking of the sure options reflecting the increasing reward amounts. Accordingly, the variability of the value estimate for the sure option across trials should be very small. For simplicity, we presume here that the slope of the sure accumulator is constant across trials (indicated by the thick blue line in Fig. 3A–A″). In contrast, when comparing a gamble against sure options, the monkeys often varied their preferences across trials (Fig. 2A). This variability did not depend on perceptual uncertainty, since the stimuli indicating the different options were easily distinguishable. It is unlikely that the monkeys were uncertain about which outcomes were associated with which visual stimuli, since their behavioral variance did not reduce even after months of exposure to the task. Instead, the behavioral variance is likely to be caused by a changing estimation of the gamble option's value across trials. We presume here that this value is drawn from a Gaussian distribution (indicated by the family of red lines in Fig. 3A–A″).

One reason for this persistent uncertainty about the value of the gamble options might be that they vary across 2 independent dimensions, reward amount and probability, both of which can affect the overall value. Options can be attractive for different reasons, for example, either because of low risk or high payoff. Hence, assessing the value of a gamble option requires a trade-off between the different attributes that should be integrated in a weighted fashion in order to generate a one-dimensional decision variable, the subjective value of the option. This process has no obvious best solution and agents can remain ambivalent with respect to which of the options is optimal. In addition, there are a number of other psychological factors that could increase the variability of the subjective value estimate for gambles, such as different states of arousal or attention to the task set.

In the model (Fig. 3A–A″), the choice is determined by the race between the gamble and the sure accumulator. Whichever accumulator reaches the decision threshold first determines the choice on that trial. Varying choices result from the noisy estimates in the subjective value of the gamble option, and do not reflect errors in the decision process (in the sense that a target is chosen, although it is believed to be of lesser value on average across trials). In other words, the same choice (e.g. a sure option) can be made, while different degrees of information supporting the alternative option have been accumulated (e.g. the red lines below the blue line in Fig. 3A). Accordingly, at the moment of choice, there are varying degrees of difference in the accumulated evidence across trials (Vickers 1979; Kiani and Shadlen 2009; Kepecs and Mainen 2012). The frequency distribution of the resulting activity differences between the accumulators is shown to the right in each of Figure 3A–A″. A positive activity difference between sure and gamble accumulator is indicated in blue, and corresponds to the choice of the sure option. A negative activity difference is indicated in red and corresponds to the choice of the gamble option. In this case, the activity difference between the winning gamble and the losing sure accumulator (indicated by the hatched vertical line) is projected on top of the threshold onto the negative part of the y-axis.

As in our experiment, each panel in Figure 3A–A″ depicts a situation in which the same gamble accumulator is matched against a sure accumulator, representing a value that is smaller (Figure 3A), equal to (Figure 3A′), or larger (Figure 3A″) than the average gamble value. For positive activity differences the sure option was chosen, whereas for negative ones the gamble option was chosen. Thus, the probability of choosing the sure option is proportional to the fraction of the distribution of differences of activity in the positive range (indicated in blue below the threshold). The resulting choice probability varies as a function of the difference between the mean value of the sure and the gamble option (Fig. 3B), similar to the behavioral choice functions of the monkeys in the gambling task (Fig. 2A).

A large activity difference between the sure and the gamble accumulators allow for high confidence that the choice was optimal, because it indicates a much larger amount of information supporting the chosen option relative to the alternative. Conversely, small activity differences result in less confidence, because in this case the 2 options were supported nearly equally strong, and the eventual choice might have been a result of noise (Vickers 1979). Thus, the activity difference between the accumulators at the moment of choice serves as an estimate of choice confidence, a measure of the likelihood that the choice in the gambling task was optimal. While confidence will vary from trial to trial, the average confidence is a function of the difference between the mean value of the sure and the gamble option, and relates to the average difference value in the blue and red sections of the activity difference distributions depicted in Figure 3A–A″. As a result, average confidence depends both on the difference in the mean value of the 2 options and on the choice, with a resulting four-fold pattern (Fig. 3C). The tendency of the relationship between average confidence and mean value difference is the same for sure and gamble choices. Therefore, in a further simplification of their relationship, we can predict that average confidence in the gambling task should be a monotonically increasing function of the difference in mean value of the chosen and unchosen option (Fig. 3D). Similar monotonically increasing relationships can be derived using other signal detection or sequential sampling models of confidence (Vickers 1979; Kepecs et al. 2008; Kiani and Shadlen 2009; Kepecs and Mainen 2012). Note that this relationship is very different from response conflict, which should be maximal when the mean value difference is zero, and then fall off symmetrically for increasingly larger value differences, independent of their direction.

Electrophysiology

After training, we placed a square chamber (20 × 20 mm) centered over the midline, 25 mm (monkey B) and 27 mm (monkey A) anterior to the interaural line (Fig. 4). During each recording session, single units were recorded using a single tungsten microelectrode with an impedance of 2–4 MΩ (Frederick Haer, Bowdoinham, ME, USA). The microelectrodes were advanced using a self-build microdrive system. Data were collected using the PLEXON MAP system. Up to four template spikes were identified using template matching and principal component analysis, and the time stamps were then collected at a sampling rate of 1000 Hz. Data were subsequently analyzed offline to identify additional units and to ensure only single units were included in consequent analyses.

Figure 4.

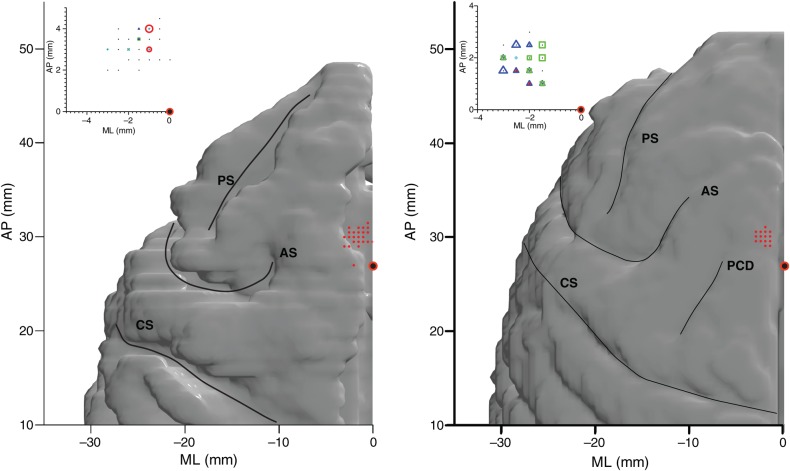
Location of the SEF and choice-dependent neurons. The red dots indicate the localization of all neurons with saccade-related activity in the left hemispheres of monkeys A (left) and B (right). The recording locations were superimposed onto a reconstruction of the cerebral cortex based on a MRI scan. The red circle with black fill is located 27 mm forward of the interaural line. The insets indicate subpopulations of cells encountered in the SEF with choice-dependent activity (red circle: Vd+; green square: UV; blue triangle: Vd−; magenta star: CV). The marker sizes indicate the number of neurons (large: 9–12 cells, medium: 5–8 cells, and small: 1–4 cells). AS: arcuate sulcus; PS: principal sulcus; CS: central sulcus; PCD: precentral dimple.

Spike Density Function

To represent neural activity as a continuous function, we calculated spike density functions by convolving the spike train with a growth-decay exponential function that resembled a post-synaptic potential. Each spike therefore exerts influence only forward in time. The equation describes rate (R) as a function of time (t):

$$R(t)=(\text{1}-\exp (-t/{\tau }_{\mathrm{g}}))\cdot \exp (-t/{\tau }_{\mathrm{d}}),$$ (3)

where τ_g is the time constant for the growth phase of the potential, and τ_d, is the time constant for the decay phase. Based on physiological data from excitatory synapses, we used 1 ms for the value of τ_g and 20 ms for the value of τ_d (Sayer et al. 1990).

Task-Related Neurons

Since we focused our analysis on neuronal activities during the delay after saccade and before the result disclosure, we restricted our analyses on the population of neurons active during this time period. We performed t-tests on the spike rates in 10 ms intervals throughout the delay period, in comparison with the baseline activity defined as the average firing rates during the 200–100 ms prior to target onset. If P-values were <0.05 for 5 or more consecutive intervals, the cell was classified as task-related in the delay period (So and Stuphorn 2010, 2012).

Choice-Selective Neurons

In a previous study (So and Stuphorn 2012), we analyzed outcome-encoding neurons in the SEF. Outcome-encoding neurons should show no difference in activity for choice and no-choice trials, since both the expected and the actual outcomes are defined with respect to the chosen target, independent of the presence of an alternative. In contrast, in this study, we are interested in the neurons whose activity differed significantly between choice- and no-choice trials. Neurons of this type are candidates for carrying choice-evaluation signals, such as confidence. To find such cells, we first analyzed the neurons using combinations of outcome-encoding variables (subjective value of the chosen target, uncertainty [i.e. a binary signal representing whether the chosen option was a sure or a gamble option], and the interaction of the choice value and the uncertainty) that we used in a previous study (So and Stuphorn 2012). We searched for a best model for each neuron, pooling all the choice and no-choice trials. Next, we added a term identifying the trial type (choice or no-choice) to the previously found best model and determined whether this explained the variance in neuronal activity better, using the BIC comparison. All subsequent analyses were conducted on the subset of neurons that showed a significant activity difference for choice- and no-choice trials.

Although we identified task-related neurons by looking at the entire delay period, we fit the neuronal activity separately for early (300 ms after saccade onset) and late delay period (300 ms prior to the outcome disclosure). We looked at those periods independently, since these 2 time periods might be functionally different, one more related to decision formation and its immediate evaluation, and the other to the outcome expectation. Among the 227 neurons that showed task-related activity during the delay period (out of 264 neurons recorded in total), 66 and 28 neurons were found to be sensitive to the trial types during the early and the late delay periods, respectively. This study analyzed specifically these neurons. Only 4 cells were choice-selective in both periods.

Regression Analysis

To quantitatively characterize individual neuron's modulation, we designed groups of linear regression models, using linear combinations of variables that were postulated to describe the neuronal modulation: the value difference (Vd), the chosen option value (CV), the unchosen option value (UV), and their interaction terms. In general, we treated the activity in each individual trial as a separate data point for the fitting of the regression models.

Choice confidence is only defined in choice trials. To investigate the neuronal correlates for the choice confidences signal, therefore, we used the delay period activity in choice trials exclusively from the choice-selective neurons that showed a significant difference between choice and no-choice trials. To quantitatively describe the choice-dependent neuronal activity modulation, one model for the regression analysis was designed as

$$\text{FR(CV},\text{Vd)}=b0+b{\text{1}}^{\ast }\text{CV}+b{\text{2}}^{\ast }\text{Vd}+b{\text{3}}^{\ast }({\text{CV}}^{\ast }\text{Vd}),$$ (4)

where CV was the subjective value of the chosen option, and Vd was defined as

$$\text{Vd}=\text{CV}-\text{UV,}$$ (5)

where UV was the subjective value of the unchosen option. In addition, we also designed an alternative model

$$\text{FR(UV},\text{Vd)}=b0+b{\text{1}}^{\ast }\text{UV}+b{\text{2}}^{\ast }\text{Vd}+b{\text{3}}^{\ast }({\text{UV}}^{\ast }\text{Vd}),$$ (6)

in which UV was exchanged for CV. We did not include CV, UV, and Vd into one model, since they are not independent of one another. The 2 alternative models and all their derivative models, including a simple constant baseline model (b0), were used to describe each neuron's mean neuronal activity during the first 300 ms after saccade initiation (early delay period), and the last 300 ms before the result disclosure (late delay period). Depending on which variables were found in the best model (see the “Model Fitting” section below), we classified the activity as carrying a chosen value (CV) signal, an unchosen value (UV) signal, and value difference (Vd)-sensitive signals (Vd, CV * Vd, or UV * Vd).

Coefficient of Partial Determination

To determine the dynamics of the strength with which the different signals modulated neuronal activity, we calculated the coefficient of partial determination (CPD) for each variable from each neuron's mean activity during different time bins (50 ms width with 10 ms step size; Neter et al. 1996). As we had 3 variables in each of the full regression models, CPD for each variable (X1) was calculated as:

$$\text{CP}{\text{D}}_{X1}=\frac{\text{SSE}(X\text{2, }X\text{3})-\text{SSE}(X\text{1},X\text{2},X\text{3)}}{\text{SSE}(X\text{2},X\text{3})}$$ (7)

For each neuron and time bin, we calculated the CPD using the best one of the 2 full model alternatives (see the “Model Fitting” section below), and set the CPD value for the variable that was not contained in the model to zero.

Model Fitting

To determine the best fitting regression model, we searched for the model that was the most likely to be correct, given the experimental data. This approach is a statistical method that has its origin in Bayesian data analysis (Gelman et al. 2004). Specifically, we used a form of model comparison, whereby the model with the smaller Bayesian information criterion (BIC) value was chosen. For each neuron, BIC values were calculated for all of the different regression models:

$$\text{BIC}=n\ast \text{log(RSS}/n)+K\ast \text{log(}n)$$ (8)

where n was the total trial number and K was the number of fitting parameters (Burnham and Anderson 2002; Busemeyer and Diederich 2010). By comparing the BIC values, the best model was determined as the one having the lowest BIC.

This procedure is related to a likelihood-ratio test, and equivalent to choosing a model based on the F-statistic (Sawa 1978). It provides a Bayesian test for nested hypotheses (Kass and Wasserman 1995). Importantly, we included a baseline model in our set of regression models. Thus, a model with one or more signals was compared against the null hypothesis that none of the signals explained any variance in neuronal activity. An alternative procedure, a series of sequential F-tests, while exact, requires the assumption of data with a normal distribution. We decided to use the BIC test, because it was computationally straightforward and more robust. An additional advantage was that we could compare all models simultaneously, using a consistent criterion (Burnham and Anderson 2002).

Residual Firing Rate Analysis

The activity of any given neuron may be influenced by many different variables. To better visualize the modulation that could be contributed by only one of the variables (variable of interest), we performed the following procedure to subtract the influence of all other variables (controlled variables). First, we determined for each trial the spike density function expected from the modulation by the controlled variables by averaging the spike density function of all trials that had the same set of values for the controlled variables as the ones in the particular trial. Secondly, we subtracted this spike density function from the spike density function of the given trial. Hence, the resulting residual firing rate represented the activity modulation on that trial due to the variable of interest as the modulation due to the controlled variables was taken into account. Thirdly, we computed the average residual firing rate across all trials belonging to a given condition.

We decided to control only the CV, UV, and saccade direction, which are related to the major alternative hypotheses to explain our Vd signals, and to ignore a number of other variables. It is important for this analysis that the spike density function of the reference trials is as smooth as possible, so that the resulting difference (the residual firing rate) reflects mostly the variance in the individual trial activity, not the noise in the reference trials. As the spike density function of individual trials is very noisy, it requires that the reference activity is constructed on as large number of trials as practical. We will discuss the practical implications of this limitation of the analysis in the context of the actual results.

Results

Subjective Value of Gamble Options

We trained 2 monkeys in a gambling task (Fig. 1A), which required them to choose between a sure and a gamble option by making an eye movement to 1 of the 2 targets. Behavioral results showed that the monkeys' choices were based on the relative value of the 2 options. For each gamble, we plotted the probability of choosing the gamble as a function of the alternative sure reward amount (Fig. 2A). The probability of a gamble choice decreased as the alternative sure reward amount increased. In addition, as the probability of receiving the maximum reward (i.e. “winning” the gamble) increased, the monkey showed more preference for the gamble over the sure option. The monkey's preferences with respect to fluid reward might depend on his satiation level (Minamimoto et al. 2009). We therefore divided the trials into the first (Fig. 2A, upper row) and the second (lower row) half of trials in each daily session. There was no difference in the choice functions, indicating that the overall behavioral preferences were stable over the course of the session.

From these behavioral data, we estimated the choice function for each gamble using a logistic regression function (equation 1). The choice functions allowed us to estimate the subjective value of the gamble to the monkeys, by finding the sure reward amount at which the monkey chooses the gamble and the sure option equally often. This sure reward amount (the CE) is presumably equal in subjective value to the gamble. This procedure only depends on the monkey's own choice curves and is independent of the exact shape of the underlying utility functions that relate physical outcome to a value. The choice functions of both monkeys show a graded shift in the gamble option preference as the alternative sure reward amount increases, rather than a sharp shift in an all-or-none fashion (Fig. 2A). This indicates that the monkeys have variable preferences with respect to gamble options over a range of sure values. This choice ambivalence is not present when the monkeys had to compare different sure options only. In that case, the monkeys indicated clear preferences and nearly always chose the option resulting in the larger reward amount. Hence, the ambivalence during the gambling task indicates uncertainty which of the 2 options is better. This ambivalence persists despite long exposure to the task, and it is systematically related to the alternative sure reward amount, rather than being random (Fig. 2A). It is therefore not likely to be the result of simple lack of knowledge about the possible outcomes of choosing each option, which can be overcome through learning and exposure. Instead, it likely reflects the probabilistic nature of the gamble options.

We plotted the subjective value of each gamble against its expected value, that is, the sum of the 2 possible reward amounts weighted by the probability (Fig. 2B). Both monkeys chose the gamble option more often than expected given the probabilities and reward amounts of the outcomes, indicating that the subjective value of the gamble option was larger than its expected value (Fig. 2B). Thus, the monkeys behaved in a risk-seeking fashion, similar to findings in other gambling tasks using macaques (McCoy and Platt 2005; O'Neill and Schultz 2010). The reasons for the general tendency for risk-seeking behavior are not clear. It might be related to the specific requirements of our experimental set-up, that is, a large number of choices with small stakes. From the point of view of the present experiment, the most important fact is that we can measure the subjective value of the gambles, which is different from the “objective” expected value.

Monkeys Evaluate Their Choice During the Delay Period

In our gambling task, there is an approximately 1 s delay between the choice (saccade onset) and the disclosure of its outcome (Fig. 1A). Nevertheless, the likelihood that the choice was optimal (i.e. choice confidence) can be evaluated immediately. This is particularly important, since our task imposes a cost associated with waiting for the outcome of the choice, due to the effort of keeping the target fixated and the opportunity cost of not advancing to the next trial sooner, which might offer potentially better options. The behavior of the monkeys strongly suggests that they indeed evaluated their choice in this way.

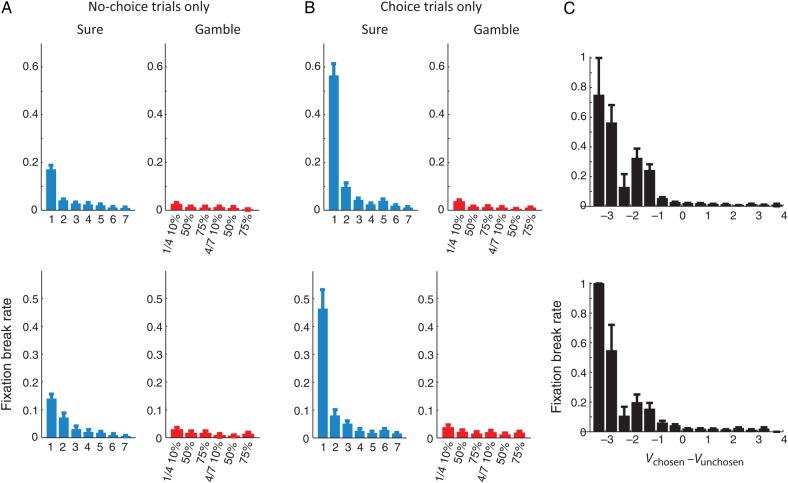
During the delay period following the saccade, both monkeys broke fixation more often the lower the reward amount they expect from the target (Fig. 5A,B). This trend was overall the same during both no-choice (Fig. 5A) and choice trials (Fig. 5B). In both monkeys, the fixation break rate is higher following the selection of a sure over a gamble option. This difference might be the result of the overall risk attitude of both monkeys. Since both monkeys had a slight preference of gambles over sure options, they might have valued the offered gamble options higher than the sure options (Fig. 2B). Since subjective value is negatively correlated with a fixation break rate, we would expect fewer fixation breaks following the choice of gamble options in general.

Figure 5.

Rate of fixation breaks during the post-choice delay. (A) Fixation break rate as a function of the value of the saccadic target during no-choice trials. (B) Fixation break rate as a function of the value of the chosen option during choice trials. (C) Fixation break rate as a function of the value difference between the chosen and unchosen option. Upper rows represent the results from monkey A and lower row the results monkey B. Error bars represent SEM.

During choice trials, in addition to the chosen option value, the monkeys were also sensitive to the value difference in the chosen and unchosen option (Fig. 5C). Both monkeys broke fixation more often when the chosen option held less subjective value than the alternative (i.e. more negative value difference). This trend was significant even after the value of the chosen option was taken into account. Linear regression analyses showed that the fixation break rate of both monkeys was significantly related to the chosen option value, the value difference between the chosen and unchosen option, and their interaction term (P < 0.001 for all 3 variables for both monkeys). During gamble choice trials, the overall fixation break rate was lower than during sure choice trials. We therefore repeated the linear regression specifically for gamble choice trials, using CV, value difference, and their interaction as dependent variables. We found both factors and their interaction to be highly significantly (P < 0.001) related to the rate of fixation breaks for both monkeys. To further test the influence of value difference independent from the CV, we repeated our regression analyses within the trials where the monkey chose a particular option. This regression conditioned on the chosen option value confirmed that value difference alone could explain the frequency of the monkey's fixation breaks (P < 0.05 for both monkeys).

This analysis suggests that confidence in the choice and willingness to wait for the outcome of the choice are related. However, the monkey might also break fixation following a momentary lapse of attention or an impulsive saccade in a way that is unrelated to the normal value comparison. While we cannot rule out the possibility of such random lapses in the decision process, they cannot explain the relationship between fixation breaks and value difference. If we presume that the animal automatically aborts the trial if such an error occurs, we should see a constant rate of fixation breaks that is independent of value difference. As Figure 5C indicates, that is not the case. Fixation breaks occur only, when the difference between the chosen and unchosen option is negative and then their frequency gradually increases as a function of increasing a value difference. It is possible that random errors occur, but only lead to fixation breaks, if they cause a disadvantageous choice. However, in that case, it is again necessary for the animal to compare the relative weight of evidence (i.e. the value of the 2 options) in order to decide whether it should break fixation or not. The relationship between fixation breaks and value difference therefore indicates that fixation breaks are related to choice confidence and are triggered by low levels of confidence, and not by random breakdowns of the normal decision process.

While the monkeys occasionally broke fixation and thereby suggested that they had low confidence in the preceding choice, most of the time the monkeys finished the trials; the number of fixation breaks during the choice trials were 487/23191 (2%) in monkey A and 514/21478 (2.4%) in monkey B. Indeed, the fixation break itself was costly, since the monkeys forfeited any reward they would have received on that trial. Thus, the monkeys might be willing to await the consequence of a choice even if they had low confidence. Hence, the fixation breaks are best understood as a measure of the minimum amount of confidence below which the monkey was no longer willing to invest time and effort in his choice, rather than a measure representing the full spectrum of confidence.

SEF Neurons Represent Choice Confidence

Many evaluative signals that are represented in the SEF, such as reward expectations, or uncertainty about the reward amount, are well defined even in the absence of an alternative option (So and Stuphorn 2012). In contrast, without a choice between alternatives, choice confidence cannot be defined. Hence, neuronal signals reflecting choice confidence should be present only during choice trials, but not during no-choice trials, where only one option is given (Fig. 1A). Indeed, immediately after the choice (early delay period; 300 ms after the saccade onset), we observed a substantial number of neurons (66/227; 29%) that showed a significant activity difference for choice and no-choice trials (choice-selective neurons). Thus, the activity of these neurons depended on the presence of an alternative target. This study analyzed specifically these neurons.

Figure 6 shows an example of such a cell. Despite identical values of the saccade targets, this neuron showed a clear difference in its activity during choice trials (“blue lines” during sure choice trials; “red lines” during gamble choice trials) compared with no-choice trials (“black lines”). In general, the neuron responded more strongly and less stereotypically on choice trials; it did not reflect only the chosen or unchosen option. The neuronal activity for any given chosen option was very different depending on what was offered as an alternative (different colored lines within each plot). Likewise, the neuronal activity varied considerably for the same unchosen option accompanying different chosen options (the same colored lines across the plots). Thus, the overall activity pattern of this neuron seems to reflect both the value of the chosen and the unchosen option. More specifically, for a particular chosen option, this neuron showed higher activity with an increasing value of the unchosen option (paler-colored lines). This implies that the neuronal activity is inversely correlated with the difference in the value between the chosen and unchosen option.

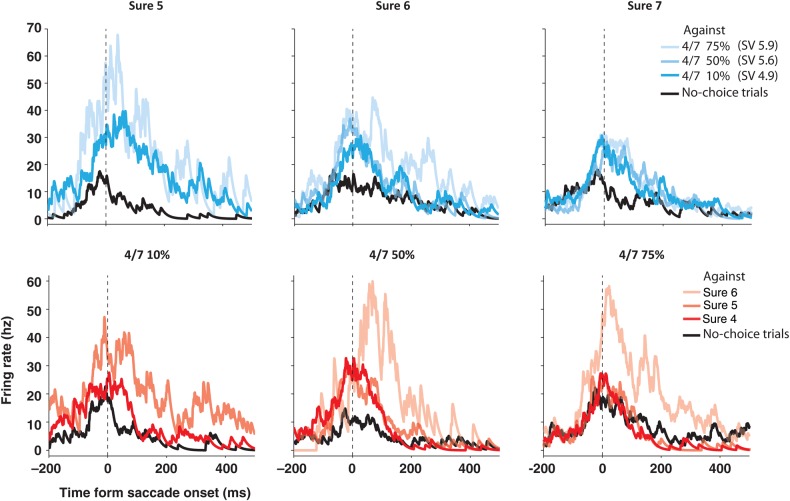
Figure 6.

SEF neuron with choice contingent activity during the delay period. Spike density histograms show activity separately for different chosen options, aligned on the saccade onset. The upper row shows the activity when sure options of increasing value were chosen (due to increasing payoff: 5–7 units of reward). The lower row shows activity when gamble options of an increasing value were chosen (due to increasing winning probability: 10–75%). Within each spike density histogram, trials were sorted by the unchosen alternative option (upper row: sure option chosen over 4 vs. 7 gamble with a winning probability of 10%: pale blue, 50%: light blue, and 75%: dark blue; lower row: 4 vs. 7 gamble chosen over sure option with a payoff of 4: pale red, 5: light red, and 6: dark red; all in units of reward). During no-choice trials, the activity (black line) was very similar across reward options, and nearly always lower than when the same option was chosen in a choice trial (blue or red lines). During choice trials, the activity was not only larger, but also systematically influenced both by the chosen and unchosen option. In general, the activity was stronger as the unchosen option was more valuable than the chosen option. This can be seen, for example, by comparing the activity when sure options of increasing value (from 5 to 7) were chosen against a 4 vs. 7 gamble option with a 75% chance of winning (pale blue lines in the upper row). When the choice was made against the same alternative, the activity was strongest for the least valuable chosen option and weakest for the most valuable chosen option. Thus, this neuron seems to be influenced by the comparative value of the chosen option.

We tested whether any of the choice-selective neurons carried signals related to choice evaluation. We used a series of nested regression models employing variables like value difference between the chosen and unchosen (Vd), CV, UV, and the interaction between the value and the value difference (CV * Vd and UV * Vd). Of the 66 choice-selective neurons in the early delay period, 15 neurons (23%) represented the Vd signal, 7 neurons (11%) the CV signal, 30 neurons (45%) the UV signal, 6 neurons (9%) the CV * Vd signal, and 12 (18%) the UV * Vd signal. Individual neurons often carried a combination of these signals (19/54; 35%; Table 1). Interestingly, for the majority of neurons carrying the Vd signal (11/15; 73%), the activity was negatively correlated with a value difference. This tendency was similar for the UV * Vd signal (10/12; 83%). On the other hand, the activity of the neurons carrying CV, UV, and CV * Vd signals was often positively correlated with each of the corresponding variables (5/7; 71% for CV signal, 28/30; 93% for UV signal, 6/6; 100% for CV * Vd signal). In total, 29 of the 66 (44%) choice-selective neurons carried Vd-sensitive, that is, choice confidence-related signals (either one of Vd, CV * Vd, and UV * Vd signals).

Table 1.

Distribution of signal types found in SEF data set

	Early			Late
CV	CV	5 (3/2)	7 (5/2)	CV	5 (3/2)	6 (3/3)
	CV + Vd	0		CV + Vd	1 (0/1)
	CV + CV * Vd	2 (2/0)		CV + CV * Vd	0
	CV + Vd + CV * Vd	0		CV + Vd + CV * Vd	0
UV	UV	20 (19/1)	30 (28/2)	UV	4 (1/3)	4 (1/3)
	UV + Vd	1 (0/1)		UV + Vd	0
	UV + UV * Vd	7 (7/0)		UV + UV * Vd	0
	UV + Vd + UV * Vd	2 (2/0)		UV + Vd + UV * Vd	0
Vd	Vd	10 (2/8)	15 (4/11)	Vd	1 (1/0)	6 (4/2)
	CV + Vd	0		CV + Vd	1 (0/1)
	Vd + CV * Vd	2 (0/2)		Vd + CV * Vd	3 (2/1)
	CV + Vd + CV * Vd	0		CV + Vd + CV * Vd	0
	UV + Vd	1 (0/1)		UV + Vd	0
	Vd + UV * Vd	0		Vd + UV * Vd	1 (1/0)
	UV + Vd + UV * Vd	2 (2/0)		UV + Vd + UV * Vd	0
CV * Vd	CV * Vd	2 (2/0)	6 (6/0)	CV * Vd	1 (0/1)	4 (1/3)
	CV + CV * Vd	2 (2/0)		CV + CV * Vd	0
	Vd + CV * Vd	2 (2/0)		Vd + CV * Vd	3 (1/2)
	CV + Vd + CV * Vd	0		CV + Vd + CV * Vd	0
UV * Vd	UV * Vd	3 (1/2)	12 (2/10)	UV * Vd	1 (1/0)	2 (1/1)
	UV + UV * Vd	7 (1/6)		UV + UV * Vd	0
	Vd + UV * Vd	0		Vd + UV * Vd	1 (0/1)
	UV + Vd + UV * Vd	2 (0/2)		UV + Vd + UV * Vd	0

Note: Four rows for each of the signal represent the cases of the best model in which the signal was observed. Numbers in parentheses represent the frequency of the positive/negative correlation with the neuronal activity, respectively. For example, “2 (2/0)” on the third row of the third column means that 2 of the CV signals were found in the neuronal activity best described with the model “CV + Vd”, and 2 among those 2 cases had positive coefficient for the CV signal in the best model. The functional types were determined separately for the early and the late delay periods.

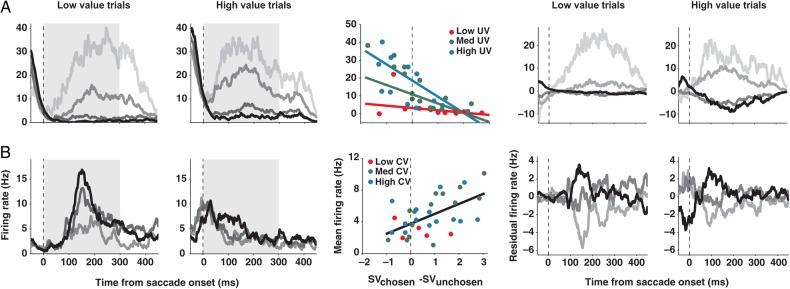
Figure 7 shows 2 example neurons carrying Vd-sensitive signals. The neuronal response in each spike density histogram is sorted into 4 groups according to the amount and sign of the value difference between the chosen and unchosen option. To demonstrate the effect of the chosen or UV, the activity is shown separately for the trials comparing high-value range options and low-value range options. An absolute value of both the chosen and unchosen option is in the range of 30–120 µL fluid reward for the low-value trials and 120–210 µL fluid reward for the high-value trials (Fig. 1B). The histograms to the left of the regression plot show the actual firing rate, whereas the histograms to the right show the residual firing rate that was due to the value difference after accounting for the influence of either chosen (CV) or UV and saccade direction. The regression plots between the histograms show the mean activity of those example neurons (“circles”) as a function of the value difference, along with the predictions based on the best regression models (“lines”). If the best model for the activity of a neuron contains any UV-related signals, the residual firing rate was generated by controlling the UV and the saccade direction. Otherwise, the CV and the saccade direction were controlled. The neuron in Figure 7A showed the highest activity when a chosen option had the lowest value compared with the alternative, and decreased its activity as a chosen option increased in relative value. This neuron was additionally modulated by the UV, in a nonlinear fashion. Being negatively correlated with the Vd, the activity of this neuron seems to be related to the belief that the choice was likely not optimal (Vd- signal). On the other hand, the neuron in Figure 7B is positively associated with the Vd, and therefore seems to reflect the belief that the choice was likely optimal (Vd + signal).

Figure 7.

SEF neurons representing decision confidence during the delay period. Spike density histograms show activity separately for trials with a low-value gamble option (1 unit of reward for losing and 4 units for winning) and for trials with a high-value gamble option (4 vs. 7 units of reward). The activity is aligned on the saccade onset. Within each spike density histogram, trials were sorted by the range of value difference (Vd) between the chosen and unchosen option (Vd = 2.5 to 1.5 [black], 1.5 to 0.5 [dark gray], 0.5 to −0.5 [medium dark gray], −0.5 to −1.5 [light gray]; all in units of reward, 1 unit = 30 µL of water). The histograms to the left of the regression plot show the actual firing rate, whereas the histograms to the right show the residual firing rate that was due to value difference after accounting for the influence of CV or UV and saccade direction. The activity of SEF neurons could be negatively (A) or positively (B) correlated with Vd. The best regression model for each example neuron is plotted in the middle of the histograms. Neuronal activities (dots) are plotted against the value difference between the chosen and unchosen option. Three different ranges of CV or UV are indicated by the dot color (low [red]: 1–3; medium [green]: 3–5; high CV or UV [blue]: 5–7; all in units of reward). Lines describe the best regression model when the CV or the UV was 7 (blue), 4 (green), and 1 (red) units of reward. When there is no modulation by CV or UV, different colored lines collapse into a single black line. Only the conditions that include more than 5 trials were plotted to make the figures less noisy.

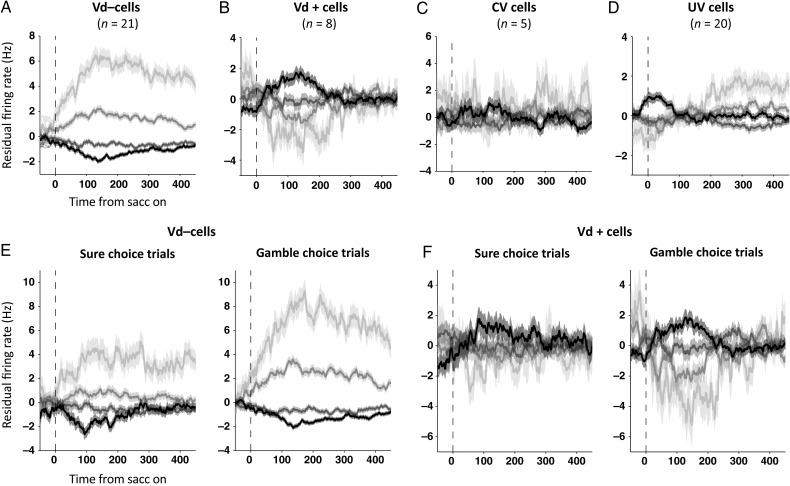
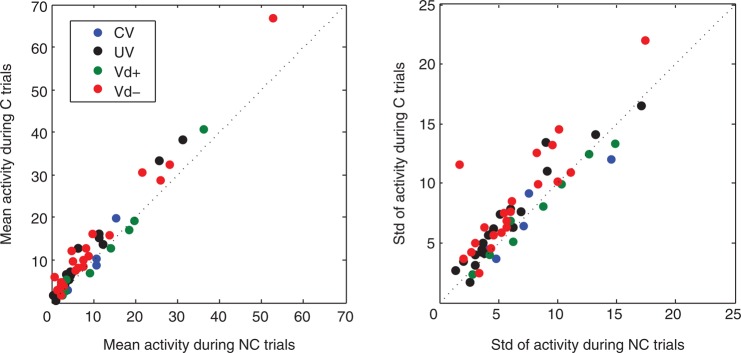
The residual firing rate histograms of the groups of SEF neurons carrying the Vd, CV, and UV signals are shown in Figure 8. When we accounted for the activity modulation due to the CV and the direction of a saccade, the residual firing rate showed clear, but opposed, activity modulation for the cells that were negatively (Fig. 8A) or positively (Fig. 8B) correlated with Vd (one-way ANOVA, P < 10⁻¹⁰). Note that the residual firing rate should be interpreted as neuronal activity that either stronger or weaker than what would be expected based on the controlled variables. That means that in case of a residual firing rate of zero, a neuron might nevertheless be very active. Likewise, a neuron that shows a negative residual firing rate in a certain condition is simply less active than what would be expected given the same CV and saccadic direction. This Vd-related modulation was observed in both gamble and sure choice trials (Fig. 8E,F). In contrast, cells that carried only a CV signal (Fig. 8C) showed no additional activity modulation (one-way ANOVA, P > 0.05), supporting the results of our regression analysis. The neurons that carried only an UV signal according to the regression analysis (Fig. 8D) showed weak modulation by the Vd, after the UV and the direction of a saccade were controlled (one-way ANOVA, P < 0.01). However, this trend was inconsistent in time and showed no regular relationship with the degree of value difference.

Figure 8.

Choice confidence-dependent residual firing rate after accounting for choice value and the direction of a saccade. Residual firing rate for all neurons carrying Vd− signals (A), Vd+ signals (B), a CV signal only (C), or a UV signal only (D). For neurons representing a UV signal only (D), the value of the unchosen option was controlled, instead of the chosen option value. Residual firing rate of SEF neurons representing confidence following sure and gamble option choices, for all neurons with activity that is negatively (E) or positively (F) correlated with Vd. Trials were sorted by the range of value difference (Vd) between the chosen and unchosen option (Vd = 2.5 to 1.5 [black], 1.5 to 0.5 [dark gray], 0.5 to −0.5 [medium dark gray], −0.5 to −1.5 [light gray]; all in units of reward). Shaded areas represent SEM.

In the residual firing rate analysis, we only controlled for CV, UV, and saccadic direction. It is possible that the residual firing rates might still reflect the influence of other variables that we did not include in the analysis, such as the outcome-related variables that we investigated in a previous study (So and Stuphorn 2012). In choice trials, on which we concentrate in this study, a CV is equivalent to expected outcome. The remaining class of potentially unaccounted variables is therefore those related to uncertainty (i.e. signals representing whether the chosen option was a sure or a gamble option; So and Stuphorn 2012). However, we observed value difference (Vd)-dependent residual firing rate modulations in both sure and gamble choice cases (Fig. 8E,F), suggesting that it is unlikely that uncertainty-sensitive variables might be the source of these activity modulations instead of value difference.

There were fewer choice-evaluation signals in the late delay period, just before the outcome was revealed (300 ms before the outcome disclosure). A smaller number of neurons (28/227; 12%) showed a significant difference depending on the trial type (choice/no-choice). Among them, the Vd signal was found in 6 neurons (21%) and its interaction with the CV (CV * Vd) and the UV (UV * Vd) was found in 4 neurons (14%) and in 2 neurons (7%), respectively (Table 1).

Our previous study showed that many SEF neurons carried outcome evaluation signals during the outcome period following the post-choice delay (So and Stuphorn 2012). However, there was no tendency of the SEF neurons carrying Vd− or Vd+ signals to encode any particular set of outcome-related signals. Specifically, the neurons carrying Vd− signals were equally likely to represent loss- or win-related signals (8 loss-related, 7 win-related, and 6 other signals). The same was true for neurons carrying Vd+ signals (1 loss-related, 3 win-related, and 4 other signals).

As mentioned earlier, neurons that carry signals related to choice evaluation should be less engaged in no-choice trials. To characterize the difference in neuronal activities between choice and no-choice trials for the neurons carrying Vd, CV, or UV signals, we compared the mean and the standard deviation in neuronal activity during the 300 ms after saccade between these 2 conditions (Fig. 9). Most of the neurons (especially the Vd− cells) showed stronger and more variable activity during the choice trials compared with no-choice trials.

Figure 9.

The strength and variance of SEF neuron activity with choice contingent activity varies for choice and no-choice trials. We compared the mean activity (left) and the standard deviation of the activity (right) in choice and no-choice trials for the SEF neurons that carried Vd (Vd+: green dots; Vd−: red dots), CV (blue dots), or UV (black dots) signals.

Population Dynamics of the Choice Confidence Signal

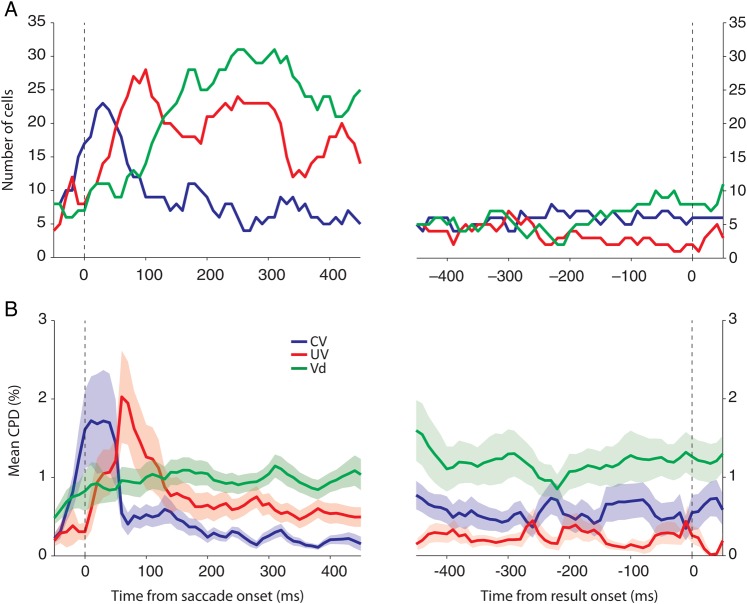
We investigated the temporal dynamics of the choice confidence signals represented in SEF neurons using a dynamic regression and a CPD analysis. First, at each time window (50 ms width; 10 ms step size), we plotted the number of cells whose mean activities during that time window were best described by a model that contained the respective variable (Fig. 10A). Since the temporal dynamics of all Vd−containing signals (Vd, CV * Vd, and UV * Vd signals) were very similar to one another, we combined them all to show the underlying temporal dynamics more clearly. At the beginning of the delay period, most neurons encoded the CV and/or the UV. Interestingly, the UV representation developed mainly after the choice, approximately 50 ms later than the CV representation. Gradually, neurons started to represent the confidence in the choice just made. The number of neurons carrying Vd-sensitive confidence signals peaked around 200 ms after the saccade. Following this peak, all of the choice confidence signals slowly became less frequent. Secondly, using the same temporal windows, we measured at each time point the CPD for each variable (Fig. 10B). The CPD value describes the additional reduction in the variance of neuronal activity that is achieved by introducing a given variable when the explanatory power of all the other variables has already been taken into account. The absolute measure of the CPD value is not informative since its scale depends on the inherent variance in spikes and the overall firing rate of the neurons (see Methods). However, the relative dynamics in CPD value over time and the strength provides a measure to compare the dynamics and the relative strength of each signal in time within the same population. Although the initial domination of the CV and the UV signals makes it less obvious in the plot, the characteristic temporal development of the Vd-sensitive signals was similar to the one revealed by the dynamic regression analysis. Moreover, the temporal difference in CV and UV representation was also observed in the CPD analysis.

Figure 10.

Temporal dynamics of signals in the SEF representing choice confidence. (A) The number of cells that include each variable in their best models was counted for each time bin (overlapping window; 50 ms width with 10 ms step). (B) Mean CPD for each variable at each time bin. Shaded areas represent SEM.

Choice Confidence Signals in SEF Neurons Were Stronger Prior to a Fixation Break

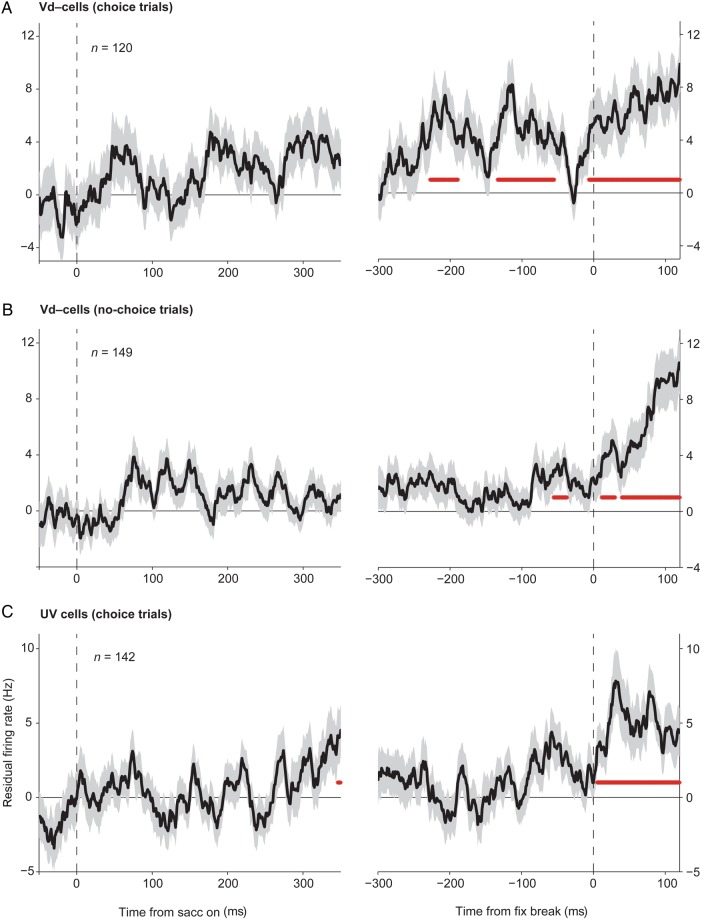
The monkeys evaluated their choice before its outcome was revealed, since they withdrew their choice by breaking fixation of the chosen target more often when the chosen option value was lower than the unchosen option value on average (Fig. 5). We wished to test whether the choice confidence-related activity in SEF neurons had any relation with such evaluative behavior of the monkeys. To test whether the neurons were differentially active on fixation break trials, we computed the residual activity on such trials, after controlling all the other possible factors influencing the neuronal activity, namely the CV, the UV, and the direction of a saccade. Unfortunately, fixation breaks were not common enough to allow us to analyze the activity of individual neurons. Instead, we compared the average of the resulting residual firing rate for all the neurons carrying Vd− signals (Fig. 11A,B), and for all the cells carrying the UV signal only (Fig. 11C). If the activity of the neurons is related to the monkey's evaluative behavior, we would expect the neuronal activity to be significantly different during the fixation break trials compared with trials with an identical condition, in which the monkey decided to stay with the current choice. We examined whether there is any time period prior to the fixation break, during which the residual activity is significantly different from zero for at least 20 ms (two-sided t-test; P < 0.05; Bonferroni adjusted). The cells carrying Vd− signals showed stronger activity for the fixation break trials (positive residual firing rate), as early as around 220 ms prior to the fixation break (Fig. 11A, right). This is a strong indication that the confidence signal carried by the SEF neurons is indeed used to decide, whether the choice should be withdrawn to avoid further costs. This relationship is specific, since during the no-choice trials these same cells showed the activity increase too late to explain the fixation breaks (Fig. 11B, right). Likewise, cells that only carried an UV signal showed stronger activity only after the fixation break had happened (Fig. 11C, right). Hence, the UV signal represented in SEF neurons was not in a position to influence the decision whether the choice should be withdrawn or not. Owing to the small number of the cells carrying Vd+ signals (8 cells and 26 fixation break trials) and of the cells carrying a CV signal only (5 cells and 15 fixation break trials), we could not perform the same analysis on those groups of neurons.

Figure 11.

Residual firing rate during fixation break trials. From the activity during the choice trials where the monkey broke the fixation of the chosen target during the post-choice delay period, the mean activity expected for the same chosen and unchosen options and the same saccade direction was subtracted for the neurons carrying Vd− signals (A), and the ones carrying a UV signal only (C). To determine the residual firing rate of the Vd− neurons before a fixation break during the no-choice trials (B), we subtracted the mean activity expected for the same chosen option and the saccade direction. The residual firing rate was aligned to the initial saccade onset (left), and to the fixation break onset (right). The number of fixation break trials used for each group is indicated in each plot.

Discussion

Using an oculomotor gambling task, we found a group of SEF neurons that carried an explicit confidence signal immediately following the choice. The Vd signals described here follow the choice and are contingent on the choice. Therefore, the causes of the choice—whether it be lapse of attention, exploration, or random fluctuations in the value estimations on which the choice is based—cannot be responsible for the Vd signals we report here. Instead, the Vd signals are likely related to an evaluation of the choice and are used to guide subsequent behavior. SEF and the medial frontal cortex, in general, are known to contain many other evaluative signals (Stuphorn et al. 2000; Ito et al. 2003; So and Stuphorn 2012) and to be involved in behavioral control (Stuphorn and Schall 2006; Chen et al. 2010; Scangos and Stuphorn 2010; So and Stuphorn 2010; Stuphorn et al. 2010). Choice confidence was strongly related to the likelihood that the monkey broke fixation before the outcome of the choice was revealed. This implies that, on some trials, the monkeys had such a low estimation of the current choice that they preferred to withdraw from it before knowing its outcome. These spontaneous fixation breaks in our task reflected therefore an evaluation of the choice process. In that sense, they are functionally similar to post-decision wagers used in other experiments to probe choice confidence (Smith et al. 1997; Kepecs et al. 2008; Kiani and Shadlen 2009; Kepecs and Mainen 2012; Middlebrooks and Sommer 2012).

Functional Role of Confidence Signals in SEF

The confidence representation in SEF is distinct from the representation of reward expectation, since it was not present during the no-choice trials (Fig. 1A), in which reward expectation exists, but an action cannot be evaluated with respect to its unchosen alternative. The Vd signals are also distinct from other evaluative signals observed in SEF, such as the actual outcome representation (win, loss, and reward amount representation) or the reward prediction error signals, all of which must appear after the outcome was revealed (So and Stuphorn 2012). Furthermore, the Vd signals still contributed significantly to the neuronal activity, even after the individual effects of CV and UV were taken into account in our analyses (Figs 7 and 8). Thus, the confidence signal we observed in SEF is distinct from reward expectation.

A recent study also attempted to disambiguate confidence and reward expectation, but used a perceptual judgment task (Middlebrooks and Sommer 2012). In this study, monkeys first had to search for a masked target, and then had to bet whether their decision was correct or not. They received different amounts of reward depending on both their decision (correct/incorrect) and the bet. The authors attempted to separate confidence and reward expectation in their task by relating different bets following the same decision to the different confidence levels, and the same bet following different decisions to the same degree of reward expectation. SEF neurons showed different activity for different betting trials on the same decision, and it was the only area showing such confidence-related activity among the 3 areas they recorded, namely orbitofrontal cortex (OFC), frontal eye field, and SEF. The authors argued that such SEF neuronal activity could not represent a reward expectation signal, since the activity was significantly different for different decisions followed by the same bet. However, the reward amount that the monkey received depended on both the decision and the bet. Hence, the reward expectation of the monkey while choosing a particular bet was also contingent on his confidence in the prior decision. Thus, confidence and reward expectations were still highly correlated in this metacognitive task (Middlebrooks and Sommer 2012). In contrast, our study provides unequivocal evidence for the existence of a confidence signal that is distinct from reward expectation. Value-based decisions such as the ones in our gambling task consist in the comparison of different reward expectations. Hence, confidence and reward expectation can be naturally separated as the balance of evidence, that is, confidence, does not necessarily coincide with the eventual reward amount expected. Our results therefore complement the study of Middlebrooks and Sommer (2012) and support their interpretation of the SEF activity as encoding choice confidence.

Many SEF neurons carried a mixture of confidence-related signals (Vd) and reward expectation (CV) signals. This seems reasonable, if the primary function of those neurons is the immediate evaluation of the choice. Since the optimal choice is associated with different reward amount across trials, the absolute reward amount is also an important measure to evaluate the choice besides the judgment on how optimal the choice is. If the eventual outcome is good enough, even a choice that was likely suboptimal might still be worth pursuing. In addition, we also found many SEF neurons that represented the alternative potential outcome, that is, the UV. In contrast to the CV signal, the UV signal developed mainly after the choice, which suggests its evaluative nature (Fig. 10). Our current study does not provide a conclusive answer on the functional role of this UV signal in decision-making. One possibility is that the UV signal might be used to compute the Vd signals. The temporal dynamics of CV, UV, and Vd signals provide some support for this possibility. Alternatively, the UV signal may reflect an independent evaluation based on the hypothetical outcome of the alternative action (Hayden et al. 2009; Abe and Lee 2011). However, the UV signal in the SEF did not seem to influence the monkey's evaluative behavior following the choice (Fig. 11B).

Activity in the lateral intraparietal area (LIP) also reflects confidence, albeit in a more implicit fashion (Kiani and Shadlen 2009). LIP neurons represent the accumulated evidence in favor of a particular choice. As expected by the balance-of-evidence models of confidence (Vickers 1979), in the time period before a choice was expressed, the LIP neurons were less active when the monkey was less certain (Kiani and Shadlen 2009). Thus, the LIP neurons seem to reflect the decision process, on which the confidence estimation is based (Gold and Shadlen 2007), while the signals in the SEF explicitly encode confidence after the decision is made. The interpretation of the Vd-sensitive signals in the SEF as internal monitoring signals that regulate future behavior might also explain why the confidence signal was found predominantly in the SEF, but not in other parts of the frontal cortex (Middlebrooks and Sommer 2012).

The majority of SEF neurons were most active when choice confidence was low. The same predominance of neurons whose activity was negatively correlated with confidence was found in rat OFC (Kepecs et al. 2008), but not in monkey SEF in the task that required to bet on a prior judgment (Middlebrooks and Sommer 2012). One possible reason for such predominance of inverse confidence signals in our study is that low confidence is behaviorally more salient in the gambling task. If the current choice is likely to be suboptimal, corrective actions become desirable, while no further action is necessary if the current choice is likely to be optimal. In contrast, in the metacognitive task, both high and low confidence was behaviorally relevant since they required different subsequent choices (Middlebrooks and Sommer 2012).

Recording studies in monkeys have shown confidence-related signals in the LIP and SEF. A recent imaging study in humans also studied the representation of confidence in value-based choice (De Martino et al. 2013). Interestingly, this study did not show activity in the parietal or dorsomedial frontal cortex. Instead, activity in the ventromedial prefrontal cortex (vmPFC) reflected confidence in the value comparison process. The degree to which this confidence signal could be reported accurately depended on the strength of the functional connection between vmPFC and a more rostral frontal area, the rostrolateral prefrontal cortex (RLPFC). There are 2 possible reasons for the apparent differences between the monkey and human studies. First, the total number of SEF neurons that carried confidence signals in our study was low (29/227 neurons; 13%). In general, due to unknown recording biases, it is complicated to extrapolate from the total number of neurons in a study the overall frequency of such neurons in a brain area. Nevertheless, the small number of confidence-related neurons in our sample implies that they might represent only a small subset of the overall neural population in the SEF. Thus, they might not have generated a signal that was strong enough to be picked up by neuroimaging techniques. Secondly, both SEF and LIP are oculomotor regions. It is likely that the confidence-related activity in these areas is present only during decisions involving selection of eye movements. Instead, the signals in the human vmPFC and RLPFC might represent a more abstract confidence signal that is not related to any specific motor system. More experiments in monkeys and humans are necessary to investigate these issues.

Alternative Interpretations

Some SEF neurons carry error-related activity (Stuphorn et al. 2000). In our gambling task, a choice that is likely to be less valuable than the alternative might also be interpreted as an error, and the Vd− signals as an error signal. The previously reported error signals evaluate the choice after the outcome is known (Stuphorn et al. 2000; So and Stuphorn 2012). In contrast, the Vd− signals are present before the outcome is known. Thus, if one wanted to interpret the Vd− signals as a type of error signals, one had to hypothesize that it represents the likelihood that a choice was incorrect or suboptimal. Error likelihood in this sense is a retroactive evaluation of a past action, and must be distinguished from “error likelihood” as a proactive control signal, indicating the likelihood that an error will be committed in the future (Brown and Braver 2005). However, an error likelihood signal in this sense is simply the inverse of a signal that represents the likelihood that a choice was correct/optimal, that is, confidence. Thus, there is only a semantic difference between “error likelihood” and “confidence”, without any functional difference in interpretation.

Another alternative interpretation is that the Vd signals represent regret, a cognitive or emotional reaction associated with the realization that an unchosen action would have yielded a better outcome (Bell 1982; Loomes and Sugden 1982; Mellers et al. 1999). Since the Vd signals reflect the value difference between the chosen and unchosen option, they might also represent a comparison with hypothetical outcomes (Coricelli et al. 2005; Hayden et al. 2009; Abe and Lee 2011). What argues against this interpretation of the Vd signals in the SEF is their timing. Regret can be represented in an anticipatory fashion, helping an agent to make a choice to minimize possible future regret. However, the Vd signals reported here cannot represent such anticipated regret, since they appear after the choice. Likewise, these signals cannot represent the regret itself, which is contingent on the actual outcome. When the actual outcome was revealed, the Vd signals were already diminished and the neurons carrying them were not consistently active after losing outcomes. Thus, the Vd-sensitive SEF activity is unlikely to represent regret.

Conflict is another monitoring signal that reflects the difference in drive supporting the choice options (Stuphorn et al. 2000; Botvinick et al. 2001). However, conflict should reach a maximum as value difference approaches zero and should fall off symmetrically as one of the options is increasingly more valuable than the alternative, regardless of what is chosen. In contrast, the Vd signals described here monotonically rise or fall across the signed value difference, contingent on the choice. Thus, the Vd-encoding SEF neurons are unlikely to represent conflict.

The Vd-encoding neurons in the SEF were significantly more active before the monkey broke fixation in choice trials (Fig. 11A). Therefore, the activity of these neurons might be correlated with a lapse of attention or disengagement from the task, rather than confidence. However, the Vd-encoding cells were not active before the fixation breaks during no-choice trials (Fig. 11B). Thus, it is unlikely that these neurons represent task disengagement as such. Instead, the neurons likely responded to the evaluation of a decision process, since the activities were closely related to the unchosen alternative in a graded fashion reflecting the entire range of Vd values, encompassing both the positive and negative domain (Fig. 8). If these neurons were representing or responding to a lapse of attention, they should not have been active during the trials with positive Vd values, in which the monkey behaved optimally. Again, the most parsimonious interpretation of the Vd-encoding SEF neurons is that their activity reflects confidence in value-based choices.

There are limitations to our study. First, all of the present results depend on linear models and we might have missed at least some neurons that might represent confidence in a nonlinear fashion. Nevertheless, the current approach seemed like the most conservative and robust one in the absence of any a priori belief about more specific nonlinear models. Secondly, even though we tried to disambiguate confidence from other cognitive or emotional signals, there might still have been other factors in our complex task that we did not control for. Finally, the absence of explicit post-decision wagers forced us to rely on spontaneous fixation breaks that were limited in number. Future experiments should compare SEF neurons directly during perceptual and value-based decisions in tasks that allow a direct behavioral estimate of confidence.

Conclusions

In conclusion, our study shows that the SEF actively represents confidence in value-based decisions. This fits with previous findings indicating a role of SEF neurons in value-based action selection (So and Stuphorn 2010), and monitoring of action outcomes (So and Stuphorn 2012). The confidence signals form a small, but substantial number of neurons in our study and might be part of a larger group of monitoring signals that affect the monkeys' present and future behavior. In addition, our current findings also support the hypothesis that choice confidence is an integral component of all forms of decision-making, whether they are based on perceptual evidence or on value estimations.

Funding

This work was supported by the National Institutes of Health through grant R01-EY019039 to V.S.