Quantitative Multivariate Analysis of Dynamic Multicellular Morphogenic Trajectories

Abstract

Interrogating fundamental cell biology principles that govern tissue morphogenesis is critical to better understanding of developmental biology and engineering novel multicellular systems. Recently, functional micro-tissues derived from pluripotent embryonic stem cell (ESC) aggregates have provided novel platforms for experimental investigation; however elucidating the factors directing emergent spatial phenotypic patterns remains a significant challenge. Computational modelling techniques offer a unique complementary approach to probe mechanisms regulating morphogenic processes and provide a wealth of spatio-temporal data, but quantitative analysis of simulations and comparison to experimental data is extremely difficult. Quantitative descriptions of spatial phenomena across multiple systems and scales would enable unprecedented comparisons of computational simulations with experimental systems, thereby leveraging the inherent power of computational methods to interrogate the mechanisms governing emergent properties of multicellular biology. To address these challenges, we developed a portable pattern recognition pipeline consisting of: the conversion of cellular images into networks, extraction of novel features via network analysis, and generation of morphogenic trajectories. This novel methodology enabled the quantitative description of morphogenic pattern trajectories that could be compared across diverse systems: computational modelling of multicellular structures, differentiation of stem cell aggregates, and gastrulation of cichlid fish. Moreover, this method identified novel spatio-temporal features associated with different stages of embryo gastrulation, and elucidated a complex paracrine mechanism capable of explaining spatiotemporal pattern kinetic differences in ESC aggregates of different sizes.

Graphical abstract

Introduction

Model organisms, such as C. elegans, Drosophila, and zebrafish, are frequently used to interrogate the complex sets of regulatory cues and gene regulatory networks governing morphogenic processes, like gastrulation and neurulation, due to the technical ease in manipulating and imaging ^1–3 these organisms. Pluripotent embryonic stem cell (ESC) aggregates present a complementary, alternative in vitro platform for investigating mechanisms of morphogenesis due to their intrinsic ability to differentiate into tissues from all three germ layers and yield formation of a variety of primitive tissues including optic cups ⁴, human intestinal lining ⁵ and cerebral organoids ⁶. Each of these multicellular systems is highly complex both in terms of the heterotypic cell types that comprise the tissue and the emergent spatiotemporal organization dynamics exhibited by heterogeneous cell populations.

Computational modeling of embryonic development has become an increasingly powerful tool to complement experimental investigations due largely to the fact that increased processing speed has reduced the barrier to multiscale simulations of complex multicellular organismal systems. Computational models have been constructed for C. elegans ⁷ and Drosophila ^8–10 to comprehend the relationships between cell signaling and lineage development in order to gain new insights into the intricate interplay of mechanisms governing development. Stage-specific models have also been developed to examine phenomena such as gastrulation ¹¹ and somite formation ¹² at a mechanical level, while computational models of the formation and differentiation of cells in the early mouse embryo ¹³ and in mouse ESC aggregates ¹⁴ explore mechanisms governing early cell fate decisions. Overall, these modeling approaches have provided a wealth of quantitative data to describe spatio-temporal events associated with morphogenesis; however it remains extremely challenging to relate spatial modeling predictions directly with experimental outcomes due primarily to the difficulty in quantifying multicellular pattern features.

This challenge of relating patterns across systems has hindered high-throughput analysis of developmental processes. In experimental systems, divergent phenotypes are often characterized largely by visual inspection, thus lacking the quantitative rigor and objective criteria necessary for direct comparison with computational models. Though several techniques exist to automatically distinguish phenotypes at various spatial scales ^15–19, they often lack the resolution of single-cell regulatory dynamics ^{18, 19}, or are customized specifically for investigation of only specific systems ^{17, 19}. As a result, quantitative metrics extracted from such studies cannot be easily translated between different modes of data analysis or across various model organisms. Hence, a portable pattern recognition pipeline capable of handling various biological and computational inputs would enable direct quantitative comparisons on previously unattainable spatial and temporal scales between different multicellular systems.

In this report, we demonstrate that deriving physiologically meaningful quantitative metrics capable of distinguishing subtleties between spatial phenotypes in a computationally tractable manner can be achieved via spatially derived networks. This novel approach extracts global metrics, such as path lengths and connectivity information, as well as local metrics based on attributes of specific clusters of cell phenotypes. Identification and comparisons of sub-networks within morphogenic systems allow for greater network quantification and significantly enriches the possible metric space by extracting specific subpopulation information. These metrics can be subsequently analyzed with standard classification methodologies and high dimensional data visualization techniques to extract biologically relevant information^20–22. Furthermore, this network-based scheme is the first classification approach currently capable of using spatial data at the single cell level to classify tissue level pattern dynamics. To demonstrate this, we first explored the use of simple network metrics to capture patterning across a large range of parameter space using computational simulations, before applying this analysis to a variety of applications. Several input formats (i.e. 2D images and 3D confocal data sets) were analyzed to demonstrate the robust nature of this technique. Consequently, we describe the creation of a powerful and modular pattern identification algorithm with sufficient portability to address meaningful questions about the spatiotemporal dynamics of biological pattern formation. This methodological tool automatically identified stages of gastrulation in cichlid fish in an unprecedented manner, provided the first quantitative description of spatio-temporal patterns associated with loss of pluripotency in ESC aggregates, and uncovered a paracrine mechanism capable of explaining the observed differences in spatiotemporal pattern kinetics associated with ESC aggregate differentiation.

Results

Network-based metric identification for spatial pattern classification

In order to identify appropriate metrics for characterizing spatial patterns, a flexible and expedient computational framework was necessary to generate a large data set comprised of various types of multicellular patterns. We generated an in silico training set by using pattern generation algorithms to simulate spatial features of differentiation in 3D multicellular aggregates ¹⁴. In total, seven different classes of general patterns were generated: random, outside-in, inside-out, snaked, globular, undifferentiated (>95% Oct4+) and differentiated (<5% Oct4+) (Fig 1A). We postulated that by applying a network-based approach, simple sets of quantitative metrics could be extracted from complex patterns. Typically, metrics extracted from intact networks include path lengths, average connection counts, and connection lengths. While these metrics are important for describing the network as a whole, they did not accurately describe the variations present in biological patterns. Therefore, clusters of cells of the same phenotypes were identified to partition the single larger network into a series of sub-networks in which various metrics related to the number, size and distribution of these sub-networks were defined (Supplementary Fig 1). In the context of stem cell differentiation, two sub-networks (Oct4+ and Oct4-) were examined because of the transitions from high to low Oct4 protein levels as a result of differentiation and loss of pluripotency^23,24.

Figure 1.

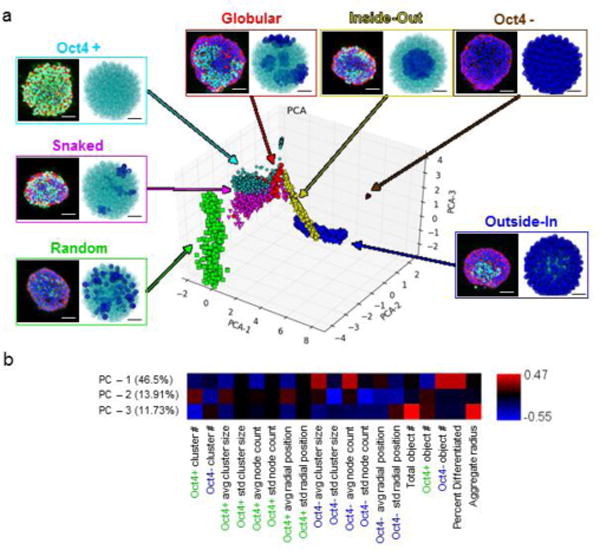
Validation of spatial network metrics for pattern classification. (a) Examples of experimental (green = Oct4 Ab, blue = DAPI, red = phalloidin) and in silico generated pattern classes (teal = Oct4+, blue = Oct4 −). Scale bars = 100 μm and 35 μm for the experimental and in silico images, respectively. Representative images are mapped onto the PCA plot of the resulting pattern space, color coded by individual pattern type. (b) PCA axis analysis indicating the relative contribution of each metric to the given principal component axis.

To examine the overall shape of the multi-dimensional data set, a dimensional reduction technique, principal component analysis (PCA), was performed. PCA generated a 2D projection of all samples based upon their network features. The scatter plot revealed some overlap between different pattern classes, particularly for the globular and snaked patterns (Fig 1A), but in general the different classes could be readily distinguished from one another. More importantly, a continuum of patterns was observed (Fig 1A), suggesting a natural pattern evolution. The model was able to explain 77.7% of the variance in the data set with three principal components (PCs): 46.5% with PC-1, 13.9% with PC-2 and 11.7% with PC-3 (Fig 1B). PC-1 represented the stage of differentiation and was positively correlated with variables associated with differentiated clusters or overall differentiation, whereas PC-2 and PC-3 were associated with spatial sub-network descriptors. PCA also revealed that each metric contributed significantly to the model, indicating that inclusion of all metrics was important to comprehensively describe the data set.

To verify that simple network-based metrics could describe complex spatial pattern classes, various classification algorithms were assessed to determine their ability to distinguish between pattern types: k nearest neighbor (KNN), state vector machines (SVM, NuSVC), stochastic gradient descent (SGD) and decision tree algorithms. Classification labeling overlapped with the true labels as assessed via PCA dimensional reduction (Supplementary Fig 2). The SVC classifier had the highest overall accuracy (.998), precision (.999), and recall scores (.987), suggesting it was the most appropriate algorithm for classifying spatial patterns. Collectively, these results suggested that novel network-based measurements provide a robust set of quantitative metrics for classification of complex spatial patterns.

Quantitative pattern trajectories of 3D pluripotent stem cell aggregates

Images of Oct 4+ to Oct4− transitions during differentiation of 3D murine ESC aggregates were acquired experimentally to determine how well network metrics captured an in vitro dynamic biological process (Fig 2A). Since pluripotent differentiation is known to be modulated by aggregate size^25–27, two starting cell densities were examined (250 and 1000 cells/aggregate). To evaluate the previously derived network metrics for pattern analysis, experimentally-obtained confocal images were converted into a network representation of the cells using a digital reconstruction pipeline (Supplementary Fig 3). A representative time course of differentiation in 1000-cell aggregates (Supplementary Fig 4) demonstrates the fidelity of this process in accurately converting images into annotated networks.

Figure 2.

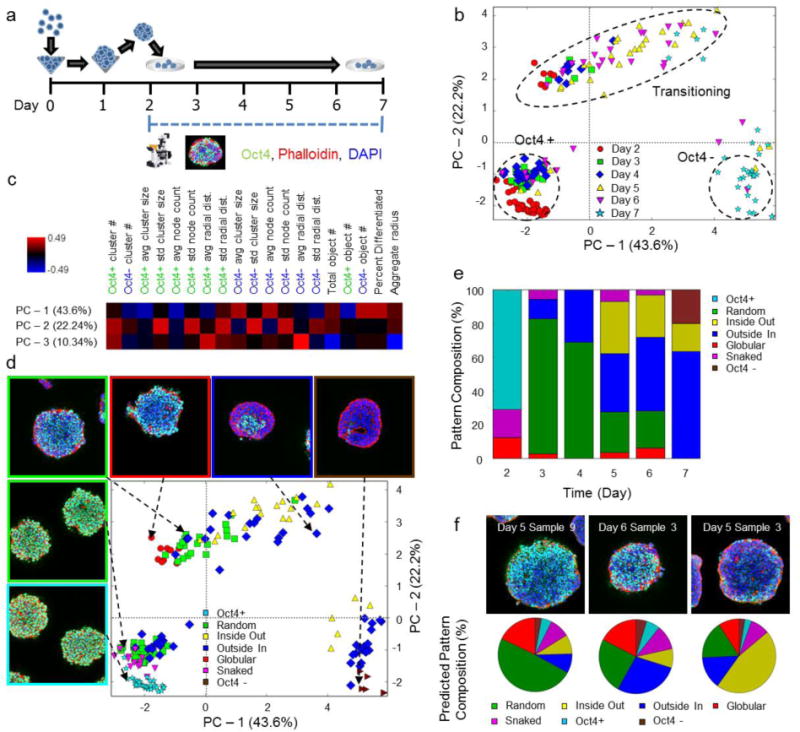
Evaluation of spatial and temporal patterns during early ESC aggregate differentiation. (a) Experimental plan and time course; confocal microscopy was performed daily (on days 2–7). (b) PCA trajectory for 1000 cell aggregates. Dashed regions highlight different cell states present. (c) Heat map of the weights of each metric in relation to each principal component. (d) Annotations for the pattern classification of each sample. (e) Pattern compositions for each day of differentiation. (f) SVC classification of samples that contain aspects of multiple core pattern classes. Experimental images (top row) and, predicted pattern composition (pie charts, bottom row). The predicted pattern composition is represented as a percent of the different sub-patterns contained within.

Next, digitized ESC aggregate networks were analyzed with the aforementioned network metrics. PCA revealed an average trajectory through latent variable space for cell aggregates in which all cells began in an undifferentiated state and proceeded through a transitioning period until finally settling into a differentiated state (Fig 2B). Regardless of size, the trajectories substantially overlapped, although the 250-cell trajectory was more truncated temporally relative to the 1000 cell aggregates, reflecting accelerated differentiation (Supplementary Fig 5). The PCA model explained 76.1% of the variance in the data: 43.6% from PC-1, 22.2% from PC-2, and 10.3% from PC-3 (Fig 2C). All metrics significantly contributed to at least one principal component, verifying that network-derived metrics capture the variance of biological spatial patterns. PC-1 represented differentiation, while PC-2 and PC-3 again correlated with spatial sub-network descriptors representing inter-pattern variation. The principal component metric weights for the experimental data closely mirrored the weights for the in silico training set, indicating that network-derived metrics comprehensively capture the inherent biological variance that transpires during the course of ESC aggregate differentiation.

While the Oct4+ and Oct4− states were quite distinct, the intermediate transitioning period displayed a great amount of variance (Fig 2B). To determine if the variation was due to differences in spatial patterns, classification was performed using the previously trained SVC classifier to characterize the distribution of spatial patterns in each state. Classification indicated that the initial state consisted largely of a mix of undifferentiated, random, and outside-in patterns, while the final state consisted of a mix of entirely differentiated and outside-in patterns (Fig 2D, Fig 2E). The variation with respect to each time-point peaked at days 5 and 6 (Fig 2B), which also displayed a diverse set of spatial patterns (Fig 2E). Furthermore, SVC classification predicted that many of the aggregates at day 5 and 6 could belong to multiple pattern classes, indicating that these patterns were more spatially complex and thus displayed components of multiple different pattern types (Fig 2F). Overall, spatial pattern evolution progressed in the following temporal order: undifferentiated, snaked, random, globular, inside-out, differentiated. Similar pattern trajectories were also observed for the 250-cell aggregates (Supplementary Fig 5). These results represent a biological trajectory describing spatial pattern evolution in a portable quantitative fashion, but even more importantly, the analysis suggests that early differentiation in ESC aggregates progresses via quantifiable spatial patterns that do not display purely random characteristics. Furthermore, this is the first description of biological trajectories using single cell information to capture spatial pattern complexity.

Pattern trajectories of computational models describing ESC differentiation

Next, to probe the mechanisms governing the formation of spatial patterns associated with differentiation, an agent-based modeling approach was employed in which cells are allowed to proliferate, migrate, and differentiate within a 3D aggregate configuration¹⁴. In our prior work, a simple set of rules based on local neighboring cell state(s) were used to govern changes in cells state; however, we found comparisons between modeling results to be nearly impossible because a quantitative set of descriptors for assessing spatial patterns did not exist. In addition, comparison with experimental data could not be directly accomplished without a validated digitization strategy. These challenges were addressed simultaneously by enabling direct comparison between spatial patterns from computational models and experimental results via the use of these newly defined network metrics.

Seven models with different rule schemes driving differentiation were investigated: random, local positive feedback, local negative feedforward, local competing regulation, paracrine activation, paracrine inhibition, and combined paracrine activation/inhibition (Fig 3A). Diffusion simulations were carried out to understand how the ratio of consumption to production of soluble factors effected gradient propagation prior to paracrine rule creation (Supplementary Figure 6). Simulations were carried out over a six-day period with different initial aggregate sizes: 250- and 1000-cells/aggregate. Each rule set was simulated with multiple parameters to explore the breadth of pattern trajectory space (Supplementary Table 1). PCA using the metrics described in figures 1 and 2, captured 76.5% of the simulation variance: 48.83% from PC-1, 17.7 from PC-2, and 9.9% from PC-3 (Supplementary Figure 7). Again, PC-1 represented differentiation, while the PC-2 was influenced by standard deviations in sub-network measurements, correlating with the formation of spatial patterns in the simulations.

Figure 3.

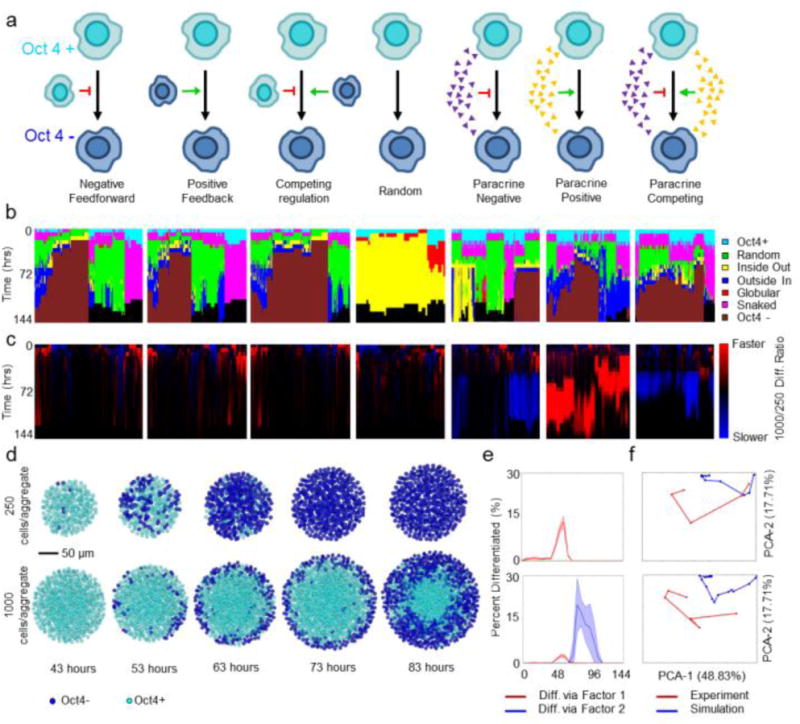
Characterization of computational pattern trajectories and comparison to experimental patterns. (a) Description of rules governing modeling. Red arrows, negative feedback; green arrows, positive feedback; small triangles indicate a soluble morphogen gradient. (b) Hierarchal clustering using a Ward linkage algorithm of the pattern trajectories for each parameter set, annotated by rule (gray scale bar). (c) Ratio of the 1000-cell to 250-cell differentiation rate. Blue represents slower differentiation in 1000-cellular aggregates, while red represents faster differentiation. (d) Representative images of the differentiation trajectories predicted by the competing paracrine rule (cells in blue are Oct4−, cells in teal are Oct4+). (e) Percent differentiation for representative 250 (top) and 1000-cell (bottom) simulations. Red represents differentiation induced via absence of inhibitor, while blue represents differentiation induced via the agonist. (f) PCA projections indicating the best fits of the 250 (top) and 1000-cell (bottom) experimental data (red) to the simulations (blue).

The previously trained pattern classifiers were applied to assess the spatial patterns generated by the computational simulations and analyzed using hierarchical clustering (Figure 3B). While the competing, negative feedforward, and positive feedback rules all generated similar pattern distributions and trajectories, the paracrine rules generated a more diverse set of pattern types. All together the rules were able to achieve a wide variety of diverse pattern types and evolutions. These results indicate that various complex pattern evolutions and temporal kinetics can be achieved using parsimonious, generalized rule sets.

Comparing computational and experimental pattern trajectories

A powerful feature of the employed network-based methodology is the ability to directly compare results across different platforms, thus allowing the modelling and experimental data sets to be merged into a single metric set. PCA was used to assess which metric axes were most important for describing the variation, resulting in a set of 5 axes responsible for ~ 90% of the variance along which to compare the different data sets (Supplementary Figure 6). Previously it was postulated that a competing regulation scheme could capture the spatial pattern evolution during differentiation, but this mechanism failed to explain kinetic differences between 250 and 1000-cell differentiation trajectories. To identify parameter sets and rules that did modulate differentiation based on aggregate size, a ratio of the differentiation rate of 250-cell to 1000-cell differentiation was calculated (Figure 3C). This ratio confirmed that local feedback rules did not exhibit significant size dependent differences, where nearly all of the soluble rules did. Both the paracrine activation and competing paracrine rules resulted in slower differentiation of 1000-cell aggregates than 250 cell aggregates, matching experimental observations. By comparing these rules to the experimental data on the PCA axes derived previously, it was determined that the paracrine competing rule set yielded the best fit (Figure 3F) because this rule accurately captured both the relevant time scales for differentiation (~24 hours in 250 cells/aggregate and ~48 hours for 1000 cells/aggregate) and the spatial pattern evolution (Figure 3D). Furthermore, this rule suggested that in 250 cell aggregates, differentiation was primarily induced by the absence of activator for the pluripotent state, while differentiation was largely caused by the accumulation of an activating factor within the 1000 cell aggregates (Figure 3E). Collectively, these results demonstrate a non-intuitive paracrine mechanism that can accurately explain differentiation of ESC aggregates and thereby demonstrate the power and utility of network based metrics for elucidating new mechanisms governing biological processes.

Network-based analysis of cichlid gastrulation

Finally, to assess the applicability of network-based analysis on a tightly regulated biological process involving multiple biological signals, gastrulation of East African cichlid fish embryos was analyzed. Gastrulation begins from a relatively undifferentiated cell aggregate that undergoes coordinated multicellular movement and differentiation to yield three tissue layers, a neural plate and rudimentary gut²⁸. This fundamental developmental process occurs under the tight spatial and temporal control of morphogens, such as bone morphogenic protein (BMP), and subsequent activation of downstream SMAD signaling via phosphorylation (designated as pSmad). BMP signaling is initially expressed across the entire embryo during gastrulation but clears dorsally to form a pSmad gradient²⁸. The subsequent amount and rate of BMP removal correlates with expression of the homeobox gene, dlx3b²⁹. As with pSmad activity, expression of the dlx3b gene goes from being ubiquitous across the majority of the embryo to specific and strong expression in the neural plate boundary (Figure 4A). Assessing the temporal and spatial patterns of multiple correlated signals during morphogenic processes represents a powerful new application of network analysis.

Figure 4.

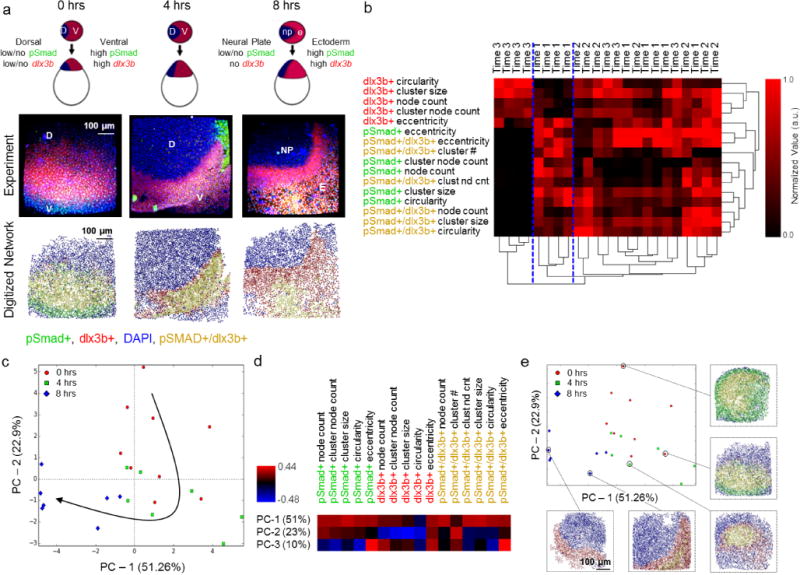
Pattern analysis during gastrulation reveals the importance of the transition from a pSmad+ dominated early gastrulation phase to dlx3b+ crescent formation in late stage gastrulation. (a) Representative schematic of gastrulation in cichlids on top, experimental confocal data in middle (red – dlx3b, green – pSmad, blue DAPI, yellow pSmad+/dlx3b+) followed by network reconstructions on the bottom (red – dlx3b, green – pSmad, blue DAPI, yellow pSmad+/dlx3b). Scale bars are 100 μm. (b) Hierarchical clustering of the data set yields three distinct sub-clusters (highlighted by dividing blue dashed lines). (c) PCA of the resulting data set reveals (n >= 7 per time point) a distinct trajectory informed by time (0 hours – red circle, 4 hours – green square, 8 hours -blue diamond). (d) Heatmap of how each metric contributes to the principal component model. Blue indicates a strong negative contribution, while red indicates a strong positive contribution. (e) Annotated PCA plot showing the evolution of pattern formation over time during gastrulation in cichlid fish. All images have the same scale bar of 100 μm.

The inherent 3D structure of cichlids presented a challenge, thus a 3D segmentation algorithm was implemented to output annotated spatial networks (Supplementary Fig 8). Using the previously defined metrics, three separate sub-networks of cells were analyzed: pSmad+, dlx3b+ and pSmad+/dlx3b (Fig 4A). In addition, several new pattern classification metrics were added, such as the ratio of pSmad+/dlx3b+ nodes to dlx3b+ nodes and pSmad+ nodes, as well as circularity and eccentricity measures for cell clusters in an effort to capture the additional spatial complexity of this system. To identify relevant metrics feature extraction analysis was performed (Supplementary Figure 9).

Initial hierarchical clustering analysis of the resulting metrics revealed segregation of the data set into three main clusters, but the majority of the data set fell into a single large cluster that made subsequent interpretation difficult (Fig 4B). Thus, in order to analyze the clusters further, a PCA model was created that explained the majority (83.8%) of the variance: 51.3% from PC-1, 22.9% from PC-2, and 9.6% from PC3 (Fig 5D). PC-1 correlated highly with metrics associated with the shape of pSmad+ and pSmad+/dlx3b+ clusters, while PC-2 was strongly inversely correlated with dlx3b+ cluster metrics, and PC-3 correlated with eccentricities metrics.

Figure 5.

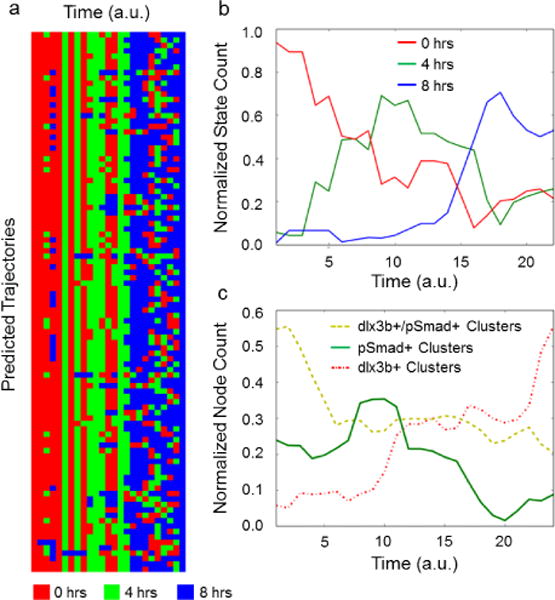
Information analysis predicts evolution of images during gastrulation. (a) Predicted pattern trajectories through time exhibit correct temporal ordering of early (0 hours, red), middle (4 hours green) and late gastrulation (8 hours blue). (b) The averages for all trajectories reflect state evolution from early to middle to late gastrulation. (c) The averages for all trajectories indicate the evolution of different cluster number during gastrulation.

This final PCA model not only revealed the initial and terminal states detected by hierarchical clustering, but more importantly, resolved the remaining data along a clear temporal trajectory (Fig 4C). Selecting various points along the trajectory revealed a set of patterns that matched the known biology, while also identifying subtle transition states between discrete time points (Fig 4E). Early development time points (0 hours – 4 hours) were characterized by a shrinking pSmad+ region with an increase in dlx3b+/pSmad+ regions, as indicated by the shift primarily in early time points along PC-2. The midpoint of gastrulation (~4 hours) exhibited an important switch in the formation and shape of the dlx3b+ region, and the final developmental stage (4 hours – 8 hours) was heavily influenced by the emergence of a crescent of dlx3b expression, as indicated by its progression along the PC-1 axis. To test how well these metrics predicted the evolution, a set of path finding simulations intended to find the most likely flow of information through a given process were performed (Figure 5A). The average trajectory for these simulations indicated the 0 hours samples peaking first, followed by a peak in the 4 hour, and 8 hour samples (Figure 5B). Analysis of the clusters indicated that early samples were marked by a high level of pSmad+ and pSmad+/dlx3b+ regions, followed by a gradual increase in the presence of solely dlx3b+ clusters (Figure 5C). Taken together, these results indicate that the biological trajectory produced by this approach can distinguish the precise state of gastrulation of a biological sample regardless of the experimental timepoint at which it was acquired during the process (Figure 4C, 4E, Figure 5B), further demonstrating the unique strength of a quantitative network-based pattern classification approach for more accurately analyzing morphogenic processes.

Discussion

Network and information theory provide a powerful tool for the analysis of many complex systems ranging from social^30,31 to biological networks^32,33. For the first time, our work applied the principles of network theory to the study of morphogenic biological systems in a spatial manner. Increasingly, examples of emergent spatial patterns are being reported from initial pluripotent states, leading to organoids such as optic cups, cerebral tissues, or others (4–6), however, quantitative descriptions of multicellular patterns are still lacking. For example Warmflash et al. recently used radial distance to delineate organization of differentiated phenotypes within micropatterned ESC colonies ^{4–6, 34}, while Herberg et al. used a similar method to compare spatial distributions of proteins in ESC colonies to computational models ³⁵, but these approaches are not sufficient to describe more complex 3D structures. Our method reconstructs cellular locations as interacting networks that can subsequently be further subdivided into biologically relevant sub-networks. This network-based approach circumvents problems associated with traditional classification methods that rely solely on standardized images ¹⁹ and use of individual pixel classification methodologies ^{36, 37}. While some systems exist for classifying spatial patterns in zebrafish ¹⁷, C. elegans ¹⁵ and Drosophila embryos ^19,38–40, previous approaches require specifically orientated and annotated images, are specific to the organism of interest, and/or often do not have single cell resolution. In particular, machine learning algorithms developed for positional dependence of patterning in Drosophila have not relied on individual cell segmentation for evolution of network connectivity over time. Our quantitative method is the first network based approach capable of integrating single cell spatial positioning and phenotypic state information to quantitatively describe dynamic tissue level patterning. The multiple examples illustrated herein highlight the broad utility of network-based analysis for identification of spatial biological patterns via the formulation of novel pattern metrics. We report the derivation of pattern trajectories associated with several systems: experimentally observed loss of Oct4 in ESC aggregates, computational models of Oct4 loss in ESC aggregates, and gastrulation in cichlids. Novel biological insights gained using our network analysis approach include: 1) differences in ESC aggregate spatiotemporal pattern kinetics can be explained by a combined paracrine signaling methodology, and 2) gastrulation in cichlid fishes can be partitioned into a set of discrete stages. In the case of ESCs, a large body of literature exists that suggests differentiation is heavily influenced by ESC aggregate size^{26,27,41–43}; soluble gp130 proteins have been identified as a paracrine mechanism which modulate of differentiation ^44,45 The two paracrine process proposed here can explain these differences (one in a secreted factor is responsible for maintain pluripotency, and the other where more differentiated cells secrete a factor which induces differentiation), and mirrors the known properties of soluble LIF and FGF4 signaling respectively^24,46–48. Surprisingly but interestingly, the lack of local neighbor-to-neighbor regulation of phenotypic state, as analyzed by our methodology, suggests that transmission of cell state information by intercellular cues, such as Notch, may impact later stages of differentiation than the time period examined here. Furthermore, this analytical approach uniquely enables the first direct quantitative comparison between computational modeling and complex emergent spatiotemporal patterns during multicellular lineage commitment in 3D ESC aggregates.

Methods

D3 murine ESCs were used for all of these experiments. All cichlid embryo experiments were performed with approval by and in compliance with Georgia Tech Institutional Animal Care and Use Committee. Modelling and comparisons were performed using custom python code. For more detailed methods on data acquisition and analysis, please refer to the supplementary methods section.

Conclusions

In summation, this novel pattern classification pipeline permits entirely new forms of quantitative analysis based upon the fundamental interconnectivity of multicellular networks, which could revolutionize the characterization of biologically complex spatiotemporal phenomena.

Insight, innovation, integration.

Decades of research have focused largely on characterizing individual cellular features, and consequently the image processing tools used to analyze biological systems have focused on identifying and quantifying cells as independent, static entities rather than interconnected, dynamic systems. Our innovation in analyzing multicellular systems arises from characterizing metrics from dynamic cell-cell networks that allows cross-comparison from virtually any modality of imaging. Because our analysis is platform independent, quantitative integration between agent-based computational models and experimental data is feasible. This approach allowed us to gain new insight in the pattern evolution of differentiation within stem cell aggregates as dictated by competing paracrine signaling mechanisms.