Abstract
Studies of individual differences in bereavement have revealed prototypical patterns of outcome. However, many of these studies were conducted prior to the advent of sophisticated contemporary data analytic techniques. For example, Bonanno, Wortman et al. (2002) used rudimentary categorization procedures to identify unique trajectories of depression symptomatology from approximately 3 years prior to 4 years following conjugal loss in a representative sample of older American adults. In the current study, we revisited these same data using Latent Class Growth Analysis (LCGA) to derive trajectories and test predictors. LCGA is a technique well-suited for modeling empirically- and conceptually-derived heterogeneous longitudinal patterns while simultaneously modeling predictors of those longitudinal patterns. We uncovered four discrete trajectories similar in shape and proportion to the previous analyses: Resilience (characterized by little or no depression; 66.3%), Chronic Grief (characterized by depression following loss, alleviated by 4 years post-loss; 9.1%), _Pre-existing Chronic Depression (ongoing high pre- through post-loss depression; 14.5%), and Depressed-Improved (characterized by high pre-loss depression that decreases following loss; 10.1%). Using this analytic strategy, we were able to examine multiple hypotheses about bereavement simultaneously. Health, financial stress, and emotional stability emerged as strong predictors of variability in depression only for some trajectories, indicating that depression levels do not have a common etiology across all the bereaved. As such, we find that identifying distinct patterns informs both the course and etiology of depression in response to bereavement.
Keywords: Latent Class Growth Analysis, Bereavement, Resilience, Depression, Emotional Stability, U.S.A
Depression in response to bereavement has often presented with confusing and seemingly paradoxical results. In a meta-analysis, bereavement was shown to be one of the most prominent and consistent risk factors for depression among the elderly (Cole & Dendurki, 2003), and longitudinal analyses of the course of psychopathology in bereavement have shown that depression sharply increases following a loss (Norris & Murrell, 1997). However, bereavement studied prospectively from before to after the loss has also shown that the bereaved are characterized by emotional stability rather than extreme reactions (Heyman & Gianturco, 1973).
What might account for these apparently conflicting findings? One possible explanation may be the high non-normal level of variability observed in depression scores following loss (Onrust et al., 2007). This variability may not be unique to bereavement, but might instead be a characteristic of measured depression in non-clinical populations (Radloff, 1977). Variability following such a distribution level may not be successfully captured in statistical models that sample from the mean, as is the case in the above studies and commonly the case in the study of bereavement (Mancini et al., 2011), because such models assume homogeneity characterized by a single normal distribution (Judd et al., 2009).
A Preliminary Map of Trajectories of Bereavement Response
Attempts to explore the variability intrinsic to depression following loss have revealed surprising results. In an attempt to ascertain if this variability fits into patterns over time, Bonanno and colleagues (2002) “mapped” distinct and clinically meaningful trajectories of response to loss over time in a sample of American older adults. These included a pattern of stable low depression (Resilience); a pattern characterized by moderate to severe depression after the loss that lasted several months or longer before gradually returning to baseline level of functioning (Common Grief or Recovery); a sharp incline in symptoms of depression following loss that did not lessen by 18 months (Chronic Grief); high pre-loss depression that continues after the loss (Chronic Depression); and high pre-loss depression that declines significantly following the loss (Depressed-Improved) (Bonanno et al., 2002; Bonanno et al. 2004; Bonanno, Moskowitz et al., 2005). As such, even among those who suffered significantly after a loss, clinically meaningful heterogeneity was observed.
While this methodology successfully revealed unique trajectories of bereavement response, it suffered from three serious methodological shortcomings (Bonanno et al., 2011). First, Bonanno et al.'s (2002) approach assessed variability solely in terms of overall sample distribution. The method they used to create the trajectories involved first placing subjects at each time-point into high or low depression categories based on their percentile scores on the distribution and then determining change in relation to those cutoffs from before loss to 6 and 18 months after the loss. Unfortunately, relying on a single estimate does not permit this source of variability to influence trajectory designation and can potentially lead to spurious conclusions, as for example in cases when the distribution is not normal (Duncan et al., 2006). Second, Bonanno et al.'s (2002) method of using a priori cut points to define trajectories is inherently arbitrary. This approach imposes the change patterns on the data rather than allowing the patterns to emerge directly from the data. Third, the operational definitions for the trajectories were based solely on theoretical assumptions about the nature of the prototypical patterns of variation across time (e.g., Bonanno, 2004) and may not have captured other patterns of response.
Given these limitations, evaluating the resulting trajectory solution is difficult if not impossible in the absence of more sophisticated statistical techniques that might adjudicate among different possible trajectory solutions. An analogous situation would be attempting to assess if variables within a scale cluster together by exploring which variables are most highly correlated. While such a technique provides useful information, it may be inadequate compared to statistical techniques such as factor analysis that are designed to assess latent relationships between variables.
These concerns become even more important as analyses move from elucidating distinct patterns to identifying predictors of those patterns. The rudimentary approach Bonanno et al. (2002) employed did not allow for identification of different parameters of the trajectories (e.g., variability in intercept or slope) and could only identify predictors of the trajectories post-hoc, independent of model building. As we detail below, more sophisticated analytic techniques are now available that can addresses these issues.
Latent Growth Modeling
A number of approaches have been developed to model patterns with high levels of variability. For example, both Hierarchical Linear Modeling (Bryk & Raudenbush, 1987) and Growth Curve Modeling (McArdle & Epstein, 1987) represent advances over traditional linear models because they allow for the exploration and prediction of individual level variability in patterns over time. However, these modeling techniques assume a common pattern that individuals fit better or worse. In situations such as stress responses, for which we find true heterogeneity, such models may be inadequate (Nagin, 1999). A number of methodologies have been developed that better serve this purpose. One such technique, the Nagin Method (Nagin, 1999) has been applied to the study of the course of depression in bereavement (Aneshensel et al., 2004). A significant advantage of this technique is that it allows for an objective comparison of progressive numbers of distinct trajectories using the Bayesian Information Criteria (BIC) as a point of comparison, where lower scores on the BIC indicate better model fit. This approach also provides information regarding the probability of correct categorization and has provided an empirical demonstration of the significant and meaningful heterogeneity in patterns of depression following bereavement (Aneshensel et al., 2004). Nagin (1999) suggested that a limitation of his technique, however, is that model comparison is limited to the BIC, which can be fallible under certain circumstances, and that advances would require the development of additional methods of evaluating model fit.
A recent set of analytic techniques that has emerged in response to this limitation is Latent Growth Modeling (LGM). Importantly, LGM allows for the empirical exploration of the underlying heterogeneity within the data, which would otherwise be treated as error (Del Boca, et al., 2004), while also providing a number of alternative tests to evaluate model fit (see methods). LGM techniques such as Latent Class Growth Analysis (LCGA) and Latent Growth Mixture Modeling (LGMM) have emerged as particularly strong methodologies for the study of homogeneous trajectories in a larger heterogeneous sample. These techniques test whether the population under study is composed of a mixture of discrete distributions characterized as classes of individuals with differing profiles of growth, with class membership determined by these different growth parameters (Curran & Hussong, 2003). LGM allows for the modeling of longitudinal data with consideration for empirical observation as well as parsimony and interpretability (Jung & Wickrama, 2008), while also allowing for the modeling of covariates as predictors, both of the emergent longitudinal patterns and of latent growth parameters such as class membership, slope, and intercept (Muthén, 2000).
The LGM approach has been applied to a wide variety of phenomena, including drinking behavior among college students (Greenbaum et al., 2005), childhood aggression (Schaeffer et al., 2003), developmental learning trajectories (Boscardin, 2008), disease epidemic (Bonanno et al., 2008), traumatic injury (deRoon-Cassini et al., 2010), life satisfaction in response to interpersonal stressors (Mancini et al., 2011), unemployment (Galatzer-Levy et al., 2010), childbirth (Galatzer-Levy et al., 2011), cancer surgery (Lam et al., 2010), and posttraumatic stress following exposure to military deployment (Bonanno et al., in press) and other life threatening events (Galatzer-Levy et al., 2011).
In the current study, we examine prospective trajectories of bereavement from pre-loss to 48 months post-loss using LGM using the same dataset examined by Bonanno et al. (2002). One previous study had also identified trajectories in this dataset through 48 months (Boerner et al., 2005). However, due to missing data, the sample size for that study was seriously constrained. Because LGM accommodates missing data, however, in the current study we are able to include a larger number of participants from the original data set. We anticipate that we will uncover heterogeneous patterns of response including resilience, chronic grief, chronic depression, recovery, and depressed-improved, and that the resilient and chronic depression trajectories will remain stable in the more encompassing LGM analyses. The stability of the depressed-improved and the chronic grief class is more questionable, as these patterns have proved more variable in previous studies.
Covariates
The literature on depression following loss in later life is rife with causal predictors, some demonstrating inconsistent findings. Trait-based personality characteristics, demographics such as age and gender, as well as non-psychological stressors such as health and financial strain, have all demonstrated a causal relationship with depression following loss.
High levels of trait neuroticism and low levels of emotional stability in particular have been shown to be a strong predictor of poor outcomes following bereavement. Trait neuroticism is characterized primarily as emotional instability (Pai & Carr, 2010). Trait neuroticism, which includes dimensions of anxiety, hostility, depression, self-consciousness, impulsiveness, and vulnerability, has been shown to predict depression following loss over and above other trait-based characteristics that are thought to be important predictors of poor psychological responses to stressors, including anxious and avoidant attachment style (Wijngaards-de Meij et al., 2007). Consistent with these findings, we anticipate that low levels of emotional stability will characterize individuals in the chronic grief, chronic depression, and depressed-improved trajectories compared to the resilient trajectory. Age has also been shown to negatively predict outcomes following loss with younger people having more psychological problems (Parks & Weiss, 1983; Onrust et al., 2007). As such, we anticipate that individuals in the chronic grief trajectory will be significantly younger then individuals in the other trajectories.
Other characteristics may also have an impact following loss, though findings are inconsistent. For example, bereavement has been shown to result in a decline in health (Sanders, 1988), which is not likely to simply be a function of age, as younger bereaved people report more initial health problems (Ball, 1977). Additionally, the relationship between bereavement and health has been shown to be rapid, with declines occurring within weeks or months of loss (Stroebe et al., 2007). Others have found that health outcomes remain stable but that financial stress is most associated with depression outcome during bereavement (Norris & Murrell, 1990). Still other findings indicate that financial stress is not predictive of depression following loss (Kurtz et al., 1997). Owing to this variability, we anticipate that greater financial stress and poor health will predict higher levels of depression within each class following the loss.
Method
In the current investigation, we use a LCGA approach to analyze prospective patterns of depression using a sample of older, conjugally bereaved adults. Assessments began approximately 3 years prior to spouse's death and again at 6, 18, and 48 months post-loss. The data comes from the U.S. Changing Lives of Older Couples (CLOC) study. The study was approved by the ethics review board of the University of Michigan.
Participants
Bereaved participants' data were obtained as part of the Changing Lives of Older Couples (CLOC) study, a prospective study of a two-stage area probability sample of 1,532 married individuals from the Detroit Standardized Metropolitan Statistical Area (SMSA). To be eligible for the CLOC study, respondents were English-speaking, married, and had a spouse 65 years of age or older. All sample members were non-institutionalized and capable of participating in a two-hour interview. Approximately 65% of those contacted for an interview participated, which is consistent with the response rate from other Detroit area studies. Baseline interviews were conducted from June 1987 through April 1988.
Participants from the CLOC study who subsequently lost a spouse were identified using daily obituaries in three Detroit-area newspapers and monthly death record tapes provided by the State of Michigan. The National Death Index (NDI) was used to confirm deaths and obtain cause of death. Widowed participants were invited for follow-up interviews at 6, 18, and 48 months after the spouses' deaths. Of the original 1,487 participants, n=545 participated in at least one follow-up interview, n=301 participated in at least two follow-up interviews, and n=104 completed all three time points. The mean length of time between the pre-loss interview and the loss was 37.15 months (sd =16.50 months; skewness = .02; kurtosis = -1.03), indicating a normal distribution. The kurtosis is sufficiently small, as to not pose a threat of type I or II error (DeCarlo, 1997). A simple regression indicated that there is not a significant association between the length of time between the pre-loss interview and depression scores at 6 months post-loss; F (1,238)= .08; p=.77.
Because LCGA is able to handle missing data effectively, we utilized data from all participants who had data on depression symptoms for at least two time points after loss. Analyses in the present study were based on the 301 widowed persons (269 women and 32 men) who had participated in at least two follow-up interviews. Participants who remained in the study or dropped out did not differ significantly in pre-loss depression (p > .15). Participants' average age at 6 months post-loss was 72 (SD = 6.5) years. For more information on the sample, see CLOC (2003).
Symptom Measures and Predictor Variables
Depression symptoms
Depression symptoms were measured using the Center for Epidemiologic Studies Depression (CES-D) scale (Radloff, 1977). The CES-D has shown adequate test-retest reliability and internal consistency across a wide range of subsamples (Roberts, 1990), and discriminates meaningfully between depressed patients and controls (Boyd, 1982). The present study used a brief, 9-item version of the CES-D that has shown comparable reliability and validity statistics (Kohout, 1993). Respondents were asked to indicate how often they felt or experienced each symptom in the week prior to the interview. Internal consistency for the 9-item version was α =.85.
Grief
Grief was measured using 16 items derived from the Bereavement Index, the Present Feelings about Loss Scale and the Texas Revised Inventory of Grief (see Boerner et al., 2005). The items represented five domains of grief symptoms: Yearning (Having painful waves of missing your spouse?); Despair (Felt life had lost its meaning?); Anxiety (Afraid of what is ahead?); Shock (Couldn't believe what was happening?); and Intrusive Thoughts (Couldn't get thoughts about him/her out of your mind?). Internal consistency for the total grief-specific symptom score was α =.88.
Financial Stress
The level of financial stress was measured at each time point using three items measured on a Likert scale where higher values denote a higher level of financial stress (α =.76). Scores on this scale reflect a mean of the three items. Data on this index was collected at all time points. This analysis used financial stress at 6 months post loss.
Functional Health Index
The Functional Health Index (called health) is a 6-item Guttman Type scale covering four progressive levels of functional impairment due to health from severe to no functional impairments. This scale does not measure the impact of specific pathology and its effects but rather measures participant's functional dependency. Scores on this scale indicate the highest level of health impairment endorsed by participants. Data on this index were collected at all time points. This analysis used the Functional Health Index at 6 months post-loss.
Emotional Stability
Emotional Stability was measured using a shortened measure meant to map onto a continuum from high trait-based neuroticism to high levels of emotional stability. This measure is based on the NEO Personality Inventory (Pai & Carr, 2010). This measure used a 13-item Likert scale querying about the frequency and intensity of emotional responses such as “It takes a lot to make me mad” and “I am an even tempered person” (α =.73). Scores were the mean with higher scores reflecting a higher level of emotional stability and lower neuroticism.
Statistical Analysis
We employed LCGA to analyze latent trajectories of depression symptomatology from 4 waves of data, beginning on average 3 years prior to the loss and concluding 48 months post-loss, as well as predictors of the qualities of these latent trajectories (Muthén & Muthén, 2000). We used Mplus 6.0 (Muthén & Muthén, 1998-2010) to identify latent classes of bereavement response. MPlus employs a robust full information maximum-likelihood (FIML) estimation procedure for handling missing data. The appropriateness of FIML is widely endorsed (Enders, 2001). FIML assumes missing data are unrelated to the outcome variable, i.e., missing at random. Participants in social science research are rarely truly missing completely at random, meaning there is no predictable pattern to the missingness. However, simulation studies have demonstrated that maximum-likelihood estimators provide unbiased estimates when data are missing at random, where the missingness may occur with some level of predictability but where that predictability is not related to the focus of the study as opposed to the assumption that data are missing completely at random. There is strong evidence that even when the assumption of missing at random does not hold up, using maximum-likelihood estimators provides more accurate estimates than removing data listwise (Muthén, 1987). Other longitudinal studies where attrition may be related to depression symptomatology in geriatric populations have demonstrated that mixed models approaches like those used here provide stronger estimates when compared to both listwise deletion or single imputation techniques (Heo, 2007).
In the study of bereavement in older adults, both depression and age represent challenges to the missing-at-random assumption. As discussed above, missing versus non-missing subjects did not differ in age or baseline depression scores. This gives some indication that missingness complies with the assumption. However, the analysis of missingness on baseline depression may be inaccurate for the same reason mean level analyses are limited in the face of heterogeneity in the data. As such, we proceeded with a set of analyses specially tailored to assess missingness in relation to latent class patterns. Using a latent dropout class model (Roy, 2003), we assessed missingness associated with class membership. Roy's latent dropout class model is considered an improvement on pattern-mixture models (Hedeker & Gibbons, 1997; Thijs, et al., 2002), which also assess for meaningful patterns of dropout related to the variables under study, because the latent dropout class model explores whether dropout is a function of time and/or class membership, while pattern-mixture models only test the former and not the latter. This analysis revealed non-significant results for patterns of missingness by class, indicating that particular patterns of depression outcomes were not more likely to be missing data at any time points. As such, we felt confident and proceeded in our analysis with the assumption of missing at random.
After establishing that we could proceed under the assumption, our analysis of the effect of bereavement on depression symptoms consisted of three steps. First we identified a univariate single-class growth model without covariates to facilitate model specification. Growth modeling techniques can be computationally intense and problems of model non-convergence are common (Duncan et al., 2006). To aid in convergence, the variance of the slope, intercept, and/or quadratic terms may be thoughtfully set to 0, indicating homogeneity within class, though setting all terms to 0 is discouraged (Jung & Wickrama, 2008). In the current model, we fixed the slope and quadratic term to aid in model convergence and left the intercept term-free. Fixing these parameters is the distinction between LGMM and LCGA. These parameters were fixed in the current model to aid in model convergence, which prevented it from becoming a full LGMM.
For this analysis, we set the intercept to 6 months post-loss so that we could assess the level of depression across all occasions following loss after conditioning on the linear, quadratic, latent class, and covariates. We created loadings for each measurement point reflecting the distance between those points. Because the baseline measurement point was normally distributed around 37.15 months between the pre-loss time point and 6 months post-loss, and the length of time did not significantly predict 6-months depression scores, we chose loadings reflecting distance divided by the common denominator 6, creating the following loading (baseline = -6.19; 6 months post-loss =1; 18 months post-loss = 3; 48 months post-loss = 8).
We compared progressive nested unconditional trajectory models (no covariates), assessing relative fit with conventional indices, including the Bayesian Information Criterion (BIC), sample-size adjusted Bayesian Information Criterion (SSBIC), Aikaike Information Criterion (AIC) indices, the Lo-Mendell-Rubin likelihood test (LRT) (Lo et al., 2001), and the Bootstrap Likelihood Ratio Test (BLRT). Model fit was assessed with the greatest weight placed on the BLRT, reduction in the BIC, and considerations were made for parsimony and interpretability consistent with Nylund, Asparouhov, & Muthén's (2007) recommendations for choosing the correct number of classes. Entropy values range from 0 to 1 and indicate the clarity of class specification with scores closer to one, indicating better fit of the data into the prescribed class structure (Duncan et al., 2006).
Second, for each class count, polynomial trends (i.e., linear vs. linear + quadratic) were compared. As discussed in Curran & Hussong (2003), the quadratic model is nested within the linear model. We sought a model with lower values for the information criterion indices, and a significant p value for the BLRT while considering parsimony and interpretability.
Finally, based on previous literature on predictors of both depression in later life and responses to loss, we nested key covariates in the model (conditional model). We utilized age and emotional stability as predictors of class membership and the intercept set at 6 months post-loss was regressed on financial stress and health. In the final step, we included the covariates as predictors of specific growth parameters. Financial stress was missing on 61 cases and health was missing on 66 cases. While FIML estimates parameters with missing values on endogenous variables such as the depression variables, it does not handle missing data on exogenous variables such as these. For this reason, we imputed missing values using MPlus 6.0's built-in multiple imputation program (Muthén & Muthén, 2010).
Results
Prior to conducting predictive analyses, we examined the relationship between depression scores across time points as well as their relationship to grief scores at 6 months post-loss using a Pearson's correlation matrix. This allowed us to quantitatively establish a relationship between grief and depression following a loss. Consistent with expectations, depression scores were significantly correlated across time points. Grief was significantly correlated with depression scores at all time points with the exception of T1 (pre-loss depression). An examination of means revealed that depression scores were highest at 6 months post-loss (Table 1).
Table 1. Descriptive Statistics and Zero-Order Correlations for CES-D and Grief Scores.
| Variable | M | SD | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|
| 1. CES-D t1 | 3.14 | 2.70 | 1 | ||||
| 2. CES-D t2 | 3.65 | 3.00 | .29** | 1 | |||
| 3. CES-D t3 | 3.12 | 2.72 | .31** | .63** | 1 | ||
| 4. CES-D t4 | 2.67 | 2.78 | .47** | .42** | .53** | 1 | |
| 5. Grief t1 | 0.56 | 0.56 | .12 | .65** | .52** | .27** | 1 |
Note.
p < .01;
CES-D = Center for Epidemiologic Studies Depression; Grief = Composite of Present Feelings about Loss Scale and the Texas Revised Inventory of Grief.
Unconditional Model
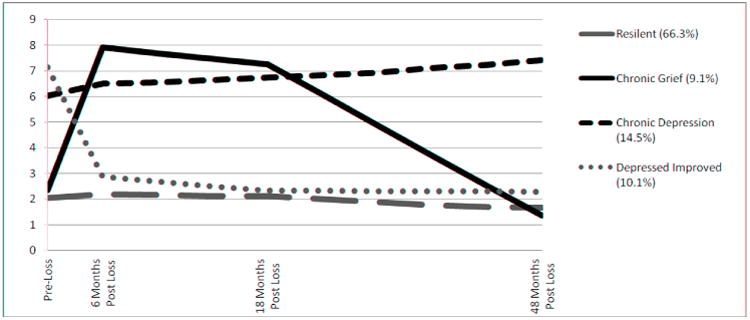
We observed the following trajectories: Resilient (66.3%), defined by a significantly lower intercept from the other three groups as well as a non-significant linear trend, and a significant but slight quadratic trend indicating a low-flat trajectory of depression scores from before the loss to 4-years after the loss; Chronic Grief (9.1%), defined by a strong quadratic trend in which depression scores increased dramatically after the loss and remained high at 18 months post-loss, but returned to pre-loss levels 4 years post-loss; Chronic Depression (14.5%), defined by a significantly higher intercept from all other groups prior to the loss and a flat non-significant slope showing no improvement in depression scores from before the loss until 4 years after the loss; and Depressed-Improved (10.1%), defined by high pre-loss depression scores, which were alleviated by 6 months post-loss. This class is characterized by significant negative slope in depression scores, which appears to be accounted for exclusively by a steep decline from before the loss to 6 months post-loss (10.1%; Table 3; Figure 1). The trajectories represent estimated means with their own variance around those means.
Table 3. Growth Factor Parameter Estimates for 4-Class unconditional Model (N = 301).
| Class | Intercept | Slope | Quadratic | |||
|---|---|---|---|---|---|---|
| Est | SE | Est | SE | Est | SE | |
| Resilient | 2.01*** | 0.16 | -0.01 | 0.02 | -0.01* | 0.003 |
| Chronic Grief | 7.88*** | 0.46 | 0.15** | 0.05 | -0.12*** | 0.01 |
| Chronic-Depression | 6.42*** | 0.40 | 0.09 | 0.05 | 0.01 | 0.01 |
| Depressed-Improved | 3.25*** | 0.59 | -0.41** | 0.09 | 0.04** | 0.01 |
Note. Est = Parameter Estimate; SE=standard error
p≤.05;
p≤.01;
p≤.001.
Figure 1. 4-Class Unconditional Trajectory Model of CED-S Scores (N=301).
The fit statistics for one- to five-class solutions for bereavement are summarized in Table 2. We conducted progressive growth models using a Maximum Likelihood (ML) estimator. The linear + quadratic parameters demonstrated better model fit. All indices demonstrated improvement through 5 classes. The LRT showed inconsistent results but the BLRT demonstrated significance up to 5 classes. The addition of a 5th class served to split the Depressed-Improved group into two relatively similar trajectories. Furthermore, the 5th class was very small (1.4%), and as such the 5-class model was less parsimonious and lent itself less to interpretation. The 4-class solution thus provided the greatest parsimony. Following recommendations for a best-fit solution (Muthén, 2003), we proceeded to the conditional model using a 4-class solution with linear + quadratic parameters (Table 2).
Table 2. Fit Indices for One- to Five-Class Growth Mixture Models of Bereavement (Unconditional n=301).
| Fit Indices | Growth Mixture Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Linear Weights Only | Linear + Quadratic | |||||||||
| Weights | ||||||||||
|
| ||||||||||
| 1 Class | 2 Classes | 3 Classes | 4 Classes | 5 Classes | 1 Class | 2 Classes | 3 Classes | 4 Classes | 5 Classes | |
| AIC | 4706.19 | 4646.64 | 4639.12 | 4633.19 | 4626.23 | 4695.74 | 4633.12 | 4578.23 | 4550.16 | 4528.58 |
| BIC | 4721.02 | 4672.59 | 4676.19 | 4681.38 | 4685.55 | 4714.28 | 4666.51 | 4626.42 | 4613.18 | 4606.43 |
| SSBIC | 4708.34 | 4650.39 | 4644.48 | 4640.15 | 4634.80 | 4698.42 | 4637.96 | 4585.19 | 4559.27 | 4539.83 |
| Entropy | --- | .81 | .85 | .88 | .78 | --- | .80 | .85 | .81 | .83 |
| LRT | --- | p<.001 | p =.56 | p =.38 | p=.20 | --- | p<=.05 | p<.001 | p =.17 | p =.16 |
| BLRT | --- | p<.001 | p<.001 | p=.10 | p=.43 | --- | p<.001 | p<.001 | p<.05 | p<.001 |
Note. AIC= Aikaike information criterion; BIC= Bayesian information criterion; SSBIC = sample size adjusted Bayesian information criterion; LRT = Lo-Mendell-Rubin test; BLRT = bootstrap likelihood ratio test.
Conditional Model
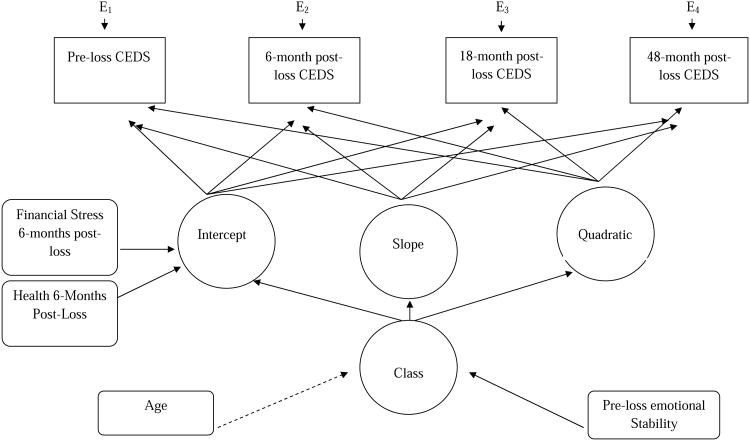
The intercepts were regressed on health and financial stress (see Table 4; Figure 2) to assess the covariates roll in predicting the level of depression across all occasions following loss. Financial stress positively predicted the intercept of the all classes, meaning that greater financial stress predicts greater levels of depression following loss even among groups that do not show high depression scores during bereavement. Health negatively predicted the intercept of the resilient and the depressed-improved classes, once again indicating that better health predicted less depression within these classes, but not for the other classes (see Table 4).
Table 4. Growth Factor Parameter Estimates for Covariates on the Intercept of the 4-Classes (n=301).
| Class | Financial Stress | Health | ||
|---|---|---|---|---|
| Est | SE | Est | SE | |
| Resilient | 0.33 | 0.13** | -0.37 | 0.14** |
| Chronic Grief | 0.56 | 0.25* | 0.07 | 0.27 |
| Chronic-Depression | 0.56 | 0.24* | -0.23 | 0.26 |
| Depressed-Improved | 0.25 | 0.12* | -1.02 | 0.03*** |
Note. Est= Parameter Estimate; SE= Standard Error
p≤.05;
p≤.01;
p≤.001.
Figure 2. Latent Growth Mixture Model Diagram.
Note: Non-significant paths from covariates are denoted by a broken line, significant paths from covariates are denoted by a solid line.
Class membership was regressed on emotional stability and age in a multinomial logistic regression framework nested in the LCGA model to assess if subjects within classes differ significantly on these pre-event characteristics. We conducted multiple comparisons within MPlus 6.0 to assess if our covariates predicted class membership. First we used the Resilient class as the reference class; next we used the Chronic Grief class as the reference class. Results of the multinomial regressions indicate that the Depressed-Improved class and the Chronic Depressed class displayed significantly lower scores on emotional stability compared to the Resilient and the Chronic Grief classes. Age demonstrated non-significance when comparing the Resilient class to the chronic depression class (see Table 5).
Table 5. Multinomial Logistic Regression for Predictors of Class Membership (n=301).
| Resilient vs. | Chronic Grief vs. | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Depressed Improved | Chronic Grief | Chronic Depression | Depressed Improved | Chronic Depression | ||||||||
| Est. | S.E. | Est. | S.E. | Est. | S.E. | Est. | S.E. | Est. | S.E. | |||
|
|
|
|||||||||||
| Age | 0.01 | 0.05 | -0.02 | 0.03 | 0.01 | 0.05 | -0.01 | .0.06 | 0.01 | 0.05 | ||
| Emotional Stability | -0.91 | 0.22*** | -0.11 | 0.26 | -1.01 | 0.34** | -1.04 | 0.41** | -1.01 | 0.33** | ||
Note. Est= Estimate; SE= Standard Error;
p≤.01;
p≤.001.
Discussion
Previous analyses of prospective data on bereavement revealed five longitudinal trajectories of depression (Boerner et al., 2005; Bonanno et al., 2002). Although these analyses were conducted prior to the advent of LGM, the observed trajectories were broadly consistent with subsequent studies of bereavement and other life events (Bonanno, 2004; Bonanno et al., 2011). Since prospective bereavement data are rare, however, in the current study we re-analyzed the data from these previous studies using the more empirical LGM approach with covariates modeled within the same analysis. Our analysis partially confirmed the original findings. Specifically, we found that four of the five trajectories, Resilient, Depressed-Improved, Chronic Depression, and Chronic Grief, remained stable using the more empirically-determined LGM.
There were also two important findings that diverged from the earlier analyses. First, the Chronic Grief trajectory indicated full recovery in depression symptomatology by 48 months, whereas the previous analyses suggested only the movement toward recovery (Boerner et al., 2005). Second and perhaps more significantly, we did not find evidence for the Common Grief or “Recovery” (Bonanno, 2004) trajectory, even when we forced a 5-class solution. It is noteworthy that the only other prospective bereavement study to employ LGM (Mancini et al., 2011) also failed to identify the Common Grief/Recovery pattern. Together these findings suggest that the more arbitrary methods used in earlier studies may have led to misclassification, pointing to an advantage of the LGM methodology. This difference suggests crucial clinical implications, as it indicates that there may not be a common pattern of bereavement response characterized by heightened levels of depression and then recovery. Rather, individuals who demonstrate heightened depression are likely to suffer significantly for some time.
We also tested a number of covariates based on evidence from the literature that health status, financial strain, emotional stability, and age. To test these variables in a single model, we regressed class membership on pre-event characteristics (age, emotional stability) and the intercept set to 6 months post-loss on health status and financial strain. We anticipated that those classes (Chronic Grief, Chronic Depression, Depressed-Improved) would be strongly predicted by the covariates because they have been shown to be indicative of poor adaptation, while the Resilient class would not because this class demonstrates both healthy adaptations to the loss and to conditions prior to the loss. Our hypotheses were only partially disconfirmed.
Financial strain positively predicted variability in levels of depression in all classes, indicating that financial stress elevates depression levels among all bereavement subpopulations, making it a generally stressor following loss. We further found that health status was only predictive of variability in the Resilient and Depressed-Improved classes. This would indicate that while poorer health does predict higher levels of depression, this seems to be the case in populations that are otherwise doing well following loss. Next, age differences did not predict trajectories of response. This indicates that variability in age, at least among the elderly, does not dictate the course of depression following loss. Finally, both the Depressed-Improved and the Chronic Depression classes demonstrated lower levels of emotional stability which is indicative of high trait neuroticism. Individuals high on trait neuroticism and low on emotional stability have been found to be less adaptive and more pathological. These findings indicate that the Chronic Grief trajectory is not comprised of individuals with a proclivity towards poor adaptation, meaning the observed psychopathology following loss may be unique to this situation rather than an ongoing endogenous depression that ebbs and flows in response to any given stressor. Also, although it is not surprising that the Chronic Depression class is low on emotional stability, it is surprising that the Depressed-Improved class is also low on this characteristic. One explanation is that their poor adaptation is observed prior to the loss, and that pre-loss events are greater stressors on this group than the loss itself, as this class does demonstrate significantly heighted depression prior to loss even if it abates by 6 months post-loss.
Our employment of an LGM framework highlights the importance of methodological precision in the study of heterogeneity in bereavement among older adults. While our analyses are certainly not exhaustive, they serve to demonstrate the capacity of LGM techniques in examining both heterogeneity in the course of bereavement and the ability to flexibly examine predictors of course in a single methodology.
It is important to note that the current investigation is not free of limitations. First, gender differences have been shown to be important in bereavement responses. Unfortunately, as our sample is predominantly female, we could not explore these differences. Further, this sample is characterized by a single population in the Detroit Michigan area in the 1980's. We may observe other patterns of adaptation among different populations or at a different time. These trajectories should not be taken as inclusive of all responses to loss among older adults, but rather serve as common patterns.
Next, the current study only examines patterns of depression in response to spousal loss. Other symptoms may be highly relevant. Complicated grief, for example has been shown to be a form of psychopathology that is unique to the grief experience and while it is closely related to depression, it has been shown to form a unique construct in the constellation of psychopathologies. Complicated grief cannot be studied prospectively and this dataset predates the strong interest among bereavement researchers in this construct. However, future studies should explore heterogeneity in complicated grief patterns, as they are highly relevant to the study of psychopathology in bereavement.
Despite these limitations, our analysis provides useful information concerning the effects of conjugal loss in older adults. First, we confirmed diversity in responses to loss while clarifying previous findings. For example, by modeling responses through 48 months, we found that the previously identified “Chronic Grief trajectory” showed full recovery over time. We also found similar to another prospective LGM study (Mancini et al., 2011) that the Common Grief or Recovery trajectory did not emerge. This has important theoretical and clinical implications as it indicates that individuals displaying high levels of depression at 6 months following loss are likely to follow a protracted course at least through 18 months.
New hypotheses related to heterogeneity in bereavement require increased analytic complexity. Reliance on statistical techniques not suited to such analyses increases the likelihood of erroneous findings. Through the use of modeling techniques that suit the study of heterogeneity, we find that psychological vulnerability prior to loss predicts heterogeneous patterns of response and that known predictors of depression following spousal loss act differently for different subpopulations, adding greater clarity in understanding how and for whom these predictors have an effect.
Research Highlights.
Conjugally bereaved older adults adapt to loss in heterogeneous ways.
Resilience is the modal outcome to conjugal bereavement
Financial Stress following a loss broadly predicts depression levels but does not differentiate adaptive from maladaptive outcomes.
People who demonstrate resilience and people who adapt poorly to the loss are more emotionally stable then people who demonstrate high pre-loss depression levels.
Latent Class Growth Analysis allows for the exploration of heterogeneous patterns of adaptation and its predictors.
Acknowledgments
The original data collection for this study was supported by NIA Grants AG610757-01 (Camille B. Wortman, P.I.), and AG05561-01 (James S. House, P.I.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Isaac R. Galatzer-Levy, New York University School of Medicine
George A. Bonanno, Columbia University
References
- Aneshensel CS, Botticello AL, Yamamoto-Mitani N. When caregiving ends: The course of depressive symptoms after bereavement. International Journal of Health and Social Behavior. 2004;45(4):422–440. doi: 10.1177/002214650404500405. [DOI] [PubMed] [Google Scholar]
- Ball JF. Widow's grief: The impact of age and mode of death. Omega. 1977;7:307–333. [Google Scholar]
- Boerner K, Wortman CB, Bonanno GA. Resilient or at risk? A 4-year study of older adults who initially showed high or low distress following conjugal loss. Journals of Gerontology Series B-Psychological Sciences & Social Sciences. 2005;60(2):67–73. doi: 10.1093/geronb/60.2.p67. [DOI] [PubMed] [Google Scholar]
- Bonanno GA. Loss, trauma, and human resilience: Have we underestimated the human capacity to thrive after extremely adverse events? American Psychologist. 2004;59:20–28. doi: 10.1037/0003-066X.59.1.20. [DOI] [PubMed] [Google Scholar]
- Bonanno GA, Ho SMY, Chan JCK, Kwong RSY, Cheung CKY, Wong CPY, Wong VCW. Psychological resilience and dysfunction among hospitalized survivors of the SARS epidemic in Hong Kong: A latent class approach. Health Psychology. 2008;27(5):659–667. doi: 10.1037/0278-6133.27.5.659. [DOI] [PubMed] [Google Scholar]
- Bonanno GA, Mancini AD, Horton JL, Powell T, LeardMann CA, Boyko EJ, Wells TS, Hooper TI, Gackstetter GD, Smith TC. Trajectories of trauma symptoms and resilience in deployed U.S. Military service members: A prospective cohort study. British Journal of Psychiatry. doi: 10.1192/bjp.bp.111.096552. in press. [DOI] [PubMed] [Google Scholar]
- Bonanno GA, Moskowitz JT, Papa A, Folkman S. Resilience to loss in bereaved spouses, bereaved parents, and bereaved gay men. Journal of Personality and Social Psychology. 2005;88:827–843. doi: 10.1037/0022-3514.88.5.827. [DOI] [PubMed] [Google Scholar]
- Bonanno GA, Westphal M, Mancini AD. Resilience to loss and potential trauma. Annual Review of Clinical Psychology. 2011;7:511–535. doi: 10.1146/annurev-clinpsy-032210-104526. [DOI] [PubMed] [Google Scholar]
- Bonanno GA, Wortman CB, Nesse RM. Prospective patterns of resilience and maladjustment during widowhood. Psychology & Aging. 2004;19(2):260–271. doi: 10.1037/0882-7974.19.2.260. [DOI] [PubMed] [Google Scholar]
- Bonanno GA, Wortman CB, Lehman DR, Tweed RG, Haring M, Sonnega J, Nesse RM. Resilience to loss and chronic grief: a prospective study from preloss to 18-months postloss. Journal of Personality & Social Psychology. 2002;83(5):1150–1164. doi: 10.1037//0022-3514.83.5.1150. [DOI] [PubMed] [Google Scholar]
- Boscardin CK. Early identification of reading difficulties using heterogeneous developmental trajectories. Journal of Educational Psychology. 2008;100(1):192–208. [Google Scholar]
- Boyd JH. Screening for depression in a community sample: Understanding the discrepancies between depression syndrome and diagnostic scales. Archives of General Psychiatry. 1982;39(10):1195–1200. doi: 10.1001/archpsyc.1982.04290100059010. [DOI] [PubMed] [Google Scholar]
- Bryk A, Raudenbush S. Application of hierarchical linear models to assessing change. Psychological Bulletin. 1987;101:147–158. [Google Scholar]
- Changing Lives of Older Couples Study (CLOC) Cloc – Changing Lives of Older Couples : A Prospective Study of Spousal Bereavement. Institute for Social Research, University of Michigan; Ann Arbor, Michigan: 2003. [Accessed 8 March 2009]. Available online at http://www.cloc.isr.umich.edu. [Google Scholar]
- Coifman KG, Bonanno GA, Ray RD, Gross JJ. Does repressive coping promote resilience? Affective-autonomic response discrepancy during bereavement. Journal of Personality & Social Psychology. 2007;92(4):745–758. doi: 10.1037/0022-3514.92.4.745. [DOI] [PubMed] [Google Scholar]
- Cole MG, Dendukuri N. Risk factors for depression among elderly community subjects; A systematic review and meta-analysis. American Journal of Psychiatry. 2003;160(6):1147–1156. doi: 10.1176/appi.ajp.160.6.1147. [DOI] [PubMed] [Google Scholar]
- Curran PJ, Hussong AM. The use of latent trajectory models in psychopathology research. Journal of Abnormal Psychology. 2003;112(4):526–544. doi: 10.1037/0021-843X.112.4.526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeCarlo LT. On the meaning and use of kurtosis. Psychological Methods. 1997;2(3):292–307. [Google Scholar]
- Del Boca FK, Darkes J, Greenbaum PE, Goldman MS. Up close and personal: temporal variability in the drinking of individual college students during their first year. Journal of Consulting & Clinical Psychology. 2004;72(2):155–164. doi: 10.1037/0022-006X.72.2.155. [DOI] [PubMed] [Google Scholar]
- deRoon-Cassini TA, Mancini AD, Rusch MD, Bonanno GA. Psychopathology and resilience following traumatic injury: a latent growth mixture model analysis. Rehabilitation Psychology. 2010;55(1):1–11. doi: 10.1037/a0018601. [DOI] [PubMed] [Google Scholar]
- Duncan TE, Duncan SC, Strycker LA. An introduction to latent variable growth curve modeling : concepts, issues, and applications. 2nd. Mahwah, N.J.: Lawrence Erlbaum Associates; 2006. [Google Scholar]
- Enders CK. The impact of nonnormality on full information maximum-likelihood estimation for structural equation models with missing data. Psychological Methods. 2001;6(4):352–370. [PubMed] [Google Scholar]
- Galatzer-Levy IR, Mazursky H, Mancini AD, Bonanno GA. What we don't expect when expecting: Evidence for heterogenaity in subjective well-being in response to parenthood. Journal of Family Psychology. 2011;25(3):384–392. doi: 10.1037/a0023759. [DOI] [PubMed] [Google Scholar]
- Galatzer-Levy IR, Bonanno GA, Mancini AD. From Marenthal to latent growth mixture modeling: A return to individual differences in response to unemployment. Journal of Neuroscience, Psychology, and Economics. 2010;3(2):116–125. [Google Scholar]
- Galatzer-Levy IR, Madan A, Neylan TC, Henn-Haase C, Marmar CR. Peritraumatic and trait dissociation differentiate police officers with resilient versus symptomatic trajectories of posttraumatic stress symptoms. Journal of Traumatic Stress. 2011;24(5):557–565. doi: 10.1002/jts.20684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenbaum P, Del Boca F, Darkes J, Wang C, Goldman MS. Variation in the drinking trajectories of freshman college students. Journal of Consulting and Clinical Psychology. 2005;73:229–238. doi: 10.1037/0022-006X.73.2.229. [DOI] [PubMed] [Google Scholar]
- Heo M. Problems in Statistical Analysis of Attrition in Randomized Controlled Clinical Trials of Antidepressant for Geriatric Depression. Current Psychiatry Reviews. 2007;3(3):178–185. [Google Scholar]
- Hedeker D, Gibbons RD. Applications of random-effects pattern-mixture models for missing data in longitudinal studies. Psychological Methods. 1997;2(1):64–78. [Google Scholar]
- Heyman DK, Gianturco DT. Long-term adaptation by the elderly to bereavement. Journal of Gerontology. 1973;28(3):359–363. doi: 10.1093/geronj/28.3.359. [DOI] [PubMed] [Google Scholar]
- Judd J, McClelland G, Ryan C. Data Analysis: A Model Comparison Approach. 2nd. New York: Rutledge; 2009. [Google Scholar]
- Jung T, Wickrama KA. An introduction to Latent Class Growth Analysis and Growth Mixture Modeling. Social and Personality Psychology Compass. 2008;2:302–317. [Google Scholar]
- Kohout FJ. Two Shorter Forms of the CES-D Depression Symptoms Index. Journal of Aging and Health. 1993;5(2):179–193. doi: 10.1177/089826439300500202. [DOI] [PubMed] [Google Scholar]
- Kurtz ME, Kurtz JC, Given CW, Given B. Predictors of postbereavement depressive symptomatology among family caregivers of cancer patients. Support Care Cancer. 1997;5:53–60. doi: 10.1007/BF01681962. [DOI] [PubMed] [Google Scholar]
- Lam WT, Bonanno GA, Mancini AD, Ho SMY, Chan M, Huan WK, Or A, Fielding R. Trajectories of psychological distress among Chinese women diagnosed with breast cancer. Psycho-oncology. 2010;19:1044–1051. doi: 10.1002/pon.1658. [DOI] [PubMed] [Google Scholar]
- Lo Y, Mendell N, Rubin D. Testing the number of components in a normal mixture. Biometrika. 2001;88:767–778. [Google Scholar]
- Mancini AD, Bonanno GA, Clark AE. Stepping off the hedonic treadmill: Individual differences in response to major life events. Journal of Individual Differences. 2011;32(2) [Google Scholar]
- McArdle JJ, Epstein D. Latent growth curves within developmental structural equation medels. Child Development. 1987;58(1):107–122. [PubMed] [Google Scholar]
- Muthén BO. On structural equation modeling with data that are not missing completely at random. Psychometrika. 1987;52(3):431–462. [Google Scholar]
- Muthén BO. Integrating Person-Centered and Variable-Centered Analyses: Growth Mixture Modeling With Latent Trajectory Classes. Alcoholism, Clinical and Experimental Research. 2000;24(6):882–891. [PubMed] [Google Scholar]
- Muthén BO. Statistical and Substantive Checking in Growth Mixture Modeling: Comment on Bauer and Curran (2003) Psychological Methods. 2003;8(3):369–377. doi: 10.1037/1082-989X.8.3.369. [DOI] [PubMed] [Google Scholar]
- Muthén BO, Muthén LK. Integrating person-centered and variable-centered analyses: growth mixture modeling with latent trajectory classes. Alcoholism, Clinical & Experimental Research. 2000;24(6):882–891. [PubMed] [Google Scholar]
- Muthén BO, Muthén LK. MPlus User's Guide. Sixth. Los Angeles, CA: Muthén & Muthén; 1998-2010. [Google Scholar]
- Nagin DS. Analyzing developmental trajectories: Semi-parametric, group-based approach. Psychological Methods. 1999;4:139–177. doi: 10.1037/1082-989x.6.1.18. [DOI] [PubMed] [Google Scholar]
- Norris FH, Murrell SA. Social support, life events, and stress as modifiers of adjustment to bereavement in older adults. Psychology and Aging. 1990;5(3):429–436. doi: 10.1037//0882-7974.5.3.429. [DOI] [PubMed] [Google Scholar]
- Nylund K, Asparouhov T, Muthén B. Deciding on the number of classes in latent class analysis and growth mixture modeling: A Monte Carlo simulation study. Structural Equation Modeling: A Multidisciplinary Journal. 2007;14(4):535–569. [Google Scholar]
- Onrust S, Cuijpers P, Smit F, Bohlmeijer E. Predictors of psychological adjustment after bereavement. International Psychogeriatrics. 2007;19(5):921–934. doi: 10.1017/S1041610206004248. [DOI] [PubMed] [Google Scholar]
- Pai M, Carr D. Do personality traits moderate the effect of late-life spousal loss on psychological distress? Journal of Health and Social Behavior. 2010;51(2):183–199. doi: 10.1177/0022146510368933. [DOI] [PubMed] [Google Scholar]
- Parks CM, Weiss R. Recovery from bereavement. New York: Basic Books; 1983. [Google Scholar]
- Radloff LS. The CES-D Scale: A Self-Report Depression Scale for Research in the General Population. Applied Psychological Measurement. 1977;1(3):385–401. [Google Scholar]
- Roberts R. Using the CES-D scale to screen for depression and anxiety: Effects of language and ethnic status. Psychiatry Research. 1990;31(1):69–83. doi: 10.1016/0165-1781(90)90110-q. [DOI] [PubMed] [Google Scholar]
- Roy J. Modeling longitudinal data with nonignorable dropouts using a latent dropout class model. Biometrics. 2003;59(4):829–836. doi: 10.1111/j.0006-341x.2003.00097.x. [DOI] [PubMed] [Google Scholar]
- Sanders CM. Risk factors in bereavement outcome. Journal of Socail Issues. 1988;44(3):97–111. [Google Scholar]
- Schaeffer CM, Petras H, Ialongo N, Poduska J, Kellam S. Modeling growth in boys' aggressive behavior across elementary school: Links to later criminal involvement, conduct disorder, and antisocial personality disorder. Developmental Psychology. 2003;39:1020–1035. doi: 10.1037/0012-1649.39.6.1020. [DOI] [PubMed] [Google Scholar]
- Stroebe M, Schut H, Stroebe W. Health outcomes of bereavement. Lancet. 2007;370:1960–1973. doi: 10.1016/S0140-6736(07)61816-9. [DOI] [PubMed] [Google Scholar]
- Thijs H, Molenberghs G, Michiels B, Verbeke G, Curran D. Straegies to fit pattern-mixture models. Biostatistics. 2002;3(2):245–265. doi: 10.1093/biostatistics/3.2.245. [DOI] [PubMed] [Google Scholar]
- Utz RL. The effect of widowhood on older adults' social participation: An evaluation of activity, disengagement, and continuity theories. The Gerontologist. 2002;42(4):522–533. doi: 10.1093/geront/42.4.522. [DOI] [PubMed] [Google Scholar]
- Wijngaards-de Meij L, Stroebe M, Schut H, Stroebe W, van den Bout J, van der Heijden P, Dijkstra I. Neuroticism and attachment insecurity as predictors of bereavement outcome. Journal of Research in Personality. 2007;41:498–505. [Google Scholar]