Abstract
A novel meal-detection algorithm is developed based on continuous glucose measurements. Bergman’s minimal model is modified and used in an unscented Kalman filter for state estimations. The estimated rate of appearance of glucose is used for meal detection. Data from nine subjects are used to assess the performance of the algorithm. The results indicate that the proposed algorithm works successfully with high accuracy. The average change in glucose levels between the meals and the detection points is 16(±9.42) [mg/dl] for 61 successfully detected meals and snacks. The algorithm is developed as a new module of an integrated multivariable adaptive artificial pancreas control system. Meal detection with the proposed method is used to administer insulin boluses and prevent most of post-prandial hyperglycemia without any manual meal announcements. A novel meal bolus calculation method is proposed and tested with the UVA/Padova simulator. The results indicate significant reduction in hyperglycemia.
Index Terms: Meal Detection, Unscented Kalman Filter, Artificial Pancreas, Type 1 Diabetes, Hyperglycemia
I. Introduction
Post-prandial glucose control in patients with type 1 diabetes (T1D) is one of the main challenges for artificial pancreas (AP) closed-loop control systems. Many studies have shown that the AP systems are able to maintain blood glucose concentrations (BGC) in target range during night time when there is no meal consumption [1]–[5]. Food intake increases plasma/serum glucose levels rapidly and can cause hyperglycemia if sufficient amount of insulin is not infused in an acceptable period of time. A hybrid closed-loop AP system may decrease the number of post-prandial hyperglycemic episodes [6]. In a hybrid AP system, meal information is used either as an announced disturbance [5], [7]–[10], or as an indicator for a constant bolus insulin infusion [11], [12]. Because of manual meal announcements, hybrid APs cannot be considered as a fully automated system. For a fully automated AP, no information should be manually entered to announce measurable disturbances for feed-forward control. Thus, there is a need for an algorithm that can detect meals from real-time measured variables. Once meals are detected, the information can be transferred to the controller and appropriate amount of insulin can be infused to prevent post-prandial hyperglycemia.
To date, only a few studies have investigated the detection of meals from real-time measurable variables such as a continuous glucose monitor (CGM) measurements. Dassau et. al [13] proposed a voting algorithm based on Kalman filter estimation, backward difference, combination of Kalman filter and backward difference and second derivative of glucose (CGM) measurements. A meal is considered to be detected when two-out-of-three or three-out-of-four algorithms detects a meal. Lee et al. [14] proposed a meal detection and meal size estimation algorithm and combined with model predictive control based AP system. Meal times and sizes are estimated based on various thresholds and if/then rules using first and second derivatives of glucose measurements. Cameron et al. [15] developed a probabilistic method for meal-detection. First, CGM signals are compared to no-meal predictions made by a simple insulin/glucose model. The residuals are fitted to predefined meal shapes used for detection of meals. Later, the method was extended for use in a model predictive control algorithm for blood glucose regulation [16].
In this paper, we propose a new method for meal-detection in patients with T1D that requires only CGM readings. A modified version of the Bergman’s minimal model [17] is used. Unscented Kalman filter (UKF) is used for simultaneous estimation of states and parameters of the minimal model. Finally, meals are detected based on rate of appearance of glucose estimations and some safety rules. An insulin bolus calculation algorithm is added for detected meals. The paper is structured as follows. Model development and UKF are described in the Methods section. The Results section presents the outcomes of the proposed method tested on nine real patients data and the performance of the bolus calculation algorithm which is tested with the UVa/Padova simulator [18]. The performance of the meal-detection algorithm as a new module for the integrated multivariable adaptive AP (IMA-AP) control system is evaluated in the Discussion section. Conclusions are provided in the last section.
II. Methods
A. Minimal Model
Bergman et al. [17] developed the first three-compartment ”minimal model” to analyze plasma glucose and insulin dynamics during an intravenous glucose tolerance test. Modifications of the minimal model have been proposed to separate the effect of glucose production from utilization [19], [20] and to capture absorption, distribution and disposal glucose/insulin dynamics [21]. The effects of free fatty acids [22] and exercise [23] are also incorporated into the minimal model. The dynamical equations for plasma glucose concentration G(t) and effective insulin concentration Ieff are given by [22]:
| (1) |
| (2) |
where Gb and Ip represent basal plasma glucose concentration and plasma insulin concentration respectively. The rate of appearance of glucose Ra(t) can be defined as a two compartment model [24]:
| (3) |
where C(t), V and τ are the amount of consumed carbohydrate, the distribution volume and the peak time of meal absorption, respectively. In the original Bergman’s model [17] and its extensions [21], [22] the unknown model parameters p1, p2, p3, p4, V and τ are not time-varying. However, due to the complexity of the human body and inter-subject variability, a constant set of parameters may not be able to describe all time-varying dynamics for a subject. Also, intra-subject variability may require different sets of parameters for different subjects. In the proposed method, all unknown parameters and the basal plasma glucose concentration Gb are defined to be time-varying in order to overcome the inter-and intra-subject variability. Using the first forward difference derivative approximation, Eqs (1)–(3) are discretized as:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
where , and h and w(k) represent sampling time and noise term, respectively. l is the length of the window that is used for calculation of Gb and selected to be 30 minutes. The notation for plasma glucose concentration G(t) in Eq (1) is replaced with subcutaneous glucose concentration (CGM) Gs(k) in Eq (4). The relation between two variables was shown to be a one compartment model with a delay parameter [25] which is neglected in our study due to validation reasons.
B. Unscented Kalman Filter
The Unscented Kalman filter [26], [27] is a powerful tool for state estimation of nonlinear systems. The drawbacks of linear approximation at an operating point and calculation of Jacobian matrices in the Extended Kalman filter (EKF) are overcome by using a minimal set of carefully chosen sample (sigma) points.
A nonlinear state space model is derived from Eqs (4)–(8):
| (9) |
where x(k) is the state vector. w(k) and v(k) are defined to be process and measurement noises, respectively. The nonlinear functions f(·) and g(·) are defined from Eqs (4)–(8). The state space model in Eq (9) has 8 states since some parameters in Eqs (4)–(8) are defined to be part of noise term w(k).
Defining L as the dimension of x vector, the scalar weights Wi are defined:
| (10) |
where i = 1, ···, 2L and μ = α2 (L + κ). The tuning parameters α, β and κ are selected to be 1, 2 and 0 [28], respectively. The sigma-points vectors χi are defined as:
| (11) |
where ηi is the ith column (i = 1, ···, L) of the squared root of the augmented covariance matrix P(k − 1) and the parameter .
Prior sigma-points estimations are calculated by propagating the sigma-points χi(k − 1) through the nonlinear function f(·). The prior sigma-points are trimmed with a nonlinear optimization to prevent non-realistic estimations such as negative values in concentrations.
| (12) |
The prior state estimations and covariance matrix are calculated as:
| (13) |
| (14) |
where Qp is the covariance matrix of the process noise. The prior sigma-points estimations are propagated through the nonlinear function g(·) for calculation of prior outputs sigma-points :
| (15) |
The measurement estimations are obtained from the output sigma-points as:
| (16) |
The innovation covariance and cross-covariance matrices are calculated as:
| (17) |
| (18) |
where Qm represent the covariance matrix for process measurement noise. Finally, the Kalman filter gain and the updated state vector estimation and covariance matrix are calculated:
| (19) |
| (20) |
| (21) |
C. Data Collection and Preprocessing
Data are collected from nine subjects undergoing multivariable AP control system experiments [29], [30] without any announcement (meal or exercise). Subjects were recruited from the University of Chicago Medical Center, Kovler Diabetes Center and were scheduled for a visit at the University of Chicago General Clinical Research Center (GCRC). Closed-loop control was performed for 32 hours for each subject. Based on the study protocol, breakfast, lunch, dinner and a late time snack were provided. Additional snacks were provided whenever requested by the subjects. The type of foods were selected based on a subject’s personal requirements. No limitation on food or snack intake was imposed. The subject’s own insulin type and pump were used during the experiments. Data were continuously collected from the subjects with a sampling time of 5 minutes. Every 10 minutes insulin infusion rates were computed by the controller and used to adjust the pump. The Guardian® REAL-time CGM (Medtronics, Northride, CA) were used to collect the glucose concentration information.
To minimize the effect of CGM measurement noise on the first forward difference derivative approximation, 1 minute sampled CGM data is obtained from original data sampled every 5 minutes, using pchip interpolation [31]. The initial conditions and tuning parameters are selected as:
| (22) |
where CGM (1) is the first measured glucose value and the initial values for p1, p2 and p4 are adapted from Roy et al. [22].
III. Results
The meal detection algorithm is developed based on the state estimations x̂(k) from the UKF algorithm. A meal is detected if the estimated rate of appearance of glucose Ra(k) is above the threshold of 2 [mg/dl/min]. Once the Ra(k) value goes below the threshold, a flag is lifted and another meal is detected when the value gets above 2 mg/dl/min. For safety from hypoglycemia, a meal detected is used for insulin bolus decision only when CGM values are above 100 [mg/dl].
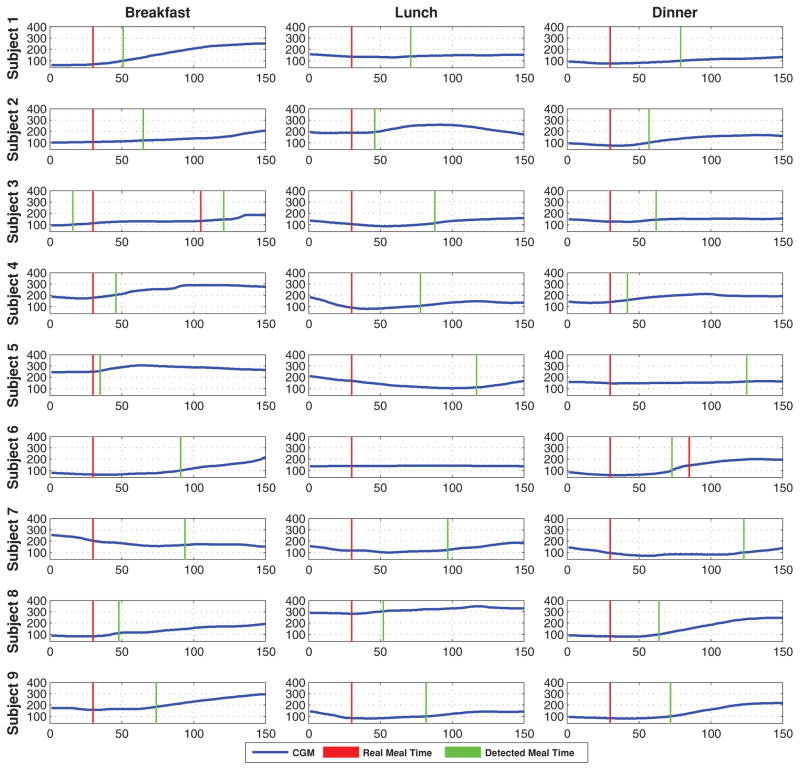
Figure 1 shows the performance of the proposed method for 27 different main meals (breakfast, lunch and dinner) for 9 subjects. Each sub-figure shows the time interval of 30 minutes before and 120 minutes after a meal. The difference in glucose values (change in glucose) between the time that meal starts and the time that meal is detected is used as the evaluation criterion. Detection time is not used as an evaluation criterion due to time-varying meal consumption lengths from subject to subject. Different types of foods have different digestion and absorption rates which also prevents using detection time as an evaluation criterion.
Fig. 1.
Meal detection of 27 different main meals for 9 subjects. (Vertical axis: glucose concentration [mg/dl], horizontal axis: sample number)
Table I summarizes the results for 9 subjects data. Overall, 51 main meal and 13 snack periods are tested. Out of 63 cases, only two meals are missed. As shown in Figure 1, the lunch for subject 6 is missed because there is almost no change in glucose values after the consumption of 45 grams of carbohydrates. This might be due to insulin on board that is already active. A meal is not detected for subject 4 because, a snack, which is detected by the algorithm, is consumed by the subject before the undetected meal. Since the glucose increase from the meal is almost linearly added to the increase from the snack, the algorithm can not distinguish between the two consumptions and interprets them as one meal. Considering only the successfully detected 61 meal and snack periods, the average change in glucose is 16 (±9.42) [mg/dl]. For all tested datasets, there is only one wrong alarm for subject 4, where there was a rapid increase in glucose but no recorded meals at that time. This might be because of a missed recorded meal.
TABLE I.
Performance of the Meal-Detection Algorithm for all Subjects
| # of meals | Carb amounts | TD | MD | FD | CGM at meal time | CGM at detection time | Change in glucose | |
|---|---|---|---|---|---|---|---|---|
| Subject 1 | 3 | 68(±7.64) | 3 | 0 | 0 | 94(±36.59) | 113(±23.09) | 19(±13.86) |
| Subject 2 | 5 | 53(±9.75) | 5 | 0 | 0 | 145(±55.57) | 159(±47.81) | 13(±8.99) |
| Subject 3 | 6 | 62(±17.3) | 6 | 0 | 0 | 104(±23.48) | 117(±21.29) | 13(±13.67) |
| Subject 4 | 6 | 71(±17.6) | 5 | 1 | 1 | 169(±61.81) | 175(±62.5) | 6(±22.4) |
| Subject 5 | 6 | 85(±21.0) | 6 | 0 | 0 | 135(±67.1) | 141(±60.44) | 6(±33.07) |
| Subject 6 | 5 | 60(±10.6) | 4 | 1 | 0 | 115(±82.5) | 155(±88.05) | 40(±8.79) |
| Subject 7 | 7 | 83(±46.36) | 7 | 0 | 0 | 133(±46.46) | 148(±36.18) | 14(±27.13) |
| Subject 8 | 6 | 58(±14.15) | 6 | 0 | 0 | 160(±86.85) | 176(±83.57) | 15(±10.27) |
| Subject 9 | 6 | 65(±6.37) | 6 | 0 | 0 | 134(±43.19) | 143(±42.19) | 9(±11.24) |
| # of snacks | Carb amounts | TD | MD | FD | CGM at meal time | CGM at detection time | Change in glucose | |
| Subject 1 | 0 | 0(±0) | 0 | 0 | 0 | 0(±0) | 0(±0) | 0(±0) |
| Subject 2 | 1 | 30(±0) | 1 | 0 | 0 | 68(±0) | 100(±0) | 32(±0) |
| Subject 3 | 1 | 30(±0) | 1 | 0 | 0 | 133(±0) | 146(±0) | 13(±0) |
| Subject 4 | 4 | 26(±7.5) | 4 | 0 | 0 | 137(±39.16) | 158(±40.39) | 20(±16.68) |
| Subject 5 | 2 | 22(±10.6) | 2 | 0 | 0 | 106(±29.69) | 119(±27.57) | 13(±2.12) |
| Subject 6 | 1 | 15(±0) | 1 | 0 | 0 | 120(±0) | 149(±0) | 29(±0) |
| Subject 7 | 1 | 30(±0) | 1 | 0 | 0 | 123(±0) | 156(±0) | 33(±0) |
| Subject 8 | 2 | 20(±0) | 2 | 0 | 0 | 122(±39.59) | 131(±38.18) | 9(±1.41) |
| Subject 9 | 1 | 15(±0) | 1 | 0 | 0 | 194(±0) | 200(±0) | 6(±0) |
| Total | 63 | 44(±9.38) | 61 | 2 | 1 | 121(±33.99) | 138(±31.74) | 16(±9.42) |
Values are shown as mean (±standard deviation). TD: true detection, MD: missed detection, FD: false detection. The units are mg/dl and grams for glucose values and carb amounts, respectively.
The rate of appearance of glucose Ra(k) estimations are used for calculation of meal boluses. A meal bolus is given when the estimated Ra(k) is above 2 [mg/dl/min] and measured CGM value is above 100 [mg/dl]. A second meal bolus can be given only after the Ra(k) values go below the 2 [mg/dl/min] threshold and 30 minutes passes over the last infused meal bolus. Once a meal bolus is infused, a flag is turned on to activate correction bolus (CB) infusion and the 2 [mg/dl/min] threshold is increased to 3 [mg/dl/min]. While the flag is on, the Ra(k) value is checked every 15 minutes and a CB is given if the Ra(k) is above the new threshold. For each given CB, the threshold is increased by 1 [mg/dl/min] and the process is repeated every 15 minutes until the flag is turned off. The correction boluses are calculated based on measured CGM values Gs(k) and subject’s body weight (BW) as a function of total daily dose (TDD) as follow:
| (23) |
| (24) |
| (25) |
where r0 and μ are the desired set-point, and the tuning parameter that affects the amount of CB infusions, respectively. The values μ are selected to be 0.55, 0.3 and 0.1 for sensitive, normal and resistant adults or adolescents and 0.8, 0.7 and 0.45 for sensitive, normal and resistant children, respectively [30]. The set-point r0 is set to 100 mg/dl.
The proposed meal bolus calculation strategy was performed on the academic version of UVa/Padova metabolic simulator [32] which has 30 subjects (10 adults, 10 adolescents and 10 children). For the consistency, the same three-day simulation scenario with the Turksoy et al. [30] was generated and 300 simulations (10 for each subject) were performed. The same scenario was used for adults and adolescents. The amount of carbohydrates in meals was reduced for children.
Turksoy et al. [30] divided the 30 subjects of the UVa/Padova metabolic simulator into 3 subgroups (sensitive, normal, resistant) based on a subject’s insulin sensitivity. In this study, the amount of meal boluses are defined based on these 3 subgroups. The meal boluses are selected to be 4 [U], 3 [U] and 2 [U] for the resistant, normal and sensitive adult and adolescent subjects and 1 [U], 0.85 [U] and 0.7 [U] for the resistant, normal and sensitive child subjects, respectively.
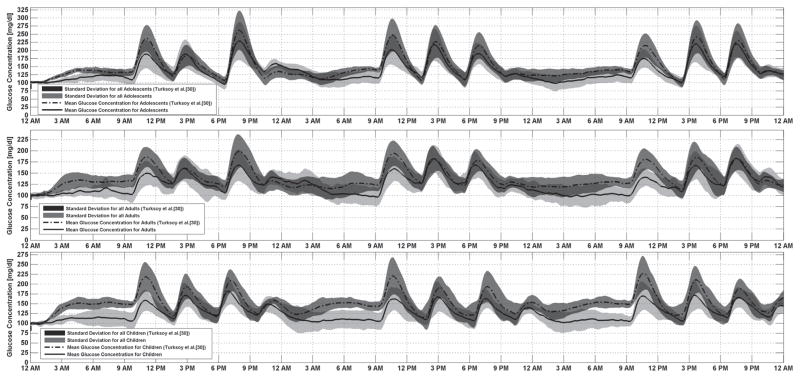
Figure 2 shows the average glucose concentration (CGM) for all 30 subjects (means and standard deviations). The mean glucose concentration for adolescents in the target range is 86.8% of the time and is stable during the night. Better glucose regulation is obtained in adults subjects. During 94.7% of the simulation time glucose concentration stayed within the target range even though meals with high carbohydrate content were provided. A successful glucose regulation was obtained for the children subjects where 92% of the time glucose concentration stayed within the target range. The time in hyperglycemic range is significantly (p < 0.01) decreased with the proposed meal bolus calculation algorithm.
Fig. 2.
Average glucose concentration (CGM) for all subjects
IV. Discussion
Many studies have shown that an AP control system is able to keep BGC in target range [5], [7]–[12], [29], [30], [33]. In addition to being able to control BGC, a fully automated AP system should not require any manual information from patients. We have already developed an integrated multivariable adaptive AP (IMA-AP) control system without any manual meal or exercise announcement [29], [30], [33]. The system has two different modules. The first module is the adaptive control algorithm that is responsible for insulin suggestions [30]. The second module is a hypoglycemia early alarm system that is able to detect hypoglycemic episodes around 25–30 minutes in advance and warn patients about potential low glucose values [34]. The two modules are able to prevent most of hypoglycemia and at the same time keep the BGC in target range. However, due to lack of meal announcements, the IMA-AP system suffers from having some post-prandial hyperglycemia.
The meal-detection algorithm developed provides the third module for the IMA-AP system. The meal-detection module is completely adaptive and does not require any subject-specific initialization. It works based on only CGM measurements. The early detection of meals by the meal-detection module enables the IMA-AP system to provide a meal bolus (without any manual announcements) that would prevent most of post-prandial hyperglycemia.
Since there are no simulators that provide physiological signals [29], [33] that are used by the IMA-AP system, a single variable (only CGM measurements) version of the algorithm was tested on the UVa/Padova simulator. The performance of the IMA-AP system for preventing of hypoglycemia and keeping BGC in target range has already been demonstrated [29], [30]. We are conducting clinical experiments by using the new version of the IMA-AP system wtih meal-detection and insulin bolus. We are expecting to significantly decrease the number of hyperglycemia without causing any additional hypoglycemic episodes.
V. Conclusions
The meal-detection algorithm developed is able to detect almost all tested meals. Simulation results indicate that using such a high performance meal-detection module in artificial pancreas control systems can prevent most of hyperglycemia by providing bolus insulin for meals before large increases in BGC without any manual information from patients.
Acknowledgments
This work is supported by the National Institutes of Health (NIH) under grants 1DP3DK101077-01 and 1DP3DK101075-01 and the Juvenile Diabetes Research Foundation International (JDRF) under grant 17-2013-472.
Biographies
 Kamuran Turksoy received the B.Sc. degree in electrical engineering from Yildiz Technical University, Istanbul, Turkey and the Ph.D. degree in biomedical engineering from Illinois Institute of Technology, Chicago, USA in 2010 and 2015, respectively.
Kamuran Turksoy received the B.Sc. degree in electrical engineering from Yildiz Technical University, Istanbul, Turkey and the Ph.D. degree in biomedical engineering from Illinois Institute of Technology, Chicago, USA in 2010 and 2015, respectively.
He is currently a posdoctoral research associate in biomedical engineering at Illinois Institute of Technology. His research interests include system identification, modeling, control, fault detection and diagnosis in biological systems. mypages.iit.edu/~syscont/turksoy.html
 Sediqeh Samadi received the M.Sc. degree in chemical engineering from Sharif University, Iran. She is currently a Ph.D. student in chemical engineering at Illinois Institute of Technology. Her research focuses on modeling and simulation of the dynamics of insulin-glucose system. mypages.iit.edu/~syscont/samadi.html
Sediqeh Samadi received the M.Sc. degree in chemical engineering from Sharif University, Iran. She is currently a Ph.D. student in chemical engineering at Illinois Institute of Technology. Her research focuses on modeling and simulation of the dynamics of insulin-glucose system. mypages.iit.edu/~syscont/samadi.html
 Jianyuan Feng received the B.Sc. degree in mechanical engineering from Changzhou University, Changzhou, China in 2012. He received the master degree in 2013 and is currently a Ph.D. student in chemical engineering at Illinois Institute of Technology.
Jianyuan Feng received the B.Sc. degree in mechanical engineering from Changzhou University, Changzhou, China in 2012. He received the master degree in 2013 and is currently a Ph.D. student in chemical engineering at Illinois Institute of Technology.
His current research interests include controller performance assessment, sensor error detection and analytical sensor redundancy for a fully automated closed-loop artificial pancreas algorithm for patients with type 1 diabetes. mypages.iit.edu/~syscont/feng.html
 Elizabeth Littlejohn received the MD degree from M. D. Rosalind Franklin University of Medicine and Science, North Chicago, IL, USA in 1988.
Elizabeth Littlejohn received the MD degree from M. D. Rosalind Franklin University of Medicine and Science, North Chicago, IL, USA in 1988.
She is an Associate Professor of pediatrics and medicine at the University of Chicago, Chicago. IL, USA. She specializes in pediatric diabetes and endocrinology, working with patients ranging from newborn to age 20. Also a clinical researcher, she is investigating innovative treatments and more efficient diagnostic tools to improve diabetes care for children and young adults. In the Kovler Diabetes Center, she focuses specifically on expanding pediatric clinical research with the goal to advance clinical care for pediatric diabetes. She has served on a number of committees including the Illinois Department of Public Health Advisory Committee on Metabolic and Genetic Screening, American Diabetes Association, and the Juvenile Diabetes Research Foundation.
 Laurie Quinn received the Ph.D. degree in nursing science from University of Illinois at Chicago, Chicago, IL, USA in 1996.
Laurie Quinn received the Ph.D. degree in nursing science from University of Illinois at Chicago, Chicago, IL, USA in 1996.
She is a Clinical Associate Professor at the College of Nursing, University of Illinois at Chicago, Chicago, IL, USA. She is experienced in the clinical management of patients with diabetes mellitus and has investigated the physiological mechanisms that contribute to their excessive rate of cardiovascular disease. Specifically, she has studied the effects of aerobic exercise on the metabolic determinants of cardiovascular disease in patients with type 2 diabetes (i.e., insulin resistance, oxidative stress, lipid, and lipoprotein abnormalities). A major focus of her work has been examining the influence of aerobic exercise on postprandial metabolism in obese nondiabetic and diabetic patients.
 Ali Cinar received the Ph.D. degree in chemical engineering from Texas A&M University, College Station, TX, USA.
Ali Cinar received the Ph.D. degree in chemical engineering from Texas A&M University, College Station, TX, USA.
He is a Professor of Chemical Engineering and Biomedical Engineering at Illinois Institute of Technology and since 2004 he has been the director of the Engineering Center for Diabetes Research and Education. His current research includes agent-based techniques for modeling, supervision, and control of complex and distributed systems, modeling of diabetes, angiogenesis and tissue formation, and adaptive control techniques for artificial pancreas systems for patients with diabetes. He has published two books, more than 190 technical papers in refereed journals and conference proceedings. A full list of publications, detailed description of research interests, presentations, and software is available at www.chbe.iit.edu/~cinar.
Dr. Cinar is a member of the IEEE and a fellow of the AIChE.
Contributor Information
Kamuran Turksoy, Email: kturksoy@hawk.iit.edu, Postdoctoral research associate in the Department of Biomedical Engineering, Illinois Institute of Technology, Chicago, IL, 60616 USA.
Sediqeh Samadi, Email: ssamadi@hawk.iit.edu, Ph.D. student in Process Modeling, Monitoring and Control Research Group, Department of Chemical and Biological Engineering, Illinois Institute of Technology, Chicago, IL, 60616 USA.
Jianyuan Feng, Email: jfeng12@hawk.iit.edu, Ph.D. student in Process Modeling, Monitoring and Control Research Group, Department of Chemical and Biological Engineering, Illinois Institute of Technology, Chicago, IL, 60616 USA.
Elizabeth Littlejohn, Email: elittlej@peds.bsd.uchicago.edu, Associate professor in the Department of Pediatrics, Kovler Diabetes Center, University of Chicago, Chicago, IL, 60637, USA.
Laurie Quinn, Email: lquinn1@uic.edu, Associate professor in the Department of Biobehavioral Health Science, College of Nursing, University of Illinois at Chicago, Chicago, IL, 60612, USA.
Ali Cinar, Email: cinar@iit.edu, Professor in the Departments of Chemical and Biological Engineering and Biomedical Engineering, IIT, Chicago, IL, 60616, USA.
References
- 1.Clarke WL, Anderson S, Breton M, Patek S, Kashmer L, Kovatchev B. Closed-loop artificial pancreas using subcutaneous glucose sensing and insulin delivery and a model predictive control algorithm: the Virginia experience. Journal of Diabetes Science and Technology. 2009 Sep;3(5):1031–1038. doi: 10.1177/193229680900300506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hovorka R, Allen JM, Elleri D, Chassin LJ, Harris J, Xing D, Kollman C, Hovorka T, Larsen AMF, Nodale M, et al. Manual closed-loop insulin delivery in children and adolescents with type 1 diabetes: a phase 2 randomised crossover trial. The Lancet. 2010;375(9716):743–751. doi: 10.1016/S0140-6736(09)61998-X. [DOI] [PubMed] [Google Scholar]
- 3.Elleri D, Allen J, Nodale M, Wilinska M, Acerini C, Dunger D, Hovorka R. Suspended insulin infusion during overnight closed-loop glucose control in children and adolescents with type 1 diabetes. Diabetic Medicine. 2010;27(4):480–484. doi: 10.1111/j.1464-5491.2010.02964.x. [DOI] [PubMed] [Google Scholar]
- 4.Steil G, Palerm C, Kurtz N, Voskanyan G, Roy A, Paz S, Kandeel F. The effect of insulin feedback on closed loop glucose control. Journal of Clinical Endocrinology & Metabolism. 2011;96(5):1402–1408. doi: 10.1210/jc.2010-2578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Breton M, Farret A, Bruttomesso D, Anderson S, Magni L, Patek S, Dalla Man C, Place J, Demartini S, Del Favero S, et al. Fully Integrated Artificial Pancreas in Type 1 Diabetes Modular Closed-Loop Glucose Control Maintains Near Normoglycemia. Diabetes. 2012;61(9):2230–2237. doi: 10.2337/db11-1445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Weinzimer SA, Steil GM, Swan KL, Dziura J, Kurtz N, Tamborlane WV. Fully automated closed-loop insulin delivery versus semiautomated hybrid control in pediatric patients with type 1 diabetes using an artificial pancreas. Diabetes Care. 2008 May;31(5):934–939. doi: 10.2337/dc07-1967. [DOI] [PubMed] [Google Scholar]
- 7.Sherr JL, Cengiz E, Palerm CC, Clark B, Kurtz N, Roy A, Carria L, Cantwell M, Tamborlane WV, Weinzimer SA. Reduced hypoglycemia and increased time in target using closed-loop insulin delivery during nights with or without antecedent afternoon exercise in type 1 diabetes. Diabetes care. 2013;36(10):2909–2914. doi: 10.2337/dc13-0010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Luijf YM, DeVries JH, Zwinderman K, Leelarathna L, Nodale M, Caldwell K, Kumareswaran K, Elleri D, Allen JM, Wilinska ME, et al. Day and night closed-loop control in adults with type 1 diabetes a comparison of two closed-loop algorithms driving continuous subcutaneous insulin infusion versus patient self-management. Diabetes care. 2013;36(12):3882–3887. doi: 10.2337/dc12-1956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nimri R, Danne T, Kordonouri O, Atlas E, Bratina N, Biester T, Avbelj M, Miller S, Muller I, Phillip M, et al. The glucositter overnight automated closed loop system for type 1 diabetes: a randomized crossover trial. Pediatric diabetes. 2013;14(3):159–167. doi: 10.1111/pedi.12025. [DOI] [PubMed] [Google Scholar]
- 10.Elleri D, Allen JM, Kumareswaran K, Leelarathna L, Nodale M, Caldwell K, Cheng P, Kollman C, Haidar A, Murphy HR, et al. Closed-loop basal insulin delivery over 36 hours in adolescents with type 1 diabetes randomized clinical trial. Diabetes Care. 2013;36(4):838–844. doi: 10.2337/dc12-0816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Russell SJ, El-Khatib FH, Sinha M, Magyar KL, McKeon K, Goergen LG, Balliro C, Hillard MA, Nathan DM, Damiano ER. Outpatient glycemic control with a bionic pancreas in type 1 diabetes. New England Journal of Medicine. 2014;371(4):313–325. doi: 10.1056/NEJMoa1314474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.El-Khatib FH, Russell SJ, Magyar KL, Sinha M, McKeon K, Nathan DM, Damiano ER. Autonomous and continuous adaptation of a bihormonal bionic pancreas in adults and adolescents with type 1 diabetes. The Journal of Clinical Endocrinology & Metabolism. 2014;99(5):1701–1711. doi: 10.1210/jc.2013-4151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dassau E, Bequette BW, Buckingham BA, Doyle FJ. Detection of a meal using continuous glucose monitoring implications for an artificial β-cell. Diabetes care. 2008;31(2):295–300. doi: 10.2337/dc07-1293. [DOI] [PubMed] [Google Scholar]
- 14.Lee H, Buckingham BA, Wilson DM, Bequette BW. A closed-loop artificial pancreas using model predictive control and a sliding meal size estimator. Journal of diabetes science and technology. 2009;3(5):1082–1090. doi: 10.1177/193229680900300511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cameron F, Niemeyer G, Buckingham BA. Probabilistic evolving meal detection and estimation of meal total glucose appearance. Journal of diabetes science and technology. 2009;3(5):1022–1030. doi: 10.1177/193229680900300505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cameron F, Niemeyer G, Bequette BW. Extended multiple model prediction with application to blood glucose regulation. Journal of Process Control. 2012;22(8):1422–1432. [Google Scholar]
- 17.Bergman RN, Phillips LS, Cobelli C. Physiologic evaluation of factors controlling glucose tolerance in man: measurement of insulin sensitivity and beta-cell glucose sensitivity from the response to intravenous glucose. Journal of Clinical Investigation. 1981;68(6):1456. doi: 10.1172/JCI110398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kovatchev B, Breton M, Dalla Man C, Cobelli C. In silico model and computer simulation environment approximating the human glucose/insulin utilization. Food and Drug Administration Master File MAF. 2008;1521 [Google Scholar]
- 19.Cobelli C, Pacini G, Toffolo G, Sacca L. Estimation of insulin sensitivity and glucose clearance from minimal model: new insights from labeled ivgtt. Am J Physiol. 1986;250(5 Pt 1):E591–8. doi: 10.1152/ajpendo.1986.250.5.E591. [DOI] [PubMed] [Google Scholar]
- 20.Cobelli C, Caumo A, Omenetto M. Minimal model sgoverestimation and siunderestimation: improved accuracy by a bayesian two-compartment model. American Journal of Physiology-Endocrinology And Metabolism. 1999;277(3):E481–E488. doi: 10.1152/ajpendo.1999.277.3.E481. [DOI] [PubMed] [Google Scholar]
- 21.Hovorka R, Shojaee-Moradie F, Carroll PV, Chassin LJ, Gowrie IJ, Jackson NC, Tudor RS, Umpleby AM, Jones RH. Partitioning glucose distribution/transport, disposal, and endogenous production during ivgtt. American Journal of Physiology-Endocrinology and Metabolism. 2002;282(5):E992–E1007. doi: 10.1152/ajpendo.00304.2001. [DOI] [PubMed] [Google Scholar]
- 22.Roy A, Parker RS. Dynamic modeling of free fatty acid, glucose, and insulin: An extended”minimal model. Diabetes Technology & Therapeutics. 2006;8(6):617–626. doi: 10.1089/dia.2006.8.617. [DOI] [PubMed] [Google Scholar]
- 23.Roy A, Parker RS. Dynamic modeling of exercise effects on plasma glucose and insulin levels. Journal of Diabetes Science and Technology. 2007;1(3):338–347. doi: 10.1177/193229680700100305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hovorka R, Canonico V, Chassin LJ, Haueter U, Massi-Benedetti M, Federici MO, Pieber TR, Schaller HC, Schaupp L, Vering T, et al. Nonlinear model predictive control of glucose concentration in subjects with type 1 diabetes. Physiological measurement. 2004;25(4):905. doi: 10.1088/0967-3334/25/4/010. [DOI] [PubMed] [Google Scholar]
- 25.Dalla Man C, Micheletto F, Lv D, Breton M, Kovatchev B, Cobelli C. The uva/padova type 1 diabetes simulator new features. Journal of Diabetes Science and Technology. 2014;8(1):26–34. doi: 10.1177/1932296813514502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Julier SJ, Uhlmann JK. Unscented filtering and nonlinear estimation. Proceedings of the IEEE. 2004;92(3):401–422. [Google Scholar]
- 27.Wan EA, Van Der Merwe R. The unscented kalman filter for nonlinear estimation. Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000. AS-SPCC. The IEEE 2000; IEEE; 2000. pp. 153–158. [Google Scholar]
- 28.Van Der Merwe R. PhD dissertation. Oregon Health & Science University; 2004. Sigma-point kalman filters for probabilistic inference in dynamic state-space models. [Google Scholar]
- 29.Turksoy K, Bayrak ES, Quinn L, Littlejohn E, Cinar A. An integrated Multivariable Artificial Pancreas Control System. Journal of Diabetes Science and Technology. 2014;8(3):498–507. doi: 10.1177/1932296814524862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Turksoy K, Quinn L, Littlejohn E, Cinar A. Multivariable adaptive identification and control for artificial pancreas systems. Biomedical Engineering, IEEE Transactions on. 2014 Mar;61(3):883–891. doi: 10.1109/TBME.2013.2291777. [DOI] [PubMed] [Google Scholar]
- 31.Fritsch FN, Carlson RE. Monotone piecewise cubic interpolation. SIAM Journal on Numerical Analysis. 1980;17(2):238–246. [Google Scholar]
- 32.Kovatchev BP, Breton M, Man CD, Cobelli C. In silico preclinical trials: a proof of concept in closed-loop control of type 1 diabetes. J Diabetes Sci Technol. 2009 Jan;3(1):44–55. doi: 10.1177/193229680900300106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Turksoy K, Bayrak ES, Quinn L, Littlejohn E, Cinar A. Multivariable Adaptive Closed-Loop Control of an Artificial Pancreas without Meal and Activity Announcement. Diabetes Technology & Therapeutics. 2013;15(5):386–400. doi: 10.1089/dia.2012.0283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Turksoy K, Bayrak ES, Quinn L, Littlejohn E, Rollins DK, Cinar A. Hypoglycemia Early Alarm Systems Based On Multivariable Models. Industrial Eng Chemical Research. 2013;52(35):12329–12336. doi: 10.1021/ie3034015. [DOI] [PMC free article] [PubMed] [Google Scholar]