Pyrrolo[3,2-b]pyrroles – from unprecedented solvatofluorochromism to two-photon absorption

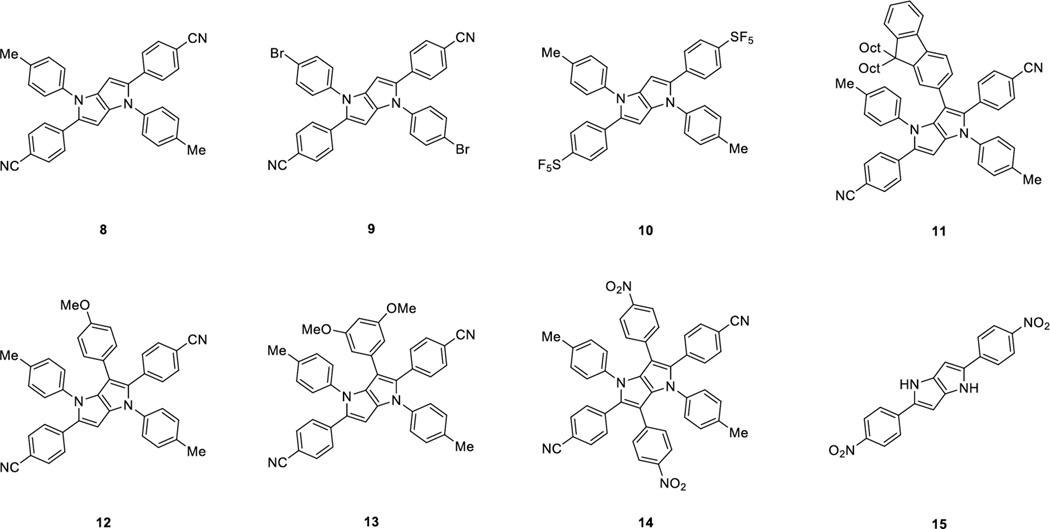
Abstract

A combined experimental and theoretical study of the two-photon absorption properties of a series of quadrupolar molecules possessing a highly electron-rich heterocyclic core, pyrrolo[3,2-b]pyrrole is presented. In agreement with quantum-chemical calculations, we observe large two-photon absorption (2PA) cross-section values, σ_2PA ~ 10²–10³ GM (1GM = 10⁵⁰ cm⁴ s photon⁻¹) at wavelengths 650–700 nm, corresponding to the 2-photon allowed but 1-photon forbidden transitions. The calculations also predict that increased planarity of this molecule via removal of two N-substituents leads to further increase in the σ_2PA values. Surprisingly, the most quadrupolar pyrrolo[3,2-b]pyrrole derivative bearing two 4-nitrophenyl substituents at positions 2 and 5 demonstrates very strong solvatofluorochromic effect, with the fluorescence quantum yield as high as 0.96 in cyclohexane, while the fluorescence vanishes in DMSO.

Introduction

The pioneering studies performed in 1990-ies put forward two basic designs for organic compounds with enhanced two-photon absorption cross-sections in the vis and near IR range of wavelengths.^[1] The first class possesses centrosymmetric structure, where the highest 2PA cross-section (σ_2PA), corresponds to the 2-photon allowed but 1-photon forbidden transition. It was observed that the maximum 2PA cross-section, increases with increasing quadrupolar character of the chromophore,^[1b,2] which is related to the increase of excited state transition dipole moments. The second class comprises dipolar molecules, where the 2-photon and 1-photon transitions are simultaneously allowed,^[1a] and the maximum σ_2PA value correlates with the change of the permanent electric dipole moment in the transition from ground- to the final excited state.^[3] In recent years, a variety of quadrupolar chromophores possessing different electron-donating and electron-accepting groups linked in a specific manner (so-called A-D-A and D-A-D structures) have been synthesized and studied,^[4] although some octupolar architectures^[5] have also been investigated. Materials based on porphyrins,^[6] multi-annulenes,^[7] radical-cations^[8] and diradicals^[9] have also been extensively explored. Although the arrangement of electron-donating and electron-withdrawing groups is crucial for modulating the non-linear response, the actual electron density of the A, D moieties may also guide the increase of the two-photon absorption cross-section. Recently we discovered a new and efficient methodology for the synthesis of pyrrolo[3,2-b]pyrroles,^[10] the most electron-rich heterocycle among aromatic two-ring systems.^[11] It became tempting to utilize this scaffold in the construction of even stronger quadrupolar A-D-A chromophores and to study their two-photon absorption properties. In a preliminary study, we found that for a series of TetraAryl-1,4-dihydroPyrrolo[3,2-b]Pyrroles (TAPPs), the two-photon absorption cross-sections reach values of σ_2PA~700 GM at 700 nm, limited by the wavelength tuning range of the laser system.^[10b,12] Tetra- and hexa-substituted pyrrole[3,2-b]pyrroles are centrosymmetric, while the pentasubstituted compounds are nominally non-centrosymmetric, even though their backbone structure still behaves in a centrosymmetric manner. The remaining uncertainty concerning the location and values of 2PA maxima and the potential use of dyes possessing large non-linear responses at wavelengths shorter than 700 nm in areas such as two-photon excited polymerization^[13] and optical limiting^[14] prompted us to undertake a more detailed study of the origin of the one- and two-photon absorption characteristics of these molecules. Here we present a comprehensive investigation of the nonlinear optical properties of the TAPPs as a function of the electron-withdrawing strength of peripheral groups using both experimental and established quantum chemical computational techniques.^[15]

Design and synthesis

Tetra-, penta- and hexa-substituted pyrrolo[3,2-b]pyrroles bearing electron-withdrawing groups of different strengths were designed for this study. Depending on the actual number of aryl substituents on the core, one can expect different levels of conjugation between these units, which should have a huge impact on the optical properties (both linear and non-linear).

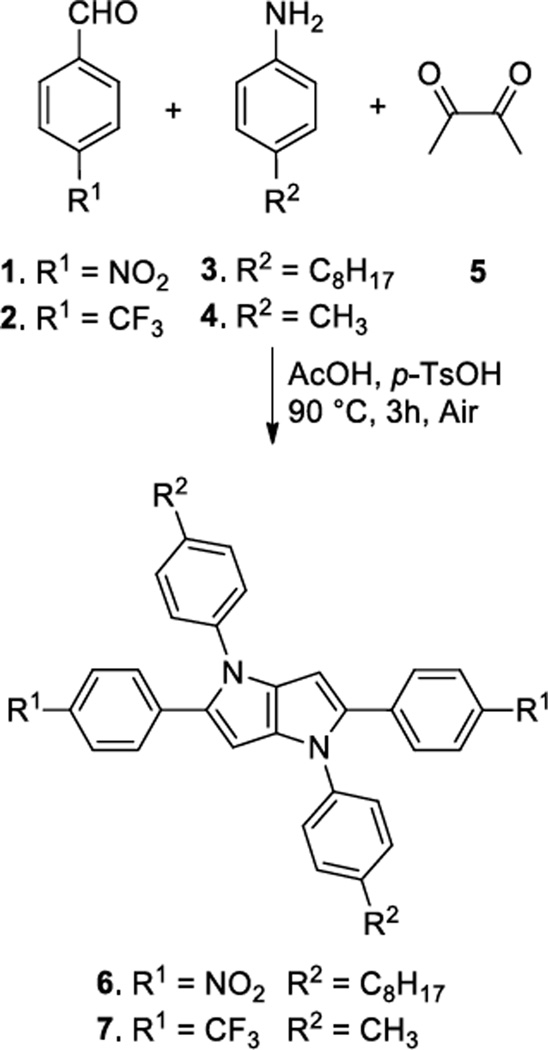
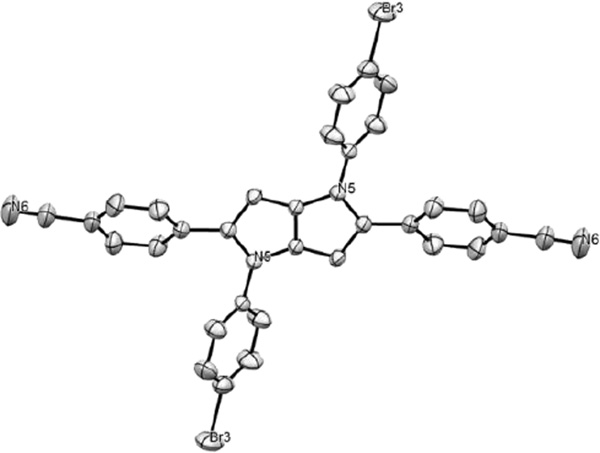
The majority of designed compounds was synthesized as described earlier employing an optimized synthesis of TAPPs together with a direct arylation methodology (Figure 1).^[10b] Two new key compounds 6 and 7 bearing 4-nitrophenyl- and 4-trifluoromethylphenyl substituents at position 2 and 5 were synthesized for this study from the corresponding aldehydes 1 and 2, primary aromatic amines 3 and 4 and diacetyl (5) (Scheme 1). These compounds have been obtained in 36% and 35% yield, respectively. In order to get insight into the molecular structure of the TAPP derivatives, we have grown crystals of compound 9 suitable for X-ray crystallography.

Figure 1.

Scheme 1.

Synthesis of pyrrolopyrroles 6 and 7.

It is noteworthy to emphasize that this is the first example of a TAPP X-ray structure (Figure 2). The molecular structure reveals that the dihedral angle between the aryl rings (originating from an aldehyde) and the pyrrolopyrrole core is 35.6 degrees in the ground state. This is a moderate value, allowing for a certain overlap of the molecular orbitals of the different parts and hence for a conjugation pathway across the different molecular parts, providing a highly polarizable link between the peripheral electron withdrawing groups through the pyrrolopyrrole core (A-D-A quadrupole). The dihedral angle between the N-aryl rings and the pyrrolopyrrole core is 45.8 degrees.

Figure 2.

X-ray structure of compound 9 (hydrogen atoms omitted for clarity) CCDC 1404494.

Linear spectroscopic characteristics

The structure of the synthesized TAPPs consists of the central electron donor framework and two terminal electron acceptor parts. Consequently, changing from nonpolar to polar solvents should influence the optical properties of these dyes, as polar solvents tend to stabilize the intramolecular charge transfer (ICT) state.^[16] In fact, linear optical properties for TAPPs 6 and 7 are very different. Compound 7 displays a sharp absorption band (ε= 31000–42000 M⁻¹∙cm⁻¹) and its λ_max is hardly sensitive to the change of the solvent polarity (Table 1). In the emission spectrum, the position of the fluorescence maxima for 7 varies in the relatively small wavelength range explored, indicating that the excited-state geometry shows only moderate dependence on the solvent polarity. The fluorescence quantum yields are very high in the majority of the solvents, with the exception of the nonpolar cyclohexane where fluorescence efficiency is somewhat lower (in the CCl₄ solution, compound 7 rapidly decomposed). The difference in the fluorescence quantum yield can be explained by the fact that in polar solvents compound 7 tends to fluoresce more efficiently from the ICT state.^[17]

Table 1.

Optical properties of TAPPs 6 and 7.

Cmpd.	Solvent	λabs, nm	ε·10−3, M−1·cm−1	ΔS, cm−1	λem, nm	Φfl
6a	C6H12	447; 469	48; 44	1160	496, 525	0.96
	CCl4	458	45	3300	540	0.93
	toluene	465	42	3400	552; 569	0.70
	dioxane	464	44	4600	590	0.25
	THF	471	44	4800	610	0.03
	CH2Cl2	477	41		nd
	CH3CN	467	40		nd
	DMSO	483	35		nd
7b	C6H12	371	31	2600	411	0.67
	toluene	375	38	2800	419	0.85
	dioxane	374	42	3000	421	0.86
	THF	376	41	2900	422	0.81
	CH2Cl2	373	39	3200	424	0.85
	CH3CN	369	39	3700	428	0.80
	DMSO	377	38	3700	438	0.87

^aDetermined with fluorescein in NaOH (0.01M) (Φ_fl = 0.9);

^bDetermined with 9,10-diphenylanthracene in cyclohexane as a standard (Φ_fl = 0.7).^[18]

nd – fluorescence spectra were not measured due to very low S/N ratio

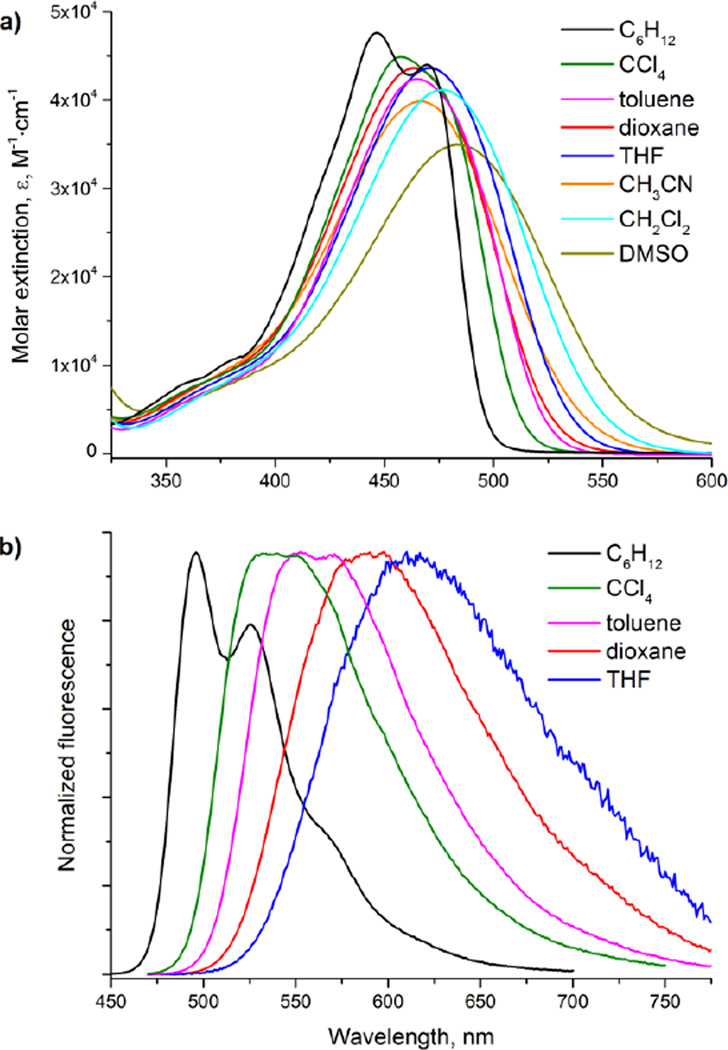
In contrast to 7, the optical properties of compound 6 are non-typical for known TAPP molecules^[10–12] as 6 is remarkably affected by the solvent polarity. The absorption bands are bathochromically shifted as a consequence of the stronger polarization of the electronic structure of 6 compared with 7. Meanwhile, the position of the absorption maxima in the different solvents varies in the narrow spectral range investigated, and compound 6 shows a strong solvatochromism of the fluorescence bands (Figure 3). In non-polar toluene compound 6 still demonstrates strong emission though the fluorescence quantum yield is somewhat decreased compared to both cyclohexane and CCl₄. When changing the solvent to 1,4-dioxane and THF the fluorescence response falls dramatically and in CH₂Cl₂ solution the fluorescence signal becomes undetectable. For the typical dipolar solvents (CH₃CN, DMSO), no fluorescence is observed (Table 1).

Figure 3.

Absorption (a) and normalized emission (b) spectra of TAPP 6.

Compound 6 also features unusual optical properties compared to other functional dyes as the molecule contains two nitro groups, yet displays strong fluorescence, and this prompted us to perform an in-depth analysis of their linear and nonlinear optical properties.

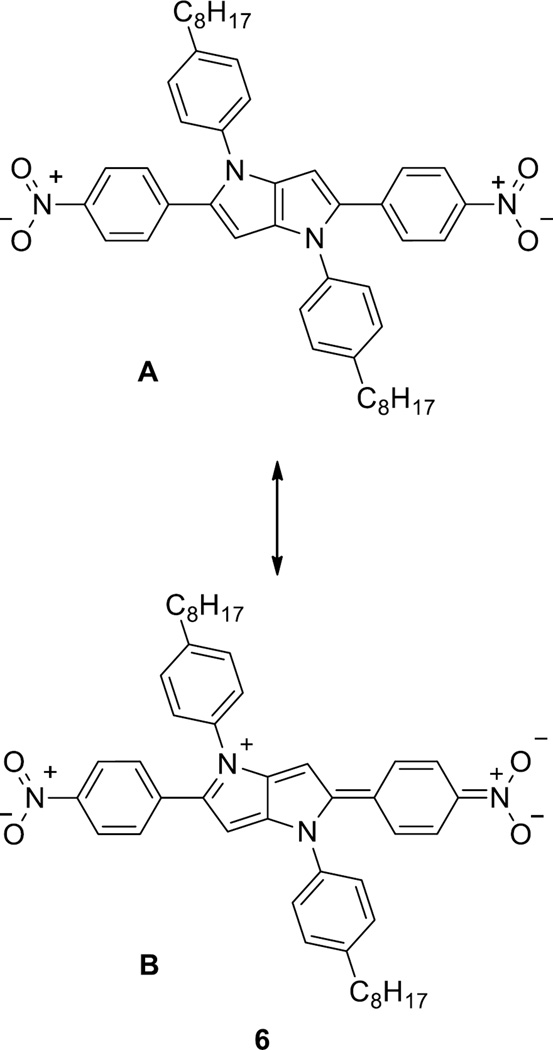
Whereas the trifluoromethyl groups in compound 7 influence the electronic structure mainly through inductive effects, the nitro group also possesses a strong mesomeric effect. In nonpolar solvents such as cyclohexane and carbon tetrachloride, the contribution of the neutral limiting form (Figure 4, form A) is much higher. In this state, the aryl substituents are most likely non-coplanar with the central framework, and the mesomeric effect of the nitro group is thus quenched. As a result, compound 6 in cyclohexane and CCl₄ solutions emits very efficiently. Although there are examples of nitro derivatives possessing fluorescence properties, they are rather rare in the literature,^{[16,17,19,20]} and to the best of our knowledge no nitro derivatives with almost 100% fluorescence quantum yield have been reported. When increasing the solvent polarity, the single bonds at positions 2 and 5 adopt a partial double-bond character in favor of the ICT state (Figure 4), form B), resulting in a more planar structure quenching the fluorescence as is typical for the nitro group.^[21]

Figure 4.

Postulated limiting forms of compound 6.

In their breakthrough paper Terenziani, Painelli and Blanchard-Desce^[22] explained the phenomenon of solvatofluorochromism of quadrupolar molecules (observed earlier) via introducing the concept of symmetry breaking in the excited state.^[23] Such phenomenon was later observed and confirmed by other groups.^[24] It has to be emphasized that although a relaxed (symmetry broken) excited state is possible due to the interactions of the excited structure with solvents molecules, the quadrupolar charge distribution cannot induce a uniform reaction field at the location of the solute. The larger solvatofluorochromism compared to solvatochromism for centrosymmetric chromophore (which puts these compounds into class I chromophores according to Terenziani classification) can arise only from two phenomena: large change in electronic distribution^[25] or symmetry breaking in the relaxed excited state.^[23] In analogy to platinum complexes described by Cooper and co-workers^[25a] the strongly electron-withdrawing nitro group acts as game-changer and it induces symmetry breaking in the S1 state.

Two-photon absorption

Femtosecond two-photon absorption (2PA) spectra were measured in the excitation wavelength range 570–900 nm using two-photon excited fluorescence (2PEF) and non-linear transmission (NLT) methods (see Experimental Section for details of the methods). The quadratic dependence of the 2PEF signal on the incident power was confirmed with an accuracy of 2.00 ± 0.05 within the considered range (for the 2PEF method). At wavelengths shorter than 570 nm, the power exponent declined from the strict quadratic dependence due to an increasing contribution from the accompanying one-photon absorption process (1PA).

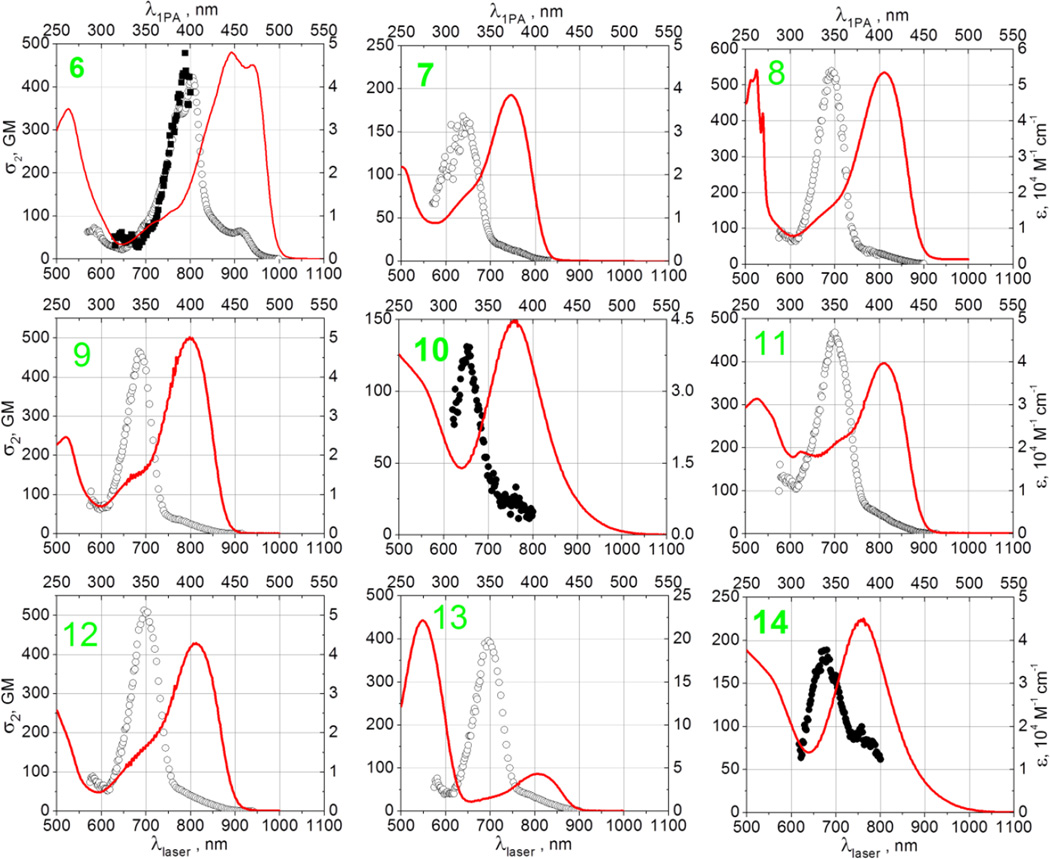
Figure 5 shows the 2-photon absorption spectra of compounds 6–14 in cyclohexane. In case of 10 and 14, which showed nearly vanishing fluorescence in all solvents, the measurements were performed using the NLT method (filled symbols) in the 570–800 nm range. For all other compounds the 2PEF method was used in the 570–1000 nm range. In addition, due to the poor solubility of compound 6 in cyclohexane, the NLT measurement was performed for 6 in dichloromethane. The 2PA spectral shapes obtained by the two alternative methods were in good agreement, indicating that excited-state absorption is relatively insignificant. Linear absorption spectra in cyclohexane (solid line) are shown for comparison.

Figure 5.

Two-photon absorption spectra of compounds 6–14 obtained by using 2PEF method (empty symbols) and NLT method (filled symbols). Linear absorption spectra (solid line) are shown for comparison Left vertical axes represent two-photon absorption cross-sections, right vertical axes represent extinction coefficients. Bottom horizontal axes are used for laser (two-photon excitation) wavelengths, top horizontal axes are used for linear (one-photon excitation) wavelengths.

The 2PA spectrum of 8 was reported earlier in the 700–900 nm range, and our values correlate well with these previous measurements.^[12a] In the 570–900 nm range, the two-photon absorption spectra show a dominant band with peak wavelengths in the range 640–800 nm. The corresponding maximum 2PA cross-section varies from the lowest value of 130 GM in 10 to the highest value 530 GM in 8. Table 2 summarizes the measured peak wavelengths and peak cross-sections. In all nine compounds studied, the lowest-energy dipole-allowed S₀→S₁ transition occurs at about 50–70 nm longer wavelengths from the dominant two-photon peak, which most likely means that the latter belongs to a different excited state, probably a higher singlet state S_n. With the exception of 6, which shows a bump at about 920 nm, the 2PA spectrum at the S₀→S₁ transition shows no distinct features in the series of compounds, whereas the 2PA cross-section stays below 5–10 GM in all systems. These observations are in accordance with the alternate parity selection rule for centrosymmetric chromophores, as is also confirmed by our theoretical calculations (vide infra). Compounds 8 and 9 are structurally rather similar, which is reflected in the fact that both the 1PA and 2PA spectra display only a slight blue shift and reduction of the corresponding peak cross-sections due to the addition of the two peripheral Br atoms.

Table 2.

Linear and non-linear optical properties of compounds 6–15 in cyclohexane.

Cmpd.	λabs [nm]	λem [nm]	Φfl	2λ1PA [nm]	(λ2PA)max [nm]		(σ2PA)max [GM]
					Exp.	Calc.a	Exp.	Calc.a
6	469	496	0.96c	938	800b	674	420b	1650
7	371	411	0.67d	752	640	564	170	561
8	406e	461	0.88f	812	690	592	530	1180
9	399e	454	0.86f	798	675	584	470	1030
10	382e	434	0.01f	764	655	570	125	867
11	404e	472	0.57f	808	700		470
12	406e	467	0.75f	812	700		510
13	401e	461	0.79f	802	695		400
14	381e	-	-	762	675		190
15	nd	nd	nd	nd	nd	668	nd	2330

^aCalculated using CAM-B3LYP;

^bDetermined in CH₂Cl₂;

^cDetermined with fluorescein in NaOH (0.01M) (Φ_fl = 0.9);

^dDetermined with 9,10-diphenylanthracene in cyclohexane as a standard (Φ_fl = 0.7).[18]

^edata from ref. [12a];

^fDetermined with quinine sulfate in H₂O (0.5 M) as a standard (Φ_fl = 0.94).

The two-photon spectrum of compound 6 follows the same bathochromic shift compared to the rest of the series as was observed in the one-photon absorption. The 2PA spectra also show some features that are not discernible in other compounds, most likely due to 6 having less line broadening which might be due to 6 possessing two partially conjugated 4-nitrophenyl groups, which are the strongest electron acceptors among all the substituents considered. Interestingly, 14 also has two NO₂ groups attached, but here these effects are less prominent.

Table 2 compares the experimental and calculated values for the maximum two-photon transition wavelength and the corresponding peak two-photon cross-section of 6–9, together with the linear optical characteristics of the whole series.

Theoretical modeling

Two-photon absorption

A computational study using density functional theory has been carried out for six molecules. Compounds 7–10 and 15 were studied using the structures shown in Figure 1. Compound 6 has been studied in a slightly modified version; to avoid too strong conformational flexibility and to reduce the computational cost, the octyl chains in TAPP 6 have been replaced by methyl groups. We will refer to this species as 6a in the following.

The calculations have been carried out using the CAM-B3LYP and PBE0 density functionals. The choice of functionals was based on several studies. Nayydar, Masunov and Tretiak have found that PBE0 reproduces experimental values of 2PA cross sections very well.^[26a] However, in comparisons with coupled cluster calculations the CAM-B3LYP functional has proven to be very reliable in the treatment especially of charge-transfer excited states^[26b] while other studies have shown that CAM-B3LYP results are lower than results from coupled cluster.^[27] We therefore decided to use both density functionals. Our results are listed in Tables 3 and 4 (comparison between two methods). We note that the excitation energies differ strongly between CAM-B3LYP and PBE0 with the energies from CAM-B3LYP being always higher and the values from PBE0 always being lower than the experimental values. This is in line with the known behavior of CAM-B3LYP.^[28] In contrast to this the 2PA cross sections from these two functional are extremely similar. We only note some deviation in the order of the states. While in 7 and 10 the 2PA active states in both cases are the S3 and the S5 states, respectively, in 8 and 9 the 2PA active state is the S3 state in PBE0 and the S2 state in CAM-B3LYP. For 6a and 15 the S2 state shows the highest 2PA cross section in all cases. Using the CAM-B3LYP functional calculations on 8 and 9 have been carried out using C₂ point group symmetry. In these cases the 2PA active state is the second highest in an energetic order and the first one with B symmetry. Comparing the computational cross sections, we note that they increase in the order σ₇ < σ₁₀ < σ₉ < σ₈ < σ_6a < σ₁₅.

Table 3.

Calculated data of the relevant states for compounds 6A, 7–10 and 15 using CAM-B3LYP functionals. The values in the fourth column are the rotationally averaged transition strengths in atomic units as obtained from the Dalton program (see Computational Details section). They are given here for the sake of reproducibility.^[27] The values in the last column resemble the denominator in eq. 1 and have the dimension of an energy, and are reported in atomic units.

Molecule state.	λex [nm]	Oscillator strength	2PA strength 103 [a.u.]	2PA cross section 103 [GM]	1/(ωi−ω01) [a.u.]
6a, 1PA-state, 1 A	394	1.352	0.222	0.002	−20.77
6a, 2PA-state, 2 A	337	0.051	166.0	1.650	-
7, 1PA-state, 1 A	340	1.227	0.023	0	−18.7
7, 2PA-state, 3 A	282	0.206	39.70	0.561	-
8, 1PA-state, 1 B	359	1.456	0.037	0	−20.01
8, 2PA-state, 1 A	296	0.004	92.00	1.180	-
9, 2PA-state, 1 B	359	0.005	0.042	0	−19.72
9, 2PA-state, 1 A	297	1.445	78.40	1.030	-
10, 1PA-state, 1 A	347	1.347	0.032	0	−19.51
10, 2PA-state, 5 A	285	0.003	62.60	0.867	-
15, 1PA-state, 1 A	405	1.621	0	0	−20.86
15, 2PA-state, 2 A	334	0	232.0	2.330	-

Table 4.

Comparison of two-photon absorption calculations using PBE0 and CAM-B3LYP functionals.

		PBE0			CAM-B3LYP
Mol.	λex [nm]	2PA strength 103 [a.u.]	2PA cross section 103 [GM]	λex [nm]	2PA strength 103 [a.u.]	2PA cross section 103 [GM]
6a	469	0.427	0.002	392	0.222	0.002
	415	230.0	1.492	336	166.0	1.650
	398	0.016	0	315	0.007	0
	359	4.482	0.039	315	4.340	0.049
	323	0.592	0.006	314	0.011	0
7	373	0.040	0	338	0.023	0
	327	0.005	0	283	0.191	0.003
	322	31.10	0.338	281	39.70	0.561
	316	0.942	0.011	273	9.570	0.144
	309	41.26	0.482	270	3.560	0.054
8	400	0.060	0	358	0.037	0
	347	0.010	0	296	92.00	1.180
	339	126.6	1.235	293	0.004	0
	317	0.042	0	276	4.990	0.073
	316	9.611	0.108	275	0.039	0.001
9	393	0.060	0	353	0.042	0
	338	0.009	0	291	78.40	1.030
	325	100.0	0.998	289	0.004	0
	321	0.062	0.001	274	6.180	0.092
	318	25.88	0.285	273	0.052	0.001
10	385	0.039	0	346	0.032	0
	384	0.042	0	289	2.190	0.029
	381	0.050	0	289	0.347	0.005
	335	0.006	0	288	0.020	0
	323	62.00	0.665	284	62.60	0.867
15	469	0	0	404	0	0
	405	273.1	1.861	333	232.0	2.330
	349	0	0	316	0.077	0.001
	324	0.547	0.006	315	5.190	0.058
	324	0.134	0.001	287	0.002	0

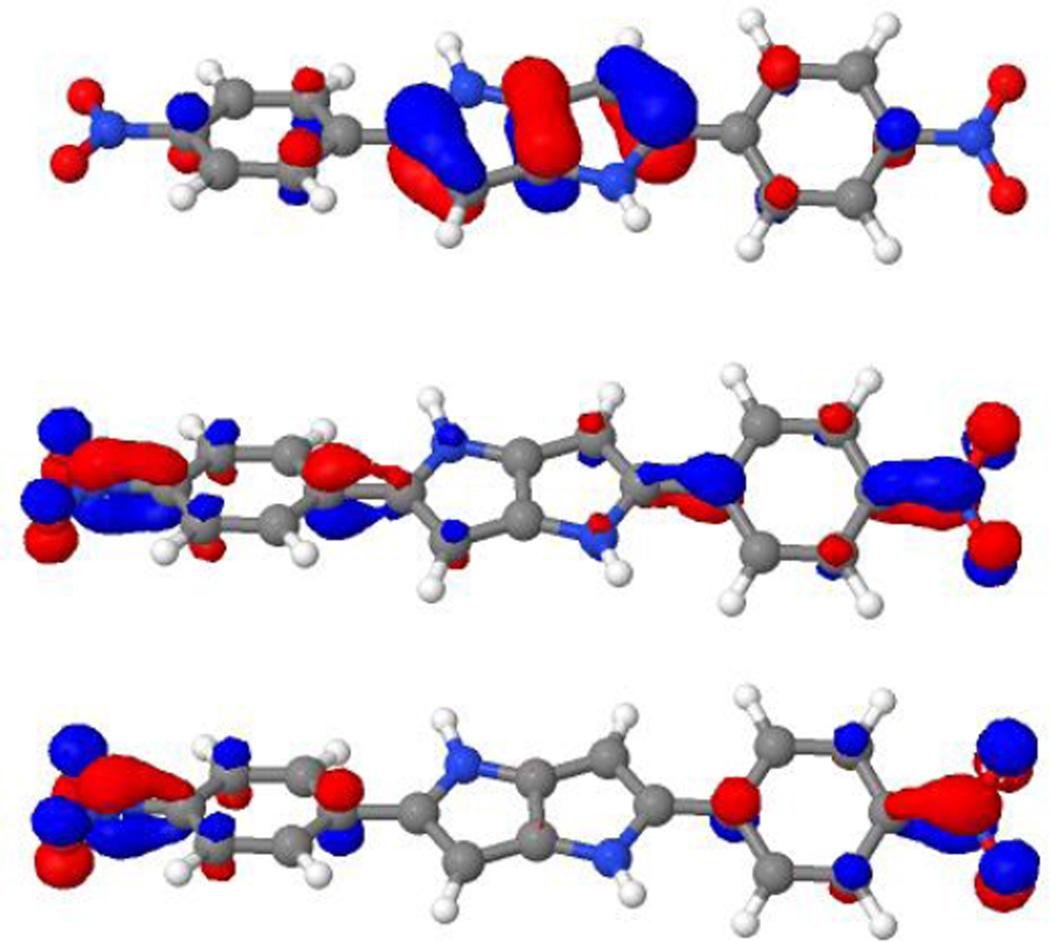
For all molecules the lowest state in energy has been found to be nearly dark in 2PA but to show a strong one-photon absorption (1PA). In the following the behavior of the 1PA- and 2PA active states will be discussed in more detail using results from the CAM-B3LYP calculations. In all cases the 1PA-active state has been found to correspond to the HOMO-LUMO excitation and the HOMO and the LUMO have very similar characteristics for all molecules: The largest part of the HOMO is located at the pyrrolo[3,2-b]pyrrole backbone, whereas the largest contributions to the LUMO are a p-orbital in para-position to the electron-withdrawing group on the rings in position 2 and 5 and the π-bond between these rings and the electron withdrawing group. We will refer for this state as the “1PA state” in in the following.

The 2PA-bright states also always have the same characteristics and corresponds to the transition from the HOMO to an orbital which is the LUMO+1 in 6a, 7, 8, 9 and 15 and the LUMO+3 in 10. In 10, there are MOs located at the SF₅ groups that lie in-between the LUMO and the LUMO+3. The main part of the relevant virtual orbital for the 2PA-state is always similar to the LUMO but has additional nodal planes. Plots of all three orbitals involved are shown in Figure 6. Another state with strong one-photon absorption has been identified above the 2PA-state. This state can always be correlated with an excitation from the HOMO-1 to the LUMO.

Figure 6.

HOMO (up), LUMO (middle) and LUMO+1 (lower panel) of compound 15. The orbital plots have been generated from a CAM-B3LYP calculation using the aug-cc-pVDZ basis set.

The strong alternation in the behaviour of the 1PA- and the 2PA state is typical for centrosymmetric molecules for which symmetry dictates the 1PA and 2PA selection rules. Although the optimized structures are not centrosymmetric, the deviations from centrosymmetry are small. All molecules have a rather low permanent dipole moment with a centrosymmetric pyrrolo[3,2-b]pyrrole. The molecules can thus be considered “pseudo-centrosymmetry” which allows us to study them using a simplified few-state model^[29] for which the contribution of permanent moments will be negligible.^[30] This few-state model is an approximation to the sum-over-states approach where transition properties are expressed in terms of transition dipole moments and excitation energies. In our simplified version of this model, the elements of the two-photon transition moment tensor S_ij (from which the two-photon absorption cross-section can be obtained^[31]) are

$$S_{ij}=\frac{1}{h}\frac{{\mu }_i^{01}{\mu }_j^{12}}{{\omega }_i-{\omega }_{01}}.$$ Equation 1

where i,j are spatial components of the electric field, 0 is the electronic ground state, 1 is an intermediate excited state and 2 is the final excited state. μ_i¹² is the i-component of the transition dipole moment between states 1 and 2, ω_i the frequency of perturbation i and ω₀₁ the excitation energy from the ground state to state 1. This is not the expression used in our calculations, but it captures the main driving forces for the observed 2PA cross-sections. Indeed, when using this formula we reproduce the dominating two-photon transition moment tensor elements of 6a, 7, 8, 10 and 15 with an error of less than 15% when we use the 1PA-state as state 1 and the 2PA-state as state 2.

Looking at the orbitals in Figure 6, we note that although the whole molecule is not centrosymmetric, the main part of the HOMO is centrosymmetric and ungerade with respect to inversion at the center of the backbone. The LUMO and the LUMO+1 show some pseudo-centrosymmetry and comparing them we note that the LUMO can be considered to be pseudo-gerade and the LUMO+1 is pseudo-ungerade with respect to inversion. This explains the strict 1PA- and 2PA-specificity of these two states as normally observed in centrosymmetric molecules.

Eq. 1 shows that there are three contributions to the two-photon transition matrix element: The transition dipole moment from the ground state to the 1PA-state, the transition dipole moment from the 1PA-state to the 2PA-state and the denominator which depends on the difference between the energy of the incident photons (which is half the excitation energy of the 2PA-state) and the excitation energy of the 1PA-state. In Table 3 we have listed the characteristics of these relevant states for all molecules considered. These data show that there is a good correlation between the 2PA cross-section and the denominator in Eq. 1, in particular the order of the denominators is the same as the order of the 2PA cross-sections. This indicates that 2PA can be tuned by designing substitution patterns of the pyrrolo[3,2-b]pyrrole backbone that aligns the energy of the 1PA-state as close as possible to half the energy of the 2PA-state.

For our class of molecules, this suggests that a key principle for the design of new chromophores is to lower the excitation energy of the 1PA state. This is well illustrated when comparing the excitation energies for the two molecules with the largest 2PA cross-sections, 6a and 15. The excitation energies of the 2PA-states are nearly the same in both molecules (337 and 334 nm, respectively) whereas the energies of the 1PA states differ more (394 and 405 nm, respectively). This results in a higher denominator and a strong boost of the 2PA cross-sections.

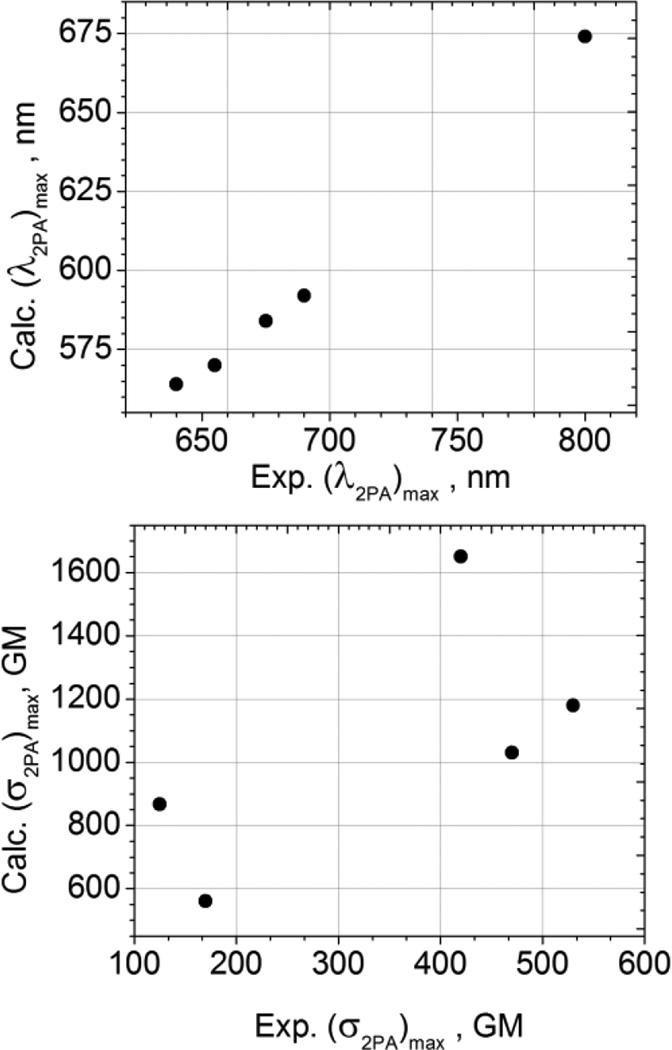
The top panel in Figure 7 shows the correlation between the measured and calculated peak wavelength values of the dominant two-photon allowed transition. Besides a constant ~80–100 nm blue shift, which is typical of most vacuum quantum-chemical calculations, the predicted wavelength maxima are in very good agreement with the observed substituent-dependent behavior, which again confirms the two-photon allowed and one-photon forbidden origin of this transition.

Figure 7.

Correlation between measured and calculated 2PA peak wavelengths (top panel) and peak 2PA cross-sections (bottom panel).

On the other hand, as shown in the bottom panel of Figure 7, the agreement between the calculated and measured peak 2-photon cross-sections is less satisfactory. The calculations tend to overestimate the peak 2PA cross-section values substantially, by a factor of 2–3 or even more. This could be due to the known limitations in the quality of DFT calculations^[27] as well as the lack of solvent effects in our calculations.

Solvatochromism

In addition to our experiments we have carried out calculations on the solvatochromism of molecule 6 in four different solvents: cyclohexane, methylene chloride, acetonitrile and dimethyl sulfoxide. The wavelengths and oscillator strengths obtained from these calculations are listed in Tab. 5. The results of our calculations show the same trend as in the experiment. We note that the oscillator strength of the lowest excited state is about the same in all solvents and just deviates slightly for the vacuum. The difference between the experimental and the calculated excitation wavelength is between 18 and 30 nanometers and the order of the wavelengths is the same as in experiment apart from the pair methylene chloride and acetonitrile. This more or less systematic shift shows the robustness and the reliability of the CAM-B3LYP functional.

Table 5.

Calculated data of solvatochromism of compound 6 in various solvents.

Solvent	Exc. energy [eV]	λexc [nm]	oscilator strength
vacuum	3.147	394	1.352
C6H12	2.925	424	1.579
CH2Cl2	2.775	447	1.608
CH3CN	2.761	449	1.619
DMSO	2.718	457	1.637

Conclusions

We have shown that the centrosymmetric nature of the tetra-, penta- and hexa-substituted pyrrolo[3,2-b]pyrroles leads to HOMO-LUMO+1 and HOMO-LUMO+3 transitions that are the only non-dark state in the two-photon spectra. Moreover, such design based on the presence of various aromatic moieties linked by biaryl linkages leads to the maxima of 2PA cross-section at a strikingly high-energy part of the spectra. Quantum-chemical calculations gave further insight into the excitation behavior of the molecules, where the molecules with the largest 2PA cross-sections being characterized by near-resonance conditions with the 1PA-active lower-energy S₁ state. This gives structural guidelines for the tuning of the two-photon absorption behavior of this class of molecules through changes in the substitution patterns of the parent pyrrolo[3,2-b]pyrrole backbone. The combination of unusually strong donor with very strong acceptor (NO₂) made it possible to break symmetry of the excited state, and in consequence leads to unusually pronounced solvatofluorochromism for this quadrupolar compound. Moreover we have shown that in this very special group of molecules it is possible to obtain compounds possessing near unity values of fluorescence quantum yield. As such, this family of compounds holds great potential for use as active materials in two-photon fluorescence microscopy, two-photon excited polymerization and optical limiting processes.

Experimental Section

Synthesis

All chemicals were used as received unless otherwise noted. All reported ¹H NMR and ¹³C NMR spectra were recorded on 500 MHz spectrometer. Chemical shifts (δ ppm) were determined with TMS as the internal reference; J values are given in Hz. Chromatography was performed on silica (Kieselgel 60, 200–400 mesh). All photophysical studies have been performed with freshly prepared air-equilibrated solutions at room temperature (298 K). Spectral and physical properties of compounds 8–14 have been compared to previously published data.^[10b]

General procedure for the synthesis of TAPPs 6–7

In a 25 ml round-bottom flask equipped with a reflux condenser and magnetic stir bar, 5 mL glacial acetic acid was placed followed by the addition of arylamine (6 mmol), aldehyde (6 mmol) and TsOH (0.6 mmol). The mixture was stirred at 90 °C for 30 minutes. After that time butane-2,3-dione (3 mmol) was slowly added via a syringe and the resulting mixture was stirred at 90 °C for 3 hours. The reaction mixture was then cooled to room temperature. The precipitate of the dye obtained was then filtered off and washed with cooled glacial acetic acid. Recrystallization from AcOEt and drying under vacuum gave the pure product.

2,5-Bis(4-nitrophenyl)-1,4-bis(4-octylphenyl)-1,4-dihydropyrrolo[3,2-b]pyrrole (6)

Red solid; yield 782 mg (36%); m.p. 248–249°C; ¹H NMR (500 MHz, CDCl₃, 25°C, TMS) 8.05 (dd, ³J(H,H) = 9.0 Hz, ⁴J(H,H) = 0.9 Hz, 4H), 7.31 (dd, ³J(H,H) = 9.0 Hz, ⁴J(H,H) = 1.0 Hz, 4H), 7.23 (dd, ³J(H,H) = 8.3 Hz, ⁴J(H,H) = 0.8 Hz, 4H), 7.18 (dd, ³J(H,H) = 8.3 Hz, ⁴J(H,H) = 0.9 Hz, 4H), 6.52 (s, 2H), 2.66 (t, ³J(H,H) = 7.7 Hz, 4H), 1.66 (m, 4H), 1.32 (m, 20H), 0.89 ppm (t, ³J(H,H) = 6.8 Hz, 6H); ¹³C NMR (125 MHz, CDCl₃, 25°C, TMS) δ 145.5, 141.9, 139.6, 136.8, 135.2, 134.1, 129.6, 127.6, 125.3, 123.7, 96.4, 35.5, 31.9, 31.3, 29.4, 29.34, 29.26, 22.7, 14.1 ppm; HRMS (ESI-TOF) m/z calcd for C₄₆H₅₂N₂O₄: 724.3989 [M]⁺; found: 724.3986.

2,5-Bis(4-(trifluoromethyl)phenyl)-1,4-bis(4-methylphenyl)-1,4-dihydropyrrolo[3,2-b]pyrrole (7)

Pale yellow solid; yield 600 mg (35%); m.p. 288–290 °C; ¹H NMR (500 MHz, CDCl₃, 25°C, TMS) δ 7.45 (d, ³J(H,H) = 8.3 Hz, 4H), 7.30 (d, ³J(H,H) = 8.2 Hz, 4H), 7.20 (dd, ³J(H,H) = 8.3 Hz, ⁴J(H,H) = 0.9 Hz, 4H), 7.16 (dd, ³J(H,H) = 8.3 Hz, ⁴J(H,H) = 0.9 Hz, 4H), 6.43 (s, 2H), 2.39 ppm (s, 6H; CH₃); ¹³C NMR (125 MHz, CDCl₃, 25°C, TMS) δ 137.06, 136.97, 136.1, 135.0, 132.7, 130.0, 127.9, 127.8, 127.6, 125.2, 125.1 (quartet), 95.4, 21.0 ppm; HRMS (ESI-TOF) m/z calcd for 574.1844 [M]⁺; found: 574.1820.

Optical measurements

Spectroscopic samples were prepared in 2 mL 1 cm path length quartz cuvettes for both 1PA and 2PA measurements. Cyclohexane (FisherChemicals, UN 1145, HPLC grade, 99.9%) and dichloromethane (OmniSolv, UN 1593, DX 0831-6, 99.96%) were used. Linear absorption measurements were performed with a PerkinElmer UV/VIS/NIR Lambda 950 spectrometer. For relative quantum yield measurements (for the 2PEF measurements) a luminescence PerkinElmer LS 50B spectrometer was used. The sample concentrations used in the 2PEF measurements were ~1 µM, while for the NLT measurements higher concentrations ~ 1–4 mM were required. For samples with high quantum yields (samples 6–9,11–13) the relative 2PA spectra were obtained using the 2PEF method. A Ti:Sapphire femtosecond laser system (Coherent, Libra) operated at 1 kHz repetition rate and producing pulses with duration ~100 fs pumped an optical parametric amplifier (1PA) (Light Conversion, OPerA Solo). The 1PA output wavelength was tuned in the wavelength region 570–900 nm with 2 nm steps. The approximate 1PA pulse spectral width was ~ 15–35 nm. For detection of the fluorescent signal, a grating spectrometer (Jobin-Yvon, Triax 550) combined with a CCD detector (Spectrum One) was used. Bis-diphenylaminostilbene (bDPAS) diluted in dichloromethane was used as the reference standard for the 2PEF measurements.^[32] The fluorescence quantum yields of compounds 10 and 14 were too low for reliable 2PEF measurements, and thus the femtosecond NLT method was used to determine the 2PA cross sections in a range of 570–800 nm.^[33] Briefly, for the NLT measurements, the same laser setup was employed, but the pulse repetition rate was reduced to 100 Hz. The 1PA beam was additionally collimated using a series of apertures and lenses. To detect the change in the transmission, a set of silicon photodetectors (Thorlabs, DET 36A) was employed. Bis-diphenylaminodistirylbenzene (bDPASDSB) diluted in tetrahydrofuran (OmniSolv, UN 2056, TX 0279-1, 99.9%) was used as the reference standard for the NLT measurements.

Calculations

The solvatochromism calculations have been carried out on geometries that have been optimized using the B3LYP^[34] density functional and the TZVP^[35] basis set (using the TURBOMOLE program package^[36]) together with the polarizable continuum model (PCM)^[37] as implemented in the Gaussian program.^[38] The excitation energy and oscillator strength calculations have been carried out using the Dalton program, the CAM-B3LYP density functional,^[39] the aug-cc-pVDZ basis set^[40] and the PCM approach. The corresponding PCM cavities have been constructed using van-der-Waals radii of 1.7 a.u. for carbon, 1.6 a.u. for nitrogen and 1.5 a.u. for oxygen. Hydrogen atoms did not get own van-der-Waals radii but were described together with the carbon atoms they were attached to. For a methyl group the radius was increased to 2 a.u. while for a CH group a radius of 1.8 a.u. was used.

The two-photon absorption calculations were carried out using two different computational approaches: Calculations with the CAM-B3LYP functional^[39] have been carried out using the DALTON program.^[41] Apart from 8 and 9 which have been treated using C₂ symmetry, all molecules were treated in the C₁ point group. For calculations with the PBE0 functional^[42] an open-ended recursive response theory code has been used which has been developed by two of us.^[43,44] In all calculations the aug-cc-pVDZ basis set has been used.^[40] The bromine atoms in 9 have been treated with the aug-cc-pVDZ-PP^[45] basis set and ecp-sdd-DZ effective core potentials to account for scalar relativistic effects. The two-photon absorption cross-sections in GM have been obtained using the following procedure: The two-photon transition moment tensors M which were obtained from the Dalton program are averaged rotationally according to ref. 31.

$$D=\frac{1}{15}\sum (M_{ab}{M}_{bb}+2M_{ab}Mab)$$

The rotationally averaged transition strengths are then converted to Göppert-Mayer units according to^[46]

$${\sigma }^{GM}=\frac{8{\pi }^3\alpha a^5{\omega }^2}{c}g(2\omega ,{\omega }_0,\Gamma )D$$

where α is the fine structure constant, ω is the circular frequency of the incident light, a is the Bohr radius and c is the speed of light. The term g(2ω,ω0,Γ) is a function which accounts for the broadening of the spectral line. Here we use a Lorentzian function which is centered at the excitation energy 2w with a full width of 0.1 eV at half maximum.