Texture Feature Ratios from Relative CBV Maps of Perfusion MRI Are Associated with Patient Survival in Glioblastoma

Abstract

BACKGROUND AND PURPOSE:

Texture analysis has been applied to medical images to assist in tumor tissue classification and characterization. In this study, we obtained textural features from parametric (relative CBV) maps of dynamic susceptibility contrast-enhanced MR images in glioblastoma and assessed their relationship with patient survival.

MATERIALS AND METHODS:

MR perfusion data of 24 patients with glioblastoma from The Cancer Genome Atlas were analyzed in this study. One- and 2D texture feature ratios and kinetic textural features based on relative CBV values in the contrast-enhancing and nonenhancing lesions of the tumor were obtained. Receiver operating characteristic, Kaplan-Meier, and multivariate Cox proportional hazards regression analyses were used to assess the relationship between texture feature ratios and overall survival.

RESULTS:

Several feature ratios are capable of stratifying survival in a statistically significant manner. These feature ratios correspond to homogeneity (P = .008, based on the log-rank test), angular second moment (P = .003), inverse difference moment (P = .013), and entropy (P = .008). Multivariate Cox proportional hazards regression analysis showed that homogeneity, angular second moment, inverse difference moment, and entropy from the contrast-enhancing lesion were significantly associated with overall survival. For the nonenhancing lesion, skewness and variance ratios of relative CBV texture were associated with overall survival in a statistically significant manner. For the kinetic texture analysis, the Haralick correlation feature showed a P value close to .05.

CONCLUSIONS:

Our study revealed that texture feature ratios from contrast-enhancing and nonenhancing lesions and kinetic texture analysis obtained from perfusion parametric maps provide useful information for predicting survival in patients with glioblastoma.

Glioblastoma multiforme (GBM) is one of the most common and aggressive types of malignant brain tumors. The prognosis for patients with GBM remains very poor with median survival rates between 12 and 15 months.^1,2 Several computer-based analyses, including image texture analysis, have been proposed to improve the diagnostic performance of imaging-derived measurements in cancer studies including GBM.³ Image texture analysis measures the local characteristic pattern of image intensity and has been applied to different image-processing domains, such as texture classification and texture segmentation, to identify distinct textural regions in an image.⁴ In recent studies, texture analysis has been applied to medical images to assist in tumor tissue classification and characterization. One study of PET and CT showed that the features for tumor heterogeneity extracted from the normalized gray-level co-occurrence matrix (GLCM) could represent an independent prognostic predictor in patients.⁵ Another texture study in PET/CT suggested that regional and local characterization of the PET tracer heterogeneity in tumors is more powerful than global measurements currently used in clinical practice.⁶ Also, a textural feature study in non-small cell lung cancer showed that baseline fluorine 18 fluorodeoxyglucose (¹⁸F-FDG) PET scan uptake values are associated with nonresponse to chemoradiotherapy.⁷ Recently, a novel method defined, as textural kinetics, was studied with breast dynamic contrast-enhanced MR imaging by Agner et al.⁸ This method attempted to capture spatiotemporal changes in breast lesion texture for classifying malignant and benign lesions.

In this work, we investigated tumor-derived texture feature ratios from relative CBV (rCBV) values (derived from dynamic contrast-enhanced MR imaging) of 2 different tumor regions: the contrast-enhancing lesion (CEL) region and the nonenhancing lesion (NEL) region. We extracted first-order statistics, such as homogeneity, mean, SD, skewness, and kurtosis from the intensity histogram, as well as Haralick texture features obtained from the intensity GLCM.⁹ Subsequently, ratios of these texture features between Laplacian-of-Gaussian (LoG) filtered and unfiltered versions of the rCBV map were also derived. Basically, the Laplacian-of-Gaussian filters are useful for detecting edges in images, and the feature ratio can give us quantitative relations of features between filtered and unfiltered versions of the rCBV map, which would provide an effective normalization to minimize the effects of any potential variations in MR images from different patients.¹⁰ In addition, we obtained textural kinetic features of brain tumor dynamic susceptibility contrast MR imaging data within these CEL/NEL ROIs. The purpose of this study was to determine the association of these DSC-MR imaging textural feature ratios with the overall survival status of GBM.

Materials and Methods

Data

We identified 24 patients with GMB from The Cancer Genome Atlas based on the availability of companion perfusion DSC-MR imaging data in The Cancer Imaging Archive. One of the patients had tumors in both the left occipital region and left frontal region. These 2 tumors are treated distinctly. Previously, these data were assessed for genomic relationships with rCBV values.¹¹ In this study, we performed 1D and 2D texture analysis and kinetic texture analysis of rCBV values within CEL and NEL regions for survival prediction. The clinical data were obtained from the cBioPortal for Cancer Genomics (http://www.cbioportal.org) (Table 1). In addition, a survival class variable was created by dichotomizing the overall survival value at 12 months based on the typical median survival time (∼15 months) in GBM.^2,12

Table 1:

Patient demographics

Age at First Diagnosis (yr) (range) (mean)	Overall Survival (mo) (range) (mean)	Disease-Free Survival (mo) (range) (mean)	Sex	Overall Status
40∼77	3.4∼56.9	2.6∼46.9	17 Males, 7 females	22 Deceased, 2 living
60.0	19.5	10.8

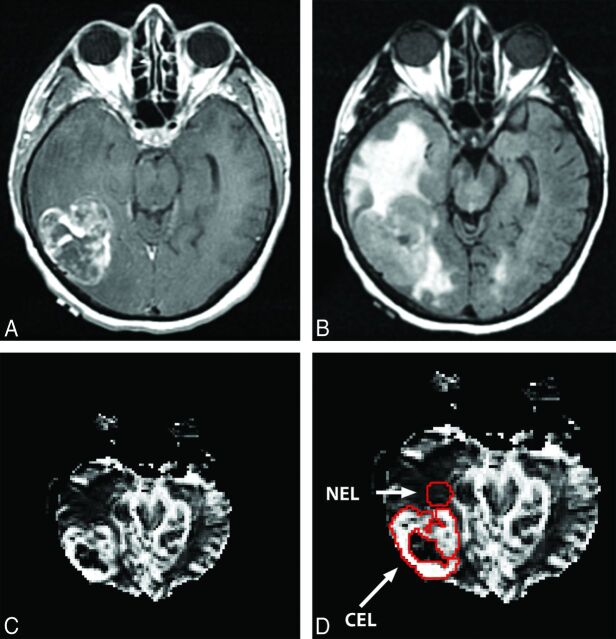
Relative cerebral blood volume values were calculated from ROIs within the CEL, the NEL, and the normal-appearing white matter, respectively, on the basis of rCBV maps obtained previously.¹¹ The methods for this processing are explained in more detail in Jain et al.¹¹ The rCBV intensities for the CEL and NEL were normalized with the mean value of the rCBV intensities for the unaffected normal-appearing white matter region.¹³ The ROIs of the CEL, NEL, and normal-appearing white matter were segmented by experts manually after co-registering rCBV parametric maps with T1 postcontrast and T2 FLAIR images, respectively. The NEL ROIs were placed adjacent to the CEL margin in the white matter within the FLAIR signal-abnormality region. Figure 1 shows an example of an rCBV map from the tumor in a female patient.

Fig 1.

A, T1 postcontrast image. B, T2 FLAIR image. C, rCBV map of the brain in a female patient. D, The CEL and NEL ROIs on the rCBV map.

Image Texture Feature Ratio Computation

Textural feature ratios were computed from the normalized rCBV data in 2 steps. First, we applied a Laplacian-of-Gaussian Equation 1, ∇²G, LoG filter to a normalized rCBV ROI to obtain filtered images.

where σ corresponds to the SD of the LoG filter (here we use a medium level of coarseness, σ = 1.8).^10,14 The filter size chosen is 11 × 11, which was determined from the SD value. The LoG filter derives edge-like features from the local-intensity variations in images. Gray-level co-occurrence matrices were derived from both unfiltered and filtered images. Next, 1D and 2D textural features were computed from the GLCMs of the unfiltered and filtered images.¹⁴ Finally, ratios of filtered texture descriptors to the unfiltered texture descriptors were calculated to yield texture feature ratios.

1D and 2D Texture Features

Image gray-level heterogeneity was quantified by using first-order statistics such as mean, SD, skewness, and kurtosis of the pixel-intensity distribution. Skewness and kurtosis are measures of the asymmetry and peakedness of the distribution, respectively. For the 2D texture features, to quantify the spatial distribution of the pixel values (rCBV values) within the ROI, we derived the GLCMs from the unfiltered and filtered images. The GLCM measures the probability of the occurrence of a specific gray-level value pair as a function of distance and direction. We used 8 gray levels, commonly used in these types of studies¹⁵ with 1 pixel offset to compute the GLCMs from the filtered and original images. We then computed 13 different second-order Haralick statistical measures from the GLCMs.¹⁶ The detailed equations for the second-order texture features are described in the Appendix.

Kinetic Texture

For the kinetic texture analysis, the gadolinium concentration time-series of the DSC perfusion data in both CEL and NEL regions were extracted by using an open-source software package: Quantitative Utility for Assessing TreatmenT RespOnse (https://github.com/rjbosca/QUATTRO).¹⁷ Each ROI voxel from the dynamic perfusion dataset was normalized by the corresponding mean normal-appearing white matter intensity, and all 18 features discussed above were calculated for each time point in the DSC series. Thus, we have 18 kinetic texture features for each perfusion dataset. Each time-series texture feature was then fitted to a third-order polynomial model (Equation 2) to yield 4 coefficients (b₀, b₁, b₂, b₃).

This 4D coefficient vector was then projected to 1D by using metric multidimensional scaling.¹⁶

Statistical Analysis

Eighteen texture feature ratios were obtained and compared between the overall survival groups (>12 or ≤12 months). The predictive accuracy of the CEL and NEL texture feature ratios for survival status was assessed by using the receiver operating characteristic (ROC) curve.

Correlations between 18 texture feature ratios and 18 kinetic texture features with P values were assessed via the Spearman rank correlation, which is a nonparametric measure of statistical dependence between 2 variables. Statistical significance was defined as a P value < .05. The Kruskal-Wallis test, a nonparametric method for testing the equality of population medians among groups, was used to determine whether the median feature value differed significantly between survival groups. Texture feature ratios were assessed with Kaplan-Meier and ROC analyses to measure their associations with overall survival. Each feature ratio was dichotomized on the basis of an optimum cutoff value derived from ROC analysis. Survival difference between the groups was assessed via a log-rank test. Multivariate Cox proportional hazards regression analysis was performed to assess the texture feature ratios as predictors, independent of volume, age, and Karnofsky Performance Status, for overall survival.¹⁸ In this study, MATLAB Version 8.0 (MathWorks, Natick, Massachusetts) and R software (R Project for Statistical Computing, http://www.r-project.org) were used for statistical analyses.

Results

The texture features with and without Laplacian-of-Gaussian filtration were obtained, and the ratios between the Laplacian-of-Gaussian filtered and unfiltered features were calculated for the CEL and NEL regions, respectively. For the CEL, there were strong positive correlations between homogeneity and inverse difference moment (IDM) (r = 0.99, P < .001), and there were strong negative correlations between angular second moment (ASM) and entropy (r = −0.94, P < .001). For the NEL, there were strong positive correlations between the variance and sum average (r = 0.94, P < .001) and between the variance and sum variance (r = 0.95, P < .001) and between the sum average and sum variance (r = 0.99, P < .001). The summaries of the Spearman rank correlations and P values for the CEL and NEL are listed in Tables 2 and 3. Information about the 4 most significant feature ratios, such as homogeneity, ASM, IDM, and entropy for the CEL and skewness, variance, sum average, and sum variance for the NEL, are listed in Tables 4 and 5.

Table 2:

Spearman rank correlation and associated P values from the following feature ratios for the CEL region

	Homogeneity	ASM	IDM	Entropy
Homogeneity	–	0.83 (<.001)	0.99 (<.001)	−0.84 (<.001)
ASM	0.83 (<.001)	–	0.84 (<.001)	−0.94 (<.001)
IDM	0.99 (<.001)	0.84 (<.001)	–	−0.85 (<.001)
Entropy	−0.84 (<.001)	−0.94 (<.001)	−0.85 (<.001)	–

Note:— – indicates not applicable.

Table 3:

The rank correlation and P values within the NEL region

	Skewness	Variance	Sum Average	Sum Variance
Skewness	–	−0.47 (.022)	−0.51 (.010)	−0.52 (.008)
Variance	−0.47 (.022)	–	0.94 (<.001)	0.95 (<.001)
Sum average	−0.51 (.010)	0.94 (<.001)	–	0.99 (<.001)
Sum variance	−0.52 (.008)	0.95 (<.001)	0.99 (<.001)	–

Note:— – indicates not applicable.

Table 4:

Range in texture feature ratios with and without LoG filtration for CEL

	Homogeneity	ASM	IDM	Entropy
LoG/unfiltered	1.08 ± 0.18	1.11 ± 0.74	1.10 ± 0.24	1.02 ± 0.18

^aData are means.

Table 5:

Range in texture feature ratios with and without LoG filtration for NEL

	Skewness	Variance	Sum Average	Sum Variance
LoG/unfiltered	3.57 ± 11.83	2.30 ± 3.77	1.37 ± 0.83	2.84 ± 5.50

^aData are means.

The areas under the ROC curve for each significant predictor of 12-month survival status (survival class) and corresponding P values were assessed and are summarized in Table 6. The areas under the curve for the CEL-derived feature ratios were 0.83 for homogeneity, 0.76 for ASM, 0.81 for IDM, and 0.80 for entropy. The areas under the curve for the NEL-derived feature ratios were 0.80 for skewness, 0.72 for variance, 0.72 for sum average, and 0.71 for sum variance. There was also a significant difference between survival classes for homogeneity (P = .008), ASM (P = .036), IDM (P = .013), and entropy (P = .015) from the CEL. However, no significant difference was found for the NEL-derived texture feature ratios (Tables 7 and 8).

Table 6:

Areas under ROC curves (for prediction of 12-month survival status) from the CEL and NEL texture feature ratios^a

	AUC	95% CI	P Value
CEL
Homogeneity	0.826	0.542–0.986	.003
ASM	0.757	0.500–0.951	.019
IDM	0.806	0.562–0.972	.006
Entropy	0.799	0.556–0.972	.007
NEL
Skewness	0.799	0.549–0.944	.007
Variance	0.715	0.465–0.896	.042
Sum average	0.715	0.465–0.889	.042
Sum variance	0.708	0.438–0.847	.048

Note:—AUC indicates area under the curve.

^aOnly features with statistically significant AUCs are shown.

Table 7:

Kruskal-Wallis test for the CEL texture feature ratios (across survival classes)

	Homogeneity	ASM	IDM	Entropy
P value	.008	.036	.013	.015

Table 8:

Kruskal-Wallis test for the NEL texture feature ratios (across survival classes)

	Skewness	Variance	Sum Average	Sum Variance
P value	.13	.19	.26	.21

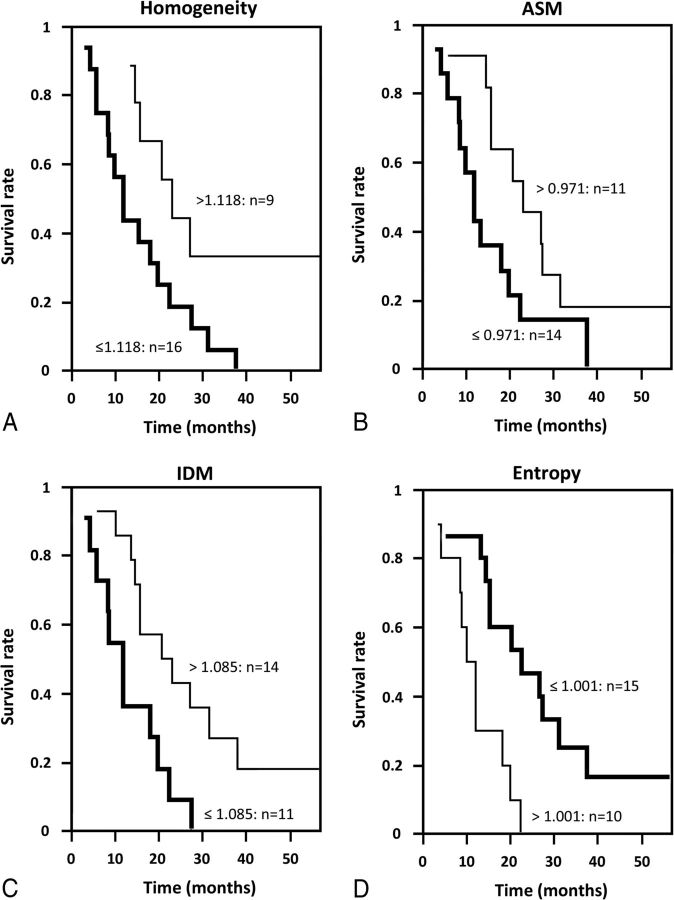
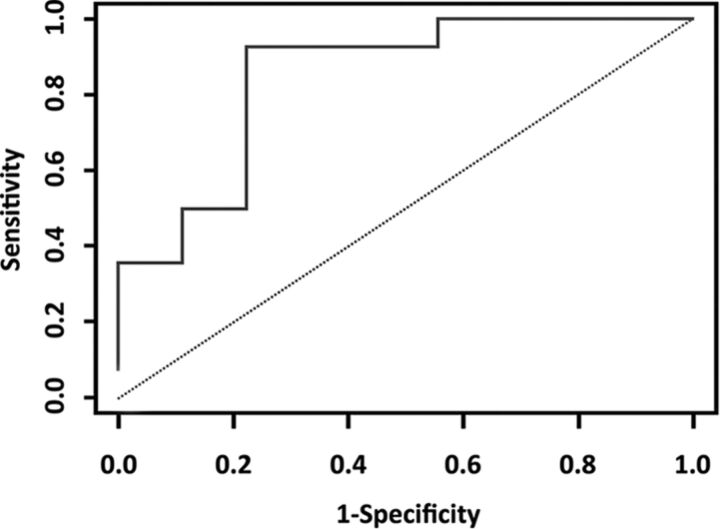
Kaplan-Meier survival curves for groups induced by the ROC-optimized cutoffs for the CEL-derived homogeneity, ASM, IDM, and entropy feature ratios were significantly different (P < .05) (Fig 2). The optimal cutoff points were 1.118 (P = .008) for homogeneity, 0.971 (P = .003) for ASM, 1.085 (P = .013) for IDM, and 1.00 (P = .008) for entropy. The median survival (in months) for each of the groups induced by the cutoff is listed in Table 9 for the CEL. Multivariate Cox proportional hazards regression analysis (including clinical variables such as volume, age, Karnofsky Performance Status) showed that CEL-derived homogeneity, ASM, IDM, and entropy feature ratios had P values of .004, .012, .006, and .001, respectively, indicating that these feature ratios were independent predictors of overall survival. For the NEL, only skewness and variance feature ratios had P values < .05 (Table 10). From the kinetic texture analysis, only the Haralick correlation feature showed a P value close to .05. All other features were not statistically significant (P > .1). Figure 3 shows the ROC curve for the kinetic Haralick correlation feature, with an area under the curve of 0.849 and a P value of .003 (Table 11).

Fig 2.

Kaplan-Meier survival curves from ROC-induced cutoffs for CEL-derived feature ratios: homogeneity (A), ASM (B), IDM (C), and entropy (D).

Table 9:

Kaplan-Meier analysis based on ROCs for the CEL texture feature ratios (only significant features are shown)

	Threshold	Median (mo) (No. of Cases)		P Value
		Above Threshold	Below Threshold
Homogeneity	1.118	23 (9)	12 (16)	.008
ASM	0.971	23 (11)	12 (14)	.003
IDM	1.085	22 (14)	12 (11)	.013
Entropy	1.001	11 (10)	23 (15)	.008

Table 10:

Multivariate Cox proportional hazards regression analysis (in a model that includes volume, age, KPS) for the CEL- and NEL-derived rCBV texture feature ratios

	Hazard Ratio	95% Confidential Interval		P Value
CEL
Homogeneity	0.019	0.001	0.272	.004
ASM	0.121	0.023	0.632	.012
IDM	0.068	0.010	0.457	.006
Entropy	96.895	7.179	1307.8	<.001
NEL
Skewness	0.79	0.638	0.977	.029
Variance	1.507	1.011	2.245	.044
Sum average	2.203	0.996	5.024	.060
Sum variance	1.207	0.929	1.568	.159

Note:—KPS indicates Karnofsky Performance Status.

Fig 3.

ROC curve for prediction of survival status based on correlation features from kinetic texture analysis. The area under the curve value was 0.849 and the 2.5% and 97.5% confidence intervals for the Mann-Whitney statistic were 0.667 and 0.952.

Table 11:

AUC for the correlation feature from kinetic texture analysis

	AUC	P Value	Confidence Interval
			2.5%	97.5%
Mann-Whitney	0.849	.003	0.667	0.952

Note:—AUC indicates area under the curve.

Discussion

Several studies have shown that the hemodynamic parameter rCBV from DSC-MR imaging is an important prognostic imaging biomarker that provides useful prognostic information in patients with GBM.^11,19 Boxerman et al¹³ have shown that the rCBV measurement is significantly correlated with GBM grade and can be used to predict time to progression and clinical outcome. Jain et al²⁰ showed that increased maximum rCBV in CEL is associated with an increased risk of death and that high rCBV in NEL and wild-type epidermal growth factor receptor mutation are associated with poor survival. In our study, we applied texture analysis to the normalized hemodynamic parameter rCBV values from the ROIs of the CEL and NEL in the rCBV map to investigate the association of the perfusion MR imaging–derived image textural feature ratios with overall survival in GBM.

Laplacian-of-Gaussian filter is a precalculated filter obtained from combining the Gaussian and Laplacian filters and is useful for detecting edges in images.¹⁰ The texture feature ratios in our study represent the quantitative relationship of features between the Laplacian-of-Gaussian filtered images and the unfiltered images.¹⁴ In a preliminary study, these feature ratios demonstrated lower dependence on scanner type compared with the original features. The purpose of the use of feature ratios (aside from following previous literature, such as Ganeshan et al²¹) is to minimize the effects of any potential systematic variations in MR images from various patients across different scanning or acquisition protocols. With these texture feature ratios, statistically significant differences were found for CEL-derived homogeneity, ASM, IDM, and entropy feature ratios between survival classes that dichotomized survival at 12 months. This finding implies that these feature ratios are associated with overall survival rates of GBM.

First-order statistics such as SD, skewness, and kurtosis describe the probability distributions of the pixel intensities; and second-order statistics, such as Haralick features, describe the spatial relationship between pairs of pixels. Tumor-derived pixel-based heterogeneity can be measured by using first- and second-order statistics. Many researchers have sought to determine whether such heterogeneity is associated with malignancy.²² Several studies of ¹⁸F-FDG PET/CT have suggested that tumor heterogeneity might provide better prognostic information, tissue characterization, and tumor segmentation.²³

Our results from the Kruskal-Wallis test indicate that the texture feature ratios for homogeneity (P = .008), ASM (P = .036), IDM (P = .013), and entropy (P = .015) from the CEL had a strong correlation with the survival group, suggesting that these texture feature ratios are associated with overall survival and could provide additional prognostic information. In addition, the results of kinetic texture analysis showed that the correlation feature from kinetic texture analysis had a high predictive (area under the curve) value (0.85). Conversely, the texture feature ratios for the NEL exhibited no significant correlation with overall survival.

There were several limitations in our study. First, this was a retrospective study performed on a publicly available patient subset, consisting of data acquired on multiple MR imaging systems with varying protocols. A study that evaluates the robustness of these feature ratios for the survival prediction task across scanning protocols, scanner resolutions, and a larger sample size is essential to establishing their predictive value. A large-sample-size study will also enable the application of appropriate multiple testing corrections to identify reliably predictive features (there is no correction for multiple testing in the current study because of its exploratory nature). In addition, variable treatment regimens with surgery, radiation, and chemotherapy may have a confounding effect on the survival rates of patients. A separate dataset with uniformity of treatment regimens is the next step to validating the predictive value of these feature ratios. Furthermore, incorporating molecular markers like IDH mutation status or molecular subtype can be useful to assess the additional predictive value of imaging-based measurements to existing molecular markers. The inclusion of other modalities or contrasts such as T1 postcontrast or FLAIR MR imaging is a great area for future work as well.

Previous studies have suggested that textural features can be used in several areas of image analysis, such as segmentation, classification, and prediction of tissue abnormality. In this study, we found that several feature ratios obtained from the rCBV map, in addition to kinetic textures, provided useful information for predicting the 12-month survival status from the CEL and NEL regions of patients with GBM.

Conclusions

The methods developed in this work are sufficiently general and might be applicable to other disease processes and sites where perfusion MR imaging is used for assessment of disease or treatment response. Our study presents the results of an exploratory study demonstrating the relationship of texture feature ratios (from 1D and 2D texture features and kinetic texture features) with survival in patients with GBM. These findings suggest that texture feature ratios from perfusion MR imaging data are promising as a clinical prognostic tool.

ABBREVIATIONS:

ASM

angular second moment

CEL

contrast-enhancing lesion

GBM

glioblastoma multiforme

GLCM

gray-level co-occurrence matrix

IDM

inverse difference moment

LoG

Laplacian of Gaussian

NEL

nonenhancing lesion

rCBV

relative CBV

ROC

receiver operating characteristic

Appendix

We provide detailed equations for 2D texture features such as 13 Haralick texture features and homogeneity features in equations A1 to A14.

The angular second moment measures the homogeneity of an image. A more homogeneous image has fewer gray levels with higher pixel elements of the GLCM and sum of square values:

where N_g is the number of gray levels present in an image and p(i, j) corresponds to the (i, j)^th element of the GLCM.

Contrast measures the luminance (differences in gray-level intensity values) present in an image:

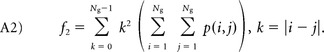Correlation measures the gray-level linear dependence of pixels at specified positions:

Variance differentially weighs the gray levels that significantly deviate from the mean value of p(i, j):

The local homogeneity or inverse difference moment enhances local homogeneous regions by reducing the weight of inhomogeneous regions where i ≠ j:

The sum and difference histograms form the principal axes of the second-order probability attenuation function. The sum average (A6) and variance (A7) quantify the mean and extent of the sum histogram, respectively. The sum entropy (A8) and difference entropy (A11) measure the homogeneity of the sum and difference histograms, respectively.

Sum average:

Sum variance:

Sum entropy:

Entropy quantifies the homogeneity of the image, suggesting that homogeneous regions have lower entropy values:

Difference variance:

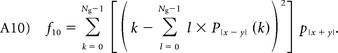Difference entropy:

Information measure of correlation I and II:

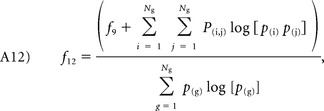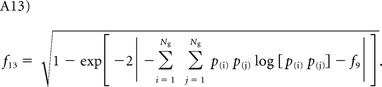In addition to the Haralick texture features, we added a homogeneity feature that measures the closeness of the distribution of elements in the GLCM to the GLCM diagonal.

The definitions for p_{x + y}(k) and p_{|x + y|}(k) are given in Equations A15 and A16, respectively: