On the Use of DSC-MRI for Measuring Vascular Permeability

Abstract

BACKGROUND AND PURPOSE:

Contrast agent extravasation has been shown to confound brain tumor perfusion measurements with DSC–MR imaging, necessitating the use of correction techniques (eg, Weisskoff, Bjornerud). Leakage parameters (K₂ and K_a) postulated to reflect vessel permeability can be extracted from these correction methods; however, the biophysical interpretation of these parameters and their relationship to commonly used MR imaging measures of vascular permeability (eg, contrast agent volume transfer constant, [K^trans]) remain unclear. Given that vascular density, as assessed by blood volume, and vascular permeability, as reflected by K^trans (and potentially K₂ or K_a), report on unique and clinically informative vascular characteristics, there is a compelling interest to simultaneously assess these features.

MATERIALS AND METHODS:

We acquired multiecho DSC–MR imaging data, allowing the simultaneous computation and voxelwise comparison of single- and dual-echo derived measures of K₂, K_a and K^trans in patients with glioma. This acquisition enabled the investigation of competing T1 and T2* leakage effects and TE dependency on these parameters.

RESULTS:

K₂ and K_a displayed nonsignificant (P = .150 and P = .060, respectively) voxelwise linear correlations with K^trans, while a significant (P < .001) inverse relationship was observed between K₂ and K_a (coefficient of determination [r²] = 0.466–0.984). Significantly different (P < .005) mean estimates were found between voxels exhibiting predominately T1 and T2* effects for K₂ and K_a. K^trans, however, was observed to be similar between these voxels (0.109 versus 0.092 minutes⁻¹). Significant differences (P < .001) in extracellular-extravascular volume fraction (v_e) (0.285 versus 0.167) were also observed between cohorts. Additionally, K₂ and K_a were found to have a significant quadratic relationship (P = .031 and P = .005, respectively) with v_e.

CONCLUSIONS:

Estimates of vascular permeability in brain tumors may be simultaneously acquired from multiple-echo DSC–MR imaging via K^trans; however, caution should be used in assuming a similar relationship for K₂ and K_a.

Brain tumors are characterized by abnormal, poorly constructed vasculature that is often permeable,¹ making them identifiable on contrast-enhanced MR images. With dynamic contrast-enhanced (DCE)–MR imaging methods, contrast agent (CA) wash-in and extravasation alter the tissue T1 relaxation time, and kinetic analysis of the associated signal change permits the computation of the CA volume transfer constant (K^trans), which reflects vascular permeability and perfusion. In dynamic susceptibility contrast MR imaging studies, CA flowing through blood vessels decreases tissue T2*, and the acquired signal changes can be used to estimate tumor blood volume. However, CA extravasation has been shown to confound measurements of tissue perfusion (eg, underestimation of blood volume), particularly in high-grade brain tumors.^2–4 When corrected for CA leakage effects, DSC–MR imaging measures of blood volume correlate with brain tumor grade and may be useful for monitoring treatment response.^2,5

CA extravasation leads to simultaneous and competing T1 and T2* effects that can substantially alter the temporal dynamics of DSC–MR imaging signals^2,6 and necessitate the use of correction techniques. One such technique, developed by Weisskoff et al⁷ and Boxerman et al,² incorporates knowledge of the average signal time course across the brain in nonenhancing voxels to model and correct time courses in tumor voxels. As a result, a leakage parameter termed “K₂” can be extracted and reflects the degree of CA extravasation. Although initially developed to correct T1 leakage effects, the Weisskoff method has been adapted to also account for T2* leakage effects.⁸ A known limitation of this method, however, is that it assumes that the mean transit times of both healthy and diseased tissue are equal; this has been observed to not be true in gliomas.⁹ To address this issue, Bjornerud et al¹⁰ recently developed an MTT-insensitive approach for correcting both T1 and T2* leakage effects on DSC–MR imaging signals.¹¹ In this method, the tissue residue function, which describes the CA passage through a voxel, is separated into an intravascular and an extravascular component, from which an apparent transfer constant “K_a” (similar to K₂) can be estimated. A third technique aims to remove T1-based CA leakage effects through the use of multiple gradient-echo acquisitions.^3,12–14 A feature of this approach is that dynamic T1-weighted information can be separated and quantified.^15–17 Traditional pharmacokinetic modeling^18,19 can then be applied to these data to extract a measure of K^trans in a manner similar to that in DCE–MR imaging. This approach has been validated in animal brain tumor models and has been recently applied in patients with high-grade gliomas.^16,17,20 For one to collect both DCE–MR imaging and DSC–MR imaging datasets, an alternative strategy is to acquire traditional DCE–MR imaging data during a preload injection of contrast agent, which is a technique also commonly used to reduce T1 leakage effects in single-echo-based DSC–MR imaging data.³

In the case of brain tumors, K^trans is largely considered to reflect vascular permeability¹⁹ and has demonstrated promise in tumor grading^21,22 and identifying disease progression and treatment response.^23–26 It has been postulated that measures of K₂ and K_a may also directly report on vascular permeability; however, their relationship with imaging biomarkers such as K^trans is not entirely clear and may be dependent on CA kinetics, tissue microstructure, and imaging parameters. Preliminary studies have also investigated the use of K₂ and K_a for assessing tumor type,²⁷ grade,^28,29 and treatment response.¹¹

Inherent to the aforementioned DSC–MR imaging correction techniques, estimates of K₂ and K_a may assume positive or negative values depending on whether T1 (+K₂, −K_a) or T2* (−K₂, +K_a) leakage effects are the dominating source of signal error. Unlike K₂ and K_a, estimates of K^trans assume the use of a “purely” T1-weighted signal and, therefore, presume insensitivity to competing T1 and T2* leakage effects. In this regard, a previous simulation study reported a nonlinear relationship between K_a and K^trans when large flip angles (>70°) were used.¹⁰ In a follow-up in vivo study,¹¹ a positive quadratic relationship between K_a and K^trans was observed. A more recent study found a positive linear correlation between K₂ and K^trans when comparing maximum whole-tumor values across patients.³⁰ These studies, however, were limited to ROI-based estimates and measures of K^trans acquired from separate DCE–MR imaging acquisition and did not take into consideration the dominating CA leakage effect.

As suggested by previous works, the presence of simultaneous T1 and T2* leakage effects within a tumor may influence the magnitude and interpretation of K₂ and K_a. The overarching goal of this study, therefore, was to investigate the contribution of both T1 and T2* effects on K₂ and K_a, while evaluating these parameters as imaging biomarkers of vascular permeability in brain tumors. This goal was achieved through voxelwise comparisons of DSC–MR imaging–derived measures of K₂, K_a, and K^trans using the previously described methods. The multiecho nature of this study allowed simultaneous measurement of these parameters from the same dataset, permitting a more accurate comparison free of registration errors and/or sequence-specific differences. In addition, the multiecho data allowed further exploration of potential TE dependencies of both Weisskoff and Bjornerud correction techniques.

Materials and Methods

MR imaging data were acquired in patients with high-grade gliomas (n = 7, Table 1) under Vanderbilt University Institutional Review Board guidelines at 3T (Achieva; Philips Healthcare, Best, the Netherlands) using a 32-channel head coil. Multiple flip angle data (TR = 7.6 ms, TE = 4.6 ms, flip angle = 2°–20° in 2° increments) were acquired to compute precontrast longitudinal relaxation rate (R₁₀) maps. Dual-echo DSC–MR imaging data were then acquired by using either a dual gradient-echo EPI or spin- and gradient-echo EPI protocol^17,31 with the following parameters: TR = 1.5 seconds (dual gradient-echo) or 1.8 seconds (spin- and gradient-echo), TE₁/TE₂ = 7.0/31.0 ms (dual gradient-echo) or 8.3/25 ms (spin- and gradient-echo), sensitivity encoding = 2, FOV = 240 × 240 mm², reconstructed voxel size = 2.5 × 2.5 × 5.0 mm³, and sections = 15. For spin- and gradient-echo data, only the first 2 echoes were used in the analysis. Measurements were made before, during, and after administration of Gd-DTPA (0.1 mmol/kg, 4-mL/s infusion rate followed by a 20-mL saline flush). The scan duration was 7.5 minutes, including 80 seconds of prebolus baseline data. A high-resolution T1-weighted dataset was collected following the DSC–MR imaging experiment. Dynamic estimates of ΔR₂* were computed for each echo (ΔR_2,TE1* and ΔR_2,TE2*) and for the dual-echo data (ΔR_2,DE*) as previously described.^12,13

Table 1:

Patient demographics

Patient	Age (yr)	Sex	Prior Resection	Pathology	OS (mo)
1	61	Female	Yes	Grade IV glioblastoma	17.9
2	66	Male	Yes	Grade IV glioblastoma	18.2
3	65	Male	Yes	Grade III anaplastic astrocytoma	NA
4	51	Male	Yes	Grade IV glioblastoma	4.3
5	55	Male	No	Grade III oligodendroglioma	13.1
6	40	Male	Yes	Grade IV glioblastoma	11.0
7	42	Female	Yes	Grade IV glioblastoma	NA

Note:—OS indicates overall survival after radiologically confirmed tumor recurrence/progression; NA, not applicable.

K₂ Computation

The method proposed by Weisskoff et al⁷ allows the extraction of K₂ from Equation 1,

where ΔR₂* is the average ΔR₂* from a mask of nonenhancing brain voxels and $\Delta \widetilde{R_2^{*}}$ is the leakage affected estimate of ΔR₂*. A voxelwise least squares fit to Equation 1 was performed to extract K₂ by using 80 seconds of prebolus baseline data and 70 seconds of postbolus data (2.5 minutes total), consistent with previous reports.^2,3,29

K_a Computation

In the presence of CA extravasation, the tissue concentration time course, C_t(t), can be represented as

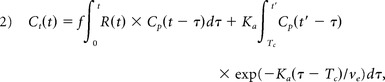where f is proportional to tissue blood flow, R(t) is defined as the tissue-specific residue function, T_c is the capillary transit time of the CA, v_e is the extracellular extravascular volume fraction (v_e), and C_p is the CA concentration in plasma (computed from an arterial input function extracted from the dual-echo data by using an automated selection process^32,33). In DSC–MR imaging, C_t(t) is estimated in relative terms through measurements of ΔR_2,t*(t),¹⁰ where ΔR_2,t*(t)α r₂* × C_t(t) and r₂* is the effective transverse relaxivity. Circular deconvolution of Equation 2 with the arterial input function³⁴ (during the same time course used in the Weisskoff correction) results in a composite residue function H(t) described by an early vascular phase (0 ≤ t < T_c) and an extravasation phase (t ≥ T_c)¹⁰:

In the context of a single-echo DSC–MR imaging acquisition, H(t) ≈ K_a for t ≫ T_c. In this study, K_a was estimated as the mean value from H(t = T_c), where T_c is equal to 1.5 × the mean transit time, to H(t = 60 seconds).

K^trans Computation

To compute an estimate of K^trans from multiecho DSC–MR imaging data, a T1-weighted signal time course [S_T1w(t)] was first extracted from dual-echo data via Equation 4.^15,16,35

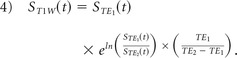A R₁₀ map was combined with the S_T1w(t) data to produce dynamic longitudinal relaxation rate time courses [R_1t(t)] for each voxel.^36,37 K^trans and v_e were estimated by fitting R_1t(t) and C_p(t) (arterial input function) with the standard Tofts model.^18,19

Voxel Selection

Voxels selected for this analysis were obtained from enhancing regions on the postgadolinium (Gd) T1-weighted images, determined using a 50% signal threshold (based on the maximum signal intensity in tumor-containing sections) over a manually drawn tumor ROI. These voxels were further categorized by the predominate leakage effect (T1 or T2*) exhibited in their dynamic ΔR₂* time course. In this study, “T2* voxels” were defined by a positive mean ΔR₂* during the last 20 seconds of the time course used for computation of K_a and K₂. “T1 voxels” were defined as those in which this estimate was negative.

Statistical Analysis

Voxelwise measures of K₂ and K_a were compared with K^trans and v_e to examine the relationship between these parameters. Associations between the aforementioned parameters were first analyzed on an individual basis by using simple linear regression and reported using the r² statistic (coefficient of determination). Unless otherwise noted, group voxelwise comparisons were conducted using analysis of covariance in a generalized linear model for repeated measures. Generalized estimating equations were used with an exchangeable covariance structure to model the correlation among voxels across patients.

Results

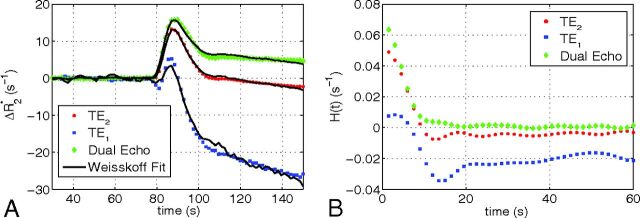
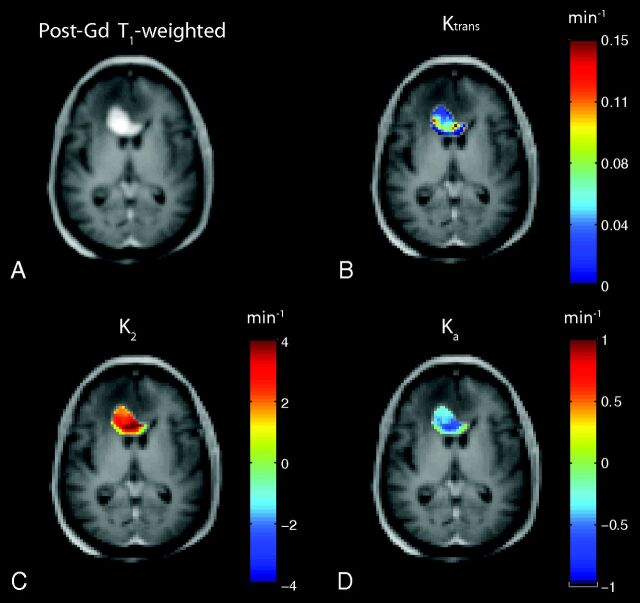
Figure 1A shows a representative uncorrected tumor ΔR₂* time course for each TE and the dual-echo signal, along with the associated Weisskoff model fit. Figure 1B shows the corresponding tissue residue functions used to compute K_a from the same patient. The computed K^trans, K₂, and K_a maps (overlaid on post-Gd T1-weighted images) for this patient (at TE₂) can be seen in Fig 2B–D, respectively, along with the corresponding post-Gd T1-weighted image (Fig 2A). Figure 3A, -B shows a sample voxelwise comparison of K₂ and K_a (computed at TE₂) with the parameter K^trans. The range of correlations at TE₂ were r² = 0.014–0.430 for K₂ and r² = 0.0001–0.403 for K_a. Across patients, both K₂ and K_a were found to have nonsignificant (P = .150 and P = .060, respectively) linear correlations with K^trans. A significant (P < .001) inverse relationship was observed (Fig 3C), however, between K₂ and K_a (r² = 0.466–0.984). To help elucidate these observed relationships, further analysis was performed.

Fig 1.

A, Representative uncorrected tumor ΔR₂* time course and the associated Weisskoff model fit (solid) used to compute K₂ at TE₁ (square), TE₂ (dot), and dual-echo (diamond). B, Corresponding tissue residue functions used to compute K_a at TE₁, TE₂, and dual-echo.

Fig 2.

A, T1-weighted post-Gd anatomic image showing a high-grade brain tumor. Sample computed permeability maps (units in minute⁻¹), K^trans (B), K₂ (C), and K_a (D).

Fig 3.

A, Sample voxelwise comparison between K₂ at TE₂ and K^trans. B, Sample voxelwise comparison between K_a at TE₂ and K^trans. C, Voxelwise comparison between K₂ (y-axis) and K_a (x-axis). Linear regression line shown in black.

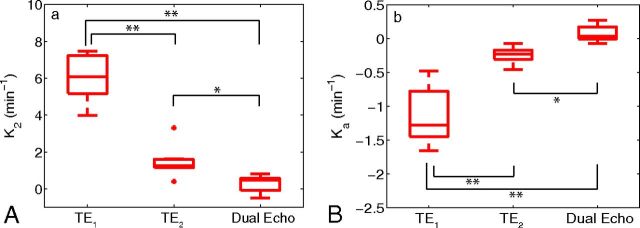
With the availability of multiecho data, the effect of TE on K₂ and K_a was investigated. Figure 4 shows boxplots using the median values of K₂ and K_a across all patients. A statistically significant difference (Mann-Whitney U test) was observed between K₂ at TE₁ and TE₂ (P < .001), K₂ at TE₁ and dual-echo (P < .001), and K₂ at TE₂ and dual-echo (P < .01) acquisitions. Similar differences were observed for K_a. For TE₂, voxelwise estimates of K₂ were observed to be predominately positive for high-grade gliomas, whereas K_a was predominately negative. A decrease in TE₁ resulted in a broader voxelwise distribution of values across patients, with estimates of K₂ becoming increasingly positive and K_a becoming increasingly negative. The computation of K₂ using the ΔR_2,DE* time course resulted in a negative shift in the distribution of values, with an increase in the number of voxels near K₂ = 0. A similar shift in the distribution toward positive values was observed for K_a.

Fig 4.

Boxplots of median parameter estimates (from all patients) calculated at various TEs for K₂ (A) and K_a (B). Boxplots display the median, 25th, and 75th percentiles (edges of box) and extreme data points (whiskers). Outliers are plotted individually (plus sign). Significance was determined by the Mann-Whitney U test. * indicates P < .01; **, P < .001. Note: Positive outlier for K₂ at TE₁ not pictured.

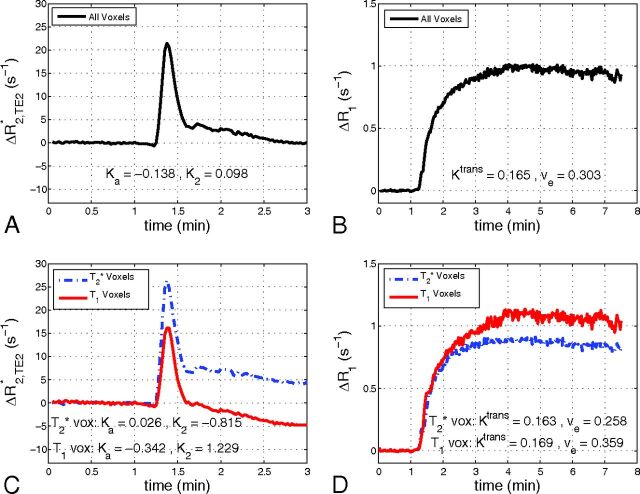
Figure 5 shows the contribution of both T1 and T2* leakage effects on the relaxation rate time courses. Figure 5A shows the mean ΔR₂* time course (TE₂) for a tumor ROI from patient 2. The resulting ΔR₁ time course from the same tumor can be seen in Fig 5B. Although the ΔR₂* time course appears to show no appreciable signs of CA leakage, the ΔR₁ time course exhibits large changes in R₁ with bolus passage. This indicates CA extravasation and results in a moderate estimate of K^trans. Similarly, focusing on the smallest 10% of all voxels (based on the magnitude of K_a) in a given patient results in K_a = −0.043 ± 0.050 minutes⁻¹, K₂ = 0.113 ± 0.553 minutes⁻¹, and K^trans = 0.060 ± 0.099 minutes⁻¹ (weighted mean ± pooled standard deviation). Figure 5C, -D shows mean ΔR₂* and ΔR₁ time courses from the same tumor with voxels separated by predominate T1 or T2* leakage effects. Note that in Fig 5C, -D, voxels from the same tumor exhibited positive and negative values of K₂ and K_a, while K^trans was observed to be almost identical between the 2 cohorts.

Fig 5.

Sample mean ΔR₂* time course (TE = 31 ms) for a tumor ROI (A) and the resulting ΔR₁ time course (B). Mean ΔR₂* (C) and ΔR₁ (D) time courses from the same tumor with voxels separated by whether they predominately exhibit T2* leakage effects (T2* voxels) or T1 leakage effects (T1 voxels).

Table 2 displays the mean estimates of K₂, K_a, and K^trans (separated by T1 and T2* voxels) across all patients. On average, 63% of voxels in the high-grade gliomas were found to predominately exhibit T1 leakage effects. In addition, a significant difference (P < .005, paired t test) was observed across patients between mean estimates from T1 and T2* voxel cohorts for both K₂ and K_a. While the difference between T1 and T2* cohorts for K^trans trended toward significance (P ≈ .05), the weighted mean for each cohort across patients was similar (0.109 minutes⁻¹ versus 0.092 minutes⁻¹). In all voxels across patients, we observed v_e = 0.241 ± 0.207. When separated by leakage effect, a significant difference (P < .001, paired t test) in mean estimates of v_e was also observed. Additionally, both K₂ and K_a were found to have a significant quadratic relationship (P = .031 and P = .005, respectively) with v_e.

Table 2:

Patient-specific estimates of DSC-MRI and DCE-MRI parameters separated by the predominant leakage effect

Patient No.	No. of Voxels (%)		K2 (min−1)		Ka (min−1)		Ktrans (min−1)		ve
	T1	T2*	T1	T2*	T1	T2*	T1	T2*	T1	T2*
1	44 (79%)	12 (21%)	1.807	1.205	−0.373	−0.250	0.223	0.066	0.221	0.072
2	214 (45%)	265 (55%)	1.229	−0.815	−0.342	0.026	0.169	0.163	0.359	0.258
3	126 (61%)	79 (39%)	2.374	0.822	−0.372	−0.117	0.089	0.038	0.328	0.150
4	368 (47%)	417 (53%)	1.767	0.700	−0.536	−0.469	0.104	0.078	0.228	0.140
5	187 (56%)	147 (44%)	1.975	0.787	−0.149	−0.025	0.069	0.044	0.284	0.107
6	734 (93%)	52 (7%)	3.726	0.240	−0.256	0.004	0.099	0.050	0.290	0.138
7	16 (64%)	9 (36%)	2.591	0.025	−0.418	0.024	0.200	0.179	0.203	0.107
Meanw			2.627	0.289	−0.329	−0.208	0.109	0.092	0.285	0.167

Note:—Mean_w indicates weighted mean.

Discussion

DCE–MR imaging estimates of vascular permeability, often reported via K^trans, have been shown to be helpful in deciphering brain tumor grade²¹ and in predicting disease prognosis.^25,38 Unlike DCE–MR imaging, DSC–MR imaging acquisitions can actually be confounded by the increased vascular permeability present in brain tumors, requiring strategies for leakage correction of the MR imaging signal time courses. Rate constants (K₂ and K_a) computed from these correction techniques have been suggested to reflect vessel permeability.^7,28 To evaluate this relationship, we performed a simultaneous comparison between K^trans and the parameters K₂ and K_a using multiecho DSC–MR imaging. In general, the range of K₂ and K_a estimates in this study was observed to be larger than that of K^trans, though they were consistent with previous measures in brain tumors.^8,10,28 Voxelwise linear relationships between K₂ and K_a and the parameter K^trans were found to be nonsignificant when computed from the same dataset. Although a nonlinear relationship between K_a and K^trans was previously presented in simulations,¹⁰ this work provides additional in vivo confirmation. The individual correlations observed here between K₂ and K^trans in gliomas were similar to those observed by Bonekamp et al³⁰ using maximum K^trans and K₂ values from whole-tumor ROIs. Although the lack of a strong linear correlation with K^trans suggests potential limitations with extracting permeability estimates from DSC–MR imaging correction methods themselves, it should not, however, be interpreted as a failure of these techniques to reliably correct CBV measures for CA leakage.

The effect of TE on K₂ and K_a was also studied. From Fig 4, we observed a significant increase (decrease) in estimates of K₂ (K_a) with a shorter TE. This is due, in part, to the decrease in T2* weighting with decreasing TE and subsequent dominance of T1 leakage effects. Liu et al⁸ previously explored the effect of TE on K₂ in numeric simulations and noted that changes in the actual vascular permeability should not affect the polarity of K₂, though changes in imaging parameters (eg, TE) could. Before the current study, a similar analysis with K_a had not yet been performed, to our knowledge.

In addition to TE, the intrinsic presence of competing and simultaneous T1 and T2* leakage effects, within a given voxel, were integral in determining the value of K₂ and K_a. As shown in Fig 5, competing T1 and T2* leakage effects can produce a ΔR₂* time course that paradoxically appears to be free of CA extravasation effects. This is misleading because the dynamic ΔR₁ information reveals appreciable CA leakage, resulting in moderate estimates of K^trans. As noted by Bjornerud et al,¹⁰ the presence of both T1 and T2* relaxation effects in the extracellular extravascular space may drive K_a (and K₂) toward zero, resulting in artifactually low estimates. As an example, in the smallest 10% of all voxels (based on the magnitude of K_a), the mean K^trans was observed to be 50% larger than |K_a|. Conversely, the magnitude of the mean K_a was ≈3× larger than K^trans when computed using all voxels. Additionally, the mean value of K₂ and K_a, computed from the aforementioned subset of voxels (smallest 10%), was almost an order of magnitude smaller than the respective mean K₂ and K_a computed using all voxels. These findings clearly have implications for the reliability of these parameters as measures of vascular permeability.

In general, the relationship of K₂ and K_a with K^trans may indicate an inaccurate assumption that these parameters solely reflect vessel permeability in brain tumors. When separated into T1 and T2* voxel cohorts, the mean values of K₂ and K_a across patients were found to be significantly different from one another (Table 2). The same was true for v_e. Similar to the previous observation between K_a and K^trans in vivo,¹¹ a significant quadratic relationship was observed between K₂ and K_a and v_e across all patients. To this end, a recent theoretic study by Liu et al³⁹ demonstrated a potential relationship between v_e and the ratio of the parameters K₁ and K₂ from the Weisskoff correction method. These results indicate that K₂ and K_a may also be influenced by the extravasation space of the CA.

The data in Table 2 also revealed that T1 voxels demonstrated larger v_e values than those found in T2* voxels. This result likely originates from the underlying biophysical basis of T1 and T2* leakage effects. As in DCE–MR imaging, T1 leakage effects result from the direct interaction of CA with the extracellular extravascular water. Accordingly, the physiologic factors that drive the tissue CA concentration (compartmental volume fractions, perfusion, and vascular permeability) and physical properties (CA T1 relaxivity, precontrast T1) and pulse sequence parameters (TR, flip angle) all influence the shape and magnitude of T1 leakage effects on DSC–MR imaging signals. In addition to physiologic factors and imaging parameters, T2* leakage effects are influenced by intravoxel susceptibility differences created by the spatial distribution of the CA within a voxel. Recently, Semmineh et al⁴⁰ demonstrated that these effects are predominantly influenced by cellular properties, including density, size, distribution, and shape. Consistent with the results presented herein, stronger T2* leakage effects were observed for tissues with higher cell density (or lower v_e). In general, the dependency of T2* leakage effects on tumor cellularity manifests as changes in the effective T2* relaxivity of the CA. So unlike T1 leakage effects, where the T1 relaxivity of the CA is essentially constant within and across tumors, the T2* relaxivity may vary from voxel to voxel as the cellular properties change.⁴¹

The variable CA T2* relaxivity also has important implications for the interpretation of the extracted K₂ and K_a parameters. Although voxels were designated as predominantly exhibiting either T1 or T2* leakage effects, the signal of each voxel is the summation of these competing effects, as previously discussed. In the limiting case in which T2* leakage effects are absent and the signals only reflect T1 leakage effects, the K₂ and K_a parameters are primarily driven by the underlying CA kinetics and the assumptions built into the correction models and can be understood accordingly. However, when there are competing T1 and T2* effects, K₂ and K_a represent a complex balance between the CA kinetics and the tissue microstructure. Practically, this implies that a positive and negative estimate of K₂ or K_a of the same absolute value may not reflect the same combination of vascular permeability, tissue compartment size, or microstructural geometry. Similarly, K₂ and K_a values that are equivalent within or across tumors may not reflect the same underlying physiologic environment because they could originate from unique combinations of competing T1 and T2* effects. This observation may help further explain the discrepancies in using K₂ and K_a to evaluate tumor grade and to assess treatment response.^11,28,29 Computational studies that account for the underlying biophysical basis of the DSC–MR imaging signal could be used to systematically investigate and provide insight into the complex interaction between T1 and T2* leakage effects and the derived K₂ and K_a values.

The use of multiecho DSC–MR imaging in this study enabled measures of DCE–MR imaging signals and, subsequently, computation of the associated K^trans maps. As mentioned above, an alternative approach to collect both datasets in the same examination is to acquire DCE–MR imaging data during a preload of CA. This step enables the use of traditional DCE–MR imaging pulse sequences, ones that typically have higher spatial (and lower temporal) resolution. For the purpose of the study, this approach would have enabled the comparison of more conventionally derived K^trans values with K₂ and K_a. However, the addition of a preload to this study would have reduced T1 leakage effects and increased T2* leakage effects. It is unclear how this change would influence the correlation among K^trans, K₂, and K_a. Another limitation of this study is the small sample size. While the findings are likely to hold in a larger population of patients with gliomas, it would be valuable to expand the tumor types considered (eg, primary central nervous system lymphoma and brain metastasis) as different histologic subtypes have been shown to express varying degrees of T1 and T2* leakage effects.

Conclusions

This study investigated the use of DSC–MR imaging for estimating vascular permeability in brain tumors. Implementation of common DSC–MR imaging leakage-correction techniques afforded the computation of rate constants (K₂ and K_a) postulated to report on vessel permeability. Additionally, the acquisition of multiecho data allowed the computation of the DCE–MR imaging pharmacokinetic parameter K^trans. A voxelwise comparison among the parameters K₂, K_a, and K^trans revealed nonsignificant linear correlations that may be attributed, in part, to competing T1 and T2* leakage effects and the effect of TE on K₂ and K_a. Further investigation also revealed a significant quadratic relationship between K₂ and K_a and the DCE–MR imaging parameter v_e. On the basis of these findings, caution should be used in assuming a direct relationship between K₂ and K_a and vascular permeability in brain tumors. Furthermore, the acquisition of K^trans from multiecho DSC–MR imaging data may provide a convenient method for simultaneously measuring vascular permeability and perfusion in brain tumors.

ABBREVIATIONS:

CA

contrast agent

DCE

dynamic contrast-enhanced

Gd

gadolinium

K_a

apparent transfer constant

K₂

leakage parameter

K^trans

volume transfer constant

R₁

longitudinal relaxation rate

R₂

transverse relaxation rate

v_e

extracellular extravascular volume fraction

R₂*

effective transverse relaxation rate