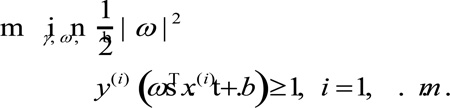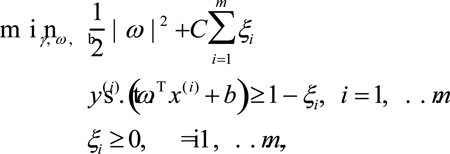Highly Predictive Support Vector Machine (SVM) Models for Anthrax Toxin Lethal Factor (LF) Inhibitors

Abstract

Anthrax is a highly lethal, acute infectious disease caused by the rod-shaped, Gram-positive bacterium Bacillus anthracis. The anthrax toxin lethal factor (LF), a zinc metalloprotease secreted by the bacilli, plays a key role in anthrax pathogenesis and is chiefly responsible for anthrax-related toxemia and host death, partly via inactivation of mitogen-activated protein kinase kinase (MAPKK) enzymes and consequent disruption of key cellular signaling pathways. Antibiotics such as fluoroquinolones are capable of clearing the bacilli but have no effect on LF-mediated toxemia; LF itself therefore remains the preferred target for toxin inactivation. However, currently no LF inhibitor is available on the market as a therapeutic, partly due to the insufficiency of existing LF inhibitor scaffolds in terms of efficacy, selectivity, and toxicity. In the current work, we present novel support vector machine (SVM) models with high prediction accuracy that are designed to rapidly identify potential novel, structurally diverse LF inhibitor chemical matter from compound libraries. These SVM models were trained and validated using 508 compounds with published LF biological activity data and 847 inactive compounds deposited in the Pub Chem BioAssay database. One model, M1, demonstrated particularly favorable selectivity toward highly active compounds by correctly predicting 39 (95.12%) out of 41 nanomolar-level LF inhibitors, 46 (93.88%) out of 49 inactives, and 844 (99.65%) out of 847 Pub Chem inactives in external, unbiased test sets. These models are expected to facilitate the prediction of LF inhibitory activity for existing molecules, as well as identification of novel potential LF inhibitors from large datasets.

Graphical abstract

1. Introduction

Anthrax is an acute, often fatal infectious disease caused by the rod-shaped, spore-forming bacterium Bacillus anthracis. Primarily a zoonotic disease affecting livestock and wild animals, anthrax has more recently emerged as a lethal bioterror agent, with the inhalational form posing a particular threat to society. Anthrax-related toxicity has been attributed primarily to its plasmid-encoded, secreted exotoxin comprising the lethal factor (LF), the edema factor (EF, a calmodulin-activated adenylate cyclase), and the protective antigen (PA).[1] LF, a zinc-dependent hydrolase, joins with PA to form the anthrax lethal toxin, which is chiefly responsible for cytotoxicity and eventual host death associated with anthrax pathogenesis.[2] The protective antigen delivers LF into the cytoplasm of host cells, where LF cleaves and inactivates mitogen-activated protein kinase kinases (MAPKKs), thereby interfering with signaling processes that are essential for cell function and survival, most notably involving the immune response.[3–5] Antibiotics such as fluoroquinolones are capable of eradicating the bacilli, however, host death from residual toxemia can occur even after B. anthracis is cleared from the system, and there is currently no extant therapeutic modality to directly combat LF-mediated cytotoxicity.[6, 7]

As Bacillus anthracis continues to pose a significant threat as a biological weapon, various experimental and computational efforts have been focused on identifying small-molecule LF inhibitors as potential drugs as adjunct therapeutics with antibiotics.[4, 8–33] Previous computational modeling efforts have been primarily directed toward structure-based virtual screening, pharmacophore mapping, and 3D-QSAR model development.[28–33] While these studies have been useful for the prediction of LF inhibitory activity and the identification of common molecular features in LF inhibitors, compounds addressed in these studies have chiefly been limited to one or two structural classes. Studies have demonstrated that models built on a structurally similar set of compounds occupying closely adjacent areas of chemical space are likely to have limited applicability in terms of identifying novel inhibitor classes, and thus may result in unreliable predictions when used in virtual screening of structurally diverse chemical databases.[34, 35]

With the goal of overcoming this roadblock, in the current work we have assembled a diverse set of active and inactive LF inhibitors collected from the literature, to develop novel support vector machine (SVM) models that can be used to accurately identify new compounds (or compounds based on novel scaffolds) that may exhibit favorable LF inhibitory activity. The SVM method has consistently demonstrated robust predictivity in lead identification and optimization, and has also proven useful in the prediction of drug metabolism, blood-brain barrier penetration, p-glycoprotein substrates, oral absorption, and the efficacy of various enzyme inhibitor therapeutics.[36] The SVM models we report here have been rigorously validated using 10-fold cross-validation, and they have demonstrated quite favorable accuracy in predicting biological activities of external, unbiased test set compounds. Specifically, as discussed below, a particularly efficacious model using MOE (Chemical Computing Group, Inc.) descriptors successfully identified 39 (95.12%) of 41 nanomolar-level LF inhibitors, while rejecting 46 (93.88%) of 49 inactives and 844 (99.65%) of 847 inactives in a series of compound set evaluations. We found that these validation and testing results support the application of our SVM models as screening tools for identifying potentially potent LF inhibitors.

2. Methodology

2.1 Data Sets

Compound structures and biological activities for 546 LF inhibitors of varying potency (database DB) were collected from the literature as described in our previously published work.[37] A total of 102 compounds with LF IC₅₀ or Ki values less than 1 µM were considered to be active LF inhibitors. These displayed high structural diversity and included sulfonamide hydroxamates, rhodanine-based derivatives, guanidinylated 2,5-dideoxystreptamine derivatives, guanidinylated derivatives of neamine, aniline, and γ-ether, an N-sulfonylated phenylfuran derivative, and an N-hydroxyhexanamide analog, among other scaffold types. 122 compounds with specified IC₅₀ or Ki values larger than 100 µM, or nonspecified IC₅₀ or Ki values larger than 40 µM, were considered to be inactive. Taken together, these 224 compounds (subset database DBA) were used for SVM model development and validation. From among the remaining 320 compounds in DB, 284 compounds (subset database DBB) with IC₅₀ or Ki values ranging from 1 µM to 40 µM were treated as weakly active compounds and were set aside for model validation. In addition to DB, 847 inactive compounds from two recently reported high-throughput screening experiments deposited on Pubchem BioAssay (AID: 602142 and 602326) were used as an external validation set and were termed database DBC. Although 13 compounds in DBC were reported to be active, they lacked specific IC₅₀ values and were therefore not included in the validation set.

2.2 Computational Methods

2.2.1 3D Structure Generation

Three-dimensional conformations of all dataset structures were generated via geometry optimization by energy minimization in Pipeline Pilot, and were further geometry optimized in MOE 2011.10 (Chemical Computing Group, Inc.) using the MMFF94s force field with a convergence criterion of 0.01 kcal/mol•Å.[38]

2.2.2 Molecular Descriptor Calculation

2.2.2.1 MOE Descriptors

Molecular descriptors were used in this study to quantitatively represent structural and physicochemical properties of compounds. A total of 334 2D and 3D molecular descriptors were calculated using MOE 2011.10.[39] These included subdivided surface areas, atom counts and bond counts, Kier & Hall connectivity and Kappa Shape indices, and physical property-related, adjacency and distance matrix, pharmacophore feature, partial charge, potential energy, MOPAC, surface area, volume and shape, and conformation-dependent charge descriptors. Any descriptors with missing values were eliminated, resulting in a final set of 313 descriptors.

2.2.2.2 Schrödinger Descriptors

We incorporated a total of 292 topological, MOPAC, and ADME-tox related descriptors (relevant to potential therapeutic design and optimization) from Schrödinger, Inc., using Maestro 9.3.[40]

2.2.2.3 ISIDA Fragment Descriptors

The Online Chemical Modeling Environment was used to calculate a series of ISIDA 2D fragment descriptors.[41] Descriptors with low variance (less than 0.01) or with fewer than two unique values were removed. Also, if the correlation coefficient between two descriptors was larger than 0.95, one descriptor was eliminated. A total of 748 ISIDA fragment descriptors were utilized in this work.

2.2.3 SVM Modeling Approaches

2.2.3.1 Data Set Division for Model Development and Validation

Database DBA was randomly split into a training set (Train1) of 134 compounds (61 actives and 73 inactives, 60% of DBA) and an external test set (Test1) of 90 compounds (41 actives and 49 inactives, 40% of DBA). In addition, in order to assess the ability of the resulting SVM models to classify compounds that are structurally dissimilar to the training set, active and inactive DBA compounds were clustered based on ECFP_4 descriptors in Pipeline Pilot 8.0 (Accelrys, Inc.). One cluster containing 44 actives and one cluster containing 51 inactives were extracted from DBA as an external test set (Test2). The remaining structures in DBA were retained as a training set (Train2), in order to ensure that Test2 compounds would be structurally dissimilar to those in Train2.

2.2.3.2 Support Vector Machine (SVM)

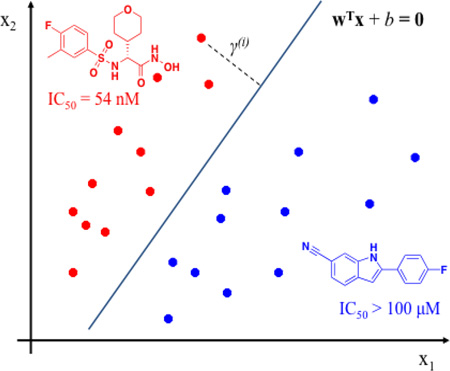
SVM is a popular and effective classification algorithm in which data points (in this case, inhibitor compounds) are mapped onto descriptor-based feature space, and a decision boundary (expressed as ω^Tx+b = 0) is identified using support vectors to separate compounds into two categories (actives and inactives) by the widest gap (margin) via a hyperplane. Support vectors often constitute a small portion of examples in the training set, allowing an SVM model to be less prone to overfitting while maintaining generalizability.[42]

Specifically, for an input set of pairs (x⁽ⁱ⁾, y⁽ⁱ⁾), i = 1, …, m, x⁽ⁱ⁾ ∈ R^P (P is defined as the dimension of the input space), y⁽ⁱ⁾ ∈ {− 1, 1}, presenting the classes of an sample x⁽ⁱ⁾, the following optimization can be formulated:

However, sometimes the data may not be easily separable. Also, where outliers exist, finding a separating hyperplane may not offer the best solution to a problem. In order for the algorithm to function for non-separable data and exhibit less sensitivity to outliers, the optimization problem can be formulated with regularization terms:

where a cost Cξ_i will be incurred for a mislabeled example.[43] The parameter C determines the relative weighting between the objectives of minimizing ‖ω‖² and maximizing correct prediction, which is essentially a trade-off between a large margin and a small classification error penalty. The optimization problem can subsequently be solved using Lagrangian multipliers.

In this study, all SVM models were built and optimized using the open source package RapidMiner.[44] The Gaussian Radial Basis Function was incorporated as the kernel type:

$$\mathrm{k}(x^{\mathit{(}i\mathit{)}},x^{\mathit{(}j\mathit{)}})=\text{exp}{(-\gamma \Vert x^{\mathit{(}i\mathit{)}}-x^{\mathit{(}j\mathit{)}}\Vert )}^2$$

Parameters C and γ were optimized by maximizing the prediction accuracy in a 10-fold cross validation of the training data. Accuracy, sensitivity (true positive rate), and specificity (true negative rate) were utilized to evaluate the predictive power of the models against the external test sets.

3. Results and Discussion

3.1 Performance of Models

Table 1 illustrates the predictive performance of the SVM models based on training set Train1, by means of 10-fold cross-validation using MOE, Schrödinger, and ISIDA descriptors. The combination of C = 5.0 and γ = 0.1 yielded the model M1 with the best cross-validated accuracy of 95.44% for Train1 using MOE descriptors. M1 was highly predictive for blind test sets: a total of 39 (95.12%) of 41 actives with IC₅₀ or Ki values less than 1 µM in Test1 were accurately classified. Only 3 (6.12%) out of 49 inactives in Test1 and 3 (0.35%) out of 847 inactives in DBC were incorrectly predicted as active. Note that M1 is less efficient in terms of identifying weak actives in DBB as active compounds, most likely because the biological activity values of DBB compounds fall between those of the actives and inactives in our training set.

Table 1.

Classification Performance of SVM Models Developed Based on Dataset Train1 with Various Descriptor Sets

	MOE	Schrödinger	ISIDA fragments
10-fold cross-validation (61 actives and 73 inactives)
Parameters	C = 5 γ = 0.1	C = 20 γ = 0.1	C = 40 γ = 0.1
Accuracy	95.44%	95.44%	91.65%
Sensitivity	96.72%	95.08%	88.52%
Specificity	94.52%	95.89%	94.52%
Prediction on external test set Test1 (41 actives and 49 inactives)
Accuracy	94.44%	90.00%	91.11%
Sensitivity	95.12%	87.80%	87.80%
Specificity	93.88%	91.84%	93.88%
Prediction on external test set DBB (284 weak actives)
Accuracy	18.31%	17.61%	22.18%
Prediction on external test set DBC (847 inactives)
Accuracy	99.65%	99.29%	96.81%

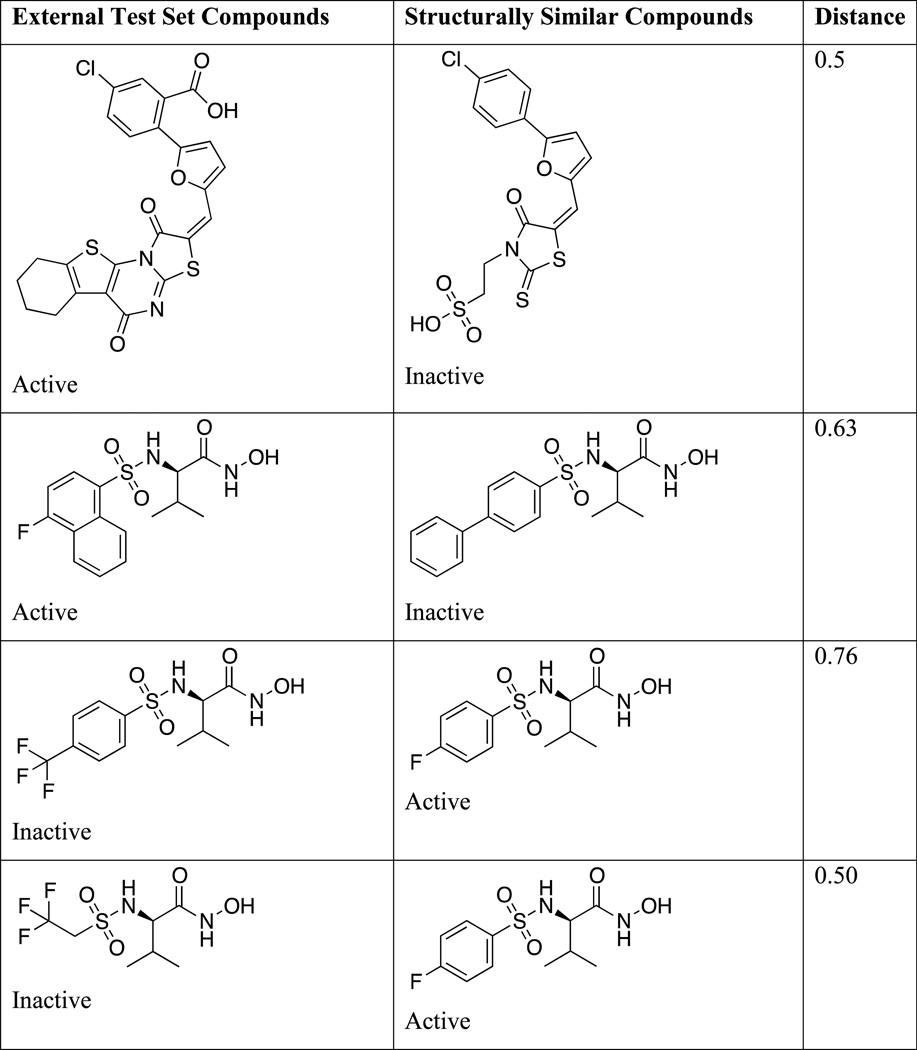
Incorrect predictions of structures in the external evaluation set were then closely analyzed. Table 3 lists structures of misclassified compounds, together with those of structurally similar compounds belonging to a different activity class. This structural similarity is most likely the cause of these errors in prediction, and it is evident that subtle structural variations may lead to significant alterations in activity. It is also possible that some compounds are outliers that cannot be directly identified by means of SVM models.

Table 3.

Examples of External Test Set Compounds Misclassified by model M1

Models were also developed using training set Train1, with Schrödinger and ISIDA fragment descriptors. The cross-validated accuracy, sensitivity, and specificity for the optimized model (M2) using Schrödinger descriptors for Train1 were 95.44%, 95.08%, and 95.89%, respectively. Internal validation performance of M2 is comparable to that of M1. However, this model’s external test set accuracy was slightly worse than that of M1. For the optimized model (M3) using ISIDA descriptors for Train1, the crossvalidated accuracy, sensitivity, and specificity of were 91.65%, 88.52%, and 94.52%. Overall, M1 slightly outperformed M3; the internal and external evaluation results are summarized in Table 1.

As mentioned in section 2.2.3.1, structural similarity-based sampling was applied to build training set Train2 and test set Test2, to ensure that these two sets would be structurally dissimilar. Corresponding models were then developed and used to predict activity vs. inactivity for the datasets Test2, DBB, and DBC. As illustrated in Table 2, performances of models built from Train2 are comparable to those constructed from Train1. The models based on Train2 using MOE (M4), Schrödinger (M5), and ISIDA descriptors (M6) exhibited cross-validated accuracies of 93.01%, 91.54%, and 90.71%, respectively. Notably, all three models are capable of differentiating actives from inactives, when all compounds tested are structurally dissimilar to the training set compounds. These results point to a major advantage of the SVM modeling method, specifically, that SVM models represent only a subset of the training data as support vectors in order to discriminate between two distinct classes, and are therefore less likely to overfit training data while maintaining favorable generalizability.

Table 2.

Classification Performance of SVM Models Developed Based on Dataset Train2 with Various Descriptor Sets

	MOE	Schrödinger	ISIDA fragments
10-fold cross-validation (58 actives and 71 inactives)
Parameters	C = 40 γ = 0.1	C = 40 γ = 0.1	C = 40 γ = 0.001
Accuracy	93.01%	91.54%	90.71%
Sensitivity	94.83%	93.10%	87.93%
Specificity	91.55%	90.14%	92.96%
Prediction on external test set Test2 (44 actives and 51 inactives)
Accuracy	92.63%	89.47%	96.84%
Sensitivity	90.90%	81.82%	100.00%
Specificity	94.12%	96.08%	92.68%
Prediction on external test set DBB (284 weak actives)
Accuracy	19.37%	31.34%	34.51%
Prediction on external test set DBC (847 inactives)
Accuracy	96.22%	99.29%	86.89%

We found that the cross-validated accuracy of models constructed from Train2 is slightly worse than those obtained from Train1. This may be because Train2 lacked information from entire clusters of actives and inactives, while Train1 incorporated a broader selection of diverse compounds occupying a wider region of chemical space, due to the random sampling strategy used to assemble that dataset. Models based on Train1 are therefore likely to identify descriptors that strongly correlate with variations among actives and inactives, leading to better prediction performance. Interestingly, however, we found that model M6 identified active compounds in Test2 quite accurately, while only 3 inactives were identified incorrectly. The performance of model M5 on Test2 was least accurate among the three models; however, in comparison to M4, M5 was able to retrieve more weak actives (89 compounds of 284) from DBB. Model M6 also identified more weak actives (98 compounds of 284) from DBB as actives, although its ability to pull out inactives (86.89%) from DBC was much less effective than other models. Notably, M6 identifies more active compounds, including weak actives, but also generates more false positives.

3.2 Analysis of Molecular Descriptors

We found that certain molecular descriptors displayed higher SVM kernel weights than others, suggesting that these may play a key role in the abilities of the respective models to classify compounds as active or inactive. These specific descriptors are listed in Table 4 (M1), Table 5 (M2), and Table 6 (M3). The mean values for active-compound descriptors differed significantly from those for inactive compounds. The MOE descriptors SlogP_VSA2, SlogP_VSA8, SlogP_VSA7, and SlogP_VSA1 are defined as the sum of accessible van der Waals surface area (in Ų) for each atom, the contribution of which to logP(o/w) is within (−0.2, 0], (0.3, 0.4], (0.25, 0.3], and (−0.4, −0.2], respectively, based on the method of Crippen et al.[45] In particular, those atom types with contributions to logP(o/w) which are in the range (−0.2, 0] (SlogP_VSA2) include 2° aromatic carbons, the 4° aromatic carbon represented by the SMARTS string “[CH0X4]a,” aliphatic ether oxygens, carbonyl aliphatic oxygens, and ionic sulfur. Atom types with contributions to logP(o/w) in the range (0.25, 0.3] (SlogP_VSA7) include aromatic bridgehead carbons, the 4° aromatic carbon represented by the SMARTS string “[c](:a)(:a)-a”, acidic hydrogens, and ionized nitrogens. Finally, atom types with contributions to logP(o/w) within the range (−0.4, −0.2] (SlogP_VSA1) include the 1° and 2° carbons represented by the SMARTS strings “[CH3][(N,O,P,S,F,Cl,Br,I)]” and “[CH2X4](N,O,P,S,F,Cl,Br,I)]”, the 3° and 4° carbons with SMARTS strings “[CH1X4][(N,O,P,S,F,Cl,Br,I)]” and “[CH0X4][(N,O,P,S,F,Cl,Br,I)]”, the carbon represented by the SMARTS string “[C]=[A#X]”, alcohol hydrogens, 3° amine nitrogens, unprotonated aromatic nitrogens, 4° amine nitrogens, alcohol oxygens, and oxide oxygens. Representative atom types for SlogP_VSA8 have not been published to date.

Table 4.

Representative MOE descriptors in model M1, with corresponding average values for actives and inactives in Train1

MOE descriptors	Weight	Average (Actives)	Average (Inactives)
SlogP_VSA2	7.77	66.96	21.89
SlogP_VSA8	6.01	45.64	8.34
b_rotR	4.85	0.33	0.16
opr_nrot	4.57	8.30	3.79
PEOE_VSA+4	4.55	3.97	1.35
SlogP_VSA7	−4.71	96.10	151.05
SlogP_VSA1	−4.59	23.98	42.98
opr_nring	−4.08	2.05	3.30
b_ar	−3.90	9.79	15.34
opr_brigid	−3.48	12.00	18.32

Table 5.

Representative Schrodinger descriptors in model M2, with corresponding average values for actives and inactives in Train1

Schrödinger descriptors	Weight	Average (Actives)	Average (Inactives)
#rtvFG	6.25	0.85	0.15
ALOGP9	5.21	19.52	1.95
#metab	4.99	4.82	2.47
#rotor	3.79	9.28	3.90
SAamideO	3.65	25.39	2.03
Maximal electrotopological negative variation (MENV)	−3.93	3.13	3.85
Dipole (Point Chg) -Y	−3.91	−1.38	0.32
PEOE4 (PEOE4)	−3.70	10.01	25.69
QPPCaco	−3.39	99.54	879.19
Molecule cyclized degree (MCD)	−3.13	0.45	0.71

Table 6.

Representative ISIDA descriptors in model M3 with corresponding average values for actives and inactives in Train1

Descriptors	Kernel Weight	Average (Actives)	Average (Inactives)
C-N-O	6.56	0.84	0.11
C-C-C-C-N	6.31	2.51	0.14
H-C*C-F	5.65	1.20	0.10
H-O-C-C-N	4.99	0.20	0.03
C-N-C-C-O	4.90	0.39	0.04
H-C*C*C-H	−5.84	2.26	3.68
C*C-C*C	−5.81	0.15	0.27
C(-H'*C'*C')	−5.59	5.18	7.47
O(CB'CB')	−5.56	0.10	0.32
CB(CB'CB'CB')	−4.26	0.15	1.04

-: single bonds

^*: aromatic bonds

H: hydrophobe

CB: aromatic C

In model M1, SlogP_VSA2 and SlogP_VSA8 exhibit higher mean values for actives than for inactives, while the mean values for SlogP_VSA7 and SlogP_VSA1 are lower for actives than for inactives. Variations among these subdivided surface area descriptor values for actives and inactives may point to specific requirements of size, shape, and spatial arrangements of atoms for active molecules. Descriptors b_rotR and opr_nrot are defined as rotatable bond related descriptors, and both exhibit higher mean values for actives than for inactives, suggesting that actives tend to have more rotatable bonds than inactives. Partial charge descriptor PEOE_VSA+4 indicates the contributions of special partial charge distribution to biological activity. while descriptors opr_nring, b_ar, and opr_brigid are defined as the number of ring bonds, aromatic bonds, and rigid bonds, respectively. Based on the mean values of these descriptors, compounds that are inactive against LF tend to have more ring, aromatic, and rigid bonds than do active inhibitors.

We note that a specific series of ADME-Tox related descriptors, including the number of reactive functional groups (#rtvFG), the number of likely metabolic reactions (#metab), the number of non-trivial rotatable bonds (#rotor), solvent-accessible surface area of amide oxygen atoms (SAamideO), and predicted apparent Caco-2 cell permeability (QPPCaco), contribute significantly to the ability of model M2 to differentiate between LF actives and inactives. The average values of these descriptors for both actives and inactives in Train1 fall within the range of 95% of known drugs, indicating that both actives and inactives exhibit predicted drug-like properties. However, the average values of #rtvFG, #metab, #rotor, and SAamideO are higher for actives than for inactives, while the opposite is true regarding the average value of QPPCaco. Notably, some active compounds in Train1 incorporate a hydroxamate moiety, which is considered to be a reactive functional group for the purposes of calculating #rtvFG, which therefore results in a somewhat misleading, higher value of #rtvFG for actives than for inactives. Our observation that compounds active against LF have more rotatable bonds is consistent with our conclusions drawn from model M1 using MOE descriptors. Also, a larger value for SAamideO in active compounds may indicate that amide groups are preferred for LF inhibition. Specific conclusions are somewhat more challenging to draw from the #metab and QPPCaco descriptor values, since these are influenced by multiple factors, and a direct correlation between structural features and these descriptor values for actives vs. inactives is therefore nontrivial.

We also analyzed the ISIDA fragment-based descriptor values in model M3 in order to gain insight into potential structure-activity relationships for effective LF inhibition. This model demonstrated that the structural fragments C-N-O, C-C-C-C-N, H-C* C-F, H-O-C-C-N, and C-N-C-C-O appear more often in active LF inhibitors than in inactive compounds. Closer analysis revealed potential H-bonding requirements for LF activity; for example, in some fragments, N and O atoms are present together in a single fragment, separated by a short distance. We note that this result correlates well with findings from our previously published comprehensive LF pharmacophore hypothesis, in which H-bond donor feature F23 and acceptor features F13 and F21 were found to be present in highly active LF inhibitors, and are located in close proximity to each other.[37] We also discovered that the fluorine-based fragment H-C*C-F was present in many active compounds, pointing to potential hydrophobic interactions favored for LF inhibition, whereas certain aromatic ring containing fragments such as H-C*C*C-H, C*C-C*C, C(-H'*C'*C'), O(CB'CB'), and CB(CB'CB'CB') are disfavored for LF activity.

4. Concluding Remarks

This work describes the development and optimization of a variety of support vector machine (SVM) based models from published LF inhibitors with experimental biological activity data, the most optimal of which were able to sharply distinguish between active and inactive compounds. Accuracy and predictivity of these models were assessed internally via 10-fold cross-validation and externally by means of test set compounds not incorporated in the original models. A wide variety of molecular descriptors were examined in this study, including subdivided surface areas, rotatable bonds, partial charge distribution, number of reactive functional groups, number of metabolic reactions, solvent-accessible surface area of amide oxygen atoms, and 2D fragments including C-N-O, C-C-C-C-N, H-C*C-F, H-O-C-C-N, and C-N-C-C-O. These fragments helped to elucidate specific H-bonding donor and acceptor and hydrophobic requirements for LF inhibitors. From among all models generated, our model M1 using MOE descriptors, based on a randomly split training set, yielded the highest cross-validated accuracy of 95.44% for the internal test set of LF inhibitors. This model achieved an accuracy of 94.44% on a heterogeneous external test set, and was able to identify 99.65% of compounds correctly in an external inactive test set. This optimal model is of potential use to complement experimental in vitro screening, as well as virtual screening, of compound libraries in order to rapidly identify novel and potent LF inhibitor compounds from large datasets.

Highlights.

• Novel support vector machine models with high prediction accuracy were developed to rapidly identify LF inhibitors from compound libraries.

• Our models demonstrate high selectivity toward nanomolar-level LF inhibitors.

• Our modeling studies suggest that specific molecular descriptors including subdivided surface areas, rotatable bonds, and partial charge distribution are likely to play a critical role in defining LF inhibitory activities.