Rapid Sampling for Visualizations with Ordering Guarantees

Abstract

Visualizations are frequently used as a means to understand trends and gather insights from datasets, but often take a long time to generate. In this paper, we focus on the problem of rapidly generating approximate visualizations while preserving crucial visual properties of interest to analysts. Our primary focus will be on sampling algorithms that preserve the visual property of ordering; our techniques will also apply to some other visual properties. For instance, our algorithms can be used to generate an approximate visualization of a bar chart very rapidly, where the comparisons between any two bars are correct. We formally show that our sampling algorithms are generally applicable and provably optimal in theory, in that they do not take more samples than necessary to generate the visualizations with ordering guarantees. They also work well in practice, correctly ordering output groups while taking orders of magnitude fewer samples and much less time than conventional sampling schemes.

1. Introduction

To understand their data, analysts commonly explore their datasets using visualizations, often with visual analytics tools such as Tableau [24] or Spotfire [45]. Visual exploration involves generating a sequence of visualizations, one after the other, quickly skimming each one to get a better understanding of the underlying trends in the datasets. However, when the datasets are large, these visualizations often take very long to produce, creating a significant barrier to interactive analysis.

Our thesis is that on large datasets, we may be able to quickly produce approximate visualizations of large datasets preserving visual properties crucial for data analysis. Our visualization schemes will also come with tuning parameters, whereby users can select the accuracy they desire, choosing less accuracy for more interactivity and more accuracy for more precise visualizations.

We show what we mean by “preserving visual properties” via an example. Consider the following query on a database of all flights in the US for the entire year:

Q : SELECT NAME, AVG(DELAY) FROM FLT GROUP BY NAME

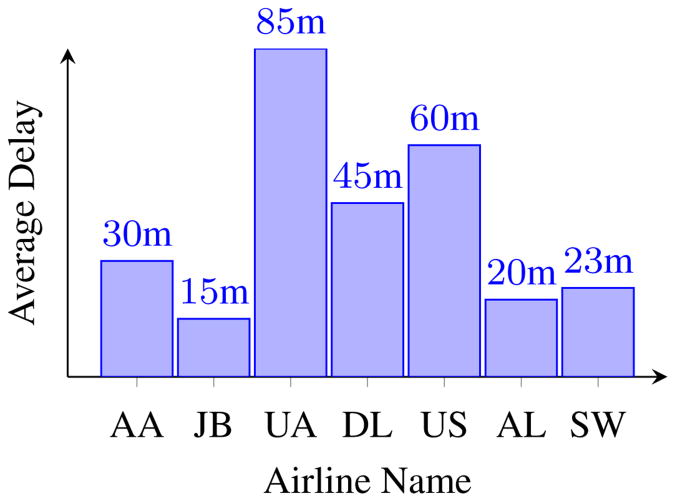
The query asks for the average delays of flights, grouped by airline names. Figure 1 shows a bar chart illustrating an example query result. In our example, the average delay for AA (American Airlines) is 30 minutes, while that for JB (Jet Blue) is just 15 minutes. If the FLT table is large, the query above (and therefore the resulting visualization) is going to take a very long time to be displayed.

Figure 1. Flight Delays.

In this work, we specifically design sampling algorithms that generate visualizations of queries such as Q, while sampling only a small fraction of records in the database. We focus on algorithms that preserve visual properties, i.e., those that ensure that the visualization appears similar to the same visualization computed on the entire database. The primary visual property we consider in this paper is the correct ordering property: ensuring that the groups or bars in a visualization or result set are ordered correctly, even if the actual value of the group differs from the value that would result if the entire database were sampled. For example, if the delay of JB is smaller than the delay of AA, then we would like the bar corresponding to JB to be smaller than the bar corresponding to AA in the output visualization. As long as the displayed visualizations obey visual properties (such as correct ordering), analysts will be able to view trends, gain insights, and make decisions—in our example, the analyst can decide which airline should receive the prize for airline with least delay, or if the analyst sees that the delay of AL is greater than the delay of SW, they can dig deeper into AL flights to figure out the cause for higher delay. Beyond correct ordering, our techniques can be applied to other visual properties, including:

• Accurate Trends: when generating line charts, comparisons between neighboring x-axis values must be correctly presented.

• Accurate Values: the values for each group in a bar chart must be within a certain bound of the values displayed to the analyst.

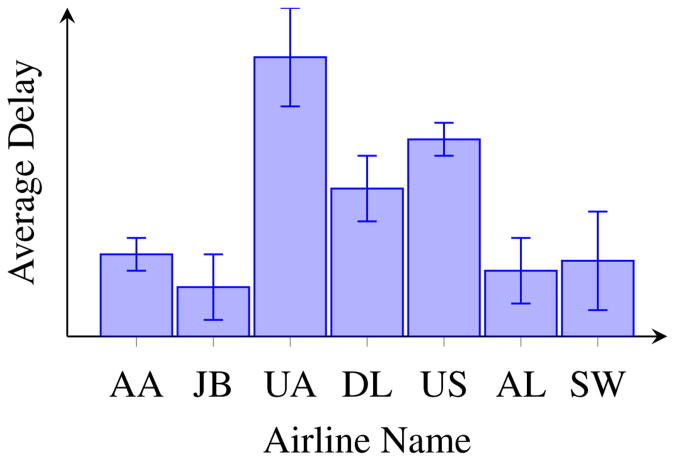
We illustrate the challenges of generating accurate visualizations using our flight example. Here, we assume we have a sampling engine that allows us to retrieve samples from any airline group at a uniform cost per sample (we describe one such sampling engine we have built in Section 4.) Then, the amount of work done by any visualization generation algorithm is proportional to the number of samples taken in total across all groups. After performing some work (that is, after doing some sampling), let the current state of processing be depicted as in Figure 2, where the aggregate for each group is depicted using confidence intervals. Starting at this point, suppose we wanted to generate a visualization where the ordering is correct (like in Figure 1). One option is to use a conventional round-robin stratified sampling strategy [8], which is the most widely used technique in online approximate query processing [25, 27, 28, 37], to take one sample per group in each round, to generate estimates with shrinking confidence interval bounds. This will ensure that the eventual aggregate value of each group is roughly correct, and therefore that the ordering is roughly correct. We can in fact modify these conventional sampling schemes to stop once they are confident that the ordering is guaranteed to be correct. However, since conventional sampling is not optimized for ensuring that visual properties hold, such schemes will end up doing a lot more work than necessary (as we will see in the following).

Figure 2. Flight Delays: Intermediate Processing.

A better strategy would be to focus our attention on the groups whose confidence intervals continue to overlap with others. For instance, for the data depicted in Figure 2, we may want to sample more from AA because its confidence interval overlaps with JB, AL, and SW while sampling more from UA (even though its confidence interval is large) is not useful because it gives us no additional information — UA is already clearly the airline with the largest delay, even if the exact value is slightly off. On the other hand, it is not clear if we should sample more from AA or DL, AA has a smaller confidence interval but overlaps with more groups, while DL has a larger confidence interval but overlaps with fewer groups. Overall, it is not clear how we may be able to meet our visual ordering properties while minimizing the samples acquired.

In this paper, we develop a family of sampling algorithms, based on sound probabilistic principles, that:

1. are correct, i.e., they return visualizations where the estimated averages are correctly ordered with a probability greater than a user-specified threshold, independent of the data distribution,

2. are theoretically optimal, i.e., no other sampling algorithms can take much fewer samples, and

3. are practically efficient, i.e., they require much fewer samples than the size of the datasets to ensure correct visual properties, especially on very large datasets. In our experiments, our algorithms give us reductions in sampling of up to 50× over conventional sampling schemes.

Our focus in this paper is on visualization types that directly correspond to a SQL aggregation query, e.g., a bar chart, or a histogram; these are the most commonly used visualization types in information visualization applications. While we also support generalizations to other visualization types (see Section 2.5), our techniques are not currently applicable to some visualizations, e.g., scatter-plots, stacked charts, timelines, or treemaps.

In addition, our algorithms are general enough to retain correctness and optimality when configured in the following ways:

1. Partial Results: Our algorithms can return partial results (that analysts can immediately peruse) improving gradually over time.

2. Early Termination: Our algorithms can take advantage of the finite resolution of visual display interfaces to terminate processing early. Our algorithms can also terminate early if allowed to make mistakes on estimating a few groups.

3. Generalized Settings: Our algorithms can be applied to other aggregation functions, beyond AVG, as well as other, more complex queries, and also under more general settings.

4. Visualization Types: Our algorithms can be applied to the generation of other visualization types, such as trend-lines or chloropleth maps [47] instead of bar graphs.

2. Formal Problem Description

We begin by describing the type of queries and visualizations that we focus on for the paper. Then, we describe the formal problem we address.

2.1 Visualization Setting

Query

We begin by considering queries such as our example query in Section 1. We reproduce the query (more abstractly) here:

Q : SELECT X, AVG(Y) FROM R(X, Y) GROUP BY X

This query can be translated to a bar chart visualization such as the one in Figure 1, where AVG(Y) is depicted along the y–axis, while X is depicted along the x–axis. While we restrict ourselves to queries with a single GROUP BY and a AVG aggregate, our query processing algorithms do apply to a much more general class of queries and visualizations, including those with other aggregates, multiple group-bys, and selection or having predicates, as described in Section 2.5 (these generalizations still require us to have at least one GROUP BY, which restricts us to aggregate-based visualizations, e.g., histograms, bar-charts, and trend-lines.

Setting

We assume we have an engine that allows us to efficiently retrieve random samples from R corresponding to different values of X. Such an engine is easy to implement, if the relation R is stored in main memory, and we have a traditional (B-tree, hash-based, or otherwise) index on X. We present an approach to implement this engine on disk in Section 4. Our techniques will also apply to the scenario when there is no index on X — we describe this in the extended technical report [34].

Notation

We denote the values that the group-by attribute X can take as x₁ … x_k. We let n_i be the number of tuples in R with X = x_i. For instance, n_i for X = UA will denote the number of flights operated by UA that year.

Let the ith group, denoted S_i, be the multiset of the n_i values of Y across all tuples in R where X = x_i. In Figure 1, the group corresponding to UA contains the set of delays of all the flights flown by UA that year.

We denote the true averages of elements in a group i as μ_i: Thus ${\mu }_i=\frac{{\sum }_{s\in S_i}s}{n_i}$. The goal for any algorithm processing the query Q above is to compute and display μ_i, ∀i ∈ 1 … k, such that the estimates for μ_i are correctly ordered (defined formally subsequently).

Furthermore, we assume that each value in S_i is bounded between [0, c]. For instance, for flights delays, we know that the values in S_i are within [0, 24 hours], i.e., typical flights are not delayed beyond 24 hours. Note however, that our algorithms can still be used when no bound on c is known, but may not have the desirable properties listed in Section 3.3.

2.2 Query Processing

Approach

Since we have an index on X, we can use the index to retrieve a tuple at random with any value of X = x_i. Thus, we can use the index to get an additional sample of Y at random from any group S_i. Note that if the data is on disk, random access through a conventional index can be slow: however, we are building a system, called NeedleTail (also described in Section 4) that will address the problem of retrieving samples satisfying arbitrary conditions.

The query processing algorithms that we consider take repeated samples from groups S_i, and then eventually output estimates ν₁,…, ν_k for true averages μ₁,…, μ_k.

Correct Ordering Property

After retrieving a number of samples, our algorithm will have some estimate ν_j for the value of the actual average μ_j for each j. When the algorithm terminates and returns the eventual estimates ν₁,… ν_k, we want the following property to hold:

for all i, j such that μ_i > μ_j, we have ν_i > ν_j

We desire that the query processing algorithm always respect the correct ordering property, but since we are making decisions probabilistically, there may be a (typically very small) chance that the output will violate the guarantee. Thus, we allow the analyst to specify a failure probability δ (which we expect to be very close to 0). The query processing scheme will then guarantee that with probability 1 – δ, the eventual ordering is correct. We will consider other kinds of guarantees in Section 2.5.

2.3 Characterizing Performance

We consider three measures for evaluating the performance of query processing algorithms:

Sample Complexity

The cost for any additional sample taken by an algorithm from any of the groups is the same¹. We denote the total number of samples taken by an algorithm from group i as m_i. Thus, the total sampling complexity of a query processing strategy (denoted 𝒞) is the number of samples taken across groups:

$$\mathcal{C}=\sum _{i\in 1\dots k}{m}_i$$

Computational Complexity

While the total time will be typically dominated by the sampling time, we will also analyze the computation time of the query processing algorithm, which we denote 𝒯.

Total Wall-Clock Time

In addition to the two complexity measures, we also experimentally evaluate the total wall-clock time of our query processing algorithms.

2.4 Formal Problem

Our goal is to design query processing strategies that preserve the right ordering (within the user-specified accuracy bounds) while minimizing sample complexity:

Problem 1 (AVG-Order)

Given a query Q, and parameter values c, δ, and an index on X, design a query processing algorithm returning estimates ν₁,…, ν_k for μ_i,…, μ_k which is as efficient as possible in terms of sample complexity 𝒞, such that with probability greater than 1 – δ, the ordering of ν₁,…, ν_k with respect to μ_i,…, μ_k is correct.

Note that in the problem statement we ignore computational complexity 𝒯, however, we do want the computational complexity of our algorithms to also be relatively small, and we will demonstrate that for all algorithms we design, that indeed is the case.

One particularly important extension we cover right away is the following: visualization rendering algorithms are constrained by the number of pixels on the display screen, and therefore, two groups whose true average values μ_i are very close to each other cannot be distinguished on a visual display screen. Can we, by relaxing the correct ordering property for groups which are very close to each other, get significant improvements in terms of sample and total complexity? We therefore pose the following problem:

Problem 2 (AVG-Order-Resolution)

Given a query Q, and values c, δ, a minimum resolution r, and an index on X, design a query processing algorithm returning estimates ν₁,…, ν_k for μ₁,…, μ_k which is as efficient as possible in terms of sample complexity 𝒞, such that with probability greater than 1 – δ, the ordering of ν₁,…, ν_k with respect to μ₁,…, μ_k is correct, where correctness is now defined as the following:

for all i, j, i ≠ j, if |μ_i–μ_j| ≤ r, then ordering ν_i before or after ν_j are both correct, while if |μ_i – μ_j| > r, then ν_i < ν_j if μ_i < μ_j and vice versa.

The problem statement says that if two true averages, μ_i, μ_j satisfy |μ_i – μ_j| ≤ r, then we are no longer required to order them correctly with respect to each other.

2.5 Extensions

In the technical report [34] we discuss other problem variants:

• Ensuring that weaker properties hold:

  • Trends and Chloropleths: When drawing trend-lines and heat maps (i.e., chloropleths [47]), it is more important to ensure order is preserved between adjacent groups than between all groups.
  • Top-t Results: When the number of groups to be depicted in the visualization is very large, say greater than 20, it is impossible for users to visually examine all groups simultaneously. Here, the analyst would prefer to view the top-t or bottom-t groups in terms of actual averages.
  • Allowing Mistakes: If the analyst is fine with a few mistakes being made on a select number of groups (so that that the results can be produced faster), this can be taken into account in our algorithms.
• Ensuring that stronger properties hold:

  • Values: We can modify our algorithms to ensure that the averages ν_i for each group are close to the actual averages μ_i, in addition to making sure that the ordering is correct.
  • Partial Results: We can modify our algorithms to return partial results as an when they are computed. This is especially important when the visualization takes a long time to be computed, so that the analyst to start perusing the visualization as soon as possible.
• Tackling other queries or settings:

  • Other Aggregations: We can generalize our techniques for aggregation functions beyond AVG, including SUM and COUNT.
  • Selection Predicates: Our techniques apply equally well when we have WHERE or HAVING predicates in our query.
  • Multiple Group Bys or Aggregations: We can generalize our techniques to handle the case where we are visualizing multiple aggregates simultaneously, and when we are grouping by multiple attributes at the same time (in a three dimensional visualization or a two dimensional visualization with a cross-product on the x-axis).
  • No indexes: Our techniques also apply to the scenario when we have no indexes.

Algorithm 1. IFocus.

3. The Algorithm and Its Analysis

In this section, we describe our solution to Problem 1. We start by introducing the new IFocus algorithm in Section 3.1. We will analyze its sample complexity and demonstrate its correctness in Section 3.3. We will then analyze its computational complexity in Section 3.4. Finally, we will demonstrate that the IFocus algorithm is essentially optimal, i.e., no other algorithm can give us a sample complexity much smaller than IFocus, in Section 3.5.

3.1 The Basic IFocus Algorithm

The IFocus algorithm is shown in Algorithm 1. We describe the pseudocode and illustrate the execution on an example below.

At a high level, the algorithm works as follows. For each group, it maintains a confidence interval (described in more detail below) within which the algorithm believes the true average of each group lies. The algorithm then proceeds in rounds. The algorithm starts off with one sample per group to generate initial confidence intervals for the true averages µ₁,…, µ_k. We refer to the groups whose confidence intervals overlap with other groups as active groups. Then, in each round, for all the groups whose confidence intervals still overlap with confidence intervals of other groups, i.e., all the active groups, a single additional sample is taken. We terminate when there are no remaining active groups and then return the estimated averages ν₁,…, ν_k We now describe an illustration of the algorithm on an example.

Example 3.1. An example of how the algorithm works is given in Table 1. Here, there are four groups, i.e., k = 4. Each row in the table corresponds to one phase of sampling. The first column refers to the total number of samples that have been taken so far for each of the active groups (we call this the number of the round). The algorithm starts by taking one sample per group to generate initial confidence intervals: these are displayed in the first row.

Table 1. Example execution trace: active groups are denoted using the letter A, while inactive groups are denoted as I.

	Group 1		Group 2		Group 3		Group 4
1	[60, 90]	A	[20, 50]	A	[10, 40]	A	[40, 70]	A
…
20	[64, 84]	A	[28, 48]	A	[15, 35]	A	[45, 65]	A
21	[66, 84]	I	[30, 48]	A	[17, 35]	A	[46, 64]	A
…
57	[66, 84]	I	[32, 48]	A	[17, 33]	A	[46, 62]	A
58	[66, 84]	I	[32, 47]	A	[17, 32]	I	[46, 61]	A
…
70	[66, 84]	I	[40, 47]	A	[17, 32]	I	[46, 53]	A
71	[66, 84]	I	[40, 46]	I	[17, 32]	I	[47, 53]	I

At the end of the first round, all four groups are active since for every confidence interval, there is some other confidence interval with which it overlaps. For instance, for group 1, whose confidence interval is [60, 90], this confidence interval overlaps with the confidence interval of group 4; therefore group 1 is active.

We “fast-forward” to round 20, where once again all groups are still active. Then, on round 21, after an additional sample, the confidence interval of group 1 shrinks to [66, 84], which no longer overlaps with any other confidence interval. Therefore, group 1 is no longer active, and we stop sampling from group 1. We fast-forward again to round 58, where after taking a sample, group 3's confidence interval no longer overlaps with any other group's confidence interval, so we can stop sampling it too. Finally, at round 71, none of the four confidence intervals overlaps with any other. Thus, the total cost of the algorithm (i.e., the number of samples) is

$$\mathcal{C}=21\times 4+(58-21)\times 3+(71-58)\times 2$$

The expression 21 × 4 comes from the 21 rounds when all four groups are active, (58 − 21) × 3 comes from the rounds from 22 to 58, when only three groups are active, and so on.

The pseudocode for the algorithm is shown in Algorithm 1; m refers to the round. We start at the first round (i.e., m = 1) drawing one sample from each of S₁,…, S_k to get initial estimates of ν₁,…, ν_k . Initially, the set of active groups, A, contains all groups from 1 to k. As long as there are active groups, in each round, we take an additional sample for all the groups in A, and update the corresponding ν_i. Based on the number of samples drawn per active group, we update ε, i.e., the half-width of the confidence interval. Here, the confidence interval [ν_i−ε,ν_i+ε ] refers to the 1−δ confidence interval on taking m samples, i.e., having taken m samples, the probability that the true average µ_i is within [ν_i−ε, ν_i + ε ] is greater than 1 − δ. As we show below, the confidence intervals are derived using a variation of Hoeffding's inequality.

Discussion

We note several features of the algorithm:

• As we will see, the sampling complexity of IFocus does not depend on the number of elements in each group, and simply depends on where the true averages of each group are located relative to each other. We will show this formally in Section 3.3.

• There is a corner case that needs to be treated carefully: there is a small chance that a group that was not active suddenly becomes active because the average ν_i of some other group moves excessively due to the addition of a very large (or very small) element. We have two alternatives at this point

  • a) ignore the newly activated group; i.e., groups can never be added back to the set of active groups
  • b) allow inactive groups to become active.

It turns out the properties we prove for the algorithm in terms of optimality of sample complexity (see Section 3.3) hold if we do a). If we do b), the properties of optimality no longer hold.

3.2 Proof of Correctness

We now prove that IFocus obeys the ordering property with probability greater than 1 − δ. Our proof involves three steps:

• Step 1: The algorithm IFocus obeys the correct ordering property, as long as the confidence intervals of each active group contain the actual average, during every round.

• Step 2: The confidence intervals of any given active group contains the actual average of that group with probability greater than (1 − δ/k) at every round, as long as ε is set according to Line 6 in Algorithm 1.

• Step 3: The confidence intervals of all active groups contains actual averages for the groups with probability greater than (1 − δ) at every round, when ε is set as per Line 6 in Algorithm 1.

Combining the three steps together give us the desired result.

Step 1: To complete this step, we need a bit more notation. For every m > 1, let A_m, ε_m, and ν₁,m,…, ν_k,m denote the values of A, ε, ν₁,…, ν_k at step 10 in the algorithm for the iteration of the loop corresponding to m. Also, for i = 1,…, k, recall that m_i is the number of samples required to estimate ν_i; equivalently, it will denote the value of m when i is removed from A. We define m_max to be the largest m_i.

Lemma 1. If for every m ∈ 1… m_max and every j ∈ A_m, we have |ν_j,m − µ_j| ≤ ε_m, then the estimates ν₁,…, ν_k returned by the algorithm have the same order as µ₁,…, µ_k, i.e., the algorithm satisfies the correct ordering property.

That is, as long as all the estimates for the active groups are close enough to their true average, that is sufficient to ensure overall correct ordering.

Proof. Fix any i ≠ j ∈ {1,…, k}. We will show that ν_i > ν_j iff µ_i > µ_j. Applying this to all i, j gives us the desired result.

Assume without loss of generality (by relabeling i and j, if needed) that m_i ≤ m_j. Since m_i ≤ m_j, j is removed from the active groups at a later stage than i. At m_i, we have that the confidence interval for group i no longer overlaps with other confidence intervals (otherwise i would not be removed from the set of active groups). Thus, the intervals [ν_i,mi − ε_mi, ν_i,mi + ε_mi] and [ν_j,mi − ε_mi, ν_j,mi + ε_mi] are disjoint. Consider the case when µ_i < µ_j. Then, we have:

$${\mu }_i\le {\nu }_{i,m_i}+{\epsilon }_{m_i}<{\nu }_{j,m_i}-{\epsilon }_{m_i}\le {\mu }_j$$ (1)

$$\Rightarrow {\nu }_{i,m_i}<{\mu }_j-{\epsilon }_{m_i}$$ (2)

The first and last inequality holds because µ_i and µ_j are within the confidence interval around ν_i and ν_j respectively at round m_i. The second inequality holds because the intervals are disjoint. (To see this, notice that if the inequality was reversed, the intervals would no longer be disjoint.) Then, we have:

$${\nu }_j={\nu }_{j,m_j}\ge {\mu }_j-{\epsilon }_{m_j}\ge {\mu }_j-{\epsilon }_{m_i}>{\nu }_{i,m_i}={\nu }_i.$$ (3)

The first equality holds because group j exits the set of active groups at m_j; the second inequality holds because the confidence interval at j contains µ_j; the third inequality holds because ε_j ≤ ε_i (since confidence intervals shrink as the rounds proceed); the next inequality holds because of Equation 2; while the last equality holds because group i exits the set of active groups at m_i. Therefore, we have ν_i < ν_j, as desired. The case where µ_i > µ_j is essentially identical: in this case Equation 1 is of the form:

$${\mu }_i\ge {\nu }_{i,m_i}-{\epsilon }_{m_i}>{\nu }_{j,m_i}+{\epsilon }_{m_i}\ge {\mu }_j$$

and Equation 3 is of the form:

$${\nu }_j={\nu }_{j,m_j}\le {\mu }_j+{\epsilon }_{m_j}\le {\mu }_j+{\epsilon }_{m_i}<{\nu }_{i,m_i}={\nu }_i.$$

so that we now have ν_i > ν_j, once again as desired.

Step 2: In this step, our goal is to prove that the confidence interval of any group contains the actual average with probability greater than (1 − δ/k) on following Algorithm 1.

For this proof, we use a specialized concentration inequality that is derived from Hoeffding's classical inequality [48]. Hoeffding [26] showed that his inequality can be applied to this setting to bound the deviation of the average of random numbers sampled from a set from the true average of the set. Serfling [44] refined the previous result to give tighter bounds as the number of random numbers sampled approaches the size of the set.

Lemma 2 (Hoeffding–Serfling inequality [44]). Let 𝒴 = y₁,…, y_N be a set of N values in [0, 1] with average value $\frac{1}{N}{\sum }_{i=1}^N{y}_i=\mu$. Let Y₁,…, Y_N be a sequence of random variables drawn from 𝒴 without replacement. For every 1 ≤ k < N and ε > 0,

$$\text{Pr}\left[\underset{k\le m\le N-1}{max}\right|\frac{{\sum }_{i=1}^m{Y}_i}{m}-\mu |\ge \epsilon ]\le 2exp(-\frac{2k{\epsilon }^2}{1-\frac{k-1}{N}}).$$

We use the above inequality to get tight bounds for the value of ${\sum }_{i=1}^m{Y}_i/m$ for all 1 ≤ m ≤ N, with probability δ. We discuss next how to apply the theorem to complete Step 2 of our proof.

Theorem 3.2. Let 𝒴 = y₁,…, y_N be a set of N values in [0, 1] with average value $\frac{1}{N}{\sum }_{i=1}^N{y}_i=\mu$. Let Y₁,…, Y_N be a sequence of random variables drawn from 𝒴 without replacement. Fix any δ > 0 and κ > 1. For 1 ≤ m ≤ N − 1, define

$${\epsilon }_m=\sqrt{\frac{(1-\frac{m/\kappa -1}{N})(2log{log}_{\kappa }(m)+log({\pi }^2/3\delta ))}{2m/\kappa }.}$$

$$\mathit{\text{Then}}:\text{Pr}[\exists m,1\le m\le N:|\frac{{\sum }_{i=1}^m{Y}_i}{m}-\mu |>{\epsilon }_m]\le \delta .$$

Proof. We have:

$$\begin{array}{c}\text{Pr}[\exists m,1\le m\le N:|\frac{{\sum }_{i=1}^m{Y}_i}{m}-\mu |>{\epsilon }_m]\\ \le \sum _{r\ge 1}\text{Pr}[\exists m,{\kappa }^{r-1}\le m\le {\kappa }^r:|\frac{{\sum }_{i=1}^m{Y}_i}{m}-\mu |>{\epsilon }_m]\\ \le \sum _{r\ge 1}\text{Pr}[\exists m,{\kappa }^{r-1}\le m\le {\kappa }^r:|\frac{{\sum }_{i=1}^m{Y}_i}{m}-\mu |>{\epsilon }_{{\kappa }^r}]\\ \le \sum _{r\ge 1}\text{Pr}\left[\underset{{\kappa }^{r-1}\le m\le N-1}{max}\right|\frac{{\sum }_{i=1}^m{Y}_i}{m}-\mu |>{\epsilon }_{{\kappa }^r}].\end{array}$$

The first inequality holds by the union bound [48]. The second inequality holds because ε_m only decreases as m increases. The third inequality holds because the condition that any of the sums on the left-hand side is greater than ε_κ^r occurs when the maximum is greater than ε_κ^r.

By the Hoeffding–Serfling inequality (i.e., Lemma 2),

$$\text{Pr}\left[\underset{{\kappa }^{r-1}\le m\le N-1}{max}\right|\frac{{\sum }_{i=1}^m{Y}_i}{m}-\mu |>{\epsilon }_{{\kappa }^r}]\le \frac{6\delta }{{\pi }^2{r}^2}.$$

The theorem the follows from the identity ${\sum }_{r\ge 1}\frac{1}{r^2}=\pi /6$.

Now, when we apply Theorem 3.2 to any group i in Algorithm 1, with ε_m set as described in Line 6 in the algorithm, N set to n_i, Y_i being equal to the ith sample from the group (taken without replacement), and δ set to δ/k, we have the following corollary.

Corollary 3.3. For any group i, across all rounds of Algorithm 1, we have: Pr [∃m, 1 ≤ m ≤ m_i : |ν_i,m − µ| > ε_m] ≤ δ/k.

Step 3: On applying the union bound [48] to Corollary 3.3, we get the following result:

Corollary 3.4. Across all groups and rounds of Algorithm 1: Pr [∃i, m, 1 ≤ i ≤ k, 1 ≤ m ≤ m_i : |ν_i,m − µ| > ε_m] ≤ δ.

This result, when combined with Lemma 1, allows us to infer the following theorem:

Theorem 3.5 (Correct Ordering). The eventual estimates ν₁,…, ν_k returned by Algorithm 1 have the same order as µ₁,…, µ_k with probability greater than 1 − δ.

3.3 Sample Complexity of IFocus

To state and prove the theorem about the sample complexity of IFocus, we introduce some additional notation which allows us to describe the “hardness” of a particular input instance. (Table 2 describes all the symbols used in the paper.) We define η_i to be the minimum distance between µ_i and the next closest average, i.e., η_i = min_j≠i |µ_i − µ_j|. The smaller η_i is, the more effort we need to put in to ensure that the confidence interval estimates for µ_i are are small enough compared to η_i.

Table 2. Table of Notation.

k	Number of groups.
n1, …, nk	Number of elements in each group.
S1, …, Sk	The groups themselves. Si is a set of ni elements from [0, 1].
μ1, …, μk	Averages of the elements in each group. μi = Ex∈Si[x].
τi,j	Distance between averages μi and μj. τi,j = |μi − μj|.
ηi	Minimal distance between μi and the other averages. ηi = minj≠i τi,j.
r	Minimal resolution, 0 ≤ r ≤ 1.
${\eta }_i^{(r)}$	Thresholded minimal distance; ${\eta }_i^{(r)}=max\{{\eta }_i,r\}$.

In this section, we prove the following theorem:

Theorem 3.6 (Sample Complexity). With probability at least 1 − δ, IFocus outputs estimates ν₁,…, ν_k that satisfy the correct ordering property and, furthermore, draws

$$O\left(c^2\sum _{i=1}^{\kappa }\frac{log\left(\frac{\kappa }{\delta }\right)+loglog\left(\frac{1}{{\eta }_i}\right)}{{\eta }_i^2}\right)\mathit{\text{samples in total}}.$$ (4)

The theorem states that IFocus obeys the correct ordering property while drawing a number of samples from groups proportional to the sum of the inverse of the squares of the η_i: that is, the smaller the η_i, the larger the amount of sampling we need to do (with quadratic scaling).

The next lemma gives us an upper bound on how large m_i can be in terms of the η_i, for each i: this allows us to establish an upper bound on the sample complexity of the algorithm.

Lemma 3. Fix i ∈ 1…k. Define $m_i^{\ast }$ to be the minimal value of m ≥ 1 for which ε_m < η_i/4. In the running of the algorithm, if for every $j\in A_{m_i^{\ast }}$, we have $|{\nu }_{j,m_i^{\ast }}-{\mu }_j|\le {\epsilon }_{m_i^{\ast }}$, then $m_i\le m_i^{\ast }$.

Intuitively, the lemma allows us to establish that $m_i<m_i^{\ast }$, the latter of which (as we show subsequently) is dependent on η_i.

Proof. If $i\notin A_{m_i^{\ast }}$, then the conclusion of the lemma trivially holds, because $m_i<m_i^{\ast }$. Consider now the case where $i\in A_{m_i^{\ast }}$. We now prove that $m_i=m_i^{\ast }$. Note that $m_i=m_i^{\ast }$ if and only if the interval $[{\nu }_{i,m_i^{\ast }}-{\epsilon }_{m_i^{\ast }},{\nu }_{i,m_i^{\ast }}+{\epsilon }_{m_i^{\ast }}]$ is disjoint from the union of intervals ${\cup }_{j\in A_{m_i^{\ast }}\backslash \{i\}}[v_{j,m_i^{\ast }}-{\epsilon }_{m_i^{\ast }},v_{j,m_i^{\ast }}+{\epsilon }_{m_i^{\ast }}]$.

We focus first on all j where µ_j < µ_i. By the definition of η_i, every $j\in A_{m_i^{\ast }}$ for which µ_j < µ_i satisfies the stronger inequality µ_j ≤ µ_i − η_i. By the conditions of the lemma (i.e., that confidence intervals always contain the true average), we have that ${\mu }_j\le {\nu }_{j,m_i^{\ast }}-{\epsilon }_{m_i^{\ast }}$ and that ${\mu }_i\le {\nu }_{i,m_i^{\ast }}+{\epsilon }_{m_i^{\ast }}$. So we have:

$${\nu }_{j,m_i^{\ast }}+{\epsilon }_{m_i^{\ast }}\le {\mu }_j+2{\epsilon }_{m_i^{\ast }}<{\mu }_j+\frac{{\eta }_i}{2}\le {\mu }_i-\frac{{\eta }_i}{2}<{\mu }_i-2{\epsilon }_{m_i^{\ast }}\le {\nu }_{i,m_j^{\ast }}-{\epsilon }_{m_i^{\ast }}$$

• The first and last inequalities follow the fact that the confidence interval for ν_j always contains µ_j, i.e., ${\mu }_j\ge {\nu }_{j,m_i^{\ast }}-{\epsilon }_{m_i^{\ast }}$;

• the second and fourth follow from the fact that ${\epsilon }_{m_i^{\ast }}<{\eta }_i/4$;

• and the third follows from the fact that µ_j ≤ µ_i−η_i.

Thus, the intervals $[{\nu }_{i,m_i^{\ast }}-{\epsilon }_{m_i^{\ast }},{\nu }_{i,m_i^{\ast }}+{\epsilon }_{m_i^{\ast }}]$ and $[{\nu }_{j,m_i^{\ast }}-{\epsilon }_{m_i^{\ast }},{\nu }_{j,m_i^{\ast }}+{\epsilon }_{m_i^{\ast }}]$ are disjoint. Similarly, for all $j\in A_{m_i^{\ast }}$ that satisfies µ_j > µ_i, we observe that the interval $[{\nu }_{i,m_i^{\ast }}-{\epsilon }_{m_i^{\ast }},{\nu }_{i,m_i^{\ast }}+{\epsilon }_{m_i^{\ast }}]$ is also disjoint from $[{\nu }_{j,m_i^{\ast }}-{\epsilon }_{m_i^{\ast }},{\nu }_{j,m_i^{\ast }}+{\epsilon }_{m_i^{\ast }}]$.

We are now ready to complete the analysis of the algorithm.

Proof of Theorem 3.6. First, we note that for i = 1,…, k, the value $m_i^{\ast }$ is bounded above by

$$m_i^{\ast }=O\left(c^2\frac{loglog\frac{1}{{\eta }_i^2}+log\frac{k}{\delta }}{{\eta }_i^2}\right).$$

(To verify this fact, note that when $m=\frac{8c^2}{{\eta }_i^2}(log\frac{{\pi }^{2}k}{3\delta }+loglog\frac{8}{\eta i^2}+1)$, then the corresponding value of ε satisfies ${\epsilon }_m<\frac{{\eta }_i}{4}$.)

By Corollary 3.4, with probability at least 1 − δ, for every i ∈ 1,…, k, every m ≥ 1, and every j ∈ A_m, we have |ν_j,m−µ_j| ≤ ε_m. Therefore, by Lemma 1 the estimates ν₁,…, ν_k returned by the algorithm satisfy the correct ordering property. Furthermore, by Lemma 3, the total number of samples drawn from the ith group by the algorithm is bounded above by $m_i^{\ast }$ and the total number of samples requested by the algorithm is bounded above by

$$\sum _{i=1}^{\kappa }{m}_i^{\ast }=O\left(c^2\sum _{i=1}^{\kappa }\frac{log\left(\frac{\kappa }{\delta }\right)+loglog\left(\frac{1}{{\eta }_i}\right)}{{\eta }_i^2}\right).$$

We have the desired result.

3.4 Computational Complexity

The computational complexity of the algorithm is dominated by the check used to determine if a group is still active. This check can be done in O(log |A|) time per round if we maintain a binary search tree — leading to O(k log k) time per round across all active groups. However, in practice, k will be small (typically less than 100); and therefore, taking an additional sample from a group will dominate the cost of checking if groups are still active.

Then, the number of rounds is the largest value that m will take in Algorithm 1. This is in fact:

$$(log\frac{k}{\delta }+log\frac{1}{\eta })\frac{c^2}{{\eta }^2},$$

where η = min_i η_i. Therefore, we have the following theorem:

Theorem 3.7. The computational complexity of the IFocus algorithm is: $O(klog(k)(log\frac{k}{\delta }+log\frac{1}{\eta })\frac{c^2}{{\eta }^2})$.

3.5 Lower bounds on Sample Complexity

We now show that the sample complexity of IFocus is optimal as compared to any algorithm for Problem 1, up to a small additive factor, and constant multiplicative factors.

Theorem 3.8 (Lower Bound). Any algorithm that satisfies the correct ordering condition with probability at least 1 − δ must make at least $\mathrm{\Omega }(log(\frac{k}{\delta }){\sum }_{i=1}^k\frac{c^2}{{\eta }_i^2})$ queries.

Comparing the expression above to Equation 4, the only difference is a small additive term: $\frac{c^2}{{\eta }_i^2}loglog(\frac{1}{{\eta }_i})$, which we expect to be much smaller than $\frac{c^2}{{\eta }_i^2}log(\frac{k}{\delta })$. Note that even when $\frac{1}{{\eta }_i}$ is 10⁹ (a highly unrealistic scenario), we have that $loglog\frac{1}{{\eta }_i}<5$, whereas $log\frac{k}{\delta }$ is greater than 5 for most practical cases (e.g., when k = 10, δ = 0.05).

The starting point for our proof of this theorem is a lower bound for sampling due to Canetti, Even, and Goldreich [7].

Theorem 3.9 (Canetti–Even–Goldreich [7]). Let $\varepsilon \le \frac{1}{8}$ and $\delta \le \frac{1}{6}$. Any algorithm that estimates μ_i within error ±ε with confidence 1−δ must sample at least $\frac{1}{8{\varepsilon }^2}\text{ln}(\frac{1}{16e\sqrt{\pi }\delta })$ elements from S_i in expectation.

In fact, the proof of this theorem yields a slightly stronger result: even if we are promised that ${\mu }_i\in \{\frac{1}{2}-\varepsilon ,\frac{1}{2}+\varepsilon \}$, the same number of samples is required to distinguish between the two cases.

The proof of Theorem 3.8 is omitted due to lack of space, and can be found in the extended technical report [34].

3.6 Discussion

We now describe a few variations of our algorithms.

Visual Resolution Extension

Recall that in Section 2, we discussed Problem 2, wherein our goal is to only ensure that groups whose true averages are sufficiently far enough to be correctly ordered. If the true averages of the groups are too close to each other, then they cannot be distinguished on a visual display, so expending resources resolving them is useless.

If we only require the correct ordering condition to hold for groups whose true averages differ by more than some threshold r, we can simply modify the algorithm to terminate once we reach a value of m for which ε_m < r/4. The sample complexity for this variant is essentially the same as in Theorem 3.6 (apart from constant factors) except that we replace each η_i with ${\eta }_i^{(r)}=max\{{\eta }_i,r\}$.

Alternate Algorithm

The original algorithm we considered relies on the standard and well-known Chernoff-Hoeffding inequality [48]. In essence, the algorithm—which we refer to as IRefine, like IFocus, once again maintains confidence intervals for groups, and stops sampling from inactive groups. However, instead of taking one sample per iteration, IRefine takes as many samples as necessary to divide the confidence interval in two. Thus, IRefine is more aggressive than IFocus. We provide the algorithm, the analysis, and the pseudocode in our technical report [34]. Needless to say, IRefine, since it is so aggressive, ends up with a less desirable sample complexity than IFocus, and unlike IFocus, IRefine is not optimal. We will consider IRefine in our experiments.

4. System Description

We evaluated our algorithms on top of a new database system we are building, called NeedleTail, that is designed to produce a random sample of records matching a set of ad-hoc conditions. To quickly retrieve satisfying tuples, NeedleTail uses in-memory bitmap-based indexes. We refer the reader to the demonstration paper for the full description of NeedleTail's bitmap index optimizations [35]. Traditional in-memory bitmap indexes allow rapid retrieval of records matching ad-hoc user-specified predicates. In short, for every value of every attribute in the relation that is indexed, the bitmap index records a 1 at location i when the ith tuple matches the value for that attribute, or a 0 when the tuple does not match that value for that attribute. While recording this much information for every value of every attribute could be quite costly, in practice, bitmap indexes can be compressed significantly, enabling us to store them very compactly in memory [36,49,50]. NeedleTail employs several other optimizations to store and operate on these bitmap indexes very efficiently. Overall, NeedleTail's in-memory bitmap indexes allow it to retrieve and return a tuple from disk matching certain conditions in constant time. Note that even if the bitmap is dense or sparse, the guarantee of constant time continues to hold because the bitmaps are organized in a hierarchical manner (hence the time taken is logarithmic in the total number of records or equivalently the depth of the tree). NeedleTail can be used in two modes: either a column-store or a row-store mode. For the purpose of this paper, we use the row-store configuration, enabling us to eliminate any gains originating from the column-store. NeedleTail is written in C++ and uses the Boost library for its bitmap and hash map implementations.

5. Experiments

In this section, we experimentally evaluate our algorithms versus traditional sampling techniques on a variety of synthetic and real-world datasets. We evaluate the algorithms on three different metrics: the number of samples required (sample complexity), the accuracy of the produced results, and the wall-clock runtime performance on our prototype sampling system, NeedleTail.

5.1 Experimental Setup

Algorithms

Each of the algorithms we evaluate takes as a parameter δ, a bound on the probability that the algorithm returns results that do not obey the ordering property. That is, all the algorithms are guaranteed to return results ordered correctly with probability 1 − δ, no matter what the data distribution is.

The algorithms are as follows:

• IFocus (δ): In each round, this algorithm takes an additional sample from all active groups, ensuring that the eventual output has accuracy greater than 1 − δ, as described in Section 3.1. This algorithm is our solution for Problem 1.

• IFocusR (δ,r): In each round, this algorithm takes an additional sample from all active groups, ensuring that the eventual output has accuracy greater than 1 − δ, for a relaxed condition of accuracy based on resolution. Thus, this algorithm is the same as the previous, except that we stop at the granularity of the resolution value. This algorithm is our solution for Problem 2.

• IRefine (δ): In each round, this algorithm divides all confidence intervals by half for all active groups, ensuring that the eventual output has accuracy greater than 1 − δ, as described in Section 3.6. Since the algorithm is aggressive in taking samples to divide the confidence interval by half each time, we expect it to do worse than IFocus.

• IRefineR (δ, r): This is the IRefine algorithm except we relax accuracy based on resolution as we did in IFocusR.

We compare our algorithms against the following baseline:

• RoundRobin (δ): In each round, this algorithm takes an additional sample from all groups, ensuring that the eventual output respects the order with probability than 1 − δ. This algorithm is similar to conventional stratified sampling schemes [8], except that the algorithm has the guarantee that the ordering property is met with probability greater than 1 − δ. We adapted this from existing techniques to ensure that the ordering property is met with probability greater than 1 − δ. We cannot leverage any pre-existing techniques since they do not provide the desired guarantee.

• RoundRobinR (δ, r): This is the RoundRobin algorithm except we relax accuracy based on resolution as we did in IFocusR.

System

We evaluate the runtime performance of all our algorithms on our early-stage NeedleTail prototype. We measure both the CPU times and the I/O times in our experiments to definitively show that our improvements are fundamentally due to the algorithms rather than skilled engineering. In addition to our algorithms, we implement a Scan operation in NeedleTail, which performs a sequential scan of the dataset to find the true means for the groups in the visualization. The Scan operation represents an approach that a more traditional system, such as PostgreSQL, would take to solve the visualization problem. Since we have both our sampling algorithms and Scan implemented in NeedleTail, we may directly compare these two approaches. We ran all experiments on a 64-core Intel Xeon E7-4830 server running Ubuntu 12.04 LTS; however, all our experiments were single-threaded. We use 1MB blocks to read from disk, and all I/O is done using Direct I/O to avoid any speedups we would get from the file buffer cache. Note that our NeedleTail system is still in its early stages and under-optimized — we expect our performance numbers to only get better as the system improves.

Key Takeaways

Here are our key results from experiments in Sections 5.2 and 5.3:

1. Our IFocus and IFocusR (r=l%) algorithms yield

   • up to 80% and 98% reduction in sampling and 79% and 92% in runtime (respectively) as compared to RoundRobin, on average, across a range of very large synthetic datasets, and
   • up to 70% and 85% reduction in runtime (respectively) as compared to RoundRobin, for multiple attributes in a realistic, large flight records dataset [18].

2. The results of our algorithms (in all of the experiments we have conducted) always respect the correct ordering property.

5.2 Synthetic Experiments

We begin by considering experiments on synthetic data. The datasets we ran our experiments on are as follows:

• Mixture of Truncated Normals (mixture): For each group, we select a collection of normal distributions, in the following way: we select a number sampled at random from {1, 2, 3, 4, 5}, indicating the number of truncated normal distributions that comprise each group. For each of these truncated normal distributions, we select a mean σ sampled at random from [0, 100], and a variance Δ sampled at random from [1, 10]. We repeat this for each group.

• Hard Bernoulli (hard): Given a parameter γ < 2, we fix the mean for group i to be 40 + γ × i, and then construct each group by sampling between two values {0, 100} with bias equal to the mean. Note that in this case, η, the smallest distance between two means, is equal to γ. Recall that c²/η² is a proxy for how difficult the input instance is (and therefore, how many samples need to be taken). We study this scenario so that we can control the difficulty of the input instance.

Our default setup consists of k = 10 groups, with 10M records in total, equally distributed across all the groups, with δ = 0.05 (the failure probability) and r = 1. Each data-point is generated by repeating the experiment 100 times. That is, we construct 100 different datasets with each parameter value, and measure the number of samples taken when the algorithms terminate, whether the output respects the correct ordering property, and the CPU and I/O times taken by the algorithms. For the algorithms ending in R, i.e., those designed for a more relaxed property leveraging resolution, we check if the output respects the relaxed property rather than the more stringent property. We focus on the mixture distribution for most of the experimental results, since we expect it to be the most representative of real world situations, using the hard Bernoulli in a few cases. We have conducted extensive experiments with other distributions as well, and the results are similar. The complete experimental results can be found in our technical report [34].

Variation of Sampling and Runtime with Data Size

We begin by measuring the sample complexity and wall-clock times of our algorithms as the data set size varies.

Summary: Across a variety of dataset sizes, our algorithm IFocusR (respectively IFocus) performs better on sample complexity and runtime than IRefineR (resp. IRefine) which performs significantly better than RoundRobinR (resp. RoundRobin). Further, the resolution improvement versions take many fewer samples than the ones without the improvement. In fact, for any dataset size greater than 10⁸, the resolution improvement versions take a constant number of samples and still produce correct visualizations.

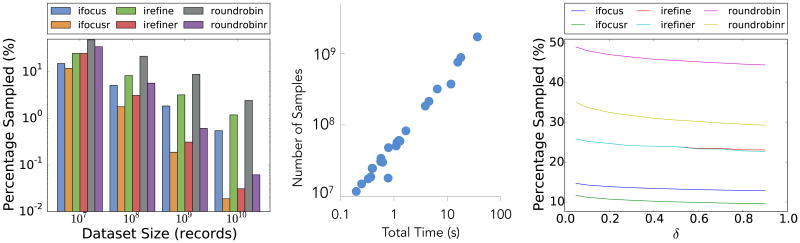
Figure 3(a) shows the percentage of the dataset sampled on average as a function of dataset size (i.e., total number of tuples in the dataset across all groups) for the six algorithms above. The data size ranges from 10⁷ records to 10¹⁰ records (hundreds of GB). Note that the figure is in log scale.

Figure 3. (a) Impact of data size (b) Scatter plot of samples vs runtime (c) Impact of δ.

Consider the case when dataset size = 10⁷ in Figure 3(a). Here RoundRobin samples ≈50% of the data, while RoundRobinR samples around 35% of the dataset. On the other hand, our IRefine and IRefineR algorithms both sample around 25% of the dataset, while IFocus samples around 15% and IFocusR around 10% of the dataset. Thus, compared to the vanilla RoundRobin scheme, all our algorithms reduce the number of samples required to reach the order guarantee, by up to 3×. This is because our algorithms focus on the groups that are actually contentious, rather than sampling from all groups uniformly.

As we increase the dataset size, we see that the sample percentage decreases almost linearly for our algorithms, suggesting that there is some fundamental upper bound to the number of samples required, confirming Theorem 3.6. With resolution improvement, this upper bound becomes even more apparent. In fact, we find that the raw number of records sampled for IFocusR, IRefineR, and RoundRobinR all remained constant for dataset sizes greater or equal to 10⁸. In addition, as expected, IFocusR (and IFocus) continue to outperform all other algorithms at all dataset sizes.

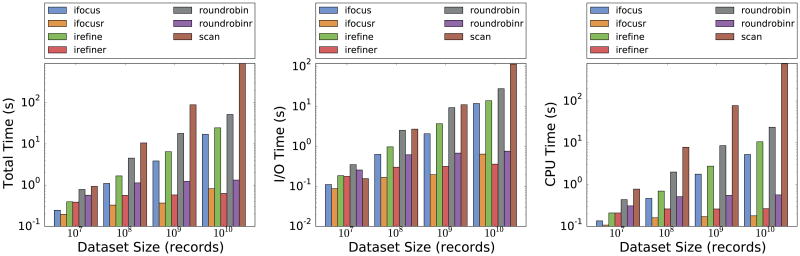
The wall-clock total, I/O, and cpu times for our algorithms running on NeedleTail can be found in Figures 4(a), 4(b), and 4(c), respectively, also in log scale. Figure 4(a) shows that for a dataset of size of 10⁹ records (8GB), IFocus/IFocusR take 3.9/0.37 seconds to complete, IRefine/IRefineR take 6.5/0.58 seconds to complete, RoundRobin/RoundRobinR take 18/1.2 seconds to complete, and Scan takes 89 seconds to complete. This means that IFocus/IFocusR has a 23× speedup and 241× speedup relative to Scan in producing accurate visualizations.

Figure 4. (a) Total time vs dataset size (b) I/O time vs dataset size (c) CPU time vs dataset size.

As the dataset size grows, the runtimes for the sampling algorithms also grow, but sublinearly, in accordance to the sample complexities. In fact, as alluded earlier, we see that the run times for IFocusR, IRefineR, and RoundRobinR are nearly constant for all dataset sizes greater than 10⁸ records. There is some variation, e.g., in I/O times for IFocusR at 10¹⁰ records, which we believe is due to random noise. In contrast, Scan yields linear scaling, leading to unusably long wall-clock (i.e., 898 seconds at 10¹⁰ records.)

We note that not only does IFocus beat out RoundRobin, and RoundRobin beat out Scan for every dataset size in total time, but this remains true for both I/O and CPU time as well. Sample complexities explain why IFocus should beat RoundRobin. It is more surprising that IFocus, which uses random I/O, outperforms Scan, which only uses sequential I/O. The answer is that so few samples are required the cost of additional random I/O is exceeded by the additional scan time; this becomes more true as the dataset size increases. As for CPU time, it highly correlated with the number of samples, so algorithms that operate on a smaller number of records outperform algorithms that need more samples.

The reason that CPU time for Scan is actually greater than the I/O time is that for every record read, it must update the mean and the count in a hash map keyed on the group. While Boost's unordered_map implementation is very efficient, our disk subsystem is able to read about 800 MB/sec, and a single thread on our machine can only perform about 10 M hash probes and updates / sec. However, even if we discount the CPU overhead of Scan, we find that total wall-clock time for IFocus and IFocusR is at least an order of magnitude better than just the I/O time for Scan. For 10¹⁰ records, compared to Scan's 114 seconds of sequential I/O time, IFocus has a total runtime of 13 seconds, and IFocusR has a total runtime in 0.78 seconds, giving a speedup of at least 146× for a minimal resolution of 1%.

Finally, we relate the runtimes of our algorithms to the sample complexities with the scatter plot presented in Figure 3(b). The points on this plot represent the number of samples versus the total execution times of our sampling algorithms (excluding Scan) for varying dataset sizes. As is evident, the runtime is directly proportional to the number of samples. With this in mind, for the rest of the synthetic datasets, we focus on sample complexity because we believe it provides a more insightful view into the behavior of our algorithms as parameters are varied. We return to runtime performance when we consider real datasets in Section 5.3.

Variation of Sampling and Accuracy with δ

We now measure how δ (the user-specified probability of error) affects the number of samples and accuracy.

Summary: For all algorithms, the percentage sampled decreases as δ increases, but not by much. The accuracy, on the other hand, stays constant at 100%, independent of δ. Sampling any less to estimate the same confidence intervals leads to significant errors.

Figure 3(c) shows the effect of varying δ on the sample complexity for the six algorithms. As can be seen in the figure, the percentage of data sampled reduces but does not go to 0 as δ increases. This is because the amount of sampling (as in Equation 4) is the sum of three quantities, one that depends on log k, the other on log δ, and another on log log(1/η_i). The first and last quantities are independent of δ, and thus the number of samples required is non-zero even as δ gets close to 1. The fact that sampling is nonzero when δ is large is somewhat disconcerting; to explore whether this level of sampling is necessary, and whether we are being too conservative, we examine the impact of sampling less on accuracy (i.e., whether the algorithm obeys the desired visual property).

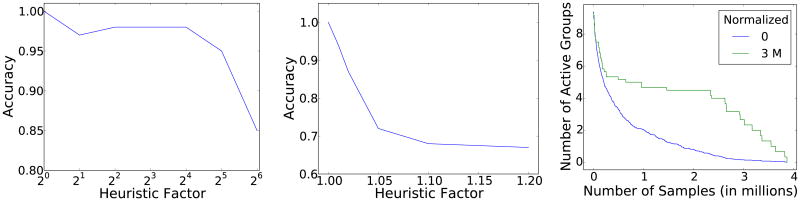
We focus on IFocusR and consider the impact of shrinking confidence intervals at a rate faster than prescribed by IFocus in Line 6 of Algorithm 1. We call this rate the heuristic factor: a heuristic factor of 4 means that we divide the confidence interval as estimated by Line 6 by 4, thereby ensuring that the confidence interval overlaps are fewer in number, allowing the algorithms to terminate faster. We plot the average accuracy (i.e., the fraction of times the algorithm violates the visual ordering property) as a function of the heuristic factor in Figure 5(a) for δ = 0.05 (other δs give identical figures, as we will see below).

Figure 5. (a) Impact of heuristic shrinking factor on accuracy (b) Impact of heuristic shrinking factor for a harder case (c) Studying the number of active intervals as computation proceeds.

First, consider heuristic factor 1, which directly corresponds to IFocusR. As can be seen in the figure, IFocusR has 100% accuracy: the reason is that IFocusR ends up sampling a constant amount to ensure that the confidence intervals do not overlap, independent of δ, enabling it to have perfect accuracy for this δ. In fact, we find that all our 6 algorithms have accuracy 100%, independent of δ and the data distributions; thus, our algorithms not only provide much lower sample complexity, but also respect the visual ordering property on all datasets.

Next, we see that as we increase the heuristic factor, the accuracy immediately decreases (roughly monotonically) below 100%, Surprisingly, even with a heuristic factor of 2, we start making mistakes at a rate greater than 2 – 3% independent of δ. Thus, even though our sampling is conservative, we cannot do much better, and are likely to make errors by shrinking confidence intervals faster than prescribed by Algorithm 1. To study this further, we plotted the same graph for the hard case with γ = 0.1 (recall that γ = η for this case), in Figure 5(b). Here, once again, for heuristic factor 1, i.e., IFocusR, the accuracy is 100%. On the other hand, even with a heuristic factor of 1.01, where we sample just 1% less to estimate the same confidence interval, the accuracy is already less than 95%. With a heuristic factor of 1.2, the accuracy is less than 70%! This result indicates that we cannot shrink our confidence intervals any faster than IFocusR does, since we may end up making up making far more mistakes than is desirable—even sampling just 1% less can lead to critical errors.

Overall, the results in Figures 5(a) and 5(b) are in line with our theoretical lower bound for sampling complexity, which holds no matter what the underlying data distribution is. Furthermore, we find that algorithms backed by theoretical guarantees are necessary to ensure correctness across all data distributions (and heuristics may fail at a rate higher than δ).

Rate of Convergence

In this experiment, we measure the rate of convergence of the IFocus algorithms in terms of the number ofgroups that still need to be sampled as the algorithms run.

Summary: Our algorithms converge very quickly to a handful of active groups. Even when there are still active groups, the number of incorrectly ordered groups is very small.

Figure 5(c) shows the average number of active groups as a function of the amount of sampling performed for IFocus, over a set of 100 datasets of size 10M. It shows two scenarios: 0, when the number of samples is averaged across all 100 datasets and 3M, when we average across all datasets where at least three million samples were taken. For 0, on average, the number of active groups after the first 1M samples (i.e., 10% of the 10M dataset), is just 2 out of 10, and then this number goes down slowly after that. The reason for this is that, with high probability, there will be two groups whose μ_i values are very close to each other. So, to verify if one is greater than the other, we need to do more sampling for those two groups, as compared to other groups whose η_i (the distance to the closest mean) is large—those groups are not active beyond 1M samples. For the 3M plot, we find that the number of samples necessary to reach 2 active groups is larger, close to 3.5M for the 3M case.

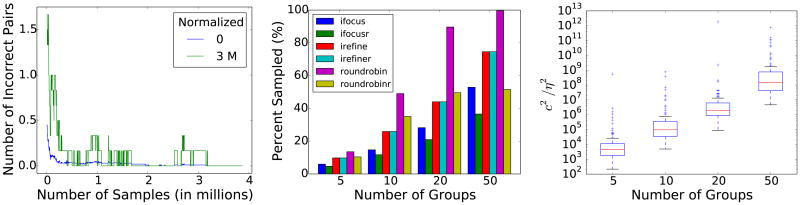
Next, we investigate if the current estimates v_i, …, v_k respect the correct ordering property, even though some groups are still active. To study this, we depict the number of incorrectly ordered pairs as a function of the number of samples taken, once again for the two scenarios described above. As can be seen in Figure 6(a), even though the number of active groups is close to two or four at 1M samples, the number of incorrect pairs is very close to 0, but often has small jumps — indicating that the algorithm is correct in being conservative and estimating that the we haven't yet identified the actual ordering. In fact, the number of incorrect pairs is nonzero up to as many as 3M samples, indicating that we cannot be sure about the correct ordering without taking that many samples. At the same time, since the number of incorrect pairs is small, if we are fine with displaying somewhat incorrect results, we can show the current results to to the user.

Figure 6. (a) Studying the number of incorrectly ordered pairs as computation proceeds (b) Impact of number of groups on sampling (c) Evaluating the difficulty as a function of number of groups.

Variation of Sampling with Number of Groups

We now look at how the sample complexity varies with the number of groups.

Summary: As the number of groups increases, the amount of sampling increases for all algorithms as an artifact of our data generation process.

To study the impact of the number of groups on sample complexity, we generate 100 synthetic datasets of type mixture where the number of groups varies from 5 to 50, and plot the percentage of the dataset sampled as a function of the dataset size. Each group has 1M items. We plot the results in Figure 6(b). As can be seen in the figure, our algorithms continue to give significant gains even when the number of groups increases from 5 to 50. However, we notice that the amount of sampling increases for IFocusR as the number of groups is increased, from less than 10% for 5 groups to close to 40% for 50 groups.

The higher sample complexity can be attributed to the dataset generation process. As a proxy for the “difficulty” of a dataset, Figure 6(c) shows the average c²/η² as a function of the number of groups (recall that η is the minimum distance between two means, c is the range of all possible values, and that the sample complexity depends on c²/η²) The figure is a a box-and-whiskers plot with the y-axis on a log scale. Note that the average difficulty increases from 10 for 5 to 10⁸ for 50–a 4 orders of magnitude increase! Since we are generating means for each group at random, it is not surprising that the more groups, the higher the likelihood that two randomly generated means will be close to each other.

Additional Experiments

In the extended technical report [34], we present additional experiments, including:

• Dataset Skew: Our algorithms continue to provide significant gains in the presence of skew in the underlying dataset.

• Variance: Sample complexities of our algorithms vary slightly with variance; sampling increases by 1-2% as variance increases.

5.3 Real Dataset Experiments

We next study the impact of our techniques on a real dataset.

Summary: IFocus and IFocusR take 50% fewer samples than RoundRobin irrespective of the attribute visualized.

For our experiments on real data, we used a flight records data set [18]. The data set contains the details of all flights within the usa from 1987–2008, with nearly 120 million records, taking up 12 GB uncompressed. From this flight data, we generated datasets of sizes 120 million records (2.4GB) and scaled-up 1.2 billion (24GB) and 12 billion records (240GB) for our experiments using probability density estimation. We focused on comparing our best algorithms—IFocus and IFocusR (r=1%)—versus the conventional sampling—RoundRobin We evaluate the runtime performance for visualizing the averages for three attributes: Elapsed Time, Arrival Delay, and Departure Delay, grouped by Airline. For all algorithms and attributes, the orderings returned were correct.

The results are presented in Table 3. The first four rows correspond to the attribute Elapsed Time. Here, RoundRobin takes 32.6 seconds to return a visualization, whereas IFocus takes only 9.70 seconds (3× speedup) and IFocusR takes only 5.04 seconds (6× speedup). We see similar speedups for Arrival Delay and Departure Delay as well. As we move from the 10⁸ dataset to 10¹⁰ dataset, we see the run times roughly double for a 100× scale-up in the dataset. The reason for any increase at all in the runtime comes from the highly conflicting groups with means very close to one another. Our sampling algorithms may read all records in the group for these groups with with η_i values. When the dataset size is increased to allow for more records to sample from, our sampling algorithms take advantage of this and sample more from the conflicting groups, leading to larger run times.

Table 3. Real Data Experiments.

Attribute	Algorithm	108 (s)	109 (s)	1010 (s)
Elapsed Time	RoundRobin	32.6	56.5	58.6
	IFocus	9.70	10.8	23.5
	IFocusR (1%)	5.04	6.64	8.46
Arrival Delay	RoundRobin	47.1	74.1	77.5
	IFocus	29.2	48.7	67.5
	IFocusR (1%)	9.81	15.3	16.1
Departure Delay	RoundRobin	41.1	72.7	76.6
	IFocus	14.3	27.5	44.3
	IFocusR (1%)	9.19	15.7	16.0

Regardless, we show that even on a real dataset, our sampling algorithms are able to achieve up to a 6× speedup in runtime compared to round-robin. We could achieve even higher speedups if we were willing to tolerate a higher minimum resolution.

6. Related Work

The work related to our paper can be placed in a few categories:

Approximate Query Processing

There are two categories of related work in approximate query processing: online, and offline. We focus on online first since it is more closely related to our work.

Online aggregation [25] is perhaps the most related online approximate query processing work. It uses conventional round-robin stratified sampling [8] (like RoundRobin) to construct confidence intervals for estimates of averages of groups. In addition, online aggregation provides an interactive tool that allows users to stop processing of certain groups when their confidence is “good enough”. Thus, the onus is on the user to decide when to stop processing groups (if not, stratified sampling is employed for all groups). Here, since our target is a visualization with correct properties, IFocus automatically decides when to stop processing groups. Hence, we remove the burden on the user, and prevent the user from stopping a group too early (making a mistake), or too late (doing extra work).

There are other papers that also use round-robin stratified sampling for various purposes, primarily for COUNT estimation respecting real-time constraints [28], respecting accuracy constraints (e.g., ensuring that confidence intervals shrink to a pre-specified size) without indexes [27], and with indexes [23, 37].

Since visual guarantees in the form of relative ordering is very different from the kind of objectives prior work in online approximate query processing considered, our techniques are quite different. Most papers on online sampling for query processing, including [25, 27, 28, 37], either use uniform random sampling or round-robin stratified sampling. Uniform random sampling is strictly worse than round-robin stratified sampling (e.g., if the dataset is skewed) and in the best case is going to be only as good, which is why we chose not to compare it in the paper. On the other hand, we demonstrate that conventional sampling schemes like round-robin stratified sampling sample a lot more than our techniques.

Next, we consider offline approximate query processing. Over the past decade, there has been a lot of work on this topic; as examples, see [9, 20, 30]. Garofalakis et al. [19] provides a good survey of the area; systems that support offline approximate query processing include BlinkDB [3] and Aqua [2]. Typically, offline schemes achieve a user-specified level of accuracy by running the query on a sample of a database. These samples are chosen a-priori, typically tailored to a workload or a small set of queries [1, 4, 5, 10, 29]. In our case, we do not assume the presence of a precomputed sample, since we are targeting ad-hoc visualizations. Even when pre-computing samples, a common strategy is to use Neyman Allocation [12], like in [11, 31], by picking the number of samples per strata to be such that the variance of the estimate from each strata is the same. In our case, since we do not know the variance up front from each strata (or group), this defaults once again to round-robin stratified sampling. Thus, we believe that round-robin stratified sampling is an appropriate and competitive baseline, even here.

Statistical Tests

There are a number of statistical tests [8,48] used to tell if two distributions are significantly different, or whether one hypothesis is better than a set of hypotheses (i.e., statistical hypothesis testing). Hypothesis testing allows us to determine, given the data collected so far, whether we can reject the null hypothesis. The t-test [8] specifically allows us to determine if two normal distributions are different from each other, while the Whitney-Mann-U-test [41] allows us to determine if two arbitrary distributions are different from each other, None of these tests can be directly applied to decide where to sample from a collection of sets to ensure that the visual ordering property is preserved.

Visualization Tools

Over the past few years, the visualization community has introduced a number of interactive visualization tools such as ShowMe, Polaris, Tableau, and Profiler [24, 32, 46]. Similar visualization tools have also been introduced by the database community, including Fusion Tables [21], VizDeck [33], and Devise [40]. A recent vision paper [42] has proposed a tool for recommending interesting visualizations of query results to users. All these tools could benefit from the algorithms outlined in this paper to improve performance while preserving visual properties.

Scalable Visualization

There has been some recent work on scalable visualizations from the information visualization community as well. Immens [39] and Profiler [32] maintain a data cube in memory and use it to support rapid user interactions. While this approach is possible when the dimensionality and cardinality is small (e.g., for simple map visualizations of a single attribute), it cannot be used when ad-hoc queries are posed. A related approach uses precomputed image tiles for geographic visualization [15].

Other recent work has addressed other aspects of visualization scalability, including prefetching and caching [13], data reduction [6] leveraging time series data mining [14], clustering and sorting [22, 43], and dimension reduction [51]. These techniques are orthogonal to our work, which focuses on speeding up the computation of a single visualization online.

Recent work from the visualization community has also demonstrated via user studies on simulations that users are satisfied with uncertain visualizations generated for algorithms like online aggregation, as long as the visualization shows error bars [16, 17]. This work supports our core premise, that analysts are willing to use inaccurate visualizations as long as the trends and comparisons of the output visualizations are accurate.

Learning to Rank

The goal of learning to rank [38] is the following: given training examples that are ranked pairs of entities (with their features), learn a function that correctly orders these entities. While the goal of ordering is similar, in our scenario we assume no relationships between the groups, nor the presence of features that would allow us to leverage learning to rank techniques.

7. Conclusions

Our experience speaking with data analysts is indeed that they prefer quick visualizations that look similar to visualizations that are computed on the entire database. Overall, increasing interactivity (by speeding up the processing of each visualization, even if it is approximate) can be a major productivity boost. As we demonstrated in this paper, we are able to generate visualizations with correct visual properties on querying less than 0.02% of the data on very large datasets (with 10¹⁰ tuples), giving us a speed-up of over 60× over other schemes (such as RoundRobin) that provide similar guarantees, and 1000× over the scheme that simply generates the visualization on the entire database.