Visualizing Functional Pathways in the Human Brain Using Correlation Tensors and Magnetic Resonance Imaging

Abstract

Functional magnetic resonance imaging usually detects changes in blood oxygenation level dependent (BOLD) signals from T₂*-sensitive acquisitions, and is most effective in detecting activity in brain cortex which is irrigated by rich vasculature to meet high metabolic demands. We recently demonstrated that MRI signals from T₂*-sensitive acquisitions in a resting state exhibit structure-specific temporal correlations along white matter tracts. In this report we validate our preliminary findings and introduce spatio-temporal functional correlation tensors to characterize the directional preferences of temporal correlations in MRI signals acquired at rest. The results bear a remarkable similarity to data obtained by diffusion tensor imaging but without any diffusion-encoding gradients. Just as in gray matter, temporal correlations in resting state signals may reflect intrinsic synchronizations of neural activity in white matter. Here we demonstrate that functional correlation tensors are able to visualize long range white matter tracts as well as short range sub-cortical fibers imaged at rest, and that evoked functional activities alter these structures and enhance the visualization of relevant neural circuitry. Furthermore, we explore the biophysical mechanisms underlying these phenomena by comparing pulse sequences, which suggest that white matter signal variations are consistent with hemodynamic (BOLD) changes associated with neural activity. These results suggest new ways to evaluate MRI signal changes within white matter.

1. INTRODUCTION

Functional magnetic resonance imaging (fMRI) usually detects hemodynamic changes associated with neural activity on the basis of blood oxygenation level dependent (BOLD) contrast, and is well established as the primary neuroimaging technique for studying the functional architecture of the brain and correlating regional activities over time (1–3). Since 1990, fMRI has been widely adopted by the neuroscience community, and has permeated many aspects of brain research, including studies of human sensory and cognitive processes and their changes with development, aging or pathological disorders.

The vast majority of fMRI studies have been focused on brain gray matter (4), in which significant changes in blood flow and oxygenation in response to variations in neural activity are known to occur, and there has been only a very limited number of reports of corresponding changes in white matter to date (5–7). The dearth of fMRI literature on white matter is conventionally attributed to an absence of significant hemodynamic changes within white matter in response to changes in electrical activity, so that any corresponding weak BOLD signals are not reliably detectable by current means. Compared to gray matter, white matter is irrigated by much less dense vasculature (8), with blood flow approximately one-fourth of that in the gray matter (9). Even if BOLD changes occur, they may produce much smaller effects. However, despite this four-fold reduction in blood flow, it has been found that the oxygen extraction fraction is relatively uniform in the resting brain (9). Thus it is at least plausible that white matter may also elicit BOLD signals that may be detected with more sensitive technology or more appropriate processing algorithms. Indeed, recent investigations in which high field MRI and prudently chosen task paradigms were employed have reported reliable detection of white matter activations (10). However, we also should emphasize that task-evoked activation is not a necessary prerequisite for the existence of resting state correlations in baseline signals.

We first reported our preliminary observations that MRI signals from T₂*-sensitive acquisitions in a resting state exhibit structure-specific temporal correlations in white matter by examining a small set of normal brains at rest (11), but we hypothesized that appropriate analysis of such signals may reveal new insights into white matter structure and represent an important type of functional synchrony which heretofore has been overlooked. In this report, we confirm the validity and significance of resting state correlations, and provide evidence of the biophysical basis of their origins. We introduce a new mathematical construct we call functional correlation tensors (FCTs) that quantifies the correlational anisotropy of resting state MRI signals among neighboring voxels in the brain. In gray matter these tensors tend to be isotropic except at the boundaries of functional domains. In white matter, the tensors tend to be anisotropic with the dominant direction grossly consistent with that of local fibers found independently by diffusion tensor imaging. These FCTs can thus be used not only to visualize white matter structures over large distances, but also to provide an entirely new way to characterize functional organization in the human brain.

We first demonstrate the ability of FCTs for depicting various fiber pathways that include the genu and splenium of corpus callosum, cingulum fibers, portions of arcuate fasciculus, and sub-cortical U-fibers, based solely on analysis of anisotropic resting state correlations of MRI signals without any prior knowledge and without any use of diffusion-encoding gradients. Second, we stimulate localized functional activity and demonstrate how these FCTs change with engagement of function and can be used to highlight pathways that are involved in these tasks. To evaluate the underlying biophysical mechanisms, we have carried out multi-echo imaging experiments with T₂*- and T₂-sensitive acquisitions acquired at different echo times, and examined the impact of different levels of T₂* and T₂ contrast on the correlational anisotropy of the signals in white matter.

2. METHODS

Human MRI data were acquired from 22 healthy subjects whose age spanned from ten years to middle-aged adults. Prior to imaging, informed consent was obtained from each subject according to protocols approved by the Vanderbilt University Institutional Review Board. All human imaging was performed on a 3T Philips Achieva scanner (Philips Healthcare, Inc., Best, Netherlands) using a 32-channel head coil. Subjects lay in a supine position with eyes closed except when performing functional tasks.

All fMRI time series acquired were corrected for slice timing and head motion using SPM software (http://www.fil.ion.ucl.ac.uk/spm/software) with our standard protocol (12). Subjects with head motion more than 4 mm of translation or 4° of rotation in any direction were excluded. Prior to analysis, a global time course of each dataset was removed by intensity normalization. Voxels in each time series were band-pass filtered to retain frequencies only of 0.01–0.08 Hz. To provide anatomical references, 3D high resolution T₁-weighted images were acquired using a multi-shot gradient echo (GE) sequence at voxel size of 1×1×1mm³, and co-registered with the mean fMRI data volume from the same subject. The subjects participated in four experimental studies, with details of imaging and analysis procedures given below.

2.1. Imaging in a resting state

T₂*-sensitive data from ten college students (5 males, age range = [18, 23]) in a resting state were collected, as well as diffusion weighted images (DWI) that were acquired during the same session.

Imaging protocol

Images sensitive to BOLD contrast were acquired using a GE, echo planar imaging (EPI) sequence and the following parameters: TR=2 s, TE=35 ms, matrix size= 80×80, FOV= 240×240 mm², 34 axial slices of 3.5 mm thick with a 0.5 mm gap, and 300 volumes. DWIs were obtained using a single-shot, spin echo (SE) EPI sequence with b=1600 s/mm², 92 diffusion-sensitizing directions, TR=8.5 s, TE=65 ms, SENSE factor=3, matrix size= 96×96, voxel size= 2.5×2.5 mm², 50 axial slices of 2.5 mm thick with zero gap.

Image processing

First, diffusion tensors were constructed from the DWI data using linear least squares fitting (13). Then slice timing and motion corrected T₂*-weighted data were co-registered with the b=0 DWI volume, along with T₁-weighted images acquired.

Construction of spatio-temporal functional correlation tensors

Methods for constructing FCTs from T₂*-weighted time series were described in detail earlier (11). Briefly, to capture intrinsic synchronization and signal correlation profiles, we measure temporal correlations among neighboring voxels and construct a tensor that characterizes directional biases of the correlations. More specifically, for each voxel, we first define a set of unit direction vectors that point to the voxels in its neighborhood, and then compute temporal correlations in T₂*-weighted signals along each of the directions. For a correlation tensor T to be constructed, the estimated correlation C_i projected along a direction vector n_i is

$$C_i={\mathbf{n}}_i·\mathbf{T}·{\mathbf{n}}_i^t,$$ (1)

where t denotes transpose.

Given a set of measured C_i, tensor T can be solved analytically, similar to the construction of diffusion tensors (13). T characterizes the local profile of temporal correlations in MRI signals, with the major eigenvector representing the dominant direction of temporal correlations.

In this experiment, we used a first tier neighborhood of 26 voxels for tensor construction, and chose C to be the squared Pearson’s linear correlation coefficient. Constructions of correlation tensors with the closest 26 neighboring voxels allow analysis of local profiles of MRI signal correlations at the finest scale available from the imaging data. To improve signal-to-noise ratio, the MRI signals were spatially smoothed prior to tensor constructions with a Gaussian filter at a small size of FWHM = 3 mm.

2.2. Imaging in a resting state and with visual stimulations

T₂*-weighted images were acquired from two adults (1 male, age=36; 1 female, age=25) both at a resting state and with visual stimulation, along with DWI data for structural references of fiber pathways.

Imaging protocol

Images sensitive to BOLD contrast were acquired using a T₂*-weighted GE EPI sequence with the following parameters: TR=3 s, TE=45 ms, matrix size= 128×128, FOV=240×240 mm², 34 axial slices of 4 mm thick with zero gap, and 200 volumes. DWIs were acquired with b=1000 s/mm², 32 diffusion-sensitizing directions, TR=10 s, TE=60 ms, SENSE factor=3, matrix size=128×128, voxel size= 2×2mm², 68 axial slices of 2 mm thick with zero gap.

Each subject was scanned twice for T₂*-weighted imaging with identical parameters as above, respectively in a resting state and with visual stimulation. The visual stimuli were a flashing (8 Hz) checkerboard, which were presented in a block design format, starting with 30 seconds of blank screen fixation followed by 30 seconds of flashing checkerboard and so on.

Image processing

Processing of the DWI data and T₂*-weighted signals was the same as in Section 2.1. Prior to constructions of functional correlation tensors, all T₂*-weighted signals were spatially smoothed with a Gaussian filter at FWHM = 2.5 mm.

2.3. Imaging in a resting state and with language task

MRI data from six school children were acquired with a language (reading) task (3 boys, age range = [10, 11]). DWI data were not acquired for this group of subjects because they were also imaged with other tasks that were not used in this study and thus there was insufficient imaging time.

Imaging protocol

Resting state T₂*-weighted signals were acquired using a GE EPI sequence and TR=2.2 s, TE=30 ms, matrix size= 128×128, FOV= 240×240 mm², 40 axial slices of 3 mm thick with zero gap, and 160 volumes. MR images acquired during the language task used the same imaging parameters as above except matrix size= 80×80 and 200 volumes.

The functional task for this experiment was passage-reading. Briefly, Coh-Metrix 2.0 was used to create eight passages that were equivalent across measures of word concreteness, syntactic simplicity, referential cohesion, causal cohesion, and narrativity. All passages were 150 words in length, and were presented one meaningful phrase at a time (details are seen in Ref. 14). The passage-reading was interleaved with reading of unconnected words and baseline as follows: passages – baseline – passages – baseline – words – baseline. The time for the passage block = 78.54±22.94s; baseline block = 47.69±1.48s; and words = 82.45 ±3.29s. The baseline was three non-alphanumeric symbols displayed horizontally on a slide.

Image processing

Slice timing and motion corrected T₂*-weighted data acquired under task conditions were first co-registered with the data acquired at resting state, and both the datasets were spatially smoothed with Gaussian filter at FWHM = 2.5 mm prior to construction of FCTs. In addition, a core language cortex, Broca’s area, was localized with SPM using our standard procedures (12).

2.4. Imaging in a resting state with multi-echo imaging sequences

Two adults (1 male, age=25, 1 female, age=22) were imaged with a multi-echo GE sequence, and two additional adults (1 male, age=26; 1 female, age=25) were imaged with a multi-echo SE sequence as well as with a GE EPI sequence. All the subjects were imaged in a resting state, from whom DWI data were also obtained during the same session.

Imaging protocol

For the first two subjects, images sensitive to T₂* contrast were acquired using a multi-echo GE EPI sequence with the following parameters: TR=3 s, TE=11/31/51/71 ms, matrix size= 80×80, FOV= 240×240 mm², 24 axial slices of 3 mm thick with zero gap, and 200 volumes. For the other two subjects, images sensitive to T₂ contrast were acquired using multi-echo SE EPI sequence and TR=3 s, TE=23/70 ms, matrix size= 80×80, FOV= 240×240 mm², 30 axial slices of 3 mm thick with zero gap, and 145 volumes. In addition, T₂*-weighted images were also acquired from these two subjects using the same parameters as above except TE=45 ms and 43 axial slices. DWIs were acquired from all the four subjects with b=1000 s/mm², 32 diffusion-sensitizing directions, TR=10 s, TE=60 ms, SENSE factor=3, matrix size= 128×128, voxel size= 2×2 mm², 68 axial slices of 2 mm thick with zero gap.

Image processing

Processing of the DWI data and T₂*/T₂-sensitive signals was the same as in the preceding experiments. In addition, from the co-registered multi-echo GE volumes, M₀ and R₂* images were also computed by non-linear fitting. For the multi-echo SE volumes, T₂-sensitive signals from both echoes were co-registered with T₂*-sensitive signals, and all of them were spatially smoothed with a Gaussian filter at FWHM = 3 mm.

Methods for constructing FCTs from the multi-echo T₂*-weighted signals were different from the preceding experiments. First, the T₂*-weighted signals along with M₀ and R₂* images were spatially smoothed with a Gaussian filter at FWHM = 6 mm. Second, a neighborhood with radius of 9 mm was used for constructing FCTs. This approximately doubles the spatial scale in the original image for tensor constructions. Analysis with an increased spatial scale allows more stable assessments of brain structures at a gross level. To facilitate constructions of FCTs with a larger neighborhood of voxels, we employed a dyadic tensor based approach which could handle arbitrary neighborhood sizes and shapes and missing voxels (e.g., at the image boundary or near cerebral-spinal fluid). The method is summarized below.

For a voxel V_i in the brain parenchyma, a Pearson’s linear correlation coefficient (C_ij) was calculated between the time course at V_i and that at V_j within its neighborhood. Then the unit vector n_ij connecting V_i and V_j was computed, from which a dyadic tensor D_ij was obtained (15):

$${\mathbf{D}}_{ij}=\left(\begin{array}{ccc}\hfill n_{ij,x}•n_{ij,x}\hfill & \hfill n_{ij,x}•n_{ij,y}\hfill & \hfill n_{ij,x}•n_{ij,z}\hfill \\ \hfill n_{ij,y}•n_{ij,x}\hfill & \hfill n_{ij,y}•n_{ij,y}\hfill & \hfill n_{ij,y}•n_{ij,z}\hfill \\ \hfill n_{ij,z}•n_{ij,x}\hfill & \hfill n_{ij,z}•n_{ij,y}\hfill & \hfill n_{ij,z}•n_{ij,z}\hfill \end{array}\right),$$ (2)

where n_ij,x, n_ij,y, n_ij,z are respectively 1^st, 2^nd and 3^rd element of the unit vector n_ij. D_ij contains only one non-zero eigenvalue, with corresponding eigenvector pointing to the direction of n_ij. Finally, the correlation tensor T at voxel V_i was defined to be the sum of all dyadic tensors in the neighborhood weighted by C_ij:

$$\mathbf{T}=\sum _j{C}_{ij}{\mathbf{D}}_{ij}.$$ (3)

In this experiment, FCTs were constructed for all the four echo times as well as for M₀ and R₂* images. Power spectra of signals were also computed for each voxel at each echo time in the frequency domain. From the power spectra, we derived the fractional power of low frequency fluctuations, the sum of signal power within the low frequency band of 0.01–0.08 Hz divided by the total signal power for all frequencies >0 (16). Fluctuations at this low frequency in gray matter are thought to reflect spontaneous brain activity in a resting state (3). The fractional power was characterized for gray and white matter separately. This was achieved by segmenting T₁-weighted images into gray and white matter, and computing the fractional power in T₂*-weighted signals in 15 slices around the middle portion of the brain (where segmentation was least ambiguous), which was then averaged individually for gray and white matter.

3. RESULTS

Among the 22 healthy subjects studied, data from three subjects were excluded due to excessive motion, leaving a total of 19 subjects for further analysis. For each subject, spatio-temporal functional correlation tensors were constructed, as well as conventional diffusion tensors (except in Section 3.3.). The results are presented with radiologic view conventions (image right = subject left), and the scheme for color coding follows that adopted by the MRI community: red = left-right direction, green = anterior-posterior direction, blue = inferior-superior direction.

3.1. Spatio-temporal functional correlation tensors obtained from resting state acquisitions visualize long range white matter tracts in brain

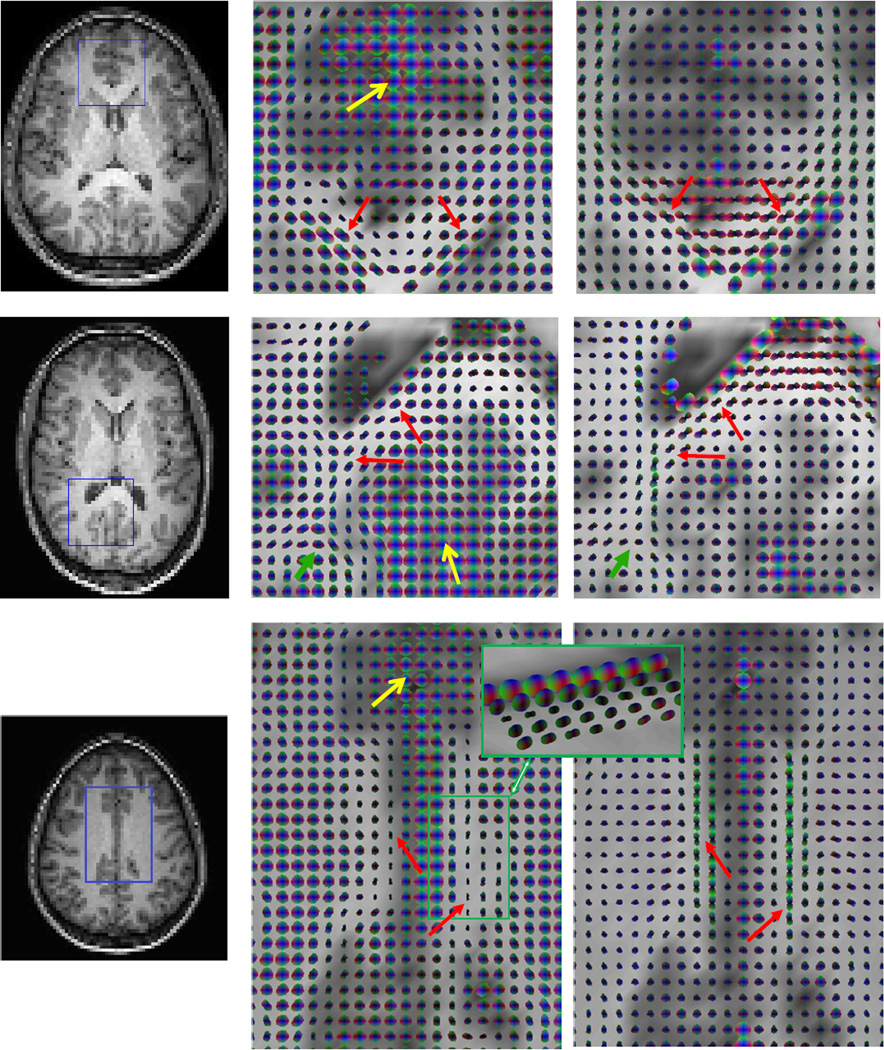
Anisotropic spatio-temporal correlations in resting state MRI signals were observed in many white matter regions in all subjects. The most common structures that exhibited anisotropic correlations along continuous pathways were the genu and splenium of the corpus callosum and cingulum, which are shown respectively in Figure 1. It can be appreciated that the pathways formed by the FCTs were grossly consistent with those revealed by diffusion tensors (red arrows). In addition to these major white matter tracts, sub-cortical U-fibers were also seen in all the subjects (green arrows). Furthermore, gray matter regions were visualized as larger tensors that appeared to be more isotropic (yellow arrows). These regions of large isotropic FCTs corresponded well to the anatomical and diffusion tensor images.

Figure 1. Spatio-temporal functional correlation tensors and diffusion tensors in the genu and splenium of the corpus callosum and the cingulum.

From left to right columns are T₁-weighted images, FCTs in the boxed region of the left column, and diffusion tensors in the same region. Top to bottom rows are the genu and splenium of the corpus callosum and the cingulum respectively. The pathways formed by the FCTs were grossly consistent with those revealed by diffusion tensors (red arrows). In addition to these major fiber tracts, sub-cortical U-fibers were also seen in all subjects (green arrows), and gray matter regions were visualized as larger tensors that appeared to be more isotropic (yellow arrows). Inset is an oblique view of the boxed region, which shows multi-layers of highly anisotropic tensors. Note that the right side of the green box is not adjacent to gray matter.

Results for the cingulum (bottom row in Figure 1) were of specific note because this white matter structure is a collection of axonal fibers projecting along the anterior-posterior direction, with its middle portion sitting right above the truncus of the corpus callosum (17). Compared to the genu and splenium of the corpus callosum, the cingulum is thinner and narrower, but was still clearly visualized by FCTs in eight subjects. The cingulum is connected to the posterior cingulate cortex, a central node in the default mode network that is in principle active when the brain is at rest (18).

3.2. Visual stimulation alters functional correlation tensors in visual pathways in white matter

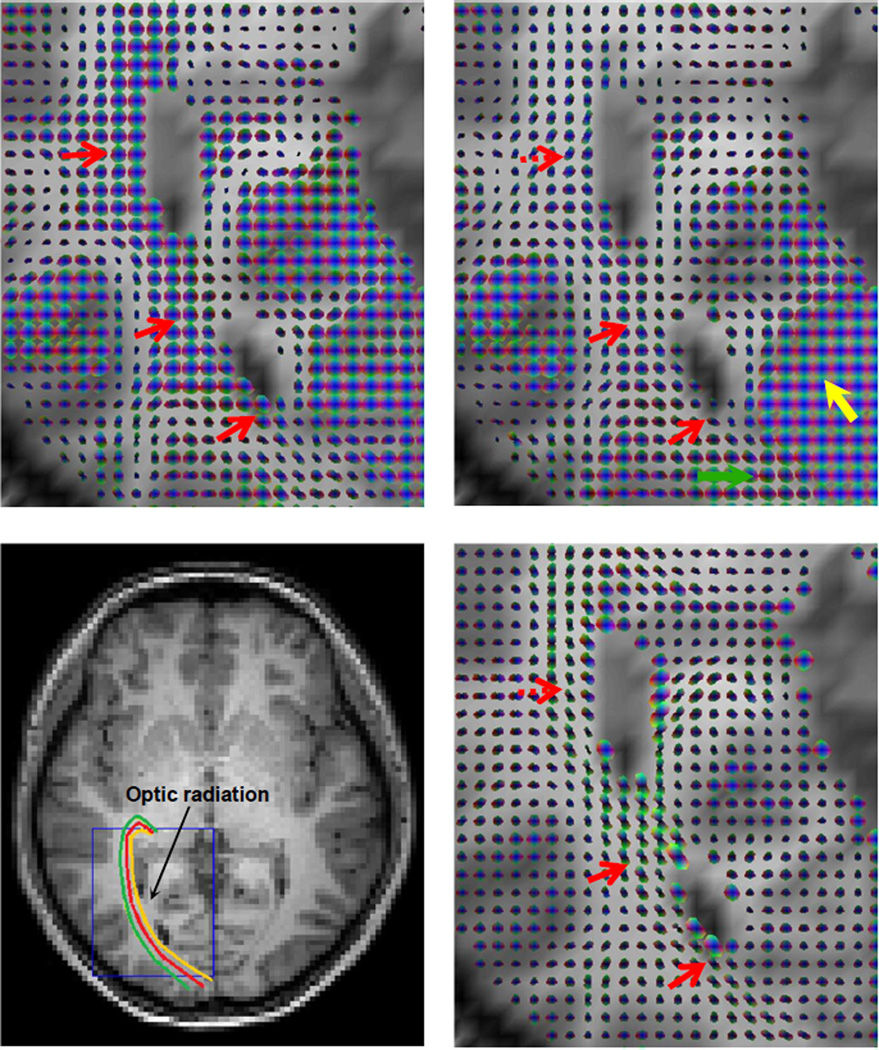
We aimed to examine the effects of functional stimulations on correlational anisotropy in long range fiber pathways. Two subjects were imaged in a resting state and with visual stimuli, when we observed significant changes in the FCTs of the optic radiations (OR), increasing the anisotropy within voxels and enhancing the visualization of tracts. The OR is a collection of long range fibers that carry visual information from the lateral geniculate nuclei of the thalamus to visual cortex (see Figure 2 for illustrations). Figure 2 shows the results from one subject (male, age=36 yrs). The spatio-temporal FCTs in the baseline resting state were largely isotropic along most portions of the right OR (top left). By contrast, visual stimulation created clear anisotropy in most of these FCTs (red arrows in top right), forming pathways similar to those defined by the diffusion tensors (bottom right). Also, FCTs in primary visual cortex appeared to be larger and more isotropic (yellow arrow) when it was activated by the visual stimuli. Note that the dominant direction of some FCTs near the dashed red arrow deviated from that of the corresponding diffusion tensors. This was perhaps due to the influence from hemodynamic effects in the U-fibers in their vicinity. Moreover, toward the end of the right OR (green arrow), correlational anisotropy observed in the resting state was lost when visual stimulation was present. This appears to be due to the spreading effect of hemodynamic responses from the visual cortex nearby. This experiment demonstrates that functional stimulations can create correlational anisotropy in BOLD-sensitive signals along long range fiber pathways that are absent in a resting state, supporting the inference that these correlations are driven by underlying neural activity.

Figure 2. Spatio-temporal functional correlation tensors and diffusion tensors along the right optic radiation of a subject.

Top left: FCTs in the boxed region in the bottom left during a resting state. Top right: FCTs in the same region during visual stimulations. Bottom left: Corresponding T1-weighted image with illustrations of putative pathways of the right OR. Bottom right: Diffusion tensors in the boxed region. The spatio-temporal FCTs in the baseline resting state were largely isotropic along most portions of the right OR. By contrast, visual stimulation created clear anisotropy in most of these FCTs, forming pathways similar to those defined by the diffusion tensors (red arrows). Also, FCTs in the primary visual cortex appeared to be larger and more isotropic (yellow arrow) when it was activated by the visual stimuli. And toward the end of the right OR (green arrow), correlational anisotropy observed in the resting state was lost when visual stimulation was present.

3.3. Language tasks alter functional correlation tensors in language pathways in white matter

To examine the effects of functional tasks on FCTs in neural circuits engaged in a cognitive function, we used standard reading tasks and analyzed correlational anisotropy in MRI signals along portions of the arcuate fasciculus (AF) and in Broca’s area (BA) and compared them between resting and task conditions. The AF is commonly recognized as connecting two core language areas in the brain: BA in the inferior frontal gyrus and Wernicke's area (WA) in the posterior superior temporal gyrus (see Figure 3 for illustrations). The AF also connects other cortical regions near the two language areas, and thus has diffuse terminations (19). As pathways of the AF traverse different axial slices, only portions near BA were analyzed in this experiment.

Figure 3. Spatio-temporal functional correlation tensors at rest and during performance of language tasks.

From top to bottom rows are T₁-weighted images and illustrations of the language circuit, resting state FCTs in the boxed region of the top row, FCTs under task conditions and with partial correlations. Left and right rows correspond to two adjacent slices. A sub-region in BA as located by standard SPM analysis contained large isotropic tensors in the presence of the task (circled region). Around this sub-region, FCTs exhibited high anisotropy during the reading task with major directions forming pathways toward (red arrow) or away from (green arrow) the BA. In contrast, FCTs around the BA in the resting state appeared to be largely isotropic. Inset is an oblique view of the boxed region, which shows multiple layers of highly anisotropic tensors. Also note that the left side of the green box is not adjacent to gray matter.

After excluding three subjects due to excessive motion, clear effects of the reading task on the AF were found in the remaining three subjects studied. Typical results from one of the subjects (male, age = 11 yrs) are presented in Figure 3, in which the 2^nd and 3^rd rows respectively show FCTs at resting state and in the task condition. A sub-region in BA as located from standard SPM analysis contained large isotropic FCTs in the task condition (circled region); around this sub-region, FCTs exhibited high anisotropy with major directions forming pathways toward (red arrow) or away from (green arrow) BA. In contrast, FCTs around the BA sub-region in the resting state appeared to be largely isotropic.

In this experiment diffusion weighted images were not acquired, but instead we analyzed a few consecutive axial slices that contained BA and found good cross-slice consistency in the connection patterns. As an example, the right column of Figure 3 is a slice right above the slice in the left column, which showed highly consistent connection patterns to those in the lower slice.

To confirm that the differences in correlational anisotropy between the resting and task conditions were not caused by factors other than the reading task (such as residual subject’s head motion), we examined the left and right ORs in the same subject, and found there were no detectable differences between the two conditions. Thus evidently, the reading task modulated the correlational profiles in the MRI signals selectively in regions engaged in language processing.

To further examine whether the correlation profiles in the fiber tracts connecting the BA sub-region were directly linked to the waveforms of the functional tasks, we computed a mean time course from the lower right four voxels in the BA sub-region, which were more isotropic, and constructed FCTs with the mean time course as a co-variate. We found that the tensor shape of only a few voxels adjacent to the BA was subtly changed, but the orientation remained similar and the overall connection patterns were almost identical, as shown in the bottom row of Figure 3. This indicates that the MR signals from white matter tracts change in response to functional tasks but differently from gray matter, and that the functional task enhanced visualization of the relevant functional pathways not by directly modulating the waveforms of their temporal responses. Furthermore, it indicates that the correlational anisotropy we observed along the white matter tracts is not driven by sharing a common draining vein with the BA, in which case the response should have been synchronized with it, but more plausibly is affected by functional modulations of electrophysiological events and accompanying hemodynamic or other MR responses along the fiber tracts.

3.4. Contrast in resting state functional correlation tensors acquired from multi-echo imaging sequences behaves similar to BOLD signals

We aimed to more fully describe the contrast mechanism underlying the correlational anisotropy of resting state signals by varying imaging echo time and analyzing the impact of different levels of T₂* contrast on the power spectra and correlational anisotropy of the signals in white matter. The findings from two subjects were similar, and results from one subject (male, age=25 yrs) are presented in Figures 4 and 5.

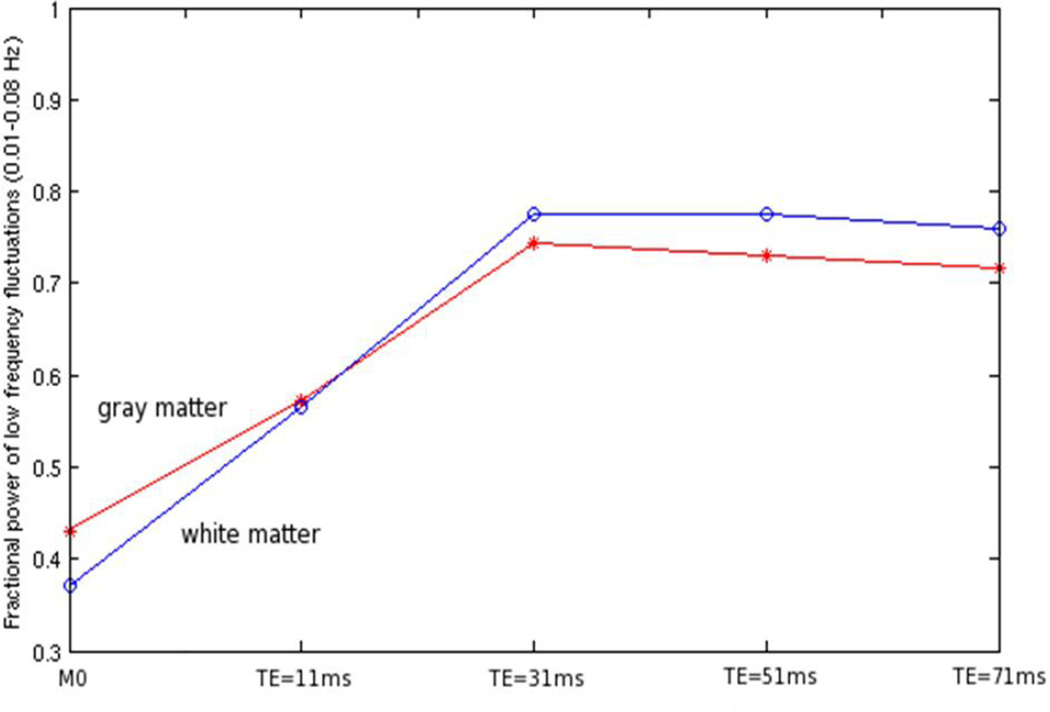
Figure 4. Variations of fractional power of low frequency fluctuations in BOLD signals with echo time.

The red line is for gray matter and the blue line is for white matter. Note that M₀ weighting corresponds to TE=0 ms.

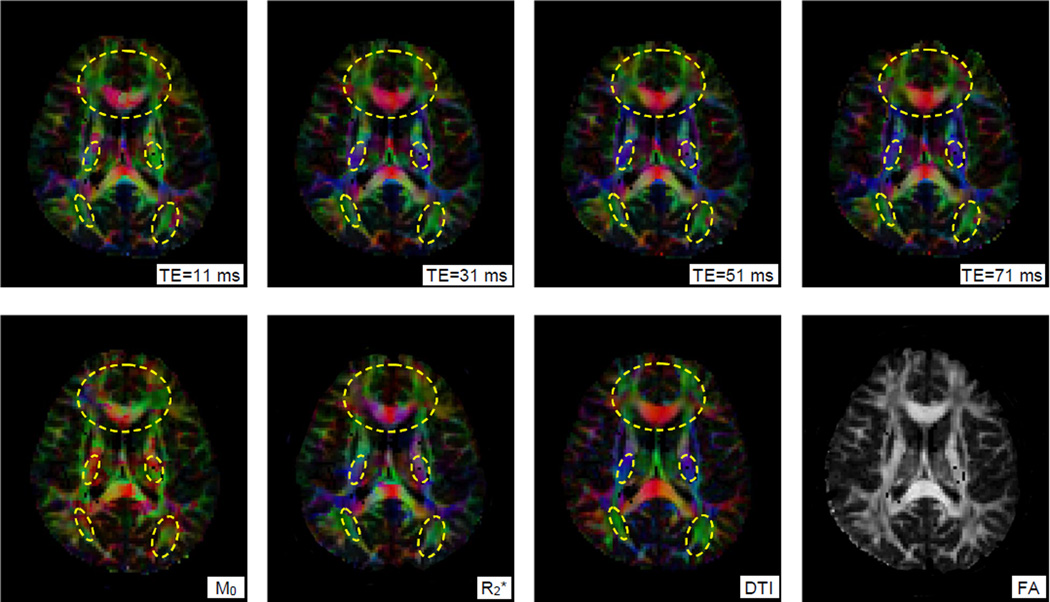
Figure 5. A slice of color-coded functional correlation tensors constructed at different echo times.

From the left to right in the top row are FCTs constructed at four different TEs, and in the bottom row are FCTs constructed from M₀ and R₂* images, diffusion tensors and a derived FA map. Circled regions show nearly identical anisotropy patterns between FCTs at TE=31 ms and diffusion tensors.

Figure 4 shows variations of the fractional power of low frequency fluctuations (FPLFF) of the MRI signals in the white and gray matter with four different TEs used in a multi-gradient echo acquisition. In both gray and white matter, the FPLFF increased with TE until TE=31 ms, beyond which it tended to decline slightly. By fitting the four images to a simple exponential and extrapolating back to TE=0, the equilibrium magnetization (M₀) was estimated, along with R₂* (=1/T₂*) at each voxel. In maps of M₀, the FPLFF in white matter was about 10% lower than in gray matter, but it became comparable to gray matter at TE=11 ms; beyond TE=31 ms, the FPLFF was slightly higher in white matter. This agrees with the fact that, although the baseline flow is lower in white matter, the oxygen extraction fraction which indicates relative metabolic demand is similar to that in gray matter, thus supporting the concept that BOLD signals in white matter may be detectable given appropriate imaging or analysis methods.

Figure 5 shows a slice of FCTs constructed from MRI signals acquired at different TEs and from computed M₀ and R₂* images. To visualize overall structures in the entire slice, major eigenvectors of the FCTs are color coded, along with major eigenvectors of corresponding diffusion tensors. To facilitate comparisons, the brightnesses of the color-coded maps are weighted by the fractional anisotropy (FA) map derived from diffusion tensor data, so that white matter tracts are highlighted. Close inspection reveals that, among all the maps of FCTs, the one constructed with TE=31 ms exhibited best directional consistency with the diffusion tensor map. Maps at TE>31 ms had a decreased directional consistency, most notably in the genu of the corpus callosum, possibly influenced by increased noise effects at longer TEs. The map at TE=11 ms had greater loss of directional consistency, presumably due to insufficient signal contrast at such a short TE. The map from the M₀* image agreed poorly with the diffusion tensor imaging (DTI) data, while that from R₂* images showed qualitatively similar patterns to those at TE=31 ms. The variations of FCTs with TE and M₀ and R₂* parameters, as well as the variations of FPLFF, suggest that anisotropic correlations in white matter behave similar to BOLD signals and represent variations in R₂* in these acquisitions, supporting one possible explanation that these are primarily driven by synchronized BOLD responses along white matter tracts.

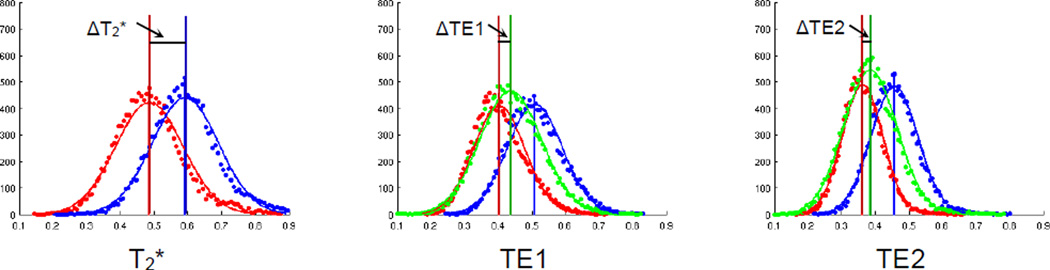
We also constructed FCTs from dual spin echo T₂-weighted images acquired from two additional subjects, and compared these to T₂*-weighted acquisitions. Experience with conventional BOLD imaging has shown that spin echo images emphasize contributions from microvasculature and are less affected by larger vessels, and the ratio of BOLD effects at 3T at TE ≈ T₂ has been found to be approximately 2–5, consistent with theoretical predictions (20). Figure 6 shows histograms of the average (red curve) and largest (i.e., major eigenvalue, blue curve) correlation values from T₂*- and dual echo T₂-weighted images (from left to right columns respectively). We also projected the FCTs from the T₂ weighting onto the tensor major eigenvector from T₂* weighting, and thus obtained T₂-based correlation values along the T₂*-based major eigenvector, which are shown as green curves in the figure. By subtracting the mean value of the average correlation from that of the projected correlation (ΔTE1 and ΔTE2 in Figure 6), and dividing by the difference between the mean average and mean largest correlations from the T₂* weighting (ΔT₂*), an estimation of relative contributions from T₂ contrast to the correlational anisotropy from T₂* contrast was obtained. Estimates from the two subjects studied are 32%, 22% and 24%, 17% for the 1^st and 2^nd echo (TE=23/70 ms) respectively. The smaller contribution from the 2^nd echo is partly attributable to increased noise when TE is longer and thus the overall correlation becomes smaller, as reflected as a shift of histograms to the left for the 2^nd echo.

Figure 6. Histograms of average, largest and projected correlations.

From left to right columns are the histograms for FCTs constructed with T₂*-weighted signals, TE1 and TE2 of T₂-weighted signals. The average correlation (red) is defined to be the average of the three eigenvalues, and the largest correlation (blue) is the largest eigenvalue. The projected correlation (green) is the projection of FCTs constructed with T₂-weighted signals onto the major eigenvector from T₂*-weighted signals, with projection of tensor T along direction v defined to be v•T•v^t. Curves are fitted values and vertical lines are the mean value of each histogram. ΔT₂*, ΔTE1 and ΔTE2 denotes the value difference between the vertical lines for T₂*, TE1 and TE2 weighting respectively. White matter voxels in the middle 15 slices of the brain are used for the histogram analysis.

4. DISCUSSION

Analyses of functional localization and inter-regional connectivity in the brain are conventionally based on statistical characterizations of changes in MRI signals from relatively large cortical regions (21–23). We present in this work a new and alternative method for characterizing functional connectivity within white matter based on the anisotropy of correlations in BOLD–like MRI signals at a voxel-level. With this approach, we are able to depict functional structures that are consistent with fiber pathways visualized by independent structural imaging without using diffusion imaging and based solely on resting state acquisitions. We have demonstrated that these putative functional pathways and related cortical regions can be detected at baseline but also change and can be emphasized by tasks that stimulate relevant functions in which they are involved.

BOLD signals are predicted to be much weaker in white matter than in gray matter, so they tend to fall below the sensitivity of detection of conventional methods that are dependent critically on the changes in signal intensity relative to noise influences. Even so, there have been a number of studies that report reliable detections of white matter activations (5–7, 24, 25). However, as only focal activations are found in these studies, the concept of BOLD response in white matter has not been widely accepted. Consequently, investigators have tended to overlook white matter activities although robustly shown in their findings (e.g., Figure 2 in Ref. 26), or attributed to the activities to nearby gray matter (e.g., Figure 1 in Ref. 27).

Unlike conventional methods, the new approach we propose for detecting connectivity does not depend on the relative changes in signal intensity to noise levels, thus offering greater sensitivity. The sensitivity gain in essence comes from two effects. First, we measure intrinsic correlations within a small spatial domain, with 26 independent directional estimates per voxel, and do not attempt to detect signal changes against a background as in conventional task studies. Second, we characterize the directional preference of temporal correlations, which is a self-normalized parameter that does not directly depend on the signal intensity. These two effects operate to improve the detectability of white matter signals.

The correlational anisotropy we observe is consistent with synchronized fluctuations in T₂*-sensitive signals along specific fiber tracts at the macro-scale available to MRI (11). These structure-specific signal correlations may not correspond to BOLD effects or neural activity, but we have adduced several pieces of evidence that show these phenomena are consistent with the same BOLD mechanism used to explain activation and connectivity between cortical regions. Our multi-echo imaging experiment demonstrates that R₂* but not M₀ images exhibit anisotropic correlations along white matter tracts, and the optimal contrast to noise occurs around TE≈T₂* just as for BOLD. Furthermore, the magnitudes of effects in SE images are reduced to a degree consistent with BOLD changes within and around microvasculature. In addition, our experiments demonstrate that functional tasks cause changes in the spatio-temporal tensors, and can induce anisotropic correlations along long range fiber tracts that were otherwise absent in the resting state, suggesting the BOLD effects we observe may be driven by neural activities along the fiber tracts. Notwithstanding, the precise biophysical substrates underlying the correlational anisotropy still require further elucidation, as other alternative explanations may exist (28). For instance, water in myelinated tissues is known to exist in various sub-compartments with distinct relaxation rates (29), and movement of water from one to another could in principle alter the average value of T₂, though such effects would not necessarily be expected to show the same temporal variations as the low frequency resting state correlations. In principle, the signal correlations along white matter tracts may also be induced by magnetic fields produced by propagating currents, though such effects are predicted to be very weak (30). Recent work in quantitative susceptibility mapping and susceptibility tensor imaging (31) have shown how magnetic susceptibility may be anisotropic within myelinated fibers in particular, but at present there is no explanation as to how such underlying static properties can produce synchronized low frequency resting state correlations as reported herein, though vasomotor activity might induce modulations of MR signals.

It can be imagined that the anisotropic patterns observed may be driven by hemodynamic fluctuations within common draining veins that run parallel to the course of fiber tracts, rather than by synchronized neural activities along them, though presumably the former are caused by the latter. Our experiments on the human language circuit have essentially ruled out the possibility that BOLD responses in long range veins modulate the anisotropic correlations observed. However, given that our multi-echo experiments suggest BOLD effects to be the origin of signal contrast and that evoked tasks selectively visualize relevant neural circuitry, it is plausible that the anisotropic patterns may be driven by small draining veins that span a few image voxels, and BOLD responses in these veins are synchronized by neural activities along the white matter tracts, yielding the observed anisotropic phenomena along long range fibers. It may be noted that this uncertainty in the origins of FCTs in white matter is little different from uncertainties about the origins of conventional BOLD signals widely used to assess neural function.

A further issue to be considered is the potential influence of structural boundaries, particularly at gray-white matter interfaces, on the detection of apparent correlation anisotropies. We expect hemodynamic profiles to differ across boundaries, and there may be complex influences from adjacent tissues due to spreading effects from hemodynamic responses or from the image formation process. On the one hand, differences in hemodynamic responses across boundaries may create artificial correlational anisotropy, leading to “false positive” tensors parallel to the boundary. On the other hand, spreading effects from hemodynamic responses or image unsharpness at the boundary may smear out correlational anisotropy, leading to “false negative” errors (see the region pointed by the green arrow in Figure 2). Of particular note, commonly used image smoothing procedures such as Gaussian smoothing reduce image sharpness at the boundary, which behaves similar to the spreading effects from hemodynamic responses, and thus tend to create “false negative” rather than “false positive” tensors.

In this work, the issue of “false positive” errors has been a major concern, i.e., whether the observed anisotropic patterns are basically driven by differences in hemodynamic profiles across gray-white matter boundaries. We have confirmed that the presence of structure boundaries is not a prerequisite to observe correlational anisotropy, as evidenced by the highly anisotropic tensors near the right side of the inset in Figure 1 and those near the left side of the inset in Figure 3; but on the contrary we have observed some highly anisotropic tensors point to the boundaries of the gray matter (see tensors indicated by the red arrows in Figure 3). Moreover, our experiments with functional tasks demonstrate that, compared to resting state conditions, functional stimulations selectively modulate correlational anisotropy in relevant neural circuits, further supporting that boundary effects are not the origin of the anisotropic patterns observed. Additionally, we have observed from our multi-echo GE experiments that M₀ images do not produce coherent anisotropic correlations along fiber tracts as the images acquired at TE>=31 ms. All these images contain identical structural boundaries, so this indicates that it is not the boundary but the hemodynamics effects that create the anisotropic patterns. “False positives”, however, may exist near some structural boundaries because of the gradient in hemodynamic profiles across them. One empirical approach for distinguishing these “false positives” from “true positives” is to analyze the shape of the correlation tensors: “true positives” tend to have a cigar-shape while “false positives” tend to have a pancake-shape typically in a single layer (e.g., see 2^nd left layer in the inset of Figure 1). The shape difference arises from the fact that “true positive” tensors have a single preferred direction. For instance, we may define a “linear index” (32) that helps identify “true positives” on the basis of tensor shape, as shown in Figure 7 for the two insets from Figure 1 and 3. Another approach is to analyze the power spectra of the MRI signals in white matter voxels, which may provide a more robust means of identifying “false positives”, given the geometric complexity of structural boundaries in the brain.

Figure 7. Functional correlation tensors and linear index of their shape.

Linear index is defined to be the difference between the two largest eigenvalues divided by the average of the three eivenvalues. Left and right two columns are axial views of the insets in Figure 1 and 3 (3^rd row) respectively. The linear index is higher for cigar-shaped tensors (red arrow), which are typically along white matter tracts, than pancake-shaped tensors (blue arrow) or spherical tensors (green arrow), which typically lie at the gray-white matter boundary or inside the gray matter region.

5. CONCLUSION

The results reported here lend credibility to the small number of reports claiming detection of focal task-evoked activity within white matter. Such signals are expected to be weaker than those observed in gray matter, but the studies described above suggest a potentially powerful new approach to their detection. White matter tracts are generally narrow, anatomically specific but extend over multiple voxels. Conventional methods for detecting activation rely on voxel-wise identification of signal changes that correlate temporally with a stimulus, but often resort to cluster analysis or spatial smoothing to increase sensitivity, in which the responses of multiple voxels within a region that show similar temporal responses are integrated. From our results it may be postulated that for white matter the natural basis for clustering is a tract along which activity-related signals are synchronized, so that attempts to detect functional changes should be based on structures first identified by DTI.