PROJECTED PRINCIPAL COMPONENT ANALYSIS IN FACTOR MODELS

Abstract

This paper introduces a Projected Principal Component Analysis (Projected-PCA), which employees principal component analysis to the projected (smoothed) data matrix onto a given linear space spanned by covariates. When it applies to high-dimensional factor analysis, the projection removes noise components. We show that the unobserved latent factors can be more accurately estimated than the conventional PCA if the projection is genuine, or more precisely, when the factor loading matrices are related to the projected linear space. When the dimensionality is large, the factors can be estimated accurately even when the sample size is finite. We propose a flexible semi-parametric factor model, which decomposes the factor loading matrix into the component that can be explained by subject-specific covariates and the orthogonal residual component. The covariates’ effects on the factor loadings are further modeled by the additive model via sieve approximations. By using the newly proposed Projected-PCA, the rates of convergence of the smooth factor loading matrices are obtained, which are much faster than those of the conventional factor analysis. The convergence is achieved even when the sample size is finite and is particularly appealing in the high-dimension-low-sample-size situation. This leads us to developing nonparametric tests on whether observed covariates have explaining powers on the loadings and whether they fully explain the loadings. The proposed method is illustrated by both simulated data and the returns of the components of the S&P 500 index.

1. Introduction

Factor analysis is one of the most useful tools for modeling common dependence among multivariate outputs. Suppose that we observe data {y_it}_i≤p,t≤T that can be decomposed as

$$y_{it}=\sum _{k=1}^K{\lambda }_{ik}{f}_{tk}+u_{it},i=1,\cdots ,p,t=1,\cdots ,T$$ (1.1)

where {f_t1, ···, f_tK} are unobservable common factors; {λ_i1, ···, λ_iK} are corresponding factor loadings for variable i, and u_it denotes the idiosyncratic component that can not be explained by the static common component. Here p and T respectively denote the dimension and sample size of the data.

Model (1.1) has broad applications in the statistics literature. For instance, y_t = (y_1t, ···, y_pt)′ can be expression profiles or blood oxygenation level dependent (BOLD) measurements for the t^th microarray, proteomic or fMRI-image, whereas i represents a gene or protein or a voxel. See, for example, Desai and Storey (2012); Efron (2010); Fan et al. (2012); Friguet et al. (2009); Leek and Storey (2008). The separations between the common factors and idiosyncratic components are carried out by the low-rank plus sparsity decomposition. See, for example, Cai et al. (2013); Candès and Recht (2009); Fan et al. (2013); Koltchinskii et al. (2011); Ma (2013); Negahban and Wainwright (2011).

The factor model (1.1) has also been extensively studied in the econometric literature, in which y_t is the vector of economic outputs at time t or excessive returns for individual assets on day t. The unknown factors and loadings are typically estimated by the principal component analysis (PCA) and the separations between the common factors and idiosyncratic components are characterized via static pervasiveness assumptions. See, for instance, Bai (2003); Bai and Ng (2002); Breitung and Tenhofen (2011); Lam and Yao (2012); Stock and Watson (2002) among others. In this paper, we consider static factor model, which differs from the dynamic factor model (Forni et al., 2000, 2015; Forni and Lippi, 2001). The dynamic model allows more general infinite dimensional representations. For this type of model, the frequency domain PCA (Brillinger, 1981) was applied on the spectral density. The so-called dynamic pervasiveness condition also plays a crucial role in achieving consistent estimation of the spectral density.

Accurately estimating the loadings and unobserved factors are very important in statistical applications. In calculating the false-discovery proportion for large-scale hypothesis testing, one needs to adjust accurately the common dependence via subtracting it from the data in (1.1) (Desai and Storey, 2012; Efron, 2010; Fan et al., 2012; Friguet et al., 2009; Leek and Storey, 2008). In financial applications, we would like to understand accurately how each individual stock depends on unobserved common factors in order to appreciate its relative performance and risks. In the aforementioned applications, dimensionality is much higher than sample-size. However, the existing asymptotic analysis shows that the consistent estimation of the parameters in model (1.1) requires a relatively large T. In particular, the individual loadings can be estimated no faster than O_P (T^−1/2). But large sample sizes are not always available. Even with the availability of “Big Data”, heterogeneity and other issues make direct applications of (1.1) with large T infeasible. For instance, in financial applications, to pertain the stationarity in model (1.1) with time-invariant loading coefficients, a relatively short time series is often used. To make observed data less serially correlated, monthly returns are frequently used to reduce the serial correlations, yet a monthly data over three consecutive years contain merely 36 observations.

1.1. This paper

To overcome the aforementioned problems, and when relevant covariates are available, it may be helpful to incorporate them into the model. Let X_i = (X_i1, ···, X_id)′ be a vector of d-dimensional covariates associated with the i^th variables. In the seminal papers by Connor and Linton (2007) and Connor et al. (2012), the authors studied the following semi-parametric factor model:

$$y_{it}=\sum _{k=1}^K{g}_k({\mathbf{X}}_i)f_{tk}+u_{it},i=1,\cdots ,p,t=1,\cdots ,T,$$ (1.2)

where loading coefficients in (1.1) are modeled as λ_ik = g_k(X_i) for some functions g_k(·). For instance, in health studies, X_i can be individual characteristics (e.g. age, weight, clinical and genetic information); in financial applications X_i can be a vector of firm-specific characteristics (market capitalization, price-earning ratio, etc).

The semiparametric model (1.2), however, can be restrictive in many cases, as it requires that the loading matrix be fully explained by the covariates. A natural relaxation is the following semiparametric model

$${\lambda }_{ik}=g_k({\mathbf{X}}_i)+{\gamma }_{ik},i=1,\cdots ,p,k=1,\cdots ,K,$$ (1.3)

where γ_ik is the component of loading coefficient that can not be explained by the covariates X_i. Let γ_i = (γ_i1, ···, γ_iK)′. We assume that {γ_i}_i≤p have mean zero, and are independent of {X_i}_i≤p and {u_it}_i≤p,t≤T. In other words, we impose the following factor structure

$$y_{it}=\sum _{k=1}^K\{g_k({\mathbf{X}}_i)+{\gamma }_{ik}\}{f}_{tk}+u_{it},i=1,\cdots ,p,t=1,\cdots ,T,$$ (1.4)

which reduces to model (1.2) when γ_ik = 0 and model (1.1) when g_k(·) = 0. When X_i genuinely explains a part of loading coefficients λ_ik, the variability of γ_ik is smaller than that of λ_ik. Hence, the coefficient γ_ik can be more accurately estimated by using regression model (1.3), as long as the functions g_k(·) can be accurately estimated.

Let Y be the p×T matrix of y_it, F be the T × K matrix of f_tk, G(X) be the p × K matrix of g_k(X_i), Γ be the p × K matrix of γ_ik, and U be p × T matrix of u_it. Then model (1.4) can be written in a more compact matrix form:

$$\mathbf{Y}=\{\mathbf{G}(\mathbf{X})+\mathbf{\Gamma }\}{\mathbf{F}}^{\prime }+\mathbf{U}.$$ (1.5)

We treat the loadings G(X) and Γ as realizations of random matrices throughout the paper. This model is also closely related to the supervised singular value decomposition model, recently studied by Li et al. (2015). The authors showed that the model is useful in studying the gene expression and single-nucleotide polymorphism (SNP) data, and proposed an EM algorithm for parameter estimation.

We propose a projected-PCA estimator for both the loading functions and factors. Our estimator is constructed by first projecting Y onto the sieve space spanned by {X_i}_i≤p, then applying PCA to the projected data or fitted values. Due to the approximate orthogonality condition of X, U and Γ, the projection of Y is approximately G(X)F′, as the smoothing projection suppresses the noise terms Γ and U substantially. Therefore, applying PCA to the projected data allows us to work directly on the sample covariance of G(X)F′, which is G(X)G(X)′ under normalization conditions. This substantially improves the estimation accuracy, and also facilitates the theoretical analysis. In contrast, the traditional PC method for factor analysis (e.g., Stock and Watson (2002), Bai and Ng (2002)) is no longer suitable in the current context. Moreover, the idea of projected-PCA is also potentially applicable to dynamic factor models of Forni et al. (2000), by first projecting the data onto the covariate space.

The asymptotic properties of the proposed estimators are carefully studied. We demonstrate that as long as the projection is genuine, the consistency of the proposed estimator for latent factors and loading matrices requires only p → ∞, and T does not need to grow, which is attractive in the typical high-dimension-low-sample-size (HDLSS) situations (e.g., Jung and Marron (2009); Shen et al. (2013a,b)). In addition, if both p and T grow simultaneously, then with sufficiently smooth g_k(·), using the sieve approximation, the rate of convergence for the estimators is much faster than those of the existing results for model (1.1). Typically, the loading functions can be estimated at a convergence rate O_P ((pT)^−1/2), and the factor can be estimated at O_P(p⁻¹). Throughout the paper, K = dim(f_t) and d = dim(X_i) are assumed to be constant and do not grow.

Let Λ be a p×K matrix of (λ_ik)_T×K. Model (1.3) implies a decomposition of the loading matrix:

$$\mathbf{\Lambda }=\mathbf{G}(\mathbf{X})+\mathbf{\Gamma },E(\mathbf{\Gamma }\mid \mathbf{X})=0,$$

where G(X) and Γ are orthogonal loading components in the sense that EG(X)Γ′ = 0. We conduct two specification tests for the hypotheses:

$$H_0^1:\mathbf{G}(\mathbf{X})=0a.s.,\text{and}{H}_0^2:\mathbf{\Gamma }=0a.s.$$

The first problem is about testing whether the observed covariates have explaining power on the loadings. If the null hypothesis is rejected, it gives us the theoretical basis to employ the projected PCA, as the projection is now genuine. Our empirical study on the asset returns shows that firm market characteristics do have explanatory power on the factor loadings, which lends further support to our projected-PCA method. The second tests whether covariates fully explain the loadings. Our aforementioned empirical study also shows that model (1.2) used in the financial econometrics literature is inadequate and more generalized model (1.5) is necessary. As claimed earlier, even if $H_0^2$ does not hold, as long as G(X) ≠ 0, the Projected-PCA can still consistently estimate the factors as p → ∞, and T may or may not grow. Our simulated experiments confirm that the estimation accuracy is gained more significantly for small T’s. This shows one of the benefits of using our projected-PCA method over the traditional methods in the literature.

In addition, as a further illustration of the benefits of using projected data, we apply the projected-PCA to consistently estimate the number of factors, which is similar to those in Ahn and Horenstein (2013) and Lam and Yao (2012). Different from these authors, our method applies to the projected data, and we demonstrate numerically that this can significantly improve the estimation accuracy.

We focus on the case when the observed covariates are time-invariant. When T is small, these covariates are approximately locally constant, so this assumption is reasonable in practice. On the other hand, there may exist individual characteristics that are time-variant (e.g., see Park et al. (2009)). We expect the conclusions in the current paper to still hold if some smoothness assumptions are added for the time varying components of the covariates. Due to the space limit, we provide heuristic discussions on this case in the supplementary material of this paper Fan et al. (2015b). In addition, note that in the usual factor model, Λ was assumed to be deterministic. In this paper, however, Λ is mainly treated to be stochastic, and potentially depend on a set of covariates. But we would like to emphasize that the results presented in Section 3 under the framework of more general factor models hold regardless of whether Λ is stochastic or deterministic. Finally, while some financial applications are presented in this paper, the projected-PCA is expected to be useful in broad areas of statistical applications (e.g., see Li et al. (2015) for applications in gene expression data analysis).

1.2. Notation and organization

Throughout this paper, for a matrix A, let ||A||_F = tr^1/2(A′A) and ${\Vert \mathbf{A}\Vert }_2={\lambda }_{max}^{1/2}({\mathbf{A}}^{\prime }\mathbf{A})$, ||A||_max = max_ij |A_ij| denote its Frobenius, spectral and max-norms. Let λ_min(·) and λ_max(·) denote the minimum and maximum eigenvalues of a square matrix. For a vector v, let ||v|| denote its Euclidean norm.

The rest of the paper is organized as follows. Section 2 introduces the new projected-PCA method and defines the corresponding estimators for the loadings and factors. Sections 3 and 4 provide asymptotic analysis of the introduced estimators. Section 5 introduces new specification tests for the orthogonal decomposition of the semi-parametric loadings. Section 6 concerns about estimating the number of factors. Section 7 presents numerical results. Finally, Section 8 concludes. All the proofs are given in the appendix and the supplementary material.

2. Projected Principal Component Analysis

2.1. Overview

In the high-dimensional factor model, let Λ be the p×K matrix of loadings. Then the general model (1.1) can be written as

$$\mathbf{Y}=\mathbf{\Lambda }{\mathbf{F}}^{\prime }+\mathbf{U}.$$ (2.1)

Suppose we additionally observe a set of covariates {X_i}_i≤p. The basic idea of the projected PCA is to smooth the observations {Y_it}_i≤p for each given day t against its associated covariates. More specifically, let {Ŷ_it}_i≤p be the fitted value after regressing {Y_it}_i≤p on {X_i}_i≤p for each given t. This results in a smooth or projected observation matrix Ŷ, which will also be denoted by PY. The projected PCA then estimates the factors and loadings by running the PCA based on the projected data Ŷ.

Here we heuristically describe the idea of projected PCA; rigorous analysis will be carried out afterwards. Let 𝒳 be a space spanned by X = {X_i}_i≤p, which is orthogonal to the error matrix U. Let P denote the projection matrix onto 𝒳 (whose formal definition will be given in (2.6) below. At the population level, P approximates the conditional expectation operator E(·|X), which satisfies E(U|X) = 0), then P² = P and PU ≈ 0. Hence, the projected data Ŷ is an approximately noiseless problem and its sample covariance has the following approximation:

$$\frac{1}{T}{\widehat{\mathbf{Y}}}^{\prime }\widehat{\mathbf{Y}}=\frac{1}{T}{\mathbf{Y}}^{\prime }\mathbf{PY}\approx \frac{1}{T}\mathbf{F}{\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda }{\mathbf{F}}^{\prime }$$ (2.2)

Hence, F and PΛ can be recovered from the projected data Ŷ under some suitable normalization condition.

The normalization conditions we imposed are

$$\frac{1}{T}{\mathbf{F}}^{\prime }\mathbf{F}={\mathbf{I}}_K,{\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda }\text{is}\mathrm{a}\text{diagonal}\text{matrix}\text{with}\text{distinct}\text{entries}.$$ (2.3)

Under this normalization, using (2.2), we conclude that the columns of F are approximately $\sqrt{T}$ times the first K eigenvectors of the T × T matrix $\frac{1}{T}{\mathbf{Y}}^{\prime }\mathbf{PY}$. Therefore, the Projected-PCA naturally defines a factor estimator F̂ using the first K principal components of $\frac{1}{T}{\mathbf{Y}}^{\prime }\mathbf{PY}$.

The projected loading matrix PΛ can also be recovered from the projected data PY in two (equivalent) ways. Given F, from $\frac{1}{T}\mathbf{PYF}=\mathbf{P}\mathbf{\Lambda }+\frac{1}{T}\mathbf{PUF},$, we see $\mathbf{P}\mathbf{\Lambda }\approx \frac{1}{T}\mathbf{PYF}$. Alternatively, consider the p × p projected sample covariance:

$$\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P}=\mathbf{P}\mathbf{\Lambda }{\mathbf{\Lambda }}^{\prime }\mathbf{P}+\stackrel{\sim }{\mathbf{\Delta }},$$

where Δ̃ is a remaining term depending on PU. Right multiplying PΛ and ignoring terms depending on PU, we obtain $(\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P})\mathbf{P}\mathbf{\Lambda }\approx \mathbf{P}\mathbf{\Lambda }({\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda })$. Hence the (normalized) columns of PΛ approximate the first K eigenvectors of $\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P}$, the p×p sample covariance matrix based on the projected data. Therefore, we can either estimate PΛ by $\frac{1}{T}\mathbf{PY}\widehat{\mathbf{F}}$ given F̂, or by the leading eigenvectors of $\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P}$. In fact, we shall see later that these two estimators are equivalent. If in addition, Λ = PΛ, that is, the loading matrix belongs to the space 𝒳, then Λ can also be recovered from the projected data.

The above arguments are the fundament of the projected-PCA, and provide the rationale of our estimators to be defined in Section 2.3. We shall make the above arguments rigorous by showing that the projected error PU is asymptotically negligible, and therefore the idiosyncratic error term U can be completely removed by the projection step.

2.2. Semiparametric Factor Model

As one of the useful examples of forming the space 𝒳 and the projection operator, this paper considers model (1.4), where X_i’s and y_it’s are the only observable data, and {g_k(·)}_k≤K are unknown nonparametric functions. The specific case (1.2) (with γ_ik = 0) was used extensively in the financial studies by Connor and Linton (2007), Connor et al. (2012) and Park et al. (2009), with X_i’s being the observed “market characteristic variables”. We assume K to be known for now. In Section 6, we will propose a projected-eigenvalue-ratio method to consistently estimate K when it is unknown.

We assume that g_k(X_i) does not depend on t, which means the loadings represent the cross-sectional heterogeneity only. Such a model specification is reasonable since in many applications using factor models: to pertain the stationarity of the time series, the analysis can be conducted within each fixed time window with either a fixed or slowly-growing T. Through localization in time, it is not stringent to require the loadings be time-invariant. This also shows one of the attractive features of our asymptotic results: under mild conditions, our factor estimates are consistent even if T is finite.

To non-parametrically estimate g_k(X_i) without the curse of dimensionality when X_i is multivariate, we assume g_k(·) to be additive: for each k ≤ K, i ≤ p, there are (g_k1, ···, g_kd) nonparametric functions such that

$$g_k({\mathbf{X}}_i)=\sum _{l=1}^d{g}_{kl}(X_{il}),d=dim({\mathbf{X}}_i).$$ (2.4)

Each additive component of g_k is estimated by the sieve method. Define {ϕ₁(x), ϕ₂(x), ···} to be a set of basis functions (e.g., B-spline, Fourier series, wavelets, polynomial series), which spans a dense linear space of the functional space for {g_kl}. Then for each l ≤ d,

$$g_{kl}(X_{il})=\sum _{j=1}^J{b}_{j,kl}{\varphi }_j(X_{il})+R_{kl}(X_{il}),k\le K,i\le p,l\le d.$$ (2.5)

Here {b_j,kl}_j≤J are the sieve coefficients of the lth additive component of g_k(X_i), corresponding to the kth factor loading; R_kl is a “remaining function” representing the approximation error; J denotes the number of sieve terms which grows slowly as p → ∞. The basic assumption for sieve approximation is that sup_x |R_kl(x)| → 0 as J → ∞. We take the same basis functions in (2.5) purely for simplicity of notation.

Define, for each k ≤ K and for each i ≤ p,

$$\begin{array}{c}{\mathbf{b}}_k^{\prime }=(b_{1,k1},\cdots ,b_{J,k1},\cdots ,b_{1,kd},\cdots ,b_{J,kd})\in {ℝ}^{Jd},\\ \varphi {({\mathbf{X}}_i)}^{\prime }=({\varphi }_1(X_{i1}),\cdots ,{\varphi }_J(X_{i1}),\cdots ,{\varphi }_1(X_{id}),\cdots ,{\varphi }_J(X_{id}))\in {ℝ}^{Jd}.\end{array}$$

Then, we can write

$$g_k({\mathbf{X}}_i)=\varphi {({\mathbf{X}}_i)}^{\prime }{\mathbf{b}}_k+\sum _{l=1}^d{R}_{kl}(X_{il}).$$

Let B = (b₁, ···, b_K) be a (Jd) × K matrix of sieve coefficients, Φ(X) = (ϕ(X₁), ···, ϕ(X_p))′ be a p × (Jd) matrix of basis functions, and R(X) be p×K matrix with the (i, k)th element ${\sum }_{l=1}^d{R}_{kl}(X_{il})$. Then the matrix form of (2.4) and (2.5) is

$$\mathbf{G}(\mathbf{X})=\mathrm{\Phi }(\mathbf{X})\mathbf{B}+\mathbf{R}(\mathbf{X}).$$

Substituting this into (1.5), we write

$$\mathbf{Y}=\{\mathrm{\Phi }(\mathbf{X})\mathbf{B}+\mathbf{\Gamma }\}{\mathbf{F}}^{\prime }+\mathbf{R}(\mathbf{X}){\mathbf{F}}^{\prime }+\mathbf{U}.$$

We see that the residual term consists of two parts: the sieve approximation error R(X)F′ and the idiosyncratic U. Furthermore, the random effect assumption on the coefficients Γ makes it also behave like noise and hence negligible when the projection operator P is applied.

2.3. The estimator

Based on the idea described in Section 2.1, we propose a Projected-PCA method, where 𝒳 is the sieve space spanned by the basis functions of X, and P is chosen as the projection matrix onto 𝒳, defined by the p × p projection matrix

$$\mathbf{P}=\mathrm{\Phi }(\mathbf{X}){(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1}\mathrm{\Phi }{(\mathbf{X})}^{\prime }.$$ (2.6)

The estimators of the model parameters in (1.5) are defined as follows. The columns of $\widehat{\mathbf{F}}/\sqrt{T}$ are defined as the eigenvectors corresponding to the first K largest eigenvalues of the T × T matrix Y′PY, and

$$\widehat{\mathbf{G}}(\mathbf{X})=\frac{1}{T}\mathbf{PY}\widehat{\mathbf{F}}.$$ (2.7)

is the estimator of G(X).

The intuition can be readily seen from the discussions in Section 2.1, which also provides an alternative formulation of Ĝ(X) as follows: let D̂ be a K×K diagonal matrix consisting of the largest K eigenvalues of the p×p matrix $\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P}$. Let Ξ̂= (ξ̂₁, …, ξ̂_K) be a p×K matrix whose columns are the corresponding eigenvectors. According to the relation $(\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P})\mathbf{P}\mathbf{\Lambda }\approx \mathbf{P}\mathbf{\Lambda }({\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda })$ described in Section 2.1, we can also estimate G(X) or PΛ by

$$\widehat{\mathbf{G}}(\mathbf{X})=\widehat{\mathbf{\Xi }}{\widehat{\mathbf{D}}}^{1/2}.$$

We shall show in Lemma A.1 that this is equivalent to (2.7). The weight matrix P projects the original data matrix onto the sieve space spanned by X. Therefore, unlike the traditional PC method for usual factor models (e.g., Bai (2003), Stock and Watson (2002)), the projected-PCA takes the principal components of the projected data PY. The estimator is thus invariant to the rotation-transformations of the sieve bases.

The estimation of the loading component Γ that can not be explained by the covariates can be estimated as follows. With the estimated factors F̂, the least-squares estimator of loading matrix is Λ̂ = YF̂/T, by using (2.1) and (2.3). Therefore, by (1.5), a natural estimator of Γ is

$$\widehat{\mathbf{\Gamma }}=\widehat{\mathbf{\Lambda }}-\widehat{\mathbf{G}}(\mathbf{X})=\frac{1}{T}(\mathbf{I}-\mathbf{P})\mathbf{Y}\widehat{\mathbf{F}}.$$ (2.8)

2.4. Connection with panel data models with time-varying coefficients

Consider a panel data model with time-varying coefficients as follows:

$$y_{it}={\mathbf{X}}_i^{\prime }{\mathit{\beta }}_t+{\mu }_t+u_{it},i\le p,t\le T,$$ (2.9)

where X_i is a d-dimensional vector of time-invariant regressors for individual i; μ_t denotes the unobservable random time effect; u_it is the regression error term. The regression coefficient β_t is also assumed to be random and time-varying, but is common across the cross-sectional individuals.

The semi-parametric factor model admits (2.9) as a special case. Note that (2.9) can be rewritten as y_it = g(X_i)′f_t + u_it with K = d + 1 unobservable “factors” ${\mathbf{f}}_t={({\mu }_t,{\mathit{\beta }}_t^{\prime })}^{\prime }$ and “loading” $g({\mathbf{X}}_i)={(1,{\mathbf{X}}_i^{\prime })}^{\prime }$. The model (1.4) being considered, on the other hand, allows more general nonparametric loading functions.

3. Projected-PCA in Conventional Factor Models

Let us first consider the asymptotic performance of the projected-PCA in the conventional factor model:

$$\mathbf{Y}=\mathbf{\Lambda }{\mathbf{F}}^{\prime }+\mathbf{U}.$$ (3.1)

In the usual statistical applications for factor analysis, the latent factors are assumed to be serially independent, while in financial applications, the factors are often treated to be weakly dependent time series satisfying strong mixing conditions.

We now demonstrate by a simple example that latent factors F can be estimated at a faster rate of convergence by Projected-PCA than the conventional PCA and that they can be consistently estimated even when sample size T is finite.

Example 3.1

To appreciate the intuition, let us consider a specific case in which K = 1 so that model (1.4) reduces to

$$y_{it}=g(X_i)f_t+{\gamma }_i{f}_t+u_{it}.$$

Assume that g(·) is so smooth that it is in fact a constant β (otherwise, we can use a local constant approximation), where β > 0. Then, the model reduces to

$$y_{it}=\beta f_t+{\gamma }_i{f}_t+u_{it}.$$

The projection in this case is averaging over i, which yields

$${\overline{y}}_{·t}=\beta f_t+{\overline{\gamma }}_{·}{f}_t+{\overline{u}}_{·t},$$

where ȳ_·t, γ̄_· and ū_·t denote the averages of their corresponding quantities over i. For the identification purpose, suppose Eγ_i = Eu_it = 0, and ${\sum }_{t=1}^T{f}_t^2=T$. Ignoring the last two terms, we obtain estimators

$$\widehat{\beta }={\left(\frac{1}{T}\sum _{t=1}^T{\overline{y}}_{·t}^2\right)}^{1/2},\text{and}{\widehat{f}}_t={\overline{y}}_{·t}/\widehat{\beta }.$$ (3.2)

These estimators are special cases of the projected-PCA estimators. To see this, define ȳ = (ȳ_·1, …, ȳ_·T)′, and let 1_p be a p-dimensional column vector of ones. Take a naive basis Φ(X) = 1_p; then the projected data matrix is in fact PY = 1_pȳ′. Consider the T × T matrix Y′PY = (1_pȳ′)′1_pȳ′ = pȳȳ′, whose largest eigenvalue is p||ȳ||². From

$${\mathbf{Y}}^{\prime }\mathbf{PY}\frac{\overline{\mathbf{y}}}{\Vert \overline{\mathbf{y}}\Vert }=p{\Vert \overline{\mathbf{y}}\Vert }^2\frac{\overline{\mathbf{y}}}{\Vert \overline{\mathbf{y}}\Vert },$$

we have the first eigenvector of Y′PY equals ȳ/||ȳ||. Hence the projected-PCA estimator of factors is $\widehat{\mathbf{F}}=\sqrt{T}\overline{\mathbf{y}}/\Vert \overline{\mathbf{y}}\Vert$. In addition, the projected PCA estimator of the loading vector β1_p is

$$\frac{1}{T}{\mathbf{1}}_p{\overline{\mathbf{y}}}^{\prime }\widehat{\mathbf{F}}=\frac{1}{\sqrt{T}}{\mathbf{1}}_p\Vert \overline{\mathbf{y}}\Vert .$$

Hence the projected PCA-estimator of β equals $\Vert \overline{\mathbf{y}}\Vert /\sqrt{T}$. These estimators match with (3.2). Moreover, since the ignored two terms γ̄_· and ū_·t are of order O_p(p^−1/2), β̂ and f̂_t converge whether or not T is large. Note that this simple example satisfies all the assumptions to be stated below, and β̂ and f̂_t achieve the same rate of convergence as that of Theorem 4.1. We shall present more details about this example in Appendix G in the supplementary material.

3.1. Asymptotic Properties of Projected-PCA

We now state the conditions and results formally in the more general factor model (3.1). Recall that the projection matrix is defined as

$$\mathbf{P}=\mathrm{\Phi }(\mathbf{X}){(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1}\mathrm{\Phi }{(\mathbf{X})}^{\prime }.$$

The following assumption is the key condition of the projected-PCA.

Assumption 3.1 (Genuine projection)

There are positive constants c_min and c_max such that, with probability approaching one (as p → ∞),

$$c_{min}<{\lambda }_{min}(p^{-1}{\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda })<{\lambda }_{max}(p^{-1}{\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda })<c_{max}.$$

Since the dimensions of Φ(X) and Λ are respectively p × Jd and p × K, Assumption 3.1 requires Jd ≥ K, which is reasonable since we assume K, the number of factors, to be fixed throughout the paper.

Assumption 3.1 is similar to the pervasive condition on the factor loadings (Stock and Watson (2002)). In our context, this condition requires the covariates X have non-vanishing explaining power on the loading matrix, so that the projection matrix Λ′PΛ has spiked eigenvalues. Note that it rules out the case when X is completely unassociated with the loading matrix Λ (e.g., when X is pure noise). One of the typical examples that satisfies this assumption is the semi-parametric factor model (model (1.4)). We shall study this specific type of factor model in Section 4, and prove Assumption 3.1 in the supplementary material Fan et al. (2015b).

Note that F and Λ are not separately identified, because for any nonsingular H, ΛF′ = ΛH⁻¹HF′. Therefore, we assume:

Assumption 3.2 (Identification)

Almost surely, T⁻¹F′F = I_K and Λ′PΛ is a K × K diagonal matrix with distinct entries.

This condition corresponds to the PC1 condition of Bai and Ng (2013), which separately identifies the factors and loadings from their product ΛF′. It is often used in factor analysis for identification, and means that the columns of factors and loadings can be orthogonalized (also see Bai and Li (2012)).

Assumption 3.3 (Basis functions)

1. (i) There are d_min and d_max > 0 so that with probability approaching one (as p → ∞),

   $$d_{min}<{\lambda }_{min}(p^{-1}\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))<{\lambda }_{max}(p^{-1}\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))<d_{max}.$$

2. max_{j≤J,i≤p,l≤d} Eϕ_j(X_il)² < ∞.

Note that $p^{-1}\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X})=p^{-1}{\sum }_{i=1}^p\varphi {({\mathbf{X}}_i)}^{\prime }\varphi ({\mathbf{X}}_i)$ and ϕ(X_i) is a vector of dimensionality Jd ≪ p. Thus, condition (i) can follow from the strong law of large numbers. For instance, {X_i}_i≤p are weakly correlated and in the population level Eϕ(X_i)′ϕ(X_i) is well-conditioned. In addition, this condition can be satisfied through proper normalizations of commonly used basis functions such as B-splines, wavelets, Fourier basis, etc. In the general setup of this paper, we allow {X_i}_i≤p’s to be cross-sectionally dependent and non-stationary. Regularity conditions about weak dependence and stationarity are imposed only on {(f_t, u_t)} as follows.

We impose the strong mixing condition. Let ${\mathcal{F}}_{-\infty }^0$ and ${\mathcal{F}}_T^{\infty }$ denote the σ-algebras generated by {(f_t, u_t) : t ≤ 0} and {(f_t, u_t) : t ≥ T} respectively. Define the mixing coefficient

$$\alpha (T)=\underset{A\in {\mathcal{F}}_{-\infty }^0,B\in {\mathcal{F}}_T^{\infty }}{sup}\mid P(A)P(B)-P(AB)\mid .$$

Assumption 3.4 (Data generating process)

1. {u_t, f_t}_t≤T is strictly stationary. In addition, Eu_it = 0 for all i ≤ p, j ≤ K; {u_t}_t≤T is independent of {X_i, f_t}_i≤p,t≤T.

2. Strong mixing: There exist r₁, C₁ > 0 such that for all T > 0,

   $$\alpha (T)<exp(-C_1{T}^{r_1}).$$
3. Weak dependence: there is C₂ > 0 so that

   $$\begin{array}{c}\underset{j\le p}{max}\sum _{i=1}^p\mid E{u}_{it}{u}_{jt}\mid <C_2,\frac{1}{pT}\sum _{i=1}^p\sum _{j=1}^p\sum _{t=1}^T\sum _{s=1}^T\mid E{u}_{it}{u}_{js}\mid <C_2,\\ \underset{i\le p}{max}\frac{1}{pT}\sum _{k=1}^p\sum _{m=1}^p\sum _{t=1}^T\sum _{s=1}^T\mid cov(u_{it}{u}_{kt},u_{is}{u}_{ms})\mid <C_2.\end{array}$$
4. Exponential tail: there exist r₂ ≥ 0, r₃ > 0 satisfying $r_1^{-1}+r_2^{-1}+r_3^{-1}>1$and b₁, b₂ > 0, such that for any s > 0, i ≤ p and j ≤ K,

   $$P(\mid u_{it}\mid >s)\le exp(-{(s/b_1)}^{r_2}),P(\mid f_{jt}\mid >s)\le exp(-{(s/b_2)}^{r_3}).$$

Assumption 3.4 is standard, especially condition (iii) is commonly imposed for high-dimensional factor analysis (e.g., Bai (2003); Stock and Watson (2002)), which requires {u_it}_i≤p,t≤T be weakly dependent both serially and cross-sectionally. It is often satisfied when the covariance matrix $E{\mathbf{u}}_t{\mathbf{u}}_t^{\prime }$ is sufficiently sparse under the strong mixing condition. We provide primitive conditions of condition (iii) in the supplementary material Fan et al. (2015b).

Formally, we have the following theorem:

Theorem 3.1

Consider the conventional factor model (3.1) with Assumptions 3.1–3.4. The projected-PCA estimators F̂ and Ĝ(X) defined in Section 2.3 satisfy, as p → ∞ (J, T may either grow simultaneously with p satisfying $J=o(\sqrt{p})$ or stay constant with Jd ≥ K),

$$\begin{array}{c}\frac{1}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{F}\Vert }_F^2=O_P\left(\frac{J}{p}\right),\\ \frac{1}{p}{\Vert \widehat{\mathbf{G}}(\mathbf{X})-\mathbf{P}\mathbf{\Lambda }\Vert }_F^2=O_P\left(\frac{J}{p^T}+\frac{J^2}{p^2}\right).\end{array}$$

To compare with the regular PC method, the convergence rate for the estimated factors is improved for small T. In particular, the projected-PCA does not require T → ∞, and also has a good rate of convergence for the loading matrix up to a projection transformation. Hence we have achieved a finite-T consistency, which is particularly interesting in the “high-dimensional-low-sample-size” (HDLSS) context, considered by Jung and Marron (2009). In contrast, the conventional PC method achieves a rate of convergence of O_P (1/p + 1/T²) for estimating factors, and O_P (1/T + 1/p) for estimating loadings. See Remarks 4.1, 4.2 below for additional details.

3.2. Projected-PCA consistency in the HDLSS context

In recent years, substantial work has been done on the PCA consistency on the spiked covariance model (e.g., Johnstone (2001) and Paul (2007)), and is extended to the HDLSS context by Ahn et al. (2007), Jung and Marron (2009) and Shen et al. (2013a). In a high-dimensional factor model y_t = Λf_t + u_t, let Σ = cov(y_t) be the p × p covariance matrix of y_t. Let Ξ = (ξ₁, …, ξ_K) be the leading eigenvectors of Σ. Under the pervasiveness condition, the first K eigenvalues of the p × p covariance matrix Σ = cov(y_t) grow at rate O(p). Due to the presence of these very spiked eigenvalues, Fan et al. (2013) showed that the leading eigenvectors of Σ can be consistently estimated by those of the p × p sample covariance matrix $\frac{1}{T}{\mathbf{YY}}^{\prime }$ as both p, T → ∞. However, either the consistency fails to hold with a finite T or the rate of convergence is slow when T grows slowly as in the HDLSS context.

With a genuine projection P that satisfies Assumption 3.1, the projected-PCA estimates Ξ using the leading eigenvectors of the sample covariance matrix based on the projected data PY. Specifically, recall that Ξ̂ is a p×K matrix whose columns are the eigenvectors corresponding to the first largest K eigenvalues of $\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P}$, and D̂ is a diagonal matrix consisting of the largest K eigenvalues of $\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P}$. The consistency of projected-PCA can be achieved up to a projection error $\frac{1}{\sqrt{p}}{\Vert \mathbf{\Lambda }-\mathbf{P}\mathbf{\Lambda }\Vert }_F$ even if T is finite, and the rate of convergence is faster when T also grows.

Let Ṽ be an orthogonal matrix whose columns are the eigenvectors of Λ′Λ, corresponding to the eigenvalues in a decreasing order. Let Σ_u be the p×p covariance matrix of u_t. We have the following result on the convergence of eigenspace spanned by the spiked eigenvalues.

Theorem 3.2

Under the conditions of Theorem 3.1, we have, as p → ∞ (J, T may either grow simultaneously with p satisfying $J=o(\sqrt{p})$ or stay constant with Jd ≥ K), for V = Ṽ′(Λ′Λ)^1/2D̂^−1/2,

$${\Vert \widehat{\mathbf{\Xi }}-\mathbf{\Xi }\mathbf{V}\Vert }_F=O_P\left(\frac{1}{p}{\Vert {\mathbf{\sum }}_u\Vert }_2+\sqrt{\frac{J}{pT}}+\frac{J}{p}+\frac{1}{\sqrt{p}}{\Vert \mathbf{P}\mathbf{\Lambda }-\mathbf{\Lambda }\Vert }_F\right).$$

Q: Not clear. What is the order of V? How does it related to Theorem 3.1? Why readers need to know all details below?

Briefly speaking, Ξ̂ approximates the space spanned by the columns of Ξ, which consists of leading eigenvectors of Σ. In addition, in the high-dimensional factor model, we shall prove in the appendix that, for Λ̄ = ΛṼ,

$${\Vert \mathbf{\Xi }-\mathbf{\Lambda }\stackrel{\sim }{\mathbf{V}}{({\overline{\mathbf{\Lambda }}}^{\prime }\overline{\mathbf{\Lambda }})}^{-1/2}\Vert }_F=O\left(\frac{1}{p}{\Vert {\mathbf{\sum }}_u\Vert }_2\right).$$ (3.3)

As a result, Theorem 3.2 follows from (3.3). There are three sources of estimation errors: (i) the error from (3.3), (ii) the error from approximating PΛ by Ξ̂D̂^1/2, which depends on the projected noise PU, and (iii) the projection error $\frac{1}{\sqrt{p}}{\Vert \mathbf{\Lambda }-\mathbf{P}\mathbf{\Lambda }\Vert }_2$. Note that the errors from (i) and (ii) are both asymptotically negligible as p → ∞, and does not require a diverging T. The error of the third type depends on the nature of the loading matrix. In the special case when Λ belongs to the space spanned by X, corresponding to G(X) = Λ, this term is also asymptotically negligible as p → ∞.

4. Projected-PCA in Semi-parametric Factor Models

4.1. Sieve approximations

In the semi-parametric factor model, it is assumed that λ_ik = g_k(X_i) + γ_ik, where g_k(X_i) is a nonparametric smooth function for the observed covariates, and γ_ik is the unobserved random loading component that is independent of X_i. Hence the model is written as

$$y_{it}=\sum _{k=1}^K\{g_k({\mathbf{X}}_i)+{\gamma }_{ik}\}{f}_{tk}+u_{it},i=1,\cdots ,p,t=1,\cdots ,T.$$

In the matrix form,

$$\mathbf{Y}=\{\mathbf{G}(\mathbf{X})+\mathbf{\Gamma }\}{\mathbf{F}}^{\prime }+\mathbf{U},$$

and G(X) does not vanish (pervasive condition, see Assumption 4.2 below).

The estimators F̂ and Ĝ (X) are the projected-PCA estimators as defined in Section 2.3. We now define the estimator of the nonparametric function g_k(·), k = 1, …, K. In the matrix form, the projected data has the following sieve approximated representation:

$$\mathbf{PY}=\mathrm{\Phi }(\mathbf{X})\mathbf{B}{\mathbf{F}}^{\prime }+\stackrel{\sim }{\mathbf{E}},$$ (4.1)

where Ẽ = PΓF′+PR(X)F′+PU is “small” because Γ and U are orthogonal to the function space spanned by X, and R(X) is the sieve approximation error. The sieve coefficient matrix B = (b₁, …, b_K) can be estimated by least squares from the projected model (4.1): Ignore Ẽ, replace F with F̂, and solve (4.1) to obtain

$$\widehat{\mathbf{B}}=({\widehat{\mathbf{b}}}_1,\dots ,{\widehat{\mathbf{b}}}_K)=\frac{1}{T}{[\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X})]}^{-1}\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathbf{Y}\widehat{\mathbf{F}}.$$

We then estimate g_k(·) by

$${\widehat{g}}_k(\mathbf{x})=\varphi {(\mathbf{x})}^{\prime }{\widehat{\mathbf{b}}}_k,\forall \mathbf{x}\in \mathcal{X},k=1,\dots ,K,$$

where 𝒳 denotes the support of X_i.

4.2. Asymptotic analysis

When Λ = G(X) + Γ, G(X) can be understood as the projection of Λ onto the sieve space spanned by X. Hence the following assumption is a specific version of Assumptions 3.1 and 3.2 in the current context.

Assumption 4.1

1. Almost surly, T⁻¹F′F = I_K and G(X)′G(X) is a K × K diagonal matrix with distinct entries.

2. There are two positive constants c_min and c_max so that with probability approaching one (as p → ∞),

   $$c_{min}<{\lambda }_{min}(p^{-1}\mathbf{G}{(\mathbf{X})}^{\prime }\mathbf{G}(\mathbf{X}))<{\lambda }_{max}(p^{-1}\mathbf{G}{(\mathbf{X})}^{\prime }\mathbf{G}(\mathbf{X}))<c_{max}.$$

In this section, we do not need to assume {γ_i}_i≤p to be i.i.d. for the estimation purpose. Cross-sectional weak dependence as in Condition (ii) would be sufficient. The i.i.d. assumption will be only needed when we consider specification tests in Section 5. Define γ_i = (γ_i1, …, γ_iK)′, and

$${\nu }_p=\underset{k\le K}{max}\frac{1}{p}\sum _{i\le p}var({\gamma }_{ik}).$$

Assumption 4.2

1. Eγ_ik = 0 and {X_i}_i≤p is independent of {γ_ik}_i≤p.

2. max_k≤K,i≤p Eg_k(X_i)² < ∞, ν_p < ∞ and

   $$\underset{k\le K,j\le p}{max}\sum _{i\le p}\mid E{\gamma }_{ik}{\gamma }_{jk}\mid =O({\nu }_p).$$

The following set of conditions is concerned about the accuracy of the sieve approximation.

Assumption 4.3 (Accuracy of sieve approximation)

∀l ≤ d, k ≤ K,

1. the loading component g_kl(·) belongs to a Hölder class 𝒢 defined by

   $$\mathcal{G}=\{g:\mid g^{(r)}(s)-g^{(r)}(t)\mid \le L{\mid s-t\mid }^{\alpha }\}$$

   for some L > 0;

2. The sieve coefficients {b_k,jl}_j≤J satisfy for κ = 2(r + α) ≥ 4, as J → ∞,

   $$\underset{x\in {\mathcal{X}}_l}{sup}{\mid g_{kl}(x)-\sum _{j=1}^J{b}_{k,jl}{\varphi }_j(x)\mid }^2=O(J^{-\kappa }),$$

   where 𝒳_l is the support of the lth element of X_i, and J is the sieve dimension.

3. ${max}_{k,j,l}{b}_{k,jl}^2<\infty$.

Condition (ii) is satisfied by common basis. For example, when {ϕ_j} is polynomial basis or B-splines, condition (ii) is implied by condition (i) (see e.g., Lorentz (1986) and Chen (2007)).

Theorem 4.1

Suppose $J=o(\sqrt{p})$. Under Assumptions 3.3, 3.4, 4.1–4.3, as p, J → ∞, T can be either divergent or bounded, we have that

$$\begin{array}{l}\frac{1}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{F}\Vert }_F^2=O_P\left(\frac{1}{p}+\frac{1}{J^{\kappa }}\right),\\ \frac{1}{p}{\Vert \widehat{\mathbf{G}}(\mathbf{X})-\mathbf{G}(\mathbf{X})\Vert }_F^2=O_P\left(\frac{J}{p^2}+\frac{J}{p^T}+\frac{J}{J^{\kappa }}+\frac{J{\nu }_p}{p}\right),\\ \underset{k\le K}{max}\underset{\mathbf{x}\in \mathcal{X}}{sup}\mid {\widehat{g}}_k(\mathbf{x})-g_k(\mathbf{x})\mid =O_P\left(\frac{J}{p}+\frac{J}{\sqrt{pT}}+\frac{J}{J^{\kappa /2}}+J\sqrt{\frac{{\nu }_p}{p}}\right)\underset{j\le J}{max}\underset{x}{sup}\mid {\varphi }_j(x)\mid .\end{array}$$

In addition, if T → ∞ simultaneously with p and J, then

$$\frac{1}{p}{\Vert \widehat{\mathbf{\Gamma }}-\mathbf{\Gamma }\Vert }_F^2=O_P\left(\frac{J}{p^2}+\frac{1}{T}+\frac{1}{J^{\kappa }}+\frac{J{\nu }_p}{p}\right).$$

The optimal $J^{\ast }={(pmin\{T,p,{\nu }_p^{-1}\})}^{1/\kappa }$ simultaneously minimizes the convergence rates of the factors and nonparametric loading function g_k(·). It also satisfies the constraint $J^{\ast }=o(\sqrt{p})$ as κ ≥ 4. With J = J^*, we have

$$\begin{array}{l}\frac{1}{T}\sum _{t=1}^T{\Vert {\widehat{\mathbf{f}}}_t-{\mathbf{f}}_t\Vert }^2=O_P\left(\frac{1}{p}\right),\\ \frac{1}{p}\sum _{i=1}^p{\mid {\widehat{g}}_k({\mathbf{X}}_i)-g_k({\mathbf{X}}_i)\mid }^2=O_P\left(\frac{1}{{(pmin\{T,p,v_p^{-1}\})}^{1-1/\kappa }}\right),\forall k\\ \underset{k\le K}{max}\underset{\mathbf{x}\in \mathcal{X}}{sup}\mid {\widehat{g}}_k(\mathbf{x})-g_k(\mathbf{x})\mid =O_P\left(\frac{{max}_{j\le J}{sup}_x\mid {\varphi }_j(x)\mid }{{(pmin\{T,p,{\nu }_p^{-1}\})}^{1/2-1/\kappa }}\right),\end{array}$$

and Γ̂ = (γ̂₁, …, γ̂_p)′ satisfies:

$$\frac{1}{p}\sum _{i=1}^p{\Vert {\widehat{\mathit{\gamma }}}_i-{\mathit{\gamma }}_i\Vert }^2=O_P\left(\frac{1}{{(pmin\{T,p,v_p^{-1}\})}^{1-1/\kappa }}+\frac{1}{T}\right).$$

Some remarks about these rates of convergence compared with those of the conventional factor analysis are in order.

Remark 4.1

The rates of convergence for factors and nonparametric functions do not require T → ∞. When T = O(1),

$$\frac{1}{T}\sum _{t=1}^T{\Vert {\widehat{\mathbf{f}}}_t-{\mathbf{f}}_t\Vert }^2=O_P\left(\frac{1}{p}\right),\frac{1}{p}\sum _{i=1}^p{\mid {\widehat{g}}_k({\mathbf{X}}_i)-g_k({\mathbf{X}}_i)\mid }^2=O_P\left(\frac{1}{p^{1-1/\kappa }}\right).$$

The rates still converge fast when p is large, demonstrating the blessing of dimensionality. This is an attractive feature of the projected-PCA in the HDLSS context, as in many applications, the stationarity of a time series and the time-invariance assumption on the loadings hold only for a short period of time. In contrast, in the usual factor analysis, consistency is granted only when T → ∞. For example, according to Fan et al. (2015a) (Lemma C.1), the regular PCA method has the following convergence rate

$$\frac{1}{T}\sum _{t=1}^T{\Vert {\stackrel{\sim }{\mathbf{f}}}_t-{\mathbf{f}}_t\Vert }^2=O_P\left(\frac{1}{p}+\frac{1}{T^2}\right),$$

which is inconsistent when T is bounded.

Remark 4.2

When both p and T are large, the projected-PCA estimates factors as well as the regular PCA does, and achieves a faster rate of convergence for the estimated loadings when γ_ik vanishes. In this case, λ_ik = g_k(X_i), the loading matrix is estimated by Λ̂ = Ĝ(X), and

$$\frac{1}{p}\sum _{i=1}^p{\mid {\widehat{\lambda }}_{ik}-{\lambda }_{ik}\mid }^2=\frac{1}{p}\sum _{i=1}^p{\mid {\widehat{g}}_k({\mathbf{X}}_i)-g_k({\mathbf{X}}_i)\mid }^2=O_P\left(\frac{1}{{(pT)}^{1-1/\kappa }}+\frac{1}{p^{2-2/\kappa }}\right).$$

In contrast, the regular PCA method as in Stock and Watson (2002) yields

$$\frac{1}{p}\sum _{i=1}^p{\mid {\stackrel{\sim }{\lambda }}_{ik}-{\lambda }_{ik}\mid }^2=O_P\left(\frac{1}{T}+\frac{1}{p}\right).$$

Comparing these rates, we see that when g_k(·)’s are sufficiently smooth (larger κ), the rate of convergence for the estimated loadings is also improved.

5. Semiparametric Specification Test

The loading matrix always has the following orthogonal decomposition:

$$\mathbf{\Lambda }=\mathbf{G}(\mathbf{X})+\mathbf{\Gamma },$$

where Γ is interpreted as the loading component that cannot be explained by X. We consider two types of specification tests: testing $H_0^1:\mathbf{G}(\mathbf{X})=0$, and $H_0^2:\mathbf{\Gamma }=0$. The former tests whether the observed covariates have explaining powers on the loadings, while the latter tests whether the covariates fully explain the loadings. The former provides a diagnostic tool as to whether or not to employ the projected PCA; the latter tests the adequacy of the semiparametric factor models in the literature.

5.1. Testing G(X) = 0

Testing whether the observed covariates have explaining powers on the factor loadings can be formulated as the following null hypothesis:

$$H_0^1:\mathbf{G}(\mathbf{X})=0a.s.$$

Due to the approximate orthogonality of X and Γ, we have PΛ ≈ G(X). Hence, the null hypothesis is approximately equivalent to

$$H_0:\mathbf{P}\mathbf{\Lambda }=0a.s.$$

This motivates a statistic ${\Vert \mathbf{P}\stackrel{\sim }{\mathbf{\Lambda }}\Vert }_F^2=\text{tr}({\stackrel{\sim }{\mathbf{\Lambda }}}^{\prime }\mathbf{P}\stackrel{\sim }{\mathbf{\Lambda }})$ for a consistent loading estimator Λ̃. Normalizing the test statistic by its asymptotic variance leads to the test statistic

$$S_G=\frac{1}{p}\text{tr}({\mathbf{W}}_1{\stackrel{\sim }{\mathbf{\Lambda }}}^{\prime }\mathbf{P}\stackrel{\sim }{\mathbf{\Lambda }}),{\mathbf{W}}_1={(\frac{1}{p}{\stackrel{\sim }{\mathbf{\Lambda }}}^{\prime }\stackrel{\sim }{\mathbf{\Lambda }})}^{-1},$$

where the K × K matrix W₁ is the weight matrix. The null hypothesis is rejected when S_G is large.

The projected PCA estimator is inappropriate under the null hypothesis as the projection is not genuine. We therefore use the least squares estimator Λ̃ = YF̃/T, leading to the test statistic

$$S_G=\frac{1}{T^{2}p}\text{tr}({\mathbf{W}}_1{\stackrel{\sim }{\mathbf{F}}}^{\prime }{\mathbf{Y}}^{\prime }\mathbf{PY}\stackrel{\sim }{\mathbf{F}}).$$

Here, we take F̃ as the regular PC estimator: the columns of $\stackrel{\sim }{\mathbf{F}}/\sqrt{T}$ are the first K eigenvectors of the T × T data matrix Y′Y.

5.2. Testing Γ = 0

Connor et al. (2012) applied the semi-parametric factor model to analyzing financial returns, who assumed that Γ = 0, that is, the loading matrix can be fully explained by the observed covariates. It is therefore natural to test the following null hypothesis of specification:

$$H_0^2:\mathbf{\Gamma }=0a.s.$$

Recall that G(X) ≈ PΛ so that Λ ≈ PΛ + Γ. Therefore essentially the specification testing problem is equivalent to testing:

$$H_0:\mathbf{P}\mathbf{\Lambda }=\mathbf{\Lambda }a.s.$$

That is, we are testing whether the loading matrix in the factor model belongs to the space spanned by the observed covariates.

A natural test statistic is thus based on the weighted quadratic form

$$\text{tr}({\widehat{\mathbf{\Gamma }}}^{\prime }{\mathbf{W}}_2\widehat{\mathbf{\Gamma }})=\text{tr}({\widehat{\mathbf{\Lambda }}}^{\prime }{(\mathbf{I}-\mathbf{P})}^{\prime }{\mathbf{W}}_2(\mathbf{I}-\mathbf{P})\widehat{\mathbf{\Lambda }}),$$

for some p × p positive definite weight matrixW₂, where F̂ is the projected-PCA estimator for factors and Λ̂ = YF̂/T. To control the size of the test, we take ${\mathbf{W}}_2={\mathbf{\sum }}_u^{-1}$, where Σ_u is a diagonal covariance matrix of u_t under H₀, assuming that (u_1t, ···, u_pt) are uncorrelated.

We replace ${\mathbf{\sum }}_u^{-1}$ with its consistent estimator: let Û = Y − Λ̂F̂′. Define

$${\widehat{\mathbf{\sum }}}_u=T^{-1}\text{diag}\{\widehat{\mathbf{U}}{\widehat{\mathbf{U}}}^{\prime }\}=T^{-1}\text{diag}\{\mathbf{Y}(\mathbf{I}-T^{-1}\widehat{\mathbf{F}}{\widehat{\mathbf{F}}}^{\prime }){\mathbf{Y}}^{\prime }\}.$$

Then the operational test statistic is defined to be

$$S_{\mathrm{\Gamma }}=\text{tr}({\widehat{\mathbf{\Lambda }}}^{\prime }{(\mathbf{I}-\mathbf{P})}^{\prime }{\widehat{\mathbf{\sum }}}_u^{-1}(\mathbf{I}-\mathbf{P})\widehat{\mathbf{\Lambda }}).$$

The null hypothesis is rejected for large values of S_Γ.

5.3. Asymptotic null distributions

For the testing purpose we assume {X_i, γ_i} to be i.i.d., and let T, p, J → ∞ simultaneously. The following assumption regulates the relation between T and p.

Assumption 5.1

Suppose

1. {X_i, γ_i}_i≤p are independent and identically distributed;

2. T^2/3 = o(p), and p(log p)⁴ = o(T²).

3. J and κ satisfy: $J=o(min\{\sqrt{p},\sqrt{T}\})$, and $max\{T\sqrt{p},p\}=o(J^{\kappa })$.

Condition (ii) requires a balance of the dimensionality and the sample size. On one hand, a relatively large sample size is desired (p(log p)⁴ = o(T²)) so that the effect of estimating ${\mathbf{\sum }}_u^{-1}$ is negligible asymptotically. On the other hand, as is common in high-dimensional factor analysis, a lower bound of the dimensionality is also required (condition T^2/3 = o(p)) to ensure that the factors are estimated accurately enough. Such a required balance is common for high-dimensional factor analysis (e.g., Bai (2003), Stock and Watson (2002)) and in the recent literature for PCA (e.g., Jung and Marron (2009), Shen et al. (2013b)). The iid assumption of covariates X_i in Condition (i) can be relaxed with further distributional assumptions on γ_i (e.g., assuming γ_i to be Gaussian). The conditions on J in Condition (iii) is consistent with those of the previous sections.

We focus on the case when u_t is Gaussian, and show that under $H_0^1$,

$$S_G=(1+o_P(1))\frac{1}{p}\text{tr}({\mathbf{W}}_1{\mathbf{\Gamma }}^{\prime }\mathbf{P}\mathbf{\Gamma }),$$

and under $H_0^2$

$$S_{\mathrm{\Gamma }}=(1+o_P(1))\frac{1}{T^2}\text{tr}({\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }{\mathbf{\sum }}_u^{-1}\mathbf{UF}),$$

whose conditional distributions (given F) under the null are χ² with degree of freedom respectively JdK and pK. We can derive their standardized limiting distribution as J, T, p → ∞. This is given in the following result.

Theorem 5.1

Suppose Assumptions 3.3, 3.4, 4.2, 5.1 hold. Then under $H_0^1$,

$$\frac{p{S}_G-\mathit{JdK}}{\sqrt{2\mathit{JdK}}}{\to }^{d}N(0,1),$$

where K = dim(f_t) and d = dim(X_i). In addition, suppose Assumptions 4.1 and 4.3 further hold, {u_t}_t≤T is i.i.d. N(0, Σ_u) with a diagonal covariance matrix Σ_u whose elements are bounded away from zero and infinity. Then under $H_0^2$,

$$\frac{T{S}_{\mathrm{\Gamma }}-pK}{\sqrt{2pK}}{\to }^{d}N(0,1).$$

In practice, when a relatively small sieve dimension J is used, one can instead use the upper α-quantile of the ${\chi }_{\mathit{JdK}}^2$ distribution for pS_G.

Remark 5.1

We require u_it be independent across t, which ensures that the covariance matrix of the leading term $\text{vec}(\frac{1}{\sqrt{T}}\mathbf{U}{\mathbf{F}}^{\prime })$ to have a simple form ${\mathbf{\sum }}_u^{-1}\otimes {\mathbf{I}}_K$. This assumption can be relaxed to allow for weakly dependent {u_t}_t≤T, but many autocovariance terms will be involved in the covariance matrix. One may regularize standard autocovariance matrix estimators such as Newey and West (1987) and Andrews (1991) to account for the high dimensionality. Moreover, we assume Σ_u be diagonal to facilitate estimating ${\mathbf{\sum }}_u^{-1}$, which can also be weakened to allow for a non-diagonal but sparse Σ_u. Regularization methods such as thresholding (Bickel and Levina (2008)) can then be employed, though they are expected to be more technically involved.

6. Estimating the Number of Factors from Projected Data

We now address the problem of estimating K = dim(f_t) when it is unknown. Once consistent estimation of K is obtained, all the results achieved carry over to the unknown K case using a conditioning argument^*. In principle, many consistent estimators of K can be employed, e.g., Bai and Ng (2002), Alessi et al. (2010), Breitung and Pigorsch (2009), Hallin and Liška (2007). More recently, Ahn and Horenstein (2013) and Lam and Yao (2012) proposed to select the largest ratio of the adjacent eigenvalues of Y′Y, based on the fact that the K largest eigenvalues of the sample covariance matrix grow fast as p increases, while the remaining eigenvalues either remain bounded or grow slowly.

We extend Ahn and Horenstein (2013)’s theory in two ways. First, when the loadings depend on the observable characteristics, it is more desirable to work on the projected data PY. Due to the orthogonality condition of U and X, the projected data matrix is approximately equal to G(X)F′. The projected matrix PY(PY)′ thus allows us to study the eigenvalues of the principal matrix component G(X)G(X)′, which directly connects with the strengths of those factors. Since the non-vanishing eigenvalues of PY(PY)′ and (PY)′PY = Y′PY are the same, we can work directly with the eigenvalues of the matrix Y′PY. Secondly, we allow p/T → ∞.

Let λ_k(Y′PY) denote the kth largest eigenvalue of the projected data matrix Y′PY. We assume 0 < K < Jd/2, which naturally holds if the sieve dimension J slowly grows. The estimator is defined as:

$$\widehat{K}=arg\underset{0<k<Jd/2}{max}\frac{{\lambda }_k({\mathbf{Y}}^{\prime }\mathbf{PY})}{{\lambda }_{k+1}({\mathbf{Y}}^{\prime }\mathbf{PY})}.$$

The following assumption is similar to that of Ahn and Horenstein (2013). Recall that U = (u₁, ···, u_T) is a p × T matrix of the idiosyncratic components, and ${\mathbf{\sum }}_u=E{\mathbf{u}}_t{\mathbf{u}}_t^{\prime }$ denote the p × p covariance matrix of u_t.

Assumption 6.1

The error matrix U can be decomposed as

$$\mathbf{U}={\mathbf{\sum }}_u^{1/2}{\mathbf{EM}}^{1/2},$$ (6.1)

where,

1. the eigenvalues of Σ_u are bounded away from both zero and infinity.

2. M is a T by T positive semi-definite non-stochastic matrix, whose eigenvalues are bounded away from 0 and infinity,

3. E = (e_it)_p×T is a p × T stochastic matrix, where e_it is independent in both i and t, and e_t = (e_1t, …, e_pt)′ are i.i.d. isotropic sub-Gaussian vectors, that is, there is C > 0, for all s > 0,

   $$\underset{\Vert \mathbf{v}\Vert =1}{sup}\underset{m\ge 1}{sup}P(\mid {\mathbf{v}}^{\prime }{\mathbf{e}}_t\mid >s)\le exp(1-s^2/C).$$
4. There are d_min, d_max > 0, almost surely,

   $$d_{min}\le {\lambda }_{min}(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X})/p)\le {\lambda }_{max}(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X})/p)\le d_{max}.$$

This assumption allows the matrix U to be both cross-sectionally and serially dependent. The T × T matrix M captures the serial dependence across t. In the special case of no-serial-dependence, the decomposition (6.1) is satisfied by taking M = I. In addition, we require u_t to be sub-Gaussian to apply random matrix theories of Vershynin (2010). For instance, when u_t is N (0, Σ_u), for any ||v|| = 1, v′e_t ~ N (0, 1). Thus condition (iii) is satisfied. Finally, the almost surely condition of (iv) seems somewhat strong, but is still satisfied by bounded basis functions (e.g., Fourier basis) and follows from the strong law of large numbers given that Eϕ(X_i)ϕ(X_i)′ is well conditioned.

We show in the supplementary material that when Σ_u is diagonal (u_it is cross-sectionally independent), both the sub-Gaussian assumption and condition (iv) can be relaxed.

The following theorem is the main result of this section.

Theorem 6.1

Under assumptions of Theorem 4.1 and Assumption 6.1, as p, T → ∞, if J satisfies $J=o(min\{\sqrt{p},T\})$ and K < Jd/2 (J may either grow or stay constant), we have

$$P(\widehat{K}=K)\to 1.$$

7. Numerical Studies

This section presents numerical results to demonstrate the performance of projected-PCA method for estimating loading and factors using both real data and simulated data.

7.1. Estimating loading curves with real data

We collected stocks in S&P500 index constituents from CRSP which have complete daily closing prices from year 2005 through 2013, and their corresponding market capitalization and book value from Compustat. There are 337 stocks in our data set, whose daily excess returns were calculated. We considered four characteristics X as in Connor et al. (2012) for each stock: size, value, momentum and volatility, which were calculated using the data before a certain data analyzing window so that characteristics are treated known. See Connor et al. (2012) for detailed descriptions of these characteristics. All four characteristics are standardized to have mean zero and unit variance. Note that the construction makes their values independent of the current data.

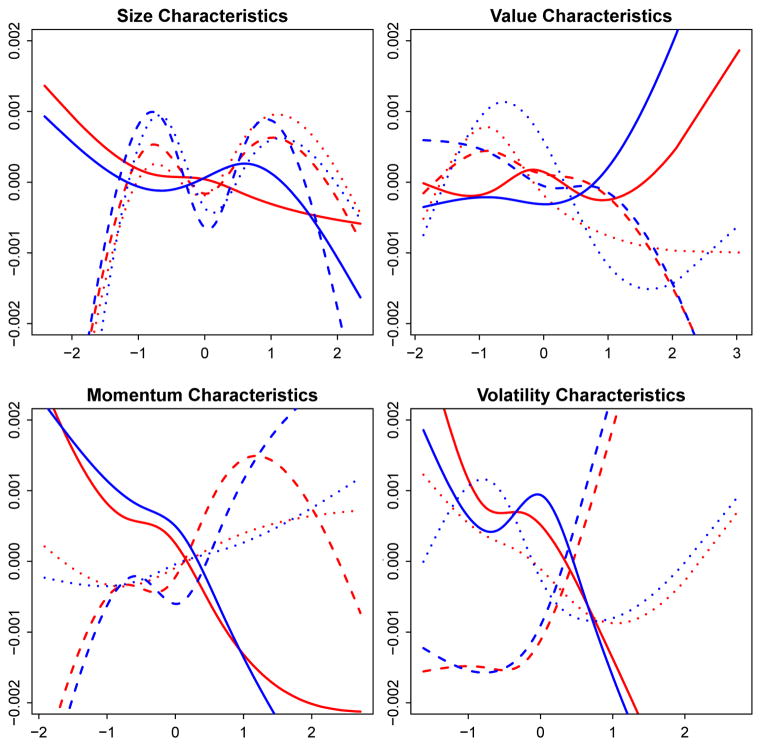
We fix the time window to be the first quarter of the year 2006, which contains T = 63 observations. Given the excess returns {y_it}_{i≤337,t≤63} and characteristics X_i as the input data and setting K = 3, we fit loading functions $g_k({\mathbf{X}}_i)={\alpha }_{ik}+{\sum }_{l=1}^4{g}_{kl}(X_{il})$ for k = 1, 2, 3 using the projected-PCA method. The four additive components g_kl(·) are fitted using the cubic spline in the R package “GAM” with sieve dimension J = 4. All the four loading functions for each factor are plotted in Figure 3. The contribution of each characteristic to each factor is quite nonlinear.

Fig. 3.

Estimated additive loading functions g_kl, l = 1, ···, 4. from financial returns of 337 stocks in S&P 500 index. They are taken as the true functions in the simulation studies. In each panel (fixed l), the true and estimated curves for k = 1, 2, 3 are plotted and compared. The solid, dashed and dotted red curves are the true curves corresponding to the first, second and third factors respectively. The blue curves are their estimates from one simulation of the calibrated model with T = 50, p = 300.

7.2. Calibrating the model with real data

We now treat the estimated functions g_kl(·) as the true loading functions, and calibrate a model for simulations. The “true model” is calibrated as follows:

1. Take the estimated g_kl(·) from the real data as the true loading functions.

2. For each p, generate {u_t}_t≤T from N(0, DΣ₀D) where D is diagonal and Σ₀ sparse. Generate the diagonal elements of D from Gamma(α, β) with α = 7.06, β = 536.93 (calibrated from the real data), and generate the off-diagonal elements of Σ₀ from $N({\mu }_u,{\sigma }_u^2)$ with μ_u = −0.0019, σ_u = 0.1499. Then truncate Σ₀ by a threshold of correlation 0.03 to produce a sparse matrix and make it positive definite by R package “nearPD”.

3. Generate {γ_ik} from the i.i.d. Gaussian distribution with mean 0 and standard deviation 0.0027, calibrated with real data.

4. Generate f_t from a stationary VAR model f_t = Af_t−1 + ε_t where ε_t ~ N(0, Σ_ε). The model parameters are calibrated with the market data and listed in Table 1.

5. Finally, generate X_i ~ N(0, Σ_X). Here Σ_X is a 4×4 correlation matrix estimated from the real data.

Table 1.

Parameters used for the factor generating process, obtained by calibration to the real data.

Σε			A
0.9076	0.0049	0.0230	−0.0371	−0.1226	−0.1130
0.0049	0.8737	0.0403	−0.2339	0.1060	−0.2793
0.0230	0.0403	0.9266	0.2803	0.0755	−0.0529

We simulate the data from the calibrated model, and estimate the loadings and factors for T = 10 and 50 with p varying from 20 through 500. The “true” and estimated loading curves are plotted in Figure 3 to demonstrate the performance of projected-PCA. Note that the “true” loading curves in the simulation are taken from the estimates calibrated using the real data. The estimates based on simulated data capture the shape of the true curve, though we also notice slight biases at boundaries. But in general, projected-PCA fits the model well.

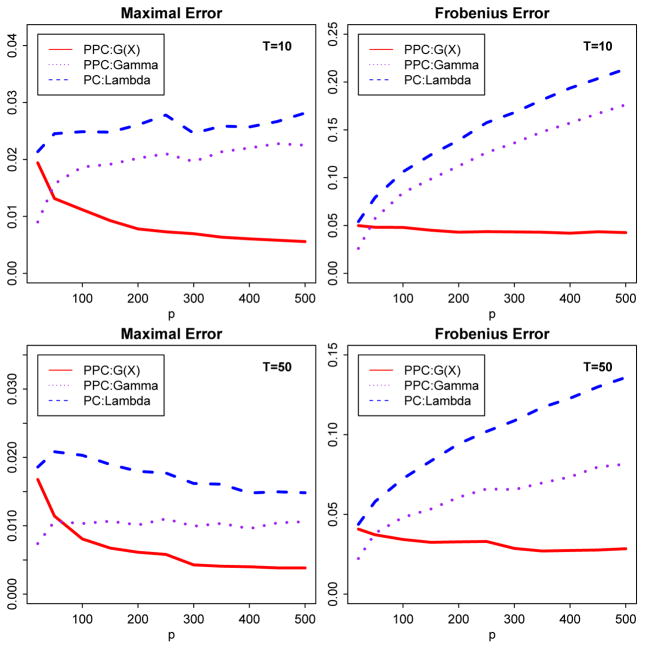
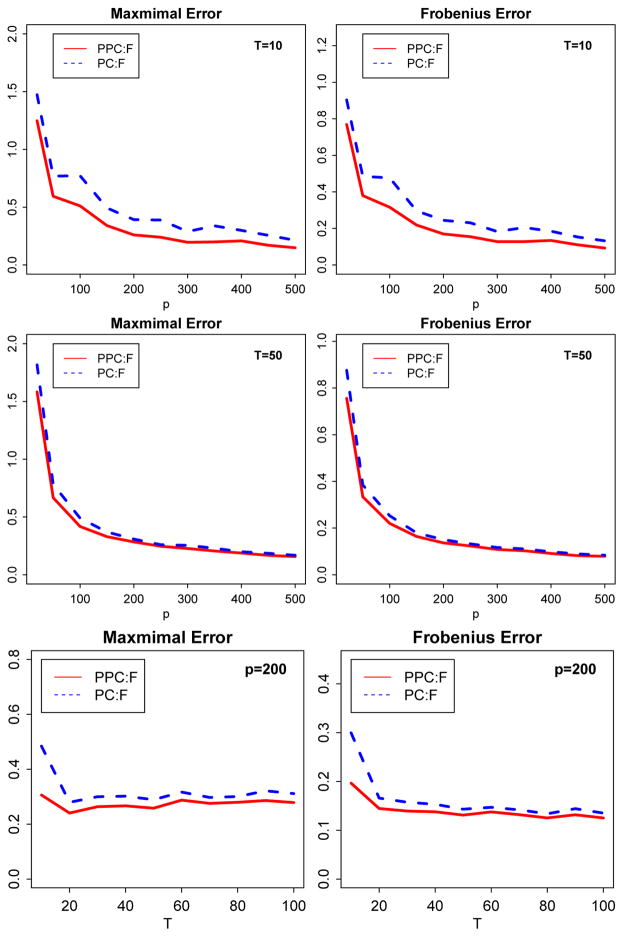
We also compare our method with the regular PC method (e.g., Stock and Watson (2002)). The mean values of ||Λ̂ − Λ||_max, ${\Vert \widehat{\mathbf{\Lambda }}-\mathbf{\Lambda }\Vert }_F/\sqrt{p}$, ||F̂ − F₀||_max and ${\Vert \widehat{\mathbf{F}}-{\mathbf{F}}_0\Vert }_F/\sqrt{T}$ are plotted in Figures 1 and 2. where Λ = G₀(X) + Γ (see section 7.3 for definitions of G₀(X) and F₀). The breakdown error or G₀(X) and Γ are also depicted in Figure 1. In comparison, projected-PCA outperforms PC in estimating both factors and loadings including the nonparametric curves G(X) and random noise Γ. The estimation errors for G(X) of projected-PCA decrease as the dimension increases, which is consistent with our asymptotic theory.

Fig. 1.

Averaged ||Λ̂ − Λ|| by projected-PCA (PPCA, red solid) and regular PC (dashed blue) and ||Ĝ − G₀||, ||Γ̂ − Γ|| by PPCA over 500 repetitions. Left panel:||_·||_max, right panel: ${\Vert .\Vert }_F/\sqrt{p}$.

Fig. 2.

Averaged ||F̂ − F₀||_max and ${\Vert \widehat{\mathbf{F}}-{\mathbf{F}}_0\Vert }_F/\sqrt{T}$ over 500 repetitions, by projected-PCA (PPCA, solid red) and regular PC (dashed blue).

7.3. Design 2

Consider a different design with only one observed covariate and three factors. The three characteristic functions are g₁ = x, g₂ = x² − 1, g₃ = x³ − 2x with the characteristic X being standard normal. Generate {f_t}_t≤T from the stationary VAR(1) model, that is f_t = Af_t−1 + ε_t where ε_t ~ N (0, I). We consider Γ = 0.

We simulate the data for T = 10 or 50 and various p ranging from 20 to 500. To ensure that the true factor and loading satisfy the identifiability conditions, we calculate a transformation matrix H such that $\frac{1}{T}\mathbf{H}{\mathbf{F}}^{\prime }\mathbf{FH}={\mathbf{I}}_K$, H⁻¹G′GH′⁻¹ is diagonal. Let the final true factors and loadings be F₀ = FH, G₀ = GH′⁻¹. For each p, we run the simulation for 500 times.

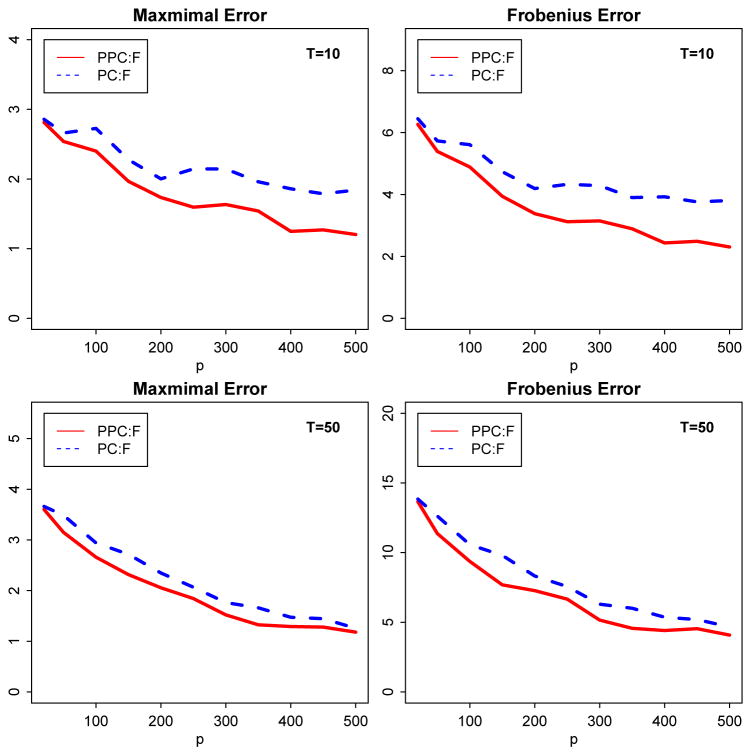
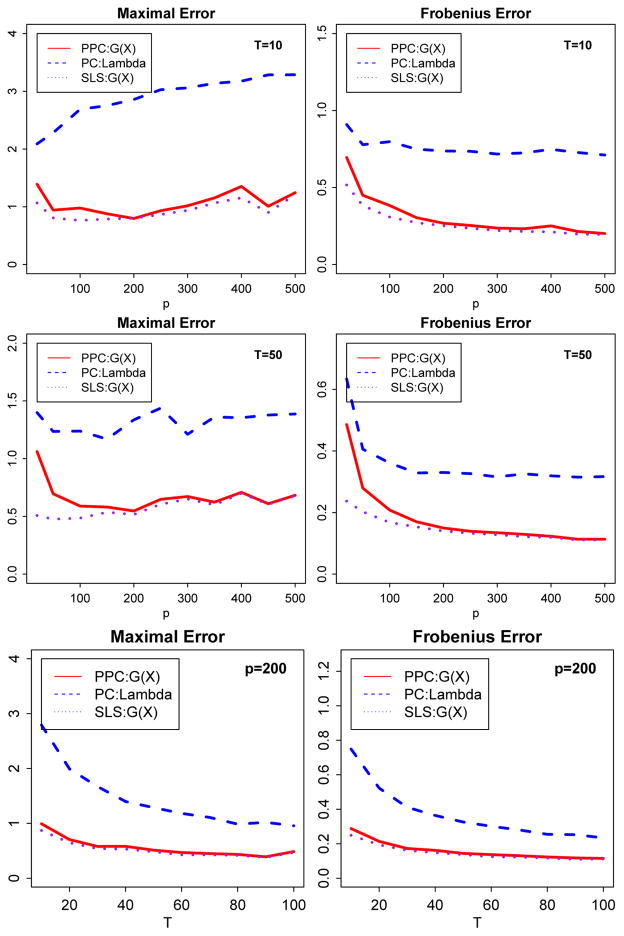
We estimate the loadings and factors using both projected-PCA and PC. For projected-PCA, as in our theorem, we choose J = C(p min(T, p))^1/κ, with κ = 4 and C = 3. To estimate the loading matrix, we also compare with a third method: sieve-least-squares (SLS), assuming the factors are observable. In this case, the loading matrix is estimated by PYF₀/T, where F₀ is the true factor matrix of simulated data.

The estimation error measured in max and standardized Frobenius norms for both loadings and factors are reported in Figures 4 and 5. The plots demonstrate the good performance of projected-PCA in estimating both loadings and factors. In particular, it works well when we encounter small T but a large p. In this design, Γ= 0, so the accuracy of estimating Λ = G₀ is significantly improved by using the projected-PCA. The projected-PCA method significantly outperforms the traditional PCA. Figure 5 shows that the factors are also better estimated by projected-PCA than the traditional one, particularly when T is small. It is also clearly seen that when p is fixed, the improvement on estimating factors is not significant as T grows. This matches with our convergence results for the factor estimators.

Fig. 4.

Averaged ||Ĝ − G₀||_max and ${\Vert \widehat{\mathbf{G}}-{\mathbf{G}}_0\Vert }_F/\sqrt{p}$ over 500 repetitions. PPCA, PC and SLS respectively represent projected-PCA, regular PCA and sieve least squares with known factors: Design 2. Here Γ = 0, so Λ = G₀. Upper two panels: p grows with fixed T; bottom panels: T grows with fixed p.

Fig. 5.

Average estimation error of factors over 500 repetitions, i.e. ||F̂ − F₀||_max and ${\Vert \widehat{\mathbf{F}}-{\mathbf{F}}_0\Vert }_F/\sqrt{T}$ by projected-PCA (solid red) and PC (dashed blue): Design 2. Upper two panels: p grows with fixed T; bottom panels: T grows with fixed p.

It is also interesting to compare projected-PCA with SLS (Sieve Least-Squares with observed factors) in estimating the loadings, which corresponds to the cases of unobserved and observed factors. As we see from Figure 4, when p is small, the projected-PCA is not as good as SLS. But the two methods behave similarly as p increases. This further confirms the theory and intuition that as the dimension becomes larger, the effects of estimating the unknown factors are negligible.

7.4. Estimating number of factors

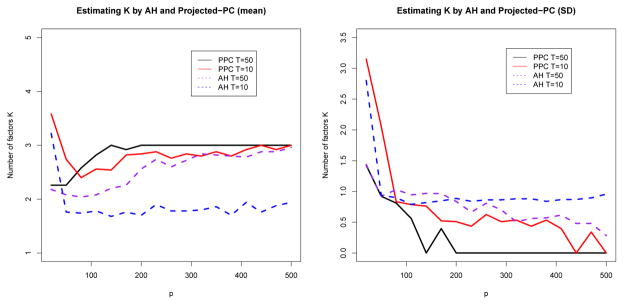
We now demonstrate the effectiveness of estimating K by the projected-PC’s eigenvalue-ratio method. The data are simulated in the same way as in Design 2. T = 10 or 50 and took the values of p ranging from 20 to 500. We compare our projected-PC based on the projected data matrix Y′PY to the eigenvalue-ratio test (AH) of Ahn and Horenstein (2013) and Lam and Yao (2012), which works on the original data matrix Y′Y.

For each pair of T, p, we repeat the simulation for 50 times and report the mean and standard deviation of the estimated number of factors in Figure 6. The projected-PCA outperforms AH after projection, which significantly reduces the impact of idiosyncratic errors. When T = 50, we can recover the number of factors almost all the time, especially for large dimensions (p > 200). On the other hand, even when T = 10, projected-PCA still obtains a closer estimated number of factors.

Fig 6.

Mean and standard deviation of the estimated number of factors over 50 repetitions. True K = 3. PPCA and AH respectively represent the methods of projected-PCA and Ahn and Horenstein (2013). Left panel: Mean; Right panel: standard deviation.

7.5. Loading specification tests with real data

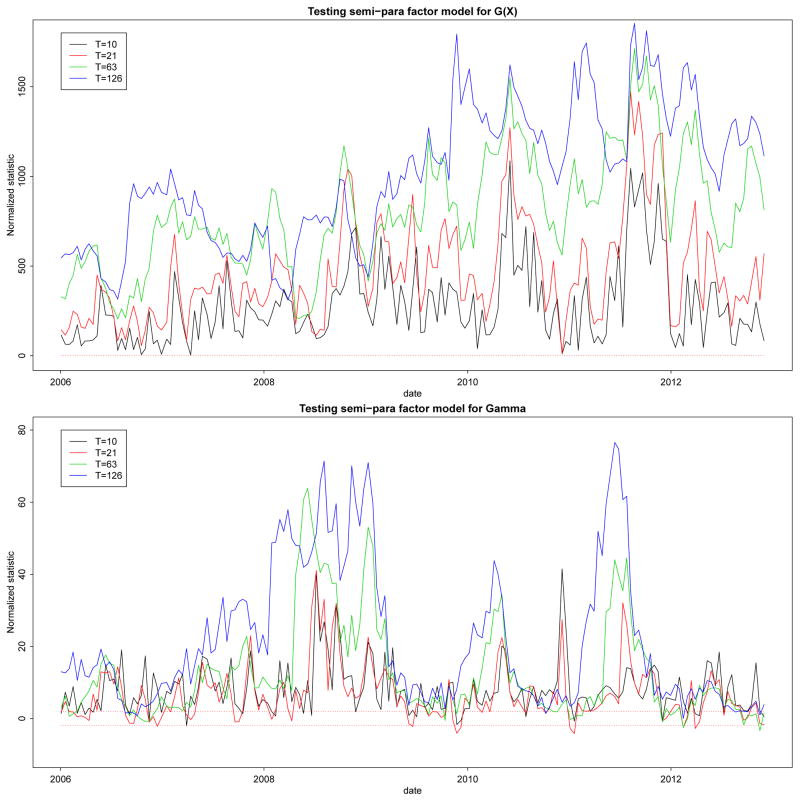
We test the loading specifications on the real data. We used the same data set as in Section 6.1, consisting of excess returns from 2005 through 2013. The tests were conducted based on rolling windows, with the length of windows spanning from 10 days, a month, a quarter, and half a year. For each fixed window-length (T), we computed the standardized test statistic of S_G and S_Γ, and plotted them along the rolling windows respectively in Figure 7. In almost all cases, the number of factors is estimated to be one in various combinations of (T, p, J).

Fig 7.

Normalized S_G, S_γ from 2006/01/03 to 2012/11/30. The dotted lines are ± 1.96.

Figure 7 suggests that the semi-parametric factor model is strongly supported by the data. Judging from the upper panel (testing $H_0^1:\mathbf{G}(\mathbf{X})=0$), we have very strong evidence of the existence of non-vanishing covariate effect, which demonstrates the dependence of the market beta’s on the covariates X. In other words, the market beta’s can be explained at least partially by the characteristics of assets. The results also provide the theoretical basis for using projected PCA to get more accurate estimation.

In the bottom panel of Figure 7 (testing $H_0^2:\mathbf{\Gamma }=0$), we see for a majority of period, the null hypothesis is rejected. In other words, the characteristics of assets cannot fully explain the market beta as intuitively expected, and model (1.2) in the literature is inadequate. However, fully nonparametric loadings could be possible in certain time range mostly before financial crisis. During 2008–2010, the market’s behavior had much more complexities, which causes more rejections of the null hypothesis. The null hypothesis Γ = 0 is accepted more often since 2012. We also notice that larger T tends to yield larger statistics in both tests, as the evidence against the null hypothesis is stronger with larger T. After all, the semi-parametric model being considered provides flexible ways of modeling equity markets and understanding the nonparametric loading curves.

8. Conclusions

This paper proposes and studies a high-dimensional factor model with nonparametric loading functions that depend on a few observed covariate variables. This model is motivated by the fact that observed variables can explain partially the factor loadings. We propose a projected PCA to estimate the unknown factors, loadings, and number of factors. After projecting the response variable onto the sieve space spanned by the covariates, the projected-PCA yields a significant improvement on the rates of convergence than the regular methods. In particular, consistency can be achieved without a diverging sample size, as long as the dimensionality grows. This demonstrates that the proposed method is useful in the typical HDLSS situations. In addition, we propose new specification tests for the orthogonal decomposition of the loadings, which fill the gap of the testing literature for semi-parametric factor models. Our empirical findings show that firm characteristics can explain partially the factor loadings, which provide theoretical basis for employing projected-PCA methods. On the other hand, our empirical study also shows that the firm characteristics can not fully explain the factor loadings so that the proposed generalized factor model is more appropriate.

APPENDIX A: PROOFS FOR SECTION 3

Throughout the proofs, p → ∞, and T may either grow simultaneously with p or stay constant. For two matrices A, B with fixed dimensions, and a sequence a_T, by writing A = B + o_P(a_T), we mean ||A − B||_F = o_P (a_T).

In the regular factor model Y = ΛF′+U, let K denote a K×K diagonal matrix of the first K eigenvalues of $\frac{1}{T_p}{\mathbf{Y}}^{\prime }\mathbf{PY}$. Then by definition, $\frac{1}{T_p}{\mathbf{Y}}^{\prime }\mathbf{PY}\widehat{\mathbf{F}}=\widehat{\mathbf{F}}\mathbf{K}$. Let $\mathbf{M}=\frac{1}{T_p}{\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda }{\mathbf{F}}^{\prime }\widehat{\mathbf{F}}{\mathbf{K}}^{-1}$. Then

$$\widehat{\mathbf{F}}-\mathbf{FM}=\sum _{i=1}^3{\mathbf{D}}_i{\mathbf{K}}^{-1},$$ (A.1)

where

$${\mathbf{D}}_1=\frac{1}{T_p}\mathbf{F}{\mathbf{\Lambda }}^{\prime }\mathbf{PU}\widehat{\mathbf{F}},{\mathbf{D}}_2=\frac{1}{T_p}{\mathbf{U}}^{\prime }\mathbf{PU}\widehat{\mathbf{F}},{\mathbf{D}}_3=\frac{1}{T_p}{\mathbf{U}}^{\prime }\mathbf{P}\mathbf{\Lambda }{\mathbf{F}}^{\prime }\widehat{\mathbf{F}}.$$

We now describe the structure of the proofs for

$$\frac{1}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{F}\Vert }_F^2=O_p\left(\frac{J}{p}\right).$$

Note that F̂ − F = F̂ − FM + F(M − I). Hence we need to bound $\frac{1}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{FM}\Vert }_F^2$ and $\frac{1}{T}{\Vert \mathbf{F}(\mathbf{M}-\mathbf{I})\Vert }_F^2$ respectively.

• Step 1: prove that $\frac{1}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{FM}\Vert }_F^2=O_P(J/p)$.

  Due to the equality (A.1), it suffices to bound ||K⁻¹||₂ as well as the $\frac{1}{T}{\Vert .\Vert }_F^2$ norm of D₁, D₂, D₃ respectively. These are obtained in Lemmas A.2, A.3 below.

• Step 2: prove that $\frac{1}{T}{\Vert {\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{FM})\Vert }_F=O_P(\sqrt{J/(pT)}+J/p)$.

  Still by the equality (A.1), $\frac{1}{T}{\Vert {\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{FM})\Vert }_F\le \frac{1}{T}{\Vert {\mathbf{K}}^{-1}\Vert }_2{\sum }_{i=1}^3{\Vert {\mathbf{F}}^{\prime }{\mathbf{D}}_i\Vert }_F$. Hence this step is achieved by bounding ||F′D_i||_F for i = 1, 2, 3. Note that in this step, we shall not apply a simple inequality ||F′D_i||_F ≤ ||F||_F ||D_i||_F, which is too crude. Instead, with the help of the result $\frac{1}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{FM}\Vert }_F^2=O_p(J/p)$ achieved in Step 1, sharper upper bounds for ||F′D_i||_F can be achieved. We do so in Lemma ?? in the supplementary material.

• Step 3: prove that ${\Vert \mathbf{M}-\mathbf{I}\Vert }_F^2=O_P(J/(pT)+{(J/p)}^2)$.

  This step is achieved in Lemma A.4 below, which uses the result in Step 2.

Before proceeding to Step 1, we first show that the two alternative definitions for Ĝ(X) described in Section 2.3 are equivalent.

Lemma A.1 $\frac{1}{T}\mathbf{PY}\widehat{\mathbf{F}}=\widehat{\mathbf{\Xi }}{\widehat{\mathbf{D}}}^{1/2}$

Proof

Consider the singular value decomposition: $\frac{1}{\sqrt{T}}\mathbf{PY}={\mathbf{V}}_1\mathbf{S}{\mathbf{V}}_2^{\prime }$, where V₁ is a p×p orthogonal matrix, whose columns are the eigenvectors of $\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P}$; V₂ is a T × T matrix whose columns are the eigenvectors of $\frac{1}{T}{\mathbf{Y}}^{\prime }\mathbf{PY}$; S is a p × T rectangular diagonal matrix, with diagonal entries as the square roots of the non-zero eigenvalues of $\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P}$. In addition, by definition, D̂ is a K × K diagonal matrix consisting of the largest K eigenvalues of $\frac{1}{T}{\mathbf{PYY}}^{\prime }\mathbf{P}$; Ξ̂ is a p × K matrix whose columns are the corresponding eigenvectors. The columns of $\widehat{\mathbf{F}}/\sqrt{T}$ are the eigenvectors of $\frac{1}{T}{\mathbf{Y}}^{\prime }\mathbf{PY}$, corresponding to the first K eigenvalues.

With these definitions, we can write V₁ = (Ξ̂, Ṽ₁), ${\mathbf{V}}_2=(\widehat{\mathbf{F}}/\sqrt{T},{\stackrel{\sim }{\mathbf{V}}}_2)$, and

$$\mathbf{S}=\left(\begin{array}{cc}{\widehat{\mathbf{D}}}^{1/2}& \mathbf{0}\\ \mathbf{0}& \stackrel{\sim }{\mathbf{D}}\end{array}\right),{\widehat{\mathbf{F}}}^{\prime }{\stackrel{\sim }{\mathbf{V}}}_2=\mathbf{0},{\widehat{\mathbf{F}}}^{\prime }\widehat{\mathbf{F}}/T={\mathbf{I}}_K,$$

for some matrices Ṽ₁, Ṽ₂ and D̃. It then follows that

$$\frac{1}{T}\mathbf{PY}\widehat{\mathbf{F}}={\mathbf{V}}_1\mathbf{S}{\mathbf{V}}_2^{\prime }\frac{1}{\sqrt{T}}\widehat{\mathbf{F}}=(\widehat{\mathbf{\Xi }},{\stackrel{\sim }{\mathbf{V}}}_1)\left(\begin{array}{cc}{\widehat{\mathbf{D}}}^{1/2}& \mathbf{0}\\ \mathbf{0}& \stackrel{\sim }{\mathbf{D}}\end{array}\right)\left(\begin{array}{c}{\widehat{\mathbf{F}}}^{\prime }/\sqrt{T}\\ {\stackrel{\sim }{\mathbf{V}}}_2^{\prime }\end{array}\right)\frac{1}{\sqrt{T}}\widehat{\mathbf{F}}=\widehat{\mathbf{\Xi }}{\widehat{\mathbf{D}}}^{1/2}.$$

Lemma A.2

||K||₂ = O_P (1), ||K⁻¹||₂ = O_P (1), ||M||₂ = O_P (1).

Proof

The eigenvalues of K are the same as those of

$$\mathbf{W}=\frac{1}{Tp}{(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2}\mathrm{\Phi }{(\mathbf{X})}^{\prime }{\mathbf{YY}}^{\prime }\mathrm{\Phi }(\mathbf{X}){(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2},$$

Substituting Y = ΛF′ + U, and F′F/T = I_K, we have $\mathbf{W}={\sum }_{i=1}^4{\mathbf{W}}_i$, where

$$\begin{array}{lll}{\mathbf{W}}_1\hfill & =\hfill & \frac{1}{p}{(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2}\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathbf{\Lambda }{\mathbf{\Lambda }}^{\prime }\mathrm{\Phi }(\mathbf{X}){(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2},\hfill \\ {\mathbf{W}}_2\hfill & =\hfill & \frac{1}{p}{(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2}\mathrm{\Phi }{(\mathbf{X})}^{\prime }(\frac{\mathbf{\Lambda }{\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }}{T})\mathrm{\Phi }(\mathbf{X}){(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2},\hfill \\ {\mathbf{W}}_3\hfill & =\hfill & {\mathbf{W}}_2^{\prime },\hfill \\ {\mathbf{W}}_4\hfill & =\hfill & \frac{1}{p}{(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2}\mathrm{\Phi }{(\mathbf{X})}^{\prime }\frac{\mathbf{U}{\mathbf{U}}^{\prime }}{T}\mathrm{\Phi }(\mathbf{X}){(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2}.\hfill \end{array}$$

By Assumption 3.3, ${\Vert \mathrm{\Phi }(\mathbf{X})\Vert }_2={\lambda }_{max}^{1/2}(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))=O_P(\sqrt{p})$,

$$\begin{array}{lll}\hfill {\Vert {(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2}\Vert }_2& =\hfill & {\lambda }_{max}^{1/2}({(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1})={\lambda }_{min}^{-1/2}(\frac{1}{p}\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))p^{-1/2}=O_P(p^{-1/2})\hfill \\ \hfill {\Vert \mathbf{P}\mathbf{\Lambda }\Vert }_2& =\hfill & {\lambda }_{max}^{1/2}(\frac{1}{p}{\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda })p^{1/2}=O_P(p^{1/2}).\hfill \end{array}$$

Hence

$${\Vert {\mathbf{W}}_2\Vert }_2\le \frac{1}{p}{\Vert {(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2}\Vert }_2^2{\Vert \mathrm{\Phi }(\mathbf{X})\Vert }_2{\Vert \mathbf{\Lambda }\Vert }_F{\Vert \frac{1}{T}{\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }\mathrm{\Phi }(\mathbf{X})\Vert }_F=O_P(\frac{1}{pT}){\Vert {\mathbf{F}}^{\prime }{\mathbf{U}}^{\prime }\mathrm{\Phi }(\mathbf{X})\Vert }_F.$$

By Lemma ?? in the supplementary material, ${\Vert W_2\Vert }_2=O_P(\frac{\sqrt{J}}{\sqrt{pT}})$. Similarly,

$${\Vert {\mathbf{W}}_4\Vert }_2\le \frac{1}{pT}{\Vert {(\mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathrm{\Phi }(\mathbf{X}))}^{-1/2}\Vert }_2^2{\Vert \mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathbf{U}\Vert }_F^2=O_P(\frac{1}{p^{2}T}){\Vert \mathrm{\Phi }{(\mathbf{X})}^{\prime }\mathbf{U}\Vert }_F^2=O_P(\frac{J}{p}).$$

Using the inequality that for the kth eigenvalue, |λ_k(W) − λ_k(W₁)| ≤ ||W − W₁||₂, we have |λ_k(W) − λ_k(W₁)| = O_P(T^−1/2 +p⁻¹), for k = 1, · · ·, K. Hence it suffices to prove that the first K eigenvalues of W₁ are bounded away from both zero and infinity, which are also the first K eigenvalues of $\frac{1}{p}{\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda }$. This holds under the theorem’s assumption (Assumption 3.1). Thus ||K⁻¹||₂ = O_P(1) = ||K||₂, which also implies ||M||₂ = O_P(1).

Lemma A.3

(i) ${\Vert {\mathbf{D}}_1\Vert }_F^2=O_P(TJ/p)$, (ii) ${\Vert {\mathbf{D}}_2\Vert }_F^2=O_P(J/p^2)$, (iii) ${\Vert {\mathbf{D}}_3\Vert }_F^2=O_P(TJ/p)$, (iv) $\frac{1}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{FM}\Vert }_F^2=O_P(J/p)$.

Proof

It follows from Lemma ?? in the supplementary material that ${\Vert \mathbf{PU}\Vert }_F=O_P(\sqrt{TJ})$. Also, ${\Vert \mathbf{F}\Vert }_F^2=O_P(T)={\Vert \widehat{\mathbf{F}}\Vert }_F^2$ and Assumption 3.1 implies ${\Vert \mathbf{P}\mathbf{\Lambda }\Vert }_2^2=O_P(p)$. So

$$\begin{array}{lll}{\Vert {\mathbf{D}}_1\Vert }_F^2\hfill & =\hfill & {\Vert \frac{1}{Tp}\mathbf{F}{\mathbf{\Lambda }}^{\prime }\mathbf{PU}\widehat{\mathbf{F}}\Vert }_F^2\le \frac{1}{T^2{p}^2}{\Vert \mathbf{F}\Vert }_F^2{\Vert \widehat{\mathbf{F}}\Vert }_F^2{\Vert \mathbf{P}\mathbf{\Lambda }\Vert }_2^2{\Vert \mathbf{PU}\Vert }_F^2=O_P(TJ/p)\hfill \\ {\Vert {\mathbf{D}}_2\Vert }_F^2\hfill & =\hfill & {\Vert \frac{1}{Tp}{\mathbf{U}}^{\prime }\mathbf{PU}\widehat{\mathbf{F}}\Vert }_F^2\le \frac{1}{T^2{p}^2}{\Vert \mathbf{PU}\Vert }_F^2{\Vert \widehat{\mathbf{F}}\Vert }_F^2=O_P(J/p^2)\hfill \\ {\Vert {\mathbf{D}}_3\Vert }_F^2\hfill & =\hfill & {\Vert \frac{1}{Tp}{\mathbf{U}}^{\prime }\mathbf{P}\mathbf{\Lambda }{\mathbf{F}}^{\prime }\widehat{\mathbf{F}}\Vert }_F^2\le \frac{1}{T^2{p}^2}{\Vert \mathbf{PU}\Vert }_F^2{\Vert \mathbf{P}\mathbf{\Lambda }\Vert }_2^2{\Vert \mathbf{F}\Vert }_F^2{\Vert \widehat{\mathbf{F}}\Vert }_F^2=O_P(TJ/p).\hfill \end{array}$$

By Lemma A.2, ||K⁻¹||₂ = O_P (1). Part (iv) then follows directly from

$$\frac{1}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{FM}\Vert }_F^2\le O_P(\frac{1}{T}{\Vert {\mathbf{K}}^{-1}\Vert }_2)({\Vert {\mathbf{D}}_1\Vert }_F^2+{\Vert {\mathbf{D}}_2\Vert }_F^2+{\Vert {\mathbf{D}}_3\Vert }_F^2).$$

Lemma A.4

In the regular factor model ${\Vert \mathbf{M}-\mathbf{I}\Vert }_F=O_P(\sqrt{J/(pT)}+J/p)$.

Proof

By Lemma ?? in the supplementary material and the triangular inequality, $\Vert \frac{1}{T}{(\widehat{\mathbf{F}}-\mathbf{FM})}^{\prime }\mathbf{F}\Vert =O_P(\sqrt{J/(pT)}+J/p)$. Hence

$${\widehat{\mathbf{F}}}^{\prime }\mathbf{F}/T={\mathbf{M}}^{\prime }+\frac{1}{T}{(\widehat{\mathbf{F}}-\mathbf{FM})}^{\prime }\mathbf{F}={\mathbf{M}}^{\prime }+O_P(\sqrt{J/(pT)}+J/p)$$

Right multiplying M to both sides ${\widehat{\mathbf{F}}}^{\prime }\mathbf{FM}/T={\mathbf{M}}^{\prime }\mathbf{M}+O_P(\sqrt{J/(pT)}+J/p)$. In addition,

$${\Vert {\widehat{\mathbf{F}}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{FM})/T\Vert }_F\le \frac{1}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{FM}\Vert }_F^2+{\Vert {\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{FM})/T\Vert }_F=O_P(\sqrt{J/(pT)}+J/p).$$

Hence

$$\mathbf{I}={\mathbf{M}}^{\prime }\mathbf{M}+O_P(\sqrt{J/(pT)}+J/p).$$

In addition, from $\mathbf{M}=\frac{1}{Tp}{\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda }{\mathbf{F}}^{\prime }\widehat{\mathbf{F}}{\mathbf{K}}^{-1}=\frac{1}{p}{\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda }\mathbf{M}{\mathbf{K}}^{-1}+O_P(\sqrt{J/(pT)}+J/p)$,

$$\mathbf{MK}=\frac{1}{p}{\mathbf{\Lambda }}^{\prime }\mathbf{P}\mathbf{\Lambda }\mathbf{M}+O_P(\sqrt{J/(pT)}+J/p).$$

Because Λ′PΛ is diagonal, the same proofs of those of Proposition ?? lead to the desired result.

Proof of Theorem 3.1

Proof

It follows from Lemmas A.3 (iv) and A.4 that

$$\frac{1}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{F}\Vert }_F^2\le \frac{2}{T}{\Vert \widehat{\mathbf{F}}-\mathbf{FM}\Vert }_F^2+2{\Vert \mathbf{M}-\mathbf{I}\Vert }_F^2=O_p(\frac{J}{p}).$$

As for the estimated loading matrix, note that

$$\widehat{\mathbf{G}}(\mathbf{X})=\frac{1}{T}\mathbf{PY}\widehat{\mathbf{F}}=\frac{1}{T}\mathbf{P}\mathbf{\Lambda }{\mathbf{F}}^{\prime }\widehat{\mathbf{F}}+\frac{1}{T}\mathbf{PU}\widehat{\mathbf{F}}=\mathbf{P}\mathbf{\Lambda }+\mathbf{E},$$

where $\mathbf{E}=\frac{1}{T}\mathbf{P}\mathbf{\Lambda }{\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{F})+\frac{1}{T}\mathbf{PU}(\widehat{\mathbf{F}}-\mathbf{F})+\frac{1}{T}\mathbf{PUF}$.

By Lemmas ?? and A.4,

$${\Vert \frac{1}{T}\mathbf{P}\mathbf{\Lambda }{\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{F})\Vert }_F\le O_P\left(\frac{\sqrt{p}}{T}\right){\Vert {\mathbf{F}}^{\prime }(\widehat{\mathbf{F}}-\mathbf{FM})\Vert }_F+O_P(\sqrt{p}){\Vert \mathbf{M}-\mathbf{I}\Vert }_F=O_P\left(\sqrt{\frac{J}{T}}+\frac{J}{\sqrt{p}}\right).$$

By Lemma ??, ${\Vert \frac{1}{T}\mathbf{PU}(\widehat{\mathbf{F}}-\mathbf{F})\Vert }_F\le \frac{1}{T}{\Vert \mathbf{PU}\Vert }_2{\Vert \widehat{\mathbf{F}}-\mathbf{F}\Vert }_F=O_P(\frac{J}{\sqrt{p}})$, and from Lemma ?? ${\Vert \frac{1}{T}\mathbf{PUF}\Vert }_F=O_P(\sqrt{\frac{J}{T}})$. Hence ${\Vert \mathbf{E}\Vert }_F=O_P(\sqrt{\frac{J}{T}}+\frac{J}{\sqrt{p}})$, which implies

$$\frac{1}{p}{\Vert \widehat{\mathbf{G}}(\mathbf{X})-\mathbf{P}\mathbf{\Lambda }\Vert }_F^2=O_P(\frac{J}{pT}+\frac{J^2}{p^2}).$$

Proof of Theorem 3.2

Proof

Since Ĝ(X) = Ξ̂D̂^1/2, by Theorem 3.1, $\frac{1}{p}{\Vert \widehat{\mathbf{\Xi }}{\widehat{\mathbf{D}}}^{1/2}-\mathbf{P}\mathbf{\Lambda }\Vert }_F^2=O_P(\frac{J}{pT}+\frac{J^2}{p^2})$. Hence $\frac{1}{p}{\Vert \widehat{\mathbf{\Xi }}{\widehat{\mathbf{D}}}^{1/2}-\mathbf{\Lambda }\Vert }_F^2=O_P(\frac{J}{pT}+\frac{J^2}{p^2})+\frac{1}{p}{\Vert \mathbf{P}\mathbf{\Lambda }-\mathbf{\Lambda }\Vert }_F^2$. By lemma A.2, ||(D̂/p)⁻¹||₂ = ||K⁻¹||₂ = O_P(1), which implies

$${\Vert \widehat{\mathbf{\Xi }}-\mathbf{\Lambda }{\widehat{\mathbf{D}}}^{-1/2}\Vert }_F^2=O_P\left(\frac{J}{pT}+\frac{J^2}{p^2}+\frac{1}{p}{\Vert \mathbf{P}\mathbf{\Lambda }-\mathbf{\Lambda }\Vert }_F^2\right).$$

On the other hand, define Λ̄ = ΛṼ = (Λ̄₁, …Λ̄_K). Then Λ̄′Λ̄ is diagonal and $\mathbf{\Lambda }{\mathbf{\Lambda }}^{\prime }{\overline{\mathbf{\Lambda }}}_j={\overline{\mathbf{\Lambda }}}_j{\Vert {\overline{\mathbf{\Lambda }}}_j\Vert }_2^2$, j = 1, …, K. This implies that the columns of Λ̄(Λ̄′Λ̄)^−1/2 are the eigenvectors of ΛΛ′ corresponding to the largest K eigenvalues. In addition, in the factor model, we have the following matrix decomposition: for Σ_u = cov(u_t), Σ = ΛΛ′ + Σ_u. Hence by the same argument of the proof of Proposition 2.2 in Fan et al. (2013),

$${\Vert \mathbf{\Xi }-\mathbf{\Lambda }\stackrel{\sim }{\mathbf{V}}{({\overline{\mathbf{\Lambda }}}^{\prime }\overline{\mathbf{\Lambda }})}^{-1/2}\Vert }_F=O\left(\frac{1}{p}{\Vert {\mathbf{\sum }}_u\Vert }_2\right).$$

Using ṼṼ′ = I, we have

$$\begin{array}{l}{\Vert \widehat{\mathbf{\Xi }}-\mathbf{\Xi }{\stackrel{\sim }{\mathbf{V}}}^{\prime }{({\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda })}^{1/2}{\widehat{\mathbf{D}}}^{-1/2}\Vert }_F\le {\Vert \widehat{\mathbf{\Xi }}-\mathbf{\Lambda }{\widehat{\mathbf{D}}}^{-1/2}\Vert }_F+{\Vert \mathbf{\Lambda }{\widehat{\mathbf{D}}}^{-1/2}-\mathbf{\Xi }{({\overline{\mathbf{\Lambda }}}^{\prime }\overline{\mathbf{\Lambda }})}^{1/2}{\stackrel{\sim }{\mathbf{V}}}^{\prime }{\widehat{\mathbf{D}}}^{-1/2}\Vert }_F+{\Vert \mathbf{\Xi }{({\overline{\mathbf{\Lambda }}}^{\prime }\overline{\mathbf{\Lambda }})}^{1/2}{\stackrel{\sim }{\mathbf{V}}}^{\prime }{\widehat{\mathbf{D}}}^{-1/2}-\mathbf{\Xi }{\stackrel{\sim }{\mathbf{V}}}^{\prime }{({\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda })}^{1/2}{\widehat{\mathbf{D}}}^{-1/2}\Vert }_F\\ \le {\Vert \widehat{\mathbf{\Xi }}-\mathbf{\Lambda }{\widehat{\mathbf{D}}}^{-1/2}\Vert }_F+{\Vert (\mathbf{\Lambda }\stackrel{\sim }{\mathbf{V}}{({\overline{\mathbf{\Lambda }}}^{\prime }\overline{\mathbf{\Lambda }})}^{-1/2}-\mathbf{\Xi }){({\overline{\mathbf{\Lambda }}}^{\prime }\overline{\mathbf{\Lambda }})}^{1/2}{\stackrel{\sim }{\mathbf{V}}}^{\prime }{\widehat{\mathbf{D}}}^{-1/2}\Vert }_F+{\Vert \mathbf{\Xi }({({\overline{\mathbf{\Lambda }}}^{\prime }\overline{\mathbf{\Lambda }})}^{1/2}{\stackrel{\sim }{\mathbf{V}}}^{\prime }-{\stackrel{\sim }{\mathbf{V}}}^{\prime }{({\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda })}^{1/2}){\widehat{\mathbf{D}}}^{-1/2}\Vert }_F.\end{array}$$

On the right hand side, the first term is $O_P(\frac{J}{pT}+\frac{J^2}{p^2}+\frac{1}{p}{\Vert \mathbf{P}\mathbf{\Lambda }-\mathbf{\Lambda }\Vert }_F^2)$, as is proved above. Still by ||(p⁻¹D̂)^−1/2||₂ = O_P(1), the second term is bounded by

$${\Vert \mathbf{\Lambda }\stackrel{\sim }{\mathbf{V}}{({\overline{\mathbf{\Lambda }}}^{\prime }\overline{\mathbf{\Lambda }})}^{-1/2}-\mathbf{\Xi }\Vert }_F{\Vert {({\overline{\mathbf{\Lambda }}}^{\prime }\overline{\mathbf{\Lambda }}/p)}^{1/2}\Vert }_F{\Vert \stackrel{\sim }{\mathbf{V}}\Vert }_2{\Vert {(\widehat{\mathbf{D}}/p)}^{-1/2}\Vert }_2=O({\Vert {\mathbf{\sum }}_u\Vert }_2/p).$$

Finally, since (Λ̄′Λ̄)^1/2 = Ṽ′(Λ′Λ)^1/2Ṽ, so (Λ̄′Λ̄)^1/2Ṽ′ − Ṽ′(Λ′Λ)^1/2 = 0, which implies the third term is zero. Hence

$${\Vert \widehat{\mathbf{\Xi }}-\mathbf{\Xi }{\stackrel{\sim }{\mathbf{V}}}^{\prime }{({\mathbf{\Lambda }}^{\prime }\mathbf{\Lambda })}^{1/2}{\widehat{\mathbf{D}}}^{-1/2}\Vert }_F\le O_P\left(\frac{J}{pT}+\frac{J^2}{p^2}+\frac{1}{p}{\Vert \mathbf{P}\mathbf{\Lambda }-\mathbf{\Lambda }\Vert }_F^2\right)+O\left(\frac{1}{p}{\Vert {\mathbf{\sum }}_u\Vert }_2\right).$$

All the remaining proofs are given in the supplementary material.