Head Impact Exposure in Youth Football: High School Ages 14 to 18 Years and Cumulative Impact Analysis

Abstract

Sports-related concussion is the most common athletic head injury with football having the highest rate among high school athletes. Traditionally, research on the biomechanics of football-related head impact has been focused at the collegiate level. Less research has been performed at the high school level, despite the incidence of concussion among high school football players. The objective of this study is to twofold: to quantify the head impact exposure in high school football, and to develop a cumulative impact analysis method. Head impact exposure was measured by instrumenting the helmets of 40 high school football players with helmet mounted accelerometer arrays to measure linear and rotational acceleration. A total of 16,502 head impacts were collected over the course of the season. Biomechanical data were analyzed by team and by player. The median impact for each player ranged from 15.2 to 27.0 g with an average value of 21.7 (±2.4) g. The 95th percentile impact for each player ranged from 38.8 to 72.9 g with an average value of 56.4 (±10.5) g. Next, an impact exposure metric utilizing concussion injury risk curves was created to quantify cumulative exposure for each participating player over the course of the season. Impacts were weighted according to the associated risk due to linear acceleration and rotational acceleration alone, as well as the combined probability (CP) of injury associated with both. These risks were summed over the course of a season to generate risk weighted cumulative exposure. The impact frequency was found to be greater during games compared to practices with an average number of impacts per session of 15.5 and 9.4, respectively. However, the median cumulative risk weighted exposure based on combined probability was found to be greater for practices vs. games. These data will provide a metric that may be used to better understand the cumulative effects of repetitive head impacts, injury mechanisms, and head impact exposure of athletes in football.

INTRODUCTION

Sports-related concussion is the most common athletic head injury.^17,34 Currently, football is noted as having the highest concussion rate in high school athletes compared to other contact sports such as soccer, basketball, and hockey.²³ It is estimated that nearly 1.1 million students play high school football in the United States,¹ 100,000 players participate in college football,²¹ and 2000 players participate in professional football.¹¹ With such a large population participating in the sport, it is very important to understand head impact exposure in the context of the risk associated with different levels of impact in order to adequately estimate cumulative risk over the course of a practice, game, season, or lifetime.

Traditionally, research on the biomechanics of football-related head impact has been focused at the collegiate level.^{8–10,13,27,28,30} Less research has been performed in the high school and youth population,^3–5,11,32 despite the incidence of concussion among high school football players.¹⁹ Approximately 5.6% (over 70,000) of high school football players and 4.4% (over 4000) Division I college football players sustain concussions in a given year.¹⁹ Approximately 15% of the concussions followed a previous concussion in the same season.¹⁹ However, these values do not reflect high rates of underreporting estimated in several studies. Underreporting rates are difficult to determine but range from 1 in 2 to 1 in 10 concussions.^22,24,29

The first analysis of head impacts at different levels of play was conducted by Schnebel et al.³² In this study, one high school team was fitted with helmets equipped with the Head Impact Telemetry (HIT) System during practices and games. The purpose of this study was to analyze the HIT System impact and kinematic data to characterize the type of session, playing position, and location of head impact and compare to head impacts occurring in National Collegiate Athletic Association (NCAA) Division I football. Schnebel et al. found a higher frequency of high-level impacts at the collegiate level compared to high school, but reported little comparative analysis.

Broglio et al. later conducted multiple analyses from consecutive seasons of high school athletes and found that the mean acceleration was 24.7 g, which was comparatively higher than values reported at the collegiate level (22.25 g).⁵ These data were obtained using the same methods as Schnebel et al.; however, the differences between high school and college athletes were not statistically significant. The data from the Broglio study included 271 impacts exceeding 70 g’s and 78 impacts exceeding 98 g’s. In this group, there were 5 diagnosed concussions. Therefore, the authors discussed the potential need for a different mild traumatic brain injury (mTBI) threshold for high school athletes. While a threshold based operational definition of concussion is outdated due to improved understanding of concussion risk,³⁰ the motivation to study head impact exposure of high school athletes is still present. Most recently, Broglio et al. reported cumulative burden of head impacts in high school football with an average annual cumulative (summed) linear acceleration of 16,746 g, and summed rotational acceleration of 1,090,067 rad/s^2.3 These values were found to be approximately 55% lower than those measured at the collegiate level. However, linear (g’s) or rotational (rad/s²) unweighted summation based metrics ignore the nonlinear relationship between peak acceleration level and concussion risk. In that sense, they may give a misleading picture of cumulative exposure for individuals or teams for many different facets of football. These may include player or team level, position, practice vs. game statistics, season, and career differences which may be very large.

The objective of this study is to collect and quantify head impact exposure data in high school football athletes. To this end, a novel cumulative exposure metric is developed and results are presented that utilize this metric with four different published analytical risk functions. These include: linear resultant acceleration (developed by Pellman et al.),²⁶ linear resultant acceleration (developed by Rowson et al.),³⁰ rotational resultant acceleration,³¹ and combined probability (linear and rotational) resultant accelerations.²⁹ These are used to elucidate individual player and team-based exposure associated with practices and games for an entire season of football.

This study adds to the ongoing investigation of head impact biomechanics in high school football, and introduces a new cumulative exposure metric that can be used for similar analyses at all levels of play. The metric developed may help researchers better understand the longitudinal effects of impacts on the brain from youth to longer football careers.

METHODS

Data Collection

The study protocol was approved by the Wake Forest School of Medicine Institutional Review Board and participant assent or consent and parental consent were appropriately obtained. Impact data were collected for the entire season, including preseason practices and scrimmages, regular season practices and games, and playoff practices and games. Head impact exposure was measured by instrumenting the helmets of high school football players with the Head Impact Telemetry (HIT) System head acceleration measurement device.^7,18 Each player participating in the study was provided a Riddell Revolution or Riddell Revolution Speed helmet instrumented with the HIT System.

The HIT System has been extensively described in the previous literature.^{2–9,13,28,30,32} For this study, the HIT System included a sideline base unit with a laptop computer connected to a radio receiver and an encoder unit for each helmet. This system collects impact data on the sidelines from each encoder equipped with six single-axis accelerometers. Data acquisition occurred each time an instrumented helmet received an impact where an accelerometer exceeded 14.4 g. The recorded impact includes 40 ms of data, including 8 ms of pre-trigger data. The data is wirelessly transmitted to the sideline computer where kinematic linear and rotational accelerations are computed, which can be analyzed in terms of the peak g’s, direction of impact, or other biomechanical indicators. All data were screened to remove any impacts that did not result from the helmet being worn on the players’ head during play (i.e., dropped helmets). A complete description of the processing algorithm and validation has been previously described.⁷ All rotational acceleration data were processed as per Rowson et al.³¹

Exposure Measurement

The Weibull probability density function (pdf) has been previously fit to helmeted impact exposure data, described in Rowson et al.³⁰ The Weibull pdf is demonstrated in Eq. (1) where α is the scale parameter, β is the shape parameter, θ is the threshold parameter, and x is the peak resultant linear or rotational head acceleration. The Weibull parameters α, β, and θ are calculated from the Weibull distribution fit for each player’s linear and rotational head acceleration from practices and games, separately. This was integrated over the respective acceleration to calculate the Weibull cumulative density function (cdf).

$$W_{\text{pdf}}=\frac{\beta {(x-\theta )}^{\beta -1}}{{\alpha }^{\beta }}{e}^{-{\left(\frac{x-\theta }{\alpha }\right)}^{\beta }}$$ (1)

In the event that a player’s impacts were not collected during a session due to a battery failure or because of late addition to the study, the player’s missing accelerations were calculated from the player’s impacts using a Weibull distribution-based model. First, the average number of impacts for that player in that respective session type (practice or game) was calculated. Next, this number was used to evenly sample the player’s Weibull cdf, resulting in an exposure-calibrated prediction of head accelerations to replace the empty data set for that season separately for games and practices. The linear and rotational head accelerations for the complete season were compiled from both the actual accelerations and the sampled accelerations. Sampled accelerations accounted for less than 5% of data.

Cumulative head impact exposure represents the concussion risk weighted sum of head impacts as measured by peak resultant linear and/or rotational acceleration. It may be measured over the course of any particular time period and activity for a particular individual or group. The risk of concussion for each impact for each player was calculated using four different risk functions previously described in the literature. The four risk functions (Figs. 1 and 2) include the logistic regression equations and regression coefficients (Table 1): (1) professional football impacts based on linear acceleration,²⁶ (2) collegiate football impacts based on linear acceleration,³⁰ (3) rotational acceleration,³¹ and (4) the combined probability (CP) from linear and rotational acceleration.²⁹ Risks associated with each head impact for each player were summed to compute the risk weighted cumulative exposure (RWE) for the season. For comparative purposes, this was repeated separately for all four risk functions, and the RWE calculated using each is referred to as RWE_Pellman, RWE_Linear, RWE_Rotational, and RWE_CP, respectively (Table 2). A non-parametric Wilcoxon test was utilized to compare differences in player-specific cumulative exposure between practices and games. Additionally, the RWE score for each player from each respective risk function was summed to calculate the team or season RWE. The data collected for this study was analyzed by impact frequency, impact location, and impact magnitude for individual high school football players.

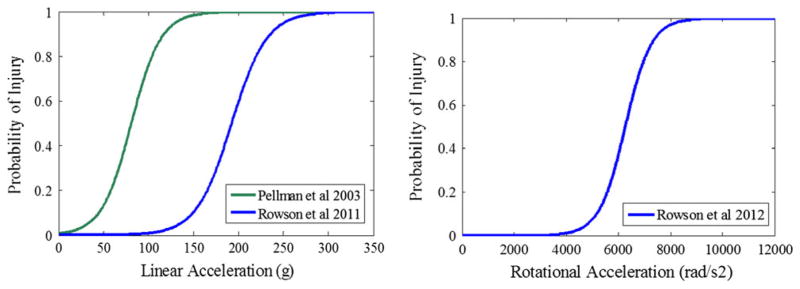
FIGURE 1.

Injury risk as a function of (left) linear acceleration^26,27 and (right) rotational acceleration.³¹

FIGURE 2.

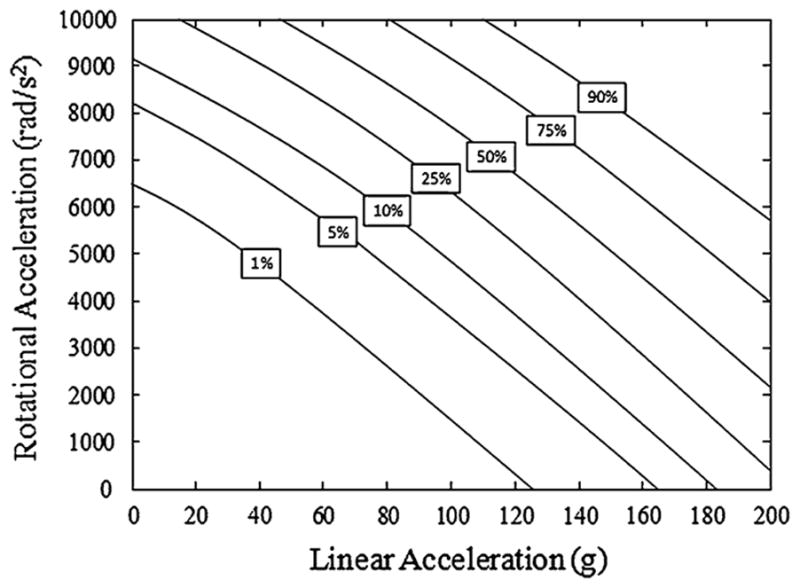
Combined probability of concussion contour given from the combined linear and rotational acceleration from Rowson et al.

TABLE 1.

Logistic regression equations and regression coefficients of the four injury risk functions utilized in the prediction of injury, where α and β are the regression coefficients and x is the measured acceleration for the Pellman, linear, and rotational risk functions.

Equation	Logistic regression equation	Risk function	Regression coefficients
(2)	$R[a]=\frac{1}{1+e^{-\alpha +\beta x}}$	Linear (NFL)	α = −4.897, β = 0.0606
		Linear (Collegiate)	α = −9.805, β = 0.0510
		Rotational	α = −12.531, β = 0.0020
(3)	$\text{CP}=\frac{1}{1+e^{-({\beta }_o+{\beta }_1\alpha +{\beta }_2\alpha +{\beta }_3\alpha \alpha )}}$	Combined Probability (CP)	β0 = −10.2, β1 = 0.0433, β2 = 0.000873, β3 = −9.2E–07

β₀, β₁, β₂, and β₃ are the regression coefficients, a is the measured linear acceleration, and α is the measured rotational acceleration for the combined probability risk function.

TABLE 2.

Risk Weighted Cumulative Exposure (RWE) equations, where a_L is the measured peak linear acceleration, a_R is the measured peak rotational acceleration, and n_hits is the number of head impacts in a season for a given player.

Risk function(s)	Equation
Pellman, Linear	${\text{RWE}}_{\text{Pellman},\text{Linear}}={\sum }_{\mathit{i}=1}^{{\mathit{n}}_{\text{hits}}}\mathit{R}{({\mathit{a}}_{\mathit{L}})}_{\mathit{i}}$
Rotational	${\text{RWE}}_{\text{Rotational}}={\sum }_{\mathit{i}=1}^{{\mathit{n}}_{\text{hits}}}\mathit{R}{({\mathit{a}}_{\mathrm{R}})}_{\mathit{i}}$
Combined Probability	${\text{RWE}}_{\text{CP}}={\sum }_{\mathit{i}=1}^{{\mathit{n}}_{\text{hits}}}\text{CP}{({\mathit{a}}_{\mathrm{L}},{\mathit{a}}_{\mathrm{R}})}_{\mathit{i}}$

RESULTS

A total of 40 high school players participated in this study. The average age of the participants at the beginning of the season was 17.1 years and ranged from 15.8 to 18.5 years. The participants in the study had an average height of 181.4 ± 6.1 cm and an average weight of 89.0 ± 16.3 kg. A total of 16,502 impacts were measured in 33 practices and 14 games, two of which were scrimmages. One player was excluded from the analysis due to an orthopedic injury that occurred within the first week of the season. The median and 95th percentile linear head acceleration and rotational head acceleration for each player is reported in Table 3.

TABLE 3.

Median and 95th percentile linear head acceleration and rotational head acceleration per player in ascending order by median linear head acceleration.

Player number	Linear acceleration (g)		Rotational acceleration (rad/s2)
	Median	95th percentile	Median	95th percentile
1	15	39	728	1878
2	19	45	685	1855
3	19	39	815	1952
4	19	43	912	2186
5	19	47	881	1907
6	19	46	712	2424
7	19	52	913	2633
8	20	44	786	1871
9	20	43	881	2006
10	20	45	871	1871
11	20	45	881	1885
12	20	51	824	1903
13	21	66	781	3198
14	21	69	870	3127
15	21	47	927	1880
16	21	65	963	2951
17	21	51	899	2346
18	21	53	1023	2358
19	21	56	983	2594
20	21	49	898	1984
21	21	70	947	3701
22	22	63	911	2705
23	22	59	938	2401
24	22	51	973	2155
25	22	66	958	3008
26	22	49	1052	2365
27	22	54	1124	2809
28	23	62	1040	2583
29	23	55	1006	2156
30	24	68	1127	3098
31	24	68	1150	2922
32	24	65	971	2466
33	24	73	1192	3274
34	24	66	1131	3470
35	25	73	1100	3521
36	25	55	921	2222
37	26	70	1098	2694
38	26	73	1065	2812
39	27	66	1232	3100

The linear accelerations recorded for the season ranged from 10.0 to 152.3 g. The data was highly right skewed with a median value of 21.9 g and 95th percentile value of 57.6 g (Fig. 3). For 33 practices, there were a total of 9167 impacts. The median linear acceleration for practices was 21.5 g, with 95th percentile value of 53.7 g. For 14 games, there were 7335 impacts with a median linear acceleration value of 22.4 g and 95th percentile value of 62.1 g. There were 76 impacts (0.46%) greater than the average linear acceleration value of 98 g’s associated with concussion. ^15,28 The average median linear acceleration for each player was 21.7 g (±2.36 g) with a range of 15.2 to 27.0 g. The average 95th percentile impact for each player was 56.4 g (±10.5 g) with a range of 38.8 to 72.9 g. The number of impacts exceeding various percentile thresholds are provided in Table 4.

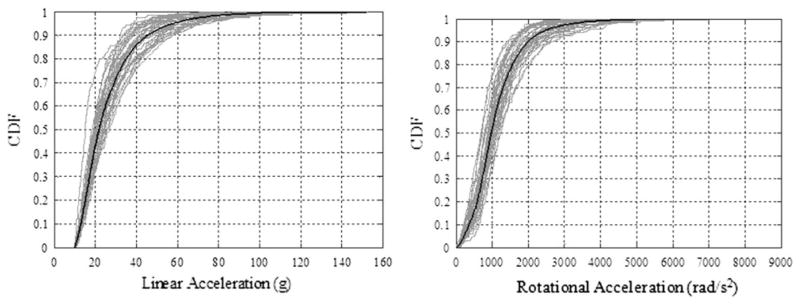
FIGURE 3.

Empirical cumulative density function (CDF) of linear (left) and rotational (right) acceleration. Each player CDF is represented in gray and the team CDF is represented in black.

TABLE 4.

Peak linear and rotational resultant acceleration percentile values and the measured number of impacts above each threshold.

Percentile	Linear acceleration value (g)	Number of impacts above	Rotational acceleration value (rad/s2)	Number of impacts above
80	35.1	3304	1563	3301
90	45.5	1655	1999	1650
95	57.6	827	2481	825
99	86.7	165	3863	165
99.5	97.2	82	4347	82
99.9	120.2	17	5463	16

The rotational accelerations for the season ranged from 2.9 to 7,701 rad/s². The data was, again, highly right skewed with a median value of 973 rad/s² and 95th percentile value of 2,481 rad/s² (Fig. 3). The impacts collected during practice had a median rotational acceleration value of 942 rad/s² and 95th percentile value of 2,263 rad/s². The impacts collected during games vs. practices demonstrate that rotational accelerations are higher for games with a median value of 1,013 rad/s² and 95th percentile value of 2,743 rad/s². The average median rotational acceleration amongst players was 953 rad/s² (±132 rad/s²), ranging from 685 to 1232 rad/s². The average 95th percentile impact amongst players was 2519 rad/s² (±536 rad/s²), ranging from 1855 to 3701 rad/s². The number of impacts exceeding various percentile thresholds are provided in Table 4.

The distribution of total number of impacts for practices and games was right skewed and the median and 95th percentile values for each were analyzed. The median (and 95th percentile) of the total number of head impacts during all practices and games was 185 (541) impacts and 138 (610) impacts, respectively. The median (and 95th percentile) of the total number of head impacts for all team sessions is 340 (1012) with the total number of impacts ranging from 129 to 1258 per player. The number of impacts per practice and per game was an average (and 95th percentile) value of 9.4 (19.0) impacts and 15.5 (43.6) impacts, respectively. A t test assuming unequal variances demonstrated the average number of impacts per player for games was significantly greater than for practices (p = 0.0017). Table 5 demonstrates the median and inter-quartile range of the number of impacts received for each player at various thresholds (30, 40, 60, 80, and 100 g).

TABLE 5.

The median and inter-quartile range (IQR) of the number of impacts exceeding various thresholds (30, 40, 60, 80, and 100 g) from each player for the complete season, as well as for practices and games.

	≥30	≥40	≥60	≥80	≥100
Season
Median	81	37	10	3	1
IQR	100	56.5	19	6.5	2
Practice
Median	47	21	6	2	0
IQR	52.5	24.5	6.5	2.5	1
Game
Median	40	17	5	1	0
IQR	68	28	10.5	5	1

The highest percentage of impacts occurred to the front of the head (45.3%), followed by the back (21.8%), and top (14.9%). Similarly, 45.7% of game impacts occurred to the front of the helmet and 45.0% of impacts during practices occurred to the front of the helmet. The impact location with the highest median peak linear acceleration for a single player was the top of the head with a median value of 34.6 g, for a player with a 95th percentile value of 91.2 g. The impact location with the highest median rotational acceleration for a single player was the back of the head with a value of 1483 rad/s², and respective 95th percentile value of 3535 rad/s² for the given player.

The results of the calculated RWE metric for each risk function are provided in Table 6. The data provided includes median, 95th percentile, minimum, and maximum RWE for each player for each risk function. The team RWE is additionally provided, which is the sum of the RWEs measured for each player for the season. The results of the multiple risk function analysis demonstrate high variability in the estimated exposure for the season based on the contribution of linear and/or rotational acceleration and the given risk function.

TABLE 6.

Results of multiple risk function comparison presented by risk function.

RWE equation	Median	95th percentile	Minimum	Maximum	Team season RWE
RWEPellman	19.40	70.82	6.123	91.07	1007
RWELinear	0.132	0.565	0.037	0.727	7.42
RWERotational	0.191	1.896	0.014	1.995	15.25
RWECP	0.497	2.799	0.094	3.228	33.75

The team season RWE is the summation of the RWE for each player resulting in the summed risk of concussion for the entire team for all practices and games for the season for each respective risk function.

The RWE_Linear, RWE_Rotational, and RWE_CP values were analyzed by session activity (practices vs. games). Themedian riskweightedcumulative exposure for practice were RWE_Linear = 0.0730, RWE_Rotational =0.0490, RWE_CP = 0.302 and for games were RWE_Linear = 0.0535, RWE_Rotational = 0.0510, RWE_CP = 0.1940. These data suggest a higher cumulative exposure to linear accelerations during practice and slightly higher exposure to rotational accelerations during games, however no statistical significance was observed (p = 0.06 and p = 0.60, respectively). Overall RWE_CP demonstrates that cumulative exposure from practices is one-third greater than that from games, however no statistical significance was observed (p = 0.47).

DISCUSSION

The goal of this study was to quantify head impact exposure in a season of high school football and develop a novel cumulative exposure metric to better understand these data. Head impact exposure has been extensively studied in the collegiate population with fewer studies investigating head impacts sustained at the high school level. This study is a vital addition to previous studies of head impact exposure in football and is a key step toward understanding the risk weighted cumulative head impact exposure in a season of football at each level of play. The frequency and severity of impacts observed are comparable to those observed at the collegiate level and consistent with data collected from different high school football data sets.

The median linear head acceleration value (21.9 g) measured in this study is similar to those values reported by Broglio et al. (21.0 g) and Eckner et al. (20.5 g) at the high school level.^4,14 The median rotational head acceleration from this study (973 rad/s²) was greater than the median value previously reported by Broglio et al. (903 rad/s²). The distribution of median linear accelerations for all individual players in this study was highly variable with average median acceleration ranging from 15.2 to 27.0 g. The median linear head acceleration value reported at the collegiate level by Rowson et al. is 18 g suggesting more frequent higher severity impacts occur at the high school level for many athletes.²⁸ The median rotational head acceleration value for each player’s impact distribution in this study ranged from 685 to 1232 rad/s².

The distribution of impacts by impact location reveals that 45% of impacts at the high school level occur to the front of the helmet and this is consistent between games and practices. This is also consistent with locations reported by Broglio et al. and Mihalik et al. for the high school level, as well as several other studies reported at the collegiate level.^4,5,25 One alarming result that has garnered attention throughout the football literature is the frequency and severity of head impacts to the top of the helmet. Broglio et al. reported mean linear head acceleration for various player positions ranging from 19 to 38 g.⁵ In the current study, the highest median value for a single player was found to be at the top of the head with a median value of 34.6 g, and 95th percentile value of 91.2 g. This value was 13 g higher than the average team median for all impacts and 10 g higher than the team median for top of the helmet impacts (Fig. 4). Although the severity is increased for impacts to this location, side impacts with a higher rotational component have been found to be the most likely impact scenario to result in concussion.^20,33

FIGURE 4.

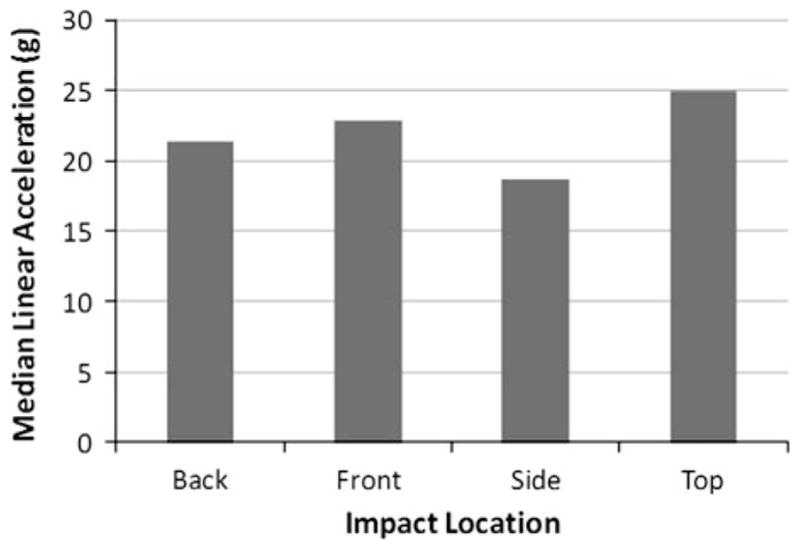
Median linear acceleration measured by impact location.

The results of the multiple risk function analysis demonstrate variability in the exposure to head impacts for the season based on the contribution of linear and/or rotational acceleration, as well as between players (Appendix Tables A1, A2, A3, and A4). The median cumulative exposure varied between practices and games. These data suggest a higher exposure to linear accelerations (RWE_Linear) during practice and slightly higher exposure to rotational accelerations (RWE_Rotational) during games. RWE_CP revealed higher cumulative exposure overall for practices. Interestingly, the average number of impacts per game were found to be higher, however the median exposure was greater during practices. This suggests that players are exposed to a greater proportion of high level impacts during practice. Interestingly, just over 60% of the team had greater than 50% of total risk weighted cumulative exposure attributed to practice impacts. Although no statistically significant difference in exposure was observed between practices and games, these data may inform and encourage teams and leagues to reduce exposure to head impacts during practices and teach proper tackling techniques to reduce exposure to impacts resulting in higher concussion risk.

TABLE A1.

RWE_Pellman for each player calculated from practice impacts, game impacts, and total impacts for the season with the linear NFL risk function.

ID	RWEPellman practice	RWEPellman game	RWEPellman total impacts	Practice impacts	Game impacts	Total impacts	Exposure per impact sample
2	33.8	57.3	91.1	365	625	990	9.20
1	36.4	34.4	70.8	648	610	1258	5.63
3	29.4	31.9	61.3	505	507	1012	6.06
7	21.1	37.9	59.0	299	415	714	8.27
11	21.2	26.0	47.2	250	331	581	8.12
10	24.7	20.6	45.3	355	218	573	7.91
6	35.3	9.06	44.3	541	169	710	6.24
13	13.74	30.3	44.1	129	346	475	9.27
4	15.08	26.5	41.6	328	458	786	5.29
5	24.5	13.94	38.5	503	306	809	4.75
18	10.3	18.95	29.3	168	245	413	7.09
23	17.42	8.38	25.8	198	120	318	8.11
8	15.82	9.73	25.6	414	252	666	3.84
12	22.2	1.832	24.1	320	46	366	6.57
14	9.62	14.01	23.6	185	306	491	4.81
24	11.12	11.47	22.6	109	153	262	8.62
9	9.91	12.38	22.3	292	323	615	3.62
16	13.28	8.10	21.4	274	182	456	4.69
27	13.83	5.79	19.62	145	91	236	8.31
15	11.31	8.09	19.40	209	179	388	5.00
17	16.76	2.30	19.05	326	29	355	5.37
28	9.25	8.41	17.66	150	89	239	7.39
25	4.21	11.80	16.01	84	211	295	5.43
21	14.02	1.772	15.79	280	46	326	4.84
19	9.19	5.91	15.11	266	138	404	3.74
29	2.36	12.62	14.98	46	204	250	5.99
26	7.97	6.22	14.19	176	128	304	4.67
22	12.14	1.500	13.64	288	52	340	4.01
30	10.61	2.13	12.74	172	44	216	5.90
32	8.69	2.25	10.94	132	41	173	6.32
36	7.18	3.32	10.50	110	40	150	7.00
39	6.74	3.56	10.30	88	50	138	7.46
35	6.55	3.63	10.18	116	50	166	6.13
20	8.24	1.584	9.82	127	35	162	6.06
37	3.94	5.84	9.77	54	75	129	7.57
31	6.28	3.24	9.51	140	106	246	3.87
34	4.47	2.65	7.13	114	62	176	4.05
33	6.42	0.650	7.07	147	15	162	4.36
38	4.65	1.469	6.12	114	38	152	4.03

Players numbered in order of total number of impacts in descending order. Players displayed in order of descending RWE_Pellman Total Season.

TABLE A2.

RWE_Linear for each player calculated from practice impacts, game impacts, and total impacts for the season with the linear collegiate risk function.

ID	RWELinear practice	RWELinear game	RWELinear total impacts	Practice impacts	Game impacts	Total impacts	Exposure per impact sample
2	0.245	0.483	0.727	365	625	990	0.0735
7	0.1631	0.402	0.565	299	415	714	0.0791
11	0.1814	0.315	0.497	250	331	581	0.0855
1	0.214	0.221	0.435	648	610	1258	0.0346
3	0.1934	0.211	0.404	505	507	1012	0.0399
13	0.0848	0.313	0.397	129	346	475	0.0837
10	0.1472	0.203	0.350	355	218	573	0.0610
4	0.0919	0.214	0.306	328	458	786	0.0389
6	0.219	0.0556	0.275	541	169	710	0.0387
5	0.1926	0.0809	0.273	503	306	809	0.0337
24	0.0731	0.1344	0.207	109	153	262	0.0792
18	0.0647	0.1411	0.206	168	245	413	0.0498
23	0.1500	0.0484	0.1981	198	120	318	0.0623
8	0.0944	0.0612	0.1556	414	252	666	0.0234
28	0.0704	0.0845	0.1549	150	89	239	0.0648
37	0.0897	0.0514	0.1410	54	75	129	0.1093
12	0.1292	0.01091	0.1401	320	46	366	0.0383
14	0.0570	0.0827	0.1397	185	306	491	0.0285
9	0.0593	0.0732	0.1324	292	323	615	0.0215
27	0.0922	0.0400	0.1322	145	91	236	0.0560
15	0.0681	0.0616	0.1300	209	179	388	0.0334
16	0.0807	0.0490	0.1297	274	182	456	0.0284
17	0.1015	0.01637	0.1179	326	29	355	0.0332
29	0.01387	0.0886	0.1025	46	204	250	0.0410
19	0.0555	0.0435	0.0993	176	128	304	0.0327
26	0.0582	0.0411	0.0990	266	138	404	0.0245
25	0.0245	0.074	0.0980	84	211	295	0.0332
21	0.0835	0.01029	0.0938	280	46	326	0.0288
31	0.0667	0.01943	0.0861	140	106	246	0.0350
22	0.0728	0.00909	0.0819	288	52	340	0.0241
39	0.0573	0.0221	0.0794	88	50	138	0.0575
30	0.0632	0.01218	0.0753	172	44	216	0.0349
35	0.0465	0.0212	0.0677	116	50	166	0.0408
36	0.0457	0.0213	0.0670	110	40	150	0.0447
32	0.0515	0.01405	0.0655	132	41	173	0.0379
20	0.0513	0.00945	0.0607	127	35	162	0.0375
33	0.0418	0.00372	0.0455	147	15	162	0.0281
34	0.0276	0.01582	0.0434	114	62	176	0.0247
38	0.0277	0.00974	0.0374	114	38	152	0.0246

Players numbered in order of total number of impacts in descending order. Players displayed in order of descending RWE_Linear Total Season.

TABLE A3.

RWE_Rotational for each player calculated from practice impacts, game impacts, and total impacts for the season with the rotational risk function.

ID	RWERotational practice	RWERotational game	RWERotational total impacts	Practice impacts	Game impacts	Total impacts	Exposure per impact sample
11	1.758	0.237	1.995	250	331	581	0.343
37	0.003	1.893	1.896	54	75	129	1.4700
10	0.1531	1.739	1.892	355	218	573	0.330
24	0.0269	1.170	1.197	109	153	262	0.457
28	0.1154	0.955	1.071	150	89	239	0.448
13	0.1681	0.681	0.849	129	346	475	0.1787
7	0.1878	0.496	0.684	299	415	714	0.0958
1	0.0823	0.439	0.521	648	610	1258	0.0414
3	0.264	0.237	0.500	505	507	1012	0.0494
29	0.00368	0.449	0.453	46	204	250	0.1812
4	0.253	0.1828	0.435	328	458	786	0.0553
23	0.361	0.0508	0.412	198	120	318	0.1296
2	0.0710	0.327	0.398	365	625	990	0.0402
6	0.1825	0.1629	0.345	541	169	710	0.0486
25	0.01807	0.277	0.295	84	211	295	0.1000
26	0.0493	0.1990	0.248	176	128	304	0.0816
18	0.0515	0.1923	0.244	168	245	413	0.0591
14	0.0378	0.1901	0.228	185	306	491	0.0464
35	0.0602	0.1492	0.209	116	50	166	0.1259
31	0.1838	0.00739	0.1911	140	106	246	0.0776
33	0.1273	0.000520	0.1278	147	15	162	0.0790
32	0.1182	0.00500	0.1232	132	41	173	0.0711
27	0.0968	0.0237	0.1205	145	91	236	0.0513
36	0.0861	0.0299	0.1159	110	40	150	0.0773
9	0.0207	0.0850	0.1057	292	323	615	0.01719
5	0.0689	0.0347	0.1035	503	306	809	0.01280
39	0.0394	0.0361	0.0749	88	50	138	0.0543
15	0.0494	0.01212	0.0615	209	179	388	0.01585
30	0.0392	0.01211	0.0513	172	44	216	0.0236
19	0.00975	0.0388	0.0486	266	138	404	0.01202
16	0.0307	0.01726	0.0481	326	29	355	0.01354
17	0.0299	0.01822	0.0480	274	182	456	0.01052
8	0.0201	0.01896	0.0391	414	252	666	0.00587
12	0.0264	0.00492	0.0313	320	46	366	0.00855
34	0.01677	0.00502	0.0218	114	62	176	0.01238
21	0.01694	0.00211	0.01905	280	46	326	0.00584
22	0.01660	0.001530	0.01813	288	52	340	0.00533
38	0.00677	0.01132	0.01809	114	38	152	0.01190
20	0.00932	0.00430	0.01361	127	35	162	0.00840

Players numbered in order of total number of impacts in descending order. Players displayed in order of descending RWE_Rotational Total Season.

TABLE A4.

RWE_CP for each player calculated from practice impacts, game impacts, and total impacts for the season with the combined probability risk function.

ID	RWECP practice	RWECP game	RWECP total impacts	Practice impacts	Game impacts	Total impacts	Exposure per impact session
11	1.813	1.415	3.23	250	331	581	0.556
2	0.732	2.07	2.80	365	625	990	0.283
10	0.573	2.06	2.63	355	218	573	0.459
13	0.428	2.05	2.47	129	346	475	0.520
7	0.634	1.74	2.38	299	415	714	0.333
3	0.865	0.941	1.806	505	507	1012	0.1785
28	0.380	1.048	1.427	150	89	239	0.597
1	0.508	0.854	1.362	648	610	1258	0.1083
24	0.450	0.887	1.323	109	153	262	0.5050
4	0.349	0.891	1.249	328	458	786	0.1578
23	0.937	0.1883	1.125	198	120	318	0.354
6	0.767	0.287	1.054	541	169	710	0.1484
18	0.233	0.724	0.956	168	245	413	0.232
37	0.1248	0.744	0.869	54	75	129	0.673
5	0.581	0.1936	0.774	503	306	809	0.0957
39	0.658	0.1883	0.700	88	50	138	0.507
29	0.0245	0.615	0.639	46	204	250	0.256
27	0.402	0.1471	0.549	145	91	236	0.232
31	0.632	0.0376	0.526	140	106	246	0.2134
25	0.0650	0.432	0.497	84	211	295	0.1686
26	0.233	0.254	0.487	176	128	304	0.1602
14	0.499	0.328	0.481	185	306	491	0.0980
16	0.302	0.220	0.442	274	182	456	0.0970
30	0.314	0.1186	0.385	172	44	216	0.1782
9	0.775	0.217	0.368	292	323	615	0.0598
35	0.212	0.1370	0.349	116	50	166	0.210
36	0.291	0.0988	0.337	110	40	150	0.225
17	0.222	0.1753	0.314	326	29	355	0.0883
15	0.1624	0.1461	0.308	209	179	388	0.0795
8	0.1672	0.1392	0.306	414	252	666	0.0460
12	0.236	0.0330	0.263	320	46	366	0.0718
19	0.0901	0.1711	0.261	266	138	404	0.0646
32	0.1985	0.0390	0.238	132	41	173	0.1373
33	0.206	0.00557	0.212	147	15	162	0.1309
21	0.1630	0.01719	0.1802	280	46	326	0.0553
22	0.1425	0.01289	0.1554	288	52	340	0.0457
34	0.0779	0.0366	0.1144	114	62	176	0.0650
20	0.0704	0.0268	0.0971	127	35	162	0.0560
38	0.0530	0.0410	0.0941	114	38	152	0.0619

Players numbered in order of total number of impacts in descending order. Players displayed in order of descending RWE_CP Total Season.

The risk weighted cumulative exposure metric presented in this study (i.e., RWE) has a different goal than metrics based on the Athlete Exposure (A-E).¹² One A-E represents one athlete participating in a single practice or game. Injury rates defined using this technique are expressed based on occurrence rate as a result of participation in one practice or competition.^9,12,16,30 In the case of football, then, A-E based injury metrics are independent of playing time, the number of impacts, and the severity of impacts received per exposure for a given player. The frequency of concussions in football can be expressed based on A-E’s, however A-E based metrics do not account for the variance in impact exposure through a single practice or game for a single athlete, nor do they account for the cumulative effects over the course of a season which may vary extensively by player or position.

Another method of defining the cumulative exposure for a given player has been previously presented by Broglio et al.³ This method directly sums the linear or rotational accelerations experienced for each athlete. Although this method captures the severity and frequency of impacts on aggregate, it does not take into consideration the nonlinear relationship between acceleration and risk of concussion, which can have substantial effects on the overall exposure. The risk weighted cumulative exposure metric introduced in this study adjusts each impact’s contribution to cumulative exposure according to its associated risk of injury. Exposure is therefore a product of each player or group’s distribution of impacts over a chosen activity and time period. RWE is different depending on the injury risk metric used, and is used to examine the cumulative exposure to each acceleration type (RWE_Linear, RWE_Rotational) or to assess the combined contribution of linear and rotational accelerations (RWE_CP).

The data provided within the appendix, includes the calculated RWE_Pellman, RWE_Linear, RWE_Rotational, and RWE_CP for each player. These data are useful to interpret within group variability for RWE. A value of interest is the risk weighted exposure per impact for each player, which represents a normalized value by which risk weighted exposure may be examined on an individual basis. These data are important to capture the risk weighted exposure independent of the number of impacts for each player, which is representative of the ‘average’ severity for that player.

One of the more interesting characteristics to study is the variation in severity between the highest and lowest exposure per impact players in games and/or practices. For example, the RWE_Linear data show an eightfold variation in the exposure per impact for practices. Some players have increased exposure during games with as high as a fivefold variation in exposure per impact. Additionally, there is a 6.5-fold variation in the exposure per impact for practices and a threefold variation in the exposure per impact for games for the RWE_Rotational data. Lastly, recorded values for RWE_CP reveal a 22-fold variation in the exposure per impact for practices and a 47-fold variation in the exposure per impact for games between players. Since the exposure metric used is risk-weighted, the players with a higher RWE per impact may reveal exposure to a greater proportion of high magnitude impacts compared to those who have a lower value. The variability in average exposure per impact that is captured when using a risk-weighted exposure metric may not be captured in a summed acceleration-based metric. Additionally, these types of analyses may provide further insight into position and player-specific exposure throughout a season of football.

If RWE exceeds one for a given risk function, it would imply that the risk function predicted at least a single concussion over the course of the season. All the assumptions inherent in the risk function apply to the cumulative exposures calculated, including assumptions about underreporting. The Pellman risk function ²⁶ for linear acceleration dramatically over-estimates the total risk weighted cumulative exposure resulting in a median RWE_Pellman per player of 19.4 and a team season RWE_Pellman value of 1,007. This might be used to argue that each player would sustain 19.4 concussions and the team would sustain approximately 1,007 concussions over the course of the season. This is further evidence that the underlying risk function for RWE_Pellman overestimates risk for each impact. More recent linear acceleration based risk functions more appropriately estimate risk and the associated risk weighted cumulative exposure.

Caution, however, should be used when interpreting RWE as the estimated number of concussions. Though it is based on a risk-weighted summation of peak resultant accelerations, a very high number of very low risk impacts may appear to give the same RWE as a smaller number of very high risk impacts. In this sense, the likelihood that the person with a smaller number of high risk impacts will have the calculated number of concussions is likely higher. However, risk weighted cumulative exposure is intended to address the importance of all impacts, given that there is no established dichotomous threshold associated with damage due to smaller vs. larger impacts.

Traditionally linear and rotational acceleration have been evaluated independently. However, more recently studies have demonstrated that a combined metric with several biomechanical inputs may be more predictive than a single measure, particularly one that includes both linear and rotational acceleration.^4,18 The combined probability of the risk of concussion is a step toward a more comprehensive assessment of cumulative exposure. This risk function was developed based on a 10× underreporting rate, however it may be beneficial moving forward to perform comparative analyses utilizing varying underreporting rates that would affect the combined probability of concussion and/or RWE_CP differently. Additionally, RWE_Linear and RWE_Rotational may be valuable metrics to be used in the understanding of the exposure to various acceleration types for an athlete. These data may be particularly useful in understanding the exposure for different playing positions in terms of linear and rotational acceleration, separately. This may be a valuable metric in capturing the lifetime exposure of an athlete and may also provide a better understanding of the role linear and rotational acceleration have on the mechanism of concussion and potential neurodegenerative changes.

The results of this study will contribute to a better understanding of head impact exposure in high school football; however, certain limitations are present. Although a large number of impacts have been collected at the high school level, analysis of position-specific distributions of impacts was not conducted due to the need for further impact data for each player position. Also, not all players on the team were enrolled in the study, but 73% of the team consented. This introduces limitations on the exposure estimates for the entire team. The exposure methods utilized are based on various injury risk functions calculated previously by Rowson et al. and Pellman et al.^26,29–31 In the future, high school specific injury risk curves may be established and utilized in the calculation of RWE, especially as more data are collected from research groups using the HIT System to characterize head impacts. However, it is estimated that the error introduced in using the risk curves described in this study is minimal, and RWE represents an improvement over A-E or acceleration sum-based measurements over the course of a season. There is a growing body of evidence that injury risk may also be directionally dependent.³⁵ The risk functions utilized in this study do not differ according to the direction of impact or axis of rotation, which may play an as yet undetermined role in injury risk, but a similar approach may incorporate such risk functions when they become available. Lastly, players receiving impacts resulting in higher levels of risk substantially affected the total season RWE calculation. In the current sample, a large portion of the RWE contribution for the team came from just a few players and impacts. Limiting the RWE calculation to particular percentile severity ranges, or otherwise excluding the highest impacts, will substantially affect the RWE value and provide a potentially better metric for comparing populations. The way that the RWE is used to compare populations vs. individuals may be very important to understand age, team, playing time, or other independent variable based variances in exposure.

This study has quantified head impact exposure in high school football, specifically focusing on the exposure to the risk of concussion for an entire football season. The cumulative risk associated with all impacts measured for each player has not yet been quantified for any sport. A method has been developed to measure cumulative exposure to the risk of injury over the course of the season and this has been quantified for each player. This metric accounts for the number of player impacts over the course of the season, as well as the severity of these impacts. RWE_Pellman was found to significantly over-estimate the total exposure risk. RWE_Linear and RWE_Rotational were found to capture the variability in exposure due to linear and/or rotational acceleration, as well as the exposure specific to session activity (i.e., practices vs. games). However, the combined risk weighted metric (CER_CP) may best capture the total linear and rotational exposure throughout the course of the season and into a lifetime. Establishment of a risk-based cumulative exposure metric is vital to understanding the biomechanical basis of head injury that may occur over the course of the football season, and potentially will have importance in correlating with potential pre- and post-season changes in the brain identified with magnetic resonance imaging, magnetoencephalography, and other neurological tests. Additionally, these metrics may also be beneficial for capturing the cumulative exposure of an athlete over a lifetime. The results presented in this paper contribute to the repository of head impact exposure data measured for various levels of play from youth football to the adult professional level which will further our understanding of the age-dependent biomechanics of head injury. These data ultimately have implications for assessment of helmet safety and improved helmet design, and ultimately can help make football a safer activity for millions of children, adolescents, and adults.

APPENDIX

See appendix Tables A1, A2, A3, and A4.