Automated, Depth-resolved Estimation of the Attenuation Coefficient From Optical Coherence Tomography Data

Abstract

We present a method for automated, depth-resolved extraction of the attenuation coefficient from Optical Coherence Tomography (OCT) data. In contrast to previous automated, depth-resolved methods, the Depth-Resolved Confocal (DRC) technique derives an invertible mapping between the measured OCT intensity data and the attenuation coefficient while considering the confocal function and sensitivity fall-off, which are critical to ensure accurate measurements of the attenuation coefficient in practical settings (e.g., clinical endoscopy). We also show that further improvement of the estimated attenuation coefficient is possible by formulating image denoising as a convex optimization problem that we term Intensity Weighted Horizontal Total Variation (iwhTV). The performance and accuracy of DRC alone and DRC+iwhTV are validated with simulated data, optical phantoms, and ex-vivo porcine tissue. Our results suggest that implementation of DRC+iwhTV represents a novel way to improve OCT contrast for better tissue characterization through quantitative imaging.

I. Introduction

Optical coherence tomography (OCT) is a confocal-like, near-infrared imaging modality capable of high-resolution, subsurface imaging of biological tissue. The attenuation of near-infrared light in biological specimens is governed by the Beer-Lambert Law, and the magnitude of this attenuation as a function of depth is characterized by the attenuation coefficient. Several studies have shown that using OCT to quantify the local attenuation coefficient is relevant to diagnostic, classification, and surveillance applications. For example, measurements of the attenuation coefficient have been implicated in atherosclerotic plaque characterization [1], renal cancer diagnosis [2], glucose diffusion measurement [3], bladder cancer tumor staging [4], burn scar assessment [5], ovarian tissue collagen content quantification [6], cerebral edema detection [7], and glaucoma diagnosis and surveillance [8].

The attenuation coefficient in biological tissue is related to the intensity of light that is back-scattered from the sample and measured by the OCT system. Faber et al. introduced the following depth-wise model:

$$I(z)\propto h(z)e^{-2\mu z},$$ (1)

where μ is the attenuation coefficient and z is the depth of interest [9]. The function h, known as the confocal function [10] (or the confocal point spread function [9]), describes the intensity profile emitted from and coupled back into the fiber as a function of depth (i.e., optical pathlength difference between the reference arm and the distance of the beamsplitter to this location) and is defined for irradiance as

$$h(z)={\left({\left(\frac{z-z_0}{z_R}\right)}^2+1\right)}^{-1},$$ (2)

where z₀ is the depth of the focal plane and z_R is the apparent Rayleigh range. The apparent Rayleigh range is related to the Rayleigh range by z_R = α_Rnz_r, where z_r is the Rayleigh range of the Gaussian beam, n is the index of refraction of the medium, and α_R equals 2 for diffuse reflectors [9]. Importantly, others have shown that a valid signal model for the back-scattered OCT intensity should account for the confocal function when the focal plane of the optical system is located within the sample, as failing to do so results in inaccurate estimates of the attenuation coefficient [10].

Several methods have been proposed to estimate the attenuation coefficient from OCT data by fitting equation (1) to a segment of an A-scan over which the attenuation coefficient is assumed to be constant [1], [4], [9]. While such “curve-fitting” algorithms are able to account for the known effect of the confocal function, they are subject to three key problems: 1) their reliance on manual segmentation to define the boundaries between regions with different expected attenuation coefficients can lead to high intraobserver and interobserver variabilities [11]; 2) the curve-fitting algorithms proposed to date are unstable when applied to very thin layers and therefore exhibit low reliability and high sensitivity to noise in these regions [12]; and 3) since entire regions are assigned a single attenuation coefficient value, small changes in the attenuation coefficient may be lost (i.e., the resolution of these algorithms is extremely poor).

To address these problems, Vermeer et al. introduced the following model:

$$I(z)=\beta L_0\alpha \mu (z)exp\left(-2{\int }_0^z\mu (\theta )d\theta \right),$$ (3)

where β is the quantum efficiency of the camera, L₀ is the intensity of the light source, α is the fraction of attenuated light that is backscattered, μ(z) is the local attenuation coefficient, θ is a variable of integration [12], and I(z) is the measured irradiance after subtraction of the noise floor and division by the sensitivity fall-off (modeled as a Gaussian). Using this model, the authors derived an invertible mapping between the measured light intensity and the attenuation coefficient that allowed them to calculate the attenuation coefficient for every pixel in the OCT image. Importantly, the Depth Resolved (DR) technique they introduced eliminated the need for manual segmentation, offering instead an algorithm that is fully automated and computationally efficient. Furthermore, since μ is not assumed to be constant within any segment, its resolution is much better than that of existing curve-fitting algorithms.

One remaining shortcoming of the DR method, however, is that it does not take the confocal function into account; hence, the obtained results are only accurate when the focal plane is positioned above the sample. Unfortunately, measurements acquired when the focal plane is located above the sample suffer from a reduced signal-to-noise ratio (SNR). Also, requiring the focal plane to be positioned above the sample restricts the applicability of the algorithm in clinical settings [13], where the position of the focal plane relative to the sample is constantly varying and is often located within the sample, even as the relative position of the focal plane to the position of zero pathlength delay doesn’t change.

Another phenomenon that influences the depth-dependent intensity of the OCT signal is sensitivity fall-off (in Fourier-domain techniques). Vermeer et al. accounted for fall-off using a Gaussian model. Yun et al. [14] have created a more comprehensive model for sensitivity fall-off in spectral domain (SD)-OCT, which is an explicit function of spectrometer and CCD parameters as follows:

$$f(z)={\left(\frac{sin\zeta }{\zeta }\right)}^2·exp\left(-\frac{{(\delta \lambda /\mathrm{\Delta }\lambda )}^2}{2ln2}{\zeta }^2\right),$$ (4)

where δλ is the spectrometer’s spectral resolution (FWHM), Δλ is the wavelength spacing between pixels, and ζ = (π/2) · (z/z_RD) represents the depth normalized to the maximum ranging depth, z_RD. The maximum ranging depth can be calculated as $z_{RD}={\lambda }_0^2/(4\mathrm{\Delta }\lambda )$, where λ₀ is the central wavelength of the source [14]. For the most accurate signal intensity model, it is important to include the effects of sensitivity fall-off.

In this work we introduce a modification of the DR method that takes into account the confocal function and the more comprehensive model for sensitivity fall-off – termed the Depth-Resolved Confocal (DRC) technique – to extend its applicability to practical measurements in clinical settings. Like DR, DRC utilizes an invertible mapping between the OCT signal intensities and the attenuation coefficient, but unlike DR it also enables accurate measurement of the attenuation coefficient independent of the position of the focal plane. Thus, DRC is the first fully automated algorithm that can estimate the attenuation coefficient when the focal plane is located within the sample.

To improve estimates of the attenuation coefficient, one of two common pre-processing methods is often implemented: 1) lateral averaging across several A-scans within a B-scan [4], [15], [16] and 2) averaging many B-scans together [1], [17]. Unfortunately, the former method degrades the image quality when the sample exhibits horizontal variations in structure while the latter is time-intensive and requires that the subject stay still during imaging, a restrictive requirement in clinical settings where motion is often present.

To improve the accuracy of the DRC estimate, we introduce a novel noise reduction technique – Intensity Weighted Horizontal Total Variation (iwhTV) denoising – that exploits the layered structure of certain biological tissues such as bladder, skin, colon, and retina. A priori knowledge of the horizontal, layered structure of the tissue is used to influence the final attenuation coefficient estimate through weighted total variation regularization in a convex optimization problem. This regularization increases the stability of the algorithm compared to modern curve-fitting algorithms.

In section III we show that iwhTV retains more of the imaged subject’s structure than other standard, post-estimation denoising techniques (i.e., Gaussian smoothing, TV denoising). It should be noted that there are other structure-preserving denoising techniques that could be utilized: bilateral filtering [18], non-local means [19], and sparsity-based dictionary techniques [20], [21] are a representative selection. We used total variation since the regularization term incorporates the prior information that the sample is approximately piece-wise constant (layered), thereby allowing us to denoise the sample with decreased blurring. The denoising algorithm iwhTV further accounts for the physical constraint that the attenuation coefficient be non-negative and accounts for depth-dependent noise in the estimate of the attenuation coefficients, leading to more accurate estimates. While it may be possible to incorporate such knowledge into the aforementioned techniques, since they are not formulated as optimization problems it is not a straightforward task and that remains something to be explored in the future.

Finally, the performances of both DRC and iwhTV denoising are validated with numerical simulations and measurements in optical phantoms comprised of Intralipid. The suitability of both techniques for clinical imaging is then tested by showing results from a layered phantom and ex-vivo tissue samples of porcine bladder and colon.

II. Methods

A. Signal Model

We utilize the following model presented by Vermeer et al.,

$$I_{fh}(z)=f(z)h(z)\beta L_0\alpha \mu (z)exp\left(-2{\int }_0^z\mu (\theta )d\theta \right).$$ (5)

The subscript fh denotes that this signal model for the intensity accounts for the confocal function and sensitivity fall-off.

For simplicity, let us consider the measurement obtained by an SD-OCT system with a 2 · M-pixel spectrometer. After resampling, apodization, and DC subtraction, sample m of the obtained M-point A-scan (one-sided) corresponds to an integration of the interferometric information over a small depth range:

$${\mathit{I}}_{\mathit{fh}}[m]={\int }_{z_m}^{z_{m+1}}{I}_{fh}(z)dz.$$ (6)

Here z_m and z_m+1 are the physical bounds of the m^th sample in depth, m ∈ {1, …, M}, and the bold emphasis denotes that the function is discrete, as is the case when sampling the data using SD-OCT. To improve the estimation accuracy, we extend the model to account for additive noise sources, such as shot-noise, dark current, read-out noise, and digitizer noise [22]. The final model of the measured signal (I_meas) is

$${\mathit{I}}_{\text{meas}}[m]={\mathit{I}}_{\mathit{fh}}[m]+\mathit{c}[m],$$ (7)

where c[m] ∈ ℝ is a random variable that accounts for additive noise typical of most SD-OCT systems.

B. Estimating the Attenuation Coefficient

Our ultimate goal is to estimate the attenuation coefficient from the measured data. One might suspect that the effects of additive noise, confocal function, and sensitivity fall-off could be removed by subtracting the mean of the additive noise and dividing by the confocal and fall-off functions. However, doing so amplifies the effects of the remaining noise; this is particularly hazardous when the noise makes up a large portion of the measured signal. Instead, these effects can be addressed in measured data by using a restoration filter, which has been shown to optimally reduce the effects of additive noise [23]:

$$\widehat{\mathit{I}}[m]={\mathit{I}}_{\text{meas}}[m]{\mathit{H}}_{\text{res}}[m],$$ (8)

where

$${\mathit{H}}_{\text{res}}[m]=\frac{1}{\mathit{f}[m]\mathit{h}[m]}\frac{{\mid {\mathit{I}}_{\text{meas}}[m]\mid }^2}{{\mid {\mathit{I}}_{\text{meas}}[m]\mid }^2+\overline{{\mid \mathit{c}[m]\mid }^2}}$$ (9)

The .^ symbol denotes an estimated parameter (i.e., parameters not directly measured using the OCT system), and the ·̄ symbol represents the expected value function. The average noise power, $\overline{{\mid \mathit{c}[m]\mid }^2}$, is a parameter of the algorithm and specified by the user. The sensitivity fall-off function can be determined from system parameters, and the confocal function can be determined experimentally using the location of the focal plane and the Rayleigh range of the scanning lens, as described in section II-E.

As shown by Vermeer et al., the attenuation coefficient associated with a given depth can then be estimated from Î using

$$\widehat{\mathit{\mu }}[m]\approx \frac{\widehat{\mathit{I}}[m]}{2\mathrm{\Delta }z{\sum }_{r=m}^M\widehat{\mathit{I}}[r]},$$ (10)

where Δz = z_m+1 − z_m [12]. Equation (10) makes it clear that the attenuation coefficient at the depth corresponding to sample m is proportional to the ratio of the intensity of light backscattered from that depth to the amount of light backscattered from all deeper positions (that is, locations further from the position of zero pathlength delay).

C. Noise Reduction

The presented algorithm, DRC, estimates the attenuation coefficient for each pixel in an A-scan. Denoising can improve the estimate; for this, we introduce a new technique – Intensity Weighted Horizontal Total Variation (iwhTV) denoising – which exploits inter-A-scan correlations to achieve smoothing across tissue layers (similar to averaging)while also preserving lateral structure in a sample. Note that vertical smoothing is also possible [24], but as the geometry is not well matched to layered structures and because variations in SNR as a function of depth complicate the smoothing, we chose to limit the current work to horizontal smoothing.

Consider the 2D matrix μ̂ ∈ ℝ^M×Nthat describes the estimated attenuation coefficient for every pixel in the collected B-scan: μ̂ is simply the concatenation of estimates from all A-scans in a single B-scan. We first formulate a regularized least squares optimization problem for each row (i.e., depth) in the B-scan:

$$\begin{array}{ll}\text{minimize}\hfill & (1/2){\Vert {\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}}-{\widehat{\mathit{\mu }}}_{\mathit{m}}\Vert }_2^2+\eta \text{Reg}({\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}})\hfill \\ \text{subject}\text{to}\hfill & {\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}}\succcurlyeq 0,\hfill \end{array}$$ (11)

where μ̂_m ∈ ℝ^1×N is the m^th row of μ̂, μ̃_m ∈ ℝ^1×N is the optimization variable, η ∈ ℝ is the regularization parameter, and Reg is a regularization function. The denoised estimate of the attenuation coefficient is denoted by ${\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}}^{★}$. The goal of the optimization problem is to find the ${\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}}^{★}$ that best fits the data while adhering to the imposed regularization and constraints. In general, regularization functions require that the estimate (i.e., the attenuation coefficient) adhere to some expected behavior, and the regularization parameter is chosen based on the degree to which the data adhere to this behavior. In the case of the layered biological tissues of interest to this work (e.g., bladder, skin, colon, and retina), we can safely assume that μ is approximately piecewise constant. Thus, total variation (TV) regularization [25] is an appropriate regularization function:

$$\text{Reg}({\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}})=\frac{1}{\mathrm{\Delta }z}{\Vert \mathit{D}{\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}}^{\mathit{T}}\Vert }_1,$$ (12)

where D ∈ ℝ^N−1×N is the discrete gradient operator with symmetric boundary conditions defined as

$$\mathit{D}=\left[\begin{array}{ccccc}-1& 1& 0& \dots & 0\\ 0& -1& 1& & \\ ⋮& & \ddots & & \\ 0& \dots & & -1& 1\end{array}\right].$$

For TV regularization, the choice of the regularization parameter η should be based on how well a piecewise constant function serves to model the data; a higher η corresponds to data that are modeled better by a piecewise constant function. Applying the regularization function to each row of the B-scan will reduce the noise laterally, much like averaging many A-scans. However, unlike averaging, the L1 norm gives the regularization function flexibility to allow for abrupt lateral variations in the attenuation coefficient due to the presence of real structures such as granules, glands, and vasculature [26]. Hence, we expect that this algorithm will essentially smooth “smartly.”

When estimating μ̂ using equation (10) (DRC), we divide by a summation representing the proportion of light backscattered from deeper positions. For large values of m (i.e., deeper in the sample), the intensity of the OCT image is small due to the attenuation of light, and the SNR at those depths becomes correspondingly low. Hence, in these regions the estimate of the back-scattered light is significantly corrupted by noise. To compensate for this effect, we replace the standard TV regularization with a weighted TV regularization [27],

$$\text{Reg}({\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}})=\frac{1}{\mathrm{\Delta }z}{\Vert \mathit{D}{\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}}^{\mathit{T}}\Vert }_{{\mathit{W}}_{\mathit{m}},1},$$ (13)

where the standard L1 norm is replaced with a weighted L1 norm, defined as

$${\Vert v\Vert }_{{\mathit{W}}_{\mathit{m}},1}=\sum _n{\mathit{W}}_{\mathit{m}}[n]\mid v[n]\mid .$$

Note that the standard TV regularization function is a special case of weighted TV regularization where all the weights have value 1.

Regions of high SNR are associated with low noise and more confident estimates. Therefore, we aim to smooth (denoise) the data more in regions where the SNR is low and less where the SNR is high. Based on this intuition, we heuristically created the following weights:

$${\mathit{W}}_{\mathit{m}}[n]=\frac{1}{{\mathit{I}}_{\text{meas}}[m,n]+\epsilon },$$ (14)

where we have used I_meas as a surrogate for the SNR, which is reasonable in the shot-noise limit. The value ε is a small number that prevents the denominator from becoming zero and limits the maximum value of the weight. The effect of ε is minimal; in our work its value was chosen experimentally to be 0.001 based on the magnitude of the measured intensities.

While μ̂[m] is a ratio of intensity at pixel m over an integration of all pixels below it as is shown in (10), the SNR of μ̂[m] is still related to I_meas[m]. When the summation of (10) covers a relatively large number of pixels, then the noise in the summation is small and the noise in the estimated attenuation coefficients is nearly equal to that of the noise in the OCT intensity data. Additionally, if Î[m] is large relative to the noise, then the numerator and denominator of equation (10) are not significantly affected by noise since Î[m] appears in both. However, if Î[m] is small relative to the noise, then we cannot be confident in the estimate of μ̂[m] at these points. Therefore, weighting μ̂[m] based on the SNR of the signal allows us to identify regions of low SNR for which we should apply increased smoothing.

Finally, to avoid blurring across the surface boundary, we introduce a mask to the data to impose regularization only in regions where the sample exists. While TV regularization could have been applied at the surface, the use of a mask reduces the computational time significantly. We first identify the surface of the tissue and then formulate a mask in the form of a diagonal matrix: X_m ∈ ℝ^N×N, where X_m[n, n] = 0 if the n^th sample lies above the tissue surface, and X_m[n, n] = 1 otherwise. The final regularization function can thus be described as

$$\text{Reg}({\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}})=\frac{1}{N_x\mathrm{\Delta }z}{\Vert \mathit{D}{\stackrel{\sim }{\mathit{\mu }}}_{\mathit{m}}^{\mathit{T}}\Vert }_{{\mathit{X}}_{\mathit{m}}{\mathit{W}}_{\mathit{m}},1},$$ (15)

where N_x is the number of nonzero elements in X_m. When combined with the regularization function presented in (15), problem (11) becomes a convex optimization problem. Thus, it can be solved using standard algorithms, such as interior point methods [26], or existing software. These algorithms converge to the unique optimal solution of the convex optimization problem. The solution to this problem is a denoised estimate of the attenuation coefficients for a given row in the B-scan. This process can be repeated for all rows to yield a denoised estimate of the attenuation coefficients for the entire image, μ̃^★.

D. Algorithm Implementation

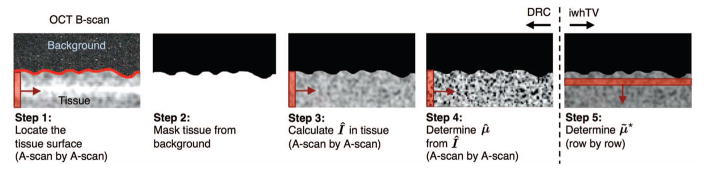
Algorithm 1 and Fig. 1 summarize the steps needed to compute μ̃^★ from I_meas with iwhTV denoising. The input to the algorithm is a processed B-scan comprised of N A-scans and M rows. A detailed description of each step of the algorithm follows.

Fig. 1.

Overview of algorithm to create a denoised reconstruction of the attenuation coefficient from an OCT B-scan.

Algorithm 1.

Attenuation Coefficient Estimation

Input: B-scan

Step 1:

for each A-scan (n = 1, 2, … N)

Locate the surface of the tissue

end

Step 2: Create an image mask, X, to isolate tissue from background

Step 3: Calculate the intensity Î using (8)

Step 4:

for each A-scan (n = 1, 2, … N)

Estimate the attenuation coefficient μ̂ using (10)

end

Step 5:

for each row in the reconstruction (m = 1, 2, … M)

Solve problem (11) with the regularization of (15) to denoise the estimate and attain μ̃★

end

• Step 1: Locate the surface of the tissue: The location of the surface was determined independently for each A-scan. We used a simple thresholding algorithm that computed two numbers: t_l, the mean of the lowest 10% of intensity values in the A-scan, and t_h, the mean of the highest 10% of intensity values. The surface location was taken to be the index of the first depth at which the intensity exceeded the threshold given by t = mean(t_l, t_h). Note that the choice of thresholding technique may be sample dependent; for example, the presence of fur or a highly reflective water surface may necessitate a more complicated surface extraction technique [28].

• Step 2: Create an image mask, X: We created a mask for the image, X ∈ ℝ^M×N, to identify tissue structures below the surface identified in Step 1. We assigned X[m, n] = 0 to all points on or above the surface and X[m, n] = 1 to all points below the surface. To avoid creation of abrupt isolated regions, the surface was smoothed by applying a morphological close operation to the image mask. Additionally, the surface itself was masked out by applying a morphological erosion operation. This was done to avoid problems from the large difference in the index of refraction between air and the biological sample, which is not accounted for in the signal model.

• Step 3: Calculate the intensity, Î: The intensity uncorrupted by the effects from additive noise, the confocal function, and sensitivity fall-off (Î) was calculated from I_meas (data obtained from the OCT system) using equation (8).

• Step 4: Estimate the attenuation coefficient, μ̂: We calculated μ̂ for every A-scan in the B-scan using equation (10).

• Step 5: Determine the denoised estimate, μ̃^★: We generated the convex optimization problem (11) with the regularization of (15) by performing the following for each row: estimate μ̂_m, assign a weight matrix W_m, and construct the mask X_m. The estimates for a single row, μ̂_m, were trivially extracted from μ̂. The weight matrix W_m was determined according to (14), and a weight was assigned to each pixel in the B-scan. The mask X_m for the m^th row of the OCT data is a diagonal matrix with diagonal elements consisting of the m^th row of the image mask, X. Once the convex optimization problem (11) was generated, we solved it using CVX, a software package for Matlab [29].

E. Experimental Design

Numerical Simulations

To test the effect of parameters such as the location of the focal plane, magnitude of the attenuation coefficient, and SNR on the accuracy of DRC, we simulated shot-noise-limited A-scans as follows: I_sim[m] = I_h[m] + p[m], where p is an independent and identically distributed Gaussian random vector with zero mean and variance σ² = 0.0004 intended to account for the additive noise. The variance of the noise was chosen to match a typical SNR value of 40 dB for tissue obtainable with OCT. The simulations were designed to mimic bi-layer tissue samples comprised of regions of constant attenuation. The true values of the layer positions, layer thicknesses and attenuation coefficients were encoded in a single vector μ_true of length M. The values for α, β and L₀ from equation (5) were chosen arbitrarily (α = 0.2, β = 1.0, L₀ = 2000); note that the choice of these values has no effect on the results of DRC as long as the regularization parameter is scaled appropriately. For each simulation, we created a B-scan by concatenating many A-scans – each having the same noise statistics – and the attenuation coefficient of the B-scan was estimated using either DR, DRC, or DRC with a denoising algorithm. The denoising algorithms tested included iwhTV, 2D Gaussian smoothing, and TV denoising [25].

For all Gaussian smoothing results, a standard deviation of 2 pixels was used for the blur kernel. For all TV results, the regularization parameter was set to 1. For all iwhTV results, unless otherwise stated, the regularization parameter was set to 6.

Phantom Experiments

To evaluate the accuracy of DRC experimentally, we fabricated several liquid optical phantoms comprised of different Intralipid concentrations. The volume to volume (v/v) ratios used were approximately 1.25%, 2.5%, 5%, 10%, 15%, and 20%. These ratios were chosen to span the range of scattering coefficients expected in soft tissue (e.g., bladder). Reference attenuation coefficients were taken from previously reported values [30]. The average attenuation coefficient using DRC was calculated for each A-scan over a range of 0.25 mm of depth just below the surface. The mean and standard deviation were calculated over all A-scans. For all Intralipid concentrations we used n = 1.353.

To better evaluate the accuracy of DRC using a sample that closely resembles the heterogeneous nature of tissue, we also fabricated a scattering optical phantom (TiO₂ dispersed in poly(dimethylsiloxane) (PDMS)) comprised of four layers with different attenuation coefficients. The attenuation coefficient of the PDMS/TiO₂ mixture was controlled by varying the percentage by weight of TiO₂ added. Layers were produced by spin-coating mixtures of PDMS/TiO₂ on a silicon wafer and were constructed sequentially with interspersed heat-curing steps. From top to bottom the level of scattering in each layer is medium, low, medium, and high. To better mimic the heterogeneous nature of tissue, we intentionally did not sonicate the PDMS/TiO₂ mixtures [31], [32]. To minimize surface reflections the phantom was submerged in water during imaging and an index of refraction n = 1.4 was used for all results.

Biological Sample Preparation

To demonstrate the performance of DRC and iwhTV in actual tissue, estimates of the attenuation coefficients of biological tissue were performed on healthy bladder and colon tissue harvested from a pig euthanized as part of an unrelated study. Pig bladder is known to closely mimic human bladder in terms of composition and mechanical properties [33]. For all tissue results we used an index of refraction n = 1.37. The pig used was a 10-month-old female Yorkshire, weighed approximately 50 kg, and was in good overall body condition. Data were collected within 12 hours of euthanization.

OCT System

All OCT measurements were collected with a commercial SD-OCT system (λ₀ = 1325 nm, TELESTO, ThorLabs) with a lateral resolution of 15 μm and an axial resolution in air of 7.5 μm. A lateral scanning lens (LSM03, ThorLabs) with a Rayleigh range of 105.91 μm was installed. To determine the parameters of the sensitivity fall-off function for our system, we imaged a neutral density filter at several depths and fit the data with a function of the form of equation (4) to obtain the following parameter values: δλ = 0.11 nm and Δλ = 0.07 nm/pixel.

Image Acquisition and Processing

Raw interferograms (1024 pixels) were collected to an imaging depth of 2.57 mm and spanned a lateral imaging range of 2.57 mm (512 pixels). Each dataset (phantom or ex-vivo tissue) comprised a single B-scan (i.e., averaging was not performed during collection) obtained by processing the raw interferograms using a custom Matlab script.

For each sample the location of the focal plane was determined visually by 1) moving the sample in and out of the focal plane and 2) determining the plane of maximum brightness. The focal plane was determined once at the beginning of the imaging session for a given position of the reference arm. All results were generated using software written in Matlab. The convex optimization problem of equation (11) was solved using the CVX software package [29]. This package allows one to set an error tolerance that dictates how close the result should be to the optimal solution prior to stopping. For all results presented, the default tolerance value of CVX was used.

III. Results and Discussion

A. Numerical Simulations

Shot-noise-limited simulations were performed to assess the accuracy of the attenuation coefficient estimates obtained using DR, DRC, and DRC with various denoising algorithms as a function of different system and sample parameters. To quantify the accuracy of the various methods, we investigated the energy (L2 norm) of the signal and defined an excess energy metric e as follows:

$$\mathit{e}[m]=\frac{{\Vert {\mathit{\mu }}_{\mathit{d}}(1:m)-{\mathit{\mu }}_{\text{true}}(1:m)\Vert }_2}{{\Vert {\mathit{\mu }}_{\text{true}}\Vert }_2}.$$ (16)

Here, μ_d is the denoised estimate of the attenuation coefficient and μ_true is a vector encoding the true layer positions, layer thicknesses, and attenuation coefficients for the simulation. For all simulations, the energy error depth, which we define as the depth at which the excess energy e exceeded 5%, was measured for each column of a 201 × 100 element simulation and the reported value is the average over all the columns (A-scans). The larger the value of e, the better the performance of the algorithm.

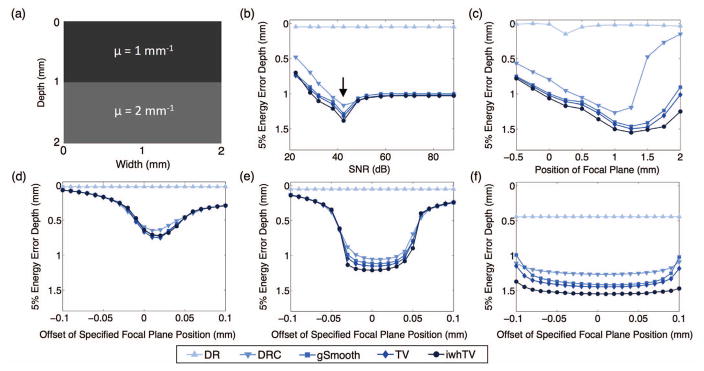
Fig. 2 shows how the energy error depth for each algorithm changes with system properties (SNR, focal plane location, and focal plane offset). Note that the energy error depth increases as we go down the vertical axis and that a larger energy error depth indicates higher accuracy. The simulation consisted of a 2-mm sample with two layers comprised of different attenuation coefficients, as shown in Fig. 2(a). For all simulations, unless otherwise specified, the focal plane was located within the sample. Recall that when the focal plane is located within the sample, the DR algorithm is predicted to fail.

Fig. 2.

(a) Simulated bi-layer sample. The effect of (b) SNR, (c) the focal plane position, and (d)–(f) error in the specified focal plane position on accuracy of the attenuation coefficient measurement. The arrow in (b) represents the value of SNR that corresponds to the noise parameter of the restoration filter that was used. In (b), (d), (e), and (f) the focal plane was located at a depth of 0.5 mm. In (b), (c), and (e) the Rayleigh range was 106 μm. In (d) and (f) the Rayleigh ranges were 50 μm and 238 μm, respectively. The superior performance of DRC with iwhTV denoising (●) is evident in all cases excluding (d), where all denoising algorithms perform similarly.

Fig. 2(b) shows how the energy error depth for each algorithm changes as a function of SNR. For these simulations, the focal plane position was kept constant at a depth of 0.5 mm. The SNR of the system was varied between 22 dB and 89 dB by altering the variance of p (described in section II-E). As expected, DRC (▼) is more accurate than standard DR (▲). The performance of DR varies little as a function of SNR, and performs worse than DRC for all values of SNR. The effect of the noise parameter from the restoration filter of equation (8) is also evident in Fig. 2(b); all simulations were run using the same restoration filter, (i.e., with the same noise parameter) in spite of changing noise levels. This restoration filter is only optimal for a single value of SNR (indicated by the arrow); for SNRs below/above the optimal point, the noise power is under/over-estimated, respectively. One might expect the results to improve with increasing SNR, as is seen when the noise power is underestimated. However, when the noise power is overestimated the restoration filter is too aggressive and filters out too much of the signal, leading to a degradation in performance. While we could have altered the noise parameter in the restoration filter to be optimal for each SNR tested, we found it informative to keep this parameter constant to explore its effect on the estimated attenuation coefficients. Interestingly, Gaussian smoothing performs worse than DRC without denoising in situations of high SNR (above 50 dB); this is because Gaussian smoothing blurs estimates at the interface of the two layers even in the absence of noise.

Fig. 2(c) shows the effect of focal plane position on the accuracy of each method. The top surface of the sample is located at 0 mm. The position of the focal plane is negative when located above the sample and positive when located within the sample. As expected, DRC (▼) is more accurate than standard DR (▲). Fig. 2(c) also shows that denoising improves the performance of DRC and reduces the dependence of accuracy on focal plane position. Notably, DRC with iwhTV denoising (●) produces the most accurate estimates.

Figs. 2(d)–(f) show how the accuracy changes for each method when the actual focal plane position is incorrectly specified to the algorithm for various Rayleigh ranges. The Rayleigh range affects the broadness of the confocal function and therefore has significant impact on the performance of both DRC and iwhTV. The Rayleigh ranges for Figs 2(d)–(f) are 50 μm, 106 μm, and 238 μm, respectively. For these simulations, the focal plane position was kept constant at a depth of 0.5 mm and the focal plane input to the algorithm varied from 0.4 to 0.6 mm. Here, the x-axis indicates the deviation (offset) in the actual and specified focal planes. The standard DR algorithm has no capacity to take into account the position of the focal plane; therefore, the obtained result is independent of the deviation, leading to a flat line for all values. In contrast, DRC preforms well even when the focal plane is incorrectly specified. The amount of offset that can be tolerated is dependent on the Rayleigh range of the system. A larger Rayleigh range allows for higher error in specifying the focal plane without sacrificing accuracy of the attenuation coefficient measurements (as demonstrated in Fig. 2(f)), while a small Rayleigh range (Fig. 2(d)) decreases the accuracy of DRC and results in similar performance by all denoising techniques. In particular, for the Rayleigh ranges tested, the amount of tolerable offset is approximately equal to the Rayleigh range of the system. For example, when the Rayleigh range is 106 μm the amount of tolerable offset is 0.1 mm (100 μm). Note that denoising further increases the accuracy of the technique, with iwhTV denoising performing best.

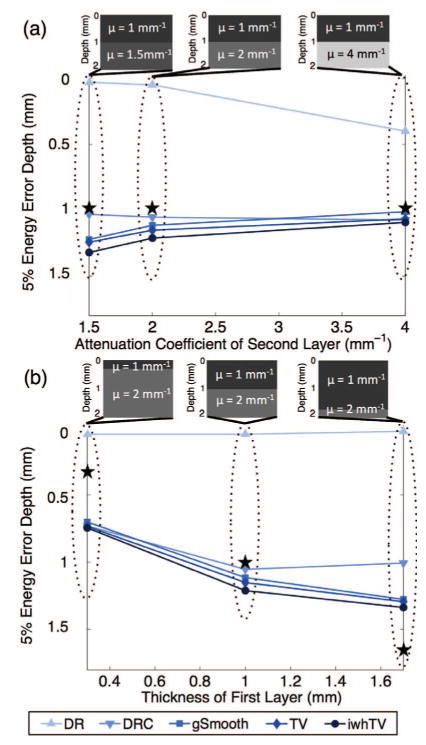
The effect of sample properties (i.e., contrast in the attenuation coefficient and relative thicknesses of the layers) on the accuracy of various estimation algorithms was investigated. Fig. 3(a) shows the effect of contrast between the layers ranging from 0.5 mm⁻¹ to 3 mm⁻¹. These values reflect the range of attenuation coefficients that are reasonable to detect using OCT [34] and that can be seen in actual tissue; for example, the three layers of the bladder visible with OCT have attenuation coefficients of approximately 0.49 mm⁻¹, 2 mm⁻¹, and 1.38 mm⁻¹ [35]. For all simulations, the attenuation coefficient of the top layer was fixed at 1 mm⁻¹, the focal plane was located at a depth of 0.5 mm, and the layer thicknesses were all 1 mm. The ★ in the graphs identifies the position of the boundary between layers. Fig. 3(a) shows the energy error depth as a function of the attenuation coefficient of the second layer. Notably, the DR result improves with increasing contrast between the layers, although the excess energy depth is still shorter than the thickness of the first layer. DRC with iwhTV denoising produces the most accurate estimates (i.e., the highest energy error depth) in all cases. It is important to note that presented results are not only a function of the contrast between layers, but will also vary with the absolute attenuation coefficients of each layer.

Fig. 3.

Bi-layer simulations used to investigate the effect of (a) attenuation coefficient contrast and (b) layer thickness on the accuracy of various algorithms. The ★ marks the position of the boundary between layers as set by the simulation. In all scenarios, DRC with iwhTV (●) outperforms all other algorithms.

Fig. 3(b) shows the energy error depth as a function of top layer thickness. For all simulations the total thickness (2 mm), attenuation coefficients (1 mm⁻¹ for the top layer and 2 mm⁻¹ for the bottom layer), SNR (40 dB) and focal plane location (0.5 mm) were kept constant. The thickness of the top layer was varied from 0.3 mm to 1.7 mm. For all algorithms, a thin top layer (left inset) results in worse energy metrics compared to layers of even thickness. All the algorithms failed to accurately measure the attenuation coefficient of a thin layer at the bottom of the sample (right inset), as evidenced by the ★ falling below the energy error depth. This is most likely due to the very low signal intensity by the time that depth is reached. Once again, DRC with iwhTV denoising outperforms all the other algorithms, yielding the highest energy error depth at approximately 1.3 mm.

Overall, Figs. 2 and 3 show that DRC with iwhTV denoising produces the most accurate estimates of attenuation coefficients when compared to other typical denoising algorithms, independent of important system and sample parameters.

B. Phantom Experiments

To validate the results obtained using DRC experimentally, we estimated the attenuation coefficient of several Intralipid phantoms. Table I shows the estimated attenuation coefficients for each phantom. The values reported for DRC are the average and standard deviation over all A-scans. The focal plane was positioned within the sample in all cases. Because the phantoms were uniform and devoid of structure, none of the denoising techniques yielded significant improvement in the results (data not shown).

TABLE I.

DRC vs reference

Intralipid Conc. (v/v)	DRC μ (mm−1)	Reference (mm −1)	Abs. difference (mm−1)
1.25%	1.2 ± 0.4	0.5	0.7
2.5%	1.7 ± 0.4	1.0	0.7
5%	2.4 ± 0.4	2.3	0.1
10%	3.8 ± 0.5	3.8	0
15%	4.4 ± 0.5	4.4	0
20%	4.6 ± 0.6	4.7	0.1

Calculated attenuation coefficients for various concentrations of Intralipid in water using DRC. Reference values from literature [30] are provided for comparison.

Table I shows that DRC achieves good agreement with values previously reported in literature [30] for all concentrations of Intralipid. The agreement is worst for 1.25% and 2.5%. We attribute this reduction in performance to the fact that these concentrations do not sufficiently attenuate the light at the bottom of the imaging range. As expected, violation of this fundamental assumption of the DR method (and DRC) will produce less reliable results. Conversely, DRC produces highly reliable results when the attenuation of light is sufficient.

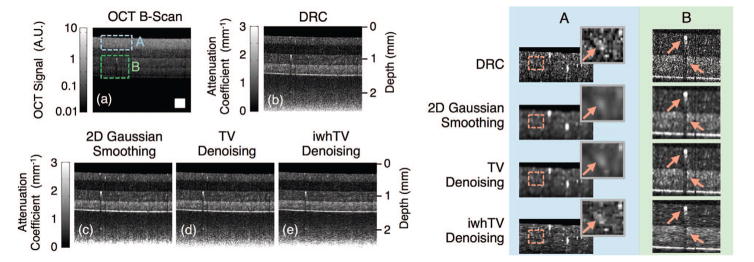
We also estimated the attenuation coefficient from a multilayer optical phantom. Fig. 4(a) shows the original OCT B-scan, while the boxed regions of interest appear magnified in the right half of the figure. Fig. 4(b) shows the results of DRC without any additional denoising, while Figs. 4(c)–(e) show the results after applying various denoising techniques. Note that the data were not averaged in any way nor was the image segmented prior to applying DRC. As expected, DRC accurately determines that the first and third layers have the same attenuation coefficient (they were made from the same mixture of PDMS/TiO₂), the second layer has the lowest attenuation coefficient, and the fourth layer has the highest attenuation coefficient. The fact that these structural properties of the sample were not obvious in the original B-scan – where the intensity decreases continually with depth – validates the relevance of the DRC method.

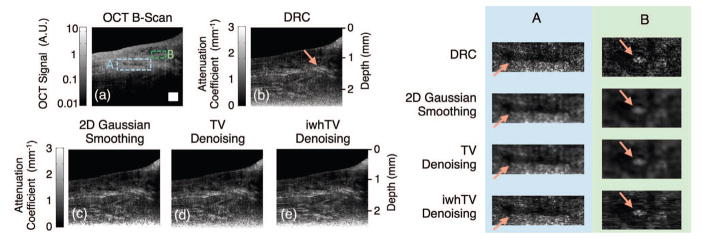
Fig. 4.

(a) OCT B-scan of a 4-layer PDMS phantom; boxed portions mark positions of the magnified views shown in the table on the right. Reconstructions were created using (b) DRC, (c) DRC with 2D Gaussian smoothing, (d) DRC with TV denoising, and (e) DRC with iwhTV denoising. iwhTV denoising reduces noise while retaining the structure of scattering particles present in the sample (highlighted in columns A and B on the right). The white square in (a) represents 250 × 250 μm².

Further improvements to the estimate of the attenuation coefficient over DRC can be attained by denoising. The choice of algorithm may affect data quality in addition to noise reduction. We compared Gaussian smoothing, TV denoising, and iwhTV. For the image portion selected in column A of Fig. 4, the SNR is high because this region of the sample is nearest the light source. In this region, the estimate provided by DRC is accurate and should not be altered much. The magnified images in column A of Fig. 4 show that Gaussian smoothing and TV denoising blur the structure of the data. In particular, the scatterers indicated by the arrow are blurred significantly by Gaussian smoothing and TV denoising. However, the structure is best retained by iwhTV denoising, and the scatterers remain in-tact. Column B of Fig. 4 shows a region of relatively low SNR. In this region, there appears a scattering particle of significant size and a resulting shadow (both indicated by arrows). The shadow remains prominent in the TV denoised image, indicating insufficient smoothing. The shadow is addressed comparably by Gaussian smoothing or iwhTV denoising; however, the structure of the scattering particle is blurred by the Gaussian smoothing algorithm. In contrast, iwhTV is able to retain the structure of the scattering particle while mitigating the shadow beneath it.

The regularization parameter, η, is an important adjustable parameter in the iwhTV algorithm. Increasing η encourages stronger piecewise constant behavior, effectively increasing the amount of smoothing to apply to the reconstruction. Fig. 5 shows the effect of changing the regularization parameter on the estimated attenuation coefficient. Fig. 5(a) shows the reconstruction of the attenuation coefficient using DRC without any additional denoising, and 5(b)–(d) show the reconstructions with iwhTV denoising and regularization parameters of η = 3, η = 6, and η = 12, respectively. Larger η leads to more lateral smoothing of the reconstruction, as evidenced by the magnified sections. The choice of which value of η to use should be governed by factors such as noise levels, confidence in the obtained data, and a priori knowledge of the amount of variation expected in the attenuation coefficient. For all instances of iwhTV denoising we set ε = 0.001. Varying ε has minimal effect on the results (data not shown).

Fig. 5.

(a) Reconstruction of the attenuation coefficient of a 4-layer PDMS phantom using DRC without any additional denoising. (b), (c), and (d) show reconstructions using DRC with iwhTV denoising and various values of the regularization parameter, η. Higher η results in more lateral blurring. The white square in (a) represents 250 × 250 μm².

C. Ex-vivo Tissue Experiments

To demonstrate the performance of DRC and iwhTV denoising on data obtained from biological samples, we estimated the attenuation coefficient of porcine bladder and colon samples. The focal plane was positioned within the sample in both cases, necessitating the use of DRC over DR to get accurate results. Fig. 6 shows comparison images between DRC (Fig. 6(b)) and DRC with various denoising conditions (Fig. 6(c)–(e)), as well as the original OCT B-scan (Fig. 6(a)). Differences between the B-scan and the attenuation coefficient reconstruction confirm that the attenuation coefficient measurement reveals information not evident in the original B-scan. For example, the region of relatively high attenuation, indicated with an arrow in Fig. 6(b) and corresponding to highly scattering muscle fibers would not have easily been identified by observing the B-scan alone.

Fig. 6.

(a) Original OCT B-scan of ex-vivo porcine bladder tissue used for creating reconstructions of the attenuation coefficient; boxed portions mark positions of magnified views shown in the table on the right. Reconstructions were created using (b) DRC, (c) DRC with 2D Gaussian Smoothing, (d) DRC with TV denoising, and (e) DRC with iwhTV denoising. The arrow in (b) indicates a region of high attenuation coefficient not obvious in the original B-scan. The arrows in columns A and B indicate boundaries that are retained with iwhTV but blurred by other techniques. The white square in (a) represents 250 × 250 μm².

Similar to observations in the phantom, pure DRC captures the overall trend of the attenuation coefficient but suffers from high speckle noise. Gaussian smoothing and TV denoising blur the image leading to a loss of resolution. Using iwhTV denoising results in reduced speckle with less degradation of resolution. Columns A and B in the right half of the figure show magnified regions of structural boundaries that are blurred by Gaussian smoothing and TV denoising. In contrast, iwhTV maintains these boundaries while still reducing speckle.

As was discussed in regards to the phantom, the user has control over the regularization parameter, η. Fig. 7 shows the effects of the regularization parameter when applied to a sample of ex-vivo porcine colon tissue. When η = 3, the image exhibits a significant amount of speckle, while increasing η leads to more smoothing, as expected.

Fig. 7.

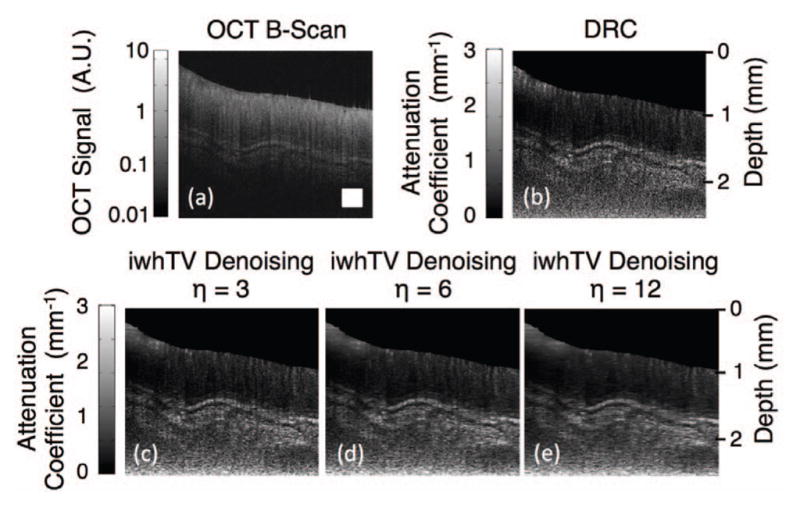
(a) OCT B-scan of ex-vivo porcine colon tissue. (b) Attenuation coefficient map created using DRC. (c), (d), and (e) show reconstructions using DRC with iwhTV denoising with various values of the regularization parameter, η. The white square in (a) represents 250 × 250 μm².

IV. Conclusion

In this paper we presented a modification to the model presented by Vermeer et al. that takes into account the confocal function and a more comprehensive estimate of sensitivity fall-off. We used this model to derive an invertible mapping between the OCT signal and the attenuation coefficient. The proposed DRC technique is the first fully automated algorithm to estimate the attenuation coefficient that simultaneously takes into account the confocal function and fall-off of the OCT system. Doing so makes the algorithm amenable to a wider variety of applications; most notably, it is able to accurately estimate the attenuation coefficient even when the focal plane is located within the sample, which is important when imaging in clinical settings.

Locating the focal plane from that data alone may be difficult; however, the focal position is often a fixed or measurable parameter in many clinical systems, suggesting that the focal plane position can be measured accurately prior to data collection and will remain constant throughout collection. To further improve upon the DRC results, we also introduced a novel denoising method based on weighted TV regularization, iwhTV denoising, that exploits the layered nature of certain biological samples.

We compared iwhTV denoising to Gaussian smoothing and TV denoising. Variations of TV denoising have been utilized previously to denoise intensity images exhibiting speckle noise [36], [37], [38]. Since we are denoising attenuation coefficient images as opposed to intensity images, these modifications are not directly applicable. Instead, the depth-dependent weights we apply based on the intensity of the standard image allow iwhTV to outperform TV.

Additionally, iwhTV denoises by optimizing a convex optimization problem, which presents at least two advantages over other types of optimization problems: 1) the availability of known algorithms and software that are guaranteed to converge to an optimal solution; and 2) the ability to attain an optimal solution while accounting for the constraint that the attenuation coefficient is non-negative, which is more difficult for other optimization formulations. The disadvantage of iwhTV is a higher computational cost. However, this disadvantage is overshadowed by the improvement in accuracy obtained when using the algorithm. Additionally, iwhTV can be dramatically sped-up by using an alternative optimization algorithm (e.g., the Alternating Direction Method of Multipliers [39]).

Currently, iwhTV takes advantage of the layered structure of many tissue types but is best suited for horizontal layers. Future modifications to the technique could incorporate the true shape of the layers, consider vertical continuity, and exploit other features of biological samples. Finally, denoising the original OCT data (prior to estimating the attenuation coefficient) could be explored as a means to further improve the accuracy of the results.

In conclusion, DRC with denoising offers a robust way to automatically extract a physical parameter from OCT data that will aid in the diagnosis and surveillance of many diseases. The elimination of user-defined ROIs and the correction for the confocal function not only make the algorithm applicable in a wider variety of situations but also increases the accuracy and reliability of the results.