Abstract
Comparison of experimental data with modeling predictions is essential for making quantitative measurements of species properties, such as diffusion coefficients and species concentrations using a T-sensor. To make valid comparisons between experimental data and model predictions, it is necessary to account for uncertainty in model predictions due to uncertain values of model parameters. We present an analysis of uncertainty induced in model predictions of a T-sensor based competitive diffusion immunoassay due to uncertainty in diffusion constants, binding reaction rate constants, and inlet flow speed. We use a non-intrusive stochastic uncertainty quantification method employing polynomial chaos expansions to represent the dependence of uncertain species concentrations on the uncertainty in model parameters. Our simulations show that the uncertainties in model parameters lead to significant spatially varying uncertainty in predicted concentration. In particular, the diffusivity of fluorescently labeled probe antigen dominates the overall uncertainty. The predicted uncertainty in fluorescence intensity is minimum near the centerline of T-sensor and relatively high in the regions with gradients in fluorescence intensity. We show that using centerline fluorescence intensity instead of first derivative of fluorescence intensity as the system response for measuring sample antigen concentration in T-sensor based competitive diffusion immunoassay leads to lower uncertainty and higher detection sensitivity.
I. INTRODUCTION
The field of microfluidics has ushered the development of lab-on-a-chip systems wherein laboratory operations, such as mixing, reaction, and detection of chemical species can be integrated on a single chip.1–3 The T-sensor is one of the simplest microfluidic devices, which leverages low Reynolds number laminar flow and controlled diffusive mixing of reactants for chemical sensing.4–8 In a T-sensor, shown schematically in Fig. 1(a), two fluid streams enter from separate inlets and flow parallel to each other in the main channel. The chemical species dissolved in these two co-flowing fluid streams diffuse into the adjacent streams creating a narrow inter-diffusion zone where they react. The reactions in this inter-diffusion zone can be quantified using several signal transduction mechanisms, including fluorescence4 and electrochemical detection.9 T-sensors have found several applications in chemistry and biochemistry, such as determination of species concentrations,5 diffusion coefficients,6,10 monitoring reaction kinetics,11 and performing immunoassays.7,12
FIG. 1.
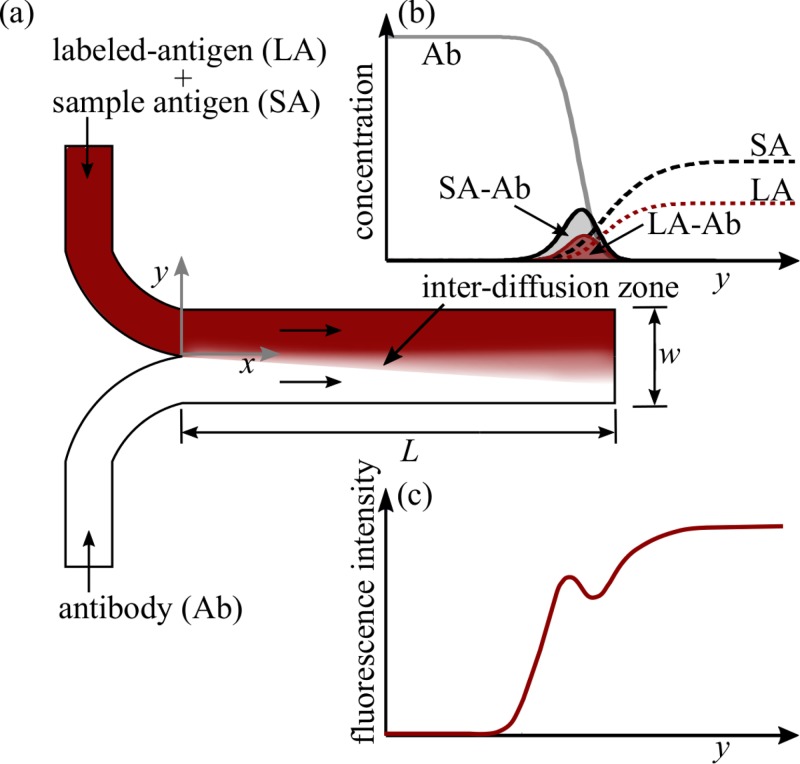
Schematic illustrating the operation of a T-sensor based competitive diffusion immunoassay. (a) Fluorescently labeled antigen and unlabeled sample antigen molecules are mixed in the upper stream, whereas the lower stream contains antibody molecules specific to the antigen. (b) The antigen and the antibody molecules diffuse into the adjacent flow streams and bind with each other in the narrow inter-diffusion zone. (c) The binding of labeled-antigen and antibody slows down the diffusive transport of labeled-antigen into the lower stream, resulting in a peak in the fluorescence intensity measured along the lateral direction (y-direction). Since labeled-antigen and sample antigen compete for the same binding sites on the antibody, the peak in fluorescence signal decreases with increase in sample antigen concentration.
Early work on T-sensors was limited to qualitative estimation of unknown analyte concentrations through basic comparisons. Subsequently, Kamholz et al.4 extended the applicability of T-sensor for making quantitative measurements through comparison of experimental data with predictions from a mathematical model for convection, diffusion, and reactions of chemical species. Kamholz et al.4 performed fluorescence visualization of binding reaction between a fluorophore (Albumin Blue 580) and human serum albumin in T-sensor and compared the experimental data with the mathematical model to determine the diffusivity of fluorophore. In a following study, Kamholz et al.6 fitted experimental data of species diffusion in a T-sensor with an analytical model to determine diffusion coefficients of fluorescently labeled biotin, insulin, ovalbumin, and streptavidin. These studies underline the importance of modeling and simulation of physico-chemical processes in T-sensor for extending its usefulness for quantitative analysis. As is true for other microfluidic systems, modeling and simulations can also help in optimizing the design of T-sensor to obtain desired results, such as the width of inter-diffusion zone and signal intensity.
The existing modeling and simulation analyses of T-sensor are based on solving deterministic convection-diffusion-reaction equations wherein the model parameters, such as species diffusivities, reaction constants, and flow rates, are assumed to be deterministic constants.4,13 In practice, these model parameters are not known exactly due to experimental measurement uncertainty or inherent variabilities. Therefore, deterministic models are unable to quantify uncertainty in the model predictions due to uncertainty in model parameters. Since experimental data fitted with model predictions is used for quantitative analysis using T-sensor, neglecting uncertainty in simulation predictions can lead to errors in estimation of physical quantities such as species concentrations, diffusivities, and reaction rates. Therefore, to make proper comparison between experimental data and modeling predictions, it is necessary to account for uncertainty in modeling and simulation results due to uncertainty in model parameters. Moreover, uncertainty quantification in simulations of T-sensor can provide valuable information regarding spatial distribution of uncertainty in measured signals. Such information can be used for choosing the detection location and developing quantification methods to minimize uncertainty in experimental measurements.
In the current work, we present uncertainty quantification in model predictions of transport and reactions of chemical species in a T-sensor. As a practical example, we consider the case of a T-sensor based competitive diffusion immunoassay described by Hatch et al.7 The working principle of a T-sensor based competitive diffusion immunoassay, illustrated in Fig. 1, is based on the changes in diffusive transport of a fluorescently labeled probe antigen upon binding with antibody molecules while the probe antigen competes with the unlabeled sample antigen (SA) for common binding sites. We elucidate the effect of uncertainty in model parameters, such as inlet flow speed, diffusivities, and reaction rate constants, on spatial variation of uncertainty in the species concentration and fluorescence intensity. Using the spatial variation of uncertainty in model predictions, we provide guidelines for performing quantitative measurements in experiments so as to improve the detection sensitivity and resolution, while reducing uncertainty.
The uncertainty in model parameters which is associated with measurement errors or inherent variability in experiments can be accounted for using stochastic uncertainty quantification techniques.14 In particular, we employ a non-intrusive stochastic uncertainty propagation approach based on Polynomial Chaos (PC) expansions14–17 as described by Reagan et al.17 Unlike deterministic simulations, in this method the model parameters are treated as uncertain. For each uncertain parameter a new stochastic dimension is used to describe its probability density function. PC expansions are used to describe the dependence of model predictions on these stochastic dimensions. The coefficients or the spectral mode strengths of the PC expansions are then evaluated using numerical quadrature through multiple solutions of the deterministic model. Such an approach readily provides the uncertainty propagation information in terms of PC expansions of model predictions. Knowing the PC expansions of model predictions, the spatial variation of uncertainty and the individual contribution of each uncertain parameter to the overall uncertainty can be computed. We note that uncertainty propagation analysis can also be performed through Monte Carlo (MC) simulations, albeit with unacceptably large number of simulations.18 Moreover, unlike PC expansion based methods, MC simulations do not provide the coupled contribution of uncertainty in model parameters to the overall uncertainty in model predictions.19
While PC expansions have been used extensively for uncertainty quantification in several fields, such as structural mechanics,20 gas dynamics,21 aerodynamics,22 and combustion,17 its potential for designing and improving microfluidic systems has not been fully utilized. Xiu and Karniadakis18 used the example of pressure-driven microchannel flow with non-uniform random boundary conditions to illustrate the application of generalized PC expansion for uncertainty quantification. Debusschere et al.19 analyzed uncertainty in protein-labeling reactions in electrokinetic flow in microchannels due to uncertainty in model parameters using PC expansions. Debusschere et al. simulated a nonlinear system in which electrokinetic transport of bands of a protein and a dye at different speeds result in band crossing and reaction. Their results provided interesting insights into the spatial variation of predicted uncertainty in species concentrations. For a similar electrokinetic system, preceding the work of Debusschere et al.,19 Gleeson23 quantified uncertainty in electroosmotic flows and associated transport of uncharged-solute due to random zeta potential. Due to the linearity of flow at low Reynolds number, Gleeson23 used superposition of fluid flows due to different random modes of zeta potential for uncertainty quantification.
The overall focus of existing work on uncertainty quantification of microfluidic systems has been on propagation of uncertainty from model parameters to model predictions. However, these studies do not focus on applying uncertainty quantification for designing or improving a microfluidic system. In contrast, the focus of current work is to elucidate the spatial variation of predicted uncertainty in a microfluidic T-sensor and use uncertainty quantification to provide guidelines for performing quantitative measurements in experiments to minimize uncertainty.
We begin by presenting the deterministic equations for modeling transport and reactions of chemical species in a microfluidic T-sensor based diffusion immunoassay. Next, we provide a description of the stochastic uncertainty quantification methodology using PC expansions. We then present results for uncertainty quantification of convection and diffusion of chemical species in T-sensor with and without accounting for chemical reactions. Based on the results, we explain the spatial variation and composition of uncertainty in predicted values of species concentrations. Thereafter, we present a comparative analysis of uncertainty associated with various methodologies for quantifying analyte concentrations in a T-sensor. We also provide practical guidelines for quantifying analyte concentration in T-sensor to minimize uncertainty and hence maximize detection sensitivity and resolution.
II. PHYSICAL MODEL FORMULATION
A. T-sensor based competitive diffusion immunoassay
In the current work, we present stochastic uncertainty quantification in simulations of a microfluidic T-sensor based competitive diffusion immunoassay shown schematically in Fig. 1. As shown in Fig. 1(a) fluorescently labeled-antigen and unlabeled sample antigen molecules are mixed in the upper flow stream, while the antibody molecules specific to the antigen are mixed in the lower flow stream. The low Reynolds number laminar flow conditions in the T-sensor result in controlled diffusive mixing of the antigen and antibody molecules into the adjacent streams forming a narrow inter-diffusion zone. In this inter-diffusion zone, the labeled-antigen (LA) and unlabeled sample antigen molecules compete to bind with the antibody molecules as shown in Fig. 1(b). Upon binding, the diffusivity of the labeled-antigen bound with antibody decreases drastically owing to the large size of antibody molecule. This decreases the downward diffusive transport of the complex of labeled-antigen and antibody, resulting in a peak in the fluorescence signal as shown in Fig. 1(c). Since labeled-antigen and sample antigen compete for the same binding sites on the antibody, the peak in fluorescence signal decreases with an increase in sample antigen concentration.
B. Mathematical modeling
Simulations of T-sensor based immunoassay require mathematical models for fluid flow, species transport due to convection and diffusion, and binding of antigen and antibody molecules. Fluid flow in a microfluidic T-sensor is characterized by low Reynolds number where inertial effects can be neglected. Here, h is the depth of the channel and u, ρ, and μ, respectively, denote the flow speed, fluid density, and fluid viscosity. Further simplification comes from the shallow geometry of T-sensor as the depth h is usually significantly smaller than the width w of the channel, . For a shallow rectangular cross-section channel with the depth-averaged velocity is uniform across the width of the channel, except for narrow regions of thickness near the side walls where velocity gradients exist to satisfy the no-slip conditions.24 Since the inter-diffusion zone at the centerline of T-sensor is relatively small compared with the width of channel, it is reasonable to assume in our analysis that the average flow velocity is uniform.
The transport of antigen and antibody molecules in a T-sensor can be described by three-dimensional mass conservation equations taking into account convective-diffusive transport and production (or elimination) terms due to binding reactions. The three-dimensional species transport equations can be simplified noting that the time scale associated with diffusion of species into the depth of T-sensor is significantly smaller than the convection time scale . Therefore, the concentration of i-th species ci in the T-sensor can be conveniently described using two-dimensional species transport equations given by
| (1) |
Here u is the depth-averaged flow speed, Di the diffusivity of i-th species, and Ri the production or elimination term to account for binding reactions. We assume that flow speed u and diffusivities Di are spatially constant. In a T-sensor, the lateral gradients in species concentration occur over narrow inter-diffusion zone with thickness , whereas the axial gradients in species concentration occur over longer distance of . Therefore, the ratio of axial diffusion to lateral diffusion scales as , where Pe is the Peclet number. For a typical T-sensor with s−1, , and m2 s−1, the Peclet number . Since the axial diffusion is three orders of magnitude lower than lateral diffusion, Equation (1) can be simplified to
| (2) |
C. Binding kinetics
The production or elimination rate Ri of various species in Equation (1) depends on the binding kinetics. Following Hatch et al.,7 we assume that each antibody molecule contains two identical binding sites for the antigens. Moreover, all binding sites are identical and have identical kinetics for the LA and SA, given by
| (3) |
| (4) |
The rates of elimination of labeled-antigen and sample antigen are given by
| (5) |
| (6) |
where k1 is the rate constant for forward reaction and Keq is the equilibrium constant for the binding reactions (3) and (4). The subscripts LA, SA, Ab, LA-Ab, and , respectively, denote labeled-antigen, sample antigen, antibody binding sites, complex of labeled-antigen and antibody, and complex of sample antigen and antibody. We note that cAb denotes the concentration of antibody binding sites. Since every antibody molecule has two binding sites, cAb is twice the concentration of antibody molecules. From Equations (3) and (4) we note that the rate of elimination of binding sites on antibody molecules is , and the production rates of the two complexes are and . To quantify the uncertainty in our simulations, we use the solutions to deterministic governing equations (2) and the above model for binding kinetics at different values of uncertain model parameters to construct the PC expansions for species concentrations. Next, we present the methodology for construction of PC expansions from deterministic simulations.
III. STOCHASTIC MODEL FORMULATION
We use a non-intrusive stochastic uncertainty quantification method based on PC expansions for propagation of uncertainty from model parameters to model predictions. This method has been presented in detail by Reagan et al.,17 and we briefly summarize it here. In this technique, we introduce an additional stochastic dimension ξ corresponding to each uncertain parameter. For normally distributed model parameters, is chosen as a random variable with standard normal probability density function. Hence a normally distributed model parameter, β, can be described in terms of ξ as
| (7) |
where is the mean value of parameter β and is the standard deviation. The species concentrations now have an additional dependence on ξ besides their spatial variation. The species concentrations ci are described using spectral PC expansions as
| (8) |
where ψk are the basis functions of PC expansion and are the corresponding spectral mode strengths for i-th species. If the model has only one uncertain parameter, the basis functions ψk are one-dimensional Hermite polynomials
| (9) |
In practice, the infinite series in Equation (8) can be truncated to a specific order p, which is the highest order polynomial used in the PC expansion. Therefore, the total number of terms in PC expansion for the case of one uncertain parameter is p + 1.
In general, for d number of uncertain model parameters, a d-dimensional stochastic space is required for which the basis functions are d-dimensional Hermite polynomials in ,
| (10) |
Here we have assumed that all stochastic dimensions are uncorrelated. The total number of terms in PC expansion in Equation (10) is , which depends on the dimensions d and highest order of polynomial p as
| (11) |
The d-dimensional Hermite polynomials are the product of one dimensional Hermite polynomials involving multi-index
| (12) |
For example, for two uncertain parameters (d = 2), the first few two-dimensional Hermite polynomials are given by
| (13) |
To describe the effect of uncertain model parameters on the species concentrations ci, we compute the coefficients of the corresponding PC expansion using a non-intrusive approach.17 To this end, we use the orthogonality of Hermite polynomials with respect to the standard normal probability density function and project the PC expansions onto the PC basis to get
| (14) |
The integrals in the numerator and denominator can be evaluated by numerical Gauss-Hermite quadrature, which approximates the integrals using weighted average of functional values at specific points within the domain of integration. For example, for a single uncertain parameter (d = 1), the coefficients (or spectral mode strengths) of the PC expansion given by Equation (8) can be calculated as
| (15) |
Here, is the weight corresponding to the quadrature point and N is the total number of quadrature points required to accurately approximate the integral; integrals consisting of a polynomial integrand of order up to can be exactly evaluated using N quadrature points. Therefore, the calculation of coefficients of PC expansion requires solutions for concentration field using the deterministic model for various realizations of the random model parameters corresponding to quadrature points . This approach for uncertainty quantification is non-intrusive in nature as the numerical solver for deterministic model need not be modified to account for uncertain model parameters.
In general, for d number of uncertain parameters, the quadrature points at which deterministic calculations are performed are given by the d-dimensional tensor product of one-dimensional quadrature points. Therefore, as the number of uncertain parameters increases, the number of solutions of the deterministic model required to perform numerical integration increases exponentially as Nd. To overcome this limitation, in the current work, we use Gauss-Hermite quadrature over Smolyak grid,25,26 which requires significantly less number of quadrature points to perform numerical integration with reasonable accuracy. For example, Gauss-Hermite quadrature with tensor product of quadrature points for N = 5 and d = 6 requires solutions of the deterministic model, whereas same accuracy of numerical integration can be obtained using Gauss-Hermite quadrature over Smolyak grid with only 85 solutions of the deterministic model. We note that, in practice, PC expansions are truncated as large number of computations is required to accurately calculate higher order terms using numerical quadrature.
Having obtained the spectral mode strengths or the coefficients of PC expansions, we can compute various statistical moments, such as the mean and standard deviation in species concentrations. As noted by Debusschere et al.,19 the zeroth-order coefficient represents the mean concentration field for i-th species because the expectations , whereas the higher order coefficients account for the uncertainty around this mean value. The standard deviation in concentration of i-th species is given by
| (16) |
The PC expansions also provide the contribution of uncertainty of individual parameters to the overall uncertainty. The contribution of each uncertain parameter to the overall uncertainty can be obtained by grouping the terms in Equation (16) which correspond to same stochastic dimension. For example, consider a second order PC expansion of concentration field with basis functions given by Equation (13) for the case of two uncertain parameters (d = 2). The individual contribution of first uncertain parameter (corresponding to ξ1) to the overall uncertainty is given by the sum of terms corresponding to and in Equation (16), whereas the term corresponding to in Equation (16) accounts for the coupled contribution of both uncertain parameters to the overall uncertainty. This feature of uncertainty quantification based on PC expansions can be used to identify the parameters that are major contributors to the overall uncertainty in model results.
IV. RESULTS AND DISCUSSION
We solved the deterministic convection-diffusion-reaction equations (2) for species concentrations numerically using a finite difference method. The governing Equations (2) were semi-discretized by approximating the derivatives along the lateral direction (y-direction) using the second-order central differencing scheme. The resulting ordinary differential equations in x-domain were solved using the fourth-order Runge-Kutta scheme. The numerical solutions to the deterministic model were used for calculating spectral mode strengths using stochastic collocation method discussed in Section III.
For all our simulations we considered a T-sensor based diffusion immunoassay system described by Hatch et al.7 The dimensions of T-sensor and the mean values of model parameters were same as those used by Hatch et al. for experimental validation of their theoretical model. The width of the T-sensor was 1200 μm and the length was 6400 μm. The sample antigen was phenytoin ( m2 s−1), the labeled-antigen was fluorescein-phenytoin conjugate ( m2 s−1), and the antibody was phenytoin-specific polyclonal antibody ( m2 s−1). Since the antibody molecule is significantly larger than the antigen molecule, we assume that the diffusivities of antibody-antigen complexes are the same as the diffusivity of unbound antibody. The forward reaction rate k1 for the binding reactions was M−1 s−1 and the equilibrium constant Keq was M−1. Both inlet flow streams of T-sensor were assumed to have same average flow speed u of 0.3475 mm s−1.
For our calculations, we assumed that the model parameters were independent, normally distributed random variables with above mentioned mean values. We assumed that the standard deviation of all diffusion coefficients was 5% of their respective mean values. The uncertainty in species diffusivity is representative of the systematic uncertainty arising from a temperature fluctuation, as diffusivity varies with temperature as ,27 where μ1 and μ2 are the viscosity values of water at temperatures T1 and T2, respectively. The standard deviation of flow speed u was taken as 0.16% of the mean value, which is in accordance with typical resolution of a syringe pump. Under the assumption that both upper and lower streams originate from a dual channel syringe pump, the two stream velocities are equal and perfectly correlated. Hence, we assigned only one stochastic dimension to account for the uncertainty in inlet stream velocity. We note that uncertainty in microchannel dimensions can also affect the flow speed. For a typical microchannel fabricated using etching, the tolerance of channel dimensions is about 0.1% of the channel thickness.28 For a shallow microchannel with fixed flow rate, this can lead to an uncertainty of 0.1% in the flow speed. This is comparable with the 0.16% standard deviation in flow speed which we have assumed in our analysis. The standard deviation in k1 and Keq were taken as 1% of their respective mean values. In our analysis, we have neglected the uncertainty due to surface roughness as typical surface roughness of order 10 nm for etched microchannels28,29 has negligible effect on fluid flow.30
We performed simulations in a rectangular domain corresponding to the main channel of T-sensor shown in Fig. 1(a). The computational domain was discretized using a uniform grid of 1500 × 200 grid points. This grid size was chosen, as doubling the grid points in both x and y directions resulted in a variation of 0.1% in the predicted values of concentrations. For all our computations, we have represented the species concentrations using third-order PC expansions. The third-order expansions were sufficiently accurate in describing the uncertainty, as higher order spectral mode strengths were significantly smaller than the lower order mode strengths.
A. Convection and diffusion of single species
To illustrate the application of uncertainty quantification methodology based on PC expansions, we begin by considering a simple case of convection-diffusion of a single species in T-sensor. We performed simulations for a T-sensor system in which labeled-antigen with inlet concentration of 19 nM flows in from the upper inlet and water flows in from the lower inlet. For this case we assumed that sample antigen and antibody are not present. Therefore, diffusivity of labeled-antigen and inlet flow speed were the only uncertain parameters. The third-order PC expansion for antigen concentration consisted of 10 coefficients. Computation of these 10 coefficients required 29 simulations using Smolyak quadrature based stochastic collocation.
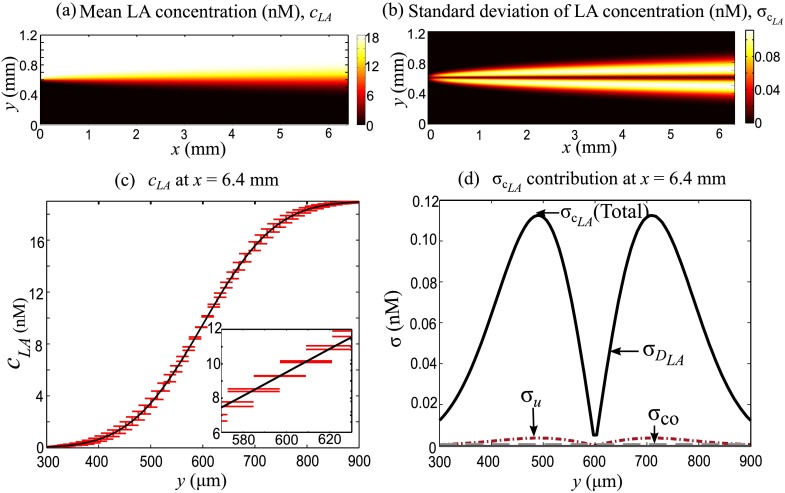
Fig. 2(a) shows the mean concentration field of labeled-antigen. The labeled-antigen flows into the T-sensor from the upper inlet and diffuses into the lower stream. This process is analogous to transient one-dimensional species diffusion with the axial direction acting as a “time-like” variable. The total predicted standard deviation in the concentration field due to uncertainty in flow speed and diffusivity of labeled-antigen is shown in Fig. 2(b). The uncertainty in concentration field in this case is minimum along the centerline and highest on either side of the centerline at nearly half the diffusion length. The uncertainty tends to “diffuse” along y-direction as the zone of uncertainty grows at downstream locations. Fig. 2(c) shows the lateral variation of mean and standard deviation () of the concentration of labeled-antigen at the exit of T-sensor (x = 6.4 mm). As expected, the mean lateral concentration variation is sigmoidal in shape. The uncertainties in model parameters induce considerable uncertainty in the simulated labeled-antigen concentration. For example, at , the uncertainty in concentration is nearly 5%.
FIG. 2.
Predicted mean and standard deviation of concentration of labeled-antigen for the case when sample antigen and antibody are absent. (a) Mean concentration field of labeled-antigen for inlet labeled-antigen concentration of 19 nM. (b) Spatial variation of total standard deviation of labeled-antigen concentration. The uncertainty is minimum along the centerline and is highest at nearly half of the diffusion length from the centerline. The uncertainty “diffuses” further in the y-direction at downstream locations. (c) Lateral concentration variation with uncertainty bars at the T-sensor exit (x = 6.4 mm). The sigmoidal shape of concentration profile is characteristic of transient one-dimensional diffusion; here x-coordinate is the “time-like” variable. (d) Individual contributions of uncertainty in model parameters to the overall uncertainty in concentration at x = 6.4 mm. The diffusivity of labeled-antigen DLA is the major contributor to uncertainty. The contributions of uncertainty in flow speed u and diffusivity of labeled-antigen DLA dip near the centerline resulting in a minima in the overall standard deviation.
In Figs. 2(b) and 2(c), we have shown the predicted values of overall uncertainty. However, the PC formalism described in Section III also provides the contribution of each uncertain parameter to the overall uncertainty. Fig. 2(d) shows the spatial variation of contribution of uncertainty in inlet flow speed and diffusivity to the overall uncertainty in exit concentration of labeled-antigen. In the current case, diffusivity of labeled-antigen is the major contributor to the overall uncertainty at all locations. However, the contribution of diffusivity nearly vanishes near the center. Such a trend is expected since the variation in diffusivity tends to flatten or steepen the lateral concentration distribution without affecting the concentration at the center. The contribution of uncertainty in flow speed follows a similar trend, although its magnitude is low due to lower uncertainty in inlet flow speed compared with that in diffusivity. Since the top and bottom stream velocities are equal, variation in inlet flow speed simply affects the residence time of molecules in the system without affecting the concentration at the center. Consequently, the overall uncertainty in concentration is minimum near the center. Fig. 2(d) also shows the contribution of coupled effects of flow speed u and diffusivity of labeled-antigen DLA, apart from their individual uncertainty, to the overall uncertainty. Even though this coupled contribution is small in comparison with individual contributions of the uncertain parameters, it reinforces the fact that stochastically independent uncertain parameters interact and give rise to coupled effects which contribute to the uncertainty in model predictions.
B. Convection, diffusion, and reaction of multiple species: Competitive diffusion immunoassay
Next, we quantify the uncertainty in simulation of competitive diffusion immunoassay in a T-sensor. The simulated system is similar to the T-sensor system described in Section IV A. However, in this case, in addition to the labeled-antigen in the upper stream, an unlabeled sample antigen flows into the T-sensor through the upper inlet and an antibody flows in through the lower inlet. The antibody molecules bind with sample and labeled-antigen molecules, forming complexes in the narrow inter-diffusion zone leading to accumulation of labeled-antigen-antibody complexes. The inlet concentrations of labeled-antigen and antibody binding sites are 19 nM and 74 nM, respectively. In this case, the uncertain parameters are the inlet velocity u, diffusivities of antibody, sample antigen and labeled-antigen (DAb, DSA, and DLA), forward reaction rate constant k1, and equilibrium constant Keq. We performed a series of simulations to analyze the uncertainty in concentration field of labeled molecules for four values of sample antigen concentration ranging from 0 to 573 nM. For these simulations, we expressed the simulation output using third-order PC expansions in six stochastically independent dimensions; there were 84 coefficients in the PC expansion. Computation of these 84 coefficients required 389 simulations using Smolyak quadrature.
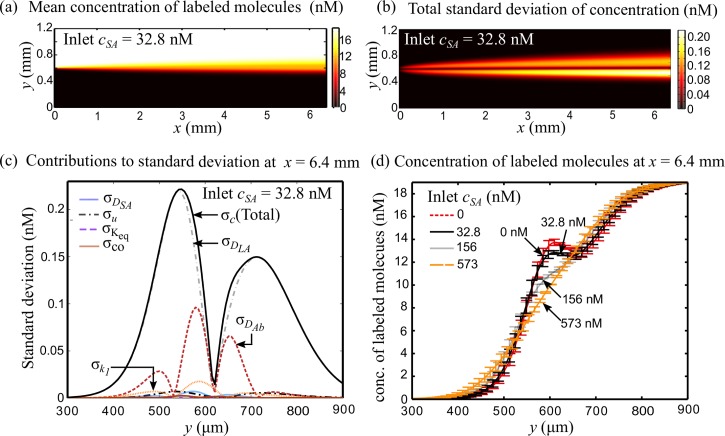
Fig. 3(a) shows the mean concentration field of labeled molecules (labeled-antigen and complex of labeled-antigen and antibody) for inlet sample antigen concentration of 32.8 nM. Here, we have chosen to plot the combined concentration of labeled-antigen and the complex of labeled-antigen and antibody because in experiments both molecules will contribute to the measured fluorescence signal. Assuming that the fluorescence signal is proportional to the concentration of fluorescently labeled molecules, the results shown in Fig. 3 can also be interpreted in terms of predicted fluorescence intensity. The binding of antibody and labeled-antigen is evidenced by the appearance of a high concentration band near the center instead of a smooth sigmoidal lateral variation in concentration of labeled molecules (see also Fig. 3(d)). The spatial variation of standard deviation in the concentration field of labeled molecules is shown in Fig. 3(b). In this case, we observe an asymmetry in the standard deviation across the centerline. That is, the uncertainty in concentration of labeled molecules is higher on the antibody side compared with that on the antigen side. This is because, the diffusion of smaller antigen molecules into the antibody stream is quicker as compared with the diffusion of bulky antibody molecules into the antigen stream, resulting in higher uncertainty on the antibody side. However, similar to the case of single species diffusion discussed in Section IV A, the standard deviation in concentration field near the centerline is conspicuously smaller compared with that in the neighboring regions.
FIG. 3.
Predicted mean and standard deviation of total concentration of labeled molecules (labeled-antigen in bound and unbound state) in T-sensor based competitive diffusion immunoassay. In these calculations, the inlet concentrations of labeled-antigen and antibody binding sites were 19 nM and 74 nM, respectively. (a)–(c) show results for the case when sample antigen concentration is 32.8 nM. (a) Mean concentration field of labeled molecules. The marked departure from smooth sigmoidal lateral variation in concentration is due to the accumulation of labeled molecules. (b) Total standard deviation in concentration of labeled molecules. The standard deviation is asymmetrically distributed about the centerline and is significantly low at the centerline. (c) Individual contribution of uncertainty in model parameters to overall uncertainty in labeled molecule concentration. The diffusivity of labeled-antigen DLA is the dominant contributor to overall uncertainty throughout the T-sensor. Since small antigen molecules diffuse faster than bulky antibody molecules, the rate of binding reactions and hence the uncertainties are higher in the antibody stream. (d) Lateral variation of concentration of labeled molecules with uncertainty bars, at T-sensor exit (x = 6.4 mm) for four values of sample antigen concentration. The accumulation of antigen molecules is evident from the peak near the center which subsides upon increase in sample antigen concentration.
To get further insight into the physico-chemical processes contributing to uncertainty of T-sensor based diffusion immunoassay, we separate out the contributions of model parameters to the overall uncertainty. As shown in Fig. 3(c), the diffusivity of labeled-antigen is the major contributor to uncertainty in concentration of labeled molecules at all locations except near the center where its contribution nearly vanishes. The contribution of antibody diffusivity to the total standard deviation follows a similar bimodal variation, albeit with lower magnitude. In contrast, the diffusivity of sample antigen has negligible contribution since sample antigen molecules do not interact directly with labeled-antigen molecules and sample antigen concentration of 32.8 nM is not large enough to significantly affect the labeled-antigen concentration. The contribution of uncertainty in inlet flow speed to the overall uncertainty also shows bimodal lateral variation which nearly vanishes at the center, similar to the case of single species diffusion discussed in Section IV A. The contribution of forward reaction rate constant to overall uncertainty attains a maxima in the antibody stream, due to higher rate of reaction in that region. Lastly, the contribution of equilibrium constant Keq is negligible since the rate of dissociation is extremely small as compared with the forward reaction rate. The coupled effect of uncertainty in different parameters taken two and three at a time, apart from their individual contributions, to the overall uncertainty is negligible as shown in Fig. 3(c).
In Fig. 3(d) we present the mean and uncertainty in lateral concentration variation of labeled molecules (or fluorescence signal) at the T-sensor exit (x = 6.4 mm) for varying sample antigen concentrations. The peak in the signal diminishes with increasing sample antigen concentration, as less number of binding sites is available on the antibody for labeled-antigen when faced with competition from higher concentration of sample antigen. Therefore, at high sample antigen concentrations, such as at 573 nM, labeled-antigen diffuses without notable binding. That is, at high sample antigen concentrations, the labeled-antigen concentration variation is similar to the case shown in Fig. 2 when antibody and sample antigen are absent. Irrespective of the sample antigen concentration, we note that the uncertainty represented by uncertainty bars in Fig. 3(d) is lowest around the center and highest in the neighborhood. The predicted uncertainty reduces very far from the center where the effects of diffusion and reaction are absent. This lateral variation in uncertainty is particularly relevant for deciding the method of quantification in experiments to minimize the uncertainty. In Section IV D, we compare different quantification methods and show that using centerline fluorescence intensity to quantify antigen concentration leads to higher detection sensitivity and resolution due to lower uncertainty in that region, whereas using the first derivative of normalized fluorescence signal as proposed by Hatch et al.7 leads to lower sensitivity and resolution as uncertainty in signal is relatively high in the regions where first derivative of signal achieves extreme values.
C. Effect of sample antigen concentration on uncertainty
We now consider the effect of sample antigen concentration on the spatial variation of predicted uncertainty. Varying the sample antigen concentration affects the binding interaction of labeled-antigen and antibody. This in turn affects the convection-diffusion transport of labeled species. Therefore, the contribution of various uncertain parameters to the overall uncertainty can vary with the concentration of sample antigen.
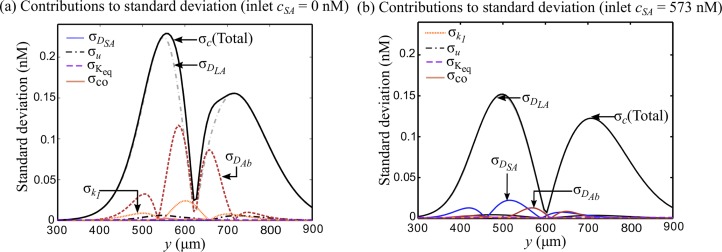
In Fig. 4, we compare the lateral variation in contributions of various uncertain parameters to the total standard deviation at two extreme values of sample antigen concentration (0 nM and 573 nM). Fig. 4(a) shows the lateral variation of standard deviation contributions at the T-sensor exit (x = 6.4 mm) when no sample antigen is added to the T-sensor. The predicted uncertainty when the sample antigen is absent qualitatively resembles the case shown in Fig. 3(c) when the sample antigen concentration is low (32.8 nM). That is, the uncertainty in diffusivity of labeled-antigen and antibody dominates the overall uncertainty in concentration of labeled molecules. When the sample antigen is present in excess (573 nM), the overall uncertainty in major part of the inter-diffusion region decreases as shown in Fig. 4(b). Moreover, the contribution of diffusivity of antibody is negligible as opposed to the cases of low sample antigen concentration shown in Figs. 3(c) and 4(a). At high sample antigen concentration, the contribution of uncertainty in diffusivity of sample antigen to overall uncertainty increases appreciably. Interestingly, at high sample antigen concentration, the spatial variation in uncertainty shown in Fig. 4(b) resembles that shown in Fig. 2(d) for the case of convection-diffusion of labeled-antigen in absence of sample antigen and antibody. This is because, at high sample antigen concentrations, the sample antigen dominates the competition for binding with the antibody. Consequently, very less amount of labeled-antigen binds with the antibody. Therefore, the labeled-antigen simply convects and diffuses as is the case shown in Fig. 2. Nevertheless, the results presented in Figs. 3(c), 4(a), and 4(b) show that the overall uncertainty for all values of sample antigen concentrations is dominated by the diffusivity of labeled-antigen, and the minimum uncertainty occurs around the centerline of T-sensor.
FIG. 4.
Effect of sample antigen concentration on uncertainty in T-sensor based diffusion immunoassay. Shown here are the contributions of various model parameters to the overall uncertainty for two cases: (a) when sample antigen is absent and (b) when inlet sample antigen concentration is 573 nM. (a) In the absence of sample antigen, the uncertainty variation is qualitatively similar to the case shown in Fig. 3(c) when antigen concentration is low. (b) At high concentration of sample antigen, the overall uncertainty decreases in most of the inter-diffusion region. Less binding sites are available for the labeled-antigen on the antibody, causing the labeled-antigen to diffuse without appreciable binding. Thus the spatial variation of uncertainty shown in (b) is qualitatively similar to the case shown in Fig. 2(d) where labeled-antigen diffuses in absence of antibody and sample antigen.
D. Comparison of analyte concentration quantification methodologies
The results presented in Sections IV A–IV C show that stochastic uncertainty propagation provides us with valuable information regarding the spatial variation of uncertainty in concentration field in a T-sensor. This information can be employed for devising strategies for quantification of sample antigen concentration from measured signal while minimizing uncertainty. In a typical T-sensor based competitive diffusion immunoassay, the fluorescence signals from the labeled molecules at known sample antigen concentrations are used to generate a calibration curve. The fluorescence signal from immunoassay of unknown sample antigen concentration is then compared with the calibration curve to predict the antigen concentration. In order to accurately determine the unknown analyte concentration in the immunoassay, it is essential that the fluorescence signals used for calibration and comparison have low uncertainty.
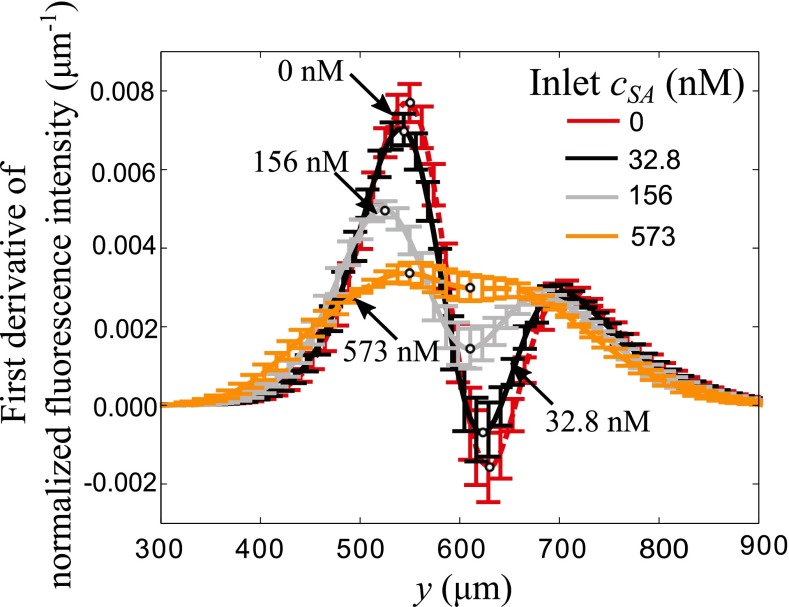
Hatch et al.7 presented a calibration technique for T-sensor based diffusion immunoassay which employs the first derivative of normalized fluorescence intensity along the lateral direction. The difference between maxima and minima in the first derivative of normalized fluorescence intensity is plotted against the known sample antigen concentrations to obtain the calibration curve. We note that here the normalized fluorescence intensity curve is the same as the normalized concentration curve of labeled molecules since fluorescence intensity of labeled molecules is assumed to be directly proportional to their concentration. Fig. 5 shows the first derivative of normalized fluorescence intensity for various sample antigen concentrations, computed from the simulation data presented in Fig. 3(d). Also shown in Fig. 5 is the predicted uncertainty in the first derivative of normalized fluorescence intensity using uncertainty bars. We calculated the uncertainty in the derivative of normalized fluorescence intensity by differentiating the PC expansion for concentration field (Equation (10)) as
| (17) |
FIG. 5.
Lateral variation of mean and uncertainty () of first derivative of normalized fluorescence intensity at T-sensor exit (x = 6.4 mm) for four values of inlet sample antigen concentration. Uncertainty in model parameters leads to significantly higher uncertainty in the first derivative of fluorescence signal. In particular, the uncertainty is highest at locations of extrema in the first derivative of normalized fluorescence intensity profile.
The uncertainty bars shown in Fig. 5 clearly indicate that significant uncertainty is introduced in the first derivative of normalized fluorescence intensity due to uncertainty in model parameters. For example, in absence of sample antigen, Fig. 5 shows that the point of local minima in the derivative of normalized fluorescence signal has almost four-fold higher uncertainty than that in the model parameters, whereas the normalized fluorescence intensity at the center has relatively low uncertainty as shown in Fig. 3(d). This suggests that using the centerline fluorescence intensity as opposed to the difference in local extrema values of first derivative in normalized fluorescence intensity for calibration would result in lower overall uncertainty.
To quantify the uncertainty in the calibration technique proposed by Hatch et al.,7 we calculate the standard deviations in the difference in local extrema values of first derivative of normalized fluorescence intensity for various sample antigen concentrations. We denote the points of local minima (depletion) and maxima (accumulation) with D and A, respectively, and the standard deviation in the difference in local extrema values with σDA. To compute σDA, we replace the PC coefficients in Equation (16) with the coefficients for PC expansion of the difference in first derivative of normalized fluorescence intensity at points D and A.
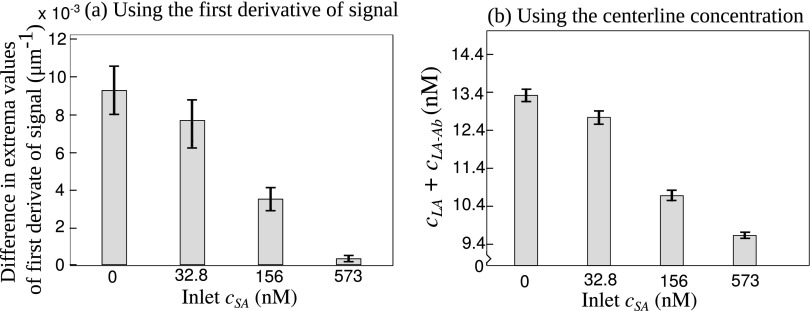
Fig. 6(a) shows the variation in difference in local extrema values of first derivative along with uncertainty bars for four values of sample antigen concentrations. The coefficient of variation for these four cases ranges from 4.7% for to 17.5% for . Clearly, such high degree of uncertainty in the system response will induce equally high inaccuracy in the prediction of sample antigen concentration. We note that the uncertainty bars for the cases with cSA = 0 nM and 32.8 nM significantly overlap, indicating that the minimum value of sample antigen concentration that can be unambiguously and accurately quantified (the limit of detection) is appreciably higher than 32.8 nM. Moreover, relatively high uncertainty for all sample antigen concentrations leads to reduced detection resolution. Therefore, using the difference in extrema values of first derivative of normalized fluorescence intensity as a response of the system to generate the calibration curve is not preferable.
FIG. 6.
Comparison of uncertainties induced in system response between two methods for quantifying sample antigen concentration in T-sensor based diffusion immunoassay: (a) using the difference between values of extrema in first derivative of normalized fluorescence intensity and (b) using centerline fluorescence intensity (or concentration of labeled molecules). (a) Since the uncertainty is high at the locations of extrema in first derivative of intensity, the uncertainty bars are large. The overlapping uncertainty bars indicate low detection sensitivity and resolution. (b) Using centerline fluorescence intensity (or concentration) as the response signal leads to reduced uncertainty, which improves detection sensitivity and resolution.
On the other hand, as shown in Figs. 3(d), 4(a), and 4(b), the uncertainty in concentration of labeled molecules near the center of T-sensor is minimum. In Fig. 6(b) we compare these central concentration values along with their associated uncertainty for four values of sample antigen concentrations. The minimum and maximum coefficient of variations are 0.1% and 0.4% for cases with cSA = 573 nM and 32.8 nM, respectively. As opposed to the case shown in Fig. 6(a), here the uncertainty bars for cSA = 0 nM and 32.8 nM do not overlap. Hence, for a T-sensor based competitive diffusion immunoassay using the centerline concentration for generating the response signal improves the detection sensitivity. Moreover, lower uncertainty for all sample antigen concentrations compared with the calibration scheme involving the first derivative of signal results in better detection resolution.
V. CONCLUSIONS
We have quantified uncertainty in modeling predictions of a T-sensor based competitive diffusion immunoassay due to the uncertainty in parameters of the mathematical model. In particular, we considered individual and coupled effects of uncertainty in species diffusivities, binding reaction rates, and inlet flow speed on spatial distribution of uncertainty in predicted concentrations. To quantify uncertainty, we modeled the dependence of solution variables (species concentrations) on stochastic dimensions associated with uncertain model parameters using PC expansions. We then evaluated the coefficients of the PC expansions using Smolyak sparse grid quadrature, which essentially involved a series of deterministic simulations for different realizations of uncertain model parameters.
Our simulations of T-sensor based competitive immunoassay show that the uncertainty in diffusivity of fluorescently labeled analyte has the maximum contribution to the overall uncertainty in predicted fluorescence signal. In practice, the uncertainty in species diffusivities can arise from even small temperature fluctuations. Therefore, our analysis suggests that precise temperature control during T-sensor operation can lead to significant reduction in uncertainty. Our simulations also show that, for all sample antigen concentrations, the uncertainty in fluorescence signal is minimum near the centerline of T-sensor, whereas high uncertainty prevails in the regions with large gradients in fluorescence intensity. Therefore, using the extreme values of first derivative of fluorescence intensity profile for quantification of antigen concentration leads to higher uncertainty, thereby reducing the detection sensitivity and resolution. On the other hand, using centerline fluorescence intensity as the system response yields reduced uncertainty, and hence higher detection sensitivity and resolution. Our simulations results are therefore directly applicable for practical T-sensor based assays wherein quantitative analysis is performed by comparing experimental data with simulation results.
Although the current work is specific to T-sensor based diffusion immunoassay, the non-intrusive stochastic uncertainty quantification methodology presented here is equally applicable for analyzing other microfluidic systems. Since the method involves a series of deterministic simulations, uncertainty propagation in microfluidic systems can be performed by post-processing simulation data obtained from existing simulation tools. Such analysis would ensure proper comparison of experimental and simulation data. Moreover, PC expansion based uncertainty quantification can elucidate the individual and coupled effects of uncertainty in model parameters to the predicted overall uncertainty.
References
- 1. Whitesides G. M., Nature 442, 368 (2006). 10.1038/nature05058 [DOI] [PubMed] [Google Scholar]
- 2. Dittrich P. S. and Manz A., Nat. Rev. Drug Discovery 5, 210 (2006). 10.1038/nrd1985 [DOI] [PubMed] [Google Scholar]
- 3. Squires T. M. and Quake S. R., Rev. Mod. Phys. 77, 977 (2005). 10.1103/RevModPhys.77.977 [DOI] [Google Scholar]
- 4. Kamholz A. E., Weigl B. H., Finlayson B. A., and Yager P., Anal. Chem. 71, 5340 (1999). 10.1021/ac990504j [DOI] [PubMed] [Google Scholar]
- 5. Weigl B. H. and Yager P., Science 283, 346 (1999). 10.1126/science.283.5400.346 [DOI] [Google Scholar]
- 6. Kamholz A. E., Schilling E. A., and Yager P., Biophys. J. 80, 1967 (2001). 10.1016/S0006-3495(01)76166-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Hatch A., Kamholz A. E., Hawkins K. R., Munson M. S., Schilling E. A., Weigl B. H., and Yager P., Nat. Biotechnol. 19, 461 (2001). 10.1038/88135 [DOI] [PubMed] [Google Scholar]
- 8. Osborn J. L., Lutz B., Fu E., Kauffman P., Stevens D. Y., and Yager P., Lab Chip 10, 2659 (2010). 10.1039/c004821f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Darling R. B., Yager P., Weigl B., Kriebel J., and Mayes K., in Micro Total Analysis Systems'98 ( Springer, Banff, Canada, 1998), pp. 105–108. [Google Scholar]
- 10. Tarn M. D., Lopez-Martinez M. J., and Pamme N., Anal. Bioanal. Chem. 406, 139 (2014). 10.1007/s00216-013-7363-6 [DOI] [PubMed] [Google Scholar]
- 11. Robinson T., Valluri P., Kennedy G., Sardini A., Dunsby C., Neil M. A., Baldwin G. S., French P. M., and de Mello A. J., Anal. Chem. 86, 10732 (2014). 10.1021/ac502732s [DOI] [PubMed] [Google Scholar]
- 12. Gervais L., De Rooij N., and Delamarche E., Adv. Mater. 23, H151 (2011). 10.1002/adma.201100464 [DOI] [PubMed] [Google Scholar]
- 13. Kamholz A. E. and Yager P., Biophys. J. 80, 155 (2001). 10.1016/S0006-3495(01)76003-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Maître L. and Knio O. M., Spectral Methods for Uncertainty Quantification ( Springer, 2010). [Google Scholar]
- 15. Wiener N., Amer. J. Math. 60, 897 (1938). 10.2307/2371268 [DOI] [Google Scholar]
- 16. Xiu D. and Karniadakis G. E., SIAM J. Sci. Comput. 24, 619 (2002). 10.1137/S1064827501387826 [DOI] [Google Scholar]
- 17. Reagan M. T., Najm H. N., Ghanem R. G., and Knio O. M., Combust. Flame 132, 545 (2003). 10.1016/S0010-2180(02)00503-5 [DOI] [Google Scholar]
- 18. Xiu D. and Karniadakis G. E., J. Comput. Phys. 187, 137 (2003). 10.1016/S0021-9991(03)00092-5 [DOI] [Google Scholar]
- 19. Debusschere B. J., Najm H. N., Matta A., Knio O. M., Ghanem R. G., and Le Maître O. P., Phys. Fluids 15, 2238 (2003). 10.1063/1.1582857 [DOI] [Google Scholar]
- 20. Ghanem R. G. and Spanos P. D., J. Eng. Mech. Div., Am. Soc. Civ. Eng. 117, 2351 (1991). 10.1061/(ASCE)0733-9399(1991)117:10(2351) [DOI] [Google Scholar]
- 21. Lin G., Su C., and Karniadakis G., Proc. Natl. Acad. Sci. U. S. A. 101, 15840 (2004). 10.1073/pnas.0405889101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Dodson M. and Parks G. T., J. Aircr. 46, 635 (2009). 10.2514/1.39419 [DOI] [Google Scholar]
- 23. Gleeson J. P., J. Colloid Interface Sci. 249, 217 (2002). 10.1006/jcis.2002.8256 [DOI] [PubMed] [Google Scholar]
- 24. Stone H. A., in CMOS Biotechnology, edited by Lee H., Westervelt R., and Ham D. ( Springer, USA, 2007), pp. 5–30. [Google Scholar]
- 25. Smolyak S. A., Dokl. Akad. Nauk SSSR 4, 240 (1963). [Google Scholar]
- 26. Gerstner T. and Griebel M., Numer. Algorithms 18, 209 (1998). 10.1023/A:1019129717644 [DOI] [Google Scholar]
- 27. Walden P., Ulich H., and B. G., Z. Phys. Chem. 123, 429 (1926). [Google Scholar]
- 28. Lin C.-H., Lee G.-B., Lin Y.-H., and Chang G.-L., J. Micromech. Microeng. 11, 726 (2001). 10.1088/0960-1317/11/6/316 [DOI] [Google Scholar]
- 29. Xu B., Ooti K., Wong N., and Choi W., Int. Commun. Heat Mass Transfer 27, 1165 (2000). 10.1016/S0735-1933(00)00203-7 [DOI] [Google Scholar]
- 30. Koo J. and Kleinstreuer C., J. Micromech. Microeng. 13, 568 (2003). 10.1088/0960-1317/13/5/307 [DOI] [Google Scholar]