Can conclusions drawn from phantom-based image noise assessments be generalized to in vivo studies for the nonlinear model-based iterative reconstruction method?

Abstract

Purpose:

Phantom-based objective image quality assessment methods are widely used in the medical physics community. For a filtered backprojection (FBP) reconstruction-based linear or quasilinear imaging system, the use of this methodology is well justified. Many key image quality metrics acquired with phantom studies can be directly applied to in vivo human subject studies. Recently, a variety of image quality metrics have been investigated for model-based iterative image reconstruction (MBIR) methods and several novel characteristics have been discovered in phantom studies. However, the following question remains unanswered: can certain results obtained from phantom studies be generalized to in vivo animal studies and human subject studies? The purpose of this paper is to address this question.

Methods:

One of the most striking results obtained from phantom studies is a novel power-law relationship between noise variance of MBIR (σ²) and tube current-rotation time product (mAs): σ² ∝ (mAs)^−0.4 [K. Li et al., “Statistical model based iterative reconstruction (MBIR) in clinical CT systems: Experimental assessment of noise performance,” Med. Phys. 41, 041906 (15pp.) (2014)]. To examine whether the same power-law works for in vivo cases, experimental data from two types of in vivo studies were analyzed in this paper. All scans were performed with a 64-slice diagnostic CT scanner (Discovery CT750 HD, GE Healthcare) and reconstructed with both FBP and a MBIR method (Veo, GE Healthcare). An Institutional Animal Care and Use Committee-approved in vivo animal study was performed with an adult swine at six mAs levels (10–290). Additionally, human subject data (a total of 110 subjects) acquired from an IRB-approved clinical trial were analyzed. In this clinical trial, a reduced-mAs scan was performed immediately following the standard mAs scan; the specific mAs used for the two scans varied across human subjects and were determined based on patient size and clinical indications. The measurements of σ² were performed at different mAs by drawing regions-of-interest (ROIs) in the liver and the subcutaneous fat. By applying a linear least-squares regression, the β values in the power-law relationship σ² ∝ (mAs)^−β were measured for the in vivo data and compared with the value found in phantom experiments.

Results:

For the in vivo swine study, an exponent of β = 0.43 was found for MBIR, and the coefficient of determination (R²) for the corresponding least-squares power-law regression was 0.971. As a reference, the β and R² values for FBP were found to be 0.98 and 0.997, respectively, from the same study, which are consistent with the well-known σ² ∝ (mAs)^−1.0 relationship for linear CT systems. For the human subject study, the measured β values for the MBIR images were 0.41 ± 0.12 in the liver and 0.37 ± 0.12 in subcutaneous fat. In comparison, the β values for the FBP images were 1.04 ± 0.10 in the liver and 0.97 ± 0.12 in subcutaneous fat. The β values of MBIR and FBP obtained from the in vivo studies were found to be statistically equivalent to the corresponding β values from the phantom study within an equivalency interval of [ − 0.1, 0.1] (p < 0.05); across MBIR and FBP, the difference in β was statistically significant (p < 0.05).

Conclusions:

Despite the nonlinear nature of the MBIR method, the power-law relationship, σ² ∝ (mAs)^−0.4, found from phantom studies can be applied to in vivo animal and human subject studies.

1. INTRODUCTION

Objective image quality assessments are indispensable in technology development, clinical evaluations, standardization/optimization of scan protocols, and routine quality check of x-ray CT systems. Due to the use of ionizing radiation in CT and other practical considerations, objective image quality assessments of CT are mostly performed using physical phantoms, which are of great stability/reproducibility, and provide the users with the needed ground truth to benchmark the physical characteristics of CT systems. Since conventional CT systems can be approximately treated as linear or quasilinear imaging systems, the use of physical phantoms as human surrogates is justifiable, and conclusions drawn from phantom-based objective image quality assessments are usually assumed to be applicable to clinical CT scans. For example, it has been hypothesized and validated that the modulation transfer function (MTF) measured with a high contrast phantom at a relatively high exposure level is representative of the MTF of clinical CT images acquired at other exposure levels, as long as other system parameters are matched.¹ Another validated assumption is that the noise magnitude of a patient image is approximately the same as that of a tissue-equivalent phantom with the same size, as long as other system parameters are matched.¹ These justified premises allow CT manufacturers to establish a correspondence between patient size and CT noise magnitude using phantoms, which can help the operators to prospectively predict the noise magnitude for each patient and tailor the radiation exposure level accordingly.

The assumption of linearity in CT systems has been violated by several new CT technologies, particularly the model-based iterative reconstruction (MBIR) method.^2–8 Since the introduction of MBIR to commercial diagnostic CT systems, there have been growing numbers of publications reporting its nonlinear image quality characteristics.^9–32

To address the challenges in objective image quality assessments introduced by those nonlinear characteristics, various task-driven methods have been developed and are gradually gaining popularity in clinical practice. The essential idea of these methods is to characterize the performance of CT imaging systems using experimental setups and image tasks that are close to those used in clinical procedures. For example, the CT acquisition parameters, particularly the radiation exposure level, are selected to be consistent with those used in the clinical scan protocol of a specific task. Moreover, the image quality metrics are narrowed down to those that can model the diagnostic task and the psychophysics of human observers who perform the diagnosis. These task-driven methods generally use anthropomorphic or customized phantoms to model the properties of the subjects being scanned for the targeted imaging task. For example, phantoms have been fabricated to include heterogeneous and high frequency structures to assess the performance of MBIR for lung imaging tasks,^12,15 while anthropomorphic abdominal phantoms with irregularly shaped low contrast features have been used to assess the performance of MBIR for liver lesion detection tasks.^21,33 However, it remains unclear whether these phantoms, despite being anthropomorphic, are able to fully characterize the complex and unique features of human anatomy. Therefore, the concept of “task-driven” itself may not guarantee the equivalence of imaging performance between phantom and clinical CT scans; the system nonlinearity dictates that some functional dependence of an output image quality metric on the input scanning parameters may change from one image object to another. Therefore, the answer to the following question is both interesting and important: are some of those functional dependence relationships drawn from phantom studies applicable to in vivo clinical CT exams?

The purpose of this work was to use experimental in vivo data to test the following central hypothesis: Certain conclusions drawn from phantom-based image noise assessments can be generalized to clinical studies for the nonlinear MBIR method.

2. METHODS AND MATERIALS

The target of this paper is to validate whether the following power-law relationship reported in phantom studies:^20,21

$${\displaystyle {\sigma }^2=\alpha {\left(\mathrm{mAs}\right)}^{-\beta },}$$ (1)

can be generalized to in vivo animal and human subject studies with similar β values. Here, α and β are two parameters of the power-law, σ² denotes the CT noise variance, mAs denotes the product of tube current and time per tube rotation (in seconds). If tube current modulation is used, milliampere is given by the effective (average) tube current per gantry rotation. This information is provided in the DICOM header of CT images. An index of β = 0.4 was found for MBIR in previous phantom studies.²⁰ In this work, the β index in Eq. (1) was measured through both an in vivo animal study and a prospective human subject trial. All CT data were acquired using the same clinical scanner (Discovery CT750HD, GE Healthcare, Waukesha, WI). For each CT data acquisition, both FBP (with the standard kernel) and MBIR (Veo™, GE Healthcare, Waukesha, WI) reconstructions were performed.

2.A. In vivo animal study

An animal study was performed with approval from the Institutional Animal Care and Use Committee. A 120-pound, 4-month-old female swine with an effective body diameter of 24 cm was scanned; an intravenous contrast injection was performed with a 50 ml bolus of Isovue-370 (Bracco Diagnostics Inc., Princeton, NJ) with an injection rate of 3 ml/s. A total of six consecutive scans were performed at six different mAs levels (10, 20, 40, 80, 150, and 290 mAs) 40 min after contrast injection. At such a late postinjection stage, the contrast concentration in the swine was almost constant over time. Based on the body size of the swine and the contrast-enhanced nature of the exam, the following acquisition parameters were used for all six scans: tube potential = 80 kV, beam collimation = 40 mm, “Medium Body” scan field of view (SFOV), helical pitch = 0.516, and rotation time = 0.5 s. The reconstruction display field of view (DFOV) was 40 cm. The CTDI_vol values corresponding to the six scans were 0.47, 0.97, 1.91, 3.90, 7.67, and 14.79 mGy, respectively. At each mAs level, the noise variance, σ², was measured in both MBIR and FBP images by drawing a 30 × 30 mm² region of interest (ROI) in the liver of the swine.

2.B. In vivo human subject study

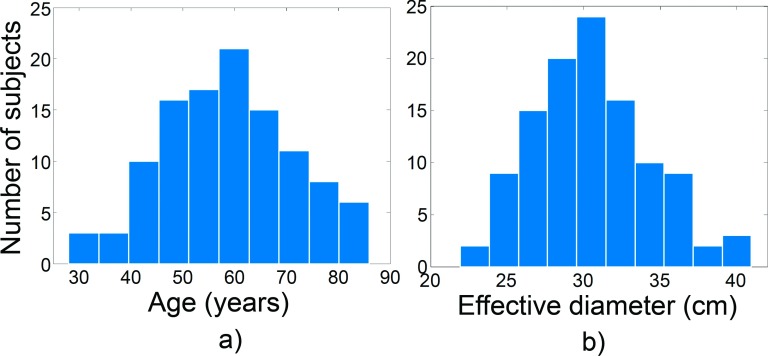
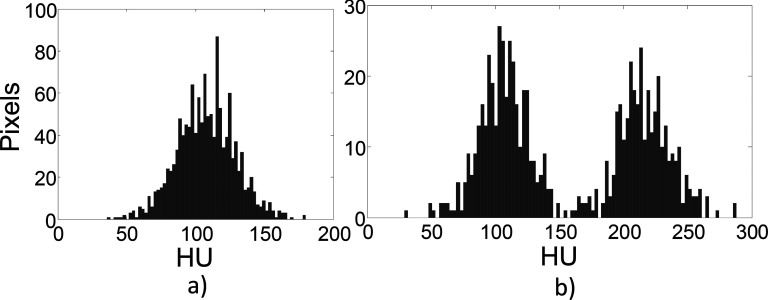
The prospective low dose human subject trial was HIPAA compliant and IRB approved. With written consent from the subjects, a total of 110 subjects (59 females and 51 males) were recruited in this study from April 2011 through January 2015. The mean and standard deviation (SD) of the age of the cohort were 59 and 13 yr, respectively [Fig. 1(a)]. The mean and SD of the body effective diameters of the subjects at the scanned sections were 30 and 4 cm, respectively [Fig. 1(b)]. The effective diameter was calculated as $\sqrt{\mathrm{AP}\times \mathrm{LAT}}$, where AP and LAT are the anterior–posterior and lateral distances, respectively. Each subject first received a routine dose chest/abdomen/pelvis or abdomen/pelvis CT scan; immediately after that, a reduced dose abdomen/pelvis scan was performed. The percent dose reduction varied across subjects and ranged from 40% to 90%. The dose reductions were achieved by lowering the tube current (mA); all other scan parameters, including the kV, SFOV, helical pitch, and rotation time, were matched between the routine and reduced dose scans for a given subject. Across subjects, however, the scan parameters varied based on the clinical indications, imaging tasks, and subject sizes. Both FBP (standard kernel) and MBIR (Veo) reconstructions were performed. For each subject and each image series, two ROIs were drawn, one in the liver and one in subcutaneous fat. To exclude those ROIs dominated by anatomical variation rather than stochastic noise, the histogram of the pixel values (HU) of each ROI was reviewed (Fig. 2). If the histogram of a ROI demonstrated more than one significant local maxima [Fig. 2(b)], or if it was significantly deviated from the normal distribution (skewness or kurtosis outside of [ − 3,  3] and [0,  6], respectively), the ROI was redrawn and the review process was repeated. After finding the appropriate ROIs for each human subject, the noise variance (σ²) was measured in both the routine and reduced dose image series for both the MBIR and FBP methods.

FIG. 1.

The distribution of age (a) and body effective diameter (b) of the 110 human subjects enrolled in this study.

FIG. 2.

Examples of the ROI selection criteria. (a): Accepted. (b) Rejected (contaminated by anatomical structures).

2.C. Statistical data analysis

For each reconstruction method and each subject, the measured σ² values were plotted as a function of mAs and then fitted to the power-law model of σ² ∝ (mAs)^−β using a least-squares regression. For the animal study, since there was only one sample, the β values measured in the in vivo data and phantom data²⁰ were directly compared without performing any statistical analysis. For the human subject study, the following statistical analyses were performed.

Test 1: For each reconstruction method, a two one-sided test (TOST) was used to determine whether the β value measured from the human subjects was statistically equivalent to that from the phantom. This method consists of testing the following null hypothesis

$${\displaystyle {\mathit{H}}_0:|{\overline{\beta }}_{\mathrm{human}}-{\beta }_{\mathrm{phantom}}|>\delta ,}$$ (2)

where δ (=0.1 in this paper) is a numerical parameter that determines the equivalence interval [ − δ, δ] ; the criteria used to select this parameter followed the guidelines described in Ref. 34. The parameter ${\overline{\beta }}_{\mathrm{human}}$ denotes the mean value of the measured β across the 110 human subjects. The value of β_phantom is 0.4 for MBIR and 1.0 for FBP, respectively. By rejecting this joint hypothesis, we can conclude that $|{\overline{\beta }}_{\mathrm{human}}-{\beta }_{\mathrm{phantom}}|\le \delta$, or the difference in β values between the human subject and phantom is within the specified equivalence interval δ.

Test 2: To test statistical equivalency between the β value measured in the liver and that in fat, the following TOST with δ = 0.1 was performed:

$${\displaystyle {\mathit{H}}_0:|{\overline{\beta }}_{\mathrm{liver}}-{\overline{\beta }}_{\mathrm{fat}}|>\delta .}$$ (3)

Test 3: To test whether there was a significant statistical difference between the β value measured in MBIR and that in FBP, a two-sided t-test with the following null hypothesis was performed:

$${\displaystyle {\mathit{H}}_0:{\overline{\beta }}_{\mathrm{MBIR}}-{\overline{\beta }}_{\mathrm{FBP}}=0.}$$ (4)

By rejecting this hypothesis, we conclude that the β values measured in MBIR and FBP are significantly different from each other.

3. RESULTS

3.A. In vivo animal study

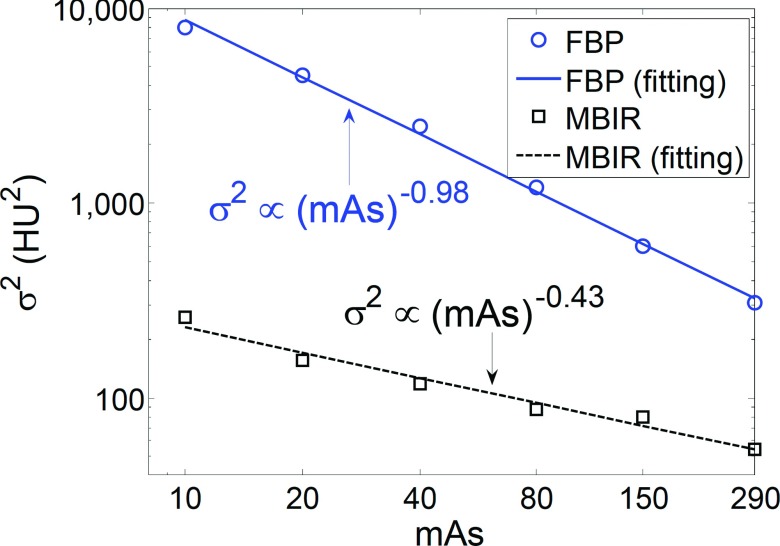
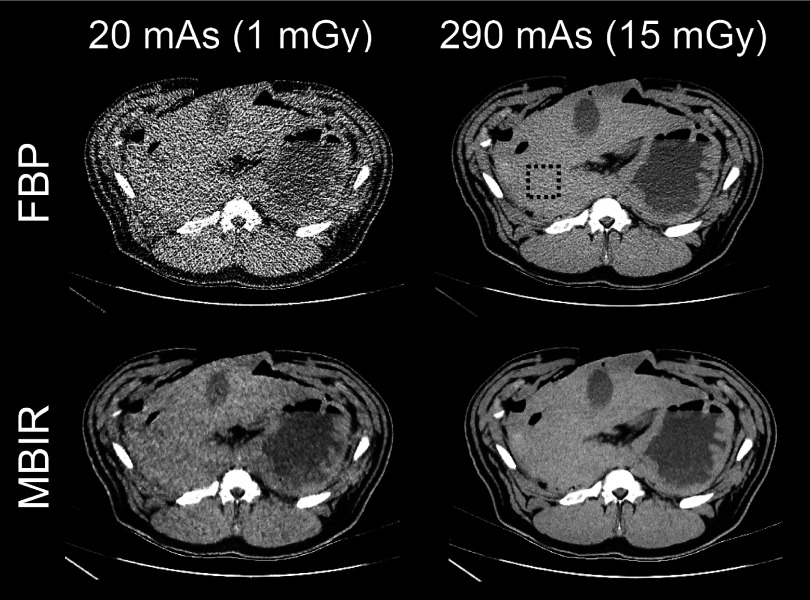
Results of the swine study are shown in Fig. 3. The β exponents of the power-law fitting, were measured to be 0.43 and 0.98 for MBIR and FBP, respectively, which were qualitatively consistent with those measured from the phantom studies.²⁰ The R² values for the power-law fittings were 0.971 and 0.997 for MBIR and FBP, respectively. Representative CT images of the swine and the ROIs used in the measurements are presented in Fig. 4.

FIG. 3.

Log–log plot of the noise variance (σ²) of the swine as a function of mAs.

FIG. 4.

Representative FBP and MBIR images of the swine. The dashed square illustrates the position of the ROI used for the noise measurements.

3.B. In vivo human subject study

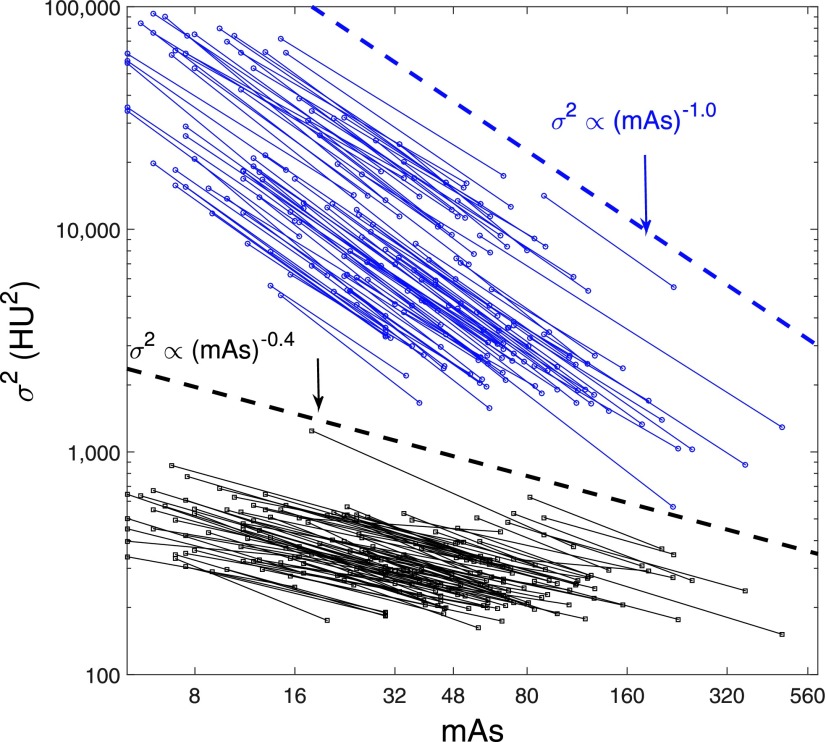
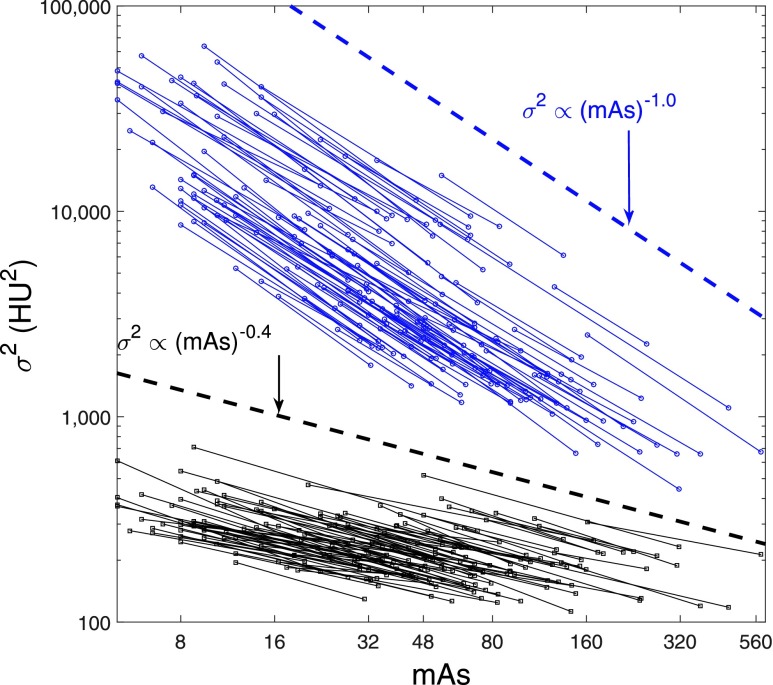
The measured σ² values for the 110 human subjects were plotted against mAs using a double-logarithmic scale in Fig. 5 (liver) and Fig. 6 (fat). The σ² values of MBIR were consistently lower than those of FBP. For a given reconstruction method, the σ²-mAs curves demonstrated similar slopes, or equivalently, similar β values in the σ² ∝ (mAs)^−β power-law. To benchmark the slopes of these curves, two reference lines of σ² ∝ (mAs)^−1.0 and σ² ∝ (mAs)^−0.4 were added to Figs. 5 and 6, which helped to demonstrate that β of MBIR was close to 0.4 and β of FBP was close to 1.0. The β values measured for the 110 subjects were pooled to generate the box–whisker plots in Fig. 7. For MBIR, the mean ± SD (standard deviation) of β is 0.41 ± 0.12 (liver ROI) or 0.37 ± 0.12 (fat ROI). For FBP, the mean ± SD of β is 1.04 ± 0.10 (liver ROI) or 0.97 ± 0.12 (fat ROI).

FIG. 5.

Noise variance of liver images as a function of mAs. The plots are displayed using a double-logarithm scale, with each line representing one subject. The dashed lines correspond to reference lines with specific slope for FBP and MBIR: σ² ∝ (mAs)^−1.0 and σ² ∝ (mAs)^−0.4.

FIG. 6.

Noise variance of fat images as a function of mAs. The plots are displayed using a double-logarithm scale, with each line representing one subject. The dashed lines correspond to reference lines with specific slope for FBP and MBIR: σ² ∝ (mAs)^−1.0 and σ² ∝ (mAs)^−0.4.

FIG. 7.

Box–whisker plots of the β values obtained for liver and fat tissues with FBP and MBIR. The central mark is the median, the edges of the box are the 25th and 75th percentiles and the whiskers extend to the lower and upper extremes of the data.

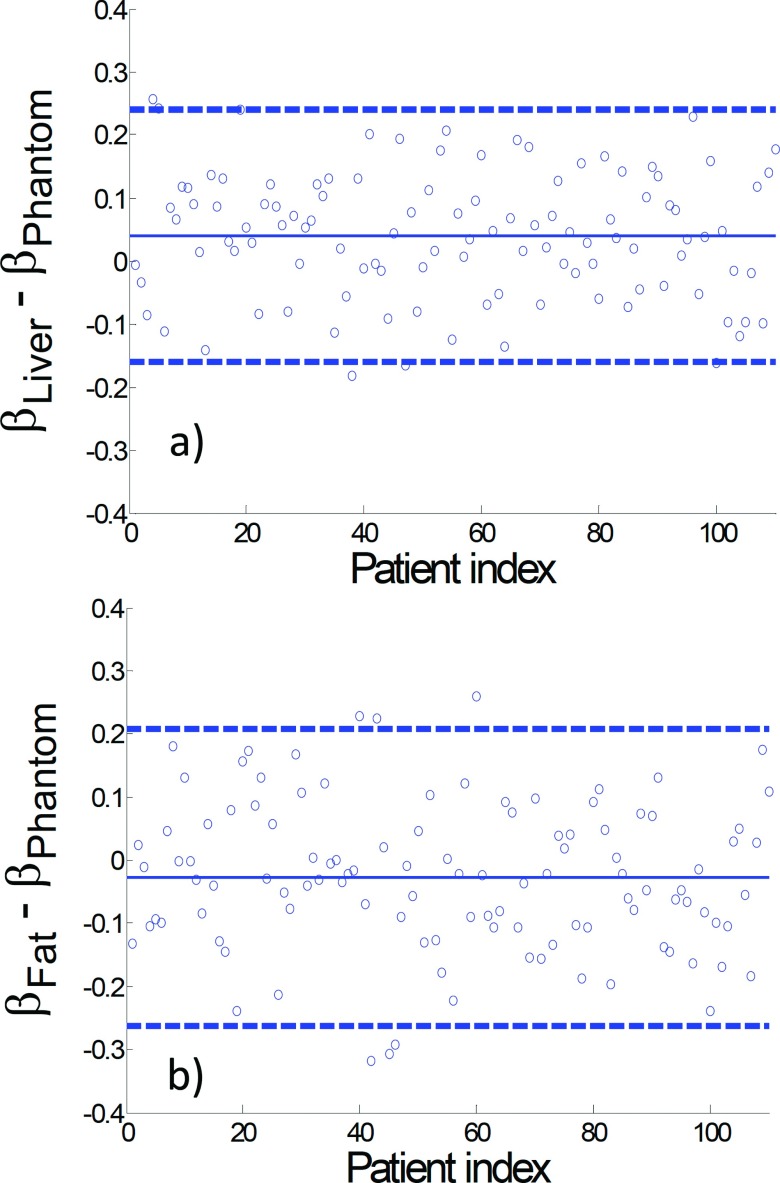
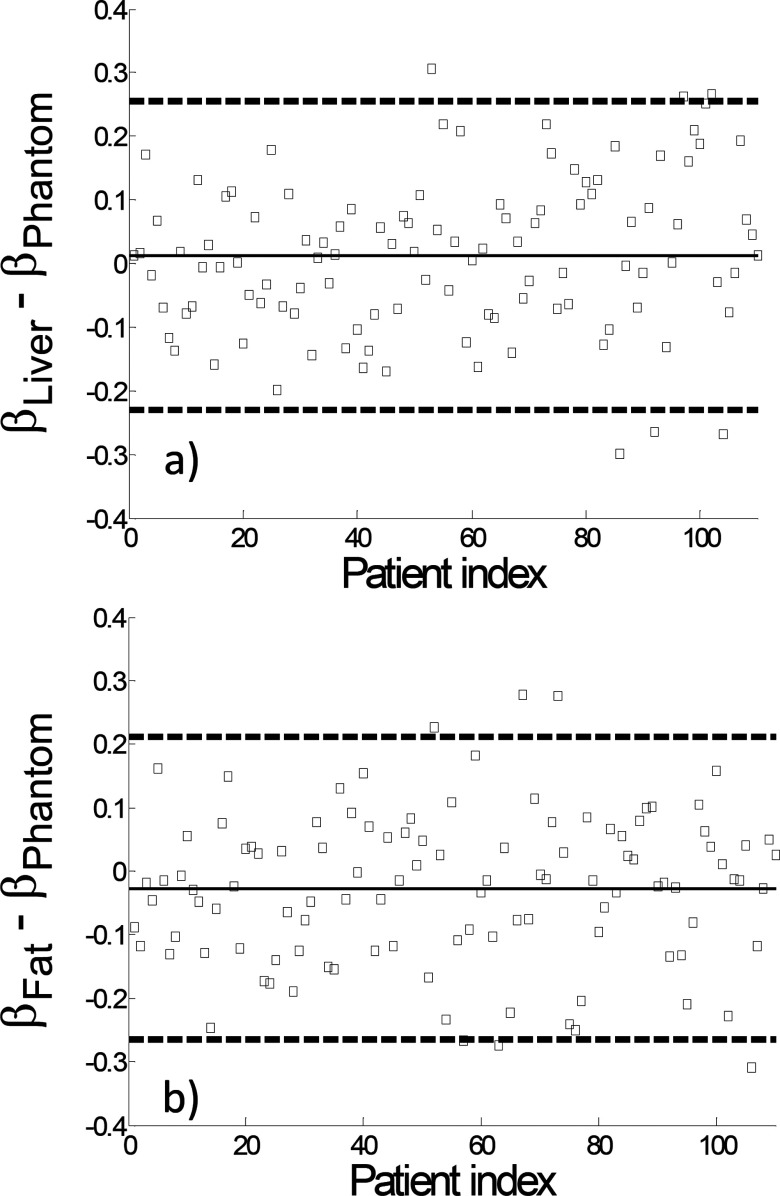
For both MBIR and FBP, results of the statistical Test 1 confirmed statistical equivalency between the β value of human and the β value of phantom (p < 0.05). The difference plots in Figs. 8 and 9 illustrate how much the human β values deviated from the phantom β values. Similarly, results from the statistical Test 2 demonstrated statistical equivalency between β of liver and β of fat for each reconstruction method (p < 0.05). Results from the statistical Test 3 led to the rejection of the hypothesis described in Eq. (4) for both of the liver and fat ROIs, meaning that there was a statistically significant difference between the β of FBP and the β of MBIR (p < 0.05).

FIG. 8.

Plots of the difference in β between the human subjects and phantom for FBP reconstructions. The dashed lines correspond to ±2 × SD (standard deviations) of the difference measurements while the solid line corresponds to the mean value.

FIG. 9.

Plots of the difference in β between the human subjects and phantom for MBIR reconstructions. The dashed lines correspond to ±2 × SD (standard deviations) of the difference measurements while the solid line corresponds to the mean value.

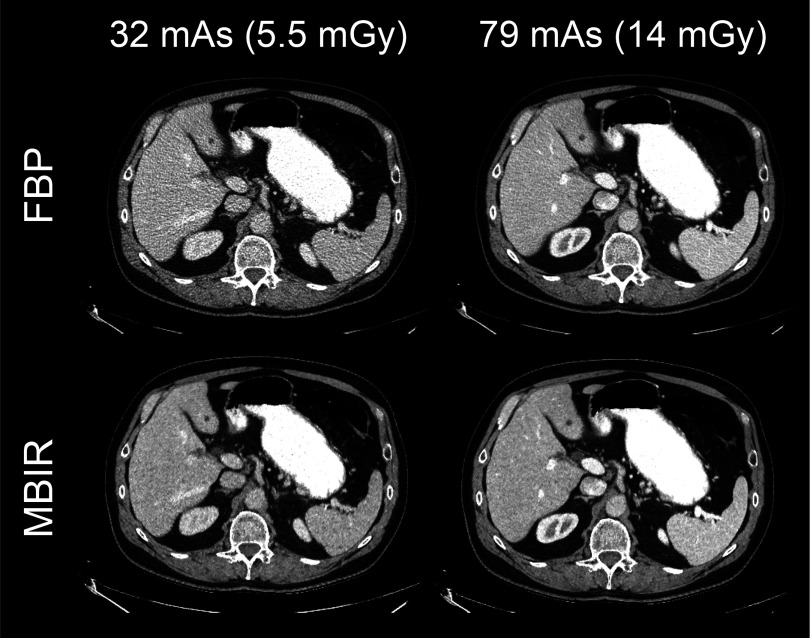
Example CT images of a human subject are shown in Fig. 10. For FBP, the image acquired at the reduced mAs was considerably noisier than the one acquired at the routine mAs; for MBIR, the noisiness of the two images acquired at the two different mAs levels was very similar, which confirmed the relatively relaxed dependence of the noise magnitude on mAs in MBIR.

FIG. 10.

FBP and MBIR images of a human subject acquired at a routine dose level and a reduced dose level.

4. DISCUSSION

Results of this work have demonstrated that the exponent, β, of the power-law relationship σ² = α(mAs)^−β observed in phantom studies can be generalized to in vivo animal and human subjects, which usually present much more complex anatomical and physiological variations. As one of the practical applications of this power-law relationship, the noise magnitude of MBIR images acquired at any mAs level can be estimated from the MBIR images acquired at a routine mAs level [denoted by (mAs)₀] using

$${\displaystyle {\sigma }^2={\sigma }_0^2{\left[\frac{\mathrm{mAs}}{{\left(\mathrm{mAs}\right)}_0}\right]}^{-\beta },}$$ (5)

where ${\sigma }_0^2$ denotes the noise variance of the routine dose images. Since the routine dose MBIR images of a given subject can be retrospectively reconstructed, the relationship in Eq. (5) could potentially be used to prospectively predict the noise magnitude of MBIR image acquired at reduced radiation dose levels before actually conducting the low dose trial. For certain clinical CT imaging tasks such as the detection of low contrast lesions, a priori knowledge about the noise magnitude of the image at any reduced mAs level could aid the judicious selection of the radiation dose reduction factor to achieve the desired diagnostic imaging performance.

Despite the aforementioned application, it is important to recognize that the development of low dose protocols for MBIR requires other measures of image quality, which is described only partially by noise variance. It has been demonstrated in several studies that MBIR introduces correlation between noise texture and mAs, which are mutually independent on each other in conventional linear CT systems.^{9,17,19,20,35} Similarly, spatial resolution has been found to be dependent on mAs,^10,18,19,22 which is rarely observed in linear CT systems. These nonlinear characteristics may confound the selection of the lowest mAs to achieve the desired image quality. Nevertheless, noise magnitude is still an important indicator of diagnostic imaging performance, especially for low contrast detection tasks.

In this work, a fixed slice thickness of 0.625 mm was used; however, a detailed analysis of the noise-mAs power-law relationship at a variety of other slice thicknesses has been performed in our previous phantom-based studies.²⁰ Based on the results of this work, it is likely that these power-law relationships at other slice thicknesses can also be generalized from phantoms to in vivo data, but this is subject to further validation in future work.

The measurement of noise variance in the human subjects was restricted to relatively uniform regions such as the liver and fat. Stochastic noise in nonuniform regions has been shown to behave differently in MBIR,²⁰ but measuring it in human subjects is difficult because of the presence of strong anatomical variations. In future work, we will explore the option of performing repeated scans and image subtractions to measure noise in nonuniform regions using in vivo animal models.

Due to the nonlinearity of the MBIR algorithm and the proprietary nature of various commercial implementation methods of MBIR, it remains unclear why the noise of MBIR images follows the power-law. In comparison, the question of “why can phantom results be generalized to in vivo data” can be answered as follows: The ROIs used in the phantom study in Ref. 20 and the in vivo studies in this work were all selected in regions with uniform tissue. Since the noise penalty term used in the objective function of MBIR is a function of the relative contrast between adjacent pixels rather than the absolute pixel values, the dependence of the noise penalty term on tissue type should be negligible, as long as the region is uniform. For these ROIs, the noise penalty term depends primarily on the noise magnitude of the projection data, which is directly determined by mAs. Therefore, it is very likely that those ROIs, no matter whether in phantoms or in human subjects, were processed by the same sets of regularization parameters. In comparison, if the ROIs in the subjects had been selected from regions with abrupt contrast changes, they would have generated results that deviated from those measured from uniform QA phantoms.^12,15

Note that how to determine the prefactor, α, in Eq. (1) is a more complex problem. Previous publications have demonstrated that α of the MBIR depends on patient size.^17,20 It is well known that in conventional linear CT systems, α also depends on other acquisition parameters (e.g., bowtie filter, beam collimation, helical pitch) and reconstruction parameters (e.g., pixel size, slice thickness).³⁶ How to quantitatively determine α from patient size and system parameters is a subject of our future work. Nevertheless, the power-law model and the β parameter itself, as demonstrated in Eq. (5), serve the need of prospective noise estimation in MBIR, as long as the routine dose MBIR image is available.

5. CONCLUSION

Despite the nonlinear nature of the MBIR method, it is still possible to generalize certain conclusions drawn from phantom-based objective image quality assessments to clinical cases. For example, the power-law relationship between noise variance and mAs found in phantom experiments was demonstrated to be applicable to relatively uniform regions from in vivo data, which potentially enables the prospective estimation of noise variance at a reduced dose level based on the images acquired at the routine dose level. This would be potentially helpful during the development of low dose CT protocols for MBIR, where a priori knowledge about the image quality at reduced dose level could significantly facilitate the protocol optimization process.