Computational model of polarized actin cables and cytokinetic actin ring formation in budding yeast

Abstract

The budding yeast actin cables and contractile ring are important for polarized growth and division, revealing basic aspects of cytoskeletal function. To study these formin-nucleated structures, we built a 3D computational model with actin filaments represented as beads connected by springs. Polymerization by formins at the bud tip and bud neck, crosslinking, severing, and myosin pulling, are included. Parameter values were estimated from prior experiments. The model generates actin cable structures and dynamics similar to those of wild type and formin deletion mutant cells. Simulations with increased polymerization rate result in long, wavy cables. Simulated pulling by type V myosin stretches actin cables. Increasing the affinity of actin filaments for the bud neck together with reduced myosin V pulling promotes the formation of a bundle of antiparallel filaments at the bud neck, which we suggest as a model for the assembly of actin filaments to the contractile ring.

Introduction

The actin cytoskeleton of budding yeast assembles into three distinct structures: actin patches, actin cables, and contractile rings [Amberg 1998; Bi and Park 2012; Moseley and Goode 2006] (Figure 1A). These actin structures contribute to the polarized growth of the bud and its separation from the mother cell. They have been studied extensively experimentally to probe fundamental aspects of polarized growth and division, including mechanistic aspects of the actin cytoskeleton. The actin patches are dense networks of branched actin filaments nucleated by the Arp2/3 complex that assemble at sites of endocytosis and are enriched at the growing bud [Bi and Park 2012; Moseley and Goode 2006]. Actin cables are long bundles of crosslinked actin filaments that extend from the bud to the mother cell. They serve as tracks for intracellular motor-driven transport of secretory vesicles, organelles, mRNA and regulate spindle alignment [Pruyne et al. 2004b]. The actin cytokinetic ring is a bundle of antiparallel actin filaments that form around the septin ring structure that recruits myosin II and other proteins at the bud neck [Bi and Park 2012; Moseley and Goode 2006]. Both actin cables and actin rings, which are the topic of this paper, are nucleated by the two budding yeast formins Bni1 and Bnr1 [Chesarone et al. 2010; Evangelista et al. 2002; Pruyne et al. 2002; Sagot et al. 2002].

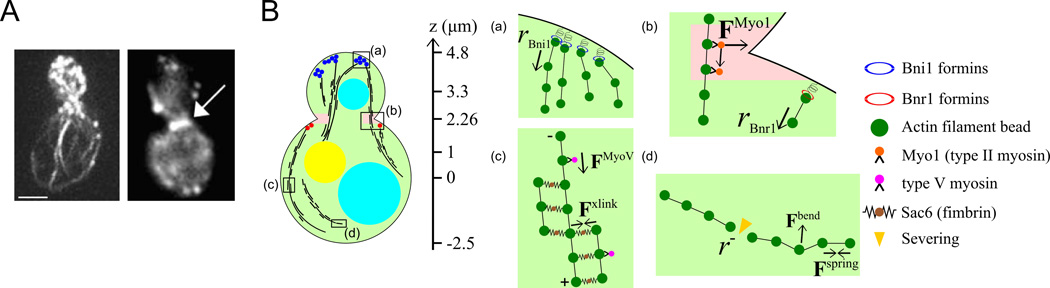
Figure 1. Model description.

(A) Experimental images of phalloidin-stained actin cables (left, reprinted from [Liu et al. 2012]) and cytokinetic ring (right, arrow, reprinted from [Tolliday et al. 2002] with permission from Elsevier) in budding yeast. Scale bar: 2 µm (B) A schematic diagram shows the geometric shape we use for budding yeast, with one sphere centered at (0,0,3.3) with radius 1.5 µm (bud) and another centered at (0,0,0) with radius 2.5 µm (mother). The two spheres intersect at z = 2.26 µm to form the neck. The two cyan and one yellow spheres represent two vacuoles and the nucleus, respectively. (Right) Schematic of implemented simulation mechanisms. (a) Beads representing Bni1 formins placed at the bud tip (blue) polymerize actin filaments (dark green beads). (b) Within the ring-shaped area around the neck (pink), the filament beads experience forces in both tangential and outward directions, representing binding to Myo1 (orange). At the neck, beads representing Bnr1 formins (red) are placed on the mother cell boundary, right below the neck where they polymerize actin filaments at a faster speed compared to Bni1. (c) Myosin V motors (violet) bind to the actin filaments at a certain rate and exert forces toward the barbed ends. An attractive interaction (brown), representing cross-linking is established when two actin filament beads come close to one another. This interaction depends on the relative orientation of the filaments. (d) Connections between filament beads are severed (yellow) with a rate that depends on the age of the connecting spring, representing age-dependent filament severing by cofilin and cofactors.

While a large amount of experimental work has focused on the study of budding yeast actin cables and contractile rings under the effect of genetic modifications, a clear picture of how molecular interactions lead to cable and ring organization at the cell scale remains a challenge. It has been established that during bud growth Bni1 localizes at the bud tip and Bnr1 at the bud neck [Buttery et al. 2007; Pruyne et al. 2004b]. The actin filaments elongated at these formin sites form bundles, likely via cross-linking proteins that can include fimbrin Sac6, Scp1, Tef1/Tef2, and Abp140 [Adams et al. 1991; Moseley and Goode 2006]. Cofilin, in coordination with other actin filament binding proteins such as coronin and Aip1, causes severing and turnover of actin filaments [Balcer et al. 2003; Iida and Yahara 1999; Moon et al. 1993; Okada et al. 2006]. Type V myosins Myo2 and Myo4 carry cargoes such as secretory vesicles, mitochondria and mRNA; they walk along actin cables towards the barbed end and accumulate at the bud [Hodges et al. 2012; Pruyne et al. 1998; Reck-Peterson et al. 2001]. Myosin passenger protein Smy1 associates with Myo2 and interacts with Bnr1 to decrease the actin filament elongation rate [Chesarone-Cataldo et al. 2011]. Type II myosin Myo1 localizes at the bud neck during both interphase and mitosis and has been reported to affect actin cable retrograde flow rates and ring formation [Bi et al. 1998; Huckaba et al. 2006]. During mitosis, Bni1 joins Bnr1 at the neck where other actin filament binding proteins such as Iqg1/Cyk1 are also recruited to the septin ring at the bud neck [Bi and Park 2012].

To systematically and quantitatively explore how the molecular interactions described in the preceding paragraph contribute to the development of cable and ring morphologies, we developed a coarse-grained 3D computational model. We focus on actin cables during the G2 phase when cables polarize towards the growing bud and are less dynamic compared to unpolarized cells [Yu et al. 2011]. By representing actin filaments as semiflexible polymers that can polymerize, sever, and respond to forces by cross-linking and motor proteins, we quantify different types of actin filament organization and the role of cell geometry. We show that a model based on these mechanisms can generate actin cable structures that resemble those in prior experiments. Quantitative results of the model include experimentally measurable quantities such as actin cable thickness, number of cables per cell, cable curvature, radial distribution, and cable orientation. The model captures the morphology of cables in bnr1Δ and bni1Δ cells. In simulations with increased Bnr1 polymerization rate, long and wavy cables result, consistent with prior observations in smy1Δ cells. We describe the predicted response of cables to changes of motor pulling forces. By varying the interaction between actin filaments and the bud neck, our model shows that actin cables structures can transform into actin rings. These results suggest that tuning of a few key interactions by the cell guides the actin system towards a different morphology in order to perform a different biological function.

We conclude this paper with a comparison to previous 3D models of actin cable and contractile ring formation in fission yeast [Bidone et al. 2014; Tang et al. 2014]. In comparison to those models, the present work includes two important changes: 1) we include explicit severing of filaments into smaller fragments while in the earlier studies turnover was simulated as whole filament removal, and 2) cross-linking interactions have an explicit orientation dependence. The latter is likely to be more important in budding yeast that has the tight cross-linker fimbrin but lacks the more flexible α-actinin.

Model and Methods

Semiflexible polymer model for actin filaments

Actin filaments are simulated using a coarse-grained bead-spring model [Nédélec and Foethke 2007; Tang et al. 2014] (Figure 1B). One bead represents a segment of the helical actin filament. The equilibrium distance between beads is l₀ = 0.1 µm (~37 subunits) connected by springs with a spring constant large enough to resist extensional forces but small enough to allow a large simulation time step ·Δt = 2.5·10⁻⁴ s. Bending deformation and stochastic forces are included. These forces together with the boundary, myosin motor, and crosslinking forces (to be described below) govern motion of the i^th bead through the following equation derived from Langevin dynamics:

$${\mathbf{F}}_i^{\text{spring}}+{\mathbf{F}}_i^{\text{bend}}+{\mathbf{F}}_i^{\text{stoch}}+{\mathbf{F}}_i^{\text{boundary}}+{\mathbf{F}}_i^{\text{crosslink}}+{\mathbf{F}}_i^{\text{motor}}={\zeta }_{\mathrm{b}}\frac{{\text{dr}}_i}{\mathrm{d}t},$$ (1)

where r_i is the 3D position vector and _·ζ_b is an effective drag coefficient of a filament segment in the cytoplasm. The spring, bending and stochastic forces are as follows:

$${\mathbf{F}}_i^{\text{spring}}=-\frac{\partial E^{\text{spring}}}{\partial r_i}=-\frac{k}{2}{\sum }_{j=1}^{N-1}\frac{\partial {(|{\mathbf{r}}_{j+1}-{\mathbf{r}}_j|-l_o)}^2}{\partial {\mathbf{r}}_i},$$

$${\mathbf{F}}_i^{\text{bend}}=-\frac{\partial E^{\text{bend}}}{\partial {\mathbf{r}}_i}=-\frac{k}{l_0}\sum _{j=2}^{N-1}|\frac{\partial ({\mathbf{t}}_j·{\mathbf{t}}_{j-1})}{\partial {\mathbf{r}}_i},$$ (2)

$${\langle {\mathbf{F}}_i^{\text{stoch}}·{\mathbf{F}}_i^{{\text{stoch}}^{\mathrm{T}}}\rangle }_{\alpha ,\beta }=\frac{2k_{\mathrm{B}}T{\zeta }_{\mathrm{b}}}{\mathrm{d}t}{\widehat{I}}_{\alpha ,\beta },$$

where ${\mathbf{t}}_i=\frac{{\mathbf{r}}_{j+1}-{\mathbf{r}}_j}{|{\mathbf{r}}_{j+1}-{\mathbf{r}}_j|}$ is the local unit tangent vector, k = k_BTl_p is the flexural rigidity, k_B is Boltzmann's constant, T is temperature, l_p is the persistence length of the filament and Î_α,β is the second-order unit tensor. This filament model reproduces the correct tangent correlation function, relaxation dynamics and equipartition of energy in thermal equilibrium [Tang et al. 2014].

Formin-mediated actin filament polymerization

Polymerization of actin filaments out of formins associated with the cell membrane is simulated as elongation of the equilibrium length of the segment between the formin and the first filament bead representing the current barbed end. If the elongating segment reaches twice the size of the spring equilibrium length l₀, a new bead is added to the middle of the segment (Figure 1B). Since formins connect to the cortex through flexible FH1 domains, we assumed the filament ends can rotate freely around their attachment point on the membrane. This is represented in the model as a freely-rotating spring connecting the first filament bead to a point on the surface (with spring constant 100 pN/nm). We assume the polymerization rate is a constant. We neglect fluctuations in formin-mediated polymerization rates that may arise from force fluctuations at the filament end [Courtemanche et al. 2013; Jegou et al. 2013]. Actin cables have been measured to extend with a retrograde flow rate of 0.2 – 0.6 µm/s [Huckaba et al. 2006; Yang and Pon 2002] while studies using TIRFM found a large range of cable movements with speeds exceeding 1 µm/s [Chesarone-Cataldo et al. 2011; Yu et al. 2011]. In vitro assays give Bni1 and Bnr1 polymerization rates that vary depending on the concentration of formins, actin, and profilin [Kovar and Pollard 2004; Moseley and Goode 2005]. As reference values in simulations we use the Bnr1 and Bni1 polymerization rates 0.6 ·µm/s and 0.3 µm/s, respectively, taking into account measurements of average cable extension rates that are higher in bni1Δ cells compared to wild type [Chesarone-Cataldo et al. 2011] (though we note that [Yu et al. 2011] provide evidence that Bni1 polymerizes at a faster rate compared to Bnr1).

Bni1 accumulates in clusters at the bud tip and is recruited and activated by polarisome complex containing Spa2, Pea2, and Bud6 [Moseley and Goode 2006]. In our simulations we assume 11 clusters of 6 Bni1 dimers. The clusters are randomly distributed at the top half of the bud sphere. The Bni1 formin sites are randomly distributed within a small area close to the centers of the clusters as in [Tang et al. 2014]. Neck formins Bnr1 are randomly distributed at the cell membrane periphery at 0.1 µm below the neck towards the mother.

Filament turnover

The precise mechanism of actin cable turnover has not been established. A large body of work suggests a significant contribution of filament severing mediated by cofilin, Aip1, coronin, twinfilin, cyclase-associated protein, and tropomyosin [Balcer et al. 2003; Iida and Yahara 1999; Moon et al. 1993; Moseley and Goode 2006; Okada et al. 2006]. As actin filaments are polymerized out of the formin sites, ATP-bound actin subunits are hydrolyzed into ADP-P_i-actin and further release phosphate to convert into ADP-actin. Cofilin binds to the sides of actin filaments, accelerates phosphate release and severs ADP-actin [Blanchoin et al. 2014]. Together these processes are expected to lead to a cooperative, age-dependent severing mechanism. Similar to [Wang and Vavylonis 2008], we use a Hill function to assign different disassembly rates for different segments of the filament:

$$r^{-}(t)=r_{\text{max}}^{-}{t}^n/(t^n+{\tau }_{\text{age}}^n),$$ (3)

where $r_{\text{max}}^{-}$ is the maximum rate of disassembly for fully aged segments, τ_age is the characteristic time of aging and n is a cooperativity coefficient. At every Δt, each segment between two filament beads is tested for severing. Upon severing, the specific segment is removed, generating two shortened filaments.

Filament crosslinking

The cross-linking interaction between actin filaments is simulated as an attractive force between the filament beads that come close to one another. This represents an effective interaction, averaged over multiple cross-links between the corresponding filament segments. Some researchers have suggested that crowding in the cytoplasm may contribute to cytoskeletal bundling [Kulp and Herzfeld 1995]. The attractive interaction between the filaments in our model may be thought to include such effects. Unlike in [Tang et al. 2014] where we used an interaction that only depends on the distance between beads, here we use an orientation-dependent spring potential to represent such force. An attractive spring force is exerted when: 1) the distance between bead i and bead j from a different filament is smaller than crosslinking interaction distance r_c, and 2) when the unit direction vector is nearly perpendicular to the local tangent vectors of the two interacting filaments:

$${\mathbf{F}}_i^{\text{xlink}}=-\frac{k_c}{2}\sum _j\frac{\partial {(|{\mathbf{r}}_i-{\mathbf{r}}_j|-r_0)}^2}{\partial {\mathbf{r}}_i}$$ (4)

for |r_i – r_j| ≤ r_c and U_ij · t_i < 0.5 and U_ij ·t_j < 0.5, where U_ij is the unit vector pointing from bead i to beady, j, t_i and t_j are the local filament tangent unit vectors, r₀ is the equilibrium length and k_c is the corresponding spring constant. This force is stronger when filaments align in parallel or anti-parallel, consistent with the ability of fission-yeast fimbrin to crosslink actin filaments to form compact bundles [Skau et al. 2011] and the lack of α-actinin in budding yeast that would allow for a large range of crosslink angles [Wu et al. 2001]. We used r₀= 12 nm, of order the size of fimbrin [Klein et al. 2004; Volkmann et al. 2001]. We use a crosslinker spring constant k_c in the range 1 – 10 pN/µm, which corresponds to the modulus of fimbrin, 10 – 10² pN/µm² [Klein et al. 2004] (assuming length 0.01 µm, cross-section 10⁻⁴ µm², 10 fimbrin proteins per 0.1 µm segment). We note that fimbrin may be redundant with other crosslinkers [Moseley and Goode 2006] (see Discussion).

Actin filament pulling by myosin motors

We account for the two types of myosin motor proteins, type II and V, that influence actin cable behavior in budding yeast. The only type II myosin in budding yeast, Myo1, localizes around the bud neck during bud growth and cytokinesis [Bi et al. 1998; Huckaba et al. 2006]. To account for the presence of Myo1 at the neck, we assume that filament beads reaching a ring-shaped area around the bud neck experience two forces due to Myo1 (Figure 1A): a pulling force toward the barbed end, ${\mathbf{F}}_{\text{pull}}^{\text{Myo}1}$, as well as an attractive force towards the closest point on the bud neck, ${\mathbf{F}}_{\text{capt}}^{\text{Myo}1}$. The reference value of the magnitude of these two forces, which represents capture and pulling, was 0.5 pN. Since typically two filament beads are within range to the bud neck, this corresponds to total forces 1 pN. Since the simulations do not implement tension-dependent actin filament elongation rates, the retrograde flow rate is not influenced significantly by Myo1 pulling [Huckaba et al. 2006]. To simulate the effects of actin filament binding to proteins bound at the septin ring at the bud neck during contractile actin ring assembly, we add a force of same direction and varying magnitude to ${\mathbf{F}}_{\text{capt}}^{\text{Myo}1}$.

Type V myosins Myo2 and Myo4 bind to the sides of the actin filaments and walk towards the barbed ends carrying secretory vesicles, mitochondria, late Golgi elements or attaching to static vacuoles [Pruyne et al. 2004b; Reck-Peterson et al. 2001]. We approximate the myosin V pulling force F^MyoV as a tangential force on filament beads of magnitude 0.8 pN, which is smaller than the myosin V stall force of 3 pN [Mehta et al. 1999] (Figure 1B). This estimate is calculated by assuming that myosin V opposes the drag force on a carried vesicle, F^MyoV = 6πηrv Here η is the cytoplasmic viscosity (see Table I) and the vesicle radius r = 100 nm as indicated in electron microscopic vesicle images [Klemm et al. 2009]. A value v = 1.4 µm/s is taken from in vitro and live cell experiments, which indicate speeds 1 – 5 µm/s [Hodges et al. 2012; Schott et al. 2002; Sheltzer and Rose 2009]. Since the duration of vesicle movement is of order 0.5 s [Schott et al. 2002], we assume that each filament bead experiences a transient tangential force for 0.5 s, with a probability giving a linear density of myosin V pulling forces ρ_MyoV. We varied ρ_MyoV to simulate the effects of deletion and overexpression of type V myosins.

Table I.

Reference parameter values used in simulations. Parameter values taken from prior experiments (see main text for justification) unless otherwise indicated by a footnote.

Parameter	Description	Value
Shape:
	Volume of the bud	14.14 µm3
	Volume of the mother cell	65.45 µm3
	Volume of the vacuole in the bud	0.9 µm3
	Volume of the vacuole in the mother cell	7.23 µm3
	Diameter of nucleus	1.6 µm
	Neck radius (wide, narrow)	1.08 µm, 0.54 µm
Filament:
T	Temperature	300 K
lp	Persistence length of actin filaments	10 µm
l0	Filament model segment equilibrium lengtha	0.1 µm
k	Spring constant between filament beadsb	100 pN/µm
n	Cytoplasmic viscosity (350 times larger than water)	0.301 pN/µm2·s
τage	Actin filament aging timec	5 s
n	Hill severing function coefficientc	6
$r_{\text{max}}^{-}$	Aged actin filament segment disassembly ratec	0.08 s−1
Formins:
NBni1	Number of active Bni1 forminsd	55
NBnr1	Number of active Bnr1 forminsd	40
rBni1	Bni1 formin polymerization rate	0.3 µm/s
rBnr1	Bnr1 formin polymerization rate	0.6 µm/s
Ncluster	Number of clusters of Bni1 forminsd	11
Crosslinking:
kc	Cross-linking spring constante	4 pN/µm
r0	Cross-linking gap distance	0.012 µm
rc	Cross-linking interaction rangee	0.10 µm
Myosin:
FMyoV	Myosin V walking force	0.8 pN
ρMyoV	Myosin V linear density along filamentf	0.7 µm1
τMyoV	Myosin V average lifetime on actin filament	0.5 s
FMyo1	Myo1 walking and outward pulling force	0.5 pN
rMyo1	Thickness of the Myo1 interaction area around the neckg	0.3 µm
hMyo1	Height of the Myo1 interaction area around the neckg	0.1 µm

^aCoarse-graining length scale in simulations

^bMaintains connectivity of filament beads, chosen small enough to allow large simulation time step.

^cEstimated values that provide an average filament and cable length comparable to experiments, see Equation (3).

^dEstimated values based on anticipated actin cable thickness and measurements of For3 cortical concentration in fission yeast [Martin et al. 2007].

^eThese parameters were varied in Figure 3. The values in the Table are large enough to produce bundles but low enough to avoid excessive cable bending. See also estimate of k_c in main text.

^fEstimated. This parameter was varied in Figure 6.

^gEstimated, comparable to the coarse-graining length scale.

Finally, we include the possibility of filament attraction to the plasma membrane, simulated as an outward force of magnitude F^cortex on the beads closer than 0.4 µm to the mother cell boundary.

Budding yeast shape and excluded volume by vacuoles and nucleus

We took into account the large excluded volume presented by the nucleus and vacuoles. We used numbers for yeast shape and location of the yeast nucleus and vacuoles from electron microscopy images [Bertin et al. 2012; Klionsky et al. 1990; Voeltz and Prinz 2007]. The shape of G2-phase budding yeast is represented by two spheres of radii 2.5 µm and 1.5 µm for the mother and daughter, respectively, intersecting at the neck (Figure 1B). These numbers correspond to the centers of the bud and mother cell volume distribution in [Chan and Marshall 2014]. They are positioned such that the bud neck has a radius of 1 µm. Narrower bud necks that are closer to typical neck radii of order 0.5 µm were also considered. We placed two vacuoles, one in the mother cell and one in the bud, with radii 1.2 µm and 0.6 µm. This gives vacuole to bud volume and mother vacuole to mother volume ratios consistent with the distributions in [Chan and Marshall 2014]. Reflecting boundary conditions are imposed at the boundaries by application of a perpendicular force of magnitude 1 pN to any bead crossing it.

Calculation of cable number, thickness, curvature and filament tension

For our analysis we picked time points after 60 s, a number higher than the characteristic severing time, which is 5 s (Table I) and the free filament relaxation time, which is 4.5 s for a 2-µm-long filament. By 60 s parameters such as number of filament beads, cable thickness and curvature reach a plateau. The longest relaxation time of the system involves slow processes such as whole filament unbundling. For this reason the results after 60 s have a small dependence on initial conditions, such as the initial angle of polymerization. By changing the initial angle of filament polymerization, we checked that the effect is not significant except for cases such as simulated bni1Δ cells that are discussed separately.

Since simulated cables are connected and branched, we measure the cable number and thickness by grouping the points of the cables intersecting the cross-sectional planes at z = 3.3, 2.26, 1, 0, −1 µm (Figure 1B). If the distance between two points is smaller than r_c, the two points form a pair. A group is defined as a collection of points with all and only their corresponding pairs. If a group contains more than 4 points, it qualifies as a cable. The filament curvature is calculated by $\kappa =\left|\frac{\mathrm{\Delta }\mathbf{t}}{\mathrm{\Delta }s}\right|=\left|\frac{\mathbf{t}(s+\mathrm{\Delta }s)-\mathbf{t}(s)}{\mathrm{\Delta }s}\right|$, Δs = 4l₀ and filaments longer than 10 beads. The average filament tension is calculated by averaging all the extension and compression of the Bnr1, Bni1, and free filament segments and multiplying by the spring constant k.

Results

Simulations reproduce actin cable structures

We examined actin cable formation in polarized budding yeast cells during the G2 phase. Simulations successfully reproduced 3D actin cable structures that are similar to those observed in fluorescence microscopy images in terms of cable distribution, number, curvature and orientation (Figure 1A). Table I shows the parameter values used in simulations (for justification of parameter values see also Model and Methods). Actin filaments elongate from the two sites of formin localization at the bud neck and bud: Bnr1 randomly distributed at the neck and Bni1 clusters at the bud tip. The elongating filaments get crosslinked and form bundles (Figure 2A and Movie S1; Bnr1-associated, Bni1-associated and free filaments are in red, blue, gray respectively). The average number of cables in the mother at z = 1 µm of Figure 1B is 5.2, which is close to the count of about 5 in previous experiments on wild type cells [Lipkin 2011]. From different perspectives, the simulated mature actin cable structures are extended and smooth structures on the cell scale (Figure 2B). Actin cables curve and connect at the bottom as a result of the mother cell boundary. As viewed from the top, clustering of Bni1 formins help bundle the actin filaments (Figure 2B). Projection of the actin filaments on a plane generates images resembling those observed in prior experiments (Figure 2C, inverted grayscale with pixel intensity proportional to the number of actin filament segments).

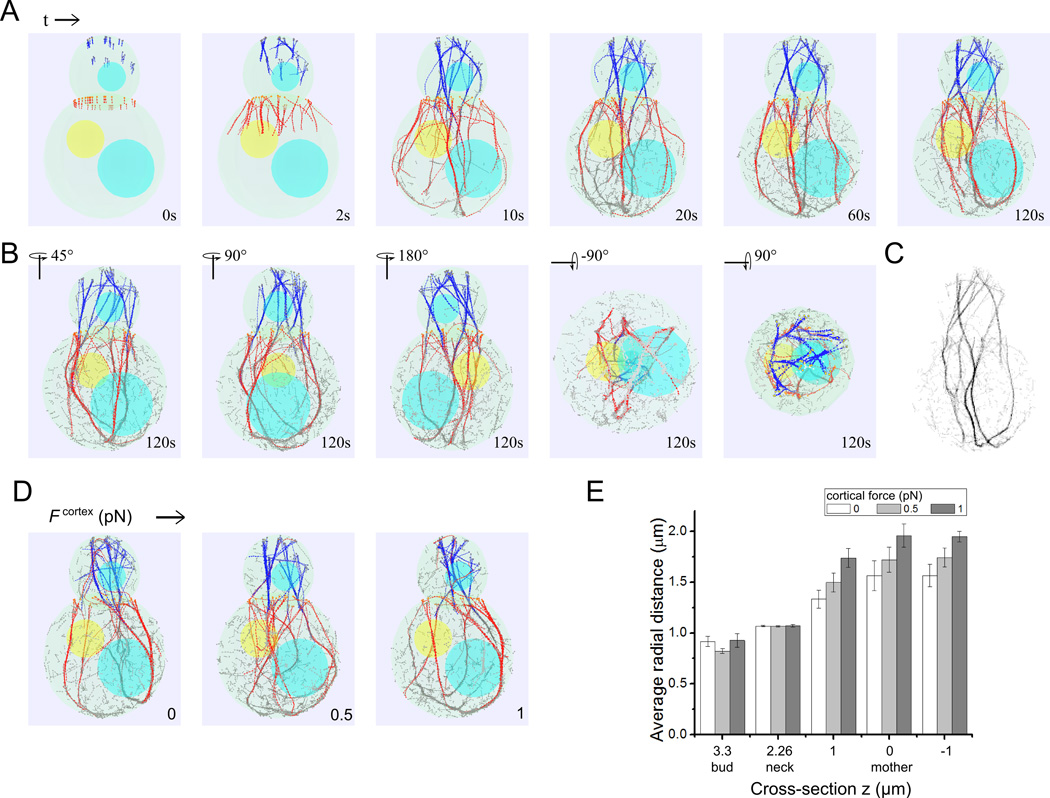
Figure 2. Simulation snapshots showing actin cable formation.

(A) Simulation snapshots using parameters from Table I show the time evolution of actin cable structures and dynamics (see also Movie S1 and 2). Bni1-associacted actin filaments shown in blue, Bnr1-associated filaments in red and severed filament segments in gray. Formin sites shown as circles at the barbed ends of filaments. The nucleus and vacuoles are shown in yellow and blue. (B) Rotated images of simulation at 120s showing a robust 3D actin cable structure. (C) Projection of the simulated actin cable structure on the y-z plane (z is along the mother-bud axis) to compare to fluorescence microscopy images. The image was calculated by assigning to each pixel (of size 0.04 µm) an intensity proportional to the sum of all filament beads with the same y, z coordinate, within a range x values and inverting the final result. (D) Simulation of the effects of a short-range attractive force, F^cortex, between actin filament beads and the mother cell boundary. Simulation snapshots show that increasing F^cortex causes the actin cables in the mother cell to get pulled close to the cell boundary. (E) Graph showing increase of average radial distance of actin filaments with increasing F^cortex.

Prior experiments have shown that the majority of actin cables in the mother cell localize very close to the cell cortex [Amberg 1998; Miao et al. 2013; Yu et al. 2011], a feature that is not captured by the simulations of Figure 2B where many actin cables run through the middle of the mother. Including a short-range attractive interaction between actin filaments and the cell cortex can pull the cables close to the cell membrane (Figure 2D, E). Since type V myosin binds to the cortical endoplasmic reticulum (ER) [Du et al. 2004], our simulations suggest that the pulling action of type V myosin could be sufficient to displace actin cables closer to the cell cortex. An alternative possibility that would require a different model is that actin cables are confined within the narrow space between the cortical ER and the plasma membrane.

The actin cables were robust to changes in the size of the bud and mother size (Figure S1A). Actin cables can also form with bud neck radii 0.5 µm, which is the typical case [Bertin et al. 2012] rather than 1 µm as in Figure 2, see Movie S2. Narrower bud necks generally result in increased bundling of the simulated Bni1 filaments. This effect is increased by the effective additional narrowing when positioning the vacuole close to the neck. Since our model is coarse-grained on the 0.1 µm scale (the distance between filament beads) larger neck diameters are better described by our model. Cables also formed in simulations where the rate of Bnr1 polymerization is slower than that of Bni1 filaments (Figure S1B, where all other parameters are unchanged); in this case the Bnr1-associated filaments are shorter than the Bni1-associated filaments and cables do not reach as close to the bottom. When Bni1 clusters are distributed uniformly around the bud surface rather than just at the bud tip, more Bni1-associated actin filaments remain in the bud (Figure S1C).

In the simulations the main body of actin cables consists of long filaments that are associated with formins while the older segments contain severed filaments. Some severed filament fragments remain as parts of actin cables while the short ones detach and depolymerize completely in the bulk of the simulated cell. We found a weak dependence of cable structure on the cooperativity coefficient n of severing kinetics in Equation (3) (Figure S2), however the aging time τ_age contributes to the length of the cables.

The results of Figure 2 indicate that the minimal set of interactions in our simulations – polymerization, thermal fluctuations, filament mechanical properties, crosslinking, myosin pulling, excluded volume and turnover – were able to represent the major features of the actin cables in budding yeast. These features include cable distribution, number, curvature, and orientation. The simulations included actin filament oligomers that may have a complex role in actin dynamics [Chen and Pollard 2011; Okreglak and Drubin 2010]. The model with whole-filament-turnover and orientation-independent filament bead crosslink mechanism of [Bidone et al. 2014; Tang et al. 2014] can also produce actin cable structures (Figure S3, see Discussion). These simulations thus provide a way for us to pry into the system and study it quantitatively.

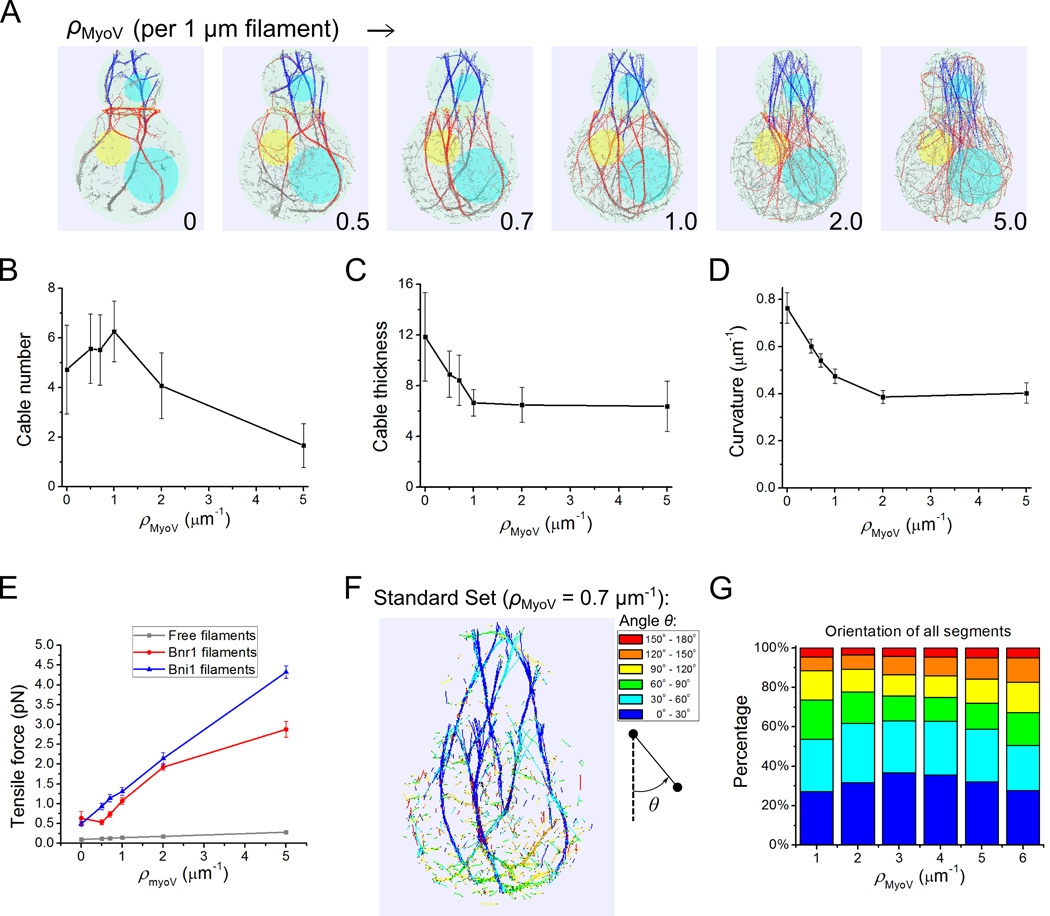
Actin cable formation requires sufficiently high crosslinking interaction strength

In our model two parameters regulate the crosslinking kinetics: r_c and k_c, which represent the cutoff range and depth of the crosslinking interaction potential. These parameters determine the rates of cross-link formation/breakage and reflect the type and concentration of cross-linker proteins in cells. Larger values of these parameters represent stronger cross-linking [Tang et al. 2014]. We explored the crosslinking parameter space and found a clear trend of increased bundling as we increase either r_c or k_c (Figure 3A). The average number of cables exhibits a plateau phase of highly bundled filaments with cable numbers between 4.5 and 5.5 at high r_c and k_c, and an unbundled phase at low r_c and k_c (Figure 3B). The cable thickness increases with r_c (Figure 3C) and is in the range 7 to 10 filaments within the highly bundled phase.

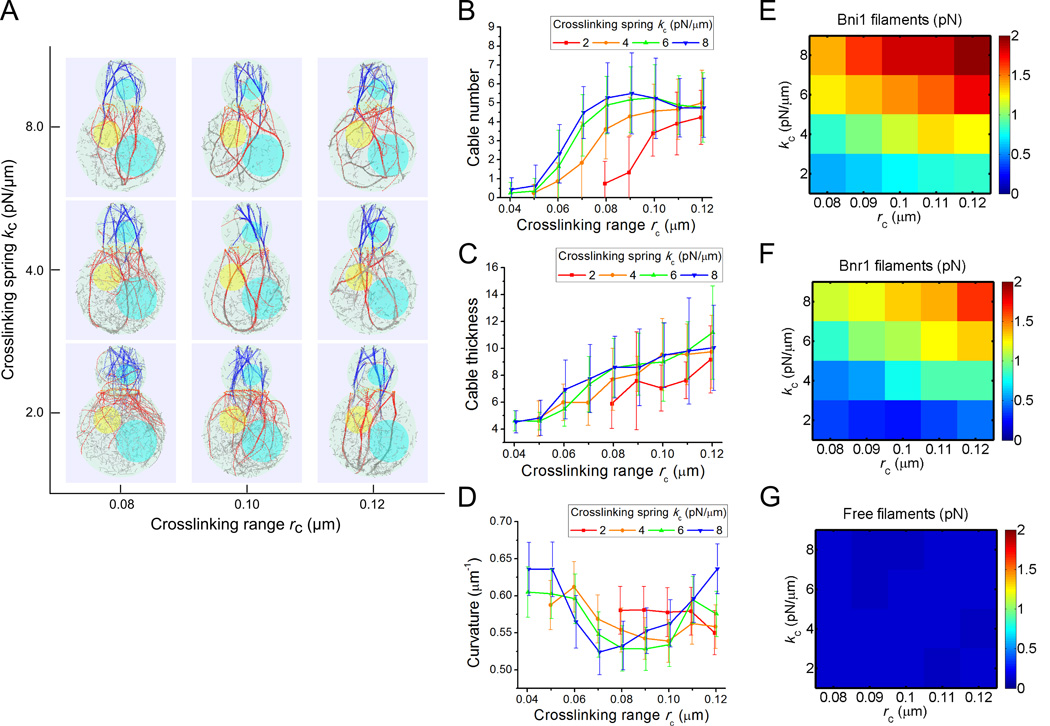
Figure 3. Effects of crosslinking interactions in cable formation.

(A) Simulation snapshots (at 80 s) under different crosslinking range r_c and spring constant k_c. Actin filaments become more bundled with increase of either parameter. (B) Average cable number as a function of r_c, for different k_c. In this and following panels, each point is an average of measurements of five cross- section measures (z = 3.3, 2.26, 1, 0, −1 µm) of 15 time points (separated by 10 s starting at 60 s) from 3 independent runs. The error bar is the standard deviation among all measurements. (C) Average cable thickness as a function of r_c for different k_c. (D) Average filament curvature as a function of r_c for different k_c. The curvature is a non-monotonic function of either variable (see main text). (E–G) Heat map of average tensile forces of Bni1-associated (E), Bnr1-associated (F) and free (G) filaments under different r_c and k_c. As cables get more bundled, forces in Bni1 and Bnr1 filaments segments increase.

We further investigated the curvature of actin cables as function of crosslinking strength. We noticed a complex behavior in Figure 3D due to two factors that affect cable curvature in simulations: 1) bundling of actin filaments results in a bundles of higher bending rigidity, which reduces the curvature and 2) the difference in polymerization rates between Bni1- and Bnr1-associated filaments causes bending of the cables due to forces that prevent filament sliding with the cable. The latter effect increases the curvature, as discussed in the prior model of fission yeast cables [Tang et al. 2014]. These two trends result in a bowl-shape curve for k_c = 4, 6, 8 pN/µm with increasing r_c in Figure 3D. Consistent with this interpretation, in simulations that lack Bni1 filaments, there is no noticeable increase in curvature at large r_c (not shown). To further quantify bundling-related deformation, we measured the average tensile forces in Bni1-associated, Bnr1-associated, and free filament segments. Increasing crosslinking parameters causes the tensile force of the Bni1 and Bnr1 filament to increase by four-fold, while in the free filaments the forces barely change (Figure 3E, F and G). In selecting the standard parameter set for the simulations, we used r_c or k_c that are large enough to produce bundles but low enough to avoid excessive cable bending.

The results of Figure 3 depend on our assumption that cross-linking does not distinguish among Bni1 and Bnr1 filaments. We are not aware of experimental evidence that directly supports or excludes the formation of mixed Bni1/Bnr1 cables.

Simulated loss of Bni1 or Bnr1 disrupts the cable numbers but not cable thickness

Many previous experiments have studied the effects of deletion of either Bni1 or Bnr1 [Buttery et al. 2007; Chesarone-Cataldo et al. 2011; Evangelista et al. 2002; Liu et al. 2012; Pruyne et al. 2004a; Yu et al. 2011]. In published images of bni1Δ cells the number of actin cables that remain in the mother cell has no drastic decrease as compared to wild type cells. Images of bnr1Δ cells show cables in both the bud and mother, presumably nucleated by Bni1 at the bud tip. The number of cables in the mother cell in bnr1Δ cells has been reported to be very close to the number in wild type cells [Yu et al. 2011]. Due to the high fluorescent intensity of actin patches inside the bud, it is hard to quantify how the number and thickness of actin cables change in the bud in prior experimental images.

We next tested if our model can reproduce the behavior in cells lacking Bni1 or Bnr1. In simulations lacking Bnr1, actin cables are observed inside the bud and extend to the mother cell (Figure 4A). Due to filament severing there are only sparse actin cables in the mother. Simulations without Bni1 show robust structures of actin cables inside the mother and occasional single filaments going into the bud, which are unable to bundle into cables (Figure 4A). Robust cables in the mother also occur when placing the Bnr1 formins at the bud neck cusp (rather than below the neck) and when the initial angle of Bnr1 polymerization is random rather than vertical (Movie S3). This occurs even though the initial number of filaments growing towards the bud is different in each case. The origin of this behavior is that myosin V pulling stretches the actin filaments and gives a preference for bundle formation in the larger mother cell.

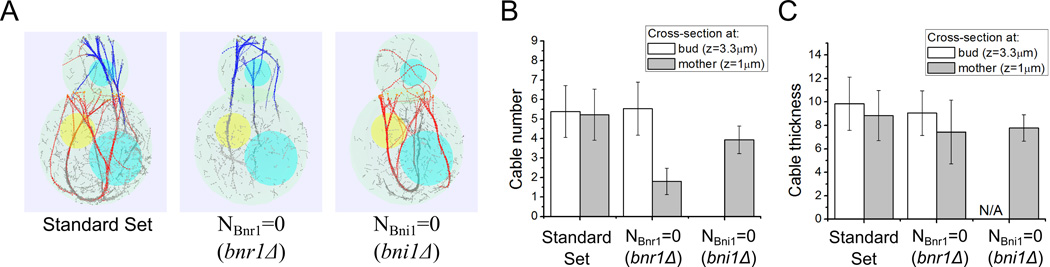
Figure 4. Simulations of formin deletion (bni1Δ and bnr1Δ).

Parameter sets taken from Table I unless otherwise indicated. (A) Simulation snapshots at 120 s using standard parameter set (left), without neck formins (middle), and without bud tip formins (right), simulating wild type, bnr1Δ and bni1Δ mutants, respectively. (B) Cable number at cross-sections z = 3.3 µm in the bud and z = 1 µm in the mother cell. With N_Bnr1 = 0, the number of cables in the bud is not significantly different from that in the standard set, but the number of cables in the mother is reduced significantly. With N_Bni1 = 0 simulations, there are slightly smaller number of cables in the mother cells and none in the bud. (C) Cable thickness at the same cross-sections as panel B. The cable thickness does not very significantly in the three cases in either bud or mother. In panels B and C, each point is an average of measurements at 15 time points, separated by 10 s starting at 80 s, from 3 independent runs; error bars are one standard deviation.

We quantified the number and thickness of actin cables by investigating the cross-sections inside the bud and the mother, at z = 3.3 µm and 1 µm, respectively, as in Figure 1B. First, taking out Bnr1 does not alter the number of cables inside the bud (5.5 ± 1.3 comparing to 5.4 ± 1.3; average ± StDev). Inside the mother the cable number decreases from 5.2 ± 1.3 to 1.8 ± 0.7 (Figure 4B). Second, taking out Bni1 leads to absence of cables inside the bud and the number of cables in the mother decreases to 3.93 ± 0.70 (Figure 4B). Third, the cable thickness (i.e. number of filaments of the cable penetrating the cross-section) inside the bud (for Bnr1 deletion) and inside mother (for either Bnr1 or Bni1 deletion) is slightly lower than the wild type case (Figure 4C). This change is small compared to the magnitude of the standard deviation. Thus by eliminating either type of formins in simulations that use the standard parameter set leads to a decrease in the number of the cables in the mother but does not significantly change the thickness of cables in either the bud or mother.

The results of Figure 4 are consistent with the prior experimental observations in bni1Δ and bnr1Δ cells, except for the larger reduction of actin cable mass in the mother in bnr1Δ cells as compared to observations [Buttery et al. 2007; Evangelista et al. 2002; Yu et al. 2011]. This discrepancy may be a result of relatively higher Bni1 polymerization rate in bnr1Δ cells, owing to greater profilin-actin monomer availability, which the model does not take into account. Another possibility is an overall underestimation of the Bni1 polymerization rate (see Figure S1B where Bni1 filaments extend further into the mother).

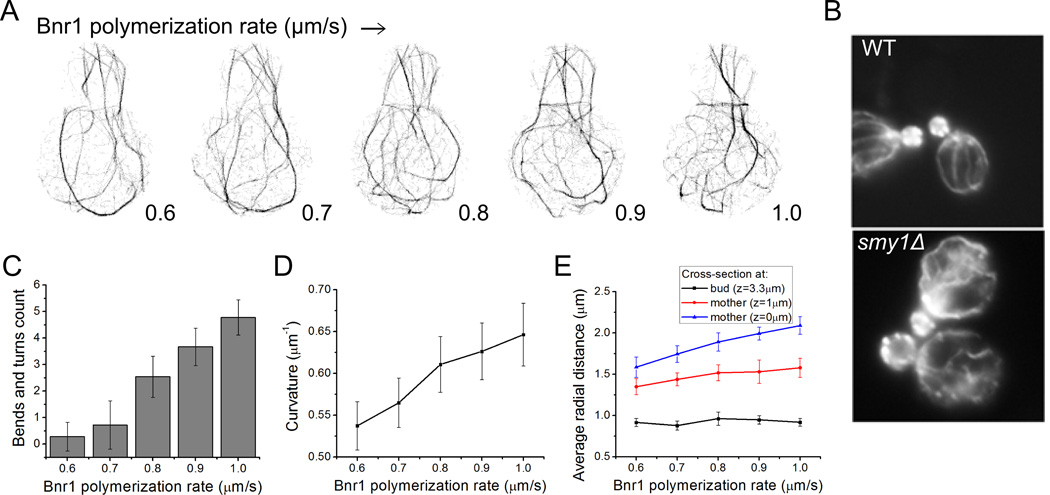
Increased Bnr1 polymerization rate reproduces actin cable defects observed in smy1Δ cells

We next performed simulations varying the Bnr1 polymerization rate from 0.6 to 1.0 µm/s, to compare to the phenotype of smy1Δ cells (Figure 5A, Movie S4). The myosin passenger protein Smy1 is transported along actin cables towards the cell cortex where it interacts with Bnr1 and decreases its polymerization rate [Chesarone-Cataldo et al. 2011]. Experimental observations (Figure 5B) show that in smy1Δ cells, actin cables are abnormally long and wavy [Chesarone-Cataldo et al. 2011]. A clear observation from simulation projection snapshots is that increasing Bnr1 rate results in a denser actin cable network with more interconnected cables (Figure 5A). It also results in cables that are highly curved with abrupt turns and bends. We manually counted the bends and turns where the change in direction is greater than 60° and found that the number of bends increases from 0.28 to 4.78 (Figure 5C). This is further confirmed by measuring the cable curvature that increases from 0.54 ± 0.03 to 0.65 ± 0.04 µm⁻¹ (Figure 5D). A comparable increase of cable curvature with Bnr1 polymerization rate was obtained in simulations that included an attractive interaction between actin filaments and the mother cell boundary where actin bundles localize close to the mother cortex (Figure S4). These results agree with the experimental observations of smy1Δ cells showing more occurrences of cables that change direction more than twice [Chesarone-Cataldo et al. 2011] (Figure 5B). Individual actin filaments would not be resolved in the experiments of Figure 5B, however the diffuse intensity near the bud neck could represent a higher density of individual filaments as in the simulations. The wavy cable structures occur at high polymerization rates, partly because filaments grow long enough such that their thermal relaxation time becomes longer than their lifetime, which is determined by the severing aging time. The longer filaments at high polymerization rates are also forced to curve when reaching the bottom part of the mother.

Figure 5. Increase of Bnr1 polymerization rate in simulations reproduces phenotype of smy1Δ cells.

(A) Projection snapshots taken at 80 s (as in Figure 2C) as a function of increasing Bnr1 polymerization rate show an increase in cable curvature, see Movie S4. (B) Experimental images of phalloidin-labeled actin cables reprinted from [Chesarone-Cataldo et al. 2011] with permission from Elsevier. The smy1Δ cells show long and more curved actin cables compared to wild type. (C) Number of cable bends and turns as a function of Bnr1 polymerization rate (manual counting using simulation projection snapshots). Data: 15 time points starting at 50 s, separated by 5 s from 3 independent runs (same for D, E). Error bar is one standard deviation. (D) Average curvature increases with increasing polymerization rate. (E) Average radial distance (measured from the axis that runs through the centers of mother and bud) of actin filaments as a function of Bnr1 polymerization rate. The average radial distance increases with increasing Bnr1 polymerization rate below the neck (z = 1 µm) and at the mother center (z = 0 µm). No significant change for cross-section at the bud center (z = 3.3 µm).

An implication of the actin cable network becoming denser and more curved is that the actin cables buckle and explore more space perpendicularly to the bud-mother axis. Inside the mother cell, at z = 1 µm (below the neck above the mother center), the average radial distance measured from the center of a horizontal cross-section increases from 1.35 ± 0.10 µm (average ± StDev) to 1.58 ± 0.12 µm at the highest Bnr1 polymerization rate. At z = 0 µm (through mother center) it increases from 1.59 ± 0.12 to 2.09 ± 0.11 µm (Figure 5E). The average radial distance does not change in the bud, which contains very few Bnr1 filaments.

Change in simulated myosin pulling density and location alters actin cable structure

Previous simulations of fission yeast actin cables [Tang et al. 2014], which implemented type V myosin pulling along actin filaments, reproduced the highly curved actin cables near the two cell tips that fail to span the cell as in myosin V deletion mutants [Lo Presti et al. 2012]. The type V myosin Myo2 is an essential protein in budding yeast that drives fast actin cable movements in unpolarized budding yeast cells [Yu et al. 2011]. Thick actin cable bars were observed in the temperature sensitive myo2-66 mutants [Johnston et al. 1991], indicating a role of Myo2 in actin cable organization. However, no significant change of actin cytoskeleton structure was observed for the same mutants in [Schott et al. 1999; Yu et al. 2011].

To explore the role of type V myosin pulling, we varied the density of simulated myosin walkers along actin filaments, similarly to what was done for fission yeast [Tang et al. 2014] (Figure 6, Movie S5). In these simulations we did not include explicit attraction of actin filaments to the cell cortex. The first observation is that the actin cables become unbundled and straighter as the myosin density, ρ_MyoV, is changed from 0 to 5 µm⁻¹ (Figure 6A). The absence of myosin V pulling occasionally leads to ring formation around the neck (Figure 6A), which we discuss in more detail in the subsequent section. The average cable number first increases from 4.7 (no myosin pulling), peaks at 6.3, and then decreases to 1.7 as ρ_MyoV is increased (Figure 6B). The cable thickness, by contrast, monotonically decreases with increasing ρ_MyoV by nearly two-fold (Figure 6C). The last two results suggest that unbundling at high ρ_MyoV consists of two phases: first, unbundling of fewer thick cables into thinner cables and second, unbundling of thin cables into individual filaments. The average curvature decreases from 0.76 to 0.4 µm⁻¹ as a result of stiffening accompanied by myosin walking (Figure 6D). Myosin V also causes the tensile force to increase in all Bni1, Bnr1 associated and free filaments (Figure 6E).

Figure 6. Myosin V pulling stretches actin filaments and influences bundling into cables in simulations.

(A) Snapshots at 60 s with increasing myosin V density ρ_MyoV (Movie S5). Filaments become unbundled and straighter along with ρ_MyoV increase. (B–E) Effects of myosin V pulling on cable number (B), thickness (C), average curvature (D) and tensile forces of Bni1, Bnr1 and free filaments segments (E). The number of cables goes through a maximum while filaments get stiffer, thinner and more tense as the myosin V density increases. All error bars are standard deviations from 15 time points (separated by 10 s starting at 60 s) of 3 independent runs. (F) Snapshot with standard parameter set (Table I, ρ_MyoV = 0.7 pN/µm) with segments colored according to their barbed-to-pointed end orientation with respect to the z axis. (G) Orientation distribution as a function of myosin V density ρ_MyoV. Legends of angle distribution are shown corresponding to the color codes in F. The degree of filament alignment goes through a maximum, similar to the cable number in panel B. Data: average from 15 time points (separated by 10 s starting at 60 s) of 3 independent runs.

We further characterized the effect of simulated myosin V pulling on actin filament segment orientation distribution. Figure 6F shows the actin filament segment orientation distribution colored according to the angle with respect to the vertical axis (cooler colors represent segments with barbed end pointing up). This figure shows that actin filament segments mostly point upwards when they are part of actin cables, except for filaments near the bottom where the cables bend and for free filaments in the cytoplasm that have a very broad distribution of orientations. We note that for cables that associate tightly with the cortex as in Figure 2D the curvature would follow the cell shape and would not change at the bottom of the cell. As a function of ρ_MyoV,, the vertical polarity of actin filament segments first increases then decreases. This is due to the fact that at low ρ_MyoV increased pulling orients and stiffens the actin cables while at high ρ_MyoV increased pulling unbundles filaments from cables leading to less cooperative orientation.

The effects of Myo1 pulling at the bud neck in actin cable organization were also explored. Figure S5 shows that in simulations with the standard parameter set, Bni1-associated filaments go very close to neck boundary of wide necks of radius 1 µm (see cross-section at the neck at lower panel). Elimination of the short-range attraction toward the neck and of the Myo1 pulling forces causes the Bni1-associated filaments to cross the neck through the middle (Figure S5A). Simulations with smaller neck radius (0.54 µm) show that Bni1 cables can go through the neck without Myo1 pulling but a larger fraction of filaments remains in the bud (Figure S5D). These results suggest that Myo1 plays a contributing role in organizing actin cables by helping to provide a complete track for transport of secretory vesicles and organelles towards the bud. Prior work using epifluorescence microscopy reported an increase of actin cable retrograde flow by Myo1[Huckaba et al. 2006] while other studies using TIRFM found no effect of Myo1 deletion on actin cable dynamics in unpolarized cells [Yu et al. 2011]. Our model does not include force- dependent polymerization rates so we do not account for the reported change in retrograde flow rate.

Formation of actin ring at the bud neck with increased bud neck binding

The computational model can also demonstrate how cells build an actin ring at the bud neck for cytokinesis using the same formins that they also use to build actin cables. The process of ring assembly is known to depend on dynamic actin filaments nucleated by Bnr1 and Bni1 [Tolliday et al. 2002], both of which localize to the bud neck during the M phase. Ring assembly also depends on binding of actin filaments to Myo1 and IQGAP-like Iqg1/Cyk1 [Bi et al. 1998; Bi and Park 2012; Shannon and Li 1999], and possibly directly to septins at the bud neck [Mavrakis et al. 2014]. The ability of the model to generate rings is already apparent in Figures 5A (highest Bnr1 polymerization rate) and 6A (no Myosin V pulling force). In both cases there is an enhanced concentration of actin filaments near the bud neck as compared to the standard parameter cases. The attraction of these filaments to the bud neck results in bundle formation around the neck.

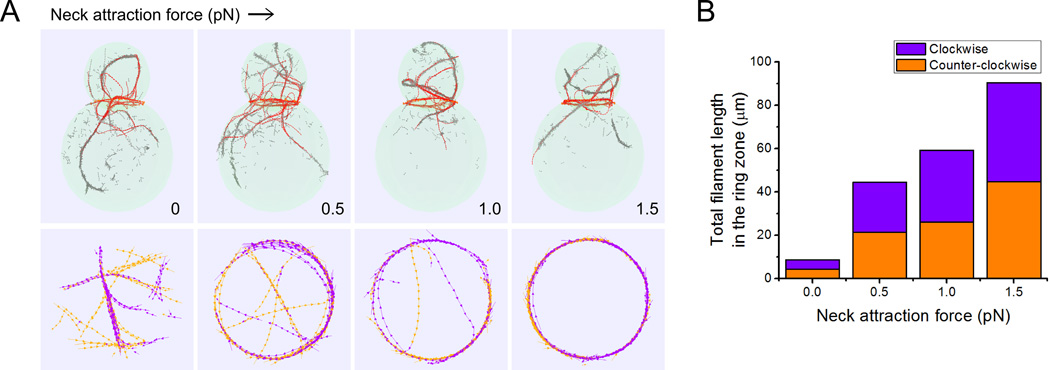
To better illustrate how the association of actin filaments to the bud neck may help in ring formation for cytokinesis, in Figure 7 we varied the force pulling actin filaments towards the bud neck but left the Myo1 pulling force towards the barbed end unchanged. In these simulations we did not include formins at the bud tip and did not include pulling by myosin V motors. To compare to the preceding results on actin cable formation, all other parameters such as cell shape and number of formins at the bud neck, including the polymerization rate at the bud neck, were unchanged as compared to Table I (here polymerization at the neck represents a combination of Bni1 and Bnr1 polymerization).

Figure 7. Increase of attraction of actin-filament to the neck region produces a ring of antiparallel filaments at the bud neck.

(A) Snapshots of simulations without Bni1 and myosin V pulling taken at 180 s (see also Movie S6), as function of force of attraction to the bud neck region. Bottom row shows actin filaments colored in orange and purple depending on their clockwise or counter-clockwise direction at a cross section of thickness 0.4 µm at the bud neck. As the neck attraction force is increased, the actin filaments at the bud neck are able to form a ring of antiparallel filaments drawn from filaments that would otherwise form parallel actin cable structures. (B) Total filament length in the ring zone (sum of all the filament segments) characterized by their directions (purple: clockwise, orange: counter-clockwise) as a function of neck region outward attraction force. Data: average from 15 time points (separated by 10 s starting at 120 s) of 3 independent runs.

Figure 7A shows that in the absence of attractive interactions with the neck, the actin filaments that nucleate at the bud neck form cables, extending towards both the bud and mother cell. The concentration of actin filaments segments is higher at the bud neck but without neck pulling they form bundles of parallel filaments oriented along random directions (see cross-section at bottom of Figure 7A). With increasing neck attraction force, actin filaments align along the bud neck, forming a ring that is a bundle of antiparallel filaments (Figure 7B). The formation of a ring results in a smaller number of filaments in cables, which can coexist with the ring structure, consistent with images of cells with both actin rings and cables [Amberg 1998]. Decreasing the neck radius closer to 0.5 µm destabilizes the ring because filaments at the neck need to bend to larger curvatures (Figure S6). This indicates that some additional fine tuning, such as a decrease in actin filament length, may be required for ring formation in cells with narrow necks.

The simulations of Figure 7 show that tuning of the strength of interactions with the bud neck may be one of the main controls for ring assembly, following the removal of Bni1 from the bud tip. This is consistent with recent findings showing premature formation of rings in cells with nonphosphorylatable Iqg1/Cyk1 mutants that cause Iqg1/Cyk1 to arrive prematurely at the bud neck [Miller et al. 2015; Naylor and Morgan 2014]. The ability of filaments to maintain antiparallel bundles relies on the use of parameters for r_c and k_c that correspond to dynamic cross-linking among filaments. Implicit in our model of ring formation is that the interactions between actin filaments and the bud neck are also dynamic, allowing filaments attached with their barbed ends at the neck to slide around the neck as they polymerize.

Discussion

The computational model in this work shows how actin cable and actin ring morphologies can arise in budding yeast through a combination of a few key interactions that take into account cell shape, nucleation geometry, motor pulling, cross-linking and turnover. The simulations highlight the degree of complexity and robustness of a system that depends on these processes. Since many regulatory proteins determine cytoskeletal interactions, the parameters of the model represent effective rate constants whose detailed dependence on molecular mechanism remains to be examined in more detail in future work. Having a model with enough elements to reproduce main experimental features of actin cables and rings is crucial in interpreting the results of genetic and pharmacological perturbations.

We did not consider the kinetics of actin patches, focusing instead on actin cables and rings. Future modeling work that accounts for all three structures should help clarify the effect of global changes in actin turnover and cross-linking. For example, deletion of cofilin is lethal but a temperature sensitive mutation of Cof1 disrupts actin cables and generates enlarged actin patches [Lappalainen and Drubin 1997]. Cells lacking Cap2, the β subunit of capping protein, show diminished cable staining [Amatruda et al. 1990]. Tropomyosin decorates and stabilizes actin filaments, and some tropomyosin mutants result in loss of actin cables [Liu and Bretscher 1992; Liu and Bretscher 1989; Okada et al. 2006]. Some of these observations may reflect the competition among actin cables, actin rings, and actin patches for a common pool of actin monomers and associated proteins [Burke et al. 2014; Gao and Bretscher 2008].

We found that our results are relatively robust with respect to the precise mechanism of actin filament turnover and cross-linking since the model with whole-filament-turnover and orientation-independent filament bead crosslink mechanism of [Bidone et al. 2014; Tang et al. 2014] can also produce actin cable structures (Figure S3). We note however that the cables in Figure S3 have slightly faster equilibration dynamics as compared to Figure 2 since it is easier for individual filaments to switch bundles by complete disassembly and regrowth from the cortex. Severing and rapid depolymerization from the exposed end as well as Bni1 detachment from the cortex [Buttery et al. 2007] could produce cable dynamics closer to that of Figure S3.

Dynamic crosslinking in the model promotes actin cable formation, which is consistent with the requirement of fimbrin Sac6 for formation of normal actin structures [Adams et al. 1991; Karpova et al. 1995] and the lethality of Sac6 overexpression [Sandrock et al. 1999]. Our simulations accounted for the orientation-dependent cross-linking activity of fimbrin, which favors parallel or antiparallel filaments. Other cross-linking proteins, such as Scp1, Tef1/Tef2, and Abp140, which may bind at large angles, could contribute to actin filament bundling [Moseley and Goode 2006]. Using a larger range of cross-linking angles allowed cable formation in simulations, however short severed actin filaments could then coalesce into disordered aggregates that have not been observed in experiments. Future studies should clarify the role of other cross-linkers and test our treatment of short actin filaments.

We found that accumulation of Bni1 at the bud tip increases the number of cables that extend from the bud into the mother (Figure S1C), which may be why Bni1 accumulates at the bud tip despite the need for isotropic bud growth. Clustering of formins at the polarisome complex at the bud tip and possible clustering of Bnr1 at the bud neck also helps formation of actin cables [Tang et al. 2014].

The simulations further suggest that pulling by type V myosins helps organize the actin cables and that there exists an optimal density of pulling forces for cable formation. In simulations lacking myosin V pulling, actin cables become more bundled and curved similar to prior simulations and experiments of myosin V deletion mutants in fission yeast [Lo Presti et al. 2012; Tang et al. 2014]. Myo2 has been shown to drive rapid cable motility in unpolarized cells [Yu et al. 2011] but its effect on cable curvature has not been characterized, partly because deletion of Myo2 is lethal for budding yeast. Overexpression of either Myo2 or Myo4 leads to cell morphological defects independent of the motor domain [Haarer et al. 1994]. Use of a temperature sensitive cell mutation myo2-66 defective in actin-binding has been reported to lead to thick actin bars in [Johnston et al. 1991]. Very few bars were however observed in [Schott et al. 1999; Yu et al. 2011], possibly a result of different strain background and growth conditions [Schott et al. 1999]. In our simulations without myosin V pulling the actin cables are 50% thicker compared to the standard parameter set, which may relate to the myo2-66 thick bar formation mechanism [Johnston et al. 1991].

We further modeled type II myosin pulling at the bud neck. We predict that Myo1 helps connect actin cables in the bud with those in the mother, consistent with experiments showing that Myo1 contributes to robustness and polarity of actin cables [Gao and Bretscher 2009; Huckaba et al. 2006]. Our study suggests that during ring formation, Myo1 motor activity may contribute to actomyosin ring formation by keeping the filaments close to the bud neck, working together with Iqg1/Cyk1 and consistent with the role of Myo1 in ring assembly [Bi and Park 2012]. Actin and myosin dynamics may change during ring constriction when actin filaments have been reported to become less dynamic and Myo1 motor activity is dispensable for constriction [Lord et al. 2005; Mendes Pinto et al. 2012].

The actin filaments within cables in our simulations are relatively long: the filament segments attached to formins have lengths on the order of microns, comparable to the total length of actin cables. Electron microscopy studies suggest that cables consist of many short actin filaments [Kamasaki et al. 2005] though studies of cable depolymerization in latrunculin A indicate the existence of long filaments [Karpova et al. 1998]. A better understanding of the severing mechanism by cofilin and cofactors such as Aip1 and tropomyosin would help in modifying the model to account for the length distribution within bundles. The precise mechanism of filament severing may change the predicted filament sliding within cables and rings, which our study suggests leads to mixed Bni1/Bnr1 cables and a ring of antiparallel filaments.

The cortical ER is associated with actin cytoskeleton [Fehrenbacher et al. 2002] and its inheritance in budding yeast cell is achieved through type V myosin transport on actin cables [Du et al. 2004; Estrada et al. 2003; Rowland and Voeltz 2012; West et al. 2011]. We tested the ER tethering effect by adding an outward pulling force for filaments come close to the cortical sites in the mother cell (Figure 2D). Such pulling forces help actin cables to organize closer to the cell cortex (Figure 2E).

In this study we made several approximations. We did not account for the turnover of formins at the cell cortex, which is faster for Bni1 as compared to Bnr1 [Buttery et al. 2007]. We also did not account for Bni1 incorporation into the body of cables, where it is presumed to remain inactive [Buttery et al. 2007]. In addition to increasing fluctuations in filament length and cable thickness, these processes may enable faster global restructuring of the actin cables through the cell. We did not explicitly account for the activation/inactivation of Bnr1formins by Bud14 that displaces the Bnr1 FH2 domain from the barbed ends and thus influences filament length and actin cable structures [Chesarone et al. 2009]. Smy1 controls Bnr1 polymerization rate in a cable length dependent manner [Chesarone-Cataldo et al. 2011; Mohapatra et al. 2015]. This feedback was not modeled here, although the overall effects of Smy1 were considered. Severing by cofilin depends on the tensile force experienced by the filament [Hayakawa et al. 2011], which may provide another mechanism for cable length control. We did not include such a feedback, however our framework that includes myosin-dependent filament tension can serve as a starting point to study this interdependence.

Future work is needed to examine actin cable dynamics in unpolarized cells where dispersed cortical Myo2 and Bni1 lead to actin cables that are more dynamic compared to polarized cells [Yu et al. 2011]. Such studies should also address the mechanism of formation and movement of short actin cables along the cell cortex at speeds larger 2 µm/s [Yu et al. 2011], a feature that was not generated by our simulations.

Finally, in the following paragraphs we compare the mechanisms for actin cable and contractile ring formation between budding yeast and fission yeast as suggested by computational modeling. In simulations of fission yeast, actin filaments polymerizing out of the cell tips by For3 meet at the cell center where they can establish straight bundles of antiparallel filaments when cross-linking interactions are dynamic enough to allow polymerizing filaments to slide past one another [Tang et al. 2014]. By contrast, simulated actin cables in budding yeast are mostly bundles of parallel filaments. Dynamic cross-linking aids in the formation of straight bundles containing filaments polymerizing at different rates from two different formins, Bni1 and Bnr1.

Unlike budding yeast where the site of ring formation is marked by septins at the bud neck, fission yeast needs to define the site of the contractile ring prior to cytokinesis. This process depends on the formation and condensation of a broad band of nodes that contain anilin Mid1, type II myosin Myo2, and formin Cdc12 [Lee et al. 2012]. Computational modeling suggests a process for broad band condensation through search, capture, pull and release and dynamic filament cross-linking that allows filaments to align in antiparallel bundles [Bidone et al. 2014; Vavylonis et al. 2008]. An alternative model envisions contractile ring formation as a process of actin cable closure followed by remodeling of actin filaments within the cables [Kamasaki et al. 2007]. These two mechanisms may coexist, reflecting the fluctuations of a finite system that is able to assemble both parallel and antiparallel bundles and transition between these two structures [Bidone et al. 2014].

Since budding yeast can place its formins and Myo1 at the septin ring, its additional task in terms of ring formation is the alignment of actin filaments around the bud neck. Here we suggest that tuning of the association of actin filaments and possibly adjusting myosin V pulling (similar to the role of myosin V in fission yeast [Huang et al. 2012] may be sufficient to reorient actin filaments and establish a bundle of antiparallel filaments, provided cross-linking interactions among actin filaments are sufficiently dynamic. Time lapse movies of simulations (Movie S6) show that the ring is formed by polymerization and aligning of filaments in a uniform manner around the ring, however cable features and cable merging into the ring are also observed. This suggests a process for ring formation as in fission yeast, but without the node condensation episode.

Since the polarity of actin filament bundles is closely related to their biological function, progress in understanding mechanistic aspects of cytoskeletal assembly mechanisms in yeast should provide insight to cytoskeletal remodeling and associated biological function across many species. For example, the mechanism of actin cable formation described here may have analogies to the formin-mediated actin bundle formation in the cortex of Dictyostelium [Diez et al. 2005] and to the DAAM1-nucleated actin asters at the cortex of animal cells [Luo et al. 2013], which regulate cell shape and mechanics. Analogies should also exist with animal cell cytokinesis where formins attached to the cell cortex nucleate actin filaments for the contractile ring, tethered to the cell cortex through septins and anilins [Green et al. 2012].