Statistical learning of temporal community structure in the hippocampus

Abstract

The hippocampus is involved in the learning and representation of temporal statistics, but little is understood about the kinds of statistics it can uncover. Prior studies have tested various forms of structure that can be learned by tracking the strength of transition probabilities between adjacent items in a sequence. We test whether the hippocampus can learn higher-order structure using sequences that have no variance in transition probability and instead exhibit temporal community structure. We find that the hippocampus is indeed sensitive to this form of structure, as revealed by its representations, activity dynamics, and connectivity with other regions. These findings suggest that the hippocampus is a sophisticated learner of environmental regularities, able to uncover higher-order structure that requires sensitivity to overlapping associations.

A growing literature suggests that the hippocampus is important for the rapid extraction of temporal structure in the environment (Bornstein & Daw, 2012; Curran, 1997; Harrison, Duggins, & Friston, 2006; Schapiro, Gregory, Landau, McCloskey, & Turk-Browne, 2014; Schapiro, Kustner, & Turk-Browne, 2012; Strange, Duggins, Penny, Dolan, & Friston, 2005; Turk-Browne, Scholl, Chun, & Johnson, 2009; Turk-Browne, Scholl, Johnson, & Chun, 2010). Such temporal structure is typically created in experiments by varying the strength of transition probabilities between adjacent items in a continuous sequence. Transitions to improbable events can drive prediction error, which has in turn been argued to support event segmentation (Reynolds, Zacks, & Braver, 2007; Zacks, Kurby, Eisenberg, & Haroutunian, 2011). Relying only on variation in strength of transition probabilities is limiting, though, as real world temporal events often involve more complex, higher-order relationships. Indeed, a recent study (Schapiro, Rogers, Cordova, Turk-Browne, & Botvinick, 2013) demonstrated that humans can learn a form of higher-order structure known as temporal community structure (Fortunato, 2010; Newman, 2003), even though strength of transition probabilities, and therefore strength of prediction errors, were uninformative. Here we show that the hippocampus can learn such higher-order structure, extending beyond its known role in statistical learning of transition probabilities. Specifically, we demonstrate that representations of items in the hippocampus cluster according to community membership, that the hippocampus deactivates at the boundaries between communities, and that the hippocampus selectively couples with other regions involved in event learning at different points in the structure.

Detailed methods can be obtained from a prior publication on which this re-analysis was based (Schapiro et al., 2013). To summarize, participants were exposed to sequences of stimuli generated from a random walk on a graph with three communities (Figure 1A) prior to, and during, an fMRI scan (prior to the scan, stimulus duration was 1.5 s with no ISI, and during the scan it was 1 s with 1, 3 or 5 s ISI to facilitate estimation of the response to individual items). In graph analysis, a community refers to a cluster of nodes that share a large number of connections among themselves, relative to the number of outgoing connections they share with other graph nodes. Each node was randomly assigned a unique abstract visual stimulus, with edges between nodes indicating possible transitions between stimuli. The graph never gave rise to moments of prediction error because each node had exactly four neighbors and the transition to each neighbor occurred with equal probability (.25). Despite this, there was strong temporal structure: nodes in the same community were preceded and followed by overlapping sets of nodes. In other words, nodes in the same community shared neighbors, whereas those from different communities did not. Participants were not informed about the structure and performed a cover task of pressing a button on each trial to indicate whether or not they thought the image was rotated from its usual orientation.

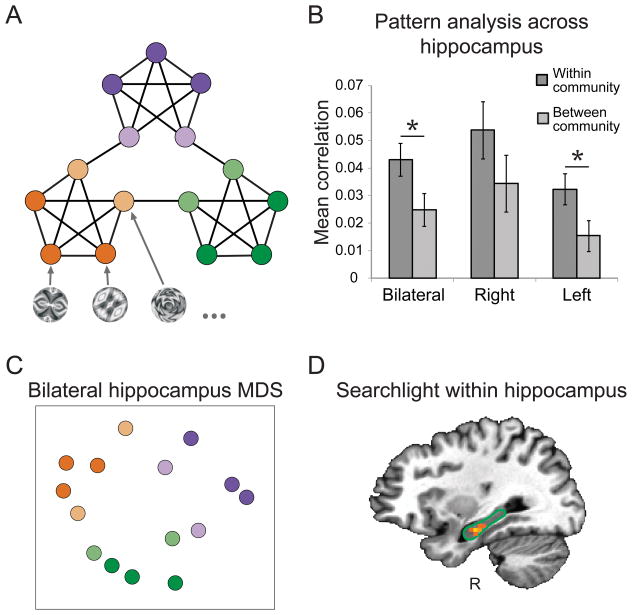
Figure 1. Pattern similarity in the hippocampus.

(A) Graph used to generate sequences of stimuli. An abstract visual stimulus was assigned to each node and the edges represent possible transitions between stimuli. The three graph communities are colored in purple, green, and orange, with community boundary nodes in a lighter shade. (B) Mean pattern similarity (Fisher transformed correlation) for within and between community pairs of items when defining patterns across all voxels in an ROI. Error bars denote ± 1 within-subject SEM (Morey, 2008). * p < .05. (C) MDS for visualization of the representational clustering in the bilateral hippocampus. Colors indicate correspondence to the nodes in the graph. (D) Voxel centers of searchlights that showed greater similarity within- vs. across-community within right hippocampus (outlined with green border). The searchlight surrounding the brightest voxel passed a threshold of p < .001 uncorrected.

Previous work, by Schapiro et al. (2012), has shown that the patterns of activity in the hippocampus evoked by two items become more similar over time if those items are part of the same event. In that work, the events were defined by a high frequency of co-occurrence of the items within an event and stronger transition probabilities within compared to between events. We first tested whether the hippocampus would show an analogous pattern similarity effect for items from the same community, despite the fact that co-occurrence frequency and transition probability strength were uniform (all sequences of a given length occur equally frequently in a random walk on the graph). Previous whole-brain searchlight analyses of the present dataset identified the left inferior frontal gyrus (IFG), left anterior temporal lobe (ATL), and left superior temporal gyrus (STG) as having representations whose similarity reflected this community structure (Schapiro et al., 2013).

We extend these findings with a hypothesis-driven region-of-interest (ROI) analysis of the hippocampus, motivated by the growing literature on the role of the hippocampus in basic statistical learning. Specifically, we assessed representational similarity in bilateral hippocampal ROIs defined from a probabilistic atlas of the medial temporal lobe (MTL; Hindy & Turk-Browne, 2015). We calculated the average blood oxygenation level-dependent (BOLD) activity patterns evoked by each of the 15 stimuli across all voxels in each ROI and across 3x3x3 voxel searchlights within these ROIs. We then calculated the Pearson correlation between the voxel pattern vector corresponding to each item and the vector for each other item, yielding a 15 by 15 similarity matrix. To look for the predicted similarity structure, we compared the mean Fisher-transformed correlation between items in the same community to that for items across different communities, controlling for distance traveled in the graph between items.

First considering stimulus-specific activity patterns across all voxels in the hippocampus (Figure 1B), we found greater within- than across-community similarity in the bilateral hippocampus (t[19] = 2.15, p = .045) and left hippocampus (t[19] = 2.14, p = .046; right hippocampus: t[19] = 1.32, p = .203). A multidimensional scaling (MDS) plot of the bilateral hippocampal representations provides a visualization of this similarity structure (Figure 1C), where each dot represents one item and the distance between two dots corresponds to the average similarity across subjects between those two items. (Statistics were calculated from the full correlation matrix for each subject, not from this scaled representation of average distances.) Items from the same community are clustered, demonstrating the learning of representations that reflect the community structure of the graph.

To explore the possibility of more local pattern similarity, we also ran searchlights within each hippocampus ROI, and found one searchlight in the right anterior hippocampus with representational structure that reflected the community structure of the graph (p < .001 uncorrected; Figure 1D). The fact that right but not left hippocampus was revealed in this analysis, whereas the reverse was true in the full ROI analysis, could potentially reflect a more focal representation in this hemisphere.

To further explore which subregions of the hippocampus might be contributing to these effects, we ran the same analyses across all voxels within hippocampal subfields CA1, CA2/3/DG, and subiculum, in each hemisphere. Though we did not scan at high enough resolution to confidently resolve these subfields, we performed exploratory analyses using probabilistic atlas labels (Hindy & Turk-Browne, 2015) derived from a database of manual anatomical segmentations. Aly and Turk-Browne (2015) describe the procedures used for these segmentations, which involved tracing based on anatomical landmarks in each coronal slice of the MTL at .44 x .44 mm in-plane, 1.5 mm thickness resolution. The only subfield that had reliably different within- vs. across-community similarity was left CA1 (t[19] = 2.60, p = .018; all other ps > .286). Though this exploratory analysis is suggestive that CA1 may be the most involved subfield of the hippocampus, it is important to note that the p value does not survive Bonferroni correction for three subregions with two hemispheres each (alpha = .05/6 = .008), and, as noted earlier, the CA1 label is only approximate at this resolution. Future work will be needed to better understand the contribution of different hippocampal subfields.

We also used the probabilistic atlas of the MTL (Hindy & Turk-Browne, 2015) to test whether MTL cortex, in addition to hippocampus, might show these pattern similarity effects, as had been found in a prior study of pattern similarity during statistical learning (Schapiro et al., 2012). We looked at pattern similarity across all voxels in each hemisphere of entorhinal cortex, perirhinal cortex, and parahippocampal cortex, and did not find evidence for greater similarity in MTL cortex for items within the same community versus from different communities (all ps > .137). However, there was a hint of an effect when the voxels in these subregions were pooled into one large MTL cortex ROI (p = .066).

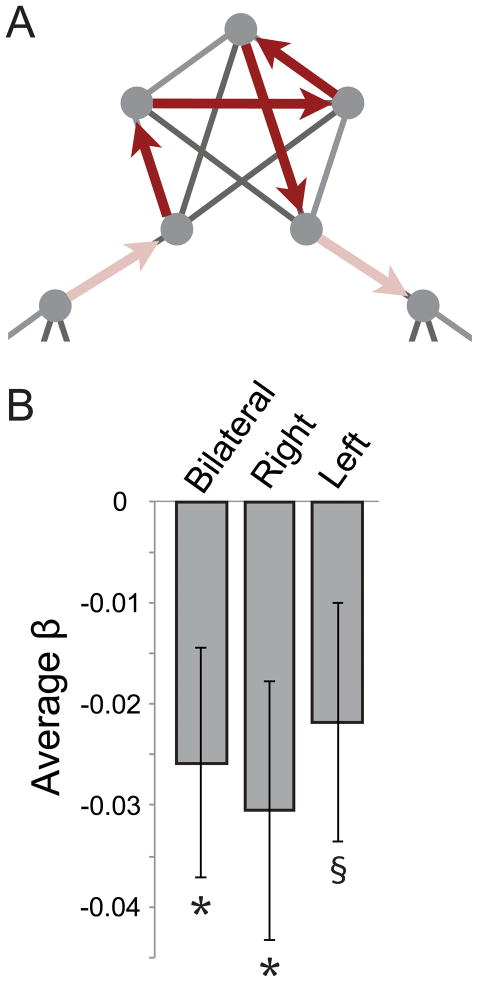
We next investigated whether the hippocampus is sensitive to the boundaries between events. In previous general linear model (GLM) analyses, we found that the medial prefrontal cortex (mPFC) was active within a community traversal and transiently deactivated at community boundaries (Schapiro et al., 2013). Using the same GLM, we averaged the beta weights for the regressor coding for community boundaries across voxels in the hippocampal ROIs (Figure 2A). The overall level of activity in the hippocampus was indeed sensitive to boundaries, in the same manner as mPFC (Figure 2B): The hippocampus was relatively active within an event, and then deactivated at event boundaries (bilateral: t[19] = 2.27, p = .035; right: t[19] = 2.38, p = .028; left: t[19] = 1.86, p = .079). We examined whether this effect was specific to the hippocampus and mPFC by testing for it within the other regions we previously found to be involved in this task, including IFG, insula, ATL, and STG (Schapiro et al., 2013). The beta weights for the boundary regressor were not reliable in any of these other ROIs (ps > .179). These results suggest that the hippocampus is not only learning representations of items that reflect community structure, but that its overall activity is sensitive to event boundaries.

Figure 2. Boundary effects in the hippocampus.

(A) Illustration of the regressor used in the GLM to examine sensitivity to boundaries, with higher activity within a community compared to at event boundaries. (B) The average beta weights from the boundary regressor across voxels in hippocampal ROIs. The negative beta values reflect lower activity at community boundaries compared to within communities. Error bars denote ± 1 SEM. * p < .05; § p < .1.

The fact that the hippocampus is both involved in item representation and shows sensitivity to boundaries suggests that it might be an important hub in the network of regions involved in learning higher-order temporal structure. To evaluate this idea, we performed a functional connectivity analysis in which we contrasted connectivity immediately after a boundary event with connectivity during periods within a community traversal. We focused on connectivity between the hippocampus (defined anatomically), the mPFC, and the left IFG (the latter two defined functionally). We chose the mPFC because it was the region sensitive to community boundaries in the whole-brain GLM (Schapiro et al., 2013). We chose the left IFG because this region was implicated by two different analyses – the pattern similarity analysis, as well as an adaptation analysis, which assessed representational similarity in a different way (Schapiro et al., 2013). The left IFG has also been implicated in other statistical learning studies (Karuza et al., 2013; Turk-Browne et al., 2009).

To assess functional connectivity, we calculated correlations between the BOLD timeseries from these ROIs. We first fit a nuisance GLM to remove sources of noise that induce spurious correlations (Fox & Raichle, 2007). The GLM included regressors for head movement in six directions, global mean signal, mean signal in ventricles, and mean signal in white matter. We excluded voxels with very high variance (more than three standard deviations outside of the mean variance), and then averaged the residual timeseries across voxels within each ROI.

Functional connectivity was contrasted between two 6-s (3 TR) periods: (1) boundary periods, 6 to 12 s after a boundary occurred within a Hamiltonian path (see Schapiro et al. (2013) for explanation of Hamiltonians); and (2) within-community periods, 4 s before to 2 s after a boundary occurred within a Hamiltonian path (see Figure S1). Taking into account the temporal lag of the hemodynamic response, these periods corresponded, respectively, to the neural response between the beginning of the boundary stimulus to a few seconds after the boundary, and to the same length of neural activity before the boundary.

We used a background connectivity approach (Al-Aidroos, Said, & Turk-Browne, 2012; Norman-Haignere, McCarthy, Chun, & Turk-Browne, 2012) to control for the potentially spurious contribution of stimulus-evoked activity to functional connectivity. Specifically, for each TR in a period, we subtracted the mean evoked activity for the corresponding timepoint across all periods of that type. The remainder thus had an across-period mean of zero at each timepoint, preventing evoked responses from confounding functional connectivity on average. All periods of a given type were then concatenated to produce a long timecourse. The activity left over from this procedure is thought to reflect spontaneous fluctuations. If such fluctuations are correlated between regions over time, these regions can be said to be part of the same functional network. Insofar as these correlations change according to the type of period (i.e., boundary vs. within-community), then different networks may underlie processing at these different points in the graph. To test for this kind of effect, we calculated the Pearson correlation of the concatenated timecourses across ROIs for each of the period types and Fisher transformed the coefficients prior to statistical testing.

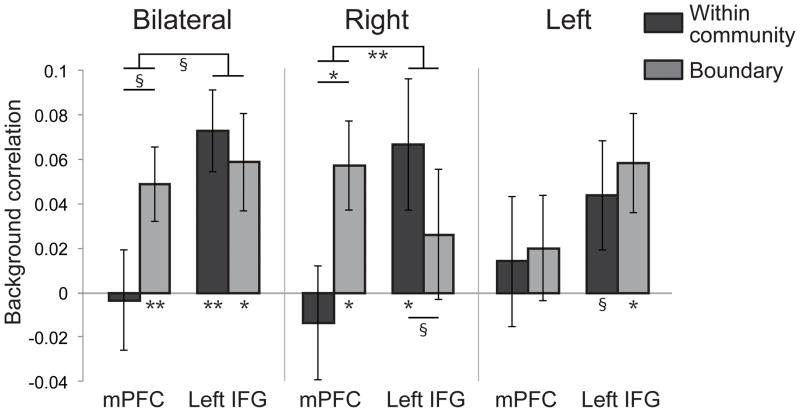
We found an interaction in the connectivity profiles in bilateral hippocampus and right hippocampus (Figure 3): The timecourses in these regions were more correlated with mPFC at community boundaries but more correlated with left IFG within communities (bilateral: t[19] = 1.88, p = .076; right: t[19] = 3.13, p = .006); we did not find this interaction in left hippocampus (t[19] = .219, p = .829). There was no change in correlation directly between mPFC and left IFG for boundary vs. within-community periods (t[19] = .115, p = .910). This double dissociation in connectivity is unlikely to be caused by factors such as differences in SNR or ROI size, as the hippocampal connectivity with left IFG and with mPFC is similar in size but present in different conditions. We ran several additional control analyses, which further validated these findings (see Supporting Information). These results therefore suggest that the hippocampus may interact more with the mPFC when processing the move to a new community (despite the fact that both regions are less active overall at this time), and may interact more with left IFG when processing the internal structure of an event.

Figure 3. Background connectivity with the hippocampus.

Connectivity between mPFC and hippocampus and between left IFG and hippocampus within a community and at community boundaries. Error bars denote ± 1 SEM. * p < .05; ** p < .01; § p < .1.

In summary, we found that the hippocampus was sensitive to higher-order, community structure. Neural representations of objects in the same vs. different communities became more similar to each other in the hippocampus. Moreover, the hippocampus was more active within a community than at a community boundary. When examining functional connectivity during the task, the hippocampus interacted more with the left IFG — a region with analogous representational similarity — within communities, and it interacted more with the mPFC — a region that also detected event boundaries — at the boundaries.

The pattern similarity results suggest that the hippocampus rapidly comes to represent items in terms of their temporal context, which is consistent with other recent findings and theories (Davachi & DuBrow, 2015; Ezzyat & Davachi, 2014; Howard, Shankar, & Jagadisan, 2011; Hsieh, Gruber, Jenkins, & Ranganath, 2014; Schapiro et al., 2012). The present findings suggest that this learning is more sophisticated than simply associating adjacent items or tracking transition probabilities. A common mechanism that might account for the previous as well as present findings is that the hippocampus can learn to represent items in terms of the similar predictions that they make about the future – here, communities can be identified by the fact that items within them make similar predictions about what items can come next (Schapiro et al., 2013).

The finding that the hippocampus was less active at event boundaries may be related to work showing that event boundaries disrupt memory processes (DuBrow & Davachi, 2013; Ezzyat & Davachi, 2011; Speer & Zacks, 2005). The hippocampus may bind the observations within each event into one episode, and clear its activity as it moves on to the next episode. The fact that functional connectivity increases between mPFC and hippocampus at boundaries may suggest that this transition phase, despite corresponding to lower activity in both areas, is still meaningfully processed.

An important goal for future work will be to understand whether learning happens independently and locally in the hippocampus, mPFC, and left IFG, or whether one region drives changes in the others. The fact that the hippocampus learns so rapidly compared to cortex (McClelland, McNaughton, & O’Reilly, 1995) and that a patient with MTL damage cannot learn new temporal structure (Schapiro et al., 2014) suggests that the representational similarity effects reported previously in left IFG, ATL, and STG (Schapiro et al., 2013) may have been mediated by the hippocampal changes. The functional connectivity finding that the hippocampus communicates with left IFG within communities and with mPFC at community boundaries lends further support to the idea that the hippocampus is a hub driving the effects in other regions. One possibility to explore is that the hippocampus mediates these changes initially, but that they can become hippocampally independent over a consolidation period (Durrant, Cairney, & Lewis, 2013; McClelland et al., 1995; Squire, 1992; Yamashita et al., 2009).

In conclusion, our findings provide new insight into the role of the hippocampus in statistical learning and event representation. The hippocampus is able to rapidly learn the structure in these community-based sequences despite there being no transition probability or frequency cues to anchor on. The findings suggest that the hippocampus may be a key player in a network of regions involved in new event learning.