Spectral fitting using basis set modified by measured B₀ field distribution

Abstract

This study sought to demonstrate and evaluate a novel spectral fitting method to improve quantification accuracy in the presence of large magnetic field distortion, especially with high fields. Magnetic resonance spectroscopy (MRS) experiments were performed using a point resolved spectroscopy (PRESS)-type sequence at 7 Tesla. A double-echo gradient echo (GRE) sequence was used to acquire B₀ maps following MRS experiments. The basis set was modified based on the measured B₀ distribution within the MRS voxel. Quantification results were obtained after fitting the measured MRS data using the modified basis set. The proposed method was validated using numerical Monte Carlo simulations, phantom measurements, and by comparing occipital lobe MRS measurements under homogeneous and inhomogeneous magnetic field conditions. In vivo results acquired from voxels placed at thalamus and prefrontal cortex regions close to the frontal sinus agreed well with published values. Instead of noise-amplifying complex division, the proposed method treats field variations as part of the signal model, thereby avoiding inherent statistical bias associated with regularization. Simulations and experiments showed that the proposed approach reliably quantified results in the presence of relatively large magnetic field distortion.

INTRODUCTION

Brain neurochemistry has frequently been studied using in vivo magnetic resonance spectroscopy (MRS). Such studies have identified abnormal neurometabolite levels in various brain regions that provide insights into a range of brain disorders, including anxiety and affective disorders (1-4), obsessive-compulsive disorder (5,6), schizophrenia (4,7,8), and autism (9). Many of these studies reported neurometabolite differences between patients and healthy controls in cortical and deep brain regions. For example, abnormally low levels of N-Acetylaspartic acid (NAA) were found in the dorsolateral prefrontal cortex of individuals with bipolar and unipolar mood disorders (1,2). Patients with social anxiety disorder showed changes in NAA and choline (Cho) levels in thalamus, caudate, and putamen of the basal ganglia circuitry (3). In addition, several studies reported that, compared to healthy controls, patients with obsessive-compulsive disorder had a higher NAA/creatine (Cr) ratio in the prefrontal cortex and left hippocampus and a lower ratio in the bilateral thalamus (5,6). Glutamate and glutamine (Glu+Gln) levels in the thalamus have also been found to correlate positively with schizophrenia symptoms (7,8). Furthermose, significantly decreased NAA concentrations have been reported in the bilateral orbitofrontal cortex of autistic patients (9).

Despite these interesting findings, it should be noted that the quality of MRS data can be severely affected by static magnetic field distortion in cortical regions close to the sinuses and in deep brain regions. Difficulties in acquiring high quality MRS data in brain regions with large magnetic field inhomogeneity have undoubtedly contributed to some of the controversies extant in the literature (4). Quantification in MRS is generally based on idealized model lineshape functions. However, the accuracy of spectral fitting using idealized model function is limited when there is severe lineshape distortion due to large static B₀ field inhomogeneities. Large susceptibility effects are present in the prefrontal cortex region where the frontal sinus is located. Deep brain structures such as the thalamus and basal ganglia are also associated with large susceptibility effects, partly due to iron deposition. B₀ field inhomogeneities due to large susceptibility effects are usually difficult to compensate for studies performed on most clinical scanners. For high magnetic field studies, uncompensated magnetic field distortion can largely offset any gains in spectral resolution associated with increased magnetic field strength. In the presence of large B₀ field inhomogeneities, spectral lineshape is significantly distorted and cannot be properly characterized by idealized lineshape model functions. Thus, using idealized lineshape models to fit the observed data may lead to unreliable metabolite concentrations.

One possible solution to this problem is changing the model function from a single Lorentzian or Gaussian type to a finite sum of Lorentzian and Gaussian type lines with the cost of increased fitting parameters (10). Another widely used method corrects lineshape distortions by complex division using a reference signal, such as the unsuppressed water signal (11). Because water signal usually decays faster than metabolite signal—especially at high magnetic fields—Tikhonov regularization (12) and Wiener filtering (13) have been introduced to lineshape deconvolution to mitigate noise amplification associated with complex division. Another deconvolution method uses the B₀ field map from a separate acquisition as the reference signal (14), and lineshape distortions derived from B₀ field inhomogeneities are removed via complex division using the free induction decay (FID) synthesized from B₀ distribution within the MRS voxel.

The current study presents a new approach for analyzing MRS data acquired from regions with large uncompensated magnetic field distortion. We used a separately acquired B₀ map to synthesize lineshape functions. Instead of complex division—which is prone to spike artifacts and noise amplification, and introduces statistical bias through regularization—we modified the spectral basis set based on the acquired B₀ map. The modified basis set was then used to fit the in vivo MRS data. Since complex division was not used, this method did not require regularization.

THEORY

If an in vivo MRS voxel yields N different lines in the nuclear magnetic resonance (NMR) spectrum with offset frequencies ν_j and transverse relaxation time T_2j (1<j< J), the measured spectra S(ν) can be expressed by:

$$S\left(v\right)=f\left(v\right)\ast \sum _{j=1}^J{A}_j∕[\frac{1}{T{2}_j}+i2\pi (v-v_j\left)\right]$$ [1a]

$$f\left(v\right)=\mathcal{F}(\int e^{-i\Delta \omega \left(\mathit{r}\right)t}{d}^3\mathit{r})$$ [1b]

where ν refers to frequencies; A_j is the individual peak amplitude; the integral ∫ e^iΔω(r)t d³r is the FID synthesized from B₀ distributions (Δω) within the MRS voxel, where r indicates locations. f(ν) is the Fourier transform ($\mathcal{F}$) of the integral, acting as a convolution factor to the measured spectra. If the MRS voxel measures M_x, M_y, and M_z in three dimensions and the corresponding image voxel measures I_x, I_y, and I_z, the required number of pixels from the B₀ map for integration is:

$$N=\frac{M_x}{I_x}\cdot \frac{M_y}{I_y}\cdot \frac{M_z}{I_z}$$ [2]

Eq. 1b can be re-written as:

$$f\left(v\right)=\mathcal{F}\left(\sum _{n=1}^N{e}^{-i\Delta {\omega }_{n}t}\right)$$ [3]

Because B₀ distributions are relatively slow-varying within a spectroscopy voxel, image interpolation can be used as an alternative to time-consuming high resolution B₀ acquisitions.

The local field distribution can be computed based on phase difference and the time difference from a two-echo sequence. The distortion-free FID S_c(t) could be obtained through deconvolution in the frequency domain, which equals complex division in the time domain:

$$S_c\left(t\right)=S\left(t\right)∕\sum _{n=1}^N{e}^{-i\Delta {\omega }_{n}t}$$ [4]

However, because the FID synthesized from B₀ distribution usually decays more slowly than the metabolite FID, complex division only restores the part of metabolite FID that is above the noise level. This partial restoration leads to spike artifacts in the frequency domain. To avoid noise amplification due to complex division, regularization of Eq. 4 is usually necessary.

The spectral model function S_m(ν) linearly combines individual basis spectra simulated from density matrix with additional parameters that characterize quantification measures of concentrations, spectral linewidth, and spectral frequency shift. With a known field distribution function f(ν), a modified signal model S_d(ν) can be constructed:

$$S_d\left(v\right)=S_m\left(v\right)\ast f\left(v\right)$$ [5]

The aforementioned quantification parameters could be solved by minimizing the difference between the measured signal and the modified model signal in the least-square sense without bias-producing regularization:

$$\mathit{min}{\Vert S\left(v\right)-S_d\left(v\right)\Vert }^2$$ [6]

MATERIALS AND METHODS

Monte Carlo Simulations

Monte Carlo simulations were performed to validate the proposed method and compare it with the frequently used lineshape deconvolution method based on unsuppressed water. The ideal FIDs were computed by multiplying trial concentration values and T₂ decay functions to the density matrix-simulated FIDs. Metabolites of NAA, N-acetyl-aspartyl-glutamate (NAAG), Glu, Gln, Cr, and Cho were simulated with trial concentrations of 13, 2.6, 10, 1.5, 10, and 3; and T₂ values of 130ms, 130ms, 90ms, 90ms, 90ms, and 150ms, respectively (15). The FID synthesized from the B₀ map was generated by integrating all pixels from the B₀ map within the MRS voxel from a typical in vivo study (vide infra). The in vivo MRS voxel was selected to cover the thalamus region where large susceptibility effects were present. The simulated metabolite FIDs were generated by multiplying the combined ideal FIDs by the synthesized FID from B₀ map plus random noise. The unsuppressed water FID was similarly generated, with a T₂ value of 45ms (15).

Two methods were used to fit the simulated metabolite FIDs. The proposed method generates a modified basis spectral model by applying the FID synthesized from the B₀ map to the basis set. Quantification results from the simulated metabolite FID were determined by minimizing the difference between reconstructed spectra from simulated FIDs and the modified signal model using non-linear fitting software developed in-house (13). Metabolite concentrations were also determined using the lineshape deconvolution method based on unsuppressed water FID with a regularization parameter of 0.007. The regularization parameter was determined using the L-curve method (12). Both methods were repeated 100 times with the same noise level but different realizations of random noise. Results from two methods were compared with the assigned trial concentrations. Simulations and fitting procedures were all programmed in Matlab (R2014a).

Phantom Studies

MRS data from spherical oil and water phantoms were collected on a Siemens 7T scanner equipped with a 32-channel receiver head coil using a point resolved spectroscopy (PRESS)-type sequence with radio frequency (RF) suppression and echo time (TE) optimization (16). The water phantom contains metabolites including NAA, Cr, Cho, Glu, and myo-inositol (mI). The PRESS-type sequence was designed to spectrally resolve Glu and Gln. Acquisition parameters were: repetition time (TR): 2.5s; TE₁/TE₂: 69/37ms; voxel size: 2 or 3 cm isotropic, suppression pulse flip angle: 90°, spectral width: 4000Hz, number of data points: 2048, and number of transients: 128 with eight interleaved unsuppressed water acquisitions. In order to mimic an inhomogeneous magnetic field, shim currents were deliberately misadjusted. Immediately following the MRS acquisition, field map data were acquired using a double echo GRE sequence with the following acquisition parameters: TR: 657ms; TE₁/TE₂: 5.5/10.5ms; in-plane resolution: 3mm; slice thickness: 3mm. Or, TR: 700ms; TE₁/TE₂: 4.5/9.5ms; in-plane resolution: 1mm.

Phase maps (φ) were first unwrapped through a magnitude image-guided unwrapping algorithm (17). The B₀ distribution was then determined by the phase difference and time difference from two echoes:

$$\Delta \omega (x,y,z)=\frac{{\phi }_1(x,y,z)-{\phi }_2(x,y,z)}{({\mathit{TE}}_1-{\mathit{TE}}_2)}$$ [7]

The offline processing pipeline can be divided into three steps. The first step prepared a single metabolite FID and a single water FID from the multi-coil and multi-transient measurements. In this step, metabolite FIDs from 128 acquisitions were first aligned after frequency and phase correction, and then averaged over different transients for each of 32 channels. The 32-channel FIDs were averaged using a generalized least square method to yield a single metabolite FID (18). The single water FID was similarly computed and was subsequently used to remove eddy current effects. In the second step, the modified spectra signal model was constructed following Eq. 5 by applying the FID synthesized from the B₀ map to the basis set signal model. In the final step, fitting software developed in-house and programmed in Matlab (R2014a) solved metabolite concentrations by minimizing the difference between reconstructed spectra from measured data and the modified signal model in a least-square sense. Besides regular quantification parameters, the minimization procedure also included a cubic spline baseline function with eight control parameters compensating for baseline distortion (16). The same post-processing pipeline was applied to each MRS dataset. Quantification results from the homogeneous field acquisition were used as the ground truth reference. Metabolite concentrations from inhomogeneous fields were then compared with the ground truth references.

In Vivo Studies

Twelve healthy volunteers (two male, 10 female, ages 22 to 38) were scanned on a Siemens 7T scanner equipped with a 32-channel receiver head coil. All procedures were approved by the institutional review board (IRB) of the NIMH. Written informed consent was obtained from all participants.

Seven healthy volunteers were scanned in the occipital lobe to validate the proposed method. Before the MRS study, a high-resolution 3D T1-weighted MP-RAGE (magnetization prepared rapid gradient echo) sequence was used to locate the MRS voxel in a white matter-dominated area of the occipital lobe for each subject. Acquisition parameters were: TR: 3s; TE: 3.9ms; voxel size: 1mm isotropic. Two sets of MRS data were acquired from the same voxel of each subject using the PRESS-type sequence (16). First and second order B₀ shim coefficients were adjusted using FASTMAP (19) to achieve an essentially homogeneous magnetic field within the MRS voxel for the first dataset. The second dataset was acquired after manually misadjusting the first order shimming coefficients by approximately 20%. The first dataset with homogeneous field was treated as the approximate ground truth reference. Acquisition parameters for the PRESS-type sequence were: TR: 2.5s; TE₁/TE₂: 26/72ms; voxel size: 2cm isotropic. Immediately following each MRS data acquisition, the field map dataset was sampled using a double-echo GRE sequence with imaging parameters: TR: 700ms; TE₁/TE₂: 4.5/9.5ms; in-plane resolution: 1mm; slice thickness: 3mm. The data processing pipeline was the same as the phantom studies. Because Cr is a relatively stable metabolite, quantification precision of the new method was evaluated by comparing metabolite over Cr concentrations from the inhomogeneous field acquisition with the ground truth reference.

Five in vivo MRS datasets were also acquired from the thalamic region and from prefrontal cortex regions. The prefrontal cortex voxel was placed close to the frontal sinus. Due to large susceptibility effects, relatively large B₀ field inhomogeneities were present in both regions after shimming. All sequence parameters and data processing pipelines were the same as in the occipital lobe experiments described above.

RESULTS

Monte Carlo Simulation

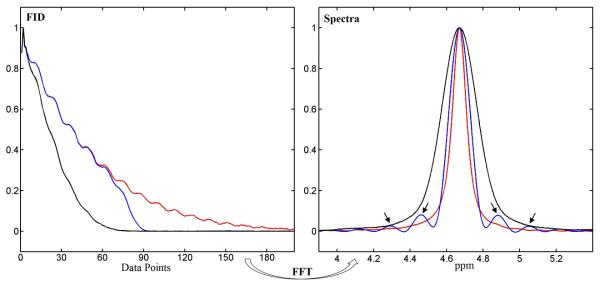
Figure 1 displays Monte Carlo simulation results of reconstructed spectra processed using the proposed method (left panel) as well as the regularized lineshape deconvolution method based on unsuppressed water signal (right panel). In each subfigure, the top trace was reconstructed from an FID with field distortion from an in vivo study and added Gaussian noise. The second trace from the top was reconstructed using parameters obtained from the spectral fitting procedure. The bottom two traces are baseline and residuals between the simulated spectrum and the reconstructed spectrum. Spike artifacts in the right subfigure are due to lineshape deconvolution where the decay rate of the reference signal was substantially different from the metabolite signals. In this case, the reference water signal decayed much faster than the metabolite signal. Comparison of quantification results from 100 simulations with known ground truth concentrations and different noise realizations are displayed in Figure 2. The proposed method, which was free of spike artifacts and statistical bias associated with regularization, yielded greatly improved accuracy compared with the lineshape deconvolution method. Because the water signal decayed much faster than the metabolite signal due to large B₀ field inhomogeneities at 7 Tesla, as expected, the regularized-unsuppressed water method had relatively large quantification errors.

Figure 1.

Linear combination fitting plots by the proposed method (left) and the line-shape deconvolution method based on unsuppressed water signal (right). Spike artifacts in the right panel were due to lineshape deconvolution when the reference signal and the metabolite signals decayed at different rates.

Figure 2.

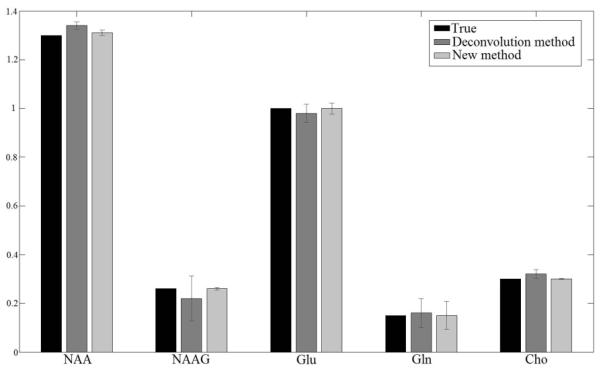
Mean and standard deviation of metabolite/Cr concentration ratios from 100 simulations with different noise realizations. Black, dark gray and light gray bars represent ground truth concentrations, simulations from regularized unsuppressed water method and the proposed method, respectively. Maximum quantification error for the water method is 14.31% and for the proposed method is 2.67%. The exact concentration numbers are provided in Table 1 of supplemental information.

Phantom study

Figure 3 shows typical spike artifacts in conventional lineshape deconvolution when metabolite signals decay faster than the reference signal. FID synthesized from the B₀ map was used as the lineshape reference. As shown in the left panel of Figure 3, in the presence of severe B₀ inhomogeneity, dividing an FID signal synthesized from the B₀ map into the metabolite FID (black) only restored the part of the metabolite FID signal above the noise level (blue). This partial restoration led to spike artifacts in the frequency domain after Fourier transformation (arrows in right panel).

Figure 3.

Left panel: Oil phantom free induction decays (FIDs) acquired with homogeneous B₀ field (red) and inhomogeneous B₀ field (black). The latter was partially restored by complex division (blue). Right panel: corresponding spectra. Arrows indicate spike artifacts.

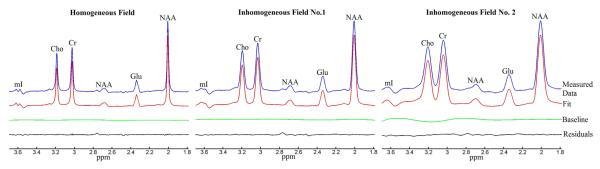
To evaluate the robustness of the proposed method, we manually distorted the magnetic field in the second phantom study. Reconstructed spectra from the second phantom study with different B₀ field inhomogeneities are shown in Figure 4. The top traces were reconstructed from measured spectral data. In the left subfigure, the magnetic field was shimmed by FASTMAP. In the middle and right subfigures, the field was distorted by misadjusting the first order shim currents by 20% and 40%, respectively. The second traces from the top were linearly combined by fitting results based on basis set spectra modified by the measured B₀ maps. The bottom two traces are baseline and residuals between the top two traces. Quantification results are shown as bar graphs in Figure 5. Compared to the ground truth reference, metabolite concentrations, as expected, tended to deviate further as the background field inhomogeneity became progressively larger. In Figure 4 and 5, the linewidth of the NAA signal was increased approximately four- and eight-fold under the first and second inhomogeneity conditions, respectively.

Figure 4.

Linear combination fitting plots of metabolite aqueous phantom data acquired at three different B₀ field inhomogeneities. Five metabolites were analyzed: NAA, Cho, Cr, Glu and mI. The small signal around 2.76 ppm was not included in the spectral model.

Figure 5.

Phantom metabolite/Cr concentration ratios from acquisitions with homogeneous field (black bar) and two different inhomogeneous fields (dark and light gray bars). The exact concentration numbers are provided in Table 2 of supplemental information.

In Vivo studies

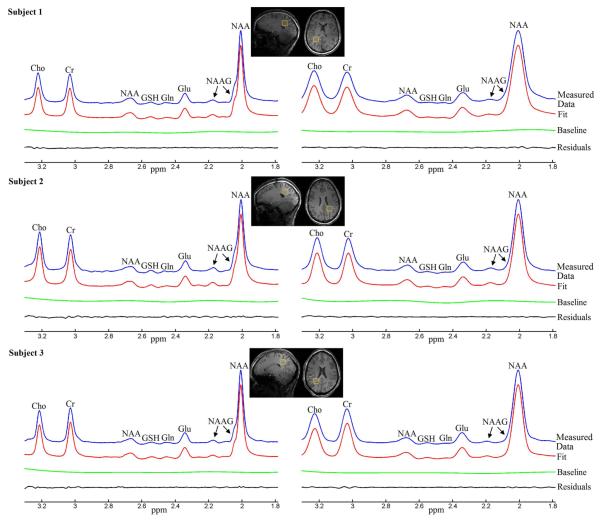
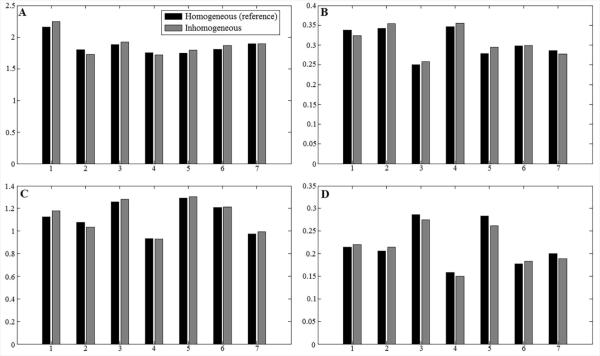
Figure 6 displays typical occipital lobe results from the in vivo method validation studies using healthy volunteers. MRS voxel locations are indicated by the yellow box overlaid on the axial and sagittal high resolution T₁-weighted images. For each subfigure, from top to bottom are reconstructed spectrum from measured FID, fitted spectrum, baseline and residuals between reconstructed spectrum and fitted spectrum. Despite deliberate misadjustment of shim currents for spectra on the right column of Figure 6, all spectra from the seven subjects yielded small residuals. Quantification results for major metabolites are displayed as bar graphs in Figure 7. Compared to the ground truth references estimated under homogeneous field conditions, most quantification results from inhomogeneous field acquisition yielded less than 5% error. The mean quantification errors across seven subjects are 0.9% for NAA, 1.18% for Cho, 0.74% for Glu and −2.10% for Gln.

Figure 6.

Linear combination fitting plots from homogeneous field acquisition (left panels) and inhomogeneous field acquisition (right panels) of three healthy volunteers (different rows). The two acquisitions of each individual subject are from the same voxel located in the occipital lobe, indicated by the yellow boxes on the sagittal and axial T1-weighted images.

Figure 7.

Metabolite/Cr concentration ratios from homogeneous (black bar) and inhomogeneous field (gray bar) acquisitions of seven healthy volunteers. Four different chemicals are compared here, including NAA (A), Cho (B), Glu (C) and Gln (D). The mean quantification errors across seven subjects are 0.9% for NAA, 1.18% for Cho, 0.74% for Glu and −2.10% for Gln. The exact concentration numbers are provided in Table 3 of supplemental information.

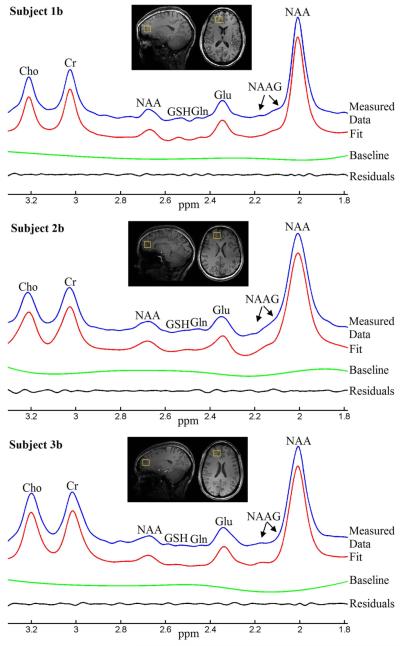
Results from thalamic and prefrontal cortical voxels are displayed in Figures 8 and 9, respectively. For each subfigure, from top to bottom are reconstructed spectrum from measured FID, fitted spectrum, baseline and residuals between reconstructed spectrum and fitted spectrum. Quantification results for the thalamus and prefrontal cortex studies are summarized in Tables 1 and 2. Previous published metabolite values were calculated as metabolite to Cr concentration ratios and compared with our quantification results. Our quantification results were generally within the range of previously published values (1-3, 7-9, 20, 21).

Figure 8.

Linear combination fitting plots from the thalamic regions of three healthy volunteers. The MRS voxels, indicated by the yellow boxes in the sagittal and axial T1-weighted images, cover the entire thalamus.

Figure 9.

Linear combination fitting plots from the prefrontal lobe voxel of three healthy volunteers. The MRS voxels were marked by the yellow boxes in the sagittal and axial T1-weighted images.

TABLE 1.

Metabolite/Creatine concentration ratios from thalamic voxel

Chemicals	NAA	CHO	GLU	GLN
Subject1a	2.0543	0.4034	1.2623	0.2078
Subject2a	1.7423	0.2870	0.9685	0.1641
Subject3a	1.5167	0.4095	1.1483	0.1517
Subject4a	1.4809	0.2949	1.1449	0.2127
Subject5a	1.3499	0.3217	1.4406	0.2995
Mean±Std	1.63±0.28	0.34±0.06	1.19±0.17	0.21±0.06
Published *	0.95-1.63	0.20-0.33	0.77-1.48	0.09-0.79

^*Published values were obtained from references 3, 8, and 20

Abbreviations: NAA: N-acetylaspartic acid; Cho: choline; Glu: glutamate; Gln: glutamine

TABLE 2.

Metabolite/Creatine concentration ratios from prefrontal lobe voxel

Chemicals	NAA	CHO	GLU	GLN
Subject1b	2.1502	0.2636	1.1505	0.2765
Subject2b	1.4570	0.3126	1.1605	0.1008
Subject3b	1.6491	0.3089	1.6001	0.5335
Subject4b	1.7694	0.2770	1.3081	0.4813
Subject5b	1.4736	0.3242	1.1660	0.1683
Mean±Std	1.70±0.28	0.30±0.03	1.28±0.19	0.31±0.19
Published *	1.03-2.00	0.12-0.75	1.05-1.27	0.26-0.36

^*Published values were obtained from references 1, 2, 7, 9, and 21

Abbreviations: NAA: N-acetylaspartic acid; Cho: choline; Glu: glutamate; Gln: glutamine

DISCUSSION

Metabolite quantification in cortical and deep brain gray matters may provide important biomarkers for a variety of neurological and psychiatric disorders. However, large susceptibility effects in basal ganglia, hippocampal, thalamic, and prefrontal cortex areas cause large spectral lineshape distortions, and introduce significant errors when fitting the distorted spectra using idealized lineshape models. Lineshape distortions may be corrected by complex division using a reference signal such as the unsuppressed water signal, or a synthesized signal using the acquired B₀ distribution. In this type of methods, regularization (either in the form of Tikhonov regularization or Wiener filtering) is required to avoid disastrous noise amplification at zero crossings (12, 13). In both Tikhonov regularization and Wiener filtering, the linear square solution is modified. As a result, these methods introduce inherent systematic errors (i.e., statistical bias) to metabolite quantification (22). In addition, because the reference signal often decays at a different rate from the metabolite signals, spike artifacts are generated; these must be carefully avoided so as not to confound MRS measurements. The widely used MRS data processing software LCModel (23) uses a built-in regularized and constrained model-free lineshape function to account for lineshape distortions. Because all regularization procedures skew the unbiased least square solution, lineshape regularization in LCModel generates statistical bias (24). At the cost of extra scans, the proposed method experimentally determines the lineshape function by measuring the B₀ map. Removing lineshape function from parameters to be determined by fitting can minimize the possibility of an inaccurate lineshape function and reduces the degree of freedom in fitting. Since no regularization is involved, the proposed method leads to the unbiased solution.

The present study used a modified signal model to minimize the difference between the observed signal and the signal model as an alternative to existing approaches. In particular, the signal model was modified by the same amount of lineshape distortion introduced by the B₀ field inhomogeneities. This was achieved by measuring the magnetic field using standard B₀ mapping and applying the measured B₀ distribution to the idealized lineshape model. The modified lineshape model was then employed to fit the measured metabolite data. One key advantage of this method is that complex multiplication instead of complex division was needed to achieve effective lineshape deconvolution. As such, the method avoids the noise amplification associated with complex division and no bias-producing regularization is required. This novel approach significantly improved the accuracy and reliability of spectral fitting in the presence of large magnetic field distortion. Since complex division has been used in a variety of lineshape correction schemes in MRS and NMR in general, we expect that the general idea proposed here will find other applications (e.g., in eddy current correction by reference signals).

Accurate and rapid measurement of the field map is a key step in this method. A variety of B₀ mapping methods have been proposed in the literature. The gold standard and most accurate B₀ mapping method collects multiple closely spaced phase data, and calculates the phase slope verse echo time from a linear square error fit. Another widely used method computes the B₀ map by measuring the linear phase shift in the frequency domain. Rapid B₀ mapping can also be achieved by using echo planar readout gradient train (25) or modified k-space trajectory (in which the center of the k-space is sampled twice (26)). Although we used a simple gradient echo method, multi-echo data point fitting may further improve the accuracy of metabolite quantification, while the echo planar readout could accelerate field map data sampling.

The single voxel MRS samples data from a small region of the human brain. On the other hand, the B₀ map acquired using the standard double echo-GRE sequence covers the whole brain slices. The current study calculated a synthesized signal from image pixels that matches the locations inside the MRS voxel. As the B₀ map covers more brain regions, the synthesized signal could be calculated from any locations within it. The current method can be easily extended to multi-voxel MRS or magnetic resonance spectroscopic imaging (MRSI). For both multi-voxel MRS and MRSI, while spectra are acquired from different brain locations to measure the metabolite variations, the B₀ field map only requires a single acquisition.

The Monte Carlo simulation study numerically validated our proposed method. Phantom studies validate the accuracy of lineshpae generated from B₀ maps using non-overlapping signals from NAA, Glu, Cr, Cho and mI under different field inhomogeneous conditions. The benefit of using non-overlapping signal is to separate the effects of lineshape function from those of overlapping signals. Since the in vivo ground truth values of metabolites were unknown, we used a voxel placed in the occipital lobe and compared metabolite quantification results under homogeneous and inhomogeneous B₀ distributions. The occipital lobe is far from the sinus. The occipital voxel is also close to the isocenter of the magnetic field. Thus, the MRS voxel located in the occipital lobe can be shimmed very well. In this study, the mean NAA linewidth under the first field homogeneity condition was 10.27+1.33Hz, indicating excellent B₀ homogeneity after adjusting both first- and second-order shim currents. We were able to use the well-shimmed occipital lobe spectra as the approximate ground truth reference to validate the proposed data fitting method based on complex multiplication. It is worthwhile to mention that although FASTMAP technique (19) has been used in this study, the more optimal shimming technique FASTEST MAP (25) could further improve field homogeneities and thus offers more reliable reference values. As shown in Figure 5, the mean quantification errors across the seven subjects under inhomogeneous B₀ distribution in the occipital lobe voxel were fairly small, providing strong in vivo validation of the proposed method. In particular and as expected, no significant systematic error was observed in metabolite quantification due to our complex-multiplication-based lineshape correction procedure as evidenced by the fact that errors with respect to the approximate ground truth values were markedly reduced upon averaging across the seven subjects.

All voxels in the current study were carefully chosen to avoid significant cerebrospinal fluid (CSF) space. However, the composition of the MRS voxel should be considered when significant amount of CSF enters the spectroscopic volume. In particular, the B₀ pixels corresponding to the CSF should be taken out of the lineshape function synthesized from B₀ map (the integral in Eq. 3). Because T₂ of CSF (~1500ms) is much longer than T₂ of brain tissue (~80ms-110ms), intensity based-segmentation could be easily applied to remove pixels originated from CSF.

Tables 1 and 2 show relatively large range in reported metabolite concentrations in the thalamus and prefrontal cortical regions. In addition to variations attributable to differences in anatomy, age, sex, and MRS method, the difficulties in acquiring high quality MRS data and fitting them also contributed to the reported discrepancies. Furthermore, previous publications are all based on relatively small sample sizes and relatively low magnetic field strength. With the above qualifications, our thalamus and prefrontal cortical results generally agree with values previously reported in the literature. However, we would expect this proposed method to fail when B₀ field inhomogeneities are very severe, and used phantom studies to evaluate the limitations of our novel method. When NAA linewidth was increased by approximately eight times in the second inhomogeneity condition, the error was still within 6.5% (see Figure 4 and 5). Therefore, we do not expect large errors in our thalamus and prefrontal cortex results although the ground truth values were unknown in this case. The unknown ground truth values in these two locations remain a limitation of our study.

Unlike spectral editing methods that directly resolve signal of interest and can be used to quantify metabolites with low concentrations, the current method only treats lineshape distortion caused by B₀ field inhomogeneity. As such, it is limited for quantifying metabolites that are known to have spectral interference and exist at low concentration.

Many clinical questions require the assessment of brain regions with large susceptibility effects. For example, most psychiatric diseases involve the frontal lobe. A general increase in the quality of MRS data acquired from regions close to the frontal sinus will thus be of great value to the field of psychiatric MRS. In addition, the problem of lineshape distortion is expected to be further aggravated by the continued growth of high magnetic field applications. Figure 1 and 2 show that at 7 Tesla, the new method markedly outperformed the Tikhonov regularization-based lineshape deconvolution method. This is not surprising considering the much shorter tissue water decay at 7 Tesla, which makes it harder to use any tissue water-based lineshape deconvolution schemes. Therefore, we expect that the proposed method will be generally useful for enhancing the quality of clinical MRS data acquired from brain regions associated with relatively large magnetic field distortions after shimming.

In conclusion, the present study demonstrates and evaluates a novel approach to spectral fitting that can be used in the presence of large magnetic field distortion, especially at high fields. The magnetic field distribution was first measured through standard B₀ mapping. An FID synthesized from the magnetic field distribution within the MRS voxel was then applied to the basis set. The modified basis set was used to fit in vivo MRS data. Monte Carlo simulations showed that the proposed approach yielded fewer errors compared to the frequently used unsuppressed water method. Phantom and in vivo validation experiments showed that the proposed approach provides reliable and improved quantification results in the presence of relatively large magnetic field distortion.

Abbreviations

Cho

choline

Cr

creatine

FID

free induction decay

Gln

glutamine

Glu

glutamate

GRE

gradient echo

mI

myo-inositol

MRS

magnetic resonance spectroscopy

NAA

N-Acetylaspartic acid

NAAG

N-acetyl-aspartyl-glutamate

NMR

nuclear magnetic resonance

φ

phase maps

PRESS

Point resolved spectroscopy

RF

radio frequency

TE

time echo

TR

repetition time

MRSI

magnetic resonance spectroscopic imaging