A penalized robust semiparametric approach for gene-environment interactions

Abstract

In genetic and genomic studies, gene-environment (G×E) interactions have important implications. Some of the existing G×E interaction methods are limited by analyzing a small number of G factors at a time, by assuming linear effects of E factors, by assuming no data contamination, and by adopting ineffective selection techniques. In this study, we propose a new approach for identifying important G×E interactions. It jointly models the effects of all E and G factors and their interactions. A partially linear varying coefficient model (PLVCM) is adopted to accommodate possible nonlinear effects of E factors. A rank-based loss function is used to accommodate possible data contamination. Penalization, which has been extensively used with high-dimensional data, is adopted for selection. The proposed penalized estimation approach can automatically determine if a G factor has an interaction with an E factor, main effect but not interaction, or no effect at all. The proposed approach can be effectively realized using a coordinate descent algorithm. Simulation shows that it has satisfactory performance and outperforms several competing alternatives. The proposed approach is used to analyze a lung cancer study with gene expression measurements and clinical variables.

1. Introduction

In genetic and genomic studies, it has been shown that gene-environment (G×E) interactions can have important implications beyond the main, additive effects. A large number of statistical methods have been developed searching for G×E interactions associated with, for example, disease outcomes and phenotypes [1]. In practice, the G factors can be gene expressions, SNPs, methylation, and other types of measurements. The E factors can be environmental exposures as well as clinical measurements of interest [2].

The existing methods, despite certain successes, may have limitations. First, some methods analyze one or a small number of G factors at a time, that is, their marginal effects [1]. Complex disease outcomes and phenotypes are associated with the joint effects of multiple G and E factors and their interactions. Marginal analysis may miss factors with weak marginal but strong joint effects. Second, most of the existing methods assume linear effects of E factors. In epidemiologic studies with low-dimensional data, it has been shown that some factors, for example age in cancer studies, often have nonlinear effects. Failing to account for the nonlinearity may result in wrong estimation and inference. Third, likelihood-based approaches have been extensively adopted. Such approaches assume that data have no contamination. Under high-dimensional settings, a few methods have been developed that can be potentially robust to data contamination. Examples include a mixture-model approach, which allows data to have different distributions [3]. The most extensively used robust approach with high-dimensional data is perhaps quantile regression [4]. However, its application to G×E interaction study is still limited. In a recent study, Shi et al. [5] developed a robust approach based on the smoothed penalized rank estimation. This approach is limited by analyzing the marginal effects. In addition, it is designed to be robust to model mis-specification. It is unclear whether it is robust to data contamination. Fourth, ineffective statistical techniques have been adopted in the selection of important G and E factors and their interactions. In the recent literature, penalization has surfaced as an effective technique for analyzing G×E [6] G×G [7] interactions, especially with the development of hierarchical LASSO and related methods [8]. However, the existing penalization methods have been applied mostly under the assumption of no contamination and linear effects. Development in this study has been motivated by the aforementioned limitations of existing methods.

In this article, we apply a penalized robust semiparametric approach for analyzing G×E interactions in high-dimensional genetic and genomic studies. It may advance from the existing studies along the following directions. First, the joint model accommodates the effects of a large number of G and E factors and their interactions. Second, a partially linear varying coefficient model (PLVCM) is adopted to accommodate possible nonlinear effects of E factors. In principle, for continuous G factors, for example gene expressions, it is also possible to consider nonlinear effects. However, when the dimensionality of G factors is high, the computational cost can be prohibitive. Thus, we limit to nonlinear effects of E factors only. Varying coefficient (VC) model has been extensively adopted because of its flexibility [9]. A large number of estimation and model selection methods have been developed for VC models under low-dimensional settings [10]. More recently, VC models have also been adopted for analyzing genetic and genomic data, however, under simpler settings [11, 12]. Third, a rank-based loss function is adopted to accommodate possible data contamination. It significantly differs from quantile regression and other robust approaches and provides a flexible alternative. It is noted that even under low-dimensional settings, there is no dominatingly better robust approach. Thus, the rank-based approach is of interest beyond quantile regression, especially under the present complicated data and model settings. Fourth, an effective penalization approach is adopted for selection. Although the penalization framework is similar to that of existing studies, the adopted approach is novel in analyzing the present more complicated data and model settings. More importantly, it can automatically determine if there is an G×E interaction, main effect only, or no genetic effect at all. These methodological advancements make the proposed approach a useful addition to the existing studies. Performance of the proposed approach is examined through simulation and the analysis of a lung cancer study with gene expression measurements.

2. Statistical Methods

2.1. Partially linear varying coefficient model

Let (X_i, Y_i, U_i, E_i), i = 1, … , n be independent and identically distributed (i.i.d.) random vectors. Y_i is the response variable. X_i is the (p + 1)-dimensional design vector of G factors, with the first component being 1. U_i and E_i are the continuous and discrete E factors, respectively. We consider only two E factors for simplicity of notation. Generalization to multiple E factors is trivial. Consider the PLVC model

$$Y_i=\sum _{k=0}^p{\alpha }_k\left(U_i\right)X_{\mathit{ik}}+\sum _{k=0}^p{\beta }_k{X}_{\mathit{ik}}{E}_i+{\epsilon }_i,$$ (1)

where α_k(·) is the smooth varying-coefficient function, X_ik is the kth component of X_i, and ε_i is the random error.

We approximate the VC function α_k(U) via basis expansion

$${\alpha }_k\left(U_i\right)\approx \sum _{l=1}^L{\tilde{\delta }}_{\mathit{kl}}{\tilde{B}}_{\mathit{kl}}\left(U_i\right),$$

where L is the number of basis functions, ${\tilde{B}}_k\left(U_i\right)={\left({\tilde{B}}_{k1}\right(U_i),\dots ,{\tilde{B}}_{\mathit{kL}}(U_i\left)\right)}^T$ is a set of normalized B spline basis, and ${\tilde{\delta }}_k={({\tilde{\delta }}_{k1},\dots ,{\tilde{\delta }}_{\mathit{kL}})}^T$ is the coefficient vector. By changing of basis, the above basis expansion is equivalent to

$${\alpha }_k(\cdot )\approx \sum _{l=1}^L{\tilde{\delta }}_{\mathit{kl}}{\tilde{B}}_{\mathit{kl}}(\cdot )\doteq {\delta }_{k1}+{\tilde{B}}_{k\ast }^T(\cdot ){\delta }_{k\ast },$$

where ${\tilde{B}}_{k\ast }\left(U_i\right)={\left({\tilde{B}}_{k2}\right(U_i),\dots ,{\tilde{B}}_{\mathit{kL}}(U_i\left)\right)}^T\cdot {\delta }_{k1}$ and δ_k∗ = (δ_k2, … , δ_kL)^T correspond to the constant and varying parts of the coefficient functional, respectively. Define ${\delta }_k={({\delta }_{k1},{\left({\delta }_{k\ast }\right)}^T)}^T$ and $B_k\left(U_i\right)={(1,{\left({\tilde{B}}_{k\ast }\right(U_i\left)\right)}^T)}^T\doteq {\left(B_{k1}\right(U_i),\dots ,B_{\mathit{kL}}(U_i\left)\right)}^T$. With the basis expansion, model (1) can be rewritten as

$$\begin{array}{cc}\hfill Y_i=& \sum _{k=0}^p\sum _{l=1}^L{\delta }_{\mathit{kl}}{B}_{\mathit{kl}}\left(U_i\right)X_{\mathit{ik}}+\sum _{k=0}^p{\beta }_k{X}_{\mathit{ik}}{E}_i+{\epsilon }_i\hfill \\ \hfill =& \sum _{k=0}^p{\left({\delta }_k\right)}^T{Z}_{\mathit{ik}}+\sum _{k=0}^p{\beta }_k{X}_{\mathit{ik}}{E}_i+{\epsilon }_i,\hfill \end{array}$$ (2)

where Z_ik = B_k(U_i)X_ik = (B_k1(U_i)X_ik, … , B_kL(U_i)X_ik)^T.

2.2. Robust estimation using a rank based loss function

Let W_i = (W_i0, … , W_ip)^T where $W_{\mathit{ik}}={(Z_{\mathit{ik}}^T,X_{\mathit{ik}}{E}_i)}^T$. Define the coefficient vector $\gamma ={({\gamma }_0^T,\dots ,{\gamma }_p^T)}^T$ with γ_k = ((δ_k)^T, β_k)^T. Then from (2), we can express the residual as ${\epsilon }_i=Y_i-W_i^T\gamma$.

In linear regression based on the Wilcoxon scores, the global rank loss function [n(n − 1)]⁻¹ ∑_i<j ∣ε_i − ε_j∣ results in the classic rank estimator. Consider the rescaled rank based loss function

$$L\left(\gamma \right)=\frac{1}{n}\sum _{i<j}\mid {\epsilon }_i-{\epsilon }_j\mid .$$ (3)

As this loss function is not differentiable, the gradient based optimization methods cannot be applied. This is especially troublesome with high-dimensional data. Following Sievers and Abebe [13], we consider the approximation

$$\sum _{i<j}\mid {\epsilon }_i-{\epsilon }_j\mid \approx \sum _{i=1}^n{\theta }_i{({\epsilon }_i-\eta )}^2,$$

where η is the median of ${\left\{{\epsilon }_i\right\}}_{i=1}^n$ and

$${\theta }_i=\{\begin{array}{cc}\frac{\frac{R\left({\epsilon }_i\right)}{n+1}-0.5}{{\epsilon }_i-\eta }\hfill & {\epsilon }_i\ne \eta \hfill \\ 0\hfill & \text{Otherwise}.\hfill \end{array}\phantom{\}}$$

Here R(ε_i) is the rank of ε_i in ${\left\{{\epsilon }_i\right\}}_{i=1}^n$.

The rank based estimation procedure provides a robust alternative to the classic likelihood based estimation. It does not make parametric distributional assumptions on the random error. The absolute value (median) based estimation makes it robust. Note that the formulation of loss function differs significantly from those in Shi et al. [5] (which is a rank correlation function), quantile regression, and others. In principle, the approximation is not necessary. In addition, there may be multiple possible smooth approximations. The adopted approximation can be preferred because of its low computational cost.

Denote Y = (Y₁, … , Y_n)^T, Σ = (W₁, … , W_n)^T, and Σ_k as the submatrix of Σ corresponding to γ_k. Without loss of generality, assume that Σ_k is orthogonalized such that $\frac{1}{n}{\Sigma }_k^T{\Sigma }_k=I\text{for}k=0,\dots ,p$. Note that this orthogonality condition is simply for ease of describing the computational algorithm. It is not essential. Without orthogonality, the update in the computational algorithm described in Section 2.4 is still solvable but does not have a simple form. Consider the approximated loss function

$$\tilde{L}\left(\gamma \right)=\frac{1}{n}{(Y-\Sigma \gamma -{\eta }^0)}^T{ϴ}^0(Y-\Sigma \gamma -{\eta }^0),$$

where η⁰ is the median of ${\{Y_i-W_i^T\gamma \}}_{i=1}^n$ and ${ϴ}^0=\mathrm{diag}\{{\theta }_1^0,\dots ,{\theta }_n^0\}$ with ${\theta }_i^0$ being the weight of the ith subject corresponding to γ. Note that both η⁰ and Θ⁰ involve the unknown parameter γ. In practice, we need an initial value for γ. In our numerical study, we use that from an unrobust penalized estimation and find that when data are not heavily contaminated, this initial value works well.

2.3. Penalized identification of G×E interactions

First consider the penalized estimate

$$\tilde{\gamma }={\mathrm{argmin}}_{\gamma }\left\{\tilde{L}\left(\gamma \right)+\lambda \sum _{k=0}^p\Vert {\gamma }_k\Vert \right\}.$$ (4)

λ is the data-dependent tuning parameter, and ∥·∥ is the ${\ell }_2$ norm. Note that the normalization of Σ_k can be equivalently achieved by replacing ∥γ_k∥ with ${\Vert {\gamma }_k\Vert }_{{\Sigma }_k}.\tilde{\gamma }$ defined above is a group LASSO type estimate. Denote γ_k,1, γ_k∗, and γ_k,(L+1) as the components of δ_k corresponding to the constant and varying parts of the coefficient functional and the discrete E factor, respectively. Denote ${\tilde{\gamma }}_{k,1},{\tilde{\gamma }}_{k\ast }$, and ${\tilde{\gamma }}_{k,(L+1)}(k=0,\dots ,p)$ as the corresponding components of the penalized estimate.

With $\tilde{\gamma }$ computed in (4), we further consider the penalized estimate

$$\widehat{\gamma }={\mathrm{argmin}}_{\gamma }\left\{\tilde{L}\left(\gamma \right)+\lambda \sum _{k=0}^p[w_{k,1}\Vert {\gamma }_{k,1}\Vert +w_{k\ast }\Vert {\gamma }_{k\ast }\Vert +w_{k,(L+1)}\Vert {\gamma }_{k,(L+1)}\Vert ]\right\}.$$ (5)

The weights are defined as $w_{k,1}={\Vert {\tilde{\gamma }}_{k,1}\Vert }^{-1},w_{k\ast }=(L-1){\Vert {\tilde{\gamma }}_{k\ast }\Vert }^{-1}$, and $w_{k,(L+1)}={\Vert {\tilde{\gamma }}_{k,(L+1)}\Vert }^{-1}$. Interactions and main effects corresponding to the nonzero components of $\widehat{\gamma }$ are identified as important. The number of identified interactions is controlled by the value of λ, which will be determined by a data-dependent approach (as described below). Note that here interaction identification is based on the penalized estimation. This strategy differs significantly from the popular significance level-based.

$\widehat{\gamma }$ defined in (5) is an adaptive group LASSO type estimate [14]. The weights come from a group LASSO estimate. With group covariates, the “LASSO + adaptive LASSO” strategy has been studied [15]. It is also closely related to the bridge penalization [16]. To determine whether an effect is varying or nonzero constant, we penalize the norm of γ_k∗, which corresponds to the spline coefficients, as a group. If ∥γ_k∗∥ = 0, the kth G factor only has a nonzero constant (or main) effect. In addition, the G factor has no main effect if ∥γ_k,1∥ = 0. Similarly, whether ∥γ_k,(L+1)∥ shrinks to 0 or not can be used to determine if there is an interaction between the G factor and discrete E factor. In this way, we can achieve the goal of simultaneous variable selection and separation of the varying/nonzero constant/zero effects. The group LASSO penalties can be replaced by other group penalties. The LASSO types penalties may be preferred because of their computational simplicity. In addition, under simpler data and model settings, the “LASSO + adaptive LASSO” strategy has been shown to have good theoretical and empirical performance [15].

Note that the proposed method does not respect the “main effects, interactions” hierarchy, which has been discussed in several recent studies [6]. That is, it is possible that an interaction is identified, but its corresponding main effect is not. Models with pure interactions in the absence of main effects have been discussed in the literature [7, 17, 18] and viewed as reasonable. As shown in published studies [6, 8], respecting the hierarchy demands significantly more complicated penalties which can lead to higher computational cost. If it is of special interest to keep the hierarchy, one can first apply the proposed method and then add back the main effects if needed.

2.4. Computational algorithm

Estimates defined in (4) and (5) can be computed using the same algorithm. Consider the group coordinate descent (GCD) algorithm, which optimizes the objective function with respect to a single predictor group at a time and iteratively cycles through all the predictor groups till convergence.

The GCD algorithm proceeds as follows. For a fixed tuning parameter λ:

• (1)Compute the initial estimate $\tilde{\gamma }$ as in (4), and initialize the vector of residuals $r=Y-{\sum }_{k=0}^p{\Sigma }_k{\tilde{\gamma }}_k-{\eta }^{\left(0\right)}$, and s = 0.
• (2)For k = 0, 1, … , p, iterate the following steps:

Denote γ_k,sub.1 = γ_k,1, γ_k,sub.2 = γ_k∗, and γ_k,sub.3 = γ_k,(L+1). Let Σ_k,sub.m be the submatrix of Σ_k corresponding to γ_k,sub.m and w_k,sub.m be the corresponding weight calculated as in (5) (m=1,2,3). Let ${ϴ}^{\left(s\right)}=\mathit{diag}\{{\theta }_1^{\left(s\right)},\dots ,{\theta }_n^{\left(s\right)}\}$ with ${\theta }_i^{\left(s\right)}$ being the weight of the ith subject in the sth iteration. For m = 1, 2, 3, repeat

• (a)Calculate $t_{k,\mathrm{sub}.m}=n^{-1}{\Sigma }_{k,\mathrm{sub}.m}^T{ϴ}^{\left(s\right)}r+{\gamma }_{k,\mathrm{sub}.m}^{\left(s\right)}$.

• (b) Calculate ${\gamma }_{k,\mathrm{sub}.m}^{(s+1)}={\left(1-\frac{\lambda w_{k,\mathrm{sub}.m}}{\Vert t_{k,\mathrm{sub}.m}\Vert }\right)}_{+}{t}_{k,\mathrm{sub}.m}$.

• (c)Update $r=r-{\Sigma }_{k,\mathrm{sub}.m}\left({\gamma }_{k,\mathrm{sub}.m}^{(s+1)}-{\gamma }_{k,\mathrm{sub}.m}^{\left(s\right)}\right)$.

Update s = s + 1.

• (3)Iterate step (2) until convergence.

Denote Q(·) as the penalized objective function. As it is minimized with respect to γ in each cycle of the GCD algorithm, we have the following descent property for the sequence of updates $\{{\widehat{\gamma }}^{\left(s\right)}:s=0,1,\dots \}$.

Proposition

Let ${\widehat{\gamma }}^{\left(s\right)}$ be the estimated coefficient vector at the convergence of the sth iteration. Then $Q\left({\widehat{\gamma }}^{\left(s\right)}\right)\le Q\left({\widehat{\gamma }}^{(s-1)}\right)$. Moreover, the sequence $\{{\widehat{\gamma }}^{\left(s\right)}:s=0,1,\dots \}$ converges to the global minimum of Q.

The proof follows from arguments similar to those in Breheny and Huang [19] and the application of Theorem 4.1 of Tseng [20]. In addition, since the sequence {Q(γ^(s)) : s = 0, 1, …} is non-increasing and bounded below by 0, it always converges.

Tuning parameter selection

To implement the proposed approach, we need to choose proper tuning parameters: the degree of B spline basis $\mathcal{D}$, number of interior knots $\mathcal{K}$, and λ.

We first select $\mathcal{D}$ and $\mathcal{K}$ using the BIC criterion. Possible values of $\mathcal{K}$ are from $\left\{\max \right(\lfloor 0.5n^{1∕(2\mathcal{D}+3)}\rfloor ,1),\lfloor 1.5n^{1∕(2\mathcal{D}+3)}\rfloor \}$, where ⌊α⌋ denotes the integer part of α. Although it is in principle possible to choose $\mathcal{D}$ and $\mathcal{K}$ for each varying coefficient function, the computational cost can be prohibitively high. Thus in the basis expansion, we take that all the varying coefficient functions are approximated with the same $\mathcal{D}$ and $\mathcal{K}$. We jointly search the optimal $(\mathcal{D},\mathcal{K})$ according to the following criteria:

$${\mathrm{BIC}}_{\mathcal{D},\mathcal{K}}=\log ({\mathrm{RSS}}_{\mathrm{I}}∕n)+(\mathcal{D}+\mathcal{K}+1)\log \left(n\right)∕n,$$

where RSS_I is the residual sum of squares of the intercept model.

Conditional on the optimal $\mathcal{D}$ and $\mathcal{K}$, we choose λ through the extended Bayesian Information Criteria (EBIC) [21] with a proper effective degree of freedom as follows:

$${\mathrm{EBIC}}_{\lambda }=\log ({\mathrm{RSS}}_{\lambda }∕n)+\mathrm{edf}\log \left(n\right)∕n,$$

where RSS_λ is the residual sum of squares with a given λ. The effective degree of freedom is defined as the number of predictor groups with non-zero estimates [22].

Remarks

It is noted that with L basis functions, the number of unknown parameters is of the order O(pL) not O(p). The proposed algorithm is casted in the group coordinate descent framework. O(npL) operations are needed for one full pass over all parameter groups. In our numerical study, we observe convergence with ~10^1–2 overall iterations. Computer code written in R is available at http://works.bepress.com/shuangge/50/.

3. Simulation

Performance of the proposed approach is evaluated using simulation. We consider both categorical and continuous G factors, corresponding to SNP and gene expression data, respectively. Under both settings, we consider four error distributions: N(0,1) (Error 1), t(3) (Error 2), 0.85N(0, 1) + 0.15LogNormal(0, 1) (Error 3), and 0.85N(0, 1) + 0.15Cauchy(0, 1) (Error 4).

We adopt two approaches to simulate SNP data. Under the first approach, the predictors are coded with three categories (2, 1, 0) for genotypes (AA, Aa, aa), respectively. We simulate the genotype data assuming the pairwise linkage disequilibrium (LD) structure. Let p_A and p_B be the minor allele frequencies (MAFs) of two alleles A and B for two adjacent SNPs, with LD denoted by ϕ. Then we have p_ab = (1 − p_A)(1 − p_B) + ϕ, p_AB = p_Ap_B + ϕ, p_aB = (1 − p_A)p_B − ϕ and p_Ab = p_A(1 − p_B) − ϕ as the frequencies of four haplotypes. With the Hardy-Weinberg equilibrium assumption, we simulate the SNP genotype (AA, Aa, aa) at locus 1 from a multinomial distribution given corresponding frequencies $(p_A^2,2p_A(1-p_A),{(1-p_A)}^2)$. Then the genotypes for locus 2 can be simulated accordingly from conditional probability. We set MAFs as 0.3 and pairwise correlation r = 0.5, which results in $\varphi =r\sqrt{p_A(1-p_A)p_B(1-p_B)}$. We refer to a recent publication [23] for more details on this approach. Under the second approach, we simulate data using the MS program [24], which generates haplotypes under the coalescent model to form individual genotype data without fixing the MAF and LD structure. The main parameters of the model are set as follows: (a) the effective diploid population size n_e=1×10⁴, (b) the scaled recombination rate for the whole region of interest =4×10⁻³, (c) the scaled mutation rate for the simulated haplotype region is 5.6×10⁻⁴, and (d) the length of sequence within the region of simulated haplotypes is 10kb. The haplotype data is generated under the above parameter settings, and the next two haplotypes are randomly drawn and paired to form the individual genotype.

For gene expression data, the predictors are generated from a multivariate normal distribution with an auto-regressive correlation structure where the correlation between the jth and kth gene is ρ_jk = ρ^∣j−k∣ with ρ = 0.5.

Under all three settings, the responses are generated under model (1) with p = 200 and n = 200. The continuous and discrete environment factors U and E are simulated from a uniform (0, 1) distribution and a binomial distribution with a success probability 0.6, respectively. The coefficients are set as α₁(u) = 2 sin(2πu), α₂(u) = 2 exp(2u − 1), α₃(u) = 6u(1 − u), α₄(u) = −4u³, α₅ = α₉ = 1.5, α₆ = α₁₀ = −1, α₇ = α₁₁ = 1.2, α₈ = α₁₂ = 1.3. β₁ = β₁₆ = 1, β₁₃ = β₁₇ = 1.2, β₁₄ = β₁₈ = 1.3, and β₁₅ = β₁₉ = −1. All of the other coefficients are 0. Note that the dimension of regression coefficients to be estimated after basis expansion is much larger than the sample size. For example, if $\mathcal{D}=2$ and $K=2$, then the effective dimension of regression is 1206.

Besides the proposed method (which is referred to as “A1”), we also consider the following alternatives: (A2) this is also a two-step procedure. It uses the same penalty functions as the proposed method. However it uses the ordinary least squared loss function, which is not robust to data contamination. (A3) This method is the same as the proposed, except that all E effects are assumed to be linear. (A4) This method conducts marginal analysis. Each marginal model includes one gene, E factors, and their interactions. The robust loss function and penalized identification are adopted. We acknowledge that multiple approaches are potentially applicable to the simulated data. The three alternatives have analysis frameworks closest to that of the proposed and are the most suitable for comparison.

Computational cost

Simulation suggests that the proposed method is computational affordable. The analysis of one simulated replicate takes about 1.6 minutes on a regular laptop. In simulation, we choose moderate n and p values, which have low computational cost but are sufficient to demonstrate properties of the proposed method. Here we note that although n = p, with the basis expansion, the number of parameters to be estimated is much larger than n. The computational cost of proposed method grows linearly with n and p. Thus the proposed method can potentially accommodate larger datasets with a reasonable computer time.

Identification and estimation results

We evaluate identification performance for the varying and constant effects of the continuous E factor and nonzero effect of the discrete E factor separately. The numbers of true positives and false positives are counted at the optimal tuning parameter values. Results are summarized in Table 1. It is observed that when there is no contamination, the proposed method may be slightly inferior to the unrobust alternative A2. This is reasonable as the unrobust alternative can be more efficient for data without contamination. With contamination, the proposed method has significant advantages. Specifically, it outperforms A2 by identifying much fewer false positives, possibly at the price of a very small loss in true positives. Method A3 identifies much fewer true positives. Method A4 is satisfactory in identifying true positives, at the price of many more false positives.

Table 1.

Simulation: marker identification results for SNP data simulation approach 1 (upper panel), approach 2 (middle panel), and gene expression data (lower panel). mean(sd) based on 100 replicates and n=200. TP/FP: true/false positives. Varying and constant effects correspond to the continuous E factor, and nonzero effect corresponds to the discrete E factor.

		Varying Effect		Constant Effect		Nonzero Effect
		TP	FP	TP	FP	TP	FP
Error 1	A1	3.60(0.49)	0.13(0.35)	6.77(0.94)	0.37(0.49)	7.57(0.63)	0.00(0.00)
	A2	3.87(0.35)	1.43(1.14)	6.50(1.01)	0.30(0.53)	7.87(0.34)	0.27(0.52)
	A3	1.17(0.74)	1.90(2.32)	0.13(0.35)	2.93(2.48)	4.17(1.32)	1.77(1.70)
	A4	3.90(0.31)	6.03(0.81)	0.17(0.38)	9.10(4.02)	7.50(0.63)	16.87(5.58)
Error 2	A1	3.23(0.62)	0.15(0.36)	5.55(0.90)	0.50(0.64)	5.98(1.21)	0.10(0.38)
	A2	3.78(0.42)	7.20(3.76)	4.83(1.34)	1.93(1.37)	6.95(0.88)	3.28(2.23)
	A3	1.73(1.01)	2.83(2.94)	0.15(0.36)	4.40(3.19)	4.08(1.23)	2.00(2.24)
	A4	3.55(0.60)	5.65(1.29)	0.35(0.48)	7.98(3.29)	6.83(0.78)	15.08(6.19)
Error 3	A1	3.35(0.70)	0.13(0.33)	5.58(0.98)	0.45(0.68)	6.00(1.06)	0.13(0.33)
	A2	3.85(0.36)	5.83(3.92)	4.73(1.18)	1.85(1.37)	6.75(0.90)	2.83(2.43)
	A3	1.58(0.90)	2.68(3.70)	0.10(0.30)	4.15(3.88)	3.90(1.00)	3.00(4.37)
	A4	3.48(0.68)	5.33(1.05)	0.30(0.52)	6.90(3.46)	6.55(0.81)	14.23(6.54)
Error 4	A1	3.00(1.03)	0.26(0.48)	5.32(1.96)	0.44(0.50)	5.84(2.13)	0.02(0.14)
	A2	3.40(1.10)	6.58(5.86)	4.46(2.04)	1.64(1.58)	6.42(2.13)	2.24(2.34)
	A3	1.24(0.96)	1.88(2.04)	0.20(0.45)	2.92(2.35)	3.54(1.28)	1.60(1.69)
	A4	3.34(1.15)	4.88(1.84)	0.42(0.67)	8.26(6.18)	6.26(1.96)	14.44(9.31)
Error 1	A1	3.83(0.38)	0.08(0.27)	7.92(0.27)	0.16(0.36)	8.00(0.00)	0.00(0.00)
	A2	3.98(0.14)	1.01(1.11)	7.04(1.00)	0.17(0.47)	8.00(0.00)	0.31(0.53)
	A3	1.72(0.92)	8.01(4.46)	0.68(0.76)	9.05(4.50)	5.58(1.26)	9.85(5.00)
	A4	3.99(0.10)	8.05(0.63)	0.04(0.19)	12.72(3.04)	8.00(0.00)	22.36(5.67)
Error 2	A1	3.60(0.38)	0.38(0.60)	7.56(0.67)	0.34(0.47)	7.90(0.36)	0.04(0.20)
	A2	3.88(0.33)	5.94(3.55)	5.74(1.19)	1.58(1.24)	8.00(0.00)	2.60(1.70)
	A3	1.64(0.66)	7.40(4.10)	0.38(0.60)	8.66(3.99)	5.34(1.39)	8.74(4.16)
	A4	3.80(0.45)	7.90(1.05)	0.18(0.48)	11.00(3.63)	7.94(0.24)	20.72(6.99)
Error 3	A1	3.67(0.47)	0.22(0.60)	7.78(0.57)	0.32(0.47)	7.98(0.14)	0.01(0.10)
	A2	3.95(0.22)	3.25(3.16)	6.20(1.36)	0.62(0.83)	8.00(0.00)	1.14(1.4)
	A3	2.09(0.95)	6.60(4.50)	0.34(0.63)	8.35(4.72)	5.20(1.59)	8.35(5.49)
	A4	3.90(0.30)	8.19(0.83)	0.08(0.27)	11.1(3.53)	7.97(0.22)	21.89(6.80)
Error 4	A1	3.67(0.81)	0.30(0.53)	7.33(1.49)	0.17(0.38)	7.60(1.48)	0.07(0.25)
	A2	3.77(0.77)	5.43(6.39)	5.83(1.88)	1.03(1.16)	7.70(1.47)	2.03(2.79)
	A3	1.40(1.04)	2.70(2.58)	0.13(0.35)	3.97(2.86)	4.53(1.80)	3.07(3.24)
	A4	3.73(0.78)	7.37(1.99)	0.13(0.35)	11.13(4.13)	7.63(1.47)	21.13(8.25)
Error 1	A1	3.36(0.55)	0.20(0.46)	6.60(1.19)	0.33(0.48)	7.13(0.86)	0.10(0.31)
	A2	3.73(0.45)	1.76(1.35)	6.23(1.28)	0.40(0.72)	7.73(0.20)	0.33(0.66)
	A3	0.87(0.68)	0.63(0.71)	0.07(0.25)	1.43(0.97)	3.97(1.09)	1.10(1.40)
	A4	3.33(0.66)	5.63(1.00)	0.33(0.66)	8.37(3.65)	7.43(0.63)	17.0(7.02)
Error 2	A1	3.10(0.66)	0.26(0.45)	5.40(0.85)	0.33(0.61)	6.10(1.16)	0.13(0.35)
	A2	3.83(0.38)	7.10(2.32)	4.57(0.94)	1.57(1.36)	7.00(0.94)	3.77(1.57)
	A3	1.90(0.99)	6.17(3.86)	0.53(0.86)	7.53(4.05)	4.73(1.21)	8.03(4.87)
	A4	3.20(0.76)	5.41(1.43)	0.40(0.56)	7.60(4.28)	6.70(0.88)	13.67(7.25)
Error 3	A1	3.25(0.54)	0.05(0.22)	6.18(1.20)	0.50(0.51)	7.10(0.93)	0.05(0.22)
	A2	3.80(0.41)	3.43(2.12)	5.65(1.10)	0.85(0.95)	7.75(0.54)	1.65(1.70)
	A3	1.53(0.88)	2.38(2.34)	0.18(0.50)	3.73(2.52)	4.18(1.26)	2.48(2.78)
	A4	3.53(0.60)	5.75(1.01)	0.25(0.49)	8.05(3.78)	7.33(0.76)	14.48(6.90)
Error 4	A1	2.90(1.07)	0.36(0.78)	5.06(1.95)	0.34(0.48)	5.86(1.98)	0.00(0.00)
	A2	3.36(1.02)	5.62(4.70)	4.84(2.02)	1.34(1.15)	6.66(1.89)	2.42(2.29)
	A3	1.16(0.79)	1.80(1.81)	0.14(0.46)	2.82(1.98)	3.82(1.44)	1.86(1.95)
	A4	3.02(1.12)	5.04(1.58)	0.38(0.60)	7.52(4.78)	6.56(1.64)	14.18(7.96)

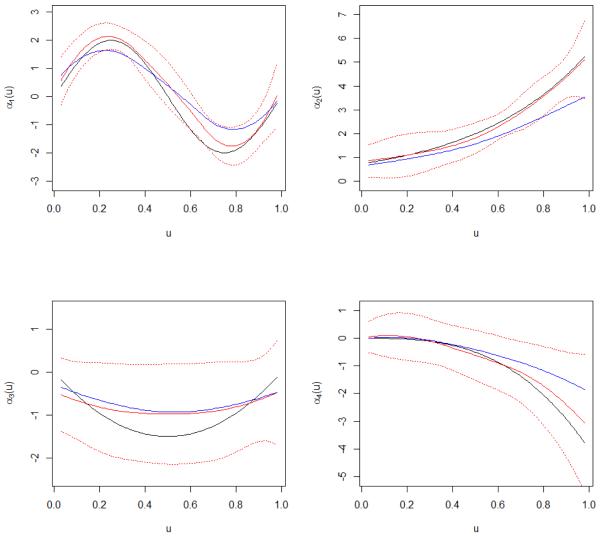
We also examine the estimation results. In Table 2, we show the integrated squared errors for α_j(u)’s, total integrated squared errors for all nonlinear estimates (TISE), and total squared errors (TSE) for all linear estimates. It is observed that without contamination, the proposed method has performance comparable to A2 but still outperforms A3 and A4. With contamination, the proposed method has significantly smaller estimation errors. As a demonstrating example, in Figure 1, for the SNP data under simulation approach 1 and Error 3, we show the average estimated varying coefficients. We observe that the proposed estimates match the true values reasonably well. They are closer to the true values than approach A2. The curves of ±2 pointwise standard deviations well cover the true parameters.

Table 2.

Simulation: estimation results for SNP data simulation approach 1 (upper panel), approach 2 (middle panel), and gene expression data (lower panel). mean(sd) based on 100 replicates and n=200. For α_j(u): ISE (integrated squared error).

		α1(u)	α2(u)	α3(u)	α4(u)	TISE	TSE
Error 1	A1	0.09(0.05)	0.06(0.06)	0.15(0.22)	0.09(0.08)	2.02(1.23)	0.75(0.84)
	A2	0.07(0.06)	0.05(0.04)	0.06(0.06)	0.07(0.06)	0.93(0.82)	0.33(0.50)
	A3	2.08(0.01)	1.96(0.74)	1.24(0.01)	1.88(0.42)	25.27(0.83)	5.70(1.63)
	A4	0.15(0.08)	0.20(0.15)	0.18(0.30)	0.38(0.63)	12.06(3.89)	1.55(0.78)
Error 2	A1	0.18(0.22)	0.20(0.30)	0.49(0.51)	0.37(0.54)	4.73(1.75)	2.75(1.51)
	A2	0.37(0.14)	0.71(0.41)	0.34(0.25)	0.57(0.36)	6.34(1.68)	3.26(1.06)
	A3	2.11(0.06)	5.81(1.95)	1.24(0.10)	1.77(0.44)	24.03(2.25)	5.95(1.81)
	A4	0.26(0.14)	0.64(0.38)	0.53(0.49)	0.94(1.59)	12.26(3.18)	3.01(0.88)
Error 3	A1	0.21(0.11)	0.17(0.24)	0.40(0.44)	0.40(0.63)	4.65(2.02)	2.80(1.46)
	A2	0.42(0.24)	0.64(0.50)	0.24(0.18)	0.57(0.47)	5.99(2.61)	3.11(1.51)
	A3	2.14(0.10)	5.41(1.99)	1.21(0.17)	1.95(0.40)	23.89(2.10)	6.12(1.47)
	A4	0.34(0.35)	0.72(2.63)	0.45(0.49)	0.95(1.49)	22.10(11.76)	2.64(1.09)
Error 4	A1	0.44(0.72)	0.66(1.72)	0.42(0.50)	0.52(0.77)	6.52(7.49)	2.74(2.81)
	A2	0.45(0.86)	0.83(1.92)	0.27(0.36)	0.40(0.60)	8.26(12.42)	2.71(2.95)
	A3	2.21(0.29)	5.75(1.99)	1.24(0.10)	1.82(0.43)	24.86(2.47)	7.26(1.92)
	A4	0.47(0.80)	0.92(1.93)	0.47(0.54)	0.75(1.06)	22.51(15.78)	3.93(3.18)
Error 1	A1	0.07(0.05)	0.04(0.03)	0.06(0.13)	0.03(0.02)	0.27(0.18)	0.08(0.04)
	A2	0.08(0.05)	0.04(0.03)	0.03(0.03)	0.04(0.04)	0.33(0.16)	0.13(0.11)
	A3	2.10(0.04)	6.47(1.51)	1.25(0.14)	1.71(0.46)	25.76(1.84)	5.36(1.63)
	A4	0.11(0.07)	0.26(0.64)	0.14(0.35)	0.10(0.13)	12.48(4.49)	0.60(0.25)
Error 2	A1	0.17(0.29)	0.09(0.12)	0.17(0.24)	0.10(0.19)	0.85(0.85)	0.29(0.41)
	A2	0.17(0.08)	0.15(0.11)	0.08(0.06)	0.13(0.09)	1.40(0.57)	0.76(0.39)
	A3	2.10(0.05)	6.41(1.67)	1.25(0.11)	1.80(0.44)	25.79(2.20)	5.54(1.80)
	A4	0.19(0.12)	0.27(0.25)	0.19(0.36)	0.35(0.63)	13.16(5.67)	1.22(0.66)
Error 3	A1	0.18(0.11)	0.06(0.04)	0.12(0.18)	0.06(0.09)	0.56(0.32)	0.15(0.16)
	A2	0.19(0.10)	0.10(0.09)	0.06(0.05)	0.08(0.07)	0.88(0.55)	0.42(0.36)
	A3	2.13(0.09)	4.80(1.89)	1.26(1.28)	1.72(0.51)	23.78(2.28)	5.64(1.88)
	A4	0.24(0.13)	0.25(0.28)	0.13(0.25)	0.22(0.53)	11.61(4.82)	0.91(0.52)
Error 4	A1	0.21(0.44)	0.29(1.28)	0.11(0.23)	0.20(0.52)	1.82(4.76)	0.66(1.88)
	A2	0.19(0.45)	0.34(1.28)	0.12(0.23)	0.22(0.53)	3.50(7.83)	0.96(1.97)
	A3	2.18(0.34)	5.17(2.22)	1.28(0.43)	1.89(0.37)	24.56(2.45)	6.77(2.62)
	A4	0.27(0.48)	0.41(1.27)	0.17(0.30)	0.46(0.72)	14.57(7.60)	1.97(2.08)
Error 1	A1	0.18(0.31)	0.16(0.17)	0.39(0.49)	0.26(0.53)	2.84(2.32)	1.22(0.98)
	A2	0.10(0.09)	0.09(0.10)	0.17(0.31)	0.08(0.06)	1.33(1.15)	0.50(0.64)
	A3	2.09(0.01)	7.02(1.01)	1.24(0.01)	2.03(0.32)	25.23(1.09)	6.12(1.28)
	A4	0.15(0.08)	0.51(0.57)	0.69(0.57)	0.52(0.74)	13.99(3.68)	1.72(0.74)
Error 2	A1	0.19(0.14)	0.41(0.39)	0.71(0.55)	0.48(0.61)	5.46(1.86)	2.63(1.42)
	A2	0.39(0.23)	1.22(0.77)	0.48(0.35)	0.69(0.41)	7.05(2.36)	3.50(1.07)
	A3	2.09(0.02)	5.61(2.17)	1.23(0.11)	1.61(0.44)	24.02(2.38)	6.00(1.69)
	A4	0.22(0.11)	0.81(0.46)	0.73(0.51)	1.19(1.10)	13.92(3.64)	2.94(0.89)
Error 3	A1	0.17(0.09)	0.22(0.24)	0.42(0.46)	0.26(0.45)	3.79(2.42)	1.36(1.20)
	A2	0.26(0.14)	0.52(0.54)	0.26(0.27)	0.31(0.27)	3.87(2.42)	1.65(1.09)
	A3	2.15(0.12)	5.45(1.53)	1.21(0.11)	2.01(0.47)	24.02(1.88)	5.66(1.39)
	A4	0.31(0.26)	0.71(0.66)	0.58(0.53)	0.42(0.67)	20.06(9.12)	1.81(1.46)
Error 4	A1	0.57(1.79)	0.68(1.45)	0.68(0.56)	0.62(0.84)	6.66(6.51)	2.63(2.49)
	A2	0.55(1.98)	0.77(1.47)	0.42(0.48)	0.43(0.66)	7.23(10.04)	2.58(2.96)
	A3	2.16(0.25)	6.06(1.75)	1.27(0.12)	1.83(0.41)	25.16(2.39)	6.85(2.03)
	A4	0.67(2.01)	1.01(1.65)	0.74(0.56)	0.88(1.68)	21.95(17.78)	3.68(2.94)

Figure 1.

Simulation study with SNP data simulation approach 1 under Error 3 (0.85N(0, 1) + 0.15LN(0, 1)). Red lines: mean estimates and ±2 pointwise standard deviation of varying coefficients for the proposed method. Solid blue lines: mean estimates of varying coefficients for ALASSO. Black lines: true parameter values.

Effect of tuning parameter selection

λ is chosen using EBIC, which is originally developed for a least squared loss. For the proposed method, with the approximation, the loss function has a least squared form. Thus adopting EBIC seems reasonable. To further examine tuning parameter selection, in Table 4 (Appendix), for one simulation scenario, we compare the results of EBIC with CV (V-fold cross validation), which has been extensively adopted and does not pose a strong constraint on the form of loss function. We see that the results are very close. Results under other simulation scenarios are similar and omitted.

Marker identification with a larger

p For one of the simulation scenarios, we also examine the performance of proposed method with p = 300 (Table 5, Appendix). Note that even before basis expansion, the number of G factors is larger than the sample size. The observed patterns are similar to those in Table 1.

Marker identification under the null model

To show that the proposed method does not identify excessive noises, we conduct simulation under the null model. Specifically, we generate SNP data under simulation approach 2. Under the null model, all of the regression parameters are zero. Marker identification results are shown in Table 6 (Appendix). Under all scenarios, the proposed method identifies none or a very small number of false positives.

4. Analysis of a lung cancer dataset

In the U.S., lung cancer is the most common cause of cancer death for both men and women. To identify genetic markers associated with the prognosis of lung cancer, gene profiling studies have been extensively conducted. The development and progression of lung cancer involves multiple genetic factors, clinical and environment factors, and their interactions. As individual studies usually have small sample sizes, we follow Xie et al [25] and collect data from four independent studies with gene expression measurements. The CAN/DF (Dana-Farber Cancer Institute) dataset has a total of 78 patients, with 35 deaths during follow-up. The median follow-up is 51 months. The HLM (Moffitt Cancer Center) dataset has a total of 79 patients, with 60 deaths during follow-up. The median follow-up is 39 months. The UM (University of Michigan Cancer Center) dataset has a total of 92 patients, with 48 deaths during follow-up. The median follow-up is 55 months. The MSKCC dataset has a total of 102 patients, with 38 deaths during follow-up. The median follow-up is 43.5 months. We refer to Xie et al [25] for more detailed information.

Gene expressions were measured by Affymetrix U133 plus 2.0 arrays. A total of 22,283 probe sets were profiled in all four datasets. We first conduct gene expression normalization for each dataset separately, and then normalization across datasets is also conducted to enhance comparability. Since genes with larger variations are often of more interest, the probe sets are ranked according to variations, and we screen the top 200 out for downstream analysis. The expression of each gene in each dataset is normalized to have mean 0 and standard deviation 1.

We consider two E factors. The first is the binary smoking status. Smoking has been identified as the most important factor for lung cancer development. The second is age at diagnosis, which is continuous and known to be an important factor for the development of most cancer types. We note that the two E factors are not “classic” environmental factors. However, as shown in Singh et al. [26] and others, the potential interactions between such clinical factors and gene expressions can still be of significant interest. The response variable is time to death. We make a log transformation of time and assume the accelerated failure time (AFT) model, which is simply model (1) with a transformed response. To accommodate possible censoring, we adopt the estimation approach in Stute [27], which assigns a non-negative weight to each observation and the value of weight does not depend on the unknown parameters. Thus the proposed approach is directly applicable. We refer to Huang and Ma [28] and references therein for more details on the weighted estimation under the AFT model. With survival data, the most popular model is the Cox model. The proposed robust approach is built on the notation of residual, which is natural with the AFT model but very difficult with the Cox model. In addition, the AFT model has been extensively adopted for genetic data because of its low computational cost and simple interpretability.

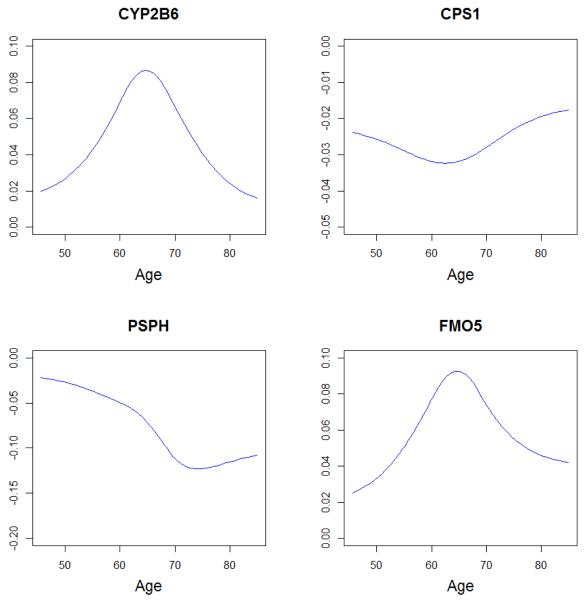
We analyze data using the proposed robust method as well as the unrobust alternative A2. As methods A3 and A4 show inferior performance in simulation, they are not considered. The estimation results are summarized in Tables 3 (proposed) and 7 (Appendix, method A2), respectively. Method A2, which is not robust, identifies 19 genes with main effects and 3 interacting with smoking status. It does not identify any gene with a varying coefficient. In contrast, the proposed approach identifies 4 and 5 genes as having interactions with age and smoking status respectively. The four varying coefficients of age are shown in Figure 2. All four estimates have clear curvature and cannot be appropriately approximated with linear effects. The proposed approach also identifies 11 genes with main effects. Although there is overlap, the two approaches identify different main effects and interactions. We conduct a brief literature search and find that some of the identified genes may have important implications. More details are provided in Appendix.

Table 3.

Analysis of the lung cancer data using the proposed approach. C: estimated coefficient of gene. E(Smoke): estimated coefficient of smoke.

Probe Set	V(Age)	C	E(Smoke)	Probe set	V(Age)	C	E(Smoke)
PAEP		0.002		DUSP4		−0.061
TFF1		−0.074		GPR116		0.042
HLA–DQA1			−0.045	PSPH	varying
CPS1		−0.027	0.002	GPX2		−0.059
CYP2B6	varying			FOLR1		0.025
WIF1			0.063	TOX3		0.059
CPS1	varying		0.079	KRT6A		−0.041
TOX3		0.067		IFI27		−0.002
SLC6A14			0.085	FMO5	varying

Figure 2.

Estimated varying coefficient effects of age under the proposed approach.

To provide additional insight, we also evaluate the prediction performance. Without additional independent dataset, we resort to the cross-validation based method [29]. This method splits samples into two risk groups with equal sizes based on the predicted risk scores and computes the logrank statistic, which measures the survival difference of the two groups. A larger logrank statistic indicates better prediction performance [6]. The logrank statistics for the proposed method and method A2 are 22.5 (p-value=2.12×10⁻⁶) and 14.6(p-value=0.000134), respectively. Although both methods have satisfactory prediction performance, the proposed has a larger logrank and hence better prediction.

5. Discussion

In this study, we have developed a penalized robust semiparametric method for the analysis of high-dimensional genetic data and identification of important G×E interactions and main effects. Advancing from the existing methods, the proposed one has the desired robustness property by adopting a rank based loss function. A convenient approximation is adopted to significantly reduce computational cost. In addition, the semiparametric modeling and “automatic” separation of varying effects, constant effects, and zero effects make the proposed method a useful addition beyond the existing alternatives. Simulation shows that the proposed method has satisfactory identification and estimation results. It outperforms three closely related alternatives. It is interesting to note that it has competitive performance when the error is not contaminated. Thus, it is a “safe” choice for data analysis when the degree of contamination is unclear. In the analysis of a lung cancer study, it identifies interesting genes and varying coefficients of age and has better prediction performance.

In modeling, we have considered a continuous response under a partially linear model. For the analyzed lung cancer prognosis data, the AFT model has a natural connection to the linear regression. Generalized linear models can be solved using the iterated weighted least squared algorithm, which defines pseudo-response and pseudo-residual. We conjecture that the proposed loss function can be extended to other types of responses under generalized linear and other models. Such extension is nontrivial and demands separate investigation. The proposed penalties are built on group LASSO. It is expected that other penalties, for example group bridge and group SCAD, are also applicable. The group LASSO penalties are adopted because of their computational simplicity and reasonable numerical performance. The development of proposed method has solid statistical basis. However, as a limitation of this study, no theoretical study is pursued. The selection, estimation, and tuning parameter selection properties are all of significant interest but will be deferred to future investigation. In simulation, we have examined three common contaminated distributions and clearly demonstrated superiority of the proposed method. More extensive numerical studies are postponed to future research. In data analysis, more extensive bioinformatics and functional studies are needed to fully comprehend the identified interactions and main effects.