The Quantitative-MFG Test: A linear mixed effect model to detect maternal-offspring gene interactions

SUMMARY

Maternal-offspring gene interactions, aka maternal-fetal genotype (MFG) incompatibilities, are neglected in complex diseases and quantitative trait studies. They are implicated in birth to adult onset diseases but there are limited ways to investigate their influence on quantitative traits. We present the Quantitative-MFG (QMFG) test, a linear mixed model where maternal and offspring genotypes are fixed effects and residual correlations between family members are random effects. The QMFG handles families of any size, common or general scenarios of MFG incompatibility, and additional covariates. We develop likelihood ratio tests (LRTs) and rapid score tests and show they provide correct inference. In addition, the LRT’s alternative model provides unbiased parameter estimates. We show that testing the association of SNPs by fitting a standard model, which only considers the offspring genotypes, has very low power or can lead to incorrect conclusions. We also show that offspring genetic effects are missed if the MFG modeling assumptions are too restrictive. With GWAS data from the San Antonio Family Heart Study, we demonstrate that the QMFG score test is an effective and rapid screening tool. The QMFG test therefore has important potential to identify pathways of complex diseases for which the genetic etiology remains to be discovered.

INTRODUCTION

Maternal and offspring gene interaction, also termed maternal-fetal genotype (MFG) incompatibility, occurs when the effects of maternal genes on the offspring’s phenotype vary depending on the offspring’s genotype. The possibility of joint maternal and offspring effects needs to be studied, especially when investigating genetic factors of developmental disorders and their associated quantitative traits. Previous studies have found that MFG interactions are associated with preterm birth, conotruncal heart defects, neural tube defects, and preeclampsia (see as examples, Liang et al., 2010, Li et al., 2014, Lupo et al., 2014, Procopciuc et al., 2014). Additionally, MFG incompatibilities have been implicated as risk factors in complex adult onset diseases, such as schizophrenia, where the effects are not evident until long after the MFG incompatibility initiated event has occurred and subsided (see as examples, Stubbs et al., 1985, Hollister et al., 1996, Dahlquist et al., 1999, Juul-Dam et al., 2001, Cannon et al., 2002, Palmer et al., 2002, Newton et al., 2004, Insel et al., 2005, Palmer et al., 2008, Freedman et al., 2011). To date, studies have not looked at the role of MFG incompatibility on the quantitative traits related to these adult onset diseases. Although there are a number of methods for investigating MFG incompatibility as a risk factor for disease (see Sinsheimer & Creek, 2013 for a review of these methods), the proposed methods to investigate the effects of maternal and offspring genes on quantitative traits typically rely on retrospective likelihoods and are limited to case-parent trios (Kistner & Weinberg, 2004, Kistner & Weinberg, 2005, Wheeler & Cordell, 2007). Moreover, the retrospective likelihood design is not easily generalized to arbitrary family structures, multiple markers, or multivariate traits (Kraft et al., 2004) and parameter interpretation can be challenging.

One way to conduct association testing with quantitative traits using pedigree data is in a measured genotype analysis (Boerwinkle et al., 1986, Lange, 2002). This method of testing uses a linear mixed model (LMM) in which the genotypes are fixed effects and familial correlations are taken into account through partitioning the variance. Hence the LMM is also called variance component modeling in the genetic literature. We have developed the Quantitative-MFG (QMFG) test, an extension to the LMM where the joint maternal and offspring effects including MFG incompatibilities are fixed effects, familial correlations are variance components, and the outcome is a trait with residuals that are reasonably modeled as normally distributed (Lange, 2002). This approach handles pedigrees of virtually any size, both general and specific scenarios of MFG incompatibility, multivariate traits, and covariates in a straightforward manner. Another advantage of this approach is the ability to quickly test genome-wide association study (GWAS) pedigree data for joint maternal and offspring effects including MFG incompatibility via the use of the score test.

MATERIALS AND METHODS

The QMFG Test

Recall that, for a single pedigree, the general multivariate normal loglikelihood for a LMM is

$$L=-\frac{1}{2}ln\mid \mathit{\Omega }\mid -\frac{1}{2}{(y-\nu )}^t{\mathit{\Omega }}^{-1}(y-\nu )$$

with observed trait vector y, mean vector ν, and covariance matrix Ω (see for example, Lange, 2002 for details regarding the variance component model in classic genetic applications). We propose an extension to this model where the maternal-offspring genotypes are fixed effects. In the QMFG test, ν = Aβ, where A is the design matrix consisting of indicator variables for the MFG combinations of interest and β is the column vector of corresponding regression coefficients. In our applications, ν always includes a grand mean μ so there is one entry of β that equals μ and one column of A is all ones. Consider the effects of a single SNP with a reference allele and a variant allele. When modeling the joint effects of maternal and offspring genotype effects, let β_amac denote the difference in the offspring’s quantitative trait value from the grand mean for a mother with a_m variant alleles and an offspring with a_c variant alleles at a given SNP. Because there are seven possible mother-offspring genotype combinations for a biallelic locus (see Table 1), in the general MFG incompatibility case for one SNP, the vector of regression coefficients is β^t =(μ, β₀₀, β₀₁, β₁₀, β₁₁, β₁₂, β₂₁, β₂₂) and the additional columns of the design matrix A are indicator variables corresponding to each of the seven possible MFG combinations. Note that just as additional covariates such as age and sex can be incorporated in the standard measured genotype analysis (Boerwinkle et al., 1986), they can be included in the fixed effect portion of the QMFG model as additional entries in theβ vector and additional columns of the A matrix. To avoid non-identifiability, one of the parameters for the MFG effects should be made the reference state or, equivalently, the sum of MFG parameters should be set to some constant. In our analyses, parameter β₀₀, denoting zero copies of the variant allele in both mother’s and offspring’s genotypes, is always set to zero and hence, at most six MFG parameters are estimated along with the grand mean.

Table 1. QMFG model parameterizations.

G_Mat and G_Off denote the maternal and offspring genotypes, respectively.

GMat	GOff	General QMFG model	RHD effects	NIMA and offspring effects
1/1	1/1	β00	β00	β00
1/1	1/2	β01	β00	β.1
1/2	1/1	β10	β00	β10
1/2	1/2	β11	β00	β.1
1/2	2/2	β12	β00	β.2
2/2	1/2	β21	β21	β.1
2/2	2/2	β22	β00	β.2

We continue to treat familial correlations as random effects by partitioning the residual variance. Here we define the partition of the covariance matrix as $\mathit{\Omega }={\mathrm{\sum }}_{i=1}^k{\sigma }_i^2{\mathrm{\Gamma }}_i$, where k is the number of variance components included in the model. Often in genetic studies a very simple version of this matrix with only two components is used, one representing the additive genetic effects and one representing environmental random effects. In this model, the familial correlations are assumed to be due to small and approximately equal effects of alleles at a number of genes each acting independently. The additive genetic and environmental variances are denoted by ${\sigma }_a^2$ and ${\sigma }_e^2$, respectively. The design matrix Γ_a corresponding to ${\sigma }_a^2$ is twice the global kinship coefficient matrix Φ. Each element Φ_ij is the probability that, at a randomly chosen autosomal locus, an allele chosen at random from subject i and an allele chosen at random from subject j match identically by descent. When i equals j the alleles are chosen with replacement. The environmental contribution is multiplied by the identity matrix I since the environment is assumed to affect each subject independently. The environmental variance ${\sigma }_e^2$ is always included even when there are thought to be no environmental factors to insure that the matrix is positive definite. Under this simple model, $\mathit{\Omega }=2{\sigma }_a^2\mathit{\Phi }+{\sigma }_e^{2}I$.

As in other LMM scenarios, likelihood ratio tests (LRTs) can be used here to determine the significance of MFG parameters. Asymptotically, the LRT statistic follows a chi-square distribution with degrees of freedom equal to the difference in the number of parameters under the null and alternative models. In addition to the LRT, we can use score tests to rapidly screen markers (Chen & Abecasis, 2007). The score statistic is given by

$$S(\theta )=dL(\theta )J{(\theta )}^{-1}\nabla L(\theta )$$

where ∇L(θ) is the gradient of the loglikelihood with the parameter vector θ, dL(θ) is the first differential of the loglikelihood, and J(θ) is the expected information matrix. Zhou et al. (2015) precompute and store key quantities for a fast score test for individual SNPs. In particular, for family i under the alternative hypothesis, the design matrix A_i can be written as (a_i, N_i) where N_i is the design matrix under the null. Additional covariates are included in the matrix N_i. The array a_i conveys the genotypes at the SNP of interest. Let the residual for family i be r_i = y_i − N_iβ̂ where β̂ are the maximum likelihood estimates (MLEs) of the fixed effects under the null (in which no SNPs are included in the model). The score statistic for n families then reduces to

$$S=R^t{\left[Q-W^t{\left(\sum _{i=1}^n{N}_i^t{\mathit{\Omega }}_i^{-1}{N}_i\right)}^{-1}W\right]}^{-1}R$$

where

$$Q=\sum _{i=1}^n{a}_i^t{\mathit{\Omega }}_i^{-1}{a}_i,R=\sum _{i=1}^n{a}_i^t{\mathit{\Omega }}_i^{-1}{r}_i,W=\sum _{i=1}^n{N}_i^t{\mathit{\Omega }}_i^{-1}{a}_i.$$

Thus the quantities ${\mathit{\Omega }}_i^{-1},{\mathit{\Omega }}_i^{-1}{r}_i,N_i^t{\mathit{\Omega }}_i^{-1}$, and ${\mathrm{\sum }}_{i=1}^n{N}_i^t{\mathit{\Omega }}_i^{-1}{N}_i$ can be computed once under the null model and then reused for the analysis of each SNP. This makes the calculation of the score test statistic for each SNP simple and rapid.

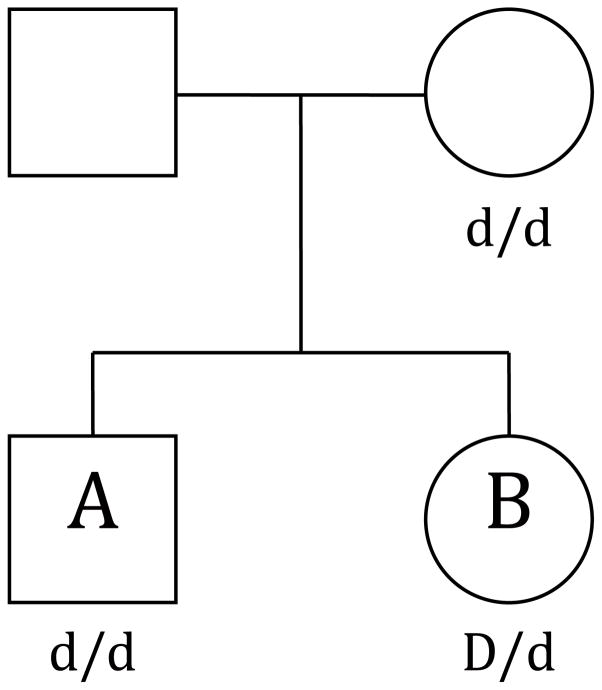
We extend this fast calculation of the score test to MFG incompatibility by replacing a_i, which previously was a vector conveying the variant allele counts at the SNP of interest for family i, with the matrix X_i. In its most general form, each column of matrix X_i represents one of the possible maternal-fetal genotype combinations and is composed of zeros and ones, indicating which MFG combination defines the joint mother-offspring genotype for each offspring within the pedigree at a particular SNP. For example, for the pedigree in Figure 1

Figure 1. Pedigree depiction of the Rhesus factor D (RHD) scenario.

The mother has two variant alleles (d/d). Offspring A has two variant alleles (d/d). Offspring B has one variant allele (D/d) and is therefore RHD incompatible with the mother.

$$X_i=\left(\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 1& 0\end{array}\right)$$

and for the pedigree in Figure 2

Figure 2. Pedigree depiction of the non-inherited maternal antigen (NIMA) scenario.

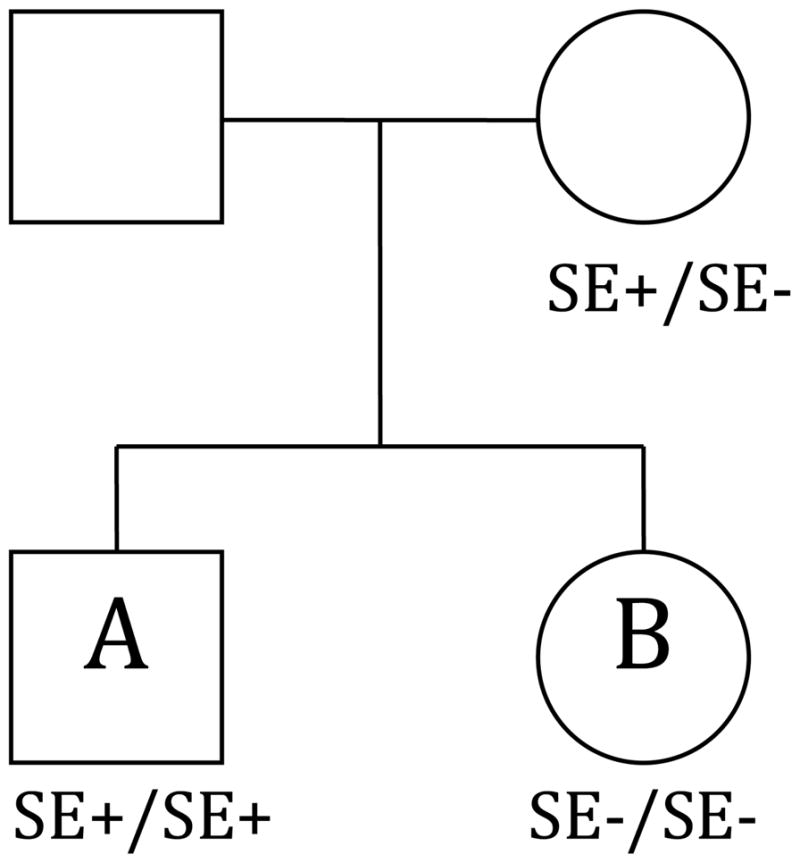
The mother has one variant allele encoding a shared epitope (SE+/SE−). Offspring A has two variant alleles encoding a shared epitope (SE+/SE+). Offspring B has no variant alleles encoding a shared epitope (SE−/SE−) and therefore illustrates the NIMA scenario.

$$X_i=\left(\begin{array}{ccccccc}0& 0& 0& 0& 1& 0& 0\\ 0& 0& 1& 0& 0& 0& 0\end{array}\right)$$

In these examples, the top row corresponds to Offspring A and the bottom row corresponds to Offspring B and each column corresponds to the maternal-fetal genotype combinations in Table 1. The columns of X_i can be combined depending on the restrictions imposed on the parameters and therefore the number of columns equals the number of parameters to be estimated. As with the LRT, the score test statistic asymptotically follows a chi-square distribution with degrees of freedom determined by the difference between the number of parameters in the null and alternative models.

There are advantages and disadvantages to both the LRT and the fast score test. For example, dealing with complex null and alternative hypotheses is better handled with the LRT. However, to calculate the LRT iterative maximization of the likelihood under both the null and alternative models is required, which can be computationally intensive when using large numbers of extended pedigrees and markers. We evaluate the ability of both tests to make correct QMFG inferences. Another advantage of the LRT is that in maximizing the likelihood we obtain parameter estimates. We also evaluate the accuracy and precision of these estimates.

Examples of MFG Incompatibility

To better illustrate how the QMFG model works, we present two well-known examples of MFG incompatibility. Although these two examples are typically framed in terms of disease, they could easily be imagined to be operating on associated quantitative traits. First, we consider the case where the mother reacts to antigens created by the offspring. The prototypical example is RHD incompatibility (Figure 1), which occurs if the mother is homozygous for the variant allele ‘d’ (RHD-negative) and the offspring is heterozygous (RHD-positive). This can lead to hemolytic disease of the newborn (Levine et al., 1941), which is associated with high levels of bilirubin resulting from the breakdown of the fetus’s red blood cells (Lee et al., 2009). In our simulation study we estimate parameter β₂₁, which denotes the expected change in the quantitative trait value of the offspring when mother and offspring are RHD incompatible, and the other six MFG parameters form the reference group, i.e., β₀₀ = β₀₁ = β₁₀ = β₁₁ = β₁₂ = β₂₂ = 0 (Table 1, Column 4).

The second example we investigate is the case where the offspring’s immune system reacts to an antigen that has its origins in the mother’s genotype. It is inspired by rheumatoid arthritis (RA) and HLA-DRB1, where non-inherited maternal antigens (NIMA) have been implicated in offspring disease susceptibility (van der Horst-Bruinsma et al., 1998, Harney et al., 2003, Newton et al., 2004). As an example of an associated quantitative trait, anti-CCP antibodies are important markers for diagnosis and prognosis in RA since they are highly specific and sensitive (Visser et al., 2002, Silveira et al., 2007) and therefore would be an interesting quantitative trait to investigate using the QMFG test. A pedigree depiction of NIMA is shown in Figure 2 and is characterized by a mother that has one variant allele encoding a shared epitope (SE-positive) and an offspring that has none (SE-negative). There is strong evidence that there is an effect when the offspring has one or more variant alleles regardless of the mother’s genotype (Gregersen et al., 1987, Jawaheer & Gregersen, 2002) and thus offspring effects must be included in the model. This model allows us to show how more complex restrictions can be handled. As shown in Table 1, Column 5, the effects of interest are the NIMA effect (β₁₀) and the offspring genotype effects (β_.1 = β₀₁ = β₁₁ = β₂₁ and β_.2 = β₁₂ = β₂₂).

Mendel Software

We implement the QMFG test by modifying the statistical genetics software package Mendel (Lange et al., 2013). When using SNPs, one allele is considered the reference allele and the other is the derived, variant allele. In order to implement the measured genotype analysis option for MFG incompatibility, the Mendel code was updated to extract the variant allele counts for mother and offspring from the genotypes included in the pedigree files. The reference allele is by default the more frequent allele but this can be changed if the user specifies in the Mendel control file. Once variant allele counts are determined, the LRT option is run by internally including a new covariate for each offspring that indicates which of the seven possible maternal-fetal gene-gene combinations describes the offspring’s and his mother’s genotypes. This enables MFG incompatibility parameters to be estimated and the likelihood to be calculated within the variance component analysis option in Mendel. The user can place restrictions on parameter estimates thus allowing for specific forms of MFG incompatibility such as offspring antigen – maternal antibody (referred in this document by the prototypical example RHD incompatibility) or maternal antigen – offspring antibody (referred in this document by the prototypical example NIMA). To program the QMFG score test, we used much of the machinery in the existing ped-GWAS option in Mendel that implements an LMM-based fast score test for GWAS on pedigree data with quantitative traits (Zhou et al., 2015). We forced the existing algorithm to include in its model the seven possible maternal-fetal genotype combinations and any user-specified restrictions on these combinations.

Simulation of Pedigrees

To evaluate the type I error or power of the QMFG tests and, for the LRT implementation, parameter estimation, we simulate data under ten specific scenarios (A-J) using the parameters shown in Table 2. Simulation A data are under the null of no genetic effects. Simulations B, E, and H involve conditions consistent with the effects of RHD incompatibility. Simulations C, D, F, and I are consistent with the effects of NIMA with and without the additional effects of offspring alleles and maternal effects. Simulation G is another possible scenario where each variant allele in the mother or offspring has the same effect on the phenotype and the effects are additive and independent; it is a special case of a scenario where there are both maternal and offspring main effects but no interaction. We use Simulation G when we want to evaluate the properties of fitting the general model. Simulation J involves offspring effects only and is used to investigate model misspecification. For power analyses, we vary selected parameters of particular interest in these simulation scenarios. The simulation design consists of 2,000 repetitions of 1,000 three-generational pedigrees (except when studying the effect of family structure or sample size), a biallelic locus, and a quantitative trait. Every three-generational pedigree is comprised of a nuclear family with two offspring, each of which have a partner and child of their own, and therefore the extended family contains a total of four founders and four offspring. Unless otherwise specified, the variant allele frequency is 0.40. Genotypes are simulated using Mendel’s gene dropping option. Additional effects include a grand mean (intercept) μ = 40 and variance components ${\sigma }_a^2=1$ and ${\sigma }_e^2=5$ (residual heritability h² = 0.167) unless otherwise specified. A univariate quantitative trait is simulated for all offspring by modifying the trait simulation option of Mendel (Lange et al., 2013).

Table 2.

Examples of QMFG data simulation scenarios.

				Simulation parameters
Simulation scenario		Constraints	Number of MFG parameters simulated	β00	β01	β10	β11	β12	β21	β22
A	No genetic effects	βij = 0 for all i = 0,1,2 and j = 0,1,2	0	0	0	0	0	0	0	0
B	RHD effect	βij = 0 for all i,j unless i = 2 & j = 1	1	0	0	0	0	0	0.55*	0
C	NIMA & offspring effects	β00 = 0 β01 = β11 = β21 β12 = β22	3	0	0.18	0.60*	0.18	0.36	0.18	0.36
D	NIMA, offspring, & maternal effects	β00 = 0	6	0	0.18	0.60	0.36	0.54	0.54	0.72
E	RHD effect	βij = 0 for all i,j unless i = 2 & j = 1	1	0	0	0	0	0	1.75	0
F	NIMA & offspring effects	β00 = 0 β01 = β11 = β21 β12 = β22	3	0	0.60	1.90	0.60	1.20	0.60	1.20
G	Count model	β00 = 0	6	0	0.17	0.17	0.34	0.51	0.51	0.68
H	RHD effect	βij = 0 for all i,j unless i = 2 & j = 1	1	0	0	0	0	0	0.70	0
I	NIMA effect	βij = 0 for all i,j unless i = 1 & j = 0	1	0	0	0.70*	0	0	0	0
J	Offspring effects	β00 = β10 = 0 β01 =β11 = β21 β12 = β22	2	0	0.27	0	0.27	0.54	0.27	0.54

^*Values varied for power analysis

Assessing the Statistical Properties of the Tests

We use a variety of full and reduced models (Table 3, Models 1–9) to analyze the simulated data, the exact choice depending on our alternative and null hypotheses. All models fit to the data estimate a grand mean (μ) and both variance components ( ${\sigma }_a^2$ and ${\sigma }_e^2$). To quantify the degree of bias in type I error, genomic control values (λ) are reported (Devlin & Roeder, 1999) and 95% confidence bounds are included on Q-Q plots. Confidence bounds are based on the standard errors of the order statistics of the comparison distribution (Fox, 2008).

Table 3.

QMFG full and reduced models.

Models		Number of MFG parameters estimated	MFG parameters estimated
1	No genetic effects model	0	None
2	RHD effect model	1	β21
3	NIMA and offspring effects model	3	β10 β01=β11=β21 β21 = β22
4	Offspring effects model	2	β01 =β11 =β21 β12 = β22
5	NIMA effect model	1	β10
6	NIMA and dominant offspring effects model	2	β10 β01 =β11 =β21= β12=β22
7	NIMA, offspring, and maternal effects model	5	β01, β10, β11, β12, β21 β22 = β12 + β21 − β11
8	General model	6	β01, β10, β11, β12, β21, β22
9	Additive offspring effect model	1	2β01 = 2β11 = 2β21 =β12 = β22

Power is defined as the rejection rate, which is the proportion of simulations in which the statistical test rejects the null model in favor of the alternative. If not otherwise specified, we used a per test significance level of 0.001 when determining power. Standard errors of power estimates are calculated using $SE=\sqrt{\frac{p(1-p)}{N}}$ where p is the proportion of rejected tests and N is the number of repetitions. The proportion of variation explained is calculated as the ratio of phenotypic variation due to the effects of interest and the total phenotypic variation, and is based on the true parameter values and allele frequencies with which the data are simulated.

The San Antonio Family Heart Study

To show the feasibility of using this approach on a real pedigree-based GWAS dataset, we use data from the San Antonio Family Heart Study (SAFHS). These data have described elsewhere (Mitchell et al., 1996) but we briefly describe the subset of the data we use. The complete study data consist of 3637 subjects in Mexican American families of various sizes. High-density lipoprotein (HDL) levels were measured at up to three time points. For the first time point, 1,397 individuals were phenotyped (Table S1). Of the subjects that were phenotyped, 1,043 also have genotype data. To reduce the computational time used to impute missing genotypes for irrelevant members of the pedigree, we first trim the data to include only subjects with a quantitative trait measurement and their connecting relatives (Lange & Sinsheimer, 2004). Because the QMFG test is an offspring-only analysis, we are interested in the subset of 855 offspring in the dataset that have both phenotype and genotype data. If an offspring’s mother is completely ungenotyped before imputation, they were not used. Our analysis therefore involves the 419 offspring from 43 families with phenotype, genotype, and maternal genotype information. In this subset of data, the largest family has 176 members and 5 generations while the smallest family has 8 members and 3 generations. Next, we use Mendel’s imputation option to fill in all missing genotypes for subjects who have some existing SNP data (Ayers & Lange, 2008). Standard imputation programs, which do not take pedigree data into account, inevitably produce impossible maternal-offspring genotype combinations. We remove SNPs that have a maternal and offspring genotype combination of either 2/2 and 1/1, respectively, or 1/1 and 2/2, respectively. Additionally, we filter out any SNPs that have a minor allele count less than 10.

RESULTS

RHD Incompatibility

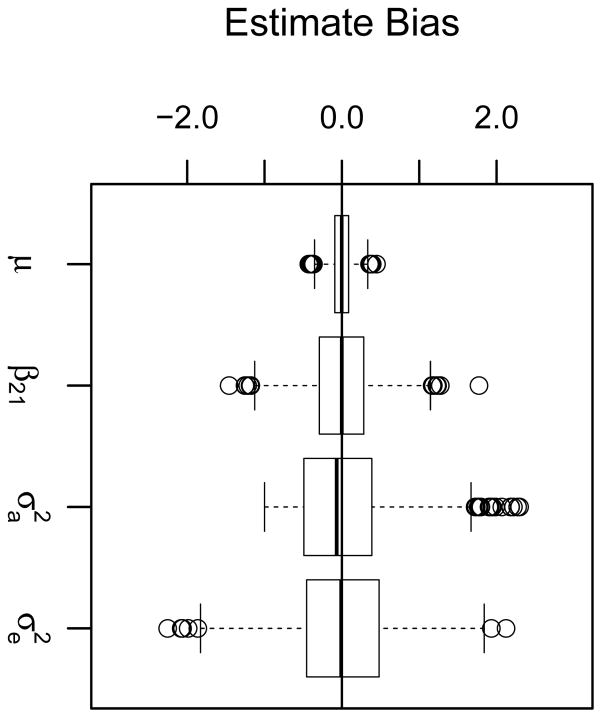
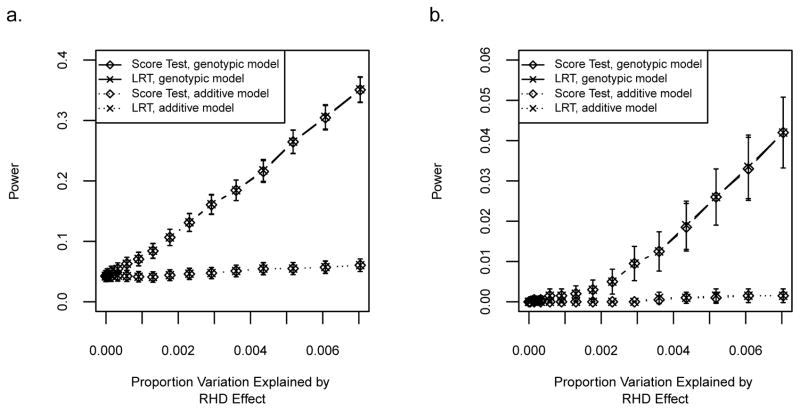
We first compare type I error rates of the LRT and score test for a simple example of maternal-fetal gene interactions that mimics RHD incompatibility. In this example, heterozygous offspring whose mothers who are homozygous for the variant allele differ in their trait value from other offspring. Figure 3a shows the results when data are simulated under the null hypothesis of no genetic effects (Simulation A) and the parameter β₂₁ is tested for significance. For the LRT, Model 1 reflects the null hypothesis and Model 2 reflects the alternative hypothesis, resulting in a one degree of freedom (df) test. The QMFG score test provides almost identical results (Figure S1a). Based on the confidence bounds on the Q-Q plot, we conclude there is little bias in the type I error for either test (genomic control value λ = 1.065). Next, data are simulated to provide a moderately small RHD effect (Simulation B). In Simulation B, the only effect associated with the offspring’s phenotype is an expected increase of 0.55 units when mother and offspring are incompatible, corresponding to 0.0044 of the variance explained by the RHD effect. Figure 4a provides boxplots of the parameter estimate bias over 2,000 replicates when the underlying MFG mechanism, RHD incompatibility, is suspected and consequently the correct model, Model 2, is fit to the data. As desired, the QMFG method produces unbiased parameter estimates. Keeping all other simulation conditions the same, we then varied the true RHD effect between 0 and 0.7, resulting in the true proportion of variation explained by the MFG effect ranging from 0 to 0.007. Figure 5a shows the LRT and score test power curves corresponding to these variations for the one degree of freedom test (solid lines) testing the significance of the RHD parameter (β₂₁). When the significance level is 0.001, the curve illustrates that 80% power is achieved when the proportion of variation explained by the RHD effect is approximately equal to 0.004 for both the LRT and score test.

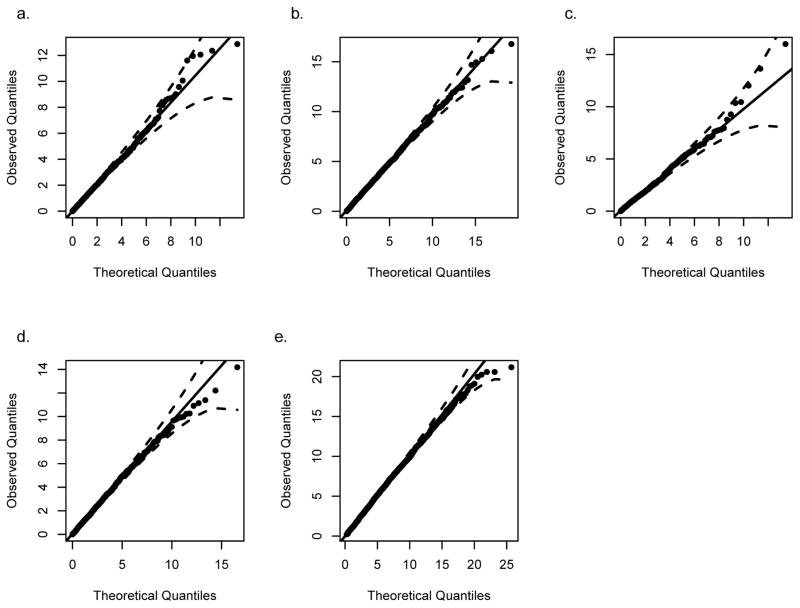
Figure 3. Q-Q plot for LRT using Simulation A data.

Genotypes and quantitative traits for each replication were simulated for 1,000 pedigrees under the null of no MFG effects and were tested with the LRT for (a) RHD effects (df = 1, λ = 1.065), (b) NIMA or offspring effects (df = 3, λ = 0.989), (c) NIMA effects in the presence of offspring genotype effects (df = 1, λ = 1.048), (d) offspring effects in the presence of NIMA effects (df = 2, λ = 0.959), and (e) any MFG effects (df = 6, λ = 1.086).

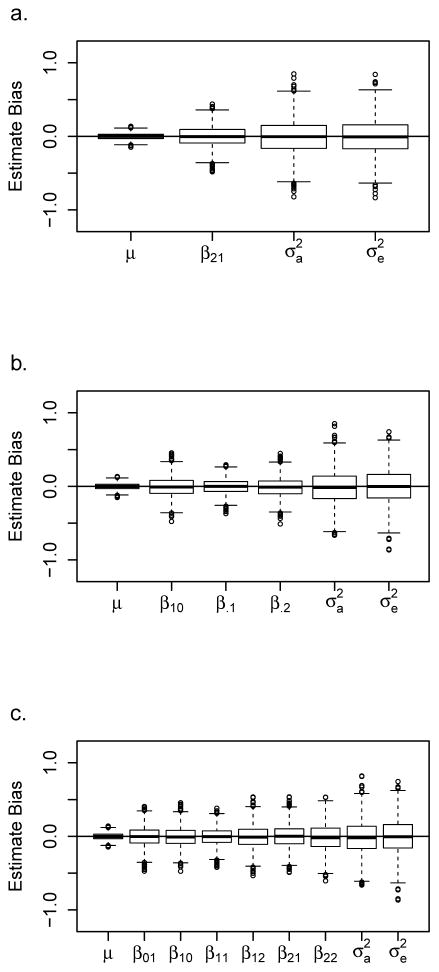
Figure 4. Parameter estimate bias.

Genotypes and quantitative traits for each replication were simulated for 1,000 pedigrees using (a) Simulation B data with an RHD effect of 0.55 (μ = 40, β₂₁ = 0.55, ${\sigma }_a^2=1,{\sigma }_e^2=5$), (b) Simulation C data with a NIMA effect of 0.60 and an additive offspring allelic effect of 0.18 (μ = 40, β₁₀ = 0.60, β_.1 = 0.18, β_.2 = 0.36, ${\sigma }_a^2=1,{\sigma }_e^2=5$), and (c) Simulation G data with a variant allele count effect of 0.17 (μ = 40, β₀₁ = 0.17, β₁₀ = 0.17, β₁₁ = 0.34, β₁₂ = 0.51, β₂₁ = 0.51, β₂₂ = 0.68, ${\sigma }_a^2=1,{\sigma }_e^2=5$). Boxplots show bias of parameter estimates, additive genetic variance, and environmental variance over 2,000 replications. A horizontal line is drawn at zero bias.

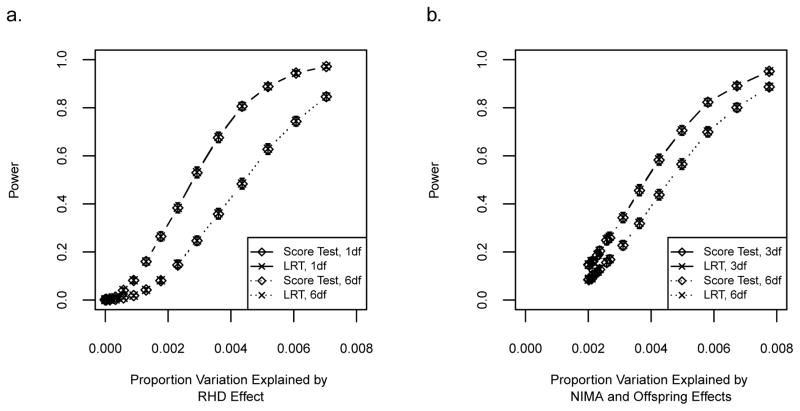
Figure 5. RHD incompatibility and NIMA power curves.

(a) Solid lines show power for the one degree of freedom test for an RHD effect (β₂₁) using the LRT and score test. Dotted lines show power when there is no specific MFG hypothesis (so all 6 MFG parameters are tested) using the LRT and score test. RHD effect sizes range from 0 to 0.7. Error bars represent approximate 95% confidence intervals. (b) Solid lines show power for the three degrees of freedom test for NIMA or offspring effects (β₁₀, β_.1, β_.2) using the LRT and score test. Dotted lines show power when there is no specific MFG hypothesis (so all 6 MFG parameters are tested) using the LRT and score test. NIMA effect sizes β₁₀ range from 0 to 0.7 and offspring effects are fixed (β_.1 = 0.18, β_.2 = 0.36). The power is not 0.001 and the proportion of variation explained is not zero when β₁₀ = 0 because β_.1, β_.2 are not zero. Error bars represent approximate 95% confidence intervals.

Non-inherited Maternal Antigen (NIMA) Effects

The case of NIMA provides a more complex model under which to investigate the properties of the QMFG test due to the added offspring allelic effects. For this more complicated case of MFG incompatibility, we start by comparing the LRT and score test type I error rates. Model 1 corresponds to the null hypothesis of no genetic effects and Model 3 corresponds to the alternative hypothesis of offspring or NIMA effects. By fitting Models 1 and 3 to data simulated with no genetic effects (Simulation A), the three degrees of freedom LRT results in the Q-Q plot in Figure 3b (λ = 0.989). Figure S1b shows that the score test for the significance of the same three parameters (β₁₀, β_.1, β_.2) is a suitable substitute for the LRT as it yields nearly identical p-values. As mentioned previously, using the LRT we can test the significance of NIMA in the presence of offspring effects or the offspring effect in the presence of NIMA. Figure 3c is the Q-Q plot (λ = 1.048) of the results of testing the significance of the NIMA parameter while allowing for offspring genotype effects (Model 3 vs Model 4) and Figure 3d is the Q-Q plot (λ = 0.959) of the results for offspring parameters in the presence of NIMA effects (Model 3 vs Model 5). Together these three Q-Q plots (Figure 3b–d) and confidence bounds demonstrate that our type I error rates are correct.

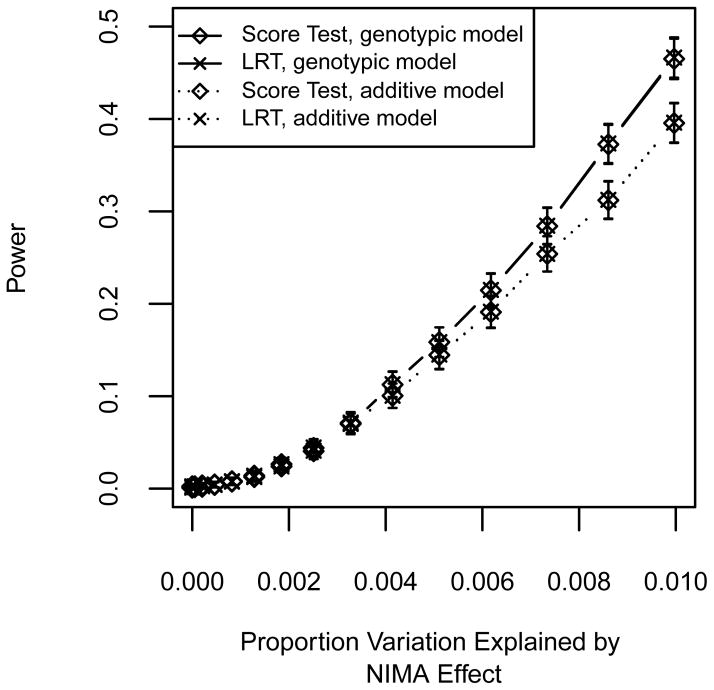
In Simulation C, a quantitative trait is simulated for offspring with a NIMA effect of 0.6 and an additive offspring allelic effect of 0.18 per allele, corresponding to 0.0058 of the variance explained by the combination of MFG and offspring effects. Mimicking a situation where there is a priori evidence for a particular model (in this case, NIMA and offspring effects), we fit Model 3 to the simulated data thus estimating three parameters (β₁₀, β_.1, β_.2) in addition to the variance components when using the LRT. The bias of each parameter estimate is shown in Figure 4b. As a valid method should, the QMFG method generates bias centered at zero. We further evaluate power over 2,000 simulation replicates for varying levels of proportion of variation explained for this model (Model 3). The power curves in Figure 5b are the results of jointly testing for NIMA or offspring effects (solid lines) when the simulated NIMA effect sizes range from 0 to 0.7 and the offspring effects are β_.1 = 0.18, and β_.2 = 0.36. These simulation parameters are consistent with proportion of variation explained ranging from 0.002 to 0.008. The power to detect NIMA or offspring effects (three degrees of freedom test) is approximately 80% when proportion of variation explained reaches 0.0055 for both the LRT and the score test. Figure S2 displays the power of the LRT for testing the significance of the NIMA effect in the presence of offspring genotype effects (one degree of freedom test) using the same collection of data. Power is approximately 80% when the proportion of variation explained by the NIMA effect reaches 0.002.

The NIMA analyses mentioned above are free of constraints on the relationship between offspring allelic effect parameters β_.1 and β_.2, that is, a genotypic model. Offspring effects may act in an additive, recessive or dominant manner. If there is a priori evidence to suggest any of these models, it is possible to impose restrictions on these parameters for the models that are fit, therefore reducing the degrees of freedom and increasing power. To demonstrate the ability of the QMFG LMM to handle such a situation, we simulate data with a NIMA effect varying from 0 to 0.6 and dominant offspring effects equal to 0.1 and analyze the data estimating again the NIMA and offspring effects, this time imposing the additional constraint β_.1 = β_.2. Figure S3 shows the power curves resulting from testing for a NIMA or dominant offspring effect. For the LRT, this involves using Model 1 corresponding to the null hypothesis and Model 6 corresponding to the alternative hypothesis, resulting in a two degrees of freedom test. The power to detect these effects remains high. There is greater than 80% to detect NIMA or dominant offspring effects when the proportion of the variance explained by these effects is 0.006.

Thus far, we have considered scenarios where just MFG and offspring effects are present. It is possible that in addition to these effects, there are maternal effects. To further demonstrate the flexibility of the QMFG method, we simulate data with both maternal and offspring main effects such that each variant allele further increases the offspring’s trait by 0.18 (Simulation D). In this scenario, the proportion of variation explained by the NIMA, offspring, and maternal effects is 0.009. For this specific scenario, we fit Model 1 corresponding to the null of no genetic effects and Model 7 corresponding to our alternative hypothesis. Model 7 is a five parameter model that is mathematically equivalent to genotypic offspring main effects, genotypic maternal main effects and a NIMA effect. Parameterized through using the coefficients for seven possible maternal-offspring genotype combinations, Model 7 requires an additional constraint β₂₂ + β₁₁ − β₁₂ − β₂₁ = 0 in addition to β₀₀ = 0. In other words, one of the parameters, β₁₁, β₁₂, β₂₁, β₂₂, is completely determined by the other three and so when using a LRT, five MFG parameters are tested (e.g. β₀₁, β₁₀, β₁₁, β₁₂, β₂₁). Figure S4 shows that there is no parameter estimate bias when we fit Model 7 to the data. The power of the LRT for this five degrees of freedom test is 0.96 (SE=0.004).

Effects of Allele Frequency and Variance Parameters

In the previous sections, the variant allele had a frequency of 0.4. For RHD incompatibility we consider ‘d’ to be the variant allele and for NIMA we consider the alleles encoding a shared epitope (SE+) to be variant. To evaluate the effect of allele frequency on our QMFG method, we compare our power results for Simulations B and C while varying the variant allele frequency from 0.1 to 0.9. Figures S5a and S5b show the impact of changing the variant allele frequency keeping the other simulation parameters the same for Simulations B and C, respectively. The power is maximized when the frequency of the ‘d’ allele is 0.67 for data simulated under RHD incompatibility. Under NIMA and offspring effects, power is maximized when the SE+ allele frequency is 0.33.

We also investigate the performance of the QMFG test when the values for additive genetic and environmental variance are changed, increasing the residual heritability. We recreate the power curves for RHD incompatibility as well as for NIMA and offspring effects, this time changing both the additive genetic and environmental variance simulation values to 3 ( ${\sigma }_a^2=3,{\sigma }_e^2=3$, h² = 0.50). Repeating the same one degree of freedom test for an RHD effect with these new variance values, we see an increase in power (Figure S6a) over our previous results (Figure 5a). Repeating the same three degrees of freedom test for NIMA or offspring effects using data simulated with these new variance values, we also see an increase in power (Figure S6b) over our previous results (Figure 5b).

Effects of Family Structure and Sample Size

To address the impact of family structure on our MFG tests, we simulate 4,000 trios, keeping the total number of offspring at 4,000, with quantitative traits with the same simulation parameters in Simulations B and C. With linear mixed models the additive and environmental variances are confounded when using a single individual per pedigree so instead of estimating ${\sigma }_a^2$ and ${\sigma }_e^2$ separately, we estimate their sum. Figure S7a shows there is no parameter estimate bias when fitting Model 2 to data simulated under RHD incompatibility (Simulation B). Power for either the LRT or the score test to detect an RHD effect (Model 2 vs Model 1) is not significantly altered. It is 0.81 (SE = 0.009) for three-generational families and 0.79 (SE = 0.009) for trios. Parameter estimates also remain unbiased (Figure S7b) when using trios with a quantitative trait simulated with NIMA and offspring effects (Simulation C) when fitting Model 3. Power with the three degrees of freedom test for NIMA or offspring effects (Model 3 vs Model 1) is not significantly changed. It is 0.82 (SE = 0.009) for three-generational families and 0.85 (SE = 0.008) for parent-offspring trios.

It is important to also consider the effect of sample size on the statistical properties of the tests. Here we run simulations with a smaller sample of 400 offspring from 100 three-generational families. As shown in Figure S8, type I error rates remain unaffected by a reduction in sample size. To achieve equivalent power to 1,000 families, we need to increase the RHD effect to 1.75. Fitting Model 2 to 100 three-generational families simulated with quantitative traits given Simulation E parameters, results in no bias for grand mean, RHD, and environmental variance parameters (Figure 6). Additive variance is slightly underestimated. The power to detect an RHD effect, which accounts for 0.042 of the trait variance in this scenario, is 0.78 (SE = 0.009). To achieve equivalent power to 1,000 families, we need to increase effect sizes for NIMA and offspring effects (Model 3) to β₀₁ = 1.90, β_.1 = 0.60, β_.2 = 1.20 when generating data for 100 three-generational families (Simulation F). We again see no bias for grand mean, NIMA, offspring, and environmental variance parameters (Figure S9). Additive variance is again slightly underestimated over the 2,000 repetitions. The proportion of variation explained by the NIMA and offspring effects in this scenario is 0.056 and the power for the three degrees of freedom test for NIMA or offspring effects is 0.82 (SE = 0.009).

Figure 6. Parameter estimate bias when data are simulated under RHD incompatibility with a smaller sample size.

Boxplots show bias of parameter estimates for the grand mean, MFG effects, additive genetic variance, and environmental variance using 100 three-generational families over 2,000 replications using parameters from Simulation E with an RHD effect of 1.75 (μ=40, β₂₁ =1.75, ${\sigma }_a^2=1,{\sigma }_e^2=5$). A horizontal line is drawn at zero bias.

Analysis when the MFG Mechanism is Unknown

Our QMFG analyses thus far assume that our outcome is associated with two well-known mechanisms of MFG incompatibility. However, it may be that there is no a priori information about the underlying MFG model that influences a trait’s value. Thus, we study the effects of using the general model, which imposes no constraints on the MFG parameters. First, we investigate the properties (type I error, power, and parameter estimates) of fitting such a model. Figure 3e shows the Q-Q plot for data simulated under the null hypothesis of no genetic effects (Simulation A) where all six MFG parameters β₀₁, β₁₀, β₁₁, β₁₂, β₂₁, β₂₂ are tested for significance (λ = 1.086). This is a six degrees of freedom test in which the full model (Model 8) is tested against the null model in which no MFG effects are estimated (Model 1) via the LRT. All the points lie within the confidence bounds; there is no bias in the type I error rate. The score test produces equivalent p-values (not shown). Parameter estimate bias is examined by simulating data given a count model (Simulation G). In Simulation G, each variant allele in the mother or offspring increases the offspring’s phenotype by 0.17 and the effects are additive and independent. In this scenario, 0.007 of the variance is explained by the MFG effect. Figure 4c shows the boxplots of the parameter estimate bias over 2,000 replicates when the general model is fit to the data. Again, unbiased parameter estimates are produced.

It is also of interest to examine the degree to which parameter estimate precision is reduced and power is lost when the underlying MFG model requires a less complex model, such as RHD or NIMA, but agnostically, the general model is fit. We consequently repeat the analysis of Simulations B and C, this time fitting the general six-parameter model (Model 8). As the boxplots displayed in Figures S10a and S10b illustrate, parameter estimates remain unbiased. The effect on power is visible in Figures 5a and 5b (dotted lines). As expected, the power curves follow a similar pattern to those from less complex models but are lower for both RHD incompatibility and NIMA examples. Under Simulation B conditions, the power of the LRT when α = 0.001 reduces from 0.751 (SE = 0.010) to 0.467 (SE = 0.011) when the proportion of variation explained is 0.0044. Under Simulation C conditions, the power of the LRT at the same significance level reduces from 0.823 (SE = 0.009) to 0.702 (SE = 0.010) when the proportion of variation explained is 0.0058. These results demonstrate that in terms of power, the QMFG test performs well when there is no prior support for a restricted model, thus avoiding possible model misspecification or misinterpretation. However, when there is prior support for a specific model (such as RHD incompatibility or NIMA), a restricted model can provide a substantial increase in power.

Power to Detect MFG Incompatibility in a Standard GWAS Analysis

Can a typical GWAS, which tests the effects of an offspring’s genotype and ignores MFG interactions, be used as a first screen for MFG incompatibility? We address this question by using data simulated with RHD incompatibility effects ranging from 0 to 0.70 and comparing the power shown in Figure 5a with the power that results when testing for either offspring genotypic and additive effects. Figure 7 shows the two degrees of freedom test for an offspring genotypic effect model and the one degree of freedom test for an additive offspring allelic effect model with significance levels α = 0.05 (Figure 7a) and α = 0.001 (Figure 7b). For the LRT, the two degrees of freedom test involves fitting Models 1 and 4 and the one degree of freedom test involves fitting Models 1 and 9. Together these figures demonstrate that, compared to the correct test for an RHD effect, power is drastically reduced. In the case of a true underlying RHD effect of 0.70 (Simulation H), the parameters representing the effect of one variant allele in the offspring genotype (β₀₁, β₁₁) are biased upward when fitting the offspring only genotypic model (Figure S11a). The parameter representing the effect of being homozygous for the variant allele remains unbiased. The parameter for the offspring allelic effect is only slightly upwardly biased when fitting the additive model (Figure S11b). We repeat both the two degrees of freedom test for offspring effects and one degree of freedom additive offspring effects analyses in data simulated with a NIMA effect ranging from 0 to 0.7 and no offspring effect. Figure 8 shows the resulting power curves for α = 0.001. In this case, the power is not as severely reduced. However, when fitting the genotypic model to data with a true NIMA effect of 0.7 (Simulation I), we see a downward bias of offspring genotype parameter estimates (Figure S12a). Figure S12b also shows there is parameter estimate bias when the additive model is fit to Simulation I data. Thus in the case of NIMA, a user may very well reject the null hypothesis but mistakenly attribute the effect to the offspring’s genotype.

Figure 7. Power using an offspring effect only test for data simulated under RHD incompatibility.

RHD effect sizes range from 0 to 0.7. Solid lines show the power for fitting the genotypic model, i.e., the two degrees of freedom test for offspring effects (β_.1, β_.2). Dotted lines show the power for fitting the additive model, i.e., the one degree of freedom test with the added constraint 2β_.1 = β_.2. Error bars represent approximate 95% confidence intervals. (a) Curves show power using the LRT and score test at significance level α=0.05. (b) Curves show power using the LRT and score test at significance level α=0.001.

Figure 8. Power using an offspring effect only test for data simulated under a NIMA effect.

Curves show power using the LRT and score test at significance level α = 0.001. NIMA effect sizes range from 0 to 0.7. Solid lines show the power for fitting the genotypic model, i.e., the two degrees of freedom test for offspring effects (β_.1, β_.2). Dotted lines show the power for fitting the additive model, i.e., the one degree of freedom test with the added constraint 2β_.1 = β_.2. Error bars represent approximate 95% confidence intervals.

Model Misspecification

We find that an RHD effect is unlikely to be detected if an investigator uses a NIMA effect model. For instance, if we take data with a true RHD effect of 0.7 (Simulation H), power drops from 0.97 (SE = 0.004) when the correct RHD effect model (Model 2) is fit to 0.008 (SE = 0.002) when an incorrect NIMA effect model is fit (Model 5). Although the parameter for a NIMA effect, β₁₀, is estimated on average to reduce the quantitative trait (Figure S13a), the estimate would not likely be found significant. Thus in the event that the model is misspecified, an RHD effect would not be misinterpreted as a NIMA effect but instead it would be missed. Likewise, misspecifying the QMFG model as an RHD effect model (Model 2) when data have a true underlying NIMA effect of 0.7 (Simulation I) would result in a missed effect. In this case, power drops from 0.999 (SE = 0.001) when the correct NIMA model is fit (Model 5) to 0.004 (SE = 0.001) when an incorrect RHD model is fit (Model 2). As shown in Figure S13b, the RHD parameter (β₁₂) is on average estimated to decrease the phenotype, though it would seldom be found significant given similar sample and effect sizes and therefore the NIMA effect would not be misinterpreted as an RHD effect. In both cases, although the true MFG effect would be missed, detecting false MFG effects is unlikely.

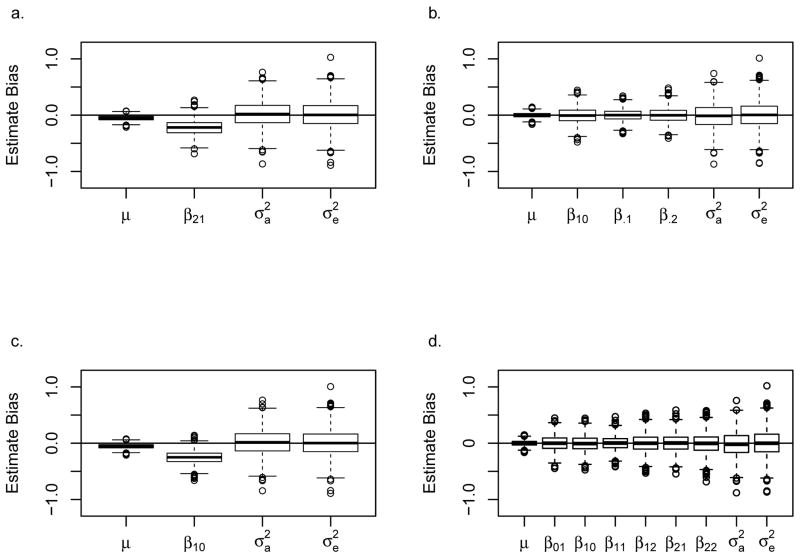
In Simulation J, a quantitative trait is simulated for offspring with an additive offspring allelic effect of 0.27. Mimicking a situation where the user incorrectly hypothesizes that there is an RHD effect on the quantitative trait, we fit Model 2 to the simulated data thus estimating the RHD parameter (β₂₁). Under these conditions where we would have power equal to 0.86 (SE= 0.008) if the correct model for offspring effects (Model 4) was used, the rejection rate when testing for an RHD effect is 0.002 (SE = 0.001). Figure 9a shows the degree of parameter estimate bias that follows from misspecifying the model. Taken together, these results show that it is possible that an offspring effect would be misinterpreted as an RHD-like effect that reduces the trait value, but that the null hypothesis of no RHD effect would rarely be rejected. If a user instead believes there may be a NIMA effect on phenotype, he or she may fit Model 3 (NIMA and offspring effects model) or Model 5 (NIMA effect only model) to the data. Because the NIMA and offspring effects model includes parameters for offspring allelic effects, we expect that the estimated parameters would not be biased although the power would be reduced. These expectations are confirmed by Figure 9b and the power for the three degrees of freedom test for NIMA or offspring effects is 0.81 (SE = 0.009). On the other hand, if the NIMA effect model (Model 5) is fit to the same data, the power when testing for a NIMA effect is 0.16 (SE = 0.008). The potential to reject the null hypothesis is higher than in the case of RHD, but a significant effect would probably not be detected. In Figure 9c it can be seen that if there was enough power, the offspring effect might be misinterpreted as a NIMA effect that decreases the quantitative phenotype. Finally, if the user has no a priori hypothesis and fits the most general model (Model 8), there is zero bias (Figure 9d) and the power to detect an effect is 0.69 (SE = 0.010). These results further demonstrate the advantage of using an MFG model that allows for offspring effects, which is a generalization of the standard GWAS analysis, when screening for MFG effects.

Figure 9. Parameter estimate bias due to model misspecification.

Genotypes and quantitative traits for each replication were simulated for 1,000 pedigrees using Simulation J data with an offspring allelic effect of 0.27 (μ = 40, β_.1 = 0.27, β_.2= 0.54, ${\sigma }_a^2=1,{\sigma }_e^2=5$). Boxplot shows bias of parameter estimates, additive variance, and environmental variance over 2,000 replications when the model is misspecified as (a) Model 2, the RHD effect model, (b) Model 3, the NIMA and offspring effects model, (c) Model 5, the NIMA effect model, and (d) Model 8, the general model. A horizontal line is drawn at zero bias.

Effect of Missing Data on Type I Error

As is often the case with real data, missing data are an issue that must be considered. Assuming genotypes are missing at random, we compare type I error rates testing for various sets of MFG parameters given 0, 5, 10, and 20% missing genotypes. Here we use Simulation A data, randomly removing a percentage of genotypes with each repetition, and estimate type I error rates with a per test significance level of 0.05. With all the models tested missing data did not significantly affect type I error rates (Table S2).

Screening for MFG Incompatibility Using Pedigree-based GWAS Data

The ability to quickly screen markers is demonstrated by running the QMFG test on data from the SAFHS. Missing genotypes for the 944,565 SNPs across the genome were imputed using Mendel’s imputation option. We removed 14,008 SNPs (1.48%) because there was at least one impossible maternal-offspring genotype combination observed at each of these SNPs in the imputation results. We omitted another 295,063 SNPs because they had minor allele counts less than 10 leaving a total of 635,494 SNPs for the analysis. Because we have no specific hypothesis regarding MFG interactions associated with HDL measures but aim to demonstrate the feasibility of using the QMFG test on pedigree-based GWAS data, we use an alternative hypothesis of NIMA or offspring effects, a straightforward generalization of the standard GWAS analysis. This model takes into account offspring effects, so in the case that there is an underlying offspring genotypic effect but no NIMA effect, we lose power by including the parameter for NIMA but avoid misspecifying the model.

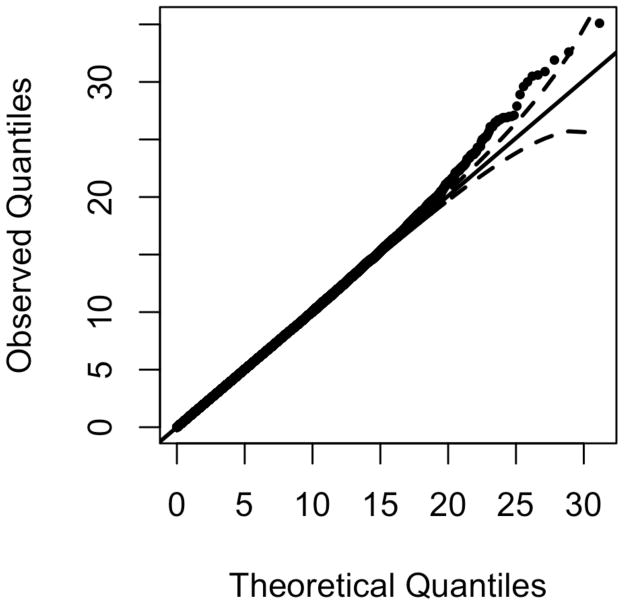
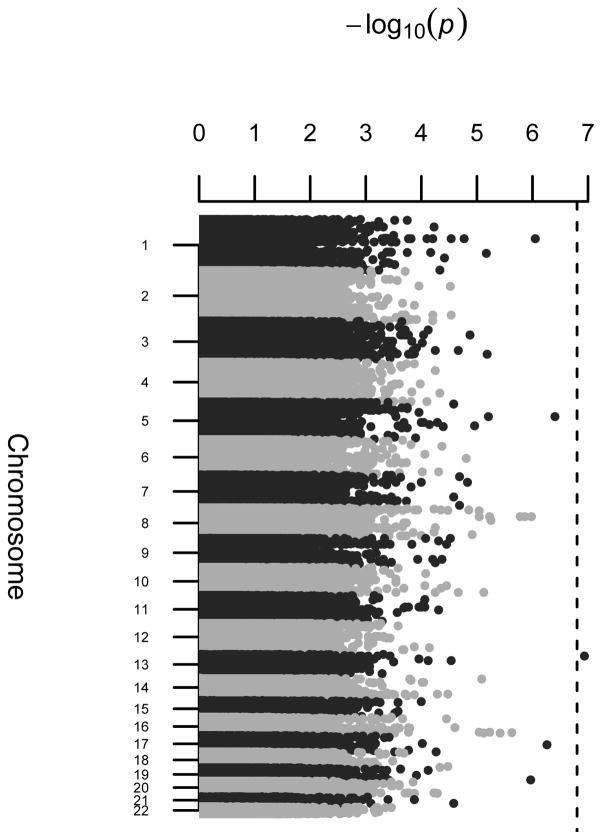
In these analyses we assume the minor allele of each SNP is the variant allele and include sex and age as fixed effects. Under the null hypothesis of no genetic effects, the estimate of the grand mean was 48.030 (SE = 2.094). The age effect estimate of 0.034 (SE = 0.069) was not significant. Women had significantly higher HDL levels than males (4.222 units higher, SE = 1.154). Figures 10 and 11 show the Q-Q plot (λ = 1.012) and Manhattan plot resulting from the three degrees of freedom QMFG score test for the alternative hypothesis of NIMA or offspring effects. The run time for Mendel to read in and perform the score tests for the 635,494 SNPs was 4 minutes and 28 seconds on a computer with 12 CPU cores (at 2.67 GHz). About 0.2% (1309) of sites fall outside the 95% confidence limits of the Q-Q plot (Figure 10). The 10 markers with the smallest p-values are shown in Table 4. Figure S14 shows the Q-Q plot of the same results with the top 10 hits removed (λ = 1.012). The lowest p-value, found with SNP rs1547189, corresponds to an FDR (Benjamini & Hochberg, 1995) of 7.5% (Table 5). The parameter estimates for this SNP are shown in Table 6.

Figure 10. Q-Q plot for score test of the SAFHS data.

Results from the three degrees of freedom test for NIMA or offspring effects (β₁₀, β_.1, β_.2) using the score test adjusting for age and sex (λ = 1.012). Data from the SAFHS consist of 635,494 SNPs from 419 offspring with HDL measurements in 43 multi-generational families.

Figure 11. Manhattan plot for score test of the SAFHS data.

Results from the three degrees of freedom test for NIMA or offspring effects (β₁₀, β_.1, β_.2) using the score test adjusting for age and sex. Data from the SAFHS consists of 635,494 SNPs from 419 offspring with HDL measurements in 43 multi-generational families. A dashed horizontal line is drawn at the initial significance cutoff for an FDR of 10%.

Table 4.

Score test for NIMA or offspring effects on HDL from the San Antonio Family Heart Study.

Chromosome	Nearby gene	SNP	Score test statistic	P-value
13	USP12	rs1547189:G>A	35.1	1.16 × 10−7
5	-	rs9293660:G>A	32.6	3.91 × 10−7
17	NGFR	rs614455:T>C	31.9	5.49 × 10−7
1	FAM69A	rs7521417:C>T	30.9	8.92 × 10−7
8	LOC102723729	rs11987150:G>A	30.6	1.03 × 10−6
19	ZNF888	rs10425203:G>A	30.5	1.08 × 10−6
8	GINS4	rs13265966:T>C	30.0	1.38 × 10−6
8	LOC102723729	rs11994079:G>T	29.6	1.68 × 10−6
16	-	rs6564175:T>C	28.9	2.35 × 10−6
16	WWOX	rs4267317:G>A	27.9	3.81 × 10−6

Table 5.

False discovery rates for the San Antonio Family Heart Study analysis.

FDR	P-value threshold	Number of significant SNPs
5%	7.87 × 10−8	0
7.5%	1.18 × 10−7	1
10%	1.57 × 10−7	1
15%	1.89 × 10−6	8

Table 6.

Parameter estimates for SNP rs1547189 from the SAFHS data.

Effect	Parameter	Estimate	Std Error
Grand mean	μ	46.10	2.72
NIMA	β10	8.51	2.15
A/G* offspring	β.1	−0.60	1.85
G/G offspring	β.2	10.19	2.84
Female	βfemale	4.32	0.55
Age	βage	0.04	0.07
Additive variance	${\sigma }_a^2$	80.66	19.64
Environmental variance	${\sigma }_e^2$	63.60	14.60

^*G is the minor allele for SNP rs1547189

For rs1547189, we further refine our analysis. The two degrees of freedom test for offspring genetic effects for SNP rs1547189 on HDL has a p-value of 0.0007. For the one degree of freedom test for additive offspring effects (2β_.1 = β_.2) using the same SNP, the p-value is 0.18. We also test for a NIMA effect in the presence of offspring effects adjusting for sex and age using an LRT. The p-value of 2.98 × 10⁻⁶ suggests that even when accounting for offspring genotypic effects, there may be an additional effect of NIMA. Taken together, these results suggest that there may be both an underlying recessive offspring effect and a NIMA effect on HDL for SNP rs1547189.

DISCUSSION

Our simulation studies show that the LRT version of the QMFG test leads to correct parameter estimates and inference and the score test version of the QMFG test provides equivalent inference to the LRT under both specific and general models of MFG incompatibility. The simulations under an RHD incompatibility scenario illustrate the QMFG test under a simple model, involving just one MFG parameter. We show that our approach has correct type I error rates for the LRT and score test, zero parameter estimation bias, and high power even when the proportion of variation explained by MFG incompatibility is small. The simulations under NIMA provide a more complicated, but still biologically pertinent, scenario to evaluate the properties of the QMFG test, requiring an MFG effect and offspring effects to be tested jointly. Under this scenario, the effect on offspring with genotypes homozygous for the reference allele depends on their mother’s genotype. With this scenario, we show the flexibility of the LRT to test effects jointly, marginally, and conditionally. When testing NIMA and offspring effects jointly and conditionally, again the LRT version of the QMFG test produces appropriate type I error rates, zero parameter estimation bias, and high power. This model can be extended by allowing for maternal genetic effects. We also demonstrate that it is possible to impose parameter restrictions to test for other situations such as a dominant offspring effects.

Additionally, we investigate MFG incompatibility testing in the case that there is no a priori information about the underlying MFG model. As expected, power is reduced when applying this general model, which imposes no constraints on the MFG parameters, to data simulated with a specific, more restricted MFG incompatibility. Our results indicate that even when the general model is fit to the data in place of the correct, simpler model, the QMFG LRT still produces unbiased parameter estimates. We also explore cases where the model is misspecified such that a model with only offspring effects is fit to data with true underlying MFG effects and find that power is greatly reduced. This is especially true in the case of testing for additive effects when the underlying MFG effect is RHD incompatibility, where power drops down to the type I error rate. This particularly low powered case with the additive model results because we have a SNP that, when viewed from the perspective of offspring effects, is displaying a weak amount of over-dominance in which a only fraction of the offspring with heterozygous genotypes are expected to have different phenotypic values from offspring with either of the two homozygous genotypes. In the case of an underlying NIMA effect, there is more power to detect a genotypic effect when fitting a model with only offspring effects but in this case, the NIMA would be misinterpreted as a weak dominant effect on the quantitative trait. These results have implications for GWAS, which typically use additive models or Armitage trend tests, since, as we have shown, the genetic effects can be detected but misinterpreted, determined with lower power, or missed all together. The QMFG test is also subject to type I or type II error when the model is misspecified. In particular, when applying the NIMA effect model to data with an RHD effect, applying the RHD effect model to data with a NIMA effect, or applying a RHD or NIMA model to data with offspring effects, the null hypothesis is rejected at very low rates, indicating that in these cases the locus would be missed. Because most effects are very likely to be offspring genotype effects, we recommend using an MFG model that includes offspring genetic effects when screening large numbers of SNPs.

Unlike other methods that have been proposed to test for an association between a quantitative trait and MFG incompatibility, the QMFG test can handle small and large pedigrees simultaneously. With actual data from the SAFHS we verify that the QMFG score test is an effective and rapid screening tool for genome wide association studies. In this data set, family size varied greatly; the smallest family had 8 members and spanned 3 generations; the largest family had 176 members and spanned 5 generations. We chose to analyze the data by jointly screening for NIMA and offspring genotypic effects using the score test. If the genetic effects only come from the offspring as typically assumed, our analysis would still be able to detect them, albeit with slightly lower power than in the typical GWAS.

Although none of the top ten markers for NIMA or offspring effects have been previously shown to be associated with HDL, the WWOX gene has been shown to be associated with HDL (Lee et al., 2008, Saez et al., 2010). Our result with the smallest p-value is for SNP rs1547189, which is an intron variant in the ubiquitin specific peptidase 12 (USP12) gene, with an FDR of 7.5%. Because it is possible that this marker’s effect could be exclusively due to offspring effects, we use the LRT with the null hypothesis of only offspring effects and the alternative hypothesis of NIMA and offspring effects to test for NIMA effects in the possible presence of offspring effects with SNP rs1547189. Combined, our results are suggestive of a NIMA effect in the presence of offspring effects. To determine whether this association is due to a previously undetected NIMA effect on HDL or, perhaps what is more likely is just a type I error, requires testing in other cohorts. However, we have clearly demonstrated the potential of the QMFG test to identify novel associations with quantitative traits that may not be detected in standard GWAS analysis models, because the standard GWAS only considers offspring allelic effects. Additionally, our analysis demonstrates that the LRT is a useful tool to refine results following the rapid screening provided by the QMFG score test.

To date, no other studies have looked at the role of MFG incompatibility on quantitative traits in families larger than trios due to the lack of appropriate models and practical software. The QPL method (Kistner & Weinberg, 2005) as well as the QCPG method (Wheeler & Cordell, 2007) are both retrospective approaches in which the offspring genotype is modeled as a function of the quantitative trait and parental genotypes and are restricted to parent-offspring trios. These methods can be easily modified to test for maternal-offspring gene interactions (Wheeler & Cordell, 2007). However, Wheeler and Cordell’s simulation results suggest that, compared to these two retrospective approaches to test for quantitative trait association in trios, a prospective, linear regression approach such as ours is likely to be more efficient but more sensitive to departures from normality. From our viewpoint, the main difficulty with retrospective approaches such as the QPL and QCPG is in generalizing them to work with a dataset composed of dramatically different sized families. Another limitation is the interpretation of the estimated effects as they are scaled by the unknown trait variance. Furthermore, including covariates such as age and sex is not straightforward. With the QMFG test we have demonstrated the benefits of a prospective approach to rapidly test for MFG incompatibility in families of any size. It is a highly flexible and accurate method, which is also easy to execute with our user-friendly software.

It should be noted that in general, LMMs used for quantitative traits do not directly apply to binary phenotypes. This limitation results from the fact that the phenotypic variance of a dichotomous disease or trait depends on its incidence in the population (Falconer, 1965). Thus, estimates must be rescaled. Unlike with continuous traits, case-control studies are additionally susceptible to ascertainment bias. As a result, using LMMs on binary traits directly can result in loss of power as sample size increases, likely due to the amplification of inaccuracies caused by ascertainment bias (Yang et al., 2014). Methods to improve power for qualitative outcomes are based on a liability threshold principle, in which it is assumed that binary traits can be represented by an underlying normally distributed liability trait. If an individual’s liability exceeds a threshold, then he or she has a phenotypic value of 1, otherwise 0, with the proportion of the normal distribution that exceeds the threshold being equal to trait incidence (Dempster & Lerner, 1950, Falconer, 1965). An approach by Hayeck et al. (2015) estimates the posterior mean liability (PML) of each individual conditional on the case-control status of all subjects, disease prevalence, and liability scale phenotypic covariance. The association between each SNP and PML is then tested. Accordingly, if the QMFG test is applied to dichotomous data, it is recommended that one adopt the Hayeck et al. (2015) approach.

We have implemented the QMFG test by modifying the statistical genetics software package Mendel. This option is scheduled for release in an upcoming version of Mendel. The validity of our method, together with the availability of convenient software, make the QMFG test a powerful tool for detecting undiscovered associations with complex diseases.

Supplementary Material

Supp FigureS1-S14 & TableS1-S2

Table S1 San Antonio Family Heart Study subject counts.

Table S2 Estimated type I error rates when a proportion of genotypes are missing.

Figure S1 Comparison of LRT and score test p-values for Simulation A data.

Figure S2 Power to detect a NIMA effect in the presence of offspring effects.

Figure S3 Power to jointly detect NIMA and dominant offspring effects.

Figure S4 Parameter estimate bias for data simulated with NIMA, offspring, and maternal effects.

Figure S5 Effect of allele frequency on power.

Figure S6 Effect of additive genetic and environmental variance on power.

Figure S7 Parameter estimate bias when data are simulated for parent-offspring trios.

Figure S8 Q-Q plot for LRT when data are simulated with a smaller sample size.

Figure S9 Parameter estimate bias when data are simulated under NIMA and offspring effects with a smaller sample size.

Figure S10 Parameter estimate bias when the general model is fit.

Figure S11 Parameter estimate bias when a misspecified model is fit using Simulation H data.

Figure S12 Parameter estimate bias when a misspecified model is fit using Simulation I data.

Figure S13 Parameter estimate bias due to model misspecification.

Figure S14 Q-Q plot for score test of the SAFHS data when top 10 hits are removed.