Sparse representation of HCP grayordinate data reveals novel functional architecture of cerebral cortex

Abstract

The recently publicly released Human Connectome Project (HCP) grayordinate‐based fMRI data not only has high spatial and temporal resolution, but also offers group‐corresponding fMRI signals across a large population for the first time in the brain imaging field, thus significantly facilitating mapping the functional brain architecture with much higher resolution and in a group‐wise fashion. In this article, we adopt the HCP grayordinate task‐based fMRI (tfMRI) data to systematically identify and characterize task‐based heterogeneous functional regions (THFRs) on cortical surface, i.e., the regions that are activated during multiple tasks conditions and contribute to multiple task‐evoked systems during a specific task performance, and to assess the spatial patterns of identified THFRs on cortical gyri and sulci by applying a computational framework of sparse representations of grayordinate brain tfMRI signals. Experimental results demonstrate that both consistent task‐evoked networks and intrinsic connectivity networks across all subjects and tasks in HCP grayordinate data are effectively and robustly reconstructed via the proposed sparse representation framework. Moreover, it is found that there are relatively consistent THFRs locating at bilateral parietal lobe, frontal lobe, and visual association cortices across all subjects and tasks. Particularly, those identified THFRs locate significantly more on gyral regions than on sulcal regions. These results based on sparse representation of HCP grayordinate data reveal novel functional architecture of cortical gyri and sulci, and might provide a foundation to better understand functional mechanisms of the human cerebral cortex in the future. Hum Brain Mapp 36:5301–5319, 2015. © 2015 Wiley Periodicals, Inc.

INTRODUCTION

Studying human brain function using in‐vivo functional neuroimaging techniques such as functional magnetic resonance imaging (fMRI) [Friston, 2009; Logothetis, 2008] has received significant interest in the brain mapping field. Specifically, task‐based fMRI (tfMRI) has been widely adopted to identify brain regions that are functionally involved in a specific task performance [Friston, 2009; Logothetis 2008]. To advance the understanding of functional localizations and interactions within the human brain based on fMRI data, there have been increasing efforts in acquiring and processing fMRI data with higher spatial/temporal resolution and correspondence across subjects and populations to better characterize the regularity and variability of human brain function [Van Essen et al., 2013]. One of such efforts is the recently publicly released Human Connectome Project (HCP) grayordinate‐based fMRI data [Barch et al., 2013; Glasser et al., 2013; Smith et al., 2013; Van Essen et al., 2013]. The HCP grayordinate data models the gray matter as combined cortical surface vertices and subcortical voxels across subjects in the standard MNI152 space [Glasser et al., 2013; Smith et al., 2013]. The HCP fMRI (including tfMRI and resting state fMRI) data in the standard grayordinate space not only has both much higher spatial and temporal resolution, but also offers group‐corresponding fMRI signals across a large population for the first time in the brain imaging field. In short, the HCP grayordinate fMRI data significantly facilitates the mapping of functional brain architecture with much higher resolution and in a group‐wise fashion, without the need to average signals within brain regions and across subjects [Mikl et al., 2008; Yue et al., 2010].

Based on tfMRI data, various studies [e.g., Bullmore and Sporns, 2009; Dosenbach et al., 2006; Fox et al., 2005; Huettel et al., 2004; Lv et al., 2015a,b] have demonstrated that there exist multiple concurrent functional networks that are spatially distributed across brain regions and are involved and interacting with each other. This phenomenon is in agreement with studies in the neuroscience field which have been widely reported and argued that there are certain brain regions and networks that exhibit strong functional heterogeneity and diversity [Anderson et al., 2013; Duncan, 2010; Fedorenko et al., 2013; Gazzaniga, 2004; Kanwisher, 2010; Pessoa, 2012]. That is, a brain region might be involved in multiple functional processes simultaneously, and a functional network might recruit heterogeneous brain regions. For instances, it was argued that “neural basis of emotion and cognition should be viewed as governed less by properties that are intrinsic to specific sites and more by interactions among multiple brain regions” [Pessoa, 2012] and that “areas of the brain that have been associated with language processing appear to be recruited across other cognitive domains” [Gazzaniga, 2004]. In short, identifying and characterizing such meaningful task‐based heterogeneous functional regions (THFRs) on cerebral cortex, i.e., the cortical regions that are activated during multiple tasks conditions and contribute to multiple task‐evoked systems during a specific task performance, could be important to understanding the functional architecture of human cerebral cortex. However, those meaningful THFRs with complex temporal patterns due to the complex composition of involved multiple functional networks/processes might have been underestimated by traditional approaches which merely consider individual tfMRI signals based on model‐driven subtraction procedures [Lv et al., 2015a,b).

The highly convoluted cortical folding, which is composed of convex gyri and concave sulci, is one of the most prominent features of human cerebral cortex [Barron, 1950; Rakic, 1988; Welker, 1990]. In recent years, there has been increasing interest in human brain mapping from both micro‐ and macroscale to investigate the possible structural/functional differences between gyri and sulci, and several interesting findings have been reported [Chen et al., 2013; Deng et al., 2014; Nie et al., 2012; Takahashi et al., 2012; Zeng et al., 2015; Zhang et al., 2014]. For instances, a recent micro‐scale study [Zeng et al., 2015] based on recently released Allen Mouse Brain Atlas demonstrated that the cerebellum gyri and sulci of rodent brains are significantly different in both axonal connectivity and gene expression patterns. For macro‐scale data analysis, our recent studies [Chen et al., 2013; Nie et al., 2012] demonstrated that the termination of streamline fibers derived from diffusion magnetic resonance imaging (dMRI) (e.g., diffusion tensor imaging (DTI) and high angular resolution diffusion imaging (HARDI)) concentrate on gyrus in human, chimpanzee, and macaque brains. This phenomenon was also observed in another analysis on human fetus brain [Takahashi et al., 2012]. Another recent study [Zhang et al., 2014] identified and characterized the U‐shapes of streamline fibers derived from dMRI (e.g., DTI, HARDI, and diffusion spectrum imaging (DSI)), and reported that most of the U‐shaped streamline fibers connect neighboring cortical gyri and course along sulci in human, chimpanzee, and macaque brains. Moreover, inspired by those structural connectivity findings, our recent study [Deng et al., 2014] demonstrated that the functional connectivity is strong between gyral‐gyral regions, weak between sulcal‐sulcal regions, and moderate between gyral‐sulcal regions based on resting state fMRI data. However, the functional brain characteristics (e.g., the possible distribution difference of THFRs in this study) of cortical gyral/sulcal regions during a specific task performance based on tfMRI data are largely unknown.

Motivated by the above‐mentioned reasons and based on the high‐quality HCP grayordinate tfMRI data, this study aims to identify and characterize the meaningful THFRs on cortical surface during a specific task performance, and to assess the possible distribution difference of identified THFRs on cortical gyral and sulcal regions. The recently publicly released HCP tfMRI data in the standard grayordinate space [Barch et al., 2013; Glasser et al., 2013; Van Essen et al., 2013] is particularly suitable for this study due to the following three reasons. (1) It is well demonstrated [e.g., Glasser et al., 2013; Smith et al., 2013; Van Essen et al., 2013] that it is of great importance to analyze cortical neuroimaging data with surface constraint information since the convoluted cortical sheet and its geometry information is better represented in two‐dimensional (2D) surface space than in commonly adopted three‐dimensional (3D) volume space. (2) The HCP grayordinate tfMRI data can sufficiently differentiate gyral/sulcal regions and relatively reliably map the tfMRI time series on cortical gyral and sulcal regions. While for the commonly used tfMRI data in 3D volume space, the possible functionally distinct regions across gyral blades or sulcal banks are only separated by a few voxels (millimeters). It is possible that the tfMRI time series from functionally distinct gyral/sulcal regions are mixed when performing 3D volumetric smoothing processing and thus inaccurate for succeeding analysis [Glasser et al., 2013]. (3) The HCP grayordinate tfMRI data has both high spatial and temporal resolution than the commonly used tfMRI data, and the spatial correspondence of the standard grayordinate tfMRI data is relatively more precise than aligned 3D volume data across different subjects [Glasser et al., 2013], and the associated tfMRI signals of grayordinates also have relatively precise correspondence across subjects, which is suitable for cross‐subject comparison and group‐wise analysis. In short, using HCP grayordinate‐based tfMRI data will significantly benefit us to identify THFRs reliably and assess their spatial patterns on cortical gyri and sulci accurately in this study.

In general, our contributions in this work are threefold: (1) We identify and characterize meaningful THFRs via our recent computational framework [Lv et al., 2015a,b] of sparse representations of whole‐brain tfMRI signals via an effective online dictionary learning algorithm [Mairal et al., 2010]. The rationales of adopting sparse representation of whole‐brain tfMRI signals to identify meaningful functional networks are explained in two fold. First, based on the argument that a brain region might be involved in multiple functional processes simultaneously [Anderson et al., 2013; Duncan, 2010; Fedorenko et al., 2013; Gazzaniga, 2004; Kanwisher, 2010; Pessoa, 2012], its tfMRI blood oxygen level dependent (BOLD) signal could be composed of various components (functional networks) simultaneously. Second, given that dictionary learning and sparse representation approaches have been successfully adopted in machine learning and pattern recognition fields to both represent signals accurately and compactly and extract meaningful patterns effectively [e.g., Wright et al., 2010], there have been several recent successes of adopting dictionary learning and sparse representation for brain fMRI signal analysis and activation/network detection under the premise that each fMRI signal's components are sparse and linearly neural integrated [e.g., Abolghasemi et al., 2015; Lee et al., 2011; Lv et al., 2015a,b; Oikonomou et al., 2012]. Specifically, our recent works [Lv et al., 2015a,b] successfully performed sparse representation of whole‐brain fMRI signals at voxel scale to infer a comprehensive collection of functional networks in the whole brain concurrently, to characterize those functional networks via spatial and temporal patterns, to assess the composition contributions of those functional networks to whole‐brain fMRI signals, and to measure the spatial overlap patterns among functional networks. A critical difference between the dictionary learning/sparse representation approach and other decomposition approaches (e.g., independent component analysis (ICA) [McKeown et al., 1998]) is that the sparse representation does not explicitly assume the independence of fMRI time series among different functional components, while ICA does. It is more appropriate to explore the THFRs with concurrent functional processes/networks based on the sparse representation‐based components in this study. (2) We apply our computational framework on the recently publicly released HCP grayordinate tfMRI data [Barch et al., 2013; Glasser et al., 2013; Van Essen et al., 2013], making the results relatively reliable, reproducible, and comparable for other studies. (3) It is the first time (as far as we know) to assess the spatial patterns of task‐based heterogeneous functional regions on cortical gyri and sulci, the results of which could provide a foundation for future exploration of functional architecture of the human cerebral cortex.

The manuscript is organized as follows. We first briefly describe HCP grayordinate‐based tfMRI data and the associated minimal preprocessing pipelines [Glasser et al., 2013]. In the methods, we first identify a comprehensive collection of functional networks of each subject during specific task performances via the recently developed computational framework [Lv et al., 2015a,b] of sparse representations of grayordinate brain tfMRI signals. Then, we identify and quantitatively characterize the meaningful task‐evoked networks and intrinsic connectivity networks in spatial and/or temporal domains. Finally, we identify the task‐based heterogeneous functional regions (THFRs) involved in multiple functional networks, and assess their spatial patterns on cortical gyri/sulci. Experimental results and discussion and conclusion are also presented.

MATERIALS AND METHODS

“Grayordinate” Data Acquisition and Preprocessing

We adopt the high‐quality task‐based fMRI (tfMRI) data from the Human Connectome Project (HCP) (first quarter (Q1) release) [Barch et al., 2013; Van Essen et al., 2013] in this study. HCP provides publicly available and easy‐to‐use multimodality MRI neuroimaging datasets for multimodal analysis of brain structure, connectivity, and function, as well as comparisons across subjects. Specifically, the HCP tfMRI datasets include seven different task paradigms (emotion, gambling, language, motor, relational, social, and working memory) which are adopted or designed to identify core functional nodes across a wide range of cerebral cortex, thus can be viewed as a comprehensive and systematic mapping of core functional nodes and functional networks across subjects [Barch et al., 2013]. The detailed designs of the seven task paradigms are referred to in Barch et al. [2013].

There are 68 subjects in the Q1 release of HCP tfMRI datasets [Barch et al., 2013; Van Essen et al., 2013]. The acquisition parameters of tfMRI data are as follows: 90 × 104 matrix, 220 mm FOV, 72 slices, TR = 0.72 s, TE = 33.1 ms, flip angle = 52°, BW = 2,290 Hz/Px, in‐plane FOV = 208 × 180 mm, 2.0 mm isotropic voxels [Barch et al., 2013]. We adopt the publicly released preprocessed tfMRI data after the minimal preprocessing pipelines which are especially defined for high spatial and temporal resolution of HCP datasets [Glasser et al., 2013]. The minimal preprocessing pipelines mainly include spatial artifacts and distortions removal, cortical surfaces generation, within‐subject cross‐modal registration, cross‐subject registration to standard volume and surface spaces, and generation of a CIFTI format of preprocessed data in the standard grayordinate space [Glasser et al., 2013]. In brief, gray matter is modeled as combined cortical surface vertices and subcortical voxels, and the term “grayordinates” is adopted to describe the spatial dimension of such combined coordinate system. The standard grayordinate space means that the cortical surface mesh and subcortical volume parcels are both in the MNI standard space (Fig. 1a). There are 91,282 maximally aligned grayordinates in total (including the gray matter sampled at about 60 k surface vertices in the standard 2 mm average vertex spacing on the cortical surface and about 30 k standard 2 mm voxels in subcortical regions) across all subjects and data modalities [Glasser et al., 2013]. The grayordinate‐based tfMRI data is represented as a 2D matrix in CIFTI format, in which one dimension represents the standard grayordinates (spatial information) which have correspondence across subjects and the other dimension represents the tfMRI time series (Fig. 1b) [Barch et al., 2013; Glasser et al., 2013].

Figure 1.

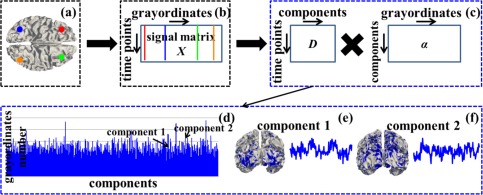
Sparse representation of grayordinate‐based whole‐brain tfMRI signals. (a) The cortical surface of an example subject in the MNI152 standard grayordinate space. Four example cortical vertices (grayordinates) are highlighted by four different colors (red, blue, green and orange). (b) The grayordinate‐based tfMRI data of the subject in (a). It is represented as a 2D matrix X, in which each row represents the standard grayordinates (spatial information) and each column represents the tfMRI time series. Four corresponding tfMRI signals of the four example grayordinates in (a) are represented as straight lines by the same color. (c): Sparse representation of X as dictionary D × sparse coefficient weight matrix α. (d)–(f): Illustrations of D and α. The blue bars in (d) show dictionary components (indexed horizontally) and the number of grayordinates that each dictionary component contains by counting the number of non‐zero elements in each row of α (vertical height). (e) and (f) show spatial distribution map on the cortical surface (highlighted by blue) and temporal time series (blue curve) of two example dictionary components, respectively. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Sparse Representation of Grayordinate‐Based Whole‐Brain TfMRI Signals

We perform dictionary learning and sparse representation of grayordinate‐based whole‐brain tfMRI data to obtain a comprehensive collection of dictionary components (functional networks) in the whole brain for each subject in each task data via our recently developed computational framework [Lv et al., 2015a,b]. All variables used in this section are summarized in Supporting Information Table I. As illustrated in Figure 1, for each subject in each task data, first, we extract tfMRI signals of whole‐brain grayordinates (Fig. 1a). After normalizing to zero mean and standard deviation of 1, all tfMRI signals are aggregated into a 2D signal matrix $\mathbf{X}=\left[{\mathbf{x}}_1,\mathrm{...},{\mathbf{x}}_n\right]\in R^{t\times n}$ (Fig. 1b), where t is the tfMRI time points and n columns are n tfMRI signals extracted from n grayordinates. Then X is factorized into an overcomplete dictionary basis matrix $\mathbf{D}=[{\mathbf{d}}_1,\mathrm{...},{\mathbf{d}}_k]\in R^{t\times k}$ (Fig. 1c, k is the dictionary component size) and a sparse coefficient weight matrix $\mathbf{\alpha }=[{\mathbf{\alpha }}_1,\mathrm{...},{\mathbf{\alpha }}_n]\in R^{k\times n}$ (Fig. 1c) via an effective online dictionary learning algorithm [Mairal et al., 2010], in which the tfMRI signal vector ${\mathbf{x}}_i$ (i=1,…n) in ith column of X is approximately modeled as ${\mathbf{x}}_i=\mathbf{D}\times {\mathbf{\alpha }}_i$, where ${\mathbf{\alpha }}_i$ (i=1,…n) is the ith column of α. Specifically, each dictionary component can be viewed as a functional network from brain science perspective, i.e., the time series vector ${\mathbf{d}}_i$ (i=1,…k) in ith column of D represents the functional BOLD (blood‐oxygen‐level dependent) activities of ith functional network (the blue curves in Fig. 1e,f), while ${\mathbf{d}}_i$'s corresponding sparse coefficient weight vector ${\mathbf{\alpha }}^i$ (i=1,…k) in ith row of α can be mapped back to the cortical surface to obtain the cortical spatial pattern of the functional network (Fig.1e,f). At the conceptual level, the computational framework of sparse representation can not only accurately and compactly represent tfMRI signals, but also effectively identify a comprehensive collection of functional networks whose temporal ( ${\mathbf{d}}_i$) and spatial ( ${\mathbf{\alpha }}^i$) patterns can be quantitatively assessed (as detailed in Identification of Functional Networks in Sparse Representation section).

We calculate D and α as follows. For sparse representation of signal matrix $\mathbf{X}\in R^{t\times n}$, we aim to learn an effective over‐complete dictionary $\mathbf{D}\in R^{t\times k}$ which satisfies the constraint that k>t and k≪n [Mairal et al., 2010]. Specifically, the empirical cost function $f_n(\mathbf{D})$ of $\mathbf{X}\in R^{t\times n}$ considering the average loss of regression to all n signal vectors using D is

$$f_n(\mathbf{D})=\frac{1}{n}{\displaystyle \sum _{i=1}^n\ell \left({\mathbf{x}}_i,\mathbf{D}\right)}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\underset{{\mathbf{\alpha }}_i\in R^k}{\min }\frac{1}{2}{\Vert {\mathbf{x}}_i-\mathbf{D}{\mathbf{\alpha }}_i\Vert }_2^2+\lambda {\Vert {\mathbf{\alpha }}_i\Vert }_1}$$ (1)

where the loss function $\ell \left(\mathbf{x},\mathbf{D}\right)$ is defined as the optimal value of sparse representation: $\ell \left(\mathbf{x},\mathbf{D}\right)=\underset{\mathbf{\alpha }\in R^k}{\min }\frac{1}{2}{\Vert \mathbf{x}-D\alpha \Vert }_2^2+\lambda {\Vert \mathbf{\alpha }\Vert }_1$. Note that the value of $\ell \left(\mathbf{x},\mathbf{D}\right)$ should be small if signal $\mathbf{x}$ is reasonably well sparse represented by D. The $l_1$ regularization is used to yield a sparse resolution of $\mathbf{\alpha }$. λ is a regularization parameter between regression residual and sparsity level. Moreover, we have the constraint to prevent the elements in D from being arbitrarily large,

$$C=\left\{\mathbf{D}\in R^{t\times k}s.t.\forall i=1,\mathrm{..}k,{\mathbf{d}}_i^T{\mathbf{d}}_i\le 1\right\}$$ (2)

So the problem of minimizing Eq. (1) is rewritten as a matrix factorization problem:

$$\underset{\mathbf{D}\in C,\mathbf{\alpha }\in R^{k\times n}}{\min }\frac{1}{2}{\Vert \mathbf{X}-D\alpha \Vert }_F^2+\lambda {\Vert \mathbf{\alpha }\Vert }_{1,1}$$ (3)

We adopt the effective online dictionary learning algorithm and the associated publicly released online dictionary learning toolbox [Mairal et al., 2010] to solve Eq. (3) and to learn the dictionary D. We briefly demonstrate the online dictionary learning approaches to solve Eq. (3) as follows. The core idea is that the two variables D and α in Eq. (3) are alternated and minimized over one while keeping the other one fixed. Specifically, we define signal training set as samples of a distribution $p\left(\mathbf{x}\right)$. ${\mathbf{D}}_m$ is defined as the updated dictionary at the iteration time m. ${\mathbf{D}}_0$ is the initial dictionary and is randomly initialized from $\mathbf{x}$. At the number of iterations m, for one element ${\mathbf{x}}_m$ drawn from $p\left(\mathbf{x}\right)$ at a time in stochastic gradient descent, the least angle regression (LARS)‐Lasso algorithm [Mairal et al., 2010] is used to compute the decomposition ${\mathbf{\alpha }}_m$ of ${\mathbf{x}}_m$ based on the dictionary ${\mathbf{D}}_{m-1}$ obtained at the previous iteration m−1. At the same time, the dictionary ${\mathbf{D}}_{m-1}$ is updated as ${\mathbf{D}}_m$ by minimizing over Eq. (2) the function in Eq. (1), where ${\mathbf{\alpha }}_m$ is computed during previous step. The block‐coordinate descent with warm starts algorithm is used for dictionary update [Mairal et al., 2010]. It has been proven that the iterations of dictionary update can achieve convergence to learn an optimal D. More detailed equations and solutions of Eq. (3) are referred to [Mairal et al., 2010]. Once D is learned and fixed in Eq. (3), the sparse representation based on the learned D can be solved as an $l_1$‐regularized linear least‐squares problem to learn an optimized α [Mairal et al., 2010]. We select the value of regularization parameter λ and dictionary size k via experimental results based on the criterion of group‐wise consistency of the inferred functional components across individual subjects [Lv et al., 2015a,b]. More details are in the Supporting Information.

Identification of Functional Networks in Sparse Representation

Once we perform dictionary learning and sparse representation of tfMRI signals to obtain a collection of dictionary components for each subject in each task data, the next step is to identify and quantitatively characterize the meaningful functional networks (including both task‐evoked networks and intrinsic connectivity networks) from the dictionary components as many as possible for each subject in each task data based on current brain science knowledge, and to seek their correspondences across individual subjects. Specifically, we identify the task‐evoked networks from the dictionary components for each subject in each tfMRI data as follows. After extensive visual inspection, it is found that certain networks (dictionary components) have similar spatial and temporal patterns compared with the activation maps derived from traditional general linear model (GLM) [Friston et al., 1994] (Fig. 2 and Supporting Information Fig. 2). In this way, we adopt the traditional GLM to perform task activation detection on tfMRI data via FSL FEAT software. The resulting activation maps under specific task contrast designs as well as the input task contrast paradigm curves in traditional GLM can be viewed as the references to identify and characterize task‐evoked networks in sparse representation. Similar to the methods in [Lv et al., 2015a,b], for ith dictionary component, we not only measure the temporal similarity (defined as Pearson's correlation coefficient) between its temporal vector ${\mathbf{d}}_i$ (blue curve in Fig. 2a,b) and each task contrast paradigm curve (black curve in Fig. 2a,b), but also measure the spatial similarity between its spatial pattern ${\mathbf{\alpha }}^i$ and the corresponding activation map obtained by GLM (Fig. 2a). The spatial similarity is defined as the spatial pattern overlap rate R between the dictionary component's spatial pattern (S) and the GLM‐derived activation map (T) on cortical surface:

$$R(S,T)=\frac{\left|S\cap T\right|}{\left|T\right|}$$ (4)

Figure 2.

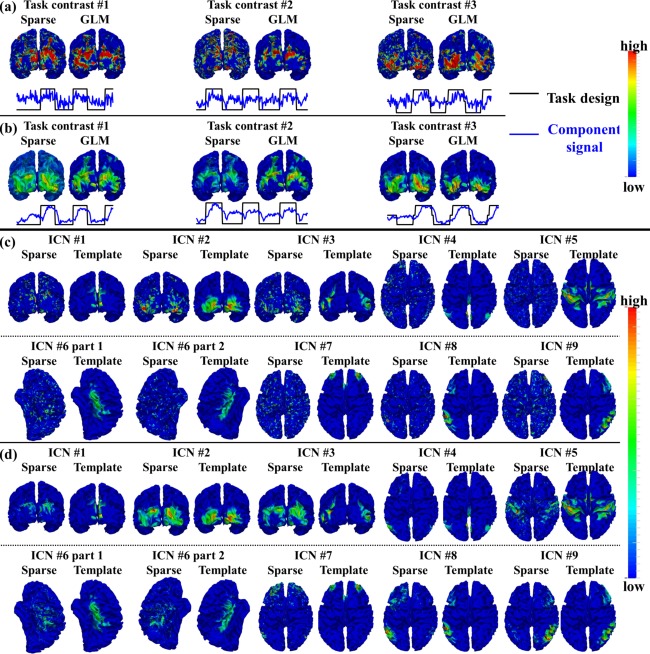
Identified task‐evoked networks and ICNs in sparse representation of emotion tfMRI data. (a) Spatial and temporal patterns of the three identified task‐evoked networks based on sparse representation compared with traditional GLM‐derived activation maps and task contrast paradigm curves in one example subject. (b) Group‐averaged spatial and temporal patterns of the three identified task‐evoked networks compared with group GLM‐derived activation maps and task contrast paradigm curves across all subjects. (c) Spatial patterns of nine identified ICNs in sparse representation compared with ICN templates in the example subject. (d) Group‐averaged spatial patterns of the nine identified ICNs compared with ICN templates across all subjects. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Note that we firstly convert S and T from continuous values to discrete labels (all values larger than 0 are labeled as 1, and others are labeled as 0) and then calculate the spatial overlap rate using Eq. (4). For each subject, we select the top 10 candidate dictionary components which have high spatial similarity with corresponding GLM‐derived activation map and have high temporal similarity with corresponding task contrast paradigm curve, respectively using the same methods in [Lv et al., 2015a,b]. Each component with high sum of value in spatial and temporal similarity is further examined by a group of seven experts separately to determine the final component with the best match of both spatial and temporal patterns with GLM based on the agreement reached by a voting procedure of all experts. Moreover, for a specific task data, we examine the group consistency of each identified meaningful task‐evoked network across all subjects by comparing the spatial and temporal patterns between group‐averaged identified meaningful task‐evoked networks and activation maps derived from group GLM (Fig. 2b), and only those consistent dictionary components across subjects are retained as identified task‐evoked networks in the specific task data. More details are in [Lv et al., 2015a,b]. Our rationale is that since temporal and spatial patterns provide crucial and complementary information of functional BOLD activities and neuroanatomic distributions of a functional network, respectively, each identified meaningful task‐evoked network in sparse representation should have both high temporal similarity with the task contrast paradigm curve and high spatial similarity with the activation map obtained from traditional GLM [Lv et al., 2015a,b].

Moreover, we identify the intrinsic connectivity networks (ICNs) [Raichle, 2010; Seeley et al., 2007; Smith et al., 2009; Lv et al., 2015a,b] from the dictionary components for each subject in each task data as follows. We measure the spatial similarity defined in Eq. (4) between dictionary components and previously identified ICN templates (Fig. 2c) to determine the correspondence [Lv et al., 2015b]. Specifically, ten previously well‐defined ICNs [Smith et al., 2009] are adopted as ICN templates in this study. We select the top 10 candidate dictionary components which have high spatial similarity with each ICN template, respectively. Each component is further examined by a group of seven experts separately to determine the final component with the best match of spatial pattern and ICN template based on the agreement reached by a voting procedure of all experts. Moreover, we examine the group consistency of each identified ICN across all subjects and all task data by comparing the spatial pattern between group‐averaged identified ICN and corresponding ICN template (Fig. 2d), and only those consistent dictionary components across subjects and across task data are retained as identified ICNs. More details are in [Lv et al., 2015a,b]. Our rationale is that each identified ICN in sparse representation should have high spatial similarity (overlap rate) with the corresponding previously identified ICN template across different subjects.

It should be noted that since there is no quantitative or effective interpretation of the comprehensive collection of all dictionary components identified by sparse representation of tfMRI signals, we adopt the independent traditional GLM‐derived contrast maps and ICN templates as the references to identify those similar meaningful functional networks from the dictionary components [Lv et al., 2015a,b], as well as to confirm that those meaningful functional networks indeed “exist” in human brain no matter what methods are adopted based on current brain science knowledge. It should also be noted that in the future, all of those hundreds of dictionary components (task‐evoked or intrinsic connectivity networks, or even noise and artifacts) should be identified with future understanding of human brain function and development of other effective methodology.

Identification of THFRs and Assessment of Spatial Patterns on Gyri/Sulci

After performing sparse representation of tfMRI signals and characterizing the meaningful functional networks, we identify task‐based heterogeneous functional regions (THFRs) and assess their spatial patterns on cortical gyri/sulci for each subject in each task data in this section. Specifically, since the dictionary components can be viewed as functional networks and the ith column ${\mathbf{\alpha }}_i$ (i = 1,…n) of α represents the functional network composition of grayordinate $g_i$ (i=1,…n), we assess the number of involved functional networks (dictionary components) of $g_i$ by counting the number of non‐zero elements in ${\mathbf{\alpha }}_i$ ( ${\Vert {\mathbf{\alpha }}_i\Vert }_0$). THFR is then defined as:

$$\text{THFR}=\forall g_{i}s.t.{\Vert {\mathbf{\alpha }}_i\Vert }_0>q$$ (5)

In brief, THFR is composed of a collection of grayordinate $g_i$ (i = 1,…n) of which the number of non‐zero elements (i.e., the number of involved functional networks) in ${\mathbf{\alpha }}_i$ is larger than a threshold q. Note that since we define q as the value of ${\Vert {\mathbf{\alpha }}_i\Vert }_0$ at the top p% across all grayordinates, the value of q is determined once value of p% is decided. The rationale of choosing value of p% is that p% should be small enough to identify the THFRs from all grayordinates, while p% should also not be too small to identify merely isolated brain grayordinates instead of continues THFR regions. We test different p% to examine the spatial pattern consistency of identified THFRs which will be detailed in Spatial Patterns of THFRs on Cortical Gyri and Sulci section. Note that we adopt a uniform p% for all tfMRI data and subjects since the values of ${\Vert {\mathbf{\alpha }}_i\Vert }_0$ across all voxels/grayordinates are typically normally distributed with similar mean and standard deviation across all subjects as illustrated in [Lv et al., 2015b] and Supporting Information Figure 1. It should also be noted that it is likely that the identified THFRs contain specific artifact or noise components which cannot be well quantitatively characterized or modeled under current brain science knowledge. However, the results in Results section will show that the identified THFRs are indeed meaningful and contain multiple identified functional networks.

After obtaining the spatial distribution of THFRs on grayordinate cortical surfaces, the further spatial pattern assessment of THFRs on gyri/sulci is straightforward. As each grayordinate already has the gyri/sulci information in each subject [Glasser et al., 2013], we could count the number of involved grayordinates in THFRs on gyral and sulcal regions respectively, then assess the ratio between the percentage of involved grayordinates in THFRs on gyri versus the percentage on sulci.

RESULTS

Identification of Meaningful Functional Networks in Sparse Representation

We adopted the temporal/spatial similarity measurement in Identification of Functional Networks in Sparse Representation section to identify meaningful task‐evoked networks and ICNs from tfMRI data of each subject. In total, we identified 3, 2, 2, 5, 2, 3, and 6 task‐evoked networks from the datasets of emotion, gambling, language, motor, relational, social, and working memory task, respectively. The detailed description of the task‐evoked networks is in Supporting Information materials. Figure 2a,b show an example consisting of the three identified task‐evoked networks in emotion tfMRI data, while the results from the other six tasks could be found in Supporting Information Figure 2. Specifically, Figure 2a shows the three task‐evoked networks in emotion tfMRI data of one example subject. We can see that all three networks have similar spatial patterns compared with corresponding GLM‐derived activation maps as well as similar temporal patterns compared with the corresponding task contrast paradigm curve. Quantitatively, the spatial overlap rate R is 0.30, 0.33, and 0.29, and the temporal similarity is 0.38, 0.30, and 0.37 for the three networks in the example subject, respectively. Figure 2b shows the group‐averaged spatial maps and temporal curves of identified task‐evoked networks across all subjects in emotion task. Table 1 provides the spatial overlap rates and temporal similarity values of all group‐averaged task‐evoked networks in seven tasks. Supporting Information Tables II and III provide the spatial overlap rate and temporal similarity value of all identified task‐evoked networks in seven tasks across all individual subjects. It is evident that all identified task‐evoked networks are consistent and have relatively high spatial overlap rate and temporal similarity across subjects.

Table 1.

Spatial overlap rate (S) and temporal similarity (T) of all identified group‐averaged task‐evoked networks (N) comparing with group GLM‐derived activation maps

	Emotion		Gambling		Language		Motor		Relational		Social		WM
	S	T	S	T	S	T	S	T	S	T	S	T	S	T
N#1	0.84	0.63	0.97	0.42	0.95	0.46	0.95	0.62	0.90	0.44	0.97	0.54	0.94	0.51
N#2	0.92	0.55	0.95	0.23	0.86	0.55	0.95	0.58	0.92	0.43	0.94	0.62	0.89	0.47
N#3	0.79	0.68					0.94	0.56			0.94	0.69	0.98	0.59
N#4							0.83	0.62					0.94	0.46
N#5							0.94	0.57					0.90	0.47
N#6													0.92	0.61

Moreover, we identified nine ICNs in all subjects and in all seven tasks. The detailed description of the nine ICNs is in Supporting Information materials. Figure 2c shows the spatial maps of the nine identified ICNs compared with ICN templates [Smith et al., 2009] in the emotion task of the example subject, while the results from the other six tasks are shown in Supporting Information Figure 2. Quantitatively, the spatial overlap rate is 0.34, 0.51, 0.37, 0.28, 0.27, 0.27, 0.23, 0.33, and 0.29 for the nine ICNs, respectively. Figure 2d shows the group‐averaged spatial maps of identified ICNs in emotion data across all subjects. Table 2 provides the spatial overlap rate of all group‐averaged ICNs. Supporting Information Table IV provides the spatial overlap rate of all nine identified ICNs in seven tasks across all subjects. We can see that all identified ICNs are consistent and have relatively high spatial overlap rate across tasks and subjects.

Table 2.

Spatial overlap rates of all identified group‐averaged ICNs

	Emotion	Gambling	Language	Motor	Relational	Social	WM
ICN#1	0.70	0.88	0.99	0.98	0.84	0.97	0.90
ICN#2	0.96	0.94	0.98	0.97	0.97	0.97	0.96
ICN#3	0.79	0.91	0.97	0.94	0.84	0.95	0.87
ICN#4	0.69	0.79	0.86	0.85	0.75	0.84	0.71
ICN#5	0.52	0.86	0.91	0.93	0.81	0.92	0.75
ICN#6	0.44	0.85	0.92	0.93	0.81	0.92	0.72
ICN#7	0.45	0.67	0.79	0.74	0.62	0.76	0.62
ICN#8	0.69	0.90	0.97	0.92	0.84	0.91	0.81
ICN#9	0.64	0.89	0.95	0.93	0.84	0.92	0.82

In summary, the identified task‐evoked networks have similar spatial patterns compared with the traditional GLM‐derived activation maps as well as similar temporal patterns compared with the task contrast paradigm curve, and the identified ICNs have similar spatial patterns with ICNs templates across all subjects and tasks based on HCP grayordinate tfMRI data, indicating that HCP grayordinate tfMRI data is sufficient to represent the whole‐brain tfMRI data (e.g., in volumetric space), to reflect whole‐brain functional activities, and to identify meaningful whole‐brain functional networks [Barch et al., 2013; Smith et al., 2013], which is also the premise to explore functional architecture of cortical gyri and sulci based on HCP grayordinate data in this article.

Identification of THFRs in Single Task and Multiple Tasks

We identified task‐based heterogeneous functional regions (THFRs) in each single task. Figure 3 shows the distribution density map of identified THFRs across subjects in each single task. In brief, since the grayordinates have correspondence across all subjects, for each task, we combine the distribution map of identified THFRs of all subjects together by counting the number of each grayordinate in the THFRs of all subjects, and calculating the mean number of each grayordinate in the THFRs to obtain the distribution density map of identified THFRs across subjects. We see that THFRs have higher distribution density at the bilateral parietal lobe, frontal lobe, and visual association cortices within each single task. Moreover, such high distribution density pattern is relatively consistent across seven tasks (as highlighted by the red arrows in Fig. 3). These findings are also consistent across all individual subjects. More individual examples are shown in Supporting Information Figures 3 and 4.

Figure 3.

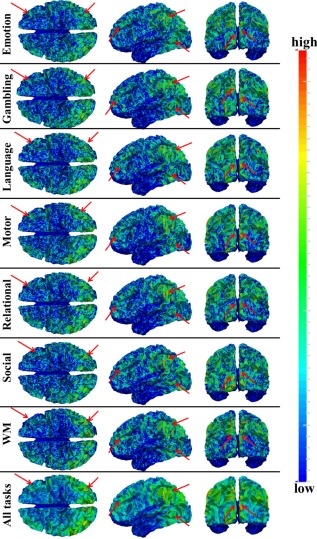
Distribution density map of identified THFRs across all subjects in each of the seven tfMRI data. Those THFRs with higher distribution density and relatively consistent across seven tasks are highlighted by red arrows. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Moreover, we identified THFRs across multiple tasks for each subject. Figure 4 shows the distribution density map of identified THFRs of all subjects across multiple tasks (at least three to seven tasks), respectively. In brief, since the grayordinates have correspondence across all subjects, for each situation (across three to seven tasks), we combine the distribution map of identified THFRs of all subjects together by counting the number of each grayordinate in the THFRs of all subjects, and calculating the mean number of each grayordinate in the THFRs to obtain the distribution density map of identified THFRs across all subjects. Interestingly, the THFRs also have higher distribution density at the bilateral parietal lobe, frontal lobe, and visual association cortices. Moreover, the higher distribution density pattern is relatively consistent across from at least three tasks to at least seven tasks (as highlighted by red arrows in Fig. 4) as those in single task (Fig. 3). These findings are also consistent across all subjects. More individual examples are shown in Supporting Information Figures 5 and 6.

Figure 4.

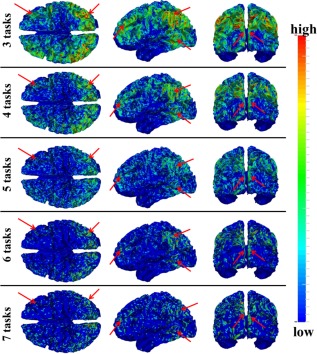
Distribution density map of identified THFRs of all subjects across multiple tasks (at least three of seven tasks in HCP data (emotion, gambling, language, motor, relational, social, and working memory)). Those THFRs with higher distribution density and relatively consistent across multiple tasks are highlighted by red arrows. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

We quantitatively characterized the identified THFRs via two measurements. First, Figure 5a,c shows the network histograms (by counting the number of involved dictionary components (functional networks)) after normalization to the sum of 1 in THFRs and task‐evoked networks of the example subject in emotion data, respectively. We can see that the histogram of THFRs (Fig. 5a) is complex and distributed across all components, while the histogram of task‐evoked networks highly concentrates on the specific components (highlighted by black in Fig. 5c), as expected. More results are in Supporting Information Figure 7. Quantitatively, the network histogram concentration (defined as summing the percentage of top three components in the histogram) is 1.22% and 8.11% for THFRs and task‐evoked networks in the example subject in emotion data, respectively. Table 3 provides the histogram concentration of THFRs and task‐evoked networks in all seven tasks across all subjects. We can see that the histogram concentration value of THFRs is statistically significantly smaller than that of task‐evoked networks (P < 0.05) across all seven tasks and subjects by using paired t‐test. Moreover, the network histogram entropy (defined as the entropy of all histogram elements [Lv et al., 2015b]) is 8.62 and 8.34 for THFRs and task‐evoked networks in the example subject in emotion data, respectively. Table 4 shows the histogram entropy of THFRs and task‐evoked networks in all seven tasks across all subjects. We can see that the histogram entropy of THFRs is statistically significantly larger than that of task‐evoked networks (P < 0.05) across all seven tasks and subjects by using paired t‐test. Second, we examined the temporal patterns of THFRs and compared with those of task‐evoked networks within the same subject. As shown in Figure 5b, the temporal patterns of all THFRs as well as two example components (R4 and R5) in THFRs of the example subject in emotion data are complex and have much less similarity with the task contrast paradigm curves, while the temporal patterns of the top three components in the histogram of task‐evoked networks have high similarity with the task contrast paradigm curves (Fig. 5d). Quantitatively, the mean temporal similarity for the temporal pattern of all THFRs and two example components (R4 and R5) is only 0.01, −0.06, and 0.01 compared with the three task contrast paradigm curves, respectively, while 0.38, 0.30, and 0.37 for the top three components in the histogram of task‐evoked networks in the same subject, respectively.

Figure 5.

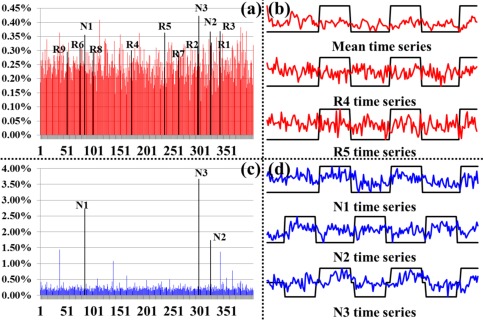
Network histogram and temporal pattern comparisons between THFRs and task‐evoked networks. (a) Network histogram (red) after normalization to the sum of 1 in THFRs of an example subject in emotion data. (b) Mean temporal pattern of identified THFRs (red) and temporal patterns of two example components identified as ICN #4 and ICN #5 in Figure 2 (R4 and R5). The task contrast paradigm curve is shown in black. (c) Network histogram (blue) after normalization to the sum of 1 in task‐evoked networks of an example subject in emotion data. Here the task‐evoked networks are the union of three identified task‐evoked networks. (d) Temporal patterns of three components identified as task‐evoked networks in Figure 2 (N1, N2, and N3). The task contrast paradigm curve is shown in black. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 3.

Network histogram concentration of THFRs and task‐evoked networks (%) in seven tasks across all subjects

	Emotion	Gambling	Language	Motor	Relational	Social	WM
THFRs	1.44 ± 0.17	1.35 ± 0.16	1.26 ± 0.11	1.31 ± 0.15	1.42 ± 0.20	1.38 ± 0.16	1.19 ± 0.09
Task‐evoked	7.20 ± 1.38	4.16 ± 0.55	3.06 ± 0.14	4.77 ± 0.89	4.75 ± 0.75	4.27 ± 0.53	3.50 ± 0.44
P	3.53E‐42	9.04E‐46	1.45E‐64	1.15E‐39	1.17E‐43	2.19E‐47	2.94E‐48

Table 4.

Network histogram entropy of THFRs and task‐evoked networks in seven tasks across all subjects

	Emotion	Gambling	Language	Motor	Relational	Social	WM
THFRs	8.61 ± 0.01	8.62 ± 0.01	8.62 ± 0.00	8.62 ± 0.01	8.61 ± 0.01	8.62 ± 0.01	8.63 ± 0.00
Task‐evoked	8.41 ± 0.07	8.56 ± 0.02	8.60 ± 0.01	8.52 ± 0.05	8.52 ± 0.03	8.56 ± 0.02	8.56 ± 0.03
p‐value	6.28E‐32	1.89E‐31	6.74E‐35	8.68E‐24	5.86E‐29	3.87E‐32	3.18E‐28

The value is represented as mean ± standard deviation. Bold values indicate P values smaller than 0.05.

We further justified the identified THFRs from two perspectives. First, Figures 3 and 4 and Supporting Information Figures 3 to 6 have illustrated that the spatial distributions of identified THFRs are reasonably consistent (bilateral parietal lobe, frontal lobe, and visual association cortices) across all subjects and tasks, and in agreement with current neuroscience knowledge [Anzai et al., 2007; Duncan, 2010; Fedorenko et al., 2013], where it has been reported that the frontal and parietal lobes have multiple‐demand patterns associated with diverse cognitive demands [Duncan, 2010; Fedorenko et al., 2013], and that visual association cortices is a heterogeneous collection of visual areas and is involved in higher level of processing, e.g., responding to visual stimuli which have complex pattern or structure [Anzai et al., 2007]. This group‐wise consistency and coincidence with current neuroscience knowledge is a reasonable verification of identified THFRs as reliable patterns which can be adopted for further investigation such as network dynamics, given the lack of ground‐truth in brain mapping.

Second, as shown in Figure 5a, the components that are identified as task‐evoked networks (N1, N2, and N3) and ICNs (R1 to R9) all have relative high percentage in the histogram of THFRs (highlighted by black in Fig. 5a) in the example subject, indicating that THFRs not only indeed involve functional networks (both task‐evoked networks and ICNs), but also involve specific regions that are participated in the task contrast paradigm (N1, N2, and N3). However, those regions with complex temporal pattern due to the complex network composition (Fig. 5a) of THFRs may have been underestimated by traditional approaches which merely consider individual tfMRI signals based on model‐driven subtraction procedures [Lv et al., 2015a,b]. Those regions that were identified by our approach but were not by traditional approaches can be further investigated in the future, which is another research topic besides this article.

Spatial Patterns of THFRs on Cortical Gyri and Sulci

We have shown the spatial distribution of THFRs on the cortical surface in each single task (Fig. 3) and across multiple tasks (Fig. 4). In this section, we further investigate how the THFRs are distributed over gyri/sulci. First, we assessed the spatial patterns of identified THFRs in each single task as illustrated in Figure 3 on cortical gyri and sulci. Figure 6a shows the segmented gyri and sulci of one example subject which is provided in HCP grayordinate data [Glasser et al., 2013]. Figure 6b,c show the spatial distributions of THFRs on gyri and sulci of the example subject in emotion task data, respectively. More examples are shown in Supporting Information Figure 8. Figure 6d shows the percentage of involved grayordinates in THFRs on gyri and sulci across all seven tasks in the example subject. More subjects are shown in Figure 7. Figure 6e shows the mean percentage of involved grayordinates in THFRs on gyri and sulci in all seven tasks. We can see that the mean percentage of involved grayordinates in THFRs on gyri is consistently larger than that on sulci in all seven tasks and all subjects. Moreover, we calculated the ratio of percentage of involved grayordinates in THFRs on gyri versus that on sulci across all subjects and tasks. Table 5 provides the mean ratio of percentage of involved grayordinates in THFRs on gyri versus that on sulci in seven tasks. We can see that the percentage of involved grayordinates in THFRs on gyri is statistically significantly larger than that on sulci (P < 0.05) across all subjects in all seven tasks by using paired t‐test. The mean ratio of percentage of involved grayordinates in THFRs on gyri versus that on sulci is 2.22, 3.14, 2.63, 2.95, 3.38, 2.50, and 2.76 in seven tasks, respectively. Supporting Information Table V provides the ratio of percentage of involved grayordinates in THFRs on gyri versus that on sulci in individual subjects. Supporting Information Tables VI and VII provide mean ratio and statistical significance of percentage of involved grayordinates in THFRs on gyri versus that on sulci across all subjects in seven tasks using different threshold p% when identifying THFRs (Eq. (5)). We can see that the percentage of involved grayordinates in THFRs on gyri is consistently significantly larger than that on sulci under different threshold p%, indicating the stability of our findings when choosing p% in a reasonable range.

Figure 6.

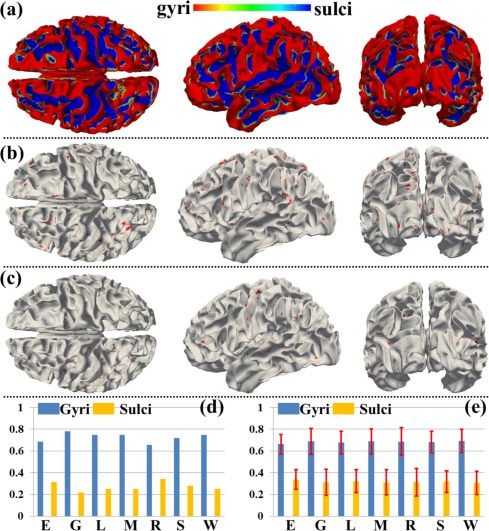
Spatial patterns of THFRs in single task on gyri/sulci and the percentages of involved grayordinates in THFRs in single task on gyri/sulci. (a) Segmented gyri and sulci of one example subject. (b) and (c) Spatial patterns of THFRs (red) on gyri (b) and sulci (c) in emotion task data of the example subject, respectively. (d) Percentages of involved grayordinates in THFRs on gyri/sulci in the example subject in all seven tasks. (e) Mean percentages of involved grayordinates in THFRs on gyri/sulci across all subjects in all seven tasks (E: emotion; G: gambling; L: language; M: motor; R: relational; S: social; W: working memory). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 7.

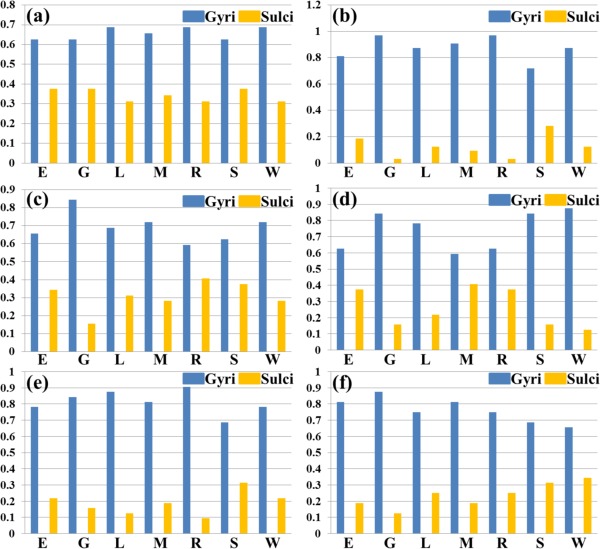
Percentages of involved grayordinates in THFRs in single task on gyri/sulci of another six subjects indexed by (a) to (f), respectively. (E: emotion; G: gambling; L: language; M: motor; R: relational; S: social; W: working memory). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 5.

Mean ratio of percentage of involved grayordinates in THFRs on gyri versus that on sulci across all subjects in seven tasks

	Emotion	Gambling	Language	Motor	Rational	Social	WM
Ratio	2.22 ± 1.09	3.14 ± 3.87	2.63 ± 2.07	2.95 ± 2.47	3.38 ± 4.29	2.50 ± 1.32	2.76 ± 1.59
P	9.48E‐22	9.60E‐19	2.98E‐20	1.56E‐19	1.49E‐17	8.25E‐22	8.29E‐22

Moreover, we assessed the spatial patterns of identified THFRs across multiple tasks (Fig. 4) on cortical gyri and sulci. Figure 8a shows the segmented gyri and sulci of the example subject which is provided in HCP grayordinate data [Glasser et al., 2013]. Figure 8b,c show the spatial patterns of THFRs on gyri/sulci of one example subject across at least four tasks. More examples are shown in Supporting Information Figure 9. Figure 8d shows the percentage of involved grayordinates in THFRs on gyri and sulci across at least three to seven tasks in the example subject. More examples are shown in Figure 9. Figure 8e shows the mean percentage of involved grayordinates in THFRs across multiple tasks on gyri and sulci across all subjects. It can be seen that the percentage of involved grayordinates in THFRs across multiple tasks on gyri is consistently larger than that on sulci. We further calculated the ratio of percentage of involved grayordinates in THFRs on gyri versus that on sulci for all subjects. Table 6 provides the mean ratio of percentage of involved grayordinates in THFRs on gyri versus that on sulci across all subjects. We can see that the percentage of involved grayordinates in THFRs across multiple tasks on gyri is statistically significantly larger than that on sulci (P < 0.05) across all subjects by using paired t‐test. Moreover, the more tasks are involved, the larger the mean ratio of percentage of involved grayordinates in THFRs on gyri versus that on sulci is (except for six tasks and seven tasks). Supporting Information Table VIII shows the ratio of percentage of involved grayordinates in THFRs across multiple tasks on gyri versus that on sulci in individual subjects.

Figure 8.

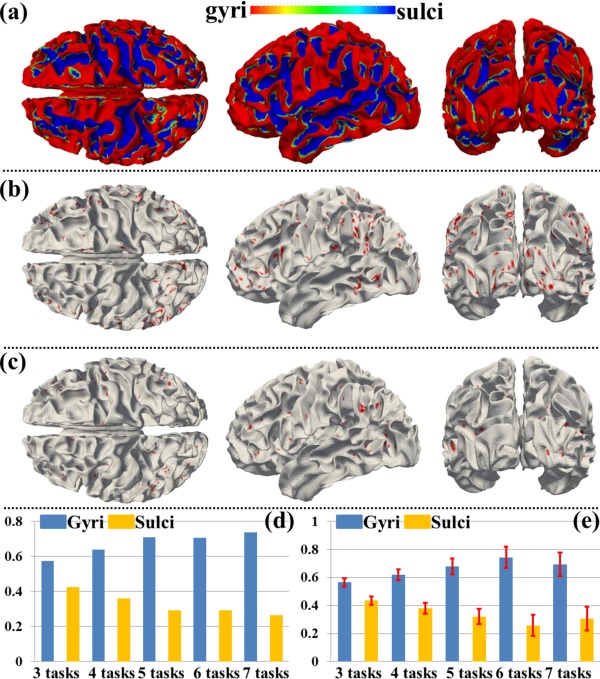
Spatial patterns of THFRs on gyri/sulci in multiple tasks and the percentages of involved grayordinates in THFRs in multiple tasks on gyri/sulci. (a) Segmented gyri and sulci of one example subject. (b) and (c): Spatial patterns of THFRs (red) on gyri (b) and sulci (c) across at least four tasks of the example subject, respectively. (d) Percentages of involved grayordinates in THFRs on gyri/sulci in the example subject across at least three tasks. (e) Mean percentages of involved grayordinates in THFRs on gyri/sulci across at least three tasks across all subjects. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 9.

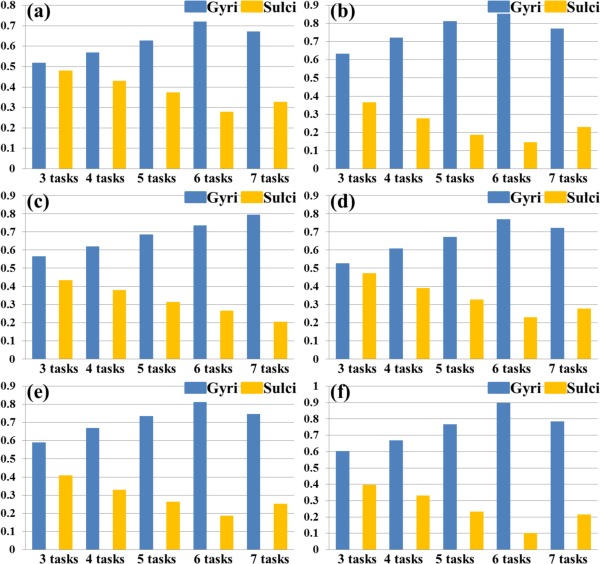
Percentages of involved grayordinates in THFRs across multiple tasks on gyri/sulci of another six subjects indexed by (a)–(f), respectively. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 6.

Mean ratio of percentage of involved grayordinates in THFRs across multiple tasks on gyri versus that on sulci across all subjects

	Three tasks	Four tasks	Five tasks	Six tasks	Seven tasks
Ratio	1.31 ± 0.16	1.66 ± 0.29	2.22 ± 0.64	3.33 ± 1.67	2.53 ± 1.05
P	2.68E‐26	2.93E‐34	3.30E‐35	2.00E‐35	2.04E‐27

The ratio is represented as mean ± standard deviation. Bold values indicate P values smaller than 0.05.

THFRs Distribution Difference Between Cortical Gyri and Sulci is not due to Signal‐to‐Noise Difference in High‐Resolution FMRI

When acquiring fMRI data at high resolution (2 mm isotropic voxels in this article or below), there can be a time series signal to noise ratio (tSNR) difference between different portions of cortex [Kruger and Glover, 2001; Weiner and Grill‐Spector, 2010]. To examine whether the identified THFRs distribution difference between cortical gyri and sulci is merely due to the possible tSNR difference between cortical gyral and sulcal regions in high‐resolution fMRI data, we measured the tSNR of each involved grayordinate in the identified THFRs. Specifically, for each grayordinate involved in the THFRs as the center, we obtained its three‐ring [about 5 mm radius, Weiner and Grill‐Spector, 2010] neighborhood grayordinates on the cortical mesh surface. We then extracted the fMRI time series of all grayordinates within the three‐ring and calculated the tSNR of the centered grayordinate as follows [Weiner and Grill‐Spector, 2010]:

$$\text{tSNR}=\frac{\text{mean}(\text{timeseries})}{\text{std}(\text{timeseries})}$$ (6)

Figure 10b shows the tSNR map of the THFRs on gyri and sulci in emotion task data of the same example subject in Figure 6b,c, respectively. We further calculated the mean tSNR of involved grayordinates in THFRs on gyri/sulci across all subjects in all seven tasks. As shown in Figure 10c, we see that the tSNR of THFRs on sulci has larger mean value while also larger standard deviation compared with that on gyri. We further examined if there is statistical tSNR difference of THFRs between gyri and sulci via unpaired two‐sample t‐test (P < 0.01). The results showed that the mean values of tSNR of gyri and sulci are statistically equal across all subjects in all seven tasks. In conclusion, the identified THFRs distribution difference between cortical gyri and sulci is not a result of the possible tSNR difference in high‐resolution fMRI data, and might truly reveal novel functional architecture of cortical gyri and sulci.

Figure 10.

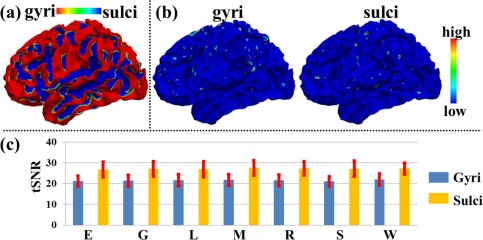
tSNR measurement: THFRs distribution difference between gyri and sulci is not due to SNR difference. (a) Segmented gyri and sulci of the same example subject in Figure 6a. (b) tSNR map of the THFRs on gyri and sulci in emotion task data of the same example subject in Figure 6b,c, respectively. (c) Mean tSNR of involved grayordinates in THFRs on gyri/sulci across all subjects in all seven tasks (E: emotion; G: gambling; L: language; M: motor; R: relational; S: social; W: working memory). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

DISCUSSION AND CONCLUSION

We proposed a data‐driven sparse representation framework on HCP grayordinate‐based whole‐brain tfMRI signals to systematically identify and characterize the task‐based heterogeneous functional regions in specific task performances and to assess their spatial pattern distribution difference on cortical gyri and sulci. Our results have shown that both consistent meaningful task‐evoked networks and ICNs were effectively and robustly reconstructed simultaneously across all subjects and seven tasks in HCP grayordinate tfMRI datasets via our proposed computational framework. Our results have also shown that the identified THFRs (involving the identified task‐evoked networks and ICNs) relatively consistently locate at the bilateral parietal lobe, frontal lobe, and visual association cortices across all subjects in both single task and across multiple tasks.

Our results finally have shown that the identified THFRs locate statistically significantly more on cortical gyral regions than on cortical sulcal regions across all subjects and tasks. Particularly, this THFRs distribution difference between gyri and sulci is not due to signal‐to‐noise difference in HCP high‐resolution fMRI. This finding suggests that cortical gyri might participate more in multiple and heterogeneous functional processes than sulci in specific task performances, and might be consistent with our previous study based on resting state fMRI data demonstrating that gyri are global functional connection centers and sulci are local functional units [Deng et al., 2014]. As demonstrated in Introduction, there have been several findings reporting the structural/functional differences between gyri and sulci [Chen et al., 2013; Deng et al., 2014; Nie et al., 2012; Takahashi et al., 2012; Zeng et al., 2015; Zhang et al., 2014]. For the first time (as far as we know), we demonstrated the functional difference during a specific task performance (i.e., THFRs distribution difference) between gyri and sulci in this article. These results revealed novel functional architecture of cortical gyri and sulci, and might help better understand functional mechanisms of the human cerebral cortex in the future.

It has been demonstrated that ICA for brain fMRI does truly recover maximal independence components, while practically it also possibly recovers overlapped components for brain fMRI like sparse representation method [Daubechies et al., 2009]. It has been demonstrated that sparse representation of whole brain fMRI signals is superior to ICA or GLM methods in reconstructing concurrent brain networks [Lv et al., 2015a,b]. Though sparse representation of fMRI signals has been relatively less studied in the field, it is worthwhile in this work to employ sparse representation of whole‐brain grayordinate‐based fMRI signals to systematically examine and characterize task‐based heterogeneous functional regions (THFRs) on cortical surface. Our experimental results have demonstrated meaningful results and several advantages, suggesting the value of this work.

More specifically, in this article, we adopt independent traditional GLM‐derived contrast maps and ICN templates as the references to identify and characterize similar task‐evoked and ICN networks in sparse representation. Similar ideas have also been used in ICA literature. It is helpful at current stage since these GLM‐derived maps and ICN templates reflect our current neuroscience knowledge and common practice. The identified meaningful functional networks in sparse representation similar as GLM‐derived contrast maps and ICN templates confirm that those meaningful functional networks indeed “exist” in the human brain no matter what different methods are adopted based on current brain science knowledge. For the identified THFRs shown in Figures 6 and 8b,c, we have verified that these THFRs are reasonably consistent across all subjects and tasks, and in agreement with current neuroscience knowledge (see details in Identification of THFRs in Single Task and Multiple Tasks section). This group‐wise consistency and coincidence with current neuroscience knowledge is a reasonable verification of the identified THFRs in Figures 6 and 8b,c as reliable and meaningful sparse patterns.

Moreover, our recent work [Lv et al., 2015b] has successfully identified 32 group‐wise consistent functional network components across individual subjects in sparse representation. They are independent of any other methods such as GLM and ICN templates. These group‐wise consistent network components can be adopted as functional network templates to define existing functional networks. These results indicate that sparse representation is not only a good method for characterizing the low‐dimensional structure of tfMRI data, but also a good method for identifying the network structure of tfMRI data. Our ongoing effort is to learn more functional networks templates in sparse representation from large populations using big‐data approaches to define a large space of existing functional networks in the future.

In general, this study can be enhanced in the future in following aspects. First, all of those dictionary components derived from sparse representation should be quantitatively characterized and modeled with future understanding of human brain function and development of other effective methodology to warrant assessment of the functional network distribution and/or removal of artifacts/noise in THFRs. Second, we can extend the THFRs spatial pattern assessment on cortical gyri/sulci to subcortical gyral/sulcal regions if effective methods are developed to perform cerebellum segmentation and cerebellar surface reconstruction with the high‐resolution HCP datasets in the future [Glasser et al., 2013]. Third, in this article, we identified and reported the spatial distributions of those relatively consistent THFRs across subjects and tasks in coarse‐scale, i.e., roughly locate on bilateral parietal lobe, frontal lobe, and visual association cortices. In the future, we can perform a finer scale assessment of THFRs spatial distributions and patterns on gyri/sulci by adopting our recently developed Anatomy‐guided Dense Individualized and Common Connectivity‐based Cortical Landmark (A‐DICCCOL) system [Jiang et al., 2015] which discovered 555 consistent cortical landmarks which have gyral/sulcal and structural (fiber connection pattern) correspondences across different subjects. In this way, the spatial distributions of the relatively consistent THFRs across subjects and tasks can be identified and reported at the cortical gyral/sulcal landmark scale. We can also correlate the spatial distribution of identified THFRs with other attributes (e.g., fiber density, cortical thickness, etc.) to explore the regularity and variability between the human brain structure and function.

Supporting information

Supporting Information