Abstract
Force field accuracy is still one of the “stalemates” in biomolecular modeling. Model systems with high quality experimental data are valuable instruments for the validation and improvement of effective potentials. With respect to protein–ligand binding, organic host–guest complexes have long served as models for both experimental and computational studies because of the abundance of binding affinity data available for such systems. Binding affinity data collected for cyclodextrin (CD) inclusion complexes, a popular model for molecular recognition, is potentially a more reliable resource for tuning energy parameters than hydration free energy measurements. Convergence of binding free energy calculations on CD host–guest systems can also be obtained rapidly, thus offering the opportunity to assess the robustness of these parameters. In this work, we demonstrate how implicit solvent parameters can be developed using binding affinity experimental data and the binding energy distribution analysis method (BEDAM) and validated using the Grid Inhomogeneous Solvation Theory analysis. These new solvation parameters were used to study protein–ligand binding in two drug targets against the HIV-1 virus and improved the agreement between the calculated and the experimental binding affinities. This work illustrates how benchmark sets of high quality experimental binding affinity data and physics-based binding free energy models can be used to evaluate and optimize force fields for protein–ligand systems.
Keywords: OPLS, force field, free energy, BEDAM, GIST
INTRODUCTION
Accurate force fields are essential for quantitative modeling of interatomic interactions that regulate biological processes such as protein folding, protein–ligand binding, and allostery. Physics-based molecular mechanics force fields make use of both quantum mechanical calculations on small fragments and experimental solution thermodynamic data for the parameterization of non-bonded terms, which is quite problematic for certain chemical groups. Measuring heats of vaporization and solvation free energies can be challenging especially for ionic molecules. Furthermore, accurate hydration free energy calculations using either quantum or classical mechanics are also very difficult for ionic molecules because of the large magnitude of their solvation free energy (Hirata et al., 1988; Hünenberger and McCammon, 1999; Shirts et al., 2003). In addition, experimental measurements for unusual ligands and functional groups are often unavailable. Therefore, alternative strategies are needed to improve the calibration of force field parameters.
Experimental binding affinity data from host–guest systems are an attractive, untapped resource for force field development. A large quantity of high quality experimental binding affinity data is available for host–guest systems, covering many different chemical functional groups. These data are obtained from isothermal calorimetric experiments, which directly account for the binding affinity, whereas IC50 measurements can also be influenced by inhibition mechanisms unrelated to ligand–receptor interactions (Cheng and Prusoff, 1973; Heeres et al., 2005; Janssen et al., 2005). Indeed, calorimetric data have already been used to evaluate the current state of the art in free energy methods in a recent Statistical Assessment of the Modeling of Proteins and Ligands (SAMPL) competition (Muddana et al., 2012; Muddana et al., 2014). In addition, a thorough assessment of force field models is contingent on achieving sufficient exploration of conformational space. In this context, host–guest systems (Chang and Gilson, 2004; Chen et al., 2004; Rekharsky et al., 2007; Moghaddam et al., 2009; Moghaddam et al., 2011; Muddana and Gilson, 2012b), being much simpler and smaller than protein–ligand complexes, can serve a useful purpose. We and others (Chang and Gilson, 2004; Chen et al., 2004; Rekharsky et al., 2007; Moghaddam et al., 2009; Moghaddam et al., 2011; Gallicchio and Levy, 2012; Hamaguchi et al., 2012; König and Brooks, 2012; Lawrenz et al., 2012; Mikulskis et al., 2012; Muddana and Gilson, 2012a; Muddana and Gilson, 2012b; Muddana et al., 2012; Wickstrom et al., 2013; Monroe and Shirts, 2014; Muddana et al., 2014) have shown that robust convergence of binding free energy estimates for these systems can be achieved with relatively modest computational cost. Computational ease allows for a thorough statistical analysis because a large number of binding affinity predictions can be used to identify, evaluate, and diagnose the potential issues with force field parameters. In addition, structure–activity relationships of host–guest complexes should be simpler to understand than protein–ligand systems, making them particularly useful for examining the accuracy of the force field for specific interactions. Lastly, but most importantly, host–guest binding free energy calculations involve the complexity of the protein–ligand binding problem, typically lacking in standard parameterization schemes using only the free energy of transfer of a solute, by including both solute–solute and solute–solvent interactions. Therefore, we propose that binding affinity measurements and calculations on host–guest complexes can be used to overcome some of the present difficulties encountered during force field parameterization, resulting in improved force fields for modeling protein–ligand binding.
The host β-cyclodextrin (β-CD) is a popular model system for studying molecular recognition (Chen et al., 2004; Rekharsky and Inoue, 1998; Rekharsky and Inoue, 2000; Rekharsky and Inoue, 2002; Szejtli, 1998; Del Valle, 2004) because of its relatively simple molecular structure and the availability of experimental binding affinities. β-CD is a torus-shaped, cyclic glucose oligosaccharide consisting of a hydrophobic core and hydrophilic rims composed of primary and secondary alcohols, respectively (Figure 1). These structural features make β-CD an attractive target for force field parameterization because they can coordinate with a variety of guests with different functional groups through nonpolar and/or polar interactions. There are also extensive experimental binding thermodynamic data for β-CD host–guest systems. Many of these experiments have been archived in a comprehensive compilation by Rekharsky and Inoue (1998).
Figure 1.
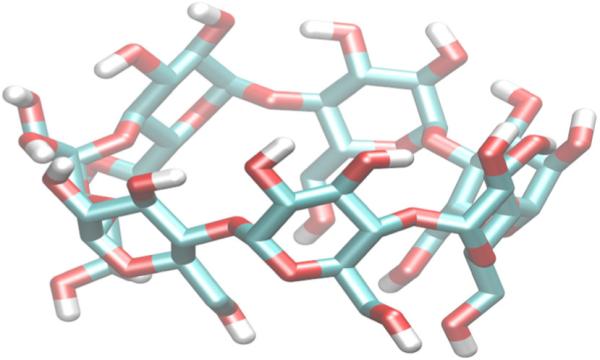
3D conformation of β-cyclodextrin. Carbon atoms are shown in cyan, oxygen atoms are shown in red, and hydrogen atoms are shown in white. Hydrogens are only shown for hydroxyl groups.
In this study, we calculate absolute binding free energies using the binding energy distribution analysis method (BEDAM; Gallicchio et al., 2010). BEDAM is based on a single direct alchemical coupling leg in implicit solvent and as a result overcomes several of the problems typically encountered by double decoupling schemes in explicit solvent. The difference between standard double decoupling in explicit solvent and BEDAM is that a standard double decoupling scheme (Gilson et al., 1997) involves two alchemical transformations: the first alchemical leg involves turning off the interactions of the ligand in the solvent, typically performed during solvation free energy calculations, and the second alchemical leg involves turning off the interactions of the ligand inside the binding site of a receptor; BEDAM only requires the second alchemical leg, which is performed using the AGBNP2 solvent model instead of explicit water molecules. The single pathway approach in BEDAM circumvents the difficulty of conventional formulations that obtain the binding free energy as the difference between large values, whose statistical errors combine additively. This feature makes our approach applicable to large and charged ligands not accessible by conventional free energy models. Implicit solvent also has several benefits over explicit solvent. The use of implicit solvent avoids the artifacts introduced by the treatment of long range forces, which are potentially an issue for charged species in explicit solvent (Reif and Oostenbrink, 2014; Rocklin et al., 2013). Convergence of the binding free energy can also be enhanced in implicit solvent, because of the lack of solvent friction and solvent fluctuations, such as when attempting to equilibrate specific waters in partially occupied sites inside the receptor binding pocket. As a result of its computational efficiency, BEDAM has been used to model very large datasets of protein–ligand complexes (Gallicchio et al., 2010; Gallicchio, 2012; Lapelosa et al., 2012; Gallicchio et al., 2014) as well as host–guest systems (Gallicchio and Levy, 2012; Wickstrom et al., 2013).
Unfortunately, there is a stigma associated with modeling solvent using standard continuum theories because of the tradeoff between speed and accuracy. One previous issue was a tendency to underestimate the desolvation penalty for specific chemical groups, leading to overestimation of the stability of salt bridges and hydrogen bonds in peptides and proteins (Okur et al., 2008; Roe et al., 2007). Secondly, structural features of water, missing from continuum models, are essential for specific interactions (Ren et al., 2012), such as bridging waters in certain protein–ligand systems. Lastly, some of the effects that drive binding, such as the expulsion of thermodynamically unfavorable water molecules, are typically missing from these models, although these effects are thought to be important for binding in many host–guest and protein–ligand systems (Deng et al., 2011; Nguyen et al., 2012; Rogers et al., 2013). Most of these problems have been addressed in the past 15 years either by adjusting or modifying the functional form of parameters within the electrostatic term of the generalized Born model (Hassan et al., 2000; Onufriev et al., 2004; Rizzo et al., 2005; Zhu et al., 2007; Zhou et al., 2008; Hassan and Steinbach, 2011; Knight and Brooks, 2011; Nguyen et al., 2013) or by adding new terms to the functional form of the solvation expression that attempt to account for the nonlinear effects of the first solvation shell (Gallicchio et al., 2009; Corbeil et al., 2010; Fennell et al., 2011).
The focus of this work is to use binding affinity calculations on a series of host-guest systems to evaluate the performance of the force field and solvent model and, where necessary, adjust the parameters in the AGBNP2 implicit solvent model (Gallicchio and Levy, 2004; Gallicchio et al., 2009). AGBNP2 features a functional form that includes a generalized Born type expression for the solvation electrostatic effects and also includes solvation energy terms that account for first shell hydration effects explicitly. Both the GB electrostatic term and the hydration shell correction term make use of algorithms from computational geometry to calculate atomic overlaps (Grant and Pickup, 1995), as briefly described below. Modifications to the parameters for this hydration free energy term will be presented in this paper. In the first part of this study, we present work on the development of parameters that account for displacing thermodynamically unfavorable waters upon ligand binding in the β-CD host–guest system. In order to validate these adjustments, we investigated the effects of displacing water in the cavity of an apo structure of β-CD using explicit solvent simulations and a grid-based implementation of Grid Inhomogeneous Solvation Theory (GIST; Lazaridis, 1998; Nguyen et al., 2012). In the first implementation of GIST, Nguyen et al. investigated the hydration of cucurbituril-7 (CB-7), noting the extreme unfavorability of water inside the cavity (Biedermann et al., 2012; Nguyen et al., 2012). For β-CD, we connect the GIST thermodynamic analysis to AGBNP2 parameters that account for water expulsion effects in the cavity (Wickstrom et al., 2013).
The second part of this study addresses the parameterization of the carboxylate functional group. We previously presented a large scale binding affinity study on β-CD host–guest systems in which we evaluated global and local binding thermodynamic trends successfully using BEDAM absolute binding free energy calculations (Wickstrom et al., 2013). This large set included guests containing alkyl, aromatic, amine, amide, and ester functional groups. Here, we expand this set to include a group of carboxylate-containing guests. Initial tests indicated particularly large errors for compounds with the carboxylate functional group. Subsequent adjustments to the solvation parameters of the carboxylates improve the agreement between the calculated and experimental binding affinities for β-CD host–guest systems. In addition, GIST analysis confirms the favorable solvation patterns, which are accounted for in the AGBNP2 model. To our knowledge, this is the first report of using large scale binding free energy calculations of host–guest systems to optimize force field parameters. Lastly, we show that implementation of these optimized parameters results in better agreement between the calculated and experimental binding affinities of several allosteric inhibitors to HIV-1 protease (HIV-PR) and improves the enrichment results from virtual screening of candidate ligands against the LEDGF binding pocket of HIV integrase.
METHODS AND MATERIALS
Computational details for β-CD simulations
BEDAM calculations were performed on 33 β-CD host–guest systems (Rekharsky and Inoue, 1998; Rekharsky and Inoue, 2000; Rekharsky and Inoue, 2002), where the guests all had ionic carboxylate functional groups (see Table S1 in the Supporting Information). Details of the guest selection and preparation are described in the previous study on β-CD host–guest systems (Wickstrom et al., 2013). Binding free energies were obtained using the OPLS-AA force field (Jorgensen et al., 1996; Kaminski et al., 2001) and the AGBNP2 (Gallicchio and Levy, 2004; Gallicchio et al., 2009) implicit solvent model. AGBNP2 includes an analytical pairwise descreening implementation of the generalized Born model for the electrostatic term (Gel), a non-polar hydration free energy estimator for the non-electrostatic term (Gnp), and a hydration correction term (Ghyd).
| (1) |
Ghyd accounts for the first shell hydration effects not accounted for by linear dielectric screening, such as hydrogen bonding with solvent and water ordering in the receptor binding site. The hydration correction term is estimated using an analytical intermolecular hydrogen bond potential described by the following expression:
| (2) |
where S(pw) is a switching function, based on the fraction pw of solvent-occupied volume in the hydration site “w” of the first solvation shell of hydrogen bonding donor and acceptor groups of the solute, and hw is an empirical parameter that accounts for the water–solute interactions not accounted for by the force field and solvation model. This correction parameter depends on the atom type of the solute (hydrogen bonding donor or acceptor, or non-polar hydrogen). The sign of this component determines whether the interactions formed with the solvent are potentially favorable or unfavorable, while its magnitude determines the strength of the excess interaction with water. In this work, we describe the parameterization of the hw correction factor for non-polar hydration sites, which model the effects of expelling unfavorable waters from the host, and polar hydration sites on the oxygen atoms of carboxylate functional groups of the guests, which account for favorable solute–water interactions (Figure S1 in the Supporting Information). Additional details about the parameterization are included in the Supporting Information.
We implemented BEDAM using Hamiltonian replica exchange molecular dynamics (H-REMD) and reservoir-REMD (Lyman et al., 2006; Okur et al., 2007; Roitberg et al., 2007) for our binding free energy simulations within the IMPACT program (Banks et al., 2005). Simulation settings with the unmodified parameters were similar to the previous study, except that the number of replicas was increased in order to optimize convergence for charged ligands. Thus, the H-REMD simulations were conducted using 24, rather than 16, replicas at values of the coupling parameter λ set to 0.0, 0.001, 0.002, 0.004, 0.005, 0.006, 0.008, 0.01, 0.02, 0.04, 0.07, 0.1, 0.25, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, and 1.0 for the BEDAM simulations using the new hydration parameters for the carboxylate guests. These simulations were performed for 5 ns per replica (Figure S2 in the Supporting Information).
Computational details for the HIV protease and HIV integrase simulations
HIV protease
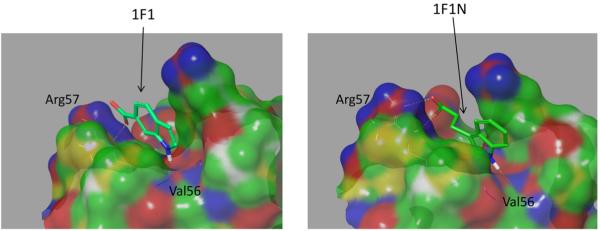
The BEDAM simulations were performed on two ligands of HIV Protease: 1F1 and 1F1-N, which bind at the flap site of the enzyme (Figure 2). The initial structures of the complexes with 1F1 and 1F1-N were obtained from the PDB (PDB IDs 3KFR (Perryman et al., 2010) and 4EJL (Tiefenbrunn et al., 2013)). The crystal structure was prepared at pH 5.6. Both PDB structures were first solvated in a TIP3P (Jorgensen et al., 1983) octahedral water box and equilibrated for 5 ns at 300 K. The waters were removed from the systems, and each system was minimized using the AGBNP2 implicit solvent model. The systems were gradually thermalized at 300 K in 75 ps and equilibrated at 300 K for an additional 75 ps before the production run.
Figure 2.
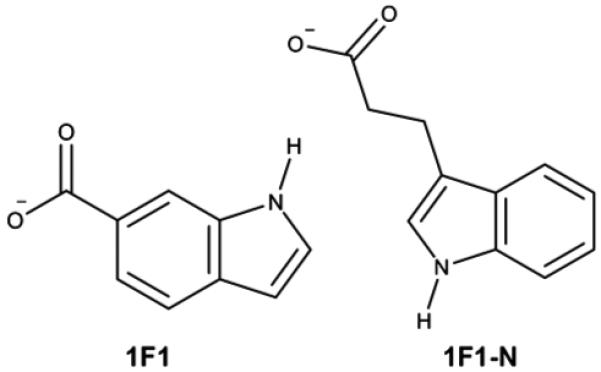
2D chemical structures of the HIV-PR allosteric inhibitors.
The BEDAM simulations of the two HIV-PR complexes were performed for 3 ns per replica (approximately 96 ns of total simulation time; Figure S3 in the Supporting Information). H-REMD simulations were conducted using 16 lambdas: 0.0, 0.001, 0.002, 0.004, 0.006, 0.008, 0.01, 0.02, 0.04, 0.07, 0.1, 0.25,0.4, 0.55, 0.75, and 1.0. The binding site is defined as a sphere with a radius of 2 Å from the center of mass of residues 44, 46, 55, and 57 of chain B of the HIV-PR dimer (Figure 3). Whenever the ligand center (here, the nitrogen atom in ligands 1F1 and 1F1N) falls within the binding site volume, the ligand is considered as in the bound state. The Cα atoms of the receptor were restrained with a force constant of 2.0 kcal/mol/Å2. Structures were saved every picosecond. The last 2 ns of data were used for analysis. Details about the parameterization and analysis are included in the Supporting Information.
Figure 3.
Predicted binding modes of 1F1 (PDB code 3KFR; Perryman et al., 2010) and 1F1N (PDB code 4EJL; Tiefenbrunn et al., 2013) in complex with HIV protease. The yellow dashed lines indicate protein-ligand intermolecular hydrogen bonds.
HIV integrase
The BEDAM simulations were performed on 10 candidate ligands targeting the LEDGF binding site of HIV integrase (Tables S5 and S6 in the Supporting Information) in the recent SAMPL4 simulation (Gallicchio et al., 2014; Mobley et al., 2014). Most of the available experimental binding affinity data determined whether these ligands were binders or non-binders (Peat et al., 2014). The only binding affinity data point available for the tested true positives is AVX17557. Five of these ligands were experimental binders, while the other five ligands were non-binders. In the previous study, the new AGBNP2 carboxylate parameters, which are described in this paper, were used for the binding affinity calculations of HIV integrase and a library of potential inhibitors. In this work, we apply the original AGBNP2 carboxylate parameters to the 10 candidate ligands using the same simulation and setup protocol as the previous study (Gallicchio et al., 2014). The ligands are ranked based on a free energy score, which takes into account the binding free energy and an energetic penalty for unfavorable ionization states.
RESULTS AND DISCUSSION
In this section, we report results involving the use of BEDAM free energy calculations to parameterize force field parameters. We focused in particular on parameters of the AGBNP2 implicit solvent model accounting for first shell hydration effects. In the present case of binding to β-CD, first shell contributions can be favorable or unfavorable toward solvation. In both cases, GIST analysis justifies these aspects of the model and the modifications we have applied. Lastly, we apply the optimized parameters to the binding of a novel class of allosteric inhibitors of HIV-PR and HIV-1-integrase and show that they lead to improved agreement with measured binding affinities and enhance enrichment in virtual screening applications.
Can implicit solvent models mimic specific water–solute interactions?
One of the challenges of using implicit solvent models is the modeling of the effects of structural waters and water expulsion upon binding. To address this, our lab developed the AGBNP2 implicit solvent model, which incorporates the effects of favorable and unfavorable hydration (Gallicchio et al., 2009; Wickstrom et al., 2013) originating from specific sites on the surface of the solute. This was achieved by geometrical and energetic predictor terms that mimic hydrogen bonding and water enclosure effects. Each accessible hydration site contributes to the overall hydration free energy of the solute according to Equation 2, where pw accounts for the accessible volume of the hydration site and hw is an adjustable interaction energy parameter. The original AGBNP2 parameterization involved training solvation free energies against experimental data for small organic molecules and comparing conformational ensembles of peptides obtained with implicit and explicit solvation models (Gallicchio et al., 2009). More recently, we reported hydration parameters to model the effects of expelling unfavorable water molecules from within the binding cavity of β-CD (Wickstrom et al., 2013). Water enclosure is a very important factor because dehydration of the cavity of β-CD and other similar host–guest systems has been noted to be key for binding (Taulier and Chalikian, 2006; Biedermann et al., 2012; Nguyen et al., 2012; Rogers et al., 2013).
The AGBNP2 parameterization was augmented to include two hydration sites for each glucose monomer pointing in toward the buried interior of the β-CD host (Figure S4 in the Supporting Information and Figure 4 Wickstrom et al., 2013). Each solvent-occupied hydration site was assigned a positive (unfavorable) hydration correction energy (hw) to mimic the effect of water enclosure. Upon binding, guests would occupy these positions in the cavity, resulting in a boost to the binding free energy of the host–guest complex because of the removal of enclosed water molecules and their transfer to the bulk. Calculated and experimental binding free energies of a small group of β-CD host–guest systems were used to train the hw parameter, representing the magnitude of the free energy of water expulsion, for these hydration sites (Table 1). Four different values were tested for the hw correction term: 0.4, 0.5, 0.6, and 0.7 kcal/mol. The best agreement between calculated and experimental binding affinities for the training set was obtained with hw = 0.6 and hw = 0.7 based on RMSD. However, the average calculated binding affinities obtained using hw = 0.6 gives the closest estimation of the average experimental binding affinity of the training set than the binding affinities obtained using hw = 0.7. From the data in Table 1, it is apparent that including water enclosure parameters is necessary to achieve reasonable agreement between our calculations and experiments and that hw = 0.6 is the suitable correction energy value to scale the free energy of water expulsion. In the next section, we discuss the further justification behind this parameterization using GIST.
Figure 4.
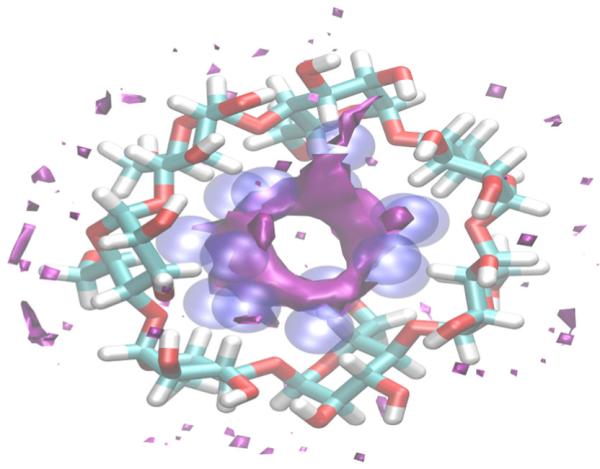
GIST contour plots of the solvation free energy density in and around β-CD. Contours at +2.0 kcal/mol/water are shown in purple. The AGBNP2 hydration sites in the cavity are shown in blue.
Table 1.
Comparison of calculated and experimental binding affinities for a training set of β-CD host–guest systems, varying the weight of the unfavorable free energy of enclosed water molecules
| hw | 0b | 0.4a | 0.5a | 0.6a | 0.7 | |
|---|---|---|---|---|---|---|
| Guests | Δ G ° exp | Δ G ° calc | Δ G ° calc | Δ G ° calc | Δ G ° calc | Δ G ° calc |
| Benzene | −2.77 | −0.37 | −2.44 ± 0.03 | −3.07 ± 0.04 | −3.69 ± 0.07 | −4.01 ± 0.05 |
| Resorcinol | −2.77 | 1.95 | −0.28 ± 0.05 | −0.78 ± 0.04 | −1.47 ± 0.05 | −1.90 ± 0.05 |
| Naproxen | −4.33 | −1.08 | −3.42 ± 0.15 | −3.79 ± 0.14 | −4.85 ± 0.13 | −5.00 ± 0.12 |
| Nabumetone | −4.59 | −1.35 | −3.18 ± 0.11 | −3.70 ± 0.06 | −4.31 ± 0.08 | −4.54 ± 0.10 |
| RMSD | 3.57 | 1.51 | 1.13 | 0.85 | 0.83 | |
| Average ΔG | −3.62 | −0.22 | −2.33 | −2.84 | −3.58 | −3.86 |
Data were included in the previous study of β-CD (Wickstrom et al., 2013).
Binding free energies were calculated from a linear extrapolation of the previous binding free energy data points.
Justification for the water site parameterization using grid inhomogeneous solvation theory analysis
The expulsion of water from unfavorable sites is a key factor in molecular recognition and binding. The recent focus of many computational groups is the development of tools that evaluate the importance of water in this process (Li and Lazaridis, 2006; Young et al., 2007; Abel et al., 2008; Michel et al., 2009; Yu and Rick, 2009; Baron et al., 2010; Nguyen et al., 2011; Nguyen et al., 2012). Some approaches, such as Watermap (Young et al., 2007; Abel et al., 2008), determine the solvation thermodynamics of high occupancy, single water sites relative to bulk water. GIST maps out the solvation patterns on a grid around a molecule of interest in order to analyze the solvation thermodynamics of high and low density regions of waters; this eliminates the need for defining specific water sites within a binding site (Nguyen et al., 2012). GIST was first used to analyze the hydration of the host CB-7, in which the binding cavity was noted to have an unfavorable free energy relative to bulk water. In this work, we evaluate the hydration pattern within and around the β-CD host using GIST in order to compare the treatment of hydration inside the cavity of β-CD by the AGBNP2 implicit solvent model with the behavior of explicit water molecules.
We calculated a GIST solvation free energy map using a 100-ns trajectory of an apo structure of β-CD in explicit solvent. Figure 4 shows the regions where the solvation free energy per water is unfavorable. Notably, there is a toroidal region (colored in purple) inside the cavity where the solvation free energy is unfavorable by 2.0 kcal/mol or more per water relative to bulk solvent. This solvation free energy is a combination of both unfavorable solvation energy, composed of slightly favorable solute–water energies and overwhelmingly unfavorable water–water energies, and the decreased entropy of the water inside this hydrophobic enclosure, relative to bulk water. The water molecules in the β-CD cavity are unfavorable energetically because of their inability to form the same number of hydrogen bonds as observed in bulk. This inability is largely due to the solvent excluded volume inside β-CD reducing the number of water neighbors available to form hydrogen bonds with each enclosed water molecule. The solvation entropy is also unfavorable inside the cavity because of the orientational and translational ordering that the water molecules need in order to form these hydrogen bonds with their limited number of water neighbors. The observation of unfavorable hydration sites inside the host cavity is consistent with previous work on a similar cylindrical enclosure for CB-7 (Nguyen et al., 2012). The 14 AGBNP2 hydration sites used in our model of β-CD have significant overlap with the toroidal region identified by GIST analysis. We therefore conclude that the modeling of water expulsion in β-CD modeled by the positive hydration correction energy terms in AGBNP2 is qualitatively justified by the GIST analysis.
Description of results with initial parameters
Computed binding free energies with original parameter set
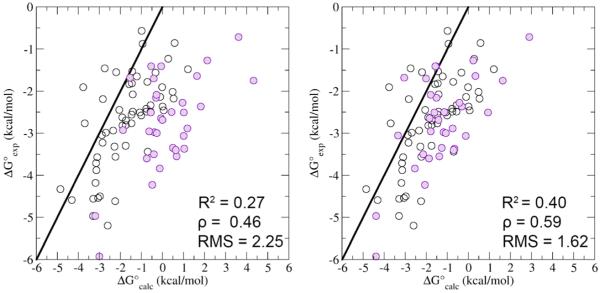
The BEDAM simulations were conducted for 33 complexes of β-CD with a diverse set of ligands containing a carboxylate functional group (Tables S1 and S2 in the Supporting Information). The results are summarized in Figure 5, along with the results from a previous study of 57 β-CD host–guest systems (Wickstrom et al., 2013) lacking carboxylate groups. Relative to the experimental standard binding free energies, the overall Spearman correlation coefficient and RMS error of the computed values are 0.46 and 2.25 kcal/mol, respectively (Figure 5, left panel). This accuracy is consistent with previous work on host–guest systems (Muddana et al., 2012; Muddana et al., 2014; Wickstrom et al., 2013). Inspection of Figure 5 reveals that guests with carboxylate groups represented the most problematic set for the computational model: β-CD host–guest systems in this class had the highest RMS deviation from the experiments (3.14 kcal/mol) and the lowest percentage of correct predictions (29%), calculated binding affinities that were within 2.0 kcal/mol of the experimental affinity, compared with the guests with other functional groups, for which the RMS deviation and percentage of correct predictions are 1.5 kcal/mol and 83%, respectively. This finding represented a clear indication that the force field parameters for the carboxylate group required further refinement.
Figure 5.
Comparison of the experimental versus the calculated standard binding free energies (ΔGb) with the original (left panel) and optimized (right panel) parameters for the AGBNP2 solvent model for all of the host–guest systems. The binding free energy data are presented for the 33 guests with (purple) and the additional 57 guests without carboxylate functional groups (black). The R2, Spearman rho (ρ), and RMS error are calculated for the set of 90 β-CD host–guest systems in each panel. The line is the x = y line.
Development of optimized hydration site parameters for carboxylate functional groups
Overall, the calculated binding affinities were underestimated relative to the experimental affinities by ~3.0 kcal/mol for carboxylate-containing guests. As detailed below, we attributed this large deviation to overestimation of the desolvation penalty for the carboxylate functional group. In order to address this issue, we focused on adjusting the hw parameter for the hydration sites surrounding the oxygen atoms on the carboxylate functional group, so as to better represent β-CD binding affinity data.
These hydration sites are located in positions where waters would potentially form hydrogen bonds with the carboxylate as described in the Methods and Materials section. The unoccupied sites are given an energetic reward for the favorable solute–solvent water interactions based on hw. This hw parameter was originally introduced to increase the desolvation penalty, which would result in a decrease in the number of salt bridges in model peptides predicted by the AGBNP model relative to explicit solvation (Gallicchio et al., 2009). However, these host–guest systems are stabilized by different interactions than observed in salt bridges; it is apparent that this parameterization strategy yielded an overly favorable hydration free energy for the carboxylate group relative to the interactions with the host. We therefore increased the value of hw solvation parameter from −1.25 kcal/mol to −0.75 kcal/mol to weaken the desolvation penalty for the carboxylate group and thereby increase the binding affinity for β-CD (Supporting Information).
The correction generally makes binding more favorable, as anticipated. When these energy parameters are applied to the full set of 33 ionic carboxylic acids, the RMS error for this set is reduced from 3.14 to 1.86 kcal/mol, and the number of correct predictions increased from 27% to 67%. Over all of the β-CD complexes investigated, the optimized parameters yield a Spearman rho of 0.59 and an RMS error of 1.62 kcal/mol, thereby providing an overall superior model (Figure 5).
In order to evaluate the realism of the updated hydration site placements, we calculated a GIST solvation free energy map using a 100-ns trajectory of hexanoate in TIP3P explicit solvent. Figure 6 shows the regions of high water density with favorable solvation (ΔGsolv ≤ −0.25 kcal/mol). Each oxygen atom of the carboxylate group is surrounded by a favorable ring of solvation free energy. Similar hydration patterns are observed around the carboxylate group of glutamate side chains in proteins based on X-ray diffraction data (Thanki et al., 1988). These maps reflect a combination of the favorable solvation energies and unfavorable solvation entropies because of the interactions between water molecules and carboxylate oxygens. The favorable solvation energy is due to the formation of approximately three hydrogen bonds between each oxygen and the surrounding waters. These interactions are penalized by the solvation entropy, which accounts for the ordering of the water around the oxygen atom allowing for favorable hydration. The AGBNP2 hydration sites overlap with these favorable regions of solvation around the carboxylate oxygens, accounting for in-plane and out-of-plane hydrogen bonding between water and the oxygen atoms. These results confirm that the locations of AGBNP2 hydration sites are appropriately selected to model the favorable hydration around the carboxylate group.
Figure 6.
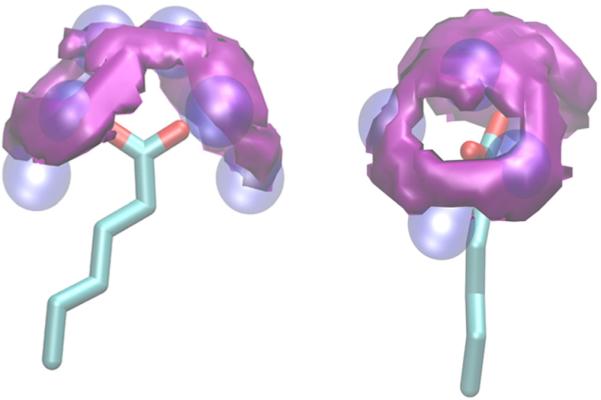
GIST contour plots of the solvation free energy around hexanoate. Contours at −0.25 kcal/mol per water are shown in purple. The hydration sites in the cavity are shown in blue. The figure is showing two orientations of the same molecule.
Physical basis for the reparameterization
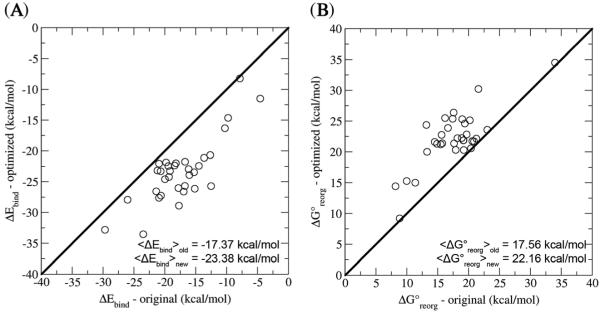
One of the strengths of physics-based models of binding, such as BEDAM, is the explicit treatment of entropic and internal conformational strain effects, collectively identified as reorganization free energy effects. Indeed, neglecting such terms produces a model in clear disagreement with the experiments (RMS deviation = 14.9 kcal/mol for the 33 carboxylate guests). It is interesting therefore to note the effect of the new parameterization on the energetic and reorganization free energy components of the binding free energies of the complexes. With the new parameters (see also Figure 7(A)), we observe a shift in the binding energies toward more favorable values (−23.4 kcal/mol on average compared with −17.4 kcal/mol). This is consistent with the goals of reparameterization, which were to adjust the free energy of solvation to strengthen host–guest interactions, thereby improving the agreement between the experimental and calculated binding affinities for these β-CD host–guest systems. The predominant effect of the new parameters on the β-CD + carboxylate guest binding modes is more hydrogen bonds between the host and the guest, because of the reduction in the solvation penalty upon binding, which translates into more favorable binding energies and affinities (Figure 8 and Tables S3 and S4 in the Supporting Information). Nevertheless, the reorganization free energies are also affected (Figure 7B and Table S3 in the Supporting Information), becoming more unfavorable with the new parameters (22.2 kcal/mol on average compared with 17.6 kcal/mol). This change is due to the decrease in the solvation penalty for binding, which enables the guest to form stronger interactions with the host, resulting in a loss of conformational entropy and an increase in the conformational strain energy for both the host and the guest. This example shows that one must be aware that modifications aimed, for example, at adjusting interaction energies could cause opposite effects to the reorganization free energy component. It is therefore crucial that both energetic and entropic effects be considered in force field parameterization of the kind described here.
Figure 7.
Comparison of the (A) binding energy and (B) the reorganization free energy of the β-CD complexes with carboxylate guests using the original and optimized parameters for the AGBNP2 solvent model.
Figure 8.
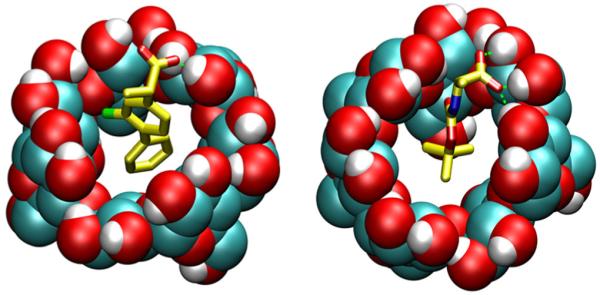
Predicted binding modes of β-CD with flurbiprofen (on the left) and N-t-boc alanine (on the right). The green dashed lines represent host-guest intermolecular hydrogen bonds.
Binding free energies of ligand inhibitors to an allosteric site on HIV Protease
Recently, a new potentially allosteric binding site has been discovered on the top of the flaps of HIV-PR using docking and experimental assays (Figures 2 and 3; Tiefenbrunn et al., 2013). Two ligands, 1F1 and 1F1N, were found to bind to this site of HIV-PR with micromolar affinity. Both ligands contain an indole and a carboxylate group but differ in the substitution position on the indole ring. In 1F1N, the carboxylate group is linked to the indole group by two methylenes. Despite the structural differences, these two ligands have similar affinity to HIV-PR (within 1.0 kcal/mol). As seen in Figure 3, the two ligands adopt similar predicted binding modes, featuring a salt bridge between the carboxylate ion and Arg57 side chain, and a hydrogen bonding interaction between the indole nitrogen on the ligand and the backbone carbonyl oxygen of Val56.
The BEDAM simulations were conducted for the HIV-PR complexes with 1F1 and 1F1N, using both carboxylate parameter sets. The results are reported in Table 2. Using the original carboxylate parameter set, the calculated binding free energies were more than 2.7 kcal/mol less favorable compared with the experimental binding affinities. With the new carboxylate parameters developed from the analysis of the host–guest systems, the binding affinities for 1F1 and 1F1N to the allosteric binding site on HIV-PR become 3.5 and 2.1 kcal/mol more favorable relative to the old parameters, which brings the calculated values to within 0.6 kcal/mol of the experimental affinities.
Table 2.
Comparison of experimental and calculated binding free energies of 1F1 and 1F1N to the allosteric site of HIV-PR using the original and optimized solvation parameter for the carboxylate moieties
| Ligand name | Parameters | Δ G ° exp | Δ G ° calc | Δ E bind | Δ G ° reorg |
|---|---|---|---|---|---|
| 1F1 | Original | −6.6 | −3.0 ± 0.53 | −19.25 ± 0.34 | 16.25 ± 0.76 |
| New | −6.6 | −6.5 ± 0.44 | −22.15 ±0.31 | 15.65 ± 0.65 | |
| 1F1N | Original | −7.3 | −4.6 ± 0.17 | −22.19 ± 0.68 | 17.59 ± 0.61 |
| New | −7.3 | −6.7 ± 0.11 | −25.15 ± 0.72 | 18.45 ± 0.81 |
The error bars are estimated by block averaging by dividing the full trajectory into five blocks. All values in kcal/mol.
In Table 2, we also report the average binding energies and reorganization free energies for the HIV-PR complexes with 1F1 and 1F1N. Relative to 1F1, 1F1N binding is associated with a more favorable binding energy offset by a more unfavorable reorganization free energy. This reflects a compensatory effect between the binding energy and reorganization free energy in these systems. The stronger binding energy for the 1F1N is attributable in part to the two extra methylene groups, which are able to form stronger hydrophobic interaction with the protein. This gain in the binding energy is however offset by the penalty because of the energetic strain and the conformational entropy loss, resulting in very similar binding free energies for the two ligands. It is also of interest to note that, for both ligands, switching to the new parameter set causes the binding energy, Ebind, to become more favorable by about −3 kcal/mol, while the associated increase in the reorganization free energy penalty is considerably smaller at ~1 kcal/mol. Examination of the BEDAM structures sampled for the fully coupled ensemble (λ = 1) confirms that there is no change in the binding mode with new parameters. Taken together, these observations suggest that the effect of the new parameters is mainly to strengthen the ligand–receptor interaction through the enhancement of the salt bridge between the carboxylate moiety on the ligand and Arg57 through the reduction of the desolvation penalty with the new parameters.
Virtual screening of HIV integrase inhibitors
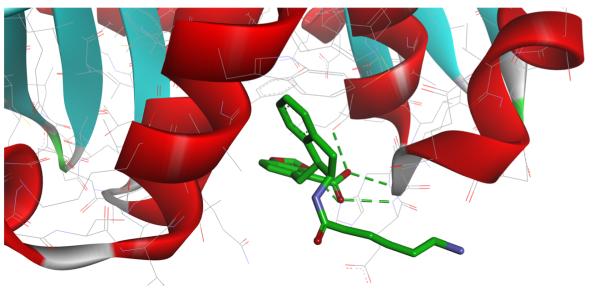
The optimized carboxylate parameters were also applied to another important drug target, HIV integrase. Recently, Gallicchio et al. reported results of a virtual screening experiment to identify binders from a library of candidate ligands against HIV integrase using AutoDock Vina, followed by BEDAM calculations in the recent SAMPL4 blind challenge (Gallicchio et al., 2014). The study focused on ligands that targeted the LEDGF binding site. Many of the ligands contained carboxylate functional groups (Figure 9 and Tables S5 and S6 in the Supporting Information). Using this docking/free energy screening protocol and new AGBNP2 parameters developed from host–guest system binding affinity data, this work reported the second highest enrichment among all 26 submissions in SAMPL4 (Mobley et al., 2014; and the highest enrichment among the 25 purely computational submissions) and identified the five experimental binders in the list of the top 10 predicted binders.
Figure 9.
Predicted binding mode of AVX17557_3 in the LEDGF binding site of HIV integrase. The green dashed lines indicate protein-ligand intermolecular hydrogen bonds.
To test whether the new parameters played a role in the accuracy of the SAMPL4 predictions, we performed BEDAM simulations of the five experimental binders and five true negatives using the original solvation parameters. Table 3 reports the free energy scores for each ligand. With the new carboxylate parameters, the binding affinities for the true binders become 3.0 kcal/mol more favorable relative to the old parameters on average. Based on these results, only three of the true experimental binders would be identified in the top 10 calculated binders with the old parameters, which would decrease the overall enrichment factor by 50%. The biggest affinity shift is observed in AVX38753_3_1, which contains two carboxylate groups unlike the other true positives. The binding affinities of the true negatives also became slightly more favorable, except for AVX38789_3, but remained in the category of non-binders. Overall, the solvation parameters improve the enrichment results from the virtual screening by making the binding affinity more favorable for true experimental binders of HIV integrase.
Table 3.
Comparison of free energy scores to the LEDGF binding site of HIV-integrase using the original and optimized solvation parameters (Gallicchio et al., 2014) for the carboxylate moieties
| True positives |
True negatives |
||||
|---|---|---|---|---|---|
| New | Original | New | Original | ||
| AVX17557_3 | −8.92 | −6.12 | AVX38784_7 | 4.38 | 4.97 |
| AVX17556_3 | −8.24 | −3.92 | AVX38787_0 | 4.51 | 4.61 |
| AVX17285_0 | −7.40 | −6.05 | AVX38782_2 | 4.52 | 4.85 |
| AVX38753_3_1 | −7.37 | −1.89 | AVX38788_2 | 4.70 | 4.92 |
| AVX101124_1 | −7.33 | −6.11 | AVX38789_3 | 4.70 | 3.25 |
All values are reported in kcal/mol.
Implications of this parameterization strategy
In this work, we show how host–guest binding affinity data can be used to optimize force field and implicit solvent model parameters. In this specific application, we developed hydration parameters for the AGBNP2 solvent model to account for the expulsion of water molecules from the binding cavity of the β-CD host and desolvation of carboxylate groups. However, host–guest affinity data are likely to be useful for potential model validation and optimization in general, including the optimization of implicit solvent models as well as explicit solvation ones.
It is worth noting that the optimized carboxylate parameters described here were also used in the blinded SAMPL4 prediction challenge, where excellent results were obtained for HIV integrase ligand screening (Gallicchio et al., 2014) and binding affinity predictions for the octa-acid host–guest system (Muddana et al., 2014; Gallicchio et al. 2015). Furthermore, the AGBNP2 polar hydration site parameters, viewed as short range corrections to the continuum electrostatic treatment, are generalizable to many different systems. The carboxylate parameters for AGBNP2 were originally trained to decrease the formation of salt bridges in peptides (Gallicchio et al., 2009) and used explicit solvent simulations as a benchmark. The revised parameters decreased the strength of the ionic interactions, which are relevant for binding (Table 2 and Table 3) of these HIV-PR and HIV-integrase inhibitor complexes. These parameters also affected the binding of β-CD host–guest systems, even though there were different groups involved in stabilizing the bound state (i.e., hydroxyl group from β-CD forming a hydrogen bond with the oxygen on the carboxylate).
In contrast, AGBNP2 hydration parameters can be specialized to account for complicated hydration patterns in binding sites. Water configurations are highly influenced by the overall chemical nature, curvature, and topology of a binding site, which is highly dependent on the cooperativity of sidechain packing. AGBNP2 hydration sites can be incorporated into a binding site to account for these effects. For example, non-polar hydration sites can be used to model the effects of unfavorably enclosed water molecules in hydrophobic enclosures, formed by several non-polar chemical groups. However, these effects are not limited to regions of non-polar hydration. Polar hydration sites can be used to model complex water structure formed within a binding site, such as a correlated H-bond network involving multiple water molecules and polar side-chains (Young et al., 2007). For simple host–guest systems, such as β-CD, these hydration sites can be placed based on the symmetrical features of the host molecule and calibrated using binding affinity data. In contrast, this type of parameterization is more challenging for a protein receptor where the structural details are more complicated and require site placement and perhaps different hydration correction energies for different regions of a binding site. In addition, the protein of interest may not have a large set of reliable binding affinity data to tune those parameters. In this situation, GIST can play an important role in characterizing the solvation profiles of different receptor binding sites, which can be used to properly calibrate the AGBNP2 hydration sites. Overall, this work illustrates the suitability of GIST to analyze hydration properties of molecules and its potential application toward the parameterization of continuum solvent models of hydration.
Furthermore, this methodology can be used with different host–guest systems to target more specific interactions in protein–ligand systems. β-CD host–guest systems are stabilized by hydrophobic packing between non-polar groups on the host and guest; however, the β-CD cavity may not be the best proxy for enclosed hydrophobic surfaces in proteins because of its shallow nature and solvent exposure. The binding of β-CD host–guest systems is also limited to polar interactions between hydroxyl groups and the chemical groups on the guests. However, experimental binding affinity data exists for other host–guest systems that are capable of targeting a variety of chemical moieties and geometries. For example, acyclic CB-7 host–guest systems studied in SAMPL3 can mimic salt–bridge interactions observed in proteins (Muddana et al., 2012), and the octa-acid host–guest systems studied in SAMPL4 provide a better model system to study the hydrophobic effect due to the hydrophobic curvature of the octa-acid cavity (Muddana et al., 2014). Nevertheless, this work should motivate the design of new host–guest systems that can serve as better models of protein–ligand systems.
CONCLUSION
We have shown that large scale binding free energy calculations and corresponding high quality experimental datasets can be useful for force field parameterization purposes. Most force field development work has focused on employing solvation free energy calculation to evaluate the quality of non-bonded parameters (Mobley et al., 2007; Mobley et al., 2012; Shivakumar et al., 2009; Shivakumar et al., 2010; Shivakumar et al., 2012; Sulea and Purisima, 2012). However, non-bonded interactions of ionic compounds are difficult to probe computationally and experimentally by hydration free energy measurements. In this work, we show that β-CD host–guest systems can be used to train force field parameters, and those parameters can then be applied to accurately model binding processes for larger protein–ligand systems. The approach demonstrated here, illustrated in the context of an implicit solvent model, is equally valid for the parameterization of explicit solvent force fields. Future work will explore the transferability of the new parameters to more diverse systems, using other host–guest systems with this parameterization method and applying quantitative GIST data to this optimization process.
Supplementary Material
Acknowledgements
This work was supported in part by NIH grants GM613000 (M. K. G.), GM30580, GM100946, and GM095417. We gratefully acknowledge Anthony Cruz-Balberdy, Steven Ramsey, and Jason Swails for providing helpful discussions. M. K. G. is a cofounder and has equity interest in the company VeraChem LLC.
Footnotes
SUPPORTING INFORMATION
Additional supporting information may be found in the online version of this article at the publisher’s web site.
REFERENCES
- Abel Robert, Young T, Farid R, Berne BJ, Friesner RA. Role of the active-site solvent in the thermodynamics of factor Xa ligand binding. J. Am. Chem. Soc. 2008;130(9):2817–2831. doi: 10.1021/ja0771033. DOI: 10.1021/ja0771033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banks JL, Beard HS, Cao Y, Cho AE, Damm W, Farid R, Felts AK, Halgren TA, Mainz DT, Maple JR, Murphy R, Philipp DM, Repasky MP, Zhang LY, Berne BJ, Friesner RA, Gallicchio E, Levy RM. Integrated modeling program, applied chemical theory (IMPACT) J. Comput. Chem. 2005;26(16):1752–1780. doi: 10.1002/jcc.20292. DOI: 10.1002/jcc.20292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baron R, Setny P, McCammon JA. Water in cavity–ligand recognition. J. Am. Chem. Soc. 2010;132(34):12091–12097. doi: 10.1021/ja1050082. DOI: 10.1021/ja1050082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biedermann F, Uzunova VD, Scherman OA, Nau WM, De Simone Alfonso. Release of high-energy water as an essential driving force for the high-affinity binding of cucurbit[n]urils. J. Am. Chem. Soc. 2012;134(37):15318–15323. doi: 10.1021/ja303309e. DOI: 10.1021/ja303309e. [DOI] [PubMed] [Google Scholar]
- Chang C-E, Gilson MK. Free energy, entropy, and induced fit in host–guest recognition: calculations with the second-generation mining minima algorithm. J. Am. Chem. Soc. 2004;126(40):13156–13164. doi: 10.1021/ja047115d. DOI: 10.1021/ja047115d. [DOI] [PubMed] [Google Scholar]
- Chen W, Chang C-E, Gilson MK. Calculation of cyclodextrin binding affinities: energy, entropy, and implications for drug design. Biophys. J. 2004;87(5):3035–3049. doi: 10.1529/biophysj.104.049494. DOI: 10.1529/biophysj.104.049494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y, Prusoff WH. Relationship between the inhibition constant (K1) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochem. Pharmacol. 1973;22(23):3099–3108. doi: 10.1016/0006-2952(73)90196-2. [DOI] [PubMed] [Google Scholar]
- Corbeil CR, Sulea T, Purisima EO. Rapid Prediction of solvation free energy. 2. The First-Shell Hydration (FiSH) continuum model. Journal of Chemical Theory and Computation. 2010;6(5):1622–1637. doi: 10.1021/ct9006037. DOI: 10.1021/ct9006037. [DOI] [PubMed] [Google Scholar]
- Del Valle EMM. Cyclodextrins and their uses: a review. Process Biochem. 2004;39(9):1033–1046. DOI: 10.1016/S0032-9592(03)00258-9. [Google Scholar]
- Deng N-j, Zhang P, Cieplak P, Lai L. Elucidating the energetics of entropically driven protein–ligand association: calculations of absolute binding free energy and entropy. J. Phys. Chem. B. 2011;115(41):11902–11910. doi: 10.1021/jp204047b. DOI: 10.1021/jp204047b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fennell CJ, Kehoe CW, Dill KA. Modeling aqueous solvation with semi-explicit assembly. Proc. Natl. Acad. Sci. U. S. A. 2011;108(8):3234–3239. doi: 10.1073/pnas.1017130108. DOI: 10.1073/pnas.1017130108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio E. Role of ligand reorganization and conformational restraints on the binding free energies of DAPY non-nucleoside inhibitors to HIV reverse transcriptase. Computational Molecular Bioscience. 2012;2(1):7–22. doi: 10.4236/cmb.2012.21002. DOI: 10.4236/cmb.2012.21002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio E, Levy RM. AGBNP: an analytic implicit solvent model suitable for molecular dynamics simulations and high-resolution modeling. J. Comput. Chem. 2004;25(4):479–499. doi: 10.1002/jcc.10400. DOI: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- Gallicchio E, Levy RM. Prediction of SAMPL3 host–guest Affinities with the binding energy distribution analysis method (BEDAM) J. Comput. Aided Mol. Des. 2012;26(5):505–516. doi: 10.1007/s10822-012-9552-3. DOI: 10.1007/s10822-012-9552-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio E, Paris K, Levy RM. The AGBNP2 implicit solvation model. Journal of Chemical Theory and Computation. 2009;5(9):2544–2564. doi: 10.1021/ct900234u. DOI: 10.1021/ct900234u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio E, Lapelosa M, Levy RM. Binding energy distribution analysis method (BEDAM) for estimation of protein–ligand binding affinities. Journal of Chemical Theory and Computation. 2010;6(9):2961–2977. doi: 10.1021/ct1002913. DOI: 10.1021/ct1002913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio E, Deng N, He P, Wickstrom L, Perryman AL, Santiago DN, Forli S, Olson AJ, Levy RM. Virtual screening of integrase inhibitors by large scale binding free energy calculations: the SAMPL4 challenge. J. Comput. Aided Mol. Des. 2014;28(4):475–490. doi: 10.1007/s10822-014-9711-9. DOI: 10.1007/s10822-014-9711-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio E, Chen H, Fitzgerald M, Gao Y, He P, Kalyanikar M, Kao C, Lu B, Niu Y, Pethe M, Zhu J, Levy RM. BEDAM Binding Free Energy Predictions for the SAMPL4 Octa-Acid Host Challenge. J. Comp. Aided Mol. Des. 2015;29:315–325. doi: 10.1007/s10822-014-9795-2. DOI: 10.1007%2Fs10822–014–9795–2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson MK, Given JA, Bush BL, McCammon JA. The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys. J. 1997;72(3):1047–1069. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant JA, Pickup BT. A Gaussian description of molecular shape. J. Phys. Chem. 1995;99(11):3503–3510. DOI: 10.1021/j100011a016. [Google Scholar]
- Hamaguchi N, Fusti-Molnar L, Wlodek S. Force-field and quantum-mechanical binding study of selected SAMPL3 host–guest complexes. J. Comput. Aided Mol. Des. 2012;26(5):577–582. doi: 10.1007/s10822-012-9553-2. DOI: 10.1007/s10822-012-9553-2. [DOI] [PubMed] [Google Scholar]
- Hassan SA, Steinbach PJ. Water-exclusion and liquid-structure forces in implicit solvation. J. Phys. Chem. B. 2011;115(49):14668–14682. doi: 10.1021/jp208184e. DOI: 10.1021/jp208184e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hassan SA, Guarnieri F, Mehler EL. Characterization of hydrogen bonding in a continuum solvent model. J. Phys. Chem. B. 2000;104(27):6490–6498. DOI: 10.1021/jp9938967. [Google Scholar]
- Heeres J, de Jonge MR, Koymans LMH, Daeyaert FFD, Vinkers M, Van Aken KJA, Arnold E, Das K, Kilonda A, Hoornaert GJ, Compernolle F, Cegla M, Azzam RA, Andries K, de Béthune MP, Azijn H, Pauwels R, Lewi PJ, Janssen PAJ. Design, synthesis, and SAR of a novel pyrazinone series with non-nucleoside HIV-1 reverse transcriptase inhibitory activity. J. Med. Chem. 2005;48(6):1910–1918. doi: 10.1021/jm040829e. DOI: 10.1021/jm040829e. [DOI] [PubMed] [Google Scholar]
- Hirata F, Redfern P, Levy RM. Viewing the Born model for ion hydration through a microscope. International Journal of Quantum Chemistry. 1988;34(S15):179–190. DOI: 10.1002/qua.560340716. [Google Scholar]
- Hünenberger PH, McCammon JA. Ewald artifacts in computer simulations of ionic solvation and ion–ion interaction: a continuum electrostatics study. J. Chem. Phys. 1999;110(4):1856–1872. DOI: 10.1063/1.477873. [Google Scholar]
- Janssen PAJ, Lewi PJ, Arnold E, Daeyaert F, de Jonge M, Heeres J, Koymans L, Vinkers M, Guillemont J, Pasquier E, Kukla M, Ludovici D, Andries K, de Béthune MP, Pauwels R, Das K, Clark AD, Jr, Frenkel YV, Hughes SH, Medaer B, De Knaep F, Bohets H, De Clerck F, Lampo A, Williams P, Stoffels P. In search of a novel anti-HIV drug: multidisciplinary coordination in the discovery of 4-[[4-[[4-[(1E)-2-cyanoethenyl]-2,6-dimethylphenyl]amino]-2-pyrimidinyl] amino]benzonitrile (R278474, Rilpivirine) J. Med. Chem. 2005;48(6):1901–1909. doi: 10.1021/jm040840e. DOI: 10.1021/jm040840e. [DOI] [PubMed] [Google Scholar]
- Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79(2):926–935. DOI: 10.1063/1.445869. [Google Scholar]
- Jorgensen WL, Maxwell DS, Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996;118(45):11225–11236. DOI: 10.1021/ja9621760. [Google Scholar]
- Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B. 2001;105(28):6474–6487. DOI: 10.1021/jp003919d. [Google Scholar]
- Knight JL, Brooks CL. Surveying implicit solvent models for estimating small molecule absolute hydration free energies. J. Comput. Chem. 2011;32(13):2909–2923. doi: 10.1002/jcc.21876. DOI: 10.1002/jcc.21876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- König G, Brooks BR. Predicting binding affinities of host–guest systems in the SAMPL3 blind challenge: the performance of relative free energy calculations. J. Comput. Aided Mol. Des. 2012;26(5):543–550. doi: 10.1007/s10822-011-9525-y. DOI: 10.1007/s10822-011-9525-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lapelosa M, Gallicchio E, Levy RM. Conformational transitions and convergence of absolute binding free energy calculations. Journal of Chemical Theory and Computation. 2012;8(1):47–60. doi: 10.1021/ct200684b. DOI: 10.1021/ct200684b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrenz M, Wereszczynski J, Ortiz-Sánchez JM, Nichols SE, McCammon JA. Thermodynamic integration to predict host–guest binding affinities. J. Comput. Aided Mol. Des. 2012;26(5):569–576. doi: 10.1007/s10822-012-9542-5. DOI: 10.1007/s10822-012-9542-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazaridis T. Inhomogeneous fluid approach to solvation thermodynamics. 1. Theory. J. Phys. Chem. B. 1998;102(18):3531–3541. DOI: 10.1021/jp9723574. [Google Scholar]
- Li Z, Lazaridis T. Thermodynamics of buried water clusters at a protein–ligand binding interface. J. Phys. Chem. B. 2006;110(3):1464–1475. doi: 10.1021/jp056020a. DOI: 10.1021/jp056020a. [DOI] [PubMed] [Google Scholar]
- Lyman E, Marty Ytreberg F, Zuckerman DM. Resolution exchange simulation. Phys. Rev. Lett. 2006;96(2):028105. doi: 10.1103/PhysRevLett.96.028105. DOI: 10.1103/PhysRevLett.96.028105. [DOI] [PubMed] [Google Scholar]
- Michel J, Tirado-Rives J, Jorgensen WL. Energetics of displacing water molecules from protein binding sites: consequences for ligand optimization. J. Am. Chem. Soc. 2009;131(42):15403–15411. doi: 10.1021/ja906058w. DOI: 10.1021/ja906058w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikulskis P, Genheden S, Rydberg P, Sandberg L, Olsen L, Ryde U. Binding affinities in the SAMPL3 trypsin and host–guest blind tests estimated with the MM/PBSA and LIE methods. J. Comput. Aided Mol. Des. 2012;26(5):527–541. doi: 10.1007/s10822-011-9524-z. DOI: 10.1007/s10822-011-9524-z. [DOI] [PubMed] [Google Scholar]
- Mobley DL, Dumont É , Chodera JD, Dill KA. Comparison of charge models for fixed-charge force fields: small-molecule hydration free energies in explicit solvent. J. Phys. Chem. B. 2007;111(9):2242–2254. doi: 10.1021/jp0667442. DOI: 10.1021/jp0667442. [DOI] [PubMed] [Google Scholar]
- Mobley DL, Liu, Cerutti DS, Swope WC, Rice JE. Alchemical prediction of hydration free energies for SAMPL. J. Comput. Aided Mol. Des. 2012;26(5):551–562. doi: 10.1007/s10822-011-9528-8. DOI: 10.1007/s10822-011-9528-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mobley DL, Liu S, Lim NM, Wymer KL, Perryman AL, Forli S, Deng N, Su J, Branson K, Olson AJ. Blind prediction of HIV integrase binding from the SAMPL4 challenge. J. Comput. Aided Mol. Des. 2014;28(4):327–345. doi: 10.1007/s10822-014-9723-5. DOI: 10.1007/s10822-014-9723-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moghaddam S, Inoue Y, Gilson MK. Host–guest complexes with protein –ligand-like affinities: computational analysis and design. J. Am. Chem. Soc. 2009;131(11):4012–4021. doi: 10.1021/ja808175m. DOI: 10.1021/ja808175m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moghaddam S, Yang C, Rekharsky M, Ko YH, Kim K, Inoue Y, Gilson MK. New ultrahigh affinity host–guest complexes of cucurbit[7]uril with bicyclo[2.2.2]octane and adamantane guests: thermodynamic analysis and evaluation of M2 affinity calculations. J. Am. Chem. Soc. 2011;133(10):3570–3581. doi: 10.1021/ja109904u. DOI: 10.1021/ja109904u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monroe JI, Shirts MR. Converging free energies of binding in cucurbit[7]uril and octa-acid host–guest systems from SAMPL4 using expanded ensemble simulations. J. Comput. Aided Mol. Des. 2014;28(4):401–415. doi: 10.1007/s10822-014-9716-4. DOI: 10.1007/s10822-014-9716-4. [DOI] [PubMed] [Google Scholar]
- Muddana HS, Gilson MK. Prediction of SAMPL3 host–guest binding affinities: evaluating the accuracy of generalized force-fields. J. Comput. Aided Mol. Des. 2012a;26(5):517–525. doi: 10.1007/s10822-012-9544-3. DOI: 10.1007/s10822-012-9544-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muddana HS, Gilson MK. Calculation of host–guest binding affinities using a quantum-mechanical energy model. Journal of Chemical Theory and Computation. 2012b;8(6):2023–2033. doi: 10.1021/ct3002738. DOI: 10.1021/ct3002738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muddana HS, Varnado CD, Bielawski CW, Urbach AR, Isaacs L, Geballe MT, Gilson MK. Blind prediction of host–guest binding affinities: a new SAMPL3 challenge. J. Comput. Aided Mol. Des. 2012;26(5):475–487. doi: 10.1007/s10822-012-9554-1. DOI: 10.1007/s10822-012-9554-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muddana HS, Fenley AT, Mobley DL, Gilson MK. The SAMPL4 host–guest blind prediction challenge: an overview. J. Comput. Aided Mol. Des. 2014;28(4):305–317. doi: 10.1007/s10822-014-9735-1. DOI: 10.1007/s10822-014-9735-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen C, Gilson MK, Young T. Structure and thermodynamics of molecular hydration via grid inhomogeneous solvation theory. 2011 doi: 10.1063/1.4733951. arXiv:1108.4876 [physics, Q-Bio], August. http://arxiv.org/abs/1108.4876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen CN, Young TK, Gilson MK. Grid inhomogeneous solvation theory: hydration structure and thermodynamics of the miniature receptor cucurbit[7]uril. J. Chem. Phys. 2012;137(4):044101. doi: 10.1063/1.4733951. DOI: 10.1063/1.4733951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen H, Roe DR, Simmerling C. Improved generalized Born solvent model parameters for protein simulations. Journal of Chemical Theory and Computation. 2013;9(4):2020–2034. doi: 10.1021/ct3010485. DOI: 10.1021/ct3010485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okur A, Roe DR, Cui G, Hornak V, Simmerling C. Improving convergence of replica-exchange simulations through coupling to a high-temperature structure reservoir. Journal of Chemical Theory and Computation. 2007;3(2):557–568. doi: 10.1021/ct600263e. DOI: 10.1021/ct600263e. [DOI] [PubMed] [Google Scholar]
- Okur A, Wickstrom L, Simmerling Carlos. Evaluation of salt bridge structure and energetics in peptides using explicit, implicit, and hybrid solvation models. Journal of Chemical Theory and Computation. 2008;4(3):488–498. doi: 10.1021/ct7002308. DOI: 10.1021/ct7002308. [DOI] [PubMed] [Google Scholar]
- Onufriev A, Bashford D, Case DA. Exploring protein native states and large-scale conformational changes with a modified generalized Born model. Proteins. 2004;55(2):383–394. doi: 10.1002/prot.20033. DOI: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- Peat TS, Dolezal O, Newman J, Mobley D, Deadman JJ. Interrogating HIV integrase for compounds that bind—a SAMPL challenge. J. Comput. Aided Mol. Des. 2014;28(4):347–362. doi: 10.1007/s10822-014-9721-7. DOI: 10.1007/s10822-014-9721-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perryman AL, Zhang Q, Soutter HH, Rosenfeld R, McRee DE, Olson AJ, Elder JE, Stout CD. Fragment-based screen against HIV protease. Chem. Biol. Drug Des. 2010;75(3):257–268. doi: 10.1111/j.1747-0285.2009.00943.x. DOI: 10.1111/j.1747-0285.2009.00943.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reif MM, Chris Oostenbrink. Net charge changes in the calculation of relative ligand-binding free energies via classical atomistic molecular dynamics simulation. J. Comput. Chem. 2014;35(3):227–243. doi: 10.1002/jcc.23490. DOI: 10.1002/jcc.23490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rekharsky MV, Inoue Y. Complexation thermodynamics of cyclodextrins. Chem. Rev. 1998;98(5):1875–1918. doi: 10.1021/cr970015o. [DOI] [PubMed] [Google Scholar]
- Rekharsky M, Inoue Y. Chiral recognition thermodynamics of Β-cyclodextrin: the thermodynamic origin of enantioselectivity and the enthalpy–entropy compensation effect. J. Am. Chem. Soc. 2000;122(18):4418–4435. DOI: 10.1021/ja9921118. [Google Scholar]
- Rekharsky MV, Inoue Yoshihisa. Solvent and guest isotope effects on complexation thermodynamics of alpha-, beta-, and 6-amino-6-deoxy-beta-cyclodextrins. J. Am. Chem. Soc. 2002;124(41):12361–12371. doi: 10.1021/ja027031+. [DOI] [PubMed] [Google Scholar]
- Rekharsky MV, Mori T, Yang C, Ko YH, Selvapalam N, Kim H, Sobransingh D, Kaifer AE, Liu S, Isaacs L, Chen W, Moghaddam S, Gilson MK, Kim K, Inoue Y. A synthetic host–guest system achieves avidin-biotin affinity by overcoming enthalpy–entropy compensation. Proc. Natl. Acad. Sci. 2007;104(52):20737–20742. doi: 10.1073/pnas.0706407105. DOI: 10.1073/pnas.0706407105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ren P, Chun J, Thomas DG, Schnieders MJ, Marucho M, Zhang J, Baker NA. Biomolecular electrostatics and solvation: a computational perspective. Q. Rev. Biophys. 2012;45(4):427–491. doi: 10.1017/S003358351200011X. DOI: 10.1017/S003358351200011X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzo RC, Aynechi T, Case DA, Kuntz ID. Estimation of absolute free energies of hydration using continuum methods: accuracy of partial charge models and optimization of nonpolar contributions. Journal of Chemical Theory and Computation. 2005;2(1):128–139. doi: 10.1021/ct050097l. DOI: 10.1021/ct050097l. [DOI] [PubMed] [Google Scholar]
- Rocklin GJ, Mobley DL, Dill KA, Hünenberger PH. Calculating the binding free energies of charged species based on explicit-solvent simulations employing lattice-sum methods: an accurate correction scheme for electrostatic finite-size effects. J. Chem. Phys. 2013;139(18):184103. doi: 10.1063/1.4826261. DOI: 10.1063/1.4826261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roe DR, Okur A, Lauren W, Hornak V, Simmerling C. Secondary structure bias in generalized Born solvent models: comparison of conformational ensembles and free energy of solvent polarization from explicit and implicit solvation. J. Phys. Chem. B. 2007;111(7):1846–1857. doi: 10.1021/jp066831u. DOI: 10.1021/jp066831u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers KE, Ortiz-Sánchez JM, Baron R, Fajer M, de Oliveira AFC, McCammon JA. On the role of dewetting transitions in host–guest binding free energy calculations. Journal of Chemical Theory and Computation. 2013;9(1):46–53. doi: 10.1021/ct300515n. DOI: 10.1021/ct300515n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roitberg AE, Okur A, Simmerling C. Coupling of replica exchange simulations to a non-Boltzmann structure reservoir. J. Phys. Chem. B. 2007;111(10):2415–2418. doi: 10.1021/jp068335b. DOI: 10.1021/jp068335b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirts MR, Pitera JW, Swope WC, Pande VS. Extremely precise free energy calculations of amino acid side chain analogs: comparison of common molecular mechanics force fields for proteins. J. Chem. Phys. 2003;119(11):5740–5761. DOI: 10.1063/1.1587119. [Google Scholar]
- Shivakumar D, Deng Y, Roux B. Computations of absolute solvation free energies of small molecules using explicit and implicit solvent model. Journal of Chemical Theory and Computation. 2009;5(4):919–930. doi: 10.1021/ct800445x. DOI: 10.1021/ct800445x. [DOI] [PubMed] [Google Scholar]
- Shivakumar D, Williams J, Wu Y, Damm W, Shelley J, Sherman W. Prediction of absolute solvation free energies using molecular dynamics free energy perturbation and the OPLS force field. Journal of Chemical Theory and Computation. 2010;6(5):1509–1519. doi: 10.1021/ct900587b. DOI: 10.1021/ct900587b. [DOI] [PubMed] [Google Scholar]
- Shivakumar D, Harder E, Damm W, Friesner RA, Sherman W. Improving the prediction of absolute solvation free energies using the next generation OPLS force field. Journal of Chemical Theory and Computation. 2012;8(8):2553–2558. doi: 10.1021/ct300203w. DOI: 10.1021/ct300203w. [DOI] [PubMed] [Google Scholar]
- Sulea T, Purisima EO. Predicting hydration free energies of polychlorinated aromatic compounds from the SAMPL-3 data set with FiSH and LIE models. J. Comput. Aided Mol. Des. 2012;26(5):661–667. doi: 10.1007/s10822-011-9522-1. DOI: 10.1007/s10822-011-9522-1. [DOI] [PubMed] [Google Scholar]
- Szejtli J. Introduction and general overview of cyclodextrin chemistry. Chem. Rev. 1998;98(5):1743–1754. doi: 10.1021/cr970022c. [DOI] [PubMed] [Google Scholar]
- Taulier N, Chalikian TV. Hydrophobic hydration in cyclodextrin complexation. J. Phys. Chem. B. 2006;110(25):12222–12224. doi: 10.1021/jp062467n. DOI: 10.1021/jp062467n. [DOI] [PubMed] [Google Scholar]
- Thanki N, Thornton JM, Goodfellow JM. Distributions of water around amino acid residues in proteins. J. Mol. Biol. 1988;202(3):637–657. doi: 10.1016/0022-2836(88)90292-6. [DOI] [PubMed] [Google Scholar]
- Tiefenbrunn T, Forli S, Baksh MM, Chang MW, Happer M, Lin YC, Perryman AL, Rhee JK, Torbett BE, Olson AJ, Elder JH, Finn MG, Stout CD. Small molecule regulation of protein conformation by binding in the flap of HIV protease. ACS Chem. Biol. 2013;8(6):1223–1231. doi: 10.1021/cb300611p. DOI: 10.1021/cb300611p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wickstrom L, He P, Gallicchio E, Levy RM. Large scale affinity calculations of cyclodextrin host–guest complexes: understanding the role of reorganization in the molecular recognition process. Journal of Chemical Theory and Computation. 2013;9(7):3136–3150. doi: 10.1021/ct400003r. DOI: 10.1021/ct400003r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young T, Abel R, Kim B, Berne BJ, Friesner RA. Motifs for molecular recognition exploiting hydrophobic enclosure in protein–ligand binding. Proc. Natl. Acad. Sci. 2007;104(3):808–813. doi: 10.1073/pnas.0610202104. DOI: 10.1073/pnas.0610202104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, Rick SW. Free energies and entropies of water molecules at the inhibitor–protein interface of DNA gyrase. J. Am. Chem. Soc. 2009;131(18):6608–6613. doi: 10.1021/ja809696s. DOI: 10.1021/ja809696s. [DOI] [PubMed] [Google Scholar]
- Zhou Baojing, Agarwal M, Wong CF. Variable atomic radii for continuum-solvent electrostatics calculation. J. Chem. Phys. 2008;129(1):014509. doi: 10.1063/1.2949821. DOI: 10.1063/1.2949821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu K, Shirts MR, Friesner RA. Improved methods for side chain and loop predictions via the protein local optimization program: variable dielectric model for implicitly improving the treatment of polarization effects. Journal of Chemical Theory and Computation. 2007;3(6):2108–2119. doi: 10.1021/ct700166f. DOI: 10.1021/ct700166f. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.