R₁ Correction in Amide Proton Transfer Imaging: Indication of the Influence of Transcytolemmal Water Exchange on CEST measurements

Abstract

Amide proton transfer (APT) imaging may potentially detect mobile proteins/peptides non-invasively in vivo, but its specificity may be reduced by contamination from other confounding effects such as asymmetry of non-specific magnetization transfer (MT) effects and spin-lattice relaxation with rate R₁ (=1/T₁). Previously reported spillover, MT and R₁ correction methods were based on a two-pool model, in which the existence of multiple water compartments with heterogeneous relaxation properties in real tissues was ignored. Such simple models may not adequately represent real tissues and thus such corrections may be unreliable. The current study investigated the effectiveness and accuracy of correcting for R₁ in APT imaging via simulations and in vivo experiments using tumor-bearing rats subjected to serial injections of Gd-DTPA that produced different tissue R₁ values in regions of blood-brain-barrier breakdown. The results suggest that conventional measurements of APT contrast (such as APT* and MTR_asym) may be significantly contaminated by R₁ variations, while the R₁-corrected metric AREX* was found to be relatively unaffected by R₁ changes over a broad range (0.4 – 1 Hz). Our results confirm the importance of correcting for spin-lattice relaxation effects in quantitative APT imaging, and demonstrate the reliability of using the observed tissue R₁ for corrections to obtain more specific and accurate measurements of APT contrast in vivo. The results also indicate that, due to relatively fast transcytolemmal water exchange, the influence of intra- and extracellular water compartments on CEST measurements with seconds long saturation time may be ignored in tumors.

Graphical Abstract

The influence of multiple water compartments and heterogeneous relaxation on APT imaging in real tissues was investigated with simulations and in vivo experiments with serial Gd-DTPA injections. The results confirm that the spin-lattice relaxation rate R₁ significantly confounds conventional APT measures; and suggest that the R₁-corrected AREX metrics based on the 1/Z method is an appropriate means to remove the influences of spin-lattice relaxation on APT measurements.

Introduction

Chemical exchange saturation transfer (CEST) imaging can measure the concentrations of relatively small solutes indirectly by detecting the attenuation of water signals induced by chemical exchange (1,2). Compared with direct MR measurements (e.g. using high resolution magnetic resonance spectroscopy) of pools of solute protons at low concentrations (typically millimolar or lower) in biological tissues, the detection of changes in the background water signal caused by saturation transfer significantly enhances the sensitivity (by up to 500,000 (3)) for detecting low levels of exchanging compounds. Thus CEST provides an attractive means to image distributions of molecules such as peptides and metabolites with potentially higher signal-to-noise ratios and higher spatial resolutions. During CEST experiments, saturated water signals (M_sat(Δω)) are usually acquired over a range of irradiation offset frequencies (Δω) around the water resonance and normalized by the corresponding unsaturated water signal M₀. The Z-spectrum (Z(Δω) = M_sat (Δω)/M₀) is then used to quantify the CEST contrast at different offsets. Amide proton transfer (APT), a specific form of CEST at Δω = 3.6 ppm relative to water, has been suggested as a surrogate biomarker of endogenous mobile proteins and peptides as well as a pH-dependent indicator of amide proton exchange rates in biological tissues. APT has been widely implemented for characterizing abnormal tissues such as tumors (3–6) and stroke (7–10).

Unfortunately, APT imaging in practice may be significantly influenced by factors other than chemical exchange, including effects caused by B₀ inhomogeneities, non-specific magnetization transfer (MT) and asymmetric MT effects, water longitudinal relaxation rate (R₁), and direct water saturation (RF spillover). Several approaches have been developed to reduce these confounding effects. For example, the WASSR method corrects for spatial B₀ field variations (11). The magnetization transfer asymmetry (MTR_asym) metric corrects for direct water saturation by subtracting the signals acquired with irradiation on the solute of interest (the label scan) from those on the corresponding other side of water (the reference scan). However, in most biological tissues the background MT effects are themselves asymmetric, and nuclear Overhauser effects (NOE) also can contribute, so that MTR_asym is still influenced by processes that are not specific for chemical exchange of amides. These significantly reduce the specificity and quantitative accuracy of APT for detecting and measuring mobile proteins/peptides, and complicate the interpretation of APT data. Furthermore, MTR_asym makes no correction for R₁ contributions.

Several refinements have been proposed to further reduce the effects of asymmetric MT (12–16). For example, Jin et al. proposed to exploit the wide spectral separation available at high field strength (e.g. 9.4T) and interpolate measurements made at three offset frequencies to better approximate APT, denoted as APT* (16). Different acquisition strategies, such as the SAFARI (13), CERT (17), and VDMP-CEST (15), have also been developed to eliminate some confounding effects. However, these methods (like MTR_asym) do not incorporate a correction for R₁ effects on CEST measurements. Recently, Zaiss et al. analyzed the behaviors of CEST measurements and developed a reciprocal Z-spectrum analysis (denoted as the 1/Z method) to eliminate RF spillover and MT effects (18–20). Moreover, this analysis indicates a simple way that the influence of R₁ on APT measurements can be eliminated. By combining the three-offset and the 1/Z methods, a new metric AREX* (apparent exchange dependent relaxation), can be obtained, which is an exchange rate-weighted APT contrast with much reduced influence from other confounding effects. This method has been successfully implemented to characterize brain cancer in rats (21) and humans (22), and stroke in rats (19,23), resulting in very different estimates of APT effects compared with more conventional methods such as MTR_asym and APT*. These results suggest strongly that the influence of R₁ plays an important role in estimates of APT contrast.

Like most other CEST models, the 1/Z analysis was originally developed based on a simple two-pool (water and amide protons) model, in which a single, measured average R₁ of water is used in corrections (19,21,23,24). Although a recent study extended the 1/Z method to a three-pool model to include the semi-solid MT pool (25), the complex arrangement of multiple water pools in real biological tissues is still not considered. It is well known that water may exist in multiple compartments such as intra- and extracellular spaces, and the relaxation properties in each compartment are likely different from each other. Moreover, not all pools necessarily have large numbers of exchanging protons, so the assumption of a single relaxation rate to represent all pools may introduce inaccuracies, especially if the water compartment fractions and relaxation rates change in pathologies such as stroke (26). There are therefore reasons to question whether R₁ correction approaches based on simple two-pool models are appropriate, and whether they can introduce extra uncertainty into estimates of APT effects.

In principle, the potentially confounding influences of water compartmentation and heterogeneous relaxation in real tissues on APT measurements may be significantly reduced if transcytolemmal water exchange occurs rapidly compared with the long (several seconds) duration of the saturation phase. For example, the apparent mean lifetime of intracellular water has been reported as 625 ± 43 ms in frontal human white matter and 344.8 ± 95.1 ms in human solid brain tumors (27). Moreover, the apparent mean lifetime of intracellular water in tumors can decrease further to 147 ± 84 ms during apoptosis (28). For a comparison, the total duration of saturation pulse(s) is on the order of several seconds, at least several times larger than the typical intracellular water lifetime. If the water molecules inside tissues can diffuse long enough so that they are well mixed at the end of the saturation phase, all the distinct water compartments can be approximated as a single mixed one, and hence a single water relaxation rate may be sufficient to describe all water molecules in the APT models. If true, this can simplify the analysis of APT data from real biological tissues, and the previously reported R₁ correction methods based on two-pool models can be applied in clinical practice.

Unfortunately, the influences of multiple water pools, heterogeneous relaxation and transcytolemmal water exchange on CEST measurements have not previously been fully investigated. Therefore in this study computer simulations and measurements in vivo were performed to evaluate such effects. Specifically, a more general four-pool model consisting of intracellular water, extracellular water, exchanging protons and an MT pool, was examined using computer simulations. Furthermore, the hypothesis of relaxation influence and compensation was directly tested in vivo: tumor-bearing rats with regions of blood-brain-barrier breakdown received serial injections of Gd-DTPA while measuring CEST signals. By such a means, the extracellular water relaxation rate was selectively altered as tracked by R₁ mapping, and hence the effectiveness and accuracy of R₁ corrections were investigated. In addition to the R₁-corrected AREX contrast, the conventional MTR_asym and APT* metrics were also calculated and compared to quantify the influence of R₁ variations on APT contrast.

Methods

Quantification of APT

For the simple two-pool (water and amide protons) model, the CEST effect is defined as a function of two Z-spectral values: the label scan Z_lab=M_lab/M₀, acquired at the amide proton frequency (3.6 ppm in biological tissues) and a reference scan Z_ref that has no contribution of amide. The conventional MTR_asym uses the opposite frequency as a reference scan Z_ref=Z(−3.6 ppm), acquired at the amide proton frequency (3,16), namely

$${\text{MTR}}_{\text{asym}}(\text{APT})=Z_{\mathit{ref}}-Z_{\mathit{lab}}=Z(-3.6\text{ppm})-Z(3.6\text{ppm}).$$ [1]

However, Z(−3.6 ppm) is contaminated by asymmetric MT and NOE effects in biological tissues. Jin et al. (2013) found that Z values at 3.0 and 4.2 ppm of rodent brain tissues on 9.4T appeared to have minimal APT saturation effect, and hence defined the apparent APT contrast APT* using the three-offset method as

$$\text{APT}\ast =Z_{\mathit{ref}}^{\ast }-Z_{\mathit{lab}}=\frac{Z(3.0\text{ppm})-Z(4.2\text{ppm})}{2}-Z(3.6\text{ppm}).$$ [2]

Zaiss et al. defined the apparent exchange-dependent relaxation (AREX) using the 1/Z analysis as (19)

$$\text{AREX}(\text{APT})=\left(\frac{1}{Z_{\mathit{lab}}}-\frac{1}{Z_{\mathit{ref}}}\right)\times R_1=\left(\frac{1}{Z(3.6\text{ppm})}-\frac{1}{Z(-3.6\text{ppm})}\right)\times R_1.$$ [3]

However, Eq.[3] was derived based on a simple two-pool model without the consideration of other confounding effects, e.g. asymmetric MT and NOE, which may play an important role in biological tissues. Specifically, Z_ref(−3.6 ppm) may suffer the contaminations from these effects and may bias the estimation of AREX(APT). To reduce these contaminations, we previously proposed to use $Z_{\mathit{ref}}^{\ast }$ in the three-offset method to replace Z_ref and obtained (21,23)

$$\text{AREX}\ast (\text{APT})=\left(\frac{1}{Z_{\mathit{lab}}}-\frac{1}{Z_{\mathit{ref}}^{\ast }}\right)\times R_1=\left(\frac{1}{Z(3.6\text{ppm})}-\frac{1}{Z(3.0\text{ppm})+Z(4.2\text{ppm})}\right)\times R_1.$$ [4]

The detailed derivations of Eq.[3] and [4] have been reported before (19,20,25), and were already applied in previous studies (19,21,23,29). The quantity AREX* corrects for spillover, R₁ and asymmetric MT effects, and hence should provide an exchange rate-weighted APT measurement relatively free of other influences (21). Note that, in principle, the AREX method is independent on how the reference value is obtained.

Numerical simulations

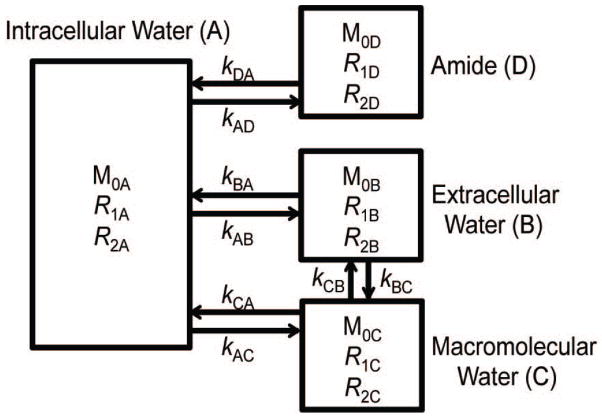
Numerical simulations based on a four-pool model were performed by solving Bloch-McConnell equations using in-house scripts written in Matlab (Mathworks, Natick, MA). The four pools were denoted as intracellular water (“A”), extracellular water (“B”), macromolecular MT (“C”), and amide (“D”) protons. Proton exchange was allowed between any two pools except that the amide (“D”) pool could only exchange with intracellular water “A”. Note that a separate work found that distinct macromolecular pools exchanging with the intra and extra cellular water pools were not necessary when fitting qMT data with rapid transcytolemmal exchange (30). Hence, we use only one macromolecular pool here. The schematic diagram with corresponding exchange rate constants is illustrated in Figure 1. The parameters used in the simulations were (7,31): M_0A = 0.6888, R_1A = 0.4 s⁻¹, R_2A = 20 s⁻¹, M_0B = 0.25, R_2B = 20 s⁻¹, M_0C = 0.06, R_1C = 1 s⁻¹, R_2C = 10⁵ s⁻¹, M_0D = 0.0012, R_1D = 1 s⁻¹, R_2D = 66.67 s⁻¹, and the extracellular water R_1B varied from 0.3 to 3.3 s⁻¹ to mimic the contrast agent induced R₁ variations 0.4 – 1 Hz observed in the experiments in vivo (see Figure 6). Other parameters were: amide water exchange rate constant k_DA = 30 s⁻¹, macromolecular water exchange rate constant k_CA = k_CB = 20 s⁻¹, transcytolemmal water exchange rate constant k_AB = 0, 1, 2, 4, or 6 s⁻¹. The observed R₁ of the whole system was simulated with a selective inversion recovery (SIR) method as described previously (31–33). MTR_asym, APT*, and AREX* were simulated and calculated according to Eqs. [1], [3] and [4]. The MR sequence parameters (TR, TE, RF duration and power) were the same as those used in the in vivo experiments (see below).

Figure 1.

Schematic diagram of a four-pool model comprised of intracellular water (A), extracellular water (B), macromolecular water (C), and amide proton (D) pools. Arrows indicate possible magnetization exchanges between pools.

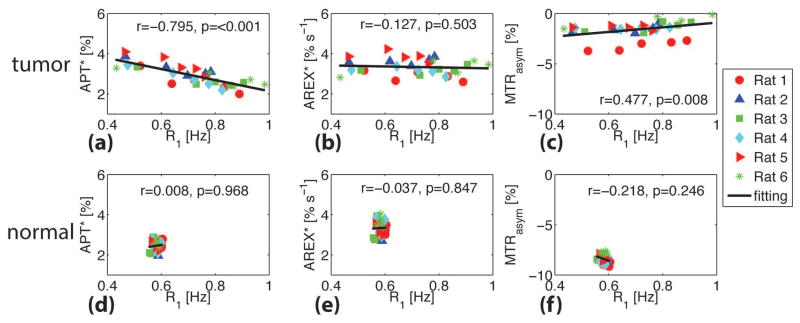
Figure 6.

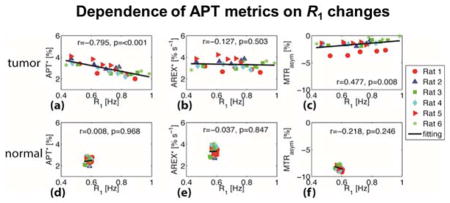
Correlations of tumor APT* (a), AREX* (b), and MTR_asym (c) with R₁ for six rats. The corresponding correlations for the contralateral normal brain tissues are shown in (d), (e), and (f). The Spearman’s coefficient r and p values are provided for each correlation. The full lines represent the linear regression of all data points in each subfigure.

MR imaging of animals

All animal-related procedures were approved by the Institutional Animal Care and Use Committee at Vanderbilt University. Six male Fisher 344 rats (280–310 g) bearing 9L brain tumors were scanned. MR images were acquired on a 9.4T Varian 21-cm-bore horizontal imaging system with a 38-mm RF volume coil for both transmission and reception. During MRI experiments, the rat rectal temperature was maintained at around 37 °C using a warm-air feedback system.

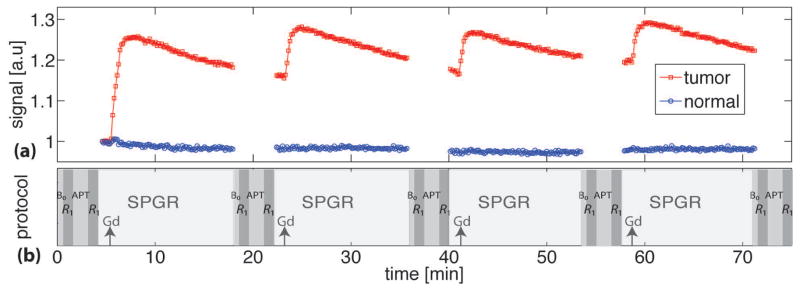
Figure 2b shows the in vivo experimental protocol of the current study. The intravenous injections of Gd-DTPA (0.083 mmol kg⁻¹) were repeated four times to obtain five (including the baseline) different accumulated Gd-DTPA concentrations as well as five different R₁ values. The measurements of B₀ field map, R₁, APT, and spoiled-gradient echo (SPGR) signals were interleaved and repeated five times to obtain multiple MR parametric maps with five different R₁’s. To assist determining the delay time between each Gd-DTPA injection and each APT measurement, the SPGR sequence was used starting from 1 minute before through 13 minutes after each Gd-DTPA injection to monitor the time course of R₁ variations caused by Gd-DTPA. Figure 2a shows the SPGR signals of the tumor (red squares) and contralateral normal brain tissue (blue circles) from a representative rat. The SPGR signals reached a relatively flat plateau after 13 minutes of Gd-DTPA injections, indicating R₁ was relatively stable after that time. Therefore, except for the baseline, all the acquisitions of multiple MR parametric maps were performed after 13 minutes of each Gd-DTPA injection. By such a means, the rapid variations of R₁ were avoided during all APT measurements. Furthermore, to quantify the R₁ changes, two R₁ maps were acquired before and after each repeated APT measurement, respectively, and hence the percentage R₁ variation δR₁ (δR₁%= 200•|R_1before−R_1after|/|R_1before+R_1after|) can be obtained showing the percentage R₁ change during each APT measurement. In order to monitor possible B₀ shifts during the whole experiments, a B₀ map was acquired before each of the five APT measurements.

Figure 2.

(a) The time course of spoiled-gradient echo (SPGR) signals of a tumor (red squares) and contralateral normal brain tissue (blue circles) from a representative rat. (b) Schematic diagram of the data acquisition protocol. The acquisitions of B₀, R₁, APT, R₁, and SPGR signals were interleaved and repeated five times. The black arrows indicate the time when Gd-DTPA was injected.

Specifically, B₀ field maps were reconstructed from four complex gradient echo images with TE = 3, 5, 7, and 9 ms. R₁ was mapped using a seven-point selective inversion recovery sequence specifically optimized for cancer imaging(30). APT measurements were acquired with 5-sec cw saturation pulses with B₁ = 1 μT. Five frequency offsets (300, 4.2, 3.6, 3, −3.6 ppm) were acquired in each APT measurement. Note that B₀ variations were monitored during experiments (see Figure 4). R₁ and APT images were acquired on a single slice of 2 mm thickness using a single-shot spin-echo echo-planar imaging (EPI) sequence (FOV = 32 × 32 mm²; matrix size = 64 × 64). After the pixel-wise mapping of B₀, R₁, MTR_asym, APT*, and AREX*, quantitative analyses were performed on regions of interest (ROIs) of the tumors and the corresponding contralateral normal tissues.

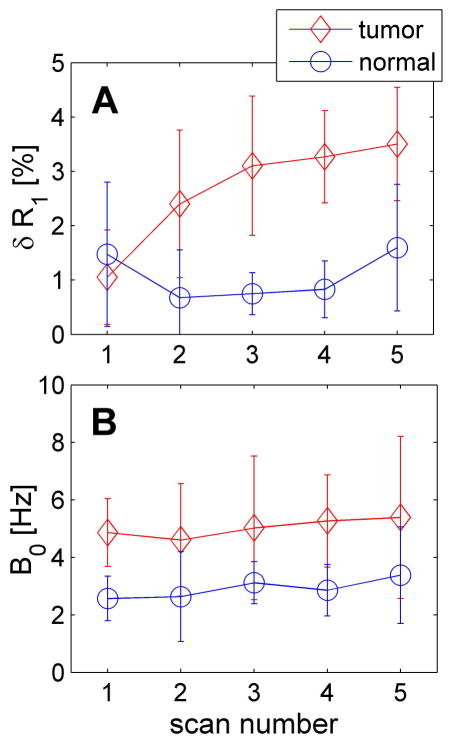
Figure 4.

The δR₁ variation between before and after each repeated APT measurement (A) and B₀ field shift at the starting point of each APT measurement (B). Scan number represents the repeated scans, and scan 1 represents the baseline acquisition.

Results

Numerical simulations

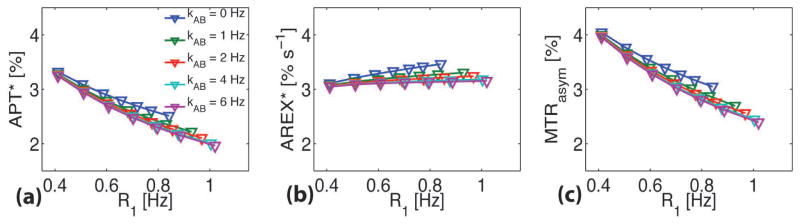
Figure 3 shows the simulated dependence of MTR_asym, APT* and AREX* on the average R₁ for the four-pool model. The change of R₁ was achieved via adjusting R_1b of the extracellular water only, mimicking the effects of injections of Gd-DTPA. The transcytolemmal water exchange rate constant k_AA was allowed to vary from 0 to 6 Hz, with corresponding intracellular water lifetime from infinity to 167 ms. MTR_asym and APT* were very dependent on R₁ at all values of k_AB e.g. ~ 41% change when R₁ changed from 0.4 to 1 Hz. The values from both methods are highly affected by R₁ no matter how fast the transcytolemmal water exchange. By contrast, although the R₁-corrected AREX* showed slight variations (~ 10%) when k_AB < 2 Hz, it became relatively independent of R₁ (< 5%) over a broad range of R₁ values from 0.4 to 1.2 Hz when transcytolemmal water exchange was faster (k_AB > 2 Hz). This suggests that R₁ effects can be eliminated in R₁-corrected AREX* if k_AB is fast enough. Even if k_AB is relatively slow (< 2 Hz), the R₁ effects are still small (~ 10%) in AREX*. In contrast, both MTR_asym and APT* are significantly influenced (~ 40%) by R₁ effects even with large k_AB values.

Figure 3.

Simulated dependence of MTR_asym (a), APT* (b), and R₁-corrected AREX* (c) on R₁ with different transcytolemmal water exchange rate constants k_AB.

In vivo MRI experiments

Figure 4 shows the δR₁ variation and B₀ field shift during the MRI scans of a representative animal. Recall that δR₁ is the percentage change of R₁ before and after each of the five APT measurements. Although δR₁ of the tumors increased slightly with the accumulation of injected Gd-DTPA, simulations indicated that the variations of APT* < 1% and the variations of MTR_asym < 5 % for δR₁ < 3.5% (data not shown). Thus the variations of R₁ that occurred during each APT measurement were ignored in the current study. Figure 4B shows that the ΔB₀ was constant in both tumors and contralateral normal tissues throughout the whole experiments. Therefore, the B₀ field shift was not considered in the data analyses of the current study since the maximum B₀ shift was only ~ 5 Hz (0.0125 ppm) in the regions of interest.

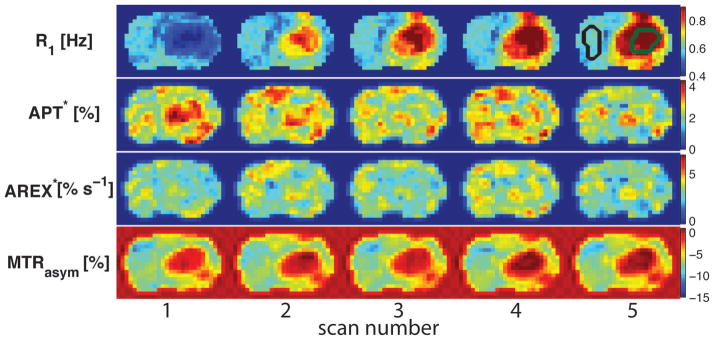
Figure 5 shows the multi-parametric maps of a representative rat brain for each of the dynamic scans. The R₁ maps confirm that the injections of Gd-DTPA affected the tumors only, as expected. The 5^th R₁ map (upper-right) shows the ROIs manually selected on the tumor (green) and contralateral normal tissues (black). Consistent with the numerical simulations (see above), APT* values were lower in tumors after the Gd-DTPA injections. By contrast, MTR_asym in tumors increased gradually with Gd-DTPA injections, which is different from the predicted results that MTR_asym should decrease with higher R₁ values. This discrepancy may be due to other effects such as the presence of NOE contributions. The R₁-corrected AREX* was constant throughout all scans, indicating it was independent on the R₁ variations caused by the Gd-DTPA injections.

Figure 5.

Temporal evolution of R₁, APT*, AREX*, and MTR_asym maps acquired from a representative rat before and after Gd-DTPA injections. The 5^th R₁ map shows the ROIs of the tumor (green) and contralateral normal tissues (black) used in the data analysis.

Figure 6 summarizes the correlations between APT measures (APT*, AREX*, and MTR_asym) and R₁ obtained in vivo. For the tumors, APT* appears to be significantly inversely correlated with R₁ (Spearman’s correlation r = −0.795 and p < 0.001), but R₁-corrected AREX* showed no significant correlation with R₁ (p = 0.503). Note also that, consistent with previous reports (21), R₁-corrected AREX* in tumors (3.34 ± 0.40 % s⁻¹) is closely similar to that in normal tissues (3.33 ± 0.35 % s⁻¹). Although MTR_asym showed a slightly positive correlation with R₁ (r = 0.477), which is different from the stronger positive correlations predicted by the simulations, the dependence of MTR_asym on R₁ is clear (p = 0.008). The predicted decrease of MTR_asym with increasing R₁ agrees with previous simulations based on a simple two-pool model (water and amide) (34), but is at variance with the experimental results found here. This may be due to the influence of NOE effects that were not considered in the simulations or to differences between the parameter values used in the simulations and the actual values present in vivo. Nevertheless, these results confirm again that MTR_asym and APT* are significantly affected by R₁ values, and hence their accuracy for quantifying mobile proteins/peptides is compromised. By contrast, R₁-corrected AREX* is immune to the large variations of R₁ (from 0.4 to 1.0 Hz) in real tissues in which multiple water compartments exist. This suggests that R₁-corrected AREX* is a more reliable indicator of levels of mobile proteins/peptides compared with other APT methods. For reference, the correlations of APT values with R₁ in contralateral normal tissues are also provided in Figure 6.

Discussion

In order to obtain reliable measurements of APT, it is necessary to remove or correct for possible influences other than chemical exchange with amides in mobile peptides and proteins. Effects such as the presence of asymmetric MT, variations in R₁, RF spillover, and NOEs can reduce the accuracy and specificity of APT in practice, and lessen its value as a molecular imaging technique. For example, any detected APT changes without corrections for confounding effects could be due to changes in R₁, MT, amide proton concentrations or combinations of these effects. This will increase the difficulty to interpret APT data and hinder its application in practice. We have previously proposed to use AREX* to correct other confounding effects and achieved a relatively “clean” exchange-rate-dependent metric. However, previous studies using AREX* are all based a simple two-pool model and the accuracy used in biological tissues with multiple physical compartments have not been fully investigated before. The current study aimed to evaluate whether the existence of multiple water compartments in real tissues with heterogeneous relaxation rates could affect the measurements of APT by different methods. The results suggest that both conventional magnetization transfer asymmetry MTR_asym and the three-offset APT* methods may be strongly affected by values of R₁, while R₁-corrected AREX* is independent of R₁ over a broad physiologically relevant range (0.4 – 1.0 Hz). This indicates that R₁ significantly confounds conventional APT measures; and the R₁-corrected AREX metrics based on the 1/Z method is an appropriate means to remove R₁ influences on APT measurements.

Note that after a single bolus injection of Gd-DTPA, tumor R₁ could change significantly during the wash-in and wash-out processes. However, such a R₁ change is relatively too fast for APT measurements especially in the first ~ 10 minutes after an injection. Note that although R₁ values were very different between different APT measurements in the current study, R₁ should be relatively stable during the acquisition of each APT measurement. Otherwise, the different R₁ weighting e.g. at control and label scans may cause a significant biased estimation of APT. The same strategy has been used to map water exchange rates using multiple bolus injections of contrast agents (35). Therefore, APT measurements were performed only when R₁ changes reached a relatively flat plateau (after 13 minutes) in the current study. Moreover, R₁ mapping was performed immediately before and after each APT measurement in order to confirm a relatively stable R₁ change during each APT measurement. Our simulations showed that the variations of APT* < 1% and the variations of MTR_asym < 5 % for δR₁ < 3.5% during each APT measurement.

A smaller value of R₁ implies a slower recovery from saturation, which should result in a larger value of MTR_asym (34). However, the observed MTR_asym in tumors showed a slight increase with increase of R₁. In biological tissues, MTR_asym may also be strongly affected by asymmetric MT and NOE effects. MTR_asym can be approximated as ≈ APTR – NOER, where APTR is the proton transfer ratio for the amide protons, and NOER is the NOE-based MT ratio (36). Both APTR and NOER should decrease with increasing R₁, but the slight increase of MTR_asym with R₁ may suggest a stronger dependence of NOER on R₁ than APTR. In addition, the variation of R₁ during the acquisitions of APT images can also slightly bias the dependence of MTR_asym on R₁ (~5% shown in simulations). A different study also observed that MTR_asym changed significantly after Gd administration to patients who were to undergo carotid endarterectomy (37). This suggests that MTR_asym is not a reliable measure of mobile proteins/peptides and may be significantly affected by variations in R₁.

The apparent dependence of APT* and independence of AREX* on R₁ demonstrates the importance of R₁ corrections for interpreting APT changes. In our previous studies, it was shown that corrections for RF spillover, MT and R₁ effects contributed differently in tumors (21) and stroke (23). APT* in tumors was higher than that in normal tissues, while R₁-corrected AREX* was similar in tumors and normal tissues (21), which was consistent with an independent study using a different approach (38). However, R₁-corrected AREX* showed a more pronounced contrast between ischemic and normal brain than APT* (23). Thus R₁ corrections may strongly affect inferences about changes within tissues in pathological conditions. Note that although AREX* significantly reduces the contrast between brain tumors and normal brain tissues, it provides unique information on mobile proteins/peptides that are not achievable by other conventional MRI methods. Moreover, considering the potentially strong influence of other variables on APT measurements, other MR parameters (R₁, R₂, quantitative MT (e.g. the pool size ratio of macromolecular vs water protons) should be measured to avoid misinterpretation of APT variations.

The amide proton pool is usually believed to be mainly within the intracellular space (7), so in our simulations we considered amide proton transfer only between amide protons and intracellular water. However, the situation when both intra- and extracellular water protons exchange with amide protons has also been simulated, and the conclusion is qualitatively the same (specific data not shown): APT* and MTR_asym would decrease with increasing R₁, but AREX* stays almost constant.

Both simulations and experiments show that R₁-corrected AREX* is independent of R₁. The intracellular exchange lifetime is much shorter than the total duration of saturation pulse(s) used in APT imaging (e.g. 5 sec in the current study). The integrated water signal from all compartments may then be approximately regarded as from a single water pool. Therefore, though Gd-DTPA selectively alters the extracellular water R₁, the overall observed R₁ is still suitable for R₁ correction of APT imaging in biological tissues. Note that this conclusion may also hold for other exchange sites, e.g. amine. Therefore, under the circumstances when intracellular water life time is much shorter than the total duration of saturation pulse(s), i.e. fast transcytolemmal water exchange rate, the influences of different water compartmentation (i.e. intra- and extracellular spaces) and relaxation properties can be ignored because all water molecules can be considered well-mixed at the end of saturation pulse(s). This may assist better data interpretation of not only APT but also other types of CEST measurements.

The present work not only represents a verification of the proposed relaxation-compensated features of the APT evaluation method AREX*, but also has practical implications. Gadolinium-based contrast agents have been widely used in clinical MRI. However, due to its strong influence on R₁ relaxation, CEST measurements were not recommended with gadolinium injections (37). The current study shows that R₁-corrected AREX* can compensate the influences caused by variations in R₁ relaxation, and hence can be measured anytime including after the gadolinium injections. This can not only increase the accuracy of APT imaging when contrast agent is present, but also increase the management flexibility of patient imaging in clinical practice.

Conclusion

The effectiveness and accuracy of R₁ correction in APT imaging has been investigated via simulations and in vivo experiments. The time courses of APT*, MTR_asym, and AREX* were measured in tumors following serial injections of Gd-DTPA to result in different R₁ values. Different from conventional APT* and MTR_asym contrasts, R₁-corrected AREX* was found independent of R₁ changes. This study establishes the importance of R₁ corrections for accurate APT imaging, and confirmed the reliability of using the overall observed tissue R₁ for R₁-correction in vivo. Our results suggest an appropriate means to correct for R₁ and MT effects in CEST imaging, and may also assist in better understanding the contrast mechanisms of CEST imaging in biological tissues.

Abbreviations

APT

amide proton transfer

MTR_asym

magnetization transfer ratio obtained using asymmetric analysis

APT*

amide proton transfer obtained using the three-offset method

AREX

apparent exchange dependent relaxation obtained using the 1/Z method

AREX*

AREX obtained using the 1/Z method and three-offset method

k_AB

transcytolemmal exchange rate from intra- to extracellular spaces

Appendix

The detailed description of the four-pool model (see Figure 1) and parameters were presented in the text. The corresponding modified Bloch-Mcconnell equations including the transcytolemmal exchange between the intracellular and extra cellular compartments can be expressed as

$$\frac{d}{dt}\left[\begin{array}{c}{M}_{xA}\\ M_{yA}\\ M_{zA}\\ M_{zC}\\ M_{xB}\\ M_{yB}\\ M_{zB}\\ M_{xD}\\ M_{yD}\\ M_{zD}\end{array}\right]=\left[\begin{array}{cccccccccc}-r_{2A}& -\mathrm{\Delta }\omega & 0& 0& k_{BA}& 0& 0& k_{DA}& 0& 0\\ \mathrm{\Delta }\omega & -r_{2A}& {\omega }_1& 0& 0& k_{BA}& 0& 0& k_{DA}& 0\\ 0& -{\omega }_1& -r_{1A}& k_{CA}& 0& 0& k_{BA}& 0& 0& k_{DA}\\ 0& 0& k_{AC}& -r_{1C}& 0& 0& 0& 0& 0& 0\\ k_{AB}& 0& 0& 0& -r_{2B}& -\mathrm{\Delta }\omega & 0& 0& 0& 0\\ 0& k_{AB}& 0& 0& \mathrm{\Delta }\omega & -r_{2B}& 0& 0& 0& 0\\ 0& 0& k_{AB}& 0& 0& 0& -r_{1B}& 0& 0& 0\\ k_{AD}& 0& 0& 0& 0& 0& 0& -r_{2D}& -\mathrm{\Delta }\omega & 0\\ 0& k_{AD}& 0& 0& 0& 0& 0& \mathrm{\Delta }\omega & -r_{2D}& 0\\ 0& 0& k_{AD}& 0& 0& 0& 0& 0& 0& -r_{1D}\end{array}\right]+\left[\begin{array}{c}0\\ 0\\ R_{1A}{M}_{0A}\\ R_{1C}{M}_{0C}\\ 0\\ 0\\ R_{1B}{M}_{0B}\\ 0\\ 0\\ R_{1D}{M}_{0D}\end{array}\right]$$ [S1]

where r_2A = R_2A + k_AB + k_AD, r_1A = R_1A + k_AB + k_AC + k_AD, r_1C = R_1C + k_CA + R_RFB,C, r_2B = R_2B + k_BA, r_1B = R_1B + k_BA, r_2D = R_2D + k_DA, r_1D = R_1D + k_DA, where $R_{\mathit{RFB}}=\pi {\omega }_1^{2}g(2\pi \mathrm{\Delta })$ is the saturation rate of the macromolecular pool, and g is the super-Lorentzian lineshape (39)

$$g(2\pi \mathrm{\Delta })=\sqrt{\frac{2}{\pi }}{T}_{2B}{\int }_0^1\frac{1}{\left|3u^2-1\right|}{e}^{-{\left(\frac{2\pi \mathrm{\Delta }{T}_{2B}}{3u^2-1}\right)}^2}du$$ [S2]

where T_2B is the transverse relaxation time of the macromolecular protons, Δ is the frequency offset. Note that only continuous-wave APT experiments were considered in the current study, so that Eq.[S1] was directly adopted and matrix operations were performed to simulate the signals. All simulations were based on in-house written scripts with Matlab (Mathworks, Natick, MA). It took ~ 4 sec on an i5-3210M 2.5GHz processor to complete one set of simulations (i.e. 4 k_AB values, 14 R₁ values, and 121 frequency offsets).