Fast macromolecular proton fraction mapping of the human liver in vivo for quantitative assessment of hepatic fibrosis

Abstract

Macromolecular proton fraction (MPF) is a quantitative MRI parameter determining the magnetization transfer (MT) effect in tissues and defined as a relative amount of immobile macromolecular protons involved into magnetization exchange with mobile water protons. MPF has a potential for quantitative assessment of fibrous tissue due to intrinsically high MPF specific for collagen. The goal of this study was to investigate a relationship between histologically determined fibrosis stage and MPF in the liver parenchyma measured using a recently developed fast single-point clinically-targeted MPF mapping method. Optimal saturation parameters for single-point liver MPF measurements were determined from the analysis of liver Z-spectra in vivo based on the error propagation model. Sixteen patients with chronic hepatitis C viral infection underwent 3T MRI using an optimized liver MPF mapping protocol. Fourteen patients had prior liver biopsy with histologically staged fibrosis (METAVIR scores F0-F3), and two patients had clinically diagnosed cirrhosis (score F4 was assigned). The protocol included four breath-hold three-dimensional scans with 2×3×6 mm³ resolution and 10 transverse sections: 1) dynamic acquisition of MT-weighted and reference images; 2) dynamic acquisition of three images for variable flip angle T1 mapping; 3) dual-echo B0 map; and 4) actual flip-angle imaging B1 map. Average liver MPF was determined as the mode of MPF histograms. MPF was significantly increased in patients with clinically significant fibrosis (scores F2-F4, n=6) compared to patients with no or mild fibrosis (scores F0-F1, n=10): 6.49±0.36% vs. 5.94±0.26%, P<0.01 (Mann-Whitney test). MPF and fibrosis score were strongly positively correlated with the Spearman's rank correlation coefficient 0.80 (P<0.001). This study demonstrates the feasibility of fast MPF mapping of the human liver in vivo and confirms the hypothesis that MPF is increased in hepatic fibrosis and associated with fibrosis stage. MPF may be useful as a non-invasive imaging biomarker of hepatic fibrosis.

Introduction

Hepatic fibrosis is a widespread pathological condition, which develops as a response to most chronic liver diseases, including alcoholic liver disease, viral hepatitis B and C, nonalcoholic steatohepatitis, and autoimmune liver disease (1). Fibrotic changes in the liver are characterized by the excessive production of collagen-rich connective tissue within the extracellular matrix and result in gradual deterioration of the organ function, which may progress to cirrhosis and liver failure. Currently, histological assessment of a liver biopsy specimen is the only widely accepted method for determining the presence and stage of hepatic fibrosis (1,2). However, liver biopsy is an invasive procedure which has a considerable risk of serious complications and frequently causes severe pain (2). Biopsy is also prone to errors due to sampling and intra-observer variability and is poorly suited to repeated or frequent monitoring (1-3). Over recent years, the development of non-invasive technologies for assessment of hepatic fibrosis has been an emerging research area. Although a number of approaches including serological markers(4-7), ultrasound or MRI-based elastography (8-12), diffusion-weighted imaging (DWI) (12-14), and targeted application of contrast agents (15) were proposed, none of them is currently capable of replacing liver biopsy, mainly due to low sensitivity to early fibrosis stages (16,17). Accordingly, the development of new methods for non-invasive diagnosis and staging of hepatic fibrosis is of critical importance for clinical hepatology.

One quantitative imaging method that could provide a prospective biomarker of hepatic fibrosis is macromolecular proton fraction (MPF) mapping (18). MPF is a key parameter determining the magnetization transfer (MT) effect in tissues and defined within the two-pool model of MT (19) as a relative amount of immobile macromolecular protons involved into magnetization exchange with mobile water protons. While MPF mapping has attracted major interest in neuroimaging applications (20,21), it also has a potential for quantitative assessment of fibrous tissue due to intrinsically high MPF specific for collagen (22). Recent studies have demonstrated sensitivity of MPF to the collagen content changes in the cartilage (23,24) and proliferation of desmoplastic fibrous tissue in tumors (25). Since an increase in the collagen content is a key histopathological feature of hepatic fibrosis (26-28), we hypothesized that MPF could allow quantitative assessment of fibrotic changes in the liver.

Among a variety of methods for quantitative mapping of MT parameters (18,29-38), the recently developed single-point MPF mapping technique (18) provides the most suitable technical approach for liver applications. The single-point method (18) allows MPF measurements in isolation from other two-pool model parameters and requires the minimal amount of source data (one MT-weighted image, reference image, independently acquired T₁ map, and B₀ and B₁ field maps), which potentially can be acquired within a few breath-hold intervals to minimize motion problems. However, determination of MPF in this method is based on constraining particular combinations of other two-pool model parameters with values that can be tissue-specific. Additionally, optimal sampling conditions in single-point MPF mapping depend on a number of factors, such as parameters of the imaging sequence, expected MPF values, distribution of constrained two-pool model parameters, and signal-to-noise ratio (SNR). Accordingly, the method (18) needs to be optimized for particular organ-specific applications.

The goals of this study were twofold. First, we aimed to develop a fast technique for liver MPF mapping based on the single-point approach (18) and breath-hold image acquisition to mitigate motion artifacts. Second, we sought to conduct a pilot clinical study to test the hypothesis that hepatic fibrosis results in an increased MPF in the liver parenchyma.

Methods

Study population

The study was approved by the Institutional Review Board, and written informed consent was obtained from all participants. For the purpose of the method optimization, one healthy volunteer was scanned using the Z-spectroscopic acquisition protocol described below. The pilot clinical study population included 16 patients with chronic hepatitis C virus (HCV) infection who were participants of a larger prospective cohort study of chronic liver disease at the Veterans Affairs Puget Sound Health Care System (39,40). Patients with chronic HCV infection were selected for this study because it is the most common etiology of cirrhosis in the United States and typically associated with progression of fibrosis. Fourteen patients underwent liver biopsy for clinical indications within one year prior to study entry (mean time interval ± SD: 4.9 ± 4.8 months). Two patients had liver cirrhosis diagnosed according to clinical criteria and did not have liver biopsy. Fibrosis and inflammatory activity were histologically staged according to the METAVIR scoring system (41). METAVIR scores include the following categories for fibrosis: no fibrosis (F0), mild fibrosis (portal fibrosis without septa, F1), moderate fibrosis (portal fibrosis and few septa, F2), severe fibrosis (numerous septa without cirrhosis, F3), and cirrhosis (F4) and inflammation: no activity (A0), mild activity (A1), moderate activity (A2), and severe activity (A3). Additionally, hepatic steatosis was graded as <5% (stage 0), 5-33% (stage 1), 34-66% (stage 2), and >66% (stage 3) of hepatocytes being steatotic at ×200 magnification (42). Relevant demographics, laboratory tests, and comorbidities were ascertained at the time of liver biopsy. The aspartate aminotransferase-to-platelet ratio index (APRI), a surrogate measure of liver fibrosis, was calculated as previously described (4,5).

MRI data acquisition

Images were acquired using a 3.0T scanner (Achieva; Philips Medical Systems, Best, Netherlands) with a phased-array six-channel torso coil. In all experiments, the following three-dimensional (3D) sequences were applied in the transverse plane to acquire source images: MT-weighted spoiled gradient-echo (GRE) with off-resonance saturation, reference GRE without MT saturation, variable flip angle (VFA) T₁ mapping, B₀ field mapping, and B₁ field mapping. In the MT-weighted sequence, off-resonance saturation was achieved by applying a single-lobe preparative sinc pulse with Gaussian apodization at effective saturation flip angles (FA_MT), offset frequencies (Δ), and durations (t_MT) specified below. For the purpose of data normalization, reference images were acquired with the same sequence at a high offset frequency where no MT effect is present (Δ=100 kHz) and the same FA_MT that was used for the MT-weighted images. VFA T₁ mapping was performed using the spoiled GRE sequence with three flip angles of the excitation pulse α=3, 10, and 20°. For B₀ mapping, the dual-T_E GRE phase-difference method (43) was used. 3D B₁ maps were obtained using the actual flip-angle imaging (AFI) method (44). The AFI and GRE sequences were implemented with optimized radiofrequency and gradient spoiling as previously described (45).

In the Z-spectroscopic experiment, the 3D GRE sequence was used with multi-shot echo-planar readout (acceleration factor 9), T_R/T_E =70/2.3 ms, and α=15°. The saturation pulse with t_MT=33 ms was applied at twelve Δ in a range 0.6-24 kHz and two FA_MT=800 and 1000°. Images were acquired with the matrix voxel size 2.2×3.1×12 mm³ in dynamic breath-hold blocks. Each block contained three images with different offset frequencies and a reference image with the total duration of 22 s. Parameters and geometry settings of the VFA T₁, B₀, and B₁ mapping sequences were similar to those used in the clinical study and specified below.

The protocol for the pilot clinical study contained four breath-hold scans with the following parameters: 1) dynamic acquisition of an MT-weighted and a reference 3D GRE images (T_R/T_E =18.5/2.3 ms, α=8°, t_MT=8 ms, FA_MT=252°, Δ= 2 and 100 kHz, respectively, scan time 17 s); 2) dynamic acquisition of 3D VFA images (T_R/T_E =18.5/2.3 ms, α=3, 10, and 20°, scan time 25 s); 3) 3D dual-T_E B₀ mapping (T_R/T_E1/T_E2=20/2.3/3.3 ms, α=8°, scan time 18 s), and 4) 3D AFI B₁ mapping (T_R1/T_R2/T_E =25/100/4.6 ms, α=60°, scan time 22 s). All images were obtained through the central portion of the liver with 3D FOV=400×300×60 mm³ and fractional k-space acquisition. Actual voxel size was 2×3×12 mm³ for all images except for B₁ maps (2.5×5.5×12 mm³). All raw data were zero-interpolated to reconstruct 10 sections with 6 mm thickness and 1×1 mm² in-plane resolution.

Analysis of Z-spectra and simulations

Z-spectroscopic measurements of the two-pool MT model parameters were performed to determine standardized non-adjustable parameter constraints in the liver tissue at 3 T for the single-point MPF mapping algorithm (18). Z-spectroscopic data were analyzed in uniform regions of interest drawn within liver parenchyma on source images. Intensities of images obtained at variable offset frequencies were normalized to the intensity of the reference images obtained at corresponding FA_MT. The four-parameter fit of the matrix pulsed steady-state MT equation (18) was performed to determine the following parameters of the two-pool model: MPF, cross-relaxation rate constant (k), and T₂ of free (water) (T₂^F) and bound (macromolecular) (T₂^B) protons. Complementary T₁ measurements were obtained by fitting Ernst equation to VFA data with B₁ correction (44). Constrained parameter combinations R₁T₂^F and R=k(1-MPF)/MPF were calculated from the primary fitted parameters.

To determine optimal sampling conditions for fast MPF mapping of the liver, the simulation approach based on the minimization of the total absolute MPF measurement error (σ_MPF) was used as described earlier (18). Simulations were carried out using the MPF error propagation model (18) with actual sequence parameters corresponding to the clinical study protocol, experimentally measured SNR for the reference image, and constrained values of R, R₁T₂^F, and T₂^B determined from the analysis of Z-spectra. To account for potential physiological variability of non-adjustable parameters, the joint distribution of constrained parameters was modeled by the product of Gaussian distributions for each parameter with standard deviations assigned as 20% of the parameter value. All analyses were performed using custom-written C language software.

Reconstruction and analysis of MPF maps

MPF maps were reconstructed using in-house written C language software according to the single-point algorithm (18). Briefly, this algorithm is based on the iterative solution of the pulsed magnetization transfer matrix equation with standardized constraints for non-adjustable two-pool model parameters and corrections for B₁ and B₀ field inhomogeneities. As input data, single-point MPF mapping utilizes an MT-weighted GRE image with off-resonance saturation, a reference GRE image without off-resonance saturation for data normalization, and an independently acquired T₁ map, which is reconstructed from VFA data with B₁ correction (44). Liver contours were manually outlined on six central sections of the reconstructed MPF maps with approximately 5 mm distance from the liver edge and excluding gallbladder to minimize partial volume effects. Then MPF histograms were calculated for the masked portion of the liver with the bin size of 0.25%, and the histogram mode was used as the measure of the central tendency. The mode was chosen to minimize influence of partial volume effects caused by blood vessels and bile ducts on MPF measurements in the liver parenchyma. The values of the mode were determined by fitting the Gaussian function to the central portion of the histogram corresponding to the MPF range of 3-10%.

Statistical analysis

The patient population was dichotomized based on the presence (defined by METAVIR scores F2-F4 or clinical diagnosis of cirrhosis) or absence (defined by METAVIR scores F0-F1) of significant fibrosis, in agreement with previous studies of other noninvasive markers (9,46). Differences between groups in distributions of histological inflammation and steatosis scores were assessed using Fisher's exact test. MPF and other clinical and demographic variables were compared between groups using Mann-Whitney U test. Associations between MPF and clinical data were tested using Spearman's rank correlation coefficient. The capability of MPF to discriminate patients with significant fibrosis (stages F2 or greater) from patients with no or mild fibrosis (F0 and F1) was evaluated using a receiver operating characteristic (ROC) curve. The area under curve (AUC) was calculated non-parametrically, and its significance was tested against the area under no-discrimination line (equal to 0.5). The optimal cutoff point was determined from Youden index. Exact binomial 95% confidence intervals (CI) were reported for the AUC and sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV) at the optimal cutoff point. P values less than 0.05 were considered to indicate statistical significance. Two-tailed tests were used in all analyses. MedCalc software (MedCalc Software bvba, Ostend, Belgium) was used for the ROC analysis, and other analyses were carried out in SPSS software (SPSS Inc, Chicago, Ill, USA).

Results

Optimization of fast MPF mapping of the liver

Experimental and fitted Z-spectra of the human liver in vivo are presented in Fig. 1. The two-pool MT model parameters determined from the fit of Z-spectra are listed in Table 1 along with the literature data for the murine liver ex vivo (47). All two-pool model parameters appear fairly consistent between our measurements and the literature (47). The constraints for non-adjustable parameters were determined from in vivo data and assigned in the reconstruction algorithm as follows: R = 55 s^-1, R₁T₂^F = 0.013, and T₂^B = 8 μs.

Figure 1.

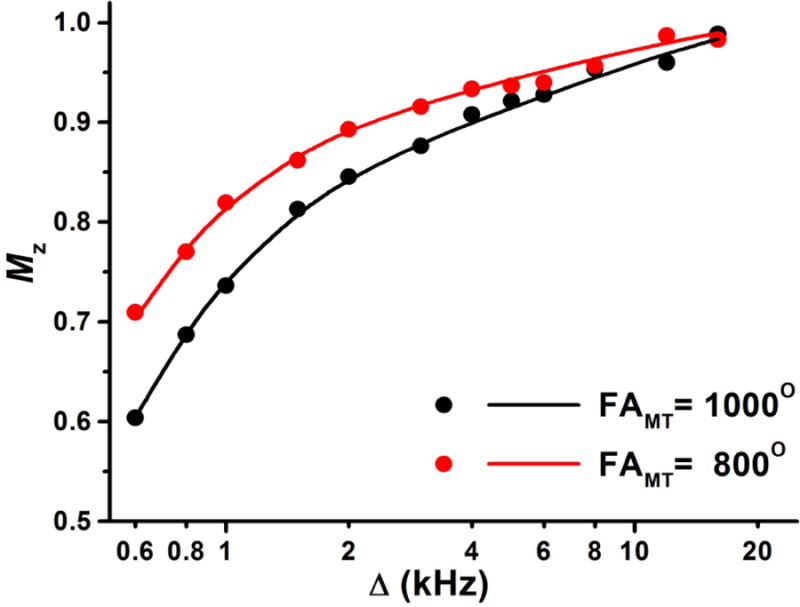
Experimental (points) and fitted (lines) Z-spectra of the human liver. Normalized longitudinal magnetization (M_z) is plotted as a function of the offset frequency (Δ) at variable FA_MT values.

Table 1.

Two-pool MT model parameters for liver tissue at 3 T determined from Z-spectra fit in this study and reported in the literature (47).

Parameter	Human liver, in vivoa	Murine liver, ex vivo (47)
MPF (SD) (%)	5.7 (0.5)	6.9 (0.7)
k (SD) (s-1)	3.3 (5.8)	3.8 (0.9)b
R (SD) (s-1)	55 (96)c	51 (10)
T2B (SD) (μs)	8.3 (0.8)	7.7 (0.2)
T2F (SD) (ms)	13.8 (0.6)	-

^aSD were determined from the covariance matrix of fitted parameters.

^bRecalculated from originally reported R and MPF.

^cRecalculated from primary fitted parameters k and MPF.

Results of simulations using the full MPF error model (18) with the above parameter constraints, experimental sequence timing parameters, and actual SNR available in human in vivo scans (around 70) are presented in Fig. 2. Minimization of the total MPF error is achieved at the offset frequencies in a range of 1.5-4 kHz depending on the effective flip angle of the saturation pulse FA_MT. Notably, the optimal FA_MT appears practically unachievable in liver imaging at 3T because of specific absorption rate (SAR) limitations. For the specified sequence parameters, the maximal allowable FA_MT within the scanner's SAR restrictions for the body transmit-receive coil was 252°, although larger values could further minimize the total MPF error (Fig. 2). Accordingly, this value and the offset frequency of 2 kHz were chosen for the clinical protocol. It also should be noted that an increase of FA_MT by applying a longer pulse with a corresponding increase of T_R does not allow circumventing the problem of suboptimal saturation conditions, because both the saturation effect and SAR are determined by the average power of the saturation pulse scaled by its duty cycle (30). Particularly, the protocols used for Z-spectroscopic acquisition (with t_MT/T_R =33/70 ms and FA_MT=1000°) and for the clinical study (with t_MT/T_R =8/18.5 ms and FA_MT=252°) are characterized by similar SAR-restricted root-mean-square amplitudes of the saturation pulse (97 and 101 Hz, respectively) and duty cycles (0.47 and 0.43, respectively), thus producing an almost equivalent saturation power and, correspondingly, resulting in similar total simulated MPF measurement errors (Fig. 2). As such, the protocol with the shortest T_R was preferred to avoid using the echo-planar readout sequence, which is prone to artifacts. Source images and parametric maps obtained with this protocol are exemplified in Fig. 3.

Figure 2.

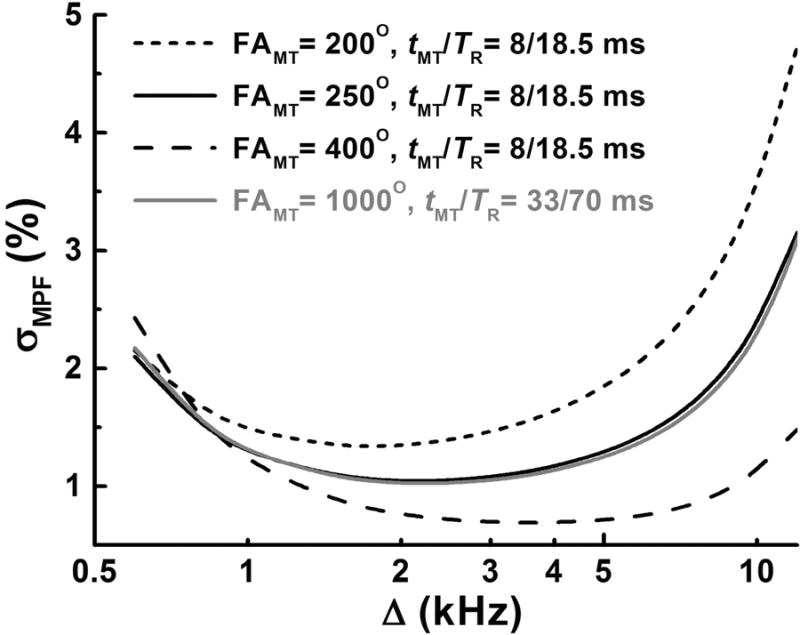
Total absolute MPF measurement error (σ_MPF) simulated using the error propagation model (18) and plotted as a function of the offset frequency (Δ) at variable FA_MT and timing parameters of the sequence (T_R and t_MT). Simulations are presented for the measured MPF value of 6%, T₁ = 1.1 s, SNR for the reference image of 70, and sequence parameters used in the protocols for the clinical study and Z-spectroscopic data acquisition.

Figure 3.

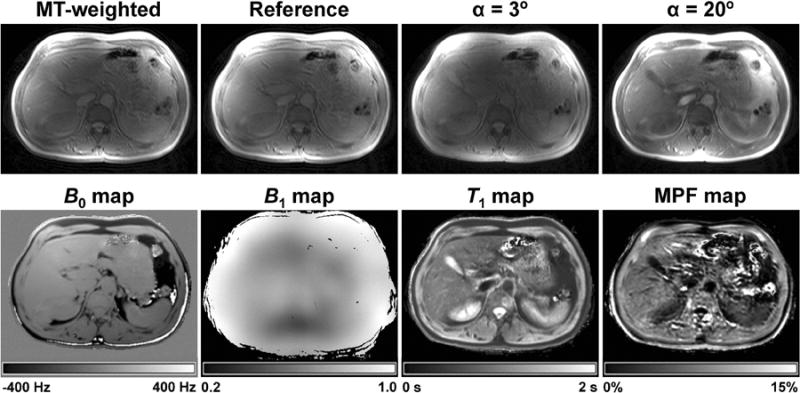
Example source images and parametric maps of the abdomen obtained from an HCV patient with fibrosis score F2 using the fast single-point MPF mapping method. Top row: MT-weighted image, reference image, and VFA images with α = 3 and 20°. Bottom row: B₀ and B₁ field maps, T₁ map, and MPF map. Grayscale ranges correspond to the frequency shift range from -400 to 400 Hz on the B₀ map, B₁ scaling factor range from 0.2 to 1.0 on the B₁ map, T₁ range from 0 to 2 s on the T₁ map, and MPF range from 0 to 15% on the MPF map.

Association between MPF and hepatic fibrosis

Clinical and demographic characteristics of the study population along with mean liver MPF histogram mode values are summarized in Table 2. MPF was significantly higher in the patients with clinically significant fibrosis compared to the patients with no or mild fibrosis. Other variables showed no significant differences between the groups. MPF histogram modes nearly monotonically increased with fibrosis severity and were characterized by the following mean ± SD values across the stages: 5.83 ± 0.27% for F0, 6.10 ± 0.18% for F1, 6.30 ± 0.92% for F2, 6.60 ± 0.64% for F3, and 6.57 ± 0.37 for F4. Example MPF maps of two patients with chronic liver disease and fibrosis scores of F0 and F3 are presented in Fig. 4. A diffuse increase of MPF in a patient with a higher fibrosis score can be visually appreciated on the color coded maps. Group liver MPF histograms of patients with and without significant fibrosis are shown in Fig. 5 and demonstrate a visible shift to higher MPF values for the significant fibrosis group.

Table 2.

Characteristics of the chronic liver disease patient groups with and without clinically significant fibrosis.

Variable	No or mild fibrosis (n=10)	Significant fibrosis (n=6)
Fibrosis score (number of patients)
F0	6	0
F1	4	0
F2	0	2
F3	0	2
F4a	0	2
Inflammation score (number of patients)
A0	1	0
A1	5	0
A2	4	3
A3	0	1
Steatosis score (number of patients)
0	8	2
1	1	2
2	1	0
Mean age (SD) (years)	55.1 (7.2)	61.7 (4.1)
Mean BMI (SD) (kg/m2)	28.1 (3.2)	27.5 (2.2)
Mean AST (SD) (IU/L)	45.9 (22.6)	121.2 (175.9)
Mean ALT (SD) (IU/L)	73.5 (48.1)	125.2 (156.8)
Mean platelet count (SD) (109/L)	197 (55)	168 (47)
Mean total bilirubin (SD) (mg/dL)	0.8 (1.3)	0.7 (0.5)
Mean albumin (SD) (g/dL)	4.55 (0.25)	4.20 (0.40)
Mean AST/ALT ratio (SD)	0.69 (0.21)	0.87 (0.15)
Mean APRI (SD)	0.66 (0.41)	2.26 (3.52)
Mean MPF histogram mode (SD) (%)b	5.94 (0.26)	6.49 (0.36)

^aScore is assigned to cirrhosis patients without biopsy based on the clinical diagnosis.

^bValues are significantly different according to Mann-Whitney U test (P=0.002)

Figure 4.

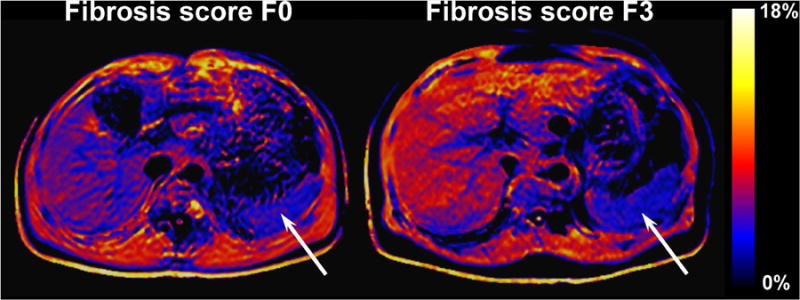
Example color-coded MPF maps of chronic HCV infection patients with fibrosis scores F0 (left) and F3 (right). Liver MPF in these patients is characterized by the histogram mode values of 5.5% and 7.1%, respectively. Note a diffuse increase of MPF in the liver of the patient with the higher score (visible as a larger proportion of the red color), whereas the spleen (arrows) has a similar appearance in both patients with the mean MPF of 3.8% and 3.9%, respectively. The color look-up table corresponds to the MPF range of 0-18%.

Figure 5.

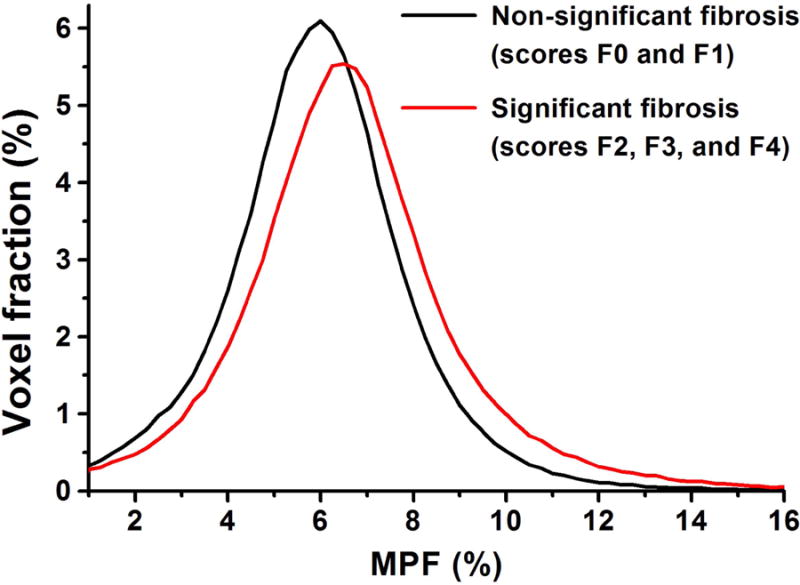
Mean group liver MPF histograms of patients with (red) and without (black) clinically significant fibrosis.

Correlations between MPF, fibrosis score, and other clinical variables are summarized in Table 3. The scatter plot of the MPF histogram mode versus fibrosis score is presented in Fig. 6. MPF showed a strong positive correlation with the fibrosis score and a weaker but significant positive correlation with the inflammation score. Fibrosis and inflammatory scores were strongly correlated with each other. No significant correlations were identified between MPF or fibrosis score and other clinical and demographic variables.

Table 3.

Spearman rank correlations between MPF, fibrosis score, and other clinical variables.

Variable	MPF histogram mode	Fibrosis score
Fibrosis score	0.80a	-
Inflammation score	0.66b	0.92a
Steatosis score	-0.04	0.30
Age	0.35	0.38
BMI	-0.20	-0.13
AST	0.12	0.20
ALT	0.05	0.10
Platelet count	-0.09	-0.28
Total bilirubin	0.10	0.26
Albumin	-0.18	-0.36
AST/ALT ratio	0.10	0.34
APRI	0.17	0.33

^aP<0.001

^bP=0.01

Figure 6.

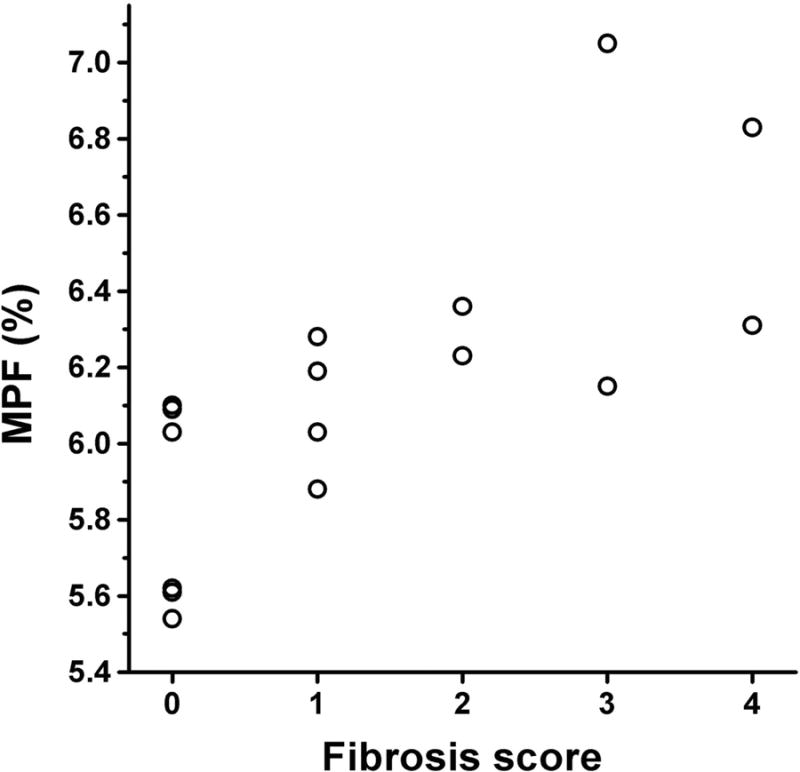
Scatter plot of the MPF histogram mode values versus the hepatic fibrosis score in 16 chronic HCV patients. The fibrosis score of 4 was assigned to cirrhosis patients without biopsy based on the clinical diagnosis.

The ROC curve for classification between clinically significant fibrosis (F2-F4) and mild or no fibrosis (F0 and F1) is plotted in Fig. 7. The AUC was 0.950 (CI: 0.715 - 0.999) which is significantly greater than 0.5 (P<0.0001), indicating that MPF can accurately discriminate clinically relevant patient groups. The optimal MPF cutoff point was 6.1%. The diagnostic performance measures at this cutoff point were as follows: sensitivity 100% (CI: 54 – 100%), specificity 80% (CI: 44 – 98%), PPV 75% (CI: 35 – 97%), and NPV 100% (CI: 63 – 100%).

Figure 7.

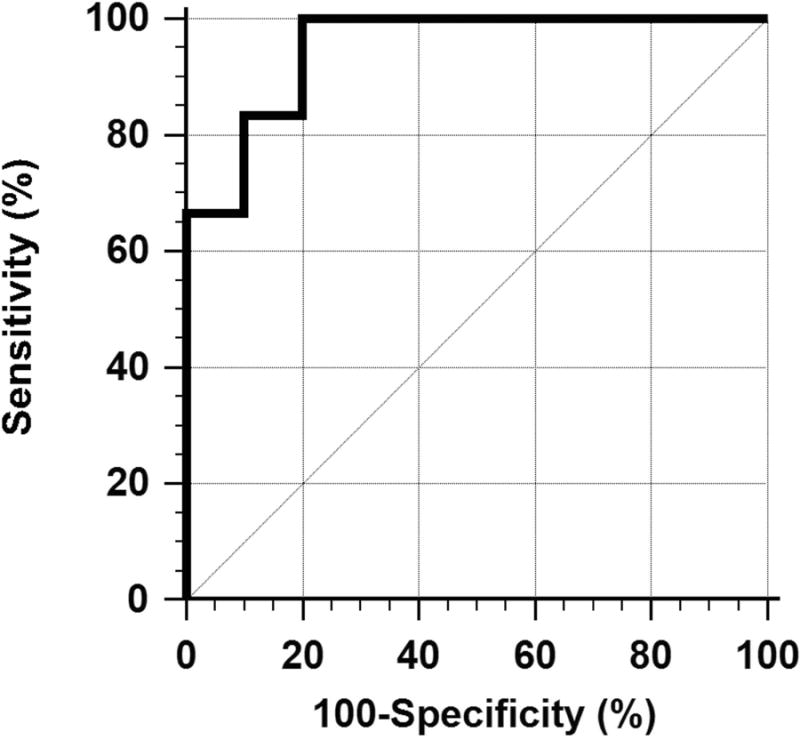
ROC curve for classification between patients with clinically significant fibrosis (F2-F4) and patients with mild or no fibrosis (F0 and F1) based on the MPF histogram mode.

Discussion

In this study, we report the first in vivo measurements of the human liver MPF and show that it may be useful in distinguishing patients with different levels of hepatic fibrosis. Our results demonstrate that fast MPF mapping is feasible in a clinical MRI setting and can be performed either as a standalone examination or as a short addition to any clinical abdominal MRI protocol. Preliminary clinical data for patients with chronic HCV infection indicate that MPF is strongly correlated with histologically confirmed fibrosis score and allows discrimination between patients with and without clinically significant fibrosis. As such, MPF mapping shows potential as a promising non-invasive method for assessing hepatic fibrosis in chronic liver diseases.

Our MPF measurements in the livers with and without significant fibrosis appear in plausible agreement with the expected effect of fibrosis on MPF values. This effect can be estimated based on the literature data about the collagen content in the normal and cirrhotic liver (26-28). In the normal liver, collagen content is about 0.5-1% by wet weight (26), and this amount increases about four-fold in cirrhosis (27,28). Taking an estimate of MPF in pure hydrated collagen as 60% based on cross-relaxation measurements (22) and assuming that MPF changes caused by fibrosis are entirely due to collagen, the range of MPF variations is expected between 1% and 2% which very well approximates the range of about 1.5% observed in our patient population (Fig. 6).

Liver biopsy is still considered the gold standard for the evaluation of hepatic fibrosis, although the number of biopsies performed in clinics has declined dramatically in the last two decades with the introduction of noninvasive tests for hepatic fibrosis (46). Such noninvasive tests generally fall into two overall classes. The first are panels of serum biomarkers (4-7) the second are ultrasound or MRI-based measurements of liver stiffness (8-12). While a discussion of the advantages and disadvantages of each of these techniques is beyond the scope of this study, attractive features of MPF as a potential clinical biomarker of hepatic fibrosis include the fact that MPF mapping can be easily implemented on a regular MRI machine, that the method allows assessment of a large portion of the liver or, potentially, the whole organ as discussed below, and that it can be performed in the setting of obesity. The pilot data of this study indicate that MPF mapping may provide the diagnostic performance comparable to other non-invasive methods. The correlation coefficient between MPF and fibrosis score and the area under ROC curve appeared slightly smaller than those reported in magnetic resonance elastography studies (11,12,48,49) but similar or larger compared to the corresponding indexes for transient elastography (8,9,49). MPF also showed better discriminating capability between significant and non-significant fibrosis relative to most serum biomarkers (4-8,17) and DWI (12,14). However, caution must be taken in the interpretation of these observations as indicators of diagnostic accuracy of MPF due to the limited sample size and the absence of direct comparisons with alternative methods.

Several earlier studies (50-56) investigated the MT effect in the liver as a potential measure of hepatic fibrosis and reported controversial findings. In an animal model of cirrhosis, Aisen et al. (50) detected a significant increase of the longitudinal relaxation rate in the presence of off-resonance saturation in the injured liver suggesting a more effective cross-relaxation caused by fibrosis though without significant correlation with the extent of fibrosis and collagen content. In another animal study, Kim et al. (51) found a trend of reduction of the MT ratio (MTR), a commonly used empirical measure of the MT effect, in fibrosis followed by an increase in cirrhosis. It is noticeable, that the development of fibrosis and cirrhosis in the rat model used in their study (51) was confounded by severe steatosis. In a similar toxic murine model of fibrosis, Fuchs et al. (52) reported that MTR was insensitive to the fibrosis score and collagen content in the liver. Guo et al. (53) found a significant increase of MTR in the murine model of Niemann-Pick disease, a genetic disorder accompanied with collagen deposition in the liver. Chen at al. (54,55) found an increased MTR in human cirrhosis but not in chronic hepatitis and early fibrosis. A recent article by Rosenkrantz et al. (56) reported the absence of significant differences in MTR between healthy and cirrhotic liver in humans. From the methodological standpoint, it should be pointed out that MT measures used in the above studies (50-56) do not reflect specific biophysical parameters describing the MT effect but rather represent compounded variables with complex dependence on several two-pool model parameters, intrinsic relaxation properties of tissues, and parameters of an imaging pulse sequence. Particularly, limitations of MTR including poor pathological sensitivity and specificity, inability to discriminate contributions from relaxation and cross-relaxation, and high variability due to instrumental factors have been noticed in many studies focused on brain (20,30,57-59) and non-brain (23-25) applications. It also has been demonstrated (20,23,58,59) that MPF overcomes these limitations, providing a physically meaningful objective parameter closely associated with pathological changes in tissues. Our results are in line with these conclusions and suggest the usefulness of MPF mapping as a prospective quantitative imaging modality for evaluation of hepatic fibrosis.

There are several methodological distinctions between the previously described brain MPF mapping technique (18,20,21) and its modification for the liver. Motion is a more critical problem for quantitative imaging of the liver and abdominal organs in general. While a number of techniques can be used to mitigate motion artifacts, we have chosen breath-hold acquisition as the most straightforward approach. The downside of the described breath-hold protocol is the limited spatial coverage that did not allow the analysis for the whole organ. Alternatively, navigator-based or respiratory-triggered techniques could be used at the expense of a longer scan time. However, adaptation of these approaches for MPF mapping may be problematic due to the need to continuously maintain the pulsed steady state required for the application of the signal model (18) in the reconstruction algorithm. Nevertheless, further advancements of the described method in the aspects of time-efficiency and spatial coverage are possible with the use of parallel imaging and improved coil technology. Of note, we used a coil with a relatively modest performance (6 channels) that impeded parallel imaging acceleration due to SNR limitations. It is expected that the breath-hold MPF mapping technique can be implemented with whole-liver coverage using contemporary 16- or 32-channel coils, which are commonly available. Another technical issue specific to abdominal applications of MPF mapping at 3 T is SAR limitations, which precluded implementing truly optimal saturation conditions according to the MPF error model (18). Such a problem does not occur in the brain MPF mapping where a range of optimal FA_MT values is completely within the allowable SAR limit (18). This aspect of liver MPF mapping is associated with both a stricter SAR margin for whole-body transmission and a relatively small MPF to be measured in combination with generally lower SNR. While larger FA_MT values could improve MPF determination, saturation power limitation in the liver MPF mapping can be partially compensated by reducing the offset frequency which was set at 2 kHz in this study (cf. the optimal range of 4-7 kHz for the brain (18)). However, care must be taken in applying this approach in the presence of high iron content because of the risk of introducing systematic MPF errors due to an increased direct saturation effect caused by shorter T₂^F. Accordingly, the described method may need to be re-optimized for studies of conditions associated with excessive iron deposition in the liver, such as haemochromatosis.

One controversial observation of this study is a significant positive correlation between MPF and the inflammatory activity histological score. This correlation is difficult to explain by biological factors, since a possible effect of inflammation (if any) would result in an increased tissue water content which could translate into a reduced MPF. As such, one would expect a negative correlation if MPF is actually affected by inflammation. However, inflammatory and fibrosis scores appeared very strongly positively correlated in the studied patient population, suggesting that the correlation between MPF and the inflammatory score is due to confounding by fibrosis score which is closely associated with both variables.

Another pathological factor that may affect MPF measurements is hepatic steatosis. Although we did not identify any statistically significant effect of steatosis in this study, the number of patients with non-zero steatosis scores was small, and therefore, a potential role of this confounder cannot be excluded. The presence of fat has been shown to reduce the observed MT saturation in traditional MT imaging of the liver (60) and cause underestimation of the pool size ratio (a measure directly related to MPF) in quantitative MT imaging of the muscle (61). As such, underestimation of MPF may potentially occur due to steatosis, and special procedures for MPF correction based on water and fat content mapping (62) may need to be developed for applications in patients with fatty liver disease.

Theoretical consideration of the effects of various pathological liver conditions on MPF suggests that only fibrosis is expected to result in increased MPF values. Hepatic fibrosis is characterized primarily by increased collagen deposition, which has a high MPF. In contrast, other histological factors, such as hepatic fat accumulation or inflammation, should decrease MPF. Therefore, an increased liver MPF is expected to be a highly specific indicator of hepatic fibrosis. On the other hand, in cases of normal or marginally increased MPF, a combination of MPF mapping with other MRI or non-MRI methods may be needed to identify clinically significant fibrosis. Appropriate diagnostic algorithms can be designed taking into account the fact that potential confounders produce opposite trends for different measures sensitive to fibrosis. For example, extrahepatic cholestasis, hepatic congestion, and hepatic inflammation (63-66) have been shown to increase liver stiffness, similar to fibrosis. However, these factors would be expected to reduce MPF due to increased accumulation of free water within liver parenchyma. Accordingly, the opposite effects of these factors on MPF and stiffness may help to develop a combined approach based on MPF mapping and elastography with better performance than each method alone. Likewise, DWI is subjected to a strong confounding effect of steatosis, which results in a decreased apparent diffusion coefficient (67,68), similar to fibrosis. Therefore, in patients with confirmed steatosis, a combination of MPF mapping and DWI may be expected to improve fibrosis staging.

This study has several limitations. First, a small sample size did not allow comprehensive comparison of MPF between all fibrosis stages and motivated us to perform dichotomized analyses. For this reason, the capability of MPF to discriminate between individual fibrosis stages remains unknown. Second, our estimates of the two-pool model parameter constraints are based on the healthy liver data and may need to be reassessed for certain pathological conditions, as discussed above. However, it is extremely unlikely that fibrosis itself would result in practically important changes of these parameters. Specifically, parameters R and T₂^B are almost identical in tissues with highly variable collagen content (47). There is a possibility that the product R₁T₂^F may decrease with fibrosis, since an increase of T₁ and a decrease of T₂* associated with fibrosis were reported (69). The use of an overestimated R₁T₂^F value in the MPF reconstruction algorithm may increase an unaccounted portion of direct saturation of free water protons and, therefore, potentially cause an overestimation of a measured MPF value. Accordingly, changes in MPF and relaxation may act synergistically and increase sensitivity of single-point MPF measurements to fibrosis. However, this effect is expected to be very small due to almost negligible direct saturation of the free water pool at high offset frequencies (33). Finally, reproducibility of liver MPF measurements has not been assessed and needs to be determined for planning larger-scale clinical studies.

In conclusion, this study has demonstrated the feasibility of fast MPF mapping of the human liver in vivo. Our results confirm the hypothesis that MPF is increased in hepatic fibrosis and associated with fibrosis stage. Based on these findings and in view of a fast image acquisition procedure, MPF can be considered a prospective non-invasive fibrosis biomarker potentially applicable in clinical settings. Future studies are warranted to investigate whether MPF mapping, alone or in combination with other biomarkers, can improve diagnosis of fibrosis and discrimination between fibrosis stages compared to existing methods.

Abbreviations used

DWI

diffusion-weighted imaging

MPF

macromolecular proton fraction

MT

magnetization transfer

SNR

signal-to-noise ratio

HCV

hepatitis C virus

APRI

aspartate aminotransferase-to-platelet ratio index

3D

three-dimensional

GRE

gradient echo

VFA

variable flip angle

FA_MT

saturation pulse flip angle

Δ

saturation pulse offset frequency

t_MT

saturation pulse duration

AFI

actual flip-angle imaging

α

excitation flip angle

FOV

field-of-view

k

cross-relaxation rate constant for transfer from water to macromolecular protons

R

cross-relaxation rate constant for transfer from macromolecular protons to water

T₂^F

T₂ of free water protons

T₂^B

T₂ of bound macromolecular protons

σ_MPF

absolute MPF measurement error

ROC

receiver operating characteristic

AUC

area under curve

CI

confidence intervals

PPV

positive predictive value

NPV

negative predictive value

SAR

specific absorption rate

MTR

magnetization transfer ratio

M_z

longitudinal magnetization

SD

standard deviation

BMI

body mass index

AST

aspartate aminotransferase

ALT

alanine aminotransferase