Quantifying Temperature-Dependent T₁ Changes in Cortical Bone Using Ultrashort Echo-Time MRI

Abstract

Purpose

To demonstrate the feasibility of using ultrashort echo-time (UTE) MRI to quantify T₁ changes in cortical bone due to heating.

Methods

Variable flip-angle T₁ mapping combined with 3D UTE imaging was used to measure T₁ in cortical bone. A calibration experiment was performed to detect T₁ changes with temperature in ex vivo cortical bone samples from a bovine femur. Ultrasound heating experiments were performed using an interstitial applicator in ex vivo bovine femur specimens, and heat-induced T₁ changes were quantified.

Results

The calibration experiment demonstrated that T₁ increases with temperature in cortical bone. We observed a linear relationship between temperature and T₁ with a linear coefficient of 0.67–0.84 ms/°C over a range of 25–70°C. The ultrasound heating experiments showed increased T₁ changes in the heated regions, and the relationship between the temperature changes and T₁ changes was similar to that of the calibration.

Conclusion

We demonstrated a temperature dependence of T₁ in ex vivo cortical bone using a variable flip-angle UTE T₁ mapping method.

Introduction

Although primary bone tumors make up only 0.2% of primary neoplasms [1], bone metastases are highly prevalent, occurring in 65–75% of patients with advanced breast and prostate cancers and in 30–40% of patients with lung cancer [2]. Image-guided thermal ablation techniques including MR-guided high-intensity focused ultrasound have proven effective in treating bone tumors and palliating painful bone metastases [3–6]. During thermal therapy, temperature mapping is desirable to ensure proper heat deposition in targeted tumors and to prevent unnecessary heating in surrounding tissues. Conventional MR thermometry exploits the proton resonant frequency shift of water protons, which is due to the alterations of hydrogen bonding between water molecules associated with temperature changes [7, 8]. However, proton resonant frequency-based MR thermometry normally requires a long echo time (TE) of 8–10 ms to yield sufficient phase changes for detection. This method cannot be applied for cortical bone because it has a short T₂* of 0.4–0.5 ms [9]. Due to this limitation, monitoring of thermal dose in cortical bone has been only possible by using temperature information in surrounding soft tissues.

Alternative temperature mapping methods have been developed to provide additional information about thermal therapy or to allow for temperature monitoring in adipose tissues, in which proton resonant frequency-based thermometry is not applicable. Since T₁-based thermometry was first proposed by Parker [10,11], it has been demonstrated in both non-adipose tissues such as muscle and liver [12–15] and adipose tissues [16–19] under ex vivo and in vivo conditions. A linear increase in T₁ on the order of 1%/°C was found over a limited temperature range for non-adipose tissues and over a larger range for adipose tissues. T₂-based thermometry has been examined to a lesser extent due to the irreversibility and nonlinear behavior observed in non-adipose tissues [20]; however, linear T₂ changes were recently observed in adipose tissues over 25–45°C or up to 70°C [17, 21, 22].

With conventional MRI sequences, the signal from cortical bone is almost not detectable due to its short T₂ and low water volume (20–25% volume) [23, 24]. However, ultrashort echotime (UTE) MRI techniques allow for detecting the signal from cortical bone. Using UTE, bone water properties such as T₁, T₂, and bone water content have been measured as well [9, 25, 26]. Recently, temperature sensitivity in cortical bone signals has been observed. Miller [27] detected a signal decrease in the heated region of cortical bone using a T₁-weighted UTE imaging sequence. Ramsay et al. [28] demonstrated a positive correlation between temperature changes and signal magnitudes using a short-TE radiofrequency (RF)-spoiled gradient-echo sequence.

The goal of our study was to determine whether T₁ changes in cortical bone can be quantified using UTE imaging and applied toward temperature mapping. A variable flip-angle method [29,30] was used to calculate T₁ in cortical bone. A calibration experiment was performed to measure T₁ changes with temperature in ex vivo cortical bone samples from a bovine femur [31]. Ex vivo heating experiments were performed using an MR compatible interstitial ultrasound applicator [32–34] to demonstrate the feasibility of using T₁-based thermometry in cortical bone [35].

Methods

Variable Flip-Angle UTE T₁ Mapping

The UTE imaging sequence used in this study was designed for a GE Discovery MR750 wide bore 3T scanner (GE Healthcare, Milwaukee, WI) equipped with gradient systems having a maximum strength of 33 mT/m and a maximum slew rate of 120 mT/m/ms. To achieve an ultrashort TE, a nonselective hard pulse with a 200 µs duration was used, followed by 3 dimensional (3D) radial trajectories [36, 37]. Data acquisition started with the rising slope of the readout gradient (ramp sampling), and TE was 175 µs, determined as the time between the middle of the RF pulse and the start of acquisition. For each readout, 256 data points were acquired with a sampling interval of 4 µs for a total readout duration of 1.024 ms. Our radial trajectories supported an anisotropic field of view, which improved scan time efficiencies for noncircular objects, and anisotropic spatial resolution [38]. RF-spoiling was performed by incorporating RF phase cycling, rewinding the readout gradients after data acquisition, and adding gradient spoilers (along all of the three axes), which allow for steady-state signals for longer T₂* tissues.

Bone T₁ mapping was performed using a variable flip-angle method, which calculates T₁ based on RF-spoiled steady-state signals at multiple flip angles [29, 30]. Given a repetition time (TR) of 11 ms and assuming a 200 ms T₁ in cortical bone at room temperature [9,39], we calculated two optimized flip angles of 8°and 44°, which provided 0.71 times the signal at the Ernst flip angle [40]. T₁ was calculated ignoring T₂* relaxation effects during excitation [41].

Calibration Study

To measure T₁ changes with temperature in cortical bone, a calibration experiment was performed in a controlled heating and cooling manner. Two cortical bone samples from a diaphysis segment of a bovine femur (with fatty bone marrow and surrounding muscle tissues removed) were placed in a thermally-insulated water bath, which was used to control the temperature. The cortical bone samples were obtained from a cow slaughtered less than a week before the experiment, and they were kept frozen and thawed one day before the experiment. Deionized water without any doping was used to heat the bone samples. A 16-channel large flex coil (NeoCoil, Pewaukee, WI), which can be wrapped around an object to provide high sensitivity, was used for imaging. To monitor temperature, fiber-optic temperature sensors (Luxtron, LumaSence Technologies, Santa Clara, CA) were positioned inside the water bath and in one of the bone samples.

T₁ mapping was performed when the heated water and cortical bone samples reached thermal equilibrium (typically 15–20 min after water temperature changed) based on fiber-optic temperature measurements. In particular, UTE T₁ mapping was performed when the equilibrium bone temperature was within ±1.4°C of 25°C, 35°C, 45°C, 55°C, 65°C, and 70°C during the heating phase, and within ±1.4°C of 55°C, 35°C, and 25°C during the cooling phase. UTE T₁ mapping was performed using 8° and 44° flip angles and 1.7 mm isotropic resolution for 8 min. Bone temperature variation during the 8 min scan was 0.2–0.6°C for all measurements.

The UTE data was reconstructed using 3D gridding followed by inverse Fourier transform. The reconstructed voxel size was 0.85 mm, isotropic. For T₁ quantification, a volume of interest for each bone sample was determined automatically. First, the two bone regions were segmented by thresholding the reconstructed UTE images slice by slice. The regions of interest (ROIs) were then determined by shrinking the boundaries of the segmented bone regions by three pixels. The ROIs in the central 25 slices corresponding to each bone sample were used to comprise the volume of interest. The mean and standard deviation of the T₁ values from the two volumes of interest were separately calculated for each temperature point.

Ultrasound Heating Experiments

Three ultrasound heating experiments were performed at 3T using different ex vivo diaphysis segments of bovine femurs (frozen for less than a week and thawed) and an eight-channel phased-array wrist coil (Invivo, Gainesville, FL). The bone segments were heated using an MR-compatible catheter-cooled interstitial ultrasound applicator with two tubular transducers sonicating at 7.6–7.8 MHz [32–34]. The transducers were sectored to provide a 180° directional heating pattern and had a 12 W/cm² surface intensity. Water cooling was achieved by circulating degassed, deionized water (at room temperature) through a plastic catheter encompassing the transducers. Heating with interstitial ultrasound applicators typically requires 10–15 min of continuous power application for tumor ablation. The applicator was inserted into the fatty yellow bone marrow in the medullary cavity of the bovine femurs, and the acoustic energy was directed toward the cortical bone (Fig. 1a). For one of the heating experiments, four holes were drilled in the cortical bone and temperature sensors were placed using glue to monitor temperatures.

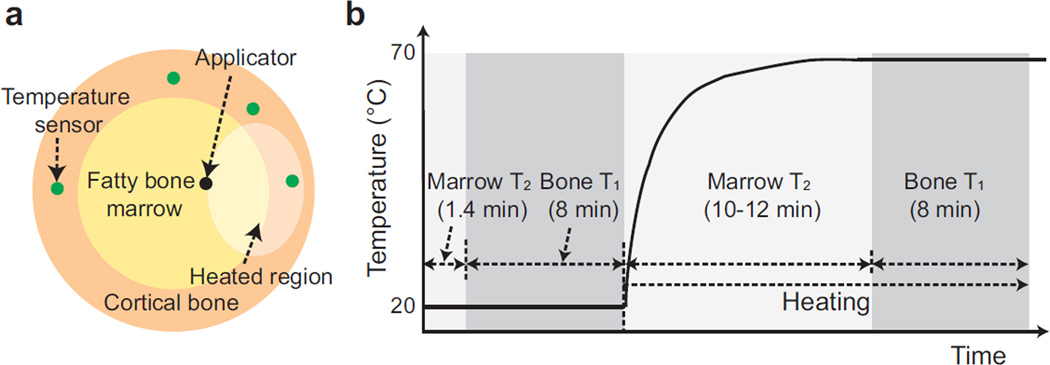
Figure 1.

Interstitial ultrasound heating experiment set-up. (a) Cross-sectional diagrams of an interstitial ultrasound applicator and temperature sensor placement in a bone segment. (b) Imaging protocols. As a reference, a plot of the expected temperature changes in a heated region is shown. To obtain a baseline, bone marrow T₂ mapping and cortical bone UTE T₁ mapping were performed. After starting heating, dynamic T₂ mapping was performed to monitor bone marrow temperatures during the transient state. The temperature was assumed to have reached steady state 10–12 min after heating began, and UTE T₁ mapping was performed again.

Before heating began, standard 3D gradient-echo imaging was performed, and T₂ mapping in fatty bone marrow [21] and UTE T₁ mapping in cortical bone were conducted as baseline measurements. After starting heating, T₂ mapping in bone marrow was performed to monitor transient temperature changes for 10–12 min. Afterwards, temperature was assumed to have reached steady state, and UTE T₁ mapping was performed again to determine T₁ changes due to heating (protocol shown in Fig. 1b). For UTE T₁ mapping, 3D UTE imaging was performed using a 1×1×1.5 mm³ spatial resolution, 9×9×9.6 cm³ field of view, 11 ms TR, and 8° and 44° flip angles. UTE imaging at each flip angle took approximately 4 min. The reconstructed isotropic voxel size was 1 mm. Double-echo 2D fast spin-echo (2D FSE) imaging was used to measure T₂ in bone marrow, using 36.3 ms and 181.7 ms TEs, a 666 ms TR, an echo train length of 40, a 12×12 cm² field of view, a 128×128 matrix size, 4 mm slice thickness, and 10 slices (total 1.4 min scan time for one time point).

Using the T₁ change maps of the specimen in which temperature was monitored with fiberoptic sensors, the relationship to actual temperature changes was assessed. To better find the four sensor locations in that specimen, UTE imaging with a higher spatial resolution (isotropic 0.5 mm resolution) was additionally performed. After denoting each sensor position on the maps of T₁ changes, an oval with an area of 20.4 mm² was centered around each sensor position. When this oval included bone/bone marrow boundary or was too close to that, it was shifted toward outside. Since the calculated T₁ in the hole itself was not reliable due to absence of tissues or presence of glue, an oval region with an area of 4.6 mm² centered at the sensor position was excluded. The resultant ring-shaped ROI was used for T₁ analysis.

Results

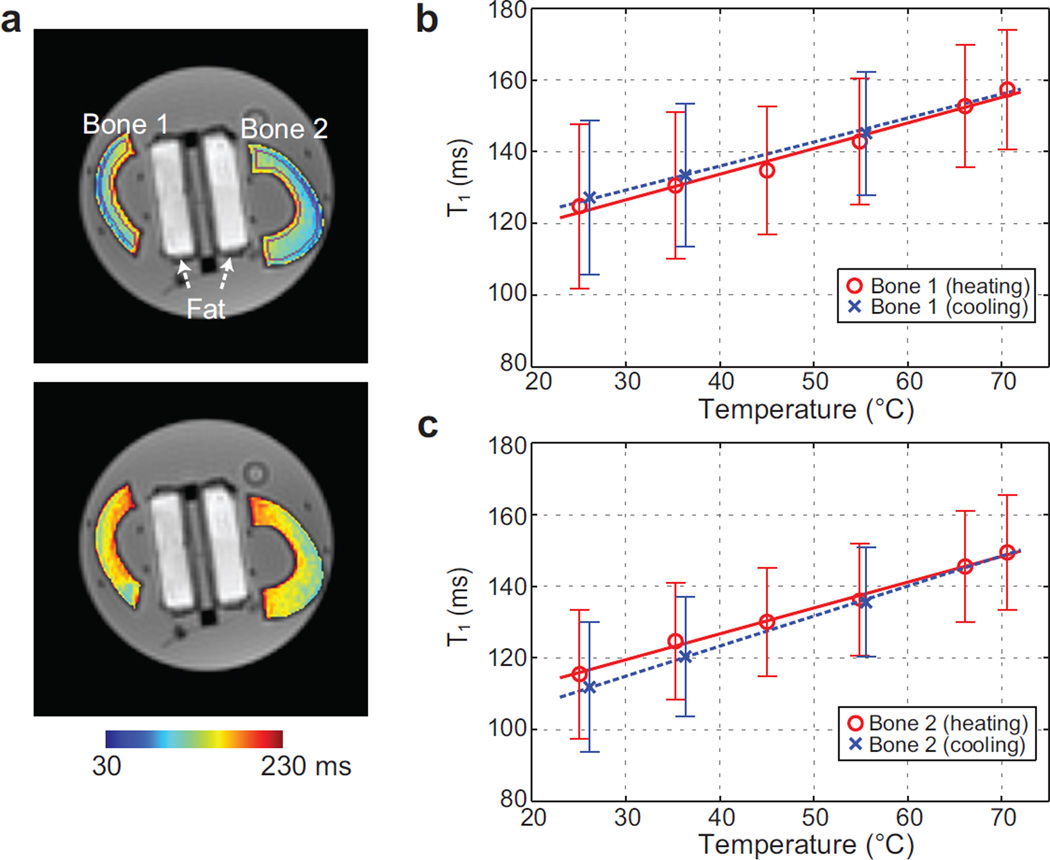
The calibration results are shown in Fig. 2. Figure 2a shows bone T₁ maps at two different temperatures, 25°C and 70°C, overlaid on UTE images. T₁ changes with temperature were observed. Figure 2b-c shows the mean T₁ values and error bar (±standard deviation) from the volumes of interest versus the bone temperatures measured by the fiber-optic sensor. An apparent linear relationship between temperature and T₁ was observed for both bone samples. For the first bone sample, the linear coefficient was 0.72±0.05 (standard error) ms/°C during heating and 0.67±0.03 ms/°C during cooling. For the second bone sample, it was 0.72±0.03 ms/°C during heating and 0.84±0.02 ms/°C during cooling.

Figure 2.

Calibration results. (a) Bone T₁ maps at temperatures of 25°C (top) and 70°C (bottom), overlaid on UTE images at 8°. Two tubes containing fat (used for a different study) are positioned between the bone samples. ROIs automatically determined to quantify T₁ in each bone sample are denoted in purple in the upper image. (b-c) The mean T₁ and error bar from the volume of interest is shown over different temperatures for each bone sample. Linear regression lines during the heating and cooling periods are plotted as well. An apparent linear increase of T₁ with temperature is demonstrated.

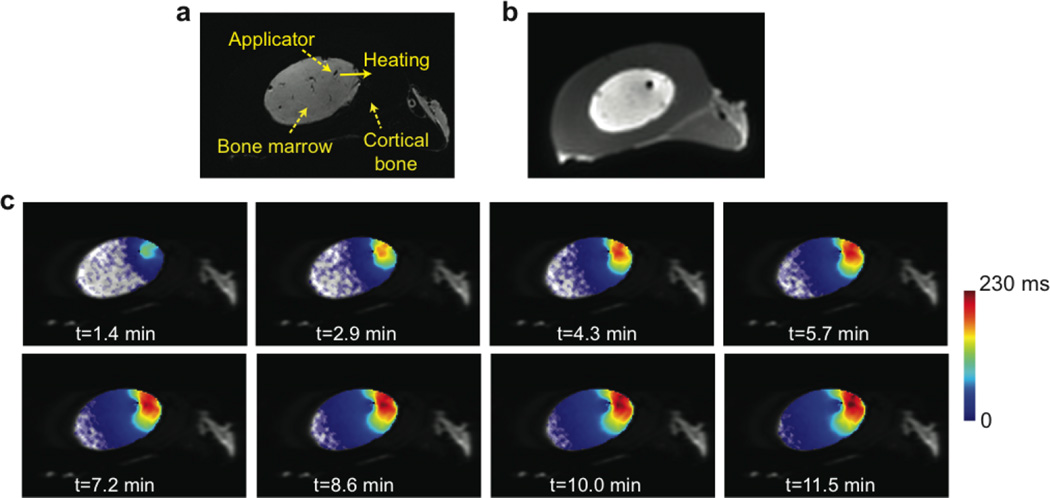
Figure 3 illustrates results from one ultrasound heating experiment. The cortical bone is dark in the gradient-echo image (Fig. 3a) but is well delineated in the UTE image (Fig. 3b). The applicator position in the fatty bone marrow and the heating direction are denoted. Figure 3c shows maps of T₂ changes between the baseline and each time point after heating began, overlaid on the FSE image at one slice location. Temperature rise in bone marrow and the approach to steady state were observed. A previous study demonstrated a linear relationship between temperature and T₂ in fatty bone marrow of a bovine femur by using an equivalent pulse sequence with similar TR/TEs [22]; the linear coefficient was 5.48 ms/°C during heating. Assuming an equivalent temperature- T₂ relationship was held in our case, a T₂ increase of 230 ms indicated a temperature increase of 42.0°C.

Figure 3.

Temperature mapping during transient state. (a) Gradient-echo image with denoted applicator location and heating direction. (b) Corresponding UTE image before heating, visually delineating cortical bone. (c) Maps of T₂ changes between the baseline and each time point after heating began, overlaid on FSE images. A T₂ increase over time in the heated region of the bone marrow can be seen. Please note limited T₂ increases near the applicator due to water cooling.

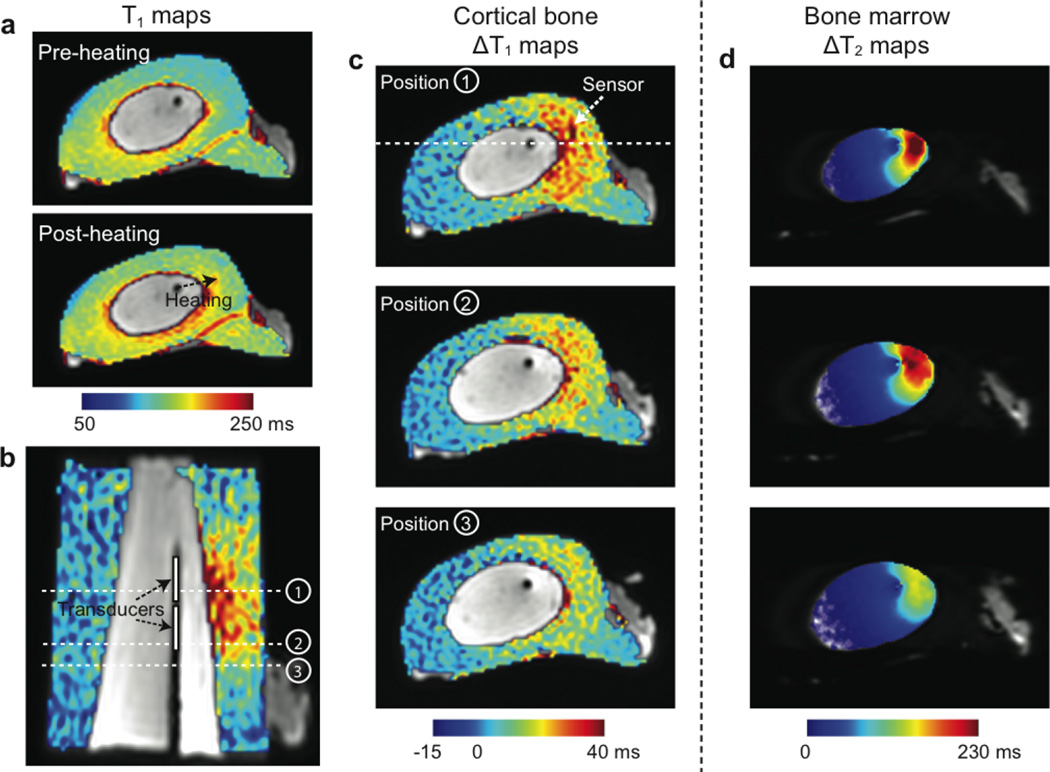
The maps of T₁ and T₁ changes in cortical bone from the equivalent experiment are illustrated in Fig. 4. Figure 4a shows T₁ maps before and after heating, overlaid on the UTE images. The baseline T₁ values were in a range of 130–170 ms. Figure 4b shows the map of T₁ changes due to heating, overlaid on the coronally-reformatted UTE image. The expected locations of the two transducers in the applicator are marked. Figure 4c shows the maps of T₁ changes at three different locations denoted in Fig. 4b. Figure 4d illustrates T₂ change maps in bone marrow of the matching locations, measured right before the second UTE T₁ mapping. T₁ increases were observed in the heated regions of cortical bone, adjacent to the regions of the bone marrow showing T₂ increases.

Figure 4.

UTE T₁ mapping. (a) Cortical bone T₁ maps before and after heating, overlaid on the UTE images. (b-c) Maps of T₁ changes between before and after heating, overlaid on the UTE images. In the coronal reformat (b), the applicator is identified as a dark line and the expected transducer positions are denoted. (c) shows T₁ change maps at the three locations denoted in (b). The slice location of (b) is denoted in the image on the top. Higher T₁ changes can be seen in the heated regions of cortical bone. (d) shows maps of T₂ changes in bone marrow right before the acquisition of the second UTE T₁ maps at the matching locations.

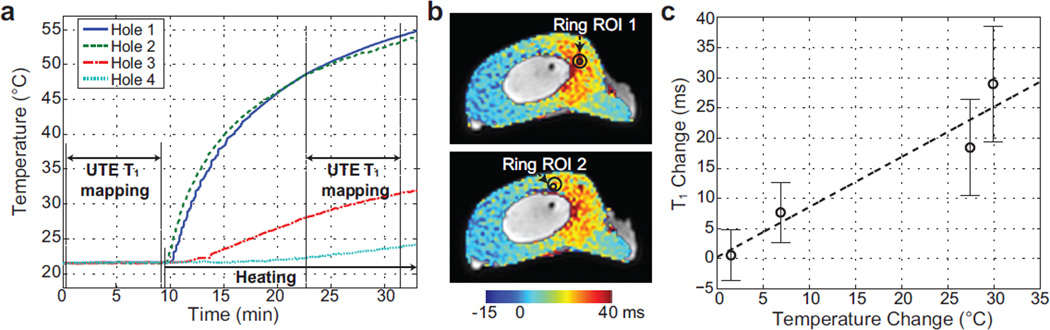
Temperatures measured with the fiberoptic temperature sensors in the four holes are displayed in Fig. 5a. Even though we assumed steady state during the second UTE T₁ mapping period, the temperature still increased. Assuming the temperature variations were negligible compared to overall temperature changes, the mean temperature changes between the two UTE T₁ mapping periods were used to associate with T₁ quantification. The mean temperature differences were 29.87°C, 27.38°C, 6.86°C, and 1.49°C in the four holes. Figure 5b denoted two ring-shaped ROIs on the T₁ change maps of the slices where two temperature sensors (providing the two highest temperatures) were located based on the high-resolution images. For the ROI in the bottom, the center of the outer oval was shifted from the sensor position not to include the bone/bone marrow boundary. Figure 5c shows a plot of the mean T₁ changes and error bars from the ring-shaped ROIs versus the mean temperature differences. This plot demonstrated increased T₁ changes with increased temperature changes. The dashed line represented a linear regression line, of which the linear coefficient was 0.83±0.18 ms/°C.

Figure 5.

Temperature changes versus T₁ changes. (a) Temperature measurements from the fiberoptic sensors over time. UTE T₁ mapping periods are denoted. (b) T₁ change maps of the slices where two temperature sensors are located and ring-shaped ROIs corresponding to the two sensors. (c) The mean T₁ changes and error bars from the four ring-shaped ROIs over mean temperature changes. The linear regression line is depicted as well.

Discussion

In this work, we have measured cortical bone T₁ changes over a temperature range relevant to thermal therapy monitoring. We achieved this using UTE imaging with a variable flip-angle method. Accurate quantification of T₁ in cortical bone is challenging due to its rapid signal decay, and flip angle errors can result in significant quantification errors when using the variable flip-angle method. Partial volume effects as well as any susceptibility-induced artifacts at interfaces with other tissues would also impact the accuracy of this method. However, our ex vivo experiments clearly demonstrated a T₁ increase with temperature in cortical bone. From the calibration experiment, an apparent linear relationship between temperature and T₁ was found with a coefficient of approximately 0.72 ms/°C, a 0.6%/°C change in T₁.

It was previously shown that temperature effects on T₁ might not be reversible in certain non-adipose tissues once the temperature threshold for protein coagulation is exceeded [42, 43]. From our ex vivo calibration study, the linear coefficients during heating and cooling were not identical; however, based on the observation that the linear coefficient was slightly higher during heating than that during cooling for one bone sample and that the opposite was the case for the other sample, there may be reversibility in T₁ in cortical bone over a temperature range of 25–70°C. As a large portion of cortical bone is composed of minerals, protein coagulation may have a lower effect on overall T₁ values in cortical bone as compared to soft tissues, resulting in potentially reversible changes in T₁ with temperature. In in vivo conditions where blood flow and inflammatory process are present, temperature-T₁ characteristics might differ from those observed in the ex vivo condition.

Variable flip-angle T₁ mapping is very sensitive to flip angle errors caused by RF-field inhomogeneities and flip angle miscalibration. In our calibration study, we measured T₁ as 120–130 ms near the body temperature. These are significantly lower than the values reported in [9,39], which measured T₁ as 230 ms for in vivo human subjects. This might be mainly due to flip angle miscalibration that occurred when imaging a container mostly filled with pure water having a very long T₁. Baseline T₁ values during the ultrasound heating experiments also ranged from 130 to 170 ms, which might result from RF-field inhomogeneities due to a presence of air near the applicator. Another concern is that T₂* relaxation in cortical bone during the RF pulse reduces the effective flip angle, which also affects T₁ calculations [41]. In our work, we used an RF pulse duration of 200 µs, with which the RF amplitude was close to the system limits (15 µT for body coil excitation) when a 44° flip angle was prescribed. The effective flip angle decrease during the 200 µs hard pulse excitation was 8% assuming a 0.5 ms T₂*. Flip angle errors and the effects of T₂* relaxation during the excitation can be reduced or corrected if the actual flip angle is measured. Actual flip-angle imaging [44] combined with UTE imaging may possibly be used to correct T₁ calculation errors [45].

The calibration study setup can be improved for more accurate quantification of T₁ in cortical bone. The deionized water has a very long T₂* and generated artifacts due to imperfect spoiling, in particular when the 44° flip angle was used. Doping the water with a MnCl₂ compound would reduce T₂* and reduce spoiling artifacts significantly. The susceptibility difference between bone and water also generated chemical shift artifacts [46] and blurring associated with radial trajectories. These affected T₁ quantification at the bone/water boundaries. Since these susceptibility-induced artifacts associated with radial trajectories become more significant farther from the iso-center [47], locating the bone samples near the iso-center would reduce T₁ quantification errors. Another concern is related to the potential change of bone water properties during the immersion of the samples in the water bath. To address this, we additionally acquired T₁ maps from a bone sample (frozen for a less than a week and thawed before the experiment) before and after immersing it in water for 7 hours. We observed almost no T₁ changes between the two time points. Since bone samples in the equivalent condition were used for our calibration study, we assumed that no significant water absorption occurred during the study. Alternatively, wrapping the bone in plastic, as done in [28], would prevent hydration regardless of the bone condition.

Cortical bone has a higher attenuation coefficient (80 Np/m/MHz) [48] compared to other soft tissues such as muscle and liver (3.4–9 Np/m/MHz over 20–70°C) [49]. However, the attenuation coefficient at 7 MHz in fatty yellow marrow is also relatively high, in a range of 11.5–36.2 Np/m/MHz over 20–70°C [50, 51]. In a phantom with low attenuation (5.6 Np/m/MHz), it was previously shown that the temperature peak occurred on the surface of cortical bone when the bone was within 10 mm of an interstitial ultrasound applicator while the peak occurred within the phantom when the applicator was located 15 mm or farther away from the bone surface [52]. In our ultrasound experiments, the applicator was located less than 10 mm from the cortical bone surface; however, a significant portion of energy might have been absorbed in the fatty marrow considering its attenuation coefficient and thus might have resulted in the peak temperature in the marrow.

Several other bone water properties might be useful to be quantified for a more accurate determination of temperature sensitivity of T₁ or for temperature mapping. In cortical bone, bone water is present in various states. Free bone water is located in porous spaces, bound water is bound to collagen and matrix substrate, and tightly bound water is embedded in the crystals of the mineral component. It was previously shown that the UTE signal from cortical bone stems from collagenbound water (T₂* ≈ 0.4 s) as well as free water (T₂* = 1 ms - 1s) [53,54]. The baseline T₁ and the temperature-T₁ linear coefficient would be affected by the bone water concentration and the proportions of free and bound water. In future studies, those values can be quantified for a more accurate characterization of temperature-T₁ dependence. Recently, Ramsay et al. [28] demonstrated that the signal from cortical bone increases with temperature, possibly due to a T₂ increase with temperature. T₂-based thermometry might be also useful for bone temperature mapping.

Direct quantification of temperature changes in cortical bone during bone tumor ablation could provide more accurate monitoring of thermal dose than the extrapolation of temperatures in surrounding soft tissues. As the ultrasound absorption coefficient is much higher in bone than in soft tissues, quantifying bone temperatures might improve the safety and efficacy of treatment. However, since bone T₁ mapping with our 3D UTE sequence is limited by a long scan time and low signal-to-noise ratio (SNR), in vivo applications are challenging. In particular, temperature monitoring during high-intensity focused ultrasound therapy requires a short update time. To reduce scan times, 2D UTE imaging sequences [55], which is more SNR efficient, can be used instead. Acceleration techniques such as parallel imaging and compressed sensing could be also combined with either 2D or 3D UTE imaging [56–58]. However, incorporating these techniques would reduce SNR and hamper accurate determination of T₁. Improvement in hardware systems including RF coil technology will be necessary to use T₁-based bone thermometry in in vivo conditions.

In conclusion, we have quantified changes in T₁ with temperature in ex vivo cortical bone using UTE MRI and demonstrated the feasibility of using T₁-based thermometry. We observed a linear relationship between temperature and T₁. Although our work was limited to ex vivo samples, the demonstration of temperature sensitivity in T₁ of cortical bone would be an important first step towards bone temperature mapping in a clinical setting.