Noninvasive Dissection of Mouse Sleep Using a Piezoelectric Motion Sensor

Abstract

Background

Changes in autonomic control cause regular breathing during NREM sleep to fluctuate during REM. Piezoelectric cage-floor sensors have been used to successfully discriminate sleep and wake states in mice based on signal features related to respiration and other movements. This study presents a classifier for noninvasively classifying REM and NREM using a piezoelectric sensor.

New Method

Vigilance state was scored manually in 4-second epochs for 24-hour EEG/EMG recordings in twenty mice. An unsupervised classifier clustered piezoelectric signal features quantifying movement and respiration into three states: one active; and two inactive with regular and irregular breathing respectively. These states were hypothesized to correspond to Wake, NREM, and REM respectively. States predicted by the classifier were compared against manual EEG/EMG scores to test this hypothesis.

Results

Using only piezoelectric signal features, an unsupervised classifier distinguished Wake with high (89% sensitivity, 96% specificity) and REM with moderate (73% sensitivity, 75% specificity) accuracy, but NREM with poor sensitivity (51%) and high specificity (96%). The classifier sometimes confused light NREM sleep—characterized by irregular breathing and moderate delta EEG power—with REM. A supervised classifier improved sensitivities to 90, 81, and 67% and all specificities to over 90% for Wake, NREM, and REM respectively.

Comparison with Existing Methods

Unlike most actigraphic techniques, which only differentiate sleep from wake, the proposed piezoelectric method further dissects sleep based on breathing regularity into states strongly correlated with REM and NREM.

Conclusions

This approach could facilitate large-sample screening for genes influencing different sleep traits, besides drug studies or other manipulations.

1. Introduction

Our understanding of sleep is advancing rapidly; yet every milestone achieved in probing the structure and function of this intriguing phenomenon reveals a new layer of complexity. Many sleep-related peculiarities are, at least in part, heritable (O’Hara and Mignot, 2000; Franken and Tafti, 2003). Genetic dissection using animal phenotypes is therefore expected to provide fundamental insights into sleep and wakefulness. Among mammals, mice have the best genetic and genomic resources for finding the genes that contribute to each sleep trait and they are increasingly being used to characterize behavior for genetic and drug studies. For instance, quantitative trait locus (QTL) analysis (Hunter and Crawford 2008) is one technique that has been used for identifying genome regions associated with polygenic traits that can be quantified on a continuous scale, such as the mean duration of sleep bouts. However, discovery of sleep-related genes involves screening large cohorts to correlate observed behavior with genetic profile, which is time-consuming.

The gold standard method for sleep analysis in mammals is polysomnography, a panel of simultaneous physiological measurements that comprises an electroencephalogram (EEG) and electromyogram (EMG) (Steriade 2000) at a minimum. Three major vigilance states are defined in mice based on EEG/EMG appearance: 1. Wakefulness (Wake), characterized by low amplitude, broadband EEG and high-powered, variable EMG; 2. Paradoxical or rapid eye movement sleep (REM), characterized by a theta EEG rhythm (6-9 Hz) and suppressed EMG (except for occasional muscle twitches); and 3. Non-REM sleep (NREM), sometimes termed slow wave sleep, characterized by low frequency, large amplitude delta EEG oscillations (0.5-4 Hz) and low, tonic EMG. EEG/EMG measurement in rodents is an invasive and resource-intensive process, a critical barrier to the discovery of sleep-related genes. While the only acceptable way to accurately discriminate vigilance state is through manual or automated scoring of the EEG/EMG signals, the required effort (surgery, recovery, etc.) limits the use of EEG/EMG in the large-scale experiments needed for genetic analysis of rodent behavior. Besides, a tether is often required for signal acquisition, which may restrict natural behavior and make simultaneous screening of multiple animals difficult. Non-tethered telemetric systems exist but still require the invasive implantation of electrodes, battery pack, preamplifier, and transmitter that may again alter behavior and hinder movement, especially in small animals like the mouse.

Many noninvasive behavioral phenotyping systems have been devised for small animals that use video tracking (Publicover et al. 2009), wheel running (Wisor et al. 2009), light beam breaking (Nairizi et al. 2009), and accelerometry (Venkatraman et al. 2010; Brodkin et al. 2014) to distinguish gross and subtle awake behaviors such as grooming, feeding, locomotion, rearing, circling, and even quiet wakefulness from sleep. Although these technologies have potential for high-throughput use, they mainly perform actigraphy: none of them reliably separate sleep into its components, namely REM and NREM, and none have been used effectively in high-throughput studies. A completely noninvasive system that discriminates between REM and NREM in mice as reliably as EEG/EMG would greatly facilitate high-throughput screening for the discovery of genes relevant to sleep and sleep-related disorders.

Physiological differences in REM regulation help us distinguish it from NREM. Skeletal muscle tone, already low in sleep, is further inhibited during REM leading to a visibly flaccid posture when compared to NREM. The feasibility of detecting this change in aspect during REM using videographic image analysis has recently been investigated (McShane et al. 2012) and appears promising, but was not deemed feasible in other video studies (Fisher et al. 2012) and is harder to perform with high throughput. Skeletal muscle paralysis is not the only peculiarity associated with REM though: mentation and irregular autonomic activity can produce ballistic eye movements (hence the name REM), variable heart rate (Calasso and Parmeggiani 2008), irregular breathing (Friedman et al. 2004), phasic muscle twitches (Geisler et al. 1987), and even middle ear muscle activity (Benson and Zarcone 1979). The observation that the regular breathing associated with NREM becomes irregular in REM (Friedman et al. 2004) suggests that a contact sensor that responds to ventilatory movement might be useful for telling them apart. In fact, a piezoelectric sensor placed on the mouse cage floor is known to detect pressure variations associated with respiratory effort when the animal is relatively still (Flores et al. 2007). The resulting quasirhythmic “piezo” signal differentiates sleep from quiet or active wakefulness with accuracy comparable to a human observer (Donohue et al. 2008). Mang et al. (2014) found that the decision statistic used by the same classifier to distinguish sleep from wakefulness (Donohue et al. 2008) appears to change in value following REM-NREM transitions as well. Sato et al. (2010) used a piezoelectric transducer to monitor mice and documented rapid increases in breathing rate during sleep with atonic posture, presumably in REM. They subsequently used this piezoelectric system to differentiate REM from NREM and Wake, but on the basis of immobility and perceived heart rate signals, in a small sample of wild type mice (Sato et al. 2014).

The literature cited above strongly suggests that the piezo could detect episodes of REM in mice based on signal changes associated with the irregular respiratory rhythm, but it does not tell us whether these measured respiratory changes occur in REM alone. The purpose of the present investigation is to determine how well behavioral states that are separable in terms of muscle tone and respiratory rhythm (as quantified by the piezo signal) correspond to electrophysiologically distinct vigilance states: namely Wake, NREM, and REM. To answer this question, first piezo signal features indicative of breathing regularity and muscle tone are extracted from 24-hour recordings in each of 20 mice in sequential epochs. Each time series of piezo signal features is automatically segmented using an unsupervised hidden Markov model (HMM) classifier into states that form natural clusters in the feature space in terms of breathing regularity and muscle tone. The states identified by the HMM are compared with the true vigilance states (Wake, NREM, and REM) determined by manual scoring of simultaneously acquired EEG/EMG measurements. The concordance between piezo-derived state scores and manual scores is assessed and analyzed for potential sources of error. Finally, conclusions are drawn regarding the feasibility of using the piezo sensor to noninvasively stage sleep in mice, which is expected to reduce the need for EEG/EMG analysis in large-sample screening of sleep phenotypes.

2. Methods

Overview

EEG, EMG, and piezo signals were acquired from mice along with video for a 24-hour period. Two human raters blinded to the piezo signal independently labeled vigilance state in sequential 4-s epochs as NREM, REM, or Wake by inspecting the EEG, EMG and video recordings and using conventional criteria. Features designed to quantify subtle movements and breathing from the piezo signal were estimated for each epoch of data. Natural clusters that separated the data into three distinct states were identified in the feature space: a relatively high activity state with variable breathing patterns; a low activity state characterized by a regular breathing rhythm; and another quiescent state but with relatively irregular breathing. Epochs of the piezo feature time series were mapped onto these three behavioral states using an unsupervised probabilistic classifier—a hidden Markov model (HMM)—with the general expectation that the states would correspond to Wake, NREM, and REM, respectively. Finally, the model-predicted states were compared against consensus human scores to assess whether this expectation was reasonable and enabled noninvasive classification of vigilance state and estimation of commonly used sleep metrics.

Animal procedures

All procedures used in the study were approved by the Institutional Animal Care and Use Committee (IACUC) of the University of Kentucky. Twenty adult male mice (C57BL/6J, Jackson Labs, Bar Harbor, Maine, USA), each 8-10 weeks old and weighing 24-29 g, were housed individually under a 14-h/10-h light/dark cycle (lights on at 7 a.m., off at 9 p.m.). EEG/EMG recordings were performed using a tethered acquisition system (Pinnacle Tech., Lawrence, Kansas, USA) in which electrodes and a head-mounted preamplifier were surgically implanted under anesthesia. The headmount is held in place by two pairs of stainless steel bone screws that serve as epidural EEG electrodes. Bipolar stainless steel wires extending from the headmount are inserted into the nuchal muscle to record EMG. Details of the EEG/EMG implantation procedure are available elsewhere (Yaghouby et al. 2014a). Two weeks were allowed prior to recording for the animals to recover completely from the procedure. Each mouse was housed with free access to food and water in a 7“×7” plexiglass cage equipped with a piezo sensor pad on the floor under 1-2 cm of bedding. Recording of EEG, EMG, piezo and video was started by cabling the headmount to a swivel commutator, which permitted continuous signal acquisition and free movement within the cage.

Monitoring and data acquisition

EEG and EMG signals were preamplified (100×) at the headmount and transmitted via the commutator to a biosignal amplifier (8200 series, Pinnacle Technology, Inc., Lawrence, Kansas, USA), which further conditioned, amplified (50×), and sampled the signals at 400 Hz and 16-bit resolution before saving them on a computer for analysis. The EEG and EMG were filtered from 0.5-100 Hz and 10-100 Hz respectively. Animals behavior was monitored continuously using digital video with infrared illumination in the dark period.

The signal from the piezo sensor pad was sampled synchronously with the EEG and EMG and written to the same data files. The piezo system (Signal Solutions, LLC, Lexington, Kentucky, USA) is described in detail elsewhere (Donohue et al. 2008; Mang et al. 2014). Briefly, the piezo sensor is a thin dielectric sheet that generates a voltage signal in response to changes in surface pressure. With the sensor placed on the cage floor, motion associated with different mouse behaviors produce characteristic signals. The response of the sensor system is designed to cover the frequency range generally associated with sleep and breathing in mice (Friedman et al. 2004). The amplified piezo signal was sampled at 400 Hz by a data acquisition board (USB-6211, National Instruments) and saved along with the EEG and EMG signals.

Manual scoring of vigilance state

A 24 hour recording of EEG, EMG, and video for each mouse was reviewed independently on a computer by two human raters (blinded to the piezo signal) to verify signal quality and assign each 4-s epoch to one of three distinct vigilance states: NREM, REM, or Wake. The visual scores were based on the following well-established guidelines. The mouse was deemed to be in Sleep when the EMG was of low amplitude and the animal was observed to be motionless with eyes closed. Epochs within sleep were scored as NREM if accompanied by large amplitude, slow EEG oscillations (delta rhythm: 0.5-4 Hz), and as REM if the EEG followed a lower amplitude but higher frequency theta rhythm (6-9 Hz). The Wake state was marked by high EMG activity and variable rhythms on the EEG.

Feature selection and extraction

The piezo signal captures instantaneous fluctuations in pressure on its surface, which is useful for characterizing behavioral state. Features were selected to quantify fine movements likely to differentiate Wake from Sleep, and to quantify the respiratory rhythm and amplitude for the inactive state in the hope of differentiating REM from NREM sleep on the basis of breathing regularity or variability (BRV). With regard to movement, it was observed that simple measures of instantaneous piezo signal power, such as the mean Teager energy (TE) (Kaiser 1990), fluctuate with EMG power, which reflects muscle tone, across Sleep-Wake transitions, even during brief arousal (Fig. 1). In quiet Wake and in Sleep, the chest and abdominal wall movement associated with mouse respiration is the main source of variation in the piezo signal; this was demonstrated using impedance pneumography (Flores et al. 2007). Examination of vigilance state transitions during Sleep shows that the quasiperiodic rhythm on the piezo signal associated with regular breathing in NREM becomes less regular in both amplitude and frequency with the onset of REM (Fig. 2). This suggests that BRV features extracted from the piezo signal could be used to differentiate REM from NREM (Fig. 3). A vector V_t of six features was estimated from each 4-second non-overlapping epoch t of the piezo signal, and comprised the following: mean Teager energy TE, mean breath rate f, breath envelope amplitude variability BRV1, two different measures of breath time regularity (the Rayleigh index BRV2 and lagged phase coherence BRV3), and finally normalized spectral mode amplitude BRV4, which is a regularity measure influenced by both time and amplitude variability. It is expected that sample feature data will form distinct clusters in this six-dimensional feature space corresponding to the three vigilance states based on the pattern and amplitude of motion and ventilation typical of those states. Computational procedures for extracting the selected features from each epoch are described in Appendix A. All analysis was performed in the Matlab^™ environment (Mathworks, Natick, MA).

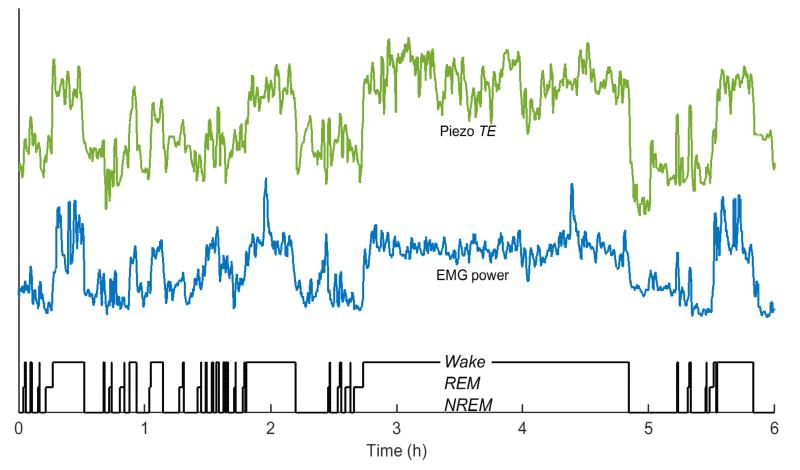
Figure 1.

Correlation between piezo signal power and muscle tone in mice. Instantaneous energy estimated in the piezo signal in 4-s epochs over a 6-h period by the mean Teager energy, TE (green) is strongly correlated with r.m.s. power (blue) of the mouse EMG. TE therefore effectively tracks sleep-wake transitions, even during brief arousals, as evidenced by comparison with the human-scored hypnogram (black) based on EEG/EMG. Feature traces are shown in arbitrary units and scaled for ease of comparison.

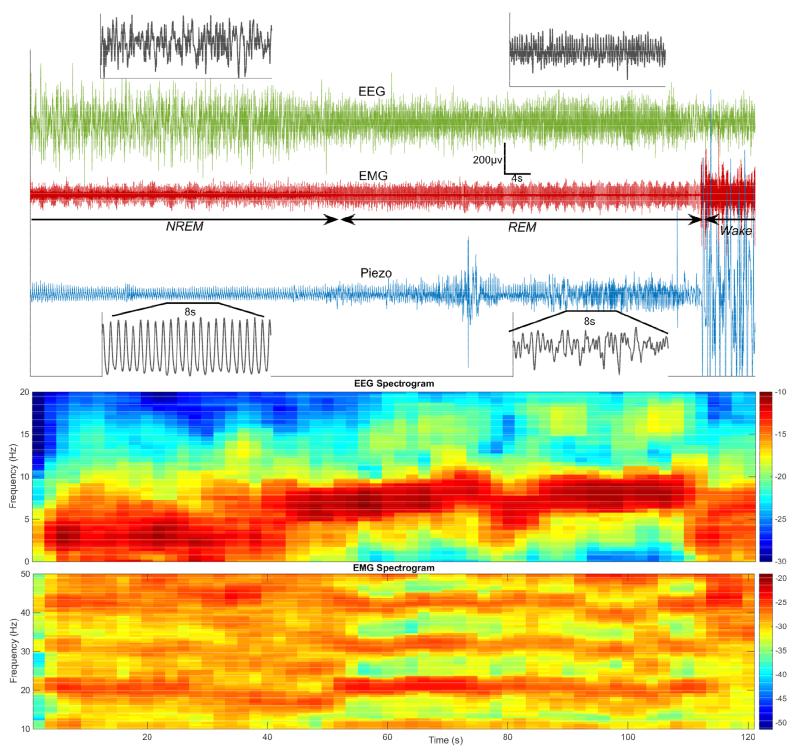
Figure 2.

Top: The respiratory pattern captured by the piezo signal (blue) changes visibly during a typical NREM-REM-Wake transition in mouse sleep. A highly regular rhythm in NREM sleep, characterized by large amplitude delta rhythm on EEG (green) and suppressed EMG (red), is disturbed in both amplitude and timing upon transition to REM (lower amplitude theta EEG rhythm, low tonic EMG). The respiratory trace is completely obscured by large amplitude motion coinciding with a surge in EMG power that signals the transition from REM to Wake. Bottom: Fourier power spectra (in decibels) of the EEG and EMG, computed in 4s increments for the signals above, clearly demonstrates the shift from a delta rhythm in NREM to a theta rhythm in REM. Muscle tone, which is high in Wake and suppressed in NREM sleep, is further inhibited in REM. The heart artifact is visible as a pronounced harmonic during REM on the EMG, which is highpass-filtered with a 10 Hz cutoff prior to sampling.

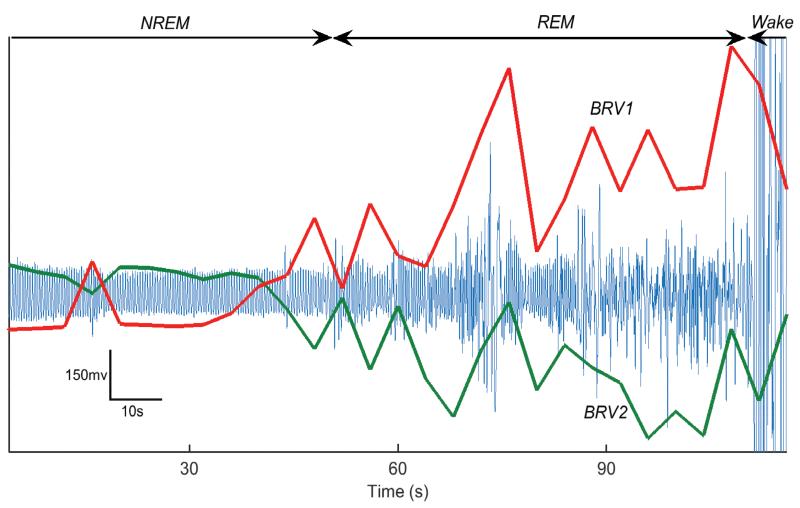
Figure 3.

Trends in breath regularity and variability (BRV) features of the piezo signal (blue) during a sample sleep transition from NREM to REM and Wake. BRV1 (red) estimates variability in the piezo envelope while BRV2 (green) tracks regularity in its period of oscillation. Both features (arbitrary units) are at stable levels that indicate regular breathing in NREM but quickly diverge upon transition to REM and Wake.

Unsupervised modeling of vigilance dynamics

Without foreknowledge of the EEG-determined vigilance states, time series of the features described above were observed to settle at different levels corresponding to low and high levels of activity suggestive of Sleep-Wake differences; and during the low activity state (presumed to be Sleep) into periods of relatively regular and irregular breathing. In keeping with the polyphasic nature of their activity cycles, mice spent variable amounts of time in each of the three states described above, and made rapid transitions between them at irregular intervals. The seemingly random nature of these transitions between discrete states suggested that their dynamics could be modeled as a Markov chain (Zung et al. 1966), in which a system occupies one of many discrete states at any instant but makes random transitions to other states in a manner determined only by the current state (the Markov property). A Markov chain in which the true state is concealed but characterized by observations whose probability distribution is conditioned on the state is known as a hidden Markov model or HMM. In this study, the piezo signal feature dynamics were fitted to an HMM with multivariate Gaussian observations whose mean and covariance depend on each state; i.e., a Gaussian observation HMM (Fraser 2008). Standard maximum likelihood estimation techniques were used to fit the vector time series of piezo signal features to an HMM in an unsupervised manner: i.e., by defining the states and their parameters as those natural partitions in the feature space that were best explained by the feature time series without the use of human-labeled training samples. This is done in order to test—in an unbiased manner—whether states that differ mainly in their motion and/or respiratory patterns correspond to electrophysiologically defined vigilance states. A set of three states are posited for the piezo signal: 1. High activity; 2. Inactive with regular breathing; and 3. Inactive with irregular breathing; these are hypothesized to correspond to Wake, NREM, and REM vigilance states, respectively, a claim that will be subsequently tested against EEG/EMG scores. Previous work has shown how HMMs can be used for automated sleep scoring based on polysomnographic recordings in humans (Yaghouby et al., 2014, Yaghouby and Sunderam 2015); here a similar modeling framework is applied to piezo recordings in mice. A more formal description of HMMs is provided in Appendix B.

Automated sleep scoring and performance assessment

Initial guesses for the HMM parameters (state-conditioned means and covariances, and state transition matrices) along with an initial partitioning of the piezo feature space were obtained by first fitting each animal’s 24-hour piezo feature time series to a three-component Gaussian mixture model (GMM). Then a three-state HMM was estimated from the feature time series and initial parameter estimates and used to decode the most likely sequence of discrete model states underlying them. The correlation between the “motion-respiration” states captured by the model from the piezo signal and the human-scored vigilance states (i.e., Wake, NREM and REM) was tested using conventional detection metrics, namely the sensitivity and specificity with respect to consensus manual scores. Sensitivity was estimated as the proportion of epochs of each state that were correctly labeled as that state (i.e., fraction of true positive detections) and specificity as the proportion of epochs that were correctly identified as belonging to one of the other two states (i.e., fraction of true negatives) rather than the state of interest.

Cohen’s kappa (κ) (Cohen 1960), a popular measure of inter-rater agreement, was used to assess the level of consensus between the two human raters. κ corrects the observed agreement (p_o), i.e., the fraction of epochs on which both raters agree, for the chance agreement (p_c) that may result simply from the overall proportions in which the states occur in the sample; that is, $\kappa =\frac{p_o-p_c}{1-p_c}$, κ > 80% indicates essentially perfect agreement, while values in the range of 60-80, 40-60, and < 40% indicate substantial, moderate, and poor agreement between the raters, respectively.

HMM-based estimates of commonly used sleep metrics, namely the % time spent, number of bouts, and mean bout duration of each state were compared against estimates based on each human rater’s sleep scores. Finally, potential sources of error were examined to account for discrepancies between the piezo states and human-scored vigilance states.

3. Results

Automated scoring of vigilance state using the piezo signal classifier

An unsupervised HMM was estimated for piezo features computed in 24-hour long recordings from each of 20 mice to predict vigilance state in 4-s windows. Scores predicted by the HMM were compared for epochs on which both human raters’ scores were identical. Agreement between the two independent human raters’ scores was excellent at 97, 95, and 98% for Wake, NREM, and REM with Cohen’s κ values of 93, 90, and 83%, respectively. Inspection of the sensitivity and specificity of detection of each individual state (Table I) by the unsupervised HMM reveals excellent discrimination of Wake (versus REM and NREM). While sensitivity and specificity were both moderately high (over 70%) for REM, they were asymmetric for NREM, with the HMM’s poor sensitivity to NREM being the most prominent source of error. A confusion matrix of HMM scores versus consensus human scores (Table II) shows that the majority of undetected NREM epochs (46%) were incorrectly assigned to REM sleep.

Table I.

Accuracy of piezo HMM classifiers assessed against manually scored vigilance state (for consensus-scored epochs only). Values reported as mean ± standard error (n = 20 mice).

Vigilance State	Unsupervised HMM		Supervised HMM
	Sensitivity (%)	Specificity (%)	Sensitivity (%)	Specificity (%)
Wake	88±1	96±1	90±2	91±2
NREM	51±1	96±1	81±3	92±1
REM	73±3	75±1	66±3	93±1

Table II.

Confusion matrices for prediction of vigilance state by piezo HMM classifiers (pooled data from n = 20 mice; consensus-scored epochs only).

True State	Predicted State (expressed as % of epochs of True State)
	Unsupervised HMM			Supervised HMM
	Wake	NREM	REM	Wake	NREM	REM
Wake	88	2	9	90	6	4
NREM	3	51	46	8	81	11
REM	9	19	72	9	26	66

To overcome the limited REM/NREM discrimination by the unsupervised HMM, a supervised HMM classifier was implemented using the same features as the unsupervised one. Leave-one-out cross validation was performed in which a model trained on data from n-1 mice is tested on that of the nth mouse (n = 20) to predict the sequence of vigilance states; this is repeated for each mouse in turn. In the training phase, HMM parameters (i.e., the state transition matrix, and the vector mean and covariance matrix of the feature distribution in each state) were estimated using piezo feature vectors and scores (of both human raters) for n-1 (i.e., 19) mice. The vector time series of piezo features from the test animal was then decoded by the trained HMM using the Viterbi algorithm (Rabiner 1989) to find the most likely sequence of vigilance states.

Table I also summarizes the sensitivity and specificity of the supervised HMM for different states of vigilance. While both are essentially unchanged for Wake classification (versus REM and NREM), NREM sensitivity and REM specificity are appreciably greater with the supervised HMM. In fact, specificity now exceeds 90% for all three states. The increased sensitivity to NREM comes at the cost of slightly reduced sensitivity (but greater specificity) to REM.

Estimation of common sleep metrics using the piezo signal classifier

The ability of the piezo classifier to predict typical sleep metrics, namely the % time spent, mean bout duration, and number of bouts in each vigilance state, which usually require EEG/EMG measurements for their estimation, was assessed. The manually scored hypnogram for each animal and for each rater was first modified to contain epoch labels for five vigilance states: i.e., prolonged bouts of Sleep, now defined as a sequence of vigilance state transitions that is not interrupted by Wake for more than five minutes at a time; prolonged bouts of Wake between consecutive Sleep bouts; and episodes of REM, NREM, and brief arousal (BA) within bouts of Sleep. This more fine-grained labeling of states intentionally makes the distinction between BA during Sleep and sustained periods of Wake, which are both hallmarks of rodent sleep (McShane et al. 2010). The three sleep metrics were then estimated for each of the five states from the modified hypnograms scored by each rater. The same metrics were derived from similarly modified HMM-predicted hypnograms for comparison with the manually derived metrics. The sample hypnogram in Fig. 4 illustrates the alternation of Sleep and Wake bouts as well as transitions between NREM, REM, and BA within Sleep.

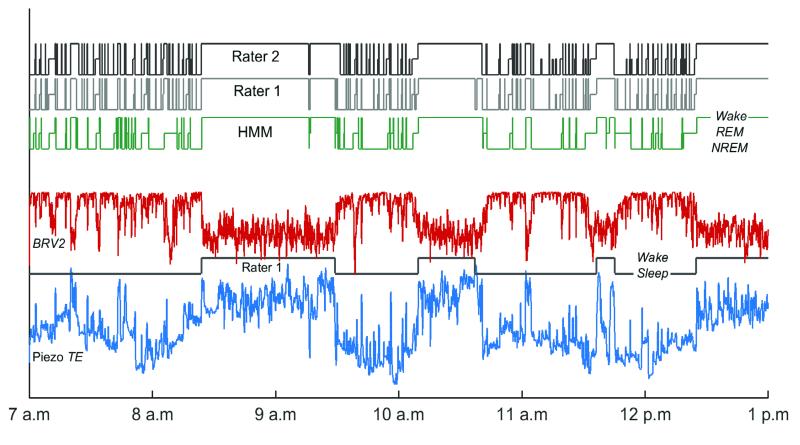
Figure 4.

Six-hour recording showing sample input features of the piezo signal that correlate with mouse movement (Piezo TE, blue) and breathing regularity (BRV2, red). Also shown are the sequence of vigilance states (i.e., the hypnogram) predicted by the unsupervised HMM from piezo features, and human-scored hypnograms (Raters 1 and 2) for comparison. The hypnogram for Rater 1 is also modified to show only the prolonged Sleep and Wake bouts (Lower). Transitions between NREM, REM, and BA on a smaller timescale can be observed by examining regions of the original hypnogram from Rater 1 (Upper) within each bout of Sleep. See Suppl. Fig. 1 for time series over the full 24 hour period of observation.

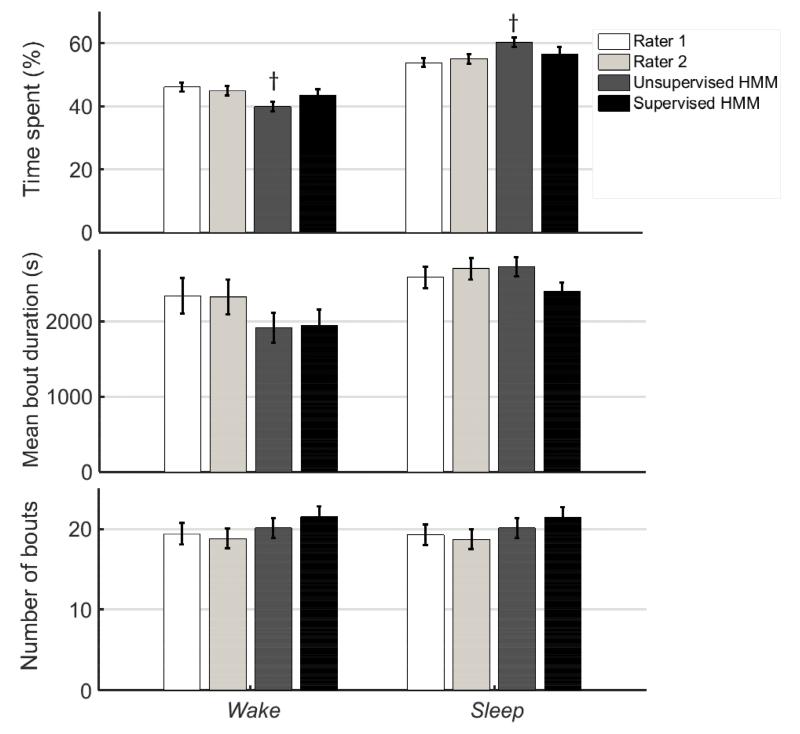
Fig. 5 compares mean metrics for Sleep and Wake bouts estimated from the supervised and unsupervised HMM predictions against values estimated independently from the manual scores of the two human raters. Matched sample comparisons were made of the values estimated by each model against the mean of the two values estimated by the human raters using the Wilcoxon sign rank test for matched samples. In order to make the test more likely to detect errors in the model-based estimates of sleep metrics, no correction was made to control for false positives (Type II error) when repeating the test for multiple outcome measures. Instead, significant differences at the 95 % (p < 0.05) and 99 % (p < 0.01) level are highlighted in the results (Figs. 5 and 6). The unsupervised HMM consistently overestimated and underestimated % time in Sleep and Wake respectively by a small margin (p < 0.05); but there was no such bias for the supervised HMM. Sleep and Wake were not significantly different in their mean bout duration and mean number of bouts for either model compared to the human rater estimates.

Figure 5.

Metrics for Wake (left) and Sleep (right) bouts estimated by manual EEG/EMG-based scores (Rater 1 and Rater 2) and from the piezo signal based on predictions made by unsupervised and supervised HMMs. Bars represent mean±standard error (n = 20 mice) of Sleep and Wake metrics estimated from independent manual scores of EEG/EMG data (Raters 1 and 2) and HMM classification of piezo signal features. † and * indicate that comparison of the HMM-estimated sleep metric is significantly different from the average of estimates by Rater 1 and Rater 2 based on a Wilcoxon sign-rank (matched sample) test at the 95 % (p < 0.05) and 99 % (p < 0.01) confidence level, respectively. Only the % time spent in Sleep (or Wake) predicted by the unsupervised HMM was significantly different from the averaged manual estimates (p < 0.05).

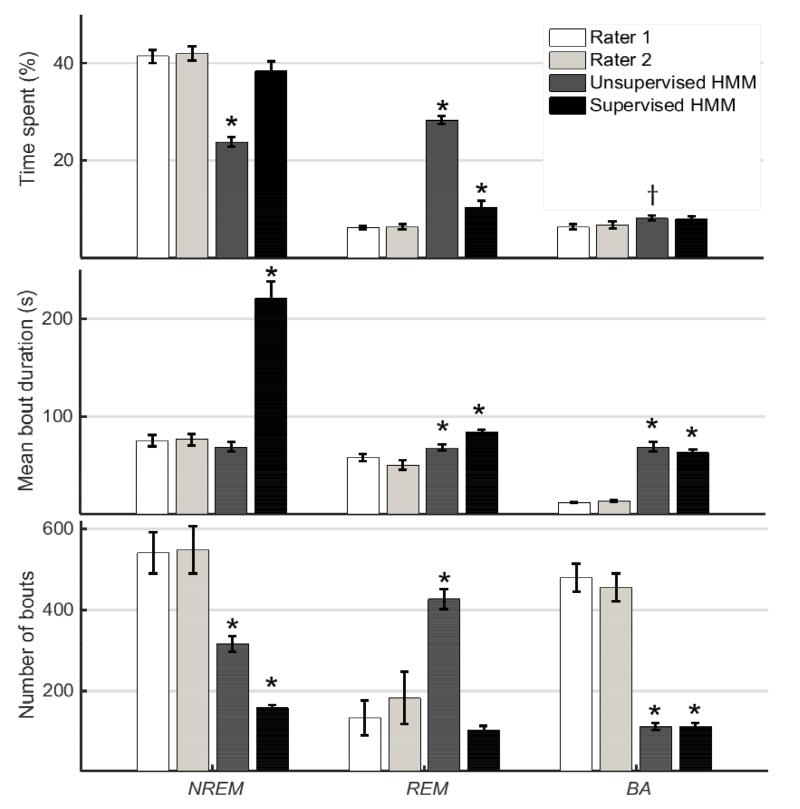
Figure 6.

Metrics for NREM (left), REM (center) and BA (right) bouts estimated by manual EEG/EMG-based scores (Rater 1 and Rater 2) and from the piezo signal based on predictions made by unsupervised and supervised HMMs. Bars represent mean±standard error (n = 20 mice) of NREM, REM, and BA metrics estimated from independent manual scores of EEG/EMG data (Raters 1 and 2) and HMM classification of piezo signal features. † and * indicate that comparison of the HMM-estimated sleep metric is significantly different from the average of estimates by Rater 1 and Rater 2 based on a Wilcoxon sign-rank (matched sample) test at the 95 % (p < 0.05) and 99 % (p < 0.01) confidence level, respectively.

Inspection of the metrics estimated for REM, NREM and BA during Sleep bouts in Fig. 6 shows that the unsupervised HMM significantly overestimated % time in REM and underestimated % time in NREM (p < 0.01) which is consistent with Tables I and II. Again, this was not the case with the supervised HMM, except for a slight overestimation of REM. The unsupervised HMM significantly overestimated % time in BA (p < 0.05) but only by a small margin. This may be explained by the tendency of HMM predictions to favor the status quo unless a future observation strongly support a transition. This smoothing behavior may cluster BAs together if they are close enough to each other, and is reflected in the significantly larger mean bout duration and lower number of bouts for BA (p < 0.01). At the same time, mean NREM bout durations were accurately estimated by the unsupervised HMM but overestimated by the supervised HMM (p < 0.01); mean REM bout durations were slightly overestimated by both HMMs (p < 0.01). The number of NREM bouts was underestimated by both HMMs (p < 0.01) but the unsupervised HMM overestimated REM bouts (p < 0.01). In general, the supervised HMM estimated % time and mean bout duration better than the unsupervised HMM.

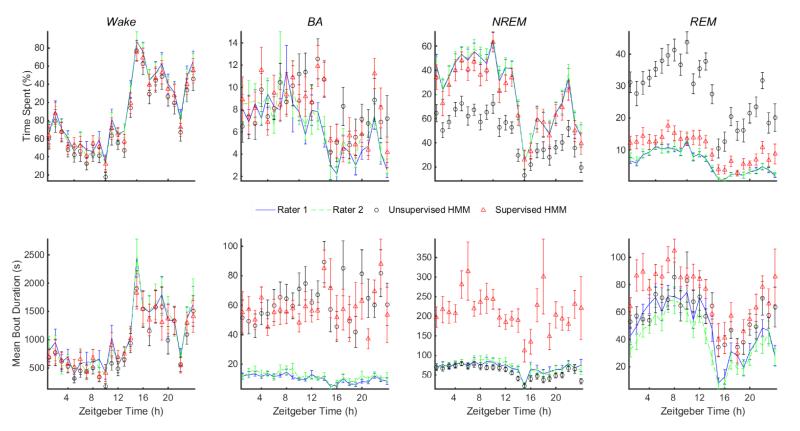
Profiles of hourly estimates of sleep metrics are shown in Fig. 7 for both HMMs and compared with estimates from human scoring. The estimated % time spent in each state tracks the diurnal variation across the Light/Dark periods well, except for the underestimation of NREM and overestimation of REM by the unsupervised HMM. Trends for Sleep bouts mirror trends for Wake and are not shown. The hourly mean bout duration also closely tracks human estimates, except that NREM is overestimated by the supervised HMM. Mean duration of BA bouts is consistently overestimated by both HMMs but not by a large extent. The hourly mean number of bouts is not shown but can be inferred from the other metrics. In general, the profiles are very similar to those seen in the literature (Brankačk et al. 2010, Martire et al. 2012, Zhou et al. 2014).

Figure 7.

Trends in hourly averages of sleep metrics for Wake, BA, NREM, and REM bouts estimated by manual EEG/EMG-based scores (Rater 1 and Rater 2) and from the piezo signal based on predictions made by unsupervised and supervised HMMs. Metrics for Sleep bouts and number of bouts for all vigilance states are not shown due to space limitations. Error bars represent mean±standard error (n = 20 mice) of metrics estimated from independent manual scores of EEG/EMG data (Raters 1 and 2) and HMM classification of piezo signal features. Zeitgeber time is measured in hours from the onset of the Light period; the Dark period begins at 14 h.

4. Discussion

In a study performed on wild type mice, an unsupervised classifier (an HMM) constructed from piezo signal features distinguished Wake from Sleep with high accuracy, and dissociated Sleep into REM and NREM components but not at the same level of performance (Table I). The main limitation was that the HMM mislabeled many NREM epochs as REM (Table II), which led to further errors in estimates of sleep metrics commonly used to summarize behavior (Figs. 5 and 6). This classification bias may result from multiple factors that warrant discussion.

The original motivation for testing whether the piezo system could distinguish REM and NREM sleep came from its ability to detect ventilation-related changes in pressure from the animal’s ventral aspect when it is relatively still. The respiratory rhythm, which is highly regular in NREM sleep, is known to become irregular during REM. Even early studies noted dramatic increases in the variability of respiration, heart rate, and blood pressure during REM compared to the different stages of NREM sleep (Snyder et al. 1964) and phasic changes in respiratory variables coinciding with instances of rapid eye movement (Pack, 1995). These phenomena point to fundamental differences in autonomic control mechanisms as the source of the observed respiratory variability. One reason proposed is the systemic suspension of homeostastic control during REM (Parmeggiani 2011), which allows cardiorespiratory variables to drift relative to their values in other stages of sleep.

Previous investigations that used piezo sensors to monitor mouse behavior suggest that they may track physiological changes during REM (Flores et al. 2007, Donohue et al. 2008, Mang et al. 2014) but do not clarify whether these changes are peculiar to REM alone, only that the piezo detects periods of relatively high and low breathing regularity that may correspond to different stages of sleep. In order to perform an unbiased test of the correlation between these respiratory patterns and REM/NREM states, an unsupervised HMM classifier was used here to capture the dynamics associated with them from signal features that quantify motion and respiration. While there was a positive correlation between REM and a piezo HMM state characterized by irregular breathing during Sleep, this state also included some periods of Sleep that were labeled NREM based on electrophysiological criteria (i.e., EEG/EMG).

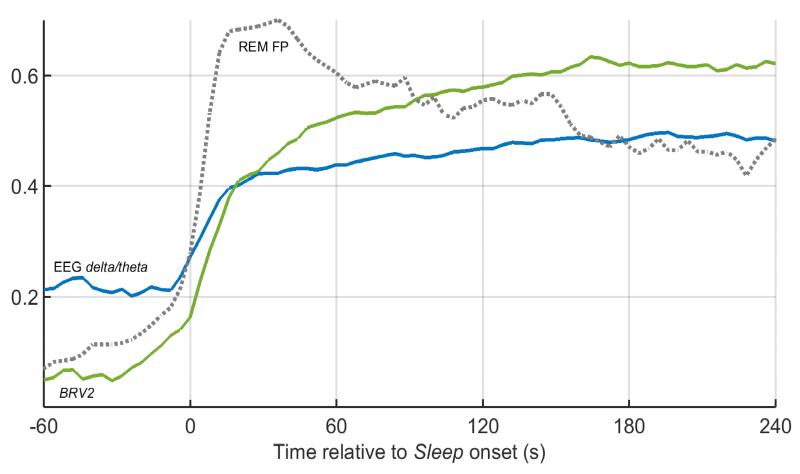
Irregular breathing during REM—just like the darting eye movements that give it its name—is episodic and need not last the entire duration of a REM bout. At the same time, breathing is known to be more regular in deep NREM than light NREM (Long et al., 2014). This suggests that periods of irregular breathing observed in mice during NREM may actually correspond to light NREM sleep and therefore be mistaken for REM (Table II). To test this hypothesis, trends in BRV features were examined time-locked to the onset of Sleep following a prolonged bout of Wake and averaged over all such Wake-Sleep transitions for all available recordings (Fig. 8). For comparison purposes, the average trend in delta band EEG power (0.5-4 Hz), a recognized index of sleep depth (Borbely and Achermann 2005), was plotted (normalized by the theta band EEG power (6-9 Hz) to emphasize the contrast with REM sleep) for the same periods. It is observed that delta EEG power steadily increases for a couple of minutes at the onset of Sleep before it saturates at a level consistent with deep NREM. Interestingly, BRV2 (and other BRV features, not shown in Fig. 8) follows the same trend on the same timescale. In addition, the probability that the unsupervised HMM classifier will falsely predict REM during this period peaks in the first minute of Sleep and then decays to settle at a lower level. These trends strongly indicate that irregular breathing accompanies light NREM, making it harder to distinguish from REM. The three-state HMM grouped REM and light NREM as one state due to the considerable overlap in their BRV features.

Figure 8.

Trends in piezo (BRV2) and EEG (delta/theta power ratio) features at the onset of Sleep following bouts of prolonged Wake. The traces represent averages computed over 385 Wake-Sleep transitions (as scored by Rater 1) in twenty mice. EEG delta/theta (blue) is the estimated delta band EEG power (0.5-4 Hz), a measure of sleep depth, normalized by the theta band EEG power (6-9 Hz). This is predictably low in Wake and gradually increases at Sleep onset, saturating within about 2-3 min. Breathing regularity, estimated by BRV2 (green) appears to follow the same trend. Furthermore, the probability that an unsupervised HMM will falsely predict REM (REM FP, dashed line) from the piezo signal increases in concert with EEG delta/theta and BRV2, and peaks in the first minute of Sleep before settling at a level consistent with its mean value in Sleep. This suggests that the unsupervised HMM confuses light NREM with REM at Sleep onset due to the irregular breathing associated with both states.

Another possible source of error could lie in the way BRV features are distributed. In periods of deep NREM sleep (slow rhythmic delta EEG oscillations and highly regular breathing), BRV measures are limited at one end of the scale by a value that corresponds to a strictly periodic signal; but during light NREM they are distributed over a broader range. The conditional distribution of BRV features in NREM is therefore a mixture of two components with very different means and variances. But here it was modeled as a single component Gaussian, which may be a poor approximation. The more variable component, even if modeled more accurately, is likely to overlap significantly with the conditional distribution for REM. As a consequence, REM and light NREM end up being modeled as one cluster denoted as REM, and the HMM overestimates REM (irregular breathing) while underestimating NREM (highly regular breathing). Lastly, REM occurs only about 5% of the time (see Fig. 6), and the HMM estimation algorithm has less to gain from minimizing the error associated with classification of a rare state. The reasons for poor REM discrimination discussed above may suggest that the piezo signal cannot be used to differentiate REM from light NREM sleep; but this is not strictly true. When labeled samples of REM, NREM, and Wake piezo data were used to supervise the estimation of HMM parameters, discrimination of these states was much improved (see Tables I and II). This could only be because REM and light NREM show some contrast in breathing regularity or variability. There is, however, a downside to the supervised approach: the requirement of labeled training data, which can only come from simultaneous EEG/EMG recordings; and the question of whether the classifier will generalize to other phenotypes than the training sample, or to other experimental situations, such as the use of vigilance-modifying drugs. These issues are beyond the scope of the present study but possible lines of future investigation.

Two important factors that govern the performance of a classifier are the choice of input features and the structure of the model. Manual feature selection is not always straightforward and can introduce subjectivity into the process of modeling data in a classification task, which may constrain performance. At the same time, feature selection can benefit from domain knowledge—in this instance the effect of sleep state on respiratory physiology—in addressing a specific classification problem. We have chosen the latter path in this study, mainly because physiologically motivated input features can produce results that are more easily interpreted. For instance, the correlated increase of breath regularity with sleep depth (as measured by the EEG delta/theta power fraction) at sleep onset (Fig. 8) was useful for understanding one potential source of error (false positive REM during light NREM sleep). Recent developments in machine learning, specifically autoencoding of features from raw data in deep belief nets to identify a set of features that best represent the natural structure in the data, offers the means for unsupervised feature selection. It would be interesting to see how features generated in this manner correlate with observed physiological variables such as muscle tone, respiration, and heart rate; and perhaps even with properties of the EEG. This would be an interesting topic for future research. With regard to model structure, the choice of HMMs was motivated by the fact that sleep dynamics are reasonably well-represented by Markov chain models (Zung et al. 1966), and the HMM’s key parameters, the transition probabilities, convey information about the dynamics and stability of the underlying states. It is possible that other more powerful machine learning techniques may provide interesting insights into piezo signal dynamics in relation to overt and subtle behaviors. Here we have chosen to work with features and a model structure that are readily interpreted in physiological terms.

Since scoring stages of sleep was the primary objective here, the piezo system was compared against EEG/EMG as the gold standard. But it is worth reviewing its attractions and limitations against other, more closely related actigraphic techniques. Actigraphy refers to the sensing of movement and can involve wheel running, photoelectric beam breaking, videography or accelerometry; the time record of periods of activity and inactivity is called an actigram. Each method of actigraphy has its trade-offs: wheel running measures locomotor activity (reliable in hamsters) but requires animal compliance in the task; beam breaking gives a binary actigram of when the animal moves and breaks one or more light beams, but does not work well when the animal stays in one location; videography requires appropriate illumination and viewing angle at all times; and in accelerometry, sensors are attached to the body of the animal.

The piezo sensor overcomes most of the limitations of actigraphy: it is completely noninvasive and nonintrusive and provides a continuous record of activity. In the absence of wake behaviors, chest/abdominal movement (and, thus, respiratory patterns) is predominant and easily detected when the animal is lying on the piezo film; comparisons with impedance pneumography (Flores et al., 2007) and thermistor airflow (Sato et al., 2006) have verified that the piezo signal provides an excellent respiratory trace during sleep (Fig. 2). The piezo sensor therefore offers the unique opportunity to noninvasively distinguish Sleep from Wake based on small movements undetectable by other techniques, and subtle changes in breathing when the animal is relatively motionless. The piezo signal has been successfully used for Sleep-Wake discrimination in mice with 95% accuracy (Flores et al., 2007; Donohue et al. 2008). In Wake, gross motor activity produces more variable signals. Even quiet Wake is typically accompanied by grooming, postural adjustments, or other distinctive movements that are captured by the sensor.

The notion that REM and NREM sleep can be discerned from signals other than EEG is not unreasonable. As noted earlier, phasic events during REM can manifest as rapid eye movement, irregular breathing, variable heart rate, altered body temperature, or middle-ear muscle activity. EEG analysis itself requires other measurements—usually EMG or EOG—to detect such phenomena and confirm the occurrence of REM. Furthermore, EEG cannot differentiate Wake behaviors; auxiliary actigraphic measurements (e.g., video, accelerometry) are needed to detect locomotion, grooming, feeding, startle response, and so on. Here, an attempt was made to extend the repertoire of the piezo system, which is essentially an actigraphic technique, to differentiate not only Sleep and Wake, but REM, NREM, and BA within Sleep based on its ability to sense the respiratory rhythm.

Have the objectives of this study been achieved? From the results, it is clear that Wake and Sleep are separated by the piezo with high accuracy. But this merely confirms findings in previous studies (Flores et al. 2007, Mang et al. 2014), except that an unsupervised classifier was used here to avoid training bias. Of greater interest, discrimination of stages within Sleep seems feasible but there was a tendency to underestimate NREM. A closer examination revealed that breathing regularity at the onset of prolonged bouts of Sleep increased with relative delta band EEG power (Fig. 8), a recognized index of sleep depth across mammals (Borbely and Achermann 2005). Hence light or transitional NREM sleep was often mistaken for REM because of their similarly variable breathing patterns. A supervised HMM classifier estimated from labeled training data significantly alleviated this bias and improved performance.

Sleep metrics estimated for each state by the unsupervised HMM were compared against values based on the manual scores (Figs. 5 and 6). The % time spent in each state was comparable to manual estimates for Wake, Sleep, and even BA, but high for REM and low for NREM as expected from our analysis of detection errors. The supervised HMM brought these estimates close to their true values. Bout durations estimated by the unsupervised HMM were reasonable not only for Sleep and Wake, but also for REM and NREM; BA durations were somewhat overestimated. Surprisingly, the supervised HMM gave poorer estimates of NREM and REM bout duration. The number of bouts was accurate for Wake and Sleep, but grossly underestimated for NREM and BA, and overestimated for REM. This is consistent with the tendency of the unsupervised HMM to mislabel light NREM sleep as REM, a flaw rectified by the supervised HMM.

To conclude, states derived from the piezo signal that differ in terms of motion and respiration are strongly correlated with conventional states of vigilance in wild type mice. The piezo system appeared to detect REM, NREM, and BA during Sleep and estimate mean metrics associated with these states with promising if limited accuracy. It is possible that more careful design and selection of signal features or advances in sensing hardware could further improve classification. Of course, the fact that REM/NREM discrimination was possible in wild type mice does not automatically imply that it will detect differences in sleep traits associated with other sleep phenotypes (e.g., narcolepsy, RBD) or vigilance modifying agents. But there is increasing evidence that the piezo signal can be mined successfully to analyze genetic differences associated with sleep-wake traits (Philip et al, 2011), and the effects of traumatic brain injury (Rowe et al. 2014) or aging and Alzheimer’s disease (Sethi et al. 2015) in protocols that include sleep deprivation. While the piezo system will never replace polysomnography, the gold standard for determination of vigilance state, it could provide a high-throughput first pass screen of genes that govern different sleep traits; a sub-sample of interesting phenotypes could then be analyzed more closely with conventional EEG/EMG monitoring. The ability to track muscle tone and respiration were shown to be of use here for REM/NREM discrimination, but it remains to be seen whether this is valid in preclinical studies of drugs and other interventions that modify sleep and respiration. The effects of sleep restriction, vigilance-modifying agents, and brain injury are possible avenues of future investigation.

Highlights.

• A piezoelectric sensor can accurately differentiate sleep from wake and sense breathing in mice.

• Piezoelectric signal features were clustered into multiple states using a hidden Markov model.

• Sleep states that differed in breathing regularity were strongly correlated with REM/NREM.

• This technology will permit high-throughput screening of sleep traits for genetic or drug studies.

Appendix A. Estimation of features that quantify motion (TE), breath rate (f), and breathing regularity or variability (BRV) from the piezo signal in mice

Let x(t_k), k = 1, … , n, be the sequence of equally spaced sample measurements of the piezo signal in a finite epoch. The first feature estimated is the mean Teager energy, TE, a nonlinear estimator of instantaneous signal power, which is computed as an average of its values for all samples in an epoch as follows:

$$\mathit{TE}=\frac{1}{n}\sum _{k=1}^n\mid x^2(t_k)-x(t_{k-1})x(t_{k+1})\mid$$ (A.1)

Next, the time-varying piezo signal x(t_k) is bandpass-filtered from 0.5 to 5 Hz to accentuate the respiratory rhythm. The breath rate and various measures that quantify the timing and amplitude regularity/variability of the respiratory trace in the signal are then estimated using the Hilbert transform as a starting point.

Amplitude fluctuations associated with breathing can be quantified from the envelope of the filtered piezo signal x(t_k). One way to estimate the envelope is from the complex “analytic signal”, z(t_k), in which the real part is x(t_k) itself and the imaginary part is its Hilbert transform $\widehat{x}\left(t_k\right)$ (described in most standard signal processing texts). The signal envelope e(t_k) is the amplitude of the analytic signal z(t_k); that is:

$$e(t_k)=\sqrt{x^2(t_k)+{\widehat{x}}^2(t_k)}$$ (A.2)

The amplitude variability BRV1 of the breathing signal can be measured as the coefficient of variation of the signal envelope e(t_k) in each epoch:

$$\mathit{BRV}1=\frac{\mathit{std}\left(e\right(t_k\left)\right)}{\langle e\left(t_k\right)\rangle }$$ (A.3)

where 〈.〉 and std (·) denote the sample mean and standard deviation, respectively. Normalization by the mean makes BRV1 insensitive to arbitrary changes in signal amplitude, which may result from changes in animal posture or amplifier gain settings.

Breathing can vary in timing as well as amplitude. To quantify irregularity in breath timing, each breath needs to be counted in order to estimate the breath rate f. Having computed the Hilbert transform earlier, each breath is marked by the time $t_i^b\in \left\{t_1,\dots ,t_n\right\}$, t =1, … M of each complete phase rotation of the complex analytic signal, where M is the number of breaths. The mean breath rate f in the epoch is estimated as the inverse of the mean inter-breath interval:

$$f=\frac{M}{{\Sigma }_{i=2}^M(t_i^b-t_{i-1}^b)}$$ (A.4)

Of course, this presumes that each oscillation of the lowpass-filtered signal corresponds to one breath, which may not always be true, especially when the animal is engaged in active behaviors such as grooming, feeding, or locomotion. But when the animal is relatively still, the respiratory trace dominates the piezo signal and the breath timing estimated from the Hilbert transform is reasonably accurate.

Now, two different estimators are proposed for breath timing regularity. First, consider the instantaneous Hilbert phase of x(t_k), given by:

$$\varphi (t_k)={\tan }^{-1}\left(\widehat{x}(t_k)/x(t_k)\right)$$ (A.5)

The instantaneous difference in Hilbert phase φ(t_k) = ϕ(t_k) − ϕ(t_k − τ) between x(t_k) in the current epoch and a time-delayed version of itself, x(t_k − τ), where τ is arbitrarily set to 1s, is computed. Breathing regularity is estimated as the amplitude of the net phasor

$$\mathit{BRV}2=1/T\sum _k\exp (-j\phi (t_k))$$ (A.6)

where $j=\sqrt{-1}$ and ∑ is the summation over all samples in the epoch. BRV2 will approach unity for highly regular breathing (each breath has the same duration), but drop toward zero as breathing becomes irregular and more ragged.

The second estimate of breath timing regularity is based on the Rayleigh statistic (Fisher 1993), which has been used extensively in astronomy to detect pulsars (Orford 1996). The time t_i^b of each breath is expressed as a complex phasor, $r_i=\exp (-jw{t}_i^b)$, rotating at a frequency w = 2πf corresponding to the estimated mean breath rate f. Individual phasors corresponding to breath times in each epoch are averaged vectorially to produce a net phasor, whose amplitude is

$$\mathit{BRV}3=1∕M\mid {\Sigma }_i{r}_i\mid$$ (A.7)

If the breath times are random (Poisson), BRV3 will be close to zero; but if there is a strong periodicity, BRV3 will approach unity. Hence, BRV3 measures how closely the phasors are clustered, a reflection of periodicity in breath timing. As Fig. 3 shows, BRV2 is almost a mirror image of BRV1 and is relatively high when breathing is regular but drops momentarily when it is variable. While both measures were used in this analysis, they followed very similar trends and excluding one or the other from the feature set did not change the results.

Finally, a measure BRV4 is computed that is sensitive to both time and amplitude variability in the piezo signal. The multitaper power spectrum (Thomson 1982) of the piezo signal was estimated in each 4s epoch and the normalized spectral amplitude of the modal frequency chosen as BRV4. Note that the modal frequency could be used as an alternative estimate of mean breath rate and its normalized spectral amplitude is a measure of the periodicity of the underlying respiratory signal.

All feature values were smoothed with a five-point (20s) moving average and expressed on a logarithmic scale to make their distributions (conditioned on state) less skewed over their dynamic range and less sensitive to outliers. This includes the breath rate estimate f, in order to stretch the dynamic range at the low end containing values in the single digits that truly pertain to breathing. Estimated values of f above this range are very unlikely to reflect the true rate since the animal is engaged in active behaviors that obscure the respiratory component of the signal even if present. But what matters is that the distributions of the estimated rate are separable enough to discriminate between Wake, NREM, and REM.

Appendix B. Hidden Markov models, parameters estimation, and prediction of state

HMMs are Bayesian graphical model that maps sequential continuous-valued observations— here the vector of features V_t estimated from the piezo signal in the time epoch t—onto one of several discrete but ‘hidden’ states S_t. Each modeled state i is associated with a prior probability P(S = i). The probability distribution of the vector V_t is conditioned on the state at that instant as P(V_t | S_t = i). At the heart of the HMM is a state transition matrix that gives the probability P(S_t+1 = j | S_t = i) that a transition from state i to state j will occur; this assumes the Markov property, by which the state S at any time t+1 depends on the state at time t but not on previous history. The parameters of the HMM are derived from a sample observation sequence V_1:T using a maximum likelihood estimation procedure known as the Baum-Welch algorithm (Rabiner 1989). Once the HMM parameters have been estimated, the sequence of model states S_1:T most likely to have generated the observations V_1:T can be determined using the Viterbi algorithm (Rabiner 1989).