Eigenanalysis of SNP Data with an Identity by Descent Interpretation

Abstract

Principal component analysis (PCA) is widely used in genome-wide association studies (GWAS), and the principal component axes often represent perpendicular gradients in geographic space. The explanation of PCA results is of major interest for geneticists to understand fundamental demographic parameters. Here, we provide an interpretation of PCA based on relatedness measures, which are described by the probability that sets of genes are identical-by-descent (IBD). An approximately linear transformation between ancestral proportions (AP) of individuals with multiple ancestries and their projections onto the principal components is found.

In addition, a new method of eigenanalysis “EIGMIX” is proposed to estimate individual ancestries. EIGMIX is a method of moments with computational efficiency suitable for millions of SNP data, and it is not subject to the assumption of linkage equilibrium. With the assumptions of multiple ancestries and their surrogate ancestral samples, EIGMIX is able to infer ancestral proportions (APs) of individuals. The methods were applied to the SNP data from the HapMap Phase 3 project and the Human Genome Diversity Panel. The APs of individuals inferred by EIGMIX are consistent with the findings of the program ADMIXTURE.

In conclusion, EIGMIX can be used to detect population structure and estimate genome-wide ancestral proportions with a relatively high accuracy.

Introduction

Principal component analysis was introduced for the study of genetic data almost thirty years ago by Menozzi et al. (1978), and has since become a standard tool. Population differentiation can be inferred from multivariate statistical methods such as PCA of allele frequencies (Menozzi et al., 1978; Cavalli-Sforza and Feldman, 2003). In a new approach, Patterson et al. (2006) applied PCA to SNP genotypic data for individuals rather than populations. Their method, implemented in a software package “EIGENSTRAT”, has been widely used to correct for population stratification in genome-wide association studies (GWAS) (Price et al., 2010). Although PCA is not based on a population genetics model, and may seem like a “black box” method, principal component axes often represent perpendicular gradients in geographic space (Cavalli-Sforza and Feldman, 2003; Price et al., 2006; Novembre et al., 2008). The relationship of PCA results to fundamental demographic parameters is of major interest to geneticists.

Novembre and Stephens (2008) showed that the gradient and wave patterns of principal components do not necessarily reflect migration events in history. From the perspective of coalescent theory, McVean (2009) provided a genealogical interpretation of PCA. He showed that the projection of samples onto the principal components could be obtained from the pairwise coalescence times between study individuals. Ma and Amos (2010) proposed a formulation of PCA based on the variance-covariance matrix of the sample allele frequencies.

We now provide an alternative interpretation of PCA based on relatedness measures: probabilities that sets of genes have descended from a single ancestral gene and so are identical by descent (ibd). The ibd concept is essential for genetic analyses such as linkage studies for mapping disease genes and forensic DNA profiling (Weir et al., 2006; Thompson, 2013). In population genetics, Weir and Hill (2002) extended the work of Weir and Cockerham (1984) by allowing different levels of coancestry for different populations, and by allowing non-zero coancestries between pairs of populations. Our further extension is to allow different coancestries between pairs of individuals and different inbreeding coefficients for individuals. The coancestry coefficient between two populations defined in the model of Weir & Hill is now replaced by the average kinship coefficient among pairs of study individuals from these two populations respectively, relative to a single ancestral population, so that the assumption of random rating can be relaxed. These individual-perspective measures of population structure can be used to explain the behavior of PCA.

Ancestral proportions (AP) of an individual refer to the fractions of the genome derived from specific ancestral populations (Pritchard et al., 2000; Falush et al., 2003; Tang et al., 2005; Alexander et al., 2009). The early approach for estimating AP can track back to Hanis et al. (1986), and the ancestral allele frequencies should be known to allow estimating allele admixture in this method. However, ancestral allele frequencies are usually estimated from surrogate ancestral samples in practice and later studies took into account in describing the uncertainty of estimated ancestral information.

A Bayesian approach, STRUCTURE, was developed to infer population substructure using unlinked genotypes (Pritchard et al., 2000). Later, it was extended to model linked markers (Falush et al., 2003) through admixture linkage disequilibrium (LD). STRUCTURE is computationally intensive and not likely to be suitable for large-scale studies, like GWAS, involved with thousands of individuals and hundreds of thousands of SNPs. SNP pruning has to be done before applying STRUCTURE, and this can introduce selection bias with respect to different SNP sets. A maximum-likelihood estimation method, frappe, has also been proposed to estimate AP with much less computation than STRUCTURE, but it assumes the markers are unlinked (Tang et al., 2005). The ADMIXTURE method was developed to analyze thousands of markers – it adopts the likelihood model embedded in STRUCTURE with an assumption of linkage equilibrium among the markers (Alexander et al., 2009).

Instead of estimating global ancestry via genome-wide markers, detection of local ancestry from chromosomal segments in admixed populations becomes of great interest. Recently, HAPMIX and MULTIMIX were proposed to infer local ancestry from dense SNP markers based on approximate coalescent models modeling linkage disequilibrium with two or more ancestries (Price et al., 2009; Churchhouse and Marchini, 2013). However, their methods require a fine genetic map.

The potential connection between ancestral proportions and principal components in the eigenanalysis has been investigated by the previous studies with a limited number of numerical simulations (Patterson et al., 2006; Engelhardt and Stephens, 2010). McVean (2009) indicated it is possible to identify relative admixture proportions from principal components. Ma and Amos (2012) showed how to estimate two-way admixture proportions with a proof under their framework of variance-covariance matrix. They also observed that an admixed population could divide the triangle of three parental populations in the PC plot into three small triangles with areas according to the three-way admixture proportions. However, none of these studies provided a sufficient proof for inferring admixture fractions from the principal components under their theoretical framework in the cases of more than two ancestral populations.

In our study, an approximately linear transformation between ancestral proportions (AP) of individuals with multiple ancestries and their projections onto the principal components is revealed, and a proof is given under the framework of identity by descent. This linear transformation could explain the perpendicular gradients in geographic space, and it also justifies the observation that the ratios of triangle areas correspond to admixture fractions in the study of Ma and Amos (2012). We also propose a new method of eigenanalysis “EIGMIX” to estimate individual ancestries. EIGMIX uses method of moments estimation with computational efficiency suitable for millions of SNP data, and it is not subject to the assumption of linkage equilibrium. Ancestral proportions can be estimated by making assumptions of surrogate samples for ancestral populations, but inferring ancestral allele frequencies is not necessary. The calculation uses all study individuals simultaneously without projecting the remaining individuals onto the existing axes of surrogates.

We applied various methods to the SNP data of 1,198 founders from the HapMap Phase 3 project and 938 unrelated individuals from the Human Genome Diversity Project (HGDP). The ancestral proportions of individuals inferred by PCA and EIGMIX are consistent with the findings of the program ADMIXTURE. All eigenanalysis in the study are implemented in the R package “SNPRelate” (Zheng et al., 2012), allowing users to apply our method to their SNP data.

Methods

We develop our approach with a series of indicator variables x_ijkl for the kth allele, k = 1, 2, at the lth locus, l = 1, 2, …, L, in the jth individual sampled from the ith population, j = 1, 2, … n_i; i = 1, 2 …, N. The total sample size is n = Σ_i n_i. The variables take the value 1 for alleles of a specific type, e.g. the reference allele, at a locus, and the value 0 otherwise. Genotypes are indicate by g_ijl = x_ij1l + x_ij2l, and these take the values 0,1,2.

Population Coancestry Framework of Weir & Hill (2002)

Under the framework of Weir & Hill (2002), the expectations for first and second moments of the x’s are

$$\begin{array}{llll}\hfill \mathcal{E}[x_{\mathit{ijkl}}]& =\hfill & p_l\hfill & \hfill \\ \hfill \mathcal{E}[x_{\mathit{ijkl}}^2]& =\hfill & p_l\hfill & \hfill \\ \hfill \mathcal{E}[x_{\mathit{ijkl}}{x}_{ij{k}^{\prime }l}]& =\hfill & p_l^2+p_l(1-p_l)F_{ij}\hfill & ,k\ne k^{\prime },\text{the}\text{same}\text{individual}\hfill \\ \hfill \mathcal{E}[x_{\mathit{ijkl}}{x}_{i{j}^{\prime }{k}^{\prime }l}]& =\hfill & p_l^2+p_l(1-p_l){\theta }_i\hfill & ,j\ne j^{\prime },\text{the}\text{same}\text{population}\hfill \\ \hfill \mathcal{E}[x_{\mathit{ijkl}}{x}_{i^{\prime }{j}^{\prime }{k}^{\prime }l}]& =\hfill & p_l^2+p_l(1-p_l){\theta }_{i{i}^{\prime }}\hfill & ,i\ne i^{\prime },\text{different}\text{populations}\hfill \end{array}$$

Here expectation is over both repeated samples from the population and over evolutionary replicates of the populations. These expressions introduce the total inbreeding coefficient F_ij, the within-population coancestries θ_i, and the between-population-pair coancestries θ_ii′. The quantities p_l are the overall, or ancestral, frequencies of the reference alleles if all study individuals can be traced back to a single reference population. This reference population could be common ancestors at a point in time of the past. The equal values for ℰ[x_ij1l x_ij2l] and ℰ[x_ijkl x_ij′k′l] require an assumption of random mating.

The coancestry coefficient θ_i refers to the ibd probability for a random pair of alleles in population i, and the pair of alleles can come from the same individual. The coancestry coefficient θ_ii′ refers to the ibd probability for a random pair of alleles, one from population i and the other is from population i′. Note that we implicitly assume θ_i and θ_ii′ are the same at each locus, and in practice θ_i and θ_ii′ are actually the average inbreeding and coancestry coefficients over all L loci.

Now consider an individual perspective measures of population structure, i.e., a special case of Weir & Hill’s model where each population i has only one sampled individual (n_i = 1) so j = 1 for each population. The assumption of random mating is relaxed, and the sample size n is also the number of populations r.

Therefore,

$$\begin{array}{lll}\hfill {\overline{p}}_l& =\hfill & \frac{1}{n}{\sum }_{i=1}^n{\overline{p}}_{il}=\frac{1}{n}{\sum }_{i=1}^n[\frac{1}{2}{\sum }_{j=1}^1(x_{ij1l}+x_{ij2l})]\hfill \\ \hfill \mathcal{E}[{\overline{p}}_l]& =\hfill & p_l\hfill \\ \hfill \text{Var}[{\overline{p}}_{il}]& =\hfill & \frac{1}{2}{p}_l(1-p_l)(1+{\theta }_i)\hfill \\ \hfill \text{Cov}[{\overline{p}}_{il},{\overline{p}}_{i^{\prime }l}]& =\hfill & p_l(1-p_l){\theta }_{i{i}^{\prime }}\hfill \\ \hfill \text{Var}[{\overline{p}}_l]& =\hfill & \frac{n-1}{n}{p}_l(1-p_l){\theta }_T+\frac{1}{2n}{p}_l(1-p_l)(1+{\theta }_I)\hfill \\ \hfill \mathcal{E}[{\overline{p}}_l(1-{\overline{p}}_l)]& =\hfill & \frac{n-1}{n}{p}_l(1-p_l)(1-{\theta }_T)+\frac{1}{2n}{p}_l(1-p_l)(1-{\theta }_I)\hfill \end{array}$$ (1)

where ${\theta }_I={\sum }_{i=1}^n{\theta }_i/n$, the average inbreeding coefficient among all study individuals, and ${\theta }_T={\sum }_{i,i^{\prime }=1,i\ne i^{\prime }}^n{\theta }_{i{i}^{\prime }}/[n(n-1)]$, the average kinship coefficient among all study individuals. The individual perspective measures do not account for familial data and the relatedness of individuals is established from evolutionary history.

Each study individual is assigned to one population, thereby the genetic covariance matrix defined by Patterson et al. (2006) at the individual level can be expressed using an index i, ${\mathbb{M}}^{\mathrm{P}}={[m_{i,i^{\prime }}^{\mathrm{P}}]}_{n\times n}$:

$$m_{i,i^{\prime }}^{\mathrm{P}}=\frac{1}{L}\sum _{l=1}^L\frac{(g_{i1l}-2{\overline{p}}_l)(g_{i^{\prime }1l}-2{\overline{p}}_l)}{{\overline{p}}_l(1-{\overline{p}}_l)}$$ (2)

The expected values of the numerator in Equation 2 is:

$$\mathcal{E}[{(g_{i1l}-2{\overline{p}}_l)}^2]=2p_l(1-p_l)(1+{\theta }_i+2\frac{n-1}{n}{\theta }_T-4{\psi }_i)+\frac{2}{n}{p}_l(1-p_l)({\theta }_I+2{\theta }_i-1),\text{for}i=i^{\prime }$$

$$\mathcal{E}[(g_{i1l}-2{\overline{p}}_l)(g_{i^{\prime }1l}-2{\overline{p}}_l)]=4p_l(1-p_l)({\theta }_{i{i}^{\prime }}+\frac{n-1}{n}{\theta }_T-{\psi }_i-{\psi }_{i^{\prime }})+\frac{2}{n}{p}_l(1-p_l)({\theta }_I+{\theta }_i+{\theta }_{i^{\prime }}-1),\text{for}i\ne i^{\prime }$$

where ${\psi }_i={\sum }_{i^{\prime }=1}^n{\theta }_{i{i}^{\prime }}/n$ (setting θ_ii = θ_i).

When the number n of study individuals is large,

$$\mathcal{E}[\frac{1}{4}{m}_{i,i^{\prime }}^{\mathrm{P}}]=\{\begin{array}{lll}\frac{1+{\theta }_i}{2(1-{\theta }_T)}+\frac{{\theta }_T-2{\psi }_i}{1-{\theta }_T}\hfill & ,\text{if}\hfill & i=i^{\prime }\hfill \\ \frac{{\theta }_{i{i}^{\prime }}}{1-{\theta }_T}+\frac{{\theta }_T-{\psi }_i-{\psi }_{i^{\prime }}}{1-{\theta }_T}\hfill & ,\text{if}\hfill & i\ne i^{\prime }\hfill \end{array}$$ (3)

Eigen-decomposition in PCA

If we are interested in individual inbreeding coefficients (1 + θ_j)/2 (the coancestry of an individual with itself) and individual-pair coancestries θ_ii′, the factors (1 − θ_T) and (θ_T − ψ_j − ψ_j′)/(1 − θ_T) in Equation 3 will confound the estimates when $\frac{1}{4}{m}_{j,j^{\prime }}^{\mathrm{P}}$ is used. This may explain why a large proportion of $m_{j,j^{\prime }}^{\mathrm{P}}$ are negative, whereas the true θ_j and θ_jj′ are always between zero and one.

The Population Perspective

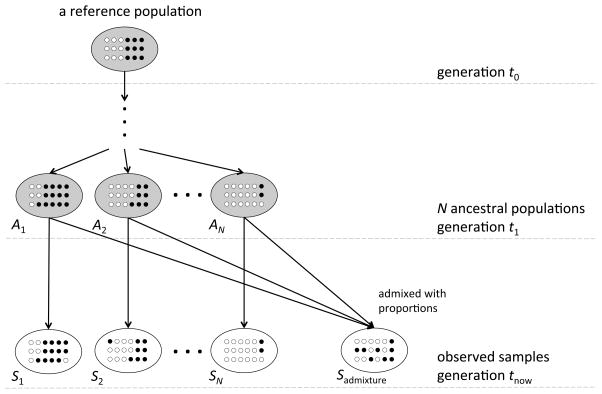
PCA conducts eigen-decomposition on the stochastic matrix 𝕄^P, and it is possible to investigate the structural features of 𝕄^P with its expectation. To illustrate what eigen-decomposition does, we introduce a genetic model consisting of populations at three points in time as shown in Figure 1. The alleles of all study individuals at t_now can be tracked to a single reference population at t₀ through at least one of distinct ancestral populations at t₁. The study samples S₁, …, S_N are directly inherited from the ancestral populations A₁, .., A_N without admixture, and the sample S_admixture is admixed from N ancestral populations.

Figure 1.

A genetic model at a single locus for observed samples. The alleles of all study individuals at t_now can be tracked to a single reference population at t₀, and there are N distinct ancestral populations at t₁. The relationships among ancestral populations are described by a coancestry matrix Θ_A.

What we can observe are the genomes of study individuals at t_now. It could be appropriate to assume there are N ancestral populations at t₁ which is between t₀ and t_now, and the samples S₁, …, S_N are good candidates (or pseudo-ancestors) to represent the ancestral populations. For example, in the initial phase of the HapMap Project, genetic data were gathered from four populations (CEU, YRI, CHB and JPT) with European, African and Asian ancestry respectively. Here, N = 3, S₁ represents CEU individuals, S₂ for YRI and S₃ for CHB+JPT.

A coancestry matrix Θ_A is used to describe the relationships among N ancestral populations at t₁ based on population perspective measures, where

$${\mathrm{\Theta }}_A=\left[\begin{array}{cccc}{\theta }_1^{\ast }& {\theta }_{12}^{\ast }& \cdots & {\theta }_{1N}^{\ast }\\ {\theta }_{12}^{\ast }& {\theta }_2^{\ast }& \cdots & {\theta }_{2N}^{\ast }\\ \cdots & \cdots & \ddots & \cdots \\ {\theta }_{1N}^{\ast }& {\theta }_{2N}^{\ast }& \cdots & {\theta }_N^{\ast }\end{array}\right]$$ (4)

That is, ${\theta }_h^{\ast }$ is the average IBD probability for a pair of alleles randomly sampled with replacement from the h^th ancestral population, and ${\theta }_{h{h}^{\prime }}^{\ast }$ is the coancestry coefficient for random pairs of individuals from the h^th and h′^th ancestral populations respectively. Since we track all individuals back to the reference population at t₀, the sample allele frequencies at t₁ are treated as random variables over a probability space, which starts from the reference population at t₀ and arrives at t₁ with the coancestry state Θ_A.

Ancestral Proportions

In practice individuals may have recent ancestors in more than one population, and an admixture model is introduced in which each individual is assumed to have inherited some proportion of its ancestry from each population. For an individual j, let the ancestral proportions be a vector a_j = (a_i,1, …, a_i,N)^T, where ${\sum }_{h=1}^N{a}_{i,h}=1$ and 0 ≤ a_i,h ≤ 1. Let Z_iklh = 1 when the k^th allele of individual i at SNP l is inherited from the h^th ancestral population at t₁, and Z_iklh = 0 otherwise. The vector Z_ikl = {Z_ikl1, …, Z_iklN}^T is modeled as a random variable with probabilities a_i, i.e., ℰ[Z_iklh] = a_i,h. Further,

$$a_{i,h}=\mathcal{E}\left[\frac{1}{L}\sum _{l=1}^L{Z}_{\mathit{iklh}}\right]$$ (5)

represent the genomic ancestral proportions. Note that Equation 5 still holds even if loci are correlated due to linkage disequilibrium. We assume that the two alleles in individual i at SNP l are independently derived from ancestral populations, since pairs of chromosomes of an individual are independently inherited from two parents respectively. Then the expected value of the inbreeding coefficient at SNP l for individual i is $\mathcal{E}[{\mathbf{Z}}_{i1l}^T{\mathrm{\Theta }}_A{\mathbf{Z}}_{i2l}]={\mathbf{a}}_i^T{\mathrm{\Theta }}_A{\mathbf{a}}_i$, the same for each SNP. The average inbreeding coefficient over L loci is ${\theta }_{i{i}^{\prime }}={\mathbf{a}}_i^T{\mathrm{\Theta }}_A{\mathbf{a}}_i$, assuming the coancestry matrix of ancestral populations is identical at each locus.

For a pair of individuals i and i′, we assume that any pair of alleles, one from i and the other from i′ are independently derived from ancestral populations. Then the expected value of the kinship coefficient at SNP l is $\mathcal{E}[{\mathbf{Z}}_{\mathit{ikl}}^T{\mathrm{\Theta }}_A{\mathbf{Z}}_{i^{\prime }{k}^{\prime }l}]={\mathbf{a}}_i^T{\mathrm{\Theta }}_A{\mathbf{a}}_{i^{\prime }}$, and the average kinship coefficient over L loci is also ${\theta }_{i{i}^{\prime }}={\mathbf{a}}_i^T{\mathrm{\Theta }}_A{\mathbf{a}}_{i^{\prime }}$. This assumption is appropriate to model relatedness in structured population with admixture, with ${\mathbf{a}}_i^T{\mathrm{\Theta }}_A{\mathbf{a}}_{i^{\prime }}$ as background relatedness due to evolutionary history. However, the validity of the assumption could be violated if individuals i and i′ are in a family, e.g., parent and offspring.

Matrix Decomposition

For a study sample, there are n unrelated individuals. Each individual i has AP a_i with respect to N ancestral populations. Let A = [a₁, a₂, …, a_n]^T be a n-by-N matrix with rows representing ancestral proportions of individuals. Then the coancestry matrix of study individuals Θ_S can be expressed as

$${\mathrm{\Theta }}_S=\mathbf{A}{\mathrm{\Theta }}_A{\mathbf{A}}^T$$ (6)

We rewrite Equation 3 in matrix notation for large n,

$$\mathcal{E}[{\mathbb{M}}^{\mathrm{P}}]=\frac{4}{1-{\theta }_T}\underset{\stackrel{\text{def}}{=}{\mathrm{\Theta }}_{\mathbf{M}}}{\underbrace{(\mathbf{A}-\frac{1}{n}{\mathbf{J}}_n\mathbf{A}){\mathrm{\Theta }}_A{(\mathbf{A}-\frac{1}{n}{\mathbf{J}}_n\mathbf{A})}^T}}+\underset{\text{bias}}{\underbrace{\text{diag}(\frac{2(1-{\theta }_1)}{1-{\theta }_T},\dots ,\frac{2(1-{\theta }_n)}{1-{\theta }_T})}}$$ (7)

where J_n is a matrix of dimension n × n with entries equal to one, since

$$\begin{array}{lll}\hfill (\frac{1}{n}{\mathbf{J}}_n\mathbf{A}){\mathrm{\Theta }}_A{(\frac{1}{n}{\mathbf{J}}_n\mathbf{A})}^T& =\hfill & \frac{1}{n^2}{\mathbf{J}}_n{\mathrm{\Theta }}_S{\mathbf{J}}_n=\frac{1}{n^2}({\sum }_{j\ne j^{\prime }}{\theta }_{j{j}^{\prime }}+{\sum }_j{\theta }_j){\mathbf{J}}_n\hfill \\ \hfill & =\hfill & \left({\theta }_T\frac{n(n-1)}{n^2}+\frac{1}{n}{\theta }_I\right){\mathbf{J}}_n\hfill \\ \hfill & \approx \hfill & {\theta }_T{\mathbf{J}}_n\hfill \\ \hfill (\frac{1}{n}{\mathbf{J}}_n\mathbf{A}){\mathrm{\Theta }}_A{\mathbf{A}}^T& =\hfill & \frac{1}{n}{\mathbf{J}}_n{\mathrm{\Theta }}_S=\left[\begin{array}{cccc}{\psi }_1& {\psi }_2& \dots & {\psi }_n\\ ⋮& ⋮& \ddots & ⋮\\ {\psi }_1& {\psi }_2& \dots & {\psi }_n\end{array}\right].\hfill \end{array}$$

The diagonal $\text{diag}(\frac{2(1-{\theta }_1)}{1-{\theta }_T},\dots ,\frac{2(1-{\theta }_n)}{1-{\theta }_T})$ is considered as a bias term in the PCA with respect to ancestral proportions.

Note that $\text{rank}(\mathbf{A}-\frac{1}{n}{\mathbf{J}}_n\mathbf{A})\le N-1$ because we lose a dimension by forcing each column to sum to zero. The eigenvectors corresponding to the largest N − 1 eigenvalues of Θ_M form a new coordinate with N − 1 dimensions while AP form an old N-dimensional coordinates. The mapping from the old coordinate to the new one is a linear transformation, and the proof is given in the appendix A1. In addition, this mapping is actually an affine transformation equivalent to a (N − 1)-dimensional linear transformation followed by a translation, and the affine transformation can be represented as an linear transformation on the higher dimensional space.

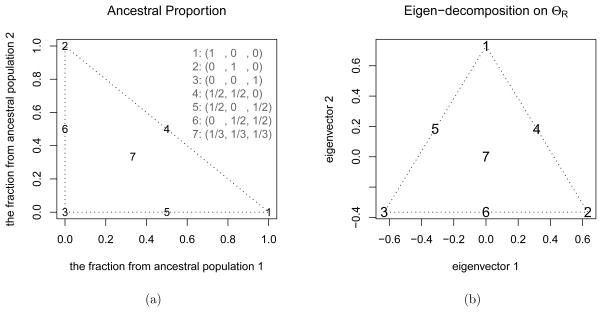
For example, assume there are three ancestral populations and seven individuals, in which individuals 1, 2, 3 are inherited from the ancestral populations without admixture, individuals 4, 5, 6 have two ancestral populations with equal contributions and individual 7 has three ancestral populations with equal contributions. The matrix A of ancestral proportions is

$$\mathbf{A}={\left[\begin{array}{ccccccc}1& 0& 0& 1/2& 1/2& 0& 1/3\\ 0& 1& 0& 1/2& 0& 1/2& 1/3\\ 0& 0& 1& 0& 1/2& 1/2& 1/3\end{array}\right]}^T,$$

and Θ_A is assumed to diag(0.05, 0.05, 0.05). The AP coordinates are shown in Figure 2a, and the new eigen-decomposition coordinates are shown in Figure 2b.

Figure 2.

The relationship between ancestral proportions and eigen-decomposition: a) seven admixture fractions from three ancestral populations are plotted in the figure; b) the first and second eigenvectors of matrix ${\mathrm{\Theta }}_{\mathbf{M}}=(\mathbf{A}-\frac{1}{n}{\mathbf{J}}_n\mathbf{R}){\mathrm{\Theta }}_A{(\mathbf{A}-\frac{1}{n}{\mathbf{J}}_n\mathbf{A})}^T$, where the ancestral coancestry matrix Θ_A is assumed to diag(0.05, 0.05, 0.05), A is an n-by-N matrix with rows representing admixture proportions of individuals, n = 7 and N = 3. The mapping from the two-dimensional coordinate in (a) to that of (b) is a linear transformation followed by a translation.

EIGMIX – Inferring Ancestral Proportions

The mapping in Figure 2 suggests an approach to estimate ancestral proportions using the largest principal components. Let S₁, …, S_N be the observed surrogate samples for the ancestral populations, as shown in Figure 1. Now we look at the largest (N − 1) principal components, and identify each location of pseudoancestor i ∈ {1, …, N} in the eigen coordinates, by averaging the locations of the sample S_i. So we have N positions in the eigen coordinates, which corresponds to N independent components in the AP coordinates. Then a linear transformation can be made to reverse the original mapping, i.e., the principal components of all study individuals are reversed to the AP coordinates by a linear transformation. In addition, the property of linear mapping makes the inferred ancestral proportions unique if N surrogate samples are specified and their locations in the eigen coordinates are distinct.

For example, the positions of individuals 1, 2 and 3 with ancestral proportions (1,0,0), (0,1,0) and (0,0,1) in the eigen coordinate of Figure 2(b) are denoted by e_s1, e_s2 and e_s3 respectively. Let T_2×2 be a linear transformation and L be a translation operator. A transformation from the AP coordinates to the eigen coordinates is:

$$\left[\begin{array}{cc}1& 0\\ 0& 1\\ 0& 0\end{array}\right]T_{2\times 2}+L_{3\times 2}=\left[\begin{array}{c}{e}_{s1}^{\prime }\\ e_{s2}^{\prime }\\ e_{s3}^{\prime }\end{array}\right]$$ (8)

Therefore, L_3×2 = [e_s3, e_s3, e_s3]′ (moving every point a constant distance) and T_2×2 = [e_s1 − e_s3, e_s2 − e_s3]′.

The inverse transformation is:

$$\text{ancestral}\text{proportion}=(e_{\text{admix}}-e_{s3})T_{2\times 2}^{-1}$$ (9)

where e_admix is an arbitrary point in the eigen coordinate.

Note that there is a bias term in the diagonal shown in Equation 7. A scheme for bias removal is to define a new genetic covariance matrix, the EIGMIX coancestry matrix ${\mathbb{M}}^{\ast }={[m_{j,j^{\prime }}^{\ast }]}_{n\times n}$, EIGMIX coancestry matrix:

$$m_{j,j^{\prime }}^{\ast }=\{\begin{array}{ll}\frac{{\sum }_{l=1}^L{(g_{jl}-2{\overline{p}}_l)}^2-g_{jl}(2-g_{jl})}{4{\sum }_{l=1}^L{\overline{p}}_l(1-{\overline{p}}_l)}\hfill & ,j=j^{\prime }\hfill \\ \frac{{\sum }_{l=1}^L(g_{jl}-2{\overline{p}}_l)(g_{j^{\prime }l}-2{\overline{p}}_l)}{4{\sum }_{l=1}^L{\overline{p}}_l(1-{\overline{p}}_l)}\hfill & ,j\ne j^{\prime }\hfill \end{array},$$ (10)

Then ℰ[𝕄^*] = Θ_M/(1 − θ_T) without any bias when there are a large number of individuals. We have previously (Weir and Cockerham, 1984) suggested the simple modification of taking the ratios of the sums over loci of the numerators and denominators instead of averaging the ratios to reduce the variance, in part by reducing the impact of rare variants. Since the ratio of expected values is an approximation for the expected value of an ratio of two random variables, our modification tends to have an advantage of bias correction due to division compared to the original PCA.

In practice, the matrix 𝕄^* of real data could have more than N − 1 significant eigenvalues when we assume the number of ancestral populations N to be a specific number (e.g., N = 3 for Europe, Asia and Africa). The largest N − 1 eigenvalues with their eigenvectors form a low-rank approximation of 𝕄^* (a real symmetric matrix), which minimizes the Frobenius norm with respect to a n-by-n matrix M with rank(M) ≤ N − 1:

$${\Vert {\mathbb{M}}^{\ast }-M\Vert }_F^2=\sum _{j=1}^n\sum _{j^{\prime }=1}^n{m}_{j,j^{\prime }}^2$$

where 𝕄^* − M = [m_j,j′]_n×n. The closest matrix to 𝕄^* is $\widehat{M}={\sum }_{i=1}^{N-1}{\lambda }_i{\mathbf{e}}_i{\mathbf{e}}_i^T$, as measured in the Frobenius norm, where |λ₁| ≥ |λ₂| ≥ … ≥ |λ_n| are the eigenvalues of 𝕄^* and e_i is the eigenvector corresponding to λ_i, and

$${\Vert {\mathbb{M}}^{\ast }-\widehat{M}\Vert }_F^2=\sum _{i=N}^n{\lambda }_i^2$$

𝕄^* is not necessarily a nonnegative definite matrix, i.e., its eigenvalues are not necessarily all nonnegative. Here “largest eigenvalues” refer to the absolute values of eigenvalues in descending order.

In addition, the estimates of EIGMIX given an arbitrary number of ancestral populations are not always bounded from 0 to 1, although we force the proportions to sum to one. If the inferred ancestral proportions lie much outside the range [0,1], signaling outliers, we could conclude that the assumption of N ancestral populations with their surrogates is not appropriate or that the SNP markers have no power to distinguish ancestral populations.

According to PCA, we might expect the eigen-decomposition of $\mathcal{E}[\frac{1}{4}{\mathbb{M}}^{\mathrm{P}}]$ and ℰ[𝕄^*] could result in similar eigenvectors corresponding to a few most significant eigenvalues when there are true structural feature in data, since the difference between $\mathcal{E}[\frac{1}{4}{\mathbb{M}}^{\mathrm{P}}]$ and ℰ[𝕄^*] depends only on the diagonal. The average difference per entry in the term of Frobenius norm becomes small when the total number of study individuals n is large:

$$\frac{1}{n^2}{\Vert \mathcal{E}[\frac{1}{4}{\mathbb{M}}^{\mathrm{P}}]-\mathcal{E}[{\mathbb{M}}^{\ast }]\Vert }_F^2=\frac{1}{4n^2}\sum _{j=1}^n\frac{{(1-{\theta }_j)}^2}{{(1-{\theta }_T)}^2}\to 0,\text{as}n\to \infty$$

A few largest eigenvalues and eigenvectors could capture the similar structure information of $\mathcal{E}[\frac{1}{4}{\mathbb{M}}^{\mathrm{P}}]$ and ℰ[𝕄^*]. Here, “similar” means similar relative positions in the eigen coordinates, since numerical calculation does not guarantee that the resulting eigenvectors will have the same absolute positions in the coordinate, e.g., if a vector v is an eigenvector then −v is also the eigenvector according to the same eigenvalue. A further numerical study is shown in the appendix A2.

Results

Materials

The Phase 3 HapMap data consist of SNP genotypes generated from 1,397 samples in total, collected using two platforms: the Illumina Human1M (by the Wellcome Trust Sanger Institute) and the Affymetrix SNP 6.0 (by the Broad Institute) (International HapMap 3 Consortium et al., 2010). Data from the two platforms have been merged for the release. The PLINK format of HapMap 3 data were downloaded from http://hapmap.ncbi.nlm.nih.gov/downloads/genotypes/hapmap3_r3/plink_format/. The consensus and polymorphic data set of 1198 founders were used in the study analyses, which include only SNPs that passed quality control in all populations, as shown in Table 1.

Table 1.

Summary of population samples in the eigenanalysis.

Name	Population	# of samples
HapMap Phase III (1,198 founders):
ASW	African ancestry in Southwest USA	53
CEU	Utah residents with Northern and Western European ancestry from the CEPH collection	112
CHB	Han Chinese in Beijing, China	137
CHD	Chinese in Metropolitan Denver, Colorado	109
GIH	Gujarati Indians in Houston, Texas	101
JPT	Japanese in Tokyo, Japan	113
LWK	Luhya in Webuye, Kenya	110
MEX	Mexican ancestry in Los Angeles, California	58
MKK	Maasai in Kinyawa, Kenya	156
TSI	Toscani in Italia	102
YRI	Yoruba in Ibadan, Nigeria	147
The Human Genome Diversity Panel (HGDP, 938 unrelated individuals):
Africa		101
Europe		157
Middle East		163
Central & South Asia		199
East Asia		228
Oceania		26
America		64

The Human Genome Diversity Panel data consists of 1043 individuals from 51 populations over the world: sub-Saharan Africa, North Africa, Europe, the Middle East, Central & South Asia, East Asia, Oceania and the Americas (Cann et al., 2002). The study individuals were genotyped on the Illumina 650K platform, and the SNP data could be downloaded from http://www.hagsc.org/hgdp/files.html. The dataset contains a small number of relatives, and 938 individuals were remained in the analysis after filtering out first and second degree relatives of which were suggested by Rosenberg (2006).

To reduce potential effects of linkage disequilibrium, SNP pruning was conducted by randomly selecting autosomal SNPs for which each pair was at least as far apart as 200kb: 9,949 remaining SNPs for HapMap Phase 3 and 9,790 for HGDP. All analyses were performed on both of the pruned and full SNP sets, and the unbound estimates of ancestral proportion are reported. In the full sets, there are 1,423,833 and 644,258 autosomal SNPs for HapMap3 and HGDP respectively.

Analyses of HapMap Phase 3 Data

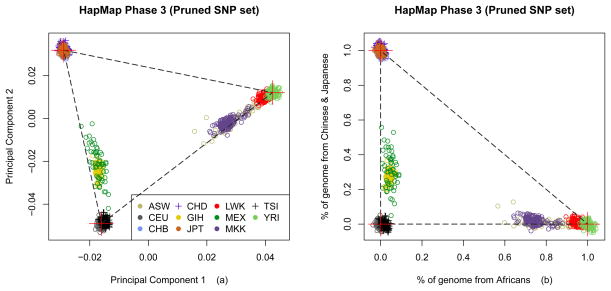
To avoid the confounding effect of relatives, 1,198 founders were selected for the PCA analysis by removing the offspring. The first two principal components are the focus, since more eigenvectors provide little additional information for inferring primary population structure. As shown in Figure 3a, the samples from CEU, YRI and CHB+JPT correspond to three vertices of a triangle, and the other populations tend to be admixtures from these three ancestries. Inferring ancestral proportions was conducted by a coordinate transformation, assuming three ancestral populations with surrogate samples: CEU, YRI and CHB+JPT. The X and Y axes in Figure 3b represent the proportions of genome from African and Asian ancestries respectively. Gujarati Indians in Houston (GIH, yellow) and Mexican ancestry in Los Angeles (MEX, green) appear to be admixtures between Europeans and Asians. ASW, MKK and LWK tend to be more related to African ancestry with some admixture, while CHD and TSI are quite close to the surrogate samples of Asia. The PCA plot with the largest two principal components generated by the full SNP set is shown in Supplemental Figure S1, which is similar to Figure 3.

Figure 3.

The principal component analysis on HapMap Phase 3 data, using a pruned set of 9,949 SNPs and 1,198 founders consisting of 11 populations: a) the first and second eigenvectors; b) a linear transformation of coordinate from a) followed by a translation, assuming three ancestral populations with surrogate samples: CEU, YRI and CHB+JPT. The average positions of three surrogate samples are masked by a red plus sign.

The population admixture proportions are estimated by averaging ancestral proportions of individuals using the full SNP set. African Americans (ASW) are a typically admixed sample, estimated with ~78% of genome from YRI and 21% from CEU, and approximately no genome from CHB+JPT. The result confirms the estimates of 78% African and 22% European ancestry shown in the supplementary materials of the HapMap Phase 3 report (International HapMap 3 Consortium et al., 2010). The HAPMIX algorithm (Price et al., 2009) was used in HapMap Phase 3 project, the optimal linear combination of 74% YRI and 26% CEU was observed for MKK, and a combination of 94% YRI and 6% CEU for LWK. In our analyses, the PCA-inferred combinations are 74% YRI + 24% CEU for MKK and 94% YRI + 5% CEU for LWK. Our results are consistent with the admixture proportions previously estimated.

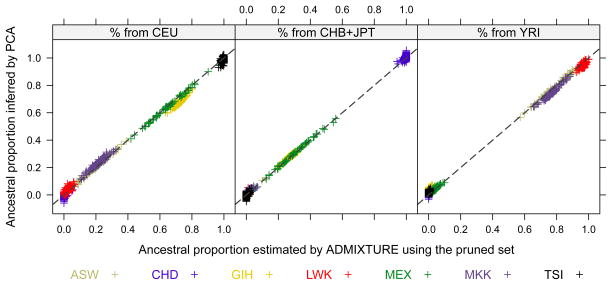
The supervised ADMIXTURE and EIGMIX methods were applied to the HapMap3 SNP data assuming three ancestral populations with surrogate samples CEU, YRI and CHB+JPT. ADMIXTURE is a model-based method with an assumption of markers in linkage equilibrium, therefore a pruned SNP set was used to avoid the strong influence of SNP clusters. The pseudo-ancestors (YRI, CHB+JPT and CEU) are specified in the analyses of ADMIXTURE according to the AP (1, 0, 0), (0, 1, 0) and (0, 0, 1). As shown in Figure 4, the AP inferred by PCA tend to be consistent with those estimated by ADMIXTURE using the same SNP set. However, the offsets are observed for admixed populations, such like GIH and MKK. The PCA-based proportions of genome from CEU are lower than ADMIXTURE for GIH, and those are higher for MKK. Actually, our inference on MKK was actually consistent with what HapMap Phase 3 has reported. Note that PCA is a dimension reduction technique and may lose information if we look only at the largest two principal components, and the assumption of pseudo-ancestors (CEU, YRI, CHB+JPT) might not truly represent the ancestors in human evolution.

Figure 4.

A comparison between PCA and supervised ADMIXTURE with respect to ancestral proportions for the HapMap Phase 3 data. A pruned set of 9,949 SNPs was used by both PCA and ADMIXTURE.

The EIGMIX coancestry matrix was used in the eigenanalysis instead of the PCA covariance matrix. As shown in Table 2, the differences of ancestral proportions at the individual level between ADMIXTURE and PCA/EIGMIX were calculated to evaluate the potential biases compared to the estimates of ADMIXTURE. The estimated proportions of EIGMIX tend to be less biased than PCA’s except Chinese in Metropolitan Denver (CHD), whereas the differences are relatively small overall for the HapMap3 data. The variances of EIGMIX are comparable to PCA if the ADMIXTURE estimates are assumed to be true values.

Table 2.

The differences on ancestral proportions of individuals between supervised ADMIXTURE and the eigenanalysis for the HapMap Phase 3 data.

Pop.	PCA – ADMIXTURE			EIGMIX – ADMIXTURE
	mean ± sd			mean ± sd
	% CEU	% CHB+JPT	% YRI	% CEU	% CHB+JPT	% YRI
ASW	0.30 ± 0.75	−0.29 ± 1.11	−0.01 ± 0.90	0.18 ± 1.09	−0.27 ± 1.24	0.09 ± 0.73
CHD	−1.10 ± 1.65	1.09 ± 1.66	0.01 ± 1.15	−1.16 ± 1.82	1.11 ± 1.70	0.05 ± 1.34
GIH	−4.15 ± 0.85	0.42 ± 0.57	3.74 ± 0.87	−3.39 ± 0.84	−0.60 ± 0.74	3.98 ± 1.12
LWK	1.50 ± 1.33	0.24 ± 1.22	−1.74 ± 1.25	0.86 ± 1.42	−0.02 ± 1.35	−0.84 ± 1.03
MEX	−0.62 ± 0.70	0.23 ± 0.57	0.40 ± 0.75	−0.31 ± 0.91	0.02 ± 0.83	0.29 ± 1.01
MKK	1.60 ± 0.85	0.61 ± 1.10	−2.21 ± 0.77	0.72 ± 1.07	0.33 ± 1.03	−1.05 ± 0.66
TSI	−1.07 ± 1.74	−0.78 ± 1.69	1.84 ± 1.12	−0.85 ± 1.73	−1.14 ± 1.80	1.99 ± 1.32

Analyses of HGDP

As suggested by Rosenberg (2006), a standardized subset of HGDP data consisting of 938 unrelated individuals was employed in the admixture analyses with a pruned set of 9,790 SNPs. The number of ancestral populations is suggested by geographic regions, the worldwide human relationship inference (Rosenberg et al., 2002; Li et al., 2008) and the plots of eigenvectors (shown in Supplementary Figure S2), and we used six ancestries in our primary analyses. The surrogate samples are suggested by the previous inferred regional ancestry (Li et al., 2008) and relative positions in the plots of eigenvectors: Sardinian for Europe (n = 28), Chinese Han for East Asia (n = 44), Kalash for Central & South Asia (n = 22), Pygmy for Africa (n = 34), Karitiana for America (n = 14) and Papuan for Oceania (n = 16).

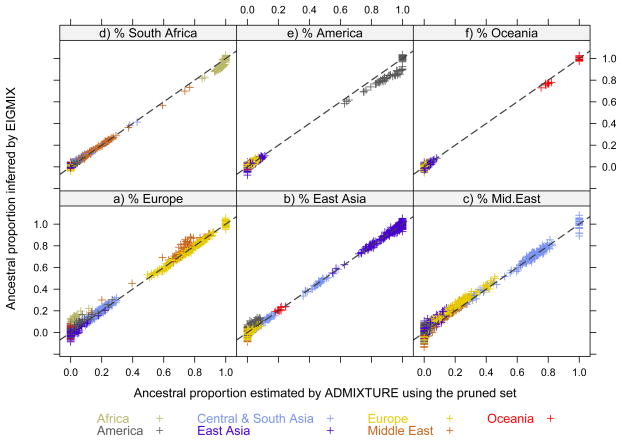
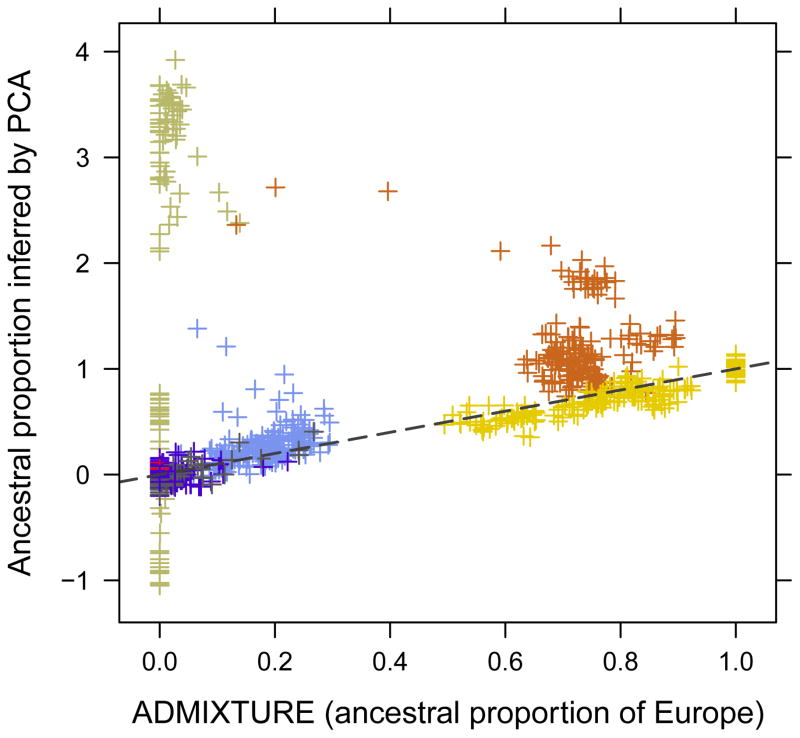
The supervised ADMIXTURE and EIGMIX methods were both applied to the HGDP SNP data with six ancestral populations. The estimated ancestral proportions of individuals are shown in Figure 5. Overall the estimates of EIGMIX are consistent with what ADMIXTURE does, however a difference of 10% admixture proportion is observed for samples from Africa and Middle East when the percents of Europe are inferred. In Figure 5e, the samples of America are also observed to be off the diagonal line. PCA was applied to the same study individuals and SNP set: the PCA-inferred admixed ancestries are shown in Figure 6 and Supplementary Figure S3. The PCA method is observed to have higher variance than EIGMIX, especially for the samples from Africa and Middle East. The variance reduction in EIGMIX is primarily due to the modification of taking the ratios of the sums over loci, rather than diagonal bias removal.

Figure 5.

A comparison of ancestral proportions between EIGMIX and supervised ADMIXTURE with 6 ancestral populations for the HGDP data. A pruned set of 9,790 SNPs was used by both EIGMIX and ADMIXTURE.

Figure 6.

A comparison of ancestral proportions between PCA and supervised ADMIXTURE with 6 ancestral populations with a pruned set of 9,790 SNPs. The color legend is as the same as Figure 5, and EIGMIX is more robust than PCA when inferring admixture fractions.

Discussion

In this study, we provide an interpretation of principal components analysis (PCA) based on relatedness measures, i.e., the probability that sets of genes are identical-by-descent. The expected values of pairwise estimates in the genetic covariance matrix of PCA are relative kinship coefficients with an additional term with respect to a single reference population in the past. An approximately linear transformation between ancestral proportions of individuals with multiple ancestries and their projections onto the principal components is revealed. A new method “EIGMIX” is proposed to estimate ancestries, allowing both linked and unlinked genetic markers regardless of linkage disequilibrium. The ancestral proportions can be estimated by making assumptions of surrogate ancestral samples. EIGMIX is a method of moments with high computational efficiency compared to existing MLE and Bayesian methods such like ADMIXTURE and STRUCTURE, and it is suitable to large-scale GWAS data with thousands of individuals and millions of SNPs. We applied the PCA, EIGMIX and supervised ADMIXTURE methods to the real SNP data from the HapMap Phase 3 project and the Human Genome Diversity Panel. The ancestral proportions inferred by PCA and EIGMIX are consistent with the findings of ADMIXTURE, but EIGMIX proportions are observed to be less biased and more robust than PCA.

Novembre et al. (2008) showed that SNP profiles of individuals within Europe can be used to infer their geographic origin with relatively high accuracy by PCA. The reason why the PC axes often represent perpendicular gradients in geographic space can be explained by ancestral proportions with two or more ancestries. In our genetic model (see Figure 1), the time t₀ of single reference population is not specified explicitly, and it could be many generations ago – even the time before modern humans’ ancestors migrated out of Africa. The repeated migration in the history of Europe could create gene frequency clines as suggested by isolation-by-distance models (Wright, 1943). Starting from the single reference population at t₀, such as the population at the time before humans migrated out of Africa, it would be possible to treat the observed alleles and the hidden pattern of ibd in the current generation as a sample from the probability space of a long-term evolutionary process. However, this strategy could be confounded by the unknown allele frequencies in the reference population. To avoid this problem, the derivation of the formulas in PCA and EIGMIX have removed explicit use of the allele frequencies.

Ma and Amos (2012) observed that a three-way admixed population could divide the triangle of parental populations in the PC plot into three small triangles with areas according to their admixture proportions. They also tried to extend this observation to the general case of more than three parental populations. A closed-form estimator of ancestral proportion is difficult to find so they solved the eigenequation numerically to confirm the observation. Our mathematical derivation of the linear transformation between ancestral proportions and eigenvectors can be used to confirm the observation of Ma and Amos (2012). Here, we adopt an three-way admixed example with four populations (P₁, P₂, P₃ and P₄) shown in Figure 5 of the paper of Ma and Amos (2012), where P₄ is an admixed population. It is shown in Supplementary Figure S4. The mapping from the two-dimensional coordinate in Figure S4 (a) to that of (b) is an affine transformation. Sets of parallel lines remain parallel after an affine transformation, and it also preserves ratios of distances between points lying on a straight line. Therefore, the ratio of heights in the triangles remain the same. Ma and Amos’s observation can be confirmed theoretically under their framework with our linear transformation proof.

It is important to realize the potential limitations and our findings should be interpreted with caution. The assumption of ancestral populations used in inferring admixture fractions from the largest principal components could be confounded by the fact that human evolution is complex and has involved repeated migration and admixture from and out of Africa (Cavalli-Sforza and Feldman, 2003; Abi-Rached et al., 2011). Therefore, the selection of surrogate samples could be biased due to lack of historical knowledge or true unknown ancestries. For example, it is known that Mexicans have mainly Native Americans and European ancestry, with a small African contribution (Price et al., 2007). The ancestral proportions of MEX in HapMap Phase 3 data are confounded by an unknown link between Amerindians and CHB+JPT, although Amerindian seems closely related to Asian rather than European and African in genetics. Also, CHB+JPT and Native Americans represent two evolution branches from their common ancestors, and it may not be appropriate to assume a simple linear combination to reflect genetic difference in Native Americans.

The number of ancestral populations N is another important issue when we infer admixture proportions. A statistical test for how many significant eigenvalues in SNP data has been proposed, which is based on the approximate Tracy–Widom distribution (Patterson et al., 2006). The potential impacts on this test include linkage disequilibrium and categorical genetic data, since the Tracy–Widom distribution was originally developed for the case of independent Gaussian matrix entries. The MLE method for selecting N based on AIC (Akaike information criterion) and BIC (Bayesian information criterion) statistics was also introduced with ADMIXTURE (Alexander et al., 2009). However, we suggest that the choice of N should rely on the knowledge of the history of a population, with limited advice from statistical significance.

In summary, we provide a genetic interpretation of PCA, and propose EIGMIX to infer ancestral proportions with relatively high accuracy. EIGMIX could help us better understand population structure for isolated and admixed populations.

Appendix

A1 Proof of Eigen-decomposition

Here, we perform eigen-decomposition on ${\mathrm{\Theta }}_{\mathbf{M}}=(\mathbf{A}-\frac{1}{n}{\mathbf{J}}_n\mathbf{A}){\mathrm{\Theta }}_A{(\mathbf{A}-\frac{1}{n}{\mathbf{J}}_n\mathbf{R})}^T$ in Equation 7, and the mapping from A to the eigenvectors of Θ_M is a linear transformation, where A is a n-by-N matrix with rows representing ancestral proportions of individuals and Θ_A is a N-by-N coancestry matrix. Let $Y=\mathbf{A}-\frac{1}{n}{\mathbf{J}}_n\mathbf{A}=(I_n-\frac{1}{n}{\mathbf{J}}_n)\mathbf{A}$, where I_n is an identity matrix and J_n is a matrix n × n with entries equal to one, then Θ_M = Y Θ_AY^T.

Proof

Note that Θ_M and Θ_A are not necessarily non-negative definite matrices, and some of the eigenvalues could be negative. To avoid a complex matrix, we perform eigen-decomposition on ${\mathrm{\Theta }}_{\mathbf{M}}^2$, since ${\mathrm{\Theta }}_{\mathbf{M}}^2$ and Θ_M have the same eigenvectors and the square of eigenvalues of Θ_M correspond to the eigenvalues of ${\mathrm{\Theta }}_{\mathbf{M}}^2$.

Note that rank(Y) ≤ N − 1, then rank(Θ_M) ≤ N − 1. Let the eigenvalues of Θ_M be |v₁| ≥ |v₂| ≥ … ≥ |v_N−1| ≥ |v_N| = … = |v_n| = 0, and Q_(M),i be the i^th eigenvector with respect to v_i. [Q_(M),1, …, Q_(M),n] forms an orthogonal matrix.

$${\mathrm{\Theta }}_{\mathbf{M}}^2=Y{\mathrm{\Theta }}_A{Y}^{T}Y{\mathrm{\Theta }}_A{Y}^T$$ (11)

We perform singular value decomposition on Y,

$$\text{SVD}:Y=U_Y{\mathrm{\sum }}_Y{V}_Y^T$$

Since rank(Y) ≤ N − 1, at least one of the singular values of Y is ZERO. Replace Y in Equation 11 by $U_Y{\mathrm{\sum }}_Y{V}_Y^T$:

$${\mathrm{\Theta }}_{\mathbf{M}}^2=(U_Y{\mathrm{\sum }}_Y{V}_Y^T{\mathrm{\Theta }}_A{V}_Y)({\mathrm{\sum }}_Y^T{\mathrm{\sum }}_Y)(V_Y^T{\mathrm{\Theta }}_A{V}_Y{\mathrm{\sum }}_Y^T{U}_Y^T)$$

where ${\mathrm{\sum }}_Y^T{\mathrm{\sum }}_Y$ forms an N × N diagonal matrix.

Let $Z_Y=U_Y{\mathrm{\sum }}_Y{V}_Y^T{\mathrm{\Theta }}_A{V}_Y{({\mathrm{\sum }}_Y^T{\mathrm{\sum }}_Y)}^{\frac{1}{2}}$, where ${\mathrm{\Theta }}_{\mathbf{M}}^2=Z_Y{Z}_Y^T$. SVD on $Z_Y=U_Z{\mathrm{\sum }}_Z{V}_Z^T$. Again, at least one of the singular values of Z is ZERO.

Since

$${\mathrm{\Theta }}_{\mathbf{M}}^2=Z_Y{Z}_Y^T=U_Z{\mathrm{\sum }}_Z{V}_Z^T{V}_Z{\mathrm{\sum }}_Z^T{U}_Z^T=U_Z{\mathrm{\sum }}_Z{\mathrm{\sum }}_Z^T{U}_Z^T,$$

U_Z is the eigenvector matrix of ${\mathrm{\Theta }}_{\mathbf{M}}^2$, i.e., [Q_(M),1, …, Q_(M),n] = U_Z and the eigenvalue |v_i| is the singular value of Z_Y (non-negative).

Note that

$$\begin{array}{lll}{U}_Z{\mathrm{\sum }}_Z=Z_Y{V}_Z& =& (U_Y{\mathrm{\sum }}_Y{V}_Y^T){\mathrm{\Theta }}_A{V}_Y{({\mathrm{\sum }}_Y^T{\mathrm{\sum }}_Y)}^{\frac{1}{2}}{V}_Z\\ & =& Y{\mathrm{\Theta }}_A{V}_Y{({\mathrm{\sum }}_Y^T{\mathrm{\sum }}_Y)}^{\frac{1}{2}}{V}_Z\\ & =& (I_n-\frac{1}{n}{\mathbf{J}}_n)\mathbf{A}{\mathrm{\Theta }}_A{V}_Y{({\mathrm{\sum }}_Y^T{\mathrm{\sum }}_Y)}^{\frac{1}{2}}{V}_Z\end{array}$$

or,

$$\underset{\text{eigen}\text{coordinate}}{\underbrace{[Q_{(\mathbf{M}),1},\dots ,Q_{(\mathbf{M}),N}]\text{diag}(\mid v_1\mid ,\dots ,\mid v_N\mid )}}=(I_n-\frac{1}{n}{\mathbf{J}}_n)\underset{\text{AP}\text{coordinate}}{\underbrace{\mathbf{A}}}{\mathrm{\Theta }}_A{V}_Y{({\mathrm{\sum }}_Y^T{\mathrm{\sum }}_Y)}^{\frac{1}{2}}{V}_Z$$ (12)

The left hand side of Equation 12 is an n×N matrix where the last column is ZERO since v_N = 0, where as the right hand side is the AP matrix times ( $I_n-\frac{1}{n}{\mathbf{J}}_n$) and ${\mathrm{\Theta }}_A{V}_Y{({\mathrm{\sum }}_Y^T{\mathrm{\sum }}_Y)}^{\frac{1}{2}}{V}_Z$. Note that this transformation matrix ${\mathrm{\Theta }}_A{V}_Y{({\mathrm{\sum }}_Y^T{\mathrm{\sum }}_Y)}^{\frac{1}{2}}{V}_Z$ is a function of A. Given an AP matrix A, the transform matrix is determined, so each data point (ancestral proportion) in A maps to a new coordinate by a linear transformation.

A2 Numerical Evaluation of Diagonal Bias in PCA

To demonstrate the similarity of relative positions in the eigen coordinates of $\mathcal{E}[\frac{1}{4}{\mathbb{M}}^{\mathrm{P}}]$ and ℰ[𝕄^*], two pseudo-ancestor populations (N = 2) and three admixed populations (admixture fractions 25%, 50%, 75%) with equal sample sizes were utilized here. As shown in Table A1, as the sample size of each population grows, the bias for estimating the true admixture fraction 25% and 75% declines from 0.0424 to 0.0004. Another example is a spatially continuous admixed population, i.e., individuals with ancestral proportions uniformly distributed from 0 to 1. E.g, if n = 11 is the total number of study individuals, there are 11 individuals with admixture fractions of 0%, 10%, 20%, …, 90% and 100%. The maximum bias of the estimated ancestral proportions is shown in Table A2, and it decreases from 0.02270 to 0.00057 as the total number of individuals n increases.

Table A1.

The bias of estimating population admixture proportions in the example of two ancestral populations and three admixed populations with equal sample size n_pop.

True ancestral proportion	0	0.25	0.5	0.75	1
Inferred population ancestral proportion from $\mathcal{E}[\frac{1}{4}{\mathbb{M}}^{\mathrm{P}}]$1:
npop = 1	0	0.20758	0.50000	0.79242	1
npop = 25	0	0.24849	0.50000	0.75151	1
npop = 50	0	0.24925	0.50000	0.75075	1
npop = 100	0	0.24962	0.50000	0.75038	1

¹calculated by averaging admixture proportion of individuals.

Table A2.

The bias of estimating ancestral proportions in the example of a spatially continuous admixed population with n individuals in total¹.

# of individuals n	11	51	101	251	501
The maximum bias of inferred ancestral proportions of individuals from $\mathcal{E}[\frac{1}{4}{\mathbb{M}}^{\mathrm{P}}]$	0.02270	0.00548	0.00281	0.00114	0.00057

¹ancestral proportions are uniformly distributed from 0 to 1 derived from two ancestral populations.